Chapter 5 Term Structure and Splines

5.1 Imagine This

Our organization is about to expand its operations into the European Union (EU). To do that we will have to raise several hundred million dollars of collateral to back employees, customers, and our supply chain in the EU. Negative interest rates abound in the markets as political events and central bankers vie for control of the euro and its relationship to major currencies. Our task is to help the Chief Financial Officer understand how the term structure of interest rates might change and thus impact the amount and pricing of the collateral our organization is about to raise.

We might ask ourselves:

What is the term structure of interest rates?
Why would the term structure matter to the CFO?

“Term” refers to the maturity of a debt instrument, the “loan” we get to buy a house. “Term structure” is the schedule of interest rates posted for each maturity. The “term structure” is also known as the “yield curve.” If the maturity on your loan (or your company’s bonds) rises, a higher yield might just convince investors (like you or TIAA/CREF or other cash-rich investor) to wait longer for a return of the principal they lend to you. Higher yields mean also that you would have to price the bond at a higher coupon rate. This means more income is paid out to lenders and bondholders than to management, staff, and shareholders. The consequence is cash flow volatility.

Our objective is to conceive a model of bond prices that reflects the underlying dynamics of the term structure of interest rates. Such a model requires us to formulate forward rates of return on bonds of various maturities, and average these rates across the time to maturity in a yield calculation. We will then need to understand how to interpolate and extrapolate rates across maturities. With that tool in hand, we can price bonds, collateral, and build discount rates to evaluate future expected cash flows.

To do all of this we will employ “regression splines” to interpolate and extrapolate values of forward rates from the term structure. The regression spline will reflect a financial model of the term structure applied to the estimation of actual term structures. We will

Start with statistical definitions and financial models of bond prices.
Move into the working example of US Treasury STRIPs (zero-coupon bonds) and explore the possibilities.
Build a financially informed model of the term structure of forward empirical rates.
Estimate the model with nonlinear least squares.
Compare and contrast two competing model specifications.

In the end we will have these tools:

Extensible quadratic spline model of the forward curve;
R skills to explore data with plots and translate theoretical forward curve model into an estimable model; and
Applications of the tools to the problem of managing the value of collateral.

5.2 The Bond

Our analysis begins with understanding the cash flows and valuation of a simple bond. A typical bond is a financial instrument that pays fixed cash flows for the maturity of the bond with a repayment of the principal (notional or face value) of the bond at maturity. In symbols,

\[ V = \sum_{t=0}^{mT} \frac{cP}{(1+y/m)^t} + \frac{P}{(1+y/m)^{mT}}, \]

where $V$ is the present value of the bond, $T$ is the number of years to maturity, $m$ is the number of periods cash flows occur per year, $y$ is the bond yield per year, $c$ is the coupon rate per year, and $P$ is the bond’s principal (notional or face value).

Using the idea of an annuity that pays $(c/m)P$ per period for $mT$ periods and $P$ at maturity period $mT$ we get a nice formula for the present value sum of coupon payments:

\[ V = (c/m) P \left( \frac{1}{y/m} - \frac{1}{(y/m)(1+y/m)^{mT}} \right) + \frac{P}{(1+y/m)^{mT}}. \]

From a financial engineering point of view this formulation is the same as constructing a position that is

long a perpetuity that pays a unit of currency starting the next compounding period and
short another perpetuity that starts to pay a unit of currency at the maturity of the bond plus one compounding period.

Our typical bond pays coupons twice a year, so $m = 2$. If the bond’s maturity in years is 10 years, then $mT = 10 \times 2 = 20$ compounding periods. We will assume that there is no accrual of interest as of the bond’s valuation date for the moment.

c <- 0.05
P <- 100
y <- c(0.04, 0.05, 0.06)
m <- 2
T <- 10
(V <- (c/m) * P * (1/(y/m) - 1/((y/m) * 
    (1 + (y/m))^(m * T))) + P/(1 + (y/m))^(m * 
    T))

## [1] 108.17572 100.00000  92.56126

5.2.1 A quick example

If the coupon rate is greater than the yield, why is the price greater than par value?
Negative interest rates abound, so set y <- c(-0.02, -0.01, 0.00, .01, .02) and recalculate the potential bond values.

One answer might be:

The bond pays out at a rate greater than what is required in the market. Buyers pay more than par to make up the difference.

Here are more results. We assign variables to assumptions in the question and then calculate the

c <- 0.05
P <- 100
y <- c(-0.02, -0.01, 0, 0.01, 0.02)
m <- 2
T <- 10
(V <- (c/m) * P * (1/(y/m) - 1/((y/m) * 
    (1 + (y/m))^(m * T))) + P/(1 + (y/m))^(m * 
    T))

## [1] 177.9215 163.2689      NaN 137.9748 127.0683

Why a NAN? Because we are dividing by ‘0’! By the way, these are some hefty premia. Check out this article on negative yields… http://www.ft.com/cms/s/0/312f0a8c-0094-11e6-ac98-3c15a1aa2e62.html

The yield in this model is an average of the forward rates the markets used to price future cash flows during future periods of time. How can we incorporate a changing forward rate into a model of bond prices? Our strategy is to use the past as a guide for the future and calibrate rates to a curve of rates versus maturities. By using a regression spline model of the term structure we can develop rates at any maturity. Then we can use the interpolated (even extrapolated) rates as building blocks in the valuation of bonds.

5.2.2 What’s a spline?

A spline is a function that is constructed piece-wise from polynomial functions. But imagine the polynomials are pieces of the term structure of interest rates. Each term structure segment is marked off by a set of price and maturity pairs. Whole sections can be marked off by a knot at a location in the term structure paired data. Knots are most commonly placed at quantiles to put more knots where data is clustered close together. A different polynomial function is estimated for each range and domain of data between each knot: this is the spline. Now we will use some finance to build a polynomial regression spline out of US Treasury zero-coupon data.

In general a polynomial is an expression that looks like this:

\[ f(x) = a_0 x^0 + a_1 x^1 + a_2 x^2 + ... + a_p x^p, \]

where the $a$’s are constant coefficients, and $x^0 = 1$ and $x^1 = x$.

If $p = 0$, then we have a constant function.
If $p = 1$, we have a linear function.
If $p = 2$, we have a quadratic function.
If $p = 3$, we have a cubic function, and so on…

In our term structure work We will be using a cubic function to build a regression spline.

5.2.3 Back to the Bond

Suppose investors give an issuer today the present value, the bond “price” $P_T$ of receiving back the 100% of the face value of a zero-coupon bond at maturity year (or fraction thereof), $T$.

The price of a zero coupon bond, quoted in terms of the percentage of face value, is this expression for discrete compounding at rate $y_T^d$ (say, monthly you get a percentage of last month’s balance):

\[ P_T = \frac{100}{(1+y^d(T))^{T}}. \]

Suppose, with the help of Jacob Bernoulli and Leonhardt Euler, we run this experiment:

Pay today at the beginning of the year $P$ to receive $1 at the end of one year AND interest $y$ is compounded only once in that year. Thus at the end of the year we receive $P + yP$. But by contract this amount is $1, so that \[ P + yP = P(1+y) = 1 \] and solving for $P$ \[ P = \frac{1}{(1+y)^1} \] where we raised $(1+y)$ to the first power to emphasize that one compounding period was modeled.
Now suppose that we can receive interest twice a year at an annual interest rate of $y$. Then at the end of the first half of the year we receive half of the interest $y/2$ so that we have in our contract account \[ P\left(1+\frac{y}{2}\right) \] We then can let this stay in the account this amount will also earn $y/2$ interest to the end of the contract year so that \[ P\left(1+\frac{y}{2}\right) + \frac{y}{2}\left[P\left(1+\frac{y}{2}\right)\right] = P\left(1+\frac{y}{2}\right)\left(1+\frac{y}{2}\right) = P\left(1+\frac{y}{2}\right)^2 \] Setting \[ P\left(1+\frac{y}{2}\right)^2 = \$1 \]

we can solve for $P$, the present value of receiving $1 at the end of the contract year when we have two compounding periods or \[ P = \frac{\$1}{\left(1+\frac{y}{2}\right)^2} \] 3. We can, again with Jacob Bernoulli’s help, more generally state for $m$ compounding periods \[ P = \frac{\$1}{\left(1+\frac{y}{m}\right)^m} \] 4. Now let’s suppose $y = 100\%$ interest and $m = 365 \times 24 \times 60 = 525600$ compounding periods (minute by minute compounding), then \[ P = \frac{\$1}{\left(1+\frac{1}{525600}\right)^525600} \]

(m <- 365 * 24 * 60)

## [1] 525600

(y <- 1)

## [1] 1

(P <- 1/(1 + (y/m))^m)

## [1] 0.3678798

This translates into continuous compounding (you get a percentage of the last nanosecond’s balance at the end of this nanosecond…as the nanoseconds get ever smaller…) as

\[ P_T(\theta) = 100 exp(-y_T T). \]

This expression is the present value of receiving a cash flow of 100% of face value at maturity. If the bond has coupons, we can consider each of the coupon payments as a mini-zero bond. Taking the sum of the present value of each of the mini-zeros gives us the value of the bond, now seen as a portfolio of mini-zeros.

The yield $y_T$ the rate from date $0$ to date $T$, maturity. It covers the stream of rates for each intermediate maturity from $0$ to $T$. Suppose we define forward rates $r(t, \theta)$, where each $t$ is one of the intermediate maturity dates between time $0$ and maturity $T$, and $\theta$ contains all of the information we need about the shape of $r$ across maturities. We can estimate the forward curve from bond prices $P(T)$ of the $T$th maturity with

\[ - \frac{\Delta log(P(T_{i}))}{\Delta T_{i}} = - \frac{log(P(T_{i})) - log(P(T_{i-1}))}{T_i - T_{i-1}}. \]

The $\Delta$ stands for the difference in one price or maturity $i$ and the previous price and maturity $i-1$. The $log()$ function is the natural logarithm. An example will follow.

The yield is then the average of the forward rates from date $0$ to date $T$ of a zero bond. We use the integral, which amounts to a cumulative sum, to compute this average:

\[ y_T(\theta) = T^{-1} \int_0^T r(t, \theta) dt. \]

The numerator is the cumulative sum of the forward rates for each maturity up to the last maturity $T$. In this expression, $r dt$ is the forward rate across a small movement in maturity. The denominator is the number of maturity years $T$.

5.2.4 An example to clarify

Load these lines of R into the RStudio console:

maturity <- c(1, 5, 10, 20, 30)  # in years
price <- c(99, 98, 96, 93, 89)  # in percentage of face value

A. Now let’s experiment on these zero-coupon prices with their respective maturities:

Calculate the log(price)/100. Then find the forward rates using using

(forward <- -diff(log(price))/diff(maturity))

Compare log(price) with price.
What does the forward rate formula indicate? What would we use it for?

B. Find the yield-to-maturity curve and recover the bond prices using

(forward.initial <- -log(price[1]/100))
(forward.integrate <- c(forward.initial, 
    forward.initial + cumsum(forward * 
        diff(maturity))))
# a rolling integration of rates
# across maturities
(price <- 100 * exp(-forward.integrate))
# present value of receiving 100% of
# face value

What is the interpretation of the forward.integrate vector?
What happened to the first bond price?
Did we recover the original prices?

Some results follow.

For question A we ran the forward rates. Let’s run the natural logarithm of price:

(forward <- -diff(log(price/100))/diff(maturity))

## [1] 0.002538093 0.004123857 0.003174870 0.004396312

(-log(price/100))

## [1] 0.01005034 0.02020271 0.04082199 0.07257069 0.11653382

-log(price/100) seems to give us the yield-to-maturity directly. But do look at -diff(log(price)) next:

(-diff(log(price/100)))

## [1] 0.01015237 0.02061929 0.03174870 0.04396312

These look like rates, because they are. They are the continuous time version of a percentage change, or growth, rate from one maturity to another maturity. We can use these numerical results to motivate an interpretation: interest rates are simply rates of change of present values relative to how much time they cover in maturity.

Now let’s calculate

(-diff(price/100)/(price[-length(price)]/100))

## [1] 0.01010101 0.02040816 0.03125000 0.04301075

These are discrete percentage changes that are similar, but not quite the same, as the continuous (using log()) version.. Note the use of the indexing of price to eliminate the last price, since what we want to compute is:

\[ \frac{P(T_i) - P(T_{i-1})}{P(T_{i-1})} \]

5.2.5 Rolling the integration

Running the code for question B we get:

forward.initial <- -log(price[1]/100)
(forward.integrate <- c(forward.initial, 
    forward.initial + cumsum(forward * 
        diff(maturity))))

## [1] 0.01005034 0.02020271 0.04082199 0.07257069 0.11653382

# a rolling integration of rates
# across maturities
(price <- 100 * exp(-forward.integrate))

## [1] 99 98 96 93 89

# present value of receiving 100% of
# face value

The rolling “integration” is an accumulative process of adding more forward rates as the maturity advances, thus a cumulative sum or in R a cumsum() is deployed.

Yields are the accumulation of forward rates. Thus the use of the cumulative sum as a discrete version of the integral. Rates add up (instead of multiply: nice feature) when we use log and exp to do our pricing.
The first forward rate is just the discount rate on the 1-year maturity bond stored in forward.initial.
All bond prices are recovered by inverting the process of producing forwards from prices and converting to yields and back to prices.

5.2.6 And now some more about that bond yield

We restate the definition of the price of a zero-coupon bond. The price of a zero-coupon bond quoted in percentage of face value is this expression for discrete compounding (say, monthly you get a percentage of last month’s balance):

\[ P_T = \frac{100}{(1+y^d(T))^{T}} \]

This translates into continuous compounding (you get a percentage of the last nanosecond’s balance at the end of this nanosecond…) as

\[ P_T(\theta) = 100 exp(-y_T T) = 100 exp( \int_0^T r(t, \theta) dt ) \]

This is the present value of receiving a cash flow of 100% of face value at maturity. If the bond has coupons we can consider each of the coupon payments as a mini-zero bond.

The term with the $\int$ symbol is a nanosecond by nanosecond way of summing the forward rates across the maturity of the bond. Equating the two statements and solving for $y_T$, the continuously compounded yield we get:

\[ P_T = \frac{100}{(1+y(T)_{d})^{T}} = 100 exp(-y_T T). \]

Rearranging with some creative algebra: $100$ drops out, and remembering that $exp(-y_T t) = 1/ exp(y_T T)$, we have:

\[ exp(y_T T) = (1+y(T)_{d})^{T}. \]

Then, taking logarithms of both sizes we get

\[ exp(y_T T)^{-T} = (1+y(T)_{d})^{T-T} = (1+y(T)_{d}). \]

Using the facts that $log(exp(x)) = x$ and $log(x^T) = T log(x)$ (very convenient):

\[ log(exp(y_T T)^{-T}) = y_T = log(1 + y(T)_{d}). \]

We now calculate discrete and continuous time versions of the yield:

y.T.d <- 0.2499  # Usury rate in NYS; d = discrete, T = maturity in years
(y.T <- log(1 + y.T.d))

## [1] 0.2230635

(y.T.d <- exp(y.T) - 1)

## [1] 0.2499

We note that the continuous time yield is always less than the discrete rate because there are so many more continuous compounding periods. This result leaps back to Jacob Bernoulli’s (17xx) derivation.

5.3 Forward Rate Parameters

Now we attend to the heretofore mysterious $\theta$, embedded in the forward rate sequence $r$. We suppose the forward rate is composed of a long-term constant, $\theta_0$; a sloping term with parameter $\theta_1$; a more shapely, even “humped” term with parameter $\theta_2$; and so on for $p$ polynomial terms:

\[ r(t, \theta) = \theta_0 + \theta_1 t + \theta_2 t^2 + ... + \theta_p t^p \]

We recall (perhaps not too painfully!) from calculus that when we integrate any variable to a power (the antiderivative), we raise the variable to the next power (and divide the term by that next power). Here we integrate the forward rate to get

\[ \int_0^T r(t, \theta) dt = \theta_0 T + \theta_1 \frac{T^2}{2} + \theta_2 \frac{T^3}{3} + ... + \theta_p \frac{T^{p+1}}{p+1}. \]

This is equivalent, after a fashion, to calculating the cumulative sum of forward rates across small increments in time $dt$ from today at maturity $t=0$ to the maturity of the term at $t=T$. We then can estimate the yield curve (and then the zero-coupon bond price) using the integrated forward rates divided by the maturity $T$ to get the yield as

\[ y_T(\theta) = \theta_0 + \theta_1 \frac{T}{2} + \theta_2 \frac{T^2}{3} + ... + \theta_p \frac{T^{p}}{p+1}. \]

Before we go any further we will procure some term structure data to see more clearly what we have just calculated.

5.3.1 Term Structure Data

Here is some (very old) data from US Treasury STRIPS (a.k.a. for “Separate Trading of Registered Interest and Principal of Securities”). The data set will prices and maturities for what are known as “zero-coupon” bonds, that is, bonds that only pay out the face value of the bond at maturity. There is more information about STRIPS at https://www.newyorkfed.org/aboutthefed/fedpoint/fed42.html.

# The data is in a directory called
# data that is a sub-directory of the
# directory from which this code
# executes.
dat <- read.table("data/strips_dec95.txt", 
    header = TRUE)

What does the data look like? Anything else? We run this code chunk to get a preliminary view of this data.

head(dat, n = 3)

##        T  price
## 1 0.1260 99.393
## 2 0.6219 96.924
## 3 1.1260 94.511

names(dat)

## [1] "T"     "price"

dat <- dat[order(dat$T), ]

We read in a table of text with a header, look at the first few observations with head(), and order the data by maturity $T_i$. A simple plot is in order now.

plot(dat$T, dat$price, main = "STRIPS", 
    xlab = "Maturity", ylab = "Price")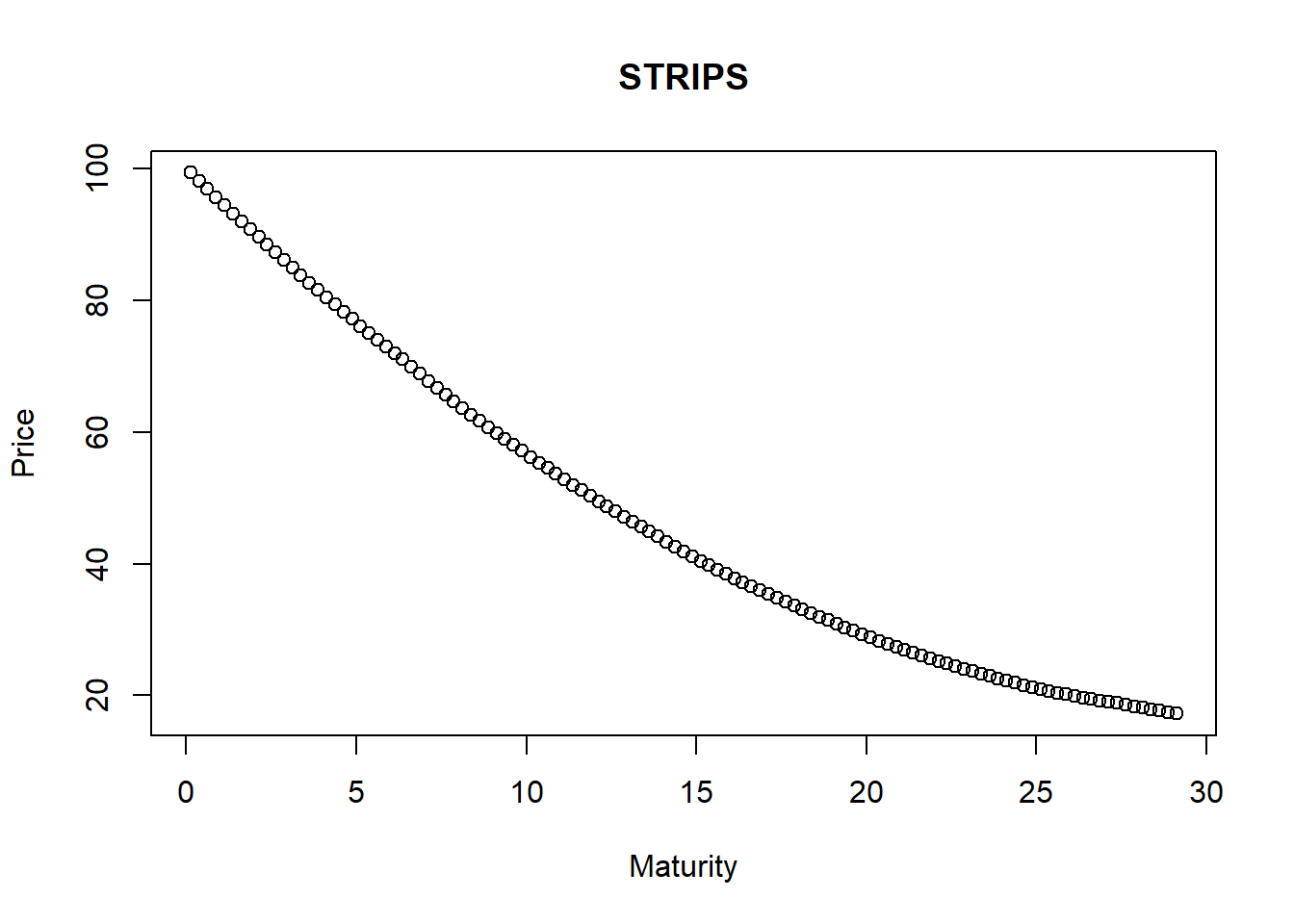

5.3.2 The empirical forward curve

We estimate the empirical forward curve using:

\[ - \frac{\Delta log(P(T_i))}{\Delta T_i} = - \frac{log(P(T_i)) - log(P(T_{i-1}))}{T_i - T_{i-1}}, \]

where $P$ is the bond price and $T_i$ is $i$th maturity,

t <- seq(0, 30, length = 100)
emp <- -diff(log(dat$price))/diff(dat$T)

The equation is translated into R with the diff function. We will use vector t later when we plot our models of the forward curve. Definitely view it from the console and check out ??seq for more information about this function.

5.3.3 Try this exercise

Let’s plot the empirical forward curves using this line of code:

plot(dat$T[2:length(dat$T)], emp, ylim = c(0.025, 
    0.075), xlab = "maturity", ylab = "empirical forward rate", 
    type = "b", cex = 0.75, lwd = 2, 
    main = "US Treasury STRIPs - 1995")

Try to answer these questions before moving on:

What exactly will dat$T[2:length(dat$T)] do when executed?
What effect will ylim, lwd, xlab, ylab, type, cex, main have on the plot?
Is there an break in the curve? Write the plot command to zoom in on maturities from 10 to 20 years.

We get these results:

What exactly will dat$T[2:length(dat$T)] do when executed?

length(dat$T)

## [1] 117

head(dat$T[2:length(dat$T)])

## [1] 0.3699 0.6219 0.8740 1.1260 1.3699 1.6219

We retrieve the T vector from the dat data frame using dat$T. Then length returns the number of maturities in the dat data frame. dat$T[2:length(dat$T)] truncates the first observation. Why? Because we differenced the prices to get forward rates and we need to align the forward rates with their respective maturities $T_i$.

5.3.4 Plot parameters

Here is the list:

ylim zooms in the y-axis data range
lwd changes the line width
xlab specifies the x-axis label
ylab specifies the y-axis label
type specifies the line
cex changes the scaling of text and symbols
main specifies the plot title.

We can go to http://www.statmethods.net/advgraphs/parameters.html to find more information and the answer to the zoom-in question.

5.3.5 The plot itself

plot(dat$T[2:length(dat$T)], emp, ylim = c(0.025, 
    0.075), xlab = "maturity", ylab = "empirical forward rate", 
    type = "b", cex = 0.75, lwd = 2, 
    main = "US Treasury STRIPS - 1995")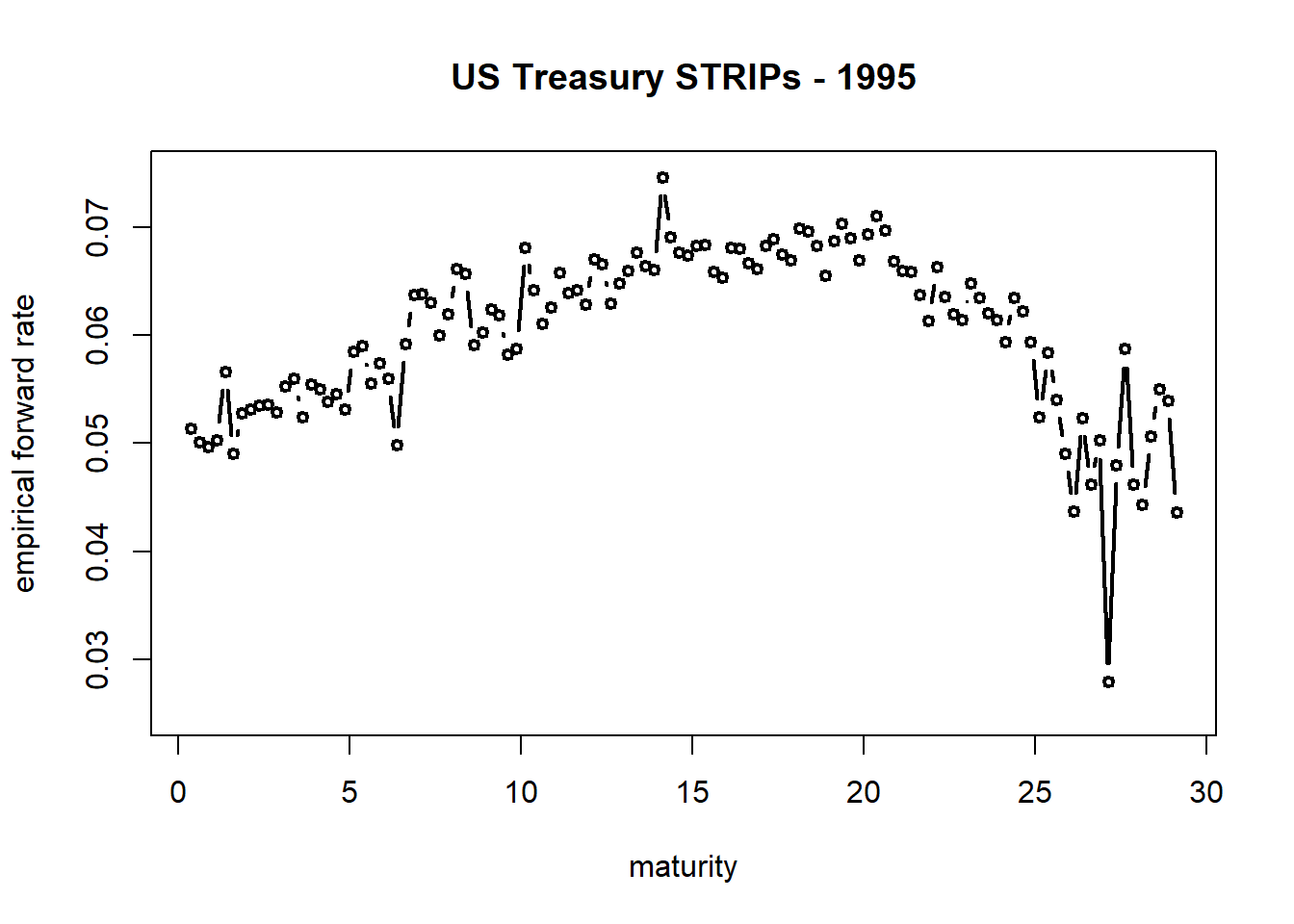

Now the zoom in:

plot(dat$T[2:length(dat$T)], emp, xlim = c(10, 
    20), ylim = c(0.025, 0.075), xlab = "maturity", 
    ylab = "empirical forward rate", 
    type = "b", cex = 0.75, lwd = 2, 
    pin = c(3, 2), main = "US Treasury STRIPS - 1995")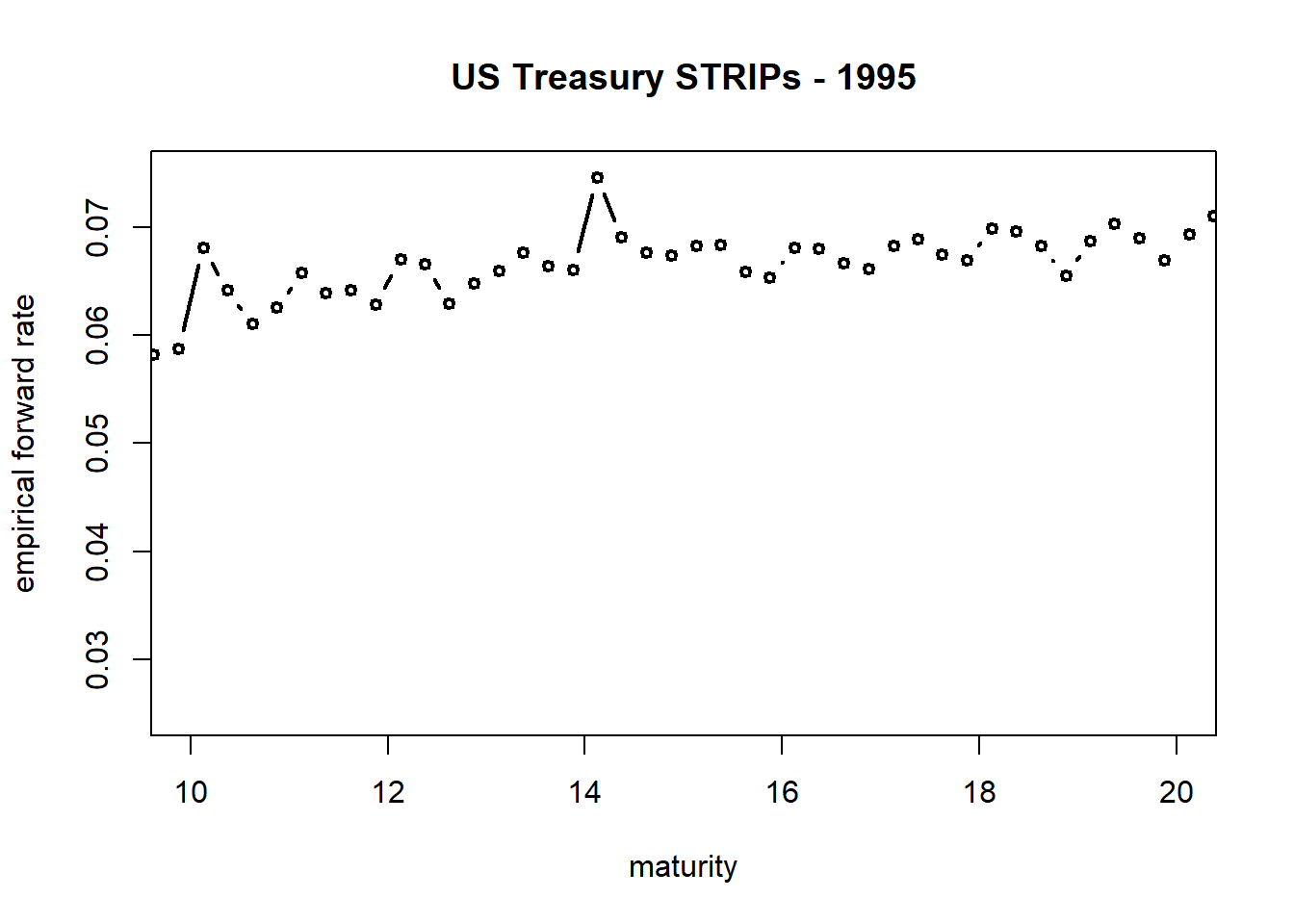

At $T_i = 14$ there appears to be an outlier. More importantly there is a break at $T_i$ = 15. This is a natural knot. Thus the possibility of a need for a spline.

5.4 Back to Our Story

Let’s add a kink in the yield curve that allows two different quadratic functions: one before the kink, and one after the kink. Let the kink be a knot $k$ at $T_i$ = 15. We evaluate a knot as $0$ if the maturities $T_i - k$ < 0, and equal $T - k$ if $T - k$ > 0. We write this as $(T - k)_{+}$. Let’s now drop the knot into our integral:

\[ \int_0^T r(t, \theta) dt = \theta_0 T + \theta_1 \frac{T^2}{2} + \theta_2 \frac{T^3}{3} + \theta_2 \frac{(T - 15)_+^3}{3} \]

We can divide by $T$ to get the yield. But to calculate the bond price we have to multiply the yield by the bond maturity $T$, so the bond price is then:

\[ P_T(\theta) = 100 exp[-(\theta_0 T + \theta_1 \frac{T^2}{2} + \theta_2 \frac{T^3}{3} + \theta_3 \frac{(T - 15)_+^3}{3})] \]

After all of that setup now we move on to estimate the thetas.

5.4.1 Gee, that’s very nonlinear of you…

Yes, the bond price is nonlinear in the $\theta$ parameters. Our statistical job now is to find a set of $\theta$ such that the difference between the actual bond prices $P$ and our clever model of bond prices (long equation that ended the last slide) is very small in the sense of the sum of squared differences (“errors”). We thus find $\theta$ that minimizes

\[ \sum_{i=0}^{N} [(P(T_i) - P(T_i, \theta)]^2 \]

To find the best set of $\theta$ we will resort to a numerical search using the R function nls, for nonlinear least squares.

5.4.2 Try this exervise as we get down to business

Back to the data: we now find the $\theta$s. The logical expression (T>k) is 1 if TRUE and 0 if FALSE. We put the R version of the bond price into the nls function, along with a specification of the data frame dat and starting values.

Run these statements to compute the (nonlinear) regression of the term structure:

fit.spline <- nls(price ~ 100 * exp(-theta_0 * 
    T - (theta_1 * T^2)/2 - (theta_2 * 
    T^3)/3 - (T > 15) * (theta_3 * (T - 
    15)^3)/3), data = dat, start = list(theta_0 = 0.047, 
    theta_1 = 0.0024, theta_2 = 0, theta_3 = -7e-05))

5.4.3 Just a couple of questions:

What are the dependent and independent variables?
Which parameter measures the sensitivity of forward rates to the knot?

The dependent variable is price. The independent variables are inside the $\exp()$ operator and include powers of T, the maturities of the bonds. The theta_3 parameter exposes the bond price to movements in maturity around the knot at $T=15$ years.

Let’s look at our handiwork using kable from the knitr package:

library(knitr)
kable(summary(fit.spline)$coefficients, 
    digits = 4)

	Estimate	Std. Error	t value
theta_0	0.0495	1e-04	536.5180
theta_1	0.0016	0e+00	51.5117
theta_2	0.0000	0e+00	-13.6152
theta_3	-0.0002	0e+00	-30.6419

(sigma <- (summary(fit.spline)$sigma)^0.5)

## [1] 0.2582649

All coefficients are significant and we have a standard error to compare with other models.

5.4.4 Build a spline

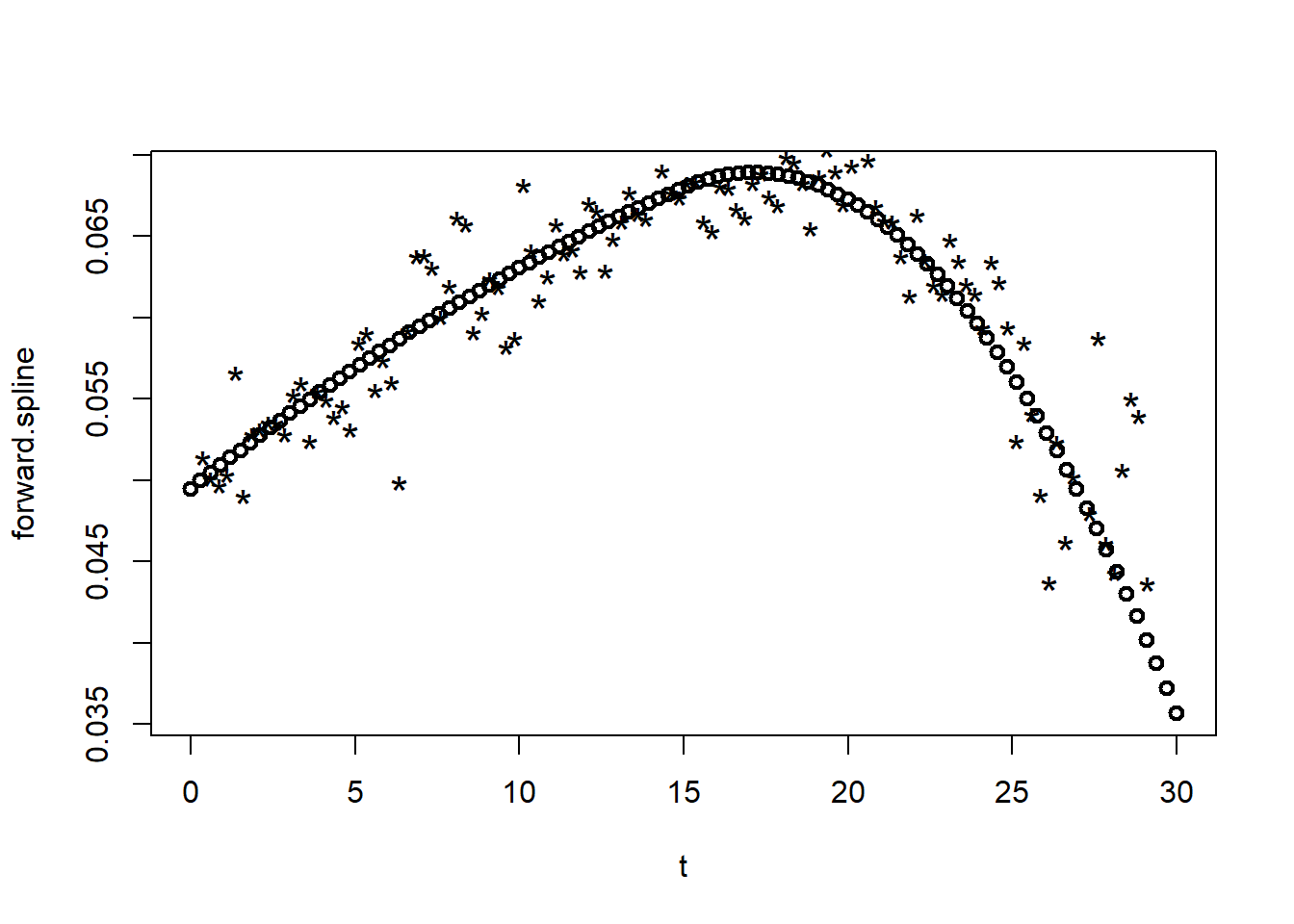
Let’s now produce a plot of our results using a sequence of maturities T. Our first task is to parse the coefficients from the nls() spline fit and build the spline prediction. Here we construct the forward rate spline across T maturities.

coef.spline <- summary(fit.spline)$coef[, 
    1]
forward.spline <- coef.spline[1] + (coef.spline[2] * 
    t)
+(coef.spline[3] * t^2)
+(t > k) * (coef.spline[4] * (t - 15)^2)

Second, pull the coefficients from a summary() of the fit.spline object for the plot.

5.5 A Summary Exercise

Let’s try these tasks to bring this analysis together.

Compare the quadratic spline we just constructed with a pure quadratic polynomial. Simply take the knot out of the nls formula and rerun. Remember that “quadratic” refers to the polynomial degree $p$ of the assumed structure of the forward rate $r(t, \theta)$.
Plot the data against the quadratic spline and the quadratic polynomial.
Interpret financially the terms in $\theta_0$, $\theta_1$, and $\theta_2$.

5.5.1 Compare

Run this code: remembering that a “cubic” term represents the integration of the “quadratic” term in

\[ r(t, \theta) = \theta_0 + \theta_1 t + \theta_2 t^2 \]

fit.quad <- nls(price ~ 100 * exp(-theta_0 * 
    T - (theta_1 * T^2)/2 - (theta_2 * 
    T^3)/3), data = dat, start = list(theta_0 = 0.047, 
    theta_1 = 0.0024, theta_2 = 0))

This estimate gives us one quadratic function through the cloud of zero-coupon price data.

knitr::kable(summary(fit.quad)$coefficients, 
    digits = 4)

	Estimate	Std. Error	t value
theta_0	0.0475	2e-04	239.0168
theta_1	0.0024	1e-04	46.5464
theta_2	-0.0001	0e+00	-33.0016

All conveniently significant.

(sigma <- (summary(fit.quad)$sigma)^0.5)

## [1] 0.4498518

The pure quadratic model produces a higher standard deviation of error than the quadratic spline.

5.5.2 Plot

We will run this code to set up the data for a plot. First some calculations based on the estimations we just performed.

coef.spline <- summary(fit.spline)$coef[, 
    1]
forward.spline <- coef.spline[1] + (coef.spline[2] * 
    t)
+(coef.spline[3] * t^2)
+(t > 15) * (coef.spline[4] * (t - 15)^2)
coef.quad <- summary(fit.quad)$coef[, 
    1]
forward.quad <- coef.quad[1] + (coef.quad[2] * 
    t) + (coef.quad[3] * t^2)

Here is the plot itself.

plot(t, forward.spline, type = "l", lwd = 2, 
    ylim = c(0.03, 0.075), xlab = "Maturity", 
    ylab = "Forward Rate", main = "US Treasury STRIPs Forward Curve: 1995")
lines(t, forward.quad, lty = 2, lwd = 2, 
    col = "red")
points(dat$T[2:length(dat$T)], emp, pch = "*", 
    cex = 1.5)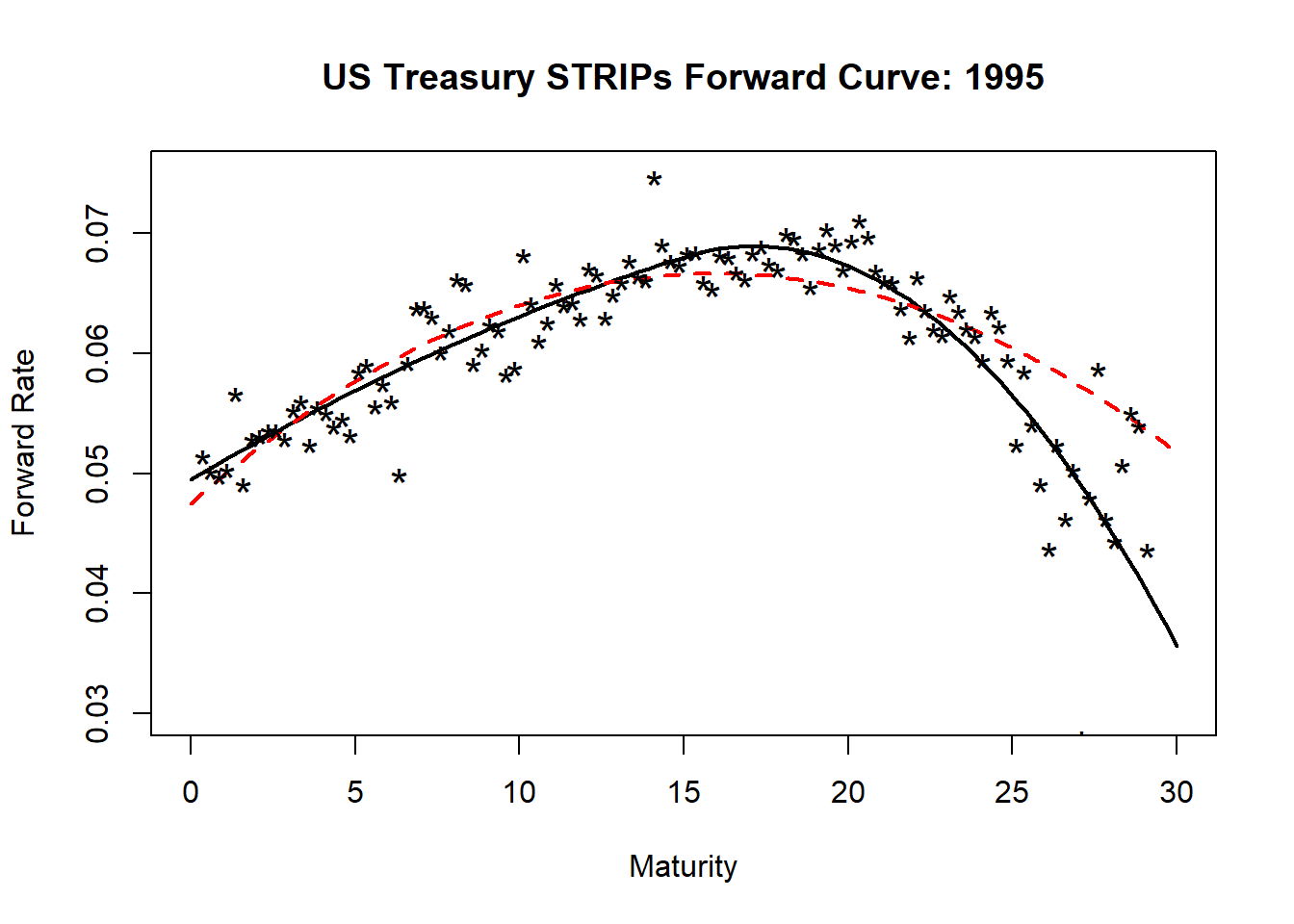

We can use “eyeball” econometrics to see what data the quadratic forward curve misses!

5.5.3 Interpret

There seem to be three components in the forward curve:

Constant
Slope
Curved (affectionately called “humped”)

Our interpretation follows what we might visualize:

$\theta_0$ is independent of maturity and thus represents the long-run average forward rate.
$\theta_1$ helps to measure the average sensitivity of forward rates to a change in maturity.
$\theta_2$ helps to measure the maturity risk of the forward curve for this instrument.

The pure quadratic forward curve seems to dramatically underfit the maturities higher than 15 years. Using a knot at the right maturity adds a boost to the reduction of error in this regression. That means that predictions of future potential term structures will apt to be more accurate than the null hypothesis of no knot.

5.6 Just one more thing

Here is the infamous So What?!, especially after all of the work we just did.

Suppose we just bought a 10 year maturity zero-coupon bond to satisfy collateral requirements for workers’ compensation in the (great) State of New York.
The forward rate has been estimated as: \[ r(t) = 0.001 + 0.002 t - 0.0003 (t-7)_{+} \]
In 6 months we then exit all business in New York State, have no employees that can claim workers’ compensation, sell the 10 year maturity zero-coupon bond. The forward curve is now \[ r(t) = 0.001 + 0.0025 t - 0.0004 (t-7)_{+} \]
How much would we gain or lose on this transaction at our exit?

5.6.1 Some bond maths to (re)consider

Let’s recall the following:

The forward rate is the rate of change of the yield-to-maturity
This means we integrate (i.e., take the cumulative sum of) forward rates to get the yield
The cumulative sum would then be some maturity times the components of the yield curve adjusted for the slope of the forward curve (the terms in $t$).
This adjustment is just one-half ($1/2$) of the slope term.

Here are some calculations to set up today’s yield curve and the curve 6 months out.

maturity.now <- 10
maturity.6m <- 9.5
(yield.now <- 0.001 * maturity.now + 
    0.002 * maturity.now^2/2 - 3e-04 * 
    (maturity.now > 7)^2/2)

## [1] 0.10985

(yield.6m <- 0.001 * maturity.6m + 0.0025 * 
    maturity.6m^2/2 - 4e-04 * (maturity.6m > 
    7)^2/2)

## [1] 0.1221125

Using these yields we can compute the bond prices for today and for 6 months out as well.

(bond.price.now <- exp(-yield.now))

## [1] 0.8959685

(bond.price.6m <- exp(-yield.6m))

## [1] 0.8850488

5.6.2 Exit

Our exit transaction is long today’s version of the bond and short the 6 month version. This translates into a 6 month return that calculates \[ R_{6m} = \frac{P(T-0.5) - P(T)}{P(T)} = \frac{P(T-0.5)}{P(T)} - 1 \] which in R is

(return = bond.price.6m/bond.price.now - 
    1)

## [1] -0.01218762

2 * return  ### annualized return

## [1] -0.02437524

It appears that we lost something in this exit from New York state as the return is negative.

5.7 Summary

This chapter covers the fundamentals of bond mathematics: prices, yields, forward curves. Using this background built two models of the forward curve and then implemented these models in R with live data. In the process We also learned something about the nonlinear least squares method and some more R programming to visualize results.

5.8 Further Reading

Ruppert and Matteson, pp. 19-43, introduces fixed income (bonds) including yield to maturity, continuous discounting, forward rates, and bond prices. From pp. 271-281 we can learn about nonlinear regression and the use of quadratic terms in term structure estimations. From pp. 645-664 we can learn about regression splines and their application to various analytical questions. McNeill et al. have similar bond mathematics discussions from pp. 329-337. They use the termstr package from CRAN to illustrate term structure models.

5.9 Practice Laboratory

5.9.1 Practice laboratory #1

5.9.1.1 Problem

5.9.1.2 Questions

5.9.2 Practice laboratory #2

5.9.2.1 Problem

5.9.2.2 Questions

5.10 Project

5.10.1 Background

5.10.2 Data

5.10.3 Workflow

5.10.4 Assessment

We will use the following rubric to assess our performance in producing analytic work product for the decision maker.

The text is laid out cleanly, with clear divisions and transitions between sections and sub-sections. The writing itself is well-organized, free of grammatical and other mechanical errors, divided into complete sentences, logically grouped into paragraphs and sections, and easy to follow from the presumed level of knowledge.
All numerical results or summaries are reported to suitable precision, and with appropriate measures of uncertainty attached when applicable.
All figures and tables shown are relevant to the argument for ultimate conclusions. Figures and tables are easy to read, with informative captions, titles, axis labels and legends, and are placed near the relevant pieces of text.
The code is formatted and organized so that it is easy for others to read and understand. It is indented, commented, and uses meaningful names. It only includes computations which are actually needed to answer the analytical questions, and avoids redundancy. Code borrowed from the notes, from books, or from resources found online is explicitly acknowledged and sourced in the comments. Functions or procedures not directly taken from the notes have accompanying tests which check whether the code does what it is supposed to. All code runs, and the R Markdown file knits to pdf_document output, or other output agreed with the instructor.
Model specifications are described clearly and in appropriate detail. There are clear explanations of how estimating the model helps to answer the analytical questions, and rationales for all modeling choices. If multiple models are compared, they are all clearly described, along with the rationale for considering multiple models, and the reasons for selecting one model over another, or for using multiple models simultaneously.
The actual estimation and simulation of model parameters or estimated functions is technically correct. All calculations based on estimates are clearly explained, and also technically correct. All estimates or derived quantities are accompanied with appropriate measures of uncertainty.
The substantive, analytical questions are all answered as precisely as the data and the model allow. The chain of reasoning from estimation results about the model, or derived quantities, to substantive conclusions is both clear and convincing. Contingent answers (for example, “if X, then Y , but if A, then B, else C”) are likewise described as warranted by the model and data. If uncertainties in the data and model mean the answers to some questions must be imprecise, this too is reflected in the conclusions.
All sources used, whether in conversation, print, online, or otherwise are listed and acknowledged where they used in code, words, pictures, and any other components of the analysis.

5.11 References

McNeill, Alexander J., Rudiger Frey, and Paul Embrechts. 2015. Quantitative Risk Management: Concepts, Techniques and Tools. Revised Edition. Princeton: Princeton University Press.

Ruppert, David and David S. Matteson. 2015. Statistics and Data Analysis for Financial Engineering with R Examples, Second Edition. New York: Springer.