Chapter 6 T-Test (two-sample using groups)
This chapter provides generic code for carrying out a T-Test analysis (two sample using groups). It is recommended that you proceed through the sections in the order they appear. If, however, you want to do a quick analysis, I recommend loading the packages, prepping your data, and then running the ggstatsplot::ggbetweenstats command in section 6.6.
Placeholders that need replacing:
- mydata – name of your dataset
- groupvar – name of your dichotomous grouping variable
- intvar – name of your interval or continuous variable
- label – any titles, axis labels, category labels
6.1 Packages Needed for T-Test
This code will check that required packages for this chapter are installed, install them if needed, and load them into your session.
req <- substitute(require(x, character.only = TRUE))
libs<-c("effsize", "ggplot2", "ggstatsplot", "patchwork", "moments", "ggpubr")
sapply(libs, function(x) eval(req) || {install.packages(x); eval(req)})6.2 Data Prep for T-Test
One of the key preparations you need to make is to declare (classify) your categorical variable as a factor variable. In the generic commands below, the ‘class’ function tells you how R currently sees the variable (e.g., double, factor, character). The second command will reclassify the specified categorical variable as a factor variable.
class(mydata$groupvar) # Will tell you how R currently views the variable (double, factor…)
mydata$groupvar <- factor(mydata$groupvar) # Will declare the variable as a factor variable6.3 Checking Data for Violations of Assumptions for T-Test
There are generally three assumptions researchers check when conducting ANOVA: 1) Relatively equal group sizes; 2) Relatively equal variances; 3) That the interval or continuous variable is normally distributed. The following generic commands offer insights on each.
6.3.1 Group Frequencies for T-Test
table(mydata$groupvar)6.3.2 Checking for Equal Variances for T-Test
Group means and standard deviations (Note: the ‘aggregate’ and ‘by’ functions give you the same results, just in slightly different formats). The var.test function offers a more direct statistical test, performing an F test to compare the variances of the two groups.
aggregate(mydata$intvar, by = list(mydata$groupvar), FUN = mean, na.rm = TRUE)
aggregate(mydata$intvar, by = list(mydata$groupvar), FUN = sd, na.rm = TRUE)
by(mydata$intvar, mydata$groupvar, mean, na.rm = TRUE)
by(mydata$intvar, mydata$groupvar, sd, na.rm = TRUE)
var.test(intvar ~ groupvar, data = mydata)6.3.3 Checking Normality for T-Test
The following generic commands can be used to check for skewness and kurtosis (a skewness of 0 and kurtosis of 3 are considered normal). You can visually inspect the data by looking at a density graph and quantile-quantile (qqplot, which draws a correlation between a sample and a normal distribution; the dots should form a relatively straight 45 degree line if htere is a normal distribution).
moments::skewness(mydata$intvar, na.rm = TRUE)
moments::kurtosis(mydata$intvar, na.rm = TRUE)
ggpubr::ggdensity(mydata$intvar, fill = "lightgray")
ggpubr::ggqqplot(mydata$intvar)Beyond a visual inspection, you can conduct a Shapiro-Wilk’s test of normality, where a p < .05 indicates a non-normal distribution and a p > .05 indicates normally distributed data. This can be a sensitive test, particularly with a large N, so use in conjunction with other information. It is also limited to a sample of 5000.
shapiro.test(mydata$intvar)6.4 T-Test Command (two sample test of group means) and Effect Size
Note that the default is for R to treat the groups as having unequal variances. If this assumption has not been violated, then you may set var.equal = TRUE, as shown below.
t.test(intvar ~ groupvar, data = mydata) # The default is for unequal variances
t.test(intvar ~ groupvar, data = mydata, var.equal = TRUE)To calculate Cohen’s d, a measure of effect size, run the following command. In general, the characterizations of effect size are: |0-.2| (small); |.2-.5| (moderate); |>.5| (large)
effsize::cohen.d(mydata$intvar, mydata$groupvar)6.5 Wilcoxon/Mann-Whitney Rank Sum Test
If you have violated any of the assumptions for t-test, you can run the Wilcoxon/Mann-Whitney Rank Sum Test, a non-parametric test of association.
wilcox.test(intvar ~ groupvar, data = mydata)6.6 Graphing Options for T-Test
Boxplots and/or violin plots are probably the most helpful graphs to complement a t-test. The ggplot2 package is the go-to package for most graphing. The ggstatsplot package and ggbetweenstats function, however, provide a one-stop shop for graphing, displaying means, and conducting a t-test. I actually recommend starting with the the ggstatsplot option. You can find helpful webpages on ggstatsplot::ggstatsbetween here, here, and here.
I also encourage you to check out the R Graph Gallery, a website that showcases different graphs and provides their associated code.
Some important arguments that can be change in ggbetweenstats include:
- plot.type = # options include “box,” “violin,” or the default “boxviolin”
- pairwise.comparisons = # Can be set to TRUE or FALSE
- var.equal = # Can be set to TRUE or FALSE (the default)
- mean.ci = # Can be set to TRUE or FALSE (the default)
- effsize.type = # Can be set to “d” for t-tests
ggstatsplot::ggbetweenstats(data = mydata, x = groupvar, y = intvar,
effsize.type = "d", mean.ci = TRUE,
pairwise.comparisons = TRUE,
messages = FALSE, bf.message = FALSE,
title = "Title of Graph", xlab = "X-axis label", ylab = "Y-axis label")This ggplot command produces a basic boxplot.
ggplot2::ggplot(data = mydata, aes(x = groupvar, y = intvar)) +
geom_boxplot() +
labs(title = "Title of Graph", x = "X-axis label", y = "Y-axis label")This version of the ggplot command includes a subcommand for plotting the means on top of the boxplots.
ggplot2::ggplot(data = mydata, aes(x = groupvar, y = intvar)) +
geom_boxplot() + stat_summary(fun.y = mean, geom = "point", shape = 8, size = 4, color = "blue", fill = "blue") +
labs(title = "Title of Graph", x = "X-axis label", y = "Y-axis label")This version of the gpplot command includes a subcommand for overlaying a violin plot atop the boxplot.
ggplot2::ggplot(data = mydata, aes(x = groupvar, y = intvar)) +
geom_boxplot() + geom_violin() +
labs(title = "Title of Graph", x = "X-axis label", y = "Y-axis label")Lastly, you may consider “patching” your desired graphs together with the patchwork. You’d only need to assign each graph to an object to do so. Here is an example of patching a bar graph and a ggstatsplot graph together (ANOVA example).
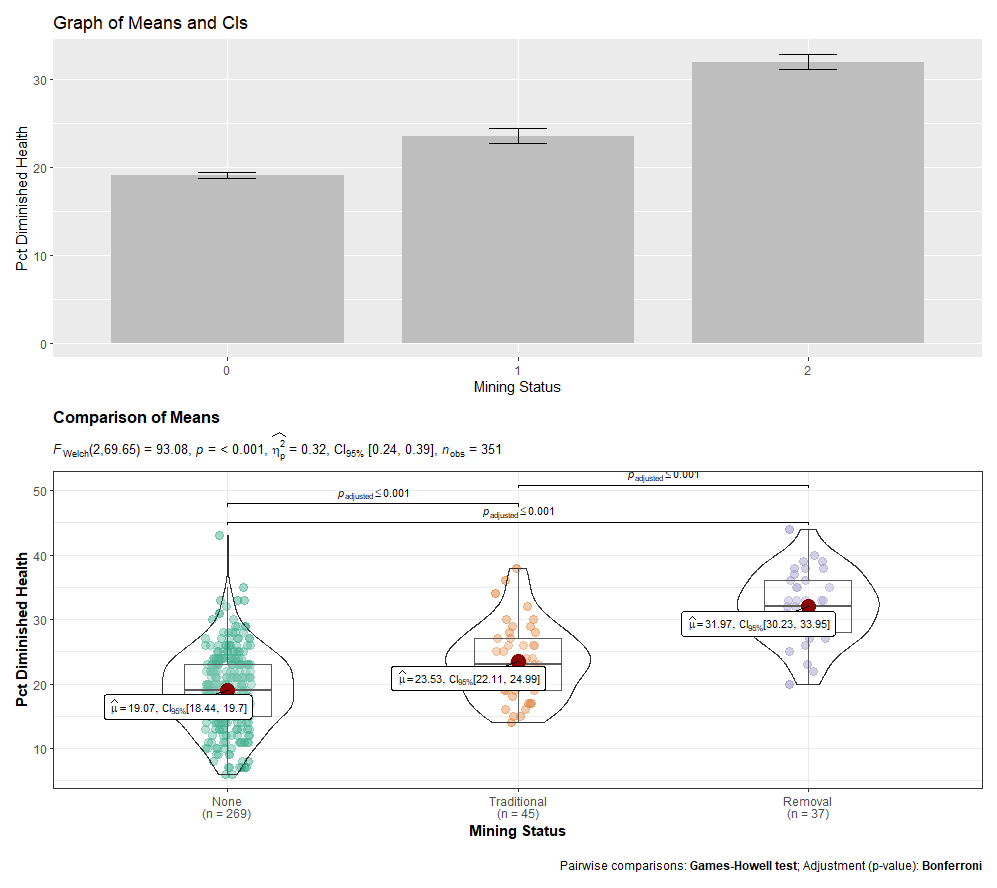
6.7 Consolidated Code for T-Test
Below is the consolidated code from this chapter. One could transfer this code into an empty RScript, which also offers the option of find/replace terms. You can also download this generic t-test RScript file here.
Placeholders that need replacing:
- mydata – name of your dataset
- groupvar – name of your categorical grouping variable
- intvar – name of your interval or continuous variable
- object – whatever you want to call your object(s)), if you generate any
- labels/title – any titles, axis labels, category labels
# 5.1 Packages Needed
req <- substitute(require(x, character.only = TRUE))
libs<-c("effsize", "ggplot2", "ggstatsplot", "patchwork", "moments", "ggpubr")
sapply(libs, function(x) eval(req) || {install.packages(x); eval(req)})
# 5.2 Prep Data
class(mydata$groupvar)
mydata$groupvar <- factor(mydata$groupvar)
# 5.3 Checking data for violations of assumptions:
## Group frequencies:
table(mydata$groupvar)
## Group means and standard deviations. Either the "aggregate" or "by" command works
aggregate(mydata$intvar, by = list(mydata$groupvar), FUN = mean, na.rm = TRUE)
aggregate(mydata$intvar, by = list(mydata$groupvar), FUN = sd, na.rm = TRUE)
by(mydata$intvar, mydata$groupvar, mean, na.rm = TRUE)
by(mydata$intvar, mydata$groupvar, sd, na.rm = TRUE)
## Test of equal variances across groups
var.test(intvar ~ groupvar, data = mydata)
## Check for Normality
moments::skewness(mydata$intvar, na.rm = TRUE)
moments::kurtosis(mydata$intvar, na.rm = TRUE)
ggpubr::ggdensity(mydata$intvar, fill = "lightgray")
ggpubr::ggqqplot(mydata$intvar)
shapiro.test(mydata$intvar)
# 5.4 T-Test command (two sample test of group means) and Cohen's d
t.test(intvar ~ groupvar, data = mydata) # The default is for unequal variances
t.test(intvar ~ groupvar, data = mydata, var.equal = TRUE)
effsize::cohen.d(mydata$intvar, mydata$groupvar)
# 5.5 Wilcoxon/Mann-Whitney Rank Sum Test (non-parametric)
wilcox.test(intvar ~ groupvar, data = mydata)
# 5.6 Graphing Options
## ggstatsplot::ggbetweeenstats is my "go to" option
ggstatsplot::ggbetweenstats(data = mydata, x = groupvar, y = intvar,
effsize.type = "d", mean.ci = TRUE,
pairwise.comparisons = TRUE,
messages = FALSE, bf.message = FALSE,
title = "Title of Graph", xlab = "X-axis label", ylab = "Y-axis label")
## ggplot commands
ggplot2::ggplot(data = mydata, aes(x = groupvar, y = intvar)) +
geom_boxplot() +
labs(title = "Title of Graph", x = "X-axis label", y = "Y-axis label")
ggplot2::ggplot(data = mydata, aes(x = groupvar, y = intvar)) +
geom_boxplot() + stat_summary(fun.y = mean, geom = "point",
shape = 8, size = 4, color = "blue", fill = "blue") +
labs(title = "Title of Graph", x = "X-axis label", y = "Y-axis label")
ggplot2::ggplot(data = mydata, aes(x = groupvar, y = intvar)) +
geom_boxplot() + geom_violin() +
labs(title = "Title of Graph", x = "X-axis label", y = "Y-axis label")