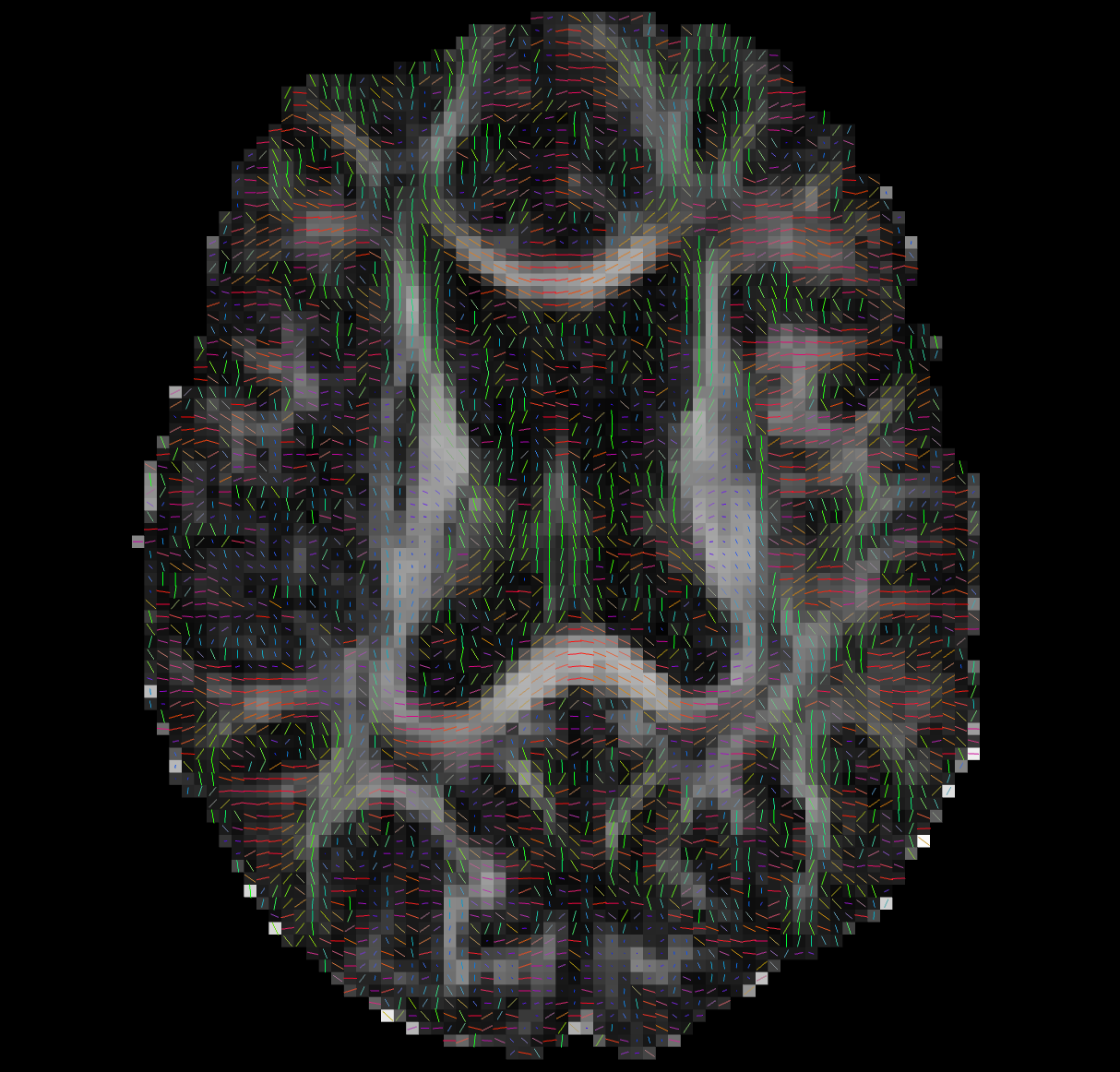
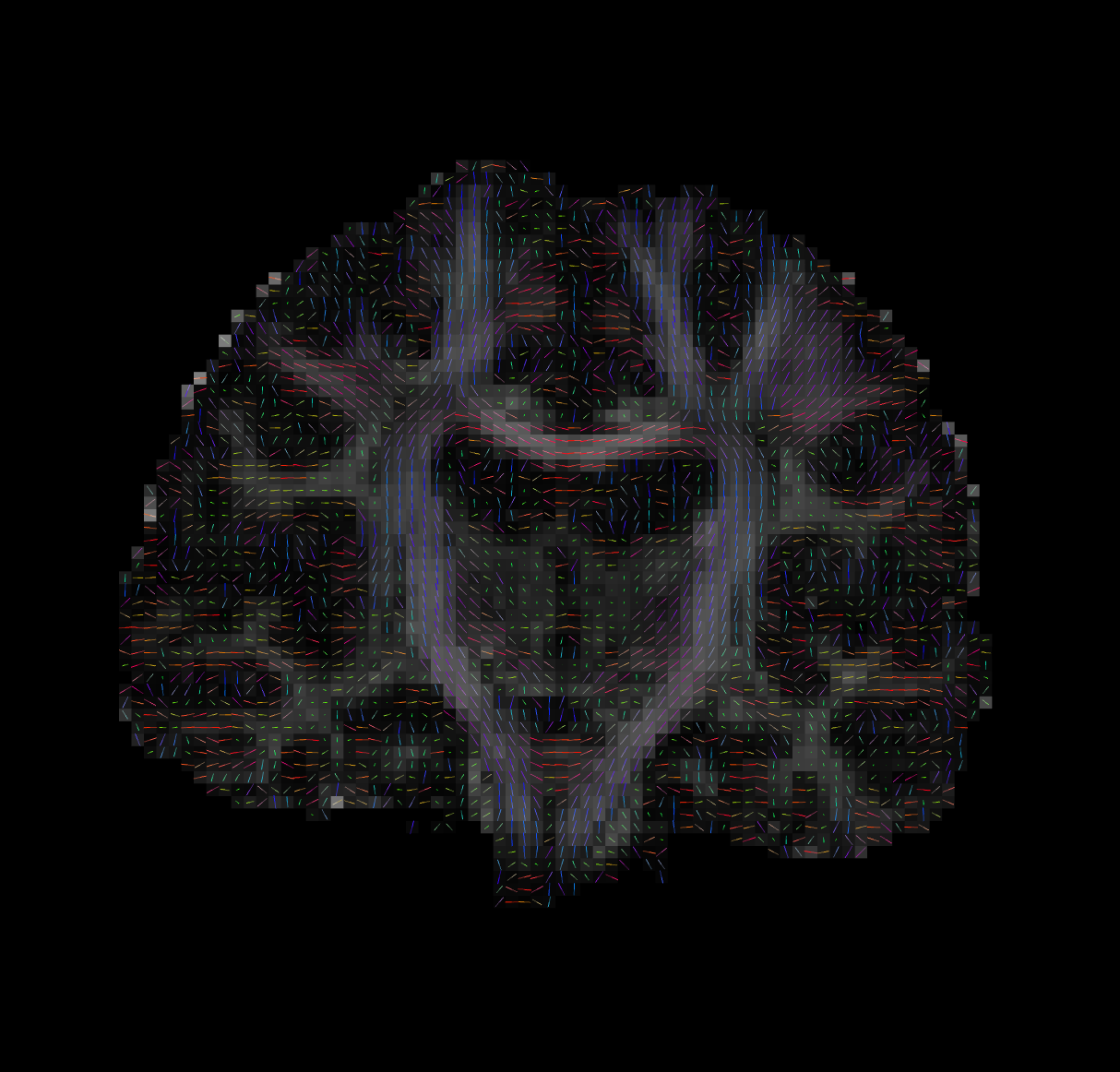
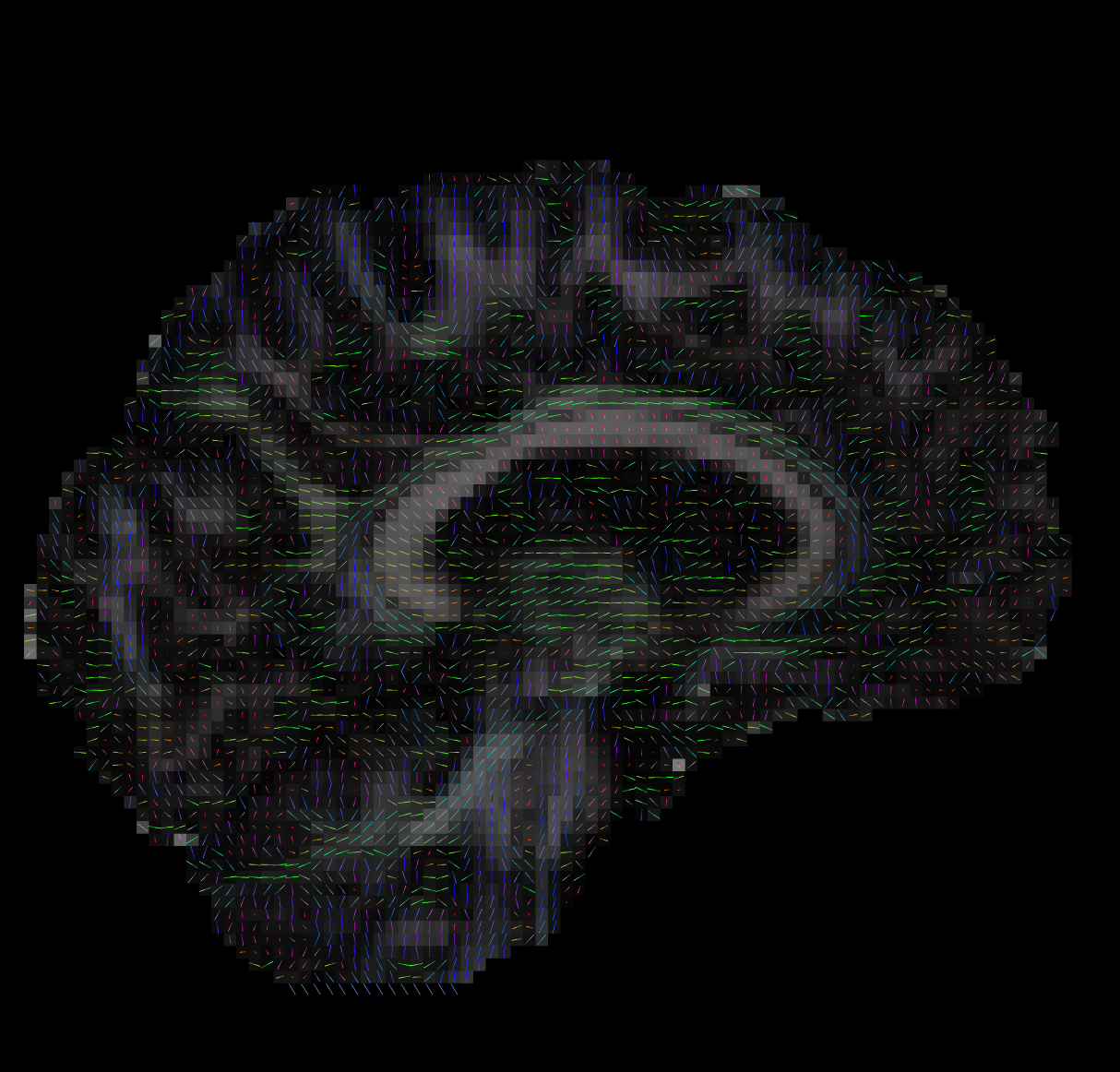
Tensor Fitting
Eigenvector vs. Eigenvalue
Eigenvectors (( e_{1}, e_{2}, e_{3} )) describe the orientation of diffusion: principal direction ((e_{1})) and “radial” directions ((e_{2}, e_{3})). Think of a 3D scatterplot and the eigenvectors are summary values of how the data are dispersed.
- ( e_{1} ) is similar to fitting a linear regression / correlation to a dataset. In the case of DWI, the data are diffusion measurements for each gradient direction.
- ( e_{2} ) is perpendicular to ( e_{1} ) and represents the error distribution in that plane.
- ( e_{3} ) is perpendicular to the xy-plane plane and represents the error distribution.
Eigenvalues (( {1}, {2}, _{3} )) describe the magnitude of the eigenvector / diffusion.
Diffusion Measurements
- Mean diffusion: molecular diffusion rate
\[MD(j) = \frac{\lambda_1(j) + \lambda_2(j) + \lambda_3(j)}{3}\]
- Axial diffusivity: diffusion rate along the main axis
\[AD(j) = \lambda_1(j)\]
- Radial diffusivity: diffusion in the transverse directions
\[RD(j) = \frac{\lambda_2(j) + \lambda_3(j)}{2}\]
- Fractional anisotropy: Variance of the 3 eigenvalues (magnitude) normalized so that (0 ) FA (), measures the strength of directional preference (i.e., anisotropy).
Calculating Tensors
If you just want to calculate single orientation (eigenvector) and magnitude (eigenvalue), use FSL dtifit. There are other options available to model diffusion (i.e., orientation distribution function (ODF), ball-and-stick):
dtifit \
--data=dwi_epi.nii.gz \
--out=dti \
--mask=dwi_epi_b0_mask.nii.gz \
--bvecs=dwi_eddy.eddy_rotated_bvecs \
--bvals=dwi.bval \
--save_tensorOutputs of dtifit:
<basename>_V1 # 1st eigenvector
<basename>_V2 # 2nd eigenvector
<basename>_V3 # 3rd eigenvector
<basename>_L1 # 1st eigenvalue
<basename>_L2 # 2nd eigenvalue
<basename>_L3 # 3rd eigenvalue
<basename>_MD # mean diffusivity
<basename>_FA # fractional anisotropy (isotropic ~ 0; stick-like ~1)
<basename>_MO # mode of the anisotropy (oblate ~ -1; isotropic ~ 0; prolate ~ 1)
<basename>_S0 # raw T2 signal with no diffusion weightingChecking Tensors
freeview \
--volume dti_V1.nii.gz:vector=1:render='line' \
dti_FA.nii.gz \
--viewport axial \
--layout 1 \
--viewsize 800 800 \
--zoom 1 \
--ras 0 0 30Bad Tensors
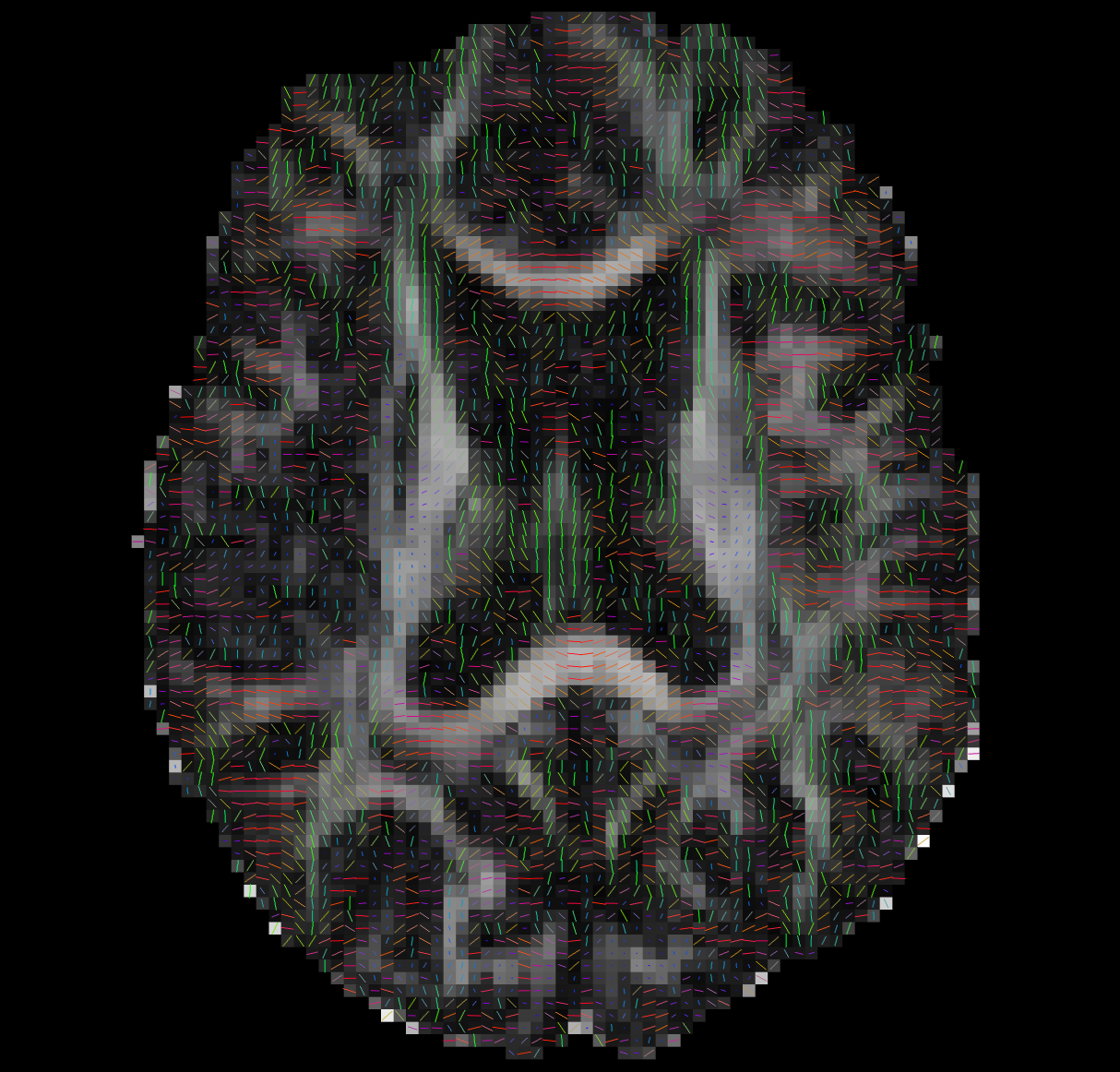
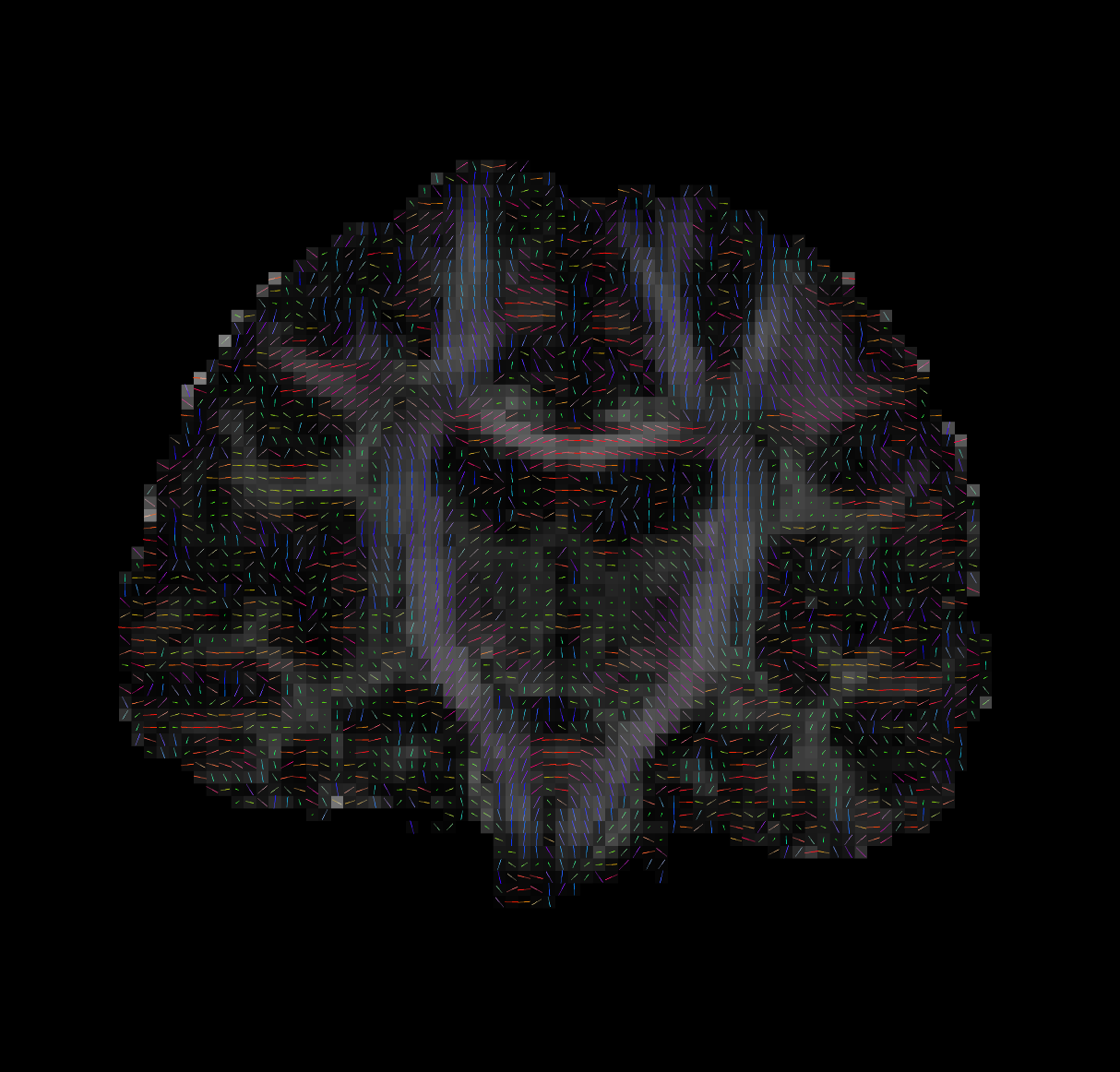
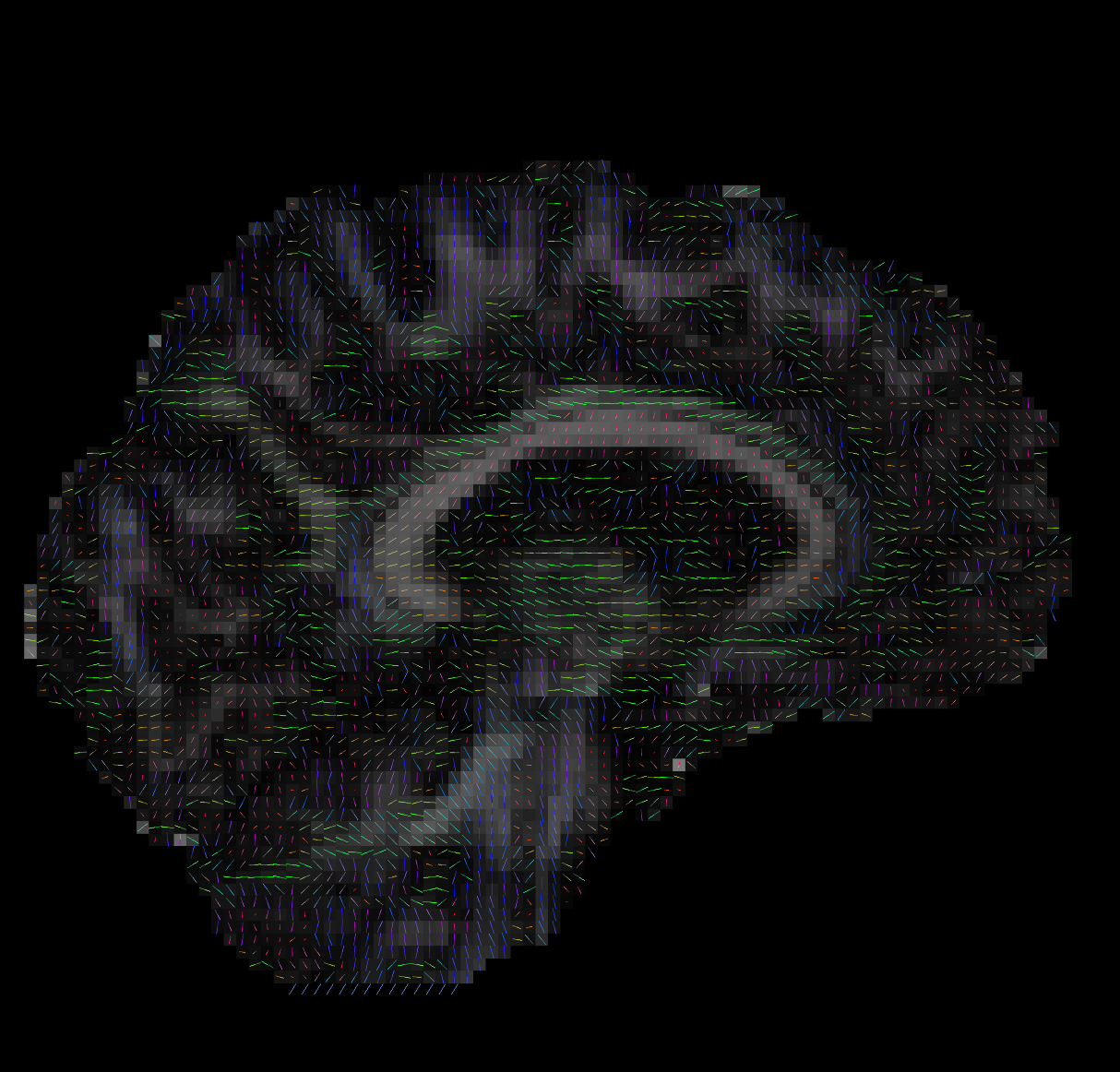
Good Tensors