Functional Connectivity

Sustained connectivity using resting-state functional MRI data are analyzed using both network level and finer-grained brain parcellation schemes. Preprocessing involves removing volumes with head motion of greater than 0.2 mm, as well as frames before and after the head motion. Time series are then extracted from volumes for each participant. Multiple volumes can be concatenated if available.

A finer parcellation is computed that consists of 333 regions in the cerebral cortex, 14 subject-specific subcortical regions from FreeSurfer derived segmentation (bilateral thalamus, caudate, putamen, amygdala, hippocampus, pallidum, and nucleus accumbens), and 14 bilateral cerebellar representations of a 7-network parcellation. This combined parcellation scheme incorporates major cortical, subcortical, and cerebellar gray matter ROIs numbering 361 regions in total. Functional connectivity is estimated as the Pearson correlation coefficient between mean time series from each ROI.

Pearson’s correlation measures the linear association between two variables. Because the correlation is bounded between [-1, 1], the sampling distribution for highly correlated variables is highly skewed. In 1921, R. A. Fisher studied the correlation of bivariate normal data and discovered a wonderful transformation that converts the skewed distribution of the sample correlation (r) into a distribution that is approximately normal. Resting state correlation coefficients are Fisher transformed. Values will range between 0 and 2.

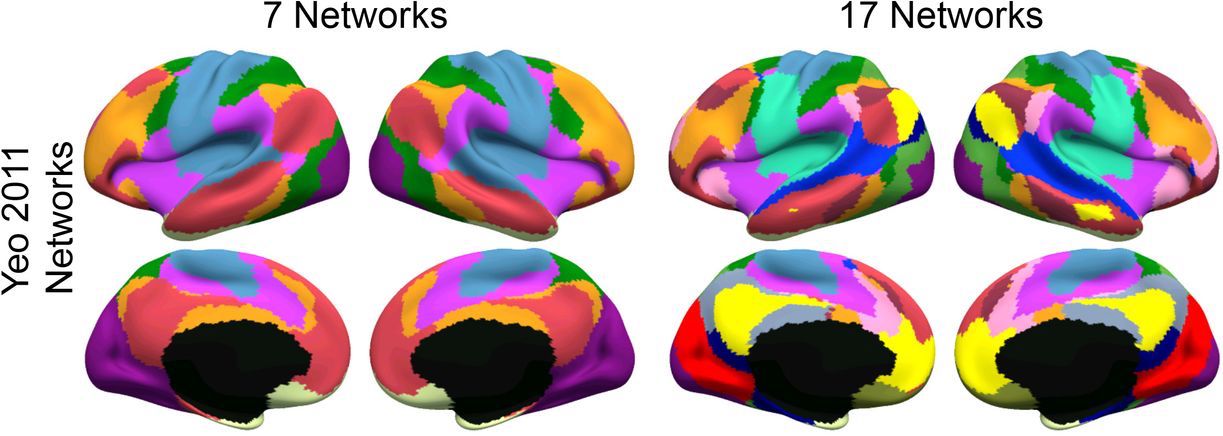
For network analyses, the mean functional connectivity between ROIs for each intrinsic network is calculated and then between-network functional connectivity is calculated as the Pearson correlation coefficient between mean time series from each network. Correlations are Fisher-transformed. Each functional network is treated as a single ROI. Mean functional connectivity outputs are available for 7 and 17 networks. The 7 networks are as follows: (1) Visual; (2) Somatomotor; (3) Dorsal Attention; (4) Ventral Attention; (5) Limbic; (6) Frontoparietal; and (7) Default. The 17 networks are as follows: (1) Central visual; (2) Peripheral visual; (3) Dorsal somatomotor; (4) Ventral somatomotor; (5) Posterior dorsal attention; (6) Somatomotor association; (7) Posterior ventral attention; (8) Anterior ventral attention; (9) Medial temporal–limbic; (10) Orbitofrontal–limbic; (11) Medial superior parietal; (12) Medial frontoparietal; (13) Lateral frontoparietal; (14) Lateral temporal–default mode network (DMN); (15) Ventral–DMN; (16) Dorsal–DMN; and (17) Lateral–DMN.

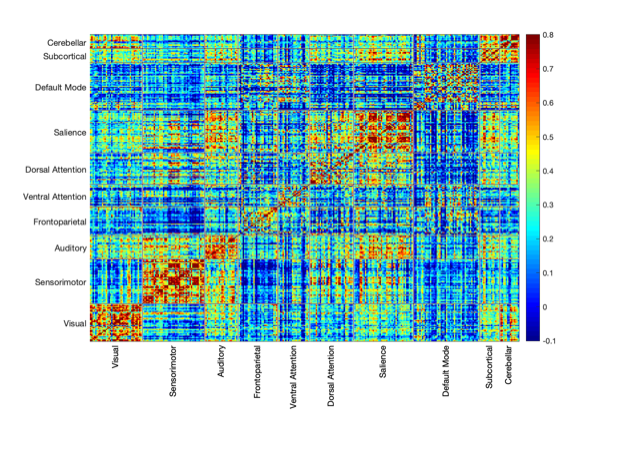
A 385x385 matrix consisting of Fisher transformed correlation coefficients representing functional connectivity is provided for each subject. The matrices can be split into 361x361 ROIs (shown above) and 17x17 networks. The larger 385x385 matrix consists of: 333 ROIs, 14 subcortical regions, 14 bilateral cerebellar representations of a 7-network parcellation, 7 brain networks from Yeo, 17 brain networks from Yeo. Within-network functional connectivity can be estimated from the mean of all ROI time series within a network of interest.

ParcelID	Hem	Community
10, 64, 65, 66, 67, 68, 69, 70, 77, 102, 104	L	Auditory
171, 224, 227, 230, 232, 233, 239, 244, 268, 269, 329, 330	R	Auditory
180, 181, 185, 187, 188, 192, 196, 198, 219, 223, 234, 235, 238, 245, 246, 248, 249, 274, 317, 318	R	CinguloOperc
21, 22, 27, 28, 34, 40, 63, 71, 72, 76, 81, 82, 84, 101, 103, 105, 111, 112, 147, 153	L	CinguloOperc
12, 89, 93	L	CinguloParietal
173, 254	R	CinguloParietal
1, 4, 6, 25, 26, 44, 94, 114, 116, 117, 126, 127, 145, 146, 150, 151, 152, 154, 156, 157	L	Default
162, 165, 184, 186, 200, 220, 225, 257, 259, 278, 279, 290, 315, 316, 321, 322, 323, 324, 325, 326, 331	R	Default
189, 199, 203, 208, 211, 236, 250, 252, 253, 262, 266, 271, 275	R	Dorsal Attention
41, 42, 43, 49, 51, 52, 55, 74, 87, 88, 91, 92, 95, 100, 106, 107, 110, 113, 155	L	Dorsal Attention
167, 168, 170, 182, 240, 260, 261, 272, 273, 276, 277, 319, 320, 327, 328	R	FrontoParietal
7, 9, 24, 78, 96, 108, 109, 148, 149	L	FrontoParietal
11, 18, 19, 73, 115, 118, 119, 120, 121, 122, 123, 124, 125, 128, 129, 133, 134, 135, 142, 144, 159	L	None
172, 178, 179, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 291, 292, 296, 297, 300, 301, 302, 303, 304, 305, 306, 312, 314	R	None
13, 14, 130, 143	L	Retrosplenial Temporal
174, 294, 295, 313	R	Retrosplenial Temporal
183, 247	R	Salience
29, 83	L	Salience
163, 190, 191, 193, 194, 195, 201, 202, 204, 205, 206, 207, 209, 210, 213, 214, 215, 216, 217, 270	R	Somatomotor Hand
2, 30, 31, 32, 33, 35, 36, 37, 38, 45, 46, 47, 48, 50, 54, 56, 57, 58	L	Somatomotor Hand
164, 197, 212, 218	R	Somatomotor Mouth
3, 39, 53, 59	L	Somatomotor Mouth
221, 222, 226, 228, 229, 231, 237, 241, 242, 243, 332, 333	R	Ventral Attention
23, 60, 61, 62, 75, 79, 80, 85, 86, 158, 161	L	Ventral Attention
166, 169, 175, 176, 177, 251, 255, 256, 258, 263, 264, 265, 267, 293, 298, 299, 307, 308, 309, 310, 311	R	Visual
5, 8, 15, 16, 17, 20, 90, 97, 98, 99, 131, 132, 136, 137, 138, 139, 140, 141	L	Visual

The follow R code can be adapted to average the correlation coefficients for each of the intrinsic networks:

# Packages
require(ppcor)

# Generate pseudo 100-by-50 correlation matrix
M <- matrix(rnorm(n=5000, mean=0, sd=1), 100, 50)
colnames(M) <- paste0('V',seq(1,50))

# View top of matrix
head(M)

# Generate correlation matrix
CM <- cor(M)

# Or a partial correlation matrix if you prefer
pCM <- ppcor::pcor(M)$estimate

# View CM
head(CM)

#### Function to get average network connectivity ####
# Function requires the correlation matrix, CM, and the IDs of the nodes of interst listed in nodes_of_interest variable

nodes_of_interest <- c('V17', 'V20', 'V33', 'V34', 'V35')

calculate_mean_network_connectivity <- function(CM, nodes){

  # subset correlation matrix by nodes of interest
  cm_ss <- CM[nodes, nodes]

  # get upper triangle values
  cm_ss_utri <- cm_ss[upper.tri(cm_ss)]

  # return mean of upper triangle
  return( mean(cm_ss_utri) )

}

# Apply the function
single_subject_result <- calculate_mean_network_connectivity(CM = CM, nodes = nodes_of_interest)
print(single_subject_result)

#### Extend this to multiple subjects, each with their own correlation matrices ####
nodes_of_interest <- c('V17', 'V20', 'V33', 'V34', 'V35')

# Generate list of 10 connectivity matrices of dimension 100-by-50 and return correlation matrices
CM_List <- lapply(1:10, function(f){
  M <- matrix(rnorm(n=5000, mean=0, sd=1), 100, 50)
  colnames(M) <- paste0('V',seq(1,50))
  CM <- cor(M)
  return(CM)
})

# Apply previous function, calculate_mean_network_connectivity, to all 10 matrices while subsetting for nodes of interest
multiple_subject_result <- sapply(CM_List, function(x) calculate_mean_network_connectivity(CM = x, nodes = nodes_of_interest))
print(multiple_subject_result)

Subcortical ROIs

	V334	V335	V336	V337	V338	V339	V340	V341	V342	V343	V344	V345	V346	V347
334	2.000	0.462	0.392	0.576	0.338	0.118	0.340	1.646	0.535	0.364	0.414	0.313	0.079	0.389
335	0.462	2.000	0.727	0.653	0.650	0.472	0.527	0.434	1.080	0.598	0.483	0.570	0.430	0.496
336	0.392	0.727	2.000	1.073	0.855	0.726	0.643	0.408	0.699	1.421	1.016	0.897	0.700	0.630
337	0.576	0.653	1.073	2.000	0.821	0.743	0.770	0.573	0.603	0.922	1.194	0.784	0.684	0.801
338	0.338	0.650	0.855	0.821	2.000	1.376	0.731	0.365	0.622	0.769	1.029	1.911	1.209	0.693
339	0.118	0.472	0.726	0.743	1.376	2.000	0.600	0.183	0.421	0.671	0.875	1.283	1.650	0.577
340	0.340	0.527	0.643	0.770	0.731	0.600	2.000	0.363	0.625	0.599	0.730	0.742	0.603	1.566
341	1.646	0.434	0.408	0.573	0.365	0.183	0.363	2.000	0.571	0.419	0.447	0.335	0.141	0.379
342	0.535	1.080	0.699	0.603	0.622	0.421	0.625	0.571	2.000	0.705	0.529	0.580	0.393	0.661
343	0.364	0.598	1.421	0.922	0.769	0.671	0.599	0.419	0.705	2.000	0.939	0.797	0.628	0.638
344	0.414	0.483	1.016	1.194	1.029	0.875	0.730	0.447	0.529	0.939	2.000	0.982	0.827	0.720
345	0.313	0.570	0.897	0.784	1.911	1.283	0.742	0.335	0.580	0.797	0.982	2.000	1.223	0.719
346	0.079	0.430	0.700	0.684	1.209	1.650	0.603	0.141	0.393	0.628	0.827	1.223	2.000	0.571
347	0.389	0.496	0.630	0.801	0.693	0.577	1.566	0.379	0.661	0.638	0.720	0.719	0.571	2.000

7-Network Cerebellar Parcellation

	V348	V349	V350	V351	V352	V353	V354	V355	V356	V357	V358	V359	V360	V361
348	2.000	0.509	0.492	0.794	0.616	0.381	-0.117	1.174	0.556	0.449	0.679	0.594	0.351	-0.021
349	0.509	2.000	0.925	1.108	0.738	0.596	0.338	0.508	1.558	0.607	1.037	0.731	0.735	0.497
350	0.492	0.925	2.000	1.243	0.762	0.717	0.401	0.520	0.835	1.108	1.066	0.665	0.689	0.366
351	0.794	1.108	1.243	2.000	0.942	0.964	0.439	0.791	1.002	0.932	1.256	0.824	0.843	0.416
352	0.616	0.738	0.762	0.942	2.000	0.804	0.322	0.612	0.713	0.778	0.773	1.395	0.711	0.358
353	0.381	0.596	0.717	0.964	0.804	2.000	0.913	0.534	0.639	0.973	0.815	0.754	1.153	0.647
354	-0.117	0.338	0.401	0.439	0.322	0.913	2.000	0.135	0.319	0.550	0.421	0.335	0.833	1.140
355	1.174	0.508	0.520	0.791	0.612	0.534	0.135	2.000	0.571	0.584	0.790	0.694	0.542	0.204
356	0.556	1.558	0.835	1.002	0.713	0.639	0.319	0.571	2.000	0.642	1.258	0.789	0.725	0.427
357	0.449	0.607	1.108	0.932	0.778	0.973	0.550	0.584	0.642	2.000	0.979	0.744	0.960	0.459
358	0.679	1.037	1.066	1.256	0.773	0.815	0.421	0.790	1.258	0.979	2.000	0.842	0.871	0.471
359	0.594	0.731	0.665	0.824	1.395	0.754	0.335	0.694	0.789	0.744	0.842	2.000	0.774	0.428
360	0.351	0.735	0.689	0.843	0.711	1.153	0.833	0.542	0.725	0.960	0.871	0.774	2.000	0.967
361	-0.021	0.497	0.366	0.416	0.358	0.647	1.140	0.204	0.427	0.459	0.471	0.428	0.967	2.000

7 Yeo Networks

	V362	V363	V364	V365	V366	V367	V368
362	2.000	1.173	1.478	1.016	1.155	1.065	0.975
363	1.173	2.000	1.356	1.270	1.069	1.126	0.999
364	1.478	1.356	2.000	1.118	1.195	1.444	1.139
365	1.016	1.270	1.118	2.000	0.787	1.080	0.858
366	1.155	1.069	1.195	0.787	2.000	1.066	1.168
367	1.065	1.126	1.444	1.080	1.066	2.000	1.282
368	0.975	0.999	1.139	0.858	1.168	1.282	2.000

17 Yeo Networks

	V369	V370	V371	V372	V373	V374	V375	V376	V377	V378	V379	V380	V381	V382	V383	V384	V385
369	2.000	1.000	0.961	1.017	1.462	1.143	0.846	0.680	0.957	1.107	0.547	1.028	0.853	0.732	0.993	0.802	0.640
370	1.000	2.000	0.937	0.929	1.055	1.020	0.817	0.736	0.825	0.672	0.685	0.738	0.585	0.899	1.121	0.863	0.635
371	0.961	0.937	2.000	1.568	0.997	1.361	1.126	0.698	0.898	0.873	0.539	1.038	0.904	0.868	0.919	0.799	0.786
372	1.017	0.929	1.568	2.000	1.049	1.343	1.485	0.835	0.952	0.854	0.510	1.140	0.872	1.012	1.008	0.845	0.818
373	1.462	1.055	0.997	1.049	2.000	1.362	0.931	0.808	1.056	0.927	0.728	1.361	1.057	1.061	1.339	0.979	0.891
374	1.143	1.020	1.361	1.343	1.362	2.000	1.253	0.867	1.048	0.874	0.524	1.280	1.049	1.056	1.061	0.931	0.960
375	0.846	0.817	1.126	1.485	0.931	1.253	2.000	1.138	0.767	0.614	0.450	0.977	0.758	0.827	0.902	0.735	0.666
376	0.680	0.736	0.698	0.835	0.808	0.867	1.138	2.000	0.633	0.464	0.518	0.698	0.712	0.650	0.748	0.737	0.676
377	0.957	0.825	0.898	0.952	1.056	1.048	0.767	0.633	2.000	0.954	0.559	0.933	0.922	1.020	1.075	1.003	1.075
378	1.107	0.672	0.873	0.854	0.927	0.874	0.614	0.464	0.954	2.000	0.563	0.833	0.913	0.638	0.805	0.807	0.726
379	0.547	0.685	0.539	0.510	0.728	0.524	0.450	0.518	0.559	0.563	2.000	0.482	0.568	0.688	0.825	0.981	0.593
380	1.028	0.738	1.038	1.140	1.361	1.280	0.977	0.698	0.933	0.833	0.482	2.000	1.216	0.975	0.998	0.804	0.952
381	0.853	0.585	0.904	0.872	1.057	1.049	0.758	0.712	0.922	0.913	0.568	1.216	2.000	0.879	0.871	0.999	1.220
382	0.732	0.899	0.868	1.012	1.061	1.056	0.827	0.650	1.020	0.638	0.688	0.975	0.879	2.000	1.182	1.049	1.199
383	0.993	1.121	0.919	1.008	1.339	1.061	0.902	0.748	1.075	0.805	0.825	0.998	0.871	1.182	2.000	1.246	0.976
384	0.802	0.863	0.799	0.845	0.979	0.931	0.735	0.737	1.003	0.807	0.981	0.804	0.999	1.049	1.246	2.000	1.159
385	0.640	0.635	0.786	0.818	0.891	0.960	0.666	0.676	1.075	0.726	0.593	0.952	1.220	1.199	0.976	1.159	2.000

Files

List of files will include a comma-separated values (.csv) file for each participant in the form of a 385 matrix.

sub-001/cor385.csv
sub-002/cor385.csv
[…]