Chapter 7 Rによるデータ分析⑤
7.1 推定結果の解釈
海上保安庁(国家公務員)への入職行動に関する重回帰分析を実施。
ここでは仮に分析モデルを以下のように設定する。
\(jcga=\beta_0+\beta_1 age18 + \beta_2 jobless +\beta_3 joboffer +\beta_4 education+u,\)
| 変数の定義 |
|---|
\(jcga=\) 各都道府県における海上保安大学校への受験者数(単位=人) \(age18=\) 各都道府県における18歳人口(単位=千人) \(jobless=\) 各都道府県における完全失業率(単位=%) \(joboffer=\) 各都道府県における有効求人倍率(単位=倍) \(education=\) 各都道府県における大学進学率(単位=%) \(u=\) 誤差項(観察されない要因) |
| 変数名 | 説明 | 出典 |
|---|---|---|
| 海保大受験者数 | 各都道府県ごとの第1次試験受験者数(2021年) | 海上保安庁総務部教育訓練管理官の提供 |
| 人口 | 各都道府県ごとの18歳人口(2021年) | 「学校基本調査」文部科学省総合教育政策局調査企画課 |
| 失業率 | 各都道府県ごとの完全失業率(%)(2021年) | 「労働力調査」総務省統計局統計調査部国勢統計課労働力人口統計室 |
| 有効求人倍率 | 各都道府県ごとの有効求人倍率(倍、年平均)(2021年) | 「一般職業紹介状況」厚生労働省職業安定局雇用政策課 |
| 大学進学率 | 各都道府県ごとの大学進学率(%)(2021年) | 「学校基本調査」文部科学省総合教育政策局調査企画課 |
※有効求人倍率は求職者1人あたり何件の求人があるかを示す指標
7.1.1 単回帰モデルの推定とその解釈
Model 1
\(jcga_i=\beta_0+\beta_1age18_i+u_i\) (海保大受験者数 = \(\beta_0\) + \(\beta_1\) 人口 + 誤差)
Model 2
\(jcga_i=\beta_0+\beta_1\,jobless_i+u_i\) (海保大受験者数 = \(\beta_0\) + \(\beta_1\) 失業率+ 誤差)
Model 3
\(jcga_i=\beta_0+\beta_1\,joboffer_i+u_i\)(海保大受験者数 = \(\beta_0\) + \(\beta_1\) 有効求人倍率 + 誤差)
Model 4
\(jcga_i=\beta_0+\beta_1\,education_i+u_i\)(海保大受験者数 = \(\beta_0\) + \(\beta_1\) 大学進学率+ 誤差)
model_1 <- lm(juken ~ age18 , data = bunseki1)
model_2 <- lm(juken ~ jobless , data = bunseki1)
model_3 <- lm(juken ~ joboffer , data = bunseki1)
model_4 <- lm(juken ~ education , data = bunseki1)推定結果をstargazerでまとめて出力する。
stargazer(model_1, model_2, model_3, model_4,
digits = 3, # 小数点以下 3 位まで示す
style = "ajps", # AJPS仕様(学術誌のスタイル),
keep.stat = c('n', 'rsq','adj.rsq', 'f'),
df = FALSE, #自由度の削除
covariate.labels = c("人口", "失業率", "有効求人倍率", "大学進学率"),
dep.var.caption = "被説明変数", # 変数の種類を明示
dep.var.labels = "海保大受験者数", # 被説明変数の名前
title = "分析結果", # タイトル
type ="html")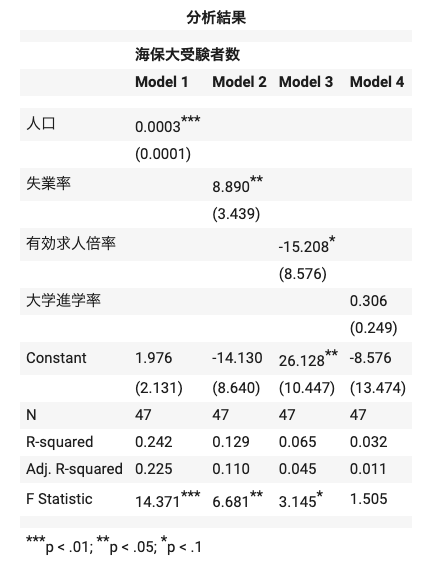
Model 1:推定結果の解釈
\(\hat{jcga}_i=1.976+0.0003\,age18_i\) (海保大受験者数 = \(1.976\) + \(0.0003\) 人口 )
\(***p<0.01\) → \(p\)値(有意確率=値が0になる確率)が1%以下=「統計的に有意である」
\(n=47\), \(R^2=0.242\)
「18歳人口(説明変数)は、正(プラス)で有意な結果となった。具体的に回帰係数の値から、人口が1人(1単位)増えると0.0003人受験者数が増える可能性が示唆される。決定係数については、0.242となりデータに対するモデルの当てはまりがあまり良くないことが示された。」
補足:決定係数\(R^2=0.242\)ということは、被説明変数(受験者数)の変動の約20%をこのモデルで説明することができるという意味である。つまり、このモデル(回帰式)の予測精度はあまり高くないが、説明変数(人口)の影響は否定できないという結果になっている。
Model 2:推定結果の解釈
\(\hat{jcga}_i=-14.130+8.890\,jobless_i\) (海保大受験者数 = \(-14.130\) + \(8.890\) 失業率)
\(**p<0.05\) → \(p\)値(有意確率=値が0になる確率)が5%以下=「統計的に有意である」
\(n=47\), \(R^2=0.129\)
「失業率(説明変数)は、正(プラス)で有意な結果となった。具体的に回帰係数の値から、失業率が1%(1単位)増えると8.890人受験者数が増える可能性が示唆される。決定係数については、0.129となりデータに対するモデルの当てはまりが良くないことが示された。」
Model 3:推定結果の解釈
\(\hat{jcga}_i=26.128-15.208\,joboffer_i\)(海保大受験者数 = \(26.128-15.208\) 有効求人倍率 )
\(*p<0.10\) → \(p\)値(有意確率=値が0になる確率)が10%以下=「統計的に有意である」
\(n=47\), \(R^2=0.129\)
「有効求人倍率(説明変数)は、負(マイナス)で有意な結果となった。具体的に回帰係数の値から、有効求人倍率が1倍(1単位)増えると15.208人受験者数が減る可能性が示唆される。決定係数については、0.065となりデータに対するモデルの当てはまりが良くないことが示された。」
Model 4:推定結果の解釈
\(jcga_i=-8.576+0.306\,education_i\)(海保大受験者数 = \(-8.576+0.306\) 大学進学率)
\(*なし\) → \(p\)値(有意確率)が高い=係数の値が0になる可能性が十分にある
\(n=47\), \(R^2=0.129\)
「大学進学率(説明変数)は、有意な結果とならなかったが係数については正(プラス)の値となっている。決定係数については、0.032となりデータに対するモデルの当てはまりが良くないことが示された。」
補足:「有意ではない」=「影響があるかどうか定かではない」という意味であり、「影響がない」とは断定できない。また変数を追加した場合に有意になることもあるので、係数の符号の向きは確認しておく必要がある。
7.1.2 重回帰モデルの推定とその解釈
重回帰モデルによる推定を行う目的は、「欠落変数」問題を解決するためである。
Example: Soybean Yield and Fertilizer
大豆の収量がモデルによって決定されるとする。
\(yield=\beta_0+\beta_1 fertilizer+u,\)
\(Y_i(yield)= 収量\)、 \(X_i(fertilizer)=肥料の量\)である。分析者は,他の要因を固定した場合の、大豆収量に対する肥料の効果に関心がある。この効果は \(\beta_1\)で与えられる。
→\(\Delta yield=\beta_1 \Delta fertilizer.\)
ここで、土地の質や降雨量などの要因を\(W_i\)とすると、\(W_i\)は\(Y_i= 収量\)や\(X_i=肥料の量\)に影響を与えることになる(上質の土地や日当たりなどの環境の良い場所では、そもそも大豆が多く収穫できるため肥料の量を減らす可能性がある)。 この\(W_i\)という変数を無視して上式のようなモデルを組み立て得ると、この\(W_i\)は誤差項\(u\)に含まれることになる。
こうなると、\(E(u_i|X_i)=0\)(\(=X_i\) と \(u_i\) の間には相関がない)が満たされず、最小二乗推定による\(\beta_1\)の推定が偏ったもの(つまり、バイアスをもったもの)になってしまう。
もう少し明示的に式で表すと、次のようになる。
日当たりを \(W_i\)、観測誤差を \(v_i\) とすると、誤差項は\(u_i=W_i+v_i\) と表すことができる。 農業者は \(W_i\) に応じて \(X_i\) を決めており、その関係を \(X_i=h(W_i)\) とする。この関係を逆に表すと \(W_i=k(X_i)\) と書ける(\(k\) は \(h\) の逆関数)。
したがって、\(u_i=k(X_i)+v_i\)となり単回帰モデルは以下のように書き直すことができる。
\(Y_i=\beta_0+\beta_1 X_i +u_i\)
\(Y_i=\beta_0+\beta_1 X_i +k(X_i)+v_i\)
\(v_i\) は観測誤差なので、\(X_i\) が変化しても平均的には \(v_i\) は変化しない
→\(E(v_i|X_i)=0\)(\(=X_i\) と \(v_i\) の間には相関がない)
ゆえに、\(X_i\) の変化がもたらす平均的な \(Y_i\) の変化は \(\beta_1 X_i\) と \(k(X_i)\) の変化の合計となる。つまり、\(X_i\) の変化を原因とする\(Y_i\) の変化を正しく測れていないことになる。このように、因果関係を推論する際に必要な変数が欠落して起こる推定値の偏りを欠落変数バイアス(omitted variable bias)といい、このバイアスをいかに取り除いていくかが欠落変数問題として定式化されているのである。 逆にいえば、誤差項が説明変数とは相関を持たなくなるまで、説明変数を加えていくことによって欠落変数のバイアスを回避するということになる。
Model 5
\(jcga=\beta_0+\beta_1 age18 + \beta_2 jobless +\beta_3 joboffer +\beta_4 education+u,\)
(海保大受験者数 = \(\beta_0\) + \(\beta_1\) 人口+\(\beta_2\) 失業率 +\(\beta_3\) 有効求人倍率 +\(\beta_4\) 大学進学率 + 誤差)
model_5<- lm(juken ~ age18 +
jobless +
joboffer +
education, data = bunseki1)先ほど出力した表にModel 5の推定結果を追加する。
stargazer(model_1, model_2, model_3, model_4, model_5,
digits = 3, # 小数点以下 3 位まで示す
style = "ajps", # AJPS仕様(学術誌のスタイル),
keep.stat = c('n', 'rsq','adj.rsq', 'f'),
df = FALSE, #自由度の削除
covariate.labels = c("人口", "失業率", "有効求人倍率", "大学進学率"),
dep.var.caption = "被説明変数", # 変数の種類を明示
dep.var.labels = "海保大受験者数", # 被説明変数の名前
title = "分析結果", # タイトル
type ="html")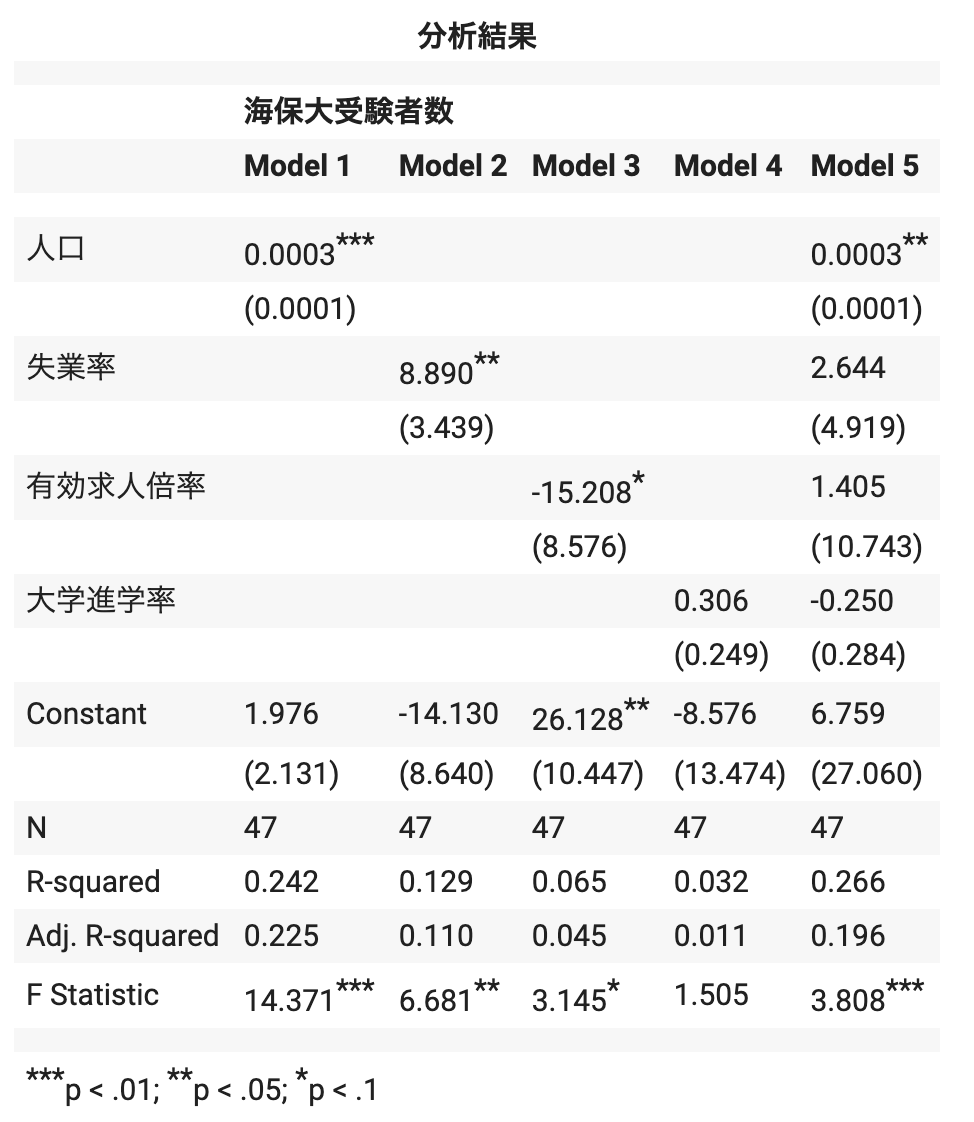
Model 5:推定結果の解釈
\(\hat{jcga}_i=6.759+0.0003\, age18 + 2.64\, jobless +1.405\, joboffer -0.250 \,education\)
(受験者数 \(=6.759+0.0003\, 人口 + 2.64\, 失業率 +1.405\, 求人倍率 -0.250 \,進学率\) )
説明変数のうち、18歳人口(\(age18\))についてのみ、
\(**p<0.01\) → \(p\)値(有意確率=値が0になる確率)が5%以下=「統計的に有意である」
\(n=47\), \(R^2=0.266\)
「欠落変数バイアスを除くためにコントロール変数を追加した結果、18歳人口(説明変数)は、正(プラス)で有意な結果となった。具体的に回帰係数の値から、人口が1人(1単位)増えると0.0003人受験者数が増える可能性が示唆される。
一方で、失業率については他の要因をコントロールしたところ、係数は正であるが有意な結果が示されなかった。このことから、単回帰分析において有意な結果が示されたのは、他の要因が作用することによって引き起こされる欠落変数バイアス(推定値の偏り)が生じていたと解釈することができる。
また、有効求人倍率についても、単回帰分析と比較して、係数の正負が逆になり、かつ、有意な結果が示されなかった。このことから、単回帰分析においては、他の要因が作用することによって引き起こされる欠落変数バイアス(推定値の偏り)が生じていたと解釈することができる。
大学進学率は、単回帰分析と同様で有意な結果とならなかった。係数については正(プラス)の値となっている。大学進学率は、他の要因をコントロールしても\(Y_i(海保大受験者数)\)に影響を与えるかどうかわからない結果となった。」
「決定係数(\(R^2\))については、0.266となっている。」← ここで注意が必要
7.2 自由度調整済み決定係数
重回帰モデルのデータへの当てはまりの良さを評価する指標としては、単回帰モデルのときと同じように決定係数 \(R^2\) を使用する。 しかし、決定係数\(R^2\)には、モデルに含める変数がデータとは無関係な変数であっても変数を増やせば増やすほど1に近づくという欠点がある。
\(R^2=1-\frac{RSS}{TSS}=1-\frac{\sum_{i=1}^{N} \hat{u}_i ^2}{\sum_{i=1}^{N}(Y_i -\overline Y)^2}\)
\(\sum_{i=1}^{N} \hat{u}_i ^2=\sum_{i=1}^{N} (Y_i-\hat Y)^2\)
\(\sum_{i=1}^{N} \hat{u}_i ^2=\sum_{i=1}^{N} (Y_i-\hat{\beta_0}-\hat{\beta_1}x_1)^2\)
モデルに含める変数を増やせば増すほど、
\(\sum_{i=1}^{N} \hat{u}_i ^2=\sum_{i=1}^{N} (Y_i-\hat{\beta_0}-\hat{\beta_1}x_1-\hat{\beta_2}x_2-...-\hat{\beta_i}x_i)^2\)
上式の残差平方和が小さくなる。
つまり、決定係数を求める式の第2項の分子が小さくなるのである。
\(R^2=1-\frac{RSS}{TSS}=1-\frac{\sum_{i=1}^{N} \hat{u}_i ^2}{\sum_{i=1}^{N}(Y_i -\overline Y)^2}\)
したがって、決定係数\(R^2\)は、モデルに含める変数がデータとは無関係な変数であっても変数を増やせば増やすほど1に近づいていってしまう。
なので通常は、モデルに入っている変数の数を調整した自由度調整済み決定係数(adjusted \(R^2\))を使用することが多い。
自由度調整済み決定係数 \(\overline{R}^2\) は、変数の数を調整した尺度であり、以下のように定義される。
\(\overline{R}^2=1-\frac{N-1}{N-k-1}\frac{\sum_{i=1}^{N}\hat{u}_i ^2}{\sum_{i=1}^{N}(Y_i-\overline{Y})^2}\)
\(k\) はモデルに含まれる(定数項以外の)変数の数である。変数の数を増やすと \(\sum_{i=1}^{N}\hat{u}_i ^2\) が小さくなるが、\(\frac{N-1}{N-k-1}\) の項が大きくなるため、変数の数を増やしても必ずしも \(\overline{R}^2\) が大きくなるとは限らない。追加した変数が十分に残差平方和\(\sum_{i=1}^{N}\hat{u}_i ^2\) を減らす場合に限って、\(\overline{R}^2\) は大きくなる。 そのため、重回帰分析の場合にはモデルの当てはまりの尺度としては \(R^2\) よりも \(\overline{R}^2\) のほうが適切であるといわれている。
再度分析結果を確認すると、「\(Adj. R-squared\)」という表記がある。これが、「自由度調整済み決定係数」である。

値を確認すると、「0.196」であり、データに対するモデルの当てはまりが良くないことが示された。
ただし、ここではある説明変数の影響を正しく推定するために重回帰分析を行う、と説明をしてきた。この目的の場合は、 重回帰モデルに含める変数は欠落変数のバイアスを避けるために選ばれるべきであり、結果として選ばれたモデルの決定係数が低くとも、欠落変数のバイアスが回避できているのであれば問題はない。
また、ある変数をモデルに含めるかどうかも欠落変数の観点から判断するべきであって、決定係数を上げる変数でも欠落変数の観点からは適切でない場合もある。
一方で、分析の目的が被説明変数の値の予測である場合は、決定係数は重要な指標になる。モデルの当てはまりが良いということは予測誤差が小さいことを意味するため、決定係数を改善する変数は予測の観点からは重要な変数となるのである。
なので、上の例における重回帰分析の決定係数に解釈については、以下のようになる。
「自由度調整済み決定係数は\(\overline{R}^2=0.196\)となっており、データに対する重回帰モデルの当てはまりが良くないことが示された(被説明変数(受験者数)の変動の約20%しかこのモデルで説明することができない)。ただし、ここでの目的は説明変数の影響を正しく推定するためであり、結果として自由度調整済み決定係数の値が小さくても欠落変数バイアスが避けられているので問題はないといえる。つまり、このモデル(回帰式)の予測精度はあまり高くないが、バイアスの影響を考慮しても18歳人口の影響は否定できないという信頼性の高い結果になっている。
7.4 付録:和演算子の基本的な性質
和演算子は、多くの数の和を含む式を操作するのに便利な速記法であり、統計学や経済学的分析において重要な役割を果たします。 もし \([x_i:i=1,...,n]\) が n 個の数列を表す場合、これらの数の和を次のように書きます。
\(\sum_{i=1}^{n}= x_1+x_2+...+x_n.\)
この定義により、和演算子は次のような性質を持つことが容易に示されます。
Property Sum.1:任意の定数 \(c\)について
\(\sum_{i=1}^{n}c= nc.\)
Property Sum.2:任意の定数 \(c\)について
\(\sum_{i=1}^{n}cx_i= c\sum_{i=1}^{n}x_i.\)
Property Sum.3:\([x_i:i=1,...,n]\)をn組の数の集合とし、a, bを定数とすると
\(\sum_{i=1}^{n}(ax_i+by_i)=a\sum_{i=1}^{n}x_i+b\sum_{i=1}^{n}y_i.\)
また、和演算子ではできないこともあるので注意が必要です。ここでも,\([x_i:i=1,...,n]\)を,各\(i\) について\(y_i\)が 0 ではない n 組の数の集合とするとき、
\(\sum_{i=1}^{n}(\frac{x_i}{y_i})\neq (\frac{\sum_{i=1}^{n}x_i}{\sum_{i=1}^{n}y_i}).\)
つまり、比の和は和の比ではないのです。n 2 の場合、おなじみの初等代数の応用でも、
\(\frac{x_1}{y_1}+\frac{x_2}{y_2} \neq \frac{x_1+x_2}{y_1+y_2}\)
というように、この等比性の欠如が明らかになる。同様に、特別な場合を除き、二乗の和は、和の二乗ではない \(n=2\)のとき \(x_1^2+x_2^2 \neq (x_1+x_2)^2=x_1^2+2x_1x_2+x_2^2\)
n 個の数 \([x_i:i=1,...,n]\) が与えられると、それらを足し算して n で割ることで、その平均または平均を計算します。
\(\overline{x}=\frac{1}{n} \sum_{i=1}^{n}x_i.\)
\(x_i\)が特定の変数(教育年数など)に関するデータの標本である場合、特定のデータ集合から計算されていることを強調するために、これを標本平均(または標本平均)と呼ぶことが多い。
標本平均は、記述的統計量の一例です;この場合、この統計量は、点\(x_i\)の集合の中心傾向を記述します。平均については、重要な基本的な特性がいくつかあります。 最初に、x上の各オブザベーションを取り、ここから平均を引くとする:\(d_i=x_i-\overline{x}\) (ここでの “d”は、平均からの偏差を表す)。そして、これらの偏差の合計は常にゼロです。
\(\sum_{i=1}^{n}d_i=\sum_{i=1}^{n}(x_i-\overline{x})=\sum_{i=1}^{n}x_i-\sum_{i=1}^{n}\overline{x}=\sum_{i=1}^{n}x_i-n\overline{x}=n\overline{x}-n\overline{x}=0\)
したがって、
\(\sum_{i=1}^{n}(x_i-\overline{x})=0\)
Example \(n=5, x_1=6,x_2=1, x_3=-2,x_4=0,x_5=5\)のとき
\(\overline{x}=\frac{1}{n} \sum_{i=1}^{n}x_i=\frac{1}{5}*6+1-2+0+5=2\)
\(\sum_{i=1}^{n}(x_i-2)=0\)
重要なことは、偏差の2乗の和は、2乗\(x_i\)から\(\overline{x}\)の2乗のn倍を引いたものの和であるということです。
\(\sum_{i=1}^{n}(x_i-\overline{x})^2=\sum_{i=1}^{n}x_i^2-n(\overline{x})^2\)
これは、和演算子の基本的な性質を使って示すことができます。
\(\sum_{i=1}^{n}(x_i-\overline{x})^2=\sum_{i=1}^{n}(x_i^2-2x_i\overline{x}+\overline{x}^2)\)
\(=\sum_{i=1}^{n}x_i^2-2\overline{x}\sum_{i=1}^{n}x_i+n(\overline{x})^2\)
\(=\sum_{i=1}^{n}x_i^2-2n(\overline{x})^2+n(\overline{x})^2\)
\(=\sum_{i=1}^{n}x_i^2-n(\overline{x})^2\) \([A.7]\)
2つの変数\([(x_i,y_i):i=1,2,...,n]\)のデータセットが与えられると、次のようになります。
\(\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})=\sum_{i=1}^{n}x_i(y_i-\overline{y})-\overline{x}\sum_{i=1}^{n}(y_i-\overline{y})\)
\(\sum_{i=1}^{n}(y_i-\overline{y})=0\)より
\(\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})=\sum_{i=1}^{n}x_i(y_i-\overline{y})\)
\(=\sum_{i=1}^{n}x_i y_i-\sum_{i=1}^{n}x_i\overline{y}\)
\(=\sum_{i=1}^{n}x_i y_i-n(\overline{x}_i*\overline{y})\)
これは式(A.7)の一般化である.(そこでは、すべてのiについて\(y_i=x_i\))。 平均は,このテキストのほとんどの部分で注目する中心傾向の尺度である. しかし、中央値(または標本の中央値)を使用して中心値を記述することが有益な場合もあります。 n 個の数 \([x_1,...,x_n]\)の中央値を求めるには、まず \(x_i\) の値を小さい順に並べます。 そして,n が奇数の場合,標本中央値は,順序付けられたオブザベーションの中間数である. 例えば、数\((-4,8,2,0,21,-10,18)\)が与えられると、中央値は2となります(順序付き配列は\((-10,-4,0,2,8,18,21)\)なので)。 このリストの最大数である21を2倍の42に変更すると、中央値は2のままです。 対照的に、標本の平均は5から8に増加し、大きな変化となります。
一般的に、中央値は、数字のリストの中の極端な値(大きいか小さいか)の変化に対して、平均値よりも感度が低い。これが、市や郡の所得や住宅価値をまとめる際に、平均ではなく「所得の中央値」や「住宅価値の中央値」が報告されることが多い理由です。nが偶数の場合、中央に2つの数字があるため、中央値を定義する独自の方法はありません。通常、中央値は、2つの中間値の平均と定義されます(再び、小さい方から大きい方へと数字を並べた後に)。このルールを使うと、数の集合\((4,12,2,6)\)の中央値は、\((4+6)/2=5\)となります。
# References {-}