Chapter 4 Rによるデータ分析②

データから因果関係を見極めることは非常に難しい。その理由としては、主に以下の3つの理由があるとされている XとYのデータの動きに関連性がある場合（つまり、XとYに相関関係がある場合）に起こりうる３つの可能性を図示している。

1. XがYに影響を与えている可能性

2. YがXに影響を与えている可能性

3. VがXとYのそれぞれに影響を与えている可能性

分析者にとって厄介なのは、XとYの相関関係を観測しただけでは、３つの可能性のうちどれが本当に起こっているのか判定ができないことである。そこで、統計学や経済学の知識を活用し「因果関係」の見極めを行っている。

以下では、データから因果関係を導き出すステップを紹介する。

4.1 STEP.1 仮説の設定

分析を行う際には、必ず何らかの理論的背景を必要とする。理論モデルや分析者の問題意識などから導出された仮説を検証するために、必要なデータを収集し、適切な分析を行うというスタンスが重要。分析によっては厳密な理論が対応しないこともあるが、そうした場合でも、少なくとも概念やロジックなど、客観的に納得できる仮説を設定する必要がある。 →この仮説の設定に役立つのが「経済学」である。

この大原則に基づいて、個人や企業、国の行動を定式化し、経済モデルを構築している。当然、人間の思考や行動というのは複雑なので、物理学並の精度で数式から行動を予測することは不可能。ただし、個人が幸福を最大化するための選択をするという仮定（効用最大化）を置くことによって、因果関係について重要な示唆を与え、この前提に基づく研究の積み重ねが社会の発展・経済の発展に大きく寄与している実績がある。

経済学の数理モデルを使った分析は、物理学並みの制度で人間行動をピタリと表すものではないが、単純化の仮定を置いて議論を見やすくし、結果として現実問題の本質的な一面を見抜くために役立つ。

この経済学の発展に大きく貢献した人物が”Gary Becker(ゲイリー・ベッカー)“である。

ベッカー氏は、従来、金銭や経済的問題にだけを分析してきた経済学の適用範囲を、人間行動のあらゆる側面を合理的選択の結果と解釈することで人間行動の説明を可能にした。

この「ベッカー理論」が、教育、職場訓練、人材育成・労務管理、人口問題、差別、結婚、離婚、虐待、信仰、犯罪、麻薬、など人間行動の様々な問題を理論的・実証的に分析して、現実の社会を変える発見や、政策形成など幅広く影響を与えた。

Example.9　ベッカーの犯罪行動理論モデル

1968年の論文の中で、個人の犯罪への参加を説明するために効用最大化の枠組みを応用した。犯罪者が犯罪を行うことによる便益と費用を比較検討して、便益が費用を上回る場合に犯罪を行うこと決定するという一種の資源配分として、理論モデルを組み立てている。

この関係を定式化すると次のような関数で表現することができる。

※経済理論ではよくあることであるが、関数 f(-)については具体的にどのような関数形であるかは指定されていない。効用最大化の枠組みでのみ構成されている。

ただこの経済理論があるおかげで、各変数が犯罪活動に与えるであろう効果を予測することができ、犯罪行動のメカニズムについて大きな示唆を得ることができる。後発の犯罪行動に関する理論的および実証研究は、ほとんどがこのモデルをベースとしている。

4.1.1 海上保安庁（国家公務員）への入職行動に関する理論モデル

先行研究のまとめ

一般に公的セクターへの入職行動については、失業率や官民賃金格差などの経済要因が負の影響を与える（不況時に入職希望者が増加する）ことがわかっている。

Krueger (1988) は、アメリカ合衆国連邦政府の求人に対する外部からの応募者数と応募者の質（応募時の保有資格で評価）の決定要因について、 Office of Personnel Management’s Open Competitive Appointment System（人事管理局の公開競争型指名制度）の時系列データ、クロスセクションデータ、パネルデータを用いて検証している。主要な結果として、政府職員の平均賃金が民間労働者の平均賃金に比べて上昇するにつれて、政府の求人への応募率が上昇し、政府と民間企業の収入格差の拡大は、政府の求人に対する応募者の質向上と関連しており、政府職員の相対的な平均賃金が上昇すると、資格を保有する求職者の比率が高まることを示した。

日本においてもこれに類似する研究があり、猪木・勇上 (1998) は、『公務員白書』の公務員競争率に関するデータを用いて、国家公務員の区分（第I 種、第II 種、第III 種）ごとの入職行動の決定要因を経済的観点から分析している。結果をみると、すべての区分で官民の賃金格差が入職行動に有意な関係にあり、とくに第III の競争率が官民賃金格差に強く反応することが示され、公共部門への入職行動については、経済状況や雇用状況に影響を受けることが示唆される。

一方で、近年の動向をみると、経済変数だけではなく通常は観察できない個人属性に係る変数について関心が持たれる傾向にある(勇上・佐々木, 2013)。Hanna and Wang (2017)は、政府の仕事に応募する個人の特性に着目し、インドの大学生および公務員（看護師）を対象にした実験と調査のデータを用いて検証を行なっている。具体的は、7 つの大学の最終学年に在籍する 669 人の学生を対象にサイコロを 42 回振ってもらい、出た目の数だけ報酬が増えるというものである。実際、個人が嘘をついたかどうかは確実に把握することはできないが、各個人の報告される分布が一様分布からどの程度離れているかを利用し、「不誠実」な特性と公務員志望の関係を測定した。結果、不誠実な行動が疑われる学生は、政府の仕事を希望する傾向があることが示された。また、実際に公務員という職についている看護師の欠勤データと前述のサイコロの実験を用いて、不誠実な特性は「汚職（不正欠勤）」に繋がるのかも検証しており、サイコロの出た目の虚偽申告が疑われる職員は、それ以外の職員よりも不正欠勤をする傾向があることが示された。

他方、Barfort et al. (2019) は、公共部門の汚職や不正行為が少ない国であるデンマークに焦点をおき、大学生を対象とした調査実験から、不正行為が少なく正直さが高い学生ほど公務員への入職を好む傾向があることを明らかにしている。具体的には、コペンハーゲン大学の法学、経済学、政治学の学部生863名を対象として、サイコロの出目を推測し当たれば報酬を受け取れるゲームを実施した。実際に推測が当たったかどうかについては、学生自身しか分からないため、不正に勝つことが選択肢として与えられており、Hanna and Wang (2017) と同様に各個人の報告される分布が一様分布からどの程度離れているかを利用し、「不誠実」な特性と公務員志望の関係を測定した。結果、公務員志望者は、不正行為を行う確率がそれ以外の者より 10 ％少ないことが示された。また、独裁者ゲームの結果から、多額の寄付をする向社会的志向を持つ学生は、系統的により正直であり、公務員のキャリアを好む傾向があることも示された。これらから国や地域における汚職の程度、制度的構造の違いにより、公共部門の職業に携わる、また、志望する人の特性は異なることが予想される。

このように、最近では経済要因だけではなく経済外的要因（教育水準、遺伝、誠実さ、親の職業、愛国心、名誉心など）への関心が高まっている。特にPSM（Public Sector Motivation)と呼ばれる個人の内発的動機が着目されており、通常は観察不可能な個人の変数をいかに数値に落とし込んで入職行動への影響を評価するかの議論が展開されている。

⇒ ここから理論モデルが組み立てられる（仮説として、影響を与えそうな変数が選定される）。

\(y=f(x_1,x_2,x_3,x_4,x_5,.....)\)

　　\(y =\) 公務員への入職行動

　　\(x_1=\) 失業率

　　\(x_2=\) 官民賃金格差（所得差）

　　\(x_3=\) 教育水準

　　\(x_4=\) 誠実さ

　　\(x_5=\) 親の職業

　　\(x_6=\) ……

　　\(x_7=\) ……

4.2 STEP.2 分析モデルの構築

理論はあくまでも理論なので、この理論を実際のデータを使用し、因果関係について検証できるような枠組みに変換する必要がある。

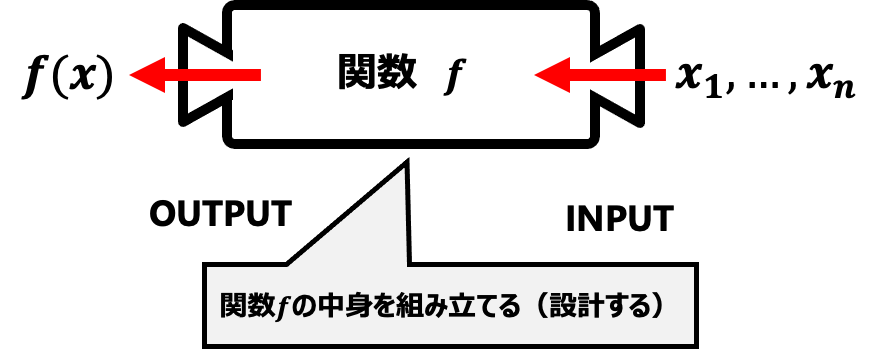
4.2.1 線形回帰分析

データを用いてある変数（事象）間の関係性を計測する手法の一つに回帰分析（ regression analysis）がある。

例えば、横軸（\(X\)軸）に失業率、縦軸（\(Y\)軸）に犯罪率をとりデータをプロットすると上図のような右肩上がりな傾向が示された。このプロットの傾向を式で表す一番良い線（モデル）を当てはめると多くの場合、

例：　\(Y\)（犯罪率） = \(\beta_0\) + \(\beta_1\) \(X\)（失業率）

という線形関係で式を組み立てることができる。これは\(X\)の変化によって\(Y\)がどの程度変化するのかを直線関係で捉えている。この式を線形回帰モデルという。

この式では、左辺（被説明変数）にある犯罪率が、右辺にある失業率（説明変数）によって説明されることを示している。

\(\beta_0\)と\(\beta_1\)は、パラメータ（回帰係数）とよばれ、実証分析では、これらパラメータをデータから推定することが主たる目的となる。このパラメータを求めることで、失業率に応じてどの程度犯罪率が増減するかといった法則性が見いだせる。

ただ、現実のデータでは、この法則性がそのまま反映されることはなく、必ずノイズが生まれる。

上図の推定式に誤差を含めているのはこのためで、法則性に誤差を加えた推定式によってデータが正しく描写され、法則性によって説明できる部分とノイズによる誤差の部分とに分けることができる。

実際のデータでは、\(Y\)と\(X\)が完全な直線関係にあることは滅多にない

• \(Y\)が、データの収集や記録の際に生じる誤差に影響される
• \(Y\)が、\(X\)以外の要因に依存していることが多い

そこで、そういった多少の乖離はあるものの２つの変数の関係が およそ直線で表されるとき、次のように書くことができる

\(Y=\beta_0+\beta_1X+u\) (1)

右辺の\(u\)は直線からの乖離の大きさを表し、これを誤差項と呼ぶ。 この\(Y\)と\(X\)について、は分野によって様々な呼び名がある。

Y	X
従属変数（Dependent variable）	独立変数（Independent variable）
被説明変数（Explained variable）	説明変数（Explanatory variable）
応答変数（Response variable）	コントロール変数（Control variable）
Predicted variable	Predictor variable
Regressand	Regressor

計量経済学で頻繁に使われるのは、“従属変数”、“独立変数”。

一般的に使われるのは、“被説明変数”と”説明変数”。

※右辺に代入するデータは、左辺と同時点もしくは左辺より過去の時点のものを使用する。

Example.9　ベッカーの犯罪行動分析モデル

犯罪行動の理論モデル（1968年）を分析のできる形（分析モデル）に変換する。

→　実証分析を行う前に、関数f(-)の形を指定する。

※上のベッカーの分析モデルも線形回帰モデルの一形態である。

理論（仮説）に基づき、影響を与えそうな変数が選定して、実際に入手できるデータをベースに分析モデルを組み立てことになる。

ただ、ここでは観測できない変数をどう扱うかが問題になる。

例えば、ある人が犯罪行為で稼げる賃金を考えてみる。このような変数は理論的には定義されているが、個々人についてこの賃金を観測することは不可能ではないにしても困難。また、逮捕される確率のような変数も、個々人について得ることは現実的に困難。

ただ、少なくとも逮捕に関連する統計を観測し、逮捕される確率に近似した変数を導出することはできる。他にも多くの要因が犯罪行動に影響を与えているが、それを全てリストアップすることはできず、観察することもできないが、何らかの形でそれらを説明できる変数を見つけ出す必要がある。

このように工夫をすることで、データから理論を検証できる分析モデルを設定することが可能になる。

ここで求めたい未知の定数は\(\beta_i\)（パラメータ）である。この\(\beta_i\)（パラメータ）を求めることにより、犯罪行動に影響を与える各変数の影響度合いを測ることができる。

犯罪行動の理論からは、例えば、\(\beta_i<0\)（平均刑期）、つまり通常は平均刑期が上がると犯罪行為の頻度は下がることが導かれる。これは重要な質的情報ではあるが、具体的に、平均刑期が１年下がると、犯罪行為の頻度がどれだけ増加するのかといった数量的な情報は与えてくれない。 つまり経済理論では、犯罪行為の増減に関する定性的な議論をすることはできても、定量的な議論をすることは難しい。そこで、定量的な議論を進めるために、実証モデルを使用して、実際の犯罪行為の頻度や平均刑期に関する観察データから、未知のパラメータ（係数＝傾き）を求めて、定量的な結果を得ることが必要になる。

\(u\) (誤差項)には、犯罪活動で得られる賃金、性格、家族背景、逮捕の確率などの観測されていない要因が含まれている。兄弟の数や両親の学歴などの家族背景変数をモデルに追加することができるが、この\(u\) (誤差項)を完全に排除することはできない。この誤差項の扱いは、すべての実証分析において最も重要となる。

4.3 STEP.3 データの選定

説明変数に当てはめるデータを選定する。

データの種類

• クロスセクションデータ：一時点における多くの主体の情報を収集したデータ（横断面データ）

• 時系列データ：一定時間の間隔で情報を収集したデータ

• パネルデータ：クロスセクションデータで収集した情報を時系列でも追跡し収集したデータ

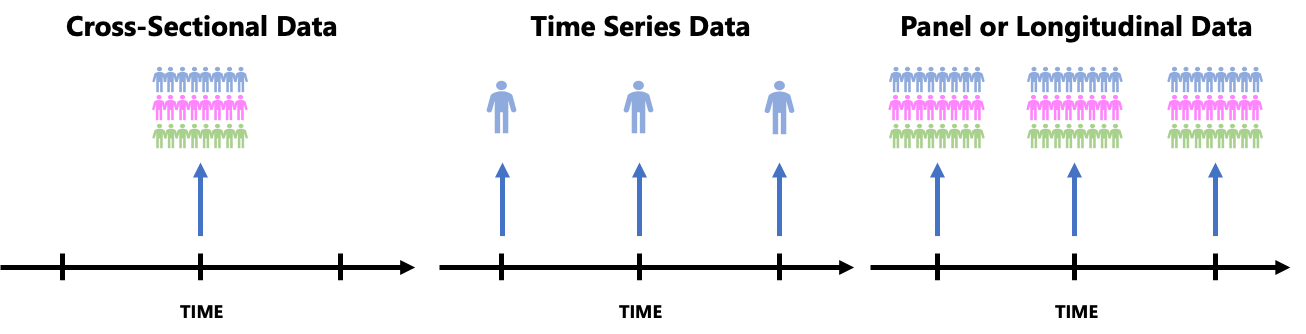
ここでは、2021年の海上保安大学校受験者と18歳人口の関係について分析を行うこととする。

\(jcga=\beta_0+\beta_1 age18 +u,\)

\(jcga\)：各都道府県における海保大校受験者数（単位＝人）

\(age18\)：各都道府県における18歳人口（単位＝千人）

\(u\)：誤差項

	説明	出典
海保大受験者数（人）	各都道府県ごとの第１次試験受験者数（2021年）	海上保安庁
18歳人口（人）	各都道府県に居住する18歳の人口（2021年）	文部科学省：学校基本調査

4.4 STEP.4 予備的分析

データが準備できたら、パラメータの推定を行う前に、エクセルや統計ソフトなどを用いて、利用するデータの特性を把握するための予備的分析を行う。

予備的分析では、まず、データの平均値、標準偏差、最大値、最小値などの基本統計量（記述統計量）を確認することが一般的で、分析に用いるデータの概観を確認する。また、被説明変数を縦軸、説明変数を横軸にとり、それぞれの組み合わせをプロットする散布図を示すことも一般的である。

まずは、データの準備、記述統計量の出力や分析に使うパッケージのインストールを行う。

セッションがタイムアウトとなり前回アップロードした「bunseki1.xlsx」が消えている場合は、再度デスクトップに保存したデータをColabにアップロードする。左タブにあるフォルダのアイコン（🗂）をクリックしフォルダを開く。その中に、分析用データ「bunseki1.xlsx」をドラッグ&ドロップしコピーする。

このとき、Colabのノートブックを新規作成した場合は、「Colab上でのRの実装手順」を再度実行する必要があるので注意してください。

1. 「ファイル」＞「ダウンロード」＞「.ipynbをダウンロード」をクリック

2. ダウンロードしたものをデスクトップへ保存

3. 保存したファイルを「メモ帳」で開く

4. 中身の書き換え

   “kernelspec” にある name と display_name を以下のように書き換える。

   “kernelspec”: {

   　　　　　　　　“name”: “ir”,

   　　　　　　　　“display_name”: “R”

   　　　　　　　}

5. Colabに戻り左上にある「ファイル」から「ノートブックをアップロード」をクリック

6. 先ほど上書き保存したファイルをアップロード（ドラッグ&ドロップ）

7. ランタイムのタイプが「R」になっていればOK

次に分析に必要なパッケージの読み込みを行う。

library(tidyverse)
library(readxl)

このほかにもstargazerというパッケージも利用するため、インストール及び読み込みを行う。

install.packages('stargazer')
library(stargazer)

アップロードしたデータの読み込みと確認を行う。

bunseki1 <- read_excel("bunseki1.xlsx")
View(bunseki1)

4.4.1 記述統計量の確認

どんな計量分析においても、まずはデータの特徴を掴むために記述統計量の確認が行われる。 データの平均値や、最大値・最小値、どのくらい偏りがあるのか（分散）を数値から把握する。 stargazerで記述統計の表を出力する。

stargazer(as.data.frame(bunseki1), 
          type = "html", 
          title = "記述統計", 
          digits = 2)

出力された以下のhtmlテキストをコピーする。

<table style="text-align:center"><caption><strong>記述統計</strong></caption>
<tr><td colspan="6" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">Statistic</td><td>N</td><td>Mean</td><td>St. Dev.</td><td>Min</td><td>Max</td></tr>
<tr><td colspan="6" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">観測番号</td><td>47</td><td>24.00</td><td>13.71</td><td>1</td><td>47</td></tr>
<tr><td style="text-align:left">年</td><td>47</td><td>2,021.00</td><td>0.00</td><td>2,021</td><td>2,021</td></tr>
<tr><td style="text-align:left">海保大受験者数</td><td>47</td><td>7.83</td><td>11.43</td><td>0</td><td>75</td></tr>
<tr><td style="text-align:left">18歳人口</td><td>47</td><td>22,393.38</td><td>21,519.57</td><td>4,844</td><td>98,235</td></tr>
<tr><td colspan="6" style="border-bottom: 1px solid black"></td></tr></table>

次のチャンクでは、コードではなくテキストを追加する。

先ほどコピーしたhtmlテキストを貼り付けると整理された表が出力される。

記述統計量の数値を確認する。

１都道府県あたり海保大を受験する者は平均（mean）で7.8人。ただし標準偏差（St.Dev.）が11.4人であることから都道府県によってバラツキが大きいことが読み取れる。最大値（Max）75人、最小値（Min）0人の数値からもその傾向が窺える。

都道府県の18歳人口についても同様で、平均（mean）22,393人で標準偏差（St.Dev.）が21,520人であることから都道府県によってバラツキが大きいことが読み取れる。最大値（Max）98,235人、最小値（Min）4,844人の数値からもその傾向が窺える。

4.4.2 ヒストグラムと散布図の確認

次に、データ処理を行いやすいように変数名（列名）を日本語からアルファベット表記に変更する。 そのまま日本語で処理を行っていも良いが、コンピュータは日本語を理解するのが苦手なのでエラーが起きやすい。 変更する際は、自身が認識できるアルファベットの羅列であれば何でも良い。

colnames()で変数名（列名）を確認。

colnames(bunseki1)

names()で変数名（列名）を変更。c( )は、『Combine Values into a Vector or List』を意味する関数であり、引数に渡したオブジェクトをベクトルかリストの形式で結合してくれる関数のことである。文字や数字の行を鎖状に繋げ、行ベクトルにすると理解しておくとよい。names()とc( )を組み合わせることで、変数名を設定することができる。数学の行列と同じ考え方で、列（変数）の数と行（c( )の中身）の数を等しくしなければエラーが起きるので注意。

names(bunseki1) <- c("num", "year", "area", "juken", "age18" )

それでは、ヒストグラムと散布図を描いていく。記述統計量は数値（平均値、標準偏差、最大値、最小値）でしか、特徴を把握することができない。そのため、分析を行うにおいてはグラフなどを用いてその全体像を把握することがよく行われる。自身が扱うデータに詳しくなることが、因果推論においては非常に重要となる。

まずは、ヒストグラム（度数分布図）を描いてみる。ヒストグラムは、あるデータを区間ごとに区切り、各区間の個数や数値のばらつきを表現する際に用いられるグラフである。

Googleの混雑状況を表すグラフをイメージしてもらうと理解しやすい。

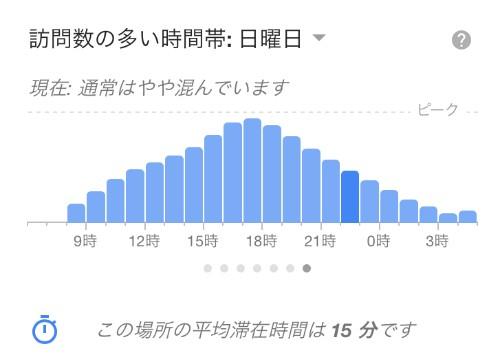
ヒストグラムにすることで、データがどのようにばらついているか把握しやすくなり、データの特徴を視覚的に理解することができる。

早速、海保大受験者のヒストグラムを描いてみる。

hist(bunseki1$juken)

もう少し見やすく装飾してみる。

hist(bunseki1$juken, 
     breaks=seq(0,80,5), 
     xaxp=c(0, 80, 10), 
     main="Histogram", 
     xlab="海保大受験者数", 
     ylim=c(0,30), 
     col="lavender")

histには様々なオプションが用意されており、それらを用いるとより綺麗なグラフが描ける。breaksでは引数にベクトルを読み込むことでヒストグラムの横軸の範囲と分割の幅 (bin) を指定できる。すなわち、ヒストグラムの階級数と階級幅を変えるオプションであり、ここでseq(0,80,5)を指定すると 0 から80までの範囲を5ずつbin分けしたヒストグラムを描くことができる。xaxpでは、x軸の両端の目盛の座標系上の位置と間隔の数を指定する。main ではグラフのタイトルを指定する。xlabではX軸の名前を指定する。ylimにはベクトルを指定することで、Y軸の範囲を指定する。col には色名を指定することでヒストグラムのバーの色を指定できる。

→　文字化け発生。フォントをインストール（CJK）。

system("apt-get install -y fonts-noto-cjk")
systemfonts::system_fonts()

familyを指定して再度グラフを出力する。

hist(bunseki1$juken, 
     breaks=seq(0,80,5), 
     xaxp=c(0, 80, 10), 
     main="Histogram", 
     xlab="海保大受験者数", 
     ylim=c(0,30), 
     col="lavender", 
     family= "Noto Sans CJK SC")

ヒストグラムから都道府県あたりの受験者は8人（平均7.8人）以下の分布に偏っていることがわかる。

同様に18歳人口のヒストグラムを描いてみる。

hist(bunseki1$age18)

横軸の目盛りについて、桁数が多いため指数表示e+されていてわかりにく。 単位を万人に変換（数値÷10000）、桁数を少なくする。

hist(bunseki1$age18/10000)

hist(bunseki1$age18/10000, 
     breaks=seq(0,10,1), 
     xaxp=c(0, 10, 10), 
     main="Histogram", 
     xlab="18歳人口（万人）", 
     ylim=c(0,20), 
     col="lavender", 
     family= "Noto Sans CJK SC")

海保大受験者と同じように右の裾野が広い分布になっている（山の形が似ている）。 次に、散布図（Scatter plot）の作成を行う。 散布図とは、縦軸と横軸に量や大きさを取り、データを当てはまる所にプロットをしたグラフのことをいう。 プロットとは、点を描くことを指す。２つの変数に関係があるかどうか（相関の有無）を、点の散らばりから確認することができる。 tidyverseのggplotを用いて18歳人口（x軸）と海保大受験者数（y軸）の散布図を描いてみる。

ggplot((bunseki1), aes(age18, juken)) +
  geom_point() +
  labs(x = "18歳人口", y = "海保大受験者数",
       title = "海保大受験数と18歳人口の散布図") 

何となく正の相関関係があるようにみえる。

点（geom_point）ではなく、都道府県名（geom_text）でプロットしてみる。

ggplot((bunseki1), aes(age18, juken)) +
  geom_text(aes(y = juken + 0.2, label = area), size = 4, vjust = 0) +
  labs(x = "18歳人口", y = "海保大受験者数",
       title = "海保大受験数と18歳人口の散布図") 

4.5 STEP.5 パラメータの推定

予備的分析でデータの特性を把握したら、回帰分析を実施し、パラメータの推定を行う。 このパラメータの推定というのは、予備的分析で作成した散布図で考えると、プロットの中心付近に一本の線を引くことを意味する（後述）。この引かれた直線のことを回帰直線という。 回帰直線の描き方はさまざまあるが、一般的には、各プロットにできるだけ近い直線を引くことが望ましいとされている。この推定方法を最小二乗法(Ordinary Least Square; OLS)という。これにより、\(\beta_0\)や\(\beta_1\)といったパラメータ（係数）が推定が可能になる。実証分析において、最も頻繁に用いられる推定方法が、この最小二乗法になる。

この式を単回帰モデルという。添字の \(i\) は、\(i\) 番目の観測値であることを示す。

このとき、\(\beta_0\) と \(\beta_1\) を回帰係数（パラメータ）といい、これらの値を実際に求めることが回帰分析の主要な目的となる。

もちろん、すべての点を通る直線を引くことはできないけれども、見たところ当てはまりの良い直線が引かれている。これは、最小２乗法（Ordinary Least Squares; 以下、OLS) と呼ばれる方法で引かれた直線であり、各点とのズレが平均的にできるだけ小さくなるように定めたものになる。

図中の赤線は、単回帰モデルにおける \(\beta_0\) と \(\beta_1\) の値についてOLSを用いて求めた結果であり、 推定回帰式（線）という。これは次の式で表すことができる。

\(\hat{Y}_i=\hat{\beta}_0+\hat{\beta}_1 X_i\)

\(\hat{\beta}_0\) と \(\hat{\beta}_1\) は、\(\beta_0\) と \(\beta_1\) の推定値という。\(\hat{Y}\) は、「ワイハット」とよみ、次図で示すように、観測値 \(Y\) に対応した推定回帰線上の値であって、\(Y\) の予測値（あるいは理論値）という。

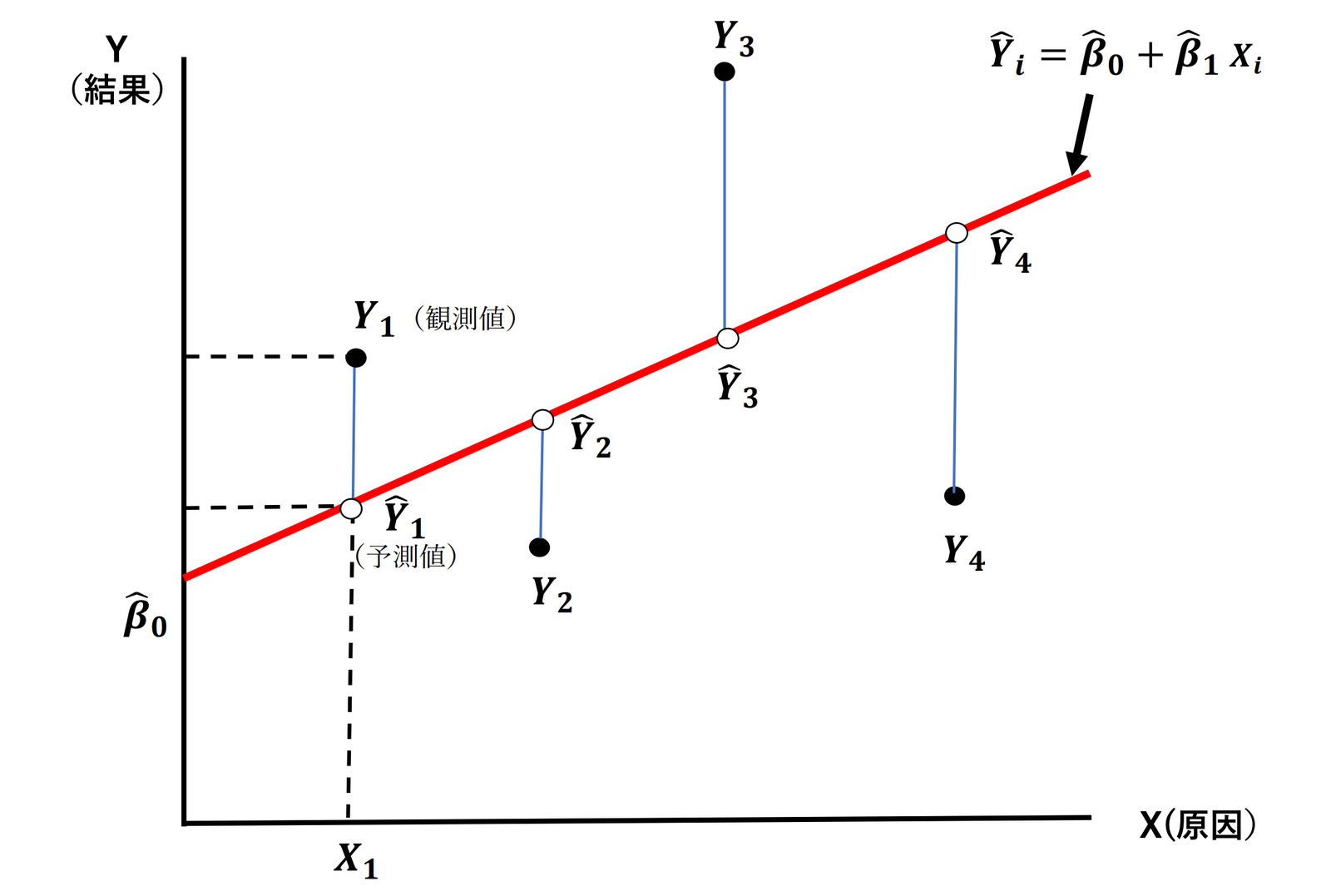
つまり、OLS推定量を用いることで、第 \(i\) データの \(Y\) の値を予測することができる。

第 \(i\) データの \(Y\)$ の値は \(Y_i\) とわかっているのに、なぜいまさら予測という言葉を使うのか？

• ここでいう予測とは、「\(X=X_i\) の個体は平均的には \(\hat{Y}\) の値を持つことが予想される」という意味。
• 言い換えれば、もう１つ観測値が得られて、\(X\) の値が再び \(X_i\) だった場合の \(Y\) の値を予想したもの。

では、この\(\beta_0\) と \(\beta_1\) の推定値（\(\hat{\beta}_0\) と \(\hat{\beta}_1\)）をどのようにして求めるか？

4.5.1 パラメータの算出

POINT: 「観測値」と「予測値」の差である「残差」

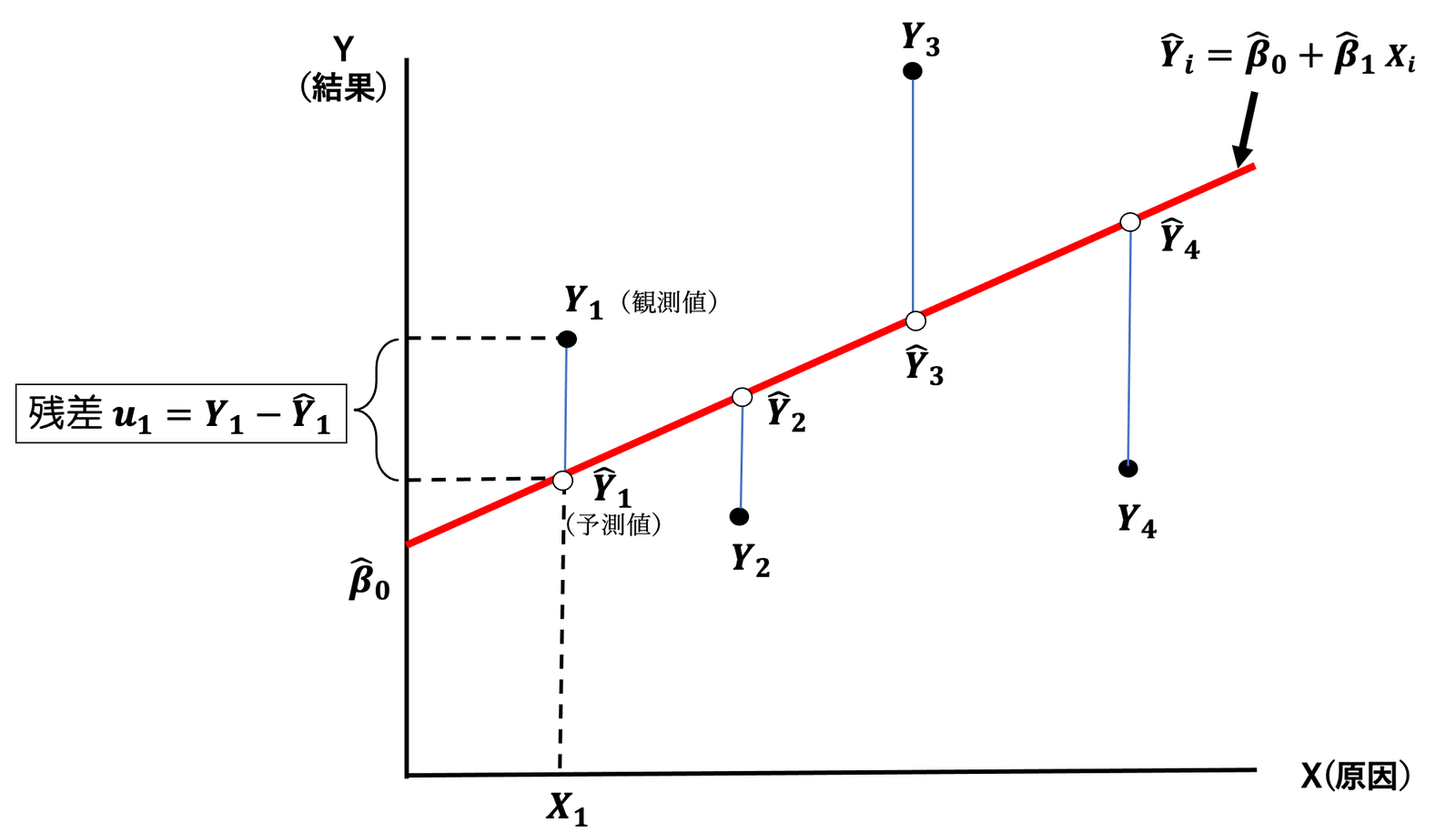
この残差は、

\(\hat{u}_i=Y_i-\hat{Y}_i=Y_i-\hat{\beta}_0-\hat{\beta}_1 X_i\)

という式で表すことができる。また上の式は、

\(Y_i=\hat{Y}_i+\hat{u}_i\)

と変形できるので、\(\hat{Y}_i\) と \(\hat{u}_i\) はそれぞれ \(Y_i\) の水準のうち、\(X_i\) で説明できる部分とできない部分に分解したものと理解することができる。 ちなみに予測値と残差にも ” \(\hat{}\) ” （ハット）を用いるのが通例である。これは \(\hat{\beta}_0\) , \(\hat{\beta}_1\) を代入して計算したものという意味合いである。

先述のなかで、最小２乗法（Ordinary Least Squares; 以下、OLS) は、各点とのズレが平均的にできるだけ小さくなるように引かれた直線であることを確認

つまり、各点との「残差」が最小となるように\(\hat{\beta}_0\) 、\(\hat{\beta}_1\)を推定する方法が、最小２乗法（OLS)の原理である。

4.5.2 †参考：残差２乗和の最小化問題

残差を最小にする→　残差の「和」が最小なるような直線式を求めればいい。 つまり、

\(\sum_{1}^{N} \hat{u}_i=\sum_{1}^{N} (Y_i-\beta_0-\beta_1 X_i)\)

ができるだけ小さくなるように（\(\hat{\beta}_0\) , \(\hat{\beta}_1\)）を算出すれば良い。 しかし、これでは点と直線の平均的なズレを小さくすることはできない。

→　直線より下にある点のズレはマイナス、上にある点のズレはプラスになるので、うまく打ち消しあってしまう。この場合、和がゼロになるような直線は無数に引くことができる。

なので、単純な和ではなく、残差の２乗和（残差２乗和）が最小になるような直線式を求めればよい。

つまり、

\(\sum_{1}^{N} \hat{u}_i^2=\sum_{1}^{N} (Y_i-\beta_0-\beta_1 X_i)^2\)

が最小になるような条件を求めることで、上記問題が解消され（\(\hat{\beta}_0\) , \(\hat{\beta}_1\)）の1つの解を算出することができる。

参考動画

https://www.youtube.com/watch?v=Zz1sgYxrA-k&t=1s

残差2乗和を最小化するための1階の条件は、上式を未知数である\(\hat{\beta}_0\) , \(\hat{\beta}_1\)でそれぞれ偏微分した値がゼロとおくことによって導くことができる。 すなわち、

\(\frac{\partial \sum \hat{u}_i}{\partial \hat{\beta}_0}=-2\sum_{1}^{N}(Y-\hat{\beta}_0-\hat{\beta}_1 X)=0\)

\(\frac{\partial \sum \hat{u}_i}{\partial \hat{\beta}_1}=-2\sum_{1}^{N} X(Y-\hat{\beta}_0-\hat{\beta}_1 X)=0\)

という２つの式が得られ、両式を整理すると以下の連立方程式を導出できる 。 \(\begin{cases} \sum Y = N\hat{\beta}_0+\hat{\beta}_1 \sum X \\ \sum XY =\hat{\beta}_0 \sum X+\hat{\beta}_1 \sum X^2 \end{cases}\)

この連立方程式を正規方程式という。 次に、この方程式を未知数である\(\hat{\beta}_0\) , \(\hat{\beta}_1\)について解くと、

\(\hat{\beta}_1=\frac{N \sum XY-\sum X \sum Y}{N \sum X^2-(\sum X)^2}\)　 　 ←　\(\frac{\sum Y}{N}=\overline{Y}\)（\(Y\)の平均値）, \(\frac{ \sum X}{N}=\overline{X}\) （\(X\)の平均値）

\(=\frac{N \sum XY-(N \overline{X})(N \overline{Y})}{N \sum X^2 -(N \overline{X})^2}\)　 　←　\(\sum X =N \overline{X}\), \(\sum Y =N \overline{Y}\) より

\(=\frac{N \sum XY- N^2 \overline{X}\, \overline{Y}}{N \sum X^2 -N^2 \overline{X}^2}\)

\(=\frac{ \sum XY- N \overline{X}\, \overline{Y}}{ \sum X^2 -N \overline{X}^2}\)　 ←　分子、分母を \(N\) で割る

ここで、分子：\(\sum XY-N \overline{X} \, \overline{Y} =\sum (X-\overline{X})(Y-\overline{Y})\) 、分母：\(\sum X^2 -N \overline{X}^2= \sum (X-\overline{X})^2\)　より

\(=\frac{ \sum (X-\overline{X})(Y- \overline{Y})}{ \sum (X -\overline{X})^2}\)
　　　　　　　　　

\(\hat{\beta}_0=\frac{ \sum X^2\sum Y-\sum X \sum XY}{N \sum X^2-(\sum X)^2}\)

\(=\frac{ \sum Y- \hat{\beta}_1 \sum X}{N}\) ←　\(\frac{\sum Y}{N}=\overline{Y}\), \(\frac{ \sum X}{N}=\overline{X}\) より

\(=\overline{Y}-\hat{\beta}_1 \, \overline{X}\)

結果をまとめると、最小2乗推定量（OLS推定量）は次式で求めることができる。

\(\begin{cases} \hat{\beta}_1=\frac{ \sum (X-\overline{X})(Y- \overline{Y})}{ \sum (X -\overline{X})^2} \\ \hat{\beta}_0=\overline{Y}-\hat{\beta}_1 \, \overline{X} \end{cases}\)

4.5.3 計算例

Example 失業率と自殺者数

次の図は、日本における失業率（％）と自殺者数（人口１０万人あたり）の推移（1975－2017年）をグラフ化したものである。

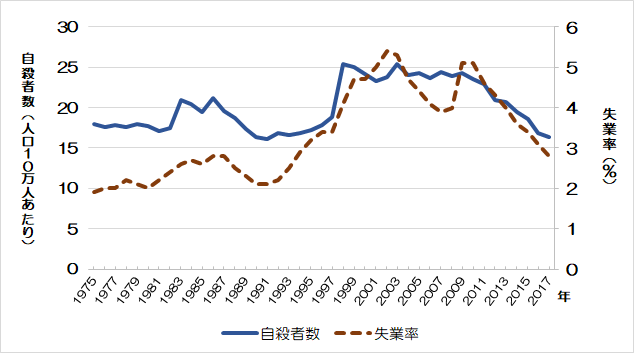
→　関係性のある動きをしている（※説明の都合上、より厳密な因果関係の立証は省略） →　２つの変数の関係性を単回帰モデルで推定する

\(Y=\beta_0+\beta_1X+u\)

ここでは、以下の表のデータを得られたとする。

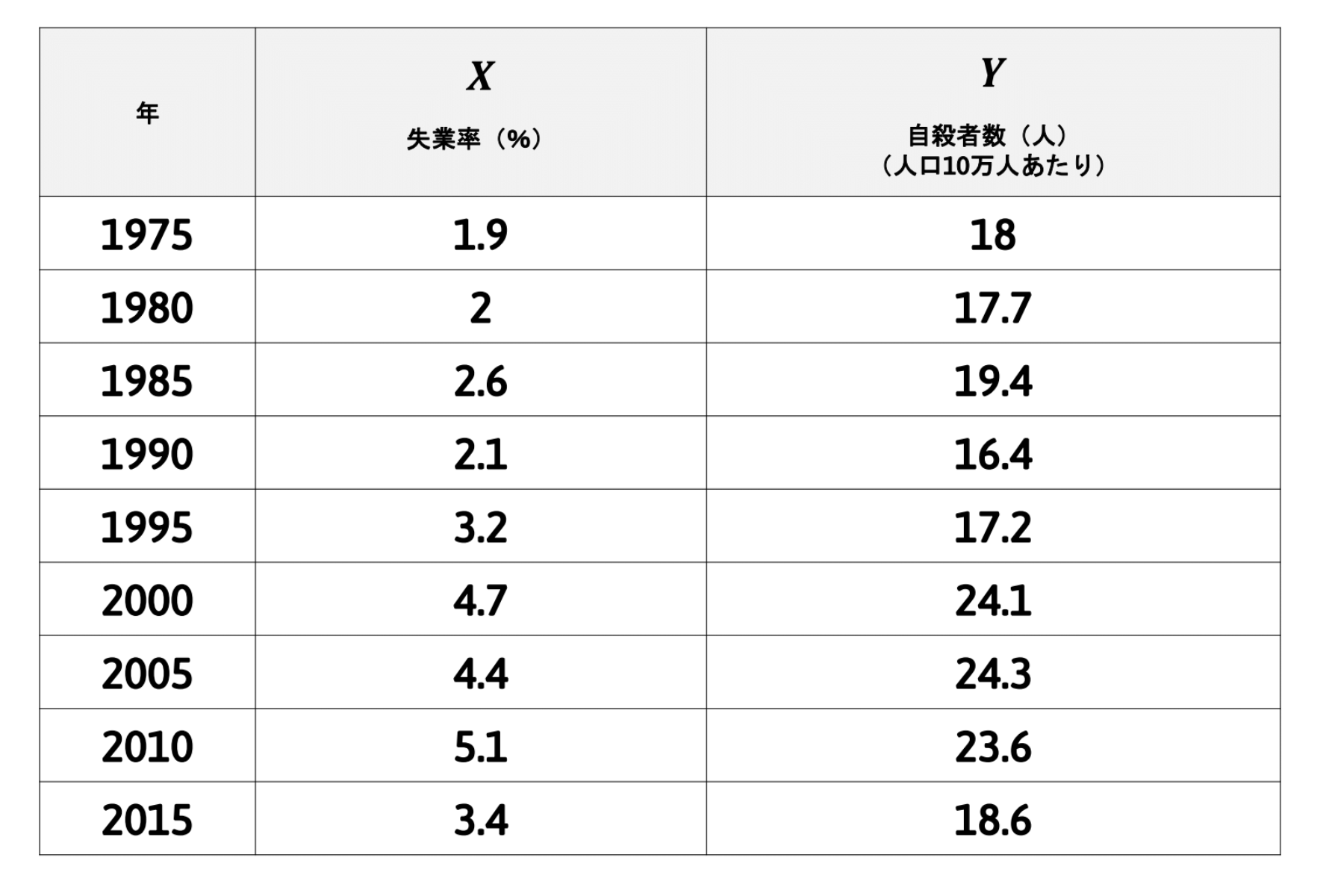
\(Y=\beta_0+\beta_1X+u\) （自殺率 = \(\beta_0\) + \(\beta_1\) 失業率 + 誤差）

最小2乗推定量（OLS推定量）は次式で求めることができるので

\(\begin{cases} \hat{\beta}_1=\frac{N \sum XY-\sum X \sum Y}{N \sum X^2-(\sum X)^2}=\frac{ \sum (X-\overline{X})(Y- \overline{Y})}{ \sum (X -\overline{X})^2} \\ \hat{\beta}_0=\frac{ \sum Y- \hat{\beta}_1 \sum X}{N}=\overline{Y}-\hat{\beta}_1 \, \overline{X} \end{cases}\)

表計算から、値を代入して、\(\hat{\beta}_0\) , \(\hat{\beta}_1\)を算出すると、

\(\hat{\beta}_1=\frac{N \sum XY-\sum X \sum Y}{N \sum X^2-(\sum X)^2}\) \(=\frac{(9)(613.31)-(29.4)(179.3)}{(9)(108.04)-(29.4)^2}\) \(=\frac{248.31}{108}\) \(=2.30\)

\(\hat{\beta}_0=\frac{ \sum Y- \hat{\beta}_1 \sum X}{N}\) \(=\frac{(179.3)-(2.30)(29.4)}{9}\) \(=12.41\)

したがって、推定した回帰式は

\(\hat{Y}=12.41+2.30X\)

となる。この推定回帰式の解釈は、１単位（１％）の失業率の増加が、人口10万人あたり2.30単位（2.30人）の自殺者数の増加をもたらす可能性があることを示している。 つまり、日本の人口が１億2,000万人だと考えると、失業率１％増加で、自殺者数が2,760人増加する可能性があるという解釈になる。また、失業率が仮に0％だとしても、平均的に1万5,000人の自殺者が潜在的に存在する可能性がある。 ただし、このモデルでは自殺者数に影響を与える失業率以外の他の要因は無視している。

4.5.4 単回帰分析

まずは、データの準備、記述統計量の出力や分析に使うパッケージのインストールを行う。

セッションがタイムアウトとなり前回アップロードした「bunseki1.xlsx」が消えている場合は、再度デスクトップに保存したデータをColabにアップロードする。左タブにあるフォルダのアイコン（🗂）をクリックしフォルダを開く。その中に、分析用データ「bunseki1.xlsx」をドラッグ&ドロップしコピーする。

このとき、Colabのノートブックを新規作成した場合は、「Colab上でのRの実装手順」を再度実行する必要があるので注意してください。

1. 「ファイル」＞「ダウンロード」＞「.ipynbをダウンロード」をクリック

2. ダウンロードしたものをデスクトップへ保存

3. 保存したファイルを「メモ帳」で開く

4. 中身の書き換え

   “kernelspec” にある name と display_name を以下のように書き換える。

   “kernelspec”: {

   　　　　　　　　“name”: “ir”,

   　　　　　　　　“display_name”: “R”

   　　　　　　　}

5. Colabに戻り左上にある「ファイル」から「ノートブックをアップロード」をクリック

6. 先ほど上書き保存したファイルをアップロード（ドラッグ&ドロップ）

7. ランタイムのタイプが「R」になっていればOK

次に分析に必要なパッケージの読み込みを行う。

library(tidyverse)
library(readxl)

このほかにもstargazerというパッケージも利用するため、インストール及び読み込みを行う。

install.packages('stargazer')
library(stargazer)

アップロードしたデータの読み込みと確認を行う。

bunseki1 <- read_excel("bunseki1.xlsx")
View(bunseki1)

データ処理を行いやすいように変数名（列名）を日本語からアルファベット表記に変更する。

names(bunseki1) <- c("num", "year", "area", "juken", "age18" )

分析用データ（“bunseki1.xlsx”）を用いて、次の単回帰モデルをOLSにより推定する。

\(jcga=\beta_0+\beta_1age18+u\)　　　(1)

（海保大受験者数 = \(\beta_0\) + \(\beta_1\) 18歳人口 + 誤差）

model_1 <- lm(juken ~ age18, data = bunseki1)

model_1に分析モデル（線形単回帰モデル）を代入する。liner model（lm）の中で、lm(被説明変数〜説明変数, data = データ)を指定して推定を行う。 推定結果をstargazerで出力する。

stargazer(model_1, type = "text")

出力結果をさらに見やすくする。

stargazer(model_1, 
          type = "html",
          covariate.labels = c("18歳人口(万人)"),
          dep.var.caption = "被説明変数", # 変数の種類を明示
          dep.var.labels = "海保大受験者数", # 応答変数の名前
          title = "分析結果") # タイトル

出力されたhtmlテキストをコピーする。

次のチャンクでは、コードではなくテキストを追加する。

先ほどコピーしたhtmlテキストを貼り付けると整理された表が出力される。

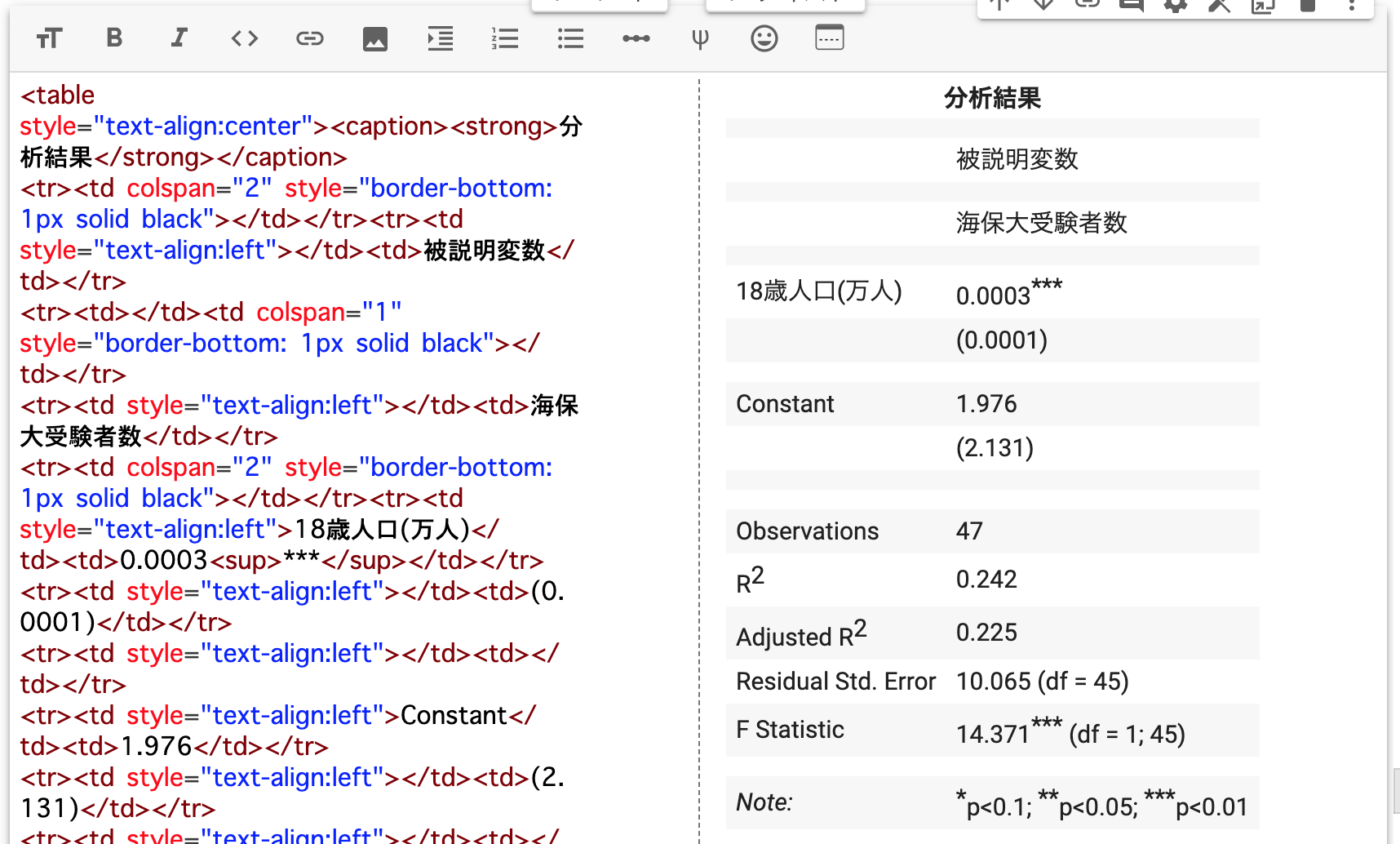
出力結果から以下の推定回帰式が得られる。

\(\hat{jcga}_i=1.976+0.0003 \,age18_i\)

この結果から、

⇒　各都道府県の18歳人口が1人増えると受験者数が「0.0003」人増える

⇒　各都道府県の18歳人口が1万人増えると受験者数が「3.0」人増える

という可能性が示唆できる。

※表中の「Constant」は「定数（切片）」を意味している。回帰式でいうと\(\beta_0\)である。