Chapter 3 Rによるデータ分析①

扱う分析事例：「海上保安庁の労働供給対策」

1. 問題背景

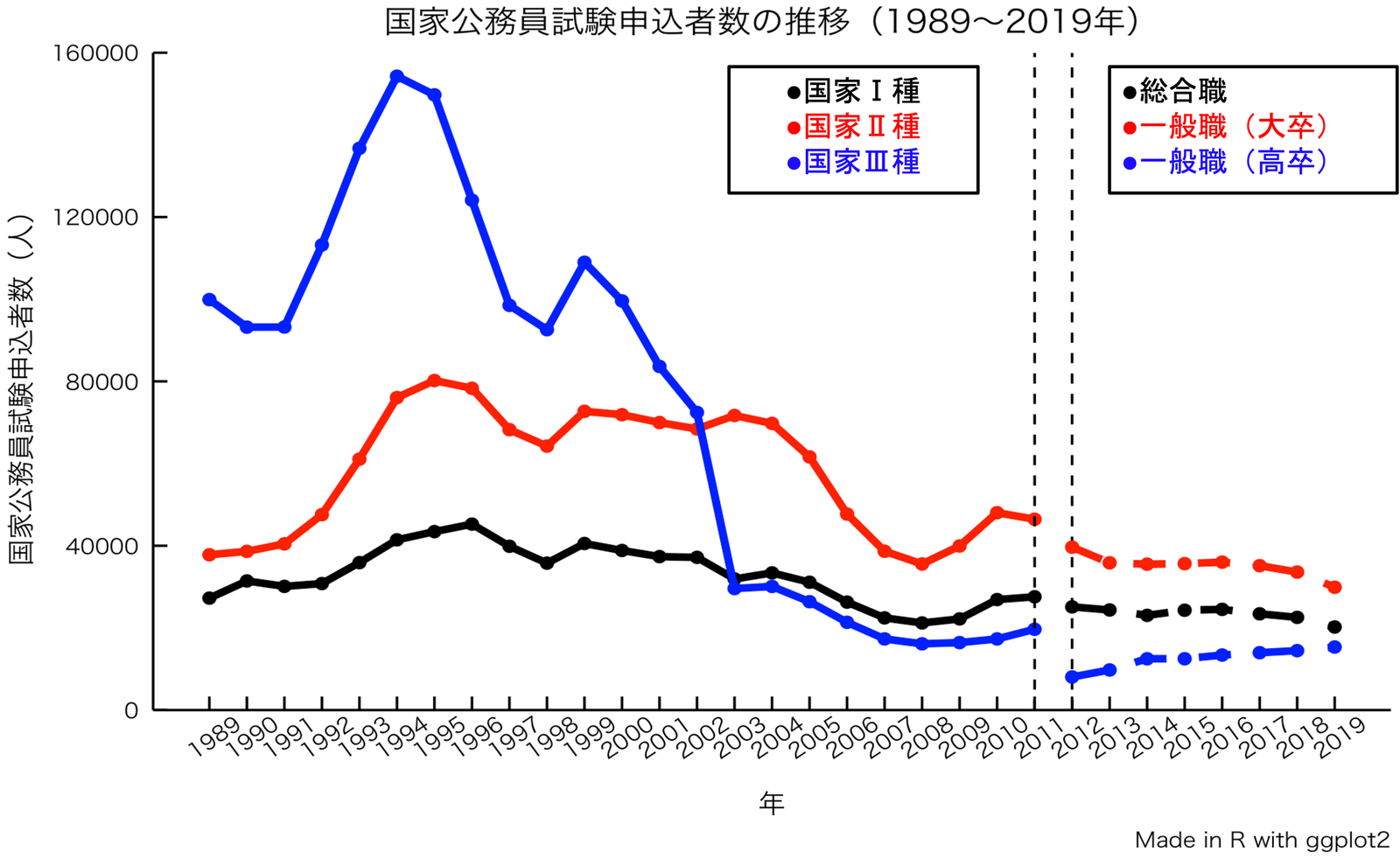
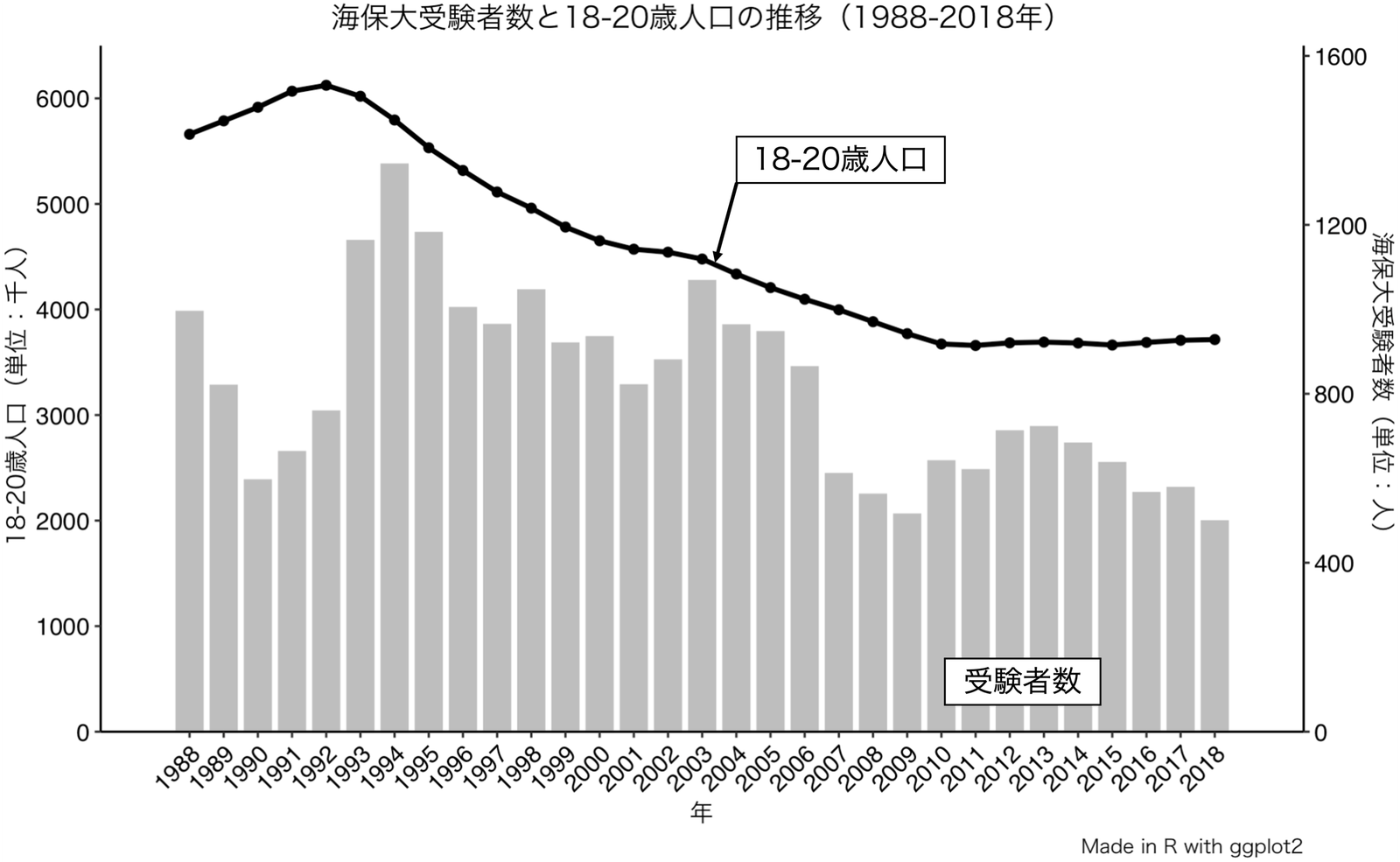
国家公務員への入職行動が減少しており、その影響を海上保安庁も受けていることが確認できる。 海上保安大学校受験者数データを用いて入職行動に影響を与える要因を突き止める。

2. 先行研究

一般に公的セクターへの入職行動については、失業率や官民賃金格差などの経済要因が負の影響を与える（不況時に入職希望者が増加する）ことがわかっている。最近では経済外的要因（遺伝、誠実さ、親の職業、愛国心、名誉心など）への関心が高まっている。 → 本演習では、主に入職行動の関係性について、データから明らかにする。

3. 参考情報

a. 最近の受験者数の推移、男女別でみた受験者数推移

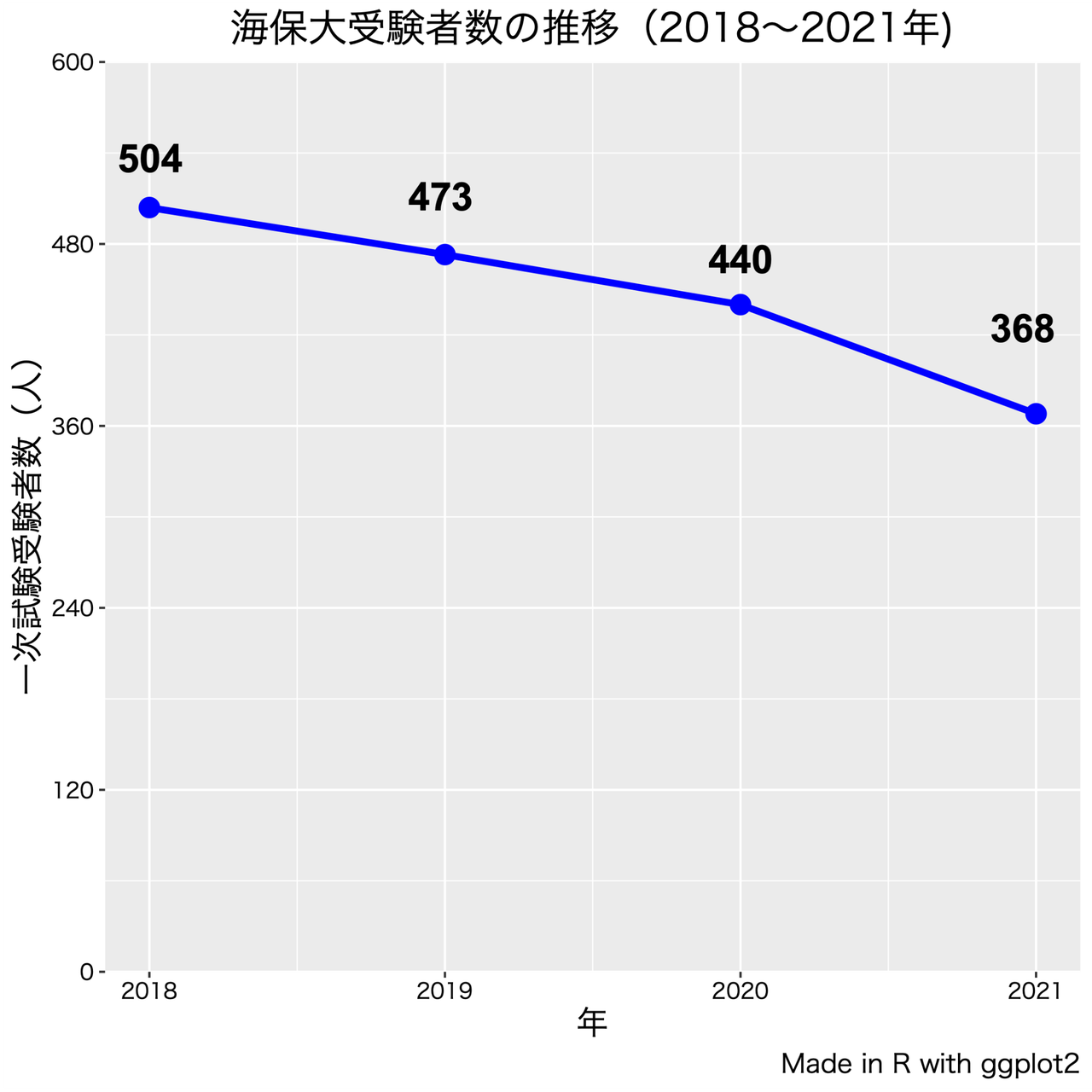
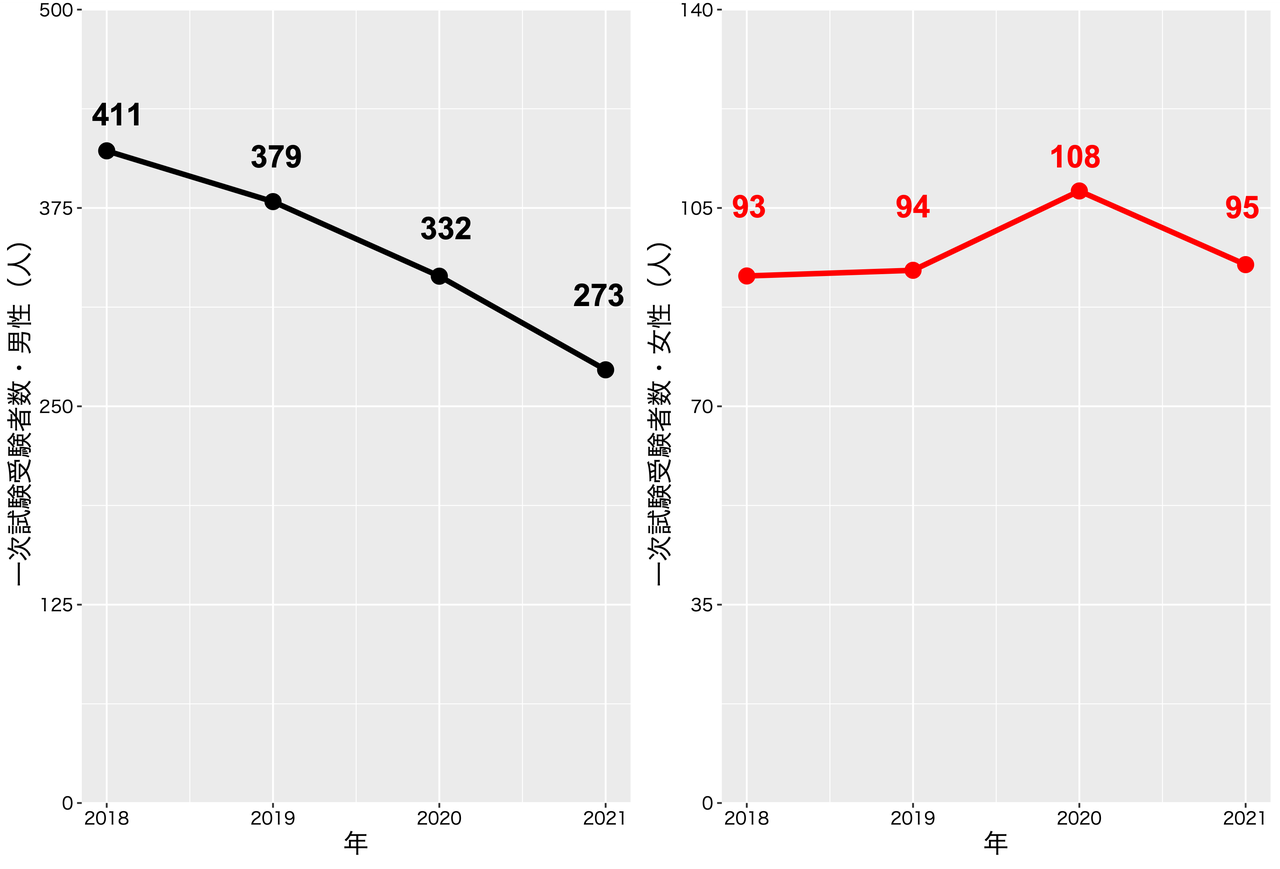
b. 現役高校受験比率の推移

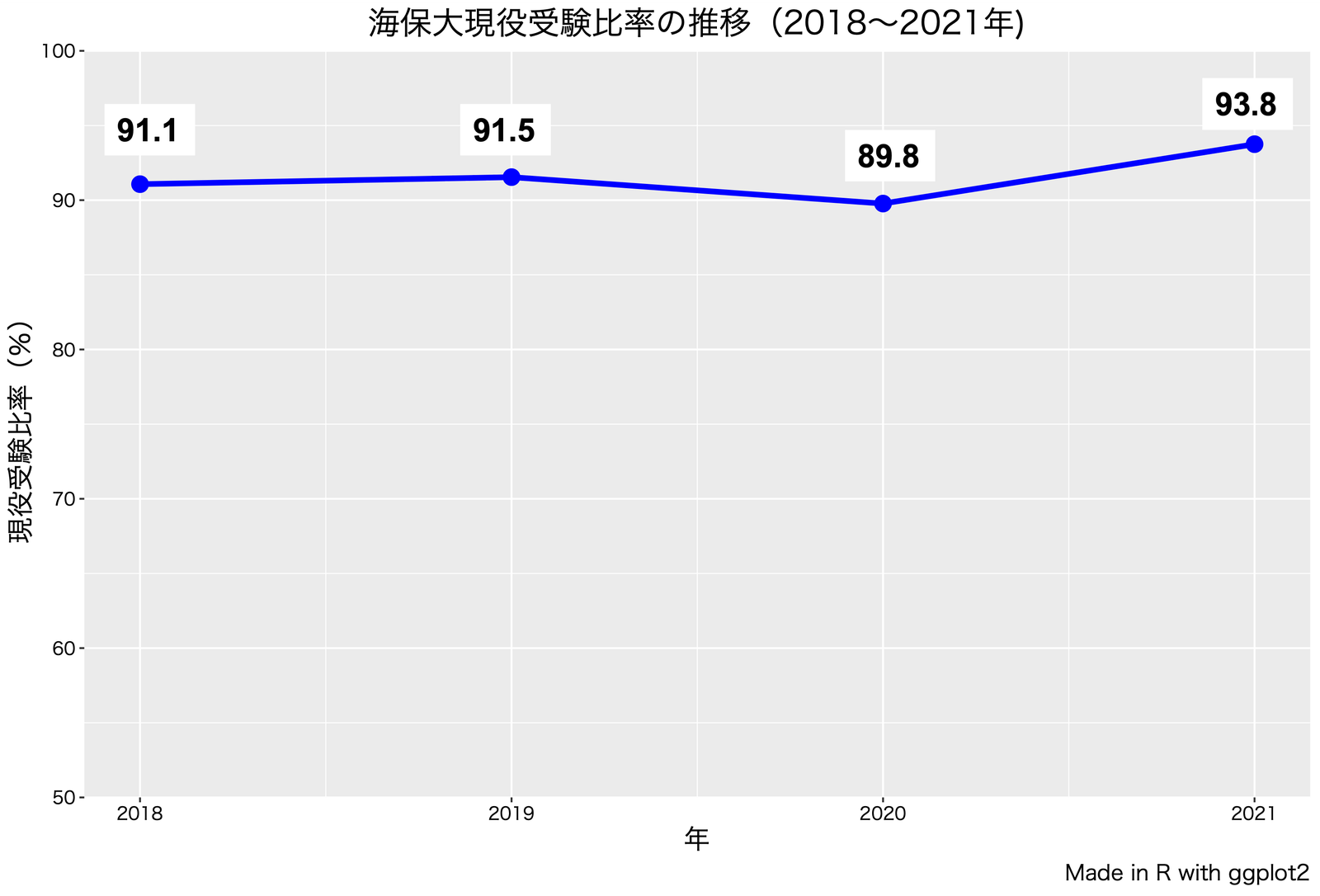
3.1 データの読み込み

Canvasから分析に用いるデータをダウンロードしデスクトップに保存する。

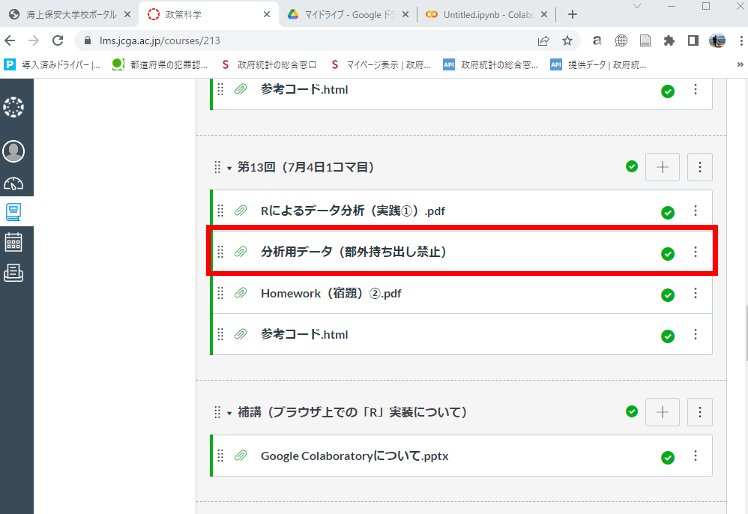
Colabに戻り、左タブにあるフォルダのアイコン（🗂）をクリックしフォルダを開く。その中に、先ほどの分析用データをドラッグ&ドロップしコピーする。このとき、当該分析用データはランタイムのリサイクル時に削除されるので留意しておくこと。

このとき、Colabのノートブックを新規作成した場合は、「Colab上でのRの実装手順」を再度実行する必要があるので注意してください。

  1. 「ファイル」＞「ダウンロード」＞「.ipynbをダウンロード」をクリック

  2. ダウンロードしたものをデスクトップへ保存

  3. 保存したファイルを「メモ帳」で開く

  4. 中身の書き換え

    “kernelspec” にある name と display_name を以下のように書き換える。

    “kernelspec”: {

    　　　　　　　　“name”: “ir”,

    　　　　　　　　“display_name”: “R”

    　　　　　　　}

  5. Colabに戻り左上にある「ファイル」から「ノートブックをアップロード」をクリック

  6. 先ほど上書き保存したファイルをアップロード（ドラッグ&ドロップ）

  7. ランタイムのタイプが「R」になっていればOK

3.2 データの確認

実際にExcelデータをRで読み込み、R上で必要な処理を行っていく。 まずは、データ処理に欠かせないパッケージを読み込む。

library(tidyverse)

さらに、ExcelデータをRに落とし込む際に必要なパッケージも読み込んでおく。

library(readxl)

それでは実際に、先ほどColab上にアップロードした分析用データ「bunseki1.xlsx」をRで開いてみる。 read関数を使用しbunseki1という変数に、“bunseki1.xlsx”を代入する。

bunseki1 <- read_excel("bunseki1.xlsx")

bunseki1という変数がどのようなデータ構造になっているか確認する。

View(bunseki1)

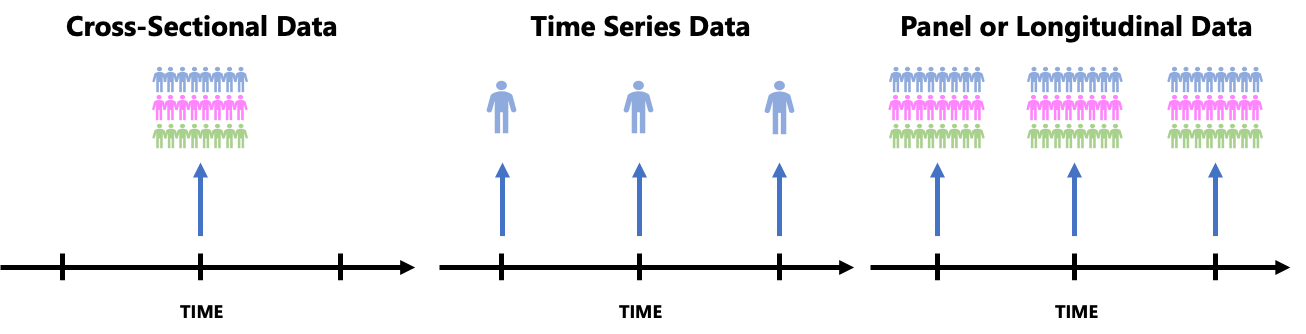
bunseki1 は、2021年における都道府県別の海上保安大学校受験者数と18歳人口のデータが格納されている。一時点を断面的に切り取ったデータであり、クロスセクションデータ（Cross-Sectional Data）というデータ構造になっている。クロスセクションデータは横断面データとも呼ばれる。

このほかにも、ある特定の対象を複数時点にわたって記録したデータである時系列データ（Time Series Data）、クロスセクションデータと時系列データの両方の側面（複数グループに対する複数期間のデータ）を持つパネルデータ（Panel or Longitudinal Data）がある。ちなみにパネルデータに関しては、原因と結果の因果関係を推定（因果推論）する場合において、パネルデータなしでは満足に答えを出すことが難しいと言われるほど重要なデータ構造になっている。

3.3 データの可視化（宿題あり）

データの特徴を掴むために可視化（グラフ化）を行う。

3.3.1 変数名（列名）の確認及び変更

データの加工、分析を行う場合には変数名（列名）をコンピュータに指定してコードを構築していくことになる。 まずは、データ処理を行いやすいように変数名（列名）を日本語からアルファベット表記に変更する。 そのまま日本語で処理を行っていも良いが、コンピュータは日本語を理解するのが苦手なのでエラーが起きやすい。 変更する際は、自身が認識できるアルファベットの羅列であれば何でも良い。

colnames()で変数名（列名）を確認。

colnames(bunseki1)

names()で変数名（列名）を変更。c( )は、『Combine Values into a Vector or List』を意味する関数であり、引数に渡したオブジェクトをベクトルかリストの形式で結合してくれる関数のことである。文字や数字の行を鎖状に繋げ、行ベクトルにすると理解しておくとよい。names()とc( )を組み合わせることで、変数名を設定することができる。数学の行列と同じ考え方で、列（変数）の数と行（c( )の中身）の数を等しくしなければエラーが起きるので注意。

names(bunseki1) <- c("num", "year", "area", "juken", "age18" )

変数名が変更されたか確認する。

View(bunseki1)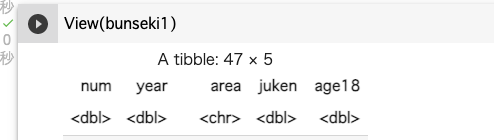

3.3.2 グラフの描画

各都道府県の受験者数の特徴を掴むため、barplot(棒グラフ)を作成してみる。グラフ化するデータ（bunseki1）とその中の変数名（juken）を$で繋ぎ、コンピュータに描画する値を指定する。さらに、その値の地域ごとの区別ができるようにnamesで各項目の名前の指定を行う。

b<- barplot(bunseki1$juken,names=bunseki1$area)

→　文字化けが発生している。これはColabに日本語フォントがインストールされていないために起こる。そのため日本語でグラフを出力する際は、以下のapt-getコマンドを使ってフォントを追加する必要がある。

system("apt-get install -y fonts-noto-cjk")

インストールしたフォント一覧を表示する（インストールには30秒ほどかかります）。

systemfonts::system_fonts()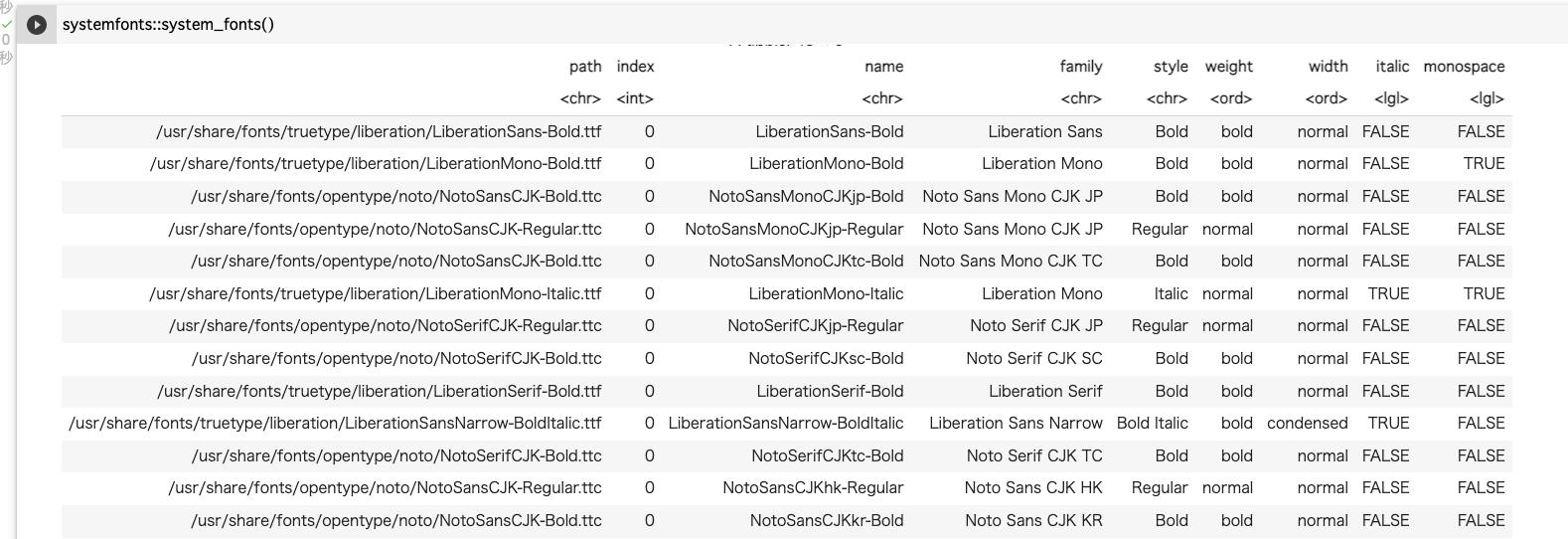

表示されたフォント一覧からfamilyに “CJK” が付いているフォントを指定することになる。 “CJK”は、Chinese Japanese Korean の略で、日本語対応しているフォントになる。

ここでは、“HiraKakuProN-W3”をフォントに指定する。barplot関数の中でfamily = "HiraKakuProN-W3"と指定すれば日本語表示に対応する。

b<- barplot(bunseki1$juken,names=bunseki1$area,family= "HiraKakuProN-W3")

ただし、これをみてもよくわからない。以降、成形してグラフを見やすくしていく。

barplot棒グラフを横向きhoriz=Tにする。

b<- barplot(bunseki1$juken,names=bunseki1$area,family="HiraKakuProN-W3", horiz=T)

x軸の目盛りを調整し、棒グラフが軸内に収まるようにする（x軸の表示範囲を拡大）。

b<- barplot(bunseki1$juken,names=bunseki1$area,family="HiraKakuProN-W3", horiz=T ,
            las=1,xlim=c(0,max(bunseki1$juken)*1.2))

グラフの色を変更する。

b<- barplot(bunseki1$juken,names=bunseki1$area,family="HiraKakuProN-W3", horiz=T ,
            las=1,xlim=c(0,max(bunseki1$juken)*1.2), col="blue")

barplotにおける項目名（地域名）のフォントサイズを変更する（0.5倍）

b<- barplot(bunseki1$juken,names=bunseki1$area,family="HiraKakuProN-W3", horiz=T ,
            las=1,xlim=c(0,max(bunseki1$juken)*1.2), col="blue", cex.names=0.5)

これでもまだわかりにくい。受験者数の多い順に並び替える。 まずは、bunseki1から受験者数jukenと都道府県areaのデータをピックアップする（bunseki2に格納）。

bunseki2 <- bunseki1[,c("juken","area")]

bunseki2について、受験者数jukenが多い順に並び替え。

bunseki2 <- bunseki2[order(bunseki2$juken),]

再度、グラフを描いてみる。

b<- barplot(bunseki2$juken,names=bunseki2$area,family="HiraKakuProN-W3", horiz=T ,
            las=1,xlim=c(0,max(bunseki2$juken)*1.2), col="blue", cex.names=0.5)

グラフのタイトルや軸ラベルを追加する。

par(mar=c(3,5,1,2))　#余白を調整
b<- barplot(bunseki2$juken,names=bunseki2$area,family="HiraKakuProN-W3", horiz=T,
            col="blue",las=1,xlim=c(0,max(bunseki2$juken)*1.2), cex.names=0.5,
            main = "都道府県ごとの海保大受験者数(2021年）", # グラフタイトル
            ylab = "都道府県", # y軸説明ラベル（y軸タイトル）
            cex.main = 1, # グラフタイトルの文字サイズ
            cex.lab = 1, # 軸説明ラベル（軸タイトル）の文字サイズ
            cex.axis = 0.6) # 軸ラベル（数値など）の文字サイズ

3.3.3 変数同士の関係性（相関関係の確認）

受験者数と他の変数（ここでは人口）との関係性を可視化してみる。

plot(bunseki1$age18, bunseki1$juken)

→　tidyverseに組み込まれているggplotを使用し、見やすくする。

ggplot(data = bunseki1) +  　　            #"bunseki1"というデータを使用        
  aes(x = age18, y = juken, label=area) +  #X軸：18歳人口、Y軸：受験者、地域で区別
  geom_text() +     　　　　　　　　　 　  #散布図のプロットをテキストで行う 
  theme_classic(base_size = 20)　#グラフのデザインをclassicにして、フォントサイズを20に指定

さらに情報を追加する。

3.3.4 Homework（宿題）②

以下のコードを実行し、グラフを出力せよ。

ggplot(bunseki1,aes(x = age18,y = juken, label=area)) +
  geom_smooth(method = "lm") +                                
  geom_text(size=5, color="black") +　　　　　　　　　　　　　　　　　　　　　
  theme_classic() +
  theme(legend.position = "none",                         
        axis.text = element_text(size = rel(1.5)), 
        axis.title.x = element_text(size= 15,face = "bold",),          
        axis.title.y = element_text(size= 15,face = "bold",),          
        plot.title = element_text(size = rel(1.5), face = "bold", 
        hjust = 0.5, margin = margin(t = 10, b = 20, unit = "pt"))) +  
  labs(x = "都道県別18歳人口（人）", y = "海保大受験者数",
       title = "受験者数と18歳人口の相関関係",
       caption = "Made in R with ggplot2")

出力したグラフをWord等に貼り付けCanvasから提出してください。

提出期限：2022年9月16日（金）2359まで

提出方法：Canvasから提出

※100点満点で成績をつけるうちの20点になります。

3.4 相関関係と因果関係


Example.1 小学生の運動能力と計算能力の関係（第一種の過誤）

ある小学校の学生を対象に計算ドリルの成績と体力テストの成績の関係を調べてみたところ以下の結果を得られた。

この結果から、体力を鍛えれば計算能力も上がるといえるのか。

直感的思考能力に従うと関係はありそうだが、実際は異なる。

先ほどの図を学年別（１〜６年をシンボルで区別）に表してみると、

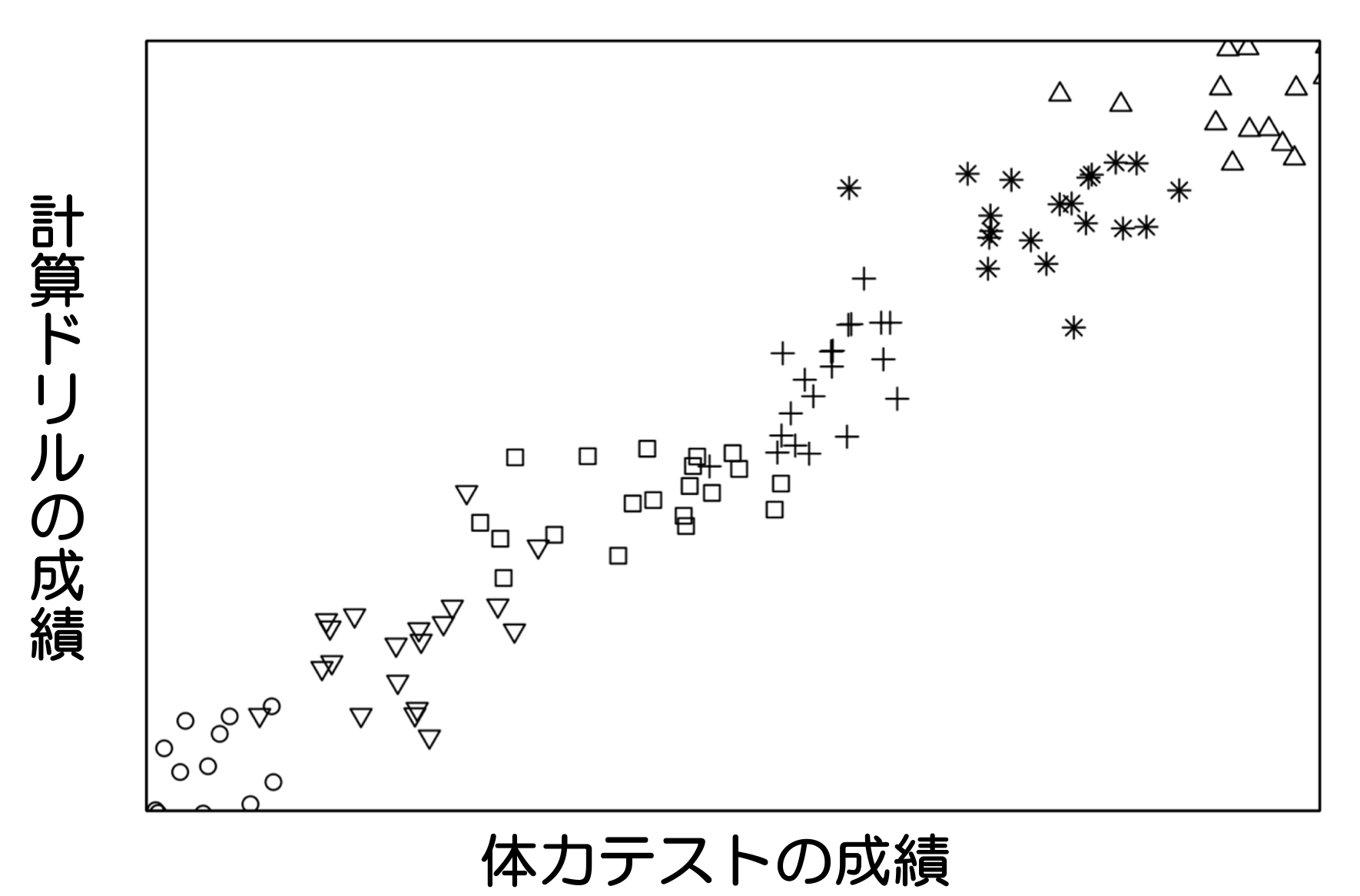
同じ学年（シンボル）だけ取り出してみると特定の傾向はなく、ばらつきがある

学年ごとに分けた場合は、運動能力と計算能力には特に関連がない

この他にも、

    • メタボ検診を受けていれば長生きできるのか

    • テレビを見せると子供の学力は下がるのか

    • 偏差値の高い大学へ行けば収入は上がるのか

という問いかけに対して「イエス」と答える人は多いはず。

⇒　しかし、先行研究によりすべて否定されている。（中室　2017）

多くの人がこれらの問いに対して「イエス」と答えてしまうのは直感的思考の中で認知バイアスが発現し、「因果関係」と「相関関係」を誤認してしまっているからである。この認知バイアスに左右されず、「因果関係」と「相関関係」を見極める必要がある

3.4.1 因果関係の識別問題

因果関係と相関関係について改めて整理する。

●因果関係

要因\(X\)を変化させたときに要因\(Y\)も変化する場合に\(X\)と\(Y\)の間に因果関係があるという

●相関関係

要因\(X\)につられてもう要因\(Y\)も変化しているように見えるものの、原因と結果の関係になっていない場合は「相関関係」があるという（相関関係の場合、何らかの関係が成り立っているものの、因果関係はない）


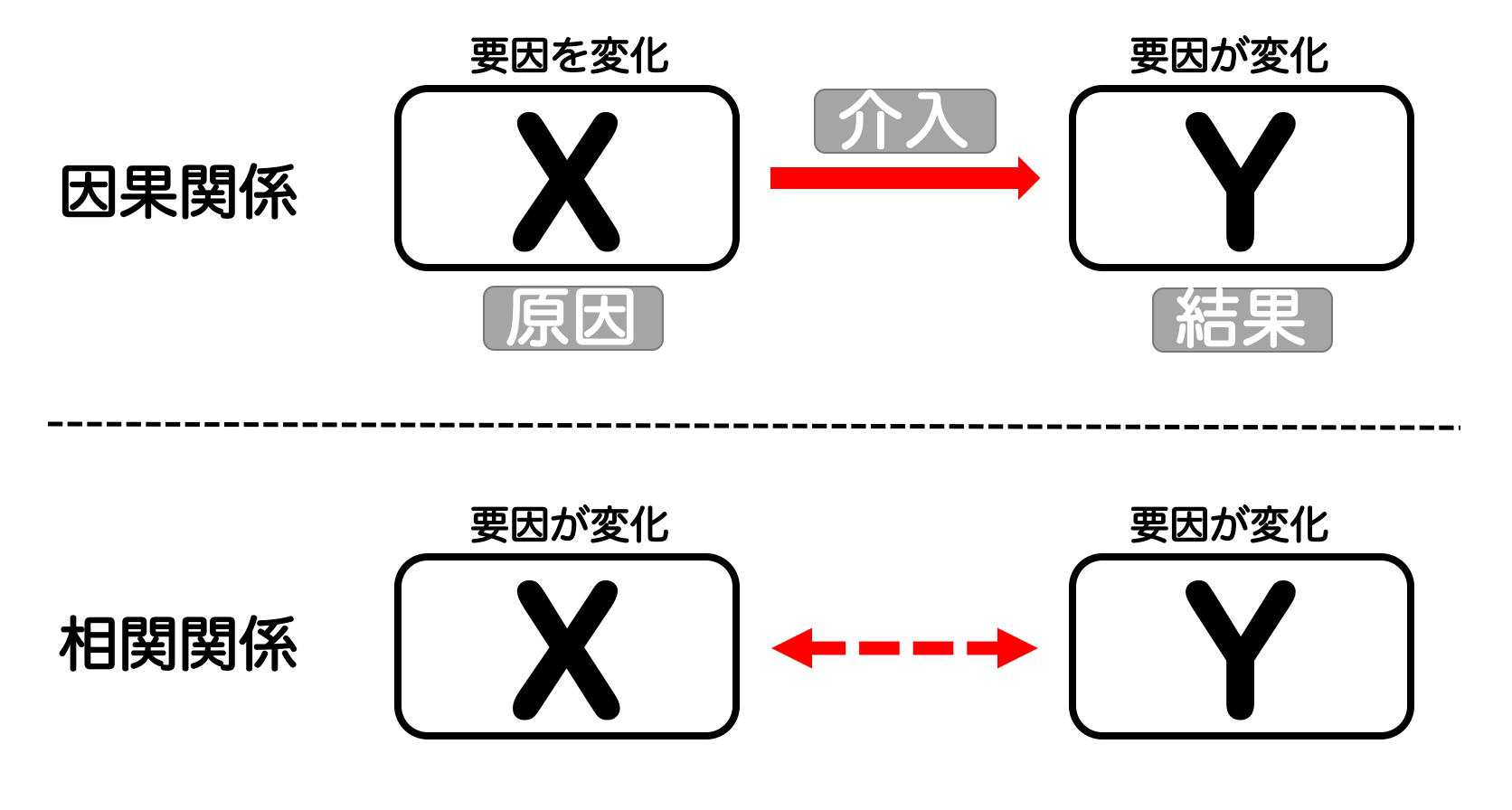
※ここでいう「要因」のように、様々な値をとるデータのことを「変数」と呼びます。変数は年齢や身長のように連続した数値のこともあれば、性別のように男性・女性いずれかの値をとる文字（１ or ０のダミー変数という）のこともある。

２つの変数の関係が因果関係なのかを明らかにするために必要な考え方が「因果推論」と呼ばれる（統計学の範囲）。

3.4.2 因果関係の識別が難しい理由

データから因果関係を見極めることは非常に難しい。その理由としては、主に以下の3つの理由があるとされている。

  • 見せかけの相関

  • 逆の因果関係

  • 他の要因（第三の変数）による影響

①　見せかけの相関

Example.2　失業率と自殺者数の関係

次の図は、日本における失業率（％）と自殺者数（人口１０万人あたり）の推移（1975ー2017年）をグラフ化したものである。

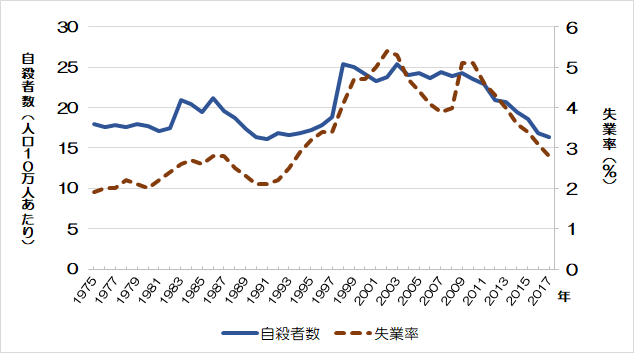
→　直感的に「失業率」が上がると「自殺者数が増える」傾向が予想できる

一方で、直感的に関連がないと思われることでも、データをみると関連した動きをしていることがある。

Example.3　地球温暖化と海賊の数

以下の図は平均気温と海賊数の推移（1820年ー2000年）をグラフ化したもの。

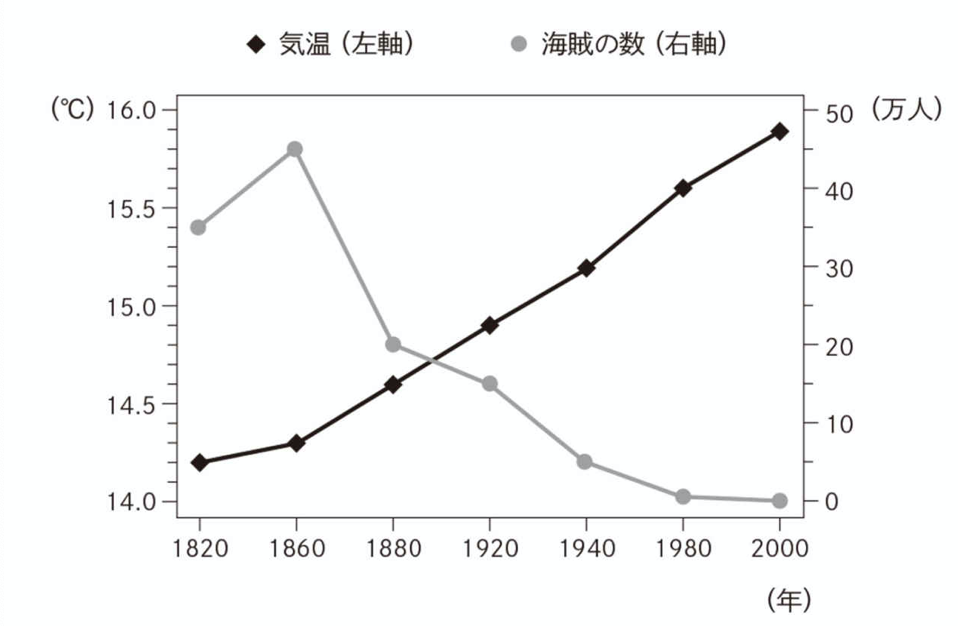
出典：中室牧子ほか（2017）より引用

→　平均気温が上がる（地球温暖化が進む）と海賊の数が減る？

→　海賊の数が減ると平均気温が上がる（地球温暖化が進む）？


Example.4　ミス・アメリカと暖房器具が原因による死者数

以下の図は、ミス・アメリカの年齢と暖房器具が原因の死者数の推移（1999ー2009年）をグラフ化したもの。

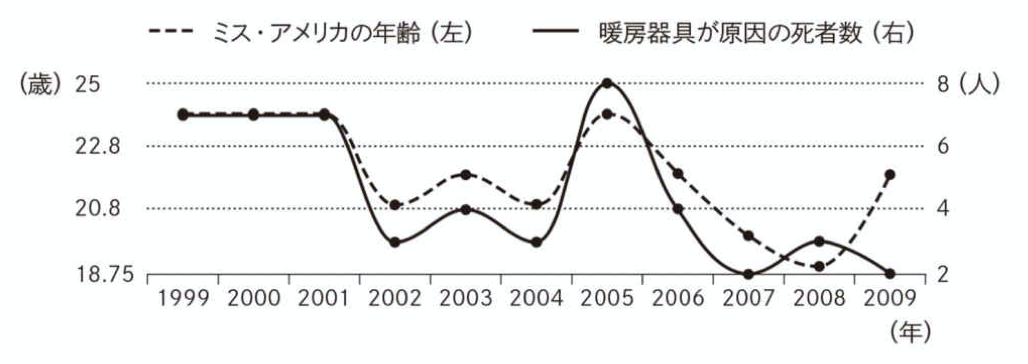
出典：中室牧子ほか（2017）より引用

→　ミス・アメリカの年齢が若いほど、その年の暖房器具が原因の死者数が減る？

→　暖房器具が原因の死者数が低いほど、その年のミス・アメリカの年齢は若い？


Example.5　ニコラス・ケイジとプールの溺死者

以下の図は、ニコラス・ケイジの映画出演本数とプールの溺死者数の推移（1999ー2009年）をグラフ化しものである。

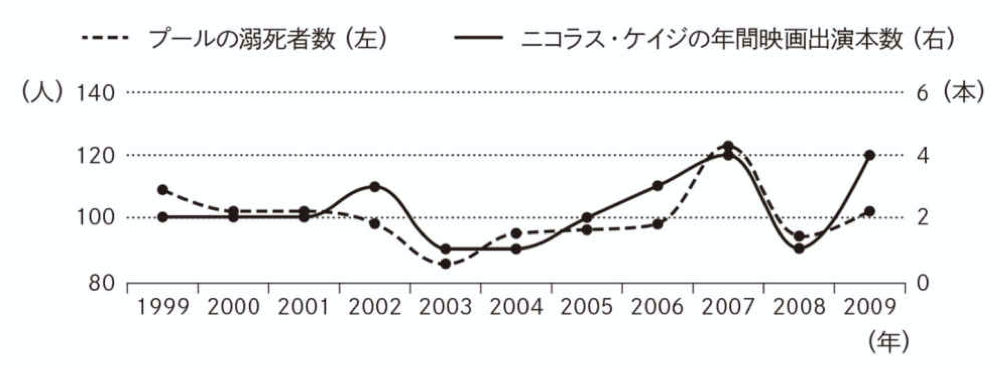
出典：中室牧子ほか（2017）より引用

→　ニコラス・ケイジの映画出演が少ないと、その年のプールの溺死者数が減る？

→　プールの溺死者数が少ないと、ニコラス・ケイジの映画出演が減る？


Example.6　博士号取得者数と商店街の収入

以下の図は、コンピューターサイエンス博士号取得者数と商店街における総収入の推移（1999ー2009年）をグラフ化したものである。

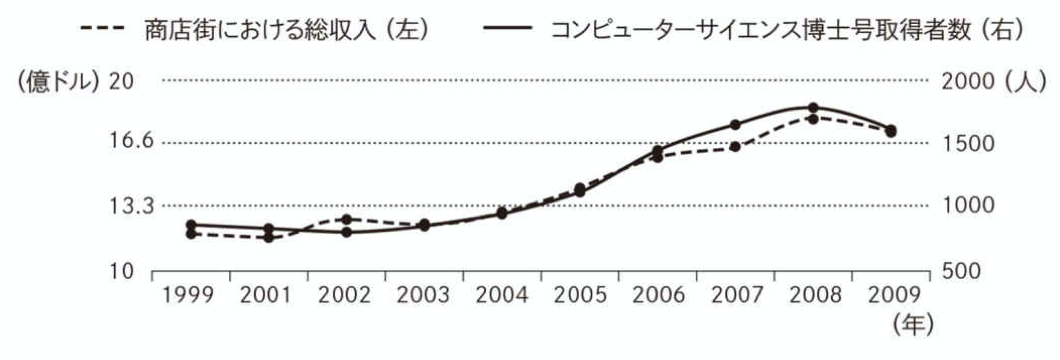
出典：中室牧子ほか（2017）より引用

→　博士号取得者が少ないと、その年の商店街の収入は減る？

→　商店街の収入が少ないと、その年の博士号取得者は減る？

いま見てきた「Example」は、一見綺麗な関係性を示しているが、「まったくの偶然」による相関関係であり、これら２変数間に因果関係は存在しない。このように単なる偶然にすぎないすが、２つの変数がよく似た動きをすることを「見せかけの相関」という。


②　逆の因果関係

「\(Y\)が\(X\)に影響を与えたのではないか」という逆の因果関係だった可能性もある

Example.7　仮想例：サンゴとその捕食者

サンゴの減少が懸念されているある地域においてサンゴの調査を行っていたところ、サンゴの生存率とサンゴの捕食者Oの個体密度の間に以下の相関関係が見られた。

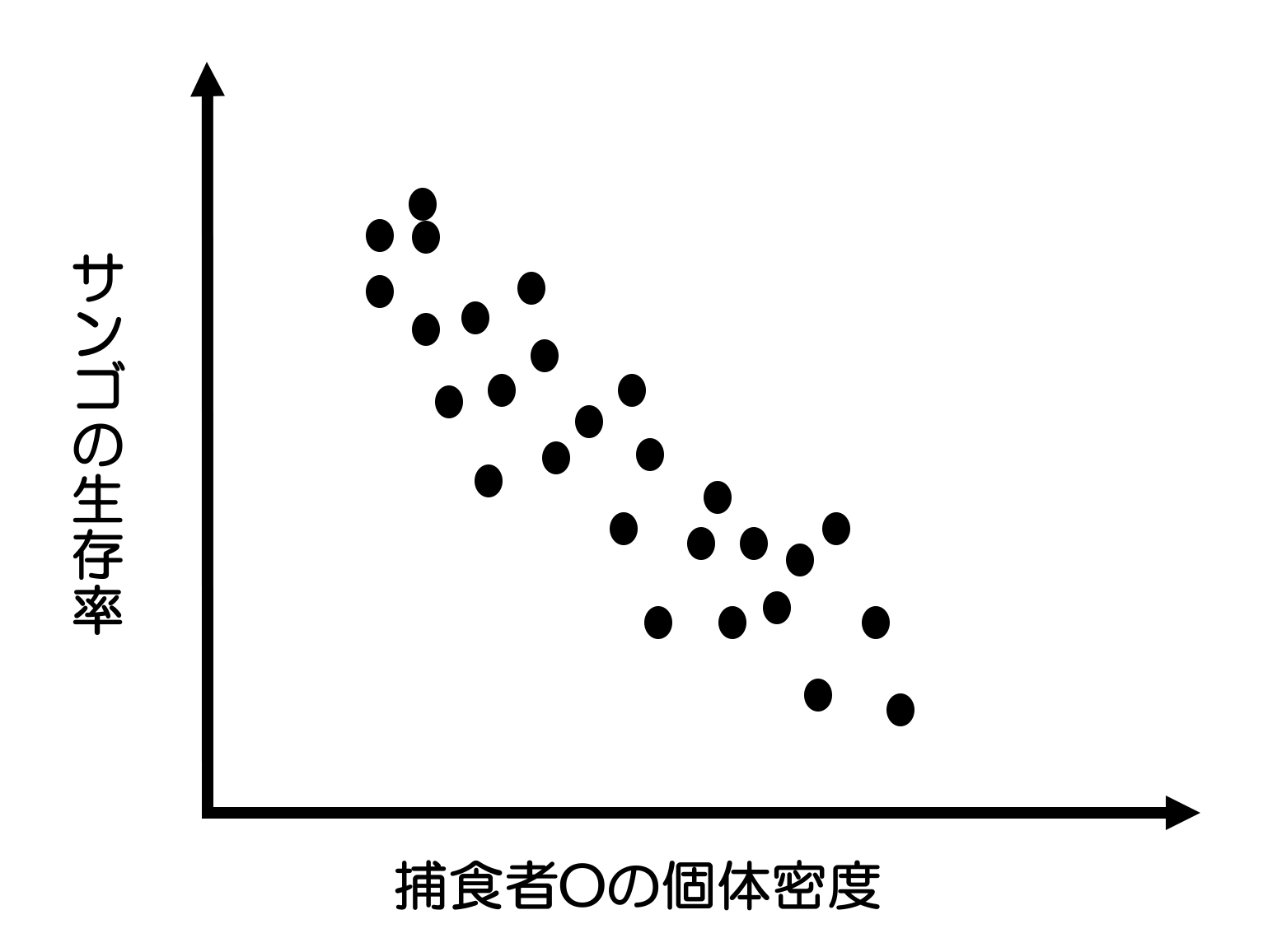
また、フィールドでの観察から、捕食者Oは実際にサンゴを捕食していることがわかった。

このとき、「捕食者Oの個体密度の増加が、サンゴの生存率の減少させた」という因果関係を想起する。

もし、このような因果関係が存在するならば、「捕食者Oの個体密度」を減少させることにより「サンゴの生存率」を増加させることができる。

⇒　しかし、より詳細なフィールド調査により、

  • 「捕食者Oは死にかけのサンゴしか食べず、生態系の中でむしろ掃除屋のような役割を果たしていた」ことがわかった。

⇒　因果の方向が、実は逆で

  • 「サンゴの生存率の低下が、捕食者Oに個体密度を増加させた」ということを示唆

もし、この因果の方向が正しいのなら、以前に想起されていた「捕食者Oの個体密度→サンゴの生存率」という因果関係は存在しない。＝「保全措置として捕食者Oの個体密度を減少させても、サンゴの生存率は変化しない」ということになる（むしろ掃除屋を排除することによりサンゴの健全な新陳代謝が妨げられる可能性さえある）。


真の「因果の向き」は、基本的にはフィールドでの観察や介入によってしか明らかにすることはできない。

因果に関する推論を行うためには、因果関係を明らかにしたい２つの要因の間の確率的な共変関係の情報だけでは不十分であり、対象とする現象についての適切な背景知識を得ることが本質的に重要となる

③　他の要因（第三の変数）による影響

「\(Y\)が変化したのは\(X\)以外の他の要因の影響だったのでは？」という問題を排除することが一番難しい

Example.8　コーヒーを飲むと心筋梗塞になる？

ある調査で、「コーヒーをよく飲む人は心筋梗塞になる」という結果がでた。これは真実か？


因果の流れを整理すると、、、

原因「コーヒーをよく飲む」→結果「心筋梗塞になる」＝明らかにおかしい！！

実際は、タバコという第三の変数（交絡因子）が影響し、見かけ上「コーヒーをよく飲む」ことと「心筋梗塞」に関連性を持たせていた可能性が高い。

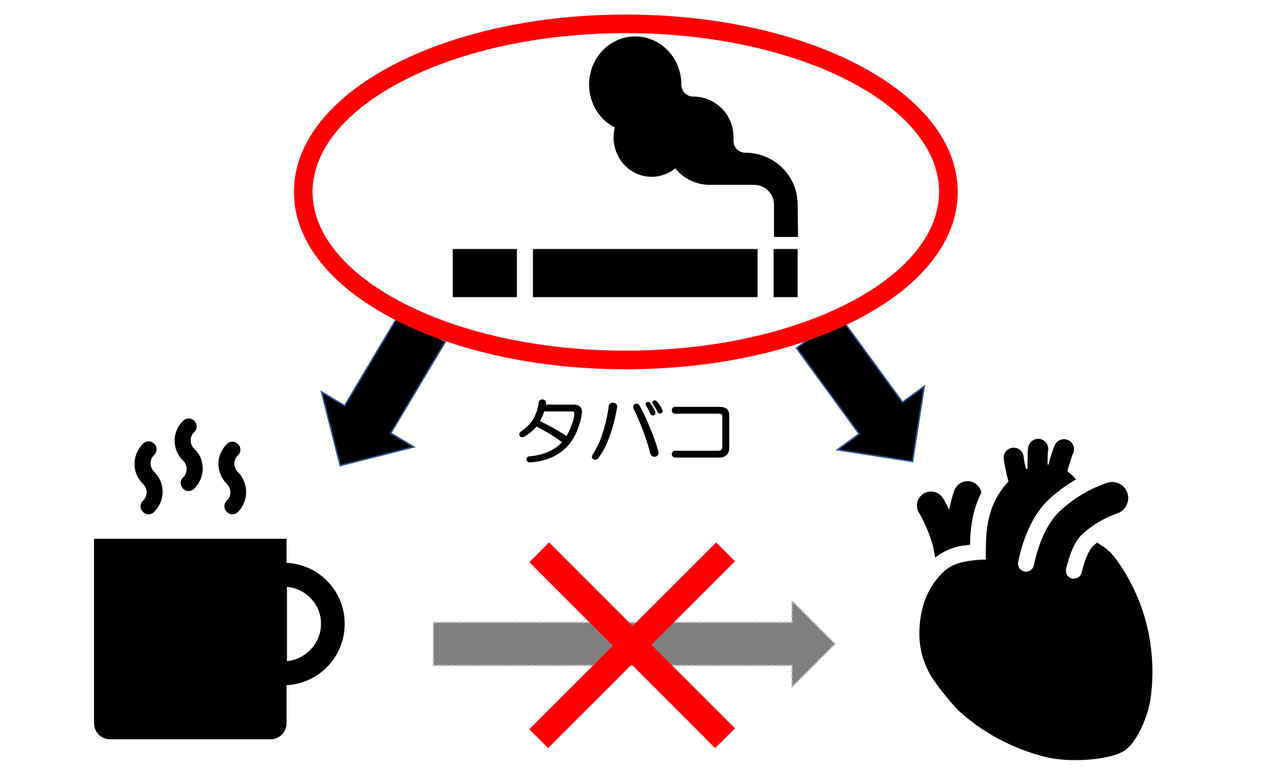
つまり、

『要因\(X\)と要因\(Y\)のデータが同時に動いているように見える場合でも、要因\(X\)が要因\(Y\)に直接影響を与えたのではなく、第三の要因\(V\)が\(X\)と\(Y\)の両方に影響を及ぼしただけ』

という可能性がある

3.4.3 まとめ

XとYのデータの動きに関連性がある場合（つまり、XとYに相関関係がある場合）に起こりうる３つの可能性を図示している。


  1. XがYに影響を与えている可能性

  2. YがXに影響を与えている可能性

  3. VがXとYのそれぞれに影響を与えている可能性


分析者にとって厄介なのは、XとYの相関関係を観測しただけでは、３つの可能性のうちどれが本当に起こっているのか判定ができないことである。そこで、統計学や経済学の知識を活用し「因果関係」の見極めを行っている。