Chapter 6 Rによるデータ分析④
6.1 決定係数
最小2乗法(OLS)を用いてデータに直線を当てはめたとき、得られた回帰式\(\hat{Y}_i=\hat{\beta}_0+\hat{\beta}_1 X_i\) がそのデータの特徴をうまく捉えているかを調べるための尺度。
→ 決定係数\(R^2\) (アール・スクエア)
\(Y\) の変動のうち \(X\) で説明される部分の比率であり、推定した回帰式の当てはまりの良さを測る指標になる。直線の当てはまりが良くないと\(R^2\) の値が小さくなる。

この決定係数を求めるために以下の3つの量を準備する
TSS(全平方和:Total Sum of Squares) → 総変動:データ全体の平均値からの各データのズレ
\(TSS=\sum_{i=1}^{N} (Y_i-\overline Y)^2\)
ESS(回帰平方和:Explaind Sum of Squares) → 回帰変動 :推定回帰式から得られた予測値とデータ全体の平均値の差
\(ESS=\sum_{i=1}^{N}(\hat{Y}_i-\overline Y)^2\)
RSS(残差平方和:Residual Sum of Squares) → 残差変動:実際のデータと推定回帰式から得られた予測値との差
\(RSS=\sum_{i=1}^{N}\hat{u}_i ^2\)
図で描画すると以下のようになる。

図からもわかるように以下の関係式が成り立つ。
\(TSS=ESS+RSS\) → 総変動=回帰変動+残差変動
という関係が成り立つ。 左辺の\(TSS\)は、\(Y\)の変動の総量を表す量(平均からの乖離)であり、これが\(ESS\)と\(RSS\)に分解される。\(RSS\)は残差の2乗和であるから、変動の総量のうち\(X\)で説明できない部分の変動を表す。\(ESS\)は変動の総量のうち\(X\)で説明される部分を表すということになる。 これらを用いて、決定係数\(R^2\)を以下のように定義する。
\(R^2=\frac{ESS}{TSS}=\frac{\sum_{i=1}^{N}(\hat{Y}_i -\overline Y)^2}{\sum_{i=1}^{N}(Y_i -\overline Y)^2}\)
これは、\(Y\)の全変動のうち説明変数\(X\)で説明される部分の比率を求めているものであり、データに対する推定回帰式の当てはまりの良さを測る指標となる。
さらに、\(R^2=\frac{ESS}{TSS}=\frac{\sum_{i=1}^{N}(\hat{Y}_i -\overline Y)^2}{\sum_{i=1}^{N}(Y_i -\overline Y)^2}\)を\(TSS=ESS+RSS\)用いて変形すると、
\(R^2=1-\frac{RSS}{TSS}=1-\frac{\sum_{i=1}^{N} \hat{u}_i ^2}{\sum_{i=1}^{N}(Y_i -\overline Y)^2}\)
とも書けることがわかる。残差の2乗\(\hat{u}_i ^2\) が全体的に大きいとき、つまり直線の当てはまりが良くないときに、\(R^2\) が小さくなることがわかる。
決定係数\(R^2\) は以下の性質を持つ。
(1) \(0\leq R^2 \leq 1\)
(2) 当てはまりが良いほど\(R^2\) の値は大きくなり、すべてのデータが一直線上にあるとき\(R^2=1\)となる
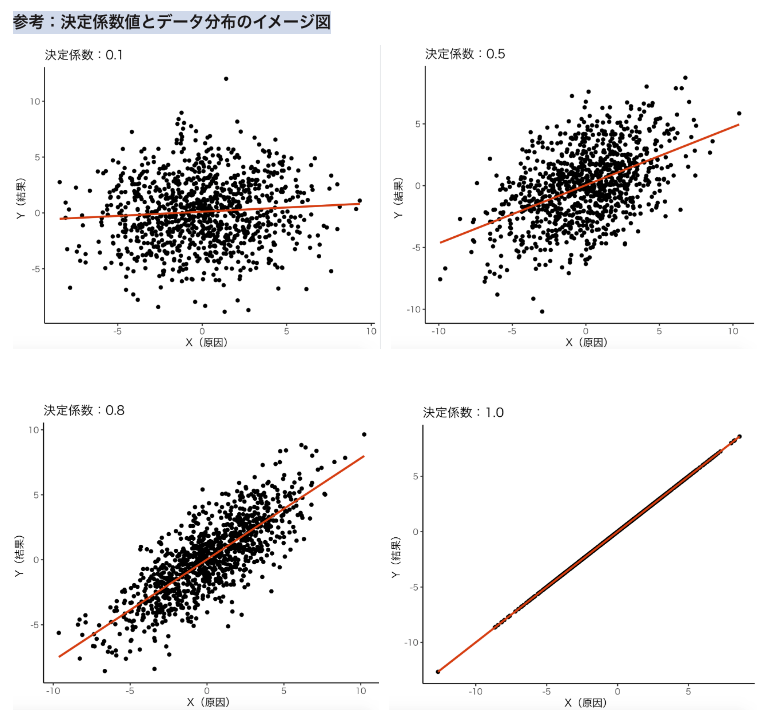
出力された結果をみると表の下部に「R2」という表記がある。これが決定係数\(R^2\) であり、推定回帰式の当てはまりの良さを表す指標になる。

値を確認すると、「0.242」であり\(0\leq R^2 \leq 1\) から判断するとデータに対する推定回帰式の当てはまりがあまり良くないことがいえる。学術的には、モデルの決定係数が0.5-0.8あれば良いとされている。
ただし、決定係数の値が重要であるかどうかは、 分析の目的に依存し、分析の目的によっては高い決定係数(あるいは自由度修正済み決定係数) を出すモデルが良いモデルとは限らない。この点の説明については後述する。
6.2 重回帰分析
前回確認した回帰分析は、説明変数が一つしかない単回帰モデル
\(Y=\beta_0+\beta_1X+u\)
だったが、通常の実証分析では、説明変数が複数になる重回帰モデルによる分析が行われる。 説明変数が増えても推定結果の見方は、ほとんど変わらないが、複数の説明変数を用いることで関心のある説明変数の効果を正しく推定することができる。
Example.9 ベッカーの犯罪行動分析モデル
犯罪行動の理論モデル(1968年)を分析のできる形(分析モデル)に変換する。

経済理論を検証する場合、あるいは公共政策を評価する場合、分析者の目標は、ある変数(例えば教育)が別の変数(例えば労働者の生産性)に因果的な影響を与えるかを推論することである。単に2つ以上の変数間の因果関係が立証されない限り、説得力を持つことはほとんどない。
ここで重要なキーフレーズがceteris paribus(セテリス・パリバス)である。 ceteris paribus とは、「他の要因が等しい(一定)」という意味で、因果関係の分析において重要な役割を果たす。経済学の入門書では、ほとんどの経済現象を ceteris paribus という条件で解明しているのである。例えば、消費者需要の分析では、所得、他の財の価格、個人の嗜好など、他のすべての要因を固定したまま、財の価格を変化させると、その需要量にどのような影響があるかを解いている。もし、他の要因が固定されていなければ、価格変化が需要量に及ぼす因果関係を知ることはできない。
Example Effects of Fertilizer on Crop Yield
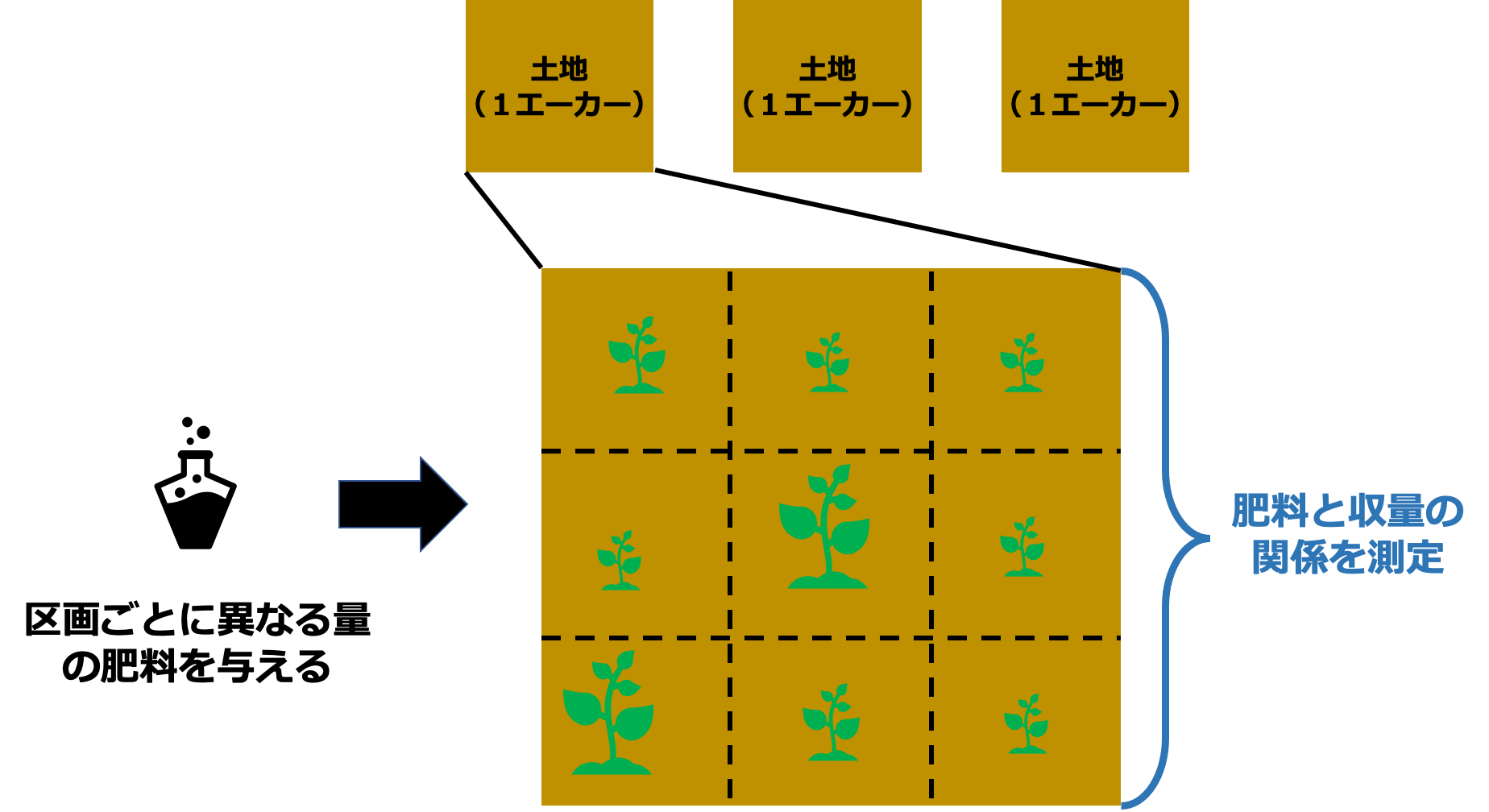
新しく開発された肥料が作物の収量に及ぼす影響を検討する。対象となる作物は大豆とする。
肥料の量は、降雨量、土地の質、寄生虫の有無など、収量を左右する要因の一つに過ぎないため、この問題は ceteris paribus の問題として取り扱わなければならない。大豆の収量に対する肥料の量の因果関係を明らかにする方法として、次のような実験が考えられる。
1エーカーの土地をいくつか選ぶ。
各区画に異なる量の肥料を施し、その後収量を測定する。これにより、横断的なデータセットが得られる。
統計的手法を用いて、収量と肥料量の関連を測定する。
ただし、肥料の量以外のすべての点で同一の土地を選ぶ(他の要因が一定である)とは言っていないので、これはあまり良い実験とはいえない。実際、このような特徴を持つ土地を選ぶことは実現不可能である。もし、肥料の量を決定する際に農場の他の特徴を完全に無視(あるいは一定にコントロール)できるなら、因果効果の測定が可能となる。
重回帰分析では、被説明変数に同時に影響を与える他の多くの要因を明示的にコントロールすることができる。このことは、経済理論を検証する上でも、非実験データに頼らざるを得ない場合に政策効果を評価する上でも重要となる。重回帰モデルは相関のある多くの説明変数に対応できるため、単純な回帰分析では誤解を招くような場合でも、因果関係を推論することが期待できる。以下その中身について確認する。
6.2.1 一般的な重回帰モデルの定義
データを \((Y_i, X_{1i}, X_{2i},...,X_{ki})\), \(i=1,...,N\) とする。\(Y_i\) が被説明変数であり、\((X_{1i}, X_{2i},...,X_{ki})\) が説明変数である。説明変数の添字は最初の\(1\) から\(k\) までのものが変数の番号であり、2つ目の\(1\) から \(N\) までのものが観測個体(人などの観測対象)の番号である。
例:\(X_{2,5}\) は5番目の観測個体の2つ目の説明変数の値を表す。
このデータでは、\(k\) 個の説明変数がある。一般的に重回帰モデルは、
\(Y_i=\beta_0+\beta_1 X_{1i}+\beta_2 X_{2i}+...+\beta_k X_{ki}+u_i\) , \(i=1,..., N\)
と書ける。\((\beta_0, \beta_1,..., \beta_k)\) は未知の回帰係数であり、\(u_i\) は、説明変数 \((X_{1i}, X_{2i}, ..., X_{ki})\) 以外の \(Y_i\) に影響を与える要素をまとめた誤差項である。
6.2.2 欠落変数バイアス
重回帰分析を行う主要な目的は、欠落変数バイアス(omitted variable bias)を避けるためである。 たとえ、興味のある説明変数が1つだけであっても、単回帰分析ではなく重回帰分析が必要となる場合も多い。その理由を欠落変数問題(omitted variable problem)として定式化する。
まず、単回帰分析では、\(X_i\) が興味のある説明変数であり、\(X_i\) が \(Y_i\) に与える効果のみを推定する。 この場合、\(Y_i\) と \(X_i\) の単回帰モデルは、
\(Y_i=\beta_0+\beta_1 X_i +u_i\)
と書ける。\(\beta_1\) が \(X_i\) の \(Y_i\) への効果を表す。したがって \(\beta_i\) を推定し統計的推測を行うことが、回帰分析の目的となる。 この単回帰モデルに最小二乗法(OLS)を適用し \(\beta_i\) の一致推定量を得るわけであるが、推定値に一致性を持たすためには、\(E(u_i|X_i)=0\) の仮定が必要になる。 この \(E(u_i|X_i)=0\) という仮定は、「\(X_i\) と \(u_i\) の間には相関がない」ことを意味する。 しかし、実際の実証分析ではこの仮定が満たされず \(E(u_i|X_i) \neq 0\) となることが多い。
どのような場合に説明変数と誤差項の間に相関が生じるのか、次の例をもとに考えてみる。
Example Soybean Yield and Fertilizer
大豆の収量がモデルによって決定されるとします。
\(yield=\beta_0+\beta_1 fertilizer+u,\)
\(Y_i(yield)= 収量\)、 \(X_i(fertilizer)=肥料の量\)である。分析者は,他の要因を固定した場合の、大豆収量に対する肥料の効果に関心がある。この効果は \(\beta_1\)で与えられる。
→\(\Delta yield=\beta_1 \Delta fertilizer.\)
ここで、土地の質や降雨量などの要因を\(V_i\)とすると、\(V_i\)は\(Y_i= 収量\)や\(X_i=肥料の量\)に影響を与えることになる(上質の土地や日当たりなどの環境の良い場所では、そもそも大豆が多く収穫できるため肥料の量を減らす可能性がある)。 この\(V_i\)という変数を無視して上式のようなモデルを組み立て得ると、この\(V_i\)は誤差項\(u\)に含まれることになる。
こうなると、\(E(u_i|X_i)=0\)(\(=X_i\) と \(u_i\) の間には相関がない)が満たされず、最小二乗推定による\(\beta_1\)の推定が偏ったもの(つまり、バイアスをもったもの)になってしまう。このように、因果関係を推論する際に必要な変数が欠落して起こる推定値の偏りを欠落変数バイアス(omitted variable bias)といい、このバイアスをいかに取り除いていくかが欠落変数問題として定式化されているのである。
6.2.3 欠落変数問題の解決法としての重回帰分析
「欠落変数問題」は重回帰分析を用いることで解決できる可能性がある。
具体的には、欠落変数問題を起こしそうな変数をモデルに含めて重回帰分析をすることで、欠落変数の問題を回避することができる。
例えば、大豆の収量と肥料の関係を検証したい場合に、日当たりの影響を考慮したいのであれば、
\(Y_i(大豆収量)=\beta_0+\beta_1 X_i(肥料)+ \beta_2 V_i(日当たり)+v_i\)
というモデルを推定することで、日当たりによって引き起こされていた欠落変数の問題は回避できる。
※懸念される要因を変数として加えることでこのモデルの誤差項 \(v_i\) は\(X_i\), \(V_i\) とは無相関になる。なお以下では、重回帰モデルの誤差項として単回帰モデルと同じく \(u_i\) を使用する。
もう少し明示的に式で表すと、次のようになる。
日当たりを \(V_i\)、観測誤差を \(v_i\) とすると、誤差項は\(u_i=V_i+v_i\) と表すことができる。 農業者は \(V_i\) に応じて \(X_i\) を決めており、その関係を \(X_i=h(V_i)\) とする。この関係を逆に表すと \(V_i=k(X_i)\) と書ける(\(k\) は \(h\) の逆関数)。
したがって、\(u_i=k(X_i)+v_i\)となり単回帰モデルは以下のように書き直すことができる。
\(Y_i=\beta_0+\beta_1 X_i +k(X_i)+v_i\)
\(v_i\) は観測誤差なので、\(X_i\) が変化しても平均的には \(v_i\) は変化しない。 ゆえに、\(X_i\) の変化がもたらす平均的な \(Y_i\) の変化は \(\beta_1 X_i\) と \(k(X_i)\) の変化の合計となる。つまり、\(X_i\) の変化を原因とする\(Y_i\) の変化を正しく測れていないことになる。
一般的には、興味のある説明変数は \(X_{1i}\) だが、ほかに \(X_{1i}\) と相関を持ち、\(Y_i\) に影響を与える変数が \(X_{2i},...,X_{ki}\)とある場合には、\(X_{1i},X_{2i},...,X_{ki}\)をすべてを含め、
\(Y_i=\beta_0+\beta_1 X_{1i}+\beta_2 X_{2i}+...+\beta_k X_{ki}+u_i\)
というモデルを考える。この \(u_i\)は、モデルに含まれている説明変数とは相関を持たない。 逆にいえば、誤差項が説明変数とは相関を持たなくなるまで、説明変数を加えていくことによって欠落変数のバイアスを回避するということになる。
このようにモデルに欠落変数問題を引き起こしそうな変数を追加することを、コントロールするという。 またその目的で追加される変数のことを、コントロール変数という。
6.3 演習(宿題あり)
授業で用いたモデルに対して、自身が考える欠落変数問題を引き起こしそうな変数(コントロール変数)を追加し、重回帰モデルによる推定を行う。

以下のステップに従い推定を行ってください。この途中経過において出力した結果をWord等に貼り付けて提出してください。
6.3.1 STEP.1 仮説の設定
ここでは、受験者数に対する人口の影響を正しく推定するということを主目的とする。 コントロール変数の選定においては、先行研究でその影響が立証されている変数(データ)を参考にすると良い。 一般に公的セクターへの入職行動については、失業率や官民賃金格差などの経済要因が負の影響を与える(不況時に入職希望者が増加する)ことがわかっている。最近では経済要因だけではなく経済外的要因(教育水準、遺伝、誠実さ、親の職業、愛国心、名誉心など)への関心が高まっている。特にPSM(Public Sector Motivation)と呼ばれる個人の内発的動機が着目されており、通常は観察不可能な個人の変数をいかに数値に落とし込んで入職行動への影響を評価するかの議論が展開されている。 先行研究以外にも自身の関心のある変数を選定しても良い。
なお、追加する変数(コントロール変数)は3つまでとする。
6.3.2 STEP.2 分析モデルの構築
理論(仮説)に基づき、影響を与えそうな変数を選定して、実際に入手できるデータをベースに分析モデルを組み立てことになる。
\(jcga=\beta_0+\beta_1 age18 + \beta_2 ??? +\beta_3 ??? +\beta_4 ???+u,\)
| 変数の説明 |
|---|
\(jcga=\) 各都道府県における海上保安大学校への受験者数(単位=人) \(age18=\) 各都道府県における18歳人口(単位=人) \(???=\)自身が考える影響を与えそうな変数① \(???=\)自身が考える影響を与えそうな変数② \(???=\)自身が考える影響を与えそうな変数③ \(u=\) 誤差項 |
| 変数名 | 説明 | 出典 |
|---|---|---|
| 海保大受験者数(人) | 各都道府県ごとの第1次試験受験者数(2021年) | 海上保安庁総務部教育訓練管理官の提供 |
| ???? | 各都道府県ごとに集計された 2021年 or 2020年のデータ |
???? |
6.3.3 STEP.3 データの選定
各府省が公表する統計データを一つにまとめ、統計データの検索をはじめとした、さまざまな機能を備えた政府統計のポータルサイト「政府統計の総合窓口(e-Stat)」からデータの選定及び収集を行う。
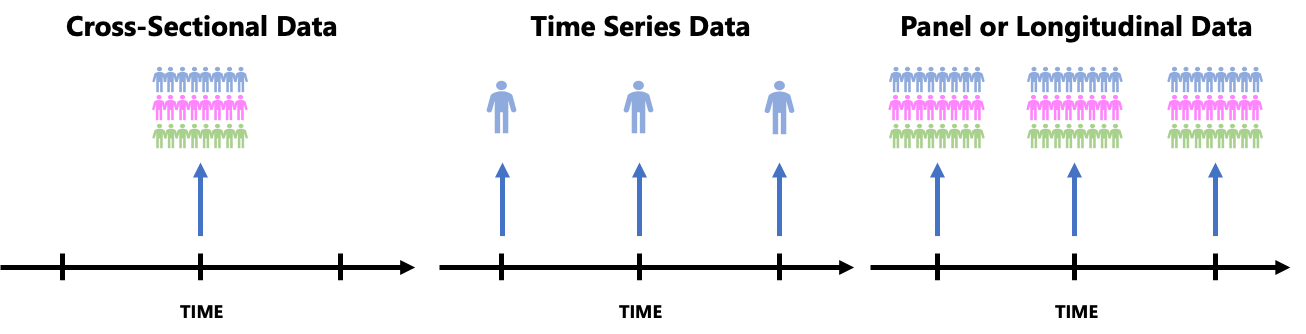
今回のデータは都道府県別・2021年の年次データであるクロスセクションデータになる。e-Statから同じ都道府県別・2021年の年次データを探すことになる。
まずはブラウザで「estat」を検索。「e-Stat 政府統計の総合窓口」にアクセス。
「e-Stat 政府統計の総合窓口」>「統計データを活用する」>「地域」タブをクリック。
「都道府県データ」を選択し、「データ表示」をクリック
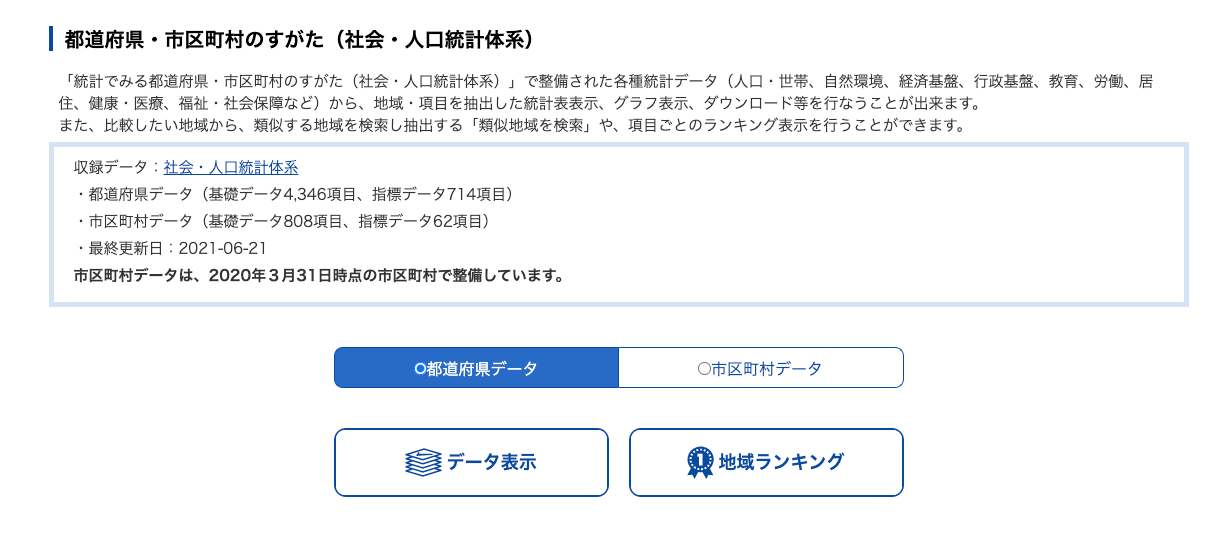
「地域選択」で47都道府県を選択

※このとき、「00000_全国」は選択しない。
「表示項目選択」で様々なデータを確認できる ⇒ 「分野🔽」で選択可能、項目を選択し確定。
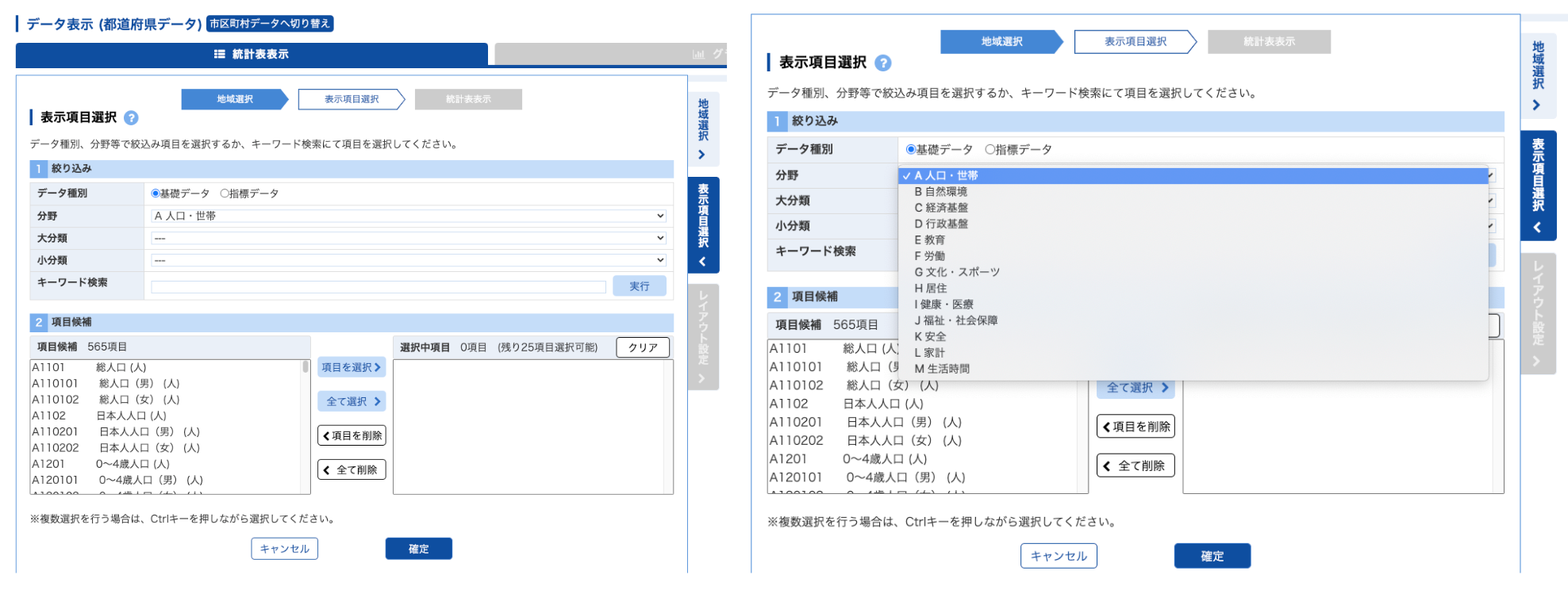
「項目」を選択し、「確定」をクリック。
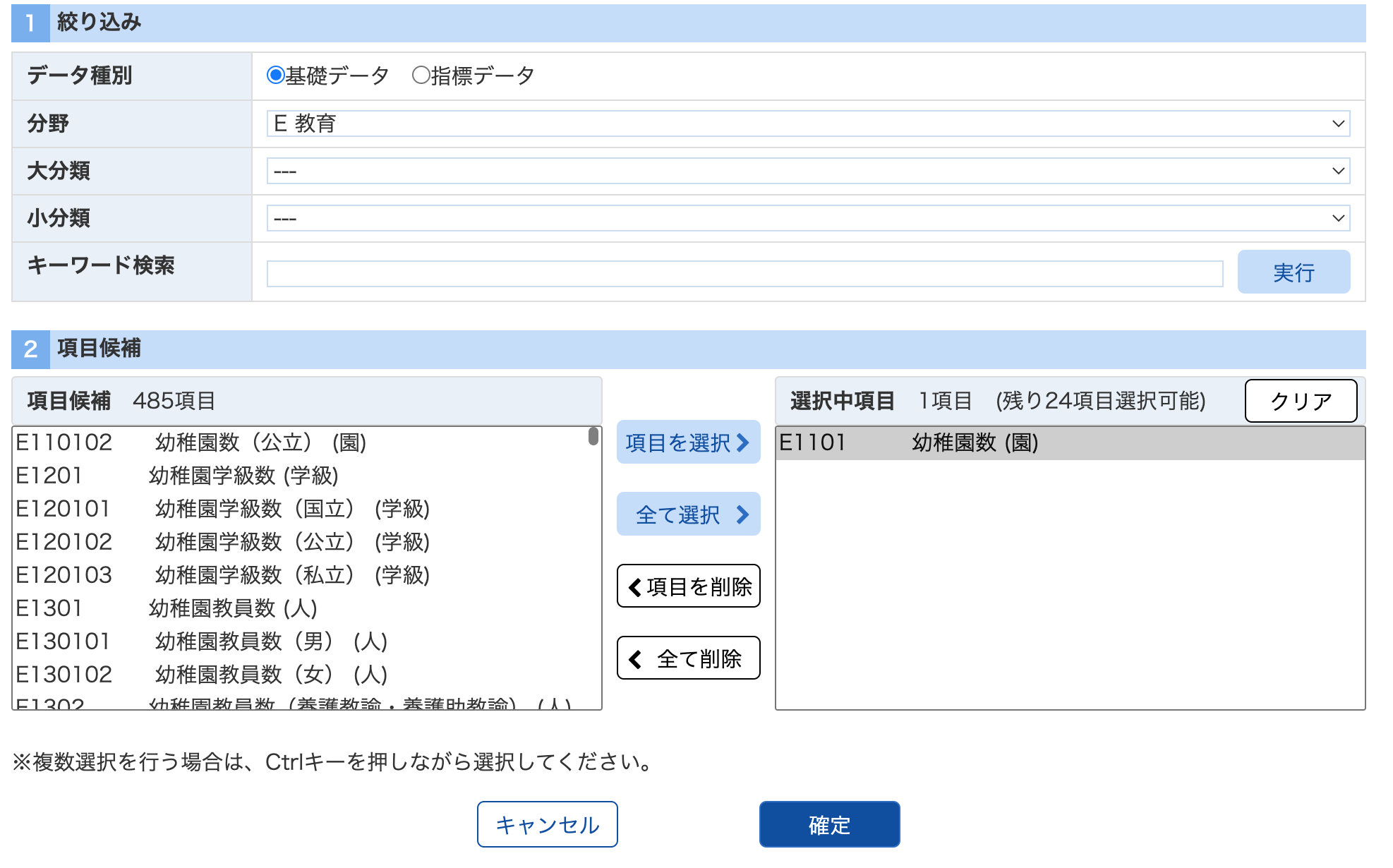
2021年、もしくは2020年があればダウンロードし、エクセルファイル「bunseki1.xlsx」にデータを追加する。


※ファイル形式は「CSV形式」で構わない。

ダウンロードしてファイルを開く。
※ただし、e-statは最新データの反映に時間がかかるので、2021年もしくは2020年のデータがない場合が多い。その際は、自身の関心のある変数について出典元を確認し、Googleから出典元にアクセスしダウンロードする。出典元については、e-Statの変数名をクリックすると確認できる。

「bunseki1.xlsx」を開き、ダウンロードしたデータの必要箇所をコピペする。
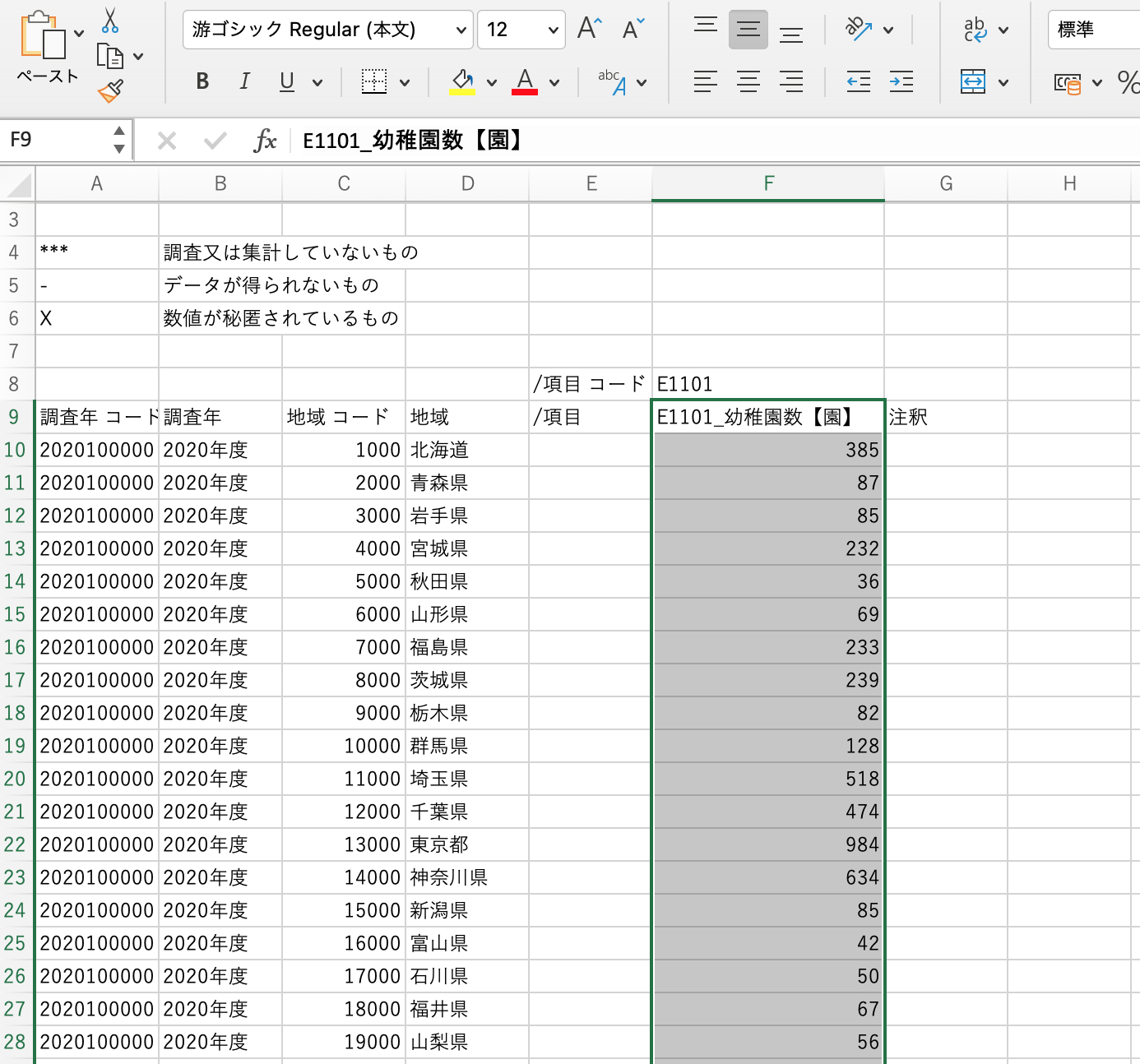

2021年の海上保安大学校受験者と人口の関係について正しく推定を行うためにコントロール変数を追加した以下の重回帰モデルを用いて分析を行うこととする。
\(jcga=\beta_0+\beta_1 age18 + \beta_2 ??? +\beta_3 ??? +\beta_4 ???+u,\)
\(jcga\):各都道府県における海保大校受験者数(単位=人)
\(age18\):各都道府県における18歳人口(単位=人)
\(???\):???(単位=???)
\(???\):???(単位=???)
\(???\):???(単位=???)
\(u\):誤差項
6.3.4 STEP.4 予備的分析(Homework③)
データが準備できたら、パラメータの推定を行う前に、エクセルや統計ソフトなどを用いて、利用するデータの特性を把握するための予備的分析を行う。
予備的分析では、
① データの平均値、標準偏差、最大値、最小値などの基本統計量(記述統計量)を確認する。
② 各変数のヒストグラムを確認する。
③ 被説明変数を縦軸、説明変数を横軸にとり、それぞれの組み合わせをプロットする散布図を示す。
まずは、データの準備、記述統計量の出力や分析に使うパッケージのインストールを行う。
library(tidyverse)
library(readxl)このほかにもstargazerというパッケージも利用するため、インストール及び読み込みを行う。
install.packages('stargazer')
library(stargazer)先ほど変数を追加したデータをアップロードし、データの読み込みと確認を行う。
bunseki1 <- read_excel("bunseki1.xlsx")
View(bunseki1)6.3.4.1 ①記述統計量の確認
まずはデータの特徴を掴むために記述統計量の確認を行う。 データの平均値や、最大値・最小値、どのくらい偏りがあるのか(分散)を数値から把握する。 stargazerで記述統計の表を出力する。
stargazer(as.data.frame(bunseki1),
type = "html",
title = "記述統計",
digits = 2)出力されたhtmlテキストをコピーする。次のセルでは、コードではなくテキストを追加し、コピーしたテキストを貼り付ける。
出力された「記述統計」の表をスクショ([Win]+[Shift]+[S]のショートカットキー)しWordに貼り付ける。
6.3.4.2 ②ヒストグラムの確認
データ処理を行いやすいように変数名(列名)を日本語からアルファベット表記に変更する。 そのまま日本語で処理を行っていも良いが、コンピュータは日本語を理解するのが苦手なのでエラーが起きやすい。 変更する際は、自身が認識できるアルファベットの羅列であれば何でも良い。
colnames()で変数名(列名)を確認。
colnames(bunseki1)names()で変数名(列名)を変更。c( )は、『Combine Values into a Vector or List』を意味する関数であり、引数に渡したオブジェクトをベクトルかリストの形式で結合してくれる関数のことである。文字や数字の行を鎖状に繋げ、行ベクトルにすると理解しておくとよい。names()とc( )を組み合わせることで、変数名を設定することができる。数学の行列と同じ考え方で、列(変数)の数と行(c( )の中身)の数を等しくしなければエラーが起きるので注意。
names(bunseki1) <- c("num", "year", "area", "juken", "age18", "???", "???" , "???" )データの特徴をさらに掴むためにヒストグラムと散布図を描く。
海保大受験者数のヒストグラム(度数分布図)を出力。
hist(bunseki1$juken,
breaks=seq(0,80,5),
xaxp=c(0, 80, 10),
main="Histogram",
xlab="海保大受験者数",
ylim=c(0,30),
col="lavender",
family= "Noto Sans CJK SC").png)
上記を参考に3つのコントロール変数(???)のヒストグラム(度数分布図)を出力しWordに貼り付ける。
6.3.5 STEP.5 パラメータの推定
予備的分析でデータの特性を把握したら、回帰分析を実施し、パラメータの推定を行う。

まずは以下の単回帰モデル設定しをOLSにより推定する。
6.3.5.1 ①分析モデル(単回帰)
\(jcga_i=\beta_0+\beta_1age18_i+u_i\) (1)
(海保大受験者数 = \(\beta_0\) + \(\beta_1\) 18歳人口 + 誤差)
\(jcga_i=\beta_0+\beta_1\,???_i+u_i\) (2)
(海保大受験者数 = \(\beta_0\) + \(\beta_1\) ??? + 誤差)
\(jcga_i=\beta_0+\beta_1\,???_i+u_i\) (3)
(海保大受験者数 = \(\beta_0\) + \(\beta_1\) ??? + 誤差)
\(jcga_i=\beta_0+\beta_1\,???_i+u_i\) (4)
(海保大受験者数 = \(\beta_0\) + \(\beta_1\) ???+ 誤差)
各変数については\(jcga\):各都道府県における海保大校受験者数(単位=人)、\(age18\):各都道府県における18歳人口(単位=人)、\(???\):???(単位=???)、\(???\):???(単位=???)、\(???\):???(単位=???)、\(u\):誤差項である。
Rでモデルを組み立てる。
model_1 <- lm(juken ~ age18 , data = bunseki1)
model_2 <- lm(juken ~ ??? , data = bunseki1)
model_3 <- lm(juken ~ ??? , data = bunseki1)
model_4 <- lm(juken ~ ??? , data = bunseki1)liner model(lm)の中で、lm(被説明変数〜説明変数, data = データ)を指定して推定を行う。
推定結果をstargazerでまとめて出力する。
stargazer(model_1, model_2, model_3, model_4,
digits = 3, # 小数点以下 3 位まで示す
style = "ajps", # AJPS仕様(学術誌のスタイル),
keep.stat = c('n', 'rsq', 'adj.rsq', 'f'),
df = FALSE, #自由度の削除
covariate.labels = c("18歳人口(万人)",
"???",
"???",
"???"),
dep.var.caption = "被説明変数", # 変数の種類を明示
dep.var.labels = "海保大受験者数", # 被説明変数の名前
title = "分析結果", # タイトル
type ="html")出力されたhtmlテキストをコピーする。次のセルでは、コードではなくテキストを追加する。

先ほどコピーしたhtmlテキストを貼り付けると整理された表が出力される。
出力された「推定結果」の表をスクショ([Win]+[Shift]+[S]のショートカットキー)しWordに貼り付ける。 ※表中の「Constant」は「定数(切片)」を意味している。回帰式でいうと\(\beta_0\)である。
6.3.5.2 ②分析モデル(重回帰)
欠落変数バイアスに対処した推定を行うために以下の重回帰モデルを用いる。
\(jcga=\beta_0+\beta_1 age18 + \beta_2 ??? +\beta_3 ??? +\beta_4 ???+u,\) (5)
(海保大受験者数 = \(\beta_0\) + \(\beta_1\) 18歳人口+\(\beta_2\) ??? +\(\beta_3\) ??? +\(\beta_4\) ??? 誤差)
Rで重回帰モデルを作成する。
model_5<- lm(juken ~ age18 + ??? + ??? + ???, data = bunseki1)推定結果をstargazerでまとめて出力する。
stargazer(model_1, model_2, model_3, model_4, model_5,
digits = 3, # 小数点以下 3 位まで示す
style = "ajps", # AJPS仕様(学術誌のスタイル),
keep.stat = c('n', 'rsq', 'adj.rsq', 'f'),
df = FALSE, #自由度の削除
covariate.labels = c("18歳人口(万人)",
"???",
"???",
"???"),
dep.var.caption = "被説明変数", # 変数の種類を明示
dep.var.labels = "海保大受験者数", # 被説明変数の名前
title = "分析結果", # タイトル
type ="html")出力されたhtmlテキストをコピーする。次のセルでは、コードではなくテキストを追加する。

先ほどコピーしたhtmlテキストを貼り付けると整理された表が出力される。
出力された「推定結果」の表をスクショ([Win]+[Shift]+[S]のショートカットキー)しWordに貼り付ける。 ※表中の「Constant」は「定数(切片)」を意味している。回帰式でいうと\(\beta_0\)である。
以上のステップをこなし、出力結果等をWord等に貼り付けレポートとして作成後、Canvasから提出してください。
提出期限:2022年9月16日(金)2359まで
提出方法:Canvasから提出