Chapter 5 Rによるデータ分析③

5.1 線形単回帰モデル

データを用いてある変数（事象）間の関係性を計測する手法の一つに回帰分析（ regression analysis）がある。

例えば、横軸（$X$軸）に失業率、縦軸（$Y$軸）に犯罪率をとりデータをプロットすると上図のような右肩上がりな傾向が示された。このプロットの傾向を式で表す一番良い線（モデル）を当てはめると多くの場合、

例：　$Y$（犯罪率） = $\beta_0$ + $\beta_1$ $X$（失業率）

という線形関係で式を組み立てることができる。これは$X$の変化によって$Y$がどの程度変化するのかを直線関係で捉えている。この式を線形回帰モデルという。

この式では、左辺（被説明変数）にある犯罪率が、右辺にある失業率（説明変数）によって説明されることを示している。

$\beta_0$と$\beta_1$は、パラメータ（回帰係数）とよばれ、実証分析では、これらパラメータをデータから推定することが主たる目的となる。このパラメータを求めることで、失業率に応じてどの程度犯罪率が増減するかといった法則性が見いだせる。

最小2乗法（OLS）を用いてデータに直線を当てはめたとき、得られた推定回帰式（図中の赤線）が以下の式である。

$\hat{Y}_i=\hat{\beta}_0+\hat{\beta}_1 X_i$

5.2 分析モデル

$jcga_i=\beta_0+\beta_1age18_i+u_i$　　　(1)

（海保大受験者数 = $\beta_0$ + $\beta_1$ 18歳人口 + 誤差）

5.3 推定結果

出力結果から以下の推定回帰式が得られる。

$\hat{jcga}_i=1.976+0.0003 \,age18_i$

この結果から、

⇒　各都道府県の18歳人口が1人増えると受験者数が「0.0003」人増える

⇒　各都道府県の18歳人口が1万人増えると受験者数が「3.0」人増える

という可能性が示唆できる。

一方で、ここで問題となるのが、回帰係数の「信頼度」である。

●$Y_i=\beta_0+\beta_1\,X_i+u_i$　（←モデル式：現実の観測値）

●$\hat{Y}_i=\hat{\beta}_0+\hat{\beta}_1 X_i$　　　（←最小二乗法から導いた推定式）

推定値である $\hat{\beta}$ は、真のパラメータ$\beta$ に近い値が出やすい確率変数である。（不偏性、一致性）

横軸は$\hat{\beta}_i$ がとり得る値、縦軸はその確率。このグラフから$\hat{\beta}_i$ は、未知の $\beta_i$ 近辺の値がでやすい確率変数であることがわかる。つまり、「当たり」が出やすいくじ引きのようなもの。

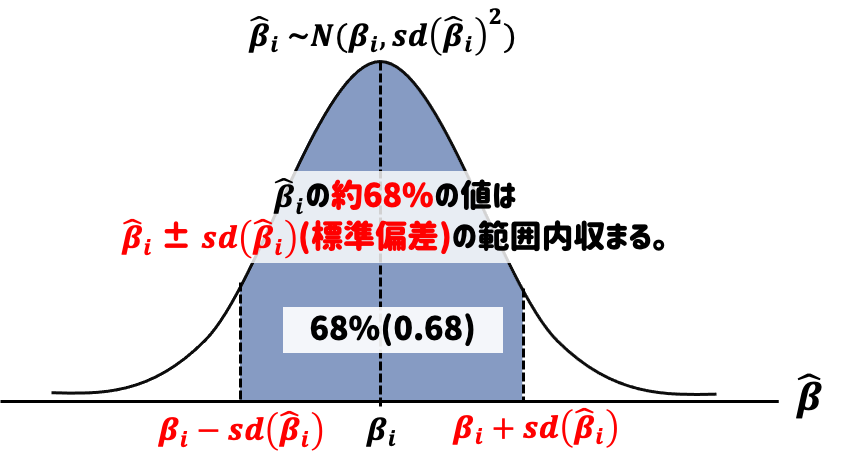
回帰分析おいて、算出した回帰係数 $\beta_i$ （パラメータ）を推定することが主目的であるが、その際には、推定値の大きさだけでなく、推定値の誤差（標準誤差）がどの程度大きいかどうかにも着目する。

→　得られた推定値の誤差が非常に大きいと、結果が安定的な法則性を示しているか疑わしい。

→　特に回帰係数 $\beta_i$がゼロの場合、説明変数が被説明変数に与える影響がないということになる

そこで、実証分析においては、得られたパラメータの推定値がゼロかどうかの仮説検定を実施する。 検定によりパラメータがゼロになる可能性が低いといえれば、この推定値は「統計的に有意である」といい、説明変数は被説明変数に影響を与えていると強く主張できる。

5.4 仮説検定の基礎

$H_0: \beta_i=\beta_i^*$ （帰無仮説）

$H_1:\beta_i \neq \beta_i^*$ （対立仮説）…..[1]　(両側検定)

回帰係数 $\beta_i$ が未知である以上、真の値 $\beta_i$ と仮説値 $\beta_i^*$ との差である $\beta_i-\beta_i^*$ もまた未知である。そこで、 $\beta_i-\beta_i^*$ を、推定値 $\hat{\beta}_i$ を用いて $\hat{\beta}_i-\beta_i^*$で推定することにする。

ある一定の条件を満たせば $\hat{\beta}_i$ は $\beta_i$ に近い値が出やすい（不偏性、一致性）確率変数である。

推定値 $\hat{\beta}_i$ は、期待値 $\beta_i$ 、分散 $V[\hat{\beta}_i]$ の正規分布に従う。 ただ、$\hat{\beta}_i$ はあくまでも確率変数なので、仮に回帰モデル式のパラメータが仮説通り $\beta_i=\beta_i^*$ であったとしても、推定値としてちょうど $\hat{\beta}_i=\beta_i^*$ が得られる見込みはない。したがって、$\hat{\beta}_i-\beta_i^*$ が「完全にゼロか否か」ではなく、「許容範囲か否か」に着目し検定を行う。

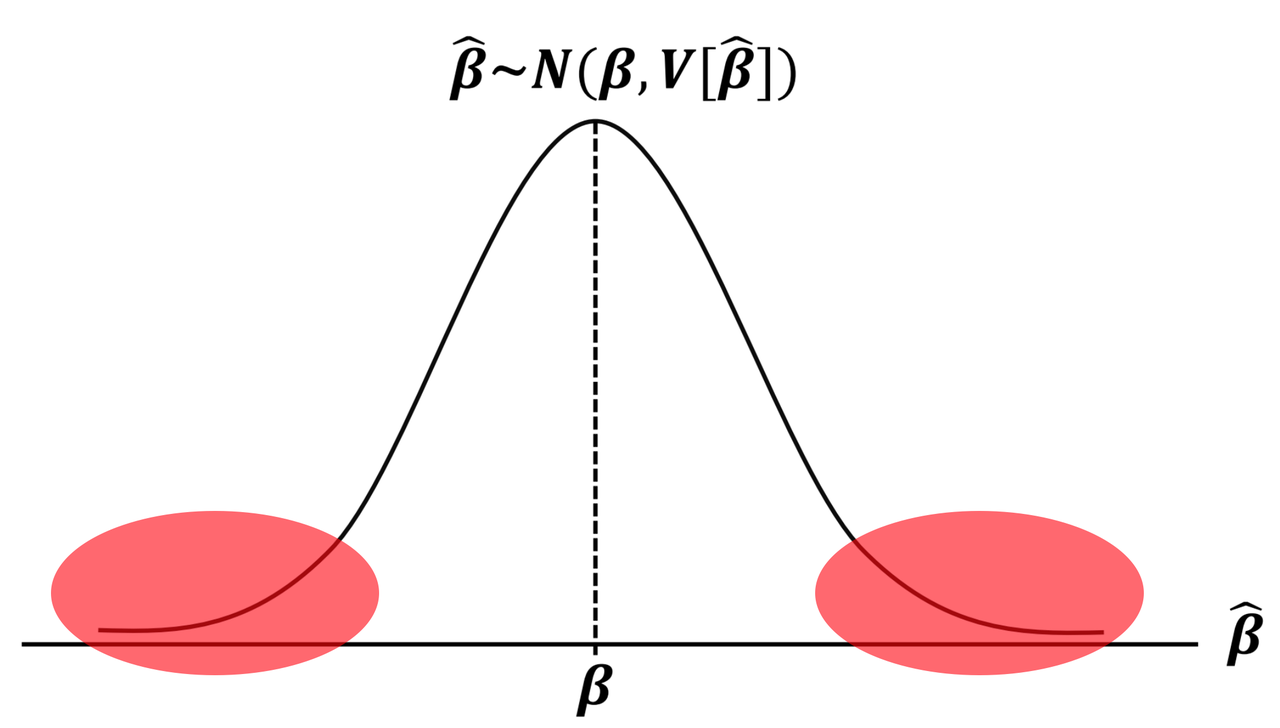
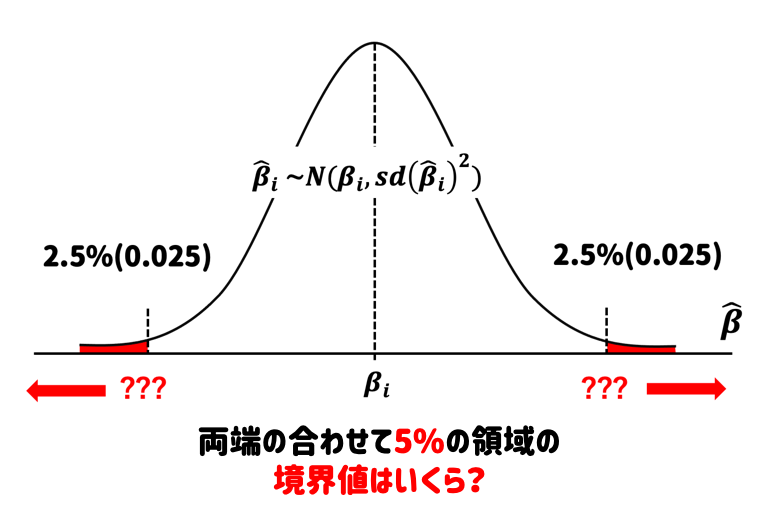
正規分布の面積は確率なので、上右図の赤の領域は、 $$\beta_i$$ の値として取りづらい領域になる。 この領域のことを棄却域という。 通常は、棄却域内の事象は確率5%以下で起きると設定する。 （⇒　有意水準：第１種の過誤を犯す確率 $\alpha=0.05$ ）

この $\alpha$ （有意水準）を低く設定したにもかかわらず、$\beta_i=\beta_i^*$が上右図の棄却域内に位置するならば、滅多に起きない稀な事象が起きたと解釈することができ、$H_1:\beta_i \neq \beta_i^*$が統計的に支持されることになる。

結論として、 「$\beta_i$は、有意水準5%で、$\beta_i^*$とは有意な差がある」を得る。

5.4.1 仮設検定の例（統計学の復習）

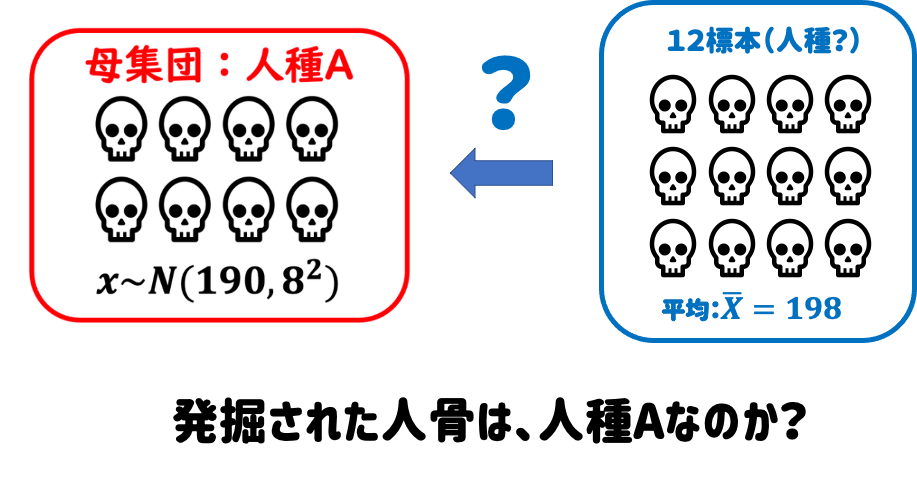
これまでに発見された頭蓋骨から、

• 人種Aの頭蓋骨の長さの平均は、190mm

• 人種Aの頭蓋骨の長さの標準偏差は、8mm

であることがわかっている。

ここで新たな人骨を発見。

確率の定理と高度な数学理論を用いれば、正規分布に従うある母集団から抽出した標本の分布は、以下の定理で正確に求めることができる。

人種Aという母集団分布から導かれた標本分布に従う本来なら、平均値190mmが期待されるが、今回は「198mm」だった。これは偶然（たまたま大きい人骨が発掘された）なのか、必然（そもそも人種Aではない人骨だった）だったのか検定を行う。

このときに必要なのが「標準正規分布」。

正規分布の面積（確率）は「1.0」で不変。

つまり、標準的な形をした正規分布を一つ定め、任意の点における面積（確率）を求めておけば、どんな形をした正規分布の面積（確率）も変形するだけで求めることが可能。

つまり、標準的な形をした正規分布を一つ定め、任意の点における面積（確率）を求めておけば、どんな形をした正規分布の面積（確率）も変形するだけで求めることが可能。

面積がわかっている標準的な粘土から、求めたい箇所を切り取る。

この切り取った粘土を変形することで様々な形をした粘土の部分面積を求めることが可能

話を戻すと、、、

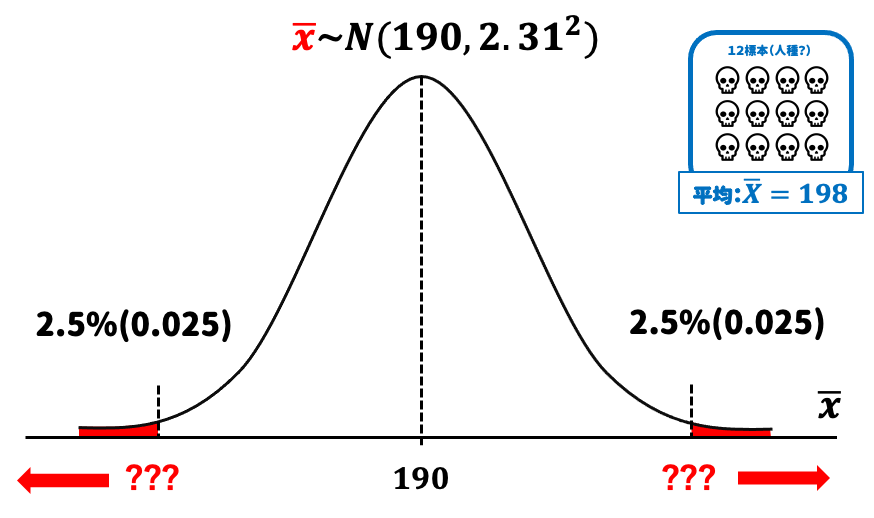
「？？？」の数値を求めたい。標準正規分布で考えると、両端の合わせて5%の領域の境界値はいくらかを求める。

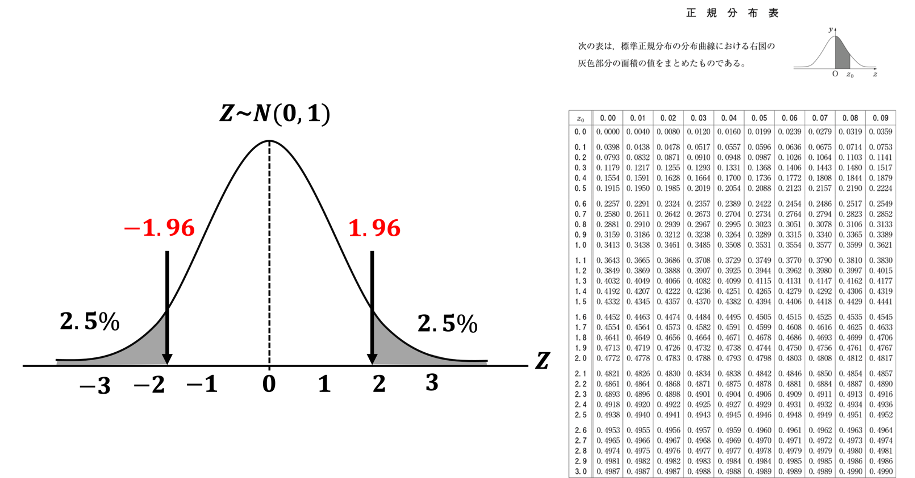
→　正規分布表から「±1.96」であることがわかった。分布の形を変形してあげる。

5.5 有意性検定

5.5.1 OLS（最小二乗法）推定量の統計的性質

OLS推定量は、一定の条件のもとで「不偏性」「一致性」「漸近正規性」といわれる統計的に望ましい性質を持つ。この「一定の条件」とは以下の仮定(1)～(4)のことをいう。

1. データ$(Y_i, X_i), i=1, ..., N$ は互いに独立で同一な分布に従い $(i.i.d.)$、 $Y_i=\beta_0+\beta_1 X_i+u_i$という関係を満たす 。

   →この条件は「無作為標本」であれば満たされる。

   

   例：味噌汁の味を決めるのに上澄みだけをすくって味見し、判断することはない。しっかり全体を混ぜて偏りをなくすことで味噌汁全体の味を判断することができる。

2. 説明変数を条件とすると、誤差項の期待値は０である。

   $E(u_i|X_i)=0$

   →「欠落変数バイアス」が解決されているときに満たされる。

   例：第三の変数が影響している場合に起きるのが「欠落変数バイアス」である。実際に$X$が$Y$の原因だとしても、 $V$のように$X$と$Y$の両者に影響する変数がある可能性がある。このような$V$は、交絡変数 (confouding variable or confounder) と呼ばれる。

   交絡変数は、必ず統制（コントロール）する必要がある。交絡変数を統制しないと、推定にバイアスが生じる。このバイアスを欠落変数バイアス (omitted variable bias)と呼ぶ。経済学では、選択バイアス（selection bias） とも呼ばれる。

   $Y$と$X$の両者に影響を与える$V$という変数があるとき、$V$を無視して、$Y_i=\beta_0+\beta_1 X_i+u_i$ という式を考えると、$V$ は誤差項$u$に含まれることになる。 そうすると、説明変数$X$と誤差項$u$の間に相関があるので、$\beta_i$ の推定が偏ったもの（つまり、バイアスをもったもの）になってしまう。

3. $x_i$ と $u_i$ の4次モーメントが有限である。

   $0<E(X_i ^4)<\infty \ , 0<E(u_i ^4)< \infty$

   →　各データに異常値がないという仮定

4. 多重共線性がない（重回帰モデルの場合）

   →　同じ変数を複数、モデルに含めてはいけないという仮定

   ここでの「同じ変数」という言葉は通常よりも広い意味で用いられている。つまり、説明変数間で極めて相関の高い変数同士をモデルに加えてはいけない。

上記仮定を満たすとき、OLS推定量は「不偏性」「一致性」「漸近正規性」という統計的に望ましい性質を持つ。

• 不偏性：推定量の期待値が推定対象の真の値に等しいという性質。

  回帰分析においては、 $E(\hat{\beta}_0)=\beta_0$ , $E(\hat{\beta}_1)=\beta_1$ が成り立つこと。

• 一致性：データ数$N$ が大きくなるとともに推定量$\hat{\beta}_1$ と $\hat{\beta}_0$ が、真の値 $\beta_0$, $\beta_1$ に近い値をとる確率が１に近づくということ。回帰分析においては、 $\hat{\beta}_0\stackrel{p}{\longrightarrow } \beta_0$ , $\hat{\beta}_1\stackrel{p}{\longrightarrow } \beta_1$ が成り立つこと。（一般に、” $\stackrel{p}{\longrightarrow }$” は統計学の用語で確率収束と呼ばれる収束を表す記号であり、大雑把にいうと $N$ が大きくなるとともに左辺の確率変数と右辺の差が小さくなることを表す。）

  不偏性と一致性は、それぞれの意味で推定量が真の値に近いことを保証しており、これらは推定量として望ましい性質である。このような性質を有するから、回帰モデルのOLS推定量は真の値 $\beta_0$, $\beta_1$ の推定量として良いものといえる。

• 漸近正規性：簡単にいうと推定量の特性のこと。

  「漸近的」とは、サンプルサイズが大きくなる（つまり、無限大に近づく）ときに推定量がどのように動作するかを指す。「正規性」は正規分布を指します。したがって、漸近的に正規である推定量は、サンプルサイズが無限に大きくなるにつれて、ほぼ正規分布になる。

  

  漸近正規性自体は、直接的に推定量の良し悪しにかかわる性質ではないかが、係数に関する仮説検定や区間推定を行う基礎となる重要な性質である。

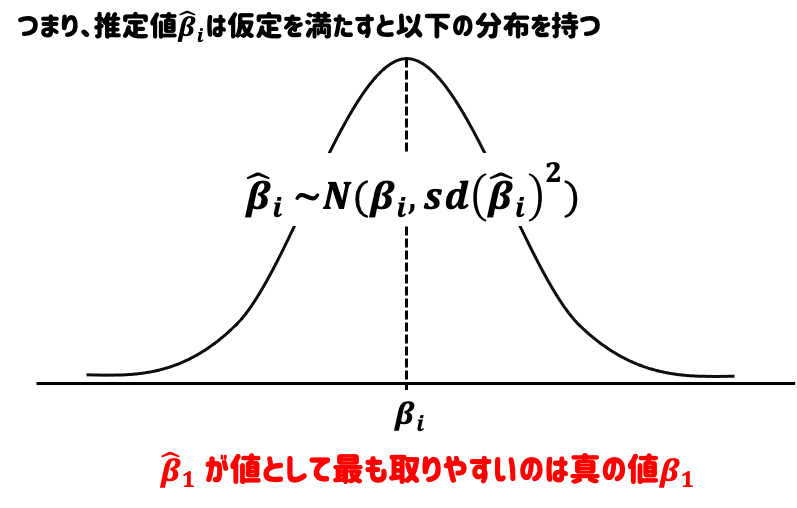
これをイメージで捉えると、

推定値$\hat{\beta}_i$のがバラツキが小さい場合は、高い確率で真の値$\beta_i$周辺の値がでる。

推定値$\hat{\beta}_i$のがバラツキが大きい場合は、真の値$\beta_i$周辺の値がでにくく、$\hat{\beta}_i=0$の可能性も排除できない。この可能性を排除することができれば、$X$が$Y$に影響を与えると強く主張することができる。そこで、推定値のバラツキに着目し、$\hat{\beta}_i=0$の可能性を検討する。 このときに使う検定が「有意性検定」である。

5.5.2 有意性検定の基礎理論

逆に捉えると、

つまり、$\hat{\beta}_i=0$が赤色の領域に落ちるなら、$\hat{\beta}_i=0$という値は滅多に取らない稀な値として、その可能性を排除することができる。そこで、赤色の領域の境界値を求めて検定を行っていくのである。

人骨の例と同じように、標準正規分布からその境界値を求めていく。

ただ、この検定には１つ問題がある。いままで触れてこなったが、 $Z$値を求めるには、$\hat{\beta}_i$ の標準偏差$sd(\hat{\beta}_i)$が必要になる。 この標準偏差$sd(\hat{\beta}_i)$は、

$sd(\hat{\beta}_i)=\sqrt {V[\hat{\beta}_i]}=\sqrt \frac{\sigma^2}{\omega_i^2}= \frac{\sigma}{\omega_i}$

という式で算出できる。分子$\sigma^2$は母集団の分散、分母$\omega_i^2$はデータから決まる定数である。

人骨の例の場合には、人種Aの頭蓋骨の長さの平均は$190mm$、人種Bの頭蓋骨の長さの平均は$196mm$であり、これら長さの標準偏差は$8mm$であることがわかっている。なので、新たに発掘された１２個の頭蓋骨（１２個の無作為標本）について、統計学の定理（約束事）から分布を定義することができる。

したがって１２個の頭蓋骨（１２個の無作為標本）は標準偏差は

→　$\frac{\sigma}{\sqrt{n}}=\frac{8}{\sqrt{12}}\fallingdotseq2.31$

となる。

しかし、今回のような推定量の検定においては、母集団の標準偏差$\sigma$や分散$\sigma^2$がすでに分かっていることはほとんどない。なので母集団の分散もどきをデータから推定して$\hat{\beta}_i$ の標準偏差$sd(\hat{\beta}_i)$の計算式に代理してあげる必要がある。

つまり、回帰係数とともにこの分散 $\sigma^2$ についても推定しなければならない。 証明は省略するが以下の推定式で、$\sigma^2$の良い推定値$s^2$を得ることができる。

$s^2=\frac{1}{n-(k+1)}Q(\hat{\beta}_0,\hat{\beta}_1,\hat{\beta}_2,..., \hat{\beta}_k)$

$n$ は観測数、$k$ は説明変数の数、$Q(\hat{\beta}_0,\hat{\beta}_1,\hat{\beta}_2,..., \hat{\beta}_k)$ は残差平方和になる。

したがって、単回帰モデルにおいて$\sigma^2$ を推定した$s^2$ は以下の式で表せる。

$s^2=\frac{\sum \hat{u}^2}{n-2}$

ここから、$s=\sqrt {s^2}$ を計算し、$\sigma$ の代役とする。こうして求めた、$\hat{\beta}_i$ の標準偏差$sd(\hat{\beta}_i)$は標準誤差$se(\hat{\beta}_i)$ と呼ばれ以下の式で定義される。

$se(\hat{\beta}_i)=\frac{s}{\omega_i}$

この標準誤差$se(\hat{\beta}_i)$ が小さいほど、高い精度で係数 $\beta_i$ が推定されたことになる。

以上をまとめると、 母集団の分散が既知のとき$Z$値は以下の式で求められるが、

$Z_i=\frac{\hat{\beta}_i-\beta_i^*}{sd(\hat{\beta}_i)}=\frac{\hat{\beta}_i-0}{sd(\hat{\beta}_i)}=\frac{\hat{\beta}_i}{sd(\hat{\beta}_i)}\sim N(1,0)$

母集団の分散が未知のときは、「母集団の分散もどき」を使用し分母である標準偏差$sd(\hat{\beta}_i)$を推定してあげる必要がある。この標準偏差$sd(\hat{\beta}_i)$を推定したものを標準誤差$se(\hat{\beta}_i)$という。

$Z$値を求める式の分母である標準偏差$sd(\hat{\beta}_i)$に対して標準誤差$se(\hat{\beta}_i)$を代理してあげると、

$t_i=\frac{\hat{\beta}_i-\beta_i}{se(\hat{\beta}_i)}\sim T(m)$

が得られる。これを $t$ 値（$t$統計量）と呼ぶ。

注意してほしいのは、この $t_i$ はもはや標準正規分布 $N(0,1)$ には従わず、 $t$ 分布という別の分布で確率が与えられることになる。これを $t_i\sim T(m)$ と表記する。

ここで、$m=n-(k+1)$ は $t$ 分布の自由度とよばれるもので、$n$ （データの観測数）と $k$ （説明変数の数）で決まる定数値である。

以下の図が示すように、$T(m)$ は $N(0,1)$ とよく似た形をしている。ただ、$T(m)$$ の厄介な点は、自由度 $m$ に依存して形状が若干変わる点である。なので$N(0,1)$ の両側 2.5% の棄却域が $\pm{1.96}$ と固定されているのに対し、$T(m)$ の棄却域は $m$ に応じて変化している。

このため、大半のテキストには、各自由度 $m$ に応じた $t$ 分布の棄却域が $t$ 分布表として掲載されている。 ただ、実際に使用するデータは、その観測数が $n=100$ を超えることも珍しくない。実は $n(m)$ が十分に大きい場合、$T(m)$ は $N(0,1)$ で近似できることがわかっている。したがって、$n$ が十分に大きいならば、$N(0,1)$ の棄却域 $Z_{0.025}=1.96$ で検定することができる。

※$n$ が十分に大きいとき 教科書的には、 $n=25$ 以上となっている。ただ、母分散が分からない場合は、とりあえず t分布を使っておけば間違いが無い（標準偏差$sd(\hat{\beta}_i)$の算出に使われる母集団の分散がすでに分かっていることはほとんどないので、$Z$値を用いた検定（$Z$検定）を使うのは稀なケースとなる。）

あとは人骨の例と同じように、$\hat{\beta}_i=0$が両端合わせて5％の領域の境界値（棄却域）にあるかを計算してあげれば良い。

5.5.3 有意性検定のまとめ

最小2乗法（OLS）を用いてデータに直線を当てはめたとき、得られた推定回帰式について、 $\hat{Y}_i=\hat{\beta}_0+\hat{\beta}_1 X_i$ 「$X$が$Y$に影響を与えた」とその因果関係を強く主張するためには、「$\hat{\beta}_1=0$」である可能性がないを立証すれば良い。統計学の仮説検定を実施する。

$H_0: \beta_i=0$ （帰無仮説） $H_1:\beta_i \neq 0$ （対立仮説）

を検定する。これを $\beta_i$ の有意性検定と呼ぶ。 この $H_0$ は、回帰式

$Y_i=\beta_0+\beta_1 X_i+u_i$

において、「説明変数 $X_i$ が不要である」と言っていることに等しい。 データの分析者は、$Y_i$ と $X_i$ の関係性を実証するために回帰分析をしている。 しかし、そこであえて「$X_i$ は不要では？」というスタンスをとり、検定により $H_0:\beta_i=0$ という「疑い」が棄却されることを示せば、$Y_i$$ と $X_i$ の関係性を裏付ける強力な証拠となる。

①　帰無仮説 $H_0:\beta_i=0$ を設定。 　　OLS推定値と仮説値の差　$\hat{\beta}_i-0$ 　を $t$ 値に換算。

　　$t_i^*=\frac{\hat{\beta}_i-0}{se(\hat{\beta}_i)}=\frac{\hat{\beta}_i}{se(\hat{\beta}_i)}$

②　$t$ 分布表から、自由度 $m=n-k-1$ の両側2.5%棄却域の境界値である$t_{0.025}(m)$ の値を求める。

③　$|t_i^*|>t_{0.025}(m)$ のとき、つまりOLS推定値と仮説値の差　$\hat{\beta}_i-0$ から求めた $t$ 値が、両側2.5%棄却域の境界値である$t_{0.025}(m)$ の値よりも大きい値であれば「$\hat{\beta}_i-0$ の乖離が甚大である→　$\beta_i=0$となる確率は低い」と判定し、帰無仮説 $$H_0:\beta_i=0$$ を棄却することができる。

この検定により $H_0:\beta_i=0$ という「疑い」が棄却されることを示せば、 回帰式$[Y_i=\beta_0+\beta_1 X_i+u_i]$において$Y_i$ と $X_i$ の関係性を裏付ける強力な証拠となる。

※$t$ 値は $t_i^*=\frac{\hat{\beta}_i}{se(\hat{\beta}_i)}$ 、つまりOLS推定値と標準誤差の比になる。 （統計ソフトで、推定値・標準誤差とともに出力される「$t$ 値」はこの $t_i^*$ ）

この有意性検定で $H_0$ が棄却された場合は、「係数 $\beta_i$ は統計的に有意である」と表現する。

5.6 出力された結果の「＊」の意味は？

出力された結果をみると、係数の横に「***」（アスタリスクが3つ）ついており、表の最後の行には「Note:　*p<0.1; **p<0.05: ***p<0.01」という見出しがついている。

まず、「p」については「p値（有意確率）」のことを意味している。「p値（有意確率）」というのは、OLS推定値と仮説値の差　$\hat{\beta}_i-0$ から求めた $t$ 値に対する確率（面積）のことである。

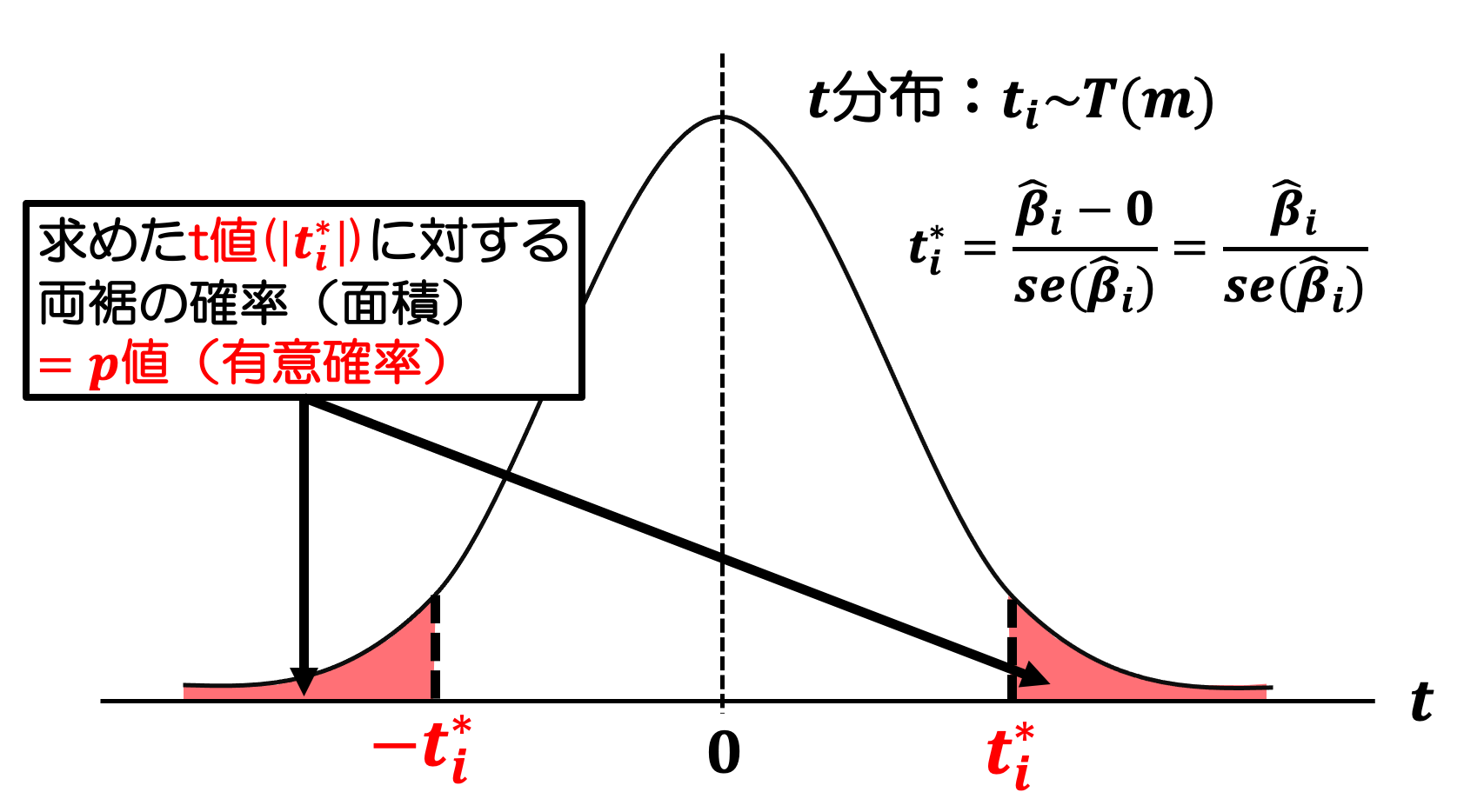
簡単にいうと、「p値（有意確率）」＝「回帰係数$\beta_i$の値が0になる確率」である。

「Note:　*p<0.1; **p<0.05: ***p<0.01」については、それぞれ、

• *p<0.1　→　p値（有意確率）が10％以下の場合は、回帰係数に「*」がつく

• **p<0.05: 　→　p値（有意確率）が5％以下の場合は。回帰係数に「**」がつく

• ***p<0.01　→　p値（有意確率）が1％以下の場合は、回帰係数に「***」がつく

という意味であり、「*」がつく回帰係数は「０」になる確率が低く、「*」の数が多いほどその係数の信頼性は高くなるのである。

今回の場合、「18歳人口」の係数「0.0003」が「0」になる確率は1％以下であり、「18歳人口」は「海保大受験者数」に影響を与えると強く主張することができるのである。

基本的には「*」がつけば係数の信頼性は高いと判断し、この「*」の有無や数により、求めた係数$\beta_i$が「統計的に有意かどうか」の判別が一目でできるようになっている。