8  ระบบสมการเชิงอนุพันธ์สำหรับนักเศรษฐศาสตร์

คำแนะนำ

ในบทนี้เป็นการศึกษาระบบสมการเชิงอนุพันธ์ จะเป็นการคำนวณเชิงตัวเลข และการคำนวณเชิงสัญลักษณ์ ผู้อ่านจะศึกษาทำความเข้าใจ การสร้างฟังก์ชันด้วยอาร์ก่อน ก็จะศึกษาบทนี้ได้โดยง่าย

ระบบสมการเชิงอนุพันธ์ ( System of Differential Equations ) คือชุดของสมการอย่างน้อยสองสมการที่เกี่ยวข้องกับ ตัวแปรมากกว่าหนึ่งตัว และ อนุพันธ์ ของตัวแปรเหล่านั้นตามตัวแปรเวลา (หรืออีกตัวแปรหนึ่ง)

8.1 นิยาม

ความหมายเชิงคณิตศาสตร์:

ระบบสมการเชิงอนุพันธ์แบบทั่วไปในตัวแปร $\mathbf{x}(t)\in {\mathbb{R}}^n$ เขียนได้ว่า: $$\frac{d\mathbf{x}}{dt}=\mathbf{f}(\mathbf{x},t)$$ โดยที่:

• $\mathbf{x}(t)=[x_1(t),x_2(t),\dots ,x_n(t){]}^{\mathrm{\top }}$ คือเวกเตอร์ของตัวแปร

• $\mathbf{f}$ คือฟังก์ชันเวกเตอร์ ที่ให้อนุพันธ์ของตัวแปรแต่ละตัว

• $t$ คือตัวแปรเวลา (หรือตัวแปรอิสระอื่น)

ตัวอย่างที่ 1 ระบบ 2 สมการเชิงเส้น $$\{\begin{array}{l}\frac{dx}{dt}=3x+4y\\ \frac{dy}{dt}=-2x+y\end{array}$$ เป็นระบบ ODE 2 ตัวแปร ซึ่งสามารถเขียนในรูปเมตริกซ์ได้ว่า: $$\frac{d}{dt}\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}3& 4\\ -2& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

ตัวอย่างที่ 2 แบบจำลองเศรษฐศาสตร์ (Price Expectation Model) $$\{\begin{array}{l}\frac{dp}{dt}=\lambda (p^e-p)\\ \frac{d{p}^e}{dt}=\gamma (p-p^e)\end{array}$$ เป็นระบบ 2 สมการไม่เชิงเส้น สมมุติว่า $p$ และ $p^e$ เปลี่ยนแปลงตามกันในเวลา $t$

8.1.1 จุดดุลยภาพ (Equilibrium Point)

คือจุด ${\mathbf{x}}^{\ast }$ ที่ทำให้ $$\frac{d\mathbf{x}}{dt}=0$$ หรือ $\mathbf{f}({\mathbf{x}}^{\ast },t)=0$ เป็นค่าที่ตัวแปรหยุดเปลี่ยนแปลง (นิ่ง)

8.1.2 ประเภทของระบบ ODE:

ประเภท	ตัวอย่าง	คำอธิบาย
เชิงเส้น (Linear)	$\frac{dx}{dt}=Ax$	คำตอบวิเคราะห์ได้ด้วยเมตริกซ์
ไม่เชิงเส้น (Nonlinear)	$\frac{dx}{dt}=x(1-x)$	วิเคราะห์ด้วย phase diagram, linearization
ระบบอิสระ (Autonomous)	$\frac{dx}{dt}=f(x)$	ไม่ขึ้นกับ $t$
ไม่อิสระ (Non-autonomous)	$\frac{dx}{dt}=f(x,t)$	มี $t$ โดยตรงในสมการ

นักเศรษฐศาสตร์ ไม่จำเป็นต้องแก้สมการเชิงอนุพันธ์ทั้งระบบเสมอไป เพราะเป้าหมายคือเข้าใจพฤติกรรมระยะยาวและโครงสร้างของแบบจำลอง มากกว่าการหาค่าตัวเลขแบบแม่นยำตลอดเวลา

เหตุผลหลัก: ทำไมจึง “ไม่นิยม” แก้ระบบสมการเชิงอนุพันธ์ (ODE) ทั้งหมด

เหตุผล	คำอธิบาย
1. แก้ยากหรือไม่มีคำตอบเชิงปิด (closed-form)	ระบบ ODE จำนวนมาก โดยเฉพาะแบบไม่เชิงเส้น (nonlinear) ไม่สามารถแก้ด้วยมือได้ หรือคำตอบอยู่ในรูปเชิงอนุพันธ์/อินทิเกรตซ้อนหลายชั้น
2. สนใจพฤติกรรมระยะยาว (long-run behavior)	เศรษฐศาสตร์ส่วนใหญ่เน้นผลลัพธ์ในระยะยาว เช่น เสถียรภาพ, จุดดุลยภาพ (steady state), หรือแนวโน้ม $\to$ การหาค่า $x^{\ast }$ ที่ทำให้ $\frac{dx}{dt}=0$ เพียงพอ
3. การวิเคราะห์เชิงคุณภาพ (qualitative analysis) เพียงพอ	นักเศรษฐศาสตร์สนใจว่า ระบบจะมุ่งไปทางไหน (converge / diverge), มีดุลยภาพหรือไม่, เสถียรหรือไม่ มากกว่าจะสนใจ trajectory แบบเจาะจงทุกจุดเวลา
4. แบบจำลองเป็นเชิงอุปมา (stylized model)	แบบจำลองเศรษฐศาสตร์มักตั้งขึ้นเพื่อเข้าใจแนวโน้ม มากกว่าจะใช้ทำนายเฉพาะเจาะจง เช่น Solow, IS-LM, Ramsey
5. จุดดุลยภาพให้ข้อมูลเพียงพอสำหรับนโยบาย	เช่น ทราบว่าอัตราภาษีหรืออัตราการออมจะส่งผลต่อ $k^{\ast }$, $y^{\ast }$ อย่างไร ก็พอแล้วสำหรับกำหนดนโยบายเศรษฐกิจ

นักเศรษฐศาสตร์มักใช้:

• Phase diagram $\to$ ดูทิศทางการเคลื่อนไหวของระบบ

• Stability analysis $\to$ วิเคราะห์ว่า equilibrium point เสถียรหรือไม่

• Comparative statics $\to$ ศึกษาผลของพารามิเตอร์ต่อจุดดุลยภาพ โดยไม่ต้องรู้ trajectory เต็ม

8.1.3 การวิเคราะห์ Phase diagram ด้วยอาร์โดยใช้ชุดคำสั่ง phaseR

แพ็กเกจ phaseR ใน R ถูกออกแบบมาเพื่อ วิเคราะห์พฤติกรรมเชิงพลวัตของระบบสมการเชิงอนุพันธ์สามัญ (ODE) โดยเฉพาะระบบแบบ 2 ตัวแปร (2D autonomous ODE systems) ซึ่งเหมาะมากกับการวาด phase portrait, direction field, และ trajectory plot

ระบบสมการเชิงอนุพนธ์ที่ phaseR ไม่รองรับโดยตรง

ประเภท	เหตุผล
ODE มากกว่า 2 ตัวแปร	แสดงผลใน phase space ไม่ได้
Non-autonomous system (ขึ้นกับ $t$ โดยตรง)	ต้องแปลงก่อนให้เป็น autonomous
PDE (สมการเชิงอนุพันธ์ย่อย)	ไม่รองรับ
DDE (สมการดีเลย์)	ไม่รองรับ

การวิเคราะห์ Phase diagram (หรือ Phase Portrait) ใน R นิยมใช้เพื่อแสดง เส้นวิถี (trajectories) ของระบบสมการเชิงอนุพันธ์สองตัวแปร $$\{\begin{array}{l}\frac{dx}{dt}=f(x,y)\\ \frac{dy}{dt}=g(x,y)\end{array}$$

ขั้นตอนการติดตั้ง (ทำครั้งเดียว)

# ติดตั้งแพ็กเกจ (ถ้ายังไม่มี)
install.packages("phaseR")

เรียกใช้งาน

library(phaseR)

การสร้างฟังก์ชันของระบบสมการเชิงอนุพันธ์ สำหรับชุดคำสั่ง phaseR ขอยกตัวอย่างสมการอนุพันธ์ในคู่มือแนะนำการใช้งาน phaseR

ตัวอย่างสมการอนุพันธ์ หนึ่งตัวแปร $$\frac{dy}{dt}=y(1-y)(2-y),$$

derivative0 <- function (t, y, parameters){
    list(y * (1 - y) * (2 - y))
}

ตัวอย่างระบบสมการ

ตัวอย่างที่ 1

$$\frac{dx}{dt}=3y,\frac{dy}{dt}=2x,$$

สามารถสร้างสมการด้วยเพื่อนำไปใช้กับ PhaseR

derivative1 <- function(t, y, parameters) {
  x  <- y[1]
  y  <- y[2]
  dy <- c(3*y, 2*x)
  list(dy)
}

ตัวอย่างที่ 2

$$\frac{dx}{dt}=\alpha y,\frac{dy}{dt}=\beta x,$$ $\alpha$ และ $\beta$ เป็นค่าพารามิเตอร์

สามารถสร้างสมการด้วยเพื่อนำไปใช้กับ PhaseR

derivative2 <- function(t, y, parameters) {
  alpha <- parameters[1]
  beta  <- parameters[2]
  x     <- y[1]
  y     <- y[2]
  dy    <- c(alpha*y, beta*x)
  list(dy)
}

ตัวอย่างที่ 3

$$\frac{dy}{dt}=a(b-3-y{)}^2,$$

สามารถสร้างสมการด้วยเพื่อนำไปใช้กับ PhaseR

derivative3 <- function(t, y, parameters) {
  a  <- parameters[1]
  b  <- parameters[2]
  dy <- a*(b - 3 - y)^2
  list(dy)
}

จากตัวอย่างทั้ง 3 สามารถสรุปได้เป็น

derivative <- function(t, y, parameters) {
  # Enter derivative computation here
  list(dy)
}

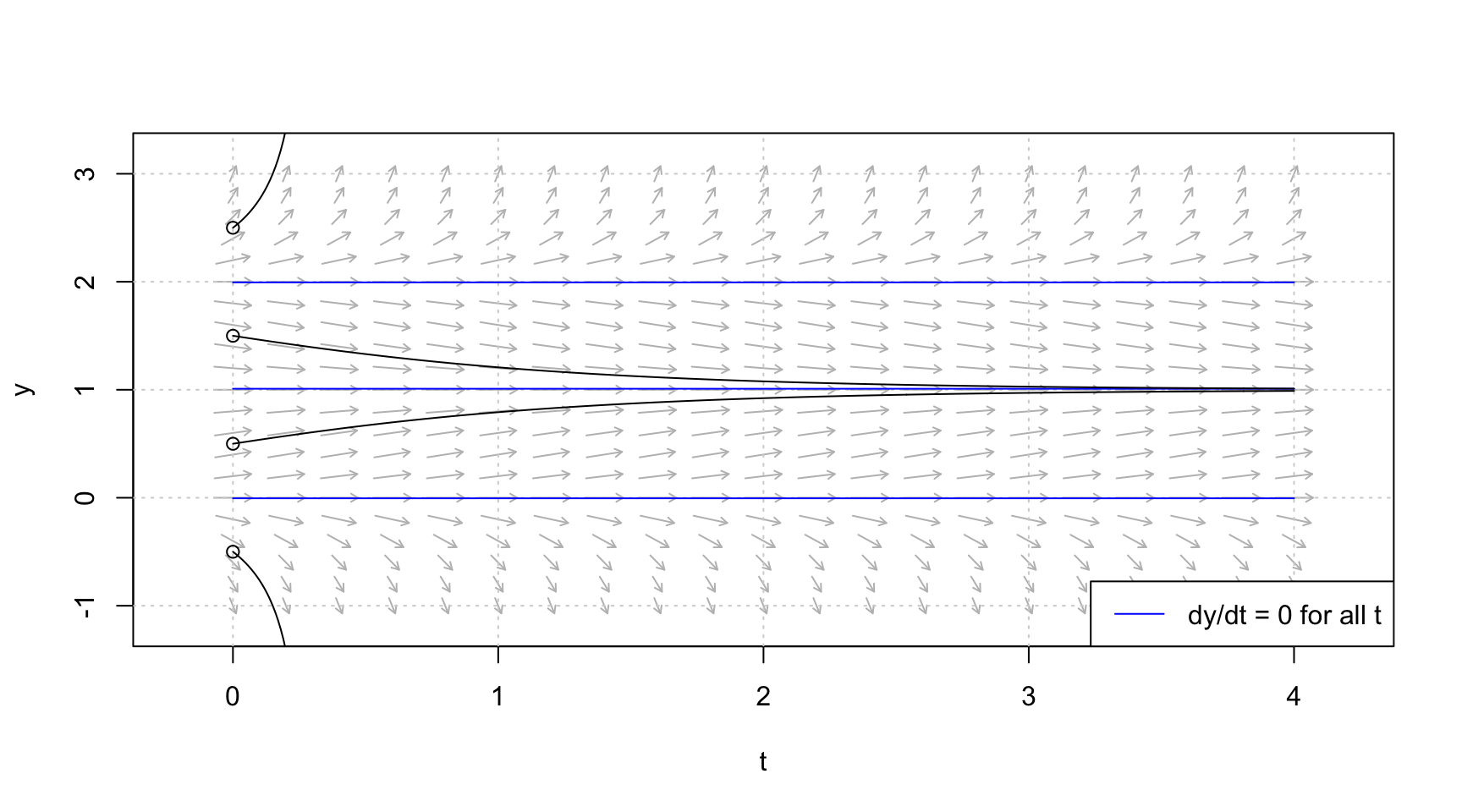
จากระบบสมการเชิงอนุพันธ์หนึ่งตัวแปร สามารถวิเคราะห์ phase diagram ได้ดังนี้

# 1. สร้าง flow field (เวกเตอร์ทิศทาง)
flowField  <- flowField(derivative0,
                        xlim   = c(0, 4),
                        ylim   = c(-1, 3),
                        system = "one.dim",
                        add    = FALSE)
# วาดกริด
grid()
# 2. สร้าง nullclines (เส้นที่อนุพันธ์ = 0)
nullclines <- nullclines(derivative0,
                         xlim   = c(0, 4),
                         ylim   = c(-1, 3),
                         system = "one.dim")
# 3. สร้างเส้นวิถี (trajectories) จากจุดเริ่มต้น y0
trajectory <- trajectory(derivative0,
                         y0     = c(-0.5, 0.5, 1.5, 2.5),
                         tlim   = c(0, 4),
                         system = "one.dim")

องค์ประกอบแต่ละอย่างใน Phase Diagram หมายถึงอะไร?

1. flowField(...) $\to$ เวกเตอร์ทิศทาง (Vector Field)

   • เป็นลูกศรเล็ก ๆ แสดงทิศทางและความเร็วที่จุดต่าง ๆ บนระนาบ (x, y)

   • แต่ละลูกศรแทนว่า ณ จุดนั้น ระบบจะ “ไหล” หรือ “เคลื่อนไป” ทางไหน

   • บอกพฤติกรรมเฉพาะจุด เช่น หมุน, วิ่งเข้า, วิ่งออก ฯลฯ

2. nullclines(...) $\to$ เส้นศูนย์อนุพันธ์

   • เส้นที่ $\frac{dx}{dt}=0$ และ $\frac{dy}{dt}=0$

   • จุดที่ nullclines ทั้งสองเส้นตัดกัน คือ จุดดุลยภาพ (equilibrium point) ของระบบ

   • ช่วยให้เข้าใจจุดสมดุล และแบ่งระนาบเป็นพื้นที่ที่ทิศทางของระบบต่างกัน

3. trajectory(...) $\to$ เส้นวิถีของระบบ (Solution Trajectories)

   • จำลองเส้นทางของระบบเมื่อเริ่มต้นจากจุดเริ่มต้นที่กำหนดใน y0

   • แต่ละแถวของ y0 เป็นจุดเริ่มต้น เช่น (2, 2), (-3, 0), (0, 2), (0, -3)

   • เส้นจะไหลไปตาม flow field $\to$ ชี้ให้เห็นว่าในระยะยาวระบบจะไปที่ใด เช่น:

     • วิ่งเข้าหาจุดดุลยภาพ (Stable Node)

     • หมุนรอบจุด (Center / Spiral)

     • หนีห่างออกไป (Unstable)

การตีความ Phase Diagram (ในทางคณิตศาสตร์/เศรษฐศาสตร์):

องค์ประกอบ	สิ่งที่ช่วยวิเคราะห์
Flow field	พฤติกรรมเฉพาะจุดของระบบ
Nullclines	ตำแหน่งจุดดุลยภาพ และการแบ่งโซนพฤติกรรม
Trajectories	การเปลี่ยนแปลงของระบบเมื่อเริ่มจากจุดต่าง ๆ

ใน phaseR แต่ละฟังก์ชัน เช่น flowField(), nullclines(), และ trajectory() มีอาร์กิวเมนต์ที่ใช้ควบคุมลักษณะการวาดแผนภาพเฟส (phase diagram)

xlim และ ylim

• ใช้กำหนด ช่วงของแกน x และ y สำหรับกราฟ

ตัวอย่าง:

xlim = c(-5, 5)  # แกน x จะเริ่มที่ -5 ถึง 5
ylim = c(-5, 5)  # แกน y จะเริ่มที่ -5 ถึง 5

system

• ระบุประเภทของระบบสมการอนุพันธ์ที่ใช้

• สำหรับระบบ 2 ตัวแปร ใช้ "two.dim"

ตัวอย่าง:

system = "two.dim"

หากเป็นระบบ 1 มิติใช้ "one.dim"
หากเป็นระบบ 2 มิติใช้ "two.dim"

y0

• ใช้ใน trajectory() เท่านั้น

• เป็น จุดเริ่มต้น (initial values) ที่จะใช้ในการวาดเส้นทาง (trajectory) ของระบบ

ตัวอย่าง:

y0 = matrix(c(1, 0, -1, 0, 2, 2), ncol = 2, byrow = TRUE)

แปลว่าเราจะเริ่ม trajectory ที่: (1, 0) (-1, 0) (2, 2)

หมายเหตุ ถ้าเป็นระบบสมการตัวแปรเดียว ให้กำหนดเป็นเวคเตอร์

tlim

• ใช้ใน trajectory() เช่นกัน

• ระบุช่วงเวลาที่จะวาด trajectory เช่น tlim = c(0, 5) แปลว่าให้วาด trajectory จากเวลา 0 ถึง 5

สรุปตารางargument หน้าที่:

Argument	ใช้ใน	ความหมาย
xlim	ทุกฟังก์ชัน	กำหนดช่วงค่าแกน x
ylim	ทุกฟังก์ชัน	กำหนดช่วงค่าแกน y
system	ทุกฟังก์ชัน	ระบุว่าระบบเป็นกี่มิติ
y0	trajectory()	จุดเริ่มต้นของ trajectory
tlim	trajectory()	ช่วงเวลาที่จะวาด trajectory

สามารถใช้ argument อื่นจากฟังก์ชัน plot ในอาร์ได้ เช่น

• col เลือกสีที่ต้องการ

• lty เลือกลักษณะเส้นที่ต้่องการ เช่น เส้นป่ะ เส้นจุด เป็นต้น

• lwd ขนาดของเส้น

• xlab, ylab ตั้งชื่อแกน x และ y

• main ตั้งชื่อกราฟ

8.2 ตัวอย่างสมการและระบบสมการเชิงอนุพันธ์ทางเศรษฐศาสตร์:

8.2.1 Price Adjustment Model (Adaptive Expectations)

8.3 แบบจำลองคือ

$$\{\begin{array}{l}\frac{dp}{dt}=\lambda (p^e-p)\\ \frac{d{p}^e}{dt}=\gamma (p-p^e)\end{array}$$

วิธีทำ ใช้ caracas หาจุดดุลยภาพ

library(caracas)
# กำหนดตัวแปร
lambda <- symbol("lambda_")
gamma <- symbol("gamma")
pe <-symbol("p_e")
p <- symbol("p")
# นิยามฟังก์ชัน
dP <- cbind(lambda*(pe-p),gamma*(p-pe))
# หาค่า  p, pe
sol <- solve_sys(dP, list(p,pe))
sol[[1]]$p

$$p_e$$

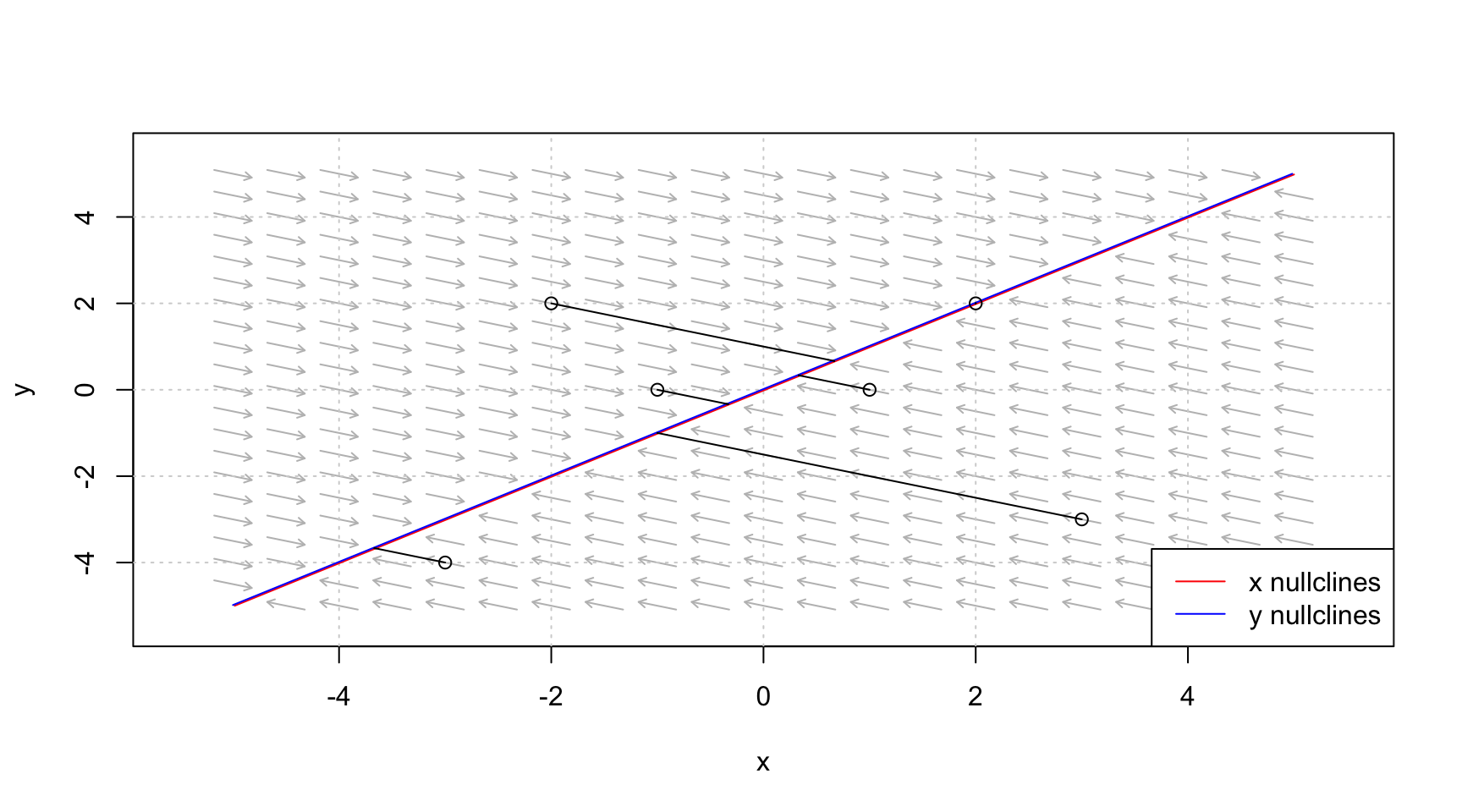
• จุดสมดุล: $p=p^e$

• ถ้า $\lambda ,\gamma >0$: ระบบจะเข้าสู่เสถียรภาพ (stable node)

• เส้น trajectory จะวิ่งเข้าแนวเส้น $p=p^e$ จากทุกจุดรอบนอก

สร้างฟังก์ชันของระบบสมการเชิงอนุพันธ์นี้ด้วย phaseR

library(phaseR)
deriv <- function(t, y, parameter){
  lambda <- parameter[1]
  gamma  <- parameter[2]
      p  <- y[1]
      pe <- y[2]
      dy <- c(lambda*(pe-p), gamma*(p-pe))
  list(dy)
    }

สมมุติให้ $\lambda =2$ และ $\gamma =1$

# วาด vector field
flowField  <- flowField(deriv,
                        xlim   = c(-5, 5),
                        ylim   = c(-5, 5),
                        parameters = c(2,1),
                        system = "two.dim",
                        add    = FALSE)
# วาดกริด
grid()
#เพิ่ม วาดเส้นจุดที่ dy/dt =0
nullclines <- nullclines(deriv,
                         xlim   = c(-5, 5),
                         ylim   = c(-5, 5),
                         parameters = c(2,1),
                         col = c("red", "blue"),
                         system = "two.dim")
#เพิ่ม วาด trajectory ตามจุด y0 ที่กำหนด
y0  <- matrix(c(1, 0, -1, 0, 2, 2, -2,
                2, 3, -3, -3, -4), ncol = 2, byrow = TRUE)
trajectory <- trajectory(deriv,
                         y0     = y0,
                         tlim   = c(0, 5),
                         parameters = c(2,1),
                         system = "two.dim")

8.3.1 Solow Growth Equation (Capital Accumulation)

แบบจำลองคือ

$$\frac{dk}{dt}=s{k}^{\alpha }-\delta k$$

วิธีทำ สามารถสมการหาจุดดุลยภาพ ที่ ${\displaystyle \frac{dk}{dt}}=0$ ดังนั้น สามารถใช้ caracas ในการจุดดุลยภาพได้ดังนี้

library(caracas)
#สร้างตัวแปร
s <- symbol("s", "positive" = TRUE)
alpha <- symbol("alpha", "positive" = TRUE)
delta <- symbol("delta", "positive" = TRUE)
k <- symbol("k")
#สร้างฟังก์ชัน
solow <- s*k^alpha - delta*k 
# หาค่า k ที่ทำให้ solow = 0
sol <- solve_sys(solow,k)
sol[[1]]$k

$${\left(\frac{\delta }{s}\right)}^{\frac{1}{\alpha -1}}$$

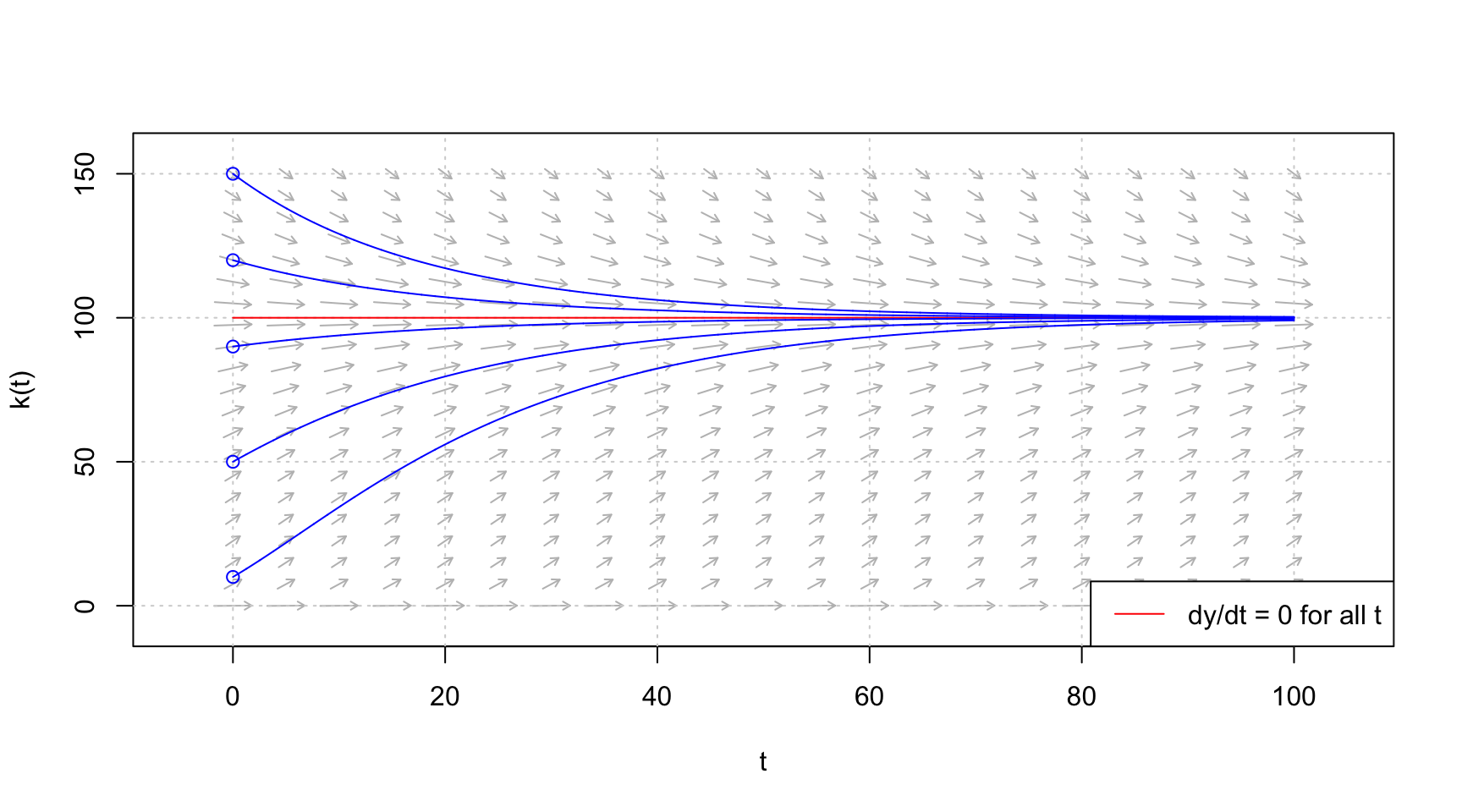
แทนค่า $s=1$ $\alpha =0.5$ และ $\delta =0.1$

(0.1/1)^(1/(.5 - 1))

[1] 100

สร้างฟังก์ชันเพื่อวิเคราะห์ด้วย phaseR

library(phaseR)
solow <- function(t, y, parameter){
      s <- parameter[1]
  alpha <- parameter[2]
  delta <- parameter[3]
      k <- y
     dy <- s*k^alpha - delta*k
     list(dy) 
     }

เหตุผลที่ต้องการจุดดุลภาพ ก็เพื่อให้พิจาณาช่วงของ $k$ ให้ครอบคลุมจุดดุลยภาพนั้นเอง วิเคราะห์ phase diagram

# กำหนด
xlim <- c(0,100)
ylim <- c(0.001,150)
para <- c(s = 1, alpha = 0.5, delta = 0.1)
tlim <- xlim
# วาด vector field
flowField  <- flowField(solow,
                        xlim   = xlim,
                        ylim   = ylim,
                        parameters = para,
                        system = "one.dim",
                        ylab = "k(t)",
                        add    = FALSE)
# วาดกริด
grid()
#เพิ่ม วาดเส้นจุดที่ dy/dt =0
nullclines <- nullclines(solow,
                         xlim   = xlim,
                         ylim   = ylim,
                         parameters = para,
                         col = "red",
                         system = "one.dim")
#เพิ่ม วาด trajectory ตามจุด y0 ที่กำหนด
y0  <- c(10,50, 90, 120, 150)
trajectory <- trajectory(solow,
                         y0     = y0,
                         tlim   = tlim,
                         col = "blue",
                         parameters = para,
                         system = "one.dim")

8.3.2 IS–LM Dynamic Model

แบบจำลอง

เป็นการอธิบายความสัมพันธ์เชิงเวลา (Time Dynamics) ระหว่างรายได้ $Y$ และอัตราดอกเบี้ย $r$ ผ่าน IS และ LM โดยใช้พฤติกรรมการปรับตัวของตลาด:

$$\{\begin{array}{l}\frac{dY}{dt}=\alpha \cdot (I(r)-S(Y))\\ \frac{dr}{dt}=\beta \cdot (L(Y,r)-M)\end{array}$$

ตัวอย่างแบบง่ายสมมุติให้:

• $I(r)=I_0-b\cdot r$: การลงทุนลดลงตาม r

• $S(Y)=s\cdot Y$: การออมเพิ่มตาม Y

• $L(Y,r)=k\cdot Y-h\cdot r$: อุปสงค์เงิน

• $M$: ปริมาณเงินคงที่

ระบบสมการแบบระบุพารามิเตอร์ $$\{\begin{array}{l}\frac{dY}{dt}=\alpha [(I_0-b\cdot r)-s\cdot Y]\\ \frac{dr}{dt}=\beta [k\cdot Y-h\cdot r-M]\end{array}$$

วิธีทำ สามารถจุดดุลภาพด้วย caracas

library(caracas)
# สร้างตัวแปร
alpha <- symbol("alpha", "positive" = TRUE)
beta <- symbol("beta", "positive" = TRUE)
#เปลี่ยน I0 เป็น ๋๋J0
J0<- symbol("J0", "positive" = TRUE) 
b <- symbol("b", "positive" = TRUE)
r <- symbol("r", "positive" = TRUE)
s <- symbol("s", "positive" = TRUE)
h <- symbol("h", "positive" = TRUE)
k <- symbol("k", "positive" = TRUE)
Y <- symbol("Y")
M <- symbol("M")
# สร้างระบบสมการ
dy <- cbind(alpha*(J0-b*r)-s*Y, beta*(k*Y -h*r -M))
dy

$$\left[\begin{array}{cc}-Ys+\alpha (J_0-br)& \beta (-M+Yk-hr)\end{array}\right]$$

แก้สมการด้วยคำสั่ง solve_sys()

sol <- solve_sys(dy, list(Y,r))

ที่จุดดุลภาพ $(Y^{\ast },r^{\ast })$ $Y^{\ast }$ มีค่าเท่ากับ

sol[[1]]$Y

$$\frac{J_0\alpha h+M\alpha b}{\alpha bk+hs}$$

และ $r^{\ast }$ มีค่าเท่ากับ

sol[[1]]$r

$$\frac{J_0\alpha k-Ms}{\alpha bk+hs}$$

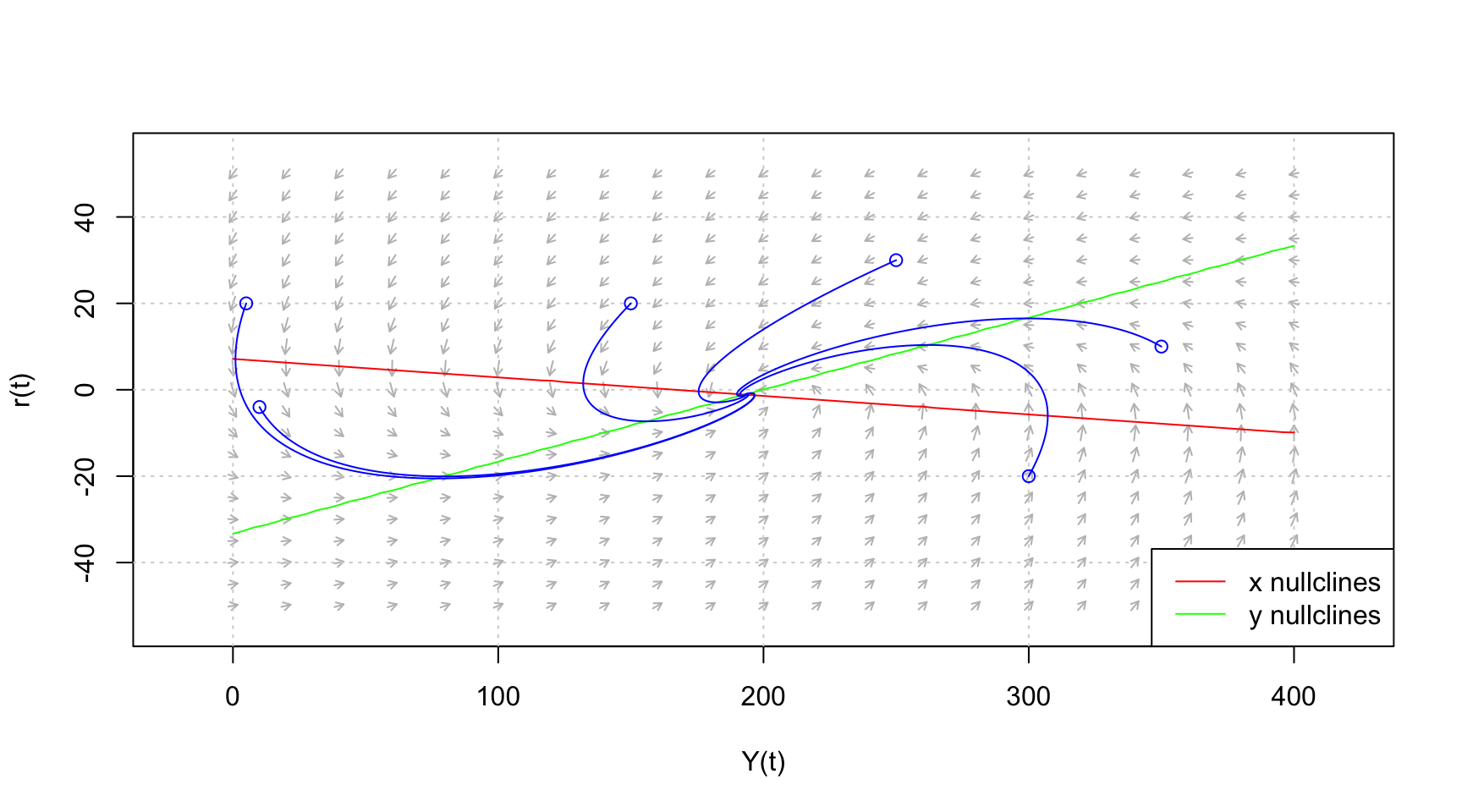
ถ้ากำหนดให้ $\alpha =1,J_0=50,b=7,s=0.3,\beta =1,k=0.5,h=3,M=100$ จะได้ Y เท่ากับ

subs(sol[[1]]$Y,list(alpha = 1, J0 = 50, b = 7, s = 0.3, beta = 1, k = 0.5, h = 3, M = 100))

$$193.181818181818$$

และ $r$ เท่ากับ

subs(sol[[1]]$r,list(alpha = 1, J0 = 50, b = 7, s = 0.3, beta = 1, k = 0.5, h = 3, M = 100))

$$-1.13636363636364$$

สร้างฟังก์ชันเพื่อวิเคราะห์ด้วย phaseR

library(phaseR)
deri <- function(t, y, parameter){
alpha <- 1
I0    <- 50
b     <- 7
s     <- 0.3
beta  <- 1
k     <- 0.5
h     <- 3
M     <- 100
  Y <- y[1]
  r <- y[2]
     dy <- c(alpha*(I0-b*r) -s*Y ,beta*(k*Y - h*r -M))
     list(dy) 
     }

จาก $(Y^{\ast },r^{\ast })=(193.1818,-1.13636)$

# กำหนด
xlim <- c(0,400)
ylim <- c(-50,50)

tlim <- xlim
# วาด vector field
flowField  <- flowField(deri,
                        xlim   = xlim,
                        ylim   = ylim,
                        parameters = NULL,
                        system = "two.dim",
                        xlab = "Y(t)",
                        ylab = "r(t)",
                        add    = FALSE)
# วาดกริด
grid()
#เพิ่ม วาดเส้นจุดที่ dy/dt =0
nullclines <- nullclines(deri,
                         xlim   = xlim,
                         ylim   = ylim,
                         parameters = NULL,
                         col = c("red","green"),
                         system = "two.dim",
                          )

#เพิ่ม วาด trajectory ตามจุด (x0,y0) ที่กำหนด
y0  <- matrix(c(10, -4, 5,20 , 150, 20, 250, 30, 350, 10, 300,-20), ncol = 2, byrow  = TRUE)
trajectory <- trajectory(deri,
                         y0     = y0,
                         tlim   = tlim,
                         col = "blue",
                         parameters = NULL,
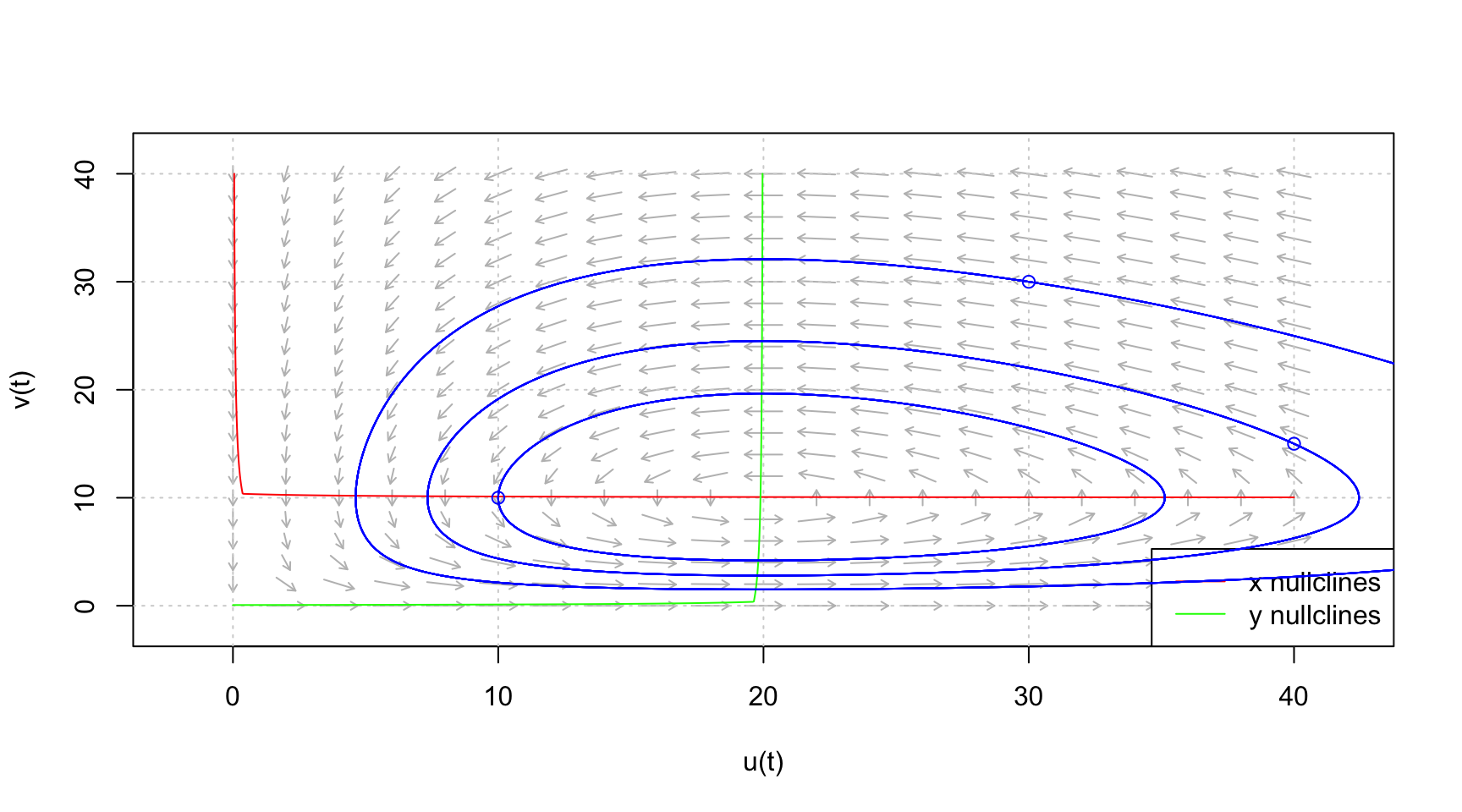
                         system = "two.dim")

8.3.3 Goodwin Growth Cycle Model (โมเดลวัฏจักรเศรษฐกิจด้านแรงงานกับทุน)

แบบจำลอง

เป็นโมเดลทางเศรษฐศาสตร์แรงงานที่วิเคราะห์พลวัตของ ส่วนแบ่งค่าจ้างแรงงาน $u$ และ การจ้างงาน $v$ $$\{\begin{array}{l}\frac{du}{dt}=u(\alpha -\beta v)\\ \frac{dv}{dt}=v(\gamma u-\delta )\end{array}$$ $$(\frac{\delta }{\gamma },\frac{\alpha }{\beta })$$

ความหมายของตัวแปร: แก - $u$: ส่วนแบ่งแรงงาน (wage share)

• $v$: อัตราการจ้างงาน (employment rate)

• $\alpha ,\beta ,\gamma ,\delta$: พารามิเตอร์เชิงเศรษฐศาสตร์ เช่น productivity growth, bargaining power

ลักษณะ: ระบบนี้สามารถแสดงวงจรวัฏจักร (limit cycle) คล้ายกับ Predator-Prey

วิธีทำ สามารถหาจุดดุลภาพด้วย caracas

library(caracas)
# สร้างตัวแปร
alpha <- symbol("alpha", "positive" = TRUE)
beta <- symbol("beta", "positive" = TRUE)
gamma <- symbol("gamma", "positive" = TRUE)
delta <- symbol("delta", "positive" = TRUE)
u <- symbol("u")
v <- symbol("v")
# สร้างระบบสมการ
dy <- cbind( u*(alpha-beta*v), v*(gamma*u-delta))
dy

$$\left[\begin{array}{cc}u(\alpha -\beta v)& v(-\delta +\gamma u)\end{array}\right]$$

แก้สมการด้วยคำสั่ง solve_sys()

sol <- solve_sys(dy, list(u,v))

ที่จุดดุลภาพ มี 2 จุดคือ $(u^{\ast },v^{\ast })$ $u^{\ast }$ มีค่าเท่ากับ

sol[[1]]$u

$$0$$

และ $r$ มีค่าเท่ากับ

sol[[1]]$v

$$0$$

นั่นคือ $(u^{\ast },v^{\ast })=(0,0)$

และ

sol[[2]]$u

$$\frac{\delta }{\gamma }$$

และ $r$ มีค่าเท่ากับ

sol[[2]]$v

$$\frac{\alpha }{\beta }$$

นั้นคือ $(u^{\ast },v^{\ast })=({\displaystyle \frac{\delta }{\gamma }},{\displaystyle \frac{\alpha }{\beta }})$

สร้างฟังก์ชันเพื่อวิเคราะห์ด้วย phaseR

สมุมติให้ $\alpha ,\beta ,\gamma ,\delta )=(1,0.1,0.075,1.5)$

library(phaseR)
deri <- function(t, y, parameter){
alpha <- 1
beta  <- 0.1
gamma <- 0.075
delta <- 1.5
  u <- y[1]
  v <- y[2]
  du <- u*(alpha - beta*v)
  dv <- v*(gamma*u - delta)
  dy <- c(du,dv)
     list(dy) 
     }

จาก $(u^{\ast },v^{\ast })=(0,0)$ และ (20, 10)

# กำหนด
xlim <- c(0,40)
ylim <- c(0,40)

tlim <- xlim
# วาด vector field
flowField  <- flowField(deri,
                        xlim   = xlim,
                        ylim   = ylim,
                        parameters = NULL,
                        system = "two.dim",
                        xlab = "u(t)",
                        ylab = "v(t)",
                        add    = FALSE)
# วาดกริด
grid()
#เพิ่ม วาดเส้นจุดที่ dy/dt =0
nullclines <- nullclines(deri,
                         xlim   = xlim,
                         ylim   = ylim,
                         parameters = NULL,
                         col = c("red","green"),
                         system = "two.dim",
                          )

#เพิ่ม วาด trajectory ตามจุด (x0,y0) ที่กำหนด
y0  <- matrix(c(30, 30, 25, -10 , 10, 10, 40,15), ncol = 2, byrow  = TRUE)
trajectory <- trajectory(deri,
                         y0     = y0,
                         tlim   = tlim,
                         col = "blue",
                         parameters = NULL,
                         system = "two.dim")

8.4 การวิเคราะห์จุดดุลยภาพสำหรับระบบสมการเชิงอนุพันธ์ตั้งแต่ 3 สมการขึ้นไป

การวิเคราะห์ ระบบสมการเชิงอนุพันธ์อันดับหนึ่งที่มี 3 ตัวแปรขึ้นไป (หรือ $n$ ตัวแปร) การใช้ Jacobian matrix และการหาค่า eigenvalues ก็ยังคงเป็น วิธีมาตรฐานและดีที่สุดในเชิงคณิตศาสตร์ สำหรับการวิเคราะห์จุดดุลยภาพ โดยเฉพาะ:

ทำไม Jacobian ยังจำเป็นเมื่อมีมากกว่า 2 ตัวแปร?

1. ยังบอกเสถียรภาพได้

   • Jacobian ยังเป็นเมทริกซ์ $n\times n$ ที่ได้จากอนุพันธ์ของระบบ

   • Eigenvalues ของเมทริกซ์นี้จะยังคงบอกถึงพฤติกรรมใกล้จุดสมดุลได้เหมือนเดิม:

   • ส่วนจริงของ eigenvalue < 0 $\to$ stable

   • ส่วนจริง > 0 $\to$ unstable

   • ค่า pure imaginary $\to$ อาจเกิด oscillation

2. ใช้วิเคราะห์ในเชิงเส้นใกล้สมดุล (linearization) ได้

   • ใกล้จุดดุลยภาพ ระบบไม่เชิงเส้นสามารถประมาณได้ด้วยระบบเชิงเส้น โดยใช้ Taylor expansion ลำดับแรก — และ Jacobian คือ “linear part” นั้น

3. ไม่สามารถวิเคราะห์พฤติกรรมเชิงภาพได้โดยตรง

   • สำหรับระบบ 2 ตัวแปร $\to$ ใช้ phase portrait วาดได้ (จากหัวข้อที่ผ่านมา)

   • สำหรับระบบ $\ge$ 3 ตัวแปร $\to$ ไม่สามารถวาด phase space ได้โดยง่าย

   • การใช้ Jacobian + eigenvalue จึงเป็นทางเลือกเดียวที่แม่นยำและคำนวณได้จริง

ตัวอย่าง: ถ้ามี 3 สมการ

$$\{\begin{array}{l}\frac{dx}{dt}=f(x,y,z)\\ \frac{dy}{dt}=g(x,y,z)\\ \frac{dz}{dt}=h(x,y,z)\end{array}$$

วิธีทำ Jacobian คือเมทริกซ์ $3\times 3$: $$J(x,y,z)=\left[\begin{array}{ccc}\frac{\partial f}{\partial x}& \frac{\partial f}{\partial y}& \frac{\partial f}{\partial z}\\ \frac{\partial g}{\partial x}& \frac{\partial g}{\partial y}& \frac{\partial g}{\partial z}\\ \frac{\partial h}{\partial x}& \frac{\partial h}{\partial y}& \frac{\partial h}{\partial z}\end{array}\right]$$

แล้วแทนค่าจุดดุลยภาพ $(x^{\ast },y^{\ast },z^{\ast })$ $\to$ หา eigenvalues $\to$ วิเคราะห์เสถียรภาพ

ตารางสรุป: ความสัมพันธ์ระหว่าง Eigenvalues กับลักษณะของจุดดุลยภาพ

ลักษณะของ Eigenvalues	สถานะของจุดดุลยภาพ	ความหมายทางพลวัต
ทุก $\mathrm{\Re }({\lambda }_i)<0$	Stable node / focus / spiral	จุดดุลยภาพ เสถียร (asymptotically stable)
มีบาง $\mathrm{\Re }({\lambda }_i)>0$	Unstable	ระบบหนีออกจากจุดนั้น
มี $\mathrm{\Re }({\lambda }_i)>0$ และ $\mathrm{\Re }({\lambda }_j)<0$	Saddle point	เสถียรบางทิศทาง ไม่เสถียรบางทิศทาง
ทุก $\mathrm{\Re }({\lambda }_i)=0$ แต่ไม่เป็นศูนย์หลายลำดับ	Center / Neutrally stable	ระบบแกว่งวนรอบจุดนั้น (ต้องใช้วิธีอื่นช่วยวิเคราะห์ต่อ)
บาง $\mathrm{\Re }({\lambda }_i)=0$	ไม่สามารถสรุปได้แน่ชัด	อาจต้องใช้ Lyapunov method หรือ nonlinear terms ตรวจสอบต่อ

8.5 ตัวอย่าง ระบบสมการเชิงอนุพันธ์ที่มีตั้งแต่ 3 สมการขึ้นไปในทางเศรษฐศาสตร์

8.5.1 แบบจำลอง IS–LM–PC (New Keynesian Model)

ใช้วิเคราะห์เศรษฐกิจระยะสั้น โดยพิจารณาการบริโภค (IS), การเงิน (LM), และเงินเฟ้อ (Phillips Curve)

แบบจำลอง

$$\{\begin{array}{ll}\frac{dY}{dt}={\alpha }_1(r-r^{\ast })& \text{(IS: รายได้ตอบสนองต่อนโยบายการเงิน)}\\ \frac{dr}{dt}={\alpha }_2(\pi -{\pi }^{\ast })& \text{(นโยบายการเงินตอบสนองต่อเงินเฟ้อ)}\\ \frac{d\pi }{dt}={\alpha }_3(Y-Y^{\ast })& \text{(PC: เงินเฟ้อตอบสนองต่อรายได้เกินดุล)}\end{array}$$

• $Y$ = รายได้จริง

• $r$ = อัตราดอกเบี้ยนโยบาย

• $\pi$ = อัตราเงินเฟ้อ

• ${\pi }^{\ast },r^{\ast },Y^{\ast }$ = ค่าดุลยภาพ

• ${\alpha }_i$ = พารามิเตอร์ตอบสนอง

วิธีทำ การคำนวณเชิงสัญลักษณ์ด้วย caracas

ขั้นที่ 1 สร้างระบบสมการด้วย caracas

library(caracas)
# สร้างตัวแปร
alpha <- as_sym(paste0("alpha",1:3))
r_e <- symbol("r_e")
pi_e <- symbol("pi_e")
Y_e <-  symbol("Y_e")
Y  <- symbol("Y")
r <- symbol("r")
pi <- symbol("pi")
# สร้างสมการ
dY <- alpha[1]*(r-r_e)
dr <- alpha[2]*(pi-pi_e)
dpi<- alpha[3]*(Y-Y_e)
Deri <- cbind(dY,dr,dpi)
Deri

$$\left[\begin{array}{ccc}{\alpha }_1(r-r_e)& {\alpha }_2(\pi -{\pi }_e)& {\alpha }_3(Y-Y_e)\end{array}\right]$$

ขั้นที่ 2 หา Jacobain matrix ด้วยคำสั่ง jacobian() ใน caracas

Jaco <-jacobian(Deri, list(Y,r,pi))
Jaco

$$\left[\begin{array}{ccc}0& {\alpha }_1& 0\\ 0& 0& {\alpha }_2\\ {\alpha }_3& 0& 0\end{array}\right]$$

ขั้นที่ 3 จุดดุลยภาพจากระบบสมการเชิงอนุพันธ์ด้วย solve_sys() ใน caracas

Sol <-solve_sys(Deri, list(Y,r, pi))

Sol[[1]]$Y

$$Y_e$$

Sol[[1]]$r

$$r_e$$

ขั้นที่ แทนค่าจุดดุลยภาพลงไปใน ่่Jacobian matrix ที่ได้ โดยใช้คำสั่ง eigenval() จาก caracas

Eigen <-eigenval(Jaco)

ค่า eigenvalue ตัวที่ 1 > 0

Eigen[[1]]$eigval

$$\sqrt[3]{{\alpha }_1{\alpha }_2{\alpha }_3}$$

ค่า eigenvalue ตัวที่ 2 ค่าจริงติดลบ

Eigen[[2]]$eigval

$$-\frac{\sqrt[3]{{\alpha }_1{\alpha }_2{\alpha }_3}}{2}-\frac{\sqrt{3}i\sqrt[3]{{\alpha }_1{\alpha }_2{\alpha }_3}}{2}$$

ค่า eigenvalue ตัวที่ 3 ค่าจริงติดลบ

Eigen[[3]]$eigval

$$-\frac{\sqrt[3]{{\alpha }_1{\alpha }_2{\alpha }_3}}{2}+\frac{\sqrt{3}i\sqrt[3]{{\alpha }_1{\alpha }_2{\alpha }_3}}{2}$$

ดังนั้น ระบบนี้เป็น Saddle focus นั่นคือ ไม่เสถียร์

8.5.2 ระบบสมการเชิงอนุพันธ์ของแบบจำลอง Goodwin

จำลองวงจรธุรกิจโดยอิงการจ้างงานและการเจรจาค่าจ้าง

แบบจำลอง

$$\{\begin{array}{l}\frac{du}{dt}=u(\alpha -\beta v)\\ \frac{dv}{dt}=v(\gamma u-\delta )\\ \frac{dw}{dt}=w(\eta u-\theta )\end{array}$$

ความหมายของตัวแปร:

สัญลักษณ์	ความหมายทางเศรษฐศาสตร์
$u(t)$	อัตราการจ้างงาน (employment rate) – สัดส่วนแรงงานที่มีงานทำ
$v(t)$	ส่วนแบ่งกำไรของทุน (profit share) – สัดส่วนของรายได้ที่ไปสู่ทุน
$w(t)$	ค่าจ้างแรงงานต่อหน่วยเวลา (real wage) หรือดัชนีค่าจ้างแรงงาน

ความหมายของพารามิเตอร์:

สัญลักษณ์	ความหมาย	ค่าคาดหวัง
$\alpha$	อัตราการเติบโตของการจ้างงานพื้นฐาน (เช่น เทคโนโลยีหรือผลผลิตแรงงาน)	บวก
$\beta$	ความไวของการจ้างงานต่อส่วนแบ่งกำไร (เมื่อ $v$ เพิ่ม $\to$ $u$ ลด)	บวก
$\gamma$	ความไวของกำไรต่อการจ้างงาน (เมื่อ $u$ เพิ่ม$\to$ กำไรเพิ่ม)	บวก
$\delta$	อัตราการลดลงของส่วนแบ่งกำไร (เช่น จากค่าแรง, ภาษี ฯลฯ)	บวก
$\eta$	ความไวของค่าจ้างต่ออัตราการจ้างงาน (bargaining power ของแรงงาน)	บวก
$\theta$	อัตราการกัดกร่อนค่าจ้างจากปัจจัยภายนอก เช่น productivity หรือแรงถ่วงของตลาด	บวก

คำอธิบายเชิงพลวัต:

• สมการที่ 1: จ้างงานเพิ่มขึ้นเมื่อกำไรไม่สูงเกินไป ($v$ ต่ำ)

• สมการที่ 2: ส่วนแบ่งกำไรเพิ่มขึ้นเมื่อมีการจ้างงานสูง (ผลิตภาพดี)

• สมการที่ 3: ค่าจ้างแรงงานเพิ่มขึ้นตามอัตราการจ้างงาน — เพราะอำนาจต่อรองแรงงานแข็งแรง

ระบบนี้สร้าง วงจรเศรษฐกิจ ที่มีลักษณะเป็น วงรอบ (limit cycle) ได้ในบางช่วง เช่น ค่าจ้างสูง $\to$ กำไรลด $\to$ การจ้างงานลด $\to$ ค่าจ้างถูกกด $\to$ กำไรเพิ่ม $\to$ กลับมาใหม่

วิธีทำ การคำนวณเชิงสัญลักษณ์ด้วย caracas

ขั้นที่ 1 สร้างระบบสมการด้วย caracas

library(caracas)
# สร้างตัวแปร
alpha <- symbol("alpha", "positive" = TRUE)
beta <- symbol("beta", "positive" = TRUE)
gamma <- symbol("gamma", "positive" = TRUE)
delta <- symbol("delta", "positive" = TRUE)
eta <- symbol("eta", "positive" = TRUE)
theta <- symbol("theta", "positive" = TRUE)
u  <- symbol("u")
v <- symbol("v")
w <- symbol("w")
# สร้างสมการ
du <- u*(alpha-beta*v)
dv <- v*(gamma*u-delta)
dw <- w*(eta*u-theta)
Deri <- cbind(du, dv, dw)
Deri

$$\left[\begin{array}{ccc}u(\alpha -\beta v)& v(-\delta +\gamma u)& w(\eta u-\theta )\end{array}\right]$$

ขั้นที่ 2 หา Jacobain matrix ด้วยคำสั่ง jacobian() ใน caracas

Jaco <-jacobian(Deri, list(u,v,w))
Jaco

$$\left[\begin{array}{ccc}\alpha -\beta v& -\beta u& 0\\ \gamma v& -\delta +\gamma u& 0\\ \eta w& 0& \eta u-\theta \end{array}\right]$$

ขั้นที่ 3 จุดดุลยภาพจากระบบสมการเชิงอนุพันธ์ด้วย solve_sys() ใน caracas

Sol <-solve_sys(Deri, list(u,v,w))

ระบบนี้ มีจุดดุลภาพ 2 จุดคือ $(u,v,w)=(0,0,0)$ และ $({\displaystyle \frac{\delta }{\gamma }},{\displaystyle \frac{\alpha }{\beta }},0)$

Sol[[1]]$u

$$0$$

Sol[[1]]$v

$$0$$

Sol[[1]]$w

$$0$$

Sol[[2]]$u

$$\frac{\delta }{\gamma }$$

Sol[[2]]$v

$$\frac{\alpha }{\beta }$$

Sol[[2]]$w

$$0$$

ขั้นที่ แทนค่าจุดดุลยภาพลงไปใน ่่Jacobian matrix ที่ได้ โดยใช้คำสั่ง
subs() และ eigenval() จาก caracas

Jaco1 <- subs(Jaco, list(u=0,v=0,w=0))
Eigen <-eigenval(Jaco1)

ค่า eigenvalue ตัวที่ 1 > 0

Eigen[[1]]$eigval

$$\alpha$$

ค่า eigenvalue ตัวที่ 2 ค่าจริงติดลบ

Eigen[[2]]$eigval

$$-\delta$$

ค่า eigenvalue ตัวที่ 3 ค่าจริงติดลบ

Eigen[[3]]$eigval

$$-\theta$$

ดังนั้น ระบบนี้เป็น Saddle focus ที่จุดดุลยภาพนี้

พิจารณาจุดดุลยภาพที่ 2

Jaco1 <- subs(Jaco, list(u= Sol[[2]]$u , v=Sol[[2]]$v , w=0))
Eigen <-eigenval(Jaco1)

ค่า eigenvalue ตัวที่ 1 ค่าจริงเท่ากับ 0

Eigen[[1]]$eigval

$$-\sqrt{-\alpha \delta }$$

ค่า eigenvalue ตัวที่ 2 ค่าจริง้ท่ากับ 0

Eigen[[2]]$eigval

$$\sqrt{-\alpha \delta }$$

ค่า eigenvalue ตัวที่ 3

Eigen[[3]]$eigval

$$\frac{\delta \eta -\gamma \theta }{\gamma }$$

จะน้อยกว่า 0 ถ้า $\delta \eta <\gamma \theta$

จะเท่ากับ 0 ถ้า $\delta \eta =\gamma \theta$

จะมากกว่า 0 ถ้า $\delta \eta >\gamma \theta$

8.5.3 แบบจำลองสามกลุ่มเศรษฐกิจ (3-sector Growth Model)

เช่น เศรษฐกิจที่ประกอบด้วย ภาคเกษตร ($A$), อุตสาหกรรม ($I$), และบริการ ($S$)

แบบจำลอง 3-Sector Growth Model

$$\{\begin{array}{l}\frac{dA}{dt}=A\cdot (f_A-{\lambda }_{AI}I-{\lambda }_{AS}S)\\ \frac{dI}{dt}=I\cdot (f_I-{\lambda }_{IA}A-{\lambda }_{IS}S)\\ \frac{dS}{dt}=S\cdot (f_S-{\lambda }_{SA}A-{\lambda }_{SI}I)\end{array}$$

ความหมายของตัวแปร

ตัวแปร	ความหมายทางเศรษฐศาสตร์
$A(t)$	ขนาดของภาคเกษตรกรรม (Agricultural sector) ณ เวลา $t$
$I(t)$	ขนาดของภาคอุตสาหกรรม (Industrial sector)
$S(t)$	ขนาดของภาคบริการ (Service sector)

ขนาดอาจวัดได้ด้วย GDP ส่วนย่อย, การจ้างงาน, หรือผลผลิตภาคเศรษฐกิจนั้น ๆ

ความหมายของพารามิเตอร์

พารามิเตอร์	ความหมาย	ค่าคาดหวัง
$f_A$	อัตราการเติบโตพื้นฐานของภาคเกษตร (endogenous growth rate)	บวก (หรือลดลงหากอิงโครงสร้างเก่า)
$f_I$	อัตราการเติบโตพื้นฐานของภาคอุตสาหกรรม	บวก (มักสูงในประเทศกำลังพัฒนา)
$f_S$	อัตราการเติบโตพื้นฐานของภาคบริการ	บวก (เพิ่มตามพัฒนาการเศรษฐกิจ)

${\lambda }_{ij}$	ความหมาย	ตีความทางเศรษฐศาสตร์
${\lambda }_{AI}$	ผลกระทบเชิงลบจากภาคอุตสาหกรรมต่อภาคเกษตร	การย้ายทรัพยากรจากเกษตรไปอุตฯ
${\lambda }_{AS}$	ผลกระทบจากภาคบริการต่อภาคเกษตร	เช่น การเปลี่ยนแรงงานไปสู่บริการ
${\lambda }_{IA}$	ผลกระทบจากเกษตรต่ออุตสาหกรรม	การแข่งขันด้านแรงงาน หรือ supply ของ input
${\lambda }_{IS}$	ผลกระทบจากบริการต่ออุตสาหกรรม	ดึงแรงงาน skilled ไปจากอุตสาหกรรม
${\lambda }_{SA}$	ผลกระทบจากเกษตรต่อบริการ	เช่น การใช้ที่ดินหรือแรงงานท้องถิ่น
${\lambda }_{SI}$	ผลกระทบจากอุตสาหกรรมต่อบริการ	อาจเป็นบวกหากเกิดการเชื่อมโยงอุตฯ–บริการ

โดยทั่วไป ${\lambda }_{ij}>0$ แสดงถึง “การแย่งทรัพยากร” ระหว่างภาคเศรษฐกิจต่าง ๆ

ซึ่งหมายถึง เมื่อภาค $j$ เติบโต จะ “กดทับ” การเติบโตของภาค $i$

ลักษณะของสมการ:

เป็นแบบจำลอง nonlinear ODEs ที่อยู่ในรูปของ Lotka–Volterra-type competition model

• การเติบโตของแต่ละภาค ขึ้นกับตัวเอง (ผ่าน $A,I,S$)

• และได้รับผลกระทบเชิงลบจากภาคอื่นผ่าน ${\lambda }_{ij}$

ตัวอย่างเชิงนโยบาย:

• ถ้า ${\lambda }_{AI}$ สูง $\to$ นโยบายเร่งอุตสาหกรรมอาจทำให้ภาคเกษตรเสื่อมถอยเร็ว

• ถ้า $f_S$ สูงแต่ ${\lambda }_{SI}$ สูงด้วย $\to$ การขยายบริการอาจบั่นทอนอุตสาหกรรม (structural unbalance)

วิธีทำ การคำนวณเชิงสัญลักษณ์ด้วย caracas

ขั้นที่ 1 สร้างระบบสมการด้วย caracas

library(caracas)
# สร้างตัวแปร
# เปลี่ยน I เป็น J ทั้งหมด
lambdaAJ <- symbol("lambda_AJ", "positive" = TRUE)
lambdaAS <- symbol("lambda_AS", "positive" = TRUE)
lambdaJA <- symbol("lambda_JA", "positive" = TRUE)
lambdaJS <- symbol("lambda_JS", "positive" = TRUE)
lambdaSA <- symbol("lambda_SA", "positive" = TRUE)
lambdaSJ <- symbol("lambda_SJ", "positive" = TRUE)                  
f <- as_sym(paste0("f",1:3))
A  <- symbol("A")
J <- symbol("J")
S <- symbol("S")
# สร้างสมการ
dA <- A*(f[1]-lambdaAJ*J-lambdaAS*S)
dJ <- J*(f[2]-lambdaJA*A-lambdaJS*S)
dS <- S*(f[3]-lambdaSA*A-lambdaSJ*J)
  
Deri <- cbind(dA, dJ, dS)
Deri

$$\left[\begin{array}{ccc}A(-J{\lambda }_{AJ}-S{\lambda }_{AS}+f_1)& J(-A{\lambda }_{JA}-S{\lambda }_{JS}+f_2)& S(-A{\lambda }_{SA}-J{\lambda }_{SJ}+f_3)\end{array}\right]$$

ขั้นที่ 2 หา Jacobain matrix ด้วยคำสั่ง jacobian() ใน caracas

Jaco <-jacobian(Deri, list(A,J,S))
Jaco

$$\left[\begin{array}{ccc}-J{\lambda }_{AJ}-S{\lambda }_{AS}+f_1& -A{\lambda }_{AJ}& -A{\lambda }_{AS}\\ -J{\lambda }_{JA}& -A{\lambda }_{JA}-S{\lambda }_{JS}+f_2& -J{\lambda }_{JS}\\ -S{\lambda }_{SA}& -S{\lambda }_{SJ}& -A{\lambda }_{SA}-J{\lambda }_{SJ}+f_3\end{array}\right]$$

ขั้นที่ 3 จุดดุลยภาพจากระบบสมการเชิงอนุพันธ์ด้วย solve_sys() ใน caracas

Sol <-solve_sys(Deri, list(A,J,S))

SympifyError: S

จะพบว่า ไม่สามารถหา คำตอบ ก็ต้องกลับใช้ทักษะ ที่ควรมี ก็คือพิจารณาด้วยตนเองก่อน จะพบว่าจุดดุลภาพแรก คือ $(A^{\ast },J^{\ast },S^{\ast })=(0,0,0)$ และจุดอื่นๆ คือ ถ้า พิจารณา ไม่มีค่าจุดใดเป็นศูนย์ จะได้

# สร้างสมการ
dA <- (f[1]-lambdaAJ*J-lambdaAS*S)
dJ <- (f[2]-lambdaJA*A-lambdaJS*S)
dS <- (f[3]-lambdaSA*A-lambdaSJ*J)
  
Another.SYS <- cbind(dA, dJ, dS)
Another.SYS

$$\left[\begin{array}{ccc}-J{\lambda }_{AJ}-S{\lambda }_{AS}+f_1& -A{\lambda }_{JA}-S{\lambda }_{JS}+f_2& -A{\lambda }_{SA}-J{\lambda }_{SJ}+f_3\end{array}\right]$$

เนื่องจกสมการนี้เป็นระบบสมการเชิงเส้นควรใช้ คำสั่ง solve_lin() แก้สมการแต่ต้องจัดอยู่ในรูปเมตริกซ์ก่อน

$$\left[\begin{array}{ccc}0& -{\lambda }_{AJ}& -{\lambda }_{AS}\\ -{\lambda }_{JA}& 0& -{\lambda }_{JS}\\ -{\lambda }_{SA}& -{\lambda }_{SJ}& 0\end{array}\right]\left[\begin{array}{c}A\\ J\\ S\end{array}\right]=\left[\begin{array}{c}-f_1\\ -f_2\\ -f_3\end{array}\right]$$

mat.A <- matrix(c(0,"-lambda_JA","-lambda_SA","-lambda_AJ",0,"-lambda_SJ",
                  "-lambda_AS","-lambda_JS",0),nrow = 3)
mat.A <- as_sym(mat.A)
mat.A

$$\left[\begin{array}{ccc}0& -{\lambda }_{AJ}& -{\lambda }_{AS}\\ -{\lambda }_{JA}& 0& -{\lambda }_{JS}\\ -{\lambda }_{SA}& -{\lambda }_{SJ}& 0\end{array}\right]$$

-f

$$\left[\begin{array}{c}-f_1\\ -f_2\\ -f_3\end{array}\right]$$

Sol <- solve_lin(mat.A,-f)
Sol

$$\left[\begin{array}{c}-\frac{f_1{\lambda }_{JS}{\lambda }_{SJ}}{{\lambda }_{AJ}{\lambda }_{JS}{\lambda }_{SA}+{\lambda }_{AS}{\lambda }_{JA}{\lambda }_{SJ}}+\frac{f_2{\lambda }_{AS}{\lambda }_{SJ}}{{\lambda }_{AJ}{\lambda }_{JS}{\lambda }_{SA}+{\lambda }_{AS}{\lambda }_{JA}{\lambda }_{SJ}}+\frac{f_3{\lambda }_{AJ}{\lambda }_{JS}}{{\lambda }_{AJ}{\lambda }_{JS}{\lambda }_{SA}+{\lambda }_{AS}{\lambda }_{JA}{\lambda }_{SJ}}\\ \frac{f_1{\lambda }_{JS}{\lambda }_{SA}}{{\lambda }_{AJ}{\lambda }_{JS}{\lambda }_{SA}+{\lambda }_{AS}{\lambda }_{JA}{\lambda }_{SJ}}-\frac{f_2{\lambda }_{AS}{\lambda }_{SA}}{{\lambda }_{AJ}{\lambda }_{JS}{\lambda }_{SA}+{\lambda }_{AS}{\lambda }_{JA}{\lambda }_{SJ}}+\frac{f_3{\lambda }_{AS}{\lambda }_{JA}}{{\lambda }_{AJ}{\lambda }_{JS}{\lambda }_{SA}+{\lambda }_{AS}{\lambda }_{JA}{\lambda }_{SJ}}\\ \frac{f_1{\lambda }_{JA}{\lambda }_{SJ}}{{\lambda }_{AJ}{\lambda }_{JS}{\lambda }_{SA}+{\lambda }_{AS}{\lambda }_{JA}{\lambda }_{SJ}}+\frac{f_2{\lambda }_{AJ}{\lambda }_{SA}}{{\lambda }_{AJ}{\lambda }_{JS}{\lambda }_{SA}+{\lambda }_{AS}{\lambda }_{JA}{\lambda }_{SJ}}-\frac{f_3{\lambda }_{AJ}{\lambda }_{JA}}{{\lambda }_{AJ}{\lambda }_{JS}{\lambda }_{SA}+{\lambda }_{AS}{\lambda }_{JA}{\lambda }_{SJ}}\end{array}\right]$$

ที่จุดดุลยภาพเท่ากับ $(A,J,S)=(0,0,0)$ Jacobian matrix คือ

Jaco1 <- subs(Jaco, list(A=0,J=0,S=0))
Jaco1

$$\left[\begin{array}{ccc}{f}_1& 0& 0\\ 0& f_2& 0\\ 0& 0& f_3\end{array}\right]$$

จากเมตริกซ์ นี้เห็นได้โดยง่ายว่า ค่า eigenvalue ทั้งหมดมีค่ามากกว่า 0 ดังนั้น ไม่เสถียร

และนำจุดดุลยภาพอีกจุดไปในแทนใน ๋Jacobian matrix เผื่อหาค่า eigenvalue จะได้เป็นคำตอบเชิงสัญลักษณ์ที่ยาว

Eigen <-eigenval(Jaco)
Eigen1 <-subs(Eigen[[1]]$eigval, list(A = Sol[1,1], 
                                      S = Sol[2,1], J = Sol[3,1]))
Eigen2 <-subs(Eigen[[2]]$eigval, list(A = Sol[1,1], 
                                      S = Sol[2,1], J = Sol[3,1]))
Eigen3 <-subs(Eigen[[3]]$eigval, list(A = Sol[1,1], 
                                      S = Sol[2,1], J = Sol[3,1]))

เหตุที่ไม่ค่าเชิงสัญลักษณ์เพราะ ยาวมาก และถ้าคำนวณด้วยมือหรือกระดาษ โอกาสผิดผลาดสูงมาก

ืทำให้การคำนวณว่า eigenvalue ในเชิงสัญลักษณ์ เป็นไปได้ยาก เพราะพิจาณาให้เห็นค่าเป็นจำนวณ หรือเชิงซ้อนทำได้ยาก จำเป็นต้องแทนตัวเลขลงที่ เพื่อวิเคราะห์

8.5.4 แบบจำลอง SIRV ทางเศรษฐศาสตร์พฤติกรรม

แบบจำลองที่คุณให้มาเป็น SIRV model ซึ่งขยายมาจากแบบจำลองโรคระบาด (SIR model) เพื่ออธิบายการแพร่กระจายของ พฤติกรรม แทนโรค โดยมีการเพิ่มกลุ่มที่ ติดพฤติกรรมอย่างถาวร ($V$) เข้าไป เช่น พฤติกรรมการใช้จ่ายอย่างไม่ระวัง การเสพติดบางอย่าง ฯลฯ

แบบจำลอง

$$\{\begin{array}{l}\frac{dS}{dt}=-\beta SI\\ \frac{dI}{dt}=\beta SI-\gamma I-\nu I\\ \frac{dR}{dt}=\gamma I\\ \frac{dV}{dt}=\nu I\end{array}$$

• $S$ = กลุ่มที่ยังไม่รับพฤติกรรม

• $I$ = กลุ่มที่กำลังมีพฤติกรรม

• $R$ = กลุ่มที่เลิกพฤติกรรมแล้ว

• $V$ = กลุ่มที่มีพฤติกรรมถาวร (เช่น ติดการใช้จ่ายแบบฟุ่มเฟือย)

คำอธิบายพารามิเตอร์

สัญลักษณ์	ความหมาย	หน่วย (โดยนัย)	ความหมายเชิงพฤติกรรม
$\beta$	อัตราการแพร่พฤติกรรม	ต่อคนต่อเวลา	ความรุนแรงของการชักจูง เช่น การโน้มน้าวจากคนรอบข้างหรือโฆษณา
$\gamma$	อัตราการเลิกพฤติกรรม	ต่อเวลา	ความเร็วที่บุคคล กลับตัว หรือหยุดพฤติกรรม เช่น เลิกใช้จ่ายฟุ่มเฟือย
$\nu$	อัตราการกลายเป็นผู้มีพฤติกรรมถาวร	ต่อเวลา	โอกาสที่บุคคลจะ ติดพฤติกรรม จนเปลี่ยนแปลงนิสัยแบบถาวร เช่น กลายเป็นนักช็อปตลอดชีวิต

ความสัมพันธ์ของสมการ

• พฤติกรรมเริ่มแพร่จาก $S$ $\to$ $I$ ผ่านการปฏิสัมพันธ์ ($\beta SI$)

• ผู้มีพฤติกรรม ($I$) สามารถ เลิก ได้ ($\gamma I$ $\to$ $R$) หรือ ติดถาวร ได้ ($\nu I$ $\to$ $V$)

• ไม่มีการกลับจาก $R$ หรือ $V$ ไปสู่ $I$ หรือ $S$ (ในโมเดลนี้ถือว่าถาวร)

วิธีทำ การคำนวณเชิงสัญลักษณ์ด้วย caracas

ขั้นที่ 1 สร้างระบบสมการด้วย caracas

library(caracas)
# สร้างตัวแปร
beta<- symbol("beta", "positive" = TRUE)
gamma <- symbol("gamma", "positive" = TRUE)
nu <- symbol("nu", "positive" = TRUE)
S <- symbol("S")
# เปลี่ยน I เป็น J ทั้งหมด
J <- symbol("J")
R <- symbol("R")
V <- symbol("V")
# สร้างสมการ
dS <- -beta*S*J 
dJ <-  beta*S*J -gamma*J -nu*J
dR <-  gamma*J
dV <-  nu*J
  
Deri <- cbind(dS, dJ, dR, dV)
Deri

$$\left[\begin{array}{cccc}-JS\beta & JS\beta -J\gamma -J\nu & J\gamma & J\nu \end{array}\right]$$

ขั้นที่ 2 หา Jacobain matrix ด้วยคำสั่ง jacobian() ใน caracas

Jaco <-jacobian(Deri, list(S, J, R, V))
Jaco

$$\left[\begin{array}{cccc}-J\beta & -S\beta & 0& 0\\ J\beta & S\beta -\gamma -\nu & 0& 0\\ 0& \gamma & 0& 0\\ 0& \nu & 0& 0\end{array}\right]$$

ขั้นที่ 3 จุดดุลยภาพจากระบบสมการเชิงอนุพันธ์ด้วย

solve_sys(Deri, list(S, J, R, V))

SympifyError: S

ระบบสมการนี้ caracas ไม่สามารถแก้ได้

ถ้าวิเคราะห์เอง จะพบว่าระบบสมการจะเป็นศูนย์ เมื่อ I=0 ส่งผลตัวแปรอื่นๆ มีค่าเป็นอะไรก็ได้

คำนวณค่า

Eigen <- eigenval(Jaco)

ค่า eigenvalue มีค่าเท่ากับ 0 อยู่ 2 ค่า และ eigenvalue ตัวอื่นเท่ากับ

Eigen[[1]]$eigval

$$-\frac{J\beta }{2}+\frac{S\beta }{2}-\frac{\gamma }{2}-\frac{\nu }{2}-\frac{\sqrt{J^2{\beta }^2-2JS{\beta }^2-2J\beta \gamma -2J\beta \nu +S^2{\beta }^2-2S\beta \gamma -2S\beta \nu +{\gamma }^2+2\gamma \nu +{\nu }^2}}{2}$$

Eigen[[2]]$eigval

$$-\frac{J\beta }{2}+\frac{S\beta }{2}-\frac{\gamma }{2}-\frac{\nu }{2}+\frac{\sqrt{J^2{\beta }^2-2JS{\beta }^2-2J\beta \gamma -2J\beta \nu +S^2{\beta }^2-2S\beta \gamma -2S\beta \nu +{\gamma }^2+2\gamma \nu +{\nu }^2}}{2}$$

Eigen[[3]]$eigval

$$0$$

8.6 แบบฝึกหัดระบบสมการเชิงอนุพันธ์

8.6.1 I. วิเคราะห์เสถียรภาพ + Jacobian (เหมาะกับ caracas)

1. ระบบ: $$\{\begin{array}{l}\frac{dx}{dt}=3x-y\\ \frac{dy}{dt}=2x+4y\end{array}$$ หาจุดสมดุล, Jacobian matrix, eigenvalue และวิเคราะห์เสถียรภาพ

2. ระบบ: $$\frac{dx}{dt}=x(1-y),\frac{dy}{dt}=y(x-2)$$ หา Jacobian ที่จุดสมดุล และตรวจสอบเสถียรภาพ

3. ระบบ: $$\frac{dx}{dt}=y,\frac{dy}{dt}=-\sin (x)-0.1y$$ หาจุดดุลยภาพ (เชิงตัวเลข), หา Jacobian โดยประมาณด้วย caracas

4. ระบบ Lotka–Volterra: $$\frac{dR}{dt}=aR-bRF,\frac{dF}{dt}=-cF+eRF$$ ใช้ caracas เพื่อหา Jacobian ที่จุดสมดุล

5. $$\frac{dx}{dt}=x(2-x-y),\frac{dy}{dt}=y(3-x-y)$$ หาจุดตัด nullclines และวิเคราะห์ Jacobian ที่แต่ละจุด

8.6.2 II. วิเคราะห์ด้วย eigen() หรือ caracas::eigenvals()

6. ให้ Jacobian: $$J=\left[\begin{array}{cc}0& 1\\ -4& -2\end{array}\right]$$ หาค่า eigenvalues และวิเคราะห์ลักษณะ trajectory

7. เมตริกซ์ระบบ: $$A=\left[\begin{array}{cc}1& 2\\ -3& -4\end{array}\right]$$

ใช้ eigen() วิเคราะห์เสถียรภาพของจุดดุลยภาพ

8. $$\frac{dx}{dt}=y,\frac{dy}{dt}=-x-y$$ เขียนระบบเป็นเมตริกซ์ แล้วใช้ eigen() วิเคราะห์จุดสมดุล

9. $$\frac{dx}{dt}=5x+y,\frac{dy}{dt}=-x+2y$$ หาค่า eigenvalues และประเภทของจุดดุลยภาพ

$$\frac{dp}{dt}=\lambda (p^e-p),\frac{d{p}^e}{dt}=\gamma (p-p^e)$$ แปลงเป็นระบบเมตริกซ์ และหา eigenvalues ของระบบ

8.6.3 III. ใช้ phaseR วิเคราะห์ flow field, nullclines, trajectory

11. $$\frac{dx}{dt}=y,\frac{dy}{dt}=-x$$ ใช้ phaseR::flowField() และ trajectory() จากจุด $(1,0)$

12. $$\frac{dx}{dt}=x-y^2,\frac{dy}{dt}=y+x^2$$ ใช้ nullclines() เพื่อหาจุดตัด และ flowField() เพื่อแสดงพฤติกรรม

13. $$\frac{dx}{dt}=x(1-x-y),\frac{dy}{dt}=y(2-x-y)$$ ใช้ flowField() เพื่อวิเคราะห์การกระจายของ trajectory

14. $$\frac{dx}{dt}=-2x+y,\frac{dy}{dt}=-x-y$$ วาด phase portrait พร้อม trajectory จากหลายจุดเริ่มต้น

15. $$\frac{dx}{dt}=-x+y,\frac{dy}{dt}=-2x-y$$ วาด nullclines + เส้นวิถีจากจุดเริ่ม $(2,0)$

16. ให้ระบบทั่วไป $$\frac{dx}{dt}=ax+by,\frac{dy}{dt}=cx+dy$$ เขียนฟังก์ชันใน R ที่รับ $a,b,c,d$ แล้วคำนวณ eigenvalues อัตโนมัติ

17. $$\frac{dx}{dt}=x+y,\frac{dy}{dt}=-x+y$$ หาค่า eigenvalue และใช้ phaseR วิเคราะห์ flowField

Andersen, M. M., & Højsgaard, S. (2023). caracas: Computer Algebra. https://github.com/r-cas/caracas

Berkelaar, M. (2024). lpSolve: Interface to ’Lp_solve’ v. 5.5 to Solve Linear/Integer Programs. https://doi.org/10.32614/CRAN.package.lpSolve

Chanaim, S. (2023). Data Visualization with R Programming. https://bookdown.org/somsak_c/data_visualization_with_r_programming/

Meurer, A., Smith, C. P., Paprocki, M., Čertı́k, O., Kirpichev, S. B., Rocklin, M., Kumar, A., Ivanov, S., Moore, J. K., Singh, S., และคณะ. (2017). SymPy: symbolic computing in Python. PeerJ Computer Science, 3, e103. https://doi.org/10.7717/peerj-cs.103

Sievert, C. (2020). Interactive Web-Based Data Visualization with R, plotly, and shiny. Chapman; Hall/CRC. https://plotly-r.com

Ushey, K., Allaire, J., & Tang, Y. (2025). reticulate: Interface to ’Python’. https://doi.org/10.32614/CRAN.package.reticulate

Wickham, H. (2016). ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org