3  การประยุกต์อนุพันธ์ในทางเศรษฐศาสตร์

ผู้อ่านควรมีความรู้และเข้าใจของนิยามของอนุพันธ์ และสามารถจดจำสูตรการหาอนุพันธ์ของฟังก์ชันต่างๆ ได้พอสมควร เพราะเนื้อหาในบทนี้จะพูดการการคำนวณเชิงสัญลักษณ์ของประยุกต์อนุพันธ์ในทางเศรษฐศาสตร์เป็นหลัก

นิยามของอนุพันธ์ (Derivative)

อนุพันธ์ของฟังก์ชัน $f(x)$ ณ จุด $x=a$ คือ อัตราการเปลี่ยนแปลงของฟังก์ชัน $f$ เมื่อ $x$ เปลี่ยนแปลงเล็กน้อยใกล้ $a$ $$f^{\prime }(a)=\underset{h\to 0}{lim}\frac{f(a+h)-f(a)}{h}$$

ถ้าลิมิตนี้มีอยู่ จะกล่าวว่า $f$ สามารถหาอนุพันธ์ได้ที่ $x=a$

3.1 ฟังก์ชันที่สามารถหาอนุพันธ์ได้ (Differentiable Functions)

ฟังก์ชันที่สามารถหาอนุพันธ์ได้ เรียกว่าเป็น ฟังก์ชันเชิงอนุพันธ์ (Differentiable Function)
ซึ่งจะต้องมีคุณสมบัติดังนี้:

เงื่อนไขสำคัญ

1. ฟังก์ชันต้องต่อเนื่องที่จุดนั้น (แต่ฟังก์ชันที่ต่อเนื่อง อาจไม่จำเป็นต้องหาอนุพันธ์ได้ เช่น $f(x)=|x|$ ที่ $x=0$)

2. ลิมิตของอัตราการเปลี่ยนแปลงจากซ้ายและขวาต้องเท่ากัน นั่นคือ ค่าอนุพันธ์จากซ้ายและขวาต้องเหมือนกัน

3.2 ตัวอย่างฟังก์ชันที่สามารถหาอนุพันธ์ได้

ฟังก์ชัน	อนุพันธ์
$f(x)=x^n$, $n\in \mathbb{R}$	$f^{\prime }(x)=n{x}^{n-1}$
$f(x)=\sin (x)$	$f^{\prime }(x)=\cos (x)$
$f(x)=\cos (x)$	$f^{\prime }(x)=-\sin (x)$
$f(x)=e^x$	$f^{\prime }(x)=e^x$
$f(x)=\ln (x)$ (เฉพาะ $x>0$)	$f^{\prime }(x)=\frac{1}{x}$

3.3 ตัวอย่างฟังก์ชันที่ไม่สามารถหาอนุพันธ์ได้ บางจุด

ฟังก์ชัน	สาเหตุ
$f(x)=|x|$	ไม่สามารถหาอนุพันธ์ได้ที่ $x=0$ เพราะกราฟหักมุม
$f(x)=x^{1/3}$	อนุพันธ์ไม่มีที่ $x=0$ เพราะความชันไม่สิ้นสุด
ฟังก์ชันที่ไม่ต่อเนื่อง	เช่น step function หรือฟังก์ชันที่กระโดด

เยี่ยมมากครับ! ต่อไปนี้คือวิธี หาอนุพันธ์ของฟังก์ชันใน R ด้วยแพ็กเกจ caracas อย่างละเอียด พร้อมตัวอย่างและคำอธิบายครบครับ

3.4 อนุพันธ์อันดับหนึ่งด้วยฟังก์ชัน der()

1. ติดตั้งและเรียกใช้แพ็กเกจ

# เรียกใช้ทุกครั้งเมื่อใช้งานครั้งแรก
library(caracas)

2. สร้างตัวแปรเชิงสัญลักษณ์ (symbolic variables)

x <- symbol("x")     # สร้างตัวแปร x
t <- symbol("t")     # สร้างตัวแปร t

3. สร้างฟังก์ชันที่ต้องการหาอนุพันธ์

ตัวอย่าง:

f <- x^3 + 2*x^2 + 5*x + 1
f

$$x^3+2x^2+5x+1$$

g <- t^3 * sin(t) + exp(t)+ log(t)
g

$$t^3\sin \left(t\right)+e^t+\log \left(t\right)$$

4. หาอนุพันธ์ด้วย der()

เช่น

df <- der(f, x)
df

$$3x^2+4x+5$$

df1 <- der(f, t)
df1

$$0$$

dg <- der(g, t)
dg

$$t^3\cos \left(t\right)+3t^2\sin \left(t\right)+e^t+\frac{1}{t}$$

การแทนคำนวณค่าอนุพันธ์ที่ ณ จุดที่ต้องการด้วยฟังก์ชัน subs() หรือจะแปลงเป็นฟังก์ชันในอาร์ด้วย as_func() ก็ได้

# f'(0)
subs(df,x, 0)

$$5$$

# g'(1)
subs(dg, t, 1)

$$\cos \left(1\right)+1+3\sin \left(1\right)+e$$

หรือถ้าต้องการผลลัพธ์เป็นตัวเลขให้เพิ่่มฟังก์ชัน N()

# g'(1)
subs(dg, t, 1) |> N()

$$6.78299708875087$$

3.4.1 ตัวอย่างฟังก์ชันอื่น ๆ ที่คุณอาจใช้

ฟังก์ชัน	คำสั่ง caracas
$f(x)=\sin (x)$	f <- sin(x)
$f(x)=\exp (x^2)$	f <- exp(x^2)
$f(x)=\ln (x+1)$	f <- log(x + 1)
$f(x)=\frac{x^2+1}{x+2}$	f <- (x^2 + 1)/(x + 2)

แล้วหาอนุพันธ์ด้วย der(f, x) ได้

3.5 อนุพันธ์อันดับสองด้วยฟังก์ชัน der2()

ขั้นตอนก็เหมือนกันการอนุพันธ์อันดับหนึ่ง ตัวอย่างเช่น

df2 <- der2(f, x)

$$6x+4$$

dg2 <- der2(g, t)

$$-t^3\sin \left(t\right)+6t^2\cos \left(t\right)+6t\sin \left(t\right)+e^t-\frac{1}{t^2}$$

การคำนวณค่าอนุพันธ์อันดับของจุดที่ต้องการ ก็สามารถใช้ฟังก์ชัน subs() ได้เช่นเดียวกัน

3.6 การหาค่าสูงสุด-ต่ำสุดของฟังก์ชันด้วยอนุพันธ์

การหาค่าสูงสุด-ต่ำสุดของฟังก์ชันด้วยอนุพันธ์เป็นเรื่องใหญ่ของ การวิเคราะห์ทางเศรษฐศาสตร์และคณิตศาสตร์ เช่น การหากำไรสูงสุด, ต้นทุนต่ำสุด, อรรถประโยชน์สูงสุด ฯลฯ

3.6.1 ขั้นตอนการหาค่าสูงสุด/ต่ำสุดด้วยอนุพันธ์

1. $f(x)$ ต้องเป็นฟังก์ชันที่ต่อเนื่องและหาอนุพันธ์ได้

หาอนุพันธ์อันดับหนึ่ง: $$f^{\prime }(x)$$

2. หาค่าของ $x$ ที่ทำให้ $f^{\prime }(x)=0$ (เรียกว่า critical points หรือจุดวิกฤติ)

3. ใช้อนุพันธ์อันดับสอง เพื่อตรวจสอบว่าแต่ละจุดเป็นค่าสูงสุดหรือค่าต่ำสุด

   • ถ้า $f^{″}(x)>0$ $\to$ จุดต่ำสุด

   • ถ้า $f^{″}(x)<0$ $\to$ จุดสูงสุด

   • ถ้า $f^{″}(x)=0$ $\to$ ต้องวิเคราะห์เพิ่มเติม

ตัวอย่างที่ 1

$$f(x)=x^3-3x+1$$

การคำนวณโดยใช้ caracas

x <- symbol("x")
f <- x^3 - 3*x + 1
f

$$x^3-3x+1$$

อนุพันธ์อันดับ 1

df <- der(f, x)
df

$$3x^2-3$$

อนุพันธ์อันดับ 2

ddf <- der2(f, x)
ddf

$$6x$$

solve_sys(df, x)

x = -1
x = 1

แทนค่าลงในอนุพันธ์อันดับสอง

subs(ddf, x, -1)

$$-6$$

ดังนั้น $f(-1)$ เป็นจุดสูงสุด

subs(ddf, x, 1)

$$6$$

ดังนั้น $f(1)$ เป็นจุดต่ำสุด

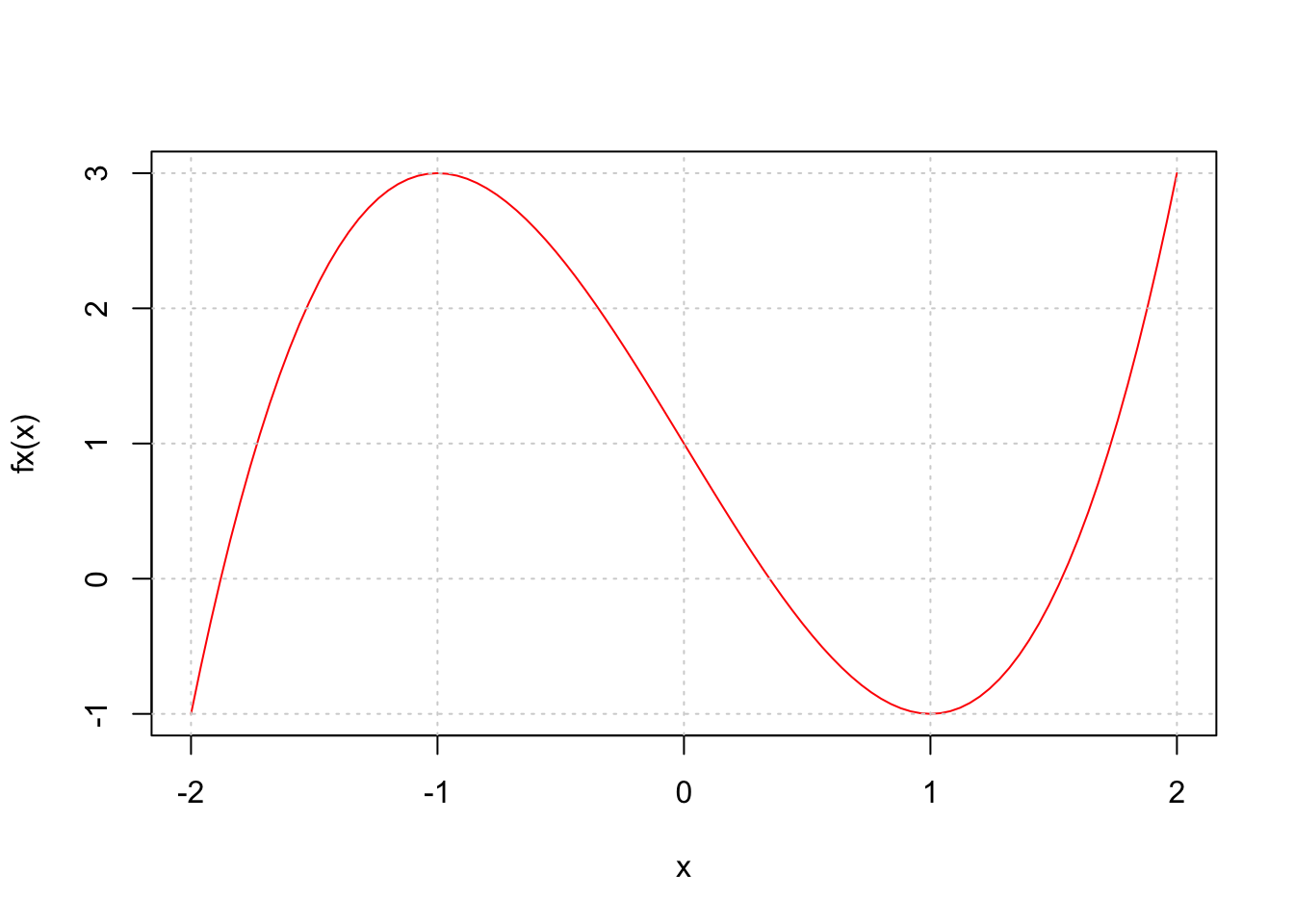
วาดกราฟ

fx <- as_func(f)
curve(fx, from = -2, to = 2, col = "red")
grid()

ที่จุด $x=-1$ และ $x=1$ เป็นค่าสูงสุดเฉพาะที่ (local maximum) และจุดต่ำสุดเฉพาะที่ (local minimum) ตามลำดับ ไม่ใช่ จุดสูงสุดสัมบูรณ์ (global maximum) และ จุดต่ำสุดสัมบูรณ์ (global minimum) ดังนั้นถ้าไม่ได้กำหนดช่วงมาให้ ต้องพิจารณาให้ดีว่าเป็นจุดสูงสุดหรือต่ำสุดแบบใด

3.7 การประยุกต์อนุพันธ์ในทางเศรษฐศาสตร์

ด้านการประยุกต์	ตัวอย่าง / คำอธิบาย
1. ต้นทุนชายขอบ (Marginal Cost, MC)	อัตราการเปลี่ยนแปลงของต้นทุนรวมเมื่อผลิตสินค้าเพิ่มขึ้นอีก 1 หน่วย $MC=\frac{dTC}{dQ}$
2. รายรับชายขอบ (Marginal Revenue, MR)	อัตราการเปลี่ยนแปลงของรายรับรวมจากการขายสินค้าเพิ่มขึ้น 1 หน่วย $MR=\frac{dTR}{dQ}$
3. อรรถประโยชน์ชายขอบ (Marginal Utility)	การเปลี่ยนแปลงของอรรถประโยชน์เมื่อบริโภคสินค้าเพิ่มขึ้น $M{U}_x=\frac{dU}{dx}$
4. การเพิ่มผลผลิต (Marginal Product)	ความเปลี่ยนแปลงของผลผลิตเมื่อเพิ่มปัจจัยการผลิต เช่น แรงงาน $M{P}_L=\frac{dQ}{dL}$
5. การหาค่าสูงสุด-ต่ำสุดของฟังก์ชัน (Optimization)	ใช้อนุพันธ์เพื่อหา จุดสูงสุดของกำไร, อรรถประโยชน์, รายได้ เป็นต้น โดยแก้ $f^{\prime }(x)=0$
6. อัตราการเปลี่ยนแปลงของราคา (Price Elasticity)	วิเคราะห์ว่าปริมาณเปลี่ยนแปลงเร็วแค่ไหนเมื่อราคาขยับ $E_p=\frac{dQ}{dP}\cdot \frac{P}{Q}$
7. การเติบโตทางเศรษฐกิจ (Growth Rate)	ใช้อนุพันธ์กับฟังก์ชันเช่น $Y(t)$, $K(t)$ เพื่อหาการเติบโตต่อเวลา $\frac{dY}{dt}$

ต้นทุนชายขอบ (Marginal Cost: MC)

ต้นทุนรวมของการผลิตสินค้าเป็นฟังก์ชัน $$TC(Q)=5Q^2+10Q+100$$
จงหาต้นทุนชายขอบเมื่อผลิต 10 หน่วย

แนวทาง:
$$MC(Q)=\frac{dTC}{dQ}=10Q+10\Rightarrow MC(10)=110$$ การคำนวณเชิงสัญลักษณ์และเชิงตัวเลขด้วย caracas

# สร้างฟังก์ชัน TQ
Q <- symbol("Q")
TC <- 5*Q^2+10*Q+100
TC

$$5Q^2+10Q+100$$

# หาอนุพันธ์ของ TC(Q)
dTC <- der(TC,Q)
dTC

$$10Q+10$$

# คำนวณ TQ'(10)
subs(dTC, Q, 10)

$$110$$

รายรับชายขอบ (Marginal Revenue: MR)

รายรับรวมจากการขายสินค้าเป็น $$TR(Q)=50Q-0.5Q^2$$
จงหารายรับชายขอบเมื่อขาย 20 หน่วย

แนวทาง:
$$MR(Q)=\frac{dTR}{dQ}=50-Q\Rightarrow MR(20)=30$$

การคำนวณเชิงสัญลักษณ์และเชิงตัวเลขด้วย caracas

# สร้างฟังก์ชัน TR
Q <- symbol("Q")
TR <- 50*Q -Q^2/2
TR

$$-\frac{Q^2}{2}+50Q$$

# หาอนุพันธ์ของ TR(Q)
dTR <- der(TR,Q)
dTR

$$50-Q$$

# คำนวณ TR'(20)
subs(dTR, Q, 20)

$$30$$

อรรถประโยชน์ชายขอบ (Marginal Utility)

ผู้บริโภคมีฟังก์ชันอรรถประโยชน์ $$U(x,y)=x^{0.5}{y}^{0.5}$$
จงหาอรรถประโยชน์ชายขอบของสินค้า $x$ เมื่อบริโภค $x=4$, $y=9$

แนวทาง:
$$M{U}_x=\frac{\partial U}{\partial x}=\frac{1}{2}{x}^{-0.5}{y}^{0.5}\Rightarrow M{U}_x(4,9)=\frac{1}{2}\cdot \frac{1}{2}\cdot 3=\frac{3}{4}$$

การคำนวณเชิงสัญลักษณ์และเชิงตัวเลขด้วย caracas

# สร้างฟังก์ชัน U(x,y)
x <- symbol("x")
y <- symbol("y")
U <- sqrt(x)*sqrt(y)
U

$$\sqrt{x}\sqrt{y}$$

# หาอนุพันธ์ของ Ux
Ux <- der(U,x)
Ux

$$\frac{\sqrt{y}}{2\sqrt{x}}$$

# คำนวณ Ux(4,9)
subs(Ux, list(x = 4, y = 9))

$$\frac{3}{4}$$

ผลผลิตชายขอบ (Marginal Product)

ฟังก์ชันการผลิต: $$Q=2L^{0.6}{K}^{0.4}$$
กำหนด $L=25$, $K=16$ จงหา $M{P}_L$

แนวทาง:
$$M{P}_L=\frac{\partial Q}{\partial L}=1.2\cdot L^{-0.4}{K}^{0.4}\Rightarrow M{P}_L=1.2\cdot {25}^{-0.4}\cdot {16}^{0.4}\approx 1.0038$$

การคำนวณเชิงสัญลักษณ์และเชิงตัวเลขด้วย caracas

# สร้างฟังก์ชัน Q(L,K)
L <- symbol("L")
K <- symbol("K")
Q <- 2*L^0.6*K^0.4
Q

$$2K^{0.4}{L}^{0.6}$$

# หาอนุพันธ์ของ MP_L
MP_L <- der(Q,L)
MP_L

$$\frac{1.2K^{0.4}}{L^{0.4}}$$

# คำนวณ MP_L(25, 26)
subs(MP_L, list(L = 25, K = 16))

$$1.00381397048762$$

การเพิ่ม-ลดฟังก์ชัน (Optimization)

กำไรของบริษัทเป็น $$\mathrm{\Pi }(Q)=120Q-4Q^2-100$$
จงหาผลผลิตที่ทำให้กำไรสูงสุด

แนวทาง:
$${\mathrm{\Pi }}^{\prime }(Q)=120-8Q\Rightarrow 120-8Q=0\Rightarrow Q=15$$

ตรวจสอบ:
$${\mathrm{\Pi }}^{″}(Q)=-8<0$$

การคำนวณเชิงสัญลักษณ์และเชิงตัวเลขด้วย caracas

# สร้างฟังก์ชัน Pi(Q)
Q <- symbol("Q")
Pi <- 120*Q-4*Q^2-100
Pi

$$-4Q^2+120Q-100$$

# หาอนุพันธ์ของ Pi(Q)
dPi <- der(Pi,Q)
dPi

$$120-8Q$$

# หาจุดที่ Pi'(Q)=0
solve_sys(dPi,Q)

Q = 15

ทดสอบค่าเป็นค่าสูงสุดจริงหรือไม่ โดยใช้อนุพันธ์อันดับสอง

# หาอนุพันธ์อันสองของ Pi(Q)
ddPi <- der2(Pi, Q)
ddPi

$$-8$$

เนื่องจาก อนุพันธ์อันดับ 2 มีค่าเป็นลบทุกจุด ดังนั้่น จึงสรุปได้ว่า ที่ Q = 15 จะมีกำไรสูงสุดคือ

subs(Pi, Q, 15) 

$$800$$

ความยืดหยุ่นของอุปสงค์ต่อราคา (Price Elasticity of Demand)

ฟังก์ชันอุปสงค์ $$Q(P)=100-2P$$
หาค่าความยืดหยุ่นที่ราคา $P=20$

แนวทาง:
$$E_p=\frac{dQ}{dP}\cdot \frac{P}{Q}=(-2)\cdot \frac{20}{100-2(20)}=-2\cdot \frac{20}{60}=-{\displaystyle \frac{2}{3}}$$ การคำนวณเชิงสัญลักษณ์และเชิงตัวเลขด้วย caracas

# สร้างฟังก์ชัน Q(P)
P <- symbol("P")
Q <- 100 - 2*P
Q

$$100-2P$$

# หาอนุพันธ์ของ Q(P)
dQ <- der(Q,P)
dQ

$$-2$$

# สร้างฟังก์ชัน Ep
Ep <- dQ*P/Q
Ep

$$-\frac{2P}{100-2P}$$

# หาค่า Ep(20)
subs(Ep, P, 20)

$$-\frac{2}{3}$$

อัตราการเติบโตทางเศรษฐกิจ (Growth Rate)

ผลผลิตตามเวลา: $$Y(t)=100e^{0.05t}$$
จงหาอัตราการเติบโตของผลผลิตเมื่อ $t=10$

แนวทาง:
$$\frac{dY}{dt}=100\cdot 0.05\cdot e^{0.05t}\Rightarrow \frac{dY}{dt}(10)=5\cdot e^{0.5}\approx 5\cdot 1.6487\approx 8.24$$

การคำนวณเชิงสัญลักษณ์และเชิงตัวเลขด้วย caracas

# สร้างฟังก์ชัน Y
t <- symbol("t")
Y <- 100*exp(0.05*t)
Y

$$100e^{0.05t}$$

# หาอนุพันธ์ของ Y
dY <- der(Y, t)
dY

$$5.0e^{0.05t}$$

# หาค่า Y'(10)
subs(dY, t, 10)

$$8.24360635350064$$

3.8 บบฝึกหัดประยุกต์อนุพันธ์ในเศรษฐศาสตร์

ให้ใช้ caracas ในการหาคำตอบ

1. กำหนดฟังก์ชันต้นทุนรวมเป็น $TC(Q)=3Q^3+5Q^2+50$ จงหาอัตราการเปลี่ยนแปลงของต้นทุน (MC) เมื่อ $Q=2$

2. รายได้รวมของผู้ผลิตให้โดย $TR(Q)=120Q-4Q^2$ จงหา MR ที่ระดับการผลิต $Q=10$

3. ให้ฟังก์ชันอรรถประโยชน์ $U(x,y)=x^2{y}^{0.5}$ จงหา Marginal Utility ของ $x$ เมื่อ $x=4$, $y=16$

4. ฟังก์ชันผลผลิตคือ $Q=20L^{0.6}{K}^{0.4}$ จงหาอนุพันธ์ของผลผลิตตามแรงงาน $L$

5. กำหนดฟังก์ชันต้นทุนเฉลี่ย $AC(Q)=Q+\frac{100}{Q}$ จงหาอัตราการเปลี่ยนแปลงของ AC เมื่อ $Q=10$

6. ให้ฟังก์ชันรายได้ $R(P)=P(300-3P)$ จงหาอัตราการเปลี่ยนแปลงของรายได้ตามราคา (dR/dP)

7. ฟังก์ชันกำไรคือ $\mathrm{\Pi }(Q)=100Q-5Q^2-200$ จงหาจุดที่กำไรเพิ่มขึ้นช้าที่สุด (ค่าต่ำสุดของ d²π/dQ²)

8. ผู้บริโภคมีฟังก์ชัน $U(x,y)=\ln (x)+2\ln (y)$ จงหาอนุพันธ์ของอรรถประโยชน์ตาม $y$

9. ให้ฟังก์ชันต้นทุนรวม $C(Q)=10Q^2+100$ จงหาอัตราการเปลี่ยนแปลงของต้นทุนเมื่อ $Q=5$

10. ฟังก์ชันผลผลิต $Q=L^{1/2}{K}^{1/2}$ จงหา MP ของทุน $K$ ที่ $L=25,K=16$

11. หากต้นทุนเพิ่ม (MC) คืออนุพันธ์ของ $TC=Q^2+5Q$ จงหาค่า MC ที่ $Q=6$

12. ให้ $TR=50Q-Q^3$ และ $TC=5Q^2+50$ จงหาค่า dπ/dQ ที่ $Q=4$

13. ฟังก์ชันต้นทุนเฉลี่ย $AC=\frac{TC}{Q}$ โดย $TC=Q^2+20$ จงหา dAC/dQ เมื่อ $Q=2$

14. ให้ฟังก์ชันอรรถประโยชน์ $U=x^{0.4}{y}^{0.6}$ จงหาอนุพันธ์ของ $U$ ตาม $x$

15. รายได้รวมคือ $R(Q)=200Q-2Q^2$ จงหาค่า Q ที่ MR = 0

16. ต้นทุนรวมคือ $C(Q)=4Q^3-20Q^2+60Q$ จงหา MC และวิเคราะห์ว่าจุดใด MC ต่ำสุด

17. ฟังก์ชันผลผลิต $Q(L)=5L-0.1L^2$ จงหา MP ที่ $L=10$

18. ให้ฟังก์ชันอรรถประโยชน์ $U(x,y)=x^2+y^2$ จงหาเส้นชั้นอรรถประโยชน์ (indifference slope) ที่ $x=3,y=4$

19. ถ้ารายได้เฉลี่ยคือ $AR=\frac{TR}{Q}$, โดย $TR=80Q-Q^2$ จงหาอัตราการเปลี่ยนแปลงของ AR ที่ $Q=10$

20. ฟังก์ชันต้นทุนรวม $TC=100+20Q+0.5Q^2$ จงหาอัตราการเปลี่ยนแปลงของ MC เมื่อ Q เพิ่มขึ้น 1 หน่วย

Andersen, M. M., & Højsgaard, S. (2023). caracas: Computer Algebra. https://github.com/r-cas/caracas

Berkelaar, M. (2024). lpSolve: Interface to ’Lp_solve’ v. 5.5 to Solve Linear/Integer Programs. https://doi.org/10.32614/CRAN.package.lpSolve

Chanaim, S. (2023). Data Visualization with R Programming. https://bookdown.org/somsak_c/data_visualization_with_r_programming/

Meurer, A., Smith, C. P., Paprocki, M., Čertı́k, O., Kirpichev, S. B., Rocklin, M., Kumar, A., Ivanov, S., Moore, J. K., Singh, S., และคณะ. (2017). SymPy: symbolic computing in Python. PeerJ Computer Science, 3, e103. https://doi.org/10.7717/peerj-cs.103

Sievert, C. (2020). Interactive Web-Based Data Visualization with R, plotly, and shiny. Chapman; Hall/CRC. https://plotly-r.com

Ushey, K., Allaire, J., & Tang, Y. (2025). reticulate: Interface to ’Python’. https://doi.org/10.32614/CRAN.package.reticulate

Wickham, H. (2016). ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org