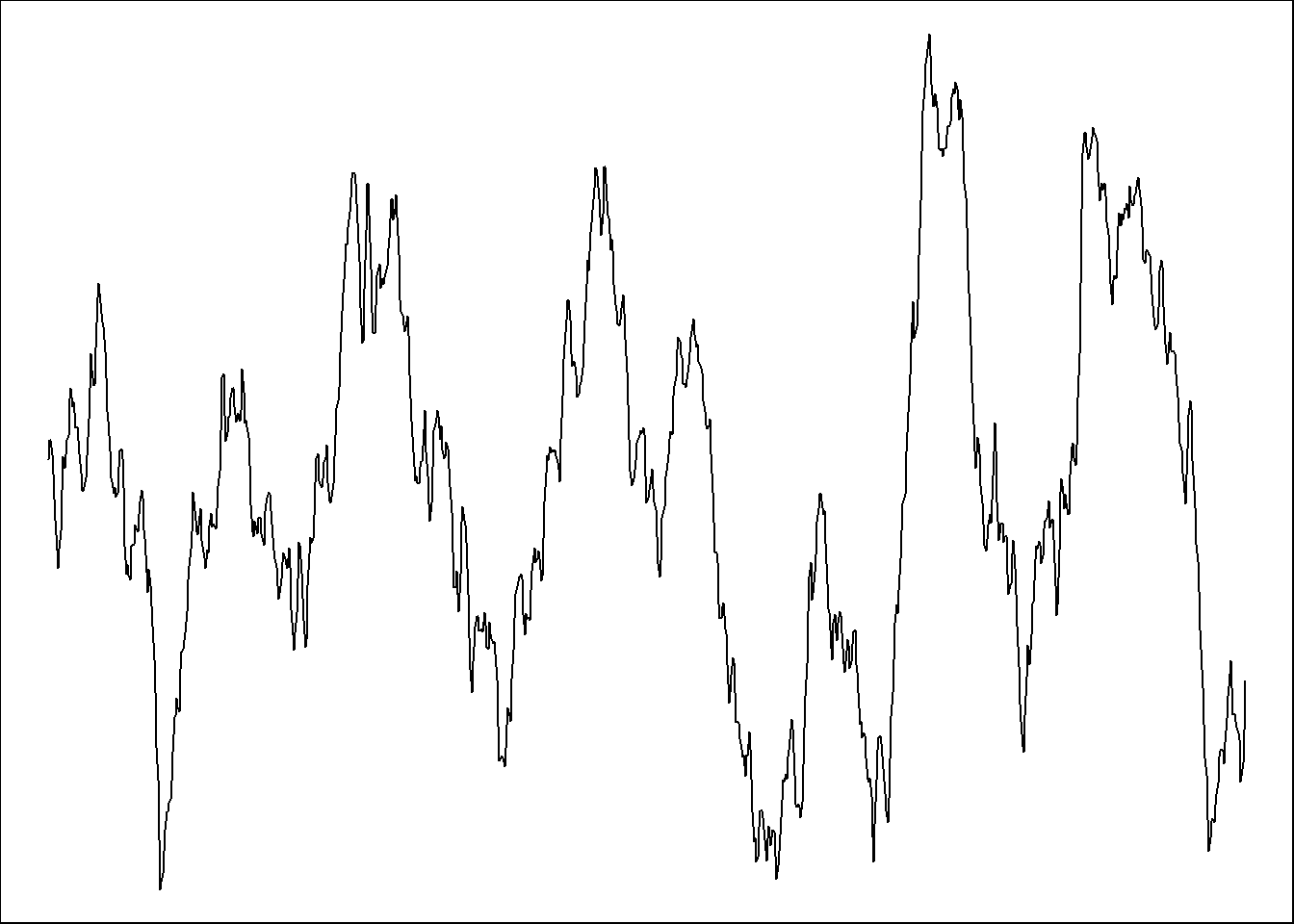Chapter 6 ARIMA Models

# preamble setting the directories and loading packages
rm(list = ls())
setwd("C:/Users/Tejendra/Desktop/FoldersOnDesktop/UdemyCourse/Section6")
require(tidyverse)
require(tidymodels)
require(data.table)
require(tidyposterior)
require(tsibble)  #tsibble for time series based on tidy principles
require(fable)  #for forecasting based on tidy principles
require(ggfortify)  #for plotting timeseries
require(forecast)  #for forecast function
require(tseries)
require(chron)
require(lubridate)
require(directlabels)
require(zoo)
require(lmtest)
require(TTR)  #for smoothing the time series

#globally setting the theme for plots
theme_set(theme_bw())
par(mar = c(1,1,1,1))

#Script
### ARIMA models
## ARIMA with auto.arima

plot(lynx)

autoplot(lynx) +
  xlab("") + ylab("") +
  ggtitle("Time Series Plot of the `lynx' Time-Series") +
  theme(plot.title = element_text(hjust = 0.5)) #for centering the text

par(mar = c(0.01,0.01,0.01,0.01))
tsdisplay(lynx) # autoregression?

ggtsdisplay(lynx,
            plot.type = "partial",
            main = "ACF & PACF plot for `lynx' Time-Series",
            smooth = TRUE)

adf.test(lynx) #to check for the stationarity of the time series

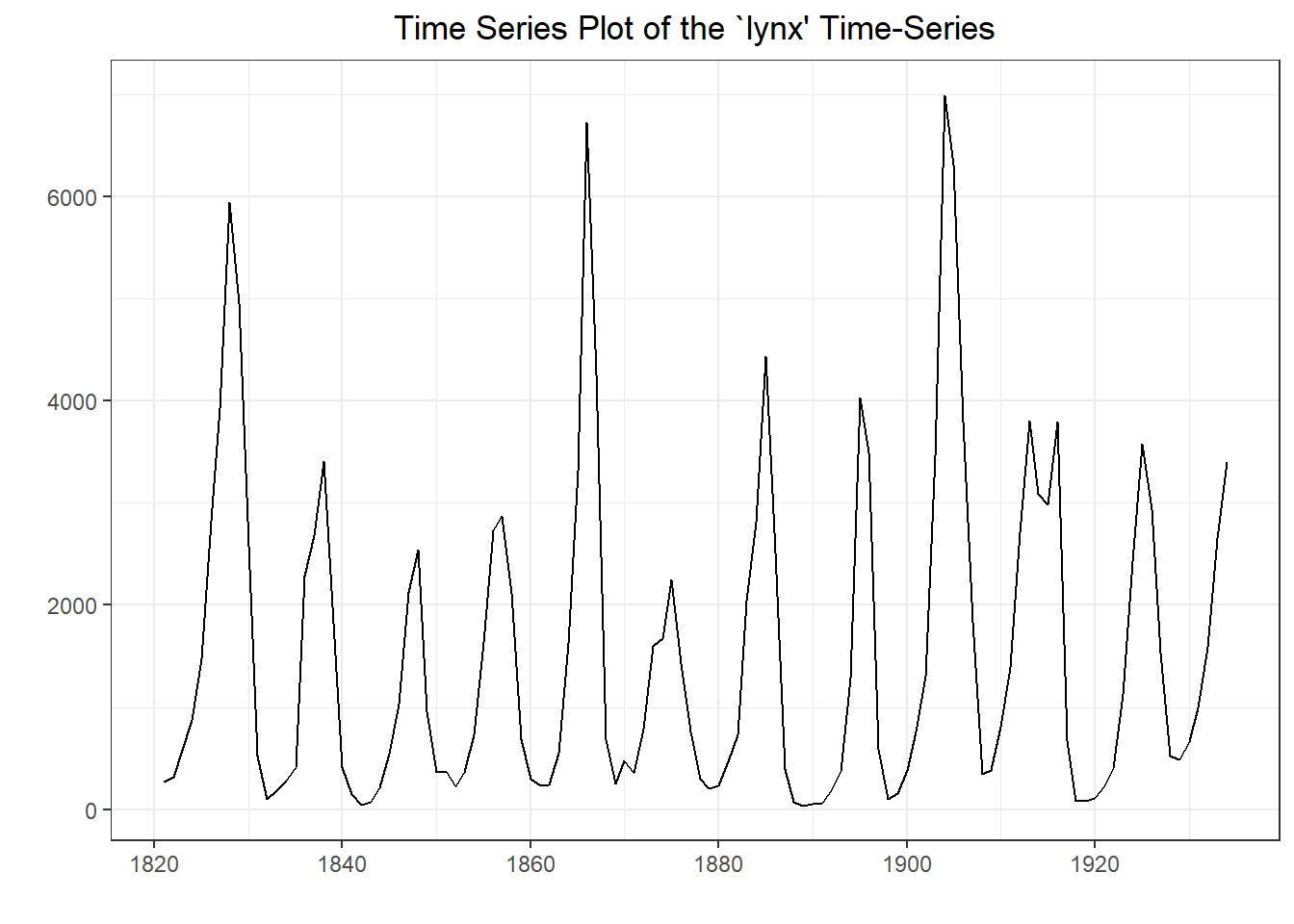
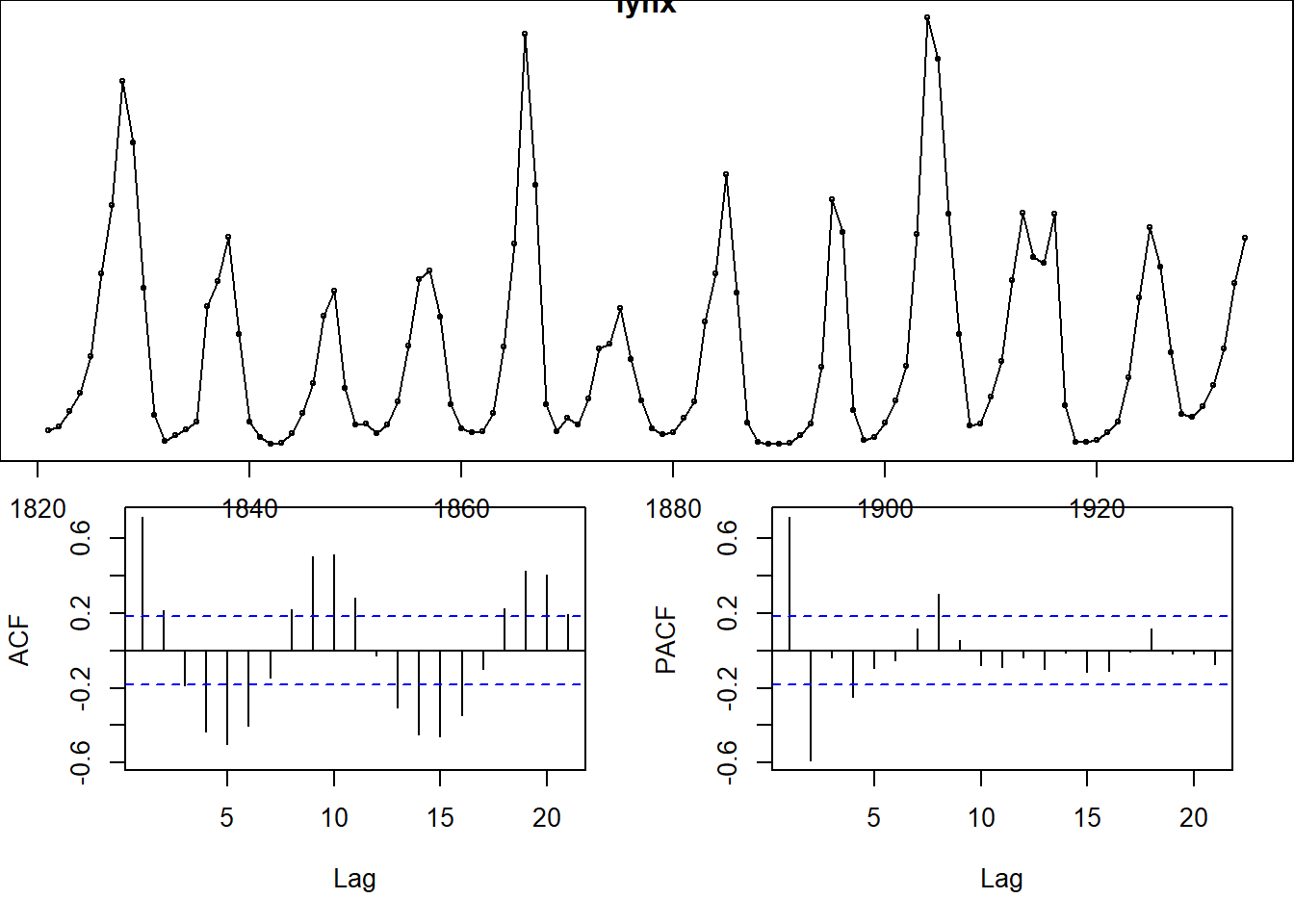
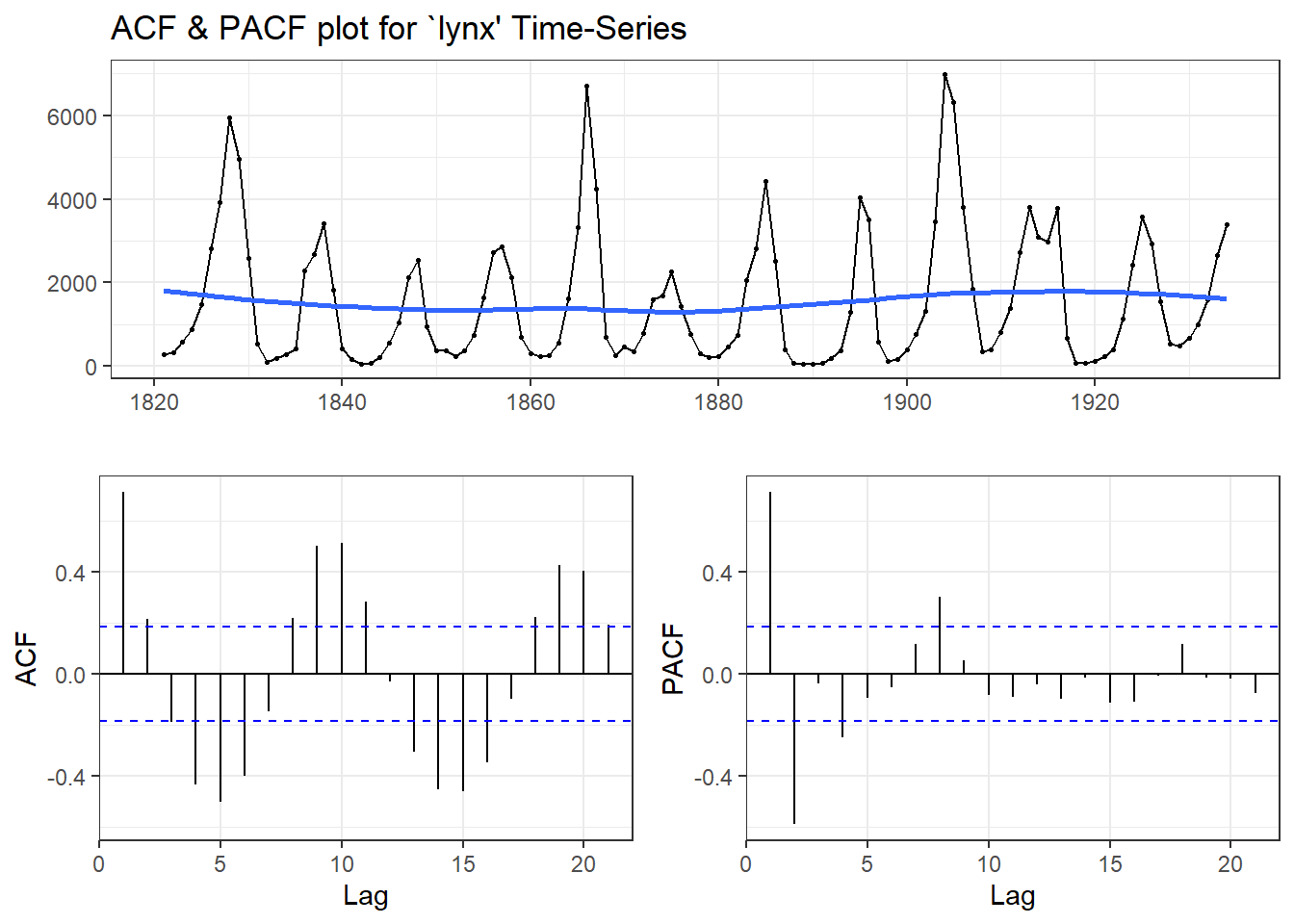
## Warning in adf.test(lynx): p-value smaller than printed p-value

## 
##  Augmented Dickey-Fuller Test
## 
## data:  lynx
## Dickey-Fuller = -6.3068, Lag order = 4, p-value = 0.01
## alternative hypothesis: stationary

auto.arima(lynx)

## Series: lynx 
## ARIMA(2,0,2) with non-zero mean 
## 
## Coefficients:
##          ar1      ar2      ma1      ma2       mean
##       1.3421  -0.6738  -0.2027  -0.2564  1544.4039
## s.e.  0.0984   0.0801   0.1261   0.1097   131.9242
## 
## sigma^2 estimated as 761965:  log likelihood=-932.08
## AIC=1876.17   AICc=1876.95   BIC=1892.58

auto.arima(lynx, trace = T)

## 
##  ARIMA(2,0,2) with non-zero mean : 1876.952
##  ARIMA(0,0,0) with non-zero mean : 2006.724
##  ARIMA(1,0,0) with non-zero mean : 1927.209
##  ARIMA(0,0,1) with non-zero mean : 1918.165
##  ARIMA(0,0,0) with zero mean     : 2080.721
##  ARIMA(1,0,2) with non-zero mean : 1888.757
##  ARIMA(2,0,1) with non-zero mean : 1880.014
##  ARIMA(3,0,2) with non-zero mean : 1878.603
##  ARIMA(2,0,3) with non-zero mean : Inf
##  ARIMA(1,0,1) with non-zero mean : 1891.442
##  ARIMA(1,0,3) with non-zero mean : 1890.03
##  ARIMA(3,0,1) with non-zero mean : 1881.962
##  ARIMA(3,0,3) with non-zero mean : 1881.515
##  ARIMA(2,0,2) with zero mean     : 1905.595
## 
##  Best model: ARIMA(2,0,2) with non-zero mean

## Series: lynx 
## ARIMA(2,0,2) with non-zero mean 
## 
## Coefficients:
##          ar1      ar2      ma1      ma2       mean
##       1.3421  -0.6738  -0.2027  -0.2564  1544.4039
## s.e.  0.0984   0.0801   0.1261   0.1097   131.9242
## 
## sigma^2 estimated as 761965:  log likelihood=-932.08
## AIC=1876.17   AICc=1876.95   BIC=1892.58

# recommended setting
auto.arima(lynx, trace = T, 
           stepwise = F, 
           approximation = F)

## 
##  ARIMA(0,0,0) with zero mean     : 2080.721
##  ARIMA(0,0,0) with non-zero mean : 2006.724
##  ARIMA(0,0,1) with zero mean     : 1972.791
##  ARIMA(0,0,1) with non-zero mean : 1918.165
##  ARIMA(0,0,2) with zero mean     : 1925.15
##  ARIMA(0,0,2) with non-zero mean : 1890.428
##  ARIMA(0,0,3) with zero mean     : 1913.118
##  ARIMA(0,0,3) with non-zero mean : 1888.326
##  ARIMA(0,0,4) with zero mean     : 1906.524
##  ARIMA(0,0,4) with non-zero mean : 1889.064
##  ARIMA(0,0,5) with zero mean     : 1908.619
##  ARIMA(0,0,5) with non-zero mean : 1886.754
##  ARIMA(1,0,0) with zero mean     : 1934.647
##  ARIMA(1,0,0) with non-zero mean : 1927.209
##  ARIMA(1,0,1) with zero mean     : 1903.345
##  ARIMA(1,0,1) with non-zero mean : 1891.442
##  ARIMA(1,0,2) with zero mean     : 1903.567
##  ARIMA(1,0,2) with non-zero mean : 1888.757
##  ARIMA(1,0,3) with zero mean     : 1905.59
##  ARIMA(1,0,3) with non-zero mean : 1890.03
##  ARIMA(1,0,4) with zero mean     : 1907.578
##  ARIMA(1,0,4) with non-zero mean : Inf
##  ARIMA(2,0,0) with zero mean     : 1906.685
##  ARIMA(2,0,0) with non-zero mean : 1878.399
##  ARIMA(2,0,1) with zero mean     : 1903.412
##  ARIMA(2,0,1) with non-zero mean : 1880.014
##  ARIMA(2,0,2) with zero mean     : 1905.595
##  ARIMA(2,0,2) with non-zero mean : 1876.952
##  ARIMA(2,0,3) with zero mean     : 1907.963
##  ARIMA(2,0,3) with non-zero mean : Inf
##  ARIMA(3,0,0) with zero mean     : 1903.728
##  ARIMA(3,0,0) with non-zero mean : 1880.512
##  ARIMA(3,0,1) with zero mean     : 1905.587
##  ARIMA(3,0,1) with non-zero mean : 1881.962
##  ARIMA(3,0,2) with zero mean     : Inf
##  ARIMA(3,0,2) with non-zero mean : 1878.603
##  ARIMA(4,0,0) with zero mean     : 1905.899
##  ARIMA(4,0,0) with non-zero mean : 1875.007
##  ARIMA(4,0,1) with zero mean     : Inf
##  ARIMA(4,0,1) with non-zero mean : 1876.407
##  ARIMA(5,0,0) with zero mean     : 1904.543
##  ARIMA(5,0,0) with non-zero mean : 1876.332
## 
## 
## 
##  Best model: ARIMA(4,0,0) with non-zero mean

## Series: lynx 
## ARIMA(4,0,0) with non-zero mean 
## 
## Coefficients:
##          ar1      ar2     ar3      ar4       mean
##       1.1246  -0.7174  0.2634  -0.2543  1547.3859
## s.e.  0.0903   0.1367  0.1361   0.0897   136.8501
## 
## sigma^2 estimated as 748457:  log likelihood=-931.11
## AIC=1874.22   AICc=1875.01   BIC=1890.64

## ARIMA calculations
# AR(2) model
myarima = arima(lynx, order = c(2,0,0))
myarima

## 
## Call:
## arima(x = lynx, order = c(2, 0, 0))
## 
## Coefficients:
##          ar1      ar2  intercept
##       1.1474  -0.5997  1545.4458
## s.e.  0.0742   0.0740   181.6736
## 
## sigma^2 estimated as 768159:  log likelihood = -935.02,  aic = 1878.03

tail(lynx)

## Time Series:
## Start = 1929 
## End = 1934 
## Frequency = 1 
## [1]  485  662 1000 1590 2657 3396

residuals(myarima)

## Time Series:
## Start = 1821 
## End = 1934 
## Frequency = 1 
##   [1]  -711.715800  -247.179068  -321.014839  -306.751202   127.414827
##   [6]   951.890591   876.687792  2428.733153  -212.432514  -237.541926
##  [11]  -164.223204   344.415030  -313.801319  -572.372533  -499.800869
##  [16]  1284.008241  -390.614888   999.532714 -1176.312892  -338.411239
##  [21]    76.614594  -581.986383  -592.092428  -537.056449  -356.640535
##  [26]  -164.773680   572.140125    13.626146 -1375.059569    84.838236
##  [31]  -162.287575  -690.094698  -371.088497  -246.153634   316.113199
##  [36]   584.894187    27.600121  -240.002495  -724.567794    85.994521
##  [41]  -395.876984  -545.490420  -286.601293   437.533551  1080.751334
##  [46]  3196.206424 -2171.180547  -862.324669  1319.008240  -106.590562
##  [51]  -730.821550   -42.121950   210.099599  -381.832131   584.871735
##  [56]  -850.724879  -229.236651  -412.244306  -387.695328  -521.330158
##  [61]  -372.233398  -363.825181   779.748247   210.328753  1731.217687
##  [66] -1586.424626  -533.760190   433.588275  -510.481277  -650.987938
##  [71]  -672.853636  -549.330544  -502.352341   273.149380  2075.597251
##  [76] -1054.463188 -1704.735336   828.545228  -314.449678  -424.603800
##  [81]  -293.316062   -29.674453  1720.888636  3099.981788  -329.627515
##  [86]    44.035737   569.799862  -185.278565   388.247443  -122.427802
##  [91]    -9.044981   905.933577   820.433050  -341.167517  1018.287679
##  [96]  1519.696544 -2583.562459   881.643131  -307.733379  -634.234854
## [101]  -545.962808  -498.009703   112.495341   673.381411   763.327803
## [106]  -406.375377  -386.254717  -173.376326   100.795394  -276.260594
## [111]  -167.745563   140.575959   733.302579   601.838001

# Check the equation for AR(2)
(2657 - 1545.45)*1.147 - (1590 - 1545.45)*0.6 + 601.84

## [1] 1850.058

3396 - 1545.45

## [1] 1850.55

# MA(2) model
myarima = arima(lynx, order = c(0,0,2))
myarima

## 
## Call:
## arima(x = lynx, order = c(0, 0, 2))
## 
## Coefficients:
##          ma1     ma2  intercept
##       1.1407  0.4697  1545.3670
## s.e.  0.0776  0.0721   224.5215
## 
## sigma^2 estimated as 855092:  log likelihood = -941.03,  aic = 1890.06

residuals(myarima)

## Time Series:
## Start = 1821 
## End = 1934 
## Frequency = 1 
##   [1]  -803.732851  -316.819775  -339.796973  -153.575542   256.164758
##   [6]  1051.017490  1062.665677  2690.592373  -162.936784   -44.605977
##  [11]  -894.921151  -405.552321  -478.418368  -530.135762  -306.914693
##  [16]  1338.739662  -243.365541  1512.454318 -1332.377780  -326.856600
##  [21]  -395.701695  -895.452231  -270.030612  -603.745610  -183.818830
##  [26]   -19.103090   691.762826   210.483679 -1153.389638    32.488716
##  [31]  -663.690549  -578.528068  -213.686644  -298.876138   533.939929
##  [36]   710.925757   263.863961   -61.283359  -915.393384  -173.356483
##  [41]  -681.659497  -441.346353  -169.735507   478.553892  1299.450551
##  [46]  3468.524287 -1858.394332  -367.558957     1.794961  -901.775190
##  [51]  -159.518680  -155.841195   301.331932  -139.911234   723.702215
##  [56]  -879.208277  -126.335608  -689.293961  -498.722732  -423.698105
##  [61]  -358.791482  -201.071547   894.524832   339.653953  2078.024947
##  [66] -1564.386859  -347.838999  -340.793301  -954.233203  -247.766795
##  [71]  -755.533899  -379.124919  -381.015812   359.344984  2254.673608
##  [76]  -791.145850 -1114.876734   203.012693 -1100.303344     1.440094
##  [81]  -272.206328    71.473327  1965.953529  3169.419791   228.755266
##  [86]   499.031993  -386.077507  -994.344061   152.258905  -444.019657
##  [91]   277.629380  1059.482295   915.638387     3.497027  1005.575888
##  [96]  1095.889333 -2593.803120   979.758850 -1364.729473  -340.749646
## [101]  -286.657856  -659.317506   473.383962   656.300763  1057.619544
## [106]  -125.095552  -362.420744  -544.182680  -269.369783  -320.487877
## [111]   -53.252771   255.911083   844.717221   766.830502

# Check the equation for MA(2)
844.72*1.141 + 255.91*0.47 + 766.83

## [1] 1850.933

3396 - 1545.37

## [1] 1850.63

## ARIMA time series simulations
set.seed(123) # for reproduction
# simulation, at least n of 1000 
asim <- arima.sim(model = list(order = c(1,0,1), 
                               ar = c(0.4), 
                               ma = c(0.3)), 
                  n = 1000) + 10
plot(asim)

autoplot(asim) +
  xlab("") + ylab("") +
  ggtitle("Time Series Plot of the `asim' Time-Series") +
  theme(plot.title = element_text(hjust = 0.5)) #for centering the text

plot(rollmean(asim, 50)) #50 days MA

plot(rollmean(asim, 25)) #25 days MA

autoplot(rollmean(asim, 50)) + #50 days MA
  xlab("") + ylab("") +
  ggtitle("50 Days MA plot for `asim' Time-Series") +
  theme(plot.title = element_text(hjust = 0.5))

autoplot(rollmean(asim, 25)) + #25 days MA
xlab("") + ylab("") +
  ggtitle("25 Days MA plot for `asim' Time-Series") +
  theme(plot.title = element_text(hjust = 0.5))

# Stationarity library(tseries) 
adf.test(asim)

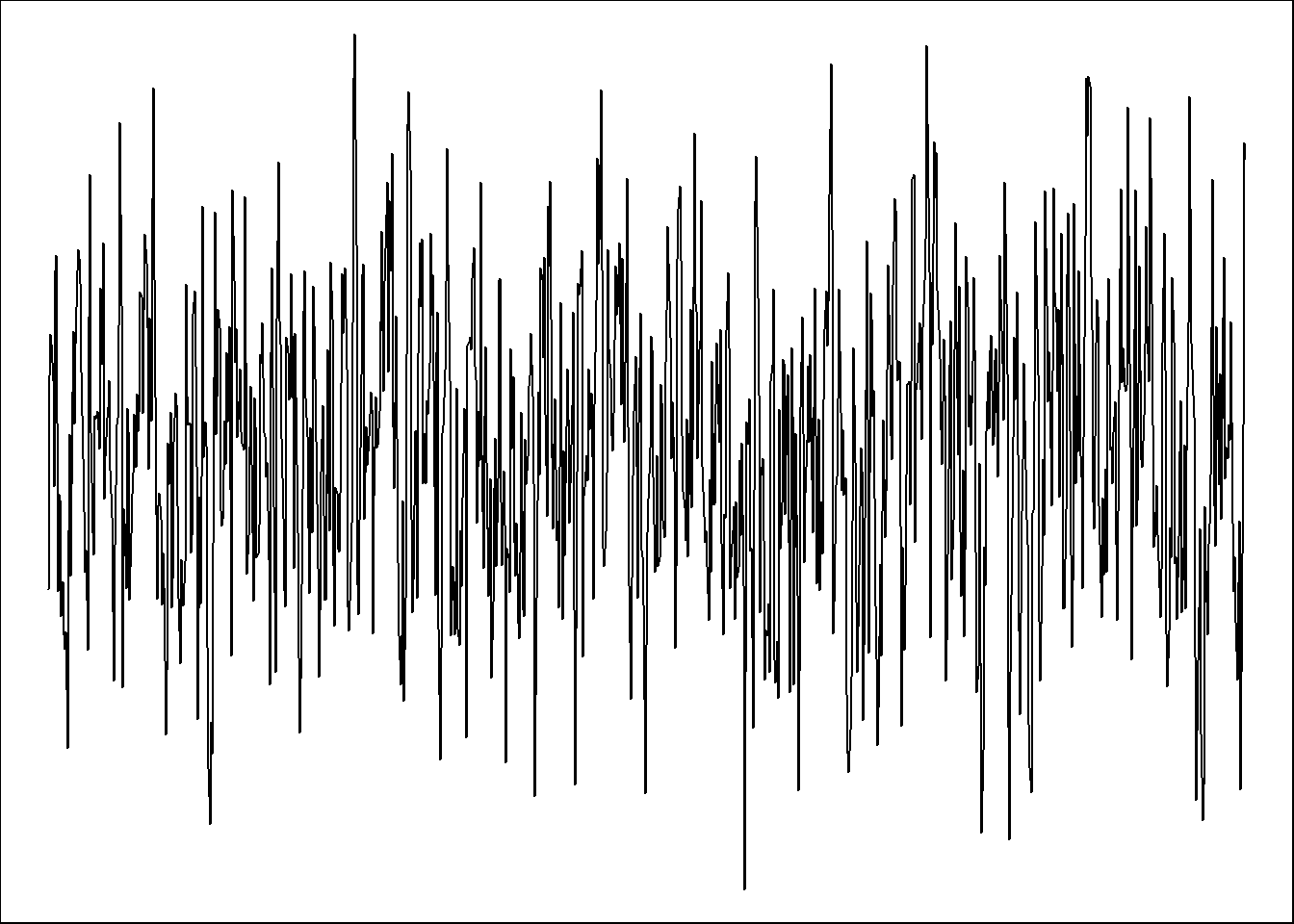
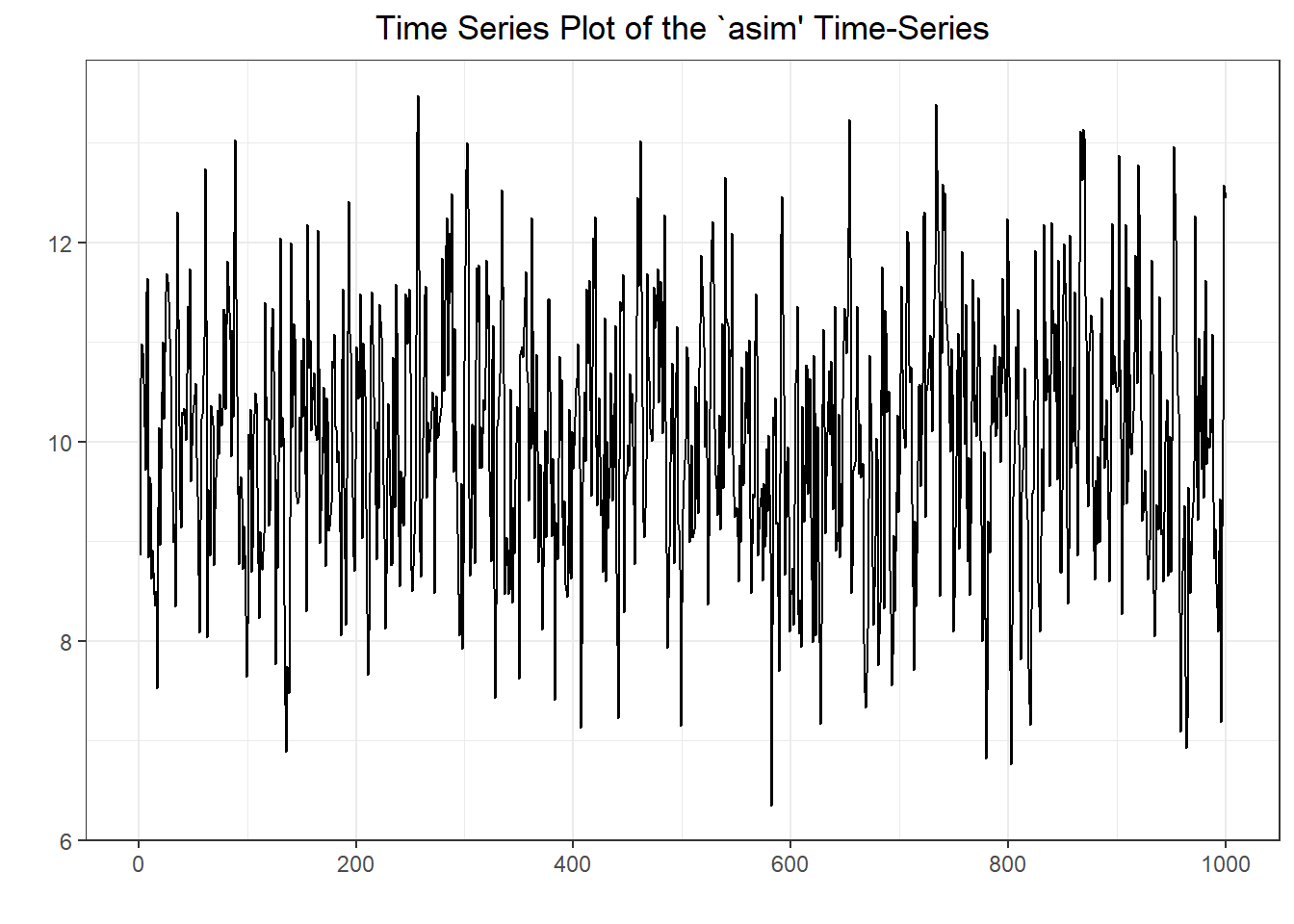
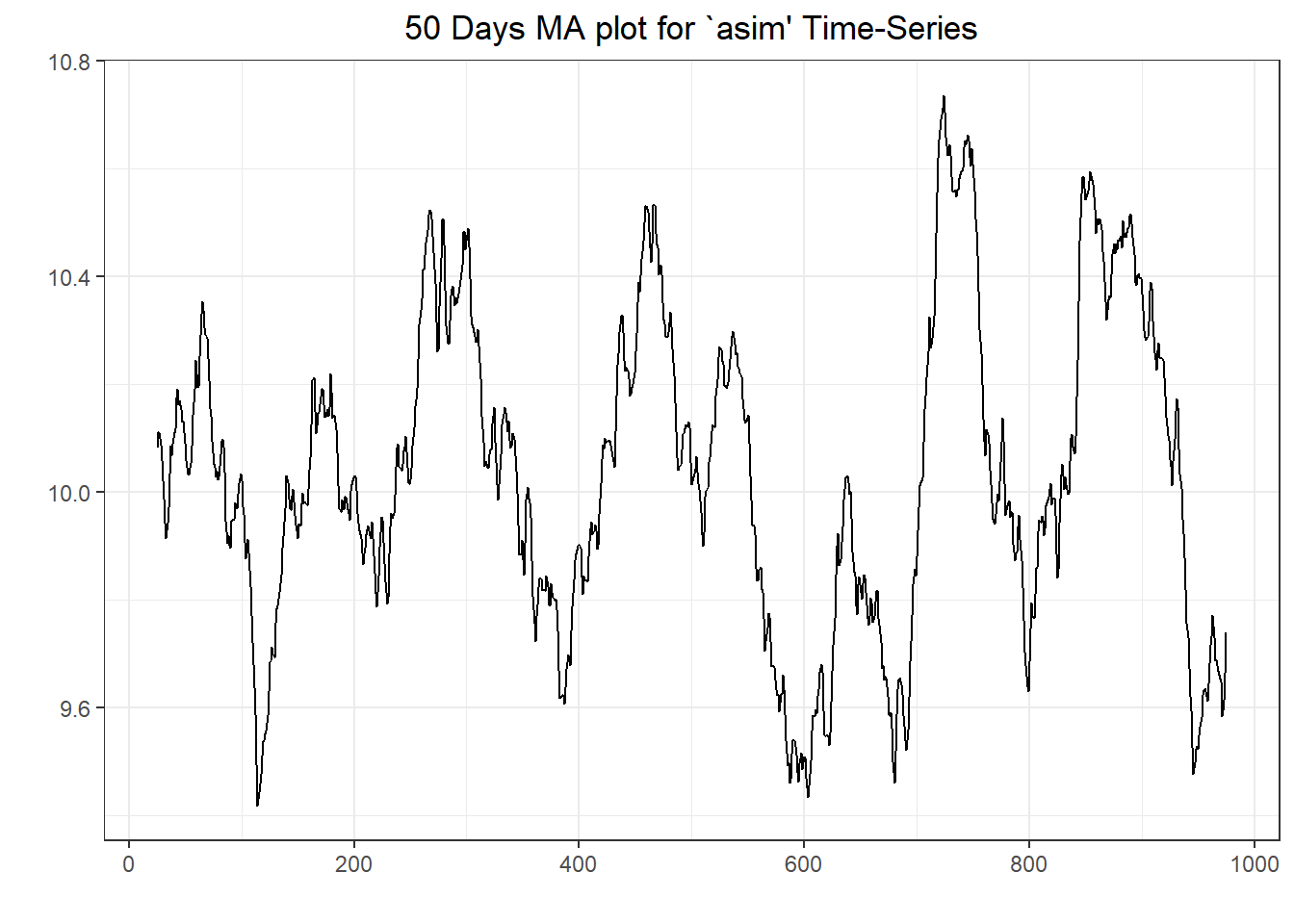
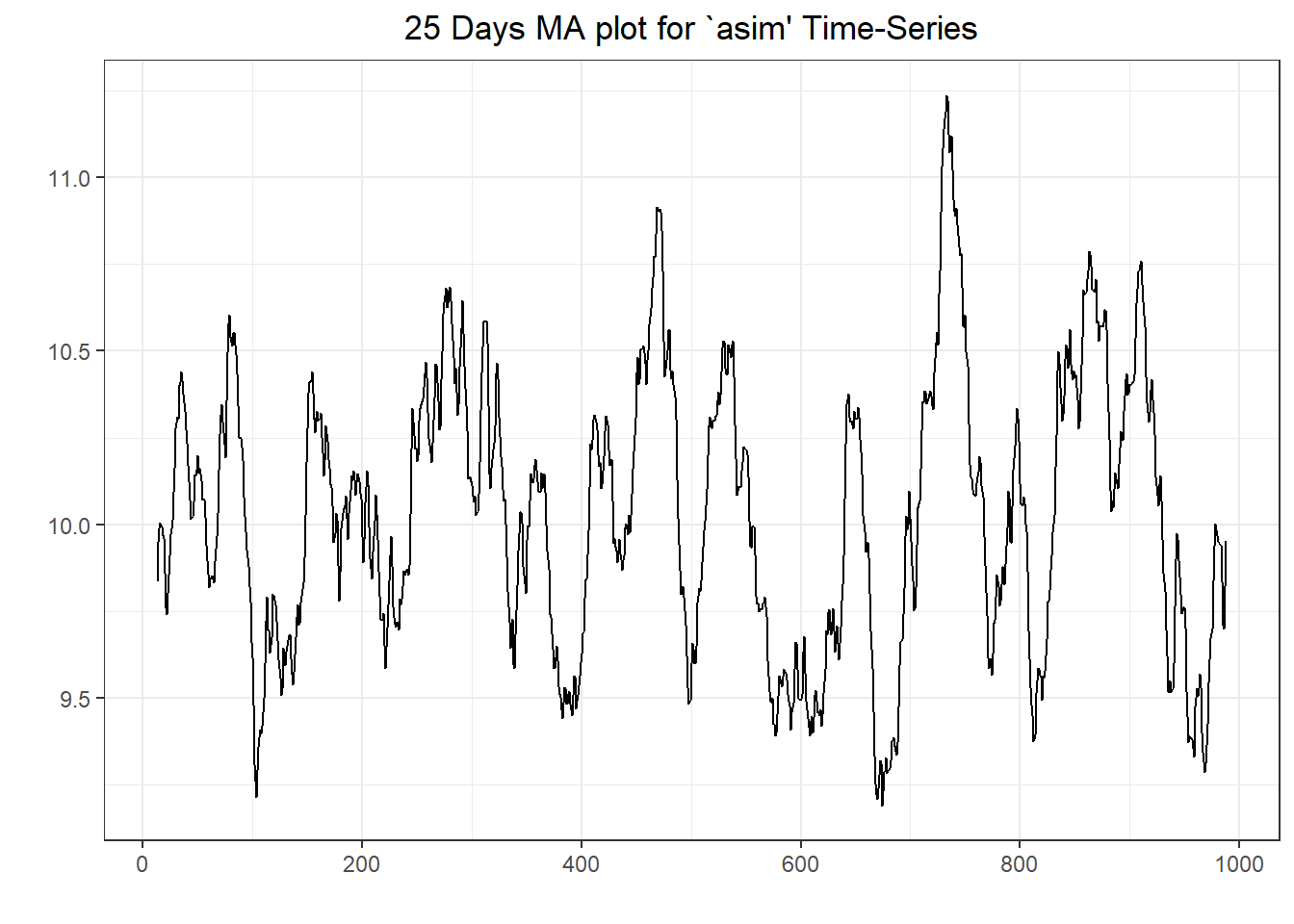
## Warning in adf.test(asim): p-value smaller than printed p-value

## 
##  Augmented Dickey-Fuller Test
## 
## data:  asim
## Dickey-Fuller = -9.0113, Lag order = 9, p-value = 0.01
## alternative hypothesis: stationary

# Autocorrelation library(forecast) tsdisplay(asim)
ggtsdisplay(asim,
            plot.type = "partial",
            main = "ACF & PACF plot for `asim' Time-Series",
            smooth = TRUE)

auto.arima(asim, 
           trace = T,  
           stepwise = F,   
           approximation = F)

## 
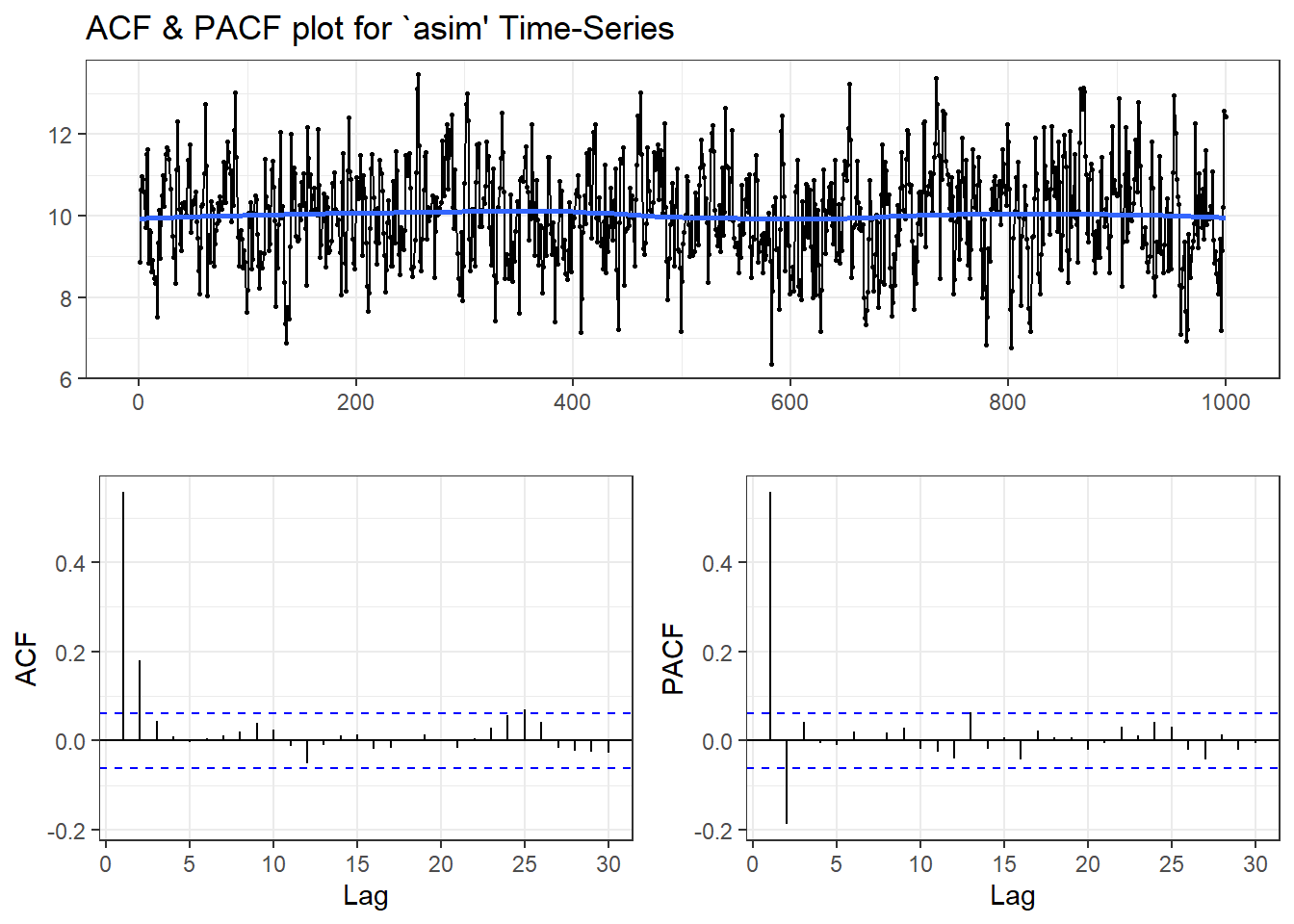
##  ARIMA(0,0,0) with zero mean     : 7465.459
##  ARIMA(0,0,0) with non-zero mean : 3241.528
##  ARIMA(0,0,1) with zero mean     : 6218.948
##  ARIMA(0,0,1) with non-zero mean : 2878.74
##  ARIMA(0,0,2) with zero mean     : 5341.968
##  ARIMA(0,0,2) with non-zero mean : 2836.895
##  ARIMA(0,0,3) with zero mean     : 4809.724
##  ARIMA(0,0,3) with non-zero mean : 2837.534
##  ARIMA(0,0,4) with zero mean     : 4450.32
##  ARIMA(0,0,4) with non-zero mean : 2838.689
##  ARIMA(0,0,5) with zero mean     : 4219.275
##  ARIMA(0,0,5) with non-zero mean : 2840.557
##  ARIMA(1,0,0) with zero mean     : Inf
##  ARIMA(1,0,0) with non-zero mean : 2870.637
##  ARIMA(1,0,1) with zero mean     : Inf
##  ARIMA(1,0,1) with non-zero mean : 2836.047
##  ARIMA(1,0,2) with zero mean     : Inf
##  ARIMA(1,0,2) with non-zero mean : 2837.165
##  ARIMA(1,0,3) with zero mean     : Inf
##  ARIMA(1,0,3) with non-zero mean : 2839.088
##  ARIMA(1,0,4) with zero mean     : Inf
##  ARIMA(1,0,4) with non-zero mean : 2840.615
##  ARIMA(2,0,0) with zero mean     : Inf
##  ARIMA(2,0,0) with non-zero mean : 2836.945
##  ARIMA(2,0,1) with zero mean     : Inf
##  ARIMA(2,0,1) with non-zero mean : 2837.319
##  ARIMA(2,0,2) with zero mean     : Inf
##  ARIMA(2,0,2) with non-zero mean : 2838.849
##  ARIMA(2,0,3) with zero mean     : Inf
##  ARIMA(2,0,3) with non-zero mean : 2840.867
##  ARIMA(3,0,0) with zero mean     : Inf
##  ARIMA(3,0,0) with non-zero mean : 2837.297
##  ARIMA(3,0,1) with zero mean     : Inf
##  ARIMA(3,0,1) with non-zero mean : 2839.296
##  ARIMA(3,0,2) with zero mean     : Inf
##  ARIMA(3,0,2) with non-zero mean : 2840.86
##  ARIMA(4,0,0) with zero mean     : Inf
##  ARIMA(4,0,0) with non-zero mean : 2839.279
##  ARIMA(4,0,1) with zero mean     : Inf
##  ARIMA(4,0,1) with non-zero mean : 2841.309
##  ARIMA(5,0,0) with zero mean     : Inf
##  ARIMA(5,0,0) with non-zero mean : 2841.162
## 
## 
## 
##  Best model: ARIMA(1,0,1) with non-zero mean

## Series: asim 
## ARIMA(1,0,1) with non-zero mean 
## 
## Coefficients:
##          ar1     ma1     mean
##       0.3494  0.3183  10.0288
## s.e.  0.0478  0.0473   0.0637
## 
## sigma^2 estimated as 0.9927:  log likelihood=-1414
## AIC=2836.01   AICc=2836.05   BIC=2855.64

## ARIMA parameter selection
adf.test(lynx)

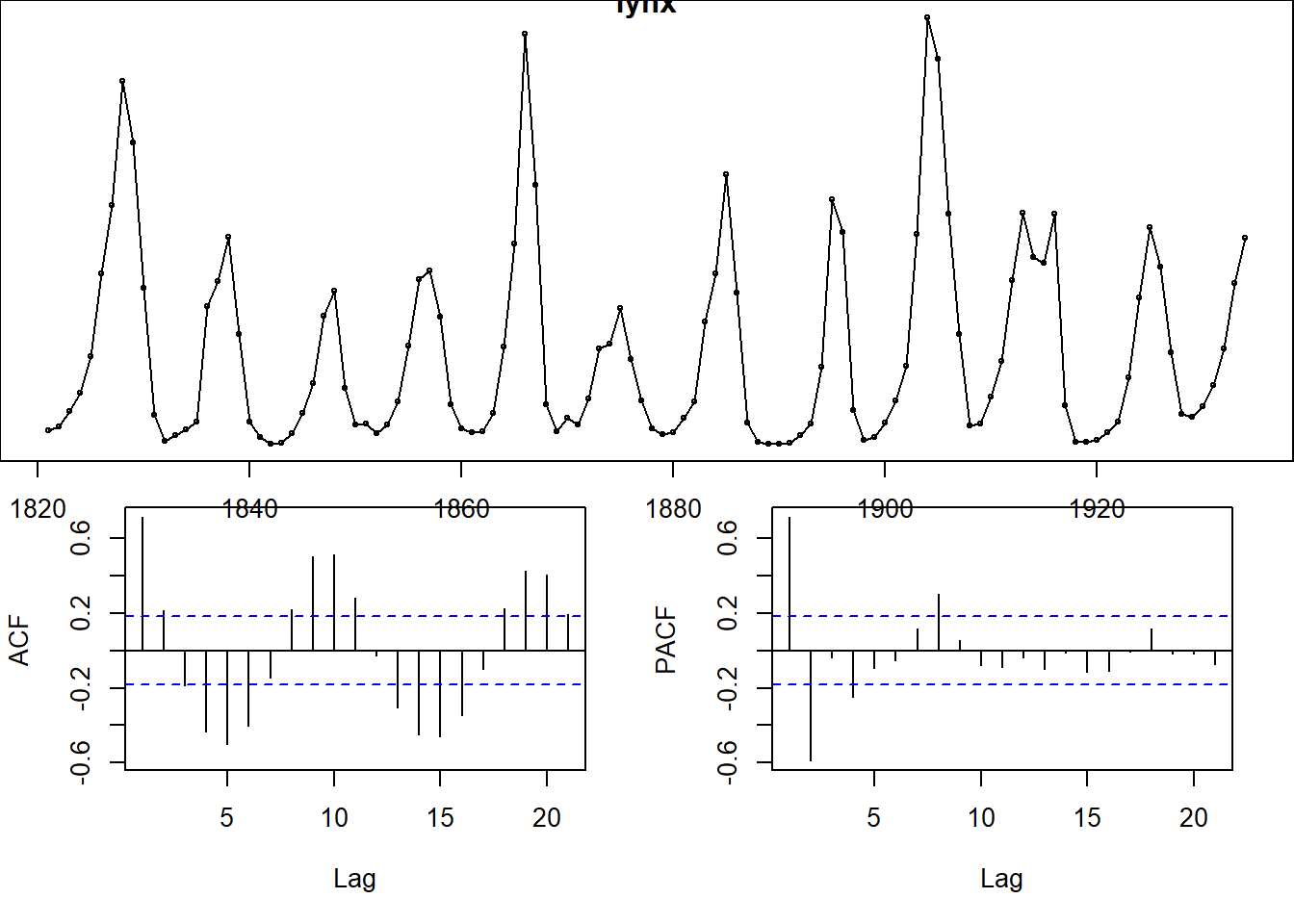
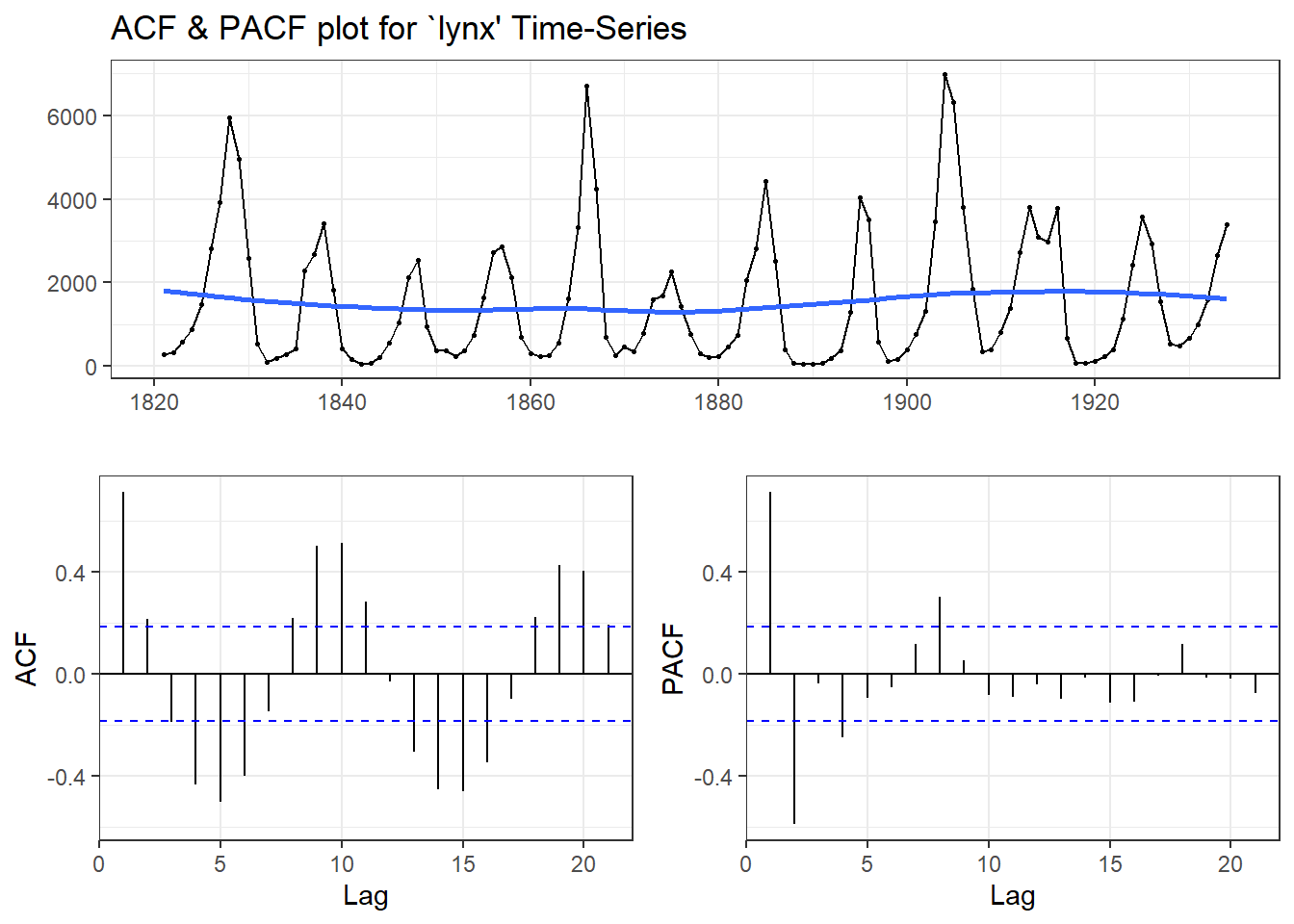
## Warning in adf.test(lynx): p-value smaller than printed p-value

## 
##  Augmented Dickey-Fuller Test
## 
## data:  lynx
## Dickey-Fuller = -6.3068, Lag order = 4, p-value = 0.01
## alternative hypothesis: stationary

tsdisplay(lynx)

ggtsdisplay(lynx,
            plot.type = "partial",
            main = "ACF & PACF plot for `lynx' Time-Series",
            smooth = TRUE)

# Arima from forecast package
myarima <- Arima(lynx, 
                 order = c(4,0,0))
checkresiduals(myarima)

## 
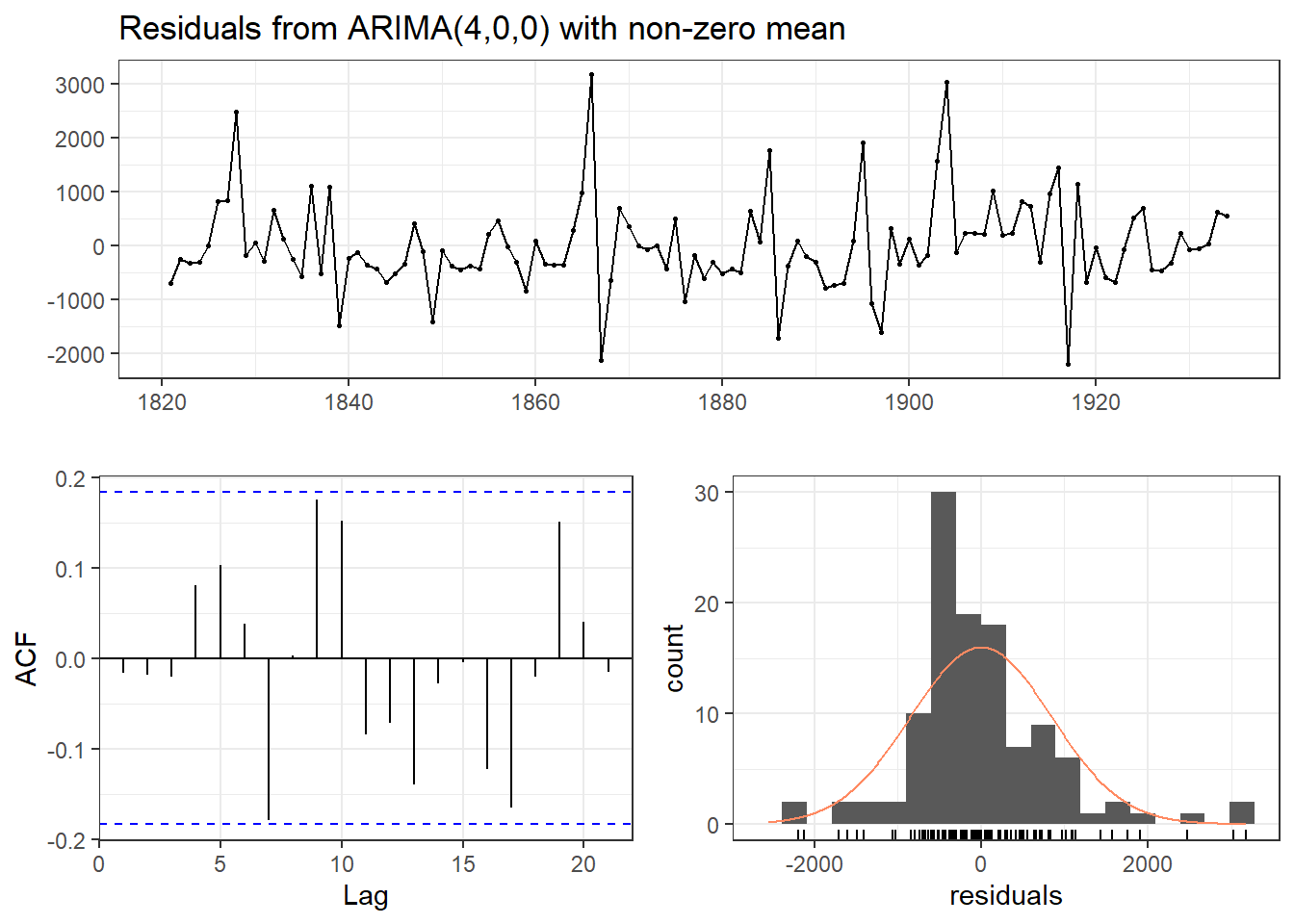
##  Ljung-Box test
## 
## data:  Residuals from ARIMA(4,0,0) with non-zero mean
## Q* = 13.201, df = 5, p-value = 0.02157
## 
## Model df: 5.   Total lags used: 10

# Example MA time series
set.seed(123) # for reproduction
# Simulation
myts <- arima.sim(model = list(order = c(0,0,2),
                               ma = c(0.3, 0.7)), n = 1000) + 10
adf.test(myts) # Stationarity

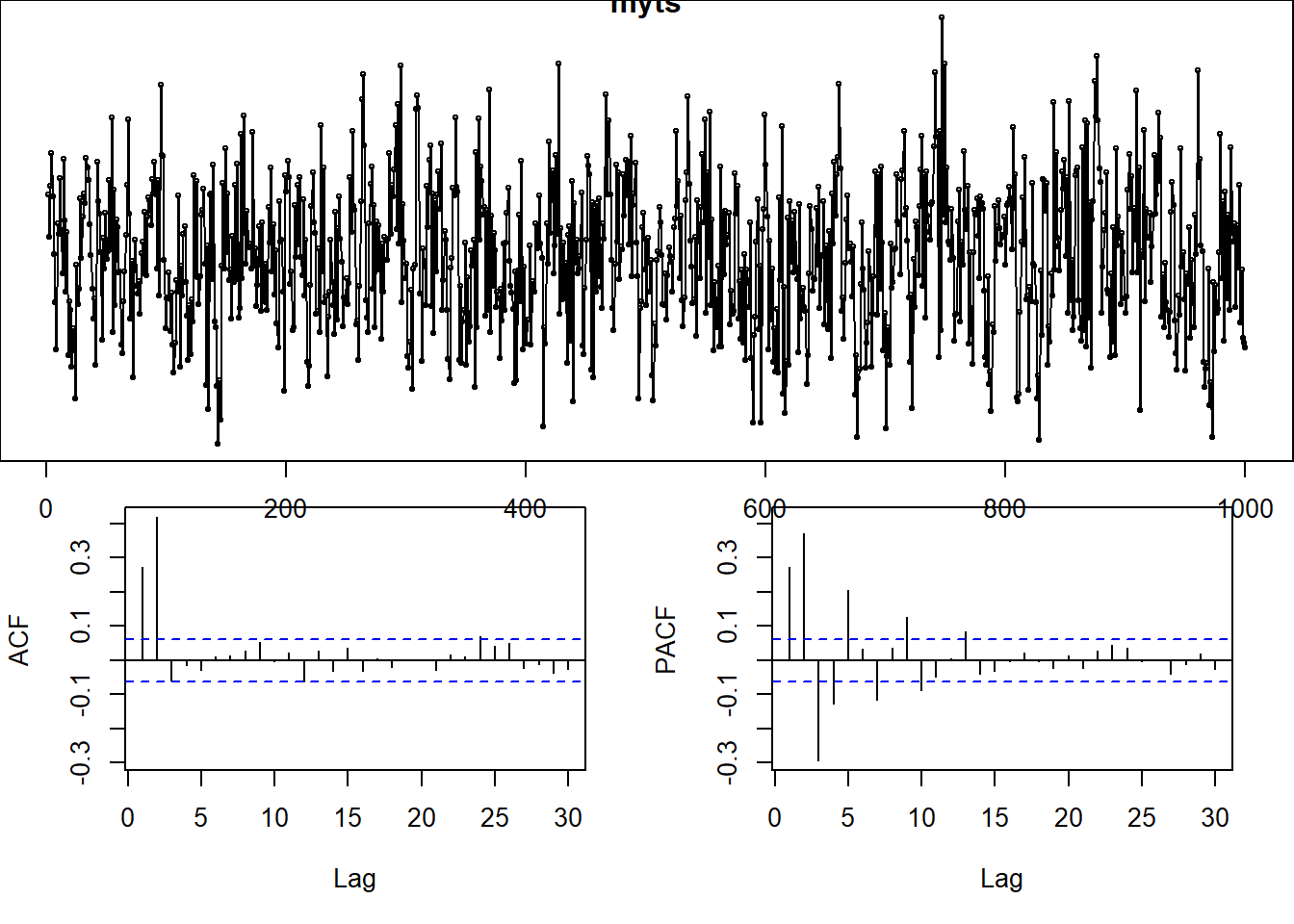
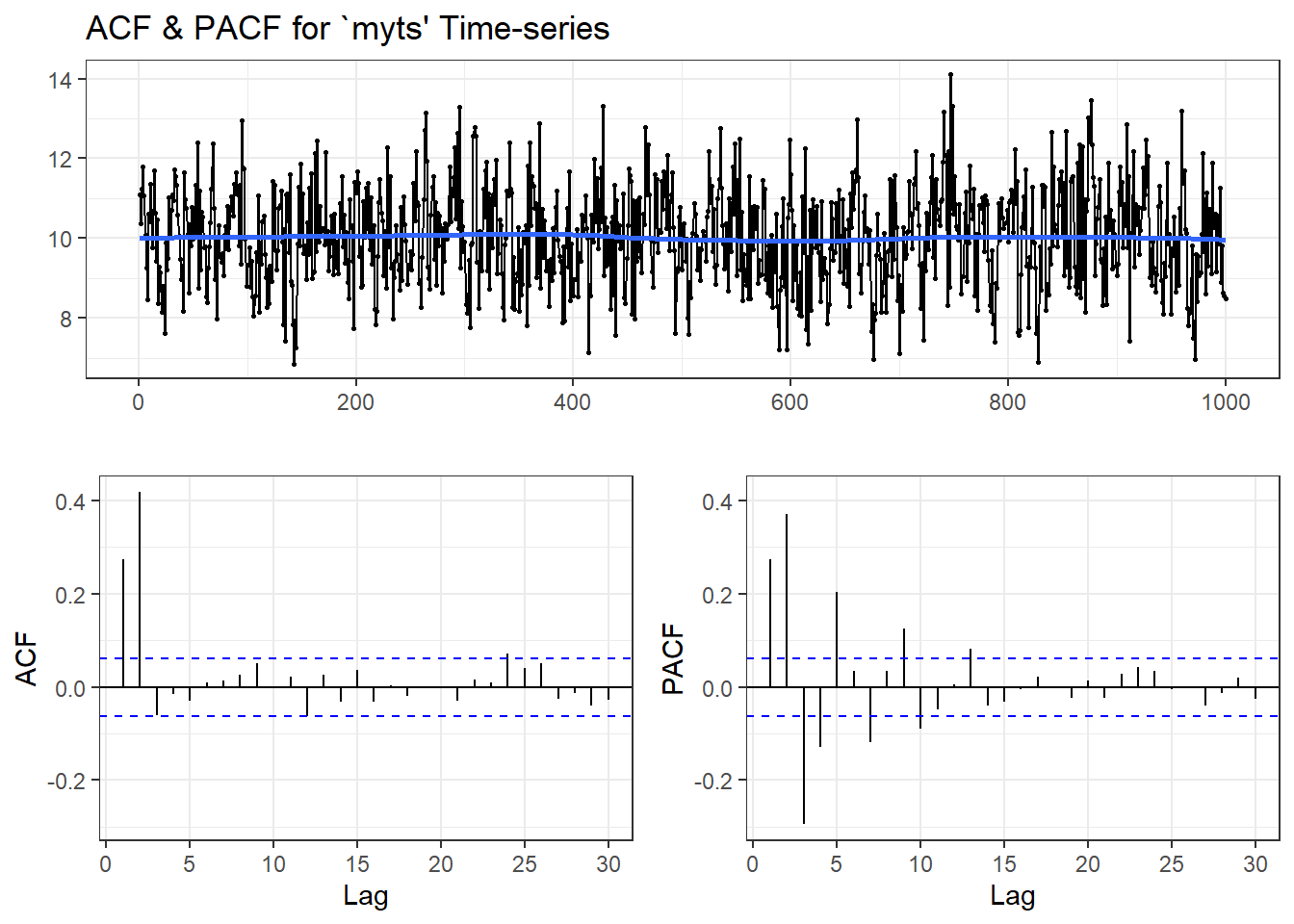
## Warning in adf.test(myts): p-value smaller than printed p-value

## 
##  Augmented Dickey-Fuller Test
## 
## data:  myts
## Dickey-Fuller = -9.0469, Lag order = 9, p-value = 0.01
## alternative hypothesis: stationary

tsdisplay(myts) # Autocorrelation

ggtsdisplay(myts,
            plot.type = "partial",
            main = "ACF & PACF for `myts' Time-series",
            smooth = TRUE)

# Arima 
myarima <- Arima(myts, order = c(0,0,3))
checkresiduals(myarima)

## 
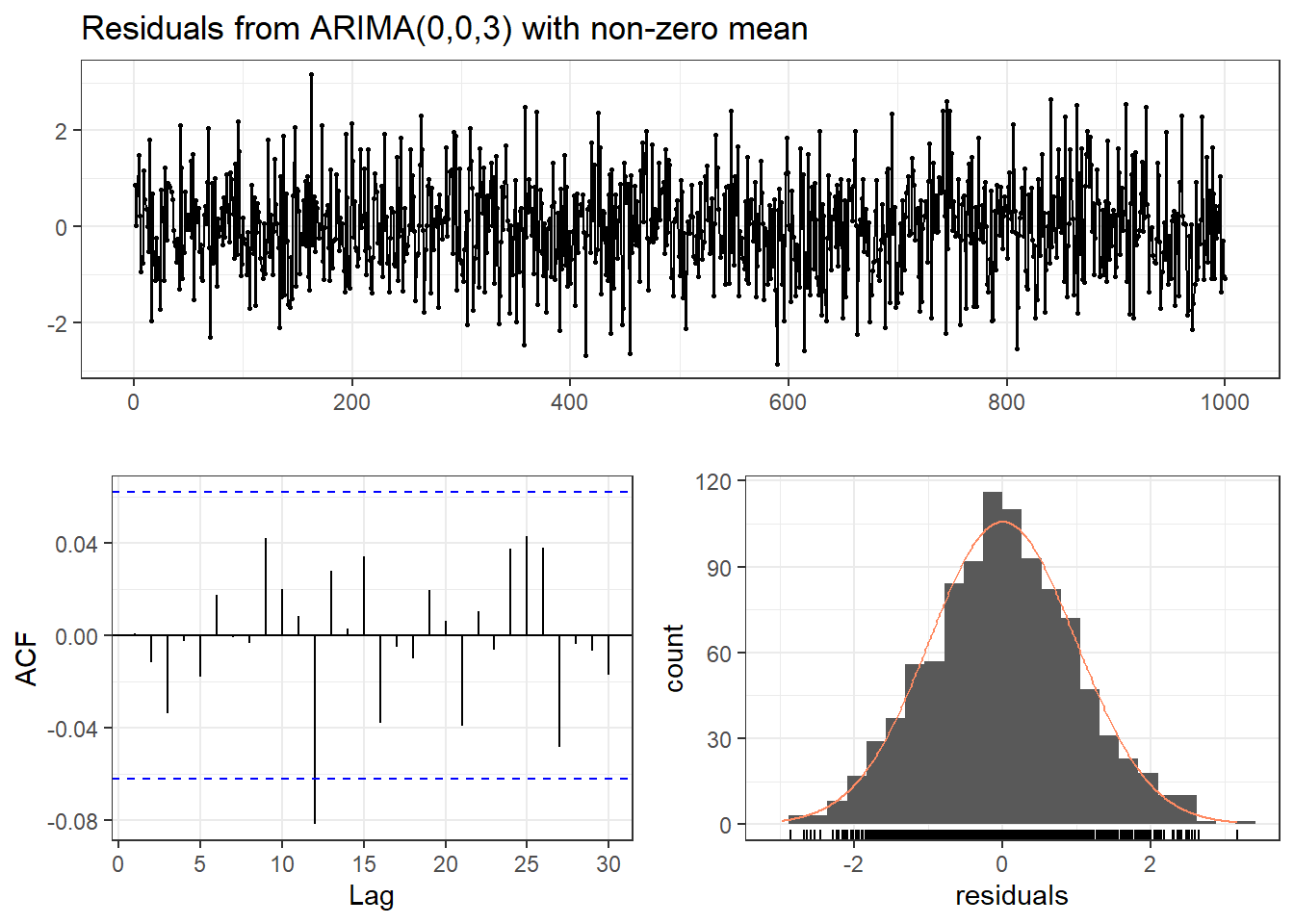
##  Ljung-Box test
## 
## data:  Residuals from ARIMA(0,0,3) with non-zero mean
## Q* = 4.1475, df = 6, p-value = 0.6567
## 
## Model df: 4.   Total lags used: 10

auto.arima(myts, 
           trace = T, 
           stepwise = F, 
           approximation = F)

## 
##  ARIMA(0,0,0) with zero mean     : 7465.902
##  ARIMA(0,0,0) with non-zero mean : 3239.597
##  ARIMA(0,0,1) with zero mean     : 6414.662
##  ARIMA(0,0,1) with non-zero mean : 3199.385
##  ARIMA(0,0,2) with zero mean     : 5571.943
##  ARIMA(0,0,2) with non-zero mean : 2828.282
##  ARIMA(0,0,3) with zero mean     : 4982.239
##  ARIMA(0,0,3) with non-zero mean : 2829.867
##  ARIMA(0,0,4) with zero mean     : 4556.587
##  ARIMA(0,0,4) with non-zero mean : 2831.522
##  ARIMA(0,0,5) with zero mean     : 4300.593
##  ARIMA(0,0,5) with non-zero mean : 2831.318
##  ARIMA(1,0,0) with zero mean     : 3610.918
##  ARIMA(1,0,0) with non-zero mean : 3163.665
##  ARIMA(1,0,1) with zero mean     : Inf
##  ARIMA(1,0,1) with non-zero mean : 3120.607
##  ARIMA(1,0,2) with zero mean     : Inf
##  ARIMA(1,0,2) with non-zero mean : 2829.89
##  ARIMA(1,0,3) with zero mean     : Inf
##  ARIMA(1,0,3) with non-zero mean : 2831.04
##  ARIMA(1,0,4) with zero mean     : Inf
##  ARIMA(1,0,4) with non-zero mean : 2832.859
##  ARIMA(2,0,0) with zero mean     : Inf
##  ARIMA(2,0,0) with non-zero mean : 3017.436
##  ARIMA(2,0,1) with zero mean     : Inf
##  ARIMA(2,0,1) with non-zero mean : 2977.38
##  ARIMA(2,0,2) with zero mean     : Inf
##  ARIMA(2,0,2) with non-zero mean : 2831.603
##  ARIMA(2,0,3) with zero mean     : Inf
##  ARIMA(2,0,3) with non-zero mean : 2832.823
##  ARIMA(3,0,0) with zero mean     : Inf
##  ARIMA(3,0,0) with non-zero mean : 2929.264
##  ARIMA(3,0,1) with zero mean     : Inf
##  ARIMA(3,0,1) with non-zero mean : 2924.325
##  ARIMA(3,0,2) with zero mean     : Inf
##  ARIMA(3,0,2) with non-zero mean : 2831.357
##  ARIMA(4,0,0) with zero mean     : Inf
##  ARIMA(4,0,0) with non-zero mean : 2914.331
##  ARIMA(4,0,1) with zero mean     : Inf
##  ARIMA(4,0,1) with non-zero mean : 2899.065
##  ARIMA(5,0,0) with zero mean     : Inf
##  ARIMA(5,0,0) with non-zero mean : 2873.303
## 
## 
## 
##  Best model: ARIMA(0,0,2) with non-zero mean

## Series: myts 
## ARIMA(0,0,2) with non-zero mean 
## 
## Coefficients:
##          ma1     ma2     mean
##       0.2878  0.6838  10.0297
## s.e.  0.0230  0.0231   0.0617
## 
## sigma^2 estimated as 0.9842:  log likelihood=-1410.12
## AIC=2828.24   AICc=2828.28   BIC=2847.87

## ARIMA Forecasting
# Our model 
myarima <- auto.arima(lynx, 
                      stepwise = F, 
                      approximation = F)

# Forecast of 10 years
arimafore <- forecast(myarima, h = 10)
plot(arimafore)

autoplot(lynx, PI = TRUE,
         shadecols = c("#596DD5", "#D5DBFF"), fcol = "#0000AA", flwd = 0.5) + 
  autolayer(forecast(myarima, h = 10), level = 95, series = "lynx")

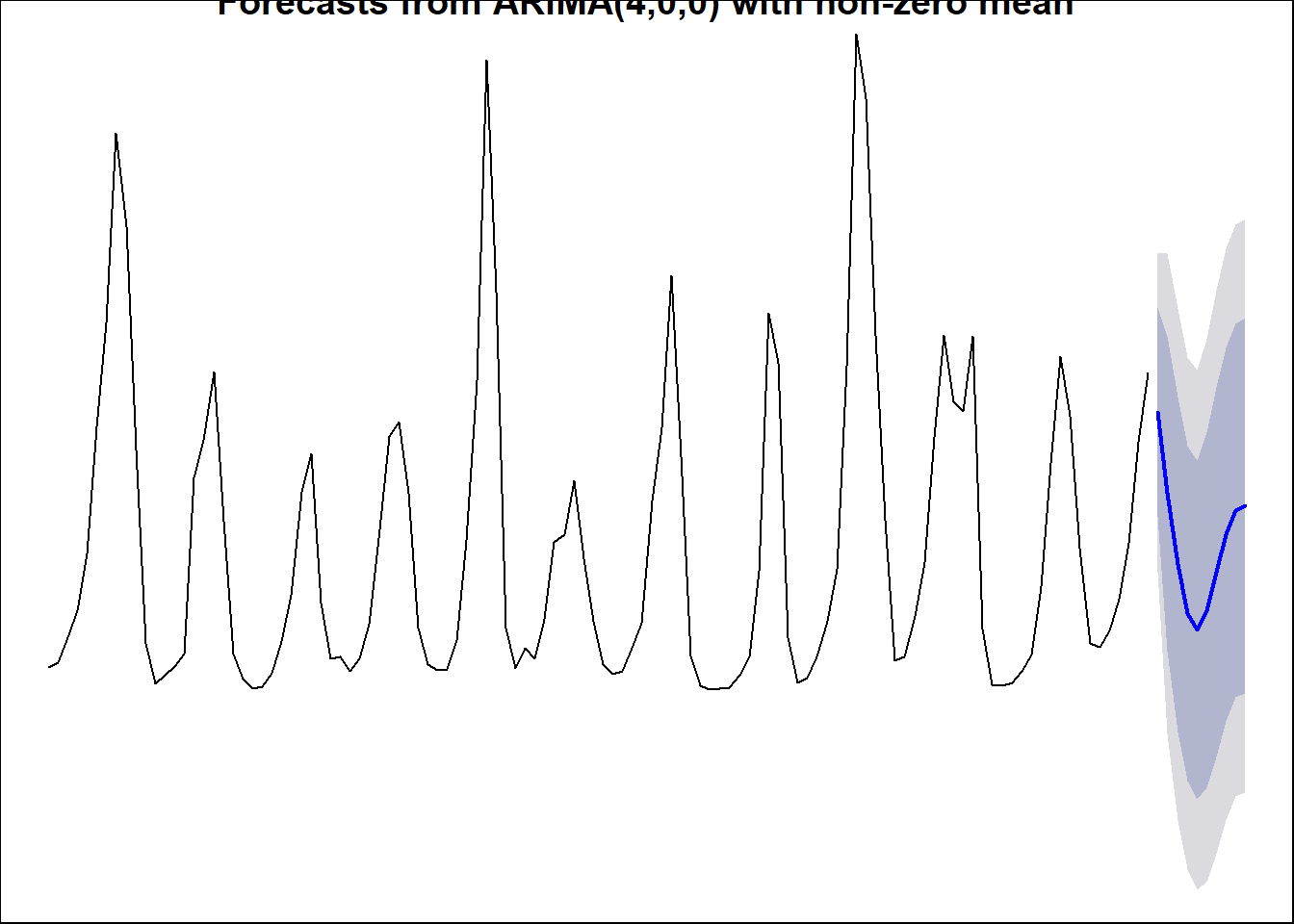
## Warning: Ignoring unknown parameters: PI, shadecols, fcol, flwd

autoplot(lynx) + geom_forecast(h = 10)

# See the forecasted values
arimafore$mean

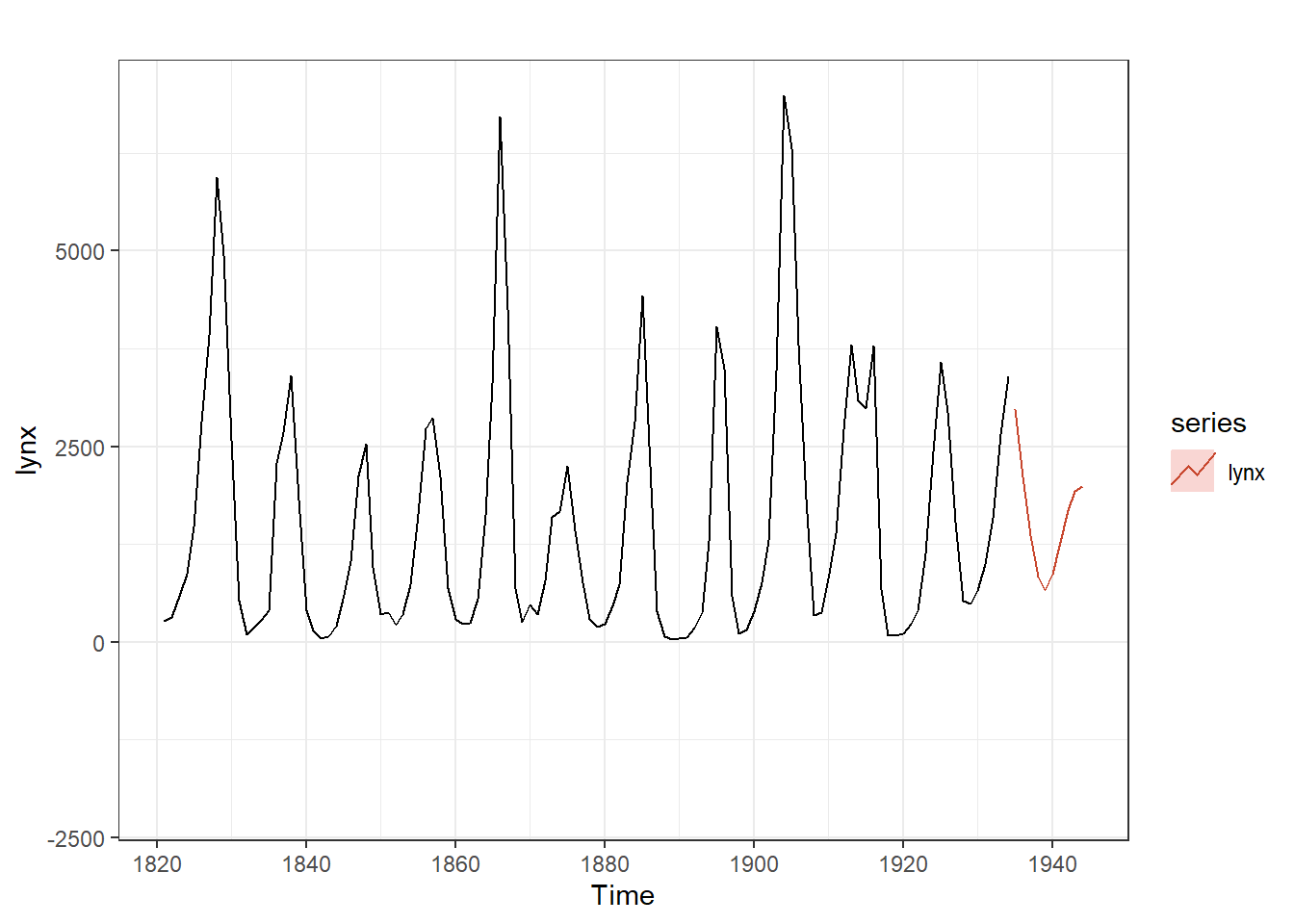
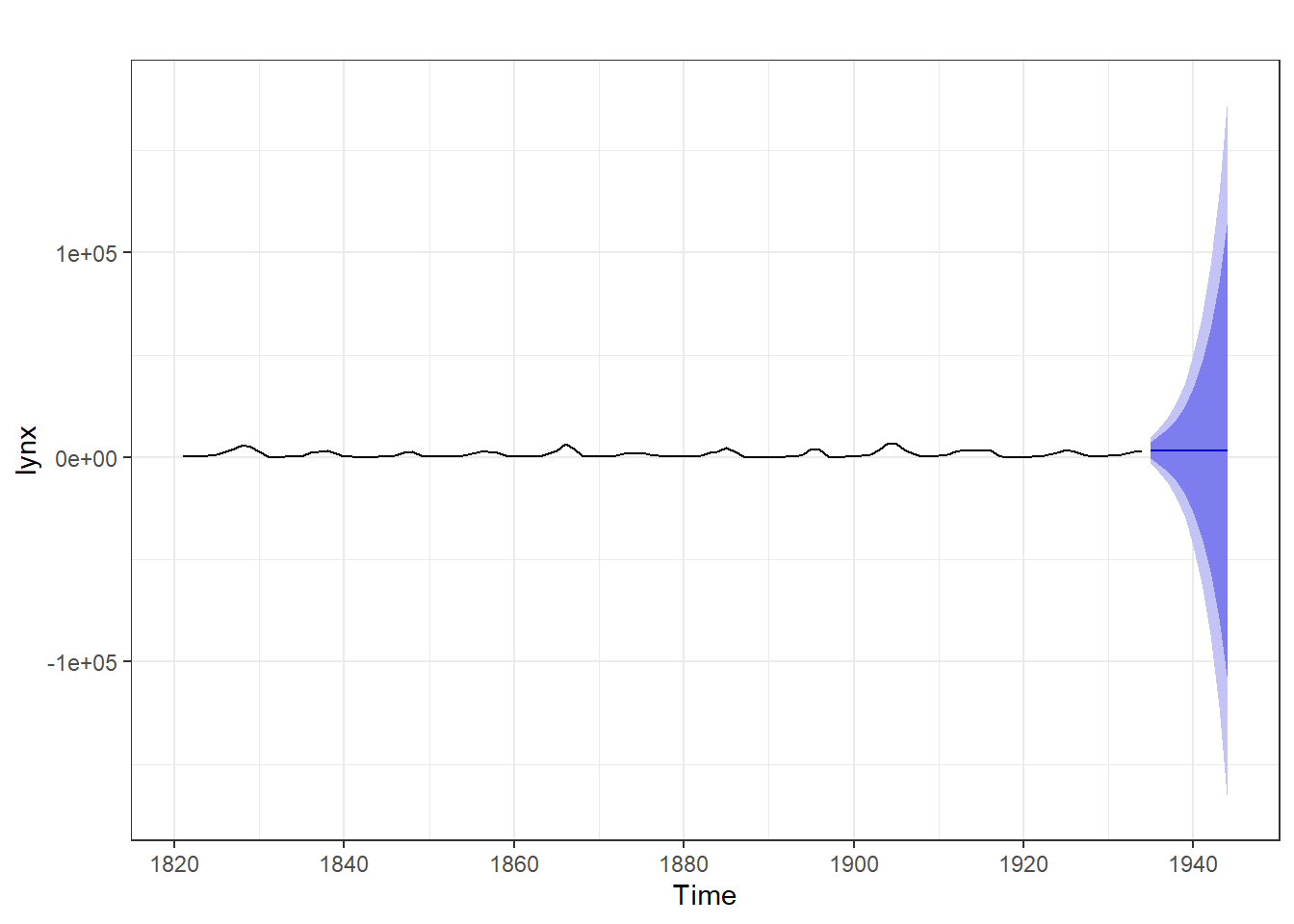
## Time Series:
## Start = 1935 
## End = 1944 
## Frequency = 1 
##  [1] 2980.7782 2114.6447 1361.7211  839.0137  668.7873  874.3079 1281.3753
##  [8] 1679.8363 1933.3503 1987.5494

# Plot last observations and the forecast
plot(arimafore, 
     xlim = c(1930, 1944))

# Ets for comparison
myets <- ets(lynx)
etsfore <- forecast(myets, h = 10)

# Comparison plot for 2 models
autoplot(lynx) +
  forecast::autolayer(etsfore$mean, series = 'ETS model') +
  forecast::autolayer(arimafore$mean, series = 'ARIMA model') +
  xlab('year') + ylab('Lynx Trappings') + 
  guides(colour = guide_legend(title = 'Forecast Method')) +
  theme(legend.position = c(0.8, 0.8))

## ARIMA with Explanatory Variables - Dynamic Regression
## Importing the cyprinidae dataset
cyprinidae <- read_csv("cyprinidae.csv")

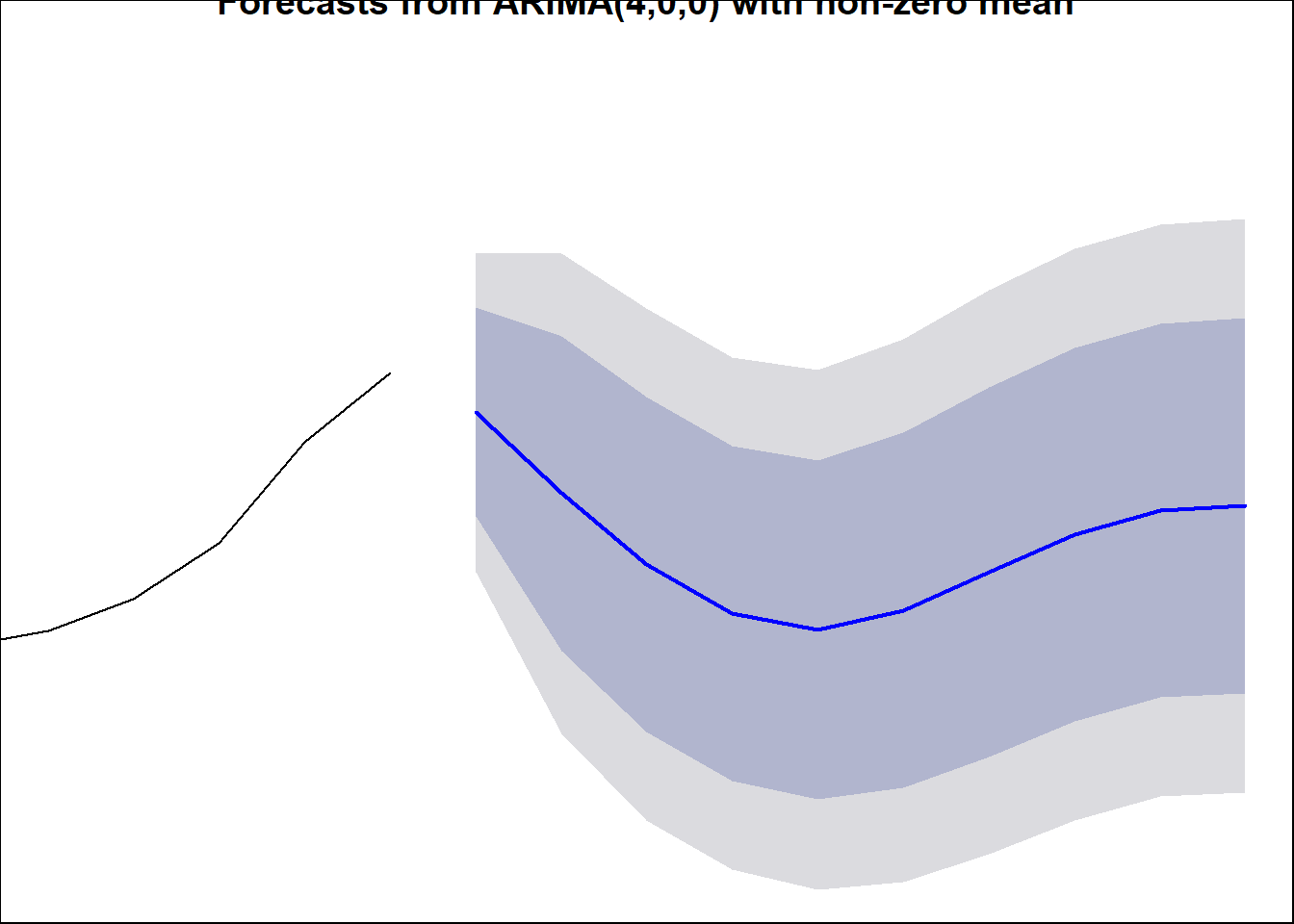
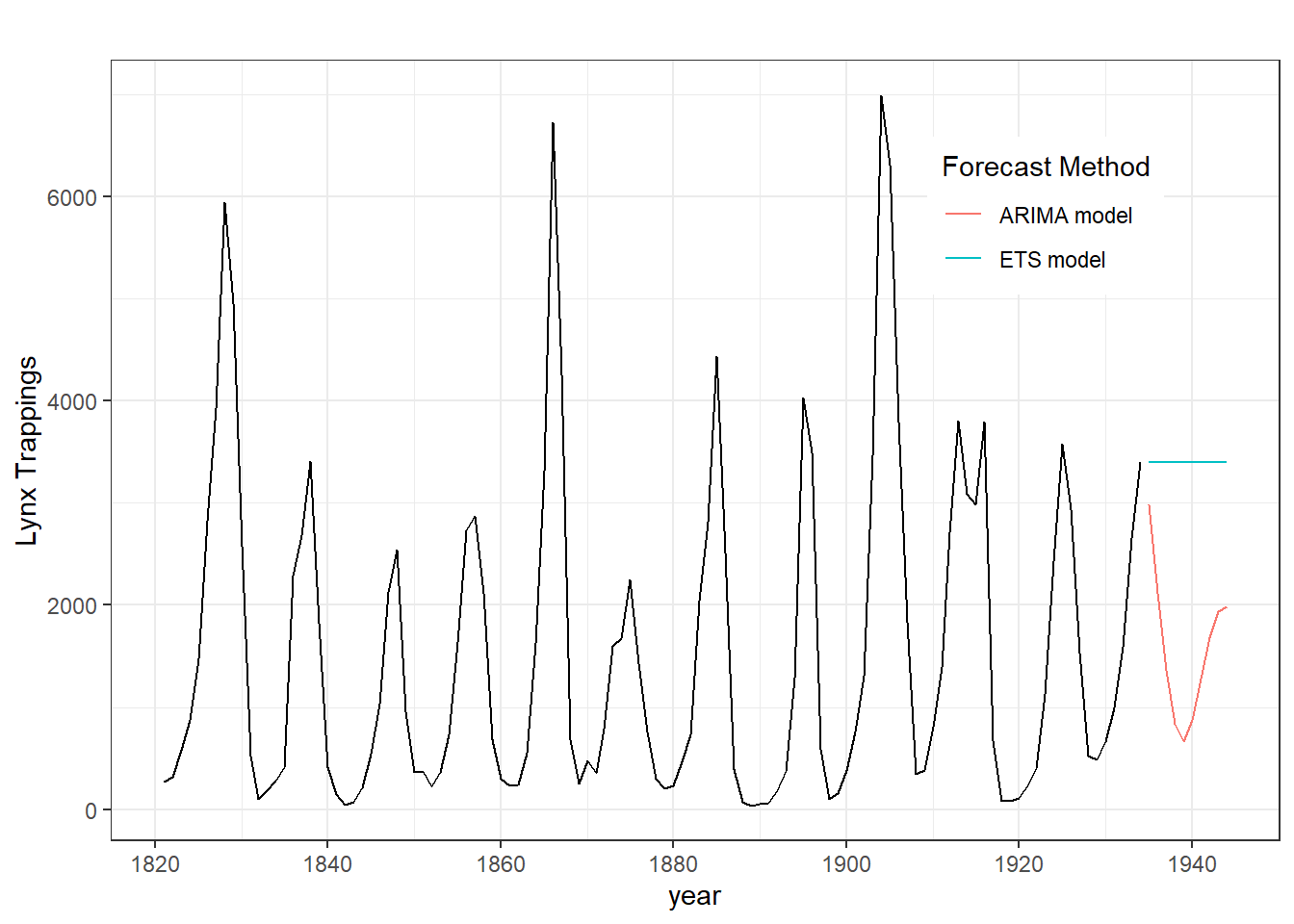
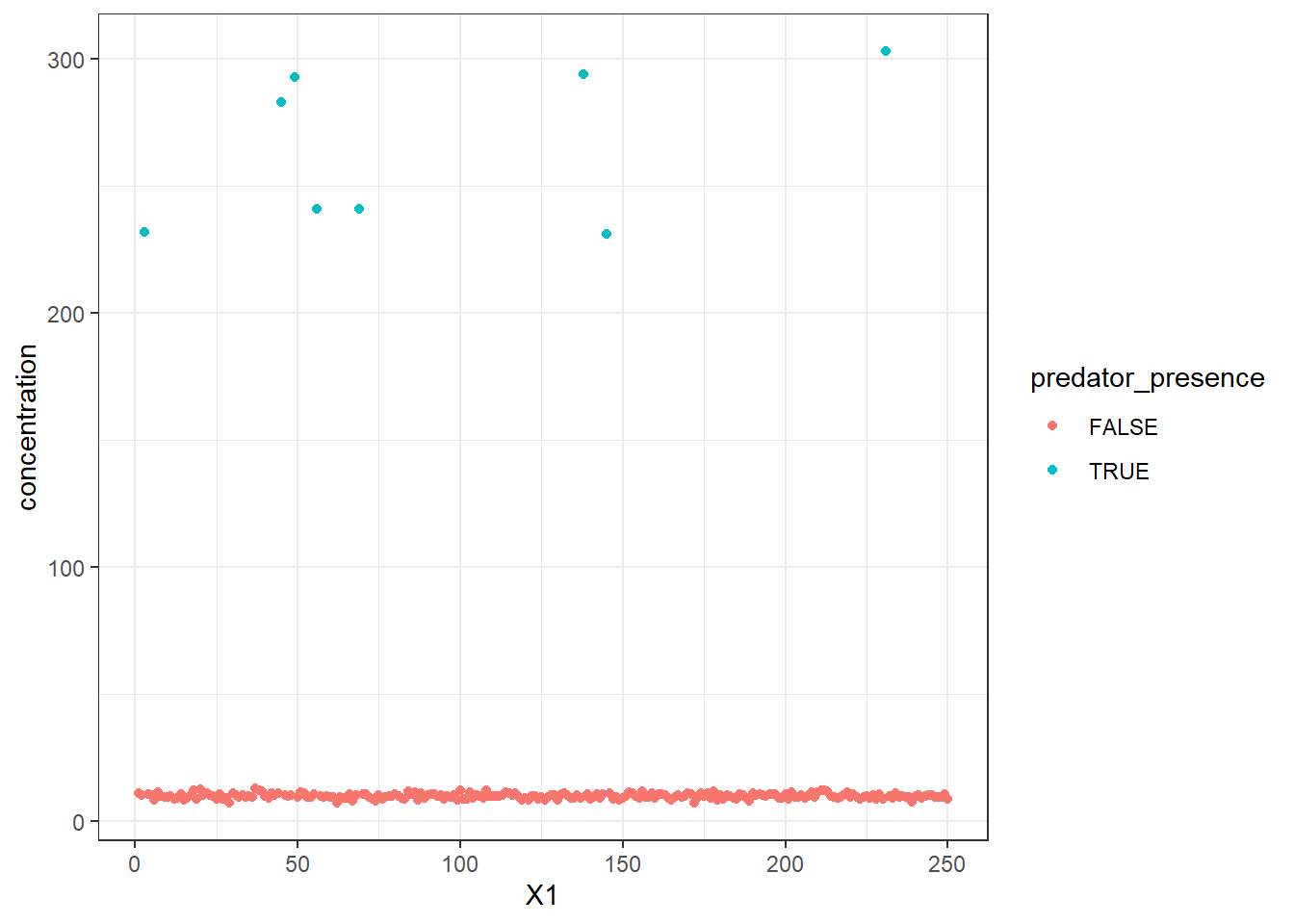
## Warning: Missing column names filled in: 'X1' [1]

## Parsed with column specification:
## cols(
##   X1 = col_double(),
##   concentration = col_double(),
##   predator_presence = col_logical()
## )

# Display the multivariate dataset
ggplot(cyprinidae,
       aes(y = concentration, x = X1)) + 
  geom_point () +
  aes(colour = predator_presence)

# Convert the variables into time series
x = ts(cyprinidae$concentration)
y = as.numeric(cyprinidae$predator_presence)

# Arima model creation
mymodel = auto.arima(x, xreg = y, 
                     stepwise = F,
                     approximation = F)
mymodel

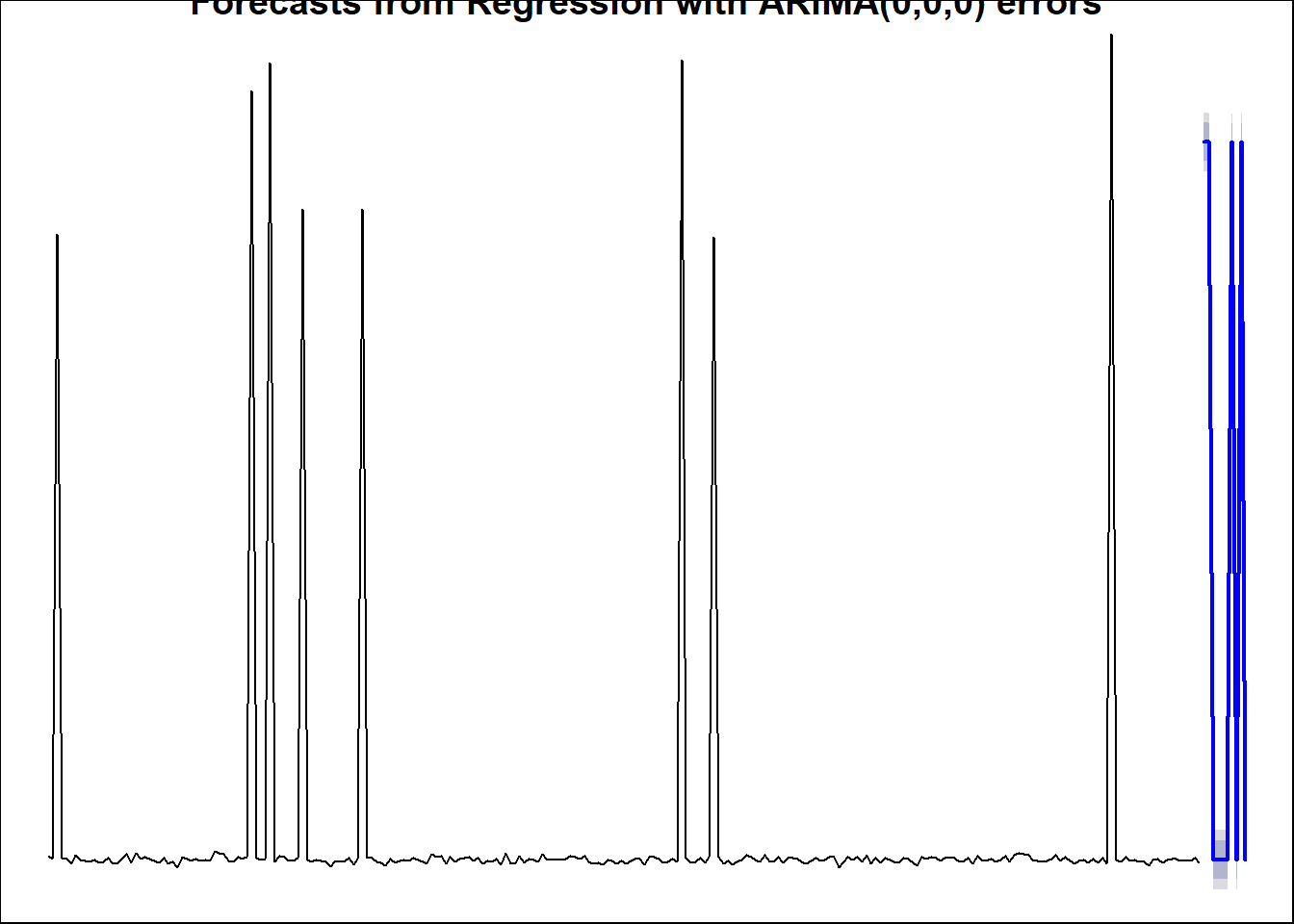
## Series: x 
## Regression with ARIMA(0,0,0) errors 
## 
## Coefficients:
##       intercept      xreg
##          9.9765  254.7735
## s.e.     0.3409    1.9059
## 
## sigma^2 estimated as 28.36:  log likelihood=-771.84
## AIC=1549.68   AICc=1549.77   BIC=1560.24

# Quick check of model quality
checkresiduals(mymodel)

## 
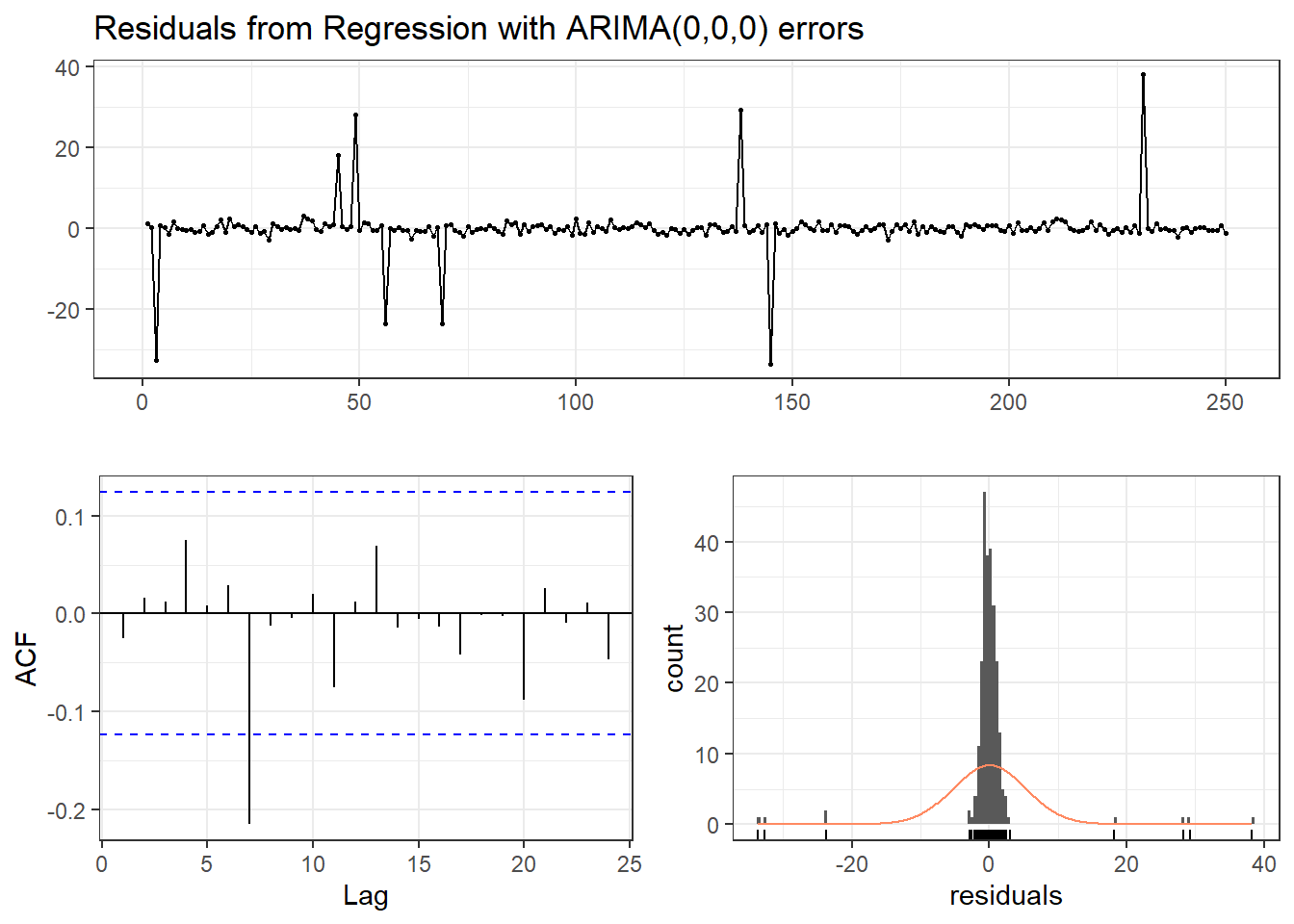
##  Ljung-Box test
## 
## data:  Residuals from Regression with ARIMA(0,0,0) errors
## Q* = 14.122, df = 8, p-value = 0.07865
## 
## Model df: 2.   Total lags used: 10

# Expected predator presence at future 10 time points
y1 = as.numeric(c(T,T,F,F,F,F,T,F,T,F))

# Getting a forecast based on future predator presence
plot(forecast(mymodel, xreg = y1))

plot(forecast(mymodel, xreg = y1),
     xlim  = c(230,260))