Chapter 1 An introduction to R programming
1.1 An introduction to R programming
Covers the elements of R programming including illustration of good practice.
1.1.1 Simple manipulations; numbers and vectors
Simple manipulations
1/2## [1] 0.5In R, Inf and -Inf exist and R can often deal with them correctly:
1/0## [1] Inf1/-0## [1] -InfAlso NaN = ‘not a number’ is available; 0/0, 0*Inf, Inf-Inf lead to NaN:
0/0 ## [1] NaNx = 0/0 # store the result in 'x'
class(x) # the class/type of 'x'; => NaN is still of mode 'numeric'## [1] "numeric"Inf is of mode ‘numeric’ (although mathematically not a number); helpful in optimization:
class(Inf)## [1] "numeric"The R NULL object (a reserved object often used as default argument of functions or to represent special cases or undefined return values):
class(NULL) ## [1] "NULL"is.null(NULL)## [1] TRUEVectors
Data structure which contains objects of the same mode.
x = c(1, 2, 3, 4, 5) # numeric vector
x # print method## [1] 1 2 3 4 5Another way of creating such a vector (and printing the output via ‘()’):
(y = 1:5) ## [1] 1 2 3 4 5(z = seq_len(5)) # and another one (see below for the 'why')## [1] 1 2 3 4 5Append to a vector (better than z = c(z, 6)); (much) more comfortable than in C/C++:
z[6] = 6
z## [1] 1 2 3 4 5 6Note
We can check whether the R objects are the same:
x == y # component wise numerically equal## [1] TRUE TRUE TRUE TRUE TRUEidentical(x, y) # identical as objects? why not?## [1] FALSEclass(x) # => x is a *numeric* vector## [1] "numeric"class(y) # => y is an *integer* vector## [1] "integer"all.equal(x, y) # numerical equality; see argument 'tolerance'## [1] TRUEidentical(x, as.numeric(y)) # => also fine## [1] TRUEUnderstanding all.equal()
all.equal # only see arguments 'target', 'current', no code (S3 method)## function (target, current, ...)
## UseMethod("all.equal")
## <bytecode: 0x0000000016ba7840>
## <environment: namespace:base>methods(all.equal) # => all.equal.numeric applies here## [1] all.equal.character all.equal.default all.equal.environment
## [4] all.equal.envRefClass all.equal.factor all.equal.formula
## [7] all.equal.language all.equal.list all.equal.numeric
## [10] all.equal.POSIXt all.equal.raw
## see '?methods' for accessing help and source codestr(all.equal.numeric) # => 'tolerance' argument; str() prints the *str*ucture of an object## function (target, current, tolerance = sqrt(.Machine$double.eps), scale = NULL,
## countEQ = FALSE, formatFUN = function(err, what) format(err), ...,
## check.attributes = TRUE)sqrt(.Machine$double.eps) # default tolerance 1.490116e-08 > 1e-8## [1] 1.490116e-08Reports for arguments all.equal(target, current) the error:
\[
\frac{\text{mean}(|\text{current} - \text{target}|)}{\text{mean}(|\text{target}|)}
\]
here: relative error
\[
\frac{|0-10^{-7}|}{10^{-7}} = 1
\]
all.equal(1e-7, 0) ## [1] "Mean relative difference: 1"Relative error: \[ \frac{|10^{-7}-0|}{0} \quad ?? \]
all.equal(0, 1e-7) ## [1] "Mean absolute difference: 1e-07"Absolute error is used instead; see ?all.equal.
Numerically not exactly the same
x = var(1:4)
y = sd(1:4)^2
all.equal(x, y) # numerical equality## [1] TRUEx == y # ... but not exactly## [1] FALSEx - y # numerically not 0## [1] 2.220446e-16Floating point numbers
1.7e+308 # = 1.7 * 10^308 (scientific notation)## [1] 1.7e+3081.8e+308 # => there is a largest positive (floating point, not real) number## [1] Inf2.48e-324 # near 0## [1] 4.940656e-3242.47e-324 # truncation to 0 => there is a smallest positive (floating point) number## [1] 01 + 2.22e-16 # near 1## [1] 11 + 2.22e-16 == 1 # ... but actually isn't (yet)## [1] FALSE1 + 1.11e-16 == 1 # indistinguishable from 1 (= 1 + 2.22e-16/2)## [1] TRUE## Note: The grid near 0 is much finer than near 1.Remark:
These phenomena are better understood with the IEEE 754 standard for floating point arithmetic:
str(.Machine) # lists important specifications of floating point numbers## List of 28
## $ double.eps : num 2.22e-16
## $ double.neg.eps : num 1.11e-16
## $ double.xmin : num 2.23e-308
## $ double.xmax : num 1.8e+308
## $ double.base : int 2
## $ double.digits : int 53
## $ double.rounding : int 5
## $ double.guard : int 0
## $ double.ulp.digits : int -52
## $ double.neg.ulp.digits : int -53
## $ double.exponent : int 11
## $ double.min.exp : int -1022
## $ double.max.exp : int 1024
## $ integer.max : int 2147483647
## $ sizeof.long : int 4
## $ sizeof.longlong : int 8
## $ sizeof.longdouble : int 16
## $ sizeof.pointer : int 8
## $ longdouble.eps : num 1.08e-19
## $ longdouble.neg.eps : num 5.42e-20
## $ longdouble.digits : int 64
## $ longdouble.rounding : int 5
## $ longdouble.guard : int 0
## $ longdouble.ulp.digits : int -63
## $ longdouble.neg.ulp.digits: int -64
## $ longdouble.exponent : int 15
## $ longdouble.min.exp : int -16382
## $ longdouble.max.exp : int 16384.Machine$double.eps # smallest positive number x s.t. 1 + x not equal 1## [1] 2.220446e-16.Machine$double.xmin # smallest normalized number > 0## [1] 2.225074e-308.Machine$double.xmax # largest normalized number## [1] 1.797693e+308Watch out
## 1
n = 0
1:n## [1] 1 0## Not the empty sequence but c(1, 0); caution in 'for loops': for(i in 1:n) ...!## 2
seq_len(n) # better: => empty sequence## integer(0)seq_along(c(3, 4, 2)) # 1:3; helpful to 'go along' objects## [1] 1 2 3## 3
1:3-1 ## [1] 0 1 21:(3-1)## [1] 1 2## ':' has higher priority; note also: the '-1' is recycled to the length of 1:3Some functions
If functions exist, use them:
(x = c(3, 4, 2))## [1] 3 4 2length(x) # as seen above## [1] 3rev(x) # change order## [1] 2 4 3sort(x) # sort in increasing order## [1] 2 3 4sort(x, decreasing = TRUE) # sort in decreasing order## [1] 4 3 2ii = order(x) # create the indices which sort x
x[ii] # => sorted## [1] 2 3 4log(x) # component-wise logarithms## [1] 1.0986123 1.3862944 0.6931472x^2 # component-wise squares## [1] 9 16 4sum(x) # sum all numbers## [1] 9cumsum(x) # compute the *cumulative* sum## [1] 3 7 9prod(x) # multiply all numbers## [1] 24seq(1, 7, by = 2) # 1, 3, 5, 7## [1] 1 3 5 7rep(1:3, each = 3, times = 2) # 1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3## [1] 1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3tail(x, n = 1) # get the last element of a vector## [1] 2head(x, n = -1) # get all but the last element## [1] 3 4Logical vectors
(ii = x >= 3) # logical vector indicating whether each element of x is >= 3## [1] TRUE TRUE FALSEx[ii] # use that vector to index x => pick out all values of x >= 3## [1] 3 4!ii # negate the logical vector## [1] FALSE FALSE TRUEall(ii) # check whether all indices are TRUE (whether all x >= 3)## [1] FALSEany(ii) # check whether any indices are TRUE (whether any x >= 3)## [1] TRUEii | !ii # vectorized logical OR (is, componentwise, any entry TRUE?)## [1] TRUE TRUE TRUEii & !ii # vectorized logical AND (are, componentwise, both entries TRUE?)## [1] FALSE FALSE FALSEii || !ii # logical OR applied to all values (is entry any TRUE?)## [1] TRUEii && !ii # logical AND applied to all values (are all entries TRUE?)## [1] FALSE3 * c(TRUE, FALSE) # TRUE is coerced to 1, FALSE to 0## [1] 3 0class(NA) # NA = 'not available' is 'logical' as well (used for missing data)## [1] "logical"z = 1:3; z[5] = 4 # two statements in one line (';'-separated)
z # => 4th element 'not available' (NA)## [1] 1 2 3 NA 4(z = c(z, NaN, Inf)) # append NaN and Inf## [1] 1 2 3 NA 4 NaN Infclass(z) # still numeric (although is.numeric(NA) is FALSE)## [1] "numeric"is.na(z) # check for NA or NaN## [1] FALSE FALSE FALSE TRUE FALSE TRUE FALSEis.nan(z) # check for just NaN## [1] FALSE FALSE FALSE FALSE FALSE TRUE FALSEis.infinite(z) # check for +/-Inf## [1] FALSE FALSE FALSE FALSE FALSE FALSE TRUEz[(!is.na(z)) & is.finite(z) & z >= 2] # pick out all finite numbers >= 2## [1] 2 3 4z[(!is.na(z)) && is.finite(z) && z >= 2] # watch out; used to fail; R >= 3.6.0: z[TRUE] => z## numeric(0)Matching in indices or names
match(1:4, table = 3:5) # positions of elements of first in second vector (or NA)## [1] NA NA 1 21:4 %in% 3:5 # logical vector## [1] FALSE FALSE TRUE TRUEwhich(1:4 %in% 3:5) # positions of TRUE in logical vector## [1] 3 4which(3:5 %in% 1:4) # close to match() but without NAs## [1] 1 2na.omit(match(1:4, table = 3:5)) # same (apart from attributes)## [1] 1 2
## attr(,"na.action")
## [1] 1 2
## attr(,"class")
## [1] "omit"## Note: na.fill() from package 'zoo' is helpful in filling NAs in time seriesCharacter vectors
x = "apple"
y = "orange"
(z = paste(x, y)) # paste together; use sep = "" or paste0() to paste without space## [1] "apple orange"paste(1:3, c(x, y), sep = " - ") # recycling ("apple" appears again)## [1] "1 - apple" "2 - orange" "3 - apple"Named vectors
(x = c("a" = 3, "b" = 2)) # named vector of class 'numeric'## a b
## 3 2x["b"] # indexing elements by name (useful!)## b
## 2x[["b"]] # drop the name## [1] 21.1.2 Arrays and matrices
Matrices
(A = matrix(1:12, ncol = 4)) # watch out, R operates on/fills by columns (column-major order)## [,1] [,2] [,3] [,4]
## [1,] 1 4 7 10
## [2,] 2 5 8 11
## [3,] 3 6 9 12(A. = matrix(1:12, ncol = 4, byrow = TRUE)) # fills matrix row-wise## [,1] [,2] [,3] [,4]
## [1,] 1 2 3 4
## [2,] 5 6 7 8
## [3,] 9 10 11 12(B = rbind(1:4, 5:8, 9:12)) # row bind## [,1] [,2] [,3] [,4]
## [1,] 1 2 3 4
## [2,] 5 6 7 8
## [3,] 9 10 11 12(C = cbind(1:3, 4:6, 7:9, 10:12)) # column bind## [,1] [,2] [,3] [,4]
## [1,] 1 4 7 10
## [2,] 2 5 8 11
## [3,] 3 6 9 12stopifnot(identical(A, C), identical(A., B)) # check whether the constructions are identical
cbind(1:3, 5) # recycling## [,1] [,2]
## [1,] 1 5
## [2,] 2 5
## [3,] 3 5(A = outer(1:4, 1:5, FUN = pmin)) # (4,5)-matrix with (i,j)th element min{i, j}## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 1 1 1 1
## [2,] 1 2 2 2 2
## [3,] 1 2 3 3 3
## [4,] 1 2 3 4 4## => Lower triangular matrix contains column number, upper triangular matrix contains row numberSome functions
nrow(A) # number of rows## [1] 4ncol(A) # number of columns## [1] 5dim(A) # dimension## [1] 4 5diag(A) # diagonal of A## [1] 1 2 3 4diag(3) # identity (3, 3)-matrix## [,1] [,2] [,3]
## [1,] 1 0 0
## [2,] 0 1 0
## [3,] 0 0 1(D = diag(1:3)) # diagonal matrix with elements 1, 2, 3## [,1] [,2] [,3]
## [1,] 1 0 0
## [2,] 0 2 0
## [3,] 0 0 3D %*% B # matrix multiplication## [,1] [,2] [,3] [,4]
## [1,] 1 2 3 4
## [2,] 10 12 14 16
## [3,] 27 30 33 36B * B # Hadamard product, i.e., element-wise product## [,1] [,2] [,3] [,4]
## [1,] 1 4 9 16
## [2,] 25 36 49 64
## [3,] 81 100 121 144Build a covariance matrix, its correlation matrix and inverse
Define L the Cholesky factor of the real, symmetric, positive definite (covariance) matrix Sigma:
L = matrix(c(2, 0, 0,
6, 1, 0,
-8, 5, 3), ncol = 3, byrow = TRUE)
Sigma = L %*% t(L)
standardize = Vectorize(function(r, c) Sigma[r,c]/(sqrt(Sigma[r,r])*sqrt(Sigma[c,c])))
(P = outer(1:3, 1:3, standardize)) # construct the corresponding correlation matrix## [,1] [,2] [,3]
## [1,] 1.0000000 0.9863939 -0.8081220
## [2,] 0.9863939 1.0000000 -0.7140926
## [3,] -0.8081220 -0.7140926 1.0000000stopifnot(all.equal(P, cov2cor(Sigma))) # a faster wayCompute \(P^{-1}\); solve(A, b) solves \(Ax = b\) (system of linear equations); if \(b\) is omitted, it defaults to \(I\), thus leading to \(A^{-1}\):
P.inv = solve(P)
P %*% P.inv # (numerically close to) I## [,1] [,2] [,3]
## [1,] 1.000000e+00 1.065814e-14 1.776357e-15
## [2,] 1.421085e-14 1.000000e+00 -8.881784e-16
## [3,] 1.421085e-14 -7.105427e-15 1.000000e+00P.inv %*% P # (numerically close to) I## [,1] [,2] [,3]
## [1,] 1.000000e+00 1.421085e-14 1.421085e-14
## [2,] 3.552714e-15 1.000000e+00 0.000000e+00
## [3,] -5.329071e-15 -7.993606e-15 1.000000e+00Another useful function is Matrix::nearPD(Sigma, corr = TRUE) which finds a correlation matrix close to the given matrix in the Frobenius norm:
Other useful functions
rowSums(A) # row sums## [1] 5 9 12 14apply(A, 1, sum) # the same## [1] 5 9 12 14colSums(A) # column sums## [1] 4 7 9 10 10apply(A, 2, sum) # the same## [1] 4 7 9 10 10## Note that there are also faster functions .rowSums(), .colSums()## Matrices are only vectors with attributes to determine when to 'wrap around'
matrix(data = NA, nrow = 1e6, ncol = 1e6) # fails to allocate a *vector* of length 1e12## Error: cannot allocate vector of size 3725.3 GbArray
Data structure which contains objects of the same mode.
Special cases: vectors (1d-arrays) and matrices (2d-arrays).
arr = array(1:24, dim = c(2,3,4), # (2,3,4)-array with dimensions (x,y,z)
dimnames = list(x = c("x1", "x2"),
y = c("y1", "y2", "y3"),
z = paste("z", 1:4, sep = "")))
arr # => also filled in the first dimension first, then the second, then the third## , , z = z1
##
## y
## x y1 y2 y3
## x1 1 3 5
## x2 2 4 6
##
## , , z = z2
##
## y
## x y1 y2 y3
## x1 7 9 11
## x2 8 10 12
##
## , , z = z3
##
## y
## x y1 y2 y3
## x1 13 15 17
## x2 14 16 18
##
## , , z = z4
##
## y
## x y1 y2 y3
## x1 19 21 23
## x2 20 22 24str(arr) # use str() to the *str*ucture of the object arr## int [1:2, 1:3, 1:4] 1 2 3 4 5 6 7 8 9 10 ...
## - attr(*, "dimnames")=List of 3
## ..$ x: chr [1:2] "x1" "x2"
## ..$ y: chr [1:3] "y1" "y2" "y3"
## ..$ z: chr [1:4] "z1" "z2" "z3" "z4"arr[1,2,2] # pick out a value## [1] 9For each combination of fixed first and second variables, sum over all other dimensions:
(mat = apply(arr, 1:2, FUN = sum)) ## y
## x y1 y2 y3
## x1 40 48 56
## x2 44 52 601.1.3 Lists (including data frames)
Data frames
Data frames are rectangular objects containing objects of possibly different type of the same length.
(df = data.frame(Year = as.factor(c(2000, 2000, 2000, 2001, 2003, 2003, 2003)), # loss year
Line = c("A", "A", "B", "A", "B", "B", "B"), # business line
Loss = c(1.2, 1.1, 0.6, 0.8, 0.4, 0.2, 0.3))) # loss in M USD, say## Year Line Loss
## 1 2000 A 1.2
## 2 2000 A 1.1
## 3 2000 B 0.6
## 4 2001 A 0.8
## 5 2003 B 0.4
## 6 2003 B 0.2
## 7 2003 B 0.3str(df) # => first two columns are factors## 'data.frame': 7 obs. of 3 variables:
## $ Year: Factor w/ 3 levels "2000","2001",..: 1 1 1 2 3 3 3
## $ Line: chr "A" "A" "B" "A" ...
## $ Loss: num 1.2 1.1 0.6 0.8 0.4 0.2 0.3is.matrix(df) # => indeed no matrix## [1] FALSEas.matrix(df) # coercion to a character matrix## Year Line Loss
## [1,] "2000" "A" "1.2"
## [2,] "2000" "A" "1.1"
## [3,] "2000" "B" "0.6"
## [4,] "2001" "A" "0.8"
## [5,] "2003" "B" "0.4"
## [6,] "2003" "B" "0.2"
## [7,] "2003" "B" "0.3"data.matrix(df) # coercion to a numeric matrix (factor are replaced according to their level index)## Year Line Loss
## [1,] 1 1 1.2
## [2,] 1 1 1.1
## [3,] 1 2 0.6
## [4,] 2 1 0.8
## [5,] 3 2 0.4
## [6,] 3 2 0.2
## [7,] 3 2 0.3Computing maximal losses per group for two different groupings
## Version 1 (leads a table structure with all combinations of selected variables):
tapply(df[,"Loss"], df[,"Year"], max) # maximal loss per Year## 2000 2001 2003
## 1.2 0.8 0.4tapply(df[,"Loss"], df[,c("Year", "Line")], max) # maximal loss per Year-Line combination## Line
## Year A B
## 2000 1.2 0.6
## 2001 0.8 NA
## 2003 NA 0.4## Version 2 (omits NAs):
aggregate(Loss ~ Year, data = df, FUN = max) # 'aggregate' Loss per Year with max()## Year Loss
## 1 2000 1.2
## 2 2001 0.8
## 3 2003 0.4aggregate(Loss ~ Year * Line, data = df, FUN = max)## Year Line Loss
## 1 2000 A 1.2
## 2 2001 A 0.8
## 3 2000 B 0.6
## 4 2003 B 0.4Playing with the data frame
(fctr = factor(paste0(df$Year,".",df$Line))) # build a 'Year.Line' factor## [1] 2000.A 2000.A 2000.B 2001.A 2003.B 2003.B 2003.B
## Levels: 2000.A 2000.B 2001.A 2003.B(grouped.Loss = split(df$Loss, f = fctr)) # group the losses according to fctr## $`2000.A`
## [1] 1.2 1.1
##
## $`2000.B`
## [1] 0.6
##
## $`2001.A`
## [1] 0.8
##
## $`2003.B`
## [1] 0.4 0.2 0.3sapply(grouped.Loss, FUN = max) # maximal loss per group## 2000.A 2000.B 2001.A 2003.B
## 1.2 0.6 0.8 0.4sapply(grouped.Loss, FUN = length) # number of losses per group; see more on *apply() later## 2000.A 2000.B 2001.A 2003.B
## 2 1 1 3(ID = unlist(sapply(grouped.Loss, FUN = function(x) seq_len(length(x))))) # unique ID per loss group## 2000.A1 2000.A2 2000.B 2001.A 2003.B1 2003.B2 2003.B3
## 1 2 1 1 1 2 3(df. = cbind(df, ID = ID)) # paste unique ID per loss group to 'df'## Year Line Loss ID
## 2000.A1 2000 A 1.2 1
## 2000.A2 2000 A 1.1 2
## 2000.B 2000 B 0.6 1
## 2001.A 2001 A 0.8 1
## 2003.B1 2003 B 0.4 1
## 2003.B2 2003 B 0.2 2
## 2003.B3 2003 B 0.3 3(df.wide = reshape(df., # reshape from 'long' to 'wide' format
v.names = "Loss", # variables to be displayed as entries in 2nd dimension
idvar = c("Year", "Line"), # variables to be kept in long format
timevar = "ID", # unique ID => wide columns have headings of the form <Loss.ID>
direction = "wide"))## Year Line Loss.1 Loss.2 Loss.3
## 2000.A1 2000 A 1.2 1.1 NA
## 2000.B 2000 B 0.6 NA NA
## 2001.A 2001 A 0.8 NA NA
## 2003.B1 2003 B 0.4 0.2 0.3Lists
is.list(df) # => data frames are indeed just lists## [1] TRUELists are the most general data structures in R in the sense that they can contain pretty much everything, e.g., lists themselves or functions or both… (and of different lengths).
(L = list(group = LETTERS[1:4], value = 1:2, sublist = list(10, function(x) x+1)))## $group
## [1] "A" "B" "C" "D"
##
## $value
## [1] 1 2
##
## $sublist
## $sublist[[1]]
## [1] 10
##
## $sublist[[2]]
## function(x) x+1Extract elements from a list
## Version 1:
L[[1]] # get first element of the list## [1] "A" "B" "C" "D"L[[3]][[1]] # get first element of the sub-list## [1] 10## Version 2: use '$'
L$group## [1] "A" "B" "C" "D"L$sublist[[1]]## [1] 10## Version 3 (most readable and fail-safe): use the provided names
L[["group"]]## [1] "A" "B" "C" "D"L[["sublist"]][[1]]## [1] 10Change a name
names(L)## [1] "group" "value" "sublist"names(L)[names(L) == "sublist"] = "sub.list"
str(L)## List of 3
## $ group : chr [1:4] "A" "B" "C" "D"
## $ value : int [1:2] 1 2
## $ sub.list:List of 2
## ..$ : num 10
## ..$ :function (x)
## .. ..- attr(*, "srcref")= 'srcref' int [1:8] 1 65 1 79 65 79 1 1
## .. .. ..- attr(*, "srcfile")=Classes 'srcfilecopy', 'srcfile' <environment: 0x000000001381c4c0>Watch out
L[[1]] # the first component## [1] "A" "B" "C" "D"L[1] # the sub-list containing the first component of L## $group
## [1] "A" "B" "C" "D"class(L[[1]]) # character## [1] "character"class(L[1]) # list## [1] "list"1.1.4 Statistical functionality
1.1.4.1 Probability distributions (d/p/q/r*) {-}
dexp(1.4, rate = 2) # density f(x) = 2*exp(-2*x)## [1] 0.1216201pexp(1.4, rate = 2) # distribution function F(x) = 1-exp(-2*x)## [1] 0.9391899qexp(0.3, rate = 2) # quantile function F^-(y) = -log(1-y)/2## [1] 0.1783375rexp(4, rate = 2) # draw random variates from Exp(2)## [1] 0.32069047 0.97641111 0.09250077 0.22965871Two-sample t-test
Ex.: Is the average loss in two different business lines equal? \(H_0\): means are equal
boxplot(Loss ~ Line, data = df) # boxplot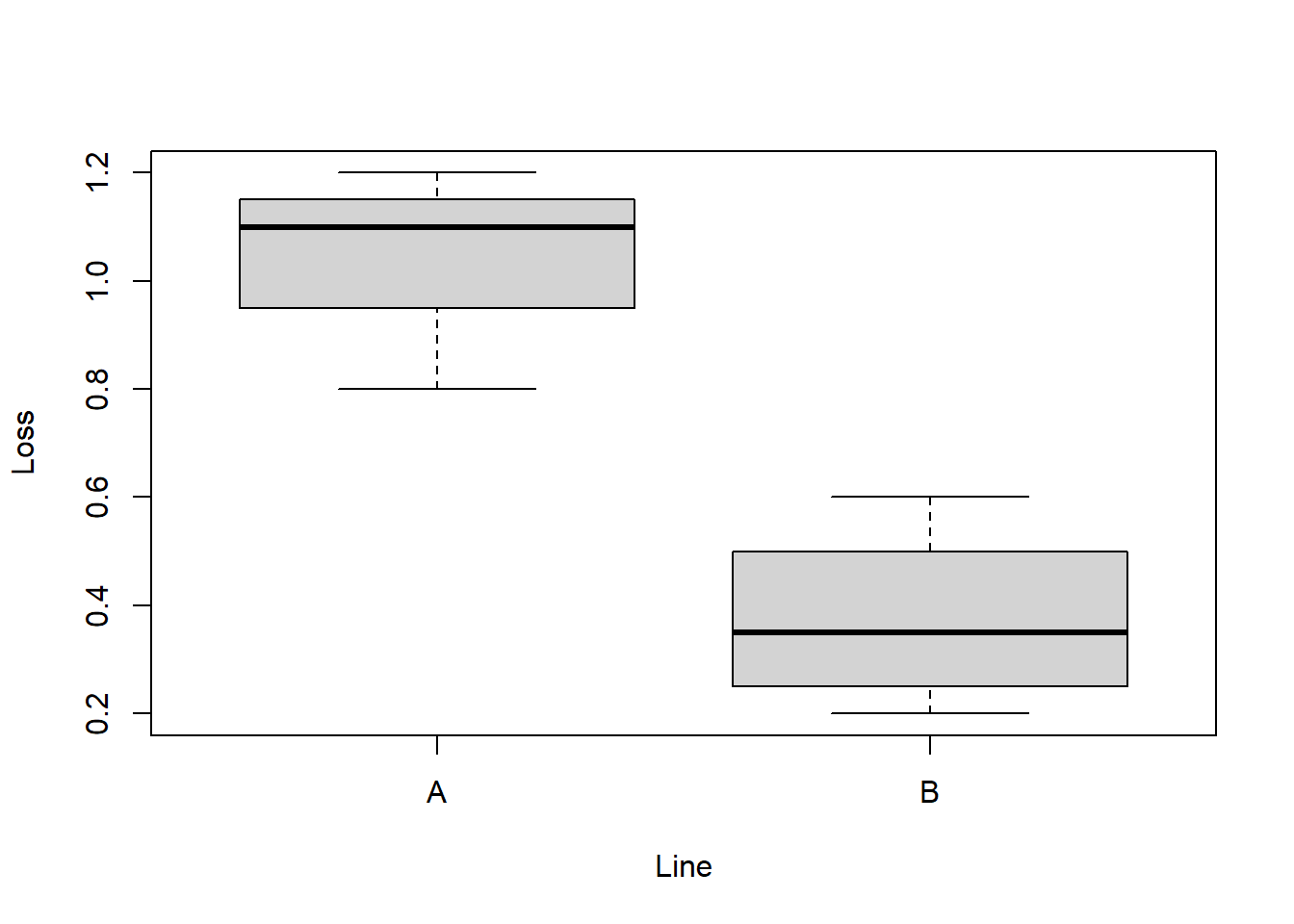
(res = t.test(Loss ~ Line, data = df)) # Two-sided Welch's t-test##
## Welch Two Sample t-test
##
## data: Loss by Line
## t = 4.4653, df = 3.8712, p-value = 0.01197
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.2435707 1.0730959
## sample estimates:
## mean in group A mean in group B
## 1.033333 0.375000str(res) # => class = "htest"## List of 10
## $ statistic : Named num 4.47
## ..- attr(*, "names")= chr "t"
## $ parameter : Named num 3.87
## ..- attr(*, "names")= chr "df"
## $ p.value : num 0.012
## $ conf.int : num [1:2] 0.244 1.073
## ..- attr(*, "conf.level")= num 0.95
## $ estimate : Named num [1:2] 1.033 0.375
## ..- attr(*, "names")= chr [1:2] "mean in group A" "mean in group B"
## $ null.value : Named num 0
## ..- attr(*, "names")= chr "difference in means"
## $ stderr : num 0.147
## $ alternative: chr "two.sided"
## $ method : chr "Welch Two Sample t-test"
## $ data.name : chr "Loss by Line"
## - attr(*, "class")= chr "htest"stopifnot(res$p.value < 0.05) # H0 rejected at 5%
t.test(subset(df, Line == "A", select = Loss), # different call
subset(df, Line == "B", select = Loss))##
## Welch Two Sample t-test
##
## data: subset(df, Line == "A", select = Loss) and subset(df, Line == "B", select = Loss)
## t = 4.4653, df = 3.8712, p-value = 0.01197
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.2435707 1.0730959
## sample estimates:
## mean of x mean of y
## 1.033333 0.375000Binomial test
Ex.: You have estimated the (\(1-p\))-quantile of 1000 losses and recorded 18 exceedances over this estimate. Is the exceedance (= success) probability really \(p\)? \(H_0: p = 0.01\)
(res = binom.test(18, n = 1000, p = 0.01)) # Two-sided binomial test##
## Exact binomial test
##
## data: 18 and 1000
## number of successes = 18, number of trials = 1000, p-value = 0.01651
## alternative hypothesis: true probability of success is not equal to 0.01
## 95 percent confidence interval:
## 0.01070195 0.02829904
## sample estimates:
## probability of success
## 0.018stopifnot(res$p.value < 0.05) # H0 rejected at 5%1.1.5 Random number generation
.Random.seed # in a new R session, this object does not exist (until RNs are drawn)## [1] 10403 4 603097374 1323527657 -1864605925 -598406870
## [7] 1665188428 -1474527729 -1875324603 1342905084 -545476270 1747048141
## [13] 2113851015 -1904363154 1528836936 -21289141 -824906071 42603512
## [19] 294275878 68049985 927985107 -1708490878 821867444 -1052718281
## [25] -57259475 2084907844 -276643734 -1253352747 -2046524305 -872301194
## [31] 234383008 1952572259 -1764521983 -1496698000 1303853838 704017785
## [37] -49737461 1296716346 2018871612 -1684158849 1243844053 1031013356
## [43] -1704225470 -2006037859 190359319 1550435966 -1846680008 2119213339
## [49] 542803577 2069938888 1361941238 1088494385 51702627 -251002574
## [55] -1447886204 512339655 228324765 -1409785580 1632161722 1960577541
## [61] 170474463 -219090330 -1984958992 866220819 603456689 916526944
## [67] 88470782 577066121 1386795963 -1168097910 637787244 1747891695
## [73] -834400731 -1636431140 700965042 -19696723 1387046759 -376548210
## [79] -626929304 1416745323 1019355913 826889624 -197466938 2006392353
## [85] 1661730483 -771578846 -1045848556 656511639 735857805 -951828060
## [91] 1472408458 -624818187 -1593899441 -1208925866 1725795328 1002505539
## [97] 753510625 934281808 1793629870 679725657 1574720107 -539494438
## [103] 644282524 -513492321 1253595381 -1334066804 -127865758 771193917
## [109] -469512521 -427020962 -430525288 -1646960645 -63552103 -1335405016
## [115] -1165685034 1808608081 1895939 1160515986 1742393124 -1551851033
## [121] -1804317123 -656631628 -490983654 2107868261 1070353663 -1737048698
## [127] -636603632 -794998861 1110469713 -1243525120 374145246 1045461801
## [133] 2118682331 -146688534 1359437196 -2098867505 -1594028411 -1624396484
## [139] 1969385490 2021474061 1494514759 1102974510 343791496 687776395
## [145] 1505006697 1077942328 -725282586 54392961 -1590173677 -1397872702
## [151] 2092367988 -580503945 1088628589 -1114761212 -128969942 -1116624747
## [157] 1511585583 1940561462 1598491232 401709219 -1950024767 161134512
## [163] -913939762 -1974239175 -679283125 -528647174 -1607973124 -2114319553
## [169] -1497758699 942350124 1268773890 586299101 -318372393 1388343486
## [175] -1414200584 1352829147 2038725433 908791432 190118454 202756721
## [181] 1662404771 -978550286 -654929596 -610006521 -812877859 -1553092396
## [187] 1661349882 1412278085 -1523301473 -851801818 1740429744 745042515
## [193] 246857073 -1990980448 423005246 -823573687 448188923 -1429326390
## [199] -1567229140 -765627601 1296673253 794719388 -192577294 1273272685
## [205] 1057773223 1101846734 -512494040 -1991934421 -1199500215 1849714008
## [211] -446170106 307822049 965068659 -657865758 1062398804 -1622022569
## [217] 309091917 -1743400476 -1304941622 2041040437 811275407 1108016534
## [223] 4137280 -1743750141 -1274266079 98715920 1992484590 -2144044391
## [229] 1296233259 236292108 -1443882916 -1166958126 122913280 958806356
## [235] 1801159912 -1304224518 -1118380336 -1423035092 -1436215052 6757778
## [241] 1636700512 2064068620 438273760 -1074427294 -182081880 220034636
## [247] -844995716 163042610 61552240 1504570180 1221596120 -753913990
## [253] -1571419600 -962192452 29360724 -1949768638 1488011424 1752222396
## [259] -2044564016 -318015646 1323109096 1949709516 -652820996 -1466537486
## [265] -158112128 833627636 1106047624 1913581370 -919474352 -882107284
## [271] 1598608788 1746408530 -229738016 -1302663988 -682739552 1801927042
## [277] -1052440344 612657900 -886614724 311546994 1660611696 -1426951132
## [283] -493682632 884060954 427216 1207485244 -705269868 1143043970
## [289] 521838016 -1211076036 -1917478512 935404066 -1863975672 775062156
## [295] -311277796 1732499602 1150978432 1843522068 -968379608 -875389382
## [301] 679428560 334759276 1136827316 1480068114 1102174688 -273794100
## [307] -1170974496 1389793314 -1902752472 -1030361588 -702657732 1568252914
## [313] 1721495280 -536022460 -93393320 892859194 628564464 1590410940
## [319] 56855828 -1186441534 1503025248 522774396 -374215728 110120226
## [325] -1263380824 1721674636 -1040827204 717285170 1247083072 1202610356
## [331] 1844439624 129699258 87826960 -1369213204 -1632225964 -1130203886
## [337] 338377120 -1387587892 1318104672 -1857782846 426666792 -371754068
## [343] -1396908228 1415019890 -162107600 1194587428 373121848 -496853286
## [349] 1209805712 -1545184516 -2013781100 1730748482 1132765440 -1814545348
## [355] 1204720976 123162786 1650378056 761547532 -1545229604 881389906
## [361] 2012457088 302222420 548496360 -700269318 1077182288 1438701356
## [367] -360080012 1634181010 -1551696800 112321932 -270249120 446100962
## [373] -95452248 -1048237876 -1522248708 -961871438 1678790128 802152388
## [379] 1589217624 2031377786 1391478704 -293487172 1042642004 1669748674
## [385] -105002976 155877564 -1388808624 -636889118 -2009130904 -1514481588
## [391] 1874904316 -1075795982 1609506048 -1121278604 479502344 -139615302
## [397] -1442347568 1738735596 -376363628 -1240391214 -911615648 -2068669620
## [403] -1406009056 930441090 -43565336 393259244 -1590163396 1910771570
## [409] 1574841968 -1724462044 193208120 -2074751846 2101449424 1167855804
## [415] -215732588 -891638142 1699307712 456853308 -926510960 1824591394
## [421] 1897163784 862588172 1211436188 389583378 1804514176 -1313130988
## [427] 21753384 488545594 -1909101104 -730118036 -1237809868 1218128530
## [433] -378122400 -641192116 26666976 -299140190 -1990370392 -1194509940
## [439] -1207796548 257032562 605677808 1434015812 914318680 560319034
## [445] 783388528 -774370244 -455998700 1169769922 -290763040 1359883132
## [451] 1293873872 -2076250974 -1559445464 553023756 1293437884 814923058
## [457] -1228671018 -687565132 1199122117 161077263 -1736087416 373840294
## [463] 590905683 -162123083 973465618 -726537760 -927417271 664029819
## [469] -153496756 1063261914 2001619663 -1929577831 -319056210 -1937472580
## [475] -688595923 527971287 -783721952 522156926 1209378123 -1445804211
## [481] 1525304698 1546981304 1847424353 1098631443 -929488588 -531399870
## [487] 692435799 208239265 -1455154330 -153709212 1444339861 -1171361345
## [493] -1939847848 356825974 -880445053 -1855022139 1133789410 427177296
## [499] -1550363527 -1656576085 1504742684 -2113893814 -1335185857 -909770103
## [505] -1084496226 -96816308 -879996131 2121851559 1313278416 -1022951058
## [511] -984257509 920970621 -853838998 -1219918328 -519095631 2064663843
## [517] 1817114148 -1442284334 -230720217 -1155311759 -1207069258 -2020614828
## [523] -1770431515 1960961519 -1221645016 -1750090362 1016773043 1086346517
## [529] -1557522574 170341312 -1076267991 150741147 338791788 -1628408454
## [535] -1629653329 -604594759 1110589390 -1939697892 -879772019 234446583
## [541] 1241125376 -1942545314 -1519886549 560999469 -453747558 371069016
## [547] 1402943425 539596915 -46100076 -1787371486 -848746697 -1172264447
## [553] -1599606010 -1376854204 -2068680075 201696223 -722073800 1494270230
## [559] -1907081949 236449509 1327191810 -1543275152 1515347225 646092043
## [565] 1745704444 1864150570 824522335 1100006889 1364031230 -1089231124
## [571] -337914307 -560560633 -911029776 2003851662 1793290171 216201629
## [577] 942356298 -438170776 -1306391215 1748082243 2035123012 1509302258
## [583] -1028858425 620471185 -1410753770 -2019840140 -916697595 930707023
## [589] -1873227192 1957217254 184151315 344318581 -1198337966 -1794104672
## [595] -2065739895 -1922495557 -639644660 -2135524966 -1200924401 -341366951
## [601] 1410386414 -865708932 1837248749 2113468311 -33812384 1562399294
## [607] -308137205 1126558093 1740346042 1420097784 -1879013727 -1995792813
## [613] -119201420 -142207230 901152663 -1112084127 905738662 341326756
## [619] 456910421 681371391 1669966744 133680310 1229236547 -900005755
## [625] -1667540702 -1201118949Generate from N(0,1)
(X = rnorm(2)) # generate two N(0,1) random variates## [1] 0.3527327 1.4526023str(.Random.seed) # encodes types of random number generators (RNGs) and the seed## int [1:626] 10403 8 603097374 1323527657 -1864605925 -598406870 1665188428 -1474527729 -1875324603 1342905084 ...Note (see ?.Random.seed):
The first integer in .Random.seed consists of…
‘03’ = \(\mathcal{U}(0,1)\) RNG (Mersenne Twister)
‘4’ = \(\mathcal{N}(0,1)\) RNG (inversion)
‘10’ = \(\mathcal{U}\{1,...,n\}\) RNG (rejection)
The remaining integers denote the actual seed.
The default kind is the “Mersenne Twister” (which needs an integer(624) as seed and the current position in this sequence, so 625 numbers).
If no random numbers were generated yet in an R session,
.Random.seedwill not exist. If you start drawing random numbers without callingset.seed(),.Random.seedis constructed from system time and the R process number. You can also dorm(.Random.seed)and callrunif(1)thereafter to convince yourself that.Random.seedis newly generated.
RNGkind() # => Mersenne Twister, with inversion for N(0,1) and rejection for U{1,..,n}## [1] "Mersenne-Twister" "Inversion" "Rejection"How can we make sure to obtain the same results (for reproducibility?)
(Y = rnorm(2)) # => another two N(0,1) random variates## [1] 0.6749304 -0.5068128all.equal(X, Y) # obviously not equal (here: with probability 1)## [1] "Mean relative difference: 1.263817"Set a ‘seed’ so that computations are reproducible
set.seed(271) # with set.seed() we can set the seed
X = rnorm(2) # draw two N(0,1) random variates
set.seed(271) # set the same seed again
Y = rnorm(2) # draw another two N(0,1) random variates
all.equal(X, Y) # => TRUE## [1] TRUEset.seed(271)
Y = rnorm(3)
all.equal(X, Y[1:2])## [1] TRUEA pseudo-random number generator which allows for easily advancing the seed is L’Ecuyer’s combined multiple-recursive generator (CMRG). Let’s see how we can call it from R:
RNGkind() # => Mersenne Twister, inversion is used for generating N(0,1)## [1] "Mersenne-Twister" "Inversion" "Rejection"RNGkind("L'Ecuyer-CMRG")
RNGkind() # => L'Ecuyer's CMRG, inversion is used for generating N(0,1)## [1] "L'Ecuyer-CMRG" "Inversion" "Rejection".Random.seed # => now of length 7 (first number similarly as above and seed of length 6)## [1] 10407 337461862 -634168913 -1336167388 -1783032619 1612283794
## [7] -1082682901(Z = rnorm(2)) # use L'Ecuyer's CMRG for generating random numbers## [1] 0.4943174 0.7258376library(parallel) # for nextRNGStream() for advancing the seed
.Random.seed = nextRNGStream(.Random.seed) # advance seed by 2^127
(Z. = rnorm(2)) # generate from next stream => will be 'sufficiently apart' from Z## [1] 2.690584 1.327619RNGkind("Mersenne-Twister") # switch back to Mersenne-Twister
RNGkind()## [1] "Mersenne-Twister" "Inversion" "Rejection"1.1.6 Control statements
R has if() else, ifelse() (a vectorized version of ‘if’), for loops (avoid or
only use if they don’t take much run time), repeat and while (with ‘break’ to
exit and ‘next’ to advance to the next loop iteration).
Without going into details, note that even ‘if()’ is a function, so
## instead of:
x = 4
if(x < 5) y = 1 else y = 0 # y is the indicator whether x < 5
## ... write (the much more readable)
y = if(x < 5) 1 else 0
## ... or even better
(y = x < 5) # ... as a logical## [1] TRUEy + 2 # ... which is internally again converted to {0,1} in calculations## [1] 3## Also, loops of the type...
x = integer(5)
for(i in 1:5) x[i] = i * i
## ... can typically be avoided by something like
x. = sapply(1:5, function(i) i * i)
stopifnot(identical(x, x.))Of course we know that this is simply (1:5)^2 which is even faster.
For efficient R programming, the following functions are useful:
## caution, we enter the 'geek zone'...
lapply(1:5, function(i) i * i) # returns a list## [[1]]
## [1] 1
##
## [[2]]
## [1] 4
##
## [[3]]
## [1] 9
##
## [[4]]
## [1] 16
##
## [[5]]
## [1] 25sapply(1:5, function(i) i * i) # returns a *s*implified version (here: a vector)## [1] 1 4 9 16 25sapply # => calls lapply()## function (X, FUN, ..., simplify = TRUE, USE.NAMES = TRUE)
## {
## FUN <- match.fun(FUN)
## answer <- lapply(X = X, FUN = FUN, ...)
## if (USE.NAMES && is.character(X) && is.null(names(answer)))
## names(answer) <- X
## if (!isFALSE(simplify) && length(answer))
## simplify2array(answer, higher = (simplify == "array"))
## else answer
## }
## <bytecode: 0x0000000014f76218>
## <environment: namespace:base>unlist(lapply(1:5, function(i) i * i)) # a bit faster than sapply()## [1] 1 4 9 16 25vapply(1:5, function(i) i * i, NA_real_) ## [1] 1 4 9 16 25## even faster but we have to know the return value of the function1.1.7 Working with additional packages
packageDescription("qrmtools") # description of an installed package## Package: qrmtools
## Version: 0.0-13
## Encoding: UTF-8
## Title: Tools for Quantitative Risk Management
## Description: Functions and data sets for reproducing selected results
## from the book "Quantitative Risk Management: Concepts,
## Techniques and Tools". Furthermore, new developments and
## auxiliary functions for Quantitative Risk Management practice.
## Authors@R: c(person(given = "Marius", family = "Hofert", role =
## c("aut", "cre"), email = "marius.hofert@uwaterloo.ca"),
## person(given = "Kurt", family = "Hornik", role = "aut", email =
## "Kurt.Hornik@R-project.org"), person(given = "Alexander J.",
## family = "McNeil", role = "aut", email =
## "alexander.mcneil@york.ac.uk"))
## Author: Marius Hofert [aut, cre], Kurt Hornik [aut], Alexander J.
## McNeil [aut]
## Maintainer: Marius Hofert <marius.hofert@uwaterloo.ca>
## Depends: R (>= 3.2.0)
## Imports: graphics, lattice, quantmod, Quandl, zoo, xts, methods,
## grDevices, stats, rugarch, utils, ADGofTest
## Suggests: combinat, copula, knitr, sfsmisc, RColorBrewer, sn
## Enhances:
## License: GPL (>= 3) | file LICENCE
## NeedsCompilation: yes
## VignetteBuilder: knitr
## Repository: CRAN
## Date/Publication: 2020-04-19 04:40:02 UTC
## Repository/R-Forge/Project: qrmtools
## Repository/R-Forge/Revision: 266
## Repository/R-Forge/DateTimeStamp: 2020-04-19 00:34:40
## Packaged: 2020-04-19 00:51:10 UTC; rforge
## Built: R 4.0.5; x86_64-w64-mingw32; 2021-04-05 23:16:30 UTC; windows
##
## -- File: C:/Users/shihs/Documents/R/win-library/4.0/qrmtools/Meta/package.rdsmaintainer("qrmtools") # the maintainer## [1] "Marius Hofert <marius.hofert@uwaterloo.ca>"citation("qrmtools") # how to cite a package##
## To cite package 'qrmtools' in publications use:
##
## Marius Hofert, Kurt Hornik and Alexander J. McNeil (2020). qrmtools:
## Tools for Quantitative Risk Management. R package version 0.0-13.
## https://CRAN.R-project.org/package=qrmtools
##
## A BibTeX entry for LaTeX users is
##
## @Manual{,
## title = {qrmtools: Tools for Quantitative Risk Management},
## author = {Marius Hofert and Kurt Hornik and Alexander J. McNeil},
## year = {2020},
## note = {R package version 0.0-13},
## url = {https://CRAN.R-project.org/package=qrmtools},
## }Generate and plot data from a multivariate t distribution
set.seed(271) # for reproducibility (see below)
library(nvmix) # for rStudent()
X = rStudent(2000, df = 4.5, scale = P) # generate data from a multivariate t_4.5 distribution
library(lattice) # for cloud()
cloud(X[,3]~X[,1]+X[,2], scales = list(col = 1, arrows = FALSE), col = 1,
xlab = expression(italic(X[1])), ylab = expression(italic(X[2])),
zlab = expression(italic(X[3])),
par.settings = list(background = list(col = "#ffffff00"),
axis.line = list(col = "transparent"), clip = list(panel = "off")))
## => not much visible; in higher dimensions even impossible ...## Pairs plot (or scatter plot matrix)
pairs(X, gap = 0, pch = ".") # ... but we can use a pairs plot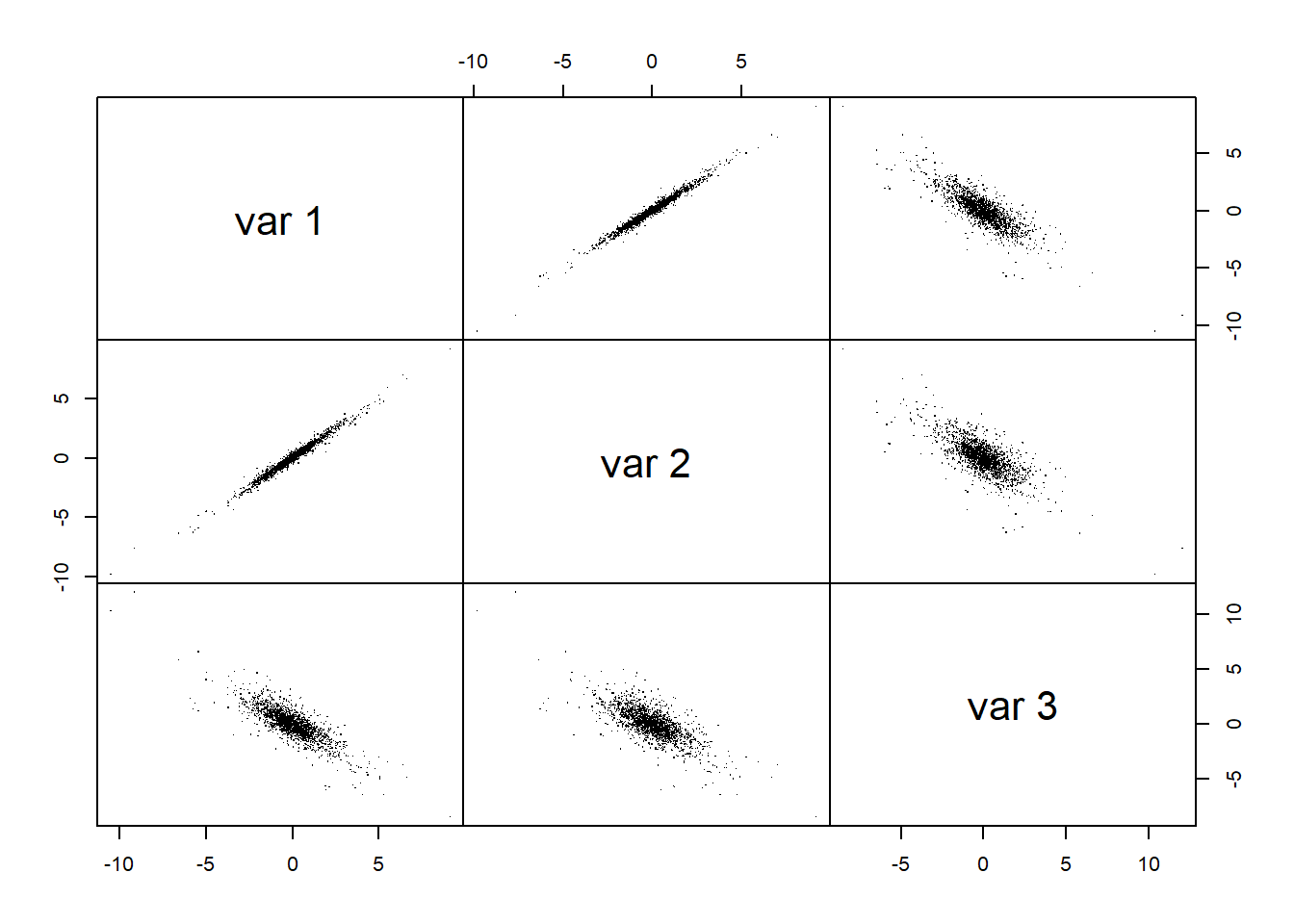
## ... or dynamically:
options(rgl.useNULL = TRUE) # Suppress the separate window.
library(rgl) # for plot3d()
plot3d(X, xlab = expression(italic(X)[1]), ylab = expression(italic(X)[2]),
zlab = expression(italic(X)[3]))
rglwidget()1.1.8 Writing functions
gap = 0 is a good default for pairs(), so we can define our own scatter plot matrix (also with nice default labels):
##' @title Scatter Plot Matrix with Defaults
##' @param x data matrix (see ?pairs)
##' @param gap see 'gap' of pairs()
##' @param labels see 'labels' of pairs()
##' @param ... additional arguments passed to the underlying pairs()
##' @return invisible(NULL); see pairs.default
##' @author Marius Hofert
mypairs = function(x, gap = 0, labels = paste("Variable", 1:ncol(x)), ...)
pairs(x, gap = gap, labels = labels, ...) # ... pass through the formal argumentsNote:
‘lazy evaluation’: as
ncol(x)is only evaluated once neededone-line functions don’t need the embracing ‘
{}’the last line of the function is returned by default, no need to call return()
## Calls
mypairs(X)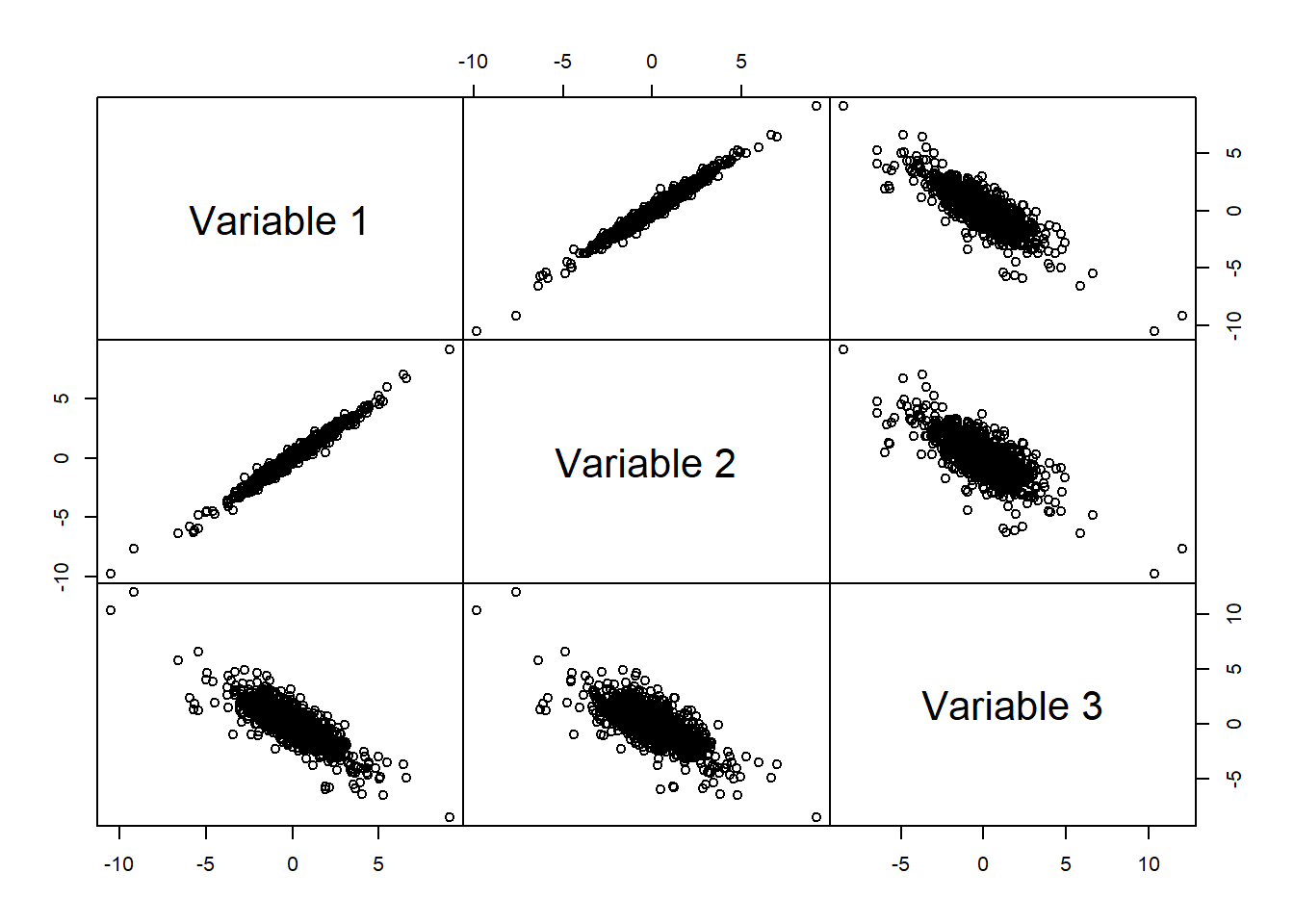
mypairs(X, pch = 19)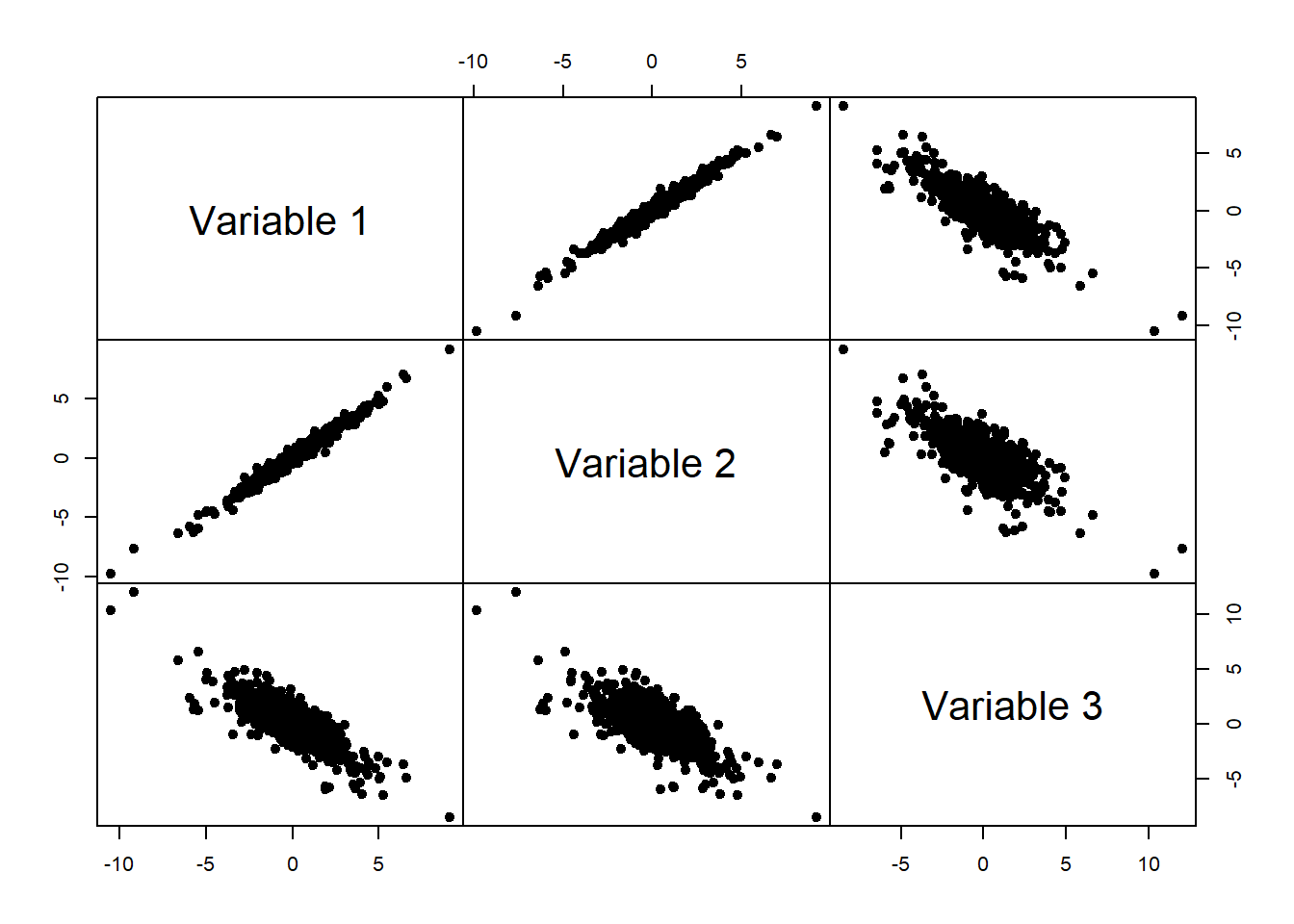
Let’s write a function for computing the mean of an Exp(lambda) analytically or via Monte Carlo:
##' @title Function for Computing the Mean of an Exp(lambda) Distribution
##' @param lambda parameter (vector of) lambda > 0
##' @param n Monte Carlo sample size
##' @param method character string indicating the method to be used:
##' "analytical": analytical formula 1/lambda
##' "MC": Monte Carlo based on the sample size 'n'
##' @return computed mean(s)
##' @author Marius Hofert
##' @note vectorized in lambda
exp_mean = function(lambda, n, method = c("analytical", "MC"))
{
stopifnot(lambda > 0) # input check(s)
method = match.arg(method) # match the provided method with the two options
switch(method, # distinguish (switch between) the two methods
"analytical" = {
1/lambda # vectorized in lambda (i.e., works for a vector of lambda's)
## Note: We did not use 'n' in this case, so although it is a
## formal argument, we do not need to provide it.
},
"MC" = {
if(missing(n)) # checks the formal argument 'n'
stop("You need to provide the Monte Carlo sample size 'n'")
E = rexp(n)
sapply(lambda, function(l) mean(E/l)) # vectorized in lambda
},
stop("Wrong 'method'"))
}Note:
We could have also omitted ‘n’ and used ‘...’. We would then need to check in the "MC" case whether ‘n’ was provided. Checking can be done with hasArg(n) in this case and ‘n’ can be obtained with list(...)$n.
## Calls
(true = exp_mean(1:4))## [1] 1.0000000 0.5000000 0.3333333 0.2500000set.seed(271)
(sim = exp_mean(1:4, n = 1e7, method = "MC"))## [1] 1.0000714 0.5000357 0.3333571 0.2500179stopifnot(all.equal(true, sim, tol = 0.001))A word concerning efficiency
## Some function mimicking a longer computation
f = function() {
## Longer computation to get 'x'
Sys.sleep(1) # mimics a longer computation
x = 1
## Longer computation to get 'y'
Sys.sleep(1) # mimics a longer computation
y = 2
## Return
list(x = x, y = y)
}
## If you need both values 'x' and 'y', then do *not* do...
x = f()$x
y = f()$y
## ... as this calls 'f' twice. Do this instead:
res = f() # only one function call
x = res$x
y = res$y1.1.9 Misc
Not discussed here:
How to read/write data from/to a file. This can be done with
read.table()/write.table(), for example. For.csvfiles, there are the convenience wrappersread.csv()/write.csv().How to load/save R objects from/to a file. This can be done using
load()/save()How to retrieve an R plot as a file (for printing, for example). For example:
doPDF = TRUE
if(doPDF) pdf(file = (file = "myfile.pdf"), width = 6, height = 6) # open plot device
plot(1:10, 10:1) # actual plot command(s)
if(doPDF) dev.off() # close plot device; or use crop's dev.off.crop(file)1.2 Evaluating \(e^x-1\)
Illustrating how R’s expm1(x) evaluates exp(x)-1 in a numerically more stable way.
1.2.1 Setup
This illustrates a potential numerical issue when evaluating exp(x)-1 appearing in the loss operator in a standard stock portfolio; see MFE (2015, Example 2.1) for detail.
Example 1.1 (stock portfolio) Consider a fixed portfolio of \(d\) stocks and denote by \(\lambda_i\) the number of shares of stock \(i\) in the portfolio at time \(t\). The price process of stock \(i\) is denoted by \((S_{t,i})_{t\in \mathbb{N}}\).
- Following standard practice in finance and risk management we use logarithmic prices as risk factors, i.e. we take \(Z_{t,i} := \ln{S_{t,i}}, \ 1 \leq i \leq d\), and we get \(V_t = \sum_{i=1}^d \lambda_i e^{Z_{t,i}}\). The risk-factor changes \(X_{t+1,i} = \ln{S_{t+1,i}} −\ln{S_{t,i}}\) then correspond to the log-returns of the stocks in the portfolio. The portfolio loss from time \(t\) to \(t+1\) is given by \[ L_{t+1} = -(V_{t+1}-V_t) = - \sum_{i=1}^d \lambda_i (e^{Z_{t,i} + X_{t+1,i}}-e^{Z_{t,i}}) = - \sum_{i=1}^d \lambda_i S_{t,i} \underbrace{(e^{X_{t+1,i}}-1)}_{\text{target}} \] Remaining contents of the example are omitted.
\(\blacksquare\)
1.2.2 Investigating exp(x)-1 vs expm1(x)
library(sfsmisc) # for eaxis()x = 10^seq(-26, 0, by = 0.25) # sequence of x values
y = exp(x)-1 # numerically critical for |x| approximately equal 0
y. = expm1(x) # numerically more stablePlot exp(x)-1 vs expm1(x) near 0
plot(x, y., type = "l", log = "xy", # expm1(x)
col = "royalblue3", ann = FALSE, xaxt = "n", yaxt = "n")
mtext(1, text = "x", line = 2) # x-axis label
eaxis(1, f.smalltcl = 2/5) # x-axis
eaxis(2, f.smalltcl = 2/5) # y-axis
lines(x, y, col = "firebrick", lwd = 1.6) # exp(x)-1
legend("bottomright", legend = c("exp(x)-1", "expm1(x)"), bty = "n",
lty = c(1,1), lwd = c(1.6,1), col = c("firebrick", "royalblue3")) # legend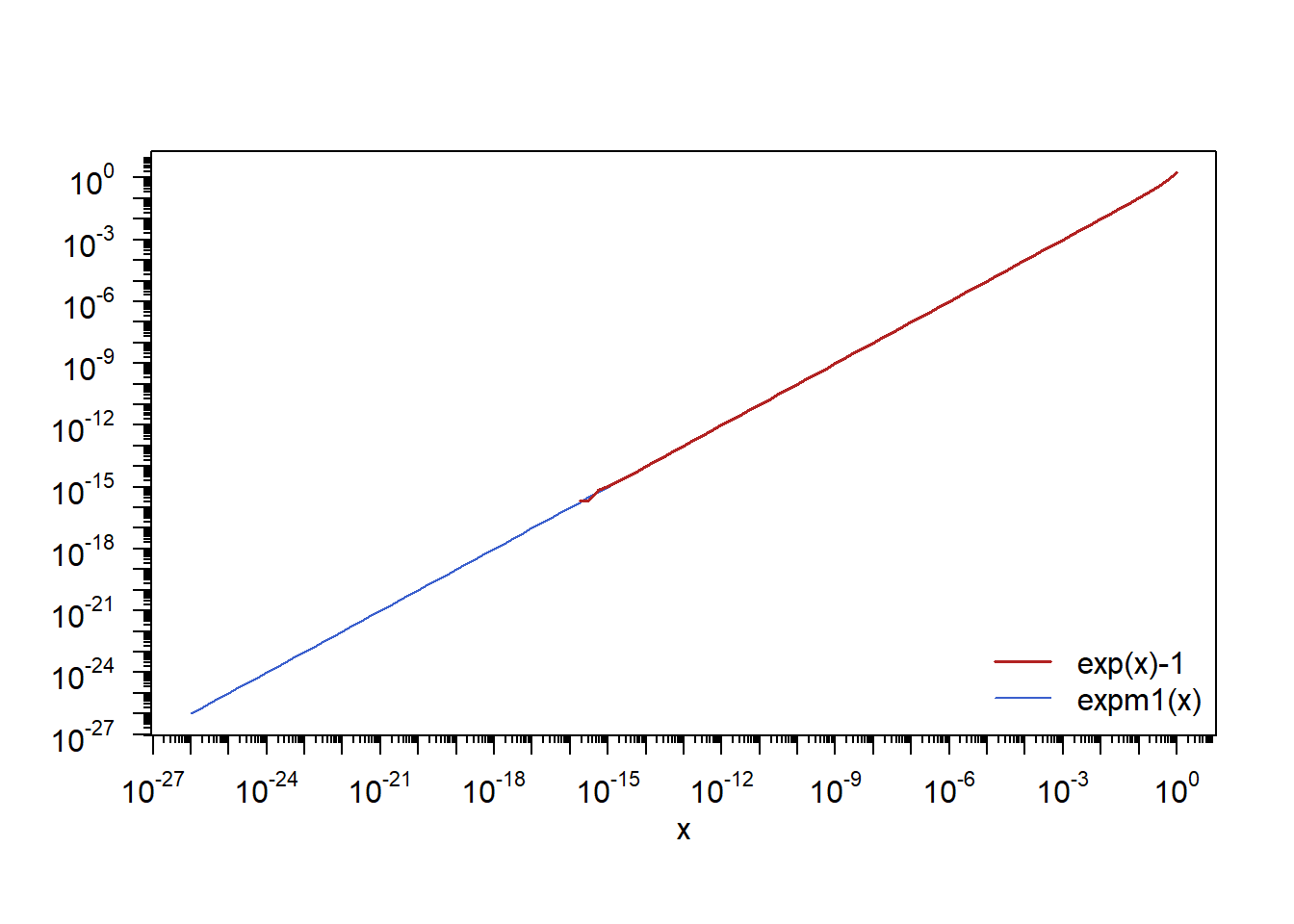
1.2.3 Illustrating how expm1(x) works
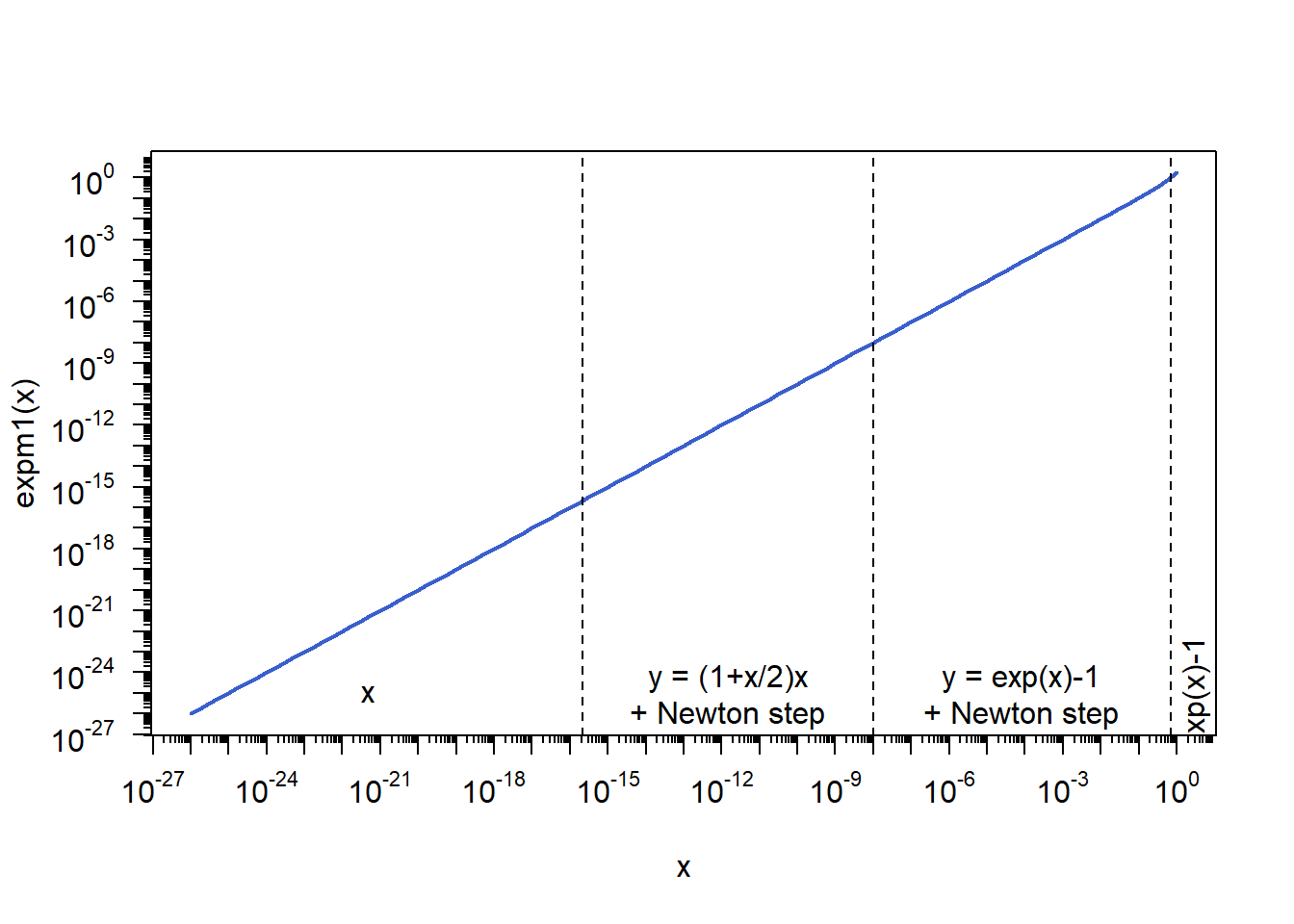
Note that this is how expm1() worked for R < 3.5.0 (where ./src/nmath/expm1.c existed). For R >= 3.5.0, expm1() is taken from gcc and also more complicated.
plot(x, y., type = "l", lwd = 2, log = "xy", col = "royalblue3",
xlab = "x", ylab = "expm1(x)", xaxt = "n", yaxt = "n") # expm1(x)
eaxis(1, f.smalltcl = 2/5) # x-axis
eaxis(2, f.smalltcl = 2/5) # y-axis
ypos = 1e-25 # y-axis height for labels
## Right-most part (non-critical)
text(x = 3, y = ypos, "exp(x)-1", srt = 90)
## Middle-right part (improvement via Newton step)
text(x = 10^(-(8+0.1681302)/2), y = ypos, "y = exp(x)-1\n+ Newton step")
abline(v = 0.697, lty = 2)
## Middle-left part (improvement via Taylor approximation + Newton step)
text(x = 10^(-(15.65356+8)/2), y = ypos, "y = (1+x/2)x\n+ Newton step")
abline(v = 1e-8, lty = 2)
## Left-most part (improvement via the identity, so again Taylor)
text(x = 10^(-(27+15.65356)/2), y = ypos, "x")
abline(v = .Machine$double.eps, lty = 2) # smallest floating-point number x>0 s.t. 1+x not equal 1