2.10 Weibull

Weibull distributions are used in time-to-event models.

If \(X\) is the time to failure in a process in which the failure rate is proportional to a power of time defined by shape \(k\) and scale \(\lambda\) parameters, then \(X\) is a random variable with a Weibull distribution \(X \sim \mathrm{WB}(k, \lambda)\)

\[ f(X = x; k, \lambda) = \begin{cases} \frac{k}{\lambda} \left(\frac{x}{\lambda}\right)^{k-1} e^{-(x / \lambda)^k}, & x \ge 0 \\ 0, & x < 0 \end{cases}\]

\(k\) is called the hazard rate. If k < 1 the failure rate decreases over time, as is the case with significant infant mortality or defective items. If k = 1 the failure rate is constant, as when external event cause failure. If k > 1 the failure rate accelerates, as with aging processes.

There are several alternative parameterizations (Wikipedia). The common one for survival analysis replaces the scale parameter with a rate parameter \(\beta = 1 / \lambda\). Then for x \(\ge\) 0,

\[f(X = x; k, \beta) = \beta k (\beta x)^{k-1} e^{-(\beta x)^k}\] with cumulative distribution function \[F(x; k, \beta) = 1 - e^{-(\beta x)^k}\] and hazard function \[h(x; k, \beta) = \beta k (\beta x)^{k-1}.\]

The “survival curve” is the compliment to the CDF: \[\begin{eqnarray} S(x; k, \beta) &=& 1 - F(x; k, \beta) \\ &=& e^{-(\beta x)^k} \end{eqnarray}\]

The probability of failing at time \(x = t\) is the probability of surviving to time time multiplied by the hazard of failing when \(x = t\), \(f(t; k, \beta) = S(t; k, \beta) \cdot h(t; k, \beta)\).

expand.grid(x = seq(from = .05, to = 2.5, by = .01),
                   k = c(.5, 1, 1.5, 5)) %>%
  mutate(f = dweibull(x, k),
         F = pweibull(x, k),
         S = pweibull(x, k, lower.tail = FALSE),
         h = f / S) %>%
  pivot_longer(cols = c(f:h)) %>%
  ggplot(aes(x = x, y = value, color = factor(k))) +
  geom_line() +
  facet_wrap(vars(name), scales = "free_y") +
  scale_colour_hue(h = c(90, 270)) +
  theme(legend.position = "top") +
  labs(x = NULL, y = NULL, color = "k", title = "Weibull (lambda = 1))")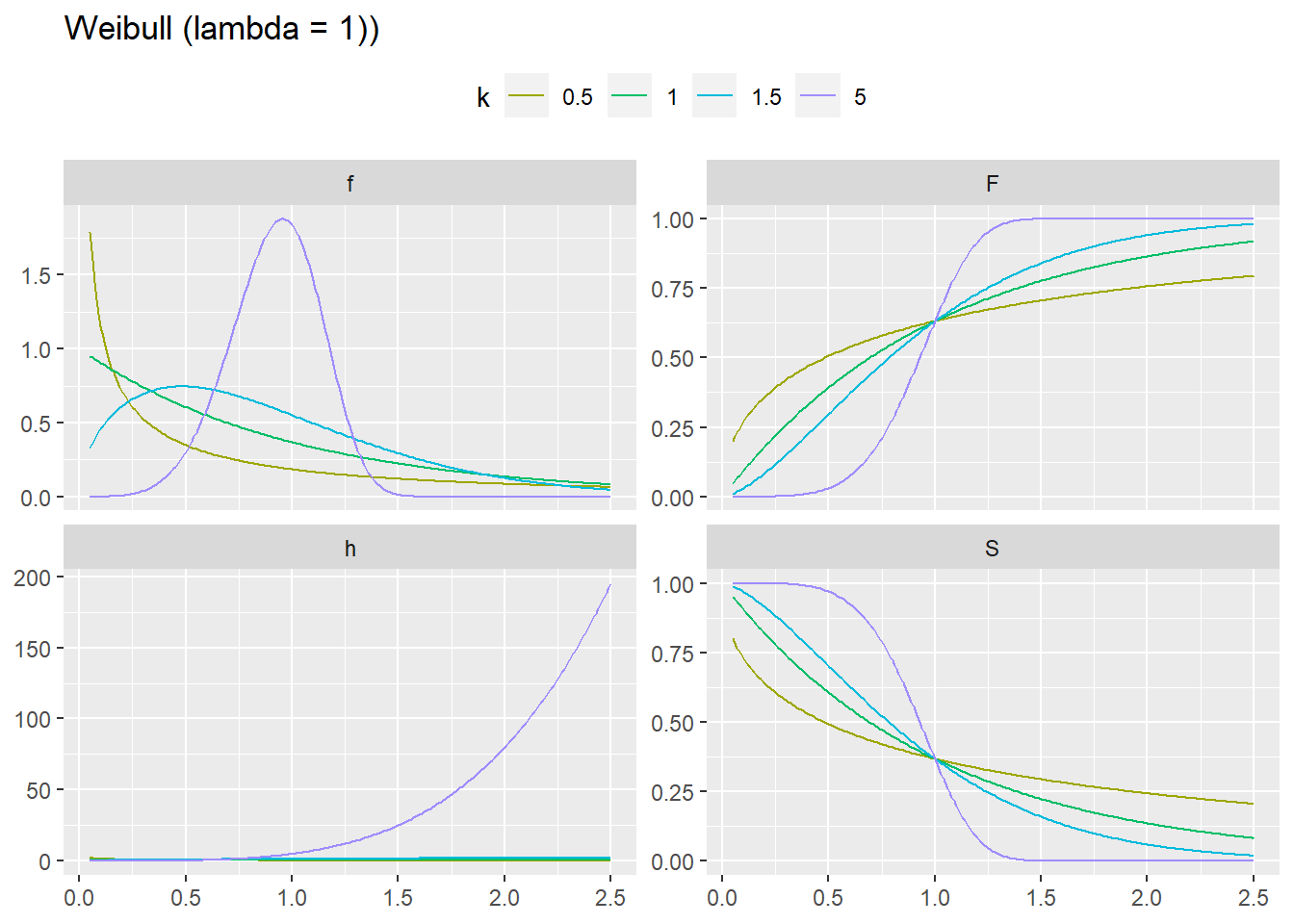

More here.