Chapter 7 Akar Persamaan Non-Linier

Persamaan non-linier dapat diartikan sebagai persamaan yang tidak mengandung syarat seperti persamaan linier, sehingga persamaan non-linier dapat merupakan:

Persamaan yang memiliki pangkat selain satu (misal: \(x^2\))
Persamaan yang mempunyai produk dua variabel (misal: \(xy\))

Dalam penyelesaian persamaan non-linier diperlukan akar-akar persamaan non-linier, dimana akar sebuah persamaan non-linier \(f\left(x\right)=0\) merupakan nilai \(x\) yang menyebabkan nilai \(f\left(x\right)\) sama dengan nol. Dalam hal ini dapat disimpulkan bahwa akar-akar penyelesaian persamaan non-linier merupakan titik potong antara kurva \(f\left(x\right)\) dengan sumbu \(x\). Ilustrasi penjelasan tersebut ditampilkan pada Gambar 7.1.

Gambar 7.1: Penyelesaian persamaan non-linier.

Contoh sederhana dari penentuan akar persamaan non-linier adalah penentuan akar persamaan kuadratik. Secara analitik penentuan akar persamaan kuadratik dapat dilakukan menggunakan Persamaan (7.1).

\[\begin{equation} x_{1,2}=\frac{-b\pm\sqrt{b^2-4a}}{2a} \tag{7.1} \end{equation}\]

Untuk masalah yang lebih rumit, penyelesaian analitik sudah tidak mungkin dilakukan. Metode numerik dapat digunakan untuk menyelesaikan masalah yang lebih kompleks. Untuk mengetahui apakah suatu persamaan non-linier memiliki akar-akar penyelesaian atau tidak, diperlukan analisa menggunakan Teorema berikut:

Teorema 7.1 (root) Suatu range x=[a,b] mempunyai akar bila f(a) dan f(b) berlawanan tanda atau memenuhi f(a).f(b)<0

Untuk memahami teorema tersebut perhatikan ilustrasi pada Gambar 7.2.

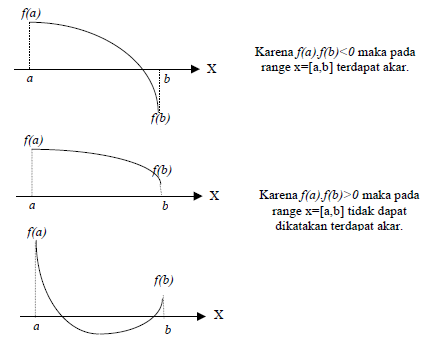
Gambar 7.2: Ilustrasi teorema Bolzano.

Pada Chapter 7 ini, akan dilakukan sejumlah pembahasan antara lain:

penentuan akar persamaan dengan metode tertutup
penentuan akar persamaan dengan metode terbuka
fungsi-fungsi R untuk mementukan akar persamaan non-linier
studi kasus

7.1 Metode Tertutup

Metode tertutup disebut juga metode bracketing. Disebut sebagai metode tertutup karena dalam pencarian akar-akar persamaan non-linier dilakukan dalam suatu selang \(\left[a,b \right]\).

7.1.1 Metode Tabel

Penyelesaian persamaan non-linier menggunakan metode tabel dilakukan dengan membagi persamaan menjadi beberapa area, dimana untuk \(x=\left[a,b \right]\) dibagi sebanyak \(N\) bagian dan pada masing-masing bagian dihitung nilai \(f\left(x \right)\) sehingga diperoleh nilai \(f\left(x \right)\) pada setian \(N\) bagian.

Bila nilai \(f\left(x_k \right)=0\) atau mendekati nol, dimana \(a \le k \le b\), maka dikatakan bahwa \(x_k\) adalah penyelesaian persamaan \(f\left(x \right)\). Bila tidak ditemukan, dicari nilai \(f\left(x_k \right)\) dan \(f\left(x_{k+1} \right)\) yang berlawanan tanda. Bila tidak ditemukan, maka persamaan tersebut dapat dikatakan tidak mempunyai akar untuk rentang \(\left[a,b \right]\).

Bila akar persamaan tidak ditemukan, maka ada dua kemungkinan untuk menentukan akar persamaan, yaitu:

Akar persamaan ditentukan oleh nilai mana yang lebih dekat. Bila \(f\left(x_k\right)\le f\left(x_{k+1}\right)\), maka akarnya \(x_k\). Bila \(f\left(x_{k+1}\right)\le f\left(x_{k}\right)\), maka akarnya \(x_{k+1}\).
Perlu dicari lagi menggunakan rentang \(x=\left[x_{k}, x_{k+1} \right]\).

Secara grafis penyelesaian persamaan non-linier menggunakan metode table disajikan pada Gambar 7.3.

Gambar 7.3: Ilustrasi metode tabel.

Algoritma Metode Tabel

Definisikan fungsi \(f\left(x \right)\)
Tentukan rentang untuk \(x\) yang berupa batas bawah \(a\) dan batas atas \(b\).
Tentukan jumlah pembagi \(N\)
Hitung step pembagi

\[\begin{equation} h=\frac{b+a}{N} \tag{7.2} \end{equation}\]

Untuk \(i=0\) s/d \(N\), hitung:

\[\begin{equation} x_i=a+i.h \tag{7.3} \end{equation}\]

\[\begin{equation} y_i=f\left(x_i \right) \tag{7.4} \end{equation}\]

Untuk \(i=0\) s/d \(N\), dimana

Bila \(f\left(x \right)=0\), maka akarnya \(x_k\)
Bila \(f\left(a \right) f\left(b \right) <0\), maka:
- \(f\left(x_k\right)\le f\left(x_{k+1}\right)\), maka akarnya \(x_k\)
- Bila tida, \(x_{k+1}\) adalah penyelesaian atau dapat dikatakan penyelesaian berada diantara \(x_k\) dan \(x_{k+1}\).

Kita dapat membuat suatu fungsi pada R untuk melakukan proses iterasi pada metode Tabel. Fungsi root_table() akan melakukan iterasi berdasarkan step algoritma 1 sampai 5. Berikut adalah sintaks yang digunakan:

root_table <- function(f, a, b, N=20){
    h <- abs((a+b)/N)
    x <- seq(from=a, to=b, by=h)
    fx <- rep(0, N+1)
    for(i in 1:(N+1)){
      fx[i] <- f(x[i])
    }
    data <- data.frame(x=x, fx=fx)
    return(data)
}

Contoh 7.1 Carilah akar persamaan \(f\left(x \right)=x+e^{x}\) pada rentang \(x=\left[-1,0 \right]\)?

Jawab:

Sebagai permulaan, jumlah pembagi yang digunakan adalah \(N=10\). Dengan menggunakan fungsi root_table() diperoleh hasil yang disajikan pada Tabel 7.1.

tabel <- root_table(f=function(x){x+exp(x)},
                     a=-1, b=0, N=10)

Tabel 7.1: Penyelesaian persamaan x+exp(x)=0
x	fx
-1.0	-0.6321
-0.9	-0.4934
-0.8	-0.3507
-0.7	-0.2034
-0.6	-0.0512
-0.5	0.1065
-0.4	0.2703
-0.3	0.4408
-0.2	0.6187
-0.1	0.8048
0.0	1.0000

Berdasarkan Tabel 7.1 diperoleh penyelesaian di antara \(-0,6\) dan \(-0,5\) dengan nilai \(f\left(x \right)\) masing-masing sebesar \(-0,0512\) dan \(-0,1065\), sehingga dapat diambil penyelesaian \(x=-0,6\). Kita dapat terus melakukan iterasi sampai memperoleh nilai \(f\left(x \right)\) < nilai toleransi dengan terus merubah rentang yang diberikan. Iterasi berikutnya dengan nilai pembagi sama dan rentang nilai \(x=\left[-0,6;-0,5\right]\) diperoleh nilai \(x=-0,57\) dan \(f\left(x \right)=0,00447\).

Untuk melihat gambaran lokasi akar, kita dapat pulang mengeplotkan data menggunakan fungsi plot. Berikut adalah fungsi yang digunakan:

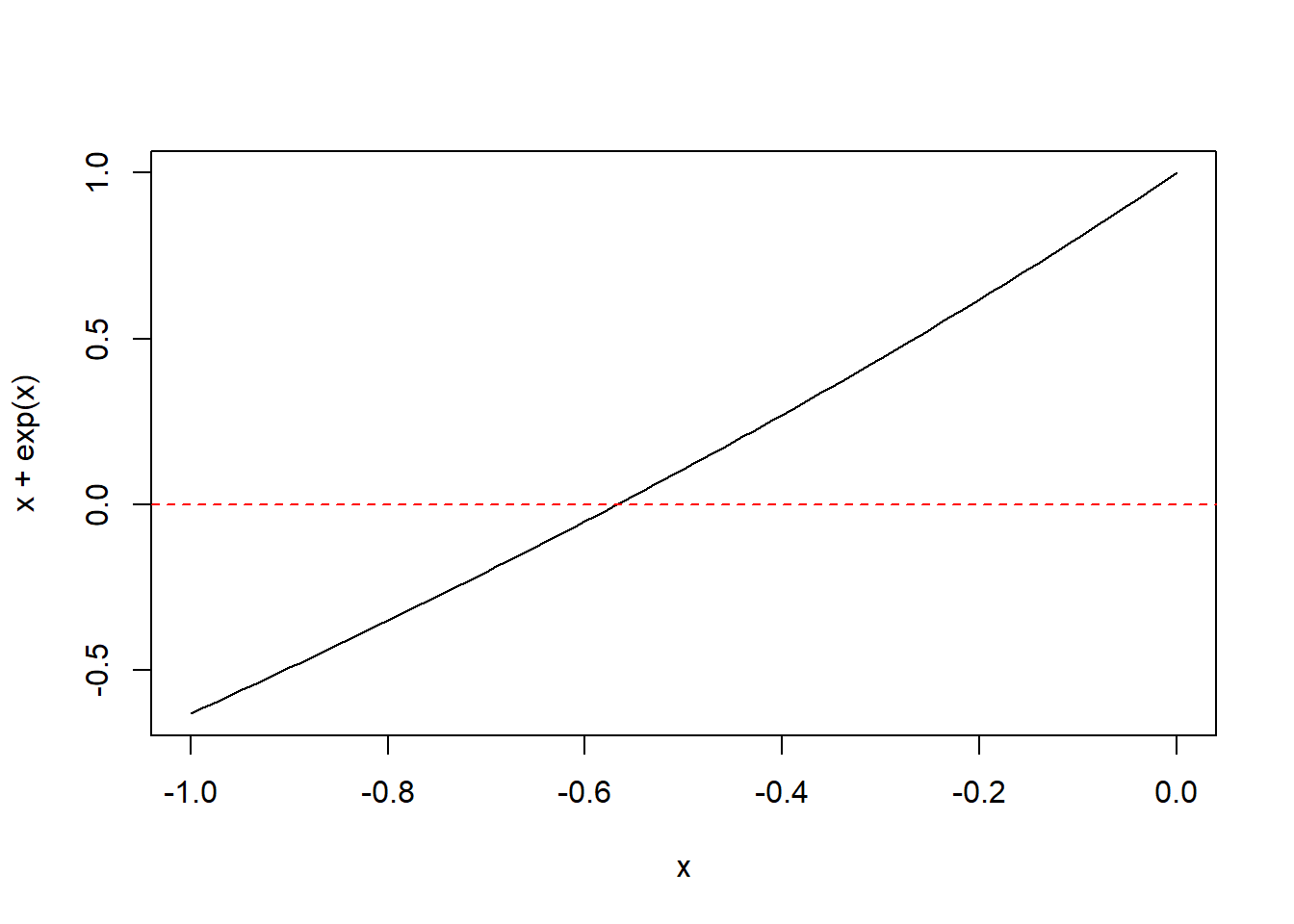
Gambar 7.4: Plot fungsi x+exp(x) pada rentang -1 sampai 0.

Untuk mengetahui lokasi akar dengan lebih jelas, kita dapat memperkecil lagi rentang nilai yang dimasukkan dalam fungsi curve().

Metode tabel pada dasarnya memiliki kelemahan yaitu cukup sulit untuk memdapatkan error penyelesaian yang cukup kecil, sehingga metode ini jarang sekali digunakan untuk menyelesaikan persamaan non-linier. Namun, metode ini cukup baik digunakan dalam menentukan area penyelesaian sehingga dapat dijadikan acuan metode lain yang lebih baik.

7.1.2 Metode Biseksi

Prinsip metode bagi dua adalah mengurung akar fungsi pada interval \(x=\left[a,b \right]\) atau pada nilai \(x\) batas bawah \(a\) dan batas atas \(b\). Selanjutnya interval tersebut terus menerus dibagi 2 hingga sekecil mungkin, sehingga nilai hampiran yang dicari dapat ditentukan dengan tingkat toleransi tertentu. Untuk lebih memahami metode biseksi, perhatikan visualisasi pada Gambar 7.5.

Gambar 7.5: Ilustrasi metode biseksi.

Metode biseksi merupakan metode yang paling mudah dan paling sederhana dibanding metode lainnya. Adapun sifat metode ini antara lain:

Konvergensi lambat
Caranya mudah
Tidak dapat digunakan untuk mencari akar imaginer
Hanya dapat mencari satu akar pada satu siklus.

Algoritma Metode Biseksi

Definisikan fungsi \(f\left(x \right)\)
Tentukan rentang untuk \(x\) yang berupa batas bawah \(a\) dan batas atas \(b\).
Tentukan nilai toleransi \(e\) dan iterasi maksimum \(N\)
Hitung \(f\left(a \right)\) dan \(f\left(b \right)\)
Hitung:

\[\begin{equation} x=\frac{a+b}{2} \tag{7.5} \end{equation}\]

Hitung \(f\left(x \right)\)
Bila \(f\left(x \right).f\left(a \right)<0\), maka \(b=x\) dan \(f\left(b \right)=f\left(x \right)\). Bila tidak, \(a=x\) dan \(f\left(a \right)=f\left(x \right)\)
Bila \(\left|b-a \right|<e\) atau iterasi maksimum maka proses dihentikan dan didapatkan akar=\(x\), dan bila tidak ulangi langkah 6.
Jika sudah diperoleh nilai dibawah nilai toleransi, nilai akar selanjutnya dihitung berdasarkan Persamaan (7.5) dengan nilai \(a\) dan \(b\) merupakan nilai baru yang diperoleh dari proses iterasi.

Berdasarkan algoritma tersebut, kita dapat menyusun suatu fungsi pada R yang dapat digunakan untuk melakukan iterasi tersebut. Fungsi root_bisection() merupakan fungsi yang telah penulis susun untuk melakukan iterasi menggunakan metode biseksi. Berikut adalah sintaks dari fungsi tersebut:

root_bisection <- function(f, a, b, tol=1e-7, N=100){
  iter <- 0
  fa <- f(a)
  fb <- f(b)
  
  while(abs(b-a)>tol){
    iter <- iter+1
    if(iter>N){
      warning("iterations maximum exceeded")
      break
    }
    x <- (a+b)/2
    fx <- f(x)
    if(fa*fx>0){
      a <- x
      fa <- fx
    } else{
      b <- x
      fb <- fx
    }
  }
  
  # iterasi nilai x sebagai return value
  root <- (a+b)/2
  return(list(`function`=f, root=root, iter=iter))
}

Contoh 7.2 Carilah akar persamaan \(f\left(x \right)=xe^{-x}+1\) pada rentang \(x=\left[-1,0 \right]\) dengan nilai toleransi sebesar \(10^-7\)?

Jawab:

Langkah pertama dalam penghitungan adalah menghitung nilai \(x\) menggunakan Persamaan (7.5).

\[ x=\frac{-1+0}{2}=-0,5 \]

Hitung nilai \(f\left(x \right)\) dan \(f\left(a \right)\).

\[ f\left(x \right)=-0,5.e^{0,5}+1=0,175639 \]

\[ f\left(a \right)=-1.e^{1}+1=-1,71828 \]

Berdasarkan hasil perhitungan diperoleh:

\[ f\left(x \right).f\left(a \right)<0 \]

Sehingga \(b=x\) dan \(f\left(b \right)=f\left(x \right)\). Iterasi dilakukan kembali dengan menggunakan nilai \(b\) tersebut.

Untuk mempersingkat waktu iterasi kita akan menggunakan fungsi root_bisection() pada R. Berikut adalah sintaks yang digunakan:

root_bisection(function(x){x*exp(-x)+1},
               a=-1, b=0)

## $`function`
## function (x) 
## {
##     x * exp(-x) + 1
## }
## <bytecode: 0x000000001d62cab0>
## 
## $root
## [1] -0.5671
## 
## $iter
## [1] 24

Berdasarkan hasil iterasi diperoleh akar persamaan \(x=-2.980232e-08\) dan iterasi yang diperlukan untuk memperolehnya sebanyak \(24\) iterasi.

7.1.3 Metode Regula Falsi

Metode regula falsi merupakan metode yang menyerupai metode biseksi, dimana iterasi dilakukan dengan terus melakukan pembaharuan rentang untuk memperoleh akar persamaan. Hal yang membedakan metode ini dengan metode biseksi adalah pencarian akar didasarkan pada slope (kemiringan) dan selisih tinggi dari kedua titik rentang. Titik pendekatan pada metode regula-falsi disajikan pada Persamaan (7.6).

\[\begin{equation} x=\frac{f\left(b\right).a-f\left(a\right).b}{f\left(b\right)-f\left(a\right)} \tag{7.6} \end{equation}\]

Ilustrasi dari metode regula falsi disajikan pada Gambar 7.6.

Gambar 7.6: Ilustrasi metode regula falsi.

Algoritma Metode Regula Falsi

Definisikan fungsi \(f\left(x \right)\)
Tentukan rentang untuk \(x\) yang berupa batas bawah \(a\) dan batas atas \(b\).
Tentukan nilai toleransi \(e\) dan iterasi maksimum \(N\)
Hitung \(f\left(a \right)\) dan \(f\left(b \right)\)
Untuk iterasi \(i=1\) s/d \(N\)

Hitung nilai \(x\) berdasarkan Persamaan (7.6)
Hitung \(f\left(x \right)\)
Hitung \(error=\left|f\left(x \right) \right|\)
Jika \(f\left(x \right).f\left(a \right)<0\), maka \(b=x\) dan \(f\left(b \right)=f\left(x \right)\). Jika tidak, \(a=x\) dan \(f\left(a \right)=f\left(x \right)\).

Akar persamaan adalah \(x\)

Fungsi root_rf() didasarkan pada langkah-langkah di atas. Sintaks fungsi tersebut adalah sebagai berikut:

root_rf <- function(f, a, b, tol=1e-7, N=100){
  iter <- 1
  fa <- f(a)
  fb <- f(b)
  x <- ((fb*a)-(fa*b))/(fb-fa)
  fx <- f(x)
  
  while(abs(fx)>tol){
    iter <- iter+1
    if(iter>N){
      warning("iterations maximum exceeded")
      break
    }
    if(fa*fx>0){
      a <- x
      fa <- fx
    } else{
      b <- x
      fb <- fx
    }
    x <- (fb*a-fa*b)/(fb-fa)
    fx <- f(x)
  }
  
  # iterasi nilai x sebagai return value
  root <- x
  return(list(`function`=f, root=root, iter=iter))
}

Contoh 7.3 Selesaikan persamaan non-linier pada Contoh 7.2 menggunakan metode regula falsi pada rentang \(x=\left[-1,0 \right]\) dengan nilai toleransi sebesar \(10^-7\)?

Jawab:

Langkah pertama penyelesaian dilakukan dengan mencari nilai \(f\left(a \right)\) dan \(f\left(b \right)\).

\[ f\left(a \right)=-1.e^{1}+1=-1,71828 \] \[ f\left(b \right)=0.e^{0}+1=1 \] Hitung nilai \(x\) dan \(f\left(x \right)\).

\[ x=\frac{\left(1.-1\right)-\left(-1,71828.0\right)}{1+1,71828}=-0.36788 \]

\[ f\left(x \right)=-0.36788.e^{0.36788}+1=0.468536 \]

Berdasarkan hasil perhitungan diperoleh:

\[ f\left(x \right).f\left(a \right)<0 \]

Sehingga \(b=x\) dan \(f\left(b \right)=f\left(x \right)\). Iterasi dilakukan kembali dengan menggunakan nilai \(b\) tersebut.

Untuk mempercepat proses iterasi, kita dapat pula menggunakan fungsi root_rf() pada R. Berikut adalah sintaks yang digunakan:

root_rf(function(x){x*exp(-x)+1},
               a=-1, b=0)

## $`function`
## function (x) 
## {
##     x * exp(-x) + 1
## }
## <bytecode: 0x000000001c7931a8>
## 
## $root
## [1] -0.5671
## 
## $iter
## [1] 15

Berdasarkan hasil perhitungan diperoleh nilai \(x=-0,5671433\) dan jumlah iterasi yang diperlukan adalah \(15\). Jumlah ini lebih sedikit dari jumlah iterasi yang diperlukan pada metode iterasi biseksi yang juga menunjukkan metode ini lebih cepat memperoleh persamaan dibandingkan metode biseksi.

7.2 Metode Terbuka

Metode terbuka merupakan metode yang menggunakan satu atau dua tebakan awal yang tidak memerlukan rentang sejumlah nilai. Metode terbuka terdiri dari beberapa jenis yaitu metode iterasi titik tetap, metode Newton-Raphson, dan metode Secant.

7.2.1 Metode Iterasi Titik Tetap

Metode iterasi titik tetap merupakan metode penyelesaian persamaan non-linier dengan cara menyelesaikan setiap variabel \(x\) yang ada dalam suatu persamaan dengan sebagian yang lain sehingga diperoleh \(x=g\left(x \right)\) untuk masing-masing variabel \(x\). Sebagai contoh, untuk menyelesaikan persamaan \(x+e^{x}=0\), maka persamaan tersebut perlu diubah menjadi \(x=e^x\) atau \(g\left(x \right)=e^x\). Secara grafis metode ini diilustrasikan seperti Gambar 7.7.

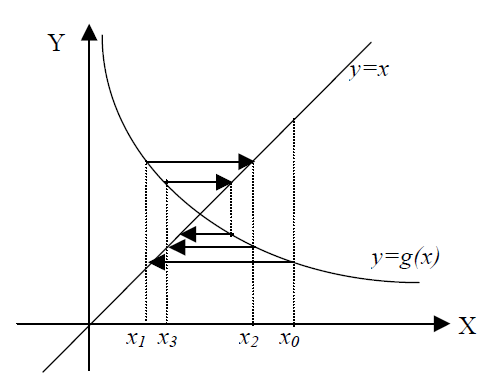
Gambar 7.7: Ilustrasi metode iterasi titik tetap.

Algoritma Metode Iterasi Titik Tetap

Definisikan \(f\left(x \right)\) dan \(g\left(x \right)\)
Tentukan nilai toleransi \(e\) dan iterasi masimum (N)
Tentukan tebakan awal \(x_0\)
Untuk iterasi \(i=1\) s/d \(N\) atau \(f\left(x_iterasi \right)\ge e \to x_i=g\left(x_{i-1} \right)\), Hitung \(f\left(x_i \right)\)
Akar persamaan adalah \(x\) terakhir yang diperoleh

FUngsi root_fpi() dapat digunakan untuk melakukan iterasi dengan argumen fungsi berupa persamaan non-linier, nilai tebakan awal, nilai toleransi, dan jumlah iterasi maksimum. Berikut adalah sintaks fungsi tersebut:

root_fpi <- function(f, x0, tol=1e-7, N=100){
  iter <- 1
  xold <- x0
  xnew <- f(xold)
  
  while(abs(xnew-xold)>tol){
    iter <- iter+1
    if(iter>N){
      stop("No solutions found")
    }
    xold <- xnew
    xnew <- f(xold)
  }
  
  root <- xnew
  return(list(`function`=f, root=root, iter=iter))
}

Contoh 7.4 Selesaikan persamaan non-linier pada Contoh 7.2 menggunakan metode iterasi titik tetap?

Jawab:

Untuk menyelesaikan persamaan non-linier tersebut kita perlu mentransformasi persamaan non-linier tersebut terlebih dahulu.

\[ xe^{-x}+1=0\ \to x=-\frac{1}{e^{-x}} \]

Untuk tebakan awal digunakan nilai \(x=-1\)

\[ x_1 = -\frac{1}{e^{1}}=-2,718282 \]

Nilai \(x\) tersebut selanjutnya dijadikan nilai input pada iterasi selanjutnya:

\[ x_2 = -\frac{1}{e^{2,718282}}=-0,06598802 \]

iterasi terus dilakukan sampai diperoleh \(\left| x_{i+1}-x_i \right|\le e\).

Untuk mempercepat proses iterasi kita dapat menggunakan bantuan fungsi root_fpi(). Berikut adalah sintaks yang digunakan:

root_fpi(function(x){-1/exp(-x)}, x0=-1)

## $`function`
## function (x) 
## {
##     -1/exp(-x)
## }
## <bytecode: 0x0000000018c9ee40>
## 
## $root
## [1] -0.5671
## 
## $iter
## [1] 29

Berdasarkan hasil iterasi diperoleh nilai \(x=-0,5671433\) dengan jumlah iterasi yang diperlukan sebanyak \(29\) kali. Jumlah iterasi akan bergantung dengan nilai tebakan awal yang kita berikan. Semakin dekat nilai tersebut dengan akar, semakin cepat nilai akar diperoleh.

7.2.2 Metode Newton-Raphson

Metode Newton-Raphson merupakan metode penyelesaian persamaan non-linier dengan menggunakan pendekatan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien. titik pendekatan dinyatakan pada Persamaan (7.7).

\[\begin{equation} x_{n+1}=x_n-\frac{f\left(x_n\right)}{f'\left(x_n\right)} \tag{7.7} \end{equation}\]

Ilustrasi metode Newton-Raphson disajikan pada Gambar 7.8.

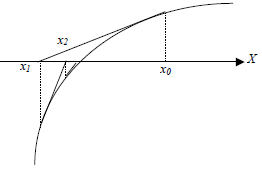
Gambar 7.8: Ilustrasi metode Newton-Raphson.

Algoritma Metode Newton-Raphson

Definisikan \(f\left(x \right)\) dan \(f'\left(x \right)\)
Tentukan nilai toleransi \(e\) dan iterasi masimum (N)
Tentukan tebakan awal \(x_0\)
Hitung \(f\left(x_0 \right)\) dan \(f'\left(x_0 \right)\)
Untuk iterasi \(i=1\) s/d \(N\) atau \(\left|f\left(x \right) \right|\ge e\), hitung \(x\) menggunakan Persamaan (7.7)
Akar persamaan merupakan nilai \(x_i\) terakhir yang diperoleh.

Fungsi root_newton() merupakan fungsi yang dibuat menggunakan algoritma di atas. Fungsi tersebut dituliskan pada sintaks berikut:

root_newton <- function(f, fp, x0, tol=1e-7, N=100){
  iter <- 0
  xold<-x0
  xnew <- xold + 10*tol
  
  while(abs(xnew-xold)>tol){
    iter <- iter+1
    if(iter>N){
      stop("No solutions found")
    }
    xold<-xnew
    xnew <- xold - f(xold)/fp(xold)  
  }
  
  root<-xnew
  return(list(`function`=f, root=root, iter=iter))
}

Contoh 7.5 Selesaikan persamaan non-linier \(x-e^{-x}=0\) menggunakan metode Newton-Raphson?

Jawab:

Untuk dapat menggunakan metode Newton-Raphson, terlebih dahulu kita perlu memperoleh turunan pertama dari persamaan tersebut.

\[ f\left(x\right)=x-e^{-x}\to f'\left(x\right)=1+e^{-x} \]

Tebakan awal yang digunakan adalah \(x=0\).

\[ f\left(x_0\right)=0-e^{-0}=-1 \] \[ f'\left(x_0\right)=1+e^{-0}=2 \]

Hitung nilai \(x\) baru:

\[ x_1=x_0-\frac{f\left(x_0\right)}{f'\left(x_0\right)}=0-\frac{-1}{2}=0,5 \]

Untuk mempercepat proses iterasi, kita dapat menggunakan fungsi root_newton(). Berikut adalah sintaks yang digunakan:

root_newton(function(x){x-exp(-x)},
            function(x){1+exp(-x)},
              x0=0)

## $`function`
## function (x) 
## {
##     x - exp(-x)
## }
## <bytecode: 0x000000001c59e158>
## 
## $root
## [1] 0.5671
## 
## $iter
## [1] 5

Berdasarkan hasil iterasi diperoleh akar penyelesaian persamaan non-linier adalah \(x=0,5671433\) dengan jumlah iterasi yang diperlukan adalah \(5\) iterasi.

Dalam penerapannya metode Newton-Raphson dapat mengalami kendala. Kendala yang dihadapi adalah sebagai berikut:

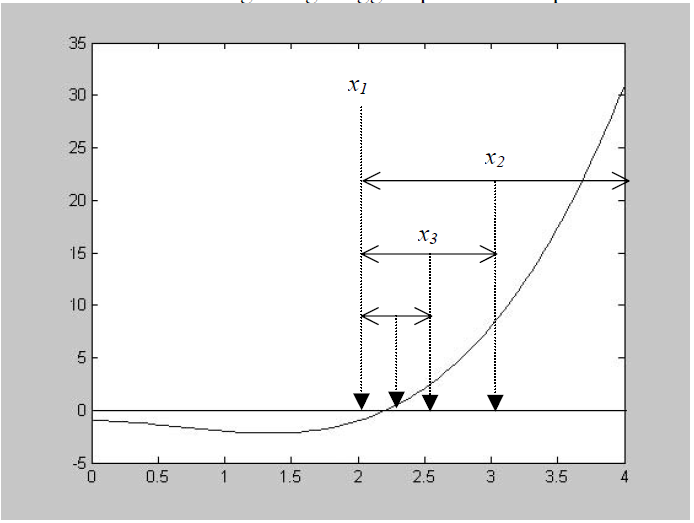
titik pendekatan tidak dapat digunakan jika merupakan titik ekstrim atau titik puncak. Hal ini disebabkan pada titik ini nilai \(f'\left(x \right)=0\). Untuk memahaminya perhatikan ilustasi yang disajikan pada Gambar 7.9. Untuk menatasi kendala ini biasanya titik pendekatan akan digeser.

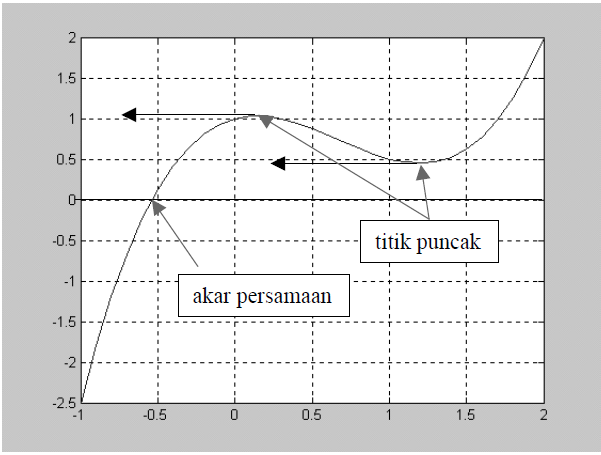
Gambar 7.9: Ilustrasi titik pendekatan di titik puncak.

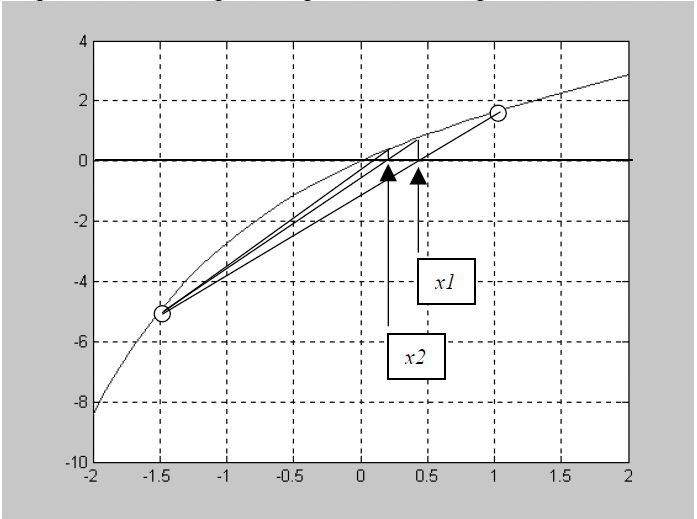
Sulit memperoleh penyelesaian ketika titik pendekatan berada diantara 2 titik stasioner. Untuk memahami kendala ini perhatikan Gambar 7.10. Untuk menghindarinya, penentuan titik pendekatan dapat menggunakan bantuan metode tabel.

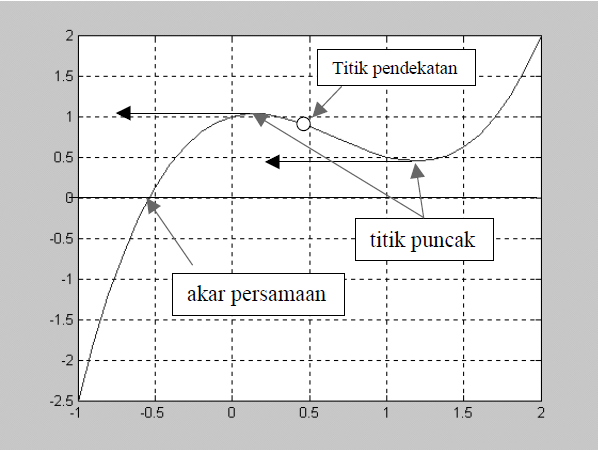
Gambar 7.10: Ilustrasi titik pendekatan diantara 2 titik stasioner.

Turunan persamaan sering kali sulit untuk diperoleh (tidak dapat dikerjakan dengan metode analitik).

7.2.3 Metode Secant

Metode Secant merupakan perbaikan dari metode regula-falsi dan Newton Raphson, dimana kemiringan dua titik dinyatakan secara diskrit dengan mengambil bentuk garis lurus yang melalui satu titik. Persamaan yang dihasilkan disajikan pada Persamaan (7.8).

\[\begin{equation} y-y_0=m\left(x-x_0\right) \tag{7.8} \end{equation}\]

Nilai \(m\) merupakan transformasi persamaan tersebut.

\[\begin{equation} m_n=\frac{f\left(x_n\right)-f\left(x_{n-1}\right)}{x_n-x_{n-1}} \tag{7.9} \end{equation}\]

Bila \(y=f\left(x\right)\) dan \(y_n\) dan \(x_n\) diketahui, maka titik ke \(n+1\) adalah:

\[\begin{equation} y_{n+1}-y_n=m_n\left(x_{n+1}-x_n\right) \tag{7.10} \end{equation}\]

Bila titik \(x_{n+1}\) dianggap akar persamaan maka nilai \(y_{n+1}=0\), sehingga diperoleh:

\[\begin{equation} -y_n=m_n\left(x_{n+1}-x_n\right) \tag{7.11} \end{equation}\]

\[\begin{equation} \frac{m_nx_n-y_n}{m_n}=x_{n+1} \tag{7.12} \end{equation}\]

atau

\[\begin{equation} x_{n+1}=x_n-y_n\frac{1}{m_n} \tag{7.13} \end{equation}\]

\[\begin{equation} x_{n+1}=x_n-f\left(x_n\right)\frac{x_n-x_{n+1}}{f\left(x_n\right)-f\left(x_{n+1}\right)} \tag{7.14} \end{equation}\]

Berdasarkan Persamaan (7.14) diketahui bahwa untuk memperoleh akar persamaan diperlukan 2 buah titik pendekatan. Dalam buku ini akan digunakan titik pendekatan kedua merupakan titik pendekatan pertama ditambah sepuluh kali nilai toleransi.

\[\begin{equation} x_1=x_0+10*tol \tag{7.15} \end{equation}\]

Algoritma Metode Secant

Definisikan \(f\left(x \right)\) dan \(f'\left(x \right)\)
Tentukan nilai toleransi \(e\) dan iterasi masimum (N)
Tentukan tebakan awal \(x_0\) dan \(x_1\)
Hitung \(f\left(x_0 \right)\) dan \(f\left(x_1 \right)\)
Untuk iterasi \(i=1\) s/d \(N\) atau \(\left|f\left(x \right) \right|\ge e\), hitung \(x\) menggunakan Persamaan (7.14)
Akar persamaan adalah nilai x yang terakhir.

Fungsi root_secant() merupakan fungsi yang penulis buat untuk melakukan iterasi menggunakan metode Secant. Berikut merupakan sintaks dari fungsi tersebut:

root_secant <- function(f, x, tol=1e-7, N=100){
  iter <- 0
  
  xold <- x
  fxold <- f(x)
  x <- xold+10*tol
  
  while(abs(x-xold)>tol){
    iter <- iter+1
    if(iter>N)
      stop("No solutions found")
    
    fx <- f(x)
    xnew <- x - fx*((x-xold)/(fx-fxold))
    xold <- x
    fxold <- fx
    x <- xnew
  }
  
  root<-xnew
  return(list(`function`=f, root=root, iter=iter))
}

Contoh 7.6 Selesaikan persamaan non-linier pada Contoh 7.5 menggunakan metode Secant?

Jawab:

Untuk menyelesaikan persamaan tersebut digunakan nilai pendekatan awal \(x_0=0\) dan \(x_1=0+10*10^{-7}=10^{-6}\).

\[ f\left(x_0 \right)=0-e^{-0}=-1 \]

\[ f\left(x_1 \right)=10^{-6}-e^{-10^{-6}}=-0,999998 \]

Hitung nilai \(x_2\) dan \(f\left(x_2 \right)\).

\[ x_2=0+0,999998\frac{10^{-6}-0}{-0,999998+1}=0,499999 \]

Untuk mempercepat proses iterasi kita dapat menggunakan fungsi root_secant() pada R. Berikut sintaks yang digunakan:

root_secant(function(x){x-exp(-x)}, x=0)

## $`function`
## function (x) 
## {
##     x - exp(-x)
## }
## <bytecode: 0x000000001b4fc6b0>
## 
## $root
## [1] 0.5671
## 
## $iter
## [1] 6

Berdasarkan hasil iterasi diperoleh nilai akar penyelesaian adalah \(x=0,5671433\) dengan iterasi dilakukan sebanyak \(6\) kali.

Secara umum metode Secant menawarkan sejumlah keuntungan dibanding metode lainnya. Pertama, seperti metode Newton-Raphson dan tidak seperti metode tertutup lainnya, metode ini tidak memerlukan rentang pencarian akar penyelesaian. Kedua, tidak seperti metode Newton-Raphson, metode ini tidak memerlukan pencarian turunan pertama persamaan non-linier secara analitik, dimana tidak dapat dilakukan otomasi pada setiap kasus.

Adapun kerugian dari metode ini adalah berpotensi menghasilkan hasil yang tidak konvergen sama seperti metode terbuka lainnya. Selain itu, kecepatan konvergensinya lebih lambat dibanding metode Newton-Raphson.

7.3 Penyelesaian Persamaan Non-Linier Menggunakan Fungsi `uniroot` dan `uniroot.all`

Paket base pada R menyediakan fungsi uniroot() untuk mencari akar persamaan suatu fungsi pada rentang spesifik. Fungsi ini menggunakan metode Brent yaitu kombinasi antara root bracketing, biseksi, dan interpolasi invers kuadrat. Format fungsi tersebut secara sederhana adalah sebagai berikut:

uniroot(f, interval, tol=.Machine$double.eps^0.25, 
        maxiter=1000)

Catatan:

f: persamaan non-linier

interval: vektor interval batas bawah dan atas

tol: nilai toleransi

maxiter: iterasi maksimum

Berikut adalah contoh penerapan fungsi uniroot():

uniroot(function(x){x*exp(-x)+1},
        interval=c(-1,0), tol=1e-7)

## $root
## [1] -0.5671
## 
## $f.root
## [1] 1.533e-08
## 
## $iter
## [1] 7
## 
## $init.it
## [1] NA
## 
## $estim.prec
## [1] 5e-08

Berdasarkan hasil iterasi diperoleh akar persamaan tersebut adalah \(-0,5671433\) dengan jumlah iterasi sebanyak \(7\) iterasi dan tingkat presisi sebesar \(5e-08\).

Fungsi lain yang dapat digunakan untuk mencari akar persamaan adalah uniroot.all() dari paket rootSolve. Fungsi ini mengatasi kelemahan dari uniroot(), dimana uniroot() tidak bekerja jika fungsi hanya menyentuh dan tidak melewati sumbu nol \(y=0\). Untuk memahaminya perhatikan contoh berikut:

uniroot(function(x){sin(x)+1}, c(-pi,0))

Bandingkan dengan sintaks berikut:

uniroot(function(x){sin(x)+1}, c(-pi,-pi/2))

## $root
## [1] -1.571
## 
## $f.root
## [1] 0
## 
## $iter
## [1] 0
## 
## $init.it
## [1] NA
## 
## $estim.prec
## [1] 0

Untuk menggunakan fungsi uniroot.all(), jalankan sintaks berikut:

library(rootSolve)

Jalankan kembali fungsi dan rentang di mana uniroot() tidak dapat bekerja:

uniroot.all(function(x){sin(x)+1}, c(-pi,0))

## [1] -1.571

7.4 Akar Persamaan Polinomial Menggunakan Fungsi `polyroot`

Fungsi polyroot() pada paket base dapat digunakan untuk memperoleh akar dari suatu polinomial. Algortima yang digunakan dalam fungsi tersebut adalah algoritma Jenkins dan Traub.

Untuk dapat menggunakannya kita hanya perlu memasukkan vektor koefisien dari polinomial. Pengisian elemen dalam vektor dimulai dari variabel dengan pangkat tertinggi menuju variabel dengan pangkat terendah. Berikut adalah contoh bagaimana fungsi polyroot() digunakan untuk mencari akar polinomial \(f\left(x\right)=x^2+1\):

polyroot(c(1,0,1))

## [1] 0+1i 0-1i

Contoh lainnya adalah mencari akar polinomial \(f\left(x\right)=4x^2+5x+6\):

polyroot(c(4,5,6))

## [1] -0.4167+0.7022i -0.4167-0.7022i

Pembaca dapat mencoba membuktikan hasil yang diperoleh tersebut menggunakan metode analitik.

7.5 Studi Kasus

Penerapan penyelesaian sistem persamaan non-linier banyak dijumpai dalam berbagai kasus di bidang lingkungan. Pada bagian ini penulis tidak akan menjelaskan seluruhnya. Penulis hanya akan menjelaskan penerapannya pada sebuah persamaan yaitu Hukum Bernoulli.

7.5.1 Persamaan Van Der Walls

7.5.2 Hukum Bernoulli

Misalkan terdapat sebuah saluran dengan penampang sesuai dengan Gambar 7.11.

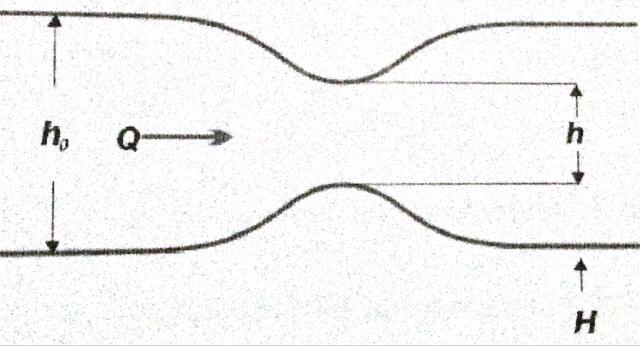
Gambar 7.11: Aliran fluida pada sebuah pipa.

Berdasarkan hukum Bernoulli, maka diperoleh persamaan berikut:

\[\begin{equation} \frac{Q^2}{2gb^2h_0^2}+h_0=\frac{Q^2}{2gb^2h^2}+h+H \tag{7.16} \end{equation}\]

Persamaan tersebut dapat dilakukan transformasi menjadi persamaan berikut:

\[\begin{equation} f\left(h\right)=h^3+\left(H-\frac{Q^2}{2gb^2h_0^2}-h_0\right)h^2+\frac{Q^2}{2gb^2}=0 \tag{7.17} \end{equation}\]

Data-data terkait saluran tersebut adalah sebagai berikut:

\(Q=1,2\ \frac{m^3}{\det\ }\) = volume aliran fluida tiap satuan waktu
\(g=9,81\ \frac{m}{s^2}\) =percepatan gravitasi
\(b=1,8\ m\) =lebar pipa
\(h_0=0,6\ m\) =ketinggian air maksimum
\(H=0,075\ m\) =tinggi pelebaran pipa
\(h\) = ketinggian air

Kita dapat menggunakan pendekatan numerik untuk menentukan \(h\). Pada studi kasus ini tidak dijelaskan lokasi dimana akar penyelesaian berada, sehingga metode terbuka seperti Secant cukup sesuai untuk menyelesaikannya:

Berikut adalah persamaan yang baru setelah seluruh data dimasukkan kedalam tiap variabelnya:

\[ f\left(h\right)=h^3+\left(0,075-\frac{1,2^2}{2\times9,81\times1,8^2\times0,6^2}-0,6\right)h^2+\frac{1,2^2}{2\times9,81\times1,8^2}=0 \]

Untuk penyelesaiannya penulis akan memberikan tebakan awal nilai \(h=h_0=0,6\). Berikut adalah sintaks penyelesaian menggunakan metode secant:

f <- function(h){
  (h^3) + ((0.075-((1.2^2)/(2*9.81*(1.8^2)*(0.6^2))))*h^2)+ (1.2^2/(2*9.81*(1.8^2)))
}
root_secant(f, 0.6)

## $`function`
## function (h) 
## {
##     (h^3) + ((0.075 - ((1.2^2)/(2 * 9.81 * (1.8^2) * (0.6^2)))) * 
##         h^2) + (1.2^2/(2 * 9.81 * (1.8^2)))
## }
## <bytecode: 0x000000001d1483f0>
## 
## $root
## [1] -0.287
## 
## $iter
## [1] 26

Berdasarkan hasil perhitungan diperoleh nilai \(h=-0,2870309\) atau ketinggian air sekitar \(0,3\ m\) dengan jumlah iterasi sebanyak \(26\) kali.

Pembaca dapat mencoba menggunakan metode lain seperti metode tertutup. Untuk dapat melakukannya, pembaca perlu memperoleh rentang lokasi akar persamaan tersebut berada menggunakan metode tabel.

7.6 Referensi

Atmika, I.K.A. 2016. Diktat Mata Kuliah: Metode Numerik. Jurusan Teknik Mesin Universitas Udayana.
Bloomfield, V.A. 2014. Using R for Numerical Analysis in Science and Engineering. CRC Press
Howard, J.P. 2017. Computational Methods for Numerical Analysis with R. CRC Press.
Jones, O. Maillardet, R. Robinson, A. 2014. Introduction to Scientific Programming and Simulation Using R. CRC Press
Kreyszig, E. 2011. Advanced Engineering Mathematics, 10th Edition. John Wiley & Sons.
Sanjaya, M. 2015. Metode Numerik Berbasis Phython. Penerbit Gava Media: Yogyakarta.
Sudiadi dan Teguh R. 2015. Metode Numerik. STMIK

7.7 Latihan

Temukan akar persamaan dari persamaan non-linier \(f\left(x\right)=x^3-2x+2\) menggunakan metode terbuka dengan \(x_0=0\) dan \(x_0=\frac{1}{2}\)!
Apakah kelebihan dari metode tertutup (contoh: metode biseksi) dibanding metode terbuka (contoh: Newton-Raphson)? (catatan: pembaca dapat pula mencari dari referensi lainnya)
Temukan akar persamaan dari persamaan \(f\left(x\right)=\frac{sin\left(x\right)}{x}\) dengan rentang pencarian \(x=0,5\) dan \(x=1\)!
Pada kondisi apakah metode Secant lebih dipilih dibanding metode Newton-Raphson?
Modifikasilah fungsi root_bisection() dan root_rf() sehingga kita tidak perlu memasukkan argumen a dan b dan hanya perlu memasukkan satu vektor interval kedalam fungsi tersebut! (contoh: interval=c(a,b))

Chapter 7 Akar Persamaan Non-Linier

7.1 Metode Tertutup

7.1.1 Metode Tabel

7.1.2 Metode Biseksi

7.1.3 Metode Regula Falsi

7.2 Metode Terbuka

7.2.1 Metode Iterasi Titik Tetap

7.2.2 Metode Newton-Raphson

7.2.3 Metode Secant

7.3 Penyelesaian Persamaan Non-Linier Menggunakan Fungsi uniroot dan uniroot.all

7.4 Akar Persamaan Polinomial Menggunakan Fungsi polyroot

7.5 Studi Kasus

7.5.1 Persamaan Van Der Walls

7.5.2 Hukum Bernoulli

7.6 Referensi

7.7 Latihan

7.3 Penyelesaian Persamaan Non-Linier Menggunakan Fungsi `uniroot` dan `uniroot.all`

7.4 Akar Persamaan Polinomial Menggunakan Fungsi `polyroot`