Chapter 10 Persamaan Diferensial

Persamaan diferensial merupakan persoalan matematis yang sering dijumpai dalam bidang teknik lingkungan. Sering kali suatu persamaan diferensial tidak dapat diselesaikan secara analitik sehingga diperlukan metode numerik untuk menyelesaikannya. Pada Chapter 10, kita akan membahas masalah-masalah dalam persamaan diferensial dan metode penyelesaiannya. Adapun yang akan dibahas pada Chapter 10 kali ini antara lain:

• Initial value problems
• Sistem persamaan diferensial
• Persamaan diferensial parsial

10.1 Initial value problems

Initial value problems merupakan permasalahan yang sering ditemukan pada proses dekomposisi zat kimia atau polutan dalam reaktor. Penyelesaiaan persamaan diferensial biasanya dipersulit dengan tidak tersedianya informasi yang cukup untuk menyelesaikannya.Sebuah persamaan diferensial \(f'\left(x,\dots\right)\) merupakan hasil diferensiasi beberapa fungsi \(f\left(x,\dots\right)\). Proses penyelesaian persamaan diferensial, dan menemukan nilai \(f \left(x,\dots\right)\) untuk beberapa nilai x,… tidak dimungkinkan karena integral dari \(f'\left(x,\dots\right)\) hanya digambarkan bentuk umum. Pergeseran vertikal, atas atau bawah, tidak diketahui. Pergeseran vertikal ini menghasilkan konstanta integrasi.

Selama proses diferensiasi, nilai apapun dari proses pergeseran vertikal (integrasi) akan hilang sebagai akibat dari eliminasi konstanta yang memiliki turunan 0. Kita biasa melakukannya ketika mengintegrasikan fungsi dengan menambahkan konstanta \(+ C\) pada proses integrasi ke integral yang tidak terbatas. Hal ini terkadang bukan menjadi permasalahan sebab jika menemukan nilai integrasi pada suatu batas tertentu syarat \(+ C\) dibatalkan dan konstanta integrasi tidak diperlukan.

Untuk persamaan diferensial biasa, tidak ada pembatalan yang nyaman, yang mengarah ke initial value problems. Initial value problems memberikan nilai \(f\left(x_0,\dots\right)\), di mana \(x_0\) biasanya bernilai 0, meski tidak diharuskan. Nilai awal ini memberikan informasi yang cukup untuk menyelesaikan persamaan dan menemukan nilai aktual dari \(f\left(x,\dots\right)\) untuk sejumlah nilai \(x\). Terdapat beberapa metode yang akan dibahas pada Chapter 10.1, antara lain:

• Metode Euler
• Metode Heun
• Metode Titik Tengah
• Metode Runge-Kutta Orde 4
• Metode multistep linier

10.1.1 Metode Euler

Metode Euler merupakan metode paling sederhana yang diturunkan dari deret Taylor. Penyelesaian initial value problems menggunakan metode Euler dilakukan melalui Persamaan (10.1).

\[\begin{equation} y_{i+1}=y_i+f\left(x_i,y_i\right)h \tag{10.1} \end{equation}\]

dimana \(i\) merupakan tahapan iterasi.

---

Algoritma Metode Euler

1. Tentukan titik awal integrasi \(x_0\) dan \(y_0\).
2. Tentukan jumlah iterasi \(n\) dan step size \(h\) yang digunakan.
3. Lakukan integrasi menggunakan Persamaan (10.1).

---

Algoritma tersebut, selanjutnya dapat disusun ke dalam sebuah fungsi R. Fungsi tersebut adalah sebagai berikut:

euler <- function(f, x0, y0, h, n){
  x <- x0
  y <- y0
  
  for(i in 1:n){
    y0 <- y0 + h*f(x0, y0)
    x0 <- x0 + h
    x <- c(x,x0)
    y <- c(y, y0)
  }
  
  return(data.frame(x=x, y=y))
}

Contoh 10.1 Selesaikan persamaan diferensial di bawah ini, jika diketahui f(0)=1 menggunakan h=0,05 dan n=100!

\[ f'\left(x,y\right)=\frac{y}{2x+1} \]

Jawab:

Penyelesaian secara analitik persamaan tersebut untuk nilai \(f\left(0\right)=1\) sebagai berikut:

\[ f\left(x\right)=\sqrt{2x+1} \]

Secara numerik persamaan tersebut dapat diselesaikan sebagai berikut:

iterasi 1

\[ y\left(0,5\right)=1+0,05\times\frac{1}{\left(2\cdot 0\right)+1}=1,05 \]

iterasi 2

\[ y\left(0,1\right)=1,05+0,05\times\frac{1}{\left(2\cdot0,05\right)+1}=1.097727 \]

Kita dapat juga menggunakan fungsi euler() untuk menyelesaikan persamaan tersebut secara numerik. Hasil yang diperoleh selanjutnya diplotkan dengan hasil yang diperoleh menggunakan metode analitik. Berikut adalah sintaks yang digunakan:

# metode numerik
f1 <- function(x,y){y/(2*x+1)}
num <- euler(f1, x0=0, y0=1, h=0.05, n=100)

# metode analitik
f2 <- function(x){sqrt(2*x+1)}
x0 <- 0
y0 <- 1
x <- x0
y <- y0

for(i in 1:100){
  y0 <- f2(x0+0.05)
  x0 <- x0+0.05
  x <- c(x, x0)
  y <- c(y, y0)
}
true <- data.frame(x=x, y=y)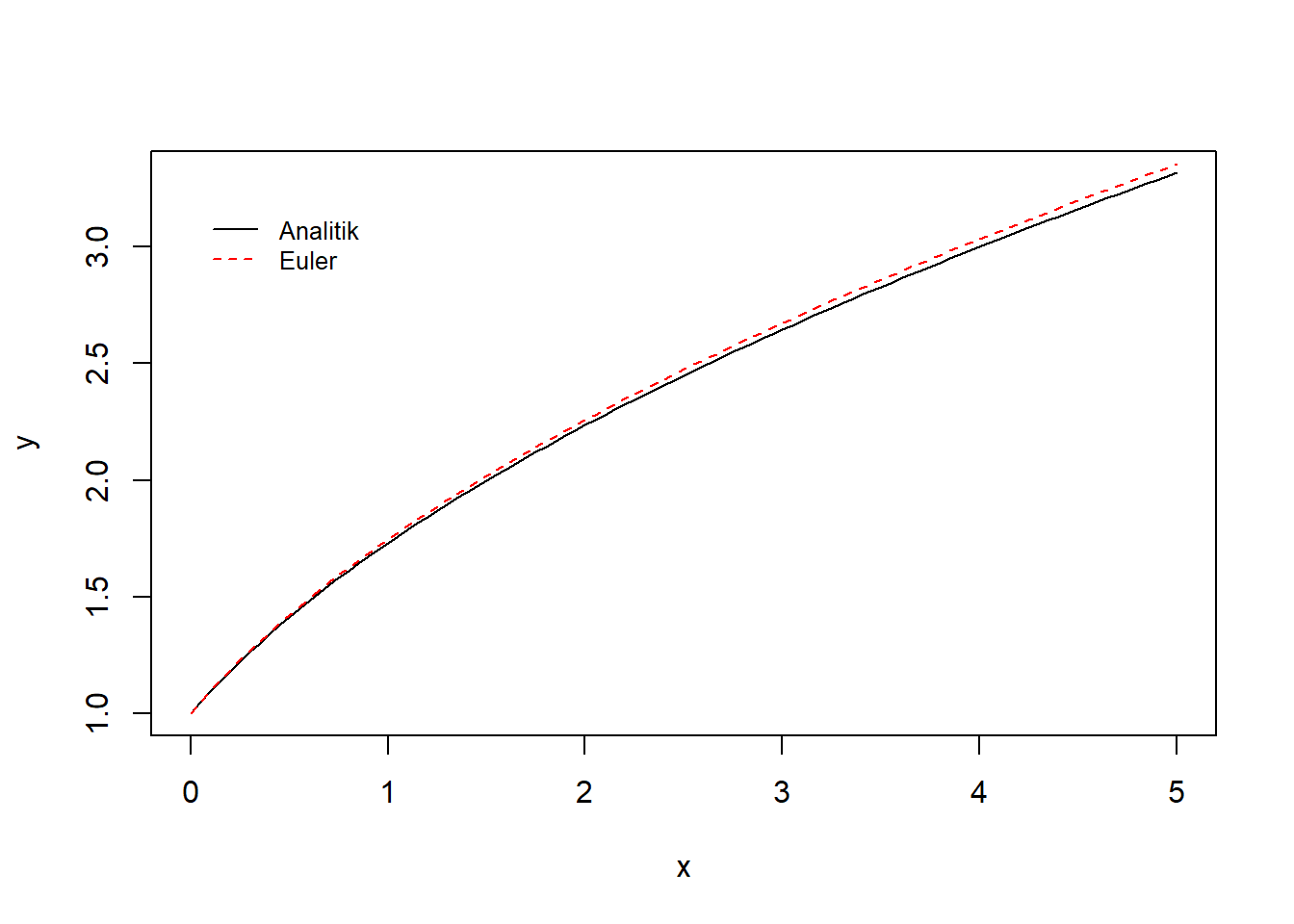

Gambar 10.1: Visualisasi integrasi numerik dengan metode Euler dan metode analitik

Berdasarkan hasil visualisasi dapat dilihat bahwa metode Euler dapat dengan baik memberikan pendekatan nilai integrasi persamaan. Pembaca dapat mencoba untuk melakukan simulasi kembali dengan nilai \(h\) yang lebih kecil.

10.1.2 Metode Heun

Metode Heun merupakan salah satu peningkatan dari metode Euler. Metode ini melibatkan 2 buah persamaan. Persamaan pertama disebut sebagai persamaan prediktor yang digunakan untuk memprediksi nilai integrasi awal (Persamaan (10.2)). Persamaan kedua disebut sebagai persamaan korektor yang mengoreksi hasil integrasi awal (Persamaan (10.3)). Metode Heun pada Chapter ini merupakan metode prediktor-korektor satu tahapan. Akurasi integrasi dapat ditingkatkan dengan melakukan koreksi ulang terhadap nilai koreksi semula menggunakan persamaan kedua.

\[\begin{equation} y_{i+1}^{0}=y_i+f\left(x_i,y_i\right)h \tag{10.2} \end{equation}\]

\[\begin{equation} y_{i+1}=y_i+\frac{f\left(x_i,y_i\right)+f\left(x_{i+1},y_{i+1}^0\right)}{2}h \tag{10.3} \end{equation}\]

---

Algoritma Metode Heun

1. Tentukan titik awal integrasi \(x_0\) dan \(y_0\).
2. Tentukan jumlah iterasi \(n\) dan step size \(h\) yang digunakan.
3. Lakukan prediksi nilai awal dengan Persamaan (10.2).
4. Lakukan koreksi nilai awal menggunakan Persamaan (10.3).
5. Lakukan koreksi terhadap nilai koreksi yang dihasilkan sebelumnya menggunakan Persamaan (10.3).

---

Kita dapat membangun sebuah fungsi yang dapat melakukan proses integrasi menggunakan metode Heun. Berikut adalah sintaks yang digunakan:

heun <- function(f, x0, y0, h, n, iter=1){
  x <- x0
  y <- y0
  
  for(i in 1:n){
    ypred0 <- f(x0,y0)
    ypred1 <- y0 + h*ypred0
    ypred2 <- f(x0+h,ypred1)
    ykor <- y0 + h*(ypred0+ypred2)/2
    if(iter!=1){
      for(i in 1:iter){
        ykor <- y0 + h*(ypred0+f(x0+h,ykor))/2
      }
    }
    y0 <- ykor
    x0 <- x0 + h
    x <- c(x, x0)
    y <- c(y, y0)
  }
  
  return(data.frame(x=x,y=y))
}

Contoh 10.2 Selesaikan kembali persamaan yang ditampilkan pada Contoh 10.1 menggunakan metode Heun!

Jawab:

Contoh perhitungan secara manual menggunakan metode Heun untuk sekali iterasi adalah sebagai berikut:

\[ f'\left(0;1\right)=\frac{1}{\left(2\cdot 0\right)+1}=1 \]

\[ y_{1}^0=1+0,05\cdot1=1,05 \]

\[ y'_1=f'\left(0,05;1,05\right)=\frac{1,05}{\left(2\cdot 0,05\right)+1}=0,9545455 \]

\[ y_1=1+0,05\cdot\frac{1+0,9545455}{2}=1,047727 \]

Penyelesaian persamaan tersebut menggunakan fungsi heun() dengan iterasi pada nilai koreksi sebanyak 1 kali disajikan pada sintaks berikut:

num <- heun(f1, x0=0, y0=1, h=0.05, n=100)

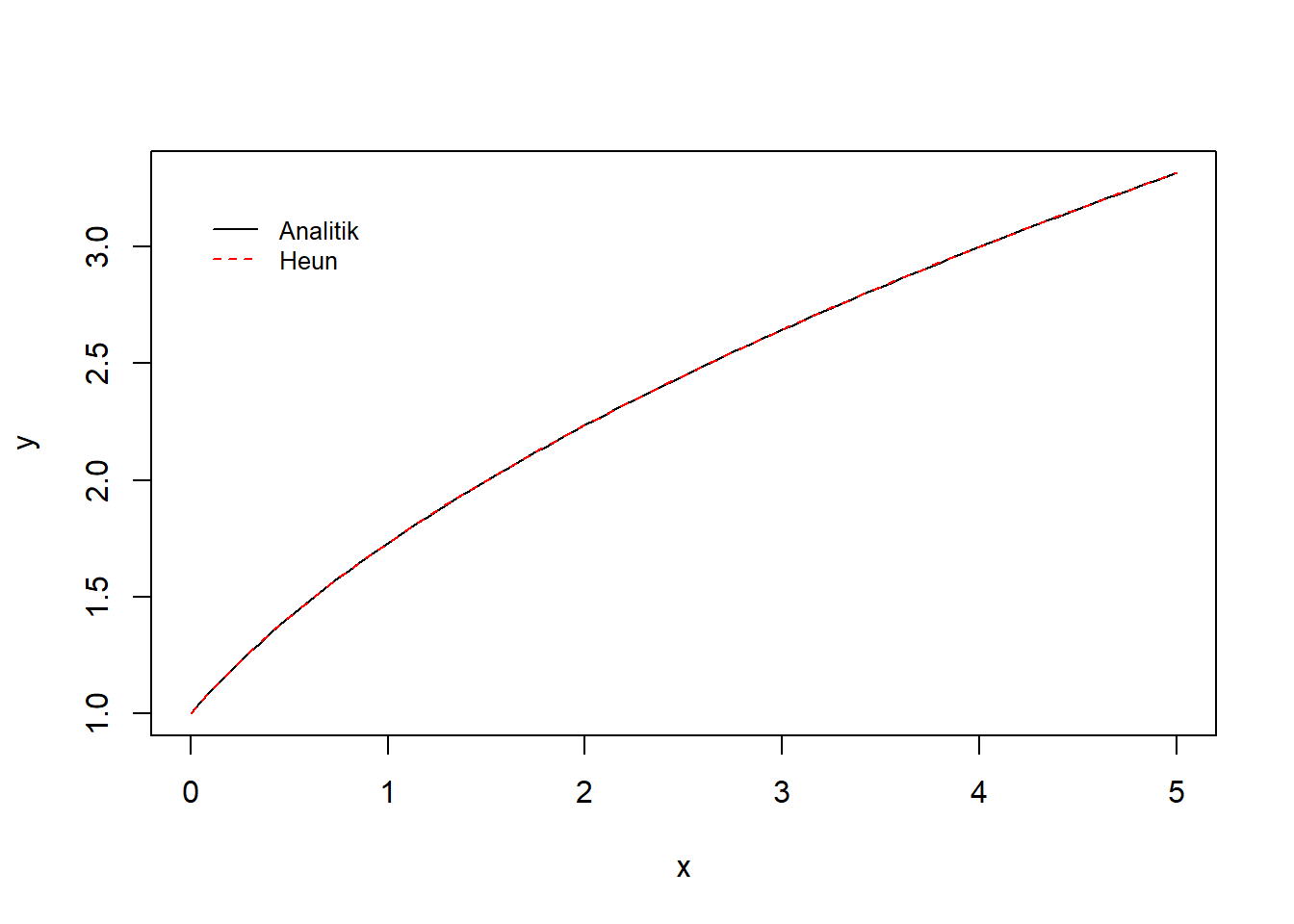
Gambar 10.2: Visualisasi integrasi numerik dengan metode Heun dan metode analitik

10.1.3 Metode Titik Tengah

Metode titik tengah menggunakan setengah step size pada metode Euler untuk melakukan estimasi terhadap integral suatu persamaan diferensial. Metode ini melakukan perhitungan melalui dua tahapan yaitu: menghitung nilai estimasi integral pada setengah step size(Persamaan (10.4)) dan menghitung nilai integral menggunkan hasil perhitungan setengah step size sebelumnya (Persamaan (10.5)).

\[\begin{equation} y_{i+\frac{1}{2}}=y_i+f\left(x_i,y_i\right)\frac{h}{2} \tag{10.4} \end{equation}\]

\[\begin{equation} y_{i+1}=y_i+f\left(x_{i+\frac{1}{2}},y_{i,\frac{1}{2}}\right)h \tag{10.5} \end{equation}\]

---

Algoritma Metode Tengah

1. Tentukan titik awal integrasi \(x_0\) dan \(y_0\).
2. Tentukan jumlah iterasi \(n\) dan step size \(h\) yang digunakan.
3. Lakukan integrasi pada setengah tahapan iterasi menggunakan Persamaan (10.4).
4. Lakukan iterasi pada setengah tahapan selanjutnya menggunakan Persamaan (10.5).

---

Berdasarkan algoritma tersebut, kita dapat membangun sebuah fungsi pada R yang adapat digunakan untuk menyelesaikan persamaan diferensial menggunakan metode titik tengah. Berikut adalah sintaks yang digunakan:

midpt <- function(f, x0, y0, h, n){
  x <- x0
  y <- y0
  
  for(i in 1:n){
    s1 <- y0 + f(x0,y0) * h/2
    s2 <- h * f(x0+h/2,s1)
    y0 <- y0 + s2
    x0 <- x0 + h
    x <- c(x, x0)
    y <- c(y, y0)
  }
  
  return(data.frame(x=x,y=y))
}

Contoh 10.3 Selesaikan kembali persamaan yang ditampilkan pada Contoh 10.1 menggunakan metode titik tengah!

Jawab:

Contoh perhitungan secara manual menggunakan metode titik tengah untuk sekali iterasi adalah sebagai berikut:

\[ y_{\frac{1}{2}}=1+\frac{1}{\left(2\cdot 0\right)+1}\cdot\frac{0,05}{2}=1,025 \]

\[ y_{1}=1+\frac{1,025}{\left(2\cdot 0,025\right)+1}\cdot0,05=1,0488 \]

Penyelesaian persamaan tersebut menggunakan fungsi midpt() dengan iterasi pada nilai koreksi sebanyak 1 kali disajikan pada sintaks berikut:

num <- midpt(f1, x0=0, y0=1, h=0.05, n=100)

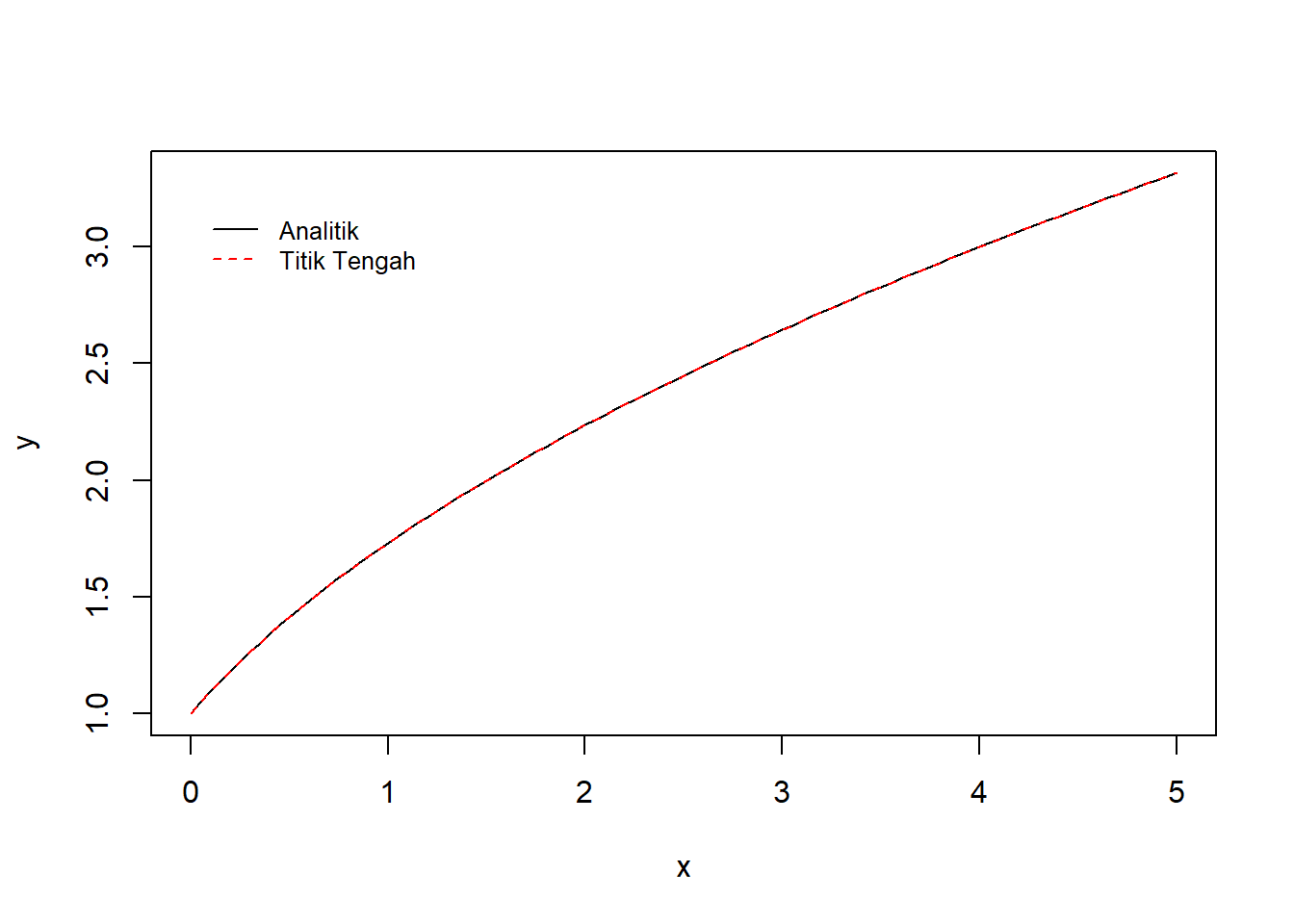
Gambar 10.3: Visualisasi integrasi numerik dengan metode titik tengah dan metode analitik

10.1.4 Metode Runge-Kutta Orde 4

Runge-Kutta orde 4 merupakan metode yang paling populer dalam penyelesaian persamaan diferensial. Metode ini dapat memperoleh akurasi deret Taylor tanpa memerlukan diferensiasi orde yang lebih tinggi. Metode Runge-Kutta orde 4 dituliskan ke dalam Persamaan (10.6).

\[\begin{equation} y_{i+1}=y_i+\frac{1}{6}\left(k_1+2k_2+2k_3+k_4\right)h \tag{10.6} \end{equation}\]

dimana

\[\begin{equation} k_1=f\left(x_i,y_i\right) \tag{10.7} \end{equation}\]

\[\begin{equation} k_2=f\left(x_i+\frac{1}{2}h,y_i+\frac{1}{2}k_1h\right) \tag{10.8} \end{equation}\]

\[\begin{equation} k_3=f\left(x_i+\frac{1}{2}h,y_i+\frac{1}{2}k_2h\right) \tag{10.9} \end{equation}\]

\[\begin{equation} k_4=f\left(x_i+h,y_i+k_3h\right) \tag{10.10} \end{equation}\]

---

Algoritma Metode Tengah

1. Tentukan titik awal integrasi \(x_0\) dan \(y_0\).
2. Tentukan jumlah iterasi \(n\) dan step size \(h\) yang digunakan.
3. Lakukan integrasi menggunakan Persamaan (10.6).

---

Berdasarkan algoritma tersebut, kita dapat membangun sebuah fungsi pada R yang adapat digunakan untuk menyelesaikan persamaan diferensial menggunakan metode Runge-Kutta orde 4. Berikut adalah sintaks yang digunakan:

rk4 <- function(f, x0, y0, h, n){
  x <- x0
  y <- y0
  
  for(i in 1:n){
    k1 <- f(x0,y0)
    k2 <- f(x0+0.5*h,y0+0.5*k1*h)
    k3 <- f(x0+0.5*h,y0+0.5*k2*h)
    k4 <- f(x0+h,y0+k3*h)
    y0 <- y0 + (1/6)*(k1+2*k2+2*k3+k4)*h
    x0 <- x0 + h
    x <- c(x, x0)
    y <- c(y, y0)
  }
  
  return(data.frame(x=x,y=y))
}

Contoh 10.4 Selesaikan kembali persamaan yang ditampilkan pada Contoh 10.1 menggunakan metode Runge-Kutta orde 4!

Jawab:

Contoh perhitungan secara manual menggunakan metode titik tengah untuk sekali iterasi adalah sebagai berikut:

\[ k_1=\frac{1}{\left(2\cdot 0\right)+1}=1 \]

\[ k_2=\frac{1+\frac{1}{2}\cdot1\cdot0,05}{\left(2\cdot 0\cdot\frac{1}{2}\cdot0,05\right)+1}=1,025 \]

\[ k_2=\frac{1+\frac{1}{2}\cdot1,025\cdot0,05}{\left(2\cdot 0\cdot\frac{1}{2}\cdot0,05\right)+1}=1,025625 \]

\[ k_2=\frac{1+1,025625\cdot0,05}{\left(2\cdot 0\cdot0,05\right)+1}=1,051281 \]

\[ y_1=1+\frac{1}{6}\left(1+2\cdot1,025+2\cdot1,025625+1,051281\right)0,05=1.051271 \]

1+(1/6)*(1+2*1.025+2*1.025625+1.051281)*0.05

## [1] 1.051

Iterasi dapat pula dilakukan dengan menggunakan fungsi rk4(). Berikut adalah sintaks yang digunakan:

num <- rk4(f1, x0=0, y0=1, h=0.05, n=100)

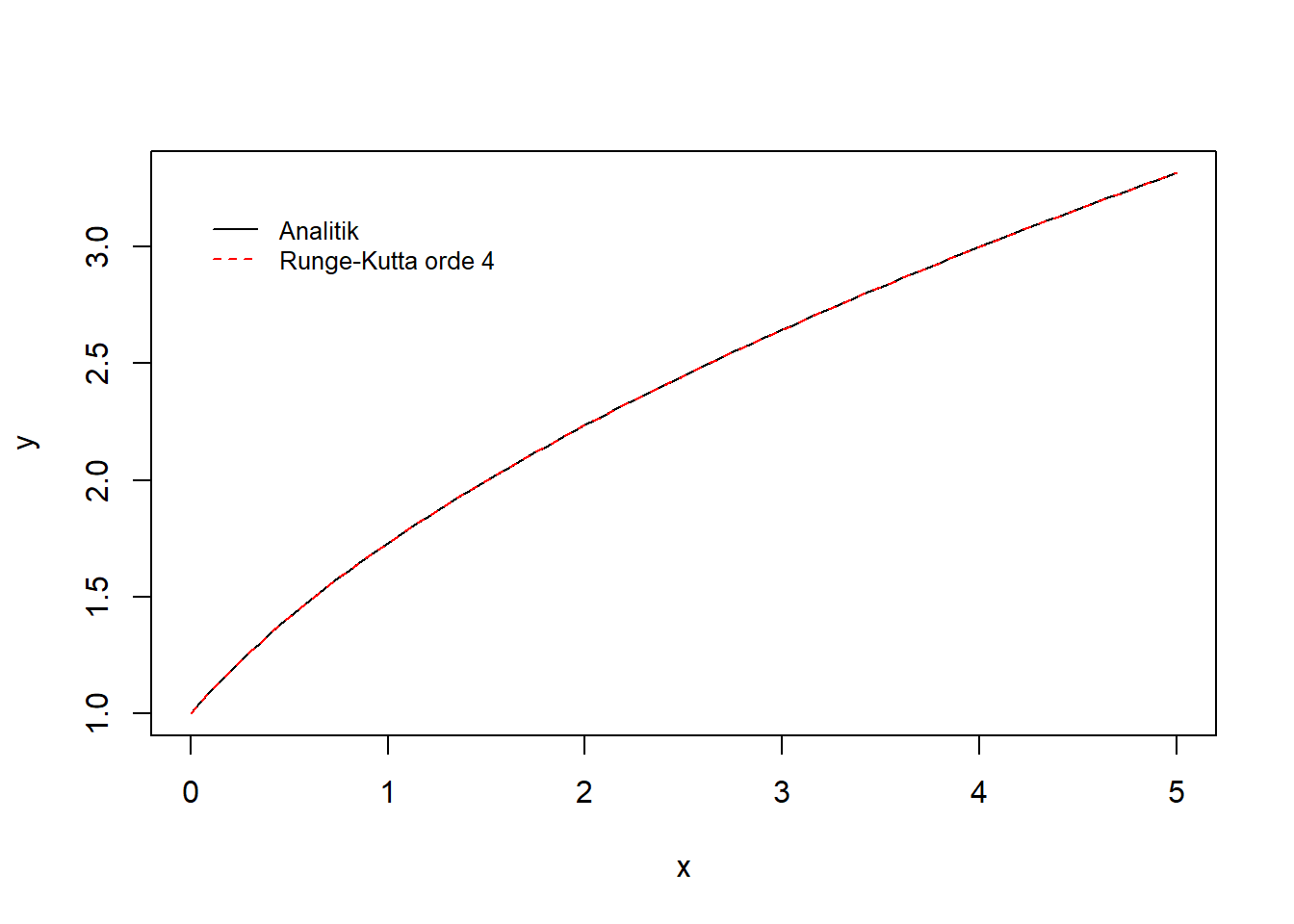
Gambar 10.4: Visualisasi integrasi numerik dengan metode Runge-Kutta orde 4 dan metode analitik

10.1.5 Metode Multistep Linier

Jika metode Runge-Kutta mengalami kesulitan karena terlalu banyak evaluasi fungsi yang digunakan, masuk akal untuk bertanya apakah kita dapat menggunakan kembali beberapa evaluasi fungsi sebelumnya, yang sudah kita buat. Sebagai contoh, kita ingin tahu apakah kita dapat menggunakan kembali estimasi \(f\left(0,1\right)\) dan \(f\left(0,2\right)\) untuk memperkirakan nilai \(f\left(0,3\right)\). Jika kita dapat menggunakan kembali perkiraan sebelumnya, kita dapat memperoleh akurasi tambahan tanpa menimbulkan penalti kinerja yang terkait dengan evaluasi fungsi tambahan. Metode multistep linier dikembangkan untuk mengatasi masalah ini.

Di satu sisi, metode multistep linier dasar untuk persamaan diferensial hanya mencakup satu titik \(x_i\), dalam perhitungan \(x_i + 1\). Ini persis bagaimana fungsi metode Euler dan metode Euler merupakan metode multistep linier dasar. Metode selanjutnya menggunakan \(x_i − 1\) dan \(x_i\) untuk menghitung \(x_i + 1\). Metode Adams-Bashforth menggunakan tambahan berbobot, termasuk bobot negatif, dari langkah dan poin untuk sampai pada langkah berikutnya. Seperti metode numerik lainnya, bobot muncul dari interpolasi polinomial titik yang tersedia.

Metode Adam-Bashforth orde 2 didasarkan pada Persamaan (10.11).

\[\begin{equation} y_{i+2}=y_{i+1}+\frac{h}{2}\left(3f\left(x_{i+1},y_{i+1}\right)-f\left(x_i,y_i\right)\right) \tag{10.11} \end{equation}\]

Pendekatan ini melakukan interpolasi antara titik sebelumnya untuk memperkirakan titik ketiga dalam grup. Titik ketiga ini menjadi titik tengah dari iterasi berikutnya saat seluruh proses berlanjut. Karena nilai sebelumnya disimpan dan digunakan kembali, evaluasi fungsi tambahan tidak diperlukan. Jika metode Runge-Kutta dapat dibandingkan dengan tip-toeing melalui bidang vektor, maka metode Adams-Bashforth dapat sama dibandingkan dengan menjalankan melalui bidang vektor. Namun, ini tidak berarti metode Adams-Bashforth lebih unggul.

---

Algoritma Metode Tengah

1. Tentukan titik awal integrasi \(x_0\) dan \(y_0\).
2. Tentukan jumlah iterasi \(n\) dan step size \(h\) yang digunakan.
3. Lakukan pendekatan pada iterasi ke-1 menggunakan metode Euler.
4. Lakukan integrasi ke-2 sampai n menggunakan Persamaan (10.11).

---

Berdasarkan algoritma tersebut, kita dapat membangun sebuah fungsi pada R yang adapat digunakan untuk menyelesaikan persamaan diferensial menggunakan metode multistep linier. Berikut adalah sintaks yang digunakan:

adambashforth <- function(f, x0, y0, h, n){
  # pendekatan Euler untuk x1 dan y1
  y1 <- y0 + h*f(x0,y0)
  x1 <- x0 + h
  
  x <- c(x0,x1)
  y <- c(y0,y1)
  n <- n-1
  
  for(i in 1:n){
    yn <- y1 + 1.5*h*f(x1,y1) - 0.5*h*f(x0,y0)
    xn <- x1 + h
    
    y0 <- y1
    x0 <- x1
    y1 <- yn
    x1 <- xn
    
    y <- c(y,y1)
    x <- c(x,x1)
  }
  
  return(data.frame(x=x,y=y))
}

Contoh 10.5 Selesaikan kembali persamaan yang ditampilkan pada Contoh 10.1 menggunakan metode Runge-Kutta orde 4!

Jawab:

Untuk melakukan iterasi, kita dapat menggunakan fungsi adambashforth(). Berikut adalah sintaks yang digunakan:

num <- rk4(f1, x0=0, y0=1, h=0.05, n=100)

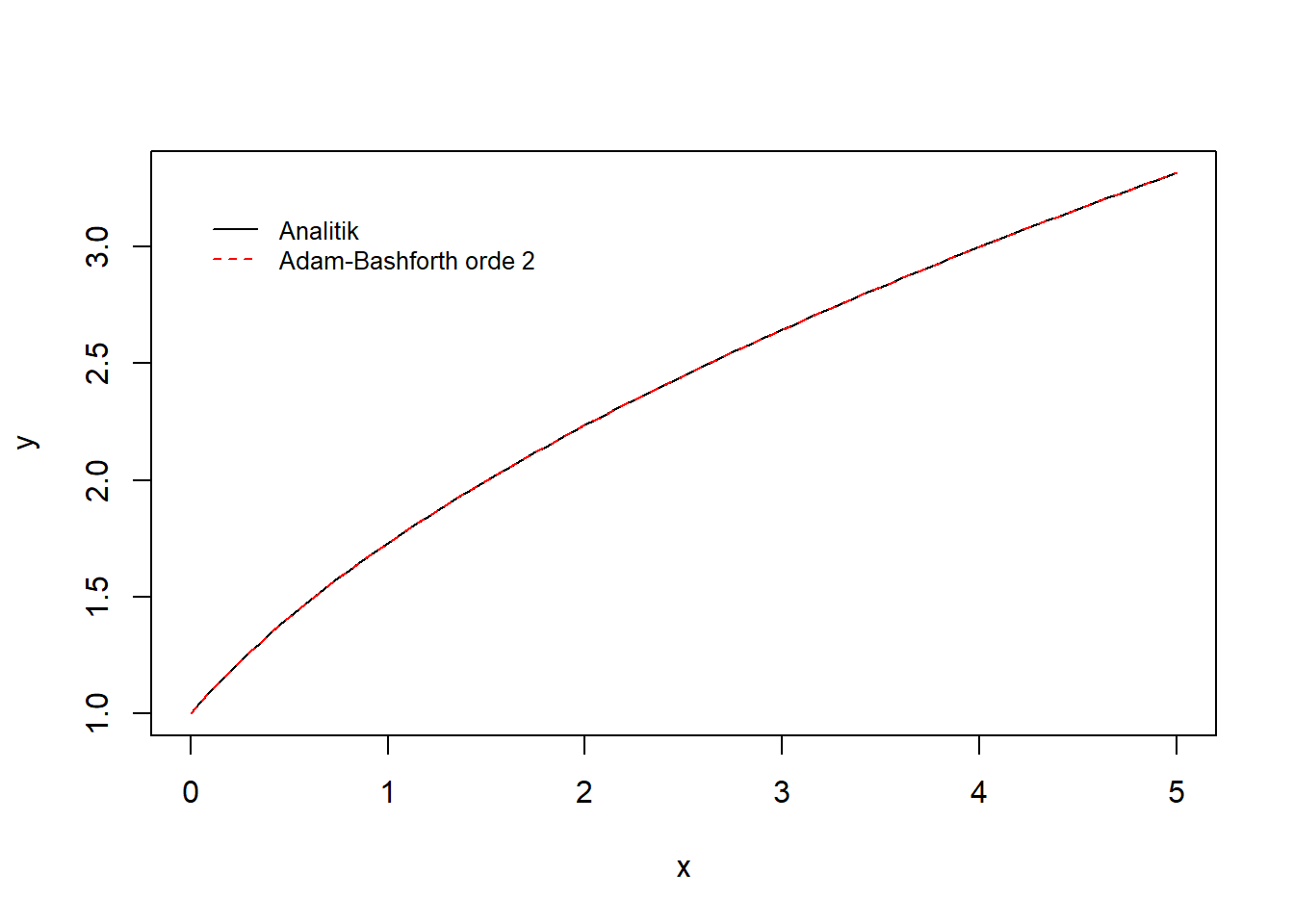
Gambar 10.5: Visualisasi integrasi numerik dengan metode Adam-Bashfoth orde 2 dan metode analitik

10.2 Sistem Persamaan Diferensial

Sistem persamaan diferensial akan sering pembaca temui dalam pemodelan sistem dinamik. Pada proses pemodelan sistem tersebut akan ditemukan aksi-interasi antar komponennya yang dinyatakan ke dalam suatu sistem persamaan diferensial.

Pada fungsi rk4sys() disusun sebuah fungsi pada R untuk melakukan iterasi terhadap sistem persamaan diferensial menggunakan metode Runge-Kutta orde 4. Berikut adalah sintaks yang digunakan:

rk4sys <- function(f, x0, y0, h, n){
  x <- x0
  y <- y0
  
  values <- data.frame(x=x,t(y0))
  for(i in 1:n){
    k1 <- f(x0,y0)
    k2 <- f(x0+0.5*h,y0+0.5*k1*h)
    k3 <- f(x0+0.5*h,y0+0.5*k2*h)
    k4 <- f(x0+h,y0+k3*h)
    y0 <- y0 + (1/6)*(k1+2*k2+2*k3+k4)*h
    x0 <- x0 + h
    values <- rbind(values, data.frame(x=x0,t(y0)))
  }
  
  return(values)
}

Contoh 10.6 Sebuah model populasi yang dibagi menjadi tiga kelompok umur: anak (0-12 tahun), melahirkan anak (13-40 tahun), dan usia (41 tahun atau lebih). Kelompok 0-12 meningkat berdasarkan kelahiran di kelompok 13-40, dan menurun dengan kematian dan lewat bagian ke kelompok 13-40. Kelompok 13–40 meningkat dengan perolehan dari kelompok 0-12, dan berkurang dengan kematian dan lewat bagian ke dalam kelompok> = 41. Kelompok> = 41 meningkat dengan keuntungan dari kelompok 13-40, dan menurun dengan kematian. Parameter dipilih untuk mewakili tingkat kelahiran dan kematian yang cukup tinggi seperti yang ditemukan di banyak masyarakat berkembang. Model interaksi tersebut dinyatakan ke dalam persamaan interkasi di bawah ini! Simulasikan dinamika populasi pada model tersebut pada 10 tahun ke depan, jika diketahui populasi semula masing-masing kelompok usia secara berurutan adalah 200,400, dan 400, serta nilai masing-masing koefisien kelahiran, kematian kelompok 1, kematian kelompok2, dan kematian kelompok 3 secara berurutan adalah 0,5;0,1;0,1;0,25!

\[ pop1' = b\cdot pop2'+\frac{11}{12}\cdot pop1'\left(1-d1\right) \]

\[ pop2' = \frac{1}{12}\cdot pop1'\cdot\left(1-d1\right)+\frac{26}{27}\cdot pop2'\cdot \left(1-d2\right) \]

\[ pop3, = \frac{1}{27}\cdot pop2,\cdot\left(1-d2\right)+ pop3'\cdot \left(1-d3\right) \]

Jawab:

Sistem persamaan diferensial perlu ditransformasi ke dalam bentuk sebuah fungsi pada R.

Population = function(x,y) {
   # parameter
   b = 0.5 # Birth rate in 13-40 group
   d1 = 0.1 # Death rate of 0-12 group
   d2 = 0.1 # Death rate of 13-40 group
   d3 = 0.25 # Death rate of 41 and older
   
   y1 = y[1] # 0-12 group population
   y2 = y[2] # 13-40 group population
   y3 = y[3] # 41 and older population
   y1.new = b*y2 + (11/12)*y1*(1 - d1)
   y2.new = (1/12)*y1*(1 - d1) + (26/27)*y2*(1 - d2)
   y3.new = (1/27)*y2*(1 - d2) + y3*(1 - d3)
   return(c(y1.new, y2.new, y3.new))
}

Nilai awal dituliskan seperti berikut:

# Nilai awal
y = c(pop1=200,pop2=400,pop3=400)

Simulasi model ditampilkan pada sintaks berikut:

pop <- rk4sys(Population, x0=0, y0=y, h=0.1, n=100)
head(pop)

##     x  pop1  pop2  pop3
## 1 0.0 200.0 400.0 400.0
## 2 0.1 239.0 437.9 432.6
## 3 0.2 283.4 479.6 467.9
## 4 0.3 334.0 525.4 506.1
## 5 0.4 391.4 575.9 547.4
## 6 0.5 456.4 631.3 592.1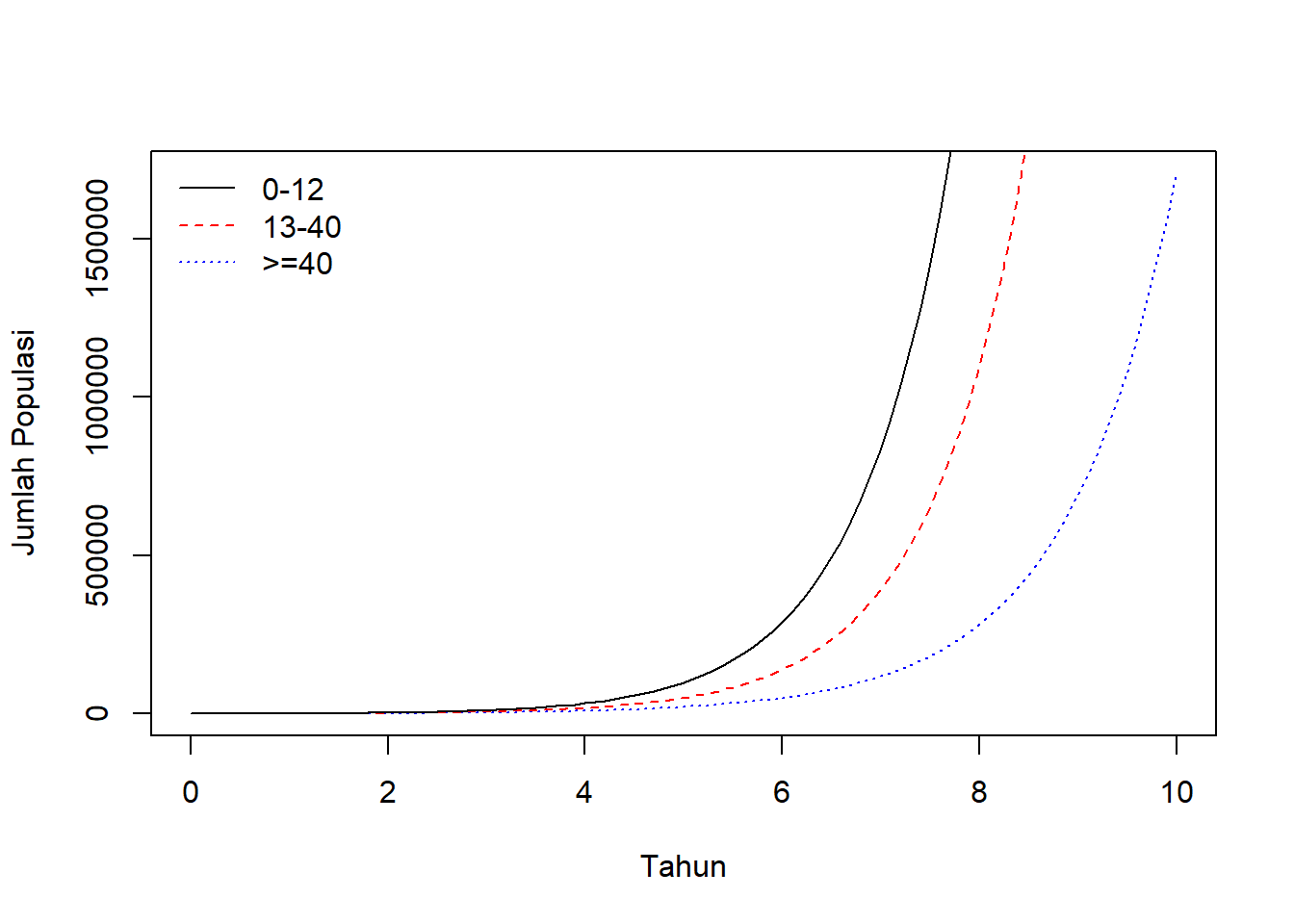

Gambar 10.6: Visualisasi hasil simulasi model dinamika populasi

10.3 Penyelesaian Persamaan Diferensial dan Sistem Persamaan Diferensial Menggunakan Fungsi ode()

Fungsi ode() pada paket deSolve merupakan salah satu fungsi yang dapat digunakan untuk menyelesaikan persamaan dan sistem persamaan diferensial. Fungsi ini mudah digunakan serta menyediakan berbagai macam metode iterasi numerik untuk menyelesaikan persamaan diferensial. Format umum fungsi ini antara lain:

ode(y, times, func, parms,method , ...)

Catatan:

• y : nilai awal (kondisi awal) suatu persamaan diferensial.
• times : deret waktu yang terdiri dari kapan simulasi dimulai, kapan simulasi berkahir dan berapa step size yang digunakan.
• func : fungsi yang berisi persamaan diferensial. Return value pada fungsi haruslah berupa list.
• parms : list parameter yang diinputan kedalam func.

• method : sebuah string yang berupa metode intgrasi yang digunakan. Metode yang tersedia dan kegunaan metode tersebut antara lain:

  • “bdf”: menangani persamaan diferensial menggunakan formula diferensiasi mundur (bacward differensiation) dan cocok untuk menangani kondisi stiff. Metode ini setara dengan method="lsode".
  • “bdf_d”: menggunakan formula diferensiasi mundur yang memanfaatkan iterasi Jacobi-Newton (mengabaikan elemen diagonal Jacobian). Cocok digunakan persamaan atau sistem persamaan diferensial kondisi stiff. Metode ini setara dengan method="lsode",mf=23.
  • “adams”: metode Adams yang menggunakan iterasi fungsional (tanpa menggunakan Jacobian). Cocok digunakan untuk persamaan atau sistem persamaan non stiff. Metode ini setara dengan method="lsode", mf=10.
  • “impAdams”: metode Adams implisit yang menggunakan iterasi Newton-Raphson. Metode ini setara dengan method="lsode",mf=12.
  • “impAdams_d”: metode Adams implisit yang menggunakan iterasi Jacobi-Newton. Metode ini setara dengan method="lsode, mf=13".
  • “euler”: metode iterasi Euler
  • “rk4”: metode iterasi Runge-Kutta orde 4.
  • metode lain: “lsoda”, “lsode”, “lsodes”, “lsodar”, “vode”, “daspk”, “ode23”, “ode45”, “radau”.

• ...: argumen tambahan untuk integrator atau method.

Contoh penerapan fungsi tersebut menggunakan Contoh 10.6, sebagai berikut:

library(deSolve)

# sistem persamaan diferensial
Population = function(t,y,param) {
  y1 = y[1] # 0-12 group population
  y2 = y[2] # 13-40 group population
  y3 = y[3] # 41 and older population
  y1.new = b*y2 + 11/12*y1*(1 - d1)
  y2.new = 1/12*y1*(1 - d1) + 26/27*y2*(1 - d2)
  y3.new = 1/27*y2*(1 - d2) + y3*(1 - d3)
  return(list(c(y1.new, y2.new, y3.new)))
}

# parameter
b = 0.5 # Birth rate in 13-40 group
d1 = 0.1 # Death rate of 0-12 group
d2 = 0.1 # Death rate of 13-40 group
d3 = 0.25 # Death rate of 41 and older

# nilai awal
y = c(pop1=200, pop2=400, pop3=400)

# waktu
Tahun = seq(0,10,0.1)

# simulasi
out = ode(func = Population, y = y, times = Tahun, 
          parms = c(b,d1,d2,d3), method = "rk4")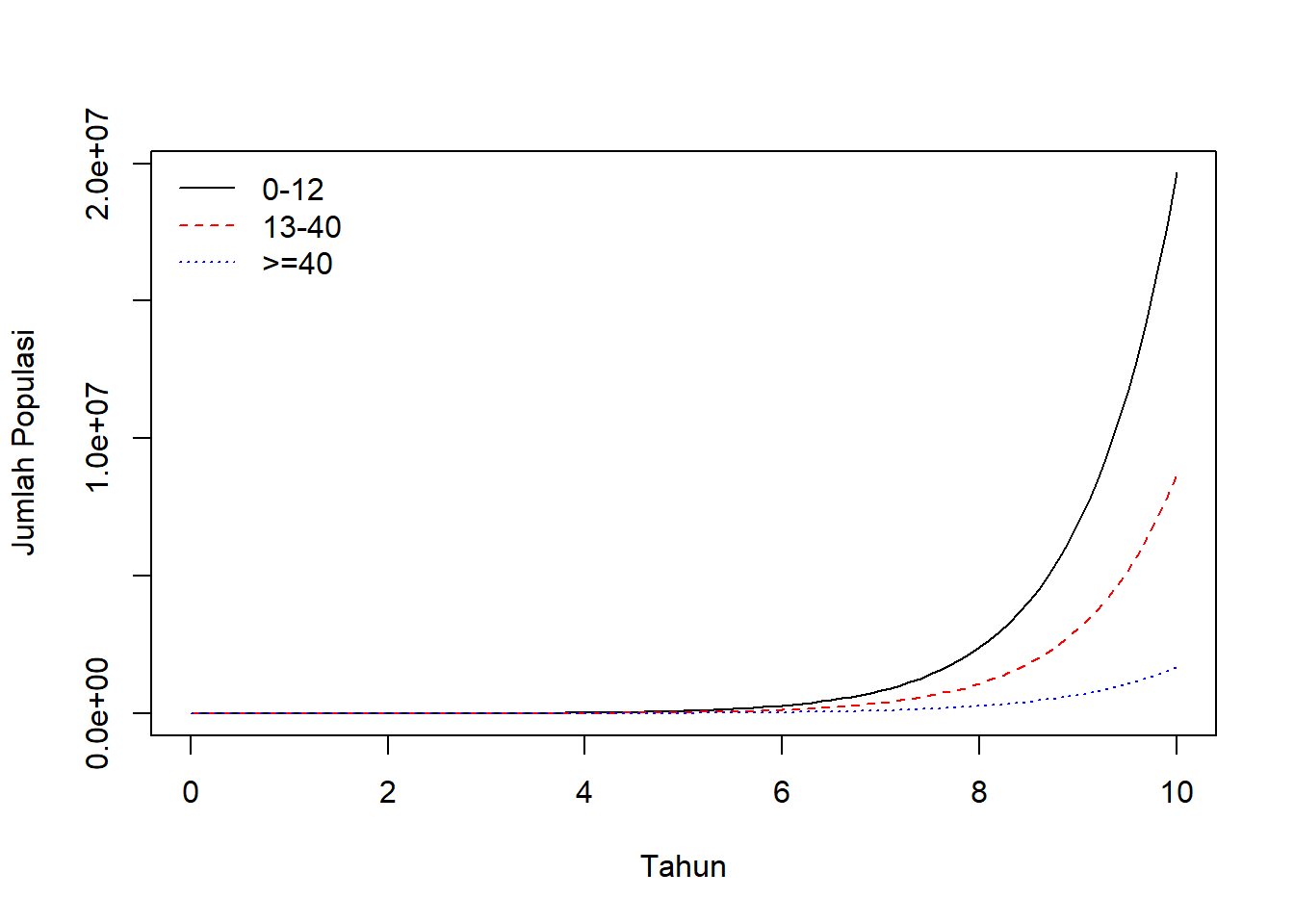

Gambar 10.7: Visualisasi hasil simulasi model dinamika populasi menggunakan paket desolve

10.4 Persamaan Diferensial Parsial

Persamaan diferensial parsial (PDE) banyak dijumpai pada pemodelan transport polutan dalam bidang teknik lingkungan. Persamaan diferensial parsial merupakan persamaan diferensial yang melibatkan lebih dari satu variabel independen, biasanya variabel waktu dan satu atau lebih variabel posisi atau beberapa variabel spasial. PDE diklasifikasikan menjadi 3 jenis: parabolik (time-dependent dan difusif), hiperbolik (time-dependent dan gelombang), dan eliptik (time-independent). Dalam penyelesaian PDE pada umumnya kita menggunakan metode FTCS (forward in time, centered in space). Untuk memahami definisi tersebut, pembaca dapat membaca kembali Chapter 9.1.

10.4.1 Persamaan Difusi

Persamaan difusi merupakan contoh PDE parabolik. Persamaan difusi satu dimensi spasial ditampilkan pada Persamaan (10.12).

\[\begin{equation} \frac{\partial C}{\partial t}=D\frac{\partial^2C}{\partial x^2} \tag{10.12} \end{equation}\]

Persamaan tersebut mirip dengan persamaan konduksi panas. Pada persamaan konduksi panas, variabel konsentrasi \(C\) diganti dengan variabel temperatur \(T\), dan koefisien difusi D diganti dengan koefsien difusi termal K.

Untuk menyelesaikan Persamaan (10.12), persamaan tersebut diubah ke dalam bentuk metode beda hingga, dimana turunan waktu menggunakan pendekatan Euler (metode beda hingga maju) dan turunan variabel spasial diubah ke dalam bentuk pendekatan titik pusat. Proses diskretisasi Persamaan (10.12), ditampilkan pada Persamaan (10.13).

\[\begin{equation} \frac{C\left(i+1,j\right)-C\left(i,j\right)}{\Delta t}=D\frac{C\left(i,j+1\right)+C\left(i,j-1\right)-2C\left(i,j\right)}{\Delta x^2} \tag{10.13} \end{equation}\]

dimana \(i\) merupakan step untuk variabel waktu \(t\) dan \(j\) merupakan step untuk variabel spasial \(x\).

Persamaan (10.13) dapat disusun kembali sehingga menjadi Persamaan (10.14) yang menyatakan persamaan konsentrasi \(C\) pada saat \(i+1\) pada posisi \(j\).

\[\begin{equation} C\left(i+1,j\right)=C\left(i,j\right)+A\left[C\left(i,j+1\right)+C\left(i,j-1\right)-2C\left(i,j\right)\right] \tag{10.14} \end{equation}\]

dimana

\[\begin{equation} A=D\frac{\Delta t}{\Delta x^2} \tag{10.15} \end{equation}\]

Untuk stabilitas komputasi, pemilihan peningkatan waktu terhadap jarak yang dinyatakan pada nilai \(A\) harus \(\le\frac{1}{2}\).

Pada contoh berikut, kita akan melakukan simulasi menggunakan Persamaan (10.14). Parameter yang digunakan dan nilai awal yang digunakan dinyatakan pada sintaks berikut:

dt    <- 3                # Timestep, s
dx    <- 0.1              # Distance step, cm
D     <- 1e-4             # Diffusion coeff, cm^2/s

# Cek apakah syarat stabilitas terpenuhi
D*dt/dx^2 <= 0.5

## [1] TRUE

# Desain grid points
L     <- 1                # Length from -L/2 to L/2
n     <- L/dx + 1         # Number of grid points
x     <- seq(-L/2,L/2,dx) # Location of grid points
steps <- 30               # Number of iterations
time  <- 0:steps

Langkah selanjutnya adalah inisiasi konsentrasi awal, dimana seluruh konsentrasi awal pada tiap grid adalah nol kecuali pada grid pusat.

C <- matrix(rep(0, (steps+1)*n), nrow = steps+1, ncol = n)
C[1, round(n/2)] <- 1/dx  # initial spike at central point

Simulasi selanjutnya dilakukan dengan melakukan iterasi pada grid points konsentrasi yang telah dibuat.

# Loop over desired number of time steps
for(i in 1:(steps-1)){
  for(j in 2:(n-1)){
    C[i+1,j] <- C[i,j] + (D*dt/dx^2)*(C[i,j+1] + C[i,j-1] - 2*C[i,j])
  }
}

Visualisasi dari hasil simulasi tersebut ditampilkan pada Gambar 10.8.

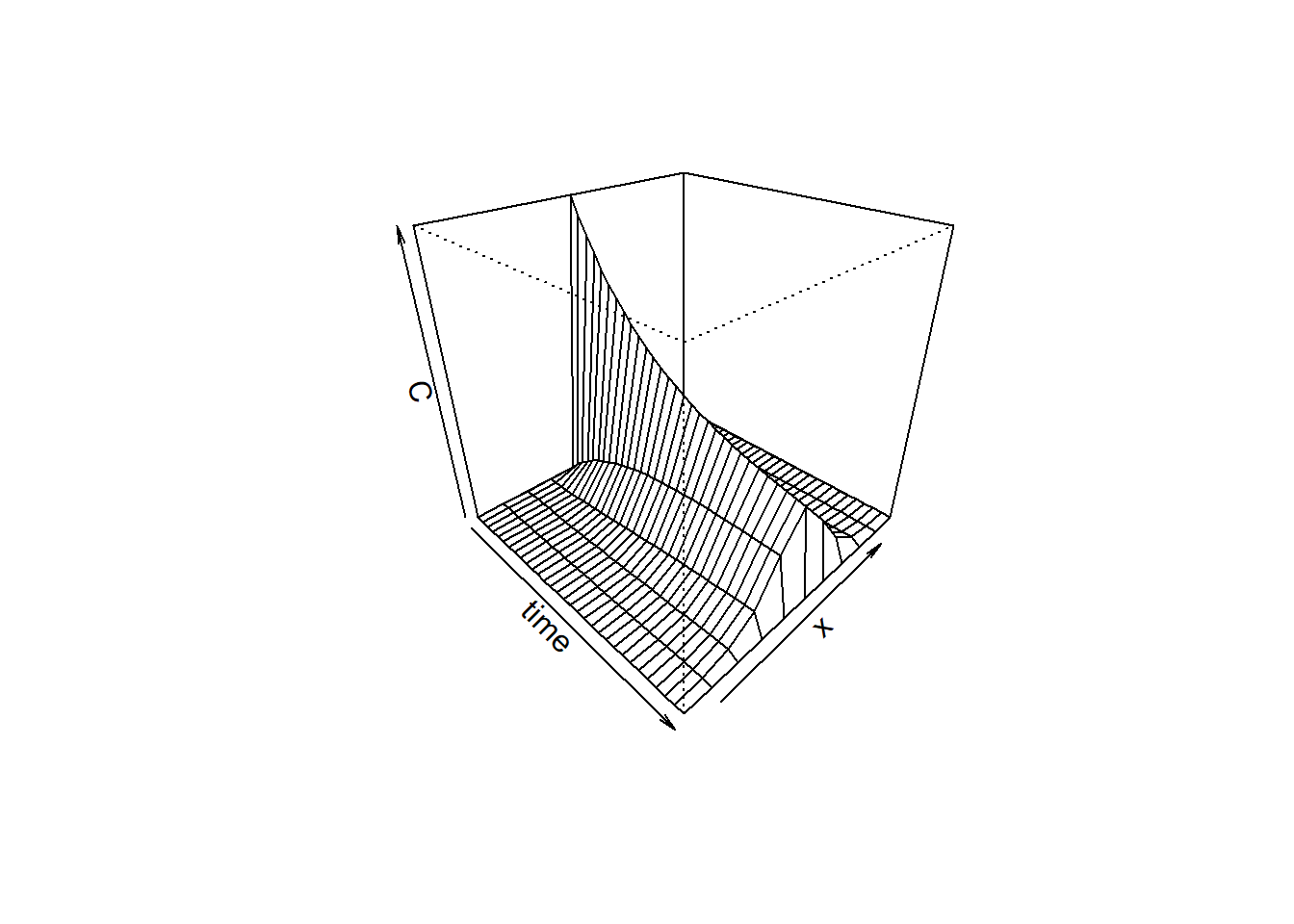
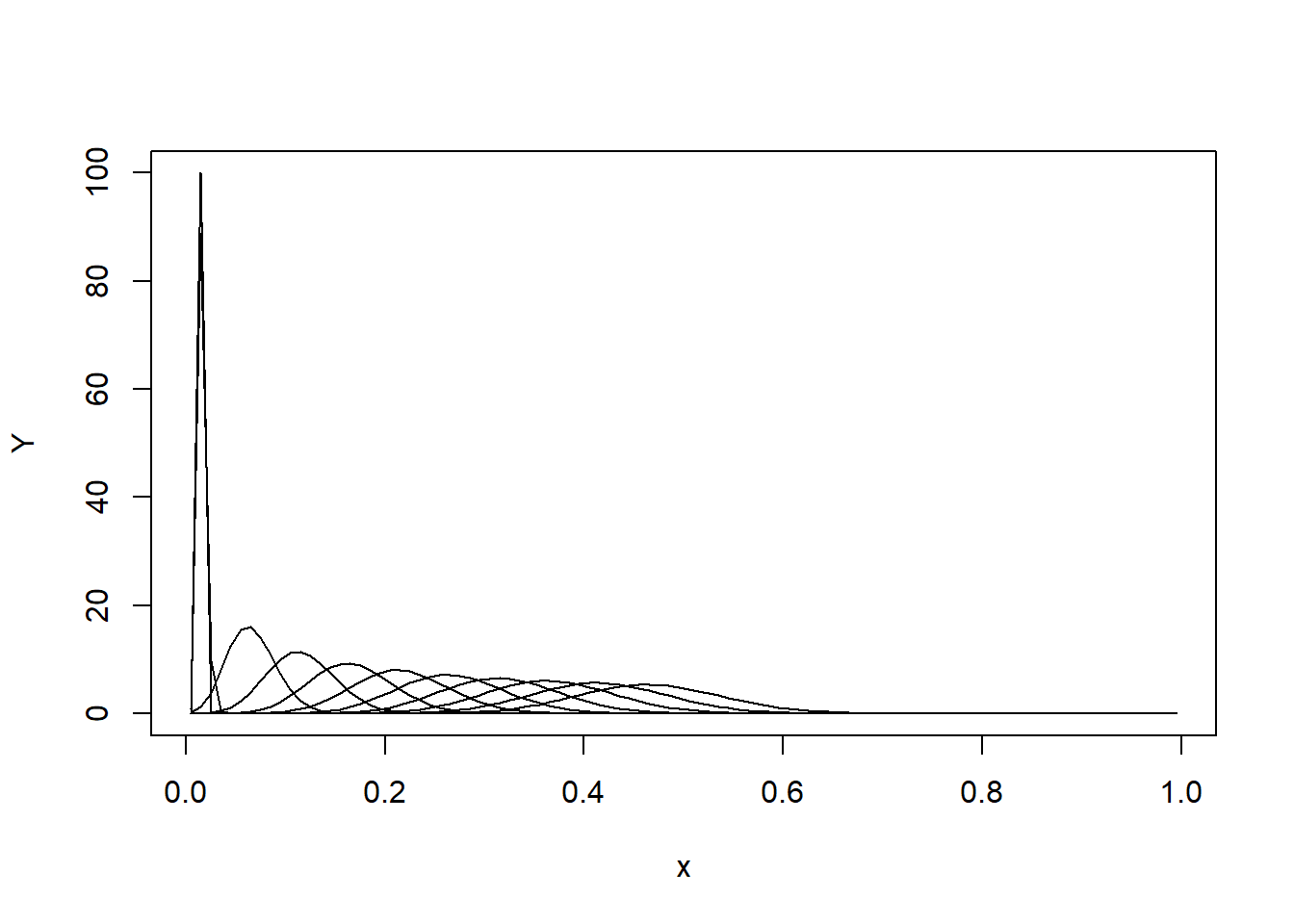
Gambar 10.8: Visualisasi 3D simulasi difusi partikulat

10.4.2 Persamaan Gelombang

Persamaan gelombang 1 dimensi ditampilkan pada Persamaan (10.16).

\[\begin{equation} \frac{\partial^2W}{\partial t^2}=c^2\frac{\partial^2W}{\partial x^2} \tag{10.16} \end{equation}\]

dimana \(W\) merupakan pemindahan dan \(c\) merupakan kecepatan gelombang. Persamaan (10.16) merupakan bentuk PDE hiperbolik. Versi lebih sederhana dari Persamaan (10.16) adalah persamaan adveksi yang ditampilkan pada Persamaan (10.17).

\[\begin{equation} \frac{\partial y}{\partial t}=-c\frac{\partial y}{\partial x} \tag{10.17} \end{equation}\]

Persamaan (10.17) menggambarkan evolusi pada bidang skalar \(y\left(x,y\right)\) dibawa oleh gelombang dengan kecepatan konstan \(c\) dan bergerak dari kiri ke kanan jika \(c>0\). Persamaan adveksi merupakan contoh palin sederhana dari persamaan konservasi flux.

Diskretisasi Persamaan (10.17) ditampilkan pada Persamaan (10.18).

\[\begin{equation} y\left(i+1,j\right)=y\left(i,j\right)-\frac{c\Delta t}{2\Delta x}\left[y\left(i,j+1\right)-y\left(i,j-1\right)\right] \tag{10.18} \end{equation}\]

Pada contoh berikut, kita akan melakukan simulasi menggunakan Persamaan (10.17). Parameter yang digunakan dan nilai awal yang digunakan dinyatakan pada sintaks berikut:

dt    <- 0.002              # Timestep, s
L     <- 1                  # Length from -L/2 to L/2
n     <- 50                 # Number of grid points
v     <- 1                  # Wavespeed, cm/s
dx    <- L/n                # Distance step, cm
x     <- (1:n-0.5)*dx-L/2   # Location of grid points
steps <- L/(v*dt)           # Number of iterations
time  <- 0:steps  
sig   <- 0.1                # Standard deviation of initial Gaussian wave
amp0  <- exp(-x^2/(2*sig^2))# Initial Gaussian amplitude

Kondisi awal dan kondisi batas periodik dinyatakan sebagai berikut:

C <- matrix(rep(0, (steps+1)*n), nrow = steps+1, ncol = n)
C[1, ] <- amp0
jplus1 <- c(2:n,1)
jminus1 <- c(n,1:(n-1))

Langkah selanjutnya melakukan interasi untuk melihat perubahan nilai pada grid points.

for(i in 1:steps){
  for(j in 1:n){
    C[i+1,j] <- C[i,j] + (v*dt/(2*dx))*(C[i,jplus1[j]] - C[i,jminus1[j]])
  }
}

Visualisasi dari hasil simulasi tersebut ditampilkan pada Gambar 10.9.

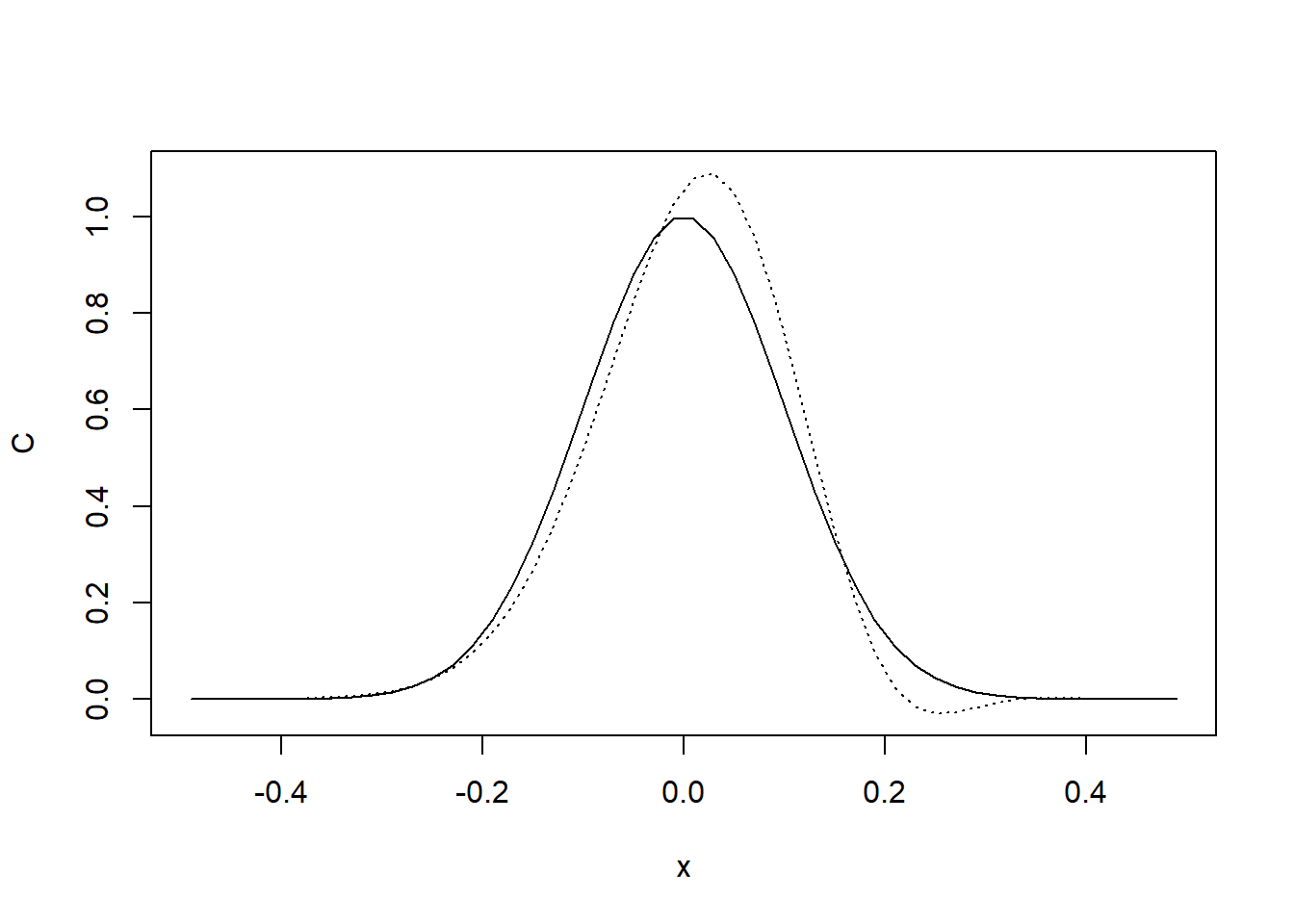
Gambar 10.9: Visualisasi simulasi adveksi

10.4.3 Persamaan Laplace

Persamaan Laplace dalam dua dimensi disajikan pada Persamaan (10.19).

\[\begin{equation} \frac{\partial V}{\partial x^2}+\frac{\partial V}{\partial y^2}=0 \tag{10.19} \end{equation}\]

Persamaan (10.19) merupakan contoh tipe ketiga PDE, persamaan elips. Persoalan ini sering muncul dalam bidang elektrostatik, gravitasi, dan bidang lain di mana potensi \(V\) harus dihitung sebagai fungsi posisi. Jika ada muatan atau massa dalam ruang, dan jika kita menggeneralisasi ke tiga dimensi, persamaannya menjadi persamaan Poisson

\[\begin{equation} \frac{\partial V}{\partial x^2}+\frac{\partial V}{\partial y^2}+\frac{\partial V}{\partial z^2}=0 \tag{10.20} \end{equation}\]

Bergantung pada geometri masalahnya, Persamaan (10.20) juga dapat ditulis dalam koordinat bola, silindris, atau lainnya.

Untuk menyelesaikan persamaan eliptik jenis ini, persamaan harus diberi syarat batas. Biasanya dengan menentukan bahwa titik, garis, atau permukaan tertentu dipertahankan pada nilai konstan potensial. Kemudian potensi di titik lain disesuaikan sampai mencapai perkiraan yang diinginkan. (Dalam kasus yang jarang terjadi, persamaan dengan kondisi batas dapat diselesaikan dengan tepat secara analitis; tetapi biasanya solusi perkiraan harus cukup.)

Ada banyak pendekatan untuk solusi numerik dari persamaan Laplace. Mungkin yang paling sederhana adalah Jacobi, di mana titik-titik interior secara berturut-turut didekati dengan rata-rata titik-titik di sekitarnya, sedangkan titik-batas dibatasi pada nilai-nilai tetap dan yang ditentukan. Kita asumsikan sebagai contoh bidang persegi, dibatasi oleh \(\left(0,1\right)\) dalam arah \(x\) dan \(y\), di mana ujung pada \(y = 1\) dipertahankan pada \(V = 1\) dan tiga tepi lainnya dipertahankan pada \(V = 0\). Kita buat tebakan awal yang paling sederhana untuk potensi di titik interior, tetapi ini akan disamakan saat solusinya menyatu.

Pada contoh berikut, kita akan melakukan simulasi persamaan Laplace menggunakan metode Jacobi. Parameter yang digunakan dalam simulasi adalah sebagai berikut:

n   <- 30                 # Number of grid points/side
L   <- 1                  # Length of a side
dx  <- L/(n-1)            # Grid spacing
x   <- y    <- 0:(n-1)*dx # x and y coorfinates

Tebakan awal untuk profil voltase adalah sebagai berikut:

V0  <- 1
V   <- matrix(V0/2*sin(2*pi*x/L)*sin(2*pi*y/L),
              nrow = n, ncol = n, byrow = TRUE)

Kondisi batas di tetapkan seperti berikut:

V[1,] <- 0
V[n,] <- 0
V[,1] <- 0
V[,n] <- V0*rep(1,n)

Selanjutnya visualisasikan tebakan awal.

Gambar 10.10: Visualisasi tebakan awal solusi persaman Laplace

Proses iterasi menggunakan metode Jacobi ditampilkan pada sintaks berikut:

newV  <- V
itmax <- n^2
tol   <- 1e-4
for(it in 1:itmax){
  dVsum <- 0
  for(i in 2:(n-1)){
    for(j in 2:(n-1)){
      newV[i,j] <- 0.25*(V[i-1,j]+V[i+1,j]+V[i,j-1]+V[i,j+1])
      dVsum <- dVsum + abs(1-V[i,j]/newV[i,j])
    }
  }
  V <- newV
  dV = dVsum/(n-2)^2 # Average deviation from prev. value
  if(dV < tol) break # Desired tolerance achived
}

it # Iterations to achieve convergence to tol

## [1] 419

dV

## [1] 9.908e-05

Hasil simulasi selanjutnya di visualisasikan kembali.

Gambar 10.11: Visualisasi hasil simulasi solusi persaman Lplace

## Penyelesaian Persamaan Diferensial Parsial Menggunakan PaketReacTran`

Package ReacTran memfasilitasi pemodelan transport reaktif dalam 1, 2, dan 3 dimensi. Paket ini "berisi rutinitas yang memungkinkan pengembangan model transportasi reaktif dalam sistem perairan (sungai, danau, lautan), media berpori (agregat flok, sedimen, …) dan bahkan organisme yang diidealkan.

Pada paket ReacTran terdapat sejumlah fasilitas fungsi, antara lain:

• Fungsi untuk menyiapkan kisi beda hingga (1D atau 2D)
• Fungsi untuk melampirkan parameter dan properti ke kisi ini (1D atau 2D)
• Fungsi untuk menghitung jangka waktu transport adveksi-difusi di atas grid (1D, 2D, 3D)
• Berbagai fungsi lainnya.

Saat paket ReacTran dimuat, paket ini juga memuat dua paket pendukung, yaitu: rootSolve dan deSolve. Paket rootSolve berguna untuk memecahkan persamaan diferensial untuk kondisi tunak baik persamaan diferensial uniform atau multikomponen (1D, 2D, dan 3D). Sedangkan deSolve berguna untuk menyediakan fungsi yang digunakan untuk memperoleh penyelesaian numerik persamaan diferensial biasa (ODE), persamaan diferensial parsial (PDE), persamaan aljabar diferensial (DAE) dan persamaan delay differential.

10.4.4 setup.grid.1D()

Fungsi setup.grid.1D() digunakan untuk membentuk kisi satu dimensi. Secara sederhana fungsi ini membagi ruang satu dimensi \(L\) antara \(x.up\) dan \(x.down\) menjadi sejumlah \(N\) kisi sebesar dx.1. Format umum fungsi tersebut, adalah sebagai berikut:

setup.grid.1D(x.up=0, x.down=NULL,L=NULL, 
              N=NULL, dx.1=NULL, 
              p.dx.1= rep(1,length(L)), 
              max.dx.1=L, dx.N=NULL, 
              p.dx.N=rep(1,length(L)), 
              max.dx.N=L)

Catatan:

• x.up : posisi hilir.
• x.down : posisi hulu.
• L : x.down-x.up.
• N : jumlah kisi = L/dx.1.

Pada situasi yang lebih kompleks, ukuran sel atau kisi dapat bervariasi, atau dapat pula lebih dari satu zona. Kondisi ini dijelaskan lebih jauh pada laman bantuan fungsi.

Nilai yang dihasilkan dari fungsi setup.grid.1D() termasuk x.mid (vektor sepanjang \(N\) yang menyatakan posisi titik tengah) dan x.int (vektor sepanjang \(N+1\) yang menyatakan posisi antar muka antara kisi sel dimana flux diukur).

Fungsi plot untuk grid.1D() memvisualissikan baik posisi sel dan ketebalan kotak, menampilkan x.mid dan x.int. Contoh di halaman bantuan menunjukkan perilaku ini.

setup.grid.1D() berfungsi sebagai titik awal untuk setup.grid.2D, yang membuat kisi di atas domain persegi panjang yang ditentukan oleh dua kisi 1D ortogonal.

10.4.5 setup.prop.1D()

Banyak model transportasi akan melibatkan kisi-kisi dengan properti konstan. Tetapi jika beberapa properti yang mempengaruhi difusi atau adveksi bervariasi dengan posisi di grid, variasi dapat digabungkan dengan fungsi setup.prop.1D() (atau setup.prop.2D() dalam dua dimensi).

Diberikan fungsi matematis atau matriks data, fungsi setup.prop.1D() menghitung nilai properti yang diminati di tengah sel kisi dan pada antarmuka antar sel. Format fungsi tersebut adalah sebagai berikut:

setup.prop.1D(func=NULL, value=NULL, xy=NULL,
              interpolate="spline",grid, ...)

Catatan:

• func : fungsi yang mengatur ketergantungan spasial properti.
• value : nilai konstan yang diberikan ke properti jika tidak ada ketergantungan spasial.
• xy : matriks data di mana kolom pertama memberikan posisi, dan kolom kedua memberikan nilai-nilai yang diinterpolasi di atas grid.
• iterpolate : metode interpolasi yang digunakan (spline atau linier).
• grid: objek yang dibentuk melalui fungsi setup.grid.1D().
• ...: argumen tambahan func.

10.4.6 tran.1D()

Fungsi ini menghitung istilah transportasi — laju perubahan konsentrasi akibat difusi dan adveksi — dalam model cairan 1D (fraksi volume = 1) atau padatan berpori (fraksi volume dapat bervariasi dan <1).tran.1D() juga digunakan untuk masalah dalam geometri bola atau silinder, meskipun dalam kasus ini antarmuka sel jaringan akan memiliki area variabel. Format fungsi ini adalah sebagai berikut:

tran.1D(C, C.up = C[1], C.down = C[length(C)], 
        flux.up = NULL, flux.down = NULL, 
        a.bl.up = NULL, a.bl.down = NULL, D = 0, 
        v = 0, AFDW = 1, VF = 1, A = 1, dx, 
        full.check = FALSE, full.output = FALSE)

Catatan:

• C : vektor konsentrasi pada titik tengah kisi sel.
• C.up, C.down : konsentrasi pada hulu dan hilir batas.
• flux.up,flux.down : flux dari dan keluar sistem pada hulu dan hilir batas.
• Jika terdapat tranport konvektif sepanjang hulu dan hilir batas, a.bl.up dan a.bl.down merupakan koefisiennya.
• D: Koefisien difusi.
• v: koefisien adveksi.
• VF: fraksi volume.
• A: fraksi area.
• dx: ketebalan kisi, baik nilai konstan atau vektor.
• full.check, full.output: nilai logik untuk memeriksa konsistensi dan mengatur output dari perhitungan. Keduanya FALSE secara default.

Ketika full.output = FALSE, nilai-nilai yang dikembalikan oleh trans.1D() adalah dC, yaitu: laju perubahan C di pusat setiap sel kisi karena transportasi, dan flux.up dan flux.down, yatu: fluks masuk dan keluar dari model di batas hulu dan hilir.

ReacTran juga memiliki fungsi untuk memperkirakan istilah difusi dan adveksi dalam model dua dan tiga dimensi, dan dalam koordinat silinder dan kutub. Jumlah input tumbuh dengan dimensi, tetapi input pada dasarnya sama seperti pada kasus 1D. Lihat halaman bantuan untuk tran.2D(), tran.3D(), tran.cylindrical(), dan tran.polar().

Namun penyempurnaan lain adalah fungsi tran.volume.1D(), yang memperkirakan istilah transportasi volumetrik dalam model 1D. Berbeda dengan tran.1D(), yang menggunakan fluks (massa per satuan luas per satuan waktu), tran.volume.1D() menggunakan aliran (massa per satuan waktu). Ini berguna untuk memodelkan saluran yang area lintas bagiannya berubah, ketika perubahan area tidak perlu dimodelkan secara eksplisit. Ini juga memungkinkan input lateral dari saluran samping.

10.4.7 ode.1D() atau steady.1D()

Setelah kisi telah diatur dan properti ditetapkan dan model transport telah diformulasikan dengan tran.1D() (atau analog 2D atau 3D-nya), maka ReacTran memanggil ode.1D() dari paket deSolve jika solusi time-dependent diperlukan, atau stable.1D() dari paket rootSolve jika solusi kondisi-stabil diinginkan. Sistem ODE yang dihasilkan dari metode pendekatan garis biasanya sparse dan non-stiff. Integrator dalam deSolve, seperti “lsoda” (metode default 1D) sangat cocok untuk menangani sistem persamaan tersebut. Jika sistem ODE non-stiff, maka “adams” umumnya merupakan metode yang baik.

10.5 Contoh Penerapan Paket ReacTran

10.5.1 Persamaan Adveksi-Difuksi 1D

Pada contoh kali ini, kita akan memodifikasi persamaan difusi satu dimensi yang telah dilakukan sebelumnya dengan menambahkan bagian adveksi serta diselesaikan menggunakan paket Reactran.

Siapkan kisi menggunakan fungsi setup.grid.1D() dan persiapkan nilai parameter persamaan.

library(ReacTran)
N     <- 100          # Number of grid cells
xgrid <- setup.grid.1D(x.up = 0, x.down = 1, N = N)
x     <- xgrid$x.mid  # Midpoints of grid cells
D     <- 1e-4         # Diffusion coefficient
v     <- 0.1          # Advection velocity

Bentuk fungsi yang menyatakan persamaan adveksi-difusi.

Diffusion <- function(t, Y, parms) {
    tran<-tran.1D(C=Y,C.up=0,C.down=0,D=D,v=v,dx= xgrid)
    list(dY = tran$dC, flux.up = tran$flux.up,
        flux.down = tran $flux.down)
}

Inisiasi konsentrasi awal pada kisi sel.

Yini <- rep(0,N) # Initial concentration = 0
Yini[2] <- 100   # Except in the second cell

Lakukan perhitungandengn menggunakan time step 0,01.

# Calculate for 5 time units
times <- seq(from = 0, to = 5, by = 0.01)
out <- ode.1D(y = Yini, times = times, func = Diffusion,
             parms = NULL,dimens = N)

Visualisasikan hasil perhitungan.

Gambar 10.12: Visualisasi hasil simulasi persamaan adveksi-difusi menggunakan paket ReacTran

10.5.2 Persamaan Gelombang 1D

Persamaan (10.16) dapat diselesaikan dengan cara yang sama dengan persamaan difusi dengan mengatur nilai \(c^2=D\), memisalkan \(W=u\) dan \(\frac{\partial u}{\partial t}=v\), dan menyelesaikannya dengan cara yang familiar untuk variabel berpasangan \(\left(u,v\right)\). Di sini kita misalkan persamaan gelombang 1D untuk senar yang dipetik, yang awalnya ditahan pada \(0\) amplitudo untuk \(x <−25\) dan \(x> 25\), dan direntangkan secara linear hingga maksimum pada \(x = 0\). ode.1D() digunakan untuk menyelesaikan set himpunan ODE simultan dengan \(c = 1\).

Langkah pertama yang harus dilakukan adalah melakukan penetapan parameter.

dx    <- 0.2          # Spacing of grid cells
# String extends from -100 to +100
xgrid <- setup.grid.1D(x.up = -100, 
                       x.down = 100, dx.1 = dx)
x     <- xgrid$x.mid  # midpoints of grid cells
N     <- xgrid$N      # number of grid cells

Menetapkan kondisi awal seperti ketinggian senar dan kecepatan.

uini  <- rep(0,N) # String height vector before stretching
vini  <- rep(0,N) # Initial string velocity vector
displ <- 10       # Initial displacement at center of string
# Impose initial triangular height profile on string between - 25
for(i in 1:N) {
  if (x[i] > -25 & x[i] <= 0) uini[i] = displ/25*(25 + x[i])else
  if (x[i] > 0 & x[i] < 25) uini[i] = displ/25*(25 - x[i])
}
yini  <- c(uini, vini)

Menetapkan deret waktu yang digunakan dalam simulasi.

times <- seq(from = 0, to = 50, by = 1)

Membangun fungsi yang akan diselesaikan secara numerik.

 wave <- function(t,y,parms) {
    u <- y[1:N] # Separate displacement and velocity vectors
    v <- y[(N+1):(2*N)]
    du<-v
    dv<-tran.1D(C=u,C.up=0,C.down=0,D=1,dx=xgrid)$dC
    return(list(c(du, dv))) 
}

Selesaikan persamaan menggunakan fungsi ode.1D() dengan metode adams.

out <- ode.1D(func = wave, y = yini, times = times,
             parms = NULL, method = "adams",
             dimens = N, names = c("u", "v"))
u <- subset(out, which = "u") # Extract displacement vector

Visualisasikan hasil perhitungan.

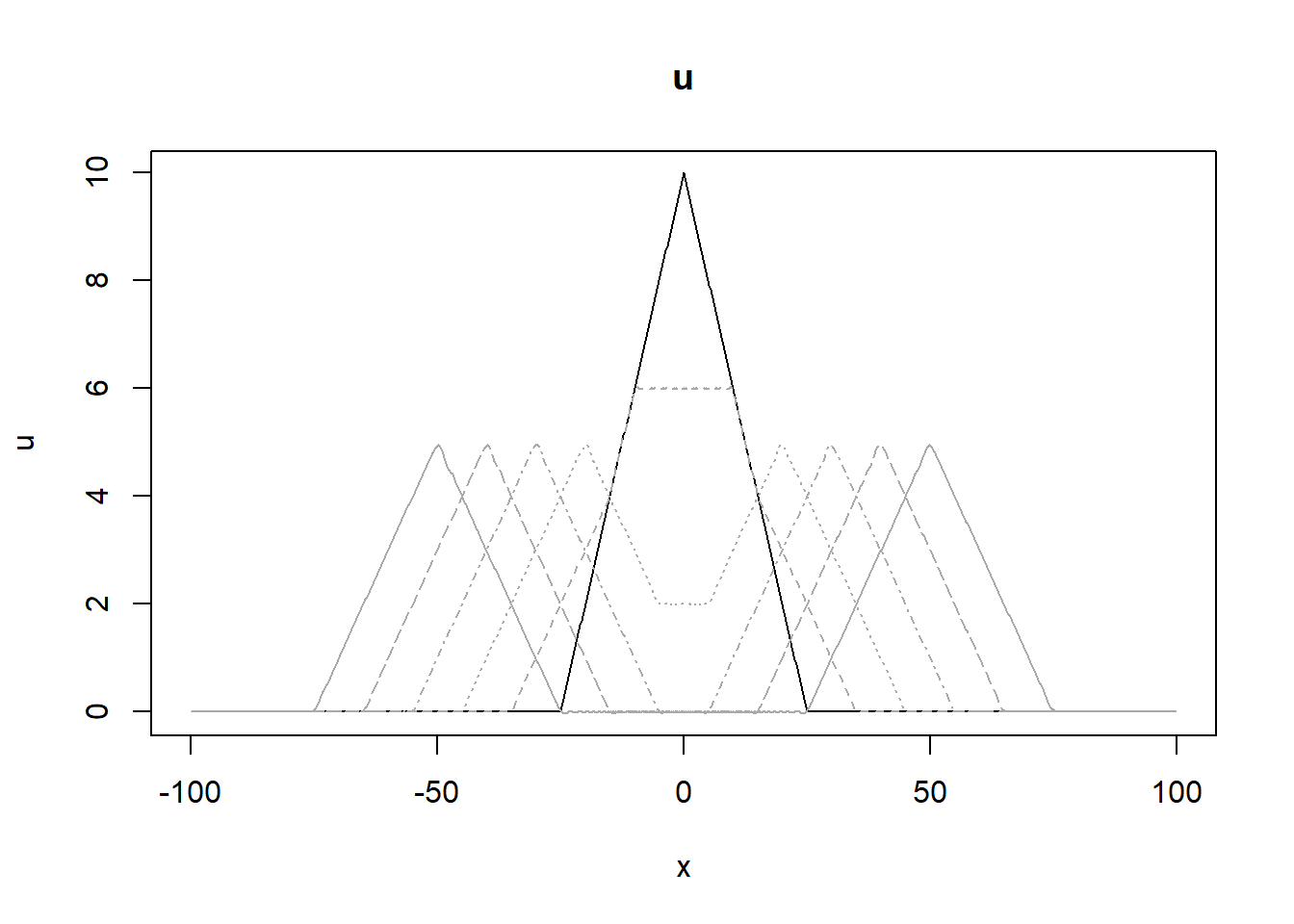
Gambar 10.13: Visualisasi hasil simulasi persamaan gelombang menggunakan paket ReacTran

10.5.3 Persamaan Laplace

Kita akan kembali melakukan simulasi terhadap Persamaan (10.19) menggunakan metode lainnya. Pada contoh kali ini, gradien pada sumbu \(y\) bernilai -1. Gradien hanyalah fluks, \(D \left(\partial C = \partial x\right)\), dengan \(D\) set sama dengan 1. Fungsi penyelesaian yang digunakan adalah steady.2D(), karena tidak ada ketergantungan waktu dalam persamaan. Sebagai kondisi awal yang arbitrer, kami menggunakan nomor acak \(N_x \times N_y\) yang terdistribusi secara seragam. Kita juga harus menentukan \(nspec\), jumlah spesies dalam model (hanya satu, potensi, dalam hal ini), \(dimens\), vektor dengan 2 nilai dengan jumlah sel dalam arah \(x\) dan \(y\), dan lrw, panjang array. Lihat halaman bantuan untuk steady.2D() untuk informasi lebih detail.

Langkah pertama dalam melakukan simulasi adalah menetapkan parameter model.

Nx    <- 100
Ny    <- 100
xgrid <- setup.grid.1D(x.up = 0, x.down = 1, N = Nx)
ygrid <- setup.grid.1D(x.up = 0, x.down = 1, N = Ny)
x     <- xgrid$x.mid
y     <- ygrid$x.mid

Bentuk fungsi yang akan diselesaikan secara numerik.

laplace <- function(t, U, parms) {
    w = matrix(nrow = Nx, ncol = Ny, data = U)
    dw = tran.2D(C = w, C.x.up = 0, C.y.down = 0,
    flux.y.up = 0,
    flux.y.down = -1,
    D.x = 1, D.y = 1,
    dx = xgrid, dy = ygrid)$dC
    list(dw) 
}

Mulia dengan bilangan acak uniform sebagai kondisi awal, kemudian selesaikan untuk memperoleh nilai pada kondisi tunak dan buat plot kontur.

out = steady.2D(y = runif(Nx*Ny), func = laplace, 
                  parms = NULL,nspec = 1, 
                  dimens = c(Nx, Ny), lrw = 1e7)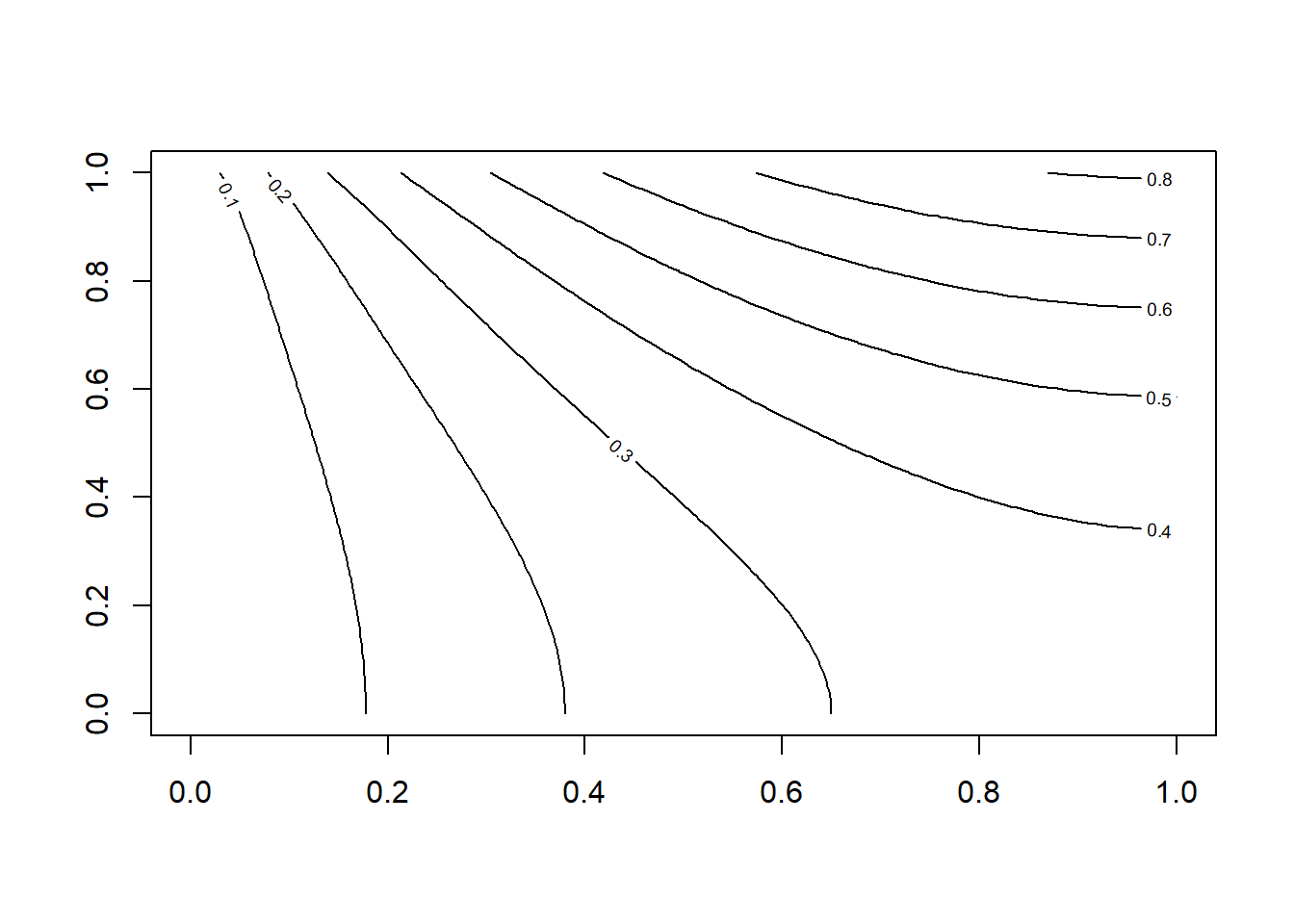

Gambar 10.14: Visualisasi hasil simulasi persamaan laplace pada kondisi tunak menggunakan paket ReacTran

10.5.4 Persamaan Poisson untuk Dipol

Pada contoh kali ini, kita akan menyelesaikan persamaan Poisson untuk dipol yang ditampilkan pada Persamaan (10.21).

\[\begin{equation} \frac{\partial^2w}{\partial x^2}+\frac{\partial^2w}{\partial y^2}=-\frac{\rho}{\varepsilon_0} \tag{10.21} \end{equation}\]

untuk dipol yang terletak di tengah selembar persegi jika tidak pada 0 potensial. Untuk mempermudah, kita dapat mengatur semua faktor skala sama dengan satu. Dalam definisi fungsi poisson, nilai-nilai dalam matriks \(N_x \times N_y\) w adalah input melalui vektor data \(U\). Seperti dalam persamaan Laplace di atas, kita menetapkan nilai awal \(w\) pada sel-sel grid sama dengan angka acak uniform.

Langkah pertama dalam melakukan simulasi adalah menetapkan parameter model.

Nx    <- 100
Ny    <- 100
xgrid <- setup.grid.1D(x.up = 0, x.down = 1, N = Nx)
ygrid <- setup.grid.1D(x.up = 0, x.down = 1, N = Ny)
x     <- xgrid$x.mid
y     <- ygrid$x.mid

Cari nilai \(x\) dan \(y\) pada titik kisi yang mendekati \(\left(0,4;0,5\right)\) untuk muatan positif dan \(\left(0,6;0,5\right)\) untuk muatan negatif.

# x and y coordinates of positive and negative charges
ipos <- which.min(abs(x - 0.4))
jpos <- which.min(abs(y - 0.50))
ineg <- which.min(abs(x - 0.6))
jneg <- which.min(abs(y - 0.50))

Bentuk fungsi Poisson yang akan diselesaikan secara numerik.

poisson <- function(t, U, parms) {
    w = matrix(nrow = Nx, ncol = Ny, data = U)
    dw = tran.2D(C = w, C.x.up = 0, C.y.down = 0,
    flux.y.up = 0,
    flux.y.down = 0,
    D.x = 1, D.y = 1,
    dx = xgrid, dy = ygrid)$dC
    dw[ipos,jpos] = dw[ipos,jpos] + 1
    dw[ineg,jneg] = dw[ineg,jneg] - 1
    list(dw) 
}

Selesaikan untuk kondisi tunak dan buat visualisasinya.

out <- steady.2D(y = runif(Nx*Ny), 
                 func = poisson, 
                 parms = NULL, 
                 nspec = 1, 
                 dimens = c(Nx, Ny), 
                 lrw = 1e7)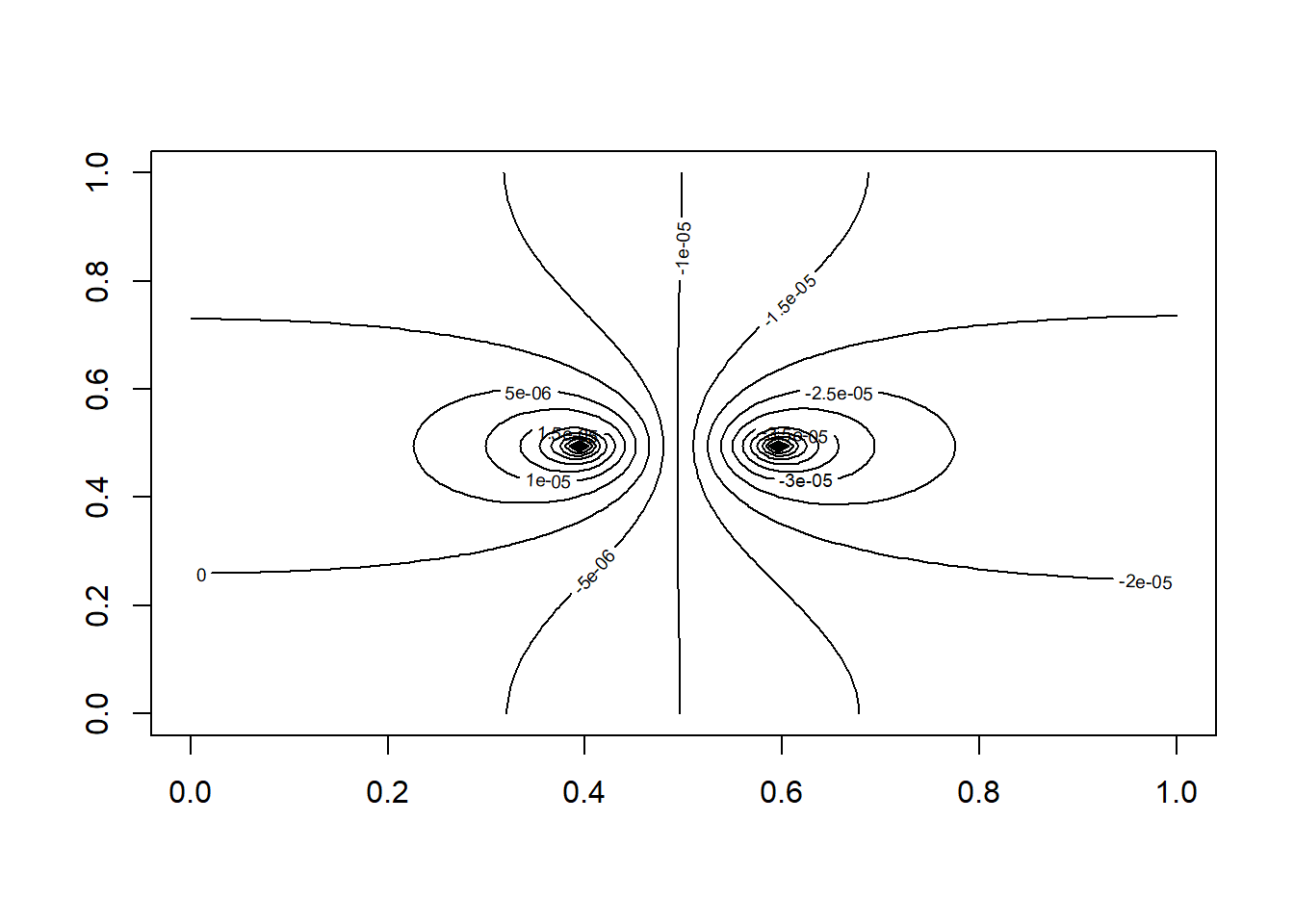

Gambar 10.15: Visualisasi hasil simulasi persamaan Poisson pada kondisi tunak menggunakan paket ReacTran

10.6 Studi Kasus

10.6.1 Model Lotka-Voltera

Model Lotka-Voltera merupakan model yang menggambarkan interaksi antara predator dan mangsa. Pada studi kasus kali ini model yang akan digunakan merupakan model dengan 3 bentuk interaksi yaitu: tanaman \(u\), herbivora \(v\), dan karnivora \(w\). Sistem persamaan diferensial sistem tersebut ditampilkan pada kumpulan persamaan berikut:

\[\begin{equation} \frac{du}{dt}=au-\alpha_1f_1\left(u,v\right) \tag{10.22} \end{equation}\]

\[\begin{equation} \frac{dv}{dt}=-bv+\alpha_1f_1\left(u,v\right)-\alpha_2f_2\left(v,w\right) \tag{10.23} \end{equation}\]

\[\begin{equation} \frac{dw}{dt}=-c\left(w-w\ast\right)+\alpha_2f_2\left(v,w\right) \tag{10.24} \end{equation}\]

dimana \(w\ast\) merupakan tingkat predasi minimum untuk menstabilkan populasi ketika populasi mangsa rendah. Interaksi antar komponen digambarkan ke dalam bentuk persamaan logistik.

\[\begin{equation} f_i\left(x,y\right)=\frac{xy}{1+k_ix} \tag{10.25} \end{equation}\]

Langkah pertama untuk menyelesaikan model adalah melakukan penentuan parameter model dan pembentukan fungsi model.

library(deSolve)
f <- function(x,y,k){x*y/(1+k*x)}
model <- function(t, xx, parms) {
    u = xx[1] # plant resource
    v = xx[2] # herbivore
    w = xx[3] # carnivore
    with(as.list(parms),{
    du = a*u - alpha1*f(u, v, k1)
    dv = -b*v + alpha1*f(u, v, k1) - alpha2*f(v, w, k2)
    dw = -c*(w - wstar) + alpha2*f(v, w, k2)
    list(c(du, dv, dw))
})}

times <- seq(0, 200, 0.1)
parms <- c(a=1, b=1, c=10, alpha1=0.2, alpha2=1,
k1<-0.05, k2=0, wstar=0.006)
xstart <- c(u=10, v=5, w=0.1)

Proses iterasi selanjutnya akan menggunakan metode lsoda, dimana metode iterasi ini dapat berganti secara otomatis dalam menangani sistem persamaan diferensial stiff dan non-stiff. Persamaan diferensial dikatakan stiff apabila variabel dependen berubah berdasarkan 2 atau lebih variabel independen yang sangat berbeda skalanya.

out = ode(xstart, times, model, parms, 
          method ="lsoda")

Ketiga variabel selanjutnya divisualisasikan.

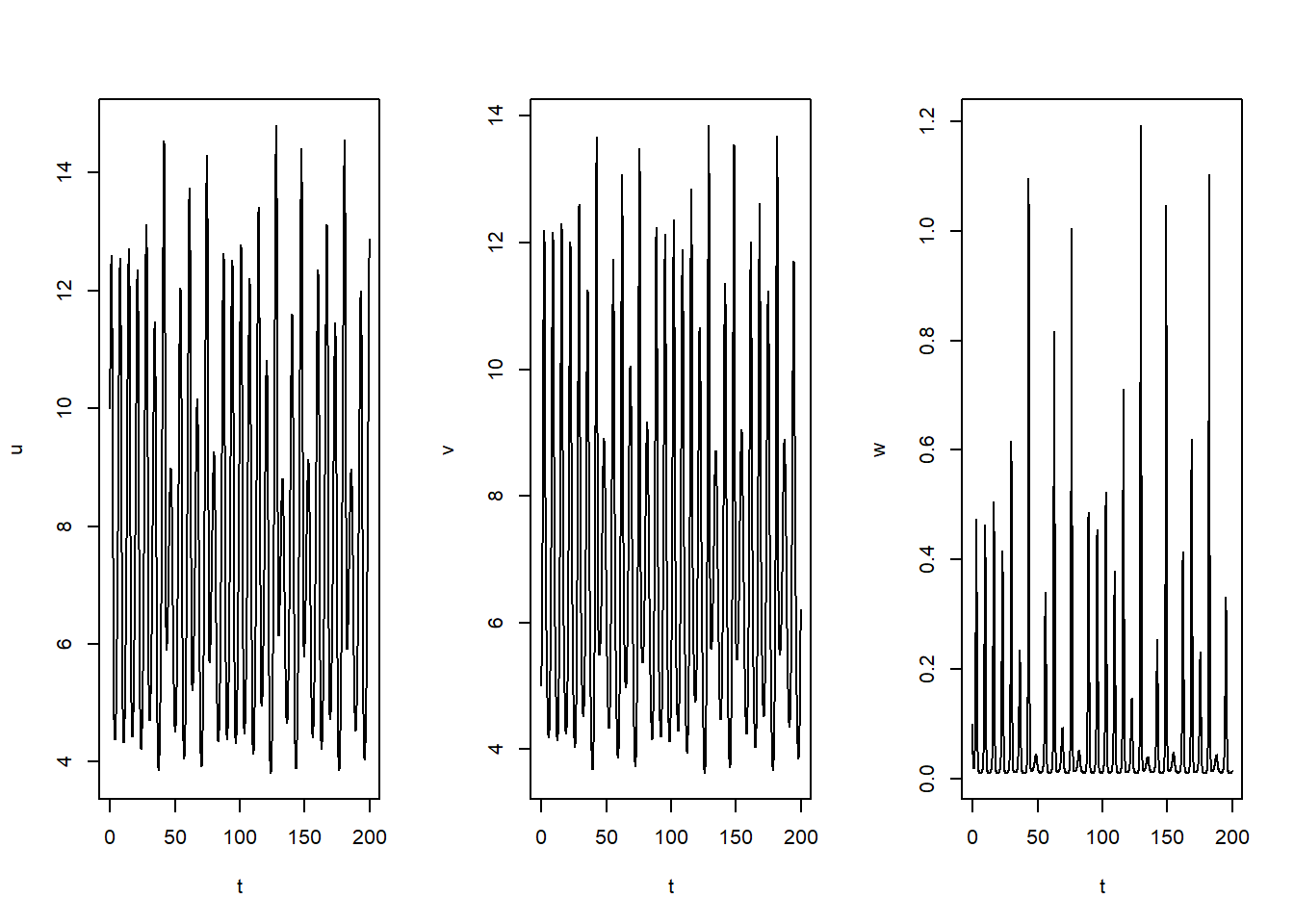
Gambar 10.16: Visualisasi simulasi model Lotka-Voltera

10.7 Referensi

1. Bloomfield, V.A. 2014. Using R for Numerical Analysis in Science and Engineering. CRC Press.
2. Chapra, S.C. Canale, R.P. 2015. Numerical Methods For Engineers, Seventh Edition. Mc Graw Hill.
3. Griffiths, G.W. 2016. Numerical analysis using R : solutions to ODEs and PDEs. Cambridge University Press.
4. Howard, J.P. 2017. Computational Methods for Numerical Analysis with R. CRC Press.
5. Kreyszig, E. 2011. Advanced Engineering Mathematics, 10th Edition. John Wiley & Sons.
6. Soetaert,K., Cash J., Mazzia F. 2012. Solving Differential Equations in R. Springer.
7. Suparno, S. 2008. Komputasi untuk Sains dan Teknik Edisi II. Departemen Fisika-FMIPA Universitas Indonesia.

10.8 Latihan

1. Tunjukkan 10 hasil iterasi metode Euler untuk persamaan diferensial \(f'\left(x,y\right)=y\) dimana \(x_0=0\), \(y_0=2\) dan step size \(h=0,1\)!
2. Kerjakan lagi soal no.1 dengan menggunakan metode lainnya dan bandingkan seluruh metode tersebut menggunakan penyelesaian analitiknya!
3. Bentuk kembali fungsi rk4sys() menggunakan algoritma metode Adams-Bashforth dan namai fungsi tersebut adamsys()!