Chapter 12 Pemodelan Data
Pada Chapter 12, kita akan membahas cara membentuk model statistik menggunakan R. Terdapat 2 buah jenis model yang akan dibahas pada Chapter ini, yaitu: regresi dan klasifikasi. Untuk informasi terkait cara untuk melakukan inferensi berdasarkan hasil yang diperoleh dan cara untuk melakukan prediksi menggunakan model yang terbentuk tidak akan dijelaskan dalam buku ini. Pembaca dapat membaca lebih lanjut pada referensi berikut:
12.1 Regresi Linier
Regresi linier merupakan model sederhana yang paling sering dibahas dalam buku-buku statistika. Modelnya cukup sederhana dimana kita berusaha membentuk model dengan pendekatan garis linier dengan prinsip meminimalkan jumlah kuadrat residual pada data. Model yang tebentuk akan menghasilkan dua buah nilai yaitu nilai konstanta (titik potong sumbu y) dan nilai slope kurva. Model yang terbentuk secara umum haruslah memenuhi asumsi dasar model linier berikut:
- Asumsi liniearitas: kurva relasi yang terbentuk antara variabel independen terhadap variabel dependen harus linier. Asumsi ini dapat dipelajari melalui plot residual terhadap nilai fitted value. Jika asumsi liniearitas terpenuhi, maka titik-titik residual yang di plotkan akan membentuk pola acak. Jika pada plot yang dihasilkan terbentuk pola tidak linear maka transformasi data pada variabel prediktor atau independen diperlukan.
- Error atau residu berdristribusi normal: normalitas error di cek menggunakan qq-plot atau uji normalitas yang telah dibahas pada Chapter 11.4.
- Outlier dan high influence point: kedua pengamatan tersebut dideteksi melalui qq-plot, plot residual terhadap nilai fitted value, dan plot residuals vs leverage. Jika outlier terjadi akibat adanya error selama pengukuran maka outlier dapat dihilangkan.
- Error bersifat independen: independensi residual dapat dideteksi melaui plot korelasi serial dengan mengeplotkan \(r_i\) vs \(r_{i-1}\).
- Varians bersifat konstan: Varians bersifat konstan dicek melalui plot square root standardize residual vs fitted value. Pada kasus dimana varians tidak bersifat konstan, kita dapat memberikan bobot pada model yang akan kita bentuk (weighted least square), dimana bobot yang diberikan proporsional dengan invers varians.
- multikolinearitas: tidak ada variabel dependen yang saling berfkorelasi. Multikolinearitas dapat dideteksi melalui plot matriks korelasi. Pada model adanya kolinearitas ditunjukkan dari nilai variance inflation factor (VIF) yang tinggi. Secara umum nilai VIF terkecil sebesar 1 dan jika kolinearitas terjadi nilainya dapat lebih besar dari 5 atau 10. Untuk mengatasi kolinearitas pada model dapat dilakukan dengan dua cara, yaitu: mengeluarkan variabel dengan nilai VIF yang tinggi pada model atau menggabungkan dua variabel prediktor yang saling berkorelasi menjadi satu variabel baru.
Pembentukan model linier pada R dilakukan dengan menggunakan fungsi lm(). Format umum fungsi tersebut adalah sebagai berikut:
Catatan:
formula: formula model yang hendak dibentuk.data: data yang digunakan untuk membentuk model.subset: subset data yang akan digunakan dalam pembentukan model.weight: nilai pembobotan dalam pembentukan model.
12.1.1 Regrasi Linier Sederhana (Simple Linear Regression)
Pada Chapter 12.1.1 akan diberikan contoh pembentukan model linier sederhana menggunakan dataset Boston dari library MASS dengan jumlah observasi sebesar 506 observasi. Pada contoh kali ini kita akan mencoba membentuk model dengan variabel dependen berupa medv (median harga rumah) dan variabel independen berupa lstat (persen rumah tangga dengan status ekonomi menengah ke bawah). Berikut adalh sintaks untuk membentuk model tersebut:
## Analysis of Variance Table
##
## Response: medv
## Df Sum Sq Mean Sq F value Pr(>F)
## lstat 1 23244 23244 602 <2e-16 ***
## Residuals 504 19472 39
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = medv ~ lstat, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.17 -3.99 -1.32 2.03 24.50
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 34.5538 0.5626 61.4 <2e-16 ***
## lstat -0.9500 0.0387 -24.5 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.22 on 504 degrees of freedom
## Multiple R-squared: 0.544, Adjusted R-squared: 0.543
## F-statistic: 602 on 1 and 504 DF, p-value: <2e-16Plot residual disajikan pada Gambar 12.1.
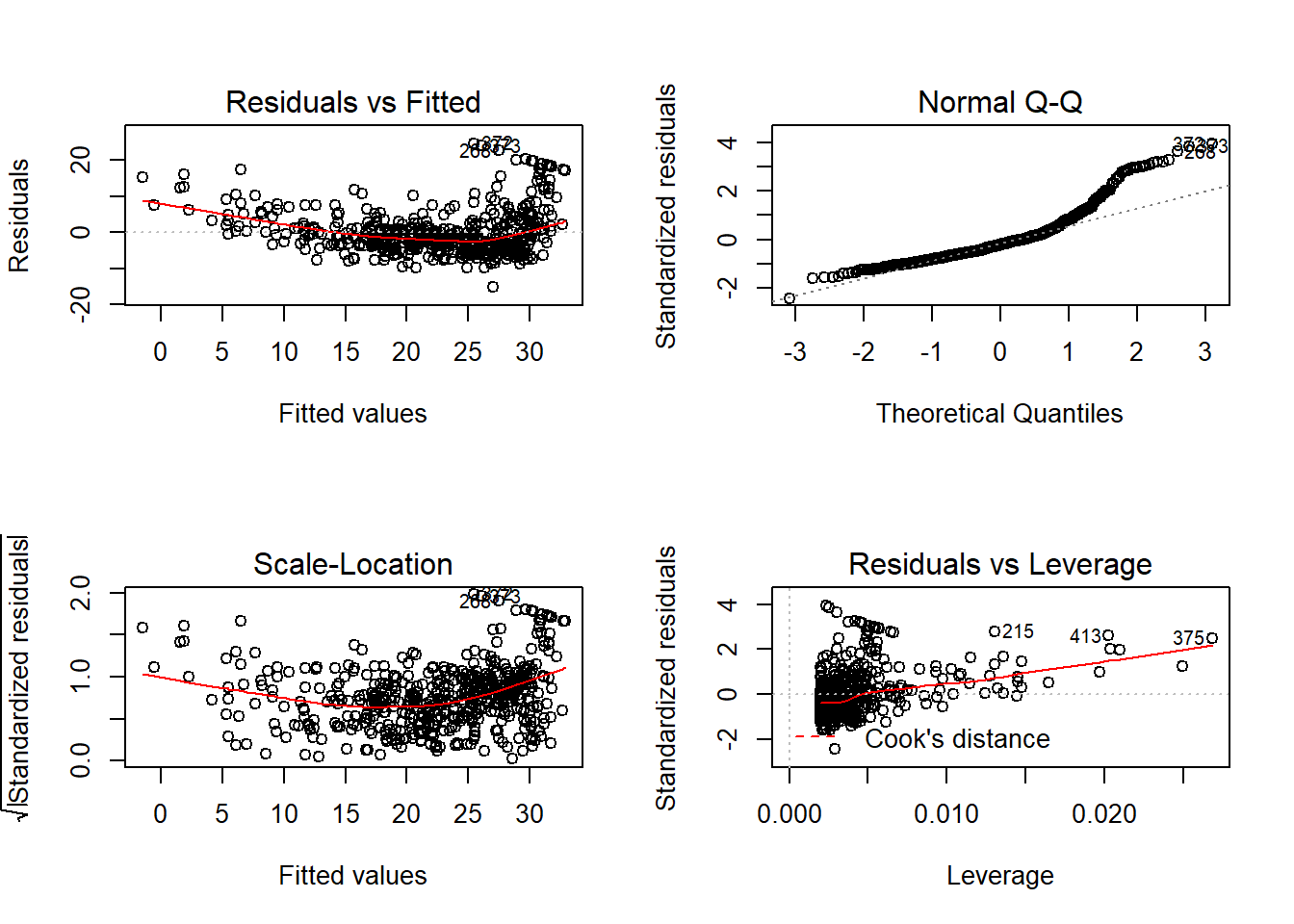
Gambar 12.1: Analisis residual model linier medv vs lstat pada dataset Boston.
Berdasarkan hasil plot dapat dilihat bahwa seluruh asumsi model linier tidak terpenuhi. Selain melalui plot residual, uji asumsi model linier dapat juga dilakukan secara matematis. Berikut adalah sintaks yang digunakan:
##
## Shapiro-Wilk normality test
##
## data: residuals(lm.fit)
## W = 0.88, p-value <2e-16## Warning: package 'lmtest' was built under R version
## 3.5.3##
## studentized Breusch-Pagan test
##
## data: lm.fit
## BP = 15, df = 1, p-value = 8e-05# error bersifat independen
# (error tidak bersifat independen)
dwtest(lm.fit, alternative = "two.sided")##
## Durbin-Watson test
##
## data: lm.fit
## DW = 0.89, p-value <2e-16
## alternative hypothesis: true autocorrelation is not 0# deteksi outlier (stdres > 2)
sres <- rstandard(lm.fit)
sres[which(abs(sres)>2)] # nomor observasi outlier## 99 142 162 163 164 167 181
## 2.038 2.038 2.759 2.787 3.000 3.058 2.003
## 187 196 204 205 215 225 226
## 3.172 2.947 2.833 2.934 2.789 2.287 3.200
## 229 234 257 258 262 263 268
## 2.560 2.822 2.001 3.274 2.488 3.201 3.628
## 281 283 284 369 370 371 372
## 2.326 2.308 2.976 2.991 3.063 2.946 3.946
## 373 375 413 506
## 3.847 2.498 2.601 -2.444# influential observation
# observasi > percentil 50
# tidak ada observasi dengan jarak cook yang extrim
cooksD <- cooks.distance(lm.fit)
p50 <- qf(0.5, df1=2, df2=560-2)
any(cooksD>p50)## [1] FALSE12.1.2 Regresi Linier Berganda (Multiple Linier Regression)
Pada Chapter 12.1.2, kita akan membuat tiga buah model regresi linier. Model pertama akan menambahkan variabel age (usia bangunan) pada model sebelumnya, model kedua akan menggunakan seluruh ariabel yang ada, dan model ketiga akan melakukan pembaharuan dengan mengeluarkan variabel dengan VIF paling tinggi dari model kedua. Berikut adalah sintaks untuk membentuk ketiag model tersebut:
## Analysis of Variance Table
##
## Response: medv
## Df Sum Sq Mean Sq F value Pr(>F)
## lstat 1 23244 23244 609.95 <2e-16 ***
## age 1 304 304 7.98 0.0049 **
## Residuals 503 19168 38
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = medv ~ lstat + age, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.98 -3.98 -1.28 1.97 23.16
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 33.2228 0.7308 45.46 <2e-16 ***
## lstat -1.0321 0.0482 -21.42 <2e-16 ***
## age 0.0345 0.0122 2.83 0.0049 **
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.17 on 503 degrees of freedom
## Multiple R-squared: 0.551, Adjusted R-squared: 0.549
## F-statistic: 309 on 2 and 503 DF, p-value: <2e-16## lstat age
## 1.569 1.569Berdasarkan hasil perhitungan diketahui nilai VIF dari model < 10, sehingga asumsi multikolinearitas terpenuhi. Untuk asumsi lainnya dapat dicek pada plot residual yang ditampilkan pada Gambar 12.2.
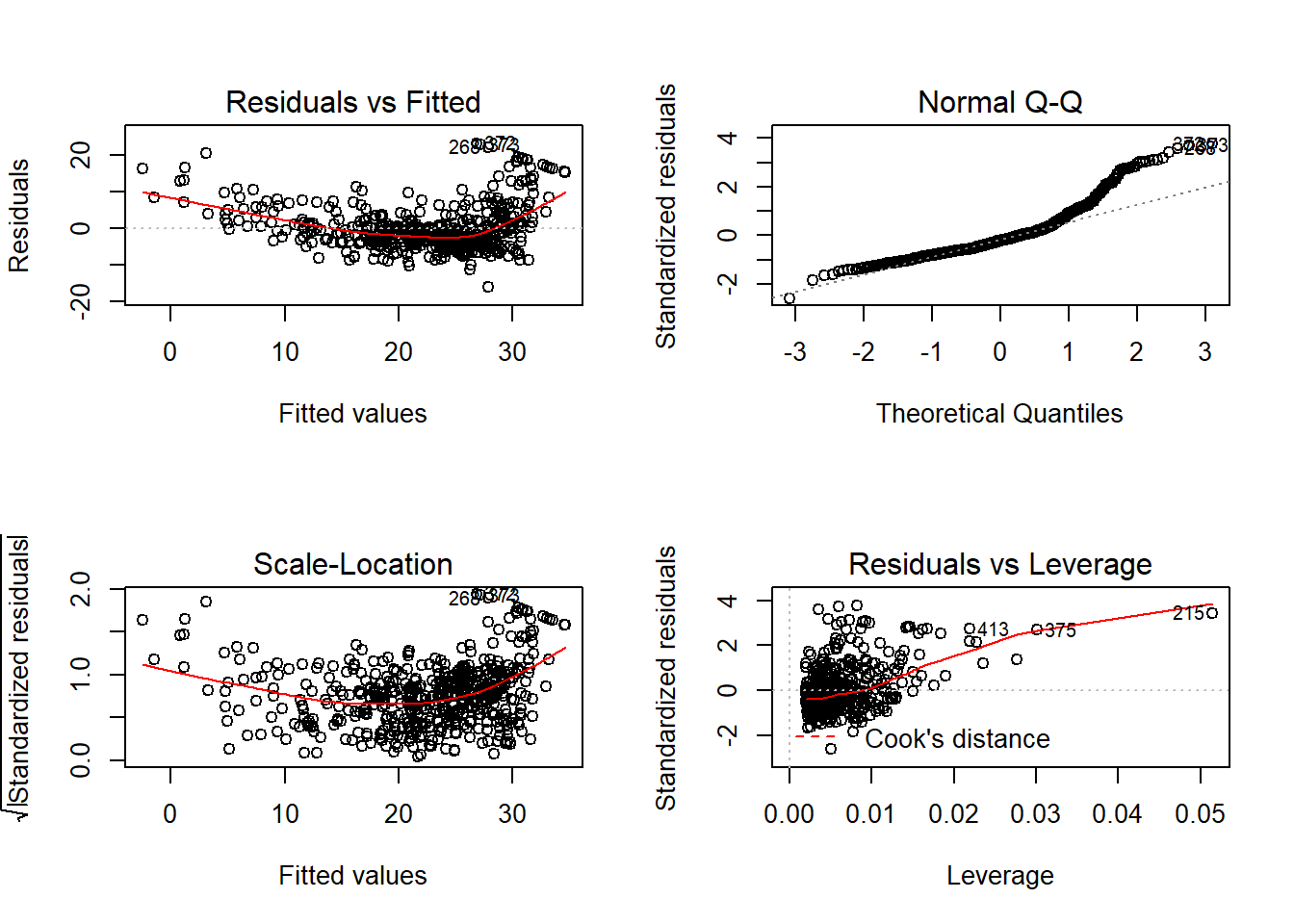
Gambar 12.2: Analisis residual model linier 1 pada dataset Boston.
## Analysis of Variance Table
##
## Response: medv
## Df Sum Sq Mean Sq F value Pr(>F)
## crim 1 6441 6441 286.03 < 2e-16 ***
## zn 1 3554 3554 157.85 < 2e-16 ***
## indus 1 2551 2551 113.30 < 2e-16 ***
## chas 1 1530 1530 67.94 1.5e-15 ***
## nox 1 76 76 3.39 0.06635 .
## rm 1 10938 10938 485.75 < 2e-16 ***
## age 1 90 90 4.01 0.04581 *
## dis 1 1780 1780 79.03 < 2e-16 ***
## rad 1 34 34 1.52 0.21883
## tax 1 330 330 14.64 0.00015 ***
## ptratio 1 1309 1309 58.15 1.3e-13 ***
## black 1 593 593 26.35 4.1e-07 ***
## lstat 1 2411 2411 107.06 < 2e-16 ***
## Residuals 492 11079 23
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = medv ~ ., data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.594 -2.730 -0.518 1.777 26.199
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.65e+01 5.10e+00 7.14 3.3e-12 ***
## crim -1.08e-01 3.29e-02 -3.29 0.00109 **
## zn 4.64e-02 1.37e-02 3.38 0.00078 ***
## indus 2.06e-02 6.15e-02 0.33 0.73829
## chas 2.69e+00 8.62e-01 3.12 0.00193 **
## nox -1.78e+01 3.82e+00 -4.65 4.2e-06 ***
## rm 3.81e+00 4.18e-01 9.12 < 2e-16 ***
## age 6.92e-04 1.32e-02 0.05 0.95823
## dis -1.48e+00 1.99e-01 -7.40 6.0e-13 ***
## rad 3.06e-01 6.63e-02 4.61 5.1e-06 ***
## tax -1.23e-02 3.76e-03 -3.28 0.00111 **
## ptratio -9.53e-01 1.31e-01 -7.28 1.3e-12 ***
## black 9.31e-03 2.69e-03 3.47 0.00057 ***
## lstat -5.25e-01 5.07e-02 -10.35 < 2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.75 on 492 degrees of freedom
## Multiple R-squared: 0.741, Adjusted R-squared: 0.734
## F-statistic: 108 on 13 and 492 DF, p-value: <2e-16## crim zn indus chas nox rm
## 1.792 2.299 3.992 1.074 4.394 1.934
## age dis rad tax ptratio black
## 3.101 3.956 7.484 9.009 1.799 1.349
## lstat
## 2.941Berdasarkan hasil perhitungan diperoleh nilai VIF untuk seluruh varaibel prediktor dalam model < 10, sehingga asumsi multikolinearitas terpenuhi. Untuk asumsi lainnya dapat dicek pada plot residual yang ditampilkan pada Gambar 12.3.
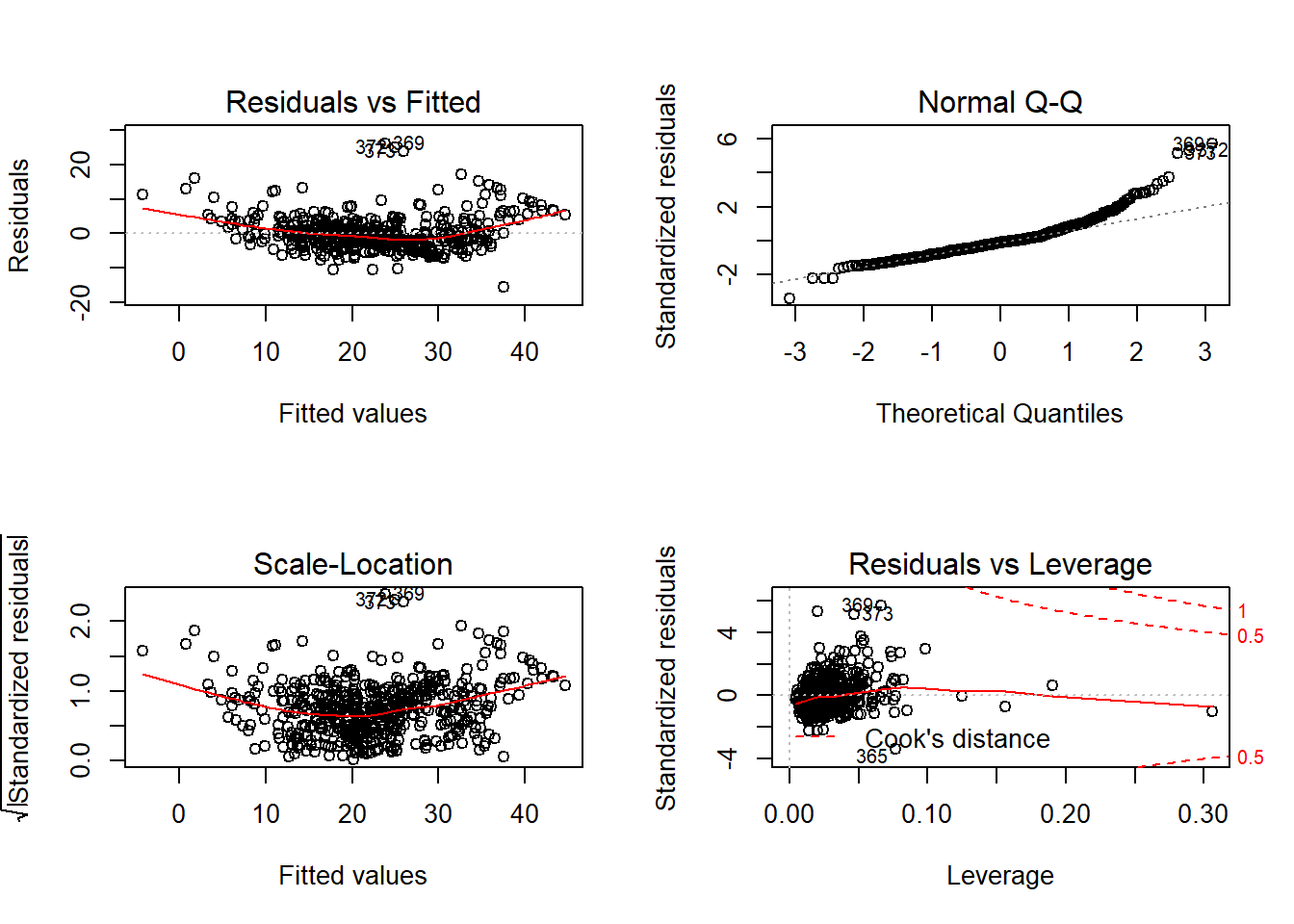
Gambar 12.3: Analisis residual model linier 2 pada dataset Boston.
Pada model ketiga, kita akan mencoba untuk melakukan pembaharuan pada model kedua dengan melakukan drop variabel dengan vif yang paling tinggi. Pada hasil perhitungan sebelumnya, variabel tax (pajak) memiliki nilai VIF yang paling tinggi, sehingga pada model ketiga variabel tersebut tidak disertakan. Terdapat dua cara untuk melakukannya berikut adalah sintaks yang digunakan:
# Model 3 (cara 1)
lm.fit3 <- lm(medv~.-tax, data=Boston)
# Model 3 (cara 2)
lm.fit3 <- update(lm.fit2, ~.-tax)
anova(lm.fit3)## Analysis of Variance Table
##
## Response: medv
## Df Sum Sq Mean Sq F value Pr(>F)
## crim 1 6441 6441 280.48 < 2e-16 ***
## zn 1 3554 3554 154.78 < 2e-16 ***
## indus 1 2551 2551 111.10 < 2e-16 ***
## chas 1 1530 1530 66.62 2.8e-15 ***
## nox 1 76 76 3.32 0.069 .
## rm 1 10938 10938 476.32 < 2e-16 ***
## age 1 90 90 3.93 0.048 *
## dis 1 1780 1780 77.49 < 2e-16 ***
## rad 1 34 34 1.49 0.223
## ptratio 1 1401 1401 61.02 3.4e-14 ***
## black 1 612 612 26.63 3.6e-07 ***
## lstat 1 2388 2388 103.99 < 2e-16 ***
## Residuals 493 11321 23
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = medv ~ crim + zn + indus + chas + nox + rm + age +
## dis + rad + ptratio + black + lstat, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.145 -2.914 -0.566 1.744 26.311
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.46e+01 5.12e+00 6.76 3.9e-11 ***
## crim -1.07e-01 3.32e-02 -3.22 0.00138 **
## zn 3.64e-02 1.35e-02 2.69 0.00735 **
## indus -6.78e-02 5.58e-02 -1.21 0.22532
## chas 3.03e+00 8.64e-01 3.51 0.00049 ***
## nox -1.87e+01 3.85e+00 -4.86 1.6e-06 ***
## rm 3.91e+00 4.21e-01 9.29 < 2e-16 ***
## age -6.05e-04 1.33e-02 -0.05 0.96380
## dis -1.49e+00 2.01e-01 -7.39 6.3e-13 ***
## rad 1.35e-01 4.13e-02 3.26 0.00118 **
## ptratio -9.85e-01 1.32e-01 -7.48 3.5e-13 ***
## black 9.55e-03 2.71e-03 3.52 0.00047 ***
## lstat -5.22e-01 5.12e-02 -10.20 < 2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.79 on 493 degrees of freedom
## Multiple R-squared: 0.735, Adjusted R-squared: 0.729
## F-statistic: 114 on 12 and 493 DF, p-value: <2e-16## crim zn indus chas nox rm
## 1.792 2.184 3.226 1.058 4.369 1.923
## age dis rad ptratio black lstat
## 3.098 3.954 2.837 1.789 1.348 2.941Plot residual ditampilkan pada Gambar 12.4.
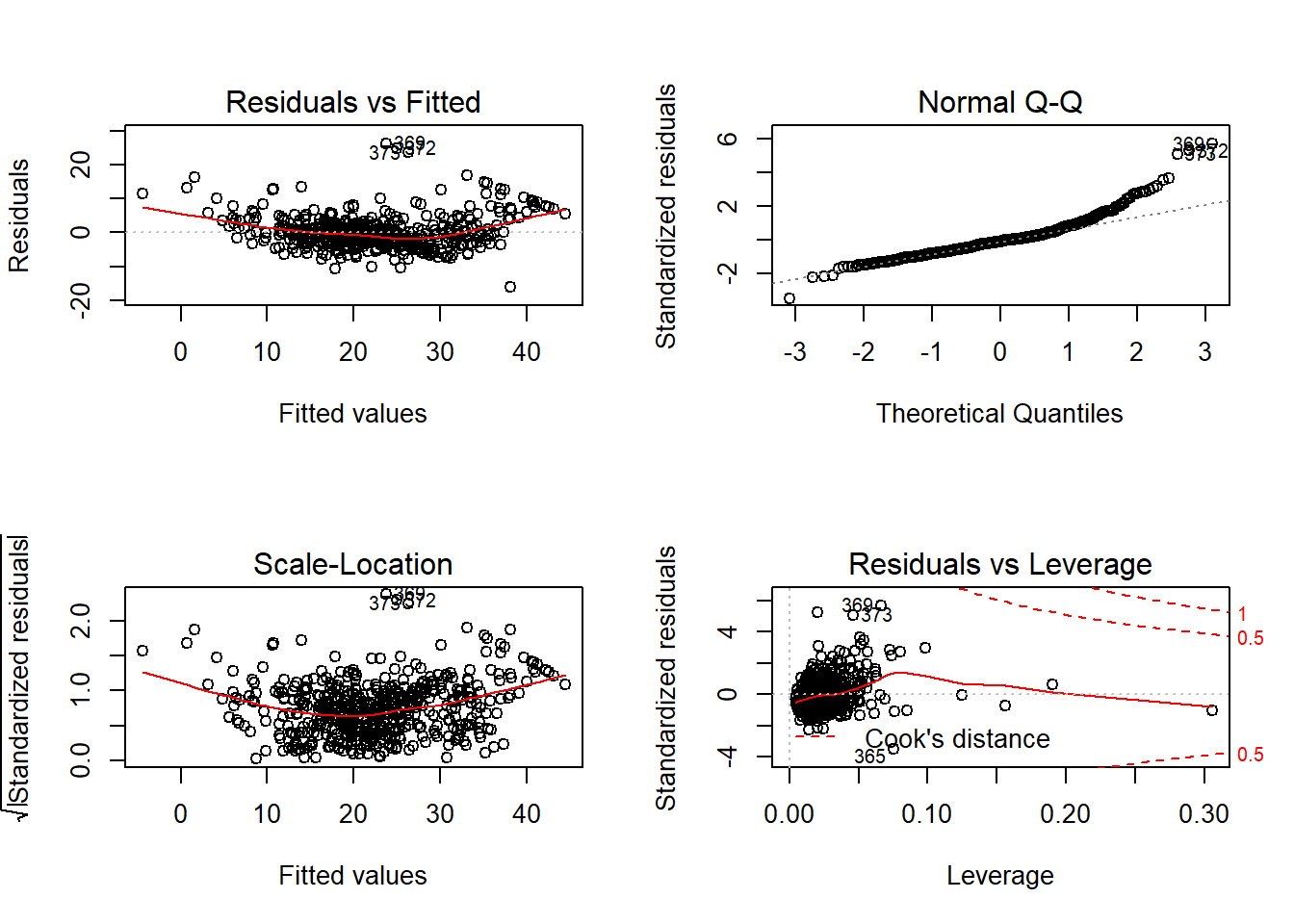
Gambar 12.4: Analisis residual model linier 3 pada dataset Boston.
12.1.3 Model Linier dengan Interaksi Antar Variabel Prediktor
Interaksi antar variabel pada model linier dapat dengan mudah dimasukkan kedalam fungsi lm(). Terdapat dua buah cara untuk melakukannya. Cara pertama dengan menggunakan tanda : pada formula (contoh: \(y1 ~ x1+x2+x1:x2\)). Tanda : menyatakan formula persamaan linier memasukkan interaksi antar variabel prediktor di dalamnya. Cara kedua adalah dengan menggunakan tanda *. Cara ini lebih sederhana, dimana fungsi lm() akan secara otomatis menerjemahkannya sebagai serangkaian variabel tunggal dan interaksinya. Berikut adalah contoh penerapannya menggunakan kedua cara tersebut:
## Analysis of Variance Table
##
## Response: medv
## Df Sum Sq Mean Sq F value Pr(>F)
## lstat 1 23244 23244 614.85 <2e-16 ***
## age 1 304 304 8.05 0.0047 **
## lstat:age 1 190 190 5.04 0.0252 *
## Residuals 502 18978 38
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = medv ~ lstat + age + lstat:age, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.81 -4.04 -1.33 2.08 27.55
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 36.088536 1.469835 24.55 < 2e-16 ***
## lstat -1.392117 0.167456 -8.31 8.8e-16 ***
## age -0.000721 0.019879 -0.04 0.971
## lstat:age 0.004156 0.001852 2.24 0.025 *
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.15 on 502 degrees of freedom
## Multiple R-squared: 0.556, Adjusted R-squared: 0.553
## F-statistic: 209 on 3 and 502 DF, p-value: <2e-16## Analysis of Variance Table
##
## Response: medv
## Df Sum Sq Mean Sq F value Pr(>F)
## lstat 1 23244 23244 614.85 <2e-16 ***
## age 1 304 304 8.05 0.0047 **
## lstat:age 1 190 190 5.04 0.0252 *
## Residuals 502 18978 38
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = medv ~ lstat * age, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.81 -4.04 -1.33 2.08 27.55
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 36.088536 1.469835 24.55 < 2e-16 ***
## lstat -1.392117 0.167456 -8.31 8.8e-16 ***
## age -0.000721 0.019879 -0.04 0.971
## lstat:age 0.004156 0.001852 2.24 0.025 *
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.15 on 502 degrees of freedom
## Multiple R-squared: 0.556, Adjusted R-squared: 0.553
## F-statistic: 209 on 3 and 502 DF, p-value: <2e-16Plot residual ditampilkan pada Gambar 12.5.
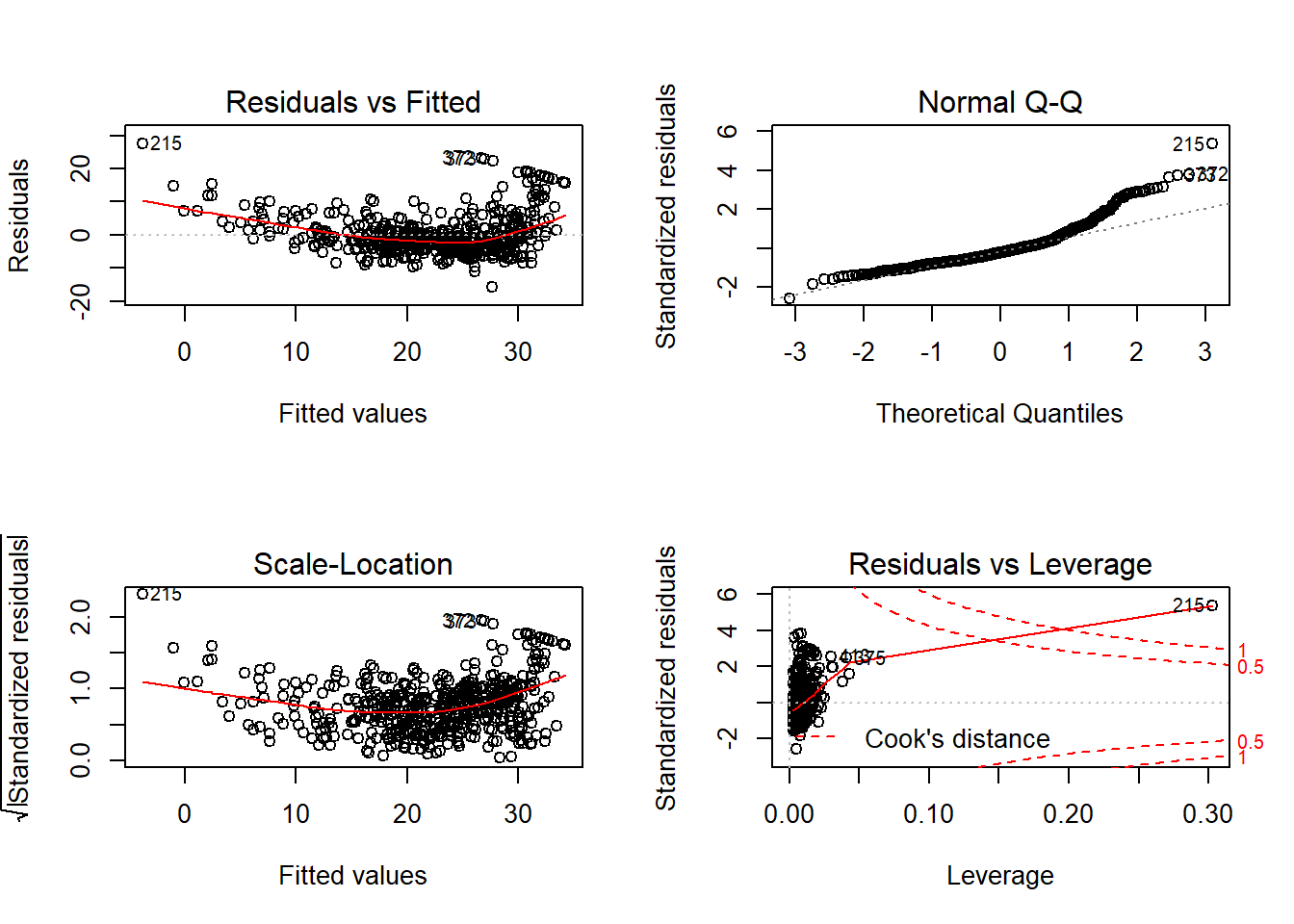
Gambar 12.5: Analisis residual model dengan melibatkan interaksi antar variabel pada dataset Boston.
12.1.4 Transformasi Non-linier Pada Prediktor
Fungsi lm() juga dapat melibatkan transformasi non-linier prediktor pada argumen formula-nya. Transformasi non-linier dilakukan dengan menambahkan fungsi identitas I(). Sebagai contoh model berikut melibatkan transformasi kuadrat pada variabel lstat:
## Analysis of Variance Table
##
## Response: medv
## Df Sum Sq Mean Sq F value Pr(>F)
## lstat 1 23244 23244 762 <2e-16 ***
## I(lstat^2) 1 4125 4125 135 <2e-16 ***
## Residuals 503 15347 31
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = medv ~ lstat + I(lstat^2), data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.28 -3.83 -0.53 2.31 25.41
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 42.86201 0.87208 49.1 <2e-16 ***
## lstat -2.33282 0.12380 -18.8 <2e-16 ***
## I(lstat^2) 0.04355 0.00375 11.6 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.52 on 503 degrees of freedom
## Multiple R-squared: 0.641, Adjusted R-squared: 0.639
## F-statistic: 449 on 2 and 503 DF, p-value: <2e-16Cara yang lebih sederhana untuk melibatkan tranformasi polinomial kedalam model linier adalah dengan menggunakan fungsi poly(). Berikut adalah contoh penerapannya:
## Analysis of Variance Table
##
## Response: medv
## Df Sum Sq Mean Sq F value Pr(>F)
## poly(lstat, 2) 2 27369 13685 449 <2e-16 ***
## Residuals 503 15347 31
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = medv ~ poly(lstat, 2), data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.28 -3.83 -0.53 2.31 25.41
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.533 0.246 91.8 <2e-16
## poly(lstat, 2)1 -152.460 5.524 -27.6 <2e-16
## poly(lstat, 2)2 64.227 5.524 11.6 <2e-16
##
## (Intercept) ***
## poly(lstat, 2)1 ***
## poly(lstat, 2)2 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.52 on 503 degrees of freedom
## Multiple R-squared: 0.641, Adjusted R-squared: 0.639
## F-statistic: 449 on 2 and 503 DF, p-value: <2e-16Plot residual ditampilkan pada Gambar 12.6.
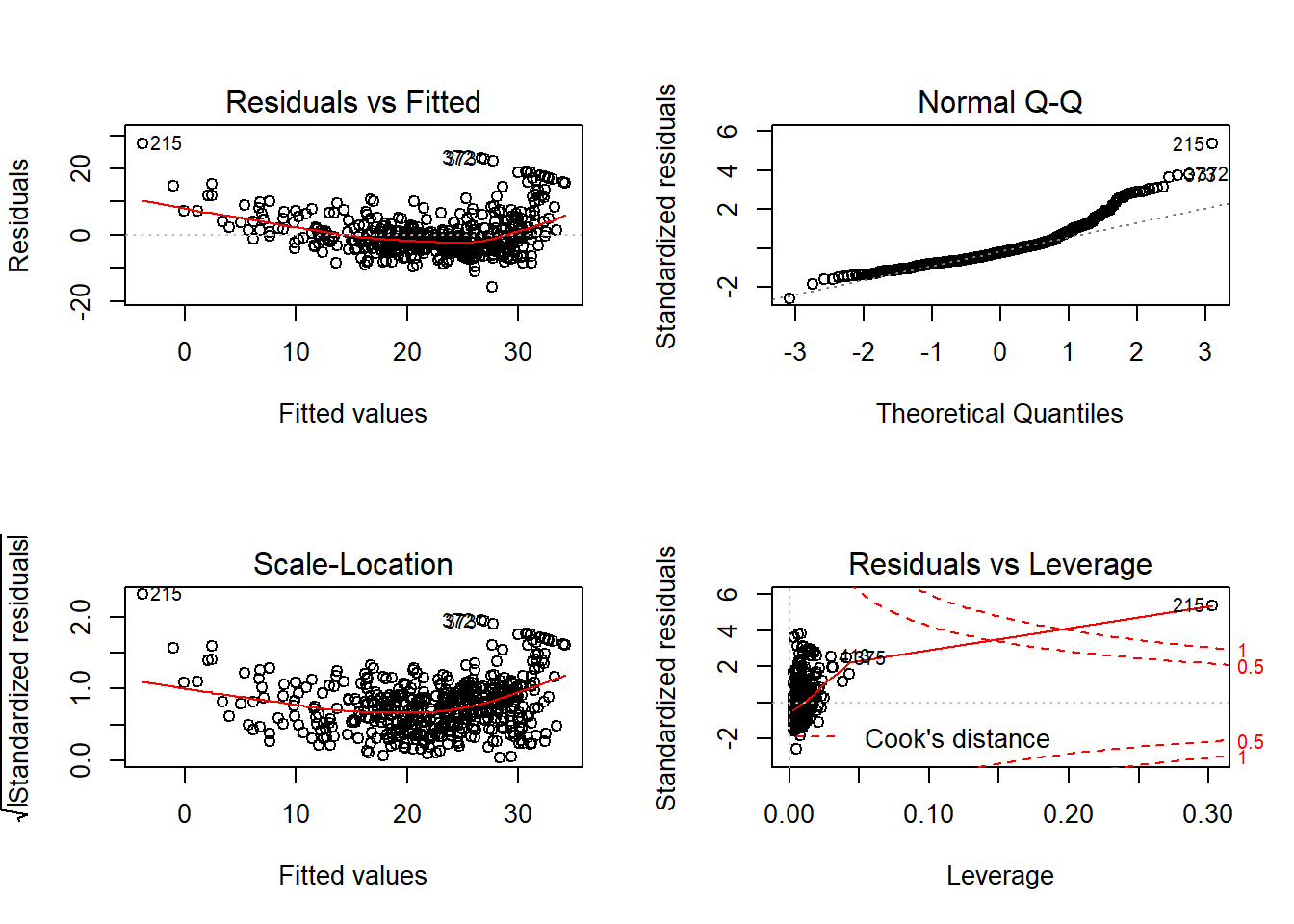
Gambar 12.6: Analisis residual model dengan melibatkan transformasi non-linier variabel prediktor pada dataset Boston.
FUngsi trasnformasi lainnya juga dapat digunakan pada pembentukan model linier. Berikut adalah contoh penerapan transformasi logaritmik dan eksponensial pada model linier:
##
## Call:
## lm(formula = medv ~ log(lstat), data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.460 -3.501 -0.669 2.169 26.013
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 52.125 0.965 54.0 <2e-16 ***
## log(lstat) -12.481 0.395 -31.6 <2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.33 on 504 degrees of freedom
## Multiple R-squared: 0.665, Adjusted R-squared: 0.664
## F-statistic: 1e+03 on 1 and 504 DF, p-value: <2e-16##
## Call:
## lm(formula = medv ~ exp(lstat), data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -17.57 -5.47 -1.37 2.43 27.43
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.26e+01 4.09e-01 55.19 <2e-16 ***
## exp(lstat) -4.44e-16 2.79e-16 -1.59 0.11
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9.18 on 504 degrees of freedom
## Multiple R-squared: 0.00501, Adjusted R-squared: 0.00303
## F-statistic: 2.54 on 1 and 504 DF, p-value: 0.11212.1.5 Model Linier dengan Prediktor Kategorikal
Regresi linier dapat pula dilakukan dengan jenis variabel prediktor berupa variabel kategorikal. Untuk dapat melakukannya jenis data variabel kategorikal terlebih dahulu dirubah kedalam factor.
Pada contoh kali ini, kita akan menggunakan dataset utds dari library edtaR untuk memodelkan konsentrasi uranium dalam air tanah menggunakan variabel TDS pada berbagai kondisi kesadahan. Berikut adalah sintaks yang digunakan
## Classes 'tbl_df', 'tbl' and 'data.frame': 44 obs. of 3 variables:
## $ TDS : num 683 819 304 1151 582 ...
## $ Uranium : num 0.931 1.938 0.292 11.904 1.567 ...
## $ Bicarbonate: num 0 0 0 0 0 0 0 0 0 0 ...# ubah variabe Bicarbonat menjadi factor
utds$Bicarbonate <- factor(utds$Bicarbonate,
levels = c(0,1),
labels = c(" <= 50%",
" > 50%"))
str(utds)## Classes 'tbl_df', 'tbl' and 'data.frame': 44 obs. of 3 variables:
## $ TDS : num 683 819 304 1151 582 ...
## $ Uranium : num 0.931 1.938 0.292 11.904 1.567 ...
## $ Bicarbonate: Factor w/ 2 levels " <= 50%"," > 50%": 1 1 1 1 1 1 1 1 1 1 ...## Analysis of Variance Table
##
## Response: Uranium
## Df Sum Sq Mean Sq F value Pr(>F)
## TDS 1 27 27.4 3.31 0.076 .
## Bicarbonate 1 220 220.2 26.56 6.8e-06 ***
## Residuals 41 340 8.3
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = Uranium ~ ., data = utds)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.710 -1.682 -0.121 1.144 7.118
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5.61188 1.87617 -2.99 0.0047
## TDS 0.01051 0.00206 5.11 7.8e-06
## Bicarbonate > 50% 6.93845 1.34623 5.15 6.8e-06
##
## (Intercept) **
## TDS ***
## Bicarbonate > 50% ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.88 on 41 degrees of freedom
## Multiple R-squared: 0.422, Adjusted R-squared: 0.393
## F-statistic: 14.9 on 2 and 41 DF, p-value: 1.34e-05Plot residual yang ditampilkan pada Gambar 12.7.
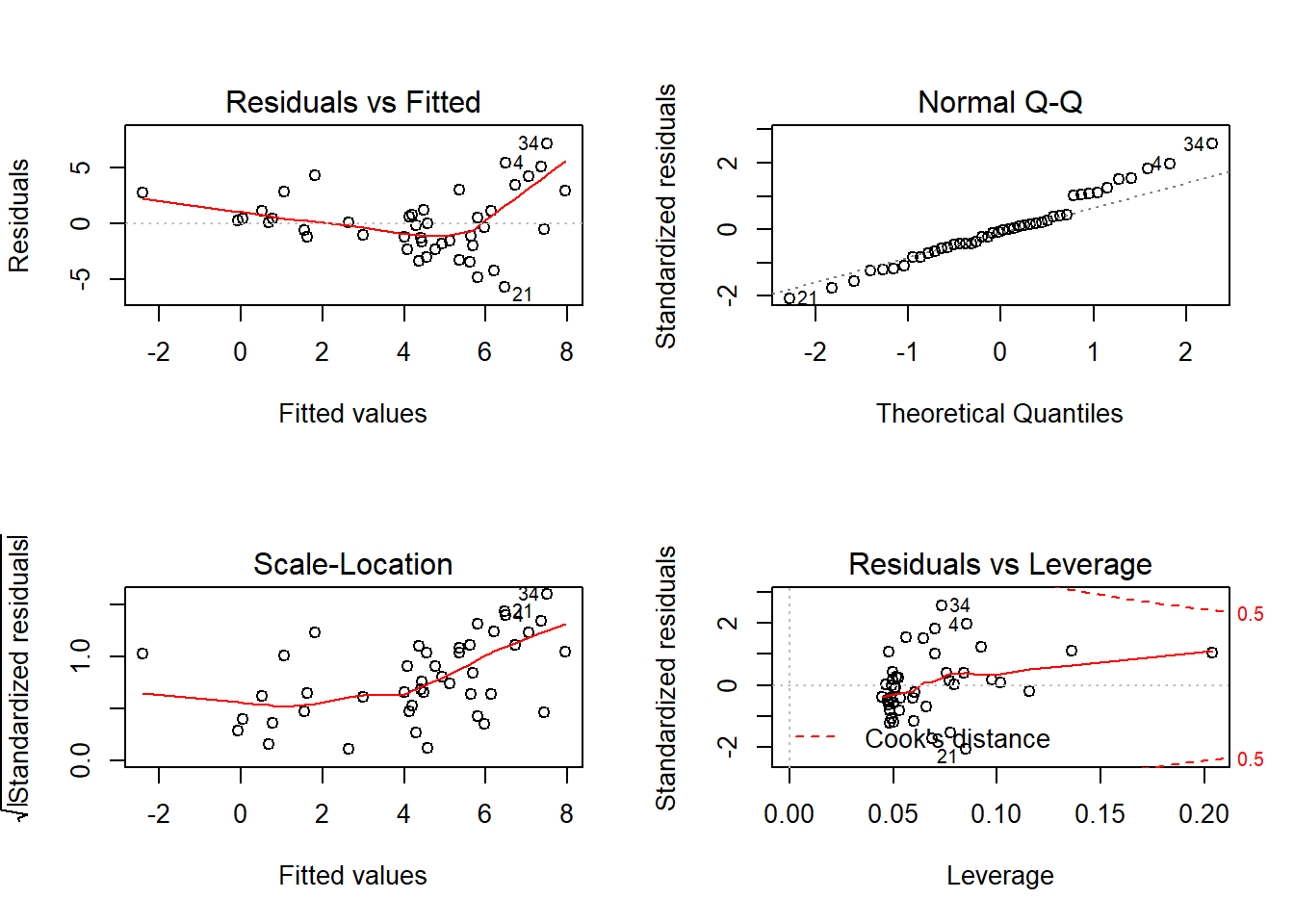
Gambar 12.7: Analisis residual model dengan melibatkan variabel kategorikal pada dataset utds.
12.1.6 Regresi linier dengan Pembobotan
Pada pembahasan sebelumnya kita telah menyaksikan bahwa sebagian model yang telah terbentuk tidak memenuhi asumsi varians yang konstan. Untuk mengatasi hal tersebut, kita dapat membentuk regresi dengan memberikan bobot sebesar invers variansnya. Untuk melakukannya diperlukan beberapa tahapan, antara lain:
- Membentuk model linier dari variabel dataset:
fit <- lm(y~(variabel prediktor)). - Menghitung error absolut (
abse <- abs(resid(fit))) dan nilai *fitted value dari model (yhat <- fitted(fit). - Membentuk kembali model menggunakan data residual absolut (
efit <- lm(abse~poly(yhat,2))) dan menghitung residual fitted value (shat <- fitted(efit)). - Gunakan nilai bobot
w <- 1/shat^2untuk membentuk model regresi dengan pembobotan (fitw <-lm(y~(variabel prediktor), weights=w)).
Kita akan membentuk kembali model menggunakan dataset Boston dengan menggunakan seluruh variabel, namun pada model kali ini kita akan memberikan bobot pada model yang terbentuk. Berikut adalah sintaks yang digunakan:
# langkah 1
fit <- lm(medv~., data=Boston)
# langkah 2
abse <- abs(resid(fit))
yhat <- fitted(fit)
# langkah 3
efit <- lm(abse~poly(yhat,2))
shat <- fitted(efit)
# langkah 4
fitw <- lm(medv~., data = Boston, weights = 1/(shat^2))
anova(fitw)## Analysis of Variance Table
##
## Response: medv
## Df Sum Sq Mean Sq F value Pr(>F)
## crim 1 367 367 188.5 < 2e-16 ***
## zn 1 148 148 76.1 < 2e-16 ***
## indus 1 125 125 63.9 9.3e-15 ***
## chas 1 41 41 21.2 5.2e-06 ***
## nox 1 38 38 19.7 1.1e-05 ***
## rm 1 363 363 186.6 < 2e-16 ***
## age 1 30 30 15.6 9.0e-05 ***
## dis 1 106 106 54.3 7.4e-13 ***
## rad 1 0 0 0.0 0.99
## tax 1 30 30 15.4 9.9e-05 ***
## ptratio 1 74 74 37.9 1.6e-09 ***
## black 1 64 64 33.1 1.6e-08 ***
## lstat 1 334 334 171.7 < 2e-16 ***
## Residuals 492 958 2
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1##
## Call:
## lm(formula = medv ~ ., data = Boston, weights = 1/(shat^2))
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -4.252 -0.795 -0.037 0.698 9.299
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 39.15845 4.47418 8.75 < 2e-16 ***
## crim -0.13738 0.03254 -4.22 2.9e-05 ***
## zn 0.03975 0.01367 2.91 0.00380 **
## indus 0.03107 0.05211 0.60 0.55129
## chas 2.88679 0.81633 3.54 0.00044 ***
## nox -15.84421 3.22177 -4.92 1.2e-06 ***
## rm 2.32247 0.41424 5.61 3.4e-08 ***
## age 0.00587 0.01147 0.51 0.60930
## dis -1.13778 0.17774 -6.40 3.6e-10 ***
## rad 0.30255 0.05805 5.21 2.8e-07 ***
## tax -0.01138 0.00328 -3.47 0.00056 ***
## ptratio -0.72178 0.11598 -6.22 1.0e-09 ***
## black 0.00878 0.00234 3.75 0.00020 ***
## lstat -0.62185 0.04746 -13.10 < 2e-16 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.4 on 492 degrees of freedom
## Multiple R-squared: 0.642, Adjusted R-squared: 0.633
## F-statistic: 68 on 13 and 492 DF, p-value: <2e-16Plot residual ditampilkan pada Gambar 12.8.
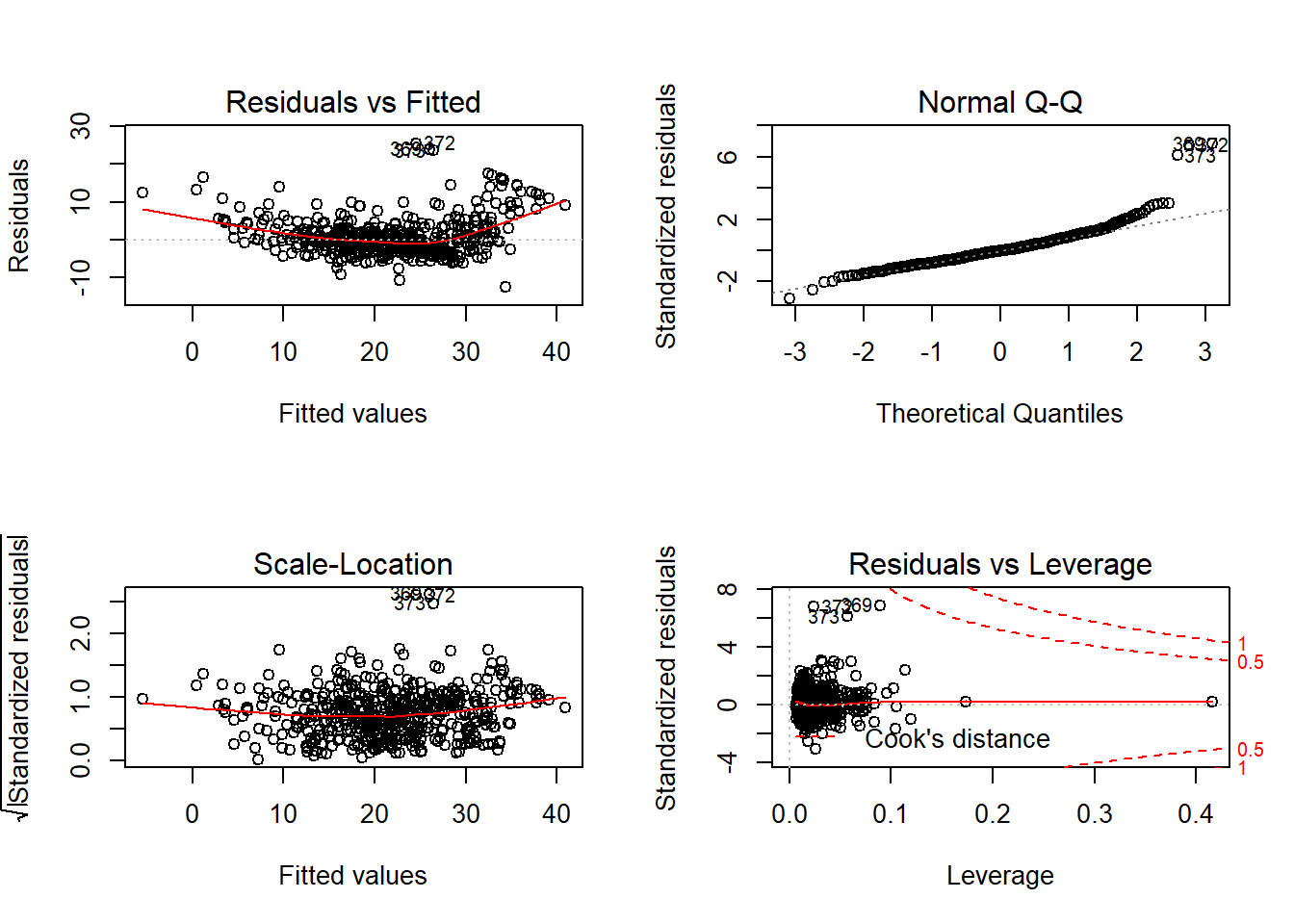
Gambar 12.8: Analisis residual model regresi linier dengan pembobotan pada dataset Boston.
12.2 Regresi Logistik
Pada Chapter 12.2, kita telah membahas cara untuk membangun model dengan output berupa variabel dengan nilai numerik. Pada Chapter 12.2, kita akan belajar cara membentuk model regresi dengan 2 respons (0 dan 1). Pada regresi ini pembentukan model didasarkan oleh kurva logistik, dimana melalui kurva tersebut nilai yang dihasilkan akan memiliki rentang dari 0 sampai 1. Karena model yang dibuat bertujuan untuk memprediksi dua buah kemungkinan (0 atau 1), maka diperlukan suatu nilai ambang (y<0,5 = 0 dan y >= 0,5 = 1).
Fungsi glm() dapat digunakan untuk membentuk model regresi logistik. Format umum fungsi tersebut adalah sebagai berikut:
Catatan:
formula: formula model yang hendak dibentuk.family: distribusi yang digunakan. Untuk regresi logistik digunakan argumenfamily=binomialdata: data yang digunakan untuk membentuk model.subset: subset data yang akan digunakan dalam pembentukan model.weight: nilai pembobotan dalam pembentukan model.
Pada contoh berikut, kita akan membuat model untuk memprediksi contamination rating menggunakan dataset contamination dari library edtaR. Berikut adalah sintaks yang digunakan:
## Analysis of Deviance Table
##
## Model: binomial, link: logit
##
## Response: CR
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev
## NULL 123 91.5
## UZT 1 12.38 122 79.1
## AY 1 4.32 121 74.8
## GWQ 1 0.01 120 74.8
## HWM 1 25.05 119 49.7##
## Call:
## glm(formula = CR ~ ., family = binomial, data = contamination)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.0945 -0.3349 -0.0857 -0.0462 2.1324
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -13.2054 3.5581 -3.71 0.00021 ***
## UZT 0.5153 0.1509 3.41 0.00064 ***
## AY 0.4291 0.2749 1.56 0.11851
## GWQ 0.0303 0.3246 0.09 0.92551
## HWM 1.0895 0.2986 3.65 0.00026 ***
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 91.474 on 123 degrees of freedom
## Residual deviance: 49.704 on 119 degrees of freedom
## AIC: 59.7
##
## Number of Fisher Scoring iterations: 712.3 Referensi
- Akritas, M. 2016. PROBABILITY & STATISTICS WITH R FOR ENGINEERS AND SCIENTISTS. Pearson.
- Bloomfield, V.A. 2014. Using R for Numerical Analysis in Science and Engineering. CRC Press.
- James, G., Witten, D., Hastie, T., Tibshirani, R. 2013. An Introduction to Statistical Learning. Springer.
- Kerns, G.J., 2018. Introduction to Probability and Statistics Using R. Course notes for University of Auckland Paper STATS 330. http://ipsur.r-forge.r-project.org/book/download/IPSUR.pdf.
- Lee, A., Ihaka, R., Triggs, C. 2012. ADVANCED STATISTICAL MODELLING.
- Primartha, R. 2018. Belajar Machine Learning Teori dan Praktik. Penerbit Informatika : Bandung.
- Rosadi,D. 2016. Analisis Statistika dengan R. Gadjah Mada University Press: Yogyakarta.
- STHDA. <(http://www.sthda.com/english/>