Chapter 8 Interpolasi dan Ekstrapolasi

Pada dunia nyata, data sering kali tidak tersaji secara lengkap. Seringkali terdapat nilai data yang hilang (missing value). Terdapat banyak penyebab dari kondisi tersebut, baik akibat kesalahan manusianya maupun keterbatasan kemampuan alat ukur.

Kondisi lain yang muncul dari data yang kita miliki adalah adanya outlier atau nilai yang berbeda jauh dengan mayoritas data yang kita miliki. Nilai tersebut akan menentukan hasil analisis atau uji statistik yang kita lakukan, terlebih lagi jika uji statistik yang kita lakukan menggunakan metode parametrik.

Terdapat banyak cara untuk menangani kondisi-kondisi tersebut. Sejumlah peneliti memilih untuk menghapus data tersebut. Hal ini dapat dilakukan jika jumlah data yang kita miliki cukup besar. Bagaimana jika data yang kita miliki sedikit dan pengukuran ulang cukup mahal atau cukup sulit dilakukan?. Salah satu cara yang dapat dilakukan adalah dengan melakukan interpolasi terhadap data.

Interpolasi dan ekstrapolasi adalah proses “menebak” nilai data dengan memperhatikan data lain yang kita miliki. Interpolasi merupakan teknik untuk mencari nilai suatu variabel yang hilang pada rentang data yang diketahui, sedangkan ektrapolasi merupakan teknik menemukan nilai suatu variabel diluar rentang data yang telah diketahui. Data lain yang kita miliki seringkali memiliki sejumlah pola. Pola yang terbentuk dapat berupa polinomial atau mengelompok. Tiap pola akan memiliki metode pendekatan yang berbeda-beda. Terdapat kemungkinan tak terbatas dari pola data tersebut. Penilaian profesional atau ahli diperlukan untuk menentukan metode mana yang sesuai berdasarkan riwayat penelitian atau pekerjaan yang pernah dilakukan sebelumnya.

Pada Chapter 8 penulis akan menjelaskan teknik-teknik interpolasi yang dapat kita lakukan. Adapun yang akan dibahas pada Chapter ini adalah sebagai berikut:

Teknik interpolasi polinomial
Teknik interpolasi piecewise
Studi kasus penerapan teknik interpolasi

8.1 Interpolasi Polinomial

Interpolasi polinomial merupakan teknik interpolasi dengan mengasumsikan pola data yang kita miliki mengikuti pola polinomial baik berderajat satu (linier) maupun berderajat tinggi. Interpolasi dengan metode ini dilakukan dengan terlebih dahulu membentuk persamaan polinomial. Persamaan polinomial yang terbentuk selanjutnya digunakan untuk melakukan interpolasi dari nilai yang diketahui atau ekstrapolasi (prediksi) dari nilai diluar rentang data yang diketahui.

Pada Chapter 8.1 pembahasan akan dibagi menjadi 3 bagian. Bagian pertama kita akan mengulang kembali teknik evaluasi polinomial, sedangkan dua bagian selanjutnya akan membahas teknik interpolasi linier dan polinomial orde tinggi dengan menjadikan pembahasan bagian pertama sebagai dasar pada dua bagian berikutnya.

8.1.1 Mengevaluasi Polinomial

Pada Chapter ini pembaca akan mempelajari teknik untuk melakukan substitusi nilai \(x\) pada persamaan polinomial untuk memperoleh nilai \(y\). Terdapat berbagai pendekatan dalam melakukan proses tersebut, mulai dari metode naive maupun metode Horner. Kedua metode akan menghasilkan hasil yang sama namun dengan proses komputasi yang berbeda. Metode naive cenderung lambat dalam proses komputasi karena jumlah proses yang dilakukan dalam sekali proses lebih banyak dari pada metode Horner.

Untuk memahami metode-metode evaluasi polinomial yang telah disebutkan tersebut, secara umum persamaan polinomial disajikan pada Persamaan (8.1).

\[\begin{equation} f\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0 \tag{8.1} \end{equation}\]

dimana \(a\) merupakan koefisien polinomial, \(x\) merupakan variabel, dan \(n\) merupakan indeks dan pangkat polinomial.

Pada metode naive kita melakukan evaluasi polinomial sama dengan cara kita melakukan evaluasi polinomial saat kita SMA. Nilai \(x\) akan disubstitusikan pada masing-masing elemen persamaan polinomial. Masing-masing elemen polinomial selanjutnya dijumkahkan untuk menghitung \(y\).

Pada R kita dapat menuliskan sebuah fungsi untuk melakukan evaluasi polinomial menggunakan metode naive tersebut. Pada fungsi tersebut, koefisien polinomial akan disimpan kedalam sebuah vektor dengan urutan pengisian mulai dari koefisien dengan pangkat \(x\) terendah ke tertinggi.

naive_poly <- function(x, coeff){
  n <- length(x)
  y <- rep(0, n)
  
  for(i in 1:length(coeff)){
    y <- y + coeff[i]*(x^(i-1))
  }
  
  return(y)
}

Contoh 8.1 Hitung nilai \(y\) pada persamaan \(f\left(x\right)=x^4+3x^3-15x^2-19x+30\), jika diketahui nilai \(x\) adalah -1, 0, dan 1!

Jawab:

Untuk dapat menghitung nilai \(y\) menggunakan fungsi naive_poly() pada persamaan tersebut dengan nilai \(x\) yang diketahui, kita perlu merubah koefisien persamaan tersebut dan nilai \(x\) yang diketahui menjadi vektor:

x <- c(-1,0,1)
coeff <- c(30,-19,-15,3,1)

Masukkan vektor-vektor yang telah terbentuk tersebut kedalam fungsi naive_poly().

naive_poly(x, coeff)

## [1] 32 30  0

Berdasarkan hasil perhitungan diperoleh nilai \(y\) masing-masing sebesar 32, 30, dan 0. Pembaca dapat mengeceknya sendiri hasil perhitungan tersebut menggunakan cara manual.

Kita dapat meningkatkan efisiensi proses perhitungan pada fungsi naive_poly() tersebut. Sebagai contoh, setiap kali kita melakukan loop untuk menghitung nilai \(y\) pada polinomial, kita dapat memperoleh eksponensial dari \(x\). Namun untuk setiap koefisien \(a_i\), nilai eksponensial yang terkait \(x_i\) merupakan seri produk.

\[\begin{equation} x^i=\prod_{j=0}^ix \tag{8.2} \end{equation}\]

Untuk \(x^i\), terdapat sebanyak \(i\) koefisien \(x\) dikalikan bersamaan. Namun, untuk setiap \(x^{i-1}\) terdapat lebih sedikit 1 perkalian dibanding koefisien \(x\) dengan pangkat yang lebih besar dan seterusnya.

Berdasarkan ilustrasi tersebut, kita dapat membentuk fungsi better_poly() sebagai perbaikan dari fungsi naive_poly(). Berikut adalah sintaks yang digunakan:

better_poly <- function(x, coeff){
  n <- length(x)
  y <- rep(0, n)
  cached_x <- 1
  
  for(i in 1:length(coeff)){
    y <- y + coeff[i]*cached_x
    cached_x <- cached_x * x
  }
  return(y)
}

Contoh 8.2 Hitung nilai \(y\) pada persamaan yang disajikan pada Contoh 8.1 menggunakan nilai \(x\) yang telah diketahui pada soal tersebut menggunakan fungsi better_poly()?

Jawab:

better_poly(x, coeff)

## [1] 32 30  0

Sejauh ini kita telah membentuk 2 fungsi yaitu naive_poly() dan better_poly(). Kedua fungsi tersebut memiliki perbedaan proses menghitung yang mempengaruhi efisiensinya masing-masing. Sebagai contoh jika diberikan polinomial berderajat 10, fungsi naive_poly() akan mengejakan perkalian dalam proses loop sebanyak 55 kali, sedangkan fungsi better_poly() akan melakukannya sebanyak 20 kali (\(2n\) perkalian).

Metode lain yang lebih efisien dalam melakukan evaluasi polinomial adalah metode Horner. Metode ini oleh William Horner pada abad ke-18. Dalam metode Horner, bentuk polinomial pada Persamaan (8.1) akan ditransformasi menjadi Persamaan (8.3).

\[\begin{equation} \begin{split} f\left(x\right)&=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\\ &= a_0+a_1x+\cdots+a_{n-1}x^{n-1}+a_nx^n\\ &= a_0+x\left(a_1+\cdots+a_{n-1}x^{n-2}+a_nx^{n-1}\right)\\ &= a_0+x\left(a_1+\cdots+x\left(a_{n-1}+x\left(a_n\right)\right)\cdots\right) \end{split} \tag{8.3} \end{equation}\]

Berdasarkan Persamaan (8.3), jika kita melakukan perhitungan pada persamaan polinomial berderajat 10, kita dapat mereduksi perhitungan menjadi 10 perkalian dan 10 penjumlahan. Jumlah tersebut sangat kecil dibandingkan kedua metode sebelumnya dan dapat dikatakan lebih efisien dibandingkan metode lainnya.

FUngsi horner_poly() merupakan fungsi yang dibentuk bedasarkan Persamaan (8.3). Sintaks fungsi tersebut adalah sebagai berikut:

horner_poly <- function(x, coeff){
  n <- length(x)
  y <- rep(0, n)
  
  for(i in length(coeff):1){
    y <- coeff[i] + x * y
  }
  return(y)
}

Contoh 8.3 Kerjakan kembali Contoh 8.2 fungsi horner_poly()?

Jawab:

horner_poly(x, coeff)

## [1] 32 30  0

8.1.2 Interpolasi Linier

Misalkan kita memiliki 3 buah data dengan dua buah variabel kita misalkan variabel \(x\) dan variabel \(y\). Pada salah satu data terdapat data yang hilang pada. Agar ketiga data tersebut tetap dapat digunakan dalam iterasi diperlukan interpolasi untuk “menebak” nilai dari data yang hilang.

Berdasarkan pengukuran yang sebelumnya pernah dilakukan diketahui bahwa pola data yang terbentuk variabel \(x\) dan \(y\) divisualisasikan menggunakan scatterplot adalah pola linier. Berdasarkan hal tersebut interpolasi dilakukan dengan menggunakan metode linier.

Interpolasi linier dilakukan dengan terlebih dahulu membentuk fungsi linier. Dengan kata lain kita perlu mencari nilai slope \(m\) dan intercept \(b\). Nilai \(m\) dihitung sebagai rasio selisih jarak dua titik pada sumbu \(y\) dan sumbu \(x\) yang dapat dituliskan melalui Persamaan (8.4).

\[\begin{equation} m=\frac{y_2-y_1}{x_2-x_1} \tag{8.4} \end{equation}\]

Nilai intercept (titik potong pada sumbu \(y\)) dihitung menggunakan Persamaan (8.5).

\[\begin{equation} b=y_2-mx_2 \tag{8.5} \end{equation}\]

Algoritma Interpolasi Linier

Tentukan dua buah titik \(\left(x,y\right)\) sebagai dasar pembentukan persaman linier.
Hitung \(m\) menggunakan Persamaan (8.4)
Hitung \(b\) menggunakan Persamaan (8.5)
Definiskan fungsi linier berdasarkan nilai \(m\) dan \(b\)
Hitung \(y\) dengan cara substitusi nilai \(x\) pada persamaan linier untuk melakukan interpolasi atau ekstrapolasi nilai \(y\) yang ingin dicari.

Algoritma poin 1 sampai 4 tersebut, kita dapat membentuk fungsi pembentuk persamaan linier dari 2 titik yang diketahui. Fungsi tersebut disajikan pada sintaks berikut:

linear_inter <- function(x, y){
  m <- (y[2]-y[1]) / (x[2]-x[1])
  b <- y[2] - m*x[2]
  
  return(c(b, m))
}

Contoh 8.4 Diketahui koordinat 2 buah titik yaitu (0,-1) dan (2,3). Jika diketahui titik ketiga memiliki koordinat sumbu \(x\) sebesar 1. Lakukan interpolasi untuk menentukan koordinat sumbu \(y\) titik ketiga tersebut!

Jawab:

Berdasarkan data-data yang terdapat pada soal terserbut, kita dapat menghitung nilai \(m\) dan \(b\). Nilai \(m\) dapat dihitung sebagai berikut:

\[ m=\frac{-1-3}{0-2}=2 \]

Dengan menggunakan nilai \(m\) tersebut kita dapat menghitung nilai \(b\).

\[ b=3-2*3=-1 \]

Berdasarkan hasil perhitungan diperoleh persamaan linier yang terbentuk adalah sebagai berikut:

\[ y=2x-1 \]

Berdasarkan persamaan linier tersebut nilai \(y\) dapat dihitung.

\[ y=2*1-1=1 \]

Kita dapat pula membentuk persamaan linier menggunakan fungsi linear_inter(). Berikut adalah sintaks yang digunakan:

x <- c(0,2)
y <- c(-1,3)

(coeff <- linear_inter(x,y))

## [1] -1  2

Setelah diperoleh koefisien persamaan linier berdasarkan dua titik tersebut, kita akan menggunakan fungsi horner_poly() untuk memperoleh nilai \(y\). Berikut adalah sintaks yang digunakan:

horner_poly(1, coeff)

## [1] 1

Hasil interpolasi yang diperoleh dapat dikatakan sesuai dengan lokasi kedua titik data yang ditunjukkan pada Gambar 8.1. Berdasarkan hal tersebut, kita dapat yakin bahwa hasil interpolasi yang telah kita lakukan telah sesuai.

Gambar 8.1: Interpolasi linier dua titik (Sumber:Howard, 2017).

Metode interpolasi linier dapat dibilang merupakan metode interpolasi yang sangat sederhana. Disamping kemudahannya, metode ini memiliki potensi error numerik jika jarak antara kedua titik cukup berdekatan terlebih lagi jika selisih penyebut (\(x_2-x_1\)) sangat kecil sehingga akan menghasilkan nilai \(y\) yang sangat besar.

Disamping adanya potensi error numerik tersebut, metode ini menjadi dasar bagi metode interpolasi lain yang lebih kompleks. Metode selanjutnya merupakan pengembangan dari metode interpolasi ini.

8.1.3 Interpolasi Polinomial Orde Tinggi

Dengan menggunakan dua titik, kita dapat membentuk garis lurus (linier) yang tepat pada dua titik tersebut. Masalah timbul jika selisih nilai \(x\) kedua titik tersebut sangat kecil atau kedua titik tersebut memiliki nilai \(x\) yang sama. Hal ini akan menyebabkan slope yang dihasilkan menjadi tidak terhingga atau garis yang terbentuk adalah garis vertikal tegak lurus.

Bagaimana jika terdapat tiga buah titik? apakah kita masih bisa menggunakan interpolasi linie?. Ya, asalkan ketiga titik tersebut membentuk pola linier atau terletak pada satu garis yang sama. Pada kenyatannya kondisi tersebut jarang terjadi, sehingga pendekatan menggunakan polinomial orde lebih tinggi diperlukan. Persamaan kuadratik (polinomial orde dua) dapat digunakan untuk membentuk persamaan polinomial pada ketiga titik tersebut, sehingga iterasi dapat dilakukan. Untuk 4 buah titik data, polinomial orde tiga dapat digunakan untuk melakukan interpolasi. Secara umum berdasarkan penjelasan tersebut, untuk \(n\) titik data interpolasi dapat dilakukan menggunakan persamaan polinomial orde \(n-1\).

Diberikan set data berpasangan yang telah diurutkan \(\left(x_i,y_i\right)\), fungsi interpolasi harus memenuhi persyaratan berikut:

\[\begin{equation} p\left(x_i\right)=y_i \tag{8.6} \end{equation}\]

Untuk setiap \(i\). Sebagai tambahan, fungsi interpolasi berupa fungsi polinomial dengan bentuk umum sebagai berikut:

\[\begin{equation} y_i=\beta_nx_i^n+\beta_{n-1}x_i^{n-1}+\cdots+\beta_1x_i+\beta_0 \tag{8.7} \end{equation}\]

Persamaan (8.7) dapat dituliskan kedalam bentuk matriks yang ditampilkan pada Persamaan (8.8).

\[\begin{equation} \begin{bmatrix} x_1^n & x_1^{n-1} & \cdots & x_1 & 1 \\[0.3em] x_2^n & x_2^{n-1} & \cdots & x_2 & 1 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] x_n^n & x_n^{n-1} & \cdots & x_n & 1 \end{bmatrix} \begin{bmatrix} \beta_n \\[0.3em] \beta_{n-1} \\[0.3em] \vdots \\[0.3em] \beta_0 \end{bmatrix} = \begin{bmatrix} y_1 \\[0.3em] y_2 \\[0.3em] \vdots \\[0.3em] y_n \end{bmatrix} \tag{8.8} \end{equation}\]

Persamaan matrik tersebut dapat dituliskan sebagai \(X\beta = y\). Untuk menyelesaikan persamaan tersebut (memperoleh nilai \(\beta\)), pembaca dapat membaca kembali Chapter 6. Matriks \(X\) disebut sebagai matriks Vandemonde dan matriks tersebut mengandung sejumlah nilai \(x\) dengan pangkat sampai dengan \(n\).

Algoritma Interpolasi Polinomial Orde Tinggi

Tentukan set titik berpasangan \(\left(x,y\right)\) yang telah diurutkan.
Bentuk matriks Vandermonde sesuai dengan Persamaan (8.8).
Definiskan persamaan matriks \(X\beta=y\)
Selesaikan persamaan matriks pada poin 3 untuk memperoleh nilai \(\beta\)
Definisikan persamaan polinomial berdasarkan koefisien \(\beta\) yang diperoleh
Lakukan substitusi \(x\) persamaan polinomial pada poin 5 untuk memperoleh nilai \(y\)

Berdasarkan algoritma poin 1 sampai 5, kita dapat membentuk suatu fungsi untuk membentuk persamaan polinomial berdasarkan Persamaan (8.8). Berikut adalah sintaks fungsi tersebut:

poly_inter <- function(x, y){
  if(length(x) != length(y))
    stop("Lenght of x and y vectors must be the same")
  
  n <- length(x)-1
  vandermonde <- rep(1, length(x))
  for(i in 1:n){
    xi <- x^i
    vandermonde <- cbind(vandermonde, xi)
  }
  beta <- solve(vandermonde, y)
  
  names(beta) <- NULL
  return(beta)
}

Contoh 8.5 Diketahui koordinat 3 buah titik yaitu (-1,-2), (1,2) dan (0,1). Jika diketahui titik keempat memiliki koordinat sumbu \(x\) sebesar -2. Lakukan interpolasi untuk menentukan koordinat sumbu \(y\) titik keempat tersebut!

Jawab:

Untuk menyelesaiakn contoh soal tersebut, kita perlu terlebih dahulu membentuk matriks sesuai dengan Persamaan (8.8). Berdasarkan soal tersebut, terdapat tiga buah titik data yang diketahui, sehingga polinomial yang hendak dibentuk selanjutnya adalah polinomial berderajat 2.

\[\begin{equation*} \begin{bmatrix} -1^2 & -1^{1} & 1 \\[0.3em] 1^2 & 1^{1} & 1 \\[0.3em] 0^2 & 0^{1} & 1 \end{bmatrix} \begin{bmatrix} \beta_2 \\[0.3em] \beta_1 \\[0.3em] \beta_0 \end{bmatrix} = \begin{bmatrix} -2 \\[0.3em] 2 \\[0.3em] 1 \end{bmatrix} \end{equation*}\]

Setelah matriks tersebut terbentuk, pembaca dapat menyelesaikannya menggunakan berbagai metode yang telah penulis jelaskan pada Chapter 6 untuk memperoleh nilai \(\beta\).

Untuk menyelesaikan contoh soal tersebut pada R, kiat perlu membentuk matriks \(x\) dan \(y\) terlebih dahulu.

x <- c(-1, 1, 0)
y <- c(-2, 2, -1)

Koefisien persamaan polinomial dihitung menggunakan fungsi poly_inter().

(coeff <- poly_inter(x, y))

## [1] -1  2  1

Berdasarkan hasil perhitungan, diperoleh nilai \(\beta\). Nilai tersebut selanjutnya digunakan untuk membentuk persamaan polinomial. Berikut merupakan persamaan polinomial yang terbentuk:

\[ f\left(x\right)=1x^2+2x-1 \]

Fungsi horner_poly() selanjutnya digunakan untuk mengevaluasi polinomial tersebut. Berikut adalah hasil substitusi \(x\) pada persamaan tersebut:

horner_poly(-2, coeff)

## [1] -1

Hasil yang diperoleh terlihat cukup sesuai jika kita perhatikan visualisasi ketiga titik tersebut pada Gambar 8.2.

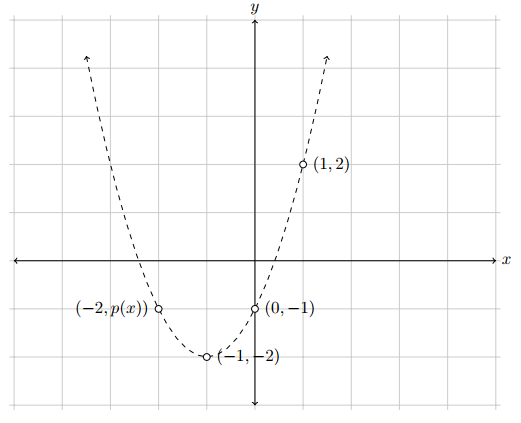
Gambar 8.2: Interpolasi kuadratik tiga titik (Sumber:Howard, 2017).

Contoh 8.6 Dengan menggunakan data pada Contoh 8.4, lakukan proses perhitungan untuk membentuk persamaan polinomial menggunakan fungsi poly_inter()

Jawab:

Berdasarkan data pada Contoh 8.4, polinomial yang terbentuk merupakan polinomial derajat 1 (linier). Berikut adalah nilai koefisien yang dihasilkan dari perhitungan menggunakan fungsi poly_inter().

x <- c(2, 0)
y <- c(3, -1)
poly_inter(x, y)

## [1] -1  2

Meskipun proses perhitungan menggunakan fungsi poly_inter() lebih rumit dibandingkan dengan fungsi linear_poly(), hasil perhitungan keduanya menggunakan data pada Contoh 8.4 menghasilkan hasil yang sama.

8.2 Interpolasi Piecewise

Interpolasi dengan polinomial sering memberikan hasil yang tidak dapat diterima. Interpolasi polinomial yang dihasilkan dari sejumlah besar data titik biasanya berderajat tinggi. Polinomial berderajat tinggi pada umumnya bersifat osilatif (grafiknya naik turun secara cepat). Akibatnya, perubahan data pada interval kecil dapat menyebabkan fluktuasi besar pada keseluruhan interval. Karena alasan ini, biasanya interpolasi hanya menggunakan polinomial berderajat rendah.

Interpolasi piecewise menawarkan alternatif lain. Pada interpolasi piecewise, pada titik yang berbeda sepanjang kurva, nilai fungsi lebih mungkin lebih baik didekati menggunakan dua atau lebih interpolasi. Pada metode ini kita akan membuat fungsi interpolasi ditiap antara dua titik observasi.

Pada sub-Chapter ini akan dijelaskan 2 buah metode interpolasi piecewise, yaitu: interpolasi linier piecewise dan interpolasi kubik spline. Interpolasi pertama dilakukan menggunakan persamaan linier, sehingga kurva yang terbentuk bukan merupakan kurva kontinu. Interpolasi selanjutnya dilakukan menggunakan persamaan polinomial berderajat tinggi sehingga kurva yang dihasilkan lebih halus (tidak ada sudut siku pada setiap titik).

8.2.1 Interpolasi Linier Piecewise

Interpolasi linier piecewise merupakan interpolasi yang menggunakan pendekatan interpolasi linier. Fungsi linier akan dibentuk pada setiap dua titik observasi. Untuk lebih memahaminya perhatikan kembali Gambar 8.2. Pada gambar tersebut sebelumnya kita telah membentuk persamaan kudratik untuk menghubungkan titik-titik tersebut. Dibanding menggunakan persamaan polinomial seperti kuadratik tersebut, interpolasi piecewise akan menghubungkan tiap dua titik observasi tersebut dengan garis lurus.

Algoritma Interpolasi Linier Piecewise

Tentukan set titik berpasangan \(\left(x,y\right)\) yang telah diurutkan berdasarkan nilai sumbu \(x\).
Hitung \(m\) pada setiap dua titik berdekatan menggunakan Persamaan (8.4)
Hitung \(b\) pada setiap dua titik berdekatan menggunakan Persamaan (8.5)
Definiskan fungsi linier berdasarkan nilai \(m\) dan \(b\)
Hitung \(y\) dengan cara substitusi nilai \(x\) pada persamaan linier untuk melakukan interpolasi nilai \(y\) yang ingin dicari.
Untuk melakukan ekstrapolasi dengan titik observasi diluar rentang titik diketahui, gunakan persamaan linier yang berada pada bagian ujung terdekat dengan nilai \(x\) yang hendak dicari nilai \(y\)-nya.

Berdasarkan algoritma tersebut, kita dapat menyusun fungsi pada R untuk membentuk persamaan linier piecewise. Berikut adalah sintaks yang digunakan:

pwise_linterp <- function(x, y){
  n <- length(x)-1
  
  y <- y[order(x)]
  x <- x[order(x)]
  
  m_vec <- b_vec <- c()
  
  for(i in 1:n){
    m <- (y[i+1]-y[i]) / (x[i+1]-x[i])
    b <- y[i+1] - m*x[i+1]
    m_vec <- c(m_vec, m)
    b_vec <- c(b_vec, b)
  }
  
  return(list(b = b_vec, m = m_vec))
}

Contoh 8.7 Tentukan persamaan-persamaan linier yang dihasilkan dari titik observasi yang ditampilkan pada Contoh 8.5?

Jawab:

Untuk menentukan persamaan-persamaan linier yang menghubungkan setiap titik, kita akan menggunakan fungsi pwise_linterp() yang telah kita buat. Berikut adalah sintaks yang digunakan:

x <- c(-1, 1, 0, -2)
y <- c(-2, 2, -1, -1)

pwise_linterp(x, y)

## $b
## [1] -3 -1 -1
## 
## $m
## [1] -1  1  3

Jika persamaan-persamaan yang terbentuk tersebut divisualisasikan akan terlihat seperti pada Gambar 8.3.

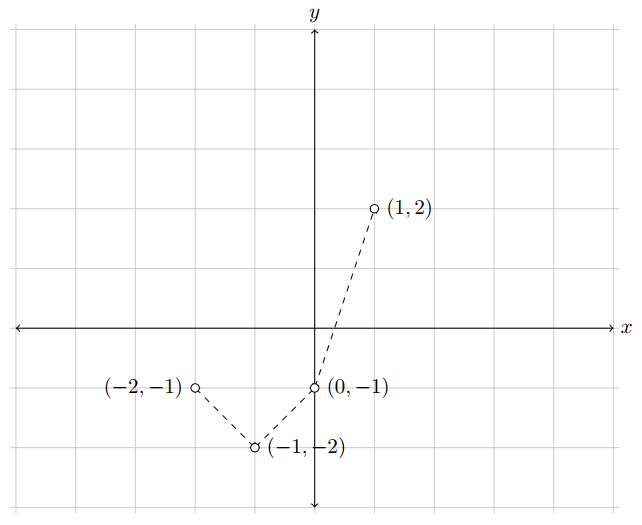
Gambar 8.3: Interpolasi linier piecewise empat titik (Sumber:Howard, 2017).

R juga menyediakan fungsi untuk melakukan interpolasi linier piecewise. Fungsi approxfun() dapat digunakan untuk melakukan interpolasi tersebut. Fungsi approxfun() hanya memerlukan dua input yaitu vektor \(x\) dan vektor \(x\). Untuk lebih memahaminya, kita akan menggunakan kembali data yang disajikan pada Contoh 8.5 untuk membuat fungsi linier piecewise. Berikut adalah sintaks yang digunakan:

f <- approxfun(x, y)

# tentukan nilai y jika x= 0
f(0)

## [1] -1

# tentukan nilai y jika x = 0.5
f(0.5)

## [1] 0.5

8.2.2 Interpolasi Spline Kubik

Jika menggunakan interpolasi polinomial berderajat satu (sebuah garis) lebih dari beberapa interval merupakan peningkatan dari satu baris interpolasi, dan jika menggunakan polinomial berderajat tinggi juga merupakan peningkatan dari satu garis interpolasi tunggal, maka dapat disimpulkan bahwa penggunaan polinomial berderajat tinggi pada selang beberapa interval juga akan menjadi peningkatan dalam proses interpolasi. Dalam beberapa kasus, hal tersebut benar, tetapi kita masih menghadapi sudut tajam di mana masing-masing kurva interpolasi tergabung (interpolasi linier piecewise). Sudut tajam ini mencegah diferensiasi dan pada prakteknya tidak dapat digunakan untuk memodelkan beberapa fungsi di dunia nyata, seperti roller coaster span.

Interpolasi spline kubik memecahkan masalah ini. Interpolasi ini akan memberikan kurva tergabung yang halus. Hal tersebut juga membuat spline terintegrasi. Karena setiap bagian individu diwakili oleh kurva kubik (polinomial derajat 3), maka masing-masing bagian individu juga dapat dianalisis sebagai kurva kubik. Dengan asumsi ada \(n\) titik data untuk interpolasi, kita akan mendefinisikan \(S_i\) sebagai fungsi polinomial kubik yang mewakili kurva pada domain \(\left[x_i; x_{i + 1}\right]\). Kemudian untuk \(n\) titik observasi, ada \(n - 1\) interpolasi polinomial kubik.

Bentuk umum seri polinomial dituliskan pada Persamaan (8.9).

\[\begin{equation} S_i=d_i\left(x-x_i\right)^3+c_i\left(x-x_i\right)^2+b_i\left(x-x_i\right)+a_i \tag{8.9} \end{equation}\]

Ini mengarah ke 4 nilai yang tidak diketahui tidak diketahui, yaitu: \(a_i\), \(b_i\), \(c_i\), dan \(d_i\) pada setiap Persamaan (8.9). Oleh karena itu, ada \(4 \left(n - 1\right) = 4n - 4\) nilai yang tidak diketahui. Karena kita ingin spline membentuk garis kontinu dan dapat didiferensiasi, ada satu set persamaan yang menentukan spline kubik:

\[\begin{equation} S_i\left(x_i\right)=y_i,\ \ \ \ \ \ \ \ \ \ i=1,\dots\dots,n-1 \tag{8.10} \end{equation}\]

\[\begin{equation} S_i\left(x_{i+1}\right)=y_{i+1},\ \ \ \ \ \ \ \ \ \ i=1,\dots\dots,n-1 \tag{8.11} \end{equation}\]

\[\begin{equation} S_i'\left(x_{i+1}\right)=S'_{i+1}\left(x_i\right),\ \ \ \ \ \ \ \ \ \ i=1,\dots\dots,n-2 \tag{8.12} \end{equation}\]

\[\begin{equation} S_i''\left(x_{i+1}\right)=S''_{i+1}\left(x_i\right),\ \ \ \ \ \ \ \ \ \ i=1,\dots\dots,n-2 \tag{8.13} \end{equation}\]

Persamaan (8.10) dan (8.11) sudah cukup jelas. Persyaratan ini memastikan bahwa jika kita mengevaluasi spline di salah satu node internal, hasil yang akan kita peroleh merupakan jawaban yang telah ditentukan, yaitu spline yang dievaluasi pada \(x_i\) untuk beberapa \(i\) adalah \(y_i\), dan setiap komponen spline bergabung dengan rapi. Persamaan (8.12) memastikan bahwa kita memiliki turunan pertama yang berkelanjutan di setiap simpul internal. Ini mencegah terbentuknya sudut tajam pada tiap node. Persamaan (8.13) memastikan turunan kedua juga kontinu, dimana kondisi ini menguntungkan karena itu berarti turunan pertama itu sendiri dapat didiferensiasi juga.

Kondisi ini menyebabkan ada \(4n − 6\) kondisi yang harus kita penuhi. Jika \(4n − 4\) kita yang tidak diketahui dipecahkan sebagai sebuah matriks, dan akhirnya matriks tersebut akan terpecahkan, matriks akan menjadi kurang ditentukan. Kita dapat menyelesaikan kondisi tersebut dengan memasukkan dua ketentuan tambahan. Dengan splines kubik, secara normal adalah menentukan akhir di kedua ujung untuk mencapai dua kondisi tambahan. Untuk contoh ini, dua kondisi yang akan kita tambahkan adalah \(S_i''\left(x_{i}\right)= 0\) dan \(S_i''\left(x_{n}\right)= 0\). Kedua kondisi ini memastikan bahwa pada titik akhir, turunan pertamanya linier dan oleh karena itu fungsi spline berlanjut ke arah yang sudah berjalan. Interpolasi spline kubik ini disebut juga sebagai “natural spline”.

Awalnya, kita dapat melihat bahwa setiap polinomial kubik \(S_i\) digeser ke kanan oleh unit \(x_i\) atau bergeser ke kiri jika \(x_i\) negatif. Pada \(x_i\) nilai fungsi adalah \(a_i\) yang berarti \(a_i = y_i\) untuk setiap nilai \(i\). Menyelesaikan sisa koefisien yang ada akan lebih kompleks, tetapi sekarang \(3n\) tidak diketahui dengan \(3n\) kondisi. Derivasi penuh tersedia dari berbagai sumber, tetapi secara garis besar dari Persamaan (8.12) kita mendapatkan \(S_i'\left(x_{i+1}\right)=S'_{i+1}\), kemudian \(S'_{i + 1} - S'_i \left(x\right) = 0\), dan kita dapat mensubstitusi Persamaan (8.9) ke dalam kedua komponen, pemecahan untuk \(d_i\) dalam hal ini \(x_i\), \(y_i\), dan \(c_i\). Proses yang sama dapat direplikasi dengan Persamaan (8.13) dan \(b_i\). Hasilnya adalah matriks tridiagonal, seperti yang ada pada Chapter 6.3.3, yang dapat dipecahkan untuk menemukan koefisien. Terdapat sebuah matriks, A, sedemikian rupa sehingga,

\[\begin{equation} AC=V \tag{8.14} \end{equation}\]

dimana \(A\) merupakan matriks tridiagonal. Pada matriks tridiagonal ini \(\left(u_1,u_2,\dots,u_{n-1}\right)\) merupakan vektor \(U\), dan vektor \(M\), \(L\), dan \(V\) ditentukan dengan cara serupa. Matriks ini sedemikian rupa,

\[\begin{equation} u_i=l_i=x_{i+1}-x_i \tag{8.15} \end{equation}\]

kecuali pada \(u_0=l_n\). Lebih jauh, diagonal utama \(D\) ditentukan menggunakan Persamaan (8.16).

\[\begin{equation} m_i=2\left(x_{i+1}-x_i+x_i-x_{i-1}\right) \tag{8.16} \end{equation}\]

kecuali pada \(d_0=d_n=1\). Akhirnya vektor \(V\) ditentukan dengan Persamaan (8.17).

\[\begin{equation} v_i=3\left(\frac{y_{i+1}-y_i}{x_{i+1}-x_i}-\frac{y_i-y_{i-1}}{x_i-x_{i-1}}\right) \tag{8.17} \end{equation}\]

kecuali pada \(v_0=v_n=0\). Sehingga,

\[\begin{equation} \begin{bmatrix} m_{1} & u_{1} & 0 & 0 & 0 \\[0.3em] l_{1} & m_{2} & u_{2} & 0 & 0 \\[0.3em] 0 & l_{2} & \ddots & \ddots & 0 \\[0.3em] 0 & 0 & \ddots & \ddots & u_{n-1} \\[0.3em] 0 & 0 & 0 &l_{n-1} & m_{n} \end{bmatrix} C = \begin{bmatrix} v_1 \\[0.3em] v_2 \\[0.3em] \vdots \\[0.3em] \vdots \\[0.3em] v_n \end{bmatrix} \tag{8.18} \end{equation}\]

Penyelesaian Persamaan (8.18) akan menghasilkan vektor koefisien \(c\), sehingga koefisien \(b\) dapat dihitung menggunakan Persamaan (8.19).

\[\begin{equation} b_i=\frac{y_{i+1}-y_i}{x_{i+1}-x_i}-\frac{x_{i+1}-x_i}{3}\left(2c_i+c_{i+1}\right) \tag{8.19} \end{equation}\]

Dengan menggunakan vektor \(C\) yang sudah diketahui, koefisien \(d\) dapat dihitung menggunakan Persamaan (8.20).

\[\begin{equation} d_i=\frac{c_{i+1}-c_i}{3\left(x_{i+1}-x_i\right)} \tag{8.20} \end{equation}\]

Algoritma Interpolasi Spline Kubik

Tentukan set titik berpasangan \(\left(x,y\right)\).
Tentukan koefisien \(a_i\) menggunakan Persamaan (8.10), dimana \(a_i = y_i\).
Hitung elemen diagonal bawah (\(l_i\)) dan elemen diagonal atas (\(u_i\)) matriks tridiagonal menggunakan Persamaan (8.15), dimana \(u_0=l_n=0\).
Hitung elemen diagonal utama (\(m_i\)) menggunakan Persamaan (8.16), dimana \(d_0=d_n=1\).
Hitung elemen vektor \(V\) menggunakan Persamaan (8.17), dimana \(v_0=v_n=0\).
Susunlah elemen \(l_i\), \(u_i\), dan \(m_i\) menjadi matriks tridiagonal \(A\).
Deifinisikan persamaan linier seperti pada Persamaan (8.14)
Selesaikan sistem persamaan linier pada Persamaan (8.14) sehingga diperoleh vektor \(C\) yang merupakan kumpulan koefisien \(c\).
Hitung koefisien \(b_i\) menggunakan Persamaan (8.19)
Hitung koefisien \(d_i\) menggunakan Persamaan (8.20).
Bentuk seri persamaan polinomial menggunakan elemen koefisien \(a\), \(b\), \(c\), dan \(d\) yang telah dihitung.
Untuk melakukan ekstrapolasi dengan titik observasi diluar rentang titik diketahui, gunakan persamaan polinomial yang berada pada bagian ujung terdekat dengan nilai \(x\) yang hendak dicari nilai \(y\)-nya.

Berdasarkan algoritma tersebut, kita dapat menyusun suatu fungsi pada R untuk mencari seri persamaan polinomial derajat tiga. Fungsi tersebut adalah sebagai berikut:

cubic_spline <- function(x, y){
  n <- length(x)
  d_vec <- b_vec <- a_vec <- rep(0, n-1)
  vec <- rep(0, n)
  delta_x <- delta_y <- rep(0, n-1)
  
  ## Menghitung nilai selisih dan vektor A
  for(i in 1:(n-1)){
    a_vec[i] <- y[i]
    delta_x[i] <- x[i+1] - x[i]
    delta_y[i] <- y[i+1] - y[i]
  }
  
  ## Menyusun matriks tridiagona
  Au <- c(0, delta_x[2:(n-1)])
  Am <- c(1, 2*(delta_x[1:(n-2)]+delta_x[2:(n-1)]), 1)
  Al <- c(delta_x[1:(n-2)], 0)
  
  vec[0] <- vec[n] <- 0
  for(i in 2:(n-1))
    vec[i] <- 3 * (delta_y[i]/delta_x[i] - 
                   delta_y[i-1]/delta_x[i-1])
  
  ## penyelesaian tridiagonal matriks
  nm <- length(Am)
  Al <- c(NA , Al)
  
  ### forward sweep
  Au[1] <- Au[1] / Am[1]
  vec[1] <- vec[1] / Am[1]
  for(i in 2:(n - 1)){
      Au[i] <- Au[i] / (Am[i] - Al[i] * Au[i - 1])
      vec[i] <- (vec[i] - Al[i] * vec[i - 1]) /
                (Am[i] - Al[i] * Au[i - 1])
  }
  vec[n] <- (vec[n] - Al[n] * vec[n - 1])/
            (Am[n] - Al[n] * Au[n - 1])
  
  ### backward sweep
  c_vec <- rep.int (0, n)
  c_vec[n] <- vec[n]
  for(i in (n - 1) :1)
      c_vec[i] <- vec[i] - Au[i] * c_vec[i + 1]
  
 ## Hitung vektor B dan D dari vektor C
 for(i in 1:(n-1)){
   b_vec[i] <- (delta_y[i]/delta_x[i])-
               (delta_x[i]/3)*(2*c_vec[i]+c_vec[i+1])
   d_vec[i] <- (c_vec[i+1]-c_vec[i]) / (3*delta_x[i])
 }
  
 return(list(a = a_vec, b = b_vec, c = c_vec[-n], d = d_vec))
}

Contoh 8.8 Tentukan persamaan-persamaan spline kubik yang dihasilkan dari titik observasi yang ditampilkan pada Contoh 8.5?

Jawab:

Untuk menentukan persamaan-persamaan linier yang menghubungkan setiap titik, kita akan menggunakan fungsi cubic_spline() yang telah kita buat. Berikut adalah sintaks yang digunakan:

x <- c(-2, -1, 0, 1)
y <- c(-1, -2, -1, 2)

cubic_spline(x, y)

## $a
## [1] -1 -2 -1
## 
## $b
## [1] -1.4 -0.2  2.2
## 
## $c
## [1] 0.0 1.2 1.2
## 
## $d
## [1]  0.4  0.0 -0.4

Sebagai contoh untuk domain \(\left[0,1\right]\), persamaan spline kubiknya adalah \(-0,4x^3+1,2x^2+2,2x-1\). Jika persamaan-persamaan yang terbentuk tersebut divisualisasikan akan terlihat seperti pada Gambar 8.4.

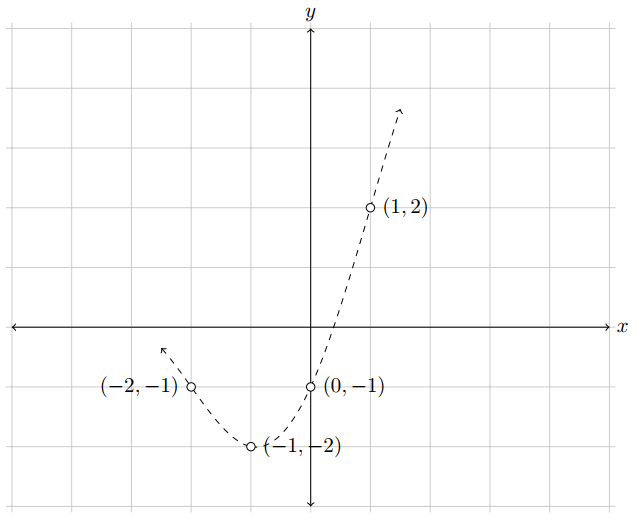
Gambar 8.4: Interpolasi spline kubik empat titik (Sumber:Howard, 2017).

Pada R juga terdapat fungsi splinefun() untuk melakukan interpolasi spline. Format fungsi tersebut adalah sebagai berikut:

splinefun(x, y = NULL,
          method = c("fmm", "periodic", "natural", "monoH.FC", "hyman"),
          ties = mean)

Catatan:

x,y : vektor titik yang akan dilakukan interpolasi

method : spesifikasi jenis spline yang digunakan. Nilai yang mungkin antara lain: "fmm", "natural", "periodic", "monoH.FC" dan "hyman".

ties : metode untuk menangani nilai imbang pada titik yang akan diinterpolasi.

Untuk melakukan interpolasi spline kubik, metode yang digunakan adalah "natural". Berikut adalah contoh interpolasi menggunakan kembali data pada Contoh 8.5:

spline <- splinefun(x, y, method="natural")

# uji dengan nilai x yang sama
spline(x)

## [1] -1 -2 -1  2

FUngsi splinefun() menghasilkan nilai yang sama persis dengan proses interpolasi yang telah kita lakukan.

8.3 Studi Kasus

Pada studi kasus kali ini, kita akan membahas teknik mengisi nilai yang hilang pada data runtun waktu. Terdapat banyak teknik untuk yang dapat digunakan untuk mengisi data yang hilang. Salah satu teknik yang dapat digunakan adalah dengan melakukan interpolasi.

8.3.1 Interpolasi Data Runtun Waktu

Pengisian data hilang pada data runtun waktu (time series) dapat dilakukan dengan berbagai cara sesuai dengan situasi yang dihadapi. Pengisian dapat menggunakan nilai rata-rata jika data memiliki pola white noise, observasi terakhir atau observasi dimasa mendatang, dan interpolasi linier.

Data yang digunakan pada contoh kasus kali ini adalah data airquality. Dataset tersebut merupakan data kualitas udara bulan Mei sampai September 1973 yang ada di New York. Berikut adalah ringkasan data airquality tersebut:

summary(airquality)

##      Ozone          Solar.R         Wind      
##  Min.   :  1.0   Min.   :  7   Min.   : 1.70  
##  1st Qu.: 18.0   1st Qu.:116   1st Qu.: 7.40  
##  Median : 31.5   Median :205   Median : 9.70  
##  Mean   : 42.1   Mean   :186   Mean   : 9.96  
##  3rd Qu.: 63.2   3rd Qu.:259   3rd Qu.:11.50  
##  Max.   :168.0   Max.   :334   Max.   :20.70  
##  NA's   :37      NA's   :7                    
##       Temp          Month           Day      
##  Min.   :56.0   Min.   :5.00   Min.   : 1.0  
##  1st Qu.:72.0   1st Qu.:6.00   1st Qu.: 8.0  
##  Median :79.0   Median :7.00   Median :16.0  
##  Mean   :77.9   Mean   :6.99   Mean   :15.8  
##  3rd Qu.:85.0   3rd Qu.:8.00   3rd Qu.:23.0  
##  Max.   :97.0   Max.   :9.00   Max.   :31.0  
##

str(airquality)

## 'data.frame':    153 obs. of  6 variables:
##  $ Ozone  : int  41 36 12 18 NA 28 23 19 8 NA ...
##  $ Solar.R: int  190 118 149 313 NA NA 299 99 19 194 ...
##  $ Wind   : num  7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
##  $ Temp   : int  67 72 74 62 56 66 65 59 61 69 ...
##  $ Month  : int  5 5 5 5 5 5 5 5 5 5 ...
##  $ Day    : int  1 2 3 4 5 6 7 8 9 10 ...

head(airquality)

##   Ozone Solar.R Wind Temp Month Day
## 1    41     190  7.4   67     5   1
## 2    36     118  8.0   72     5   2
## 3    12     149 12.6   74     5   3
## 4    18     313 11.5   62     5   4
## 5    NA      NA 14.3   56     5   5
## 6    28      NA 14.9   66     5   6

Pada contoh kasus kali ini kita akan mencoba melakukan pengisian data hilang pada data Solar.R pada dataset airquality. Langkah pertama yang perlu dilakukan adalah membuat objek data runtun waktu pada data tersebut.

Solar <- ts(airquality[,"Solar.R"])

Visualisasi data tersebut disajikan pada Gambar 8.5.

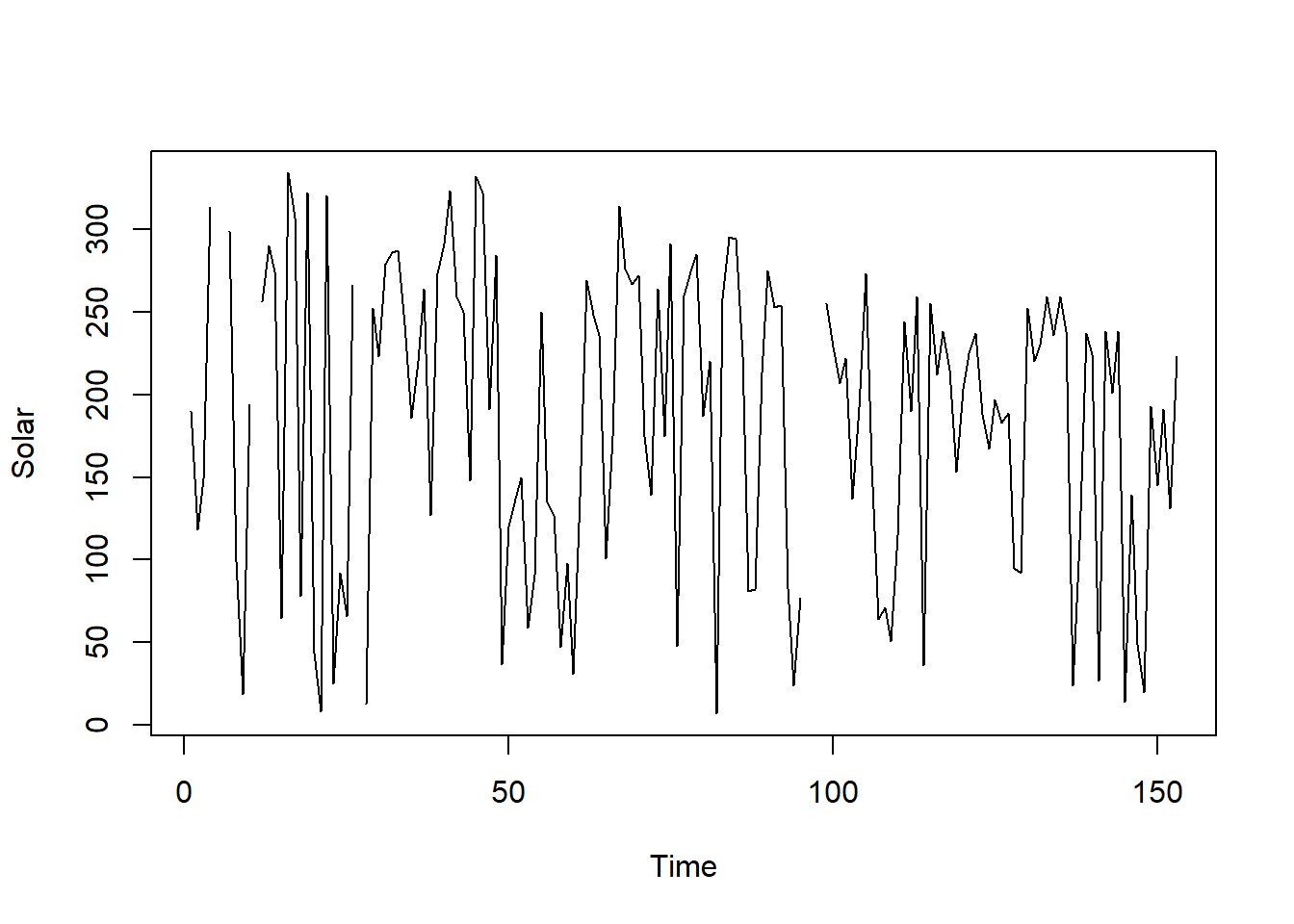
Gambar 8.5: Visualisasi variabel radiasi matahari pada dataset airquality.

Berdasarkan visualisasi tersebut terdapat garis yang terputus yang menunjukkan data yang hilang. Agar garis tersebut dapat tersambung, kita perlu melakukan pengisian nilai yang hilang pada data tersebut. Berikut adalah sintaks yang digunakan untuk melakukan pengisian nilai hilang tersebut:

library(xts)

## Warning: package 'xts' was built under R version 3.5.3

## Loading required package: zoo

## Warning: package 'zoo' was built under R version 3.5.3

## 
## Attaching package: 'zoo'

## The following objects are masked from 'package:base':
## 
##     as.Date, as.Date.numeric

# metode nilai rata-rata
Solar_mean <- na.fill(Solar, fill=mean(Solar, na.rm=TRUE))

# metode last observation carried forward
Solar_locf <- na.locf(Solar)

# metode next observation caried backward
Solar_nocb <- na.locf(Solar, fromLast = TRUE)

# metode interpolasi linier
Solar_linterp <- na.approx(Solar)

Berikut adalah visualisasi menggunakan metode nilai rata-rata:

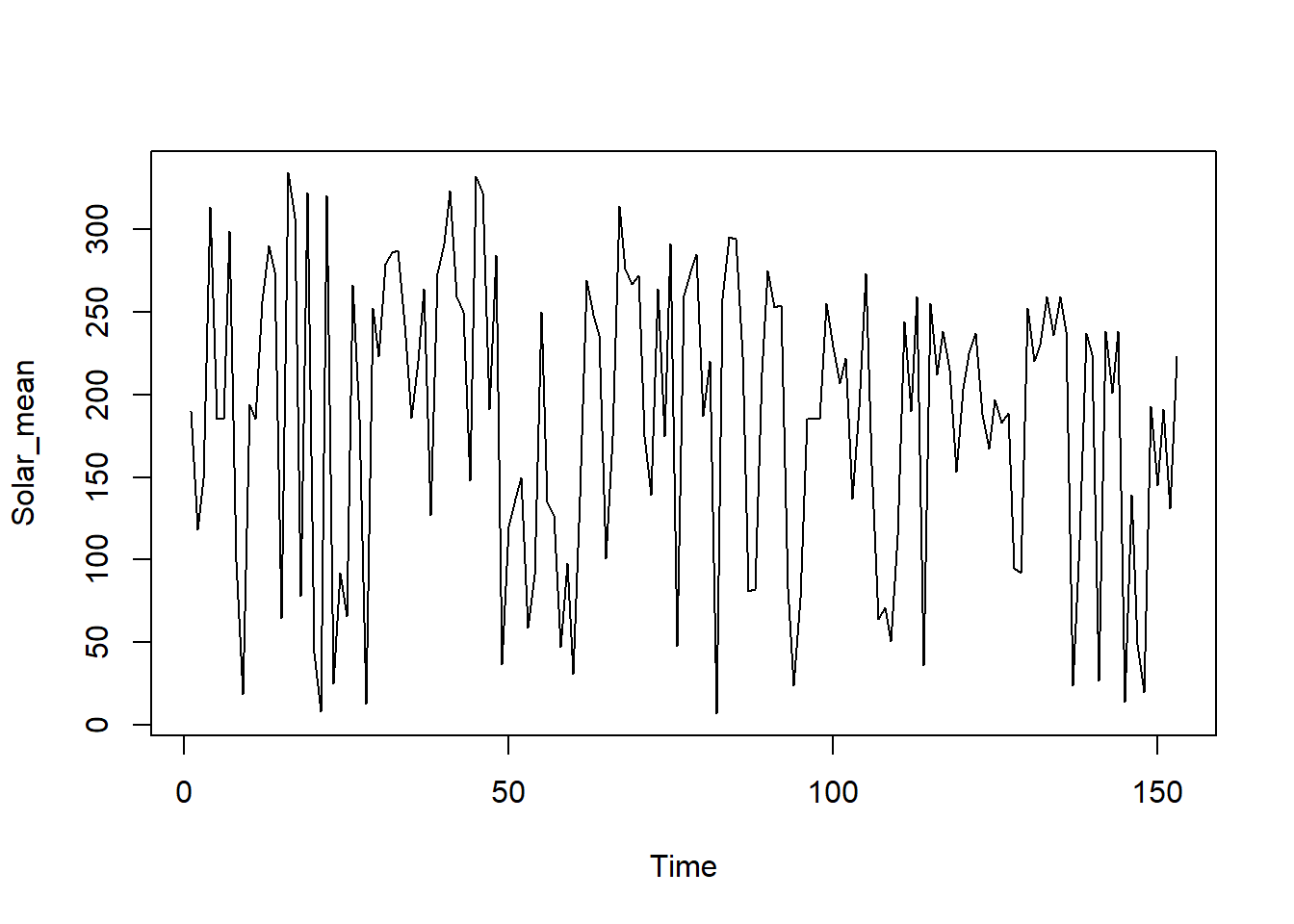
Gambar 8.6: Visualisasi data radiasi matahari menggunakan metode nilai rata-rata.

Secara berturut-turut berikut adalah visualisasi dari metode locf, nocb, dan interpolasi linier:

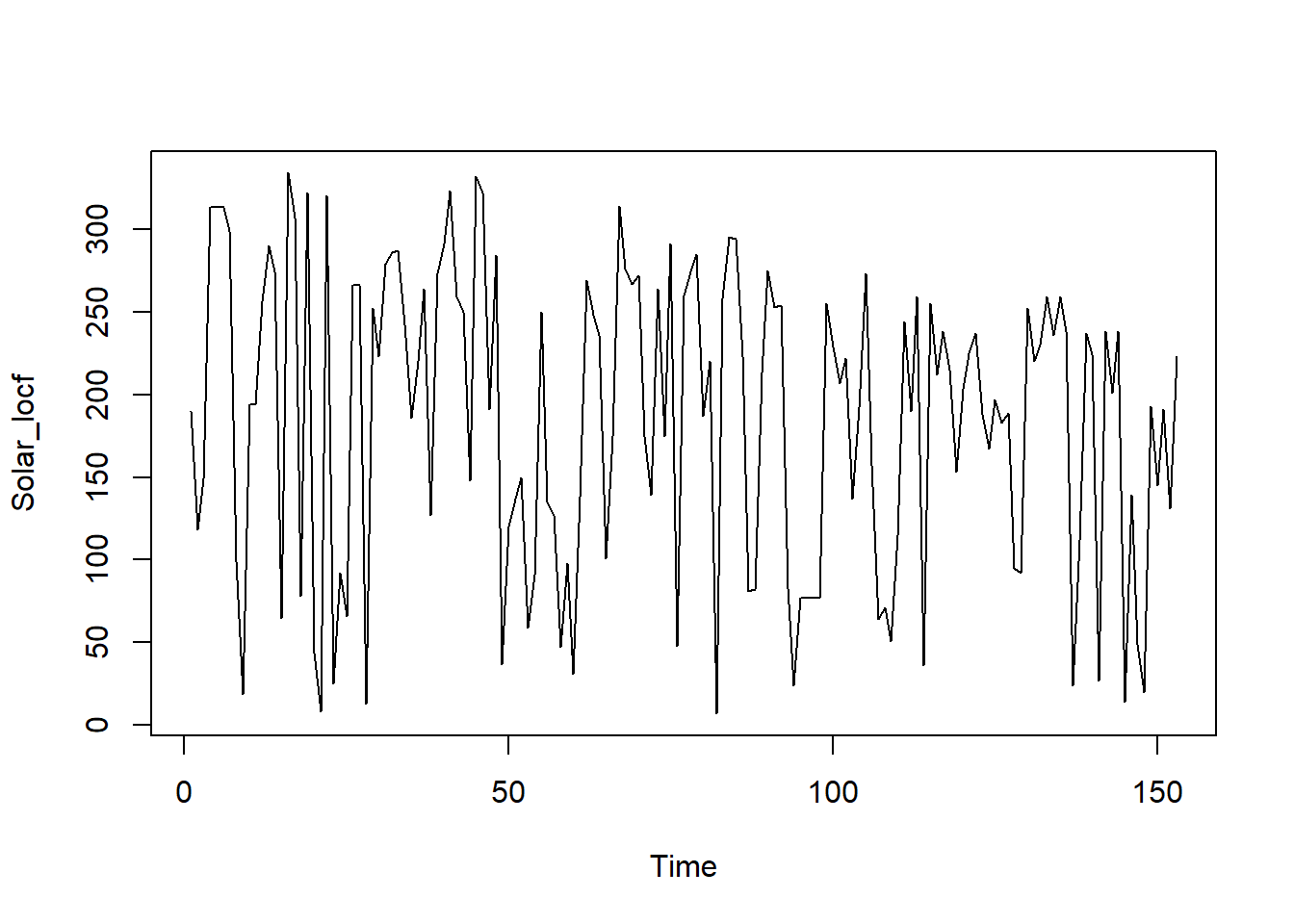
Gambar 8.7: Visualisasi data radiasi matahari menggunakan metode locf.

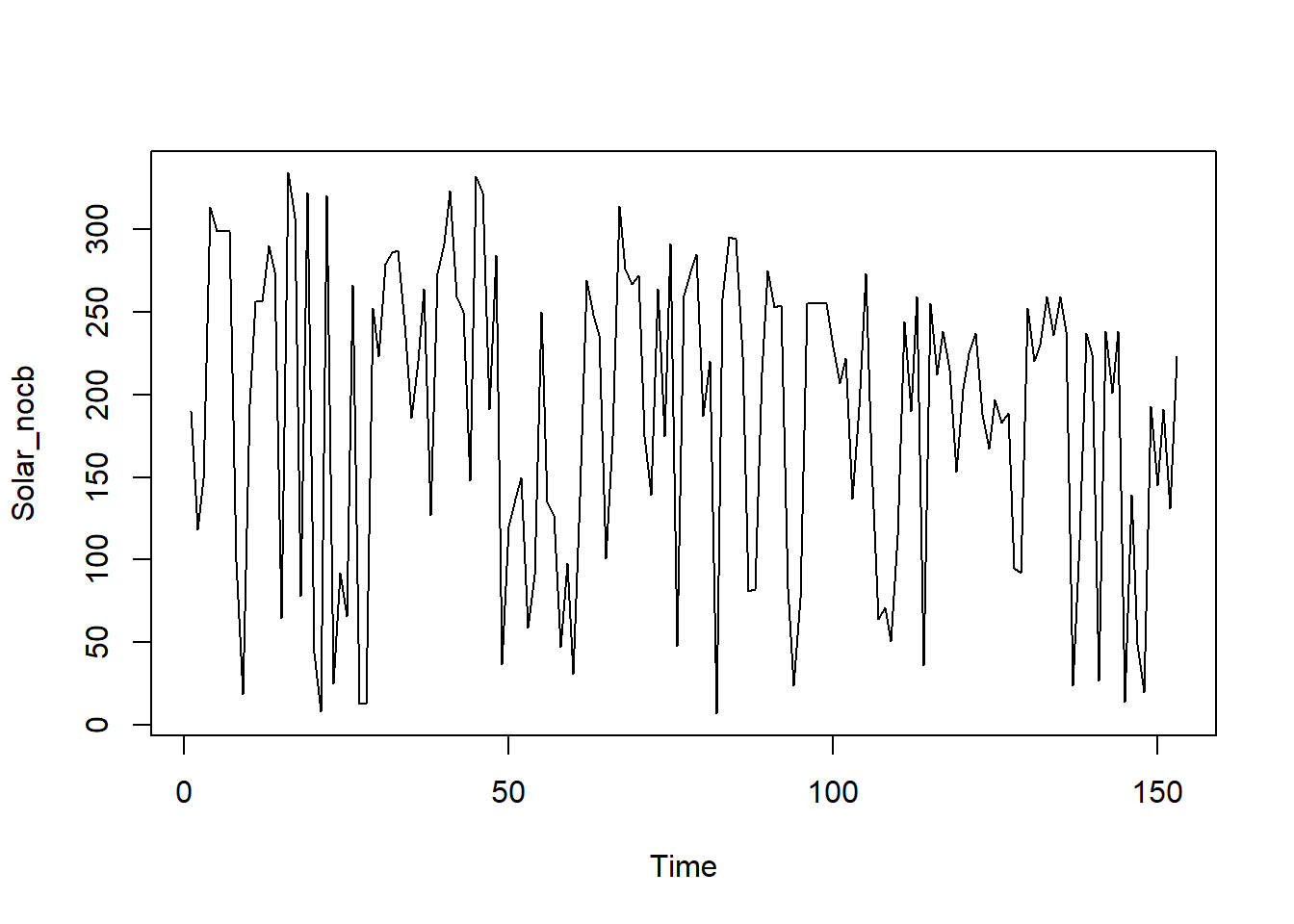
Gambar 8.8: Visualisasi data radiasi matahari menggunakan metode nocb.

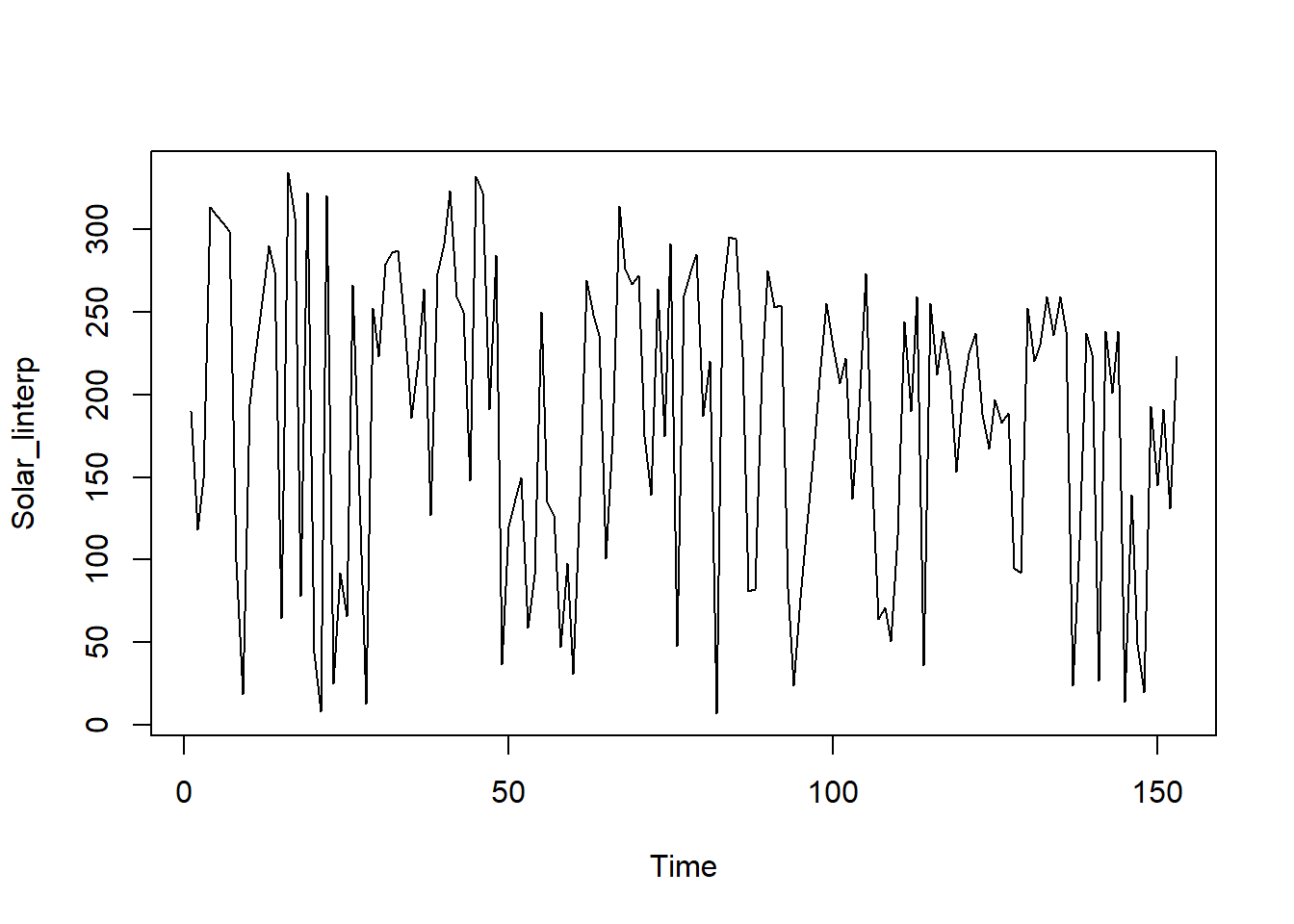
Gambar 8.9: Visualisasi data radiasi matahari menggunakan metode interpolasi linier.

Pemilihan metode interpolasi mana yang sesuai akan berbeda pada setiap situasi dan jenis data yang akan dilakukan interpolasi. Interpolasi data runtun waktu pada bidang lingkungan umumnya menggunakan metode interpolasi nilai rata-rata dan linier dan tidak menutup kemungkinan interpolasi dengan metode lain yang telah dijelaskan pada buku ini dapat pula digunakan.

Pada situasi dimana data membentuk pola white noises (pola acak disekitar nilai rata-rata dan memiliki varians yang konstan) seperti yang ditunjukkan variabel Solar.R, interpolaasi dengan nilai rata-rata cukup sesuai untuk digunakan untuk mengisi nilai hilang (missing value) pada data runtun waktu tersebut.

8.4 Referensi

Howard, J.P. 2017. Computational Methods for Numerical Analysis with R. CRC Press.
Kreyszig, E. 2011. Advanced Engineering Mathematics, 10th Edition. John Wiley & Sons.
Suparno, S. 2008. Komputasi untuk Sains dan Teknik Edisi II. Departemen Fisika-FMIPA Universitas Indonesia.

8.5 Latihan

Diberikan data titik (3,5), (0,-2), dan (4,1). Tentukan persamaan polinomial untuk melakukan interpolasi pada ketiga titik tersebut!
Jika diberikan 13 titik observasi, apakah saudara cenderung akan menggunakan interpolasi polinomial atau spline? jelaskan alasan saudara?
Bentuklah kembali fungsi poly_inter() dengan menambahkan metode evaluasi polinomial ke dalam fungsi tersebut!
Pada Latihan No.1, bentuklah persamaan spline kubik menggunakan titik observasi tersebut!