Chapter 6 Aljabar Linier

Pada chapter ini penulis akan menjelaskan mengenai cara untuk menyelesaikan sistem persamaan linier. Adapun yang akan dibahas pada chapter ini antara lain:

  • operasi Vektor dan matriks
  • Metode Eliminasi Gauss
  • Metode Dekomposisi matriks
  • Studi Kasus

6.1 Vektor dan matriks

Pada Chapter 2.7 dan Chapter 2.8 telah dijelaskan sekilas bagaimana cara melakukan operasi pada vektor dan matriks. Pada chapter ini, penulis akan menambahkan operasi-operasi lain yang dapat dilakukan pada vektor dan matriks. Dasar-dasar operasi ini selanjutnya akan digunakan sebagai dasar menyusun algoritma penyelesaian sistem persamaan linier.

6.1.1 Operasi Vektor

Misalkan saja diberikan vektor \(u\) dan \(v\) yang ditunjukkan pada Persamaan (6.1).

\[\begin{equation} u = \begin{bmatrix} u_1 \\[0.3em] u_2 \\[0.3em] \vdots \\[0.3em] u_n \end{bmatrix} dan\ v\ = \begin{bmatrix} v_1 \\[0.3em] v_2 \\[0.3em] \vdots \\[0.3em] v_n \end{bmatrix} \tag{6.1} \end{equation}\]

Jika kita menambahkan atau mengurangkan nilai elemen vektor dengan suatu skalar (konstanta yang hanya memiliki besaran), maka operasi penjumlahan/pengurangan akan dilakukan pada setiap elemen vektor.

\[\begin{equation} u \pm x = \begin{bmatrix} u_1 \\[0.3em] u_2 \\[0.3em] \vdots \\[0.3em] u_n \end{bmatrix} \pm x = \begin{bmatrix} u_1 \pm x \\[0.3em] u_2 \pm x \\[0.3em] \vdots \\[0.3em] u_n \pm x \end{bmatrix} \tag{6.2} \end{equation}\]

Jika kita melakukan penjumlahan pada vektor \(u\) dan \(v\), maka operasi akan terjadi pada masing-masing elemen dengan indeks yang sama.

\[\begin{equation} u \pm v = \begin{bmatrix} u_1 \\[0.3em] u_2 \\[0.3em] \vdots \\[0.3em] u_n \end{bmatrix} \pm v\ = \begin{bmatrix} v_1 \\[0.3em] v_2 \\[0.3em] \vdots \\[0.3em] v_n \end{bmatrix} = \begin{bmatrix} u_1 \pm v_1 \\[0.3em] u_2 \pm v_2 \\[0.3em] \vdots \\[0.3em] u_n \pm v_n \end{bmatrix} \tag{6.3} \end{equation}\]

Untuk lebih memahami operasi tersebut, berikut penulis berikan contoh penerapannya pada R:

## [1]  7  9 11 13 15
## [1] -5 -5 -5 -5 -5

Bagaimana jika kita melakukan operasi dua vektor, dimaana salah satu vektor memiliki penjang yang berbeda?. Untuk memnjawab hal tersebut, perhatikan sintaks berikut:

## Warning in u + x: longer object length is not a
## multiple of shorter object length
## [1] 2 4 4 6 6

Berdasarkan contoh tersebut, R akan mengeluarkan peringatan yang menunjukkan operasi dilakukan pada vektor dengan panjang berbeda. R akan tetap melakukan perhitungan dengan menjumlahkan kembali vektor \(u\) yang belum dijumlahkan dengan vektor \(x\) sampai seluruh elemen vektor \(u\) dilakukan operasi penjumlahan.

Operasi lain yang dapat dilakukan pada vektor adalah menghitung inner product dan panjang vektor. Inner product dihitung menggunakan Persamaan (6.4).

\[\begin{equation} u.v=\sum_{i=1}^nu_1v_1+u_2v_2+\dots+u_nv_n \tag{6.4} \end{equation}\]

Panjang vektor atau vektor yang telah dinormalisasi dihitung menggunakan Persamaan (6.5)

\[\begin{equation} \left|u\right|=\sqrt{u_1^2+u_2^2+\dots+u_n^2} \tag{6.5} \end{equation}\]

Berikut adalah contoh bagaimana cara menghitung inner product dan panjang vektor menggunakan R:

##      [,1]
## [1,]  130
## [1] 7.416

6.1.2 Operasi matriks

Misalkan kita memiliki 2 buah matriks \(A\) dan \(B\).

\[\begin{equation} A = \begin{bmatrix} a_{1.1} & a_{1.2} &\cdots& a_{1.n} \\[0.3em] a_{2.1} & a_{2.2} &\cdots& a_{2.n} \\[0.3em] \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m.1} & a_{m.2} &\cdots& a_{m.n} \end{bmatrix} dan\ B = \begin{bmatrix} b_{1.1} & b_{1.2} &\cdots& b_{1.n} \\[0.3em] b_{2.1} & b_{2.2} &\cdots& b_{2.n} \\[0.3em] \vdots & \vdots &\ddots& \vdots \\[0.3em] b_{m.1} & b_{m.2} &\cdots& b_{m.n} \end{bmatrix} \tag{6.6} \end{equation}\]

Jika salah satu matriks tersebut dijumlahkan atau dikurangkan dengan skalar.

\[\begin{equation} A \pm x = \begin{bmatrix} a_{1.1} & a_{1.2} &\cdots& a_{1.n} \\[0.3em] a_{2.1} & a_{2.2} &\cdots& a_{2.n} \\[0.3em] \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m.1} & a_{m.2} &\cdots& a_{m.n} \end{bmatrix} \pm x = \begin{bmatrix} a_{1.1}\pm x & a_{1.2}\pm x &\cdots& a_{1.n}\pm x \\[0.3em] a_{2.1}\pm x & a_{2.2}\pm x &\cdots& a_{2.n}\pm x \\[0.3em] \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m.1}\pm x & a_{m.2}\pm x &\cdots& a_{m.n}\pm x \end{bmatrix} \tag{6.7} \end{equation}\]

Jika kedua matriks \(A\) dan \(B\) saling dijumlahkan atau dikurangkan. Perlu diperhatikan bahwa penjumlahan dua buah matriks hanya dapat dilakukan pada matriks dengan ukuran yang seragam.

\[\begin{equation} \begin{split} A \pm B & = \begin{bmatrix} a_{1.1} & a_{1.2} &\cdots& a_{1.n} \\[0.3em] a_{2.1} & a_{2.2} &\cdots& a_{2.n} \\[0.3em] \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m.1} & a_{m.2} &\cdots& a_{m.n} \end{bmatrix} \pm \begin{bmatrix} b_{1.1} & b_{1.2} &\cdots& b_{1.n} \\[0.3em] b_{2.1} & b_{2.2} &\cdots& b_{2.n} \\[0.3em] \vdots & \vdots &\ddots& \vdots \\[0.3em] b_{m.1} & b_{m.2} &\cdots& b_{m.n} \end{bmatrix} \\ & = \begin{bmatrix} a_{1.1}\pm b_{1.1} & a_{1.2}\pm b_{1.2} &\cdots& a_{1.n}\pm b_{1.n} \\[0.3em] a_{2.1}\pm b_{2.1} & a_{2.2}\pm b_{2.2} &\cdots& a_{2.n}\pm b_{2.n} \\[0.3em] \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m.1}\pm b_{m.1} & a_{m.2}\pm b_{m.2} &\cdots& a_{m.n}\pm b_{m.n} \end{bmatrix} \end{split} \tag{6.8} \end{equation}\]

Untuk lebih memahaminya, berikut disajikan contoh operasi penjumlahan pada matriks:

##      [,1] [,2] [,3]
## [1,]    2    5    8
## [2,]    3    6    9
## [3,]    4    7   10
##      [,1] [,2] [,3]
## [1,]   11   17   23
## [2,]   13   19   25
## [3,]   15   21   27

Operasi pehitungan lain yang penting pada matriks adalah operasi perkalian matriks. Perlu diperhatikan bahwa untuk perkalian matriks, jumlah kolom matriks sebelah kiri harus sama dengan jumlah baris pada matriks sebelah kanan. Perkalian antara dua matriks disajikan pada Persamaan (6.9).

\[\begin{equation} A_{m.n}\times B_{n.r}=AB_{m.r} \tag{6.9} \end{equation}\]

Pada R perkalian matriks dilakukan menggunakan operator %*%. Berikut adalah contoh perkalian matriks pada R:

##      [,1] [,2] [,3]
## [1,]  138  174  210
## [2,]  171  216  261
## [3,]  204  258  312

6.2 Operasi Baris Elementer

Terdapat tiga buah operasi dasar pada baris matriksoperasi baris elementer. Ketiga operasi ini akan menjadi dasar operasi sub-chapter selanjutnya. Ketiga operasi dasar tersebut antara lain:

  1. Row Scalling. Mengalikan baris matriks dengan konstanta bukan nol.
  2. Row Swaping. Menukar urutan baris pada sebuah matriks (contoh: menukar baris 1 dengan baris 2 dan sebaliknya).
  3. Row Replacement. Baris matriks diganti dengan hasil penjumlahan atau pengurangan baris matriks tersebut dengan baris matriks lainnya, dimana baris matriks lainnya yang akan dijumlahkan/dikurangkan dengan matriks tersebut telah dilakukan proses row scalling. Luaran yang diperoleh pada umumnya adalah nilai nol pada baris matriks awal atau akhir.

Ketiga proses tersebut akan terjadi secara berulang, khusunya jika kita hendak mengerjakan sistem persamaan linier menggunakan algoritma eliminasi Gauss. Untuk mempermudah proses tersebut, kita dapat membuat masing-masing fungsi untuk masing-masing operasi tersebut. Algoritma fungsi-fungsi tersebut selanjutnya menjadi dasar penyusunan algoritma fungsi-fungsi eliminasi Gauss dan dekomposisi matriks yang akan dijelaskan pada chapter selanjutnya.

Fungsi row scalling pada R dapat dituliskan pada sintaks berikut:

Berikut adalah contoh penerapannya:

##      [,1] [,2] [,3]
## [1,]    1    6   11
## [2,]    2    7   12
## [3,]    3    8   13
## [4,]    4    9   14
## [5,]    5   10   15
##      [,1] [,2] [,3]
## [1,]    1    6   11
## [2,]   20   70  120
## [3,]    3    8   13
## [4,]    4    9   14
## [5,]    5   10   15

Catatan: Untuk menyimpan hasil perhitungan, simpan proses perhitungan dalam sebuah objek (lihat Chapter 2.5).

Row swapping merupakan proses yang berulang, kita perlu menyimpan terlebih dahulu baris matriks pertama kedalam sebuah objek. Baris matriks pertama selanjutnya diganti dengan baris matriks kedua, sedangkan baris matriks kedua selanjutnya akan diganti dengan baris matriks pertama yang telah terlebih dahulu disimpan dalam sebuah objek. Fungsi row swapping pada R dapat dituliskan pada sintaks berikut:

Berikut merupakan contoh penerapan fungsi swap_row():

##      [,1] [,2] [,3]
## [1,]    1    6   11
## [2,]    5   10   15
## [3,]    3    8   13
## [4,]    4    9   14
## [5,]    2    7   12

Pada proses row replacement, proses perhitungan dilakukan dengan melakukan penjumlahan suatu baris matriks dengan baris matriks lainnya dengan terlebih dahulu melakukan row scalling terhadap matriks lainnya. Berikut adalah fungsi replace_row() yang ditulis pada R:

Berikut adalah contoh penerapan fungsi replace_row():

##      [,1] [,2] [,3]
## [1,]    1    6   11
## [2,]    2    7   12
## [3,]    0  -10  -20
## [4,]    4    9   14
## [5,]    5   10   15

6.3 Eliminasi Gauss

Pada sub-chapter ini kita akan menggunakan operasi baris elementer yang telah dijelaskan pada Chapter 2.5. Terdapat dua topik yang akan dibahas pada sub-chapter ini, yaitu: row echelon form termasuk reduced row echelon form dan matriks tridiagonal.

Eliminasi Gauss merupakan sebuah cara untuk mencari penyelesaian sistem persamaan linier. Ide dasar dari eliminasi Gauss adalah melakukan operasi matematika pada baris matriks (lihat Chapter 2.5) dan melanjutkannya sampai hanya tersisa satu variabel saja. Kita dapat melakukan lebih dari satu operasi baris elementer pada proses elmininasi ini (contoh: mengalikan sebuah baris dengan konstanta dan menjumlahkan hasilnya pada baris lain).

6.3.1 Row Echelon Form

Sebuah matriks merupakan row echelon form jika matriks tersebut memenuhi beberapa kondisi:

  1. Angka bukan nol pertama dari kiri (leading coefficient) selalu di sebelah kanan angka bukan nol pertama pada baris di atasnya.
  2. Baris yang terdiri dari semua nol ada di bagian bawah matriks.

Misalkan terdapat persamaan linier seperti yang ditunjukkan pada Persamaan (6.10).

\[\begin{equation} \begin{matrix} a_{1.1}x_1+a_{1.2}x_2+a_{1.3}x_3+\cdots+a_{1.n}x_n=b_1 \\ a_{2.1}x_1+a_{2.2}x_2+a_{2.3}x_3+\cdots+a_{2.n}x_n=b_2 \\ a_{3.1}x_1+a_{3.2}x_2+a_{3.3}x_3+\cdots+a_{3.n}x_n=b_3 \\ \cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots \\ a_{m.1}x_1+a_{m.2}x_2+a_{m.3}x_3+\cdots+a_{m.n}x_n=b_n \end{matrix} \tag{6.10} \end{equation}\]

dimana \(a_{i.j}\) untuk \(i=1\) sampai dengan \(m\) dan \(j=1\) sampai dengan \(n\) merupakan koefisien persamaan linier. \(x_i\) untuk \(i=1\) sampai dengan \(n\) merupakan variabel bebas pada sistem persamaan linier.

Persamaan linier pada Persamaan (6.10) dapat dinyatakan ke dalam bentuk matriks pada Persamaan (6.11).

\[\begin{equation} \begin{bmatrix} a_{1.1} & a_{1.2} & a_{1.3} &\cdots& a_{1.n} \\[0.3em] a_{2.1} & a_{2.2} & a_{2.3} &\cdots& a_{2.n} \\[0.3em] a_{3.1} & a_{3.2} & a_{3.3} &\cdots& a_{3.n} \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m.1} & a_{m.2} & a_{m.3} &\cdots& a_{m.n} \end{bmatrix} \begin{bmatrix} x_1 \\[0.3em] x_2 \\[0.3em] x_3 \\[0.3em] \cdots \\[0.3em] x_n \end{bmatrix} = \begin{bmatrix} b_1 \\[0.3em] b_2 \\[0.3em] b_3 \\[0.3em] \cdots \\[0.3em] b_n \end{bmatrix} \tag{6.11} \end{equation}\]

\[\begin{equation} AX=B \tag{6.12} \end{equation}\]

dimana:

  • matriks A merupakan matriks koefisien / Jacobian
  • vaktor X merupakan vaktor variabel
  • vektor B merupakan vektor konstanta

matriks pada Persamaan (6.11) dapat diubah menjadi augmented matrix, yaitu: perluasan matriks A dengan menambahkan vektor B pada kolom terakhirnya.

\[\begin{equation} \begin{bmatrix} a_{1.1} & a_{1.2} & a_{1.3} &\cdots& a_{1.n} & b_1 \\[0.3em] a_{2.1} & a_{2.2} & a_{2.3} &\cdots& a_{2.n} & b_2 \\[0.3em] a_{3.1} & a_{3.2} & a_{3.3} &\cdots& a_{3.n} & b_3 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m.1} & a_{m.2} & a_{m.3} &\cdots& a_{m.n} & b_n \end{bmatrix} \tag{6.13} \end{equation}\]

\[\begin{equation} A=\left[A|B\right] \tag{6.14} \end{equation}\]

Teorema 6.1 (spltheorem) Suatu sistem persamaan linier mempunyai penyelesaian tunggal bila memenuhi syarat-syarat sebagai berikut:
  • ukuran persamaan linier simultan bujursangkar (jumlah persamaan sama dengan jumlah variabel bebas).
  • sistem persamaan linier non-homogen di mana minimal ada satu nilai vektor konstanta \(B\) tidak nol atau terdapat \(b_{n}\neq 0\).
  • Determinan dari matriks koefisiensistem persamaan linier tidak sama dengan nol.

Untuk memperoleh penyelesaian sistem persamaan linier, Persamaan (6.13) perlu dilakukan operasi baris elementer. Hasil operasi baris dasar akan menghasilkan matriks row echelon form yang disajikan pada Persamaan (6.15).

\[\begin{equation} \begin{bmatrix} a_{1.1} & a_{1.2} & a_{1.3} &\cdots& a_{1.n} & b_1 \\[0.3em] a_{2.1} & a_{2.2} & a_{2.3} &\cdots& a_{2.n} & b_2 \\[0.3em] a_{3.1} & a_{3.2} & a_{3.3} &\cdots& a_{3.n} & b_3 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m.1} & a_{m.2} & a_{m.3} &\cdots& a_{m.n} & b_n \end{bmatrix} \implies \begin{bmatrix} c_{1.1} & c_{1.2} & c_{1.3} &\cdots& c_{1.n} & d_1 \\[0.3em] 0 & c_{2.2} & c_{2.3} &\cdots& c_{2.n} & d_2 \\[0.3em] 0 & 0 & c_{3.3} &\cdots& c_{3.n} & d_3 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] 0 & 0 & 0 &\cdots& c_{m.n} & d_n \end{bmatrix} \tag{6.15} \end{equation}\]

Sehingga penyelesaian sistem persamaan linier dapat diperoleh menggunakan Persamaan (6.16).

\[\begin{equation} \begin{matrix} x_n=\frac{d_n}{c_{m.n}} \\ x_{n-1}=\frac{1}{C_{m-1.n-1}}\left(d_{n-1}-c_{m-1.n}x_n\right) \\ \cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots \\ x_2=\frac{1}{c_{2.2}}\left(d_2-c_{2.3}x_3-c_{2.4}x_4-\dots-c_{2.n}x_n\right) \\ x_1=\frac{1}{c_{1.1}}\left(d_1-c_{1.2}x_2-c_{1.3}x_3-\dots-c_{1.n}x_n\right) \end{matrix} \tag{6.16} \end{equation}\]

Contoh 6.1 Selesaikan sistem persamaan berikut:

\[ \begin{matrix} x_1+x_2+x_3=6 \\ x_1+2x_2-x_3=2 \\ 2x_1+x_2+2x_3=10 \\ \end{matrix} \]

Jawab:

Augmented matrix sistem persamaan linier tersebut adalah sebagai berikut:

\[ \begin{bmatrix} 1 & 1 & 1 & 6 \\[0.3em] 1 & 2 & -1 & 2 \\[0.3em] 2 & 1 & 2 & 10 \end{bmatrix} \]

Operasi baris elementer selanjutnya dilakukan pada matriks tersebut. Pada langkah pertama, baris ke-2 dikurangkan dengan baris ke-1 (\(B_2-B_1\)) dan baris ke-3 dikurangkan oleh dua kali baris ke-1 (\(B_3-2B_1\)).

\[\begin{equation*} \begin{bmatrix} 1 & 1 & 1 & 6 \\[0.3em] 1 & 2 & -1 & 2 \\[0.3em] 2 & 1 & 2 & 10 \end{bmatrix} \begin{matrix} B_2-B_1 \\ \implies \\ B_3-2B_1 \end{matrix} \begin{bmatrix} 1 & 1 & 1 & 6 \\[0.3em] 0 & 1 & -2 & -4 \\[0.3em] 0 & -1 & 0 & -2 \end{bmatrix} \end{equation*}\]

Hasil dari langkah pertama tersebut, selanjutnya menjadi input dari langkah selanjutnya. Pada langkah selanjutnya operasi baris elementer kembali dilanjutkan. Baris ke-3 dikurangkan denganbaris ke-2 (\(B_3-B_2\)).

\[\begin{equation*} \begin{bmatrix} 1 & 1 & 1 & 6 \\[0.3em] 0 & 1 & -2 & -4 \\[0.3em] 0 & -1 & 0 & -2 \end{bmatrix} \begin{matrix} B_3-B_2 \\ \implies \end{matrix} \begin{bmatrix} 1 & 1 & 1 & 6 \\[0.3em] 0 & 1 & -2 & -4 \\[0.3em] 0 & 0 & -2 & -6 \end{bmatrix} \end{equation*}\]

Setelah diperoleh matriks row echelon form selanjutnya penyelesaian persamaan dapat dikerjakan menggunakan Persamaan (6.16).

\[\begin{equation*} \begin{matrix} x_3=\frac{-6}{-2}=3 \\ x_2=\frac{1}{1}\left(-4-\left(2\right)3\right)=2 \\ x_1=\frac{1}{1}\left(6-2-3\right)=1 \end{matrix} \end{equation*}\]

Algoritma Row Echelon Form

  1. Masukkan matriks \(A\), dan vektor \(B\) beserta ukurannya \(n\)
  2. Buat augmented matrix \(\left[A|B\right]\) namakan dengan \(A\)
  3. Untuk baris ke-\(i\) dimana \(i=1\) s/d \(n\), perhatikan apakah nilai \(a_{i,j}\) sama dengan nol. a) Bila iya, lakukan row swapping antara baris ke-\(i\) dan baris ke-\(i+k\leq n\), dimana \(a_{i+k,j}\) tidak sama dengan nol. Bila tidak ada berarti perhitungan tidak bisa dilanjutkan dan proses dihentikan dengan tanpa penyelesaian, b) Bila tidak, lanjutkan.
  4. Untuk baris ke-\(j\), dimana \(j=i+1\) s/d \(n\), lakukan operasi baris elementer:a) Hitung \(c=\frac{a_{j,i}}{a_{i,i}}\), b) untuk kolom \(k\), dimana \(k=1\) s/d \(n+1\), hitung \(a_{j,k}=a_{j,k}-c.a_{i,k}\).
  5. Hitung akar, untuk \(i=n\) s/d 1 (bergerak dari baris pertama) menggunakan Persamaan (6.16).

Berdasarkan algoritma tersebut, kita dapat menyusun fungsi pada R untuk menyelesaikan sistem persamaan linier menggunakan matriks row echelon form. Fungsi yang akan dibentuk hanya sampai pada algoritma ke-4. Proses substitusi akan dilakukan secara manual. Berikut adalah sintaks yang digunakan:

Dengan menggunakan fungsi ref_matrix(), kita dapat membentuk matriks row echelon form pada Contoh 6.1.

##      [,1] [,2] [,3] [,4]
## [1,]    1    1    1    6
## [2,]    1    2   -1    2
## [3,]    2    1    2   10
##      [,1] [,2] [,3] [,4]
## [1,]    1    1    1    6
## [2,]    0    1   -2   -4
## [3,]    0    0   -2   -6

matriks yang diperoleh selanjutnya dapat diselesaikan menggunakan Persamaan (6.16).

Contoh 6.2 Dengan menggunakan fungsi ref_matrix(), buatlah matriks row echelon form dari sistem persamaan linier berikut:

\[ \begin{matrix} 2x_1+x_2-x_3=1 \\ 3x_1+2x_2-2x_3=1 \\ x_1-5x_2+4x_3=3 \\ \end{matrix} \]

Jawab:

Augmented matrix dari sistem persamaan tersebut adalah sebagai berikut:

\[ \begin{bmatrix} 2 & 1 & -1 & 1 \\[0.3em] 3 & 2 & -2 & 1 \\[0.3em] 1 & -5 & 4 & 3 \end{bmatrix} \]

Penyelesaian matriks tersebut adalah sebagai berikut:

##      [,1] [,2] [,3] [,4]
## [1,]    2    1   -1    1
## [2,]    3    2   -2    1
## [3,]    1   -5    4    3
##      [,1] [,2] [,3] [,4]
## [1,]    2  1.0 -1.0  1.0
## [2,]    0  0.5 -0.5 -0.5
## [3,]    0  0.0 -1.0 -3.0

Proses lebih lanjut akan menghasilkan penyelesaian sebagai berikut:

\[ \begin{matrix} x_1=1 \\[0.3em] x_2=2 \\[0.3em] x_3=3 \end{matrix} \]

6.3.2 Eliminasi Gauss-Jordan

Berbeda dengan metode eliminasi Gauss yang telah dijelaskan pada Chapter 6.3.1, metode eliminasi Gauss-Jordan membentuk matriks menjadi bentuk reduced row echelon form. Metode ini merupakan pengembangan metode eliminasi Gauss, dimana matriks sebelah kiri augmented matrix diubah menjadi matriks diagonal (lihat Persamaan (6.17)).

\[\begin{equation} \begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} &\cdots& a_{1,n} & b_1 \\[0.3em] a_{2,1} & a_{2,2} & a_{2,3} &\cdots& a_{2,n} & b_2 \\[0.3em] a_{3,1} & a_{3,2} & a_{3,3} &\cdots& a_{3,n} & b_3 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m,1} & a_{m,2} & a_{m,3} &\cdots& a_{m,n} & b_n \end{bmatrix} \implies \begin{bmatrix} 1 & 0 & 0 &\cdots& 0 & d_1 \\[0.3em] 0 & 1 & 0 &\cdots& 0 & d_2 \\[0.3em] 0 & 0 & 1 &\cdots& 0 & d_3 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] 0 & 0 & 0 &\cdots& 1 & d_n \end{bmatrix} \tag{6.17} \end{equation}\]

Sehingga penyelesaian persamaan linier tersebut adalah nilai \(d_1,d_2,d3,\dots,d_n\) dan atau:

\[\begin{equation} \begin{matrix} x_1=d_1 \\ x_2=d_2 \\ x_3=d_3 \\ \cdots\cdots\cdots\cdots\cdots\cdots\cdots\cdots \\ x_n=d_n \end{matrix} \tag{6.18} \end{equation}\]

Contoh 6.3 Selesaikan sistem persamaan berikut:

\[ \begin{matrix} x_1+x_2=3 \\ 2x_1+4x_2=8 \\ \end{matrix} \]

Jawab:

Augmented matrix dari persamaan linier tersebut adalah sebagai berikut:

\[ \begin{bmatrix} 1 & 1 & 3 \\[0.3em] 2 & 4 & 8 \end{bmatrix} \]

Operasi baris elementer selanjutnya dilakukan pada matriks tersebut.

\[\begin{equation*} \begin{bmatrix} 1 & 1 & 3 \\[0.3em] 2 & 4 & 8 \end{bmatrix} \begin{matrix} B_2-2B_1 \\ \implies \end{matrix} \begin{bmatrix} 1 & 1 & 3 \\[0.3em] 0 & 2 & 2 \end{bmatrix} \end{equation*}\]

\[\begin{equation*} \begin{bmatrix} 1 & 1 & 3 \\[0.3em] 0 & 2 & 2 \end{bmatrix} \begin{matrix} \frac{B_2}{2} \\ \implies \end{matrix} \begin{bmatrix} 1 & 1 & 3 \\[0.3em] 0 & 1 & 1 \end{bmatrix} \end{equation*}\]

\[\begin{equation*} \begin{bmatrix} 1 & 1 & 3 \\[0.3em] 0 & 1 & 1 \end{bmatrix} \begin{matrix} B_1-B_2 \\ \implies \end{matrix} \begin{bmatrix} 1 & 0 & 2 \\[0.3em] 0 & 1 & 1 \end{bmatrix} \end{equation*}\]

Penyelesaian persamaan linier tersebut adalah sebagai berikut:

\[ x_1=2\ dan\ x_2=1 \]

Algoritma Metode Eliminasi Gauss-Jordan

  1. Masukkan matriks \(A\) dan vektor \(B\) beserta ukurannya \(n\)
  2. Buat augmented matrix \(\left[A|B\right]\) namakan dengan \(A\)
  3. Untuk baris ke-\(i\) dimana \(i=1\) s/d \(n\)

  • Perhatikan apakah nilai \(a_{i.i}\) sama dengan nol:

    • Bila ya: pertukakan baris ke-\(i\) dan baris ke-\(i+k\le n\), dimana \(a_{i+k.i}\) tidak sama dengan nol, bila tidak ada berarti perhitungan tidak bisa dilanjutkan dan proses dihentikan dengan tanpa penyelesaian.
    • Bila tidak: lanjutkan

  • Jadikan nilai diagonalnya menjadi satu dengan cara untuk setiap kolom \(k\) dimana \(k=1\) s/d \(n+1\), hitung \(a_{i.k}=\frac{a_{i.k}}{a_{i.i}}\)

  1. Untuk baris ke-\(j\), dimana \(j=i+1\) s/d \(n\). Lakukan operasi baris elementer untuk kolom \(k\) dimana \(k=1\) s/d \(n\).
  • Hitung \(c=a_{j.i}\)
  • Hitung \(a_{j.k}=a_{j.k}-c.a_{i.k}\)
  1. Penyelesaian untuk \(i=n\) s/d 1 disajikan pada Persamaan (6.18).

Dari algoritma tersebut, kita dapat membangun sebuah fungsi menggunakan R. Fungsi tersebut adalah sebagai berikut:

Dengan menggunakan fungsi gauss_jordan(), sistem persamaan linier pada Contoh 6.3:

##      [,1] [,2] [,3]
## [1,]    1    1    3
## [2,]    2    4    8
##      [,1] [,2] [,3]
## [1,]    1    0    2
## [2,]    0    1    1
Contoh 6.4 Dengan menggunakan fungsi gauss_jordan(), carilah penyelesaian sistem persamaan linier pada Contoh 6.1 dan Contoh 6.2:

Jawab:

Untuk Contoh 6.1:

##      [,1] [,2] [,3] [,4]
## [1,]    1    0    0    1
## [2,]    0    1    0    2
## [3,]    0    0    1    3

Untuk Contoh 6.2:

##      [,1] [,2] [,3] [,4]
## [1,]    1    0    0    1
## [2,]    0    1    0    2
## [3,]    0    0    1    3

6.3.3 Matrik Tridiagonal

Metode eliminasi Gauss merupakan metode yang sederhana untuk digunakan khususnya jika semua koefisien bukan nol berkumpul pada diagonal utama dan beberapa diagonal sekitarnya. Suatu sistem yang bersifat demikian disebut sebagai banded dan banyaknya diagonal yang memuat koefisien bukan nol disebut sebagai bandwidth. Contoh khusus yang sering dijumpai adalah matriks tridiagonal yang memiliki bandwidth tiga.

Proses eliminasi untuk matriks tridiagonal bersifat trivial karena dengan membentuk sebuah subdiagonal tambahan, proses substitusi mundur segera dapat dilakukan. Bentuk matriks tridiagonal disajikan pada Persamaan (6.19).

\[\begin{equation} \begin{bmatrix} a_{1,1} & a_{1,2} & 0 &\cdots& 0 \\[0.3em] a_{2,1} & a_{2,2} & a_{2,3} &\cdots& 0 \\[0.3em] 0 & a_{3,2} & a_{3,3} &\cdots& 0 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] 0 & 0 & 0 &\cdots& a_{m,n} \end{bmatrix} \begin{bmatrix} x_1 \\[0.3em] x_2 \\[0.3em] x_3 \\[0.3em] \cdots \\[0.3em] x_n \end{bmatrix} = \begin{bmatrix} b_1 \\[0.3em] b_2 \\[0.3em] b_3 \\[0.3em] \cdots \\[0.3em] b_n \end{bmatrix} \tag{6.19} \end{equation}\]

Penyelesaian persamaan tersebut disajikan pada Persamaan (6.20).

\[\begin{equation} x_n=\frac{b_n}{a_{m.n}};\ x_i=\frac{b_i-a_{i,j+1}x_{i+1}}{a_{i,j}} \tag{6.20} \end{equation}\]

dimana \(i=n-1,n-2,\dots,1\).

Pada beberapa textbook, diagonal matriks sering dilambangkan dengan \(l\)(diagonal bawah), \(d\)(diagonal tengah), dan \(u\) (diagonal atas). Bentuk matriksnya disajikan pada Persamaan (6.21).

\[\begin{equation} \begin{bmatrix} d_{1} & u_{2} & 0 &\cdots& 0 \\[0.3em] l_{2} & d_{2} & u_{3} &\cdots& 0 \\[0.3em] 0 & l_{3} & d_{3} &\cdots& 0 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] 0 & 0 & 0 &\cdots& d_{n} \end{bmatrix} \begin{bmatrix} x_1 \\[0.3em] x_2 \\[0.3em] x_3 \\[0.3em] \cdots \\[0.3em] x_n \end{bmatrix} = \begin{bmatrix} b_1 \\[0.3em] b_2 \\[0.3em] b_3 \\[0.3em] \cdots \\[0.3em] b_n \end{bmatrix} \tag{6.21} \end{equation}\]

Algoritma Penyelesaian Matrik Tridiagonal

  1. Bentuk sistem persamaan linier menjadi matriks pada Persamaan (6.21).
  2. Lakukan foward sweep. Setiap elemen diagonal \(l\) dieliminasi menggunakan reduksi baris.

  • Untuk \(i=1\)

    • Hitung \(u_1=\frac{u_1}{d_1}\)
    • Hitung \(b_1=\frac{b_1}{d_1}\)

  • Untuk \(i=2\) s/d \(n-1\)

    • Hitung \(u_i=\frac{u_i}{d_i-l_i\times u_{i-1}}\)
    • Hitung \(b_i=\frac{b_i-l_i\times u_{i-1}}{d_i-l_i\times u_{i-1}}\)

  • Hitung \(b_n=\frac{b_n-l_n\times u_{n-1}}{d_n-l_n\times u_{n-1}}\)

  1. Lakukan backward sweep. Setiap elemen diagonal \(u\) dilakukan eliminasi.

  • Untuk \(i=n-1\) s/d \(1\)

    • Hitung \(x_n=b_i-u_i\times x_{i+1}\)

  • Hitung \(x_n=b_n\)

Berdasarkan algoritma tersebut, kita dapat membangun sebuah fungsi pada R. Fungsi penyelesaian matriks tridiagonal disajikan sebagai berikut:

Contoh 6.5 Selesaikan sistem persamaan berikut menggunakan fungsi tridiagmatrix() dan fungsi gauss_jordan()!

\[ \begin{matrix} 3x_1+4x_2=20 \\ 4x_1+5x_2-2x_3=28 \\ 2x_2+5x_3-3x_4=18 \\ 3x_3+5x_4=18 \end{matrix} \]

Jawab:

Langkah pertama untuk menyelesaikannya, kita harus merubah persamaan tersebut kedalam bentuk matriks

\[\begin{equation*} \begin{bmatrix} 3 & 4 & 0 & 0 \\[0.3em] 4 & 5 & 2 & 0 \\[0.3em] 0 & 2 & 5 & 3 \\[0.3em] 0 & 0 & 3 & 5 \end{bmatrix} x = \begin{bmatrix} 20 \\[0.3em] 28 \\[0.3em] 18 \\[0.3em] 18 \end{bmatrix} \end{equation*}\]

Untuk menyelesaikan persamaan tersebut menggunakan fungsi tridiagmatrix(), kita perlu membentuk vektor diagonal \(l\), \(d\), \(u\), dan \(b\).

Setelah terbentuk, vektor tersebut dapat langsung dimasukkan ke dalam fungsi tridiagmatrix().

## [1] 4 2 1 3

Untuk menyelesaikannya menggunakan fungsi gauss_jordan(), kita perlu membentuk augmented matrix-nya terlebih dahulu.

##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    0    0    0    4
## [2,]    0    1    0    0    2
## [3,]    0    0    1    0    1
## [4,]    0    0    0    1    3

6.3.4 Penyelesaian Sistem Persamaan Linier Menggunakan Fungsi solve()

R menyediakan fungsi bawaan solve() untuk menyelesaiakan sistem persamaan linier. Format fungsi solve() adalah sebagai berikut:

Catatan:

  • a: matriks koefisien atau matriks segiempat
  • b: vektor konstanta

Berikut adalah contoh penerapan fungsi solve() pada sistem persamaan linier yang disajikan pada Contoh 6.2:

## [1] 1 2 3

Jika kita hanya memasukkan matriks persegi, maka output yang akan dihasilkan adalah invers dari matriks yang kita masukkan.

##      [,1] [,2]       [,3]
## [1,]    2   -1  7.401e-17
## [2,]   14   -9 -1.000e+00
## [3,]   17  -11 -1.000e+00

Jika kita mengalikan invers dengan matriks semula, maka akan dihasilkan output berupa matriks identitas.

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1

6.3.5 Penyelesaian Sistem Persamaan Linier Menggunakan Fungsi ’Solve.tridiag()`

Penyelesaian matriks tridiagonal selain menggunakan fungsi solve(), juga dapat menggunakan fungsi Solve.tridiag() dari Paket limSolve. Untuk menginstall dan mengaktifkan Paket tersebut, jalankan sintaks berikut:

Fungsi Solve.tridiag() memiliki format sebagai berikut:

Catatan:

  • diam1: vektor bukan nol di bawah diagonal matriks
  • dia: vektor bukan nol pada diagonal matriks
  • diap1: vektor bukan nol di atas diagonal matriks
  • B: vektor konstanta

Untuk memahami penerapannya, kita akan menggunakan kembali matriks yang ada pada Contoh 6.5.

##      [,1]
## [1,]    4
## [2,]    2
## [3,]    1
## [4,]    3

6.4 Dekomposisi Matriks

Seringkali kita diminta untuk memperoleh nilai penyelesaian suatu persamaan linier \(Ax=B\), dimana nilai vektor \(B\) yang selalu berubah-ubah. Penggunaan metode eliminasi Gauss mengharuskan untuk menyelesaikan sistem persamaan linier \(Ax=B\) secara terpisah untuk setiap perubahan vektor \(B\). Untuk menghindari pekerjaan eliminasi yang selalu berulang-ulang, faktorisasi menjadi suatu hal yang dapat dilakukan untuk mempersingkat prosesnya. Faktorisasi atau dekomposisi matriks merupakan suatu algoritma untuk memecah matriks \(A\), hasil pemecahan ini selanjutnya digunakan untuk memperoleh penyelesaian sistem persamaan linier melalui perkalian antara vektor \(B\) dan hasil faktorisasi matriks \(A\).

6.4.1 Dekomposisi LU

Misalkan kita memiliki persamaan linier seperti yang ditunjukkan oleh Persamaan (6.12). Pada metode dekomposisi LU, matriks \(A\) difaktorkan menjadi matriks \(L\) dan matriks \(U\), dimana ukuran kedua matriks tersebut harus sama dengan ukuran matriks \(A\) atau dapat kita tuliskan bahwa hasil perkalian kedua matriks tersebut akan menghasilkan matriks \(A\).

\[\begin{equation} A=LU \tag{6.22} \end{equation}\]

Sehingga Persamaan (6.12) akan menjadi Persamaan (6.23).

\[\begin{equation} LUx=b \tag{6.23} \end{equation}\]

Langkah penyelesaian sistem persamaan linier, diawali dengan menghadirkan vektor \(t\) yang ditunjukkan pada Persamaan (6.24).

\[\begin{equation} Ux=t \tag{6.24} \end{equation}\]

Langkah pada Persamaan (6.24) tidak dimaksudkan untuk menghitung vektor \(t\), melainkan untuk menghitung vektor \(x\). Vektor \(t\) diperoleh dengan menggunakan Persamaan (6.25).

\[\begin{equation} Lx=t \tag{6.25} \end{equation}\]

Kita dapat menyelesaikan sistem persamaan yang ditunjukkan pada Persamaan (6.24) dan Persamaan (6.25) menggunakan berbagai algoritma penyelesaian yang telah dibahas sebelumnya. Namun, karena matriks \(L\) merupakan matriks segitiga bawah dengan nilai nol berada pada bagian atas diagonal utama, penyelesaian \(t\) mengambil langkah yang lebih sedikit. Kondisi ini sama dengan kondisi penyelesaian matriks tridiagonal, dimana kita memanfaatkan sejumlah jalan pintas penyelesaiaannya guna mempercepat komputasi. Matriks segitia bawah \(L\) akan berupa matriks persegi dengan ukuran \(m\), di mana \(m\) merupakan jumlah baris matriks \(A\). Persamaan (6.25) dalam bentuk matriks akan terlihat seperti Persamaan (6.26).

\[\begin{equation} Lt= \begin{bmatrix} 1 & 0 & 0 &\cdots& 0 \\[0.3em] l_{2,1} & 1 & 0 &\cdots& 0 \\[0.3em] l_{3,1} & l_{3,2} & 1 &\cdots& 0 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] l_{m,1} & l_{m,2} & l_{m,3} &\cdots& 1 \end{bmatrix} \begin{bmatrix} t_1 \\[0.3em] t_2 \\[0.3em] t_3 \\[0.3em] \cdots \\[0.3em] t_n \end{bmatrix} = \begin{bmatrix} b_1 \\[0.3em] b_2 \\[0.3em] b_3 \\[0.3em] \cdots \\[0.3em] b_n \end{bmatrix} \tag{6.26} \end{equation}\]

Berdasarkan Persamaan (6.26), diketahui nilai \(t_1=b_1\). Nilai ini selanjutnya dapat digunakan untuk melakukan proses substitusi guna memperoleh seluruh nilai vektor \(t\). Proses ini disebut sebagai foward substitution. Proses substitusi dapat dituliskan menggunakan Persamaan (6.27).

\[\begin{equation} t_i=b_i-\sum_{j=1}^{i-1}l_{i,j}t_i \tag{6.27} \end{equation}\]

Seteleh nilai vektor \(t\) dihitung, kita dapat menghitung nilai \(x\) pada Persamaan (6.28).

\[\begin{equation} Ux= \begin{bmatrix} u_{1,1} & u_{1,2} & u_{1,3} &\cdots& u_{1,n} \\[0.3em] 0 & u_{2,2} & u_{2,3} &\cdots& u_{2,n} \\[0.3em] 0 & 0 & u_{3,3} &\cdots& u_{3,n} \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] 0 & 0 & 0 &\cdots& u_{m,n} \end{bmatrix} \begin{bmatrix} x_1 \\[0.3em] x_2 \\[0.3em] x_3 \\[0.3em] \cdots \\[0.3em] x_n \end{bmatrix} = \begin{bmatrix} t_1 \\[0.3em] t_2 \\[0.3em] t_3 \\[0.3em] \cdots \\[0.3em] t_n \end{bmatrix} \tag{6.28} \end{equation}\]

Jika diperhatikan, kita dapat mengetahui mengetahui nilai \(x_n=\frac{t_n}{u_{m,n}}\). Nilai tersebut selanjutnya dapat digunakan untuk melakukan proses susbtitusi pada nilai lainnya. Proses substitusi ini disebut sebagai backward substitution. Proses dekomposisi atau faktorisasi LU digambarkan pada Gambar 6.1.

Tahapan dekomposisi LU.

Gambar 6.1: Tahapan dekomposisi LU.

Dekomposisi LU didasarkan pada operasi baris elementer. Pertama, kita perlu menemukan matriks segitiga atas yang sesuai dengan matriks \(A\). Solusi untuk melakukan dekomposisi bisa jadi tak terhingga, namun solusi yang paling sederhana adalah mengubah matriks \(A\) menjadi matriks row echelon form. Kedua, \(L\) harus menjadi matriks segitiga bawah yang mereduksi ke-\(l\) dengan mengikuti operasi baris yang sama yag menghasilkan \(U\). Kita dapat menggunakan algoritma Doolittle untuk menghasilkan \(L\), di mana nilai setiap entri dalam matriks segitiga bawah merupakan pengali yang digunakan untuk menghilangkan entri yang sesuai untuk setiap proses row replacement.

Pada praktiknya, proses eliminasi Gauss untuk memperoleh matriks \(U\) kadang menghasilkan nol di kolom pivotnya. Kondisi tersebut mengharuskan kita untuk melakukan proses row swapping atau pertukaran baris (biasanya dengan baris bawahnya) untuk pivot bukan nol. Jika proses tersebut berhasil dilakukan bisa jadi matriks \(A\) mungkin setara dengan matriks LU, tetapi tidak sama dalam hal urutan nilai pada tiap barisnya. Agar kita dapat memperoleh hasil yang sama (matriks A sama dengan matriks LU), diperlukan matriks ketiga, \(P\). Matriks ini merupakan matriks identitas dengan ukuran sama dengan matriks \(A\). Jika pertukaran baris dilakukan selama proses pembentukan matriks \(U\), maka pertukaran baris yang sama juga akan diimplemenntasikan pada matriks \(P\). oleh karena itu, dalam praktiknya matriks \(A=PLU\) dan perkalian dengan matriks \(P\) berfungsi untuk mengembalikan urutan baris.

Contoh 6.6 Selesaikan sistem persamaan linier berikut menggunakan faktorisasi LU

\[ \begin{matrix} x_1+x_2+3x_4=4 \\ 2x_1+x_2-x_3+x_4=1 \\ 3x_1-x_2-x_3+2x_4=-3 \\ -x_1-2x_2+3x_3-x_4=4 \end{matrix} \]

Jawab:

Nayatakan sistem persamaan tersebut ke dalam bentuk matriks \(Ax=b\).

\[\begin{equation*} Ux= \begin{bmatrix} 1 & 1 & 0 & 3 \\[0.3em] 2 & 1 & -1 & 1 \\[0.3em] 3 & -1 & -1 & 2 \\[0.3em] -1 & 2 & 3 & -1 \end{bmatrix} \begin{bmatrix} x_1 \\[0.3em] x_2 \\[0.3em] x_3 \\[0.3em] x_4 \end{bmatrix} = \begin{bmatrix} 4 \\[0.3em] 1 \\[0.3em] -3 \\[0.3em] 4 \end{bmatrix} \end{equation*}\]

Lakukan operasi baris elementer pada matriks \(A\) untuk memperoleh matriks \(U\). Urutan operasi baris elementer yang dilakukan adalah sebagai berikut:

  • \(\left(B_2-2B_1\right)\to B_2 \to l_{2,1}=2\),
  • \(\left(B_3-3B_1\right)\to B_3 \to l_{3,1}=3\),
  • \(\left(B_4+B_1\right)\to B_4 \to l_{4,1}=-1\),
  • \(\left(B_3-4B_2\right)\to B_3\to l_{3,2}=4\),
  • \(\left(B_4+3B_2\right)\to B_4 \to l_{4,2}=-3\),
  • \(l_{4,3}=0\)

Simpan pengali tiap tahapan pada masing-masing elemen matriks \(L\). Hasil operasi tersebut akan menghasilkan matriks triangular \(U\).

\[ U= \begin{bmatrix} 1 & 1 & 0 & 3 \\[0.3em] 0 & -1 & -1 & -5 \\[0.3em] 0 & 0 & 3 & 13 \\[0.3em] 0 & 0 & 0 & -13 \end{bmatrix} \]

Untuk matriks \(L\) sebagai berikut:

\[ L= \begin{bmatrix} 1 & 0 & 0 & 0 \\[0.3em] 2 & 1 & 0 & 0 \\[0.3em] 3 & 4 & 1 & 0 \\[0.3em] -1 & -3 & 0 & 1 \end{bmatrix} \]

Karena pada proses operasi baris elementer tidak terdapat operasi pertukaran baris, maka matriks \(P\) tidak mengalami perubahan:

\[ P= \begin{bmatrix} 1 & 0 & 0 & 0 \\[0.3em] 0 & 1 & 0 & 0 \\[0.3em] 0 & 0 & 1 & 0 \\[0.3em] 0 & 0 & 0 & 1 \end{bmatrix} \]

Lakukan operasi forward substitution menggunakan Persamaan (6.26).

\[\begin{equation*} \begin{bmatrix} 1 & 0 & 0 & 0 \\[0.3em] 2 & 1 & 0 & 0 \\[0.3em] 3 & 4 & 1 & 0 \\[0.3em] -1 & -3 & 0 & 1 \end{bmatrix} \begin{bmatrix} t_1 \\[0.3em] t_2 \\[0.3em] t_3 \\[0.3em] t_4 \end{bmatrix} = \begin{bmatrix} 4 \\[0.3em] 1 \\[0.3em] -3 \\[0.3em] 4 \end{bmatrix} \end{equation*}\]

Berdasarkan hasil perhitungan diperoleh nilai vektor \(t\).

\[ t_1=4, t_2=1, t_3=-3, t_4=4 \]

Operasi terakhir yang perlu dilakukan untuk memperoleh nilai \(x\) adalah dengan melakukan backward substitution menggunakan nilai vektor \(t\) yang telah dihitung.

\[\begin{equation*} \begin{bmatrix} 1 & 1 & 0 & 3 \\[0.3em] 0 & -1 & -1 & -5 \\[0.3em] 0 & 0 & 3 & 13 \\[0.3em] 0 & 0 & 0 & -13 \end{bmatrix} \begin{bmatrix} x_1 \\[0.3em] x_2 \\[0.3em] x_3 \\[0.3em] x_4 \end{bmatrix} = \begin{bmatrix} 4 \\[0.3em] 7 \\[0.3em] 13 \\[0.3em] -13 \end{bmatrix} \end{equation*}\]

Berdasarkan hasil perhitungan diperoleh nilai \(x\) sebagai berikut:

\[ x_1=-1, x_2=2, x_3=0, x_4=1 \]

Algoritma Dekomposisi LU

  1. Masukkan matriks \(A\), dan vektor \(B\) beserta ukurannya \(n\)
  2. Lakukan langkah poin ke-4 s/d poin 5 untuk meperoleh matriks \(U\).
  3. Untuk baris ke-\(i\) di mana \(i=1\) s/d \(n\), perhatikan apakah nilai \(a_{i,j}\) sama dengan nol.
  • Bila iya, lakukan row swapping antara baris ke-\(i\) dan baris ke-\(i+k\leq n\), dimana \(a_{i+k,j}\) tidak sama dengan nol. Bila tidak ada berarti perhitungan tidak bisa dilanjutkan dan proses dihentikan dengan tanpa penyelesaian.
  • Bila tidak, lanjutkan.
  1. Untuk baris ke-\(j\), dimana \(j=i+1\) s/d \(n\), lakukan operasi baris elementer:
  • Hitung \(c=\frac{a_{j,i}}{a_{i,i}}\)
  • untuk kolom \(k\), dimana \(k=1\) s/d \(n+1\), hitung \(a_{j,k}=a_{j,k}-c_i.a_{i,k}\)
  1. Lakukan langkah poin ke-7 s/d poin 9 untuk memperoleh matriks \(L\)
  2. Untuk diagonal matriks \(L\) isikan dengan nilai 1 dan elemen di atas diagonal dengan nilai nol.
  3. Untuk elemen di bawah diagonal isikan dengan faktor pengali operasi baris elementer matriks \(U\).
  4. Lakukan proses forward substitution menggunakan Persamaan (6.27) untuk memperoleh nilai vektor \(t\).
  5. Lakukan backward substituion menggunakan Persamaan (6.16).

Berdasarkan algoritma tersebut, kita dapat menyusun algoritma faktorisasi LU menggunakan R. Berikut adalah sintaks yang digunakan:

Kita dapat menyelesaikan sistem persamaan linier pada Contoh 6.6 menggunakan fungsi yang telah kita buat.

Untuk membentuk kembali matriks \(A\), kita dapat mengalikan matriks \(L\), \(U\), dan \(P\).

##      [,1] [,2] [,3] [,4]
## [1,]    1    1    0    3
## [2,]    2    1   -1    1
## [3,]    3   -1   -1    2
## [4,]   -1    2    3   -1
Contoh 6.7 Lakukan dekomposisi LU pada matriks berikut dan lakukan pengecekan apakah perkalian hasil dekomposisi matriks akan menghasilkan matriks semula!

\[ \begin{bmatrix} 0 & 1 & -1 \\[0.3em] 1 & 5 & 9 \\[0.3em] 7 & -1 & -5 \end{bmatrix} \]

Jawab:

Lakukan proses dekomposisi menggunakan fungsi lu_solve().

##      [,1] [,2] [,3]
## [1,]    0    1   -2
## [2,]    1    5    9
## [3,]    7   -1   -5

Lakukan pengecekan apakah matriks hasil dekomposisi akan menghasilkan matriks \(A\).

##      [,1] [,2] [,3]
## [1,]    0    1   -2
## [2,]    1    5    9
## [3,]    7   -1   -5

Fungsi lu() pada Paket Matrix dapat digunakan untuk melakukan dekomposisi LU. Untuk meggunakan fungsi tersebut, kita harus menginstall dan mengaktifkan Paket Matrix.

Untuk dapat menggunakannya kita hanya perlu menginputkan matriks kedalam fungsi tersebut. Berikut adalah contoh penerapannya:

## 'MatrixFactorization' of Formal class 'denseLU' [package "Matrix"] with 4 slots
##   ..@ x       : num [1:9] -0.95 0.705 0.589 0.53 -0.604 ...
##   ..@ perm    : int [1:3] 2 3 3
##   ..@ Dimnames:List of 2
##   .. ..$ : NULL
##   .. ..$ : NULL
##   ..@ Dim     : int [1:2] 3 3

Untuk menampilkan hasil dekomposisi, jalankan fungsi expand().

## $L
## 3 x 3 Matrix of class "dtrMatrix" (unitriangular)
##      [,1]    [,2]    [,3]   
## [1,]  1.0000       .       .
## [2,]  0.7053  1.0000       .
## [3,]  0.5895 -0.2279  1.0000
## 
## $U
## 3 x 3 Matrix of class "dtrMatrix"
##      [,1]    [,2]    [,3]   
## [1,] -0.9500  0.5300  1.7600
## [2,]       . -0.6038 -0.7513
## [3,]       .       .  0.1913
## 
## $P
## 3 x 3 sparse Matrix of class "pMatrix"
##           
## [1,] . . |
## [2,] | . .
## [3,] . | .

6.4.2 Dekomposisi Cholesky

Dekomposisi Cholesky memberikan faktorisasi matriks alternatif sehingga \(A = LL^T\), di mana \(L^T\) merupakan transpose konjugat dari matriks \(L\). Dalam kasus ini, penulis hanya bekerja dengan matriks rill dengan nilai rill dan bagian imajiner nol. Jadi untuk tujuan sub-chapter ini, matriks \(L^T\) hanyalah transpose dari matriks \(L\).

Seperti dekomposisi LU, dekomposisi Cholesky dapat digunakan untuk menyelesaikan sistem persamaan linier. Kelebihannya, Menemukan dekomposisi Cholesky jauh lebih cepat daripada dekomposisi LU. Namun, dekomposisi ini hanya terbatas pada matriks tertentu saja. Dekomposisi Cholesky hanya dapat digunakan pada matriks definit positif dan simetris. Matriks simeteris merupakan matriks yang nilai di atas dan di bawah diagonalnya simetris atau sama; secara matematis, untuk semua \(i\) dan \(j\) pada matriks \(A\), \(a_{i;j}=a_{j;i}\). Definit positif berarti bahwa setiap entri pivot (nilai elemen diagonal utama) selelu bernilai positif. Selain itu, untuk matriks definit positif, hubungan \(xAx>0\) untuk semua vektor, \(x\).

Karena \(L^∗\) transpose dari matriks \(L\), maka \(l^{T}_{i,j} = l_{j,i}\) untuk semua nilai \(i\) dan \(j\). Tanpa kendala (constraint) ini, dekomposisi Cholesky akan mirip dekomposisi LU. Tetapi dengan kendala ini, nilai elemen matriks \(L\) dan \(L^T\) harus dipilih dengan cermat sehingga hubungan \(A = LL^T\) berlaku. Bentuk dekomposisi Cholesky disajikan pada Persamaan (6.29).

\[\begin{equation} \begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} &\cdots& a_{1,m} \\[0.3em] a_{2,1} & a_{2,2} & a_{2,3} &\cdots& a_{2,m} \\[0.3em] a_{3,1} & a_{3,2} & a_{3,3} &\cdots& a_{3,m} \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] a_{m,1} & a_{m,2} & a_{m,3} &\cdots& a_{m,m} \end{bmatrix} = \begin{bmatrix} l_{1,1} & 0 & 0 &\cdots& 0 \\[0.3em] l_{2,1} & l_{2,2} & 0 &\cdots& 0 \\[0.3em] l_{3,1} & l_{3,2} & l_{3,3} &\cdots& 0 \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] l_{m,1} & l_{m,2} & l_{m,3} &\cdots& l_{m,m} \end{bmatrix} \begin{bmatrix} l_{1,1} & l_{1,2} & l_{1,3} &\cdots& l_{1,m} \\[0.3em] 0 & l_{2,2} & l_{2,3} &\cdots& l_{2,m} \\[0.3em] 0 & 0 & l_{3,3} &\cdots& l_{3,m} \\[0.3em] \vdots & \vdots & \vdots &\ddots& \vdots \\[0.3em] 0 & 0 & 0 &\cdots& l_{m,m} \end{bmatrix} \tag{6.29} \end{equation}\]

Untuk setiap elemen matriks \(A\) memiliki hubungan yang dituliskan pada Persamaan (6.30).

\[\begin{equation} a_{i,j}=\sum_{k=1}^mL_{i,k}L_{k,j} \tag{6.30} \end{equation}\]

Berdasarkan Persamaan (6.29), sejumlah nilai elemen \(L_{i,k}\) dan \(L_{k,j}\) adalah nol. Nilai tiap elemen diagonal utama yang tidak bernilai nol dihitung menggunakan Persamaan (6.31).

\[\begin{equation} l_{i,i}=\sqrt{\left(a_{i,i}-\sum_{k=1}^{i-1}l_{i,k}^2\right)} \tag{6.31} \end{equation}\]

Elemen diagonal dihitung menggunakan Persamaan (6.32)

\[\begin{equation} l_{i,j}=\frac{1}{l_{i,i}}\left(a_{i,j}-\sum_{k=1}^{i-1}l_{i,k}l_{j,k}\right) \tag{6.32} \end{equation}\]

Algoritma Dekomposisi Cholesky

  1. Masukkan matriks \(A\), dan vektor \(B\) beserta ukurannya \(n\).
  2. Untuk elemen matriks \(L\), hitung menggunakan Persamaan (6.32).
  3. Untuk nilai diagonal utama matriks \(L\), hitung menggunakan Persamaan (6.31).
  4. Untuk memperoleh matriks \(L^T\), lakukan transpose pada matriks \(L\).
  5. Untuk memperoleh nilai \(x\),
  • Hitung vektor \(t\) menggunakan Persamaan (6.25).
  • Hitung vektor \(x\) menggunakan Persamaan (6.24), dimana matriks \(U=L^T\).

Berdasarkan algoritma tersebut, kita dapat menyusun fungsi pada R untuk melakukan dekomposisi Cholesky. Fungsi tersebut disajikan pada sintaks berikut:

Contoh 6.8 Dengan menggunakan fungsi cholesky_solve(), lakukan dekomposisi pada matriks berikut! Lakukan pengecekan pada hasil dekomposisi apakah hasil kali matriks dekomposisi akan menghasilkan matriks semula!

\[ \begin{bmatrix} 9 & -3 & 6 \\[0.3em] -3 & 17 & -10 \\[0.3em] 6 & -10 & 12 \end{bmatrix} \]

Jawab:

Dekomposisi Cholesky menggunakan fungsi cholesky_solve(), disajikan pada sintaks berikut:

## $L
##      [,1] [,2] [,3]
## [1,]    3   -1    2
## [2,]    0    4   -2
## [3,]    0    0    2
## 
## $tL
##      [,1] [,2] [,3]
## [1,]    3    0    0
## [2,]   -1    4    0
## [3,]    2   -2    2
## 
## $a
##      [,1] [,2] [,3]
## [1,]    9   -3    6
## [2,]   -3   17  -10
## [3,]    6  -10   12
##      [,1] [,2] [,3]
## [1,]    9   -3    6
## [2,]   -3   17  -10
## [3,]    6  -10   12

Fungsi lain yang dapat digunakan untuk melakukan dekomposisi Cholesky adalah menggunakan fungsi chol() pada Paket Matrix. Pada fungsi tersebut, kita hanya perlu menginputkan objek matrik kedalamnya. Berikut adalah contoh penerapan fungsi tersebut menggunakan matriks pada Contoh 6.8.

##      [,1] [,2] [,3]
## [1,]    3   -1    2
## [2,]    0    4   -2
## [3,]    0    0    2

Penting!!!

Fungsi chol() hanya menampilkan matriks \(L^T\). Untuk menampilkan matriks \(L\), kita perlu melakukan transpose

6.4.3 Dekomposisi Lainnya

Terdapat beberapa algoritma lain yang telah dikembangkan untuk melakukan dekomposisi matriks. Pada buku ini hanya akan dijelaskan secara singkat terkait fungsi yang digunakan dalam melakukan dekomposisi matriks. Algoritma yang akan dijelaskan pada sub-chapter ini antara lain: QR, singular value decomposition (SVD), dan dekomposisi eigen. Untuk algoritma lainnya, pembaca dapat membaca buku terkait atau mengecek dokumentasinya pada Paket base.

6.4.3.1 Dekomposisi QR

Dekomposisi QR merupakan dekomposisi yang penting dalam menyelesaikan sistem persamaan linier. Dekomposisi ini juga berperan penting untuk menghitung koefisien regresi dan pengaplikasian algoritma Newton-Raphson.

Untuk memperoleh informasi terkait dekomposisi ini, pembaca dapat mengetikkan sintaks berikut pada R:

Berikut merupakan contoh penerapan fungsi qr() untuk menyelesaikan sistem persamaan linier:

## $qr
##         [,1]     [,2]     [,3]
## [1,] -6.3778 -12.1257 -19.8501
## [2,]  0.2775  -6.3105  -7.9392
## [3,]  0.7148  -0.6461   2.3512
## [4,]  0.6382  -0.5654   0.2767
## 
## $rank
## [1] 3
## 
## $qraux
## [1] 1.069 1.513 1.961
## 
## $pivot
## [1] 1 2 3
## 
## attr(,"class")
## [1] "qr"
## [1]  0.3046 -0.1111  0.3237

6.4.3.2 Singular Value Decomposition

Singular value decomposition (SVD) merupakan algoritma faktorisasi matriks yang mendekomposisi matriks segiempat menjadi matriks \(UDV_H\), dimana \(D\) merupakan mmatriks diagonal non negatif, \(U\) dan \(V\) merupakan matriks unitary, dan \(V_H\) merupakan matriks tanspose konjugat dari matriks \(V\). Algoritma ini banyak digunakan dalam analisis principal component.

Pada R, SVD dapat dilakukan menggunakan fungsi svd() dari Paket base. Berikut adalah sintaks untuk memperoleh informasi terkait fungsi tersebut:

Berikut adalah contoh penerapan fungsi svd():

## $d
## [1] 26.094  2.727  1.330
## 
## $u
##         [,1]    [,2]    [,3]
## [1,] -0.3685 -0.5661  0.6651
## [2,] -0.4707 -0.5703 -0.6113
## [3,] -0.5740  0.4324 -0.2590
## [4,] -0.5596  0.4089  0.3419
## 
## $v
##         [,1]     [,2]    [,3]
## [1,] -0.2257  0.87169 -0.4350
## [2,] -0.5202 -0.48536 -0.7028
## [3,] -0.8237  0.06764  0.5630

6.4.3.3 Dekomposisi Eigen

Proses umum yang digunakan untuk menemukan nilai eigen dan vektor eigen suatu matriks segiempat dapat dilihat sebagai proses dari dekomposisi eigen. Proses ini akan mendekomposisi matriks menjadi \(VDV^{-1}\), dimana \(D\) merupakan matriks diagonal yang terbentuk dari nilai eigen, dan \(V\) merupakan vektor eigen. Proses dekomposisi ini akan berguna bagi pembaca yang ingin mempelajari principal component analysis.

Fungsi eigen() pada Paket base dapat digunakan untuk melakukan dekomposisi eigen. Untuk mempelajari lebih jauh terkait fungsi ini, pambaca dapat menjalankan sintaks berikut:

Berikut adalah contoh sintaks untuk melakukan dekomposisi eigen:

## eigen() decomposition
## $values
## [1] 3.4142 2.0000 0.5858
## 
## $vectors
##         [,1]       [,2]   [,3]
## [1,] -0.5000 -7.071e-01 0.5000
## [2,]  0.7071  1.099e-15 0.7071
## [3,] -0.5000  7.071e-01 0.5000

6.5 Metode Iterasi

Pada Chapter 6.5 kita akan membahas penyelesaian persamaan linier dengan menggunakan metode iterasi. Terdapat dua metode iterasi yang akan dibahas yaitu iterasi Jacobi dan Gauss-Seidel.

Metode iterasi dimulai dengan estimasi nilai akhir. Setelah menerapkan beberapa perlakuan pada nilai estimasi, hasil perlakuan selanjutnya menjadi nilai estimasi untuk iterasi berikutnya. Proses tersebut akan berlangsung secara terus-menerus hingga ambang batas dipenuhi. Nilai ambang batas dapat berupa jumlah iterasi maksimum atau selisih antara nilai estimasi baru dan estimasi semula lebih kecil dari suatu nilai toleransi yang ditetapkan.

Jumlah kuadrat merupakan metode yang sering digunakan untuk mengecek apakah selisih nilai estimasi baru terhadap estimasi lama lebih kecil dari nilai toleransi yang ditetapkan. Persamaan (6.33) menampilkan hubungan antara jumlah kuadrat dan nilai toleransi pada proses iterasi.

\[\begin{equation} \sqrt{\sum_{i=1}^n\left(x_i^{n+1}-x_i^{n}\right)^2}<t_0 \tag{6.33} \end{equation}\]

dimana \(x^{n}\) merupakan iterasi ke-\(n\) dari algoritma dan \(t_0\) merupakan nilai toleransi maksimum yang diterima.

6.5.1 Iterasi Jacobi

Untuk menyelesaikan matriks menggunakan metode iterasi, kita dapat mulai dengan premis terdapat matriks \(A\) dan vektor \(x\) dan b, sehingga \(Ax = b\). Dengan menggunakan metode Jacobi, pertama-tama kita dapat amati bahwa terdapat matriks \(R\) dan \(D\) yang memiliki hubungan \(A = R + D\). Berdasarkan kedua hubungan tersebut, dapat diturunkan operasi matriks melalui persamaan berikut:

\[\begin{equation} Ax=b \tag{6.34} \end{equation}\]

\[\begin{equation} Rx+Dx=b \tag{6.35} \end{equation}\]

\[\begin{equation} Dx=b-Rx \tag{6.36} \end{equation}\]

\[\begin{equation} x=D^{-1}\left(b-Rx\right) \tag{6.37} \end{equation}\]

Persamaan (6.37) merupakan persamaan yang dapat kita gunakan untuk memperoleh nilai \(x\). Jika kita menulis kembali persamaan tersebut, maka kita akan memperoleh persamaan yang digunakan sebagai acuan iterasi Jacobi.

\[\begin{equation} x^{n+1}=D^{-1}\left(b-Rx^{n}\right) \tag{6.38} \end{equation}\]

dimana \(D\) merupakan matriks diagonal dengan nilai elemen diagonal berupa diagonal utama matriks \(A\). Invers dari matriks \(D\) secara sederhana sebagai matriks diagonal sama dengan satu dibagi dengan elemen diagonal utama matriks \(A\). Matriks \(R\) identik dengan matriks \(A\). Namun, diagonal utamanya bernilai nol. Suatu iterasi dikatakan konvergen jika jumlah kuadrat dari vektor \(x^{\left(n+1\right)}\) dan vektor \(x^{\left(n\right)}\) semakin mengecil.

Suatu persamaan linier yang hendak diselesaikan dengan menggunakan metode iterasi Jacobi harus memenuhi syarat nilai elemen diagonal utama matriks harus lebih dominan. Maksudnya adalah nilai absolut diagonal utama matriks harus lebih besar dari jumlah nilai absolut elemen matriks lainnya pada satu kolom.

Contoh 6.9 Selesaikan sistem persamaan berikut menggunakan iterasi Jacobi!

\[\begin{equation*} \begin{bmatrix} 5 & 2 & 3 \\[0.3em] 2 & 7 & 4 \\[0.3em] 1 & 3 & 8 \end{bmatrix} x = \begin{bmatrix} 40 \\[0.3em] 39 \\[0.3em] 55 \end{bmatrix} \end{equation*}\]

Jawab:

Berdasarkan matriks \(A\) (matriks koefisien), kita dapat memastikan bahwa matriks tersebut memiliki nilai dominan pada elemen diagonal utama. Sebagai contoh:

\[ \left|5\right|>\left|2\right|+\left|1\right|\ \ \ \left(kolom\ 1\right) \]

\[ \left|7\right|>\left|2\right|+\left|3\right|\ \ \ \left(kolom\ 2\right) \] Untuk mempermudah proses iterasi, kita akan menggunakan bantuan R untuk melakukan komputasi. Langkah pertama yang perlu dilakukan adalah menyiapkan matriks \(A\), vektor \(b\), dan vektor \(x\) (nilai taksiran awal).

##      [,1] [,2] [,3]
## [1,]    5    2    3
## [2,]    2    7    4
## [3,]    1    3    8
## [1] 40 39 55
## [1] 0 0 0

Langkah selanjutnya adalah memperoleh invers matriks \(D\).

##      [,1]   [,2]  [,3]
## [1,]  0.2 0.0000 0.000
## [2,]  0.0 0.1429 0.000
## [3,]  0.0 0.0000 0.125

Persiapan terakhir sebelum iterasi dilakukan adalah menyiapkan matriks \(R\).

##      [,1] [,2] [,3]
## [1,]    0    2    3
## [2,]    2    0    4
## [3,]    1    3    0

Iterasi selanjutnya dilakukan menggunakan Persamaan (6.38).

iterasi 1

##       [,1]
## [1,] 8.000
## [2,] 5.571
## [3,] 6.875

iterasi 2

##         [,1]
## [1,]  1.6464
## [2,] -0.6429
## [3,]  3.7857

iterasi 3

##       [,1]
## [1,] 5.986
## [2,] 2.938
## [3,] 6.910

Selama proses iterasi,jumlah akar jumlah kuadrat dihitung. Sebagai contoh berikut disajikan akar jumlah kuadrat pada iterasi ke-3:

## [1] 11.04

Selama proses iterasi nilai tersebut terus mengecil. Iterasi dihantikan jika nilai akar jumlah kuadrat tersebut lebih kecil dari nilai toleransi. Pada contoh ini digunakan nilai toleransi \(10^{-7}\).

Proses iterasi berlangsung sampai dengan iterasi ke-62 dengan nilai \(x\) akhir sebagai berikut:

\[ x = \begin{bmatrix} 4 \\[0.3em] 1 \\[0.3em] 6 \end{bmatrix} \]

Algoritma Iterasi Jacobi

  1. Masukkan matriks \(A\), dan vektor \(B\) beserta ukurannya \(n\).
  2. Hitung invers matriks \(D\), dimana nilai invernya merupakan matriks diagonal dari satu per diagonal utama matriks \(A\).
  3. Hitung matriks \(R\), dimana \(R\) merupakan selisih matriks \(A\) dikurangi dengan matriks diagonal dengan entri dari diagonal utama matriks \(A\).
  4. Tetapkan vektor \(x\) estimasi.
  5. Tetapkan nilai toleransi maksimum yang dapat diterima.
  6. Lakukan iterasi menggunakan Persamaan (6.38).
  7. Hitung akar jumlah kuadrat dari vektor \(x^{n+1}\) dan vektor \(x^n\).
  8. Jadikan nilai \(x^{n+1}\) sebagai nilai taksiran \(x\) untuk iterasi berikutnya.
  9. Hentikan proses iterasi jika telah memenuhi syarat yang ditampilkan pada Persamaan (6.33).

Berdasarkan algoritma tersebut, kita dapat menyusun fungsi sebuah fungsi untuk melakukan iterasi Jacobi. Berikut sintaks yang digunakan:

Berikut adalah penerpan fungsi jacobi() tersebut:

## $X
##      [,1]
## [1,]    4
## [2,]    1
## [3,]    6
## 
## $iter
## [1] 62
Contoh 6.10 Selesaikan sistem persamaan berikut menggunakan fungsi jacobi()

\[ \begin{bmatrix} 27 & 6 & -1 \\[0.3em] 6 & 15 & 2 \\[0.3em] 1 & 1 & 54 \end{bmatrix} x = \begin{bmatrix} 85 \\[0.3em] 72 \\[0.3em] 110 \end{bmatrix} \]

Jawab:

Matriks \(A\) (matriks koefisien) berdasarkan sistem persamaan linier tersebut telah memenuhi syarat dari algoritma Jacobi (nilai diagonal utama dominan dibanding nilai lainnya pada satu kolom). Penyelesaian sistem persamaan tersebut, sebagai berikut:

## $X
##       [,1]
## [1,] 2.425
## [2,] 3.573
## [3,] 1.926
## 
## $iter
## [1] 17

Nilai vektor \(x\) sesungguhnya dapat diperoleh menggunakan fungsi solve().

## [1] 2.425 3.573 1.926

Berdasarkan hasil perhitungan, vektor \(x\) hasil iterasi memiliki nilai identik dengan nilai penyelesaian yang sebenarnya.

Perlu diperhatikan dalam penggunaan fungsi jacobi() syarat utama matriks haruslah terpenuhi, seperti: nilai diagonal matriks \(A\) lebih besar dari nilai elemen lainnya pada satu kolom. Selain itu, nilai diagonal matriks \(D\) tidak boleh sama dengan nol agar inver matriks \(D\) dapat diperoleh. Jika syarat-syarat tersebut terpenuhi, maka metode Jacobi dapat diterapkan. Jika tidak terpenuhi, maka penyelesaian yang konvergen mungkin masih dapat diperoleh meskipun penulis tidak dapat menjamin hal tersebut dapat terjadi.

6.5.2 Iterasi Gauss-Seidel

Metode iterasi Gauss-Seidel melakukan dekomposisi pada matriks \(A\) menjadi matriks segitiga atas \(U\) dan matriks segitiga bawah \(L\). Dekomposisi ini tidak sama dengan dekomposisi LU pada Chapter 6.4.1. Matriks \(U\) pada metode Gauss-Seidel merupakan elemen (entri) matriks \(A\) pada bagian atas diagonal utama, sedangkan matriks \(L\) merupakan elemen diagonal utama dan bagian bawah diagonal utama matriks \(A\). Elemen selain yang penulis sebutkan pada kedua matriks tersebut akan bernilai nol. Persamaan iterasi Gauss-Seidel ditampilkan pada Persamaan (6.39).

\[\begin{equation} x^{n+1}=L^{-1}\left(b-Ux^{n}\right) \tag{6.39} \end{equation}\]

Syarat agar suatu sistem persamaan linier dapat diselesaikan menggunakan metode Gauss-Seidel adalah matriks harus memiliki nilai diagonal utama yang dominan. Maksudnya, nilai absolut diagonal utama lebih besar dari jumlah nilai absolut elemen lainnya dalam satu kolom. Jika syarat ini tidak terpenuhi maka metode ini tidak akan memperoleh penyelesaian yang konvergen.

Contoh 6.11 Selesaikan sistem persamaan pada Contoh 6.10 menggunakan iterasi Gauss-Seidel!

Jawab:

Kita akan kembali menggunakan bantuan R untuk melakukan kalkulasi pada proses iterasi Gauss-Seidel. Kita telah melakukan pengecekan pada sistem persamaan linier pada contoh tersebut dan menghasilkan kesimpulan bahwa persamaan linier tersebut dapat diselesaikan dengan metode Gauss-Seidel. Langkah selanjutnya adalah membentuk matriks \(L\) dan \(U\).

##      [,1] [,2] [,3]
## [1,]   27    6   -1
## [2,]    6   15    2
## [3,]    1    1   54
##      [,1] [,2] [,3]
## [1,]   27    0    0
## [2,]    6   15    0
## [3,]    1    1   54
##      [,1] [,2] [,3]
## [1,]    0    6   -1
## [2,]    0    0    2
## [3,]    0    0    0

Selanjutya lakukan invers terhadap matriks \(L\) menggunakn fungsi solve().

##            [,1]      [,2]    [,3]
## [1,]  0.0370370  0.000000 0.00000
## [2,] -0.0148148  0.066667 0.00000
## [3,] -0.0004115 -0.001235 0.01852

Tetapkan nilai estimasi awal dan nilai toleransi yang dikehendaki. Nilai toleransi pada proses ini ditetapkan sebesar \(10^-7\).

## [1] 0 0 0

Lakukan iterasi menggunakan Persamaan (6.39).

Iterasi 1

##       [,1]
## [1,] 3.148
## [2,] 3.541
## [3,] 1.913
## [1] 8.602

Iterasi 2

##       [,1]
## [1,] 2.432
## [2,] 3.572
## [3,] 1.926
## [1] 0.672

Iterasi terus dilakukan sampai dengan nilai akar jumlah kuadrat lebih kecil dari nilai toleransi. Setelah iterasi ke-7 diperoleh nilai vektor \(x\) sebesar:

\[ x = \begin{bmatrix} 2,425476 \\[0.3em] 3,573016 \\[0.3em] 1,925954 \end{bmatrix} \]

Algoritma Iterasi Gauss-Seidel

  1. Masukkan matriks \(A\), dan vektor \(B\) beserta ukurannya \(n\).
  2. Lakukan dekomposisi LU, dimana matriks \(L\) merupakan matriks segitiga bawah dengan nilai entri diagonal utama matriks \(A\) dan bagian bawah diagonalnya dan matriks \(U\) merupakan matriks segitiga atas dengan entri berasal dari elemen atas diagonal utama matriks \(A\). Isi elemen lain yang tidak disebut pada kedua matriks tersebut dengan nol.
  3. Tetapkan vektor \(x\) estimasi.
  4. Tetapkan nilai toleransi maksimum yang dapat diterima.
  5. Lakukan iterasi menggunakan Persamaan (6.39).
  6. Hitung akar jumlah kuadrat dari vektor \(x^{n+1}\) dan vektor \(x^n\).
  7. Jadikan nilai \(x^{n+1}\) sebagai nilai taksiran \(x\) untuk iterasi berikutnya.
  8. Hentikan proses iterasi jika telah memenuhi syarat yang ditampilkan pada Persamaan (6.33).

Berdasarkan algoritma tersebut, kita dapat menyusun fungsi sebuah fungsi untuk melakukan iterasi Gauss-Seidel. Berikut sintaks yang digunakan:

Contoh 6.12 Selesaikan sistem persamaan pada Contoh 6.10 menggunakan fungsi gauss_seidel()!

Jawab:

Penyelesaiansistem persamaan linier tersebut menggunakan fungsi gauss_seidel() disajikan pada sintaks berikut:

## $X
##       [,1]
## [1,] 2.425
## [2,] 3.573
## [3,] 1.926
## 
## $iter
## [1] 7

6.6 Studi Kasus

Aljabar linier banyak diaplikasikan baik dalam bidang engineering, fisika, sampai dengan statistika. Pada sub-chapter ini penulis akan menjelaskan penerapan aljabar linier pada metode kuadrat terkecil dan aliran massa dalam reaktor. Untuk penerapan lainnya pembaca dapat membaca buku lainnya terkait aljabar linier.

6.6.1 Metode Kuadrat Terkecil

Metode kuadrat terkecil merupakan salah satu aplikasi penerapan aljabar linier yang paling populer. Intuisi dibalik metode ini adalah bagaimana kita meminimalkan jarak antara sejumlah titik dengan garis regresi. Misalkan kita menggambarkan scatterplot antara dua buah variabel. Pola yang terbentuk dari plot tersebut adalah terjadi korelasi positif antara variabel pada sumbu \(x\) dan sumbu \(y\). Kita ingin menggambarkan garis regresi terbaik yang dapat menangkap seluruh pola tersebut. Garis regresi terbaik terjadi ketika jumlah kuadrat jarak antara titik observasi dan garis regresi yang terbentuk seminimal mungkin.

Untuk lebih memahaminya kita akan melakukan latihan menggunakan dataset trees yang berisi data hasil pengukuran kayu dari pohon yang ditebang. Pada dataset ini terdapat 31 observasi dan 3 buah kolom. Keterangan dari ketiga buah kolom tersebut adalah sebagai berikut:

  • Girth: diameter pohon dalam satuan inch.
  • Height: tinggi pohon dalam satuan feet.
  • Volume: volume kayu dalam satuan cubic feet.

Untuk mengecek 6 observasi pertama dan struktur data, jalankan sintaks berikut:

##   Girth Height Volume
## 1   8.3     70   10.3
## 2   8.6     65   10.3
## 3   8.8     63   10.2
## 4  10.5     72   16.4
## 5  10.7     81   18.8
## 6  10.8     83   19.7
## 'data.frame':    31 obs. of  3 variables:
##  $ Girth : num  8.3 8.6 8.8 10.5 10.7 10.8 11 11 11.1 11.2 ...
##  $ Height: num  70 65 63 72 81 83 66 75 80 75 ...
##  $ Volume: num  10.3 10.3 10.2 16.4 18.8 19.7 15.6 18.2 22.6 19.9 ...

Scatterplot matriks sangat bagus untuk mengecek korelasi antar variabel dalam dataset tersebut. Berikut adalah sintaks untuk membuatnya:

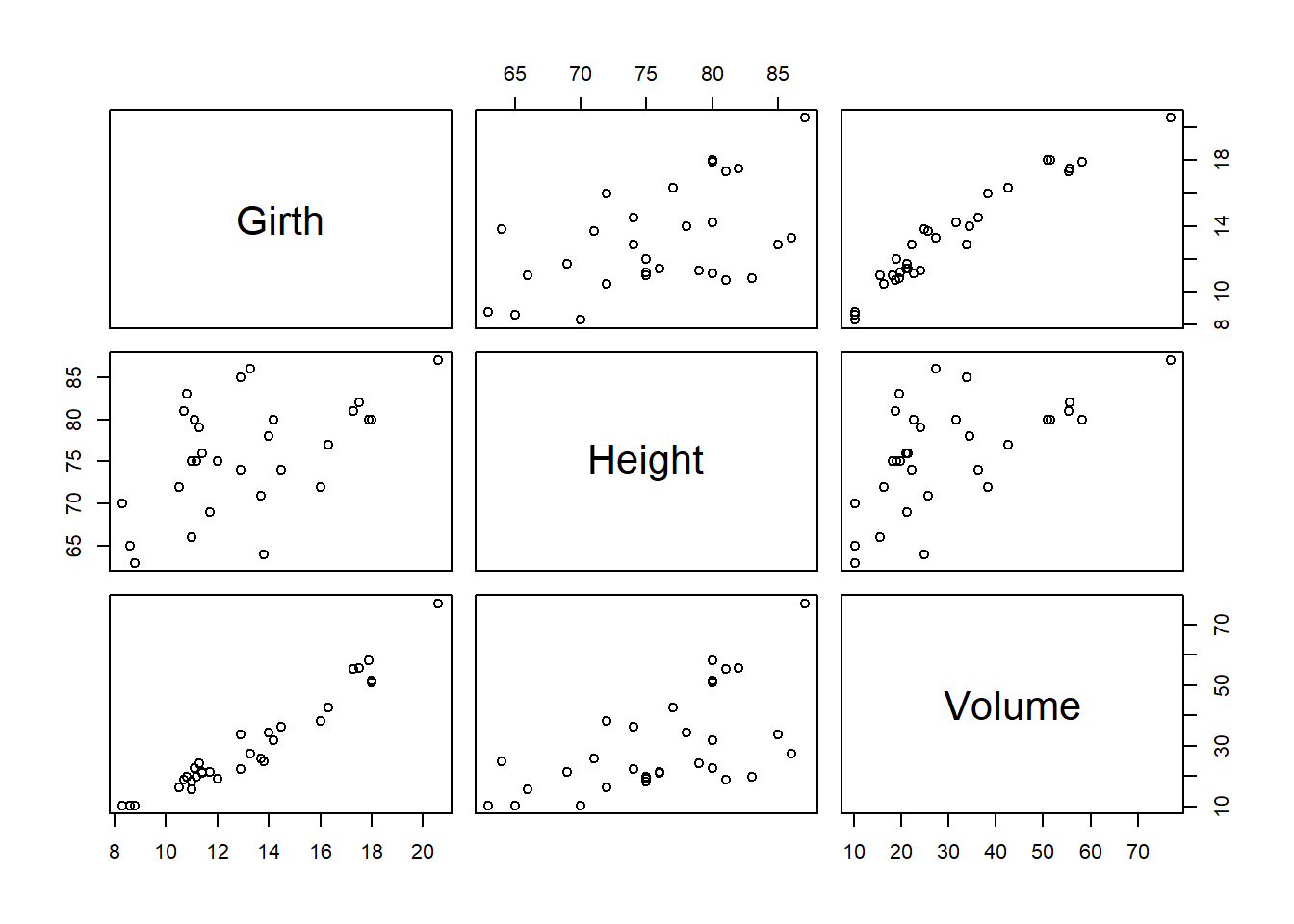
Scatterplot matriks dataset trees

(#fig:trees, LUfig)Scatterplot matriks dataset trees

Kita ingin membuat sebuah model linier untuk memprediksi Volume kayu berdasarkan variabel Girth dan Heiht atau volume sebagia fungsi dari variabel Girth dan Heiht. Kita dapat menuliskan relasi antara variabel volume sebagai fungsi dari variabel Girth dan Heiht menggunakan Persamaan (6.40).

\[\begin{equation} Volume=\beta_{girth} Girth+\beta_{height}Height+\beta_0 \tag{6.40} \end{equation}\]

dimana \(\beta_0\) merupakan intersep persamaan regresi linier dan nilai \(\beta\) lainnya merupakan koefisien dari variabel Girth dan Heiht. Variabel Volume disebut sebagai variabel respon, sedangkan variabel Girth dan Heiht disebut sebagai variabel prediktor.

Metode kuadrat terkecil berusaha memperoleh seluruh koefisien variabel dan intersep dari persamaan regresi linier. Berdasarkan yang telah penulis jelaskan garis regresi terbaik adalah garis yang memiliki nilai kuadrat terkecil jarak antara titik observasi dan garis regresi. Dasar dari metode kuadrat terkecil merupakan persamaan yang relatif sederhana yang ditunjukkan pada Persamaan (6.41).

\[\begin{equation} A^{T}A=A^{T}b \tag{6.41} \end{equation}\]

dimana \(b\) merupakan vektor dari variabel respon (Volume) dan matrik \(A\) merupakan matriks variabel prediktor (variabel Girth dan Heiht).

Untuk menginputkan intercept kedalam persamaan linier kita perlu menmabhakan satu kolom di awal matriks \(A\) yang berisi nilai 1. Berikut adalah sintaks yang digunakan untuk membentuk matriks \(A\):

##      [,1] [,2] [,3]
## [1,]   27    6   -1
## [2,]    6   15    2
## [3,]    1    1   54

Langkah selanjutnya adalah membentuk matriks \(b\). Berikut adalah sintaks yang digunakan:

## [1] 10.3 10.3 10.2 16.4 18.8 19.7

Untuk memperoleh koefisien \(\beta\), kita dapat mencarinya dengan cara menyelesaikan Persamaan (6.41). Berikut adalah sintaks yang digunakan:

##           intercept Girth Height         
## intercept         1     0      0 -57.9877
## Girth             0     1      0   4.7082
## Height            0     0      1   0.3393

Berdasarkan hasil yang diperoleh, persamaan linier yang terbentuk disajikan pada Persamaan (6.42).

\[\begin{equation} Volume=4.7081605 Girth + 0.3392512 Height -57.9876589 \tag{6.42} \end{equation}\]

Pembaca juga dapat menggunakan fungsi lain untuk memperoleh nilai koefisien tersebut, seperti: lu_solve()dansolve(). untuk fungsi jacobi() dan gauss_seidel(), kita harus pastikan syarat-syarat terkait metode tersebut. Berikut adalah contoh penyelesaian menggunakan sintaks lainnya:

## $P
##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1
## 
## $L
##       [,1]  [,2] [,3]
## [1,]  1.00 0.000    0
## [2,] 13.25 1.000    0
## [3,] 76.00 1.054    1
## 
## $U
##           intercept Girth Height
## intercept        31 410.7 2356.0
## Girth             0 295.4  311.5
## Height            0   0.0  889.6
## 
## $result
##          [,1]
## [1,] -57.9877
## [2,]   4.7082
## [3,]   0.3393
##               [,1]
## intercept -57.9877
## Girth       4.7082
## Height      0.3393

R juga menyediakan fungsi untuk membentuk model regresi linier. Fungsi yang digunakan adalah lm(). Berikut sintaks yang digunakan untuk membentuk model linier menggunakan fungsi lm():

## 
## Call:
## lm(formula = Volume ~ Girth + Height, data = trees)
## 
## Coefficients:
## (Intercept)        Girth       Height  
##     -57.988        4.708        0.339

6.6.2 Aliran Massa Dalam Reaktor

Pada sub-chapter ini penulis akan memberikan penerapan aljabar linier untuk menghitung konsentrasi suatu zat atau parameter lingkungan dalam reaktor yang saling terhubung. Pada contoh kasus kali ini diasumsikan terdapat lima buah reaktor yang saling terhubung satu sama lain sesuai Gambar 6.2. Debit air (\(\frac{m^{3}}{detik}\)) dan konsentrasi zat pencemar (\(\frac{mg}{m^3}\)) disajikan pula diagram alir tersebut. Diasumsikan kelima buah reaktor tersebut dalam kondisi steady dan volume reaktor diasumsikan sama. Kesetimbangan massa persatuan waktu dalam kondisi steady disajikan pada Persamaan (6.43).

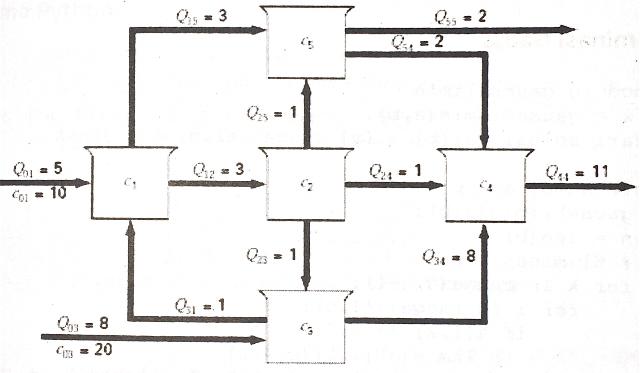
Aliran massa dalam reaktor.

Gambar 6.2: Aliran massa dalam reaktor.

\[\begin{equation} m_in=m_out \tag{6.43} \end{equation}\]

\[\begin{equation} Q_{in}C_{in}= Q_{out}C_{out} \tag{6.44} \end{equation}\]

Berdasarkan Gambar 6.2, dapat dibentuk lima buah sistem persamaan linier. Persamaan linier yang terbentuk disajikan sebagai berikut:

\[ \begin{matrix} 6c_{1}-c_{3}=50 \\ -3c_{1}+3c_{2}=0 \\ -c_{2}+9c_{3}=160 \\ -c_{2}-8c_{3}+11c_{4}-2c_{5}=0 \\ -3c_{1}-c_{2}+4c_{5}=0 \end{matrix} \]

Untuk menyelesaiakan sistem persamaan linier tersebut dan memperoleh nilai \(c\) dari masing-masing reaktor, kiat perlu mengubahnya dulu kedalam bentuk matriks \(Ax=b\). Berikut adalah matriks yang terbentuk:

\[\begin{equation*} \begin{bmatrix} 6 & 0 & -1 & 0 & 0 \\[0.3em] -3 & 3 & 0 & 0 & 0 \\[0.3em] 0 & -1 & 9 & 0 & 0 \\[0.3em] 0 & -1 & -8 & 11 & -2 \\[0.3em] -3 & -1 & 0 & 0 & 4 \end{bmatrix} c = \begin{bmatrix} 50 \\[0.3em] 0 \\[0.3em] 160 \\[0.3em] 0 \\[0.3em] 0 \end{bmatrix} \end{equation*}\]

Kita akan menyelesaikannya dengan menggunakan metode elminasi Gauss-Jordan, dekomposisi LU, iterasi Jacobi, dan iterasi Gauss-Seidel. Untuk dapat menyelesaikannya menggunakan metode-metode tersebut pada R, kita perlu membentuk matriksnya terlebih dahulu:

##      [,1] [,2] [,3] [,4] [,5]
## [1,]    6    0   -1    0    0
## [2,]   -3    3    0    0    0
## [3,]    0   -1    9    0    0
## [4,]    0   -1   -8   11   -2
## [5,]   -3   -1    0    0    4
## [1]  50   0 160   0   0

Metode Eliminasi Gauss-Jordan

##                    b
## [1,] 1 0 0 0 0 11.51
## [2,] 0 1 0 0 0 11.51
## [3,] 0 0 1 0 0 19.06
## [4,] 0 0 0 1 0 17.00
## [5,] 0 0 0 0 1 11.51

Metode Dekomposisi LU

## $P
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    0    0    0    0
## [2,]    0    1    0    0    0
## [3,]    0    0    1    0    0
## [4,]    0    0    0    1    0
## [5,]    0    0    0    0    1
## 
## $L
##      [,1]    [,2]     [,3] [,4] [,5]
## [1,]  1.0  0.0000  0.00000    0    0
## [2,] -0.5  1.0000  0.00000    0    0
## [3,]  0.0 -0.3333  1.00000    0    0
## [4,]  0.0 -0.3333 -0.92453    1    0
## [5,] -0.5 -0.3333 -0.07547    0    1
## 
## $U
##      [,1] [,2]       [,3] [,4] [,5]
## [1,]    6    0 -1.000e+00    0    0
## [2,]    0    3 -5.000e-01    0    0
## [3,]    0    0  8.833e+00    0    0
## [4,]    0    0  0.000e+00   11   -2
## [5,]    0    0  1.110e-16    0    4
## 
## $result
## [1] 11.51 11.51 19.06 17.00 11.51

Metode Iterasi Jacobi

## $X
##       [,1]
## [1,] 11.51
## [2,] 11.51
## [3,] 19.06
## [4,] 17.00
## [5,] 11.51
## 
## $iter
## [1] 17

Metode Iterasi Gauss-Seidel

## $X
##       [,1]
## [1,] 11.51
## [2,] 11.51
## [3,] 19.06
## [4,] 17.00
## [5,] 11.51
## 
## $iter
## [1] 7

Berdasarkan seluruh metode tersebut, diperoleh konsentrasi zat pencemar pada masing-masing reaktor adalah sebagai berikut:

\[ \begin{matrix} c_{1}=11,50943 \frac{mg}{m^3} \\ c_{2}=11,50943 \frac{mg}{m^3} \\ c_{3}=19,05660 \frac{mg}{m^3} \\ c_{4}=16,99828 \frac{mg}{m^3} \\ c_{5}=11.50943 \frac{mg}{m^3} \end{matrix} \]

6.7 Referensi

  1. Bloomfield, V.A. 2014. Using R for Numerical Analysis in Science and Engineering. CRC Press
  2. Howard, J.P. 2017. Computational Methods for Numerical Analysis with R. CRC Press.
  3. Kreyszig, E. 2011. Advanced Engineering Mathematics, 10th Edition. John Wiley & Sons.
  4. Primartha, R. 2018. Belajar Machine Learning Teori dan Praktik. Penerbit Informatika : Bandung.
  5. Sanjaya, M. 2015. Metode Numerik Berbasis Phython. Penerbit Gava Media: Yogyakarta.
  6. Suparno, S. 2008. Komputasi untuk Sains dan Teknik Edisi II. Departemen Fisika-FMIPA Universitas Indonesia.

6.8 Latihan

  1. Selesaikan sistem persamaan linier berikut menggunakan eliminasi Gauss!

\[ \begin{matrix} -4x+4y=-1 \\ -2x+2y-3z=-3 \\ 3x+1y-3z=-3 \end{matrix} \]

  1. Carilah penyelesaian dari sistem persamaan linier soal no.1 menggunakan algoritma dekomposisi LU!
  2. Tunjukan 5 iterasi pertama sistem persamaan linier berikut menggunakan algoritma Jacobi dan Gauss-Seidel!

\[ \begin{matrix} 3x+2y-1z=-3 \\ -3x-3y-3z=9 \\ 1y-1z=-1 \end{matrix} \]

  1. Gunakan fungsi jacobi() dan gauss_seidel() untuk menyelesaikan sistem persamaan linier pada soal no.4 dan tentukan metode mana yang paling cepat memperoleh penyelesaian? (petunjuk: gunakan fungsi system.time() dan jumlah iterasi yang diperlukan untuk memperoleh hasil yang konvergen)
  2. Apakah yang terjadi jika kita menginputkan matriks segiempat \(A\) kedalam fungsi solve() dan apa yang akan terjadi jika selanjutnya argumen pada fungsi tersebut juga menyertakan vektor \(b\)?
  3. Dengan menggunakan dataset mtcars buatlah persamaan linier variabel mpg sebagai fungsi dari variabel wt, hp, dan qsec menggunakan algoritma dekomposisi LU?