Chapter 11 Analisis Data
Pada Chapter 11, kita akan membahas mengenai cara melakukan analisis data pada R. Pada Chapter ini penulis akan memperkenalkan fungsi-fungsi yang ada pada R yang dapat membantu kita menganalisis data dan melakukan sejumlah uji statistik.
Pada Chapter ini kita tidak akan berfokus pada persamaan-persamaan matematika yang menjadi dasar suatu uji statistik. Chapter ini menitik beratkan pada bagaimana pembaca dapat melakukan sejumlah uji statistik pada R dan gambaran metode yang digunakan.
11.1 Import Data
Kita dapat melakukan import data dalam berbagai format pada R. Namun, pada sub-chapter ini hanya akan dibahas bagaimana cara mengimport data dari file dengan format .csvdan .txt. Secara umum fungsi-fungsi yang digunakan untuk membaca data pada file dengan format tersebut adalah sebagai berikut:
read.table(file, header = FALSE, sep = "", dec = ".",
stringsAsFactors = default.stringsAsFactors())
read.csv(file, header = TRUE, sep = ",", dec = ".")
read.csv2(file, header = TRUE, sep = ";", dec = ",")
read.delim(file, header = TRUE, sep = "\t", dec = ".")
read.delim2(file, header = TRUE, sep = "\t", dec = ",")Catatan:
file: lokasi dan nama file yang akan dibaca diakhiri dengan format file. Secara default fungsi akan membaca file yang ada pada working directory. Untuk mengetahui lokasi working directory, jalankan fungsigetwd(). Salin file yang akan dibaca pada lokasi working directory.header: nilai logik yang menunjukkan apakah baris pertama pada file yang dibaca akan dibaca sebagai nama kolom.sep: simbol yang menujukkan pemisah antar data. Pemisah antar data dapat berupa “",”;“,”.", dll.dec: simbol yang menujukkan desimal. Pemisah desimal dapat berupa “.” atau “,”.stringsAsFactors: nilai logik yang menunjukkan apakah jenis datastringakan dikonversi menjadifactor.
Kelima fungsi tersebut digunakan untuk membaca data tabular atau data yang disusun kedalam format tabel. Fungsi read.table() merupakan bentuk umum dari keempat fungsi lainnya. Fungsi tersebut dapat digunakan untuk membaca data dalam kedua format yang telah disebutkan sebelumnya. Fungsi lainnya lebih spesifi, dimana fungsi read.csv() dan read.csv2() digunakan untuk membaca data dengan ekstensi .csv, sedangkan read.delim() dan read.delim2() untuk membaca data dengan ekstensi .txt. Berikut adalah contoh bagaimana cara membaca data dengan nama data.csv yang ada pada working directory dengan pemisah antar data berupa ; dan tanda koma berupa ,:
11.2 Membaca Data Dari Library
Untuk keperluan pendidikan atau pengujian sebuah fungsi biasanya dalam sebuah library disediakan dataset yang siap digunakan. R melalui library datasets menyediakan sejumlah data yang dapat digunakan untuk berlatih menggunakan R. Berikut adalah fungsi yang digunakan untuk mengecek dataset apa saja yang tersedia pada sebuah library:
Catatan:
package: nama library yang hendak dicek dataset yang tersedia.
Berikut adalah contoh cara melakukan pengecekan pada dataset yang tersedia pada library datasets:
11.3 Ringkasan Data
Terdapat sejumlah fungsi yang akan pembaca sering gunakan untuk mengecek dataset yang akan pembaca analisa. Fungsi-fungsi tersebut antara lain:
head(): mengecek \(n\) (default 6) observasi teratas.tail(): mengecek \(n\) (default 6) observasi terbawah.str(): mengecek struktur data atau jenis data pada masing-masing kolom. Jenis data yang ada padaRdapat berupanum(numerik),int(integer),Factor(factor),date(tanggal), danchr(karakter atau string).summary(): ringkasan data.
Berikut adalah contoh penerapan fungsi-fungsi tersebut pada dataset iris:
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 1 5.1 3.5 1.4 0.2
## 2 4.9 3.0 1.4 0.2
## 3 4.7 3.2 1.3 0.2
## 4 4.6 3.1 1.5 0.2
## 5 5.0 3.6 1.4 0.2
## 6 5.4 3.9 1.7 0.4
## 7 4.6 3.4 1.4 0.3
## 8 5.0 3.4 1.5 0.2
## 9 4.4 2.9 1.4 0.2
## 10 4.9 3.1 1.5 0.1
## Species
## 1 setosa
## 2 setosa
## 3 setosa
## 4 setosa
## 5 setosa
## 6 setosa
## 7 setosa
## 8 setosa
## 9 setosa
## 10 setosa## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 141 6.7 3.1 5.6 2.4
## 142 6.9 3.1 5.1 2.3
## 143 5.8 2.7 5.1 1.9
## 144 6.8 3.2 5.9 2.3
## 145 6.7 3.3 5.7 2.5
## 146 6.7 3.0 5.2 2.3
## 147 6.3 2.5 5.0 1.9
## 148 6.5 3.0 5.2 2.0
## 149 6.2 3.4 5.4 2.3
## 150 5.9 3.0 5.1 1.8
## Species
## 141 virginica
## 142 virginica
## 143 virginica
## 144 virginica
## 145 virginica
## 146 virginica
## 147 virginica
## 148 virginica
## 149 virginica
## 150 virginica## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...## Sepal.Length Sepal.Width Petal.Length
## Min. :4.30 Min. :2.00 Min. :1.00
## 1st Qu.:5.10 1st Qu.:2.80 1st Qu.:1.60
## Median :5.80 Median :3.00 Median :4.35
## Mean :5.84 Mean :3.06 Mean :3.76
## 3rd Qu.:6.40 3rd Qu.:3.30 3rd Qu.:5.10
## Max. :7.90 Max. :4.40 Max. :6.90
## Petal.Width Species
## Min. :0.1 setosa :50
## 1st Qu.:0.3 versicolor:50
## Median :1.3 virginica :50
## Mean :1.2
## 3rd Qu.:1.8
## Max. :2.5Fungsi-fungsi lainnya yang dapat digunakan untuk melakukan analisis statistika deskriptif adalah sebagai berikut:
mean(): menghitung nilai rata-rata variabel numerik.sd(): menghitung simpangan baku variabel numerik.var(): menghitung varians variabel numerik.median(): menghitung median suatu variabel numerik.range(): memperoleh nilai minimum dan maksimum suatu variabel numerik.IQR(): memperoleh nilai jarak antar kuartil.quantile(): memperoleh kuantil variabel numerik.
Berikut adalah contoh penerapan fungsi-fungsi tersebut:
## [1] 42.13## [1] 31.5## [1] 32.99## [1] 1088## [1] 1 168## [1] 45.25## 25% 50% 75%
## 18.00 31.50 63.2511.4 Uji Normalitas Data Tunggal
Pada analisis statistik inferensial khususnya pada pengujian hipotesis, asumsi normalitas merupakan sesuatu yang harus terpenuhi jika prosedur uji yang digunakan merupakan prosedur uji parametrik. Terdapat dua buah cara untuk melakukan uji tersebut, antara lain:
- Metode grafis (qq-plot, ECDF, plot densitas, histogram, dan boxplot).
- Metode matematis (Shapiro-Wilk, Cramer-von Mises, Shapiro-Francia, Anderson-Darling, Liliefors, Pearson Chi-square, dll).
Pada Chapter ini, kita akan berfokus pada uji matematis karena cara pengujian dengan menggunakan metode grafis telah penulis jabarkan pada Chapter visualisasi data.
Metode uji normalitas yang sering digunakan pada R adalah metode Shapiro-Wilk. Metode ini merupakan metode uji yang memiliki power yang besar khusunya untuk ukuran sampel yang relatif kecil. Versi awal metode ini terbatas dengan jumlah sampel 3 sampai 50 sampel. Versi selanjutnya mengalami modifikasi sehingga dapat menangani sampel sampai dengan 5000 sampel bahkan lebih.
Untuk melakukan uji SHapiro-Wilk pada R, pembaca dapat menggunakan fungsi shapiro.test(). Format fungsi tersebut adalah sebagai beriku:
Catatan:
x: vektor numerik.
Untuk lebih memahami impelementasi fungsi tersebut pada data, berikut adalah contoh penerapan fungsi tersebut untuk menguji normalitas distribusi konsentrasi ozon pada dataset airquality:
##
## Shapiro-Wilk normality test
##
## data: airquality$Ozone
## W = 0.88, p-value = 3e-08Berdasarkan hasil uji diperoleh nilai p-value < 0,05, sehingga \(H_0\) ditolak dan dapat disimpulkan bahwa distribusi konsentrasi ozon tidak mengikuti distribusi normal. Untuk lebih memahami prosedur pengujian normalitas distribusi suatu data pembaca dapat membaca lebih lanjut pada tautan Environmental Data Modelin.
11.5 Uji Rata-Rata Satu dan Dua Sampel
Uji rata-rata satu sampel merupakan uji statistik untuk menguji apakah rata-rata suatu sampel berasal dari suatu populasi yang telah diketahui nilai rata-ratanya. Sedangkan uji rata-rata untuk dua populasi dilakukan untuk menguji apakah kedua selisis rata-rata populasi tersebut bernilai nol yang menujukkan bahwa kedua populasi tersebut memiliki nilai rata-rata yang sama. Uji rata-rata dua populasi dapat dilakukan untuk sampel independen (contoh: uji rata-rata performa dua buah IPAL) dan berpasangan (contoh: uji rata-rata input dan output IPAL).
Untuk melakukan uji rata-rata pada R dapat digunakan fungsi t.test() untuk uji parametrik dan wilcox.test() untuk melakukan uji non-parametrik sign rank test. Format fungsi-fungsi tersebut adalah sebagai berikut:
t.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE, var.equal = FALSE,
conf.level = 0.95, ...)
wilcox.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE, conf.level = 0.95, ...)Catatan:
x,y: vektor numerik. Jika argumenxdanydiisikan maka uji hipotesis dilakukan untuk dua buah populasi.alternative: digunakan untuk menentukan jenis uji hipotesis apakah satu sisi(“less” dan “greater”), atau dua sisi (“two.sided”).mu: nilai rata-rata populasi atau nilai rata-rata selisih antar populasi jika dilakukan uji hipotesis terhadap dua populasi. Secara default nilainya 0.paired: nilai logikal yang menentukan apakah uji dua populasi digunakan untuk sampel berpasangan (TRUE) atau tidak (FALSE).var.equal: nilai logikal yang menunjukkan apakah varians kedua populasi diasumsikan sama atau berbeda.conf.level: tingkat kepercayaan. Secara default tingkat kepercayaan yang digunakan adalah 95%.
Berikut adalah contoh penerapan fungsi tersebut untuk uji hipotesis satu dan dua populasi:
# Uji hipotesis konsentrasi ozon = 40 ppm
# parametrik
t.test(x=airquality$Ozone, alternative = "two.sided",
mu = 40)##
## One Sample t-test
##
## data: airquality$Ozone
## t = 0.7, df = 120, p-value = 0.5
## alternative hypothesis: true mean is not equal to 40
## 95 percent confidence interval:
## 36.06 48.20
## sample estimates:
## mean of x
## 42.13##
## Wilcoxon signed rank test with continuity
## correction
##
## data: airquality$Ozone
## V = 3200, p-value = 0.7
## alternative hypothesis: true location is not equal to 40# Uji hipotesis dua populasi
dni3 <- dimnames(iris3)
ii <- data.frame(matrix(aperm(iris3, c(1,3,2)), ncol = 4,
dimnames = list(NULL, sub(" L.",".Length",
sub(" W.",".Width", dni3[[2]])))),
Species = gl(3, 50, labels = sub("S", "s", sub("V", "v", dni3[[3]]))))
# parametrik
t.test(x=iris$Sepal.Length[iris$Species=="setosa"],
y=ii$Sepal.Length[iris$Species=="versicolor"])##
## Welch Two Sample t-test
##
## data: iris$Sepal.Length[iris$Species == "setosa"] and ii$Sepal.Length[iris$Species == "versicolor"]
## t = -11, df = 87, p-value <2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -1.1057 -0.7543
## sample estimates:
## mean of x mean of y
## 5.006 5.936# nonparametrik
wilcox.test(x=iris$Sepal.Length[iris$Species=="setosa"],
y=ii$Sepal.Length[iris$Species=="versicolor"])##
## Wilcoxon rank sum test with continuity
## correction
##
## data: iris$Sepal.Length[iris$Species == "setosa"] and ii$Sepal.Length[iris$Species == "versicolor"]
## W = 170, p-value = 8e-14
## alternative hypothesis: true location shift is not equal to 0Fungsi t.test() akan menghasilkan output berupa nilai t uji, derajat kebebasan (df), nilai p-value, rentang estimasi nilai rata-rata berdasarkan tingkat kepercayaan yang digunakan, serta estimasi nilai rata-rata sampel. Fungsi wilcox.test() akan menghasilkan dua buah output yaitu nilai W dan p-value berdasarkan nilai W yang dihasilkan.
11.6 Korelasi Antar Variabel
Pada sebuah analisa, kita sering kali tertarik untuk menganalisa hubungan atau korelasi antara satu variabel terhadap variabel lainnya. Pengamatan adanya korelasi antar variabel dapat dilakukan melalui visualisasi menggunakan scatterplot dan perhitungan matematis menggunakan metode Pearson untuk metode parametrik dan metode rangking Spearman dan Kendall untuk metode non-parametrik. Pada Chapter ini kita akan berfokus untuk melakukan uji korelasi menggunakan R menggunakan metode matematis.
Pada R uji korelasi dapat dilakukan dengan menggunakan fungsi cor.test(). Format fungsi tersebut adalah sebagai berikut:
cor.test(x, y,
alternative = c("two.sided", "less", "greater"),
method = c("pearson", "kendall", "spearman"),
conf.level = 0.95)Catatan:
x,y: vektor numerik.alternative: digunakan untuk menentukan jenis uji hipotesis apakah satu sisi(“less” dan “greater”), atau dua sisi (“two.sided”).method: metode perhitungan korelasi yang digunakan.conf.level: tingkat kepercayaan. Secara default tingkat kepercayaan yang digunakan adalah 95%.
Berikut adalah penerapan fungsi cor.test() berdasarkan metode-metode yang telah disediakan pada fungsi tersebut:
# Pearson
cor.test(x = airquality$Ozone, y = airquality$Solar.R,
alternative = "two.sided",
method = "pearson")##
## Pearson's product-moment correlation
##
## data: airquality$Ozone and airquality$Solar.R
## t = 3.9, df = 110, p-value = 2e-04
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.1732 0.5021
## sample estimates:
## cor
## 0.3483# Kendall
cor.test(x = airquality$Ozone, y = airquality$Solar.R,
alternative = "two.sided",
method = "kendall")##
## Kendall's rank correlation tau
##
## data: airquality$Ozone and airquality$Solar.R
## z = 3.7, p-value = 2e-04
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
## tau
## 0.2403# Spearman
cor.test(x = airquality$Ozone, y = airquality$Solar.R,
alternative = "two.sided",
method = "spearman")## Warning in cor.test.default(x = airquality$Ozone, y =
## airquality$Solar.R, : Cannot compute exact p-value with
## ties##
## Spearman's rank correlation rho
##
## data: airquality$Ozone and airquality$Solar.R
## S = 150000, p-value = 2e-04
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.3482Berdasarkan output yang dihasilkan, metode Pearson menghasilkan output berupa nilai t uji, derajat kebebasan, nilai p-value, rentang estimasi nilai korelasi berdasarkan tingkat kepercayaan, dan estimasi nilai korelasi. Metode Kendall dan Spearman disisi lai menghasilkan output berupa nilai z uji dan S untuk masing-masing metode serta nilai p-value berdasarkan nilai statistika uji dan estimasi koefisien korelasi.
11.7 Analisis Varians
Pada sub-Chapter sebelumnya penulis telah menjelaskan uji rata-rata untuk satu sampel dan dua sampel. Pada kenyataannya dalam sebuah percobaan laboratorium, kita tidak hanya membandingkan dua buah grup sampel saja, namun beberapa grup dan sejumlah faktor. Untuk menganalisa apakah variasi perlakuan pada kelompok sampel akan memberikan hasil yang berbeda-beda pada rata-rata tiap grup atau tidak diperlukan analisis varians untuk menganilisa variasi perlakuan atau faktor pada masing-masing grup. Analisis varians dapat dilakukan baik untuk satu faktor maupun dua faktor atau lebih. Untuk melakukannya pada R, kita dapat menggunakan fungsi aov() untuk analisis varians dengan metode parametrik dan kruskal.test() untuk analisis varians dengan menggunakan metode nonparametrik. Berikut adalah format kedua fungsi tersebut:
Catatan:
formula: formula model yang digunakan.data: dataset yang akan digunakan.
Berikut adalah contoh penerapan kedua fungsi tersebut untuk melihat apakah terdapat beda pada rata-rata konsentrasi bulanan ozon menggunakan dataset airquality:
## Df Sum Sq Mean Sq F value Pr(>F)
## Month 1 3387 3387 3.17 0.078 .
## Residuals 114 121756 1068
## ---
## Signif. codes:
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 37 observations deleted due to missingness##
## Kruskal-Wallis rank sum test
##
## data: Ozone by Month
## Kruskal-Wallis chi-squared = 29, df = 4, p-value
## = 7e-06Berdasarkan hasil yang diperoleh diketahui bahwa rata-rata konsentrasi bulanan ozon tidak sama tiap bulannya atau minimal terdapat satu bulan dimana konsentrasi ozonnya berbeda secara signifikan dengan konsentrasi ozon pada bulan-bulan lainnya. Untuk lebih memahami terkait analisis varians pada R dan cara membaca output kedua fungsi tersebut, pembaca dapat membaca tulisan pada halaman situs sthda.
11.8 Analisis Komponen Utama
Analisis komponen utama menggunakan transformasi ortogonal (umumnya nilai singular atau dekomposisi nilai eigen) untuk mengubah seperangkat variabel pengamatan yang mungkin berkorelasi menjadi seperangkat variabel tidak berkorelasi (ortogonal) yang disebut komponen utama. Transformasi didefinisikan sedemikian rupa sehingga komponen utama pertama memiliki varians setinggi mungkin (menyumbang variabilitas pada data sebanyak mungkin), dan masing-masing komponen berikutnya pada gilirannya memiliki varians tertinggi yang mungkin di bawah kendala, dimana komponen tersebut menjadi ortogonal ke komponen sebelumnya.
Dalam R, analisis komponen utama umumnya dilakukan dengan fungsi prcomp (). Format fungsi tersebut adalah sebagai berikut:
Catatan:
x: data frame atau matriks kompleks numerik.retx: nilai logik yang mengindikasikan apakah variabel hasil rotasi perlu ditampilkan.center: nilai logik yang mengidikasikan apakah variabel perlu dilakukan pergeseran sehingga nilai rata-ratanya berpusat pada nilai nol.scale: nilai logik yang mengidikasikan apakah variabel perlu dilakukan penskalaan sebelum dilakukan analisis.tol: nilai toleransi yang menunjukkan batas nilai bagi komponen yang akan dipertahankan. Komponen yang dihilangkan jika simpangan bakunya kurang dari atau sama dengantol x simpangan baku pc1.
Untuk memahami penerapan fungsi tersebut, kita akan melakukan simulasi menggunakan dataset iris. Output yang dihasilkan di bawah ini menunjukkan bagaimana empat variabel numerik ditransformasikan menjadi empat komponen utama. Penskalaan data mungkin tidak diperlukan dalam kasus ini, karena keempat pengukuran memiliki unit yang sama dan besarnya sama. Namun, penskalaan umumnya merupakan praktik yang baik.
iris_use <- iris[,-5] # menghilangkan variabel non-numerik
iris_pca <- prcomp(iris_use, scale. = TRUE)
iris_pca## Standard deviations (1, .., p=4):
## [1] 1.7084 0.9560 0.3831 0.1439
##
## Rotation (n x k) = (4 x 4):
## PC1 PC2 PC3 PC4
## Sepal.Length 0.5211 -0.37742 0.7196 0.2613
## Sepal.Width -0.2693 -0.92330 -0.2444 -0.1235
## Petal.Length 0.5804 -0.02449 -0.1421 -0.8014
## Petal.Width 0.5649 -0.06694 -0.6343 0.5236Fungsi summary memberikan proporsi varians total yang dikaitkan dengan masing-masing komponen utama, dan proporsi kumulatif ketika masing-masing komponen ditambahkan. Kita melihat bahwa dua komponen pertama berperan lebih dari 95% dari total varians.
## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 1.71 0.956 0.3831 0.14393
## Proportion of Variance 0.73 0.229 0.0367 0.00518
## Cumulative Proportion 0.73 0.958 0.9948 1.00000Histogram (hasil plot dalam analisis prcomp) secara grafis merekapitulasi proporsi varian yang disumbangkan oleh masing-masing komponen utama, sementara biplot menunjukkan bagaimana variabel awal diproyeksikan pada dua komponen utama pertama (Gambar 11.1). Ini juga menunjukkan koordinat dari masing-masing sampel dalam ruang (PC1, PC2). Satu spesies iris (yang berubahmenjadi setosa dari analisis kluster di bawah ini) secara jelas dipisahkan dari dua spesies lain dalam ruang koordinat ini.
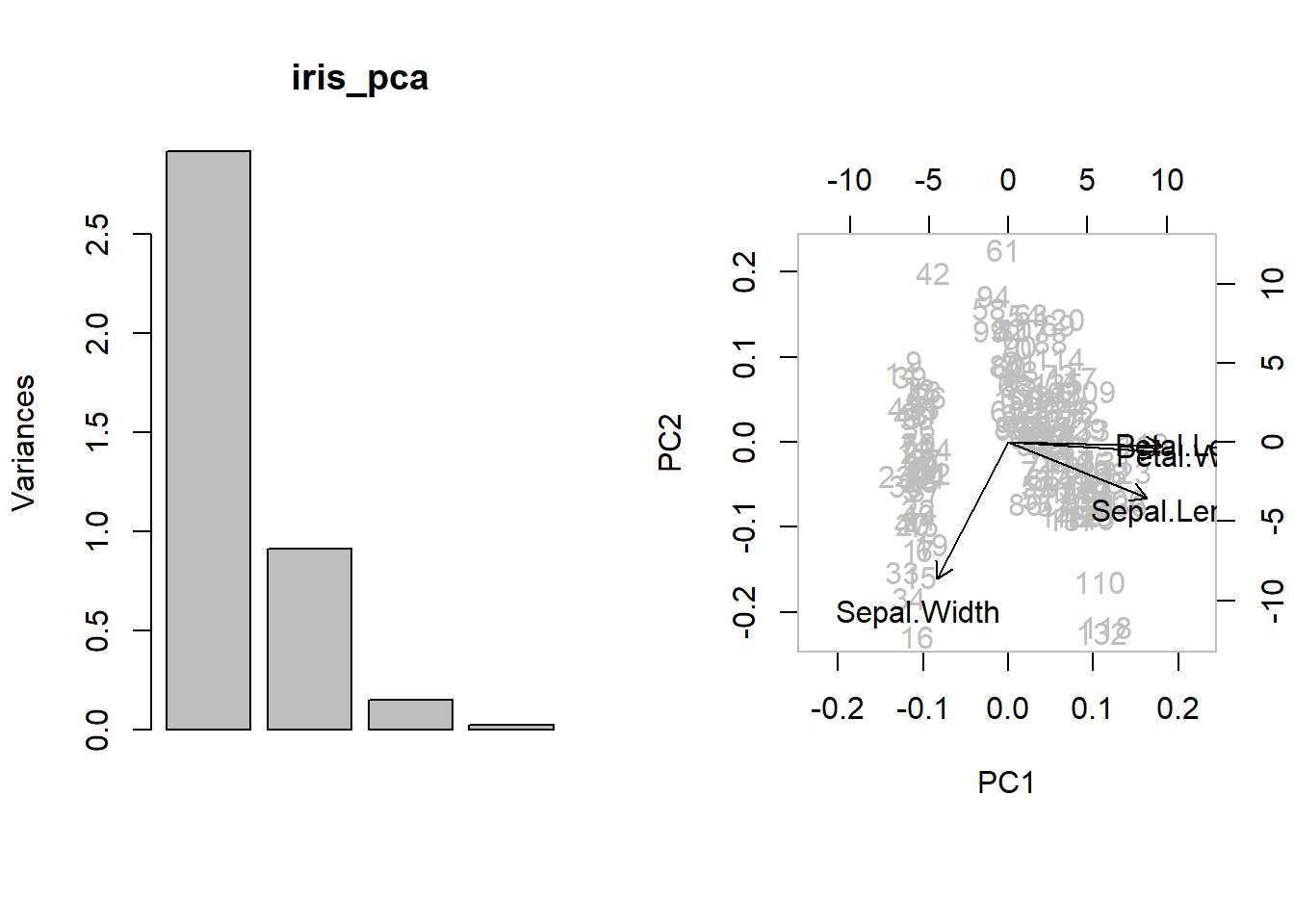
Gambar 11.1: Analisis komponen utama data iris.
Untuk informasi lebih lanjut terkait metode analisis komponen utama, pembaca dapat membacanya pada laman Little Book of R for Multivariate Analysis.
11.9 Analisis Cluster
Analisis cluster mencoba untuk mengurutkan satu set objek ke dalam kelompok (cluster) sedemikian rupa sehingga objek dalam cluster yang sama lebih mirip satu sama lain dibandingkan objek pada cluster lainnya. Ini digunakan untuk analisis eksplorasi melalui proses penambangan data (data mining) di banyak bidang, seperti bioinformatika, biologi evolusi, analisis gambar, lingkungan, dan pembelajaran mesin.
Menurut Wikipedia: “Analisis Cluster itu sendiri bukanlah salah satu algoritma spesifik, tetapi tugas umum yang harus dipecahkan. Ini dapat dicapai dengan berbagai algoritma yang berbeda secara signifikan dalam pengertian mereka tentang apa yang merupakan sebuah cluster dan bagaimana cara menemukannya secara efisien. Gagasan populer mengenai cluster termasuk kelompok dengan jarak rendah di antara anggota cluster, area padat ruang data, interval atau distribusi statistik tertentu. Algoritma pengelompokan dan pengaturan parameter yang sesuai (termasuk nilai-nilai seperti fungsi jarak yang akan digunakan, ambang kepadatan atau jumlah cluster yang diharapkan) tergantung pada dataset individual dan tujuan penggunaan hasil. Analisis cluster seperti itu bukan tugas otomatis, tetapi proses berulang penemuan pengetahuan yang melibatkan trial and error. Seringkali diperlukan untuk memodifikasi preprocessing dan parameter sampai hasilnya mencapai properti yang diinginkan.
11.9.1 Analisis Cluster Menggunakan Algoritma Pengelompokan Hierarkis Aglomeratif
Hierarchical clustering membangun hierarki cluster, di mana metrik hierarki adalah suatu ukuran ketidaksamaan antar cluster. Menurut halaman bantuan untuk hclust(), metode pengelompokan hierarkis aglomeratif, “Fungsi ini melakukan analisis hierarki cluster menggunakan seperangkat ketidaksamaan untuk n objek yang dikelompokkan. Awalnya, masing-masing objek ditugaskan ke cluster sendiri dan kemudian algoritma melanjutkan secara iteratif, pada setiap tahap bergabung dengan dua cluster yang paling mirip, terus sampai hanya ada satu cluster. Pada setiap tahap, jarak antar kluster dihitung ulang dengan formula pembaruan ketidaksamaan Lance Williams sesuai dengan metode pengelompokan tertentu yang digunakan.”Ada tujuh metode aglomerasi yang tersedia, dengan lengkap — yang mencari kluster kompak, bola — sebagai default. Format umum fungsi hclust() adalah sebagai berikut:
Catatan:
d: struktur ketidaksamaan yang dihasilkan dengan fungsidist.method: metode alglomerasi yang digunakan. Metode yang dapat digunakan antara lain: “ward.D”, “ward.D2”, “single”, “complete”, “average” (= UPGMA), “mcquitty” (= WPGMA), “median” (= WPGMC) atau “centroid” (= UPGMC)members: NULL atau vektor dengan ukuran sama dengand. Untuk info lebih lanjut jalankan sintaks?hclust.
Untuk memahami penerapan fungsi hclust(), kita akan kembali menggunakan data iris_use. Berikut adalah sintaks yang digunakan:
# menghitung jarak antar observasi
iris_hclust <- dist(iris_use)
# Pembentukan Cluster
hc <- hclust(iris_hclust)
hc##
## Call:
## hclust(d = iris_hclust)
##
## Cluster method : complete
## Distance : euclidean
## Number of objects: 150Visualisasi cluster dibentuk melalui dendogram yang ditampilkan pada Gambar 11.2.
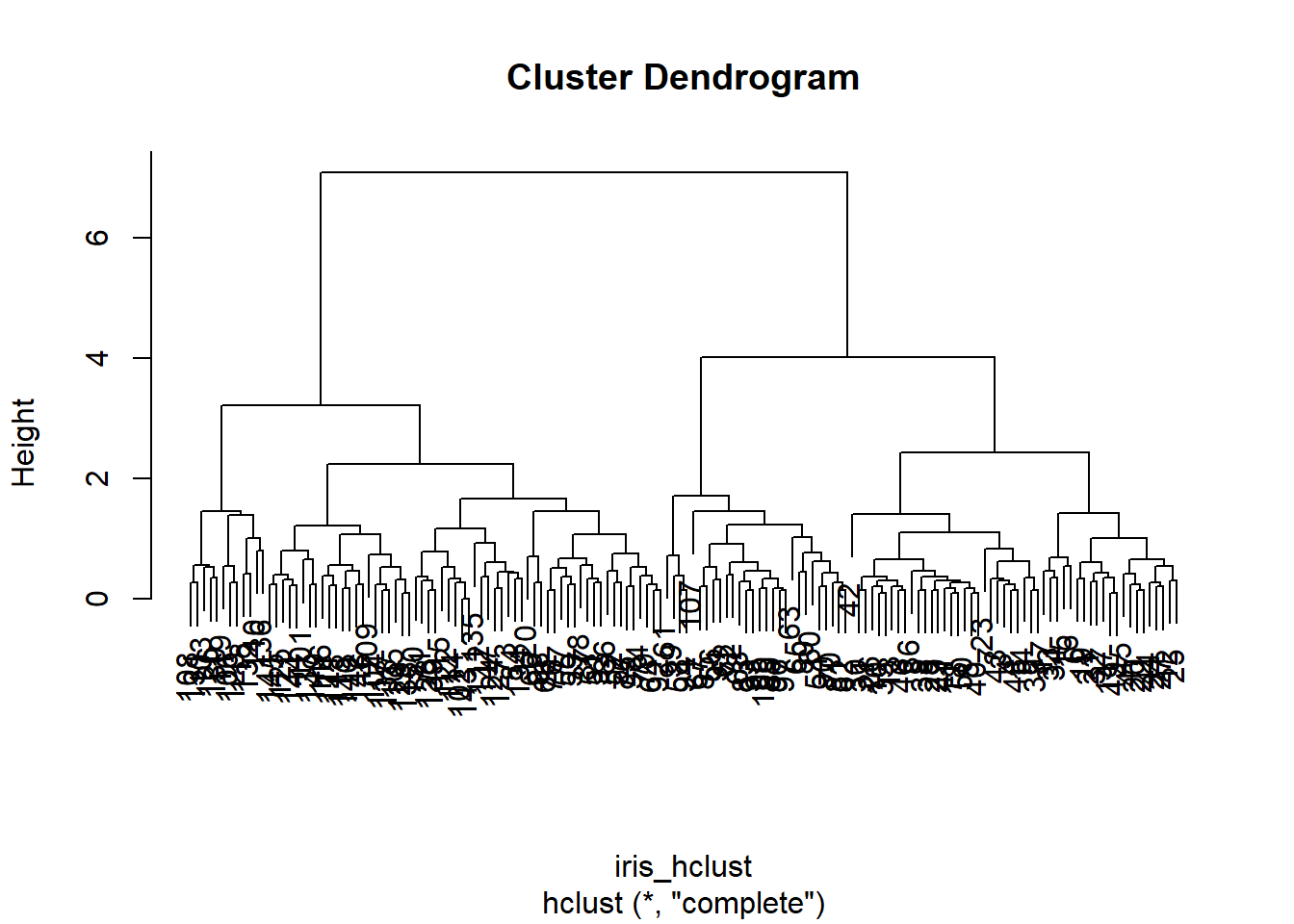
Gambar 11.2: Analisis pengelompokan hierarkis alglomeratif data iris.
11.9.2 Pengelompokan Hierarkis Divisif
Menurut halaman bantuan diana() (DIvisive ANAlysis Clustering) dalam library cluster, “Algoritma diana membangun hierarki pengelompokan, dimulai dengan satu kluster besar yang berisi semua n pengamatan. Cluster dibagi sampai masing-masing cluster hanya berisi satu pengamatan. Pada setiap tahap, cluster dengan diameter terbesar dipilih. Format fungsi diana() adalah sebagai berikut:
Catatan:
x: struktur ketidaksamaan yang dihasilkan dengan fungsidistatau data frame.metric: karakter string yang menyatakan metode pengukuran jarak yang digunakan. Metode pengukuran jarak dapat berupa “euclidean” dan “manhattan”.stand: vektor logik yang menyatakan apakah data akan dilakukan standardisasi terlebih dahulu sebelum dilakukan analisis.
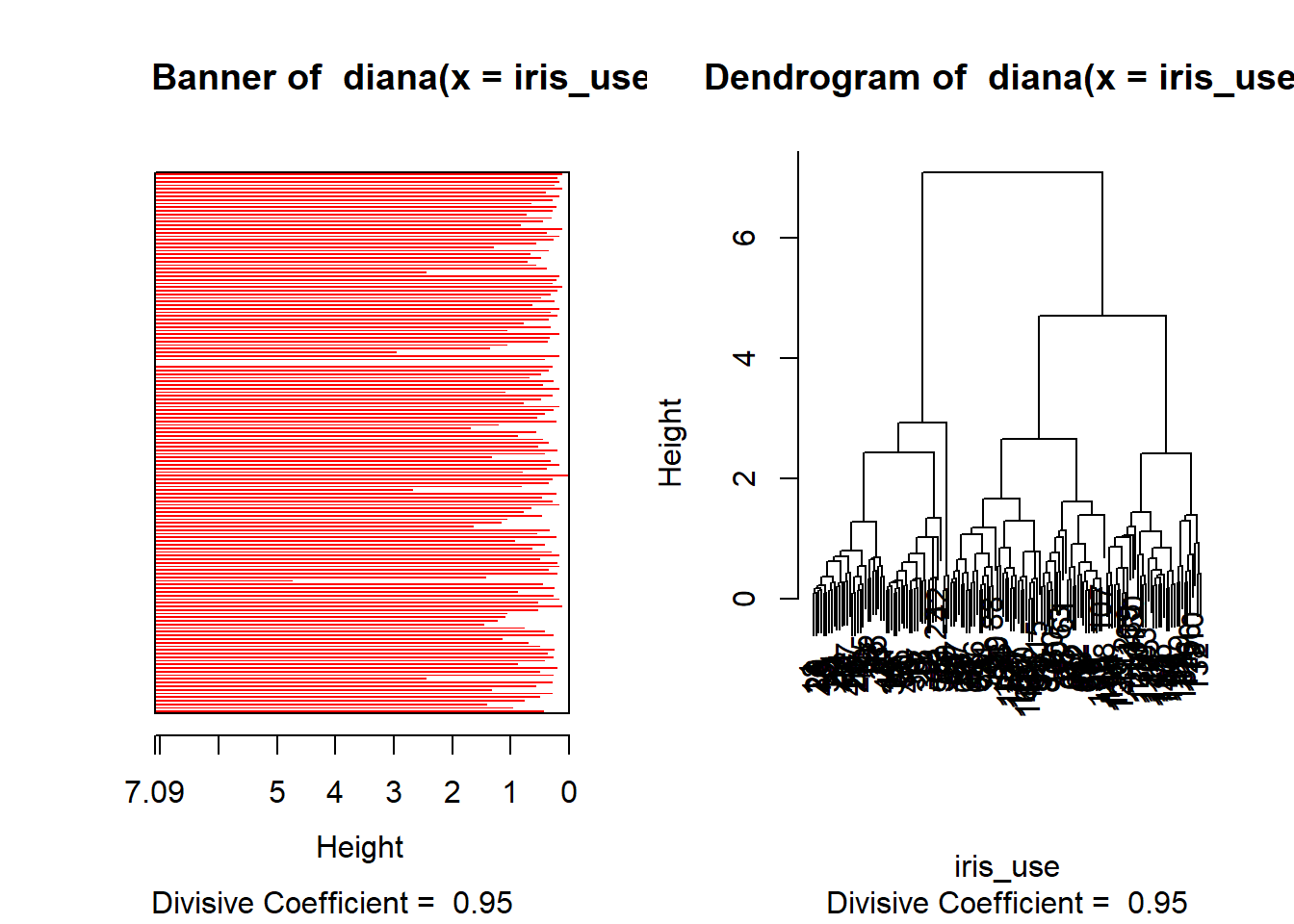
Gambar 11.3: Analisis pengelompokan divisif data iris.
11.9.3 Pengelompokan Menggunakan Algoritma K-Mean
k-means melakukan pengelompokan n pengamatan ke dalam k cluster di mana setiap pengamatan akan tergabung dengan pusat cluster terdekat. Pengguna harus menentukan jumlah pusat (cluster) yang diinginkan sebagai output. Untuk melakukan pengelompokan dengan algoritma k-means pada R dapat menggunakan fungsi kmeans(). Format fungsi tersebut secara umum adalah sebagai berikut:
Catatan:
x: data frame.centers: jumlah cluster yang ingin di buat.iter.max: jumlah iterasi maksimum yang diijinkan.algorithm: algoritma pengelompokan yang digunakan. Untuk informasi lebih lanjut jalankan sintaks?kmeans.
## K-means clustering with 3 clusters of sizes 50, 38, 62
##
## Cluster means:
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 1 5.006 3.428 1.462 0.246
## 2 6.850 3.074 5.742 2.071
## 3 5.902 2.748 4.394 1.434
##
## Clustering vector:
## [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [26] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [51] 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
## [76] 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
## [101] 2 3 2 2 2 2 3 2 2 2 2 2 2 3 3 2 2 2 2 3 2 3 2 3 2
## [126] 2 3 3 2 2 2 2 2 3 2 2 2 2 3 2 2 2 3 2 2 2 3 2 2 3
##
## Within cluster sum of squares by cluster:
## [1] 15.15 23.88 39.82
## (between_SS / total_SS = 88.4 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss"
## [4] "withinss" "tot.withinss" "betweenss"
## [7] "size" "iter" "ifault"# menghitung lokasi pusat cluster
ccent = function(cl) {
f = function(i) colMeans(iris_use[cl==i,])
x = sapply(sort(unique(cl)), f)
colnames(x) = sort(unique(cl))
return(x)
}
ccent(iris_kmeans$cluster)## 1 2 3
## Sepal.Length 5.006 6.850 5.902
## Sepal.Width 3.428 3.074 2.748
## Petal.Length 1.462 5.742 4.394
## Petal.Width 0.246 2.071 1.43411.9.4 Pengelompokan Menggunakan Algoritma PAM
pam mem-partisi data menjadi k cluster di sekitar medoid. Medoid dari set data yang terbatas merupakan titik data dengan nilai ketidaksamaan rata-rata untuk semua titik data adalah minimum. Hal tersebut menujukkan bahwa medoid merupakan pusat dari set cluster. Menurut halaman bantuan pam(), pendekatan k-medoid lebih kuat daripada pendekatan k-means “karena meminimalkan jumlah ketidaksamaan daripada jumlah jarak euclidean kuadrat”. Format umum fungsi pam() adalah sebagai berikut:
Catatan:
x: data frame.k: jumlah cluster yang ingin di buat.method: metode perhitungan jarak yang digunakan. Untuk informasi lebih lanjut jalankan sintaks?pam.
## Medoids:
## ID Sepal.Length Sepal.Width Petal.Length
## [1,] 8 5.0 3.4 1.5
## [2,] 79 6.0 2.9 4.5
## [3,] 113 6.8 3.0 5.5
## Petal.Width
## [1,] 0.2
## [2,] 1.5
## [3,] 2.1
## Clustering vector:
## [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [26] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [51] 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
## [76] 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
## [101] 3 2 3 3 3 3 2 3 3 3 3 3 3 2 2 3 3 3 3 2 3 2 3 2 3
## [126] 3 2 2 3 3 3 3 3 2 3 3 3 3 2 3 3 3 2 3 3 3 2 3 3 2
## Objective function:
## build swap
## 0.6709 0.6542
##
## Available components:
## [1] "medoids" "id.med" "clustering"
## [4] "objective" "isolation" "clusinfo"
## [7] "silinfo" "diss" "call"
## [10] "data"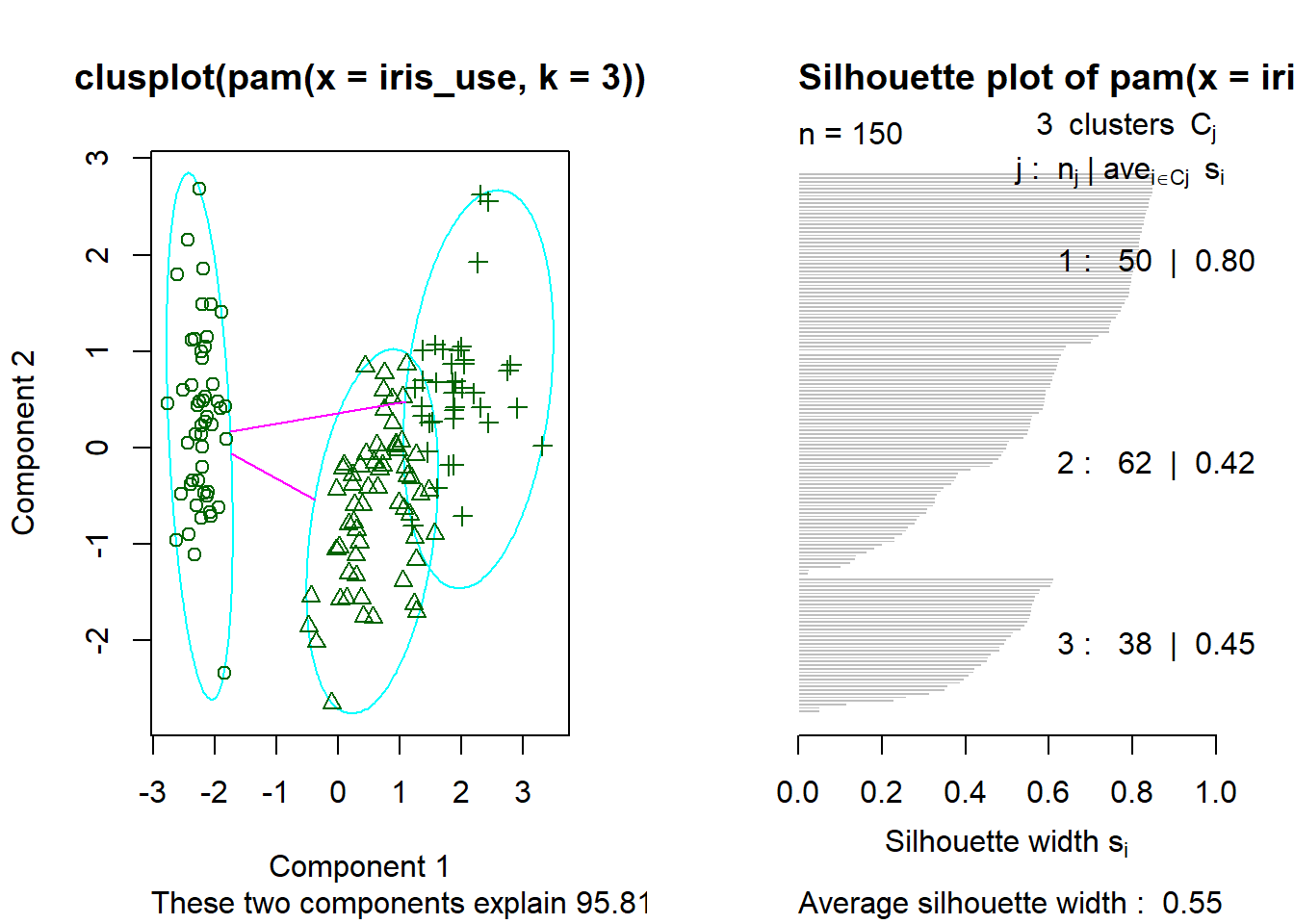
Gambar 11.4: Analisis pengelompokan metode pam data iris.
11.10 Referensi
- Bloomfield, V.A. 2014. Using R for Numerical Analysis in Science and Engineering. CRC Press.
- Coqhlan, A. Tanpa Tahun. Using R for Multivariate Analysis. https://little-book-of-r-for-multivariate-analysis.readthedocs.io/en/latest/src/multivariateanalysis.html#principal-component-analysis.
- Primartha, R. 2018. Belajar Machine Learning Teori dan Praktik. Penerbit Informatika : Bandung
- Rosadi,D. 2016. Analisis Statistika dengan R. Gadjah Mada University Press: Yogyakarta.
- Rosidi, M. 2019. Uji Hipotesis. https://environmental-data-modeling.netlify.com/tutorial/11_uji_hipotesis/.
- STHDA. Tanpa Tahun. Comparing Means in R. http://www.sthda.com/english/wiki/comparing-means-in-r.