Chapter 2 R Lab 1 - 17/03/2021

In this lecture we will learn how to implement the K-nearest neighbors (KNN) method for classification and regression problems.

The following packages are required: class, FNN and tidyverse.

library(class)
library(FNN)
## 
## Attaching package: 'FNN'
## The following objects are masked from 'package:class':
## 
##     knn, knn.cv
library(tidyverse)
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.0 ──
## ✓ ggplot2 3.3.3     ✓ purrr   0.3.4
## ✓ tibble  3.1.2     ✓ dplyr   1.0.6
## ✓ tidyr   1.1.3     ✓ stringr 1.4.0
## ✓ readr   1.3.1     ✓ forcats 0.5.0
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

2.1 KNN for regression problems

For KNN regression we will use data regarding bike sharing (link). The data are stored in the file named bikesharing.csv which is available in the e-learning. The data regard the bike sharing counts aggregated on daily basis.

We start by importing the data. Please, note that in the following code my file path is shown; obviously for your computer it will be different:

bike = read.csv("~/Dropbox/UniBg/Didattica/Economia/2020-2021/MLFE_2021/RLabs/Lab1/bikesharing.csv")
head(bike)
##   instant     dteday season yr mnth holiday weekday workingday weathersit
## 1       1 2011-01-01      1  0    1       0       6          0          2
## 2       2 2011-01-02      1  0    1       0       0          0          2
## 3       3 2011-01-03      1  0    1       0       1          1          1
## 4       4 2011-01-04      1  0    1       0       2          1          1
## 5       5 2011-01-05      1  0    1       0       3          1          1
## 6       6 2011-01-06      1  0    1       0       4          1          1
##       temp    atemp      hum windspeed casual registered  cnt
## 1 0.344167 0.363625 0.805833 0.1604460    331        654  985
## 2 0.363478 0.353739 0.696087 0.2485390    131        670  801
## 3 0.196364 0.189405 0.437273 0.2483090    120       1229 1349
## 4 0.200000 0.212122 0.590435 0.1602960    108       1454 1562
## 5 0.226957 0.229270 0.436957 0.1869000     82       1518 1600
## 6 0.204348 0.233209 0.518261 0.0895652     88       1518 1606
glimpse(bike)
## Rows: 731
## Columns: 16
## $ instant    <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, …
## $ dteday     <chr> "2011-01-01", "2011-01-02", "2011-01-03", "2011-01-04", "20…
## $ season     <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ yr         <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
## $ mnth       <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ holiday    <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0,…
## $ weekday    <int> 6, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4,…
## $ workingday <int> 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1,…
## $ weathersit <int> 2, 2, 1, 1, 1, 1, 2, 2, 1, 1, 2, 1, 1, 1, 2, 1, 2, 2, 2, 2,…
## $ temp       <dbl> 0.3441670, 0.3634780, 0.1963640, 0.2000000, 0.2269570, 0.20…
## $ atemp      <dbl> 0.3636250, 0.3537390, 0.1894050, 0.2121220, 0.2292700, 0.23…
## $ hum        <dbl> 0.805833, 0.696087, 0.437273, 0.590435, 0.436957, 0.518261,…
## $ windspeed  <dbl> 0.1604460, 0.2485390, 0.2483090, 0.1602960, 0.1869000, 0.08…
## $ casual     <int> 331, 131, 120, 108, 82, 88, 148, 68, 54, 41, 43, 25, 38, 54…
## $ registered <int> 654, 670, 1229, 1454, 1518, 1518, 1362, 891, 768, 1280, 122…
## $ cnt        <int> 985, 801, 1349, 1562, 1600, 1606, 1510, 959, 822, 1321, 126…

The dataset is composed by 731 rows (i.e. days) and 16 variables. We are in particular interested in the following quantitative variables (in this case \(p=3\) regressors):

  • atemp: normalized feeling temperature in Celsius
  • hum: normalized humidity
  • windspeed: normalized wind speed
  • cnt: count of total rental bikes (response variable)

The response variable cnt can be summarized as follows:

summary(bike$cnt)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##      22    3152    4548    4504    5956    8714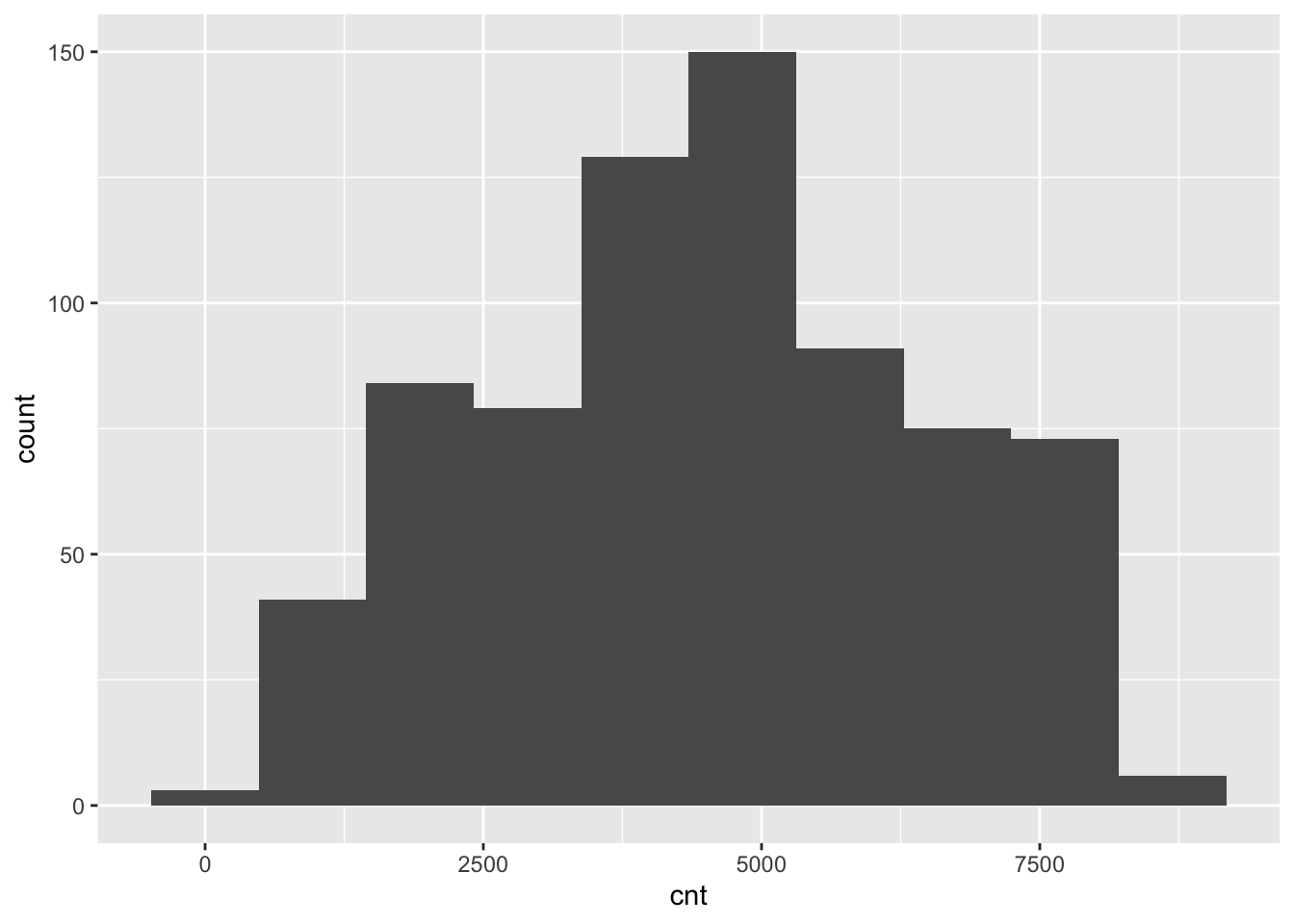
bike %>% 
  ggplot()+
  geom_histogram(aes(cnt),bins=10)

Obviously, the number of bike rentals depends strongly on weather conditions. In the following plot we represent cnt as a function of atemp and windspeed, specifying a scale color from yellow to dark blue with 12 levels:

bike %>% 
  ggplot()+
  geom_point(aes(x=atemp,y=windspeed,col=cnt))+
  scale_colour_gradientn(colours = rev(hcl.colors(12)))

It can be observed that the number of bike rentals increases with temperature.

2.1.1 Creation of the training and testing set: method 1

We divide the dataset into 2 subsets:

  • training set: containing 70% of the observations
  • test set: containing 30% of the observations

The procedure is done randomly by using the function sample. In order to have reproducible results, it is necessary to set the seed.

set.seed(1, sample.kind = "Rejection")
# Sample the indexes for the training observations
training_index = sample(1:nrow(bike),
                        0.70*nrow(bike),
                        replace=F) #the same unit can't be sample more than once
head(training_index)
## [1] 679 129 509 471 299 270
# Create a new dataframe selecting the training observations
bike_training = bike[training_index,] 
head(bike_training)
##     instant     dteday season yr mnth holiday weekday workingday weathersit
## 679     679 2012-11-09      4  1   11       0       5          1          1
## 129     129 2011-05-09      2  0    5       0       1          1          1
## 509     509 2012-05-23      2  1    5       0       3          1          2
## 471     471 2012-04-15      2  1    4       0       0          0          1
## 299     299 2011-10-26      4  0   10       0       3          1          2
## 270     270 2011-09-27      4  0    9       0       2          1          2
##         temp    atemp      hum windspeed casual registered  cnt
## 679 0.361667 0.355413 0.540833  0.214558    709       5283 5992
## 129 0.532500 0.525246 0.588750  0.176000    664       3698 4362
## 509 0.621667 0.584612 0.774583  0.102000    766       4494 5260
## 471 0.606667 0.573875 0.507917  0.225129   2846       4286 7132
## 299 0.484167 0.472846 0.720417  0.148642    404       3490 3894
## 270 0.636667 0.574525 0.885417  0.118171    477       3643 4120
# Create a new test dataframe omitting the training observations
bike_test = bike[-training_index,]
head(bike_test)
##    instant     dteday season yr mnth holiday weekday workingday weathersit
## 10      10 2011-01-10      1  0    1       0       1          1          1
## 12      12 2011-01-12      1  0    1       0       3          1          1
## 13      13 2011-01-13      1  0    1       0       4          1          1
## 14      14 2011-01-14      1  0    1       0       5          1          1
## 17      17 2011-01-17      1  0    1       1       1          0          2
## 23      23 2011-01-23      1  0    1       0       0          0          1
##         temp     atemp      hum windspeed casual registered  cnt
## 10 0.1508330 0.1508880 0.482917  0.223267     41       1280 1321
## 12 0.1727270 0.1604730 0.599545  0.304627     25       1137 1162
## 13 0.1650000 0.1508830 0.470417  0.301000     38       1368 1406
## 14 0.1608700 0.1884130 0.537826  0.126548     54       1367 1421
## 17 0.1758330 0.1767710 0.537500  0.194017    117        883 1000
## 23 0.0965217 0.0988391 0.436522  0.246600    150        836  986

The test set will be used to tune the model, i.e. to choose the best value of the tuning parameter (the number of neighbors) which minimizes the test error.

2.1.2 Implementation of KNN regression with \(k=1\)

The function used to implement KNN regression is knn.reg from the FNN package (see ?knn.reg). We start by considering the case when \(k=1\), corresponding to the most flexible model, when only one neighbor is considered.

In the argument train and test of the knn.reg function it is necessary to provide the 3 regressors from the training and test dataset. It would be possible to create two new objects (dataframes) containing this selection of variables. In this case however we select directly the necessary variables from the existing dataframes (bike_training and bike_test) by using the function select from the dplyr package. Finally, the arguments y and k refer to the training response variable vector and the number of neighbors, respectively.

KNNpred1 = knn.reg(train = dplyr::select(bike_training,atemp,windspeed,hum),
                   test = dplyr::select(bike_test,atemp,windspeed,hum),
                   y = bike_training$cnt,
                   k = 1)

The object KNNpred1 contains different objects

names(KNNpred1)
## [1] "call"      "k"         "n"         "pred"      "residuals" "PRESS"    
## [7] "R2Pred"

We are in particular interested in the object pred which contains the predictions \(\hat y_0\) for the test observations. It is then possible to compute the test mean square error (MSE): \[ \text{mean}(y_0-\hat y_0)^2 \] where average is computed over all the obsevations in the test set.

# Compute the MSE
mean((bike_test$cnt - KNNpred1$pred)^2)
## [1] 2557907

It is also possible to plot observed and predicted values. To do this we first create a new dataframe containing the observed values (\(y_0\)) and the KNN predictions (\(\hat y_0\)):

pred_df_k1 = data.frame(obs=bike_test$cnt,
                        pred=KNNpred1$pred)
head(pred_df_k1)
##    obs pred
## 1 1321 1605
## 2 1162  959
## 3 1406 1550
## 4 1421 1746
## 5 1000 1450
## 6  986 1538

Then we represent graphically the observed and predicted values and assign to the points a color given by the values of the squared error:

pred_df_k1 %>% 
  ggplot() +
  geom_point(aes(x=obs,y=pred,col=(obs-pred)^2)) +
  scale_color_gradient(low="blue",high="red")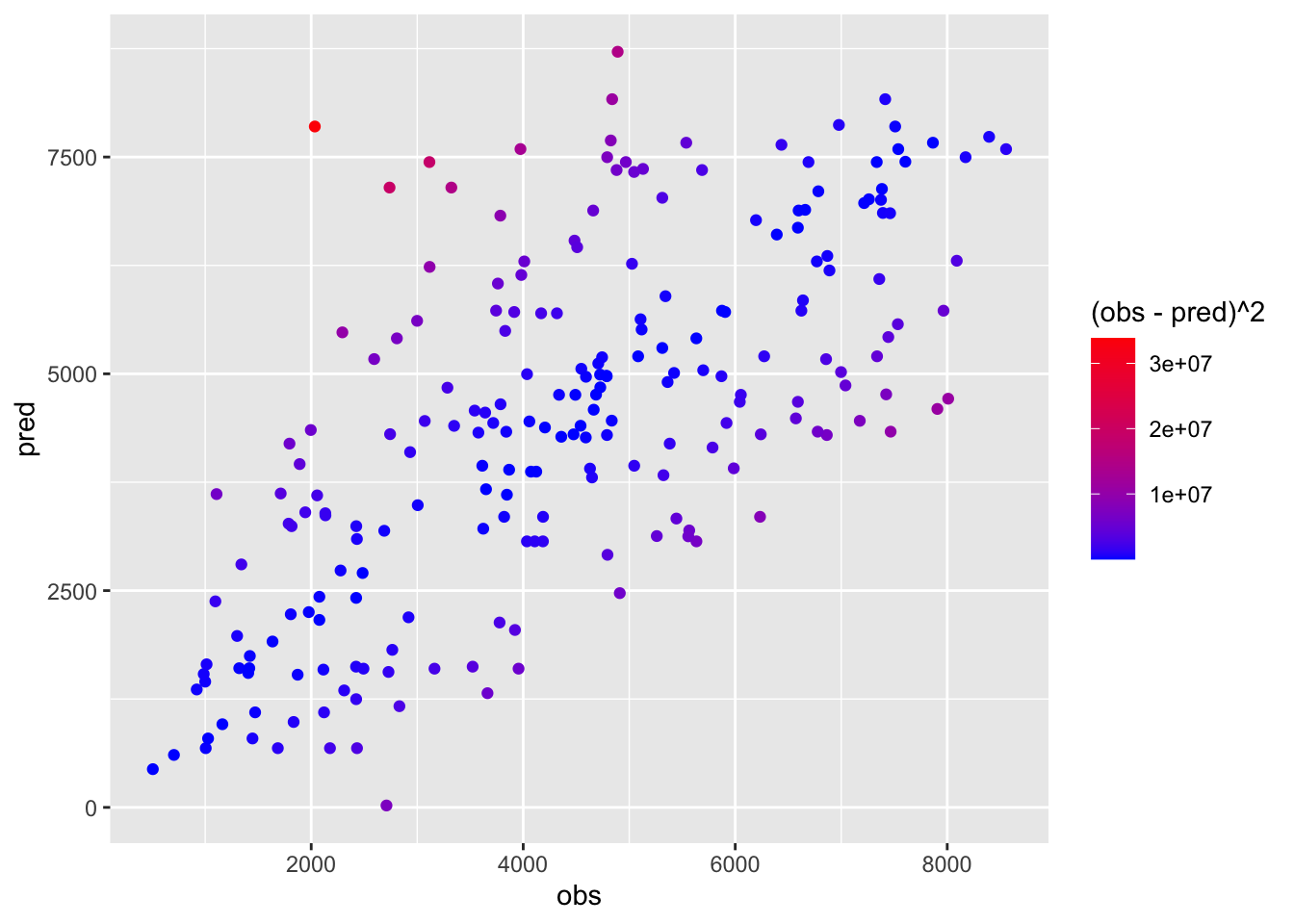

Blue observations are characterized by a smaller squared error meaning that predictions are close to observed values.

2.1.3 Implementation of KNN regression with different values of \(k\)

We now use a for loop to implement automatically the KNN regression for different values of \(k\) (in particular we consider the values 1, 10, 25, 50,100, 200, and 500). Each step of the loop, indexed by a variable i, considers a different value of \(k\). We want to save in a vector all the values of the test MSE.

# Create an empty vector where values of the MSE will be saved
mse_vec = c()
# Create a vector with the values of k
k_vec = c(1, 10, 25, 50, 100, 200, 500)

# Start the for loop
for(i in 1:length(k_vec)){
  
  # Run KNN
  KNNpred = knn.reg(train = dplyr::select(bike_training,atemp, windspeed,hum),
                     test = dplyr::select(bike_test,atemp, windspeed,hum),
                     y = bike_training$cnt,
                     k = k_vec[i])
  # Save the MSE
  mse_vec[i] = mean((bike_test$cnt-KNNpred$pred)^2)
  
}

The value of the test MSE are the following:

mse_vec
## [1] 2557907 1615815 1654941 1760180 2012120 2395182 3952574

It is useful to plot the values of the test MSE as a function of \(k\):

plot(k_vec,mse_vec,type="b")

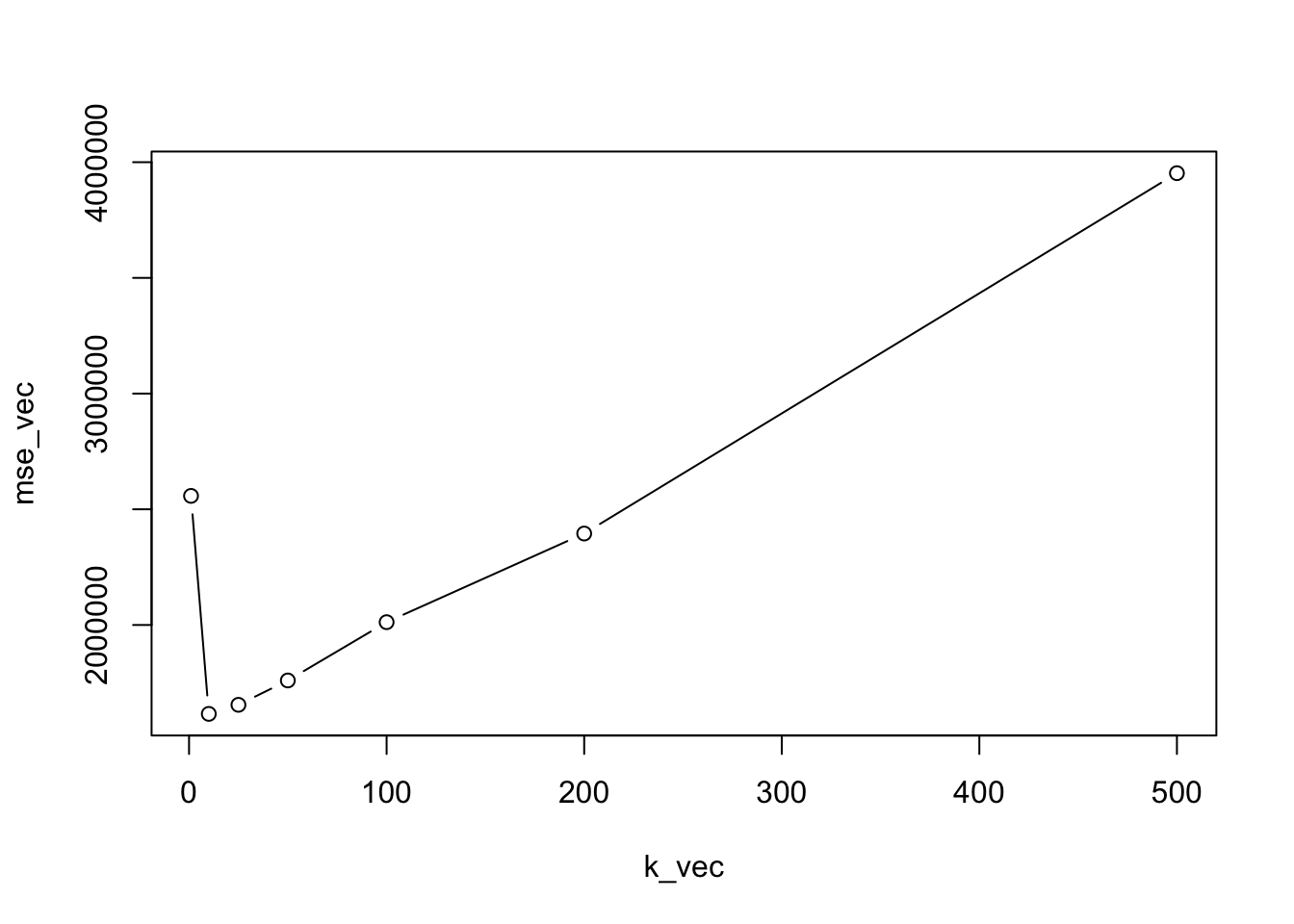
Note the U-shape of the plotted line which is typical of the test error.

The value of \(k\) which minimizes the MSE is in position 2 and is given by \(k\) equal to 10:

# Smallest MSE
MSE_KNN = min(mse_vec)
MSE_KNN
## [1] 1615815
# Its position
which.min(mse_vec)
## [1] 2
# Corresponding value of k
k_vec[which.min(mse_vec)]
## [1] 10

2.1.4 Comparison of KNN with the multiple linear model

We consider for the same set of data also the multiple linear model with 3 regressors: \[ Y = \beta_0+\beta_1 X_1+\beta_2 X_2+\beta_3 X_3 +\epsilon \]

This can be implemented by using the lm function applied to the training set of data:

lm_bike = lm(cnt ~ atemp+windspeed+hum, data=bike_training)
summary(lm_bike)
## 
## Call:
## lm(formula = cnt ~ atemp + windspeed + hum, data = bike_training)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4916.6 -1060.8   -23.3  1071.1  4341.7 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   3791.4      406.5   9.327  < 2e-16 ***
## atemp         7447.4      397.8  18.722  < 2e-16 ***
## windspeed    -4292.0      844.3  -5.084 5.22e-07 ***
## hum          -3148.6      463.8  -6.788 3.19e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1408 on 507 degrees of freedom
## Multiple R-squared:  0.4594,	Adjusted R-squared:  0.4562 
## F-statistic: 143.6 on 3 and 507 DF,  p-value: < 2.2e-16

The corresponding predictions and test MSE can be obtained as follows by making use of the predict function:

predlm = predict(lm_bike,newdata = bike_test)
MSE_lm = mean((bike_test$cnt-predlm)^2)
MSE_lm
## [1] 2119593

Note that the test MSE of the linear regression model is higher than the KNN MSE with \(k=10\).

2.1.5 Comparison of KNN with the multiple linear model with quadratic terms

We extend now the previous linear model by including quadratic terms of the regressors: \[ Y = \beta_0+\beta_1 X_1+\beta_2 X_2+\beta_3 X_3 + \beta_4 X_1^2 + \beta_5 X_2^2 + \beta_6 X_3^2+\epsilon \]

This is still a linear model in the parameters (not in the variables). Polynomial regression models are able to produce non-linear fitted functions.

This model can be implemented by using the poly function (with degree=2 in this case) in the formula specification. This specifies a model including \(X\) and \(X^2\).

lm_bike2 = lm(cnt ~ poly(atemp,2) +
                    poly(windspeed,2)+
                    poly(hum,2), data=bike_training)

As before we compute the test MSE:

predlm2 = predict(lm_bike2,newdata = bike_test)
MSE_lm2 = mean((bike_test$cnt-predlm2)^2)
MSE_lm2
## [1] 1614600

2.1.6 Final comparison

We can now compare the MSE of the best KNN model and of the 2 linear regression models:

MSE_KNN
## [1] 1615815
MSE_lm
## [1] 2119593
MSE_lm2
## [1] 1614600

Results show that the multiple linear regression model has the worst performance. The polynomial model and the KNN with \(k=10\) have a similar performance.

2.2 KNN for classification problems

For KNN classification we will use the iris dataset which is included in R (see ?iris). It contains the measurements in centimeters of the variables sepal length and width and petal length and width, respectively, for 50 flowers from each of 3 species of iris. The species are Iris setosa, versicolor, and virginica.

glimpse(iris)
## Rows: 150
## Columns: 5
## $ Sepal.Length <dbl> 5.1, 4.9, 4.7, 4.6, 5.0, 5.4, 4.6, 5.0, 4.4, 4.9, 5.4, 4.…
## $ Sepal.Width  <dbl> 3.5, 3.0, 3.2, 3.1, 3.6, 3.9, 3.4, 3.4, 2.9, 3.1, 3.7, 3.…
## $ Petal.Length <dbl> 1.4, 1.4, 1.3, 1.5, 1.4, 1.7, 1.4, 1.5, 1.4, 1.5, 1.5, 1.…
## $ Petal.Width  <dbl> 0.2, 0.2, 0.2, 0.2, 0.2, 0.4, 0.3, 0.2, 0.2, 0.1, 0.2, 0.…
## $ Species      <fct> setosa, setosa, setosa, setosa, setosa, setosa, setosa, s…
summary(iris)
##   Sepal.Length    Sepal.Width     Petal.Length    Petal.Width   
##  Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100  
##  1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300  
##  Median :5.800   Median :3.000   Median :4.350   Median :1.300  
##  Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199  
##  3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800  
##  Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500  
##        Species  
##  setosa    :50  
##  versicolor:50  
##  virginica :50  
##                 
##                 
##

The variable Species is the response categorical variables with 3 categories.

As usual we start with visualizing the data with a plot. In this case we represent Species as a function of Sepal.Length and Sepal.Width:

iris %>% 
  ggplot()+
  geom_point(aes(Sepal.Length, Sepal.Width,col=Species))+
  geom_smooth(aes(Sepal.Length, Sepal.Width,col=Species))
## `geom_smooth()` using method = 'loess' and formula 'y ~ x'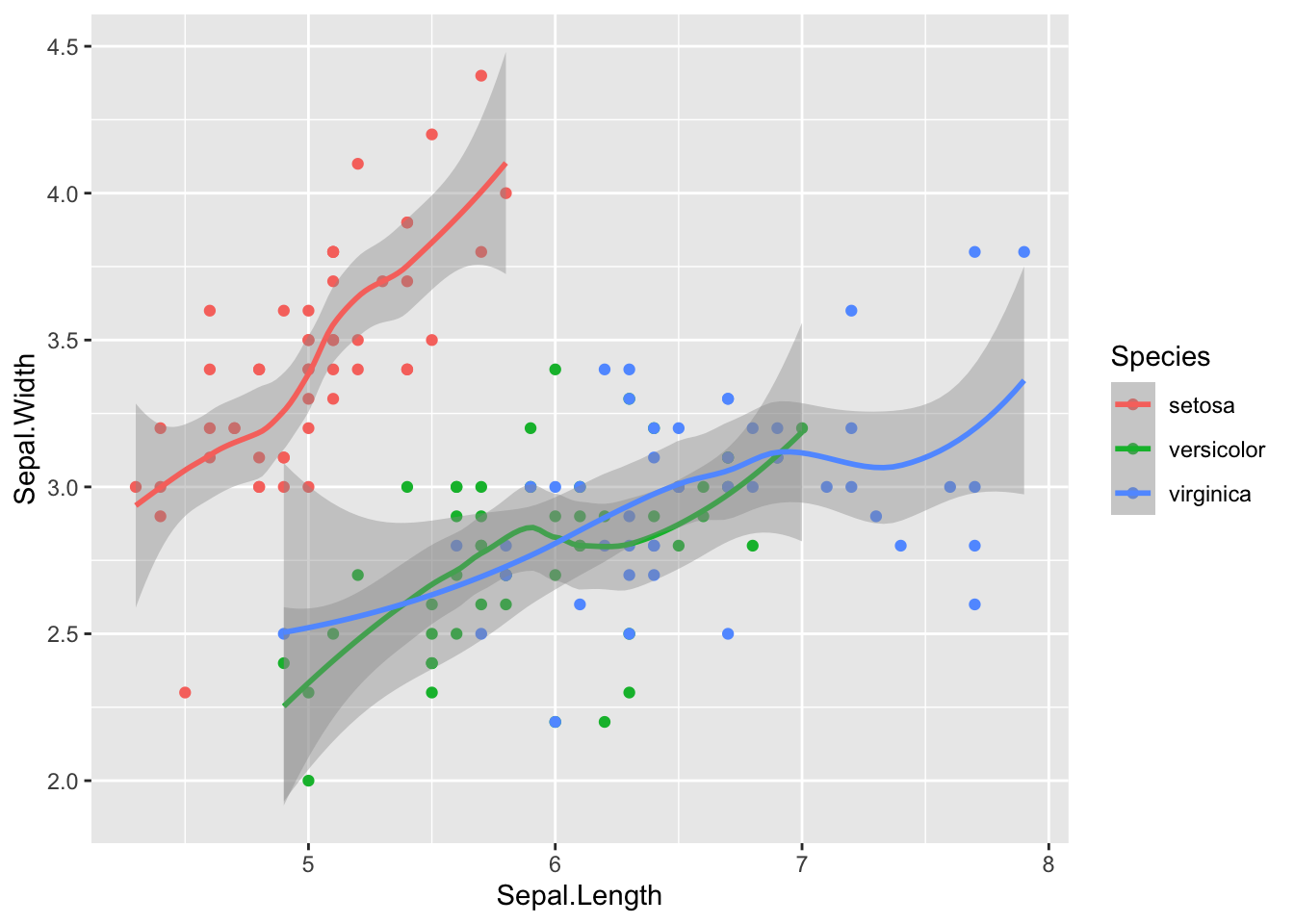

The following plot instead considers Species as a function of Petal.Length and Petal.Width by using separate plots:

iris %>% 
  ggplot()+
  geom_point(aes(Petal.Length, Petal.Width,col=Species))+
  facet_wrap(~Species)

We split the dataset into 2 subsets:

  • training set: containing 70% of the observations
  • test set: containing 30% of the observations

The procedure is done randomly by using the function sample. In order to have reproducible results, it is necessary to set the seed.

set.seed(1, sample.kind="Rejection")
# sample a vector of indexes/positions 
training_index = sample(1:nrow(iris),0.7*nrow(iris))
training_index
##   [1]  68 129  43  14  51  85  21 106  74   7  73  79  37 105 110  34 143 126
##  [19]  89  33  84  70 142  42  38 111  20  28 124  44  87 149  40 121  25 119
##  [37]  39 146 127   6  24  32 147   2  45  18  22  78 102  65 115 120 100  75
##  [55]  81  13 118 132  48  93  23 130  29  95 104 123  92 131 134 144  31  17
##  [73] 140  91  64  60 113 135  10   1 148  59  26  15  58  88 136 112  77  53
##  [91]  12 114  76  61 145  86  94  83  19 150  35  98  71 101 108
iris_training = iris[training_index,]
iris_test = iris[-training_index,]

2.2.1 KNN classification with \(k=1\)

We now implement KNN classification with \(k=1\) by using the knn function from the class package (see ?knn). Note that there are two functions both named knn in the class and FNN package. In order to specify that we want to use the function in the class package we use class::knn. As before we have to specify the regressor dataframe for the training and test observations and the response variable vector (cl). The option prob makes it possible to get the probability of the majority class.

out1 = class::knn(train = dplyr::select(iris_training,-Species),
           test = dplyr::select(iris_test,-Species),
           cl = iris_training$Species,
           k = 1, #just 1 neighbors
           prob=T) 

out1
##  [1] setosa     setosa     setosa     setosa     setosa     setosa    
##  [7] setosa     setosa     setosa     setosa     setosa     setosa    
## [13] setosa     setosa     setosa     versicolor versicolor versicolor
## [19] versicolor versicolor versicolor versicolor versicolor versicolor
## [25] versicolor versicolor versicolor versicolor versicolor versicolor
## [31] versicolor versicolor virginica  versicolor virginica  virginica 
## [37] virginica  virginica  virginica  virginica  virginica  virginica 
## [43] virginica  versicolor virginica 
## attr(,"prob")
##  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [39] 1 1 1 1 1 1 1
## Levels: setosa versicolor virginica

Predictions are contained in the out1 object; in this case all the probabilities are equal to one because just 1 neighbor is considered (and thus the majority class will have a 100% probability).

To compare predictions \(\hat y_0\) and observed values \(y_0\) it is useful to create the confusion matrix which is a double-entry matrix with predicted and observed categories and the corresponding frequencies:

table(out1, iris_test$Species)
##             
## out1         setosa versicolor virginica
##   setosa         15          0         0
##   versicolor      0         17         2
##   virginica       0          0        11

In the main diagonal we can read the number of correctly classified observations. Outside from the main diagonal we have the number of missclassified observations. In this case we have 1 flower for which the species prediction is versicolor but actually the flower is of the virginica flower.

The percentage test error rate is computed as follows:

#test error rate
mean(out1!=iris_test$Species)*100
## [1] 4.444444

In this case we see that 4.44% of the observations are missclassified.

2.2.2 KNN classification with different values of \(k\)

We now consider different values for \(k\). In particular we run the KNN algorithm for all the values of \(k\) from 1 to 100 and save the test error rate in a vector:

maxK = 100
errorrate = c() 
for(i in 1:maxK){
  # KNN classification
  out = class::knn(train = dplyr::select(iris_training,-Species),
                    test = dplyr::select(iris_test,-Species),
                    cl = iris_training$Species,
                    k = i,
                    prob=T) 
  
  # Test error rate (save in the i-th position of the vector)
  errorrate[i] = mean(out!=iris_test$Species)
}

To plot the test error rate as a function of \(k\) by using ggplot we can proceed as follows. First we need to create a new dataframe containing the values of \(k\) and of the error rate:

outfinal = data.frame(k=1:maxK,testER = errorrate)

Then we plot the data

outfinal %>% 
  ggplot() +
  geom_line(aes(x=k,y=testER))

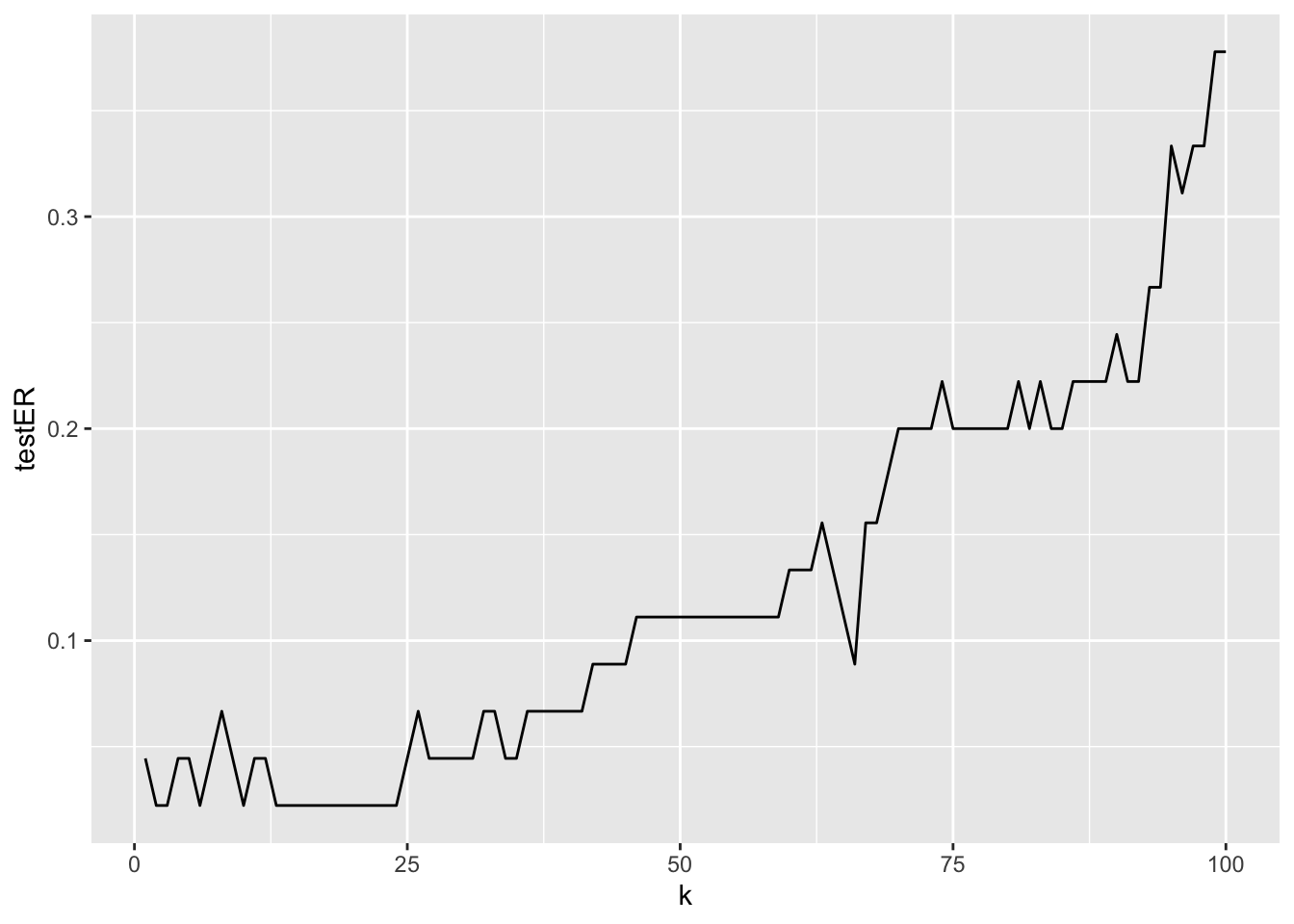
The best value of \(k\) which minimizes the test error rate is given by \(k=\) 2:

which.min(errorrate) 
## [1] 2

Note that there are other bigger values of \(k\) which provide the same lowest error rate (0.0222222):

which(errorrate==min(errorrate))
##  [1]  2  3  6 10 13 14 15 16 17 18 19 20 21 22 23 24

This gives us the possibility to choose a different level of flexibility without worsening the test error.

2.3 Exercises Lab 1

2.3.1 Exercise 1

Use the Weekly data set contained in the ISLR package. See ?Weekly.

library(ISLR)
library(tidyverse)
?Weekly
head(Weekly)
##   Year   Lag1   Lag2   Lag3   Lag4   Lag5    Volume  Today Direction
## 1 1990  0.816  1.572 -3.936 -0.229 -3.484 0.1549760 -0.270      Down
## 2 1990 -0.270  0.816  1.572 -3.936 -0.229 0.1485740 -2.576      Down
## 3 1990 -2.576 -0.270  0.816  1.572 -3.936 0.1598375  3.514        Up
## 4 1990  3.514 -2.576 -0.270  0.816  1.572 0.1616300  0.712        Up
## 5 1990  0.712  3.514 -2.576 -0.270  0.816 0.1537280  1.178        Up
## 6 1990  1.178  0.712  3.514 -2.576 -0.270 0.1544440 -1.372      Down
glimpse(Weekly)
## Rows: 1,089
## Columns: 9
## $ Year      <dbl> 1990, 1990, 1990, 1990, 1990, 1990, 1990, 1990, 1990, 1990, …
## $ Lag1      <dbl> 0.816, -0.270, -2.576, 3.514, 0.712, 1.178, -1.372, 0.807, 0…
## $ Lag2      <dbl> 1.572, 0.816, -0.270, -2.576, 3.514, 0.712, 1.178, -1.372, 0…
## $ Lag3      <dbl> -3.936, 1.572, 0.816, -0.270, -2.576, 3.514, 0.712, 1.178, -…
## $ Lag4      <dbl> -0.229, -3.936, 1.572, 0.816, -0.270, -2.576, 3.514, 0.712, …
## $ Lag5      <dbl> -3.484, -0.229, -3.936, 1.572, 0.816, -0.270, -2.576, 3.514,…
## $ Volume    <dbl> 0.1549760, 0.1485740, 0.1598375, 0.1616300, 0.1537280, 0.154…
## $ Today     <dbl> -0.270, -2.576, 3.514, 0.712, 1.178, -1.372, 0.807, 0.041, 1…
## $ Direction <fct> Down, Down, Up, Up, Up, Down, Up, Up, Up, Down, Down, Up, Up…
  1. How many data are available for each year? What is the temporal frequency of the data?
  2. Produce the boxplot which represents Today returns as a function of Year. Do you observe any difference across years?
  3. Provide the scatterplot matrix for Today and Lag1. Do you observe strong correlations?
  4. Plot the distribution of the variable Direction (with a barplot) for year 2010. Use percentage and not absolute frequencies.
  5. Plot the distribution of the variable Direction (with a barplot) separately for all the available years. Use percentage and not absolute frequencies. Attention: percentages should be computed by considering the number of observations available for each year and not the total number of observations.
  6. Consider as training set the data available from 1990 to 2008 with Lag1, Lag2 and Lag3 as predictors and Direction as response variable. How many data do you have in the training and test datasets?
  7. Compute the test error rate for the KNN classifier with \(k=1\).
  8. Compute the test error rate for the KNN classifier for \(k\) from 1 to 50. Use the for loop and save the results in a vector.
  9. Plot the error rate as a function of \(k\). Which value of \(k\) do you suggest to use?

2.3.2 Exercise 2

In this exercise we will develop a classifier to predict if a given car gets high or low gas mileage using the Auto dataset. The data are included in the ISLR package (see Auto).

library(ISLR)
?Auto
  1. Explore the data.
  2. Create a binary variable, named mpg01, that is equal to 1 if mpg is bigger than its median, and a 0 otherwise. Add the variable mpg01 to the existing dataframe. How many observations are classified with 1?
  3. Study how cylinders, weight, displacement and horsepower vary according to the factor mpg01.
  4. Consider as training set the cars released in even years. Use as regressor the following variables: cylinders, weight, displacement and horsepower. How many data do you have in the training and test datasets? Suggestion: use the modulus operator %% to check if a year is even (e.g. 4%%2 and 5%%2).
  5. Run KNN with \(k=1\). Which is the value of the test error rate?
  6. Perform KNN with \(k\) from 1 to 50 using a for loop.
  7. Plot the test error rate as a function of \(k\).
  8. For which value of \(k\) do we get the lowest test error rate?

2.3.3 Exercise 3

Consider the Carseats data set available from the ISLR library. Read the help to understand which variables are available (and if they are qualitative or quantitative).

library(ISLR)
library(tidyverse)
?Carseats

  1. Plot Sales as a function of Price.

  2. Split the dataset in two separate sets: the training set with 70% of the observations and 30% for the test set. Use 14 as seed.

  3. Fit a regression model to predict Sales using Price.

  4. Compute the MSE for the model with Sales as dependent variable and Price as regressor.

  5. Now implement KNN regression using the same variables you used for the linear regression model above. Consider all the values of \(k\) between 1 and 200. Which is the best value of \(k\) in terms of validation error?

  6. Compare the regression model and the KNN regression (with the chosen value of \(k\)). Which is the best model?

2.3.4 Exercise 4

This exercise uses simulated data.

  1. Use the rnorm function to create a vector named x containing \(n=100\) values simulated from a N(0,1) distribution. Set the seed equal to 1. These values represent the predictor’s values.

  2. Use the rnorm function to create a vector named eps containing \(n=100\) values simulated from a N(0,0.025) distribution (variance=0.025). Set the seed equal to 2. These values represent the error’s values (\(\epsilon\)).

  3. Using x and eps, obtain a vector y (the response values) according to the following (true) model. Create also a data frame containing the values of x and y. \[ Y = -1+0.5X+\epsilon \]

    1. Which is the length of y? What are the values of \(\beta_0\) and \(\beta_1\) in this model?

    2. Plot the simulated data.

    3. Fit a least squares linear model to predict y using x. Compare the true values of the parameters with the corresponding estimates.

    4. Display the least squares line in the scatterplot obtained before. Add to the plot also the straight line corresponding to the true model (suggestion: use geom_abline).

  4. Fit a polynomial regression model to predict y using x and x^2. Is there evidence that the quadratic term improves the model fit?

  5. Repeat points 1.-3. changing the data generation process in such a way that there is less noise in the data (the values of x don’t change). Consider for example a variance for the error equal to 0.001 (use a new name for the response data frame, for example data2). Describe your results.

  6. Repeat points 1.-3. changing the data generation process in such a way that there is more noise in the data (the values of x don’t change). Consider for example a variance for the error equal to 1 (use a new name for the response data, for example data3). Describe your results.