4 Exponential Smoothing Methods

Smoothers: technique to separate the signal and the noise as much as possible

A smoother acts as a fitter to obtain an “estimate” for the signal. See figure 4.1.

We have seen some smoothers:

  • moving average
  • centered moving averages
  • Hanning filter
  • moving medians

4.1 Consider the “constant” process:

\(y_{t} = \mu + \epsilon_{t}; \space \epsilon_{t} \sim(0, \sigma_{\epsilon}^{2})\)

We can “smooth” this by replacing the current observation with the best estimate for \(\mu \to \hat \mu\)

We know the least squares estimate of \(\mu\) is:

\(\hat \mu = \frac{1}{T} \sum_{t=1}^{T} y_{t} \space (\text{min SSE } \mu = \sum_{t=1}^{T}(y_{t}-\mu)^{2}\)

See figure 4.2 and figure 4.3

Why does 4.3 not work? The smoother does not react quickly enough to changes in the process.

We could use a simple moving average, because it allows us to attach less weight to earlier observations, making the smoother “faster-to-react” to changes.

\(M_{T} = \frac{1}{N}[y_{t} + y_{t-1} + ... + y_{T+N-1}] = \frac{1}{N} \sum_{t = T-N+1}^{N} y_{t}\)

If span N is small, the smoother reacts faster. However, recall that \(var(M_{T}) = \frac{\sigma^{2}}{N}\)

So, as span decreases, the smoother reacts faster, but is more “jittery” (variance is larger).

Are observations in \(M_{T}\) correlated? Yes! Successive moving averages contain the same N-1 observations

\(\therefore\) the ACF of MA that are k-lags apart is: \[ \rho_{k} = \begin{cases} 1-\frac{\lvert k \rvert}{N}; \space k \lt N \\ 0; \space k \ge N \end{cases} \]

4.2 First-Order Exponential Smoothing

Let \(\lvert \Theta \rvert \lt 1\) be a discounted factor. Then, to discount past observations in a geometrically decreasing fashion, we can create an exponentially weighted smoother as follows:

\[ y_{T} + \theta y_{T-1} + \theta^{2}y_{T-2} + ... + \theta^{T-1}y_{1} = \sum_{t=0}^{T-1}\theta^{t}y_{T-t} \]

Note that weights do not add up to 1.

\[ \sum_{t=0}^{T-1}\theta^{t} = \frac{1-\theta^{t}}{1-\theta} \]

So to adjust the smoother, multiply by \(\frac{1-\theta}{1-\theta^{t}}\)

\[ \text{If } T \to \infty, \space \sum_{t=0}^{T-1}\theta^{t} = \frac{1-\theta^{t}}{1-\theta} \to \frac{1}{1-\theta} \]

So, multiply smoother by \(1-\theta\)

\(\therefore\) First order exponential smoother is:

\[ \tilde y_{T} = (1-\theta) \sum_{t=0}^{T-1} \theta^{t} y_{T-t} \\ = (1-\theta)[y_{T} + \theta y_{t-1} + \theta^{2}y_{T-2}+...+\theta^{T-1}y_{1}] \\ =(1-\theta)y_{T} + (1-\theta)[\theta y_{T-1}+\theta^{2}y_{T-2} + ...+ \theta^{T-1}y_{1}] \\ \to \tilde y_{T} = (1-\theta) y_{T} + (1-\theta)\theta[y_{T-1}+\theta y_{T-2}+...+\theta^{T-2}y_{1}] \\ = (1-\theta) y_{t} + \theta \{ (1-\theta)[y_{T-1} + \theta^{1}y_{T-2}+...+\theta^{T-2}y_{1}]\} \\ \therefore \tilde y_{T} = (1-\theta)y_{T} + \theta \tilde y_{T-1} \]

This is a linear combination of the current observation (\(y_{T}\)) and the smoother observation at the previous time unit (\(y_{T-1}\)).

  • Linear combination of the current observation (\(y_{t}\)) and the discounted sum of all previous observations.

Setting \(\lambda = 1 - \theta\), can rewrite the first-order exponential smoother as:

\[ \tilde y_{T} = \lambda y_{T}+(1-\lambda)\tilde y_{T-1}, \text{ where} \\ \lambda = \text{discount factor = weight put on the last observation; and } \\ (1-\lambda) = \text{ weight put on the smoothed value of the previous observations} \]

Questions:

  • How to choose \(\lambda\)?
  • What about \(\tilde y_{0}\)?

A. The initial value of \(\tilde y_{0}\)

\[ \text{Recall } \tilde y_{T} = \lambda y_{T} + (1-\lambda)\tilde y_{T-1} \\ \text{So, } \tilde y_{1} = \lambda y_{1} + (1-\lambda)\tilde y_{0} \\ \tilde y_{2} = \lambda y_{2} + (1-\lambda)\tilde y_{0} \\ = \lambda y_{2} + (1-\lambda)[\lambda y_{1} + (1-\lambda)\tilde y_{0}] \\ = \lambda(y_{2}+(1-\lambda)y_{1}) + (1-\lambda)^{2} \tilde y_{0} \\ \tilde y_{3} = \lambda y_{3} + (1-\lambda)\tilde y_{2} \\ = \lambda(y_{3} + (1-\lambda)y_{2} + (1-\lambda)^{2}y_{1}) + (1-\lambda)^{3} \tilde y_{0} \\ ... \\ \therefore \tilde y_{T} = \lambda(y_{T} + (1-\lambda)y_{T-1}+...+(1-\lambda)^{T-1}y_{1}) + (1-\lambda)^{T}\tilde y_{0} \\ \text{Note: If } T \text{ is large, } (1-\lambda)^{T} \to 0 \\ \therefore \tilde y_{0} \text{ contributes little to } \tilde y_{T} \]

Possibilities:

  1. If process is locally constant in the beginning, take the average of a subset of available data, \(\tilde y\), and set \(\tilde y_{0} = \bar y\).
  2. If process begins to change early, set \(\tilde y_{0} = y_{1}\).

B. The value of \(\lambda\): If \(\lambda = 1 \to\) unsmoothed version of original time series, because \(\tilde y_{t} = y_{T}\).

If \(\lambda = 0\), \(\tilde y_{T} = \tilde y_{0} =\) constant!

\(\therefore\) Variance of the simple exponential smoother varies between zero (when \(\lambda = 0\)) and the variance of the original time series (when \(\lambda = 1\)).

If \(y_{i}\)’s are independent and have constant variance,

\[ var(\tilde y_{T}) = var(\lambda(y_{T} + (1-\lambda)y_{T-1}+...+(1-\lambda)^{T-1}y_{1}) + (1-\lambda)^{T}\tilde y_{0}) \\ = var(\lambda \sum_{t=0}^{\infty}(1-\lambda)^{t}y_{T-t} + (1-\lambda)^{T} \tilde y_{0}) \\ = \lambda^{2} var \sum_{t=0}^{\infty}(1-\lambda)^{t}y_{T-t} + 0 \\ = \lambda^{2} \sum_{t=0}^{\infty} (1-\lambda)^{2t} var(y_{T-t}) \\ = \lambda^{2} * var(y_{T}) \sum_{t=0}^{\infty}(1-\lambda)^{2t} \\ = \lambda^{2}*var(y_{T})*\frac{1}{1-(1-\lambda)^{2}} \\ \text{Note: sum of infinite geomentric series is:} = \frac{a_{1}}{1-r} \\ =\frac{\lambda}{2-\lambda}*var(y_{T}) \]

Usually, values of \(\lambda\) between 0.1 and 0.4 are recommended.

Measures of accuracy:

\[ MAPE = \frac{1}{T} \sum_{t=1}^{T} \lvert \frac{y_{t}-\tilde y_{t-1}}{y_{t}} \rvert * 100; \space (y_{t} \ne 0) \\ MAD = \frac{1}{T} \sum_{t=1}^{T} \lvert y_{t} - \tilde y_{t-1} \rvert \\ MSD = \frac{1}{T} \sum_{t=1}^{T}(y_{t} - \tilde y_{t-1})^{2} \]

4.3 Modeling Time Series Data

\[ \text{Let } y_{t} = f(t; \beta) + \epsilon_{t}, \text{ where} \\ \beta = \text{vector of unknown parameters, and } \\ \epsilon_{t} \sim (0, \sigma^{2}_{e}) = \text{uncorrelated errors} \]

For example, the constant-only model is: \(y_{t} = \beta_{0} + \epsilon_{t}\)

To see how the simple exponential smoother can be used for model estimation, consider \(SSE = \sum_{t=1}^{T}(y_{t} - \beta_{0})^{2}\).

We can consider a modified version of the SSE which assigns geometrically decreasing weights:

\[ SSE^{*} = \sum_{t=0}^{T-1} \theta^{t}(y_{t} - \beta_{0})^{2}; \space \lvert \theta \rvert \lt 1 \\ \]

Minimizing \(SSE^{*}\) w.r.t. \(\beta_{0}\),

\[ \frac{\delta}{\delta \beta_{0}} SSE^{*} = -2 \sum_{t=0}^{T-1} \theta^{t}(y_{T-t} - \hat \beta_{0}) = 0 \\ \to \hat \beta_{0}\sum_{t=0}^{T-1} \theta^{t} = \sum_{t=0}^{T-1} \theta^{t}y_{T-t} \\ \text{Recall } \sum_{t=0}^{T-1} \theta^{t} = \frac{1-\theta^{t}}{1-\theta}, \text{ and for large T} \\ \sum_{t=0}^{\infty} \theta^{t} = \frac{1}{1-\theta} \\ \therefore \hat \beta_{0} = \frac{1-\theta}{1-\theta^{t}} \sum_{t=0}^{T-1} \theta^{t} y_{T-t}, \text{ and for large T} \\ \hat \beta_{0} =1-\theta \sum_{t=0}^{\infty} \theta^{t} y_{T-t}\\ \text{Notice here that: }\hat \beta_{0} \text{ is } = \tilde y_{T}! \\ \therefore \text{ Exponential smoother(for constant-only model) is like a WLS!!} \\ \]

4.4 Second-Order Exponential Smoothing

Recall: \[ \tilde y_{t} = \lambda y_{T} + (1-\lambda) \tilde y_{T-1} \\ = \lambda(y_{T} + (1-\lambda)y_{T-1}+...+(1-\lambda)^{T-1}y_{1}) + (1-\lambda)^{T} \tilde y_{0} \\ = \lambda \sum_{t=0}^{\infty}(1-\lambda)^{t}y_{T-t} \\ E(\tilde y_{T}) = E(\lambda \sum_{t=0}^{\infty}(1-\lambda)^{t}y_{T-t}) \\ = \lambda \sum_{t=0}^{\infty}(1-\lambda)^{t} E(y_{T-t}) \\ \text{For model with linear trend: } y_{t} = \beta_{0} + \beta_{1}t + \epsilon_{t}; \space \epsilon_{t} \sim (0, \sigma^{2}_{\epsilon}) \\ \therefore \space E(\tilde y_{T}) = \lambda \sum_{t=0}^{\infty} (1-\lambda)^{t} E(Y_{T-t}) \\ = \lambda \sum_{t=0}^{\infty}(1-\lambda)^{t}[\beta_{0}+ \beta_{1}(T-t)] \\ = \lambda \sum_{t=0}^{\infty}(1-\lambda)^{t}(\beta_{0}+\beta_{1}T) - \lambda \sum_{t=0}^{\infty}(1-\lambda)^{t}(\beta_{1}t) \\ =(\beta_{0}+\beta_{1}T)\lambda \sum_{t=0}^{\infty} (1-\lambda)^{t} - \lambda \beta_{1} \sum_{t=0}^{\infty} (1-\lambda)^{t}t \\ \text{Now, } \sum_{t=0}^{\infty}(1-\lambda)^{t} = \frac{1}{1-(1-\lambda)} = \frac{1}{\lambda} \\ \text{and } \sum_{t=0}^{\infty}(1-\lambda)^{t}t = \frac{1-\lambda}{\lambda^{2}} \\ \therefore E(\tilde y_{T}) = (\beta_{0} + \beta_{1}T)*\lambda*\frac{1}{\lambda} - \lambda \beta_{1}*\frac{(1-\lambda)}{\lambda^{2}} \\ = (\beta_{0}+\beta_{1}T) - \frac{(1-\lambda)}{\lambda}\beta_{1} \\ \therefore E(\tilde y_{T}) = E(y_{T}) - \frac{(1-\lambda)}{\lambda} \beta_{1} \\ \text{Simple exponential smoother is a biased estimate for the linear trend model} \\ \text{Amount of bias } = E(\tilde y_{T}) - E(y_{T}) = -(\frac{1-\lambda}{\lambda})\beta_{1} \]

  1. If \(\lambda \to 1\), bias \(\to 0\)
  2. But, large value of \(\lambda\) fails to smooth out the constant pattern in the data!

So, what do we do?

Apply simple exponential smoothing to the smoothed series! That is, use second-order exponential smoother!

Let \(\tilde y_{T}^{(1)} =\) first-order smoothed exponentials, and \(\tilde y_{T}^{(2)} =\) second order smoothed exponentials.

Then, \(\tilde y_{T}^{(2)} = \lambda \tilde y_{T}^{(1)} + (1-\lambda) \tilde y_{T-1}^{(2)}\).

If the last-order exponential is biased, so is the second order! In fact \(E(\tilde y_{T}^{(2)}) = E(\tilde y_{T}^{(1)}) - \frac{1-\lambda}{\lambda} \beta_{1}\)

And, with several substitutions we can show that

\[ \text{a.) } \hat \beta_{1, T} = \frac{\lambda}{1-\lambda}(\tilde y_{T}^{(1)} - \tilde y_{T}^{(2)}) \text{, and } \\ \text{(b.0) } \hat \beta_{0, T} = \tilde y_{T}^{(1)} - T \hat \beta_{1,T} + \frac{1-\lambda}{\lambda} \hat \beta_{1,T} \\ \text{b.) } \to \hat \beta_{0,T} = (2-T*\frac{\lambda}{1-\lambda}) \tilde y_{T}^{(2)} \\ \therefore \text{ we have a predictor for } y_{T} \text{ as} \\ \hat y_{T} = \hat \beta_{0,T} + \hat \beta_{1,T}*T \\ \to \hat y_{T} = 2 \tilde y_{T}^{(1)} - \tilde y_{T}^{(2)} \]

Exercise: Shows that \(\hat y_{T}\) is an unbiased predictor of \(y_{T}\).

See R-code for Examples 4.1 and 4.2.

4.5 Higher-Order Exponential Smoothing

\[ \text{For } y_{t} = \beta_{0} + \epsilon_{t}, \space \epsilon_{t} \sim (0, \sigma_{\epsilon}^{2}) \to \text{1st-order exponential smoother} \\ \text{For } y_{t} = \beta_{0} + \beta_{1} t + \epsilon_{t}, \space \epsilon_{t} \sim (0,\sigma_{\epsilon}^{2}) \to \text{2nd-order exponential smoother} \\ \]

For n’th degree polynomial model of the forum:

\[ y_{t} = \beta_{0} + \beta_{1} t + \beta_{2} t^{2} + ... + \beta_{n} t^{n} + \epsilon_{t}, \space \epsilon_{t} \sim (0, \sigma_{\epsilon}^{2}) \]

We can use the \((n+1)\)’th-order exponential smoother to estimate the model parameters

\[ \tilde y_{T}^{(1)} = \lambda y_{T} + (1-\lambda) \tilde y_{T-1}^{(1)} \\ \tilde y_{T}^{(2)} = \lambda \tilde y_{T}^{(1)} + (1-\lambda) \tilde y_{T-1}^{(2)} \\ ... \\ \tilde y_{T}^{(n)} = \lambda \tilde y_{T}^{(n-1)} + (1-\lambda) \tilde y_{T-1}^{(n)} \]

However, even with a quadratic trend model (2nd-degree polynomial), calculations are difficult analytically. So, we would prefer to use an ARIMA model, which is the subject of the next chapter.

4.6 Forecasting

Let the \(\tau\)-step-ahead forecast note at time \(T\) be \(\hat y_{T+\tau}(T)\).

4.6.1 Constant Process

\[ y_{t} = \beta_{0} + \epsilon_{t}, \space \epsilon_{t} \sim (0, \sigma_{\epsilon}^{2}). \]

In this case, forecast for future observations is simply the current value of the exponential smoother:

\[ \to \hat y_{T+\tau}(T) = \tilde y_{T} = \lambda y_{T} + (1-\lambda) \tilde y_{T-1} \]

When \(y_{T+1}\) becomes available, we can UPDATE our forecast: \(\tilde y_{T+1} = \lambda y_{T+1} + (1-\lambda) \tilde y_{T}\)

\[ \text{Therefore, } \hat y_{T+1+\tau}(T+1) = \lambda y_{T+1} + (1-\lambda) \tilde y_{T} \\ = \lambda y_{T+1} + (1-\lambda) \hat y_{T+\tau}(T) \]

E.g. When \(\tau = 1\),

\[ \hat y_{T+2}(T+1) = \lambda y_{T+1} + (1-\lambda) \hat y_{T+1}(T) \\ = \lambda y_{T+1} + \hat y_{T+1}(T) - \lambda \hat y_{T+1}(T) \\ \text{Rearranging, we have:} \\ = \hat y_{T+1}(T) + \lambda(y_{T+1} - \hat y_{T+1}(T)) \\ \hat y_{T+1} = \text{previous forecast for current observation} \\ y_{T+1} - \hat y_{T+1}(T) = \text{forecast error node in forecast of current observation} \\ \therefore \space \hat y_{T+2}(T+1) = \hat y_{T+1}(T) + \lambda*e_{T+1}(1) \\ \lambda*e_{T+1}(1) = \text{one-step ahead forecast error} \\ \therefore \space \text{Forecast for next observation} = \\ \text{previous forecast for current observation } + \\ \text{fraction of forecast error in forecasting current observation!} \]

So .. \(\lambda\)(discount factor) determines HOW FAST our forecast reacts to the forecast error

Large \(\lambda \to\) fast reaction to forecast error, BUT large \(\lambda\) also \(\to\) forecast reacts fast to random fluctuations!

So … how to choose \(\lambda\)?

Choose the \(\lambda\) that minimizes the sum of squared forecast errors!!

\[ SSE(\lambda) = \sum_{t=1}^{T} e_{t}^{2}(1) \\ \text{ (calculate for various values of } \lambda \text{)} \]

We need to always supply intervals for our forecasts.

A \((100 - \alpha)\)% prediction interval for any lead time \(\tau\) is:

\[ \tilde y_{T} \pm z_{\frac{\alpha}{2}} * \hat \sigma_{\epsilon} \text{, where } \\ \tilde y_{T} = \text{1st-order exponential smoother;} \\ z_{\frac{\alpha}{2}} = \text{the relevant value from the standard normal distribution} \\ \text{and } \hat \sigma_{\epsilon}^{2} = \text{standard error of the forecast errors} \]

This gives constant prediction intervals. NOT GOOD

Example 4.4: Note the \(\hat y_{T+\tau}(7)\) and prediction intervals for the forecasts: all constant!

4.6.2 Example 4.5: First-order exponential smoother for a model with LINEAR TREND.

Problem: SSE decreases as \(lambda\) increases \(\to\) data are autocorrelated! See ACF

\(\therefore \space\) ARIMA may be better. Chapter 6!

OR, try 2nd-order exponential smoothing. And try

  • 1-step-ahead-forecasts, 2-step-ahead-forecasts, …; OR
  • 1-step-ahead-forecasts

The latter performs better

4.6.3 Standard error of forecasts, \(\hat \sigma_{e}\)

Assuming the model is correct (and constant in time) define 1-step-ahead forecast error as:

\[ e_{T}(1) = y_{T} - \hat y_{T}(T-1) \\ \text{Then, } \hat \sigma_{e}^{2} = \frac{1}{T} \sum_{t=1}^{T} e^{2}_{t}(1) = \frac{1}{T} \sum_{t=1}^{T}[y_{t} - \hat y_{t}(t-1)]^{2} \\ \text{And } \sigma^{2}_{e}(\tau) = \tau \text{-step-ahead forecast variance} \\ = \frac{1}{T-\tau+1} \sum_{t=\tau}^{T} e^{2}_{1}(\tau) \text{(not same as } e_{\tau}^{2}(1)\text{)} \]

4.6.4 Adaptive updating of \(\lambda\), the discount factor

Trigg-Leach Method:

\[ \hat y_{T} = \lambda_{T}y_{T} + (1-\lambda) \tilde y_{t-1} \]

Let Mean Absolute Deviation, \(\Delta\), be defined as:

\[ \Delta = E(\lvert e - E(e) \rvert ) \]

Then, the estimate of MAD is:

\[ \hat \Delta_{T} = \delta \vert e_{T}(1)\vert + (1-\delta) \hat \Delta_{T-1} \]

Also define the smoothed error as:

\[ Q_{T} = \delta e_{T}(1)+(1-\delta)Q_{T-1} \]

Finally, let the “tracking signal” be defined as:

\[ \frac{Q_{T}}{\hat \Delta_{T}} \]

Then, setting \(\lambda_{T} = \vert \frac{Q_{T}}{\hat \Delta_{T}} \vert\) will allow for automatic updating of the discount factor.

Example 4.6: see R code

4.6.5 Model Assessment

Plot ACF of forecast errors. If sample ACF exceeds \(\pm 2\) standard error, it violates the assumption of uncorrelated errors.

4.7 Exponential Smoothing for Seasonal Data

4.7.1 Additive seasonal model

\[ \text{Let } y_{t} = L_{t} + S_{t} + \epsilon_{t} \text{, where } \\ L_{t} = \beta_{0} + \beta_{1}t = \text{level and trend component} = \text{ permenant component} \\ S_{t} = \text{ seasonal component, with } \\ S_{t} = S_{t+s} = S_{t+2s} = \space ... \text{ for }t=1,2,..,s-1, \text{ where} \\ s = \text{length of season, or period of cycles; } \\ \text{and} \\ \epsilon_{t} = \text{random component, } \sim (0, \sigma^{2}_{\epsilon}) \\ \text{Also, } \sum _{t=1}^{s}S_{t} = 0 \to \text{seasonal adjustments add to zero during one season} \]

To forecast future observations; we use first-order exponential smoothing:

Assuming that the current observations, \(y_{T}\) is obtained, we would like to make \(\tau\)-step-ahead forecasts.

The principal idea is to update estimates of \(\hat L, \hat \beta_{1,T},\) and \(\hat S_{T}\), so that \(\tau\)-step-ahead forecast of \(y\) is:

\[ \hat y _{T+\tau}(T) = \hat L_{T} + \hat \beta_{1,T} * \tau + \hat S_{T}(\tau - s) \\ \text{Here, } \hat L_{T} = \lambda_{1}(y_{T} - \hat S_{T-s})+(1+\lambda_{1})(\hat L_{T-1} + \hat \beta_{1, T-1}) \\ y_{T} - \hat S_{T-s} = \text{current value of }L_{T} \\ \hat L_{T-1} + \hat \beta_{1, T-1} = \text{forecast of } L_{T} \text{ based on estimates at }T-1 \\ \text{Similarly, } \hat \beta_{1,T} = \lambda_{2}(\hat L_{T} - \hat L_{T-1}) + (1-\lambda_{2})\hat \beta_{1,T-1} \\ \hat L_{T} - \hat L_{T-1} = \text{current value of } \beta_{1} \\ \hat \beta_{1,T-1} = \text{forecast of } \beta_{1} \text{ at time }T-1 \\ \text{and }\hat S_{T} = \lambda_{3}(y_{T} - \hat L_{T}) + (1-\lambda_{3}) \hat S_{T-s} \\ \text{Note that }0 \lt \lambda_{1}, \lambda_{2}, \lambda_{3} \lt 1 \\ \text{Once again, we need initial values of the exponential smoothers (at time t = 0):} \\ \hat \beta_{0, 0 \to T} = \hat L_{0} = \hat \beta_{0} \\ \hat \beta_{1, 0 \to T} = \hat \beta_{1} \\ \hat S_{j-s} = \hat y_{j} \text{ for } 1 \le j \le s+1 \\ \hat S_{0} = - \sum_{j=1}^{s-1} \hat y_{j} \]

Example 4.7: See R-code

4.7.2 Multiplicative Seasonal Model

What if the seasonality is proportional to the average level of the seasonal time series.

\[ y_{t} = L_{t}*S_{t} + \epsilon_{t} \text{, where } L_{t}, S_{t} \text{, and } \epsilon_{t} \text{ are as before.} \]

Once again, we can use three exponential smoothers to obtain parameter estimates in the equation.

Example 4.8: See R-code

4.8 Biosurveillance Data

Please read pp 286-299 carefully! (DIY)

4.9 Exponential Smoothing and ARIMA models

\[ \text{Recall: }\tilde y_{T} = \lambda y_{T} + (1-\lambda)\tilde y_{T-1} \\ \text{forecast error: } e_{T} = y_{T} - \hat y_{T-1} \text{, and } \\ \therefore \space e_{T-1} = y_{T-1} - \hat y_{T-2} \\ (1-\lambda)*e_{T-1} = (1-\lambda)y_{T-1} - (1-\lambda)*\hat y_{T-2} \\ \to (1-\lambda)e_{T-1} = y_{T-1} - \lambda y_{T-1} - (1-\lambda) \hat y_{T-2} \\ \text{subtract } (1-\lambda)e_{T-1} \text{ from } e_{T}: \\ \to e_{T}-(1-\lambda)e_{T-1} = (y_{T} - \hat y_{T-1})-(1-\lambda)[y_{T-1} - \hat y_{T-2}] \\ \to e_{T}- (1-\lambda)e_{T-1} = y_{T}-\hat y_{T-1} - y_{T-1} + \lambda y_{T-1} + (1-\lambda) \hat y_{T-2} \\ \hat y_{T-1} = \lambda y _{T-1} + (1-\lambda)\hat y_{T-2} \\ \to e_{T}-(1-\lambda)e_{T-1} = y_{T} - \hat y_{T-1} - y_{T-1} + \hat y_{T-1} \\ = y_{T} - y_{T-1} \\ \therefore \space y_{T} - y_{T-1} = e_{T} - (1-\lambda)e_{T-1} \\ = e_{T} - \theta e_{T-1}, \text{ where }\theta = 1-\lambda \\ \therefore \space (1-B)y_{T} = (1-\theta B)e_{T} \text{, where } B = \text{ backshift operator} \]

This is an integrated moving average model of order (1,1) = (I,MA)

We will do ARIMA models in detail next.

4.10 Chapter 4 R-Code

First, I will call all necessary packages.

library(ggplot2)
library(tidyverse)
library(zoo)
library(stats)
library(fpp3)
library(gt)

4.10.1 Defining Exponential Smoothing Functions

Before covering exponential smoothing models in fable, we will do it ourselves using custom functions. First, in the code chunk below, I define the function for first-order exponential smoothing from the textbook, firstsmooth(y, lambda).32

# take in 3 components - y vector, lambda, starting value of smoothed version
firstsmooth <- function(y, lambda, start=y[1]){ # write a new function: firstsmooth
  ytilde <- y # create a vector with the same length as y to hold y tilde
  ytilde[1] <- lambda*y[1] + (1-lambda)*start # calculate the first values of y tilde
  for (i in 2:length(y)){ #code for a for loop
    # loops T-1 times iterating from the second element to the end
    ytilde[i] <- lambda*y[i] + (1-lambda)*ytilde[i-1] # calculate y tilde at time t = i
  }
  ytilde # print y tilde
}

Next, I will define measacc.fs(y, lambda), which wraps firstsmooth() (contains a call of it within the function), and then calculates the measures of error for the first order smoothing procedure. When using custom functions it is vitally important to understand the parameters, what the function does, and what it returns.

# writing another new function
measacc.fs <- function(y,lambda){
  out <- firstsmooth(y,lambda) # smooths the data and saves it to out
  T <- length(y) # find the length of the vector
  #Smoothed version of the original is the one step ahead prediction
  #Hence the predictions (forecasts) are given as
  pred <- c(y[1],out[1:(T-1)]) # sames the smoothed data to predictions
  prederr <- y-pred # prediction error
  SSE <- sum(prederr^2) # sum of squared errors
  MAPE <- 100*sum(abs(prederr/y))/T # mean absolute percent error
  MAD <- sum(abs(prederr))/T # mean absolute deviation
  MSD <- sum(prederr^2)/T # mean squared deviation
  ret1 <- c(SSE,MAPE,MAD,MSD) # puts them all together
  names(ret1) <- c("SSE","MAPE","MAD","MSD") # assigns them the correct name
  return(ret1) # things to return
  return(prederr)
}

4.10.2 Example 4.1: Simple Exponential Smoothing

For this example we will use the data on the Dow Jones industrial average from DowJones.csv.33 Note, the time variable must be modified into year month format so the yearmonth() function can parse it.

(dow_jones <- read_csv("data/DowJones.csv") |> 
  rename(time = 1, index = `Dow Jones`) |> 
  mutate(time = case_when(str_sub(time, start = 5, end = 5) == "9" ~ str_c("19", 
                                                                           str_sub(time, start = 5, end = 6),
                                                                           "-",
                                                                           str_sub(time, start = 1, end = 3)),
                          str_sub(time, start = 5, end = 5) == "0" ~ str_c("20", 
                                                                           str_sub(time, start = 5, end = 6), 
                                                                           "-", 
                                                                           str_sub(time, start = 1, end = 3)),
                          str_sub(time, start = 1, end = 1) != "0" | str_sub(time, start = 1, end = 1) != "9" ~ str_c("20", 
                                                                                                                      time))) |>
   mutate(time = yearmonth(time)) |>
   as_tsibble(index = time))
## Rows: 85 Columns: 2
## ── Column specification ───────────────────────────────────────
## Delimiter: ","
## chr (1): Date
## dbl (1): Dow Jones
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
## # A tsibble: 85 x 2 [1M]
##        time  index
##       <mth>  <dbl>
##  1 1999 Jun 10971.
##  2 1999 Jul 10655.
##  3 1999 Aug 10829.
##  4 1999 Sep 10337 
##  5 1999 Oct 10730.
##  6 1999 Nov 10878.
##  7 1999 Dec 11497.
##  8 2000 Jan 10940.
##  9 2000 Feb 10128.
## 10 2000 Mar 10922.
## # ℹ 75 more rows

Next, we will apply the functions declared above to the data. First, I generate the smoothed data as a new variable in the dow_jones tsibble, and then I plot the smoothed data against the original data. Finally, I run the measures of accuracy function.

(dow_jones <- dow_jones |> 
   mutate(smooth1 = firstsmooth(dow_jones$index, lambda = 0.4)))
## # A tsibble: 85 x 3 [1M]
##        time  index smooth1
##       <mth>  <dbl>   <dbl>
##  1 1999 Jun 10971.  10971.
##  2 1999 Jul 10655.  10845.
##  3 1999 Aug 10829.  10838.
##  4 1999 Sep 10337   10638.
##  5 1999 Oct 10730.  10675.
##  6 1999 Nov 10878.  10756.
##  7 1999 Dec 11497.  11052.
##  8 2000 Jan 10940.  11008.
##  9 2000 Feb 10128.  10656.
## 10 2000 Mar 10922.  10762.
## # ℹ 75 more rows
dow_jones |> 
  ggplot() +
  geom_line(aes(x = time, y = index, color = "Data")) + 
  geom_point(aes(x = time, y = index, color = "Data"), size = 0.5) + 
  geom_line(aes(x = time, y = smooth1, color = "Fitted")) +
  geom_point(aes(x = time, y = smooth1, color = "Fitted"), size = 0.5) +
  scale_color_manual(values = c(Data = "black", Fitted = "red")) + 
  labs(title = "Plot of Original vs. First Smoothed Dow Jones Index", 
       x = "Time", 
       y = "Index")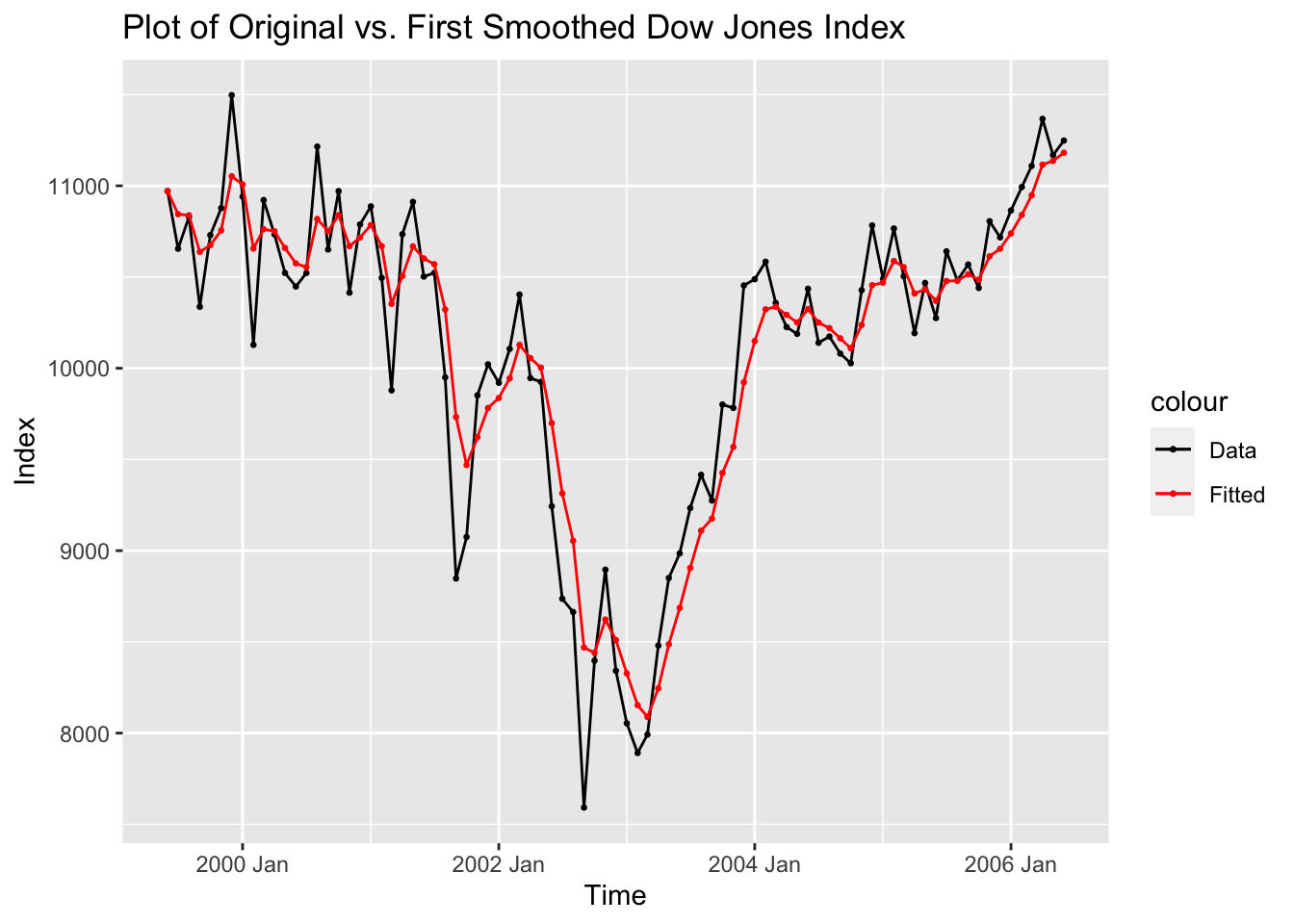

measacc.fs(dow_jones$index, 0.4)
##          SSE         MAPE          MAD          MSD 
## 1.665968e+07 3.461342e+00 3.356325e+02 1.959962e+05

An alternative method of generating smoothed data is to use the HoltWinters(data, alpha = , beta = , gamma = ) function, available through the stats package. stats is automatically included with R, so there is no need to call it. Since we are only doing simple exponential smoothing below, the beta = and gamma = parameters are set to FALSE. When the alpha =, beta =, and gamma = parameters are not specified, the optimal value of the parameter is calculated by minimizing the squared prediction error.

In the code chunk below, I calculate a simple exponential smoother when alpha = 0.4 and another simple exponential smoother where I let alpha be optimized. Then I plot the fitted values from both simple smoothers against the original data. Note: the HoltWinters() function fitted values contain one less observation than the original data. To plot it against the original data the first observation must be filtered out.

dj_smooth1 <- HoltWinters(dow_jones$index, alpha = 0.4, beta = FALSE, gamma = FALSE)
dj_smooth2 <- HoltWinters(dow_jones$index, beta = FALSE, gamma = FALSE)

dow_jones |>
  filter(time != yearmonth("1999 Jun")) |>
  ggplot(aes(x = time, y = index)) + 
    geom_point(aes(color = "Original"), size = 0.5) + 
    geom_line(aes(color = "Original")) + 
    geom_line(aes(y= dj_smooth1[["fitted"]][,1], color = "alpha = 0.4"), na.rm = TRUE) +
    geom_point(aes(y= dj_smooth1[["fitted"]][,1], color = "alpha = 0.4"), size = 0.5, na.rm = TRUE) +
    geom_line(aes(y= dj_smooth2[["fitted"]][,1], color = "alpha = 0.841"), na.rm = TRUE) +
    geom_point(aes(y= dj_smooth2[["fitted"]][,1], color = "alpha = 0.841"), size = 0.5, na.rm = TRUE) +
    scale_color_manual(values = c(Original = "black", "alpha = 0.4" = "red", "alpha = 0.841" = "blue")) + 
    labs(title = "Plot Dow Jones Index and First Smoothed Data", 
         x = "Time", 
         y = "Index",
         color = "Data")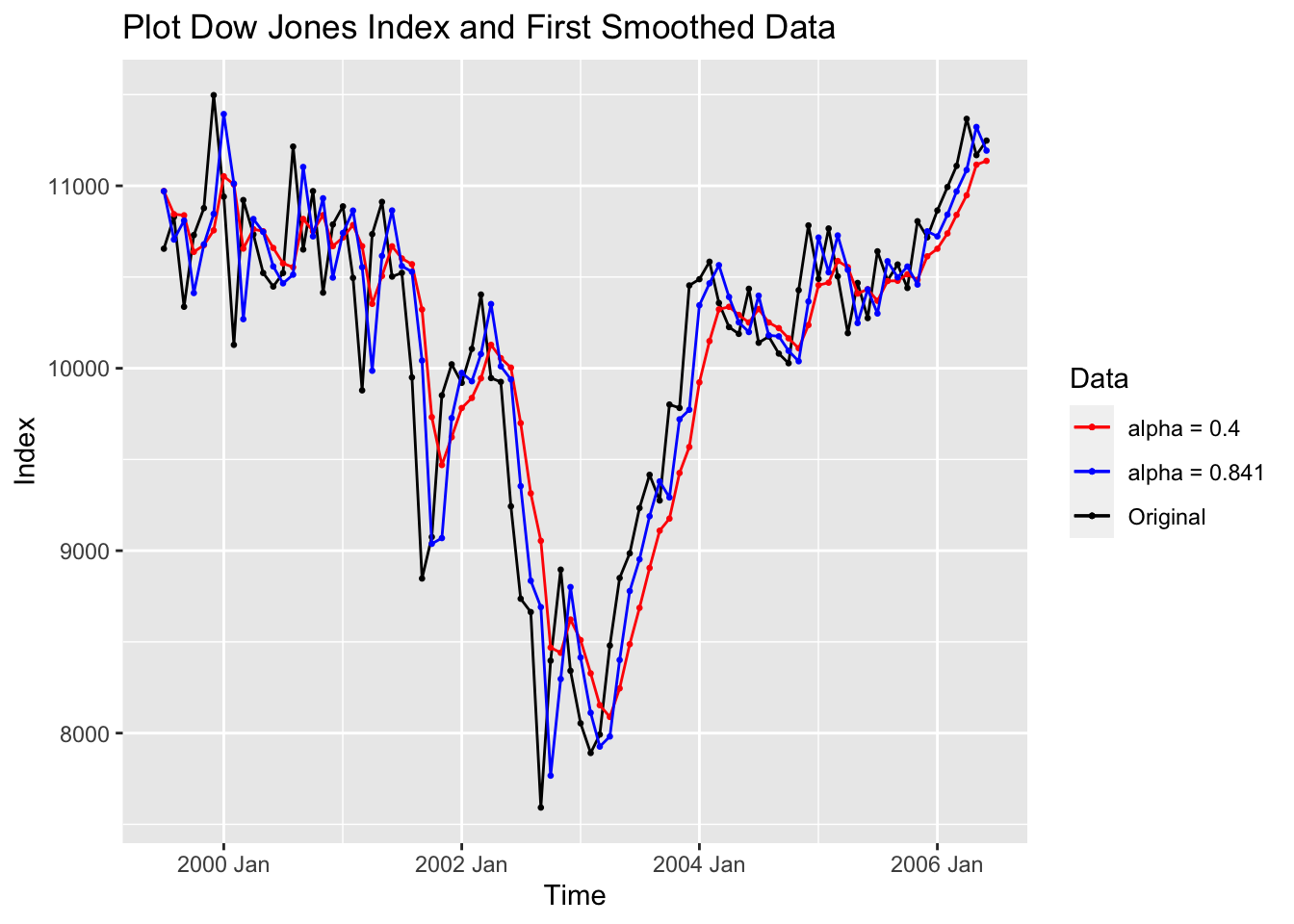

The fpp3 packages use the same method of estimating exponential smoothing within model objects, but they use a different method to choose the initial value of the smoother. Instead of either setting the first value of the smoother to the first value of the series or the mean of the series, the ETS() function chooses the optimal value by minimizing SSE through log-likelihood. The optimization process can be changed using the opt_crit = parameter. The documentation for ETS() can be found here. For further insight into ETS() and the equations for all the possible exponential smoothing model with this function, check out the tables at the bottom of this page as well as the rest of chapter 8.34 The simple exponential smoothing demonstrated below only has an error term (alpha parameter), so trend (beta) and season (gamma) are set to “N” signifying NULL. alpha = and beta = can both be set within the trend parameter and gamma = can be set within the season parameter.

dow_jones.fit <- dow_jones |>
  model(model1 = ETS(index ~ error("A") + trend("N", alpha = 0.4) + season("N")),
        model2 = ETS(index ~ error("A") + trend("N") + season("N")))

The table below contains both the alpha parameter and optimized starting value (l[0]) for both models. Additionally, I calculate the measures of accuracy for both models and compare them within the second table. The fable simple smoother optimization chooses an alpha parameter of 0.8494 instead of 0.841 chosen by the HoltWinters() function. Note: if the alpha parameter of the smoother is above 0.4, the smoother is not doing much smoothing.

dow_jones.fit |> tidy() |> mutate(estimate = round(estimate, digits = 3)) |> gt()
.model term estimate
model1 alpha 0.400
model1 l[0] 10805.637
model2 alpha 0.839
model2 l[0] 10923.490
 
dig <- function(x) (round(x, digits = 3))
dow_jones.fit |> accuracy() |> mutate_if(is.numeric, dig) |> gt()
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
model1 Training 11.047 442.152 336.732 -0.074 3.471 0.391 0.402 0.434
model2 Training 4.423 400.592 315.600 -0.061 3.208 0.366 0.364 0.017

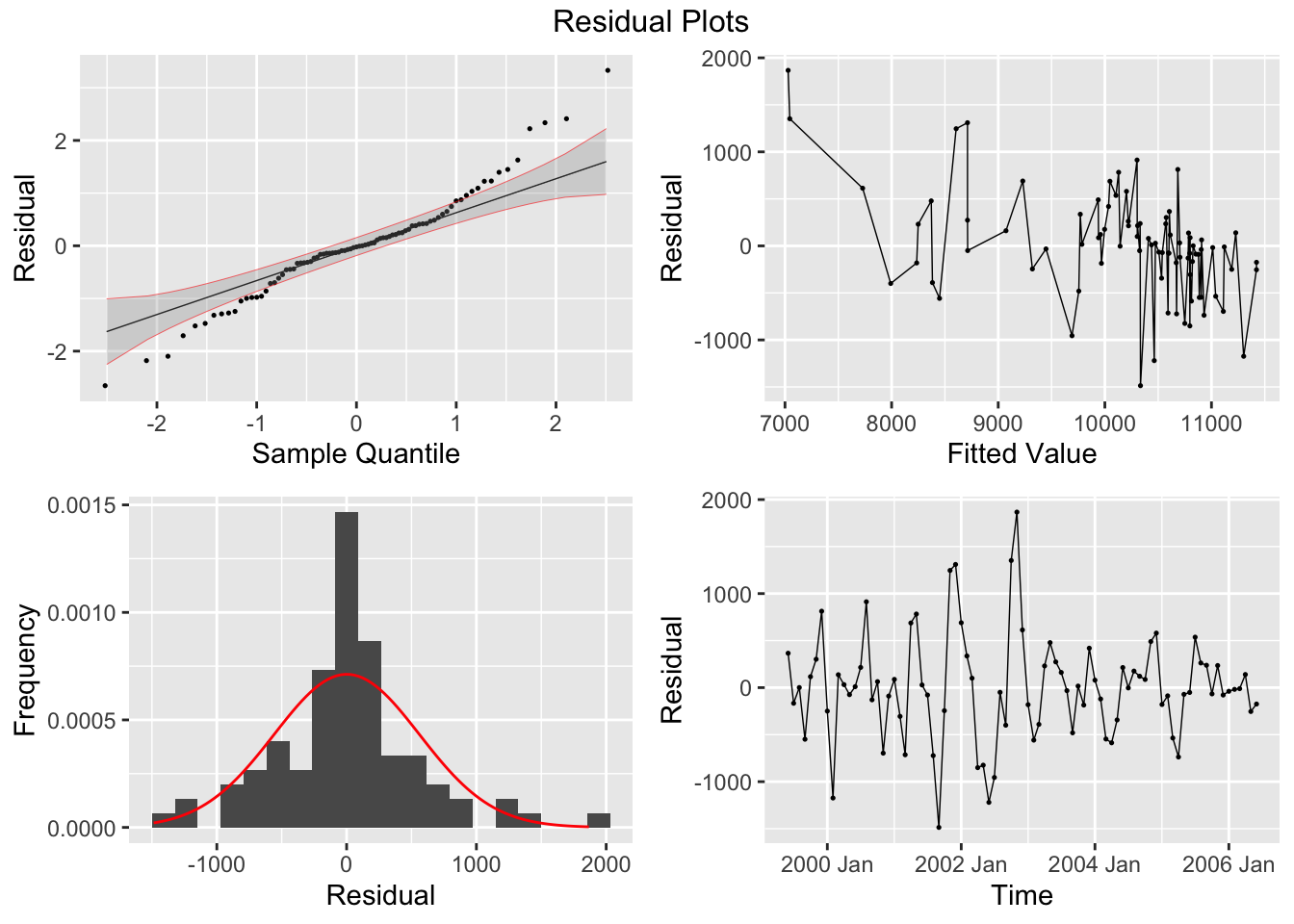
Finally, I analyze the residuals of each model using the plot_residuals() function.

augment(dow_jones.fit) |> filter(.model == "model1") |> plot_residuals()
## # A tibble: 1 × 3
##   .model lb_stat lb_pvalue
##   <chr>    <dbl>     <dbl>
## 1 model1    16.6 0.0000469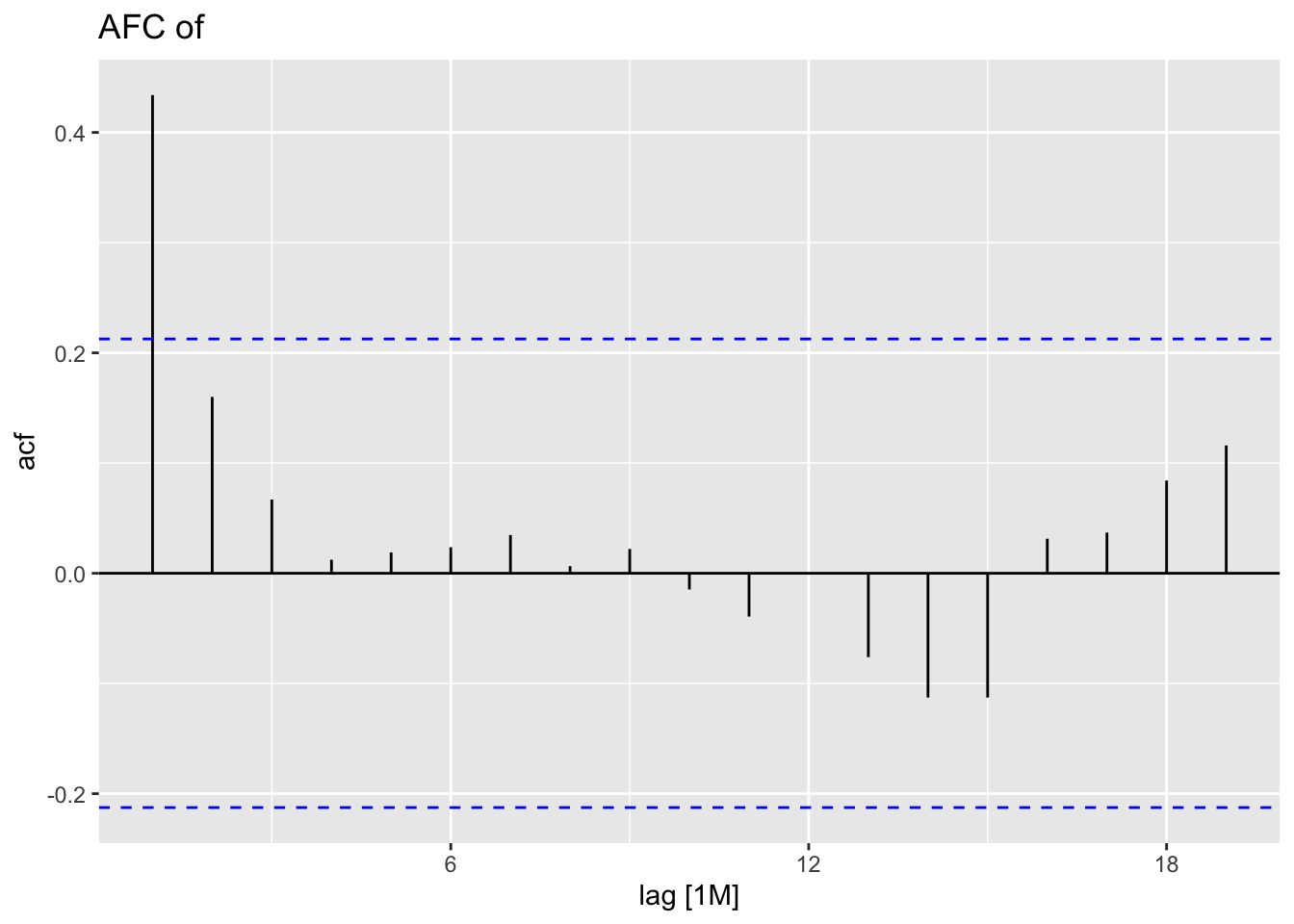

augment(dow_jones.fit) |> filter(.model == "model2") |> plot_residuals()
## # A tibble: 1 × 3
##   .model lb_stat lb_pvalue
##   <chr>    <dbl>     <dbl>
## 1 model2  0.0267     0.870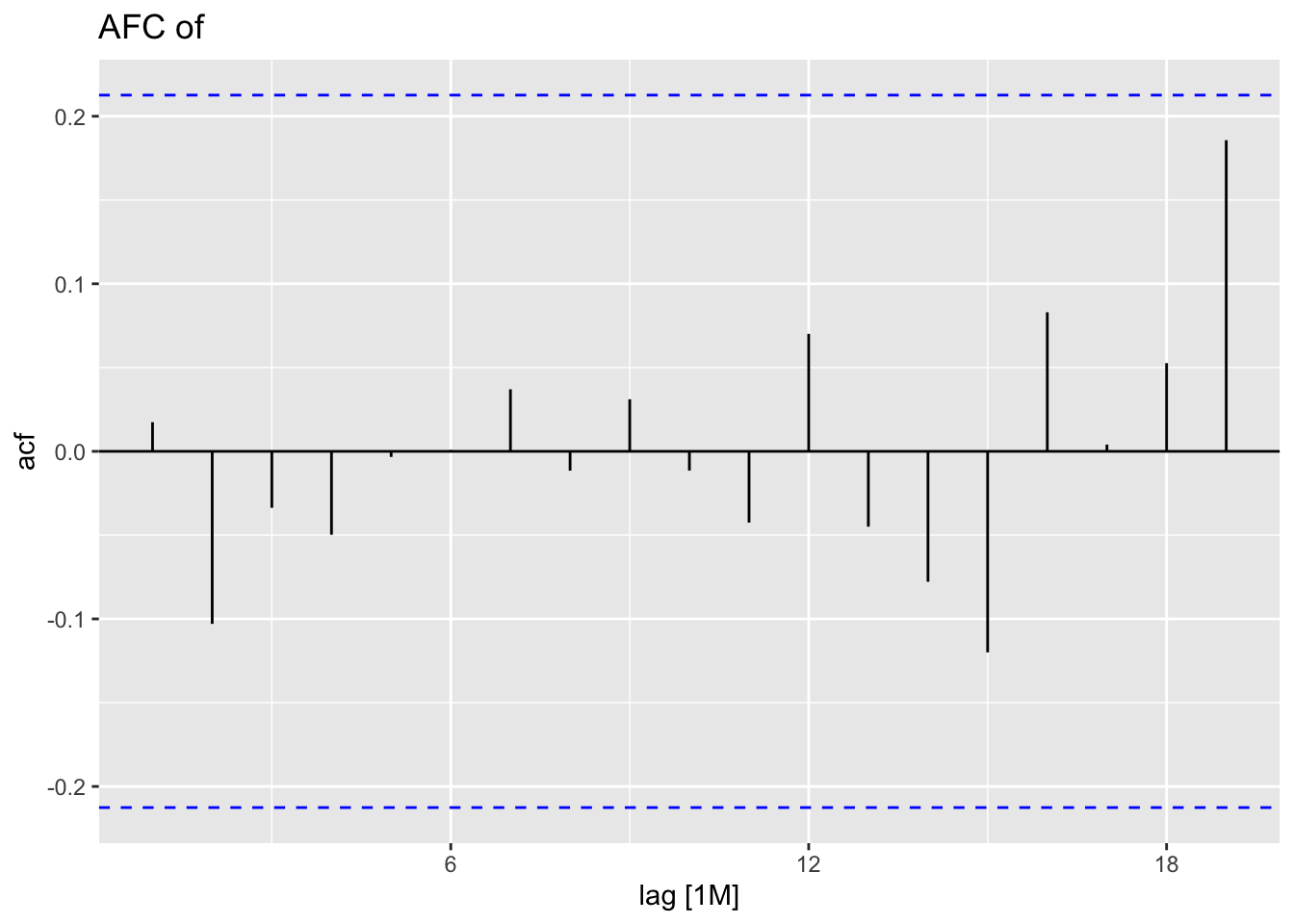

4.10.3 Example 4.2: Double Exponential Smoothing

First, I read in the U.S. consumer price index data from US_CPI.csv and create a tsibble object for it in the code chunk below. This data has issues with how time is kept, so it requires conditional formatting so the yearmonth() function can read it.

(cpi.data <- read_csv("data/US_CPI.csv") |> 
  rename("time" = 1, "index" = 2) |> 
  mutate(time = case_when(str_sub(time, start = 5, end = 5) == "9" ~ str_c("19",
                                                                           str_sub(time, start = 5, end = 6), 
                                                                           "-", 
                                                                           str_sub(time, start = 1, end = 3)), 
  str_sub(time, start = 5, end = 5) == "0" ~ str_c("20",
                                                   str_sub(time, start = 5, end = 6),
                                                   "-", str_sub(time, start = 1, end = 3)))) |>
  mutate(time = yearmonth(time)) |> 
  as_tsibble(index = time))
## Rows: 120 Columns: 2
## ── Column specification ───────────────────────────────────────
## Delimiter: ","
## chr (1): Month-Year
## dbl (1): CPI
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
## # A tsibble: 120 x 2 [1M]
##        time index
##       <mth> <dbl>
##  1 1995 Jan  150.
##  2 1995 Feb  151.
##  3 1995 Mar  151.
##  4 1995 Apr  152.
##  5 1995 May  152.
##  6 1995 Jun  152.
##  7 1995 Jul  152.
##  8 1995 Aug  153.
##  9 1995 Sep  153.
## 10 1995 Oct  154.
## # ℹ 110 more rows

After reading in the data appropriately, I calculate the first smoothed series and then the second smoothed series, both with a smoothing parameter of 0.3. Then, I calculate the predicted values by adjusting for bias.

cpi.smooth1 <- firstsmooth(y=cpi.data$index, lambda=0.3) # first order smoothing
cpi.smooth2 <- firstsmooth(y=cpi.smooth1, lambda=0.3) # second order smoothing
# take the first smoothed values as the y vector and choose the same lambda value
cpi.hat <- 2*cpi.smooth1 - cpi.smooth2 #Predicted value of y
# fitted value is twice the first smoother minus the second smoother
# these are the unbiased predicted values of y

I plot the original data, the predicted values, and the results of the first and second smoother all together in the code chunk below. The first and second smoother systematically underestimate the data, as seen in the plot.

cpi.data |>
  ggplot(aes(x = time, y = index)) +
    geom_point(aes(color = "Original"), size = 0.25) + 
    geom_line(aes(color = "Original")) + 
    geom_point(aes(y = cpi.hat, color = "Predicted Values"), size = 0.25) + 
    geom_line(aes(y = cpi.hat, color = "Predicted Values")) + 
    geom_point(aes(y = cpi.smooth1, color = "First Smoother"), size = 0.25) + 
    geom_line(aes(y = cpi.smooth1, color = "First Smoother")) + 
    geom_point(aes(y = cpi.smooth2, color = "Second Smoother"), size = 0.25) + 
    geom_line(aes(y = cpi.smooth2, color = "Second Smoother")) +
    scale_color_manual(values = c(`Original` = "black", 
                                  `Predicted Values` = "red", 
                                  `First Smoother` = "blue", 
                                  `Second Smoother` = "green")) +
    labs(title = "Plot of Original Data and Doubly Smoothed Fitted Values", 
         x = "Time", 
         y = "Index", 
         color = "Data")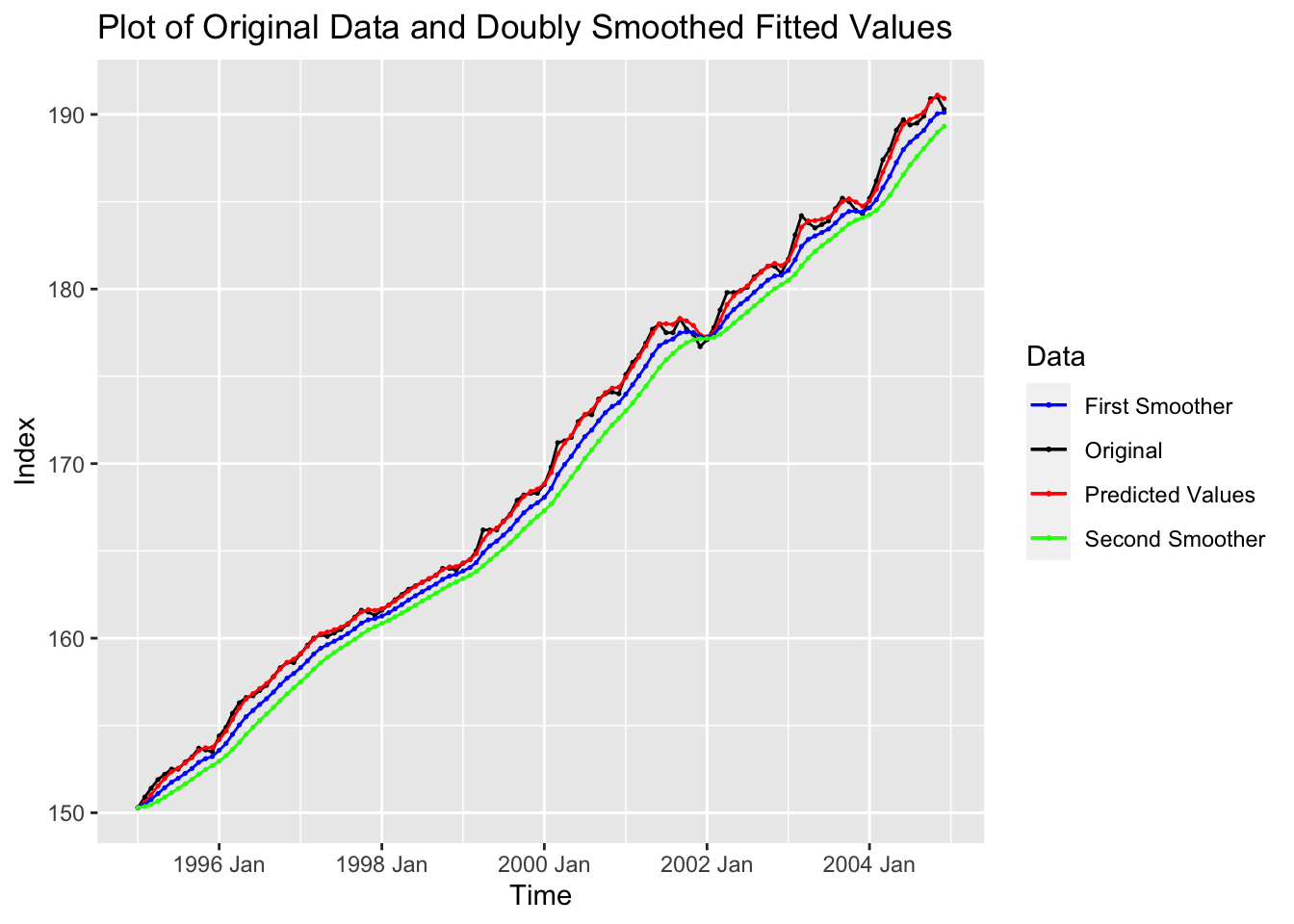

Next, I will replicate this using the methods from fpp3. I set both alpha and beta equal to 0.3 within trend().

cpi.fit <- cpi.data |> 
  model(ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")))

cpi.fit |> tidy() |> mutate(estimate = round(estimate, digits = 3)) |> gt()
.model term estimate
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) alpha 0.300
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) beta 0.300
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) l[0] 149.952
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) b[0] 0.628
 
augment(cpi.fit) |> 
  autoplot(index) + 
  geom_point(size = 0.25) + 
  autolayer(augment(cpi.fit), .fitted, color = "red") + 
  geom_point(aes(y = .fitted), color = "red", size = 0.25) + 
  labs(title = "Plot of CPI Index and Second Smoothed Data over Time", 
       subtitle = "Alpha = 0.3, Beta = 0.3", 
       x = "Time",
       y = "Index")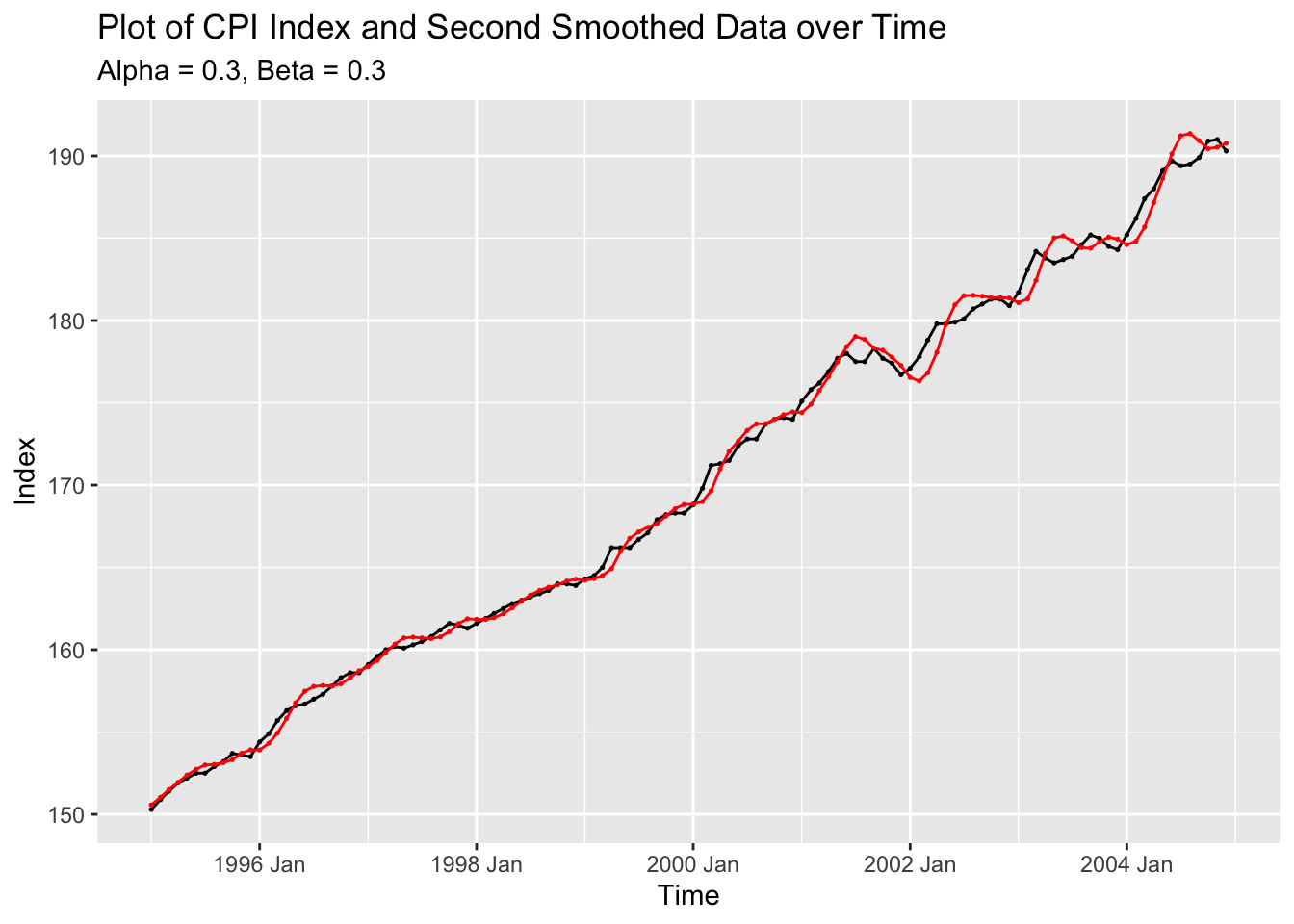

cpi.fit |> accuracy() |> mutate_if(is.numeric, dig) |> gt()
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) Training -0.019 0.723 0.535 -0.011 0.306 0.132 0.171 0.625
 
plot_residuals(augment(cpi.fit))
## # A tibble: 1 × 3
##   .model                                                       lb_stat lb_pvalue
##   <chr>                                                          <dbl>     <dbl>
## 1 "ETS(index ~ error(\"A\") + trend(\"A\", alpha = 0.3, beta …    48.1  4.04e-12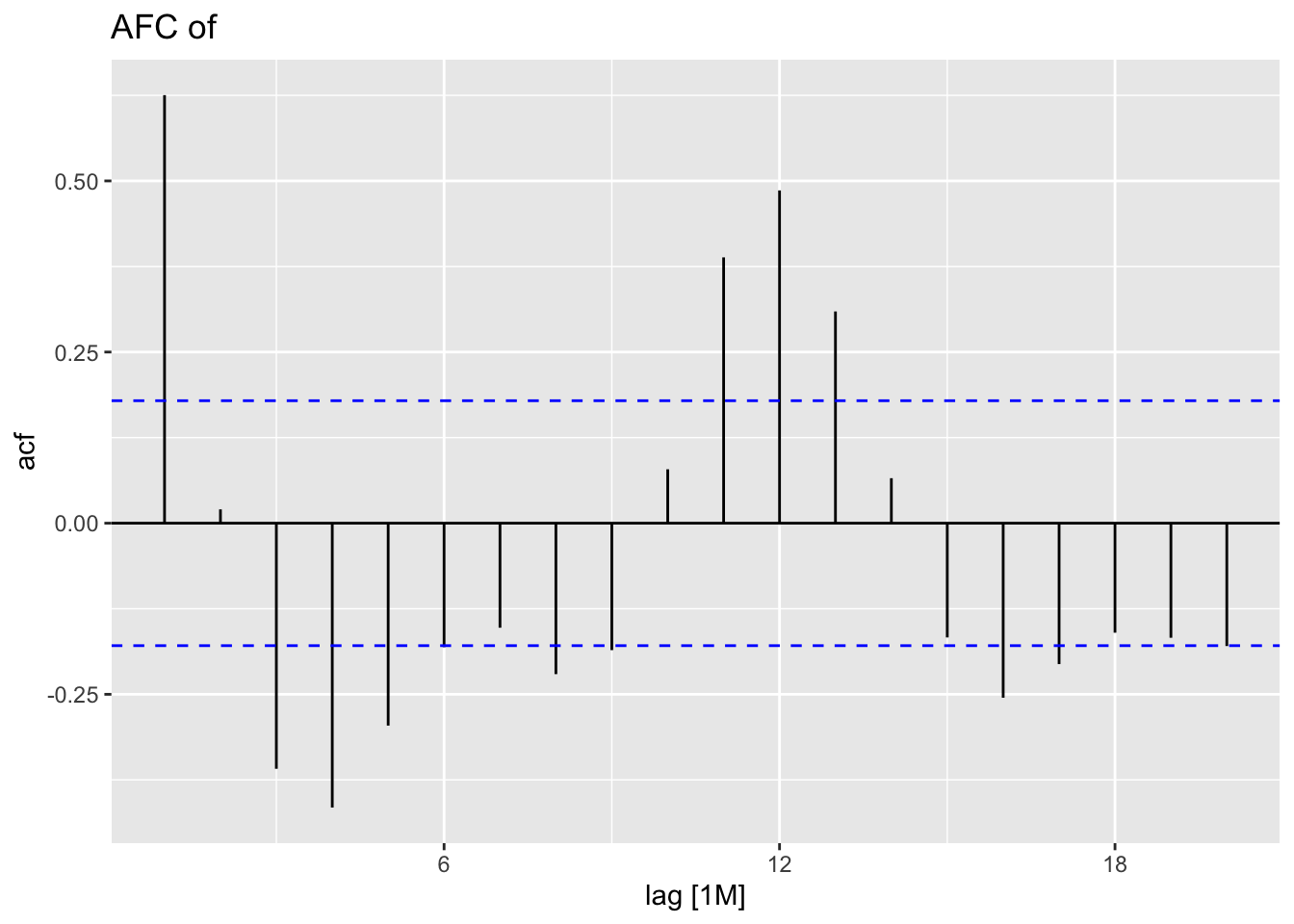

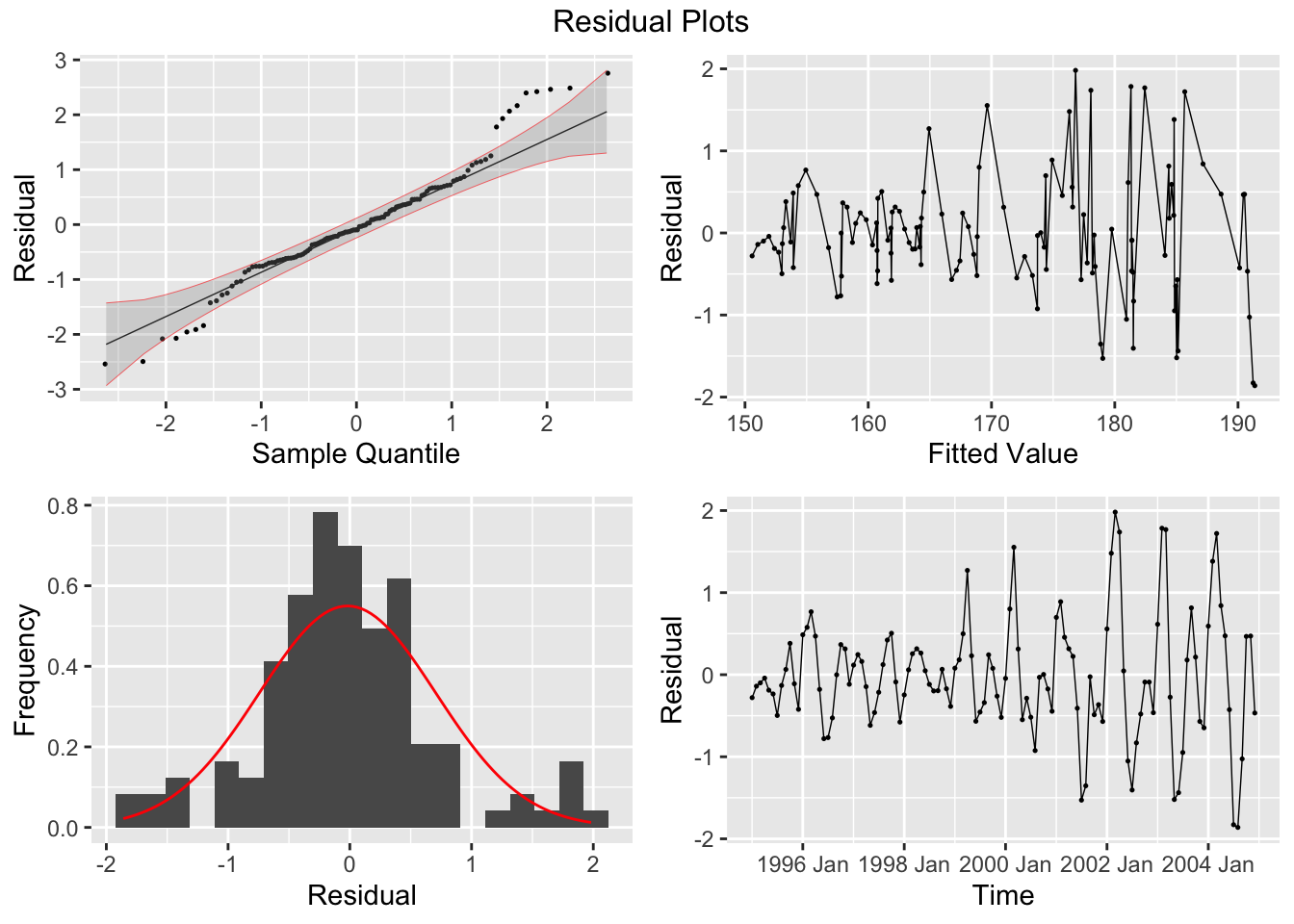
4.10.4 Example 4.3: Double Exponential Smoothing

Next I will use the same double exponential smoothing procedure from the last example on the Dow Jones index data. In the code chunk below, I use the firstsmooth() custom function to doubly smooth the data and then calculate the fitted values.

dji.smooth3 <- firstsmooth(y=dow_jones$index, lambda=0.3) # first order smoothing
dji.smooth4 <- firstsmooth(y=dji.smooth3, lambda=0.3) # second order smoothing
dji.hat <- 2*dji.smooth3 - dji.smooth4 #Predicted value of y
# twice the first smoother minus the second smoother

Then, I plot the fitted values against the original data.

dow_jones |>
  ggplot(aes(x = time, y = index)) + 
  geom_point(aes(color = "Original"), size = 0.5) +
  geom_line(aes(color = "Original")) + 
  geom_point(aes(y = dji.hat, color ="Fitted"), size = 0.5) + 
  geom_line(aes(y = dji.hat, color = "Fitted")) + 
  scale_color_manual(values = c(Fitted = "red", Original = "black")) + 
  labs(title = "Plot of Dow Jones Index and Doubly Smoothed Data over Time", 
       subtitle = "alpha = 0.3, beta = 0.3", 
       x = "Time", 
       y = "Index",
       color = "Data")

I then replicate this process using the methods from fable as done in the last example.

dow_jones.fit2 <- dow_jones |> 
  model(ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")))

dow_jones.fit2 |> tidy() |> mutate(estimate = round(estimate, digits = 3)) |> gt()
.model term estimate
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) alpha 0.300
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) beta 0.300
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) l[0] 10608.072
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) b[0] -3.073
 
augment(dow_jones.fit2) |> 
  autoplot(index) + 
  geom_point(size = 0.25) + 
  autolayer(augment(dow_jones.fit2),.fitted, color = "red") + 
  geom_point(aes(y = .fitted), size = 0.25, color = "red") + 
  labs(title = "Plot of Dow Jones Index and Doubly Smoothed Data over Time", 
       subtitle = "Alpha = 0.3, Beta = 0.3", 
       x = "Time", 
       y = "Index")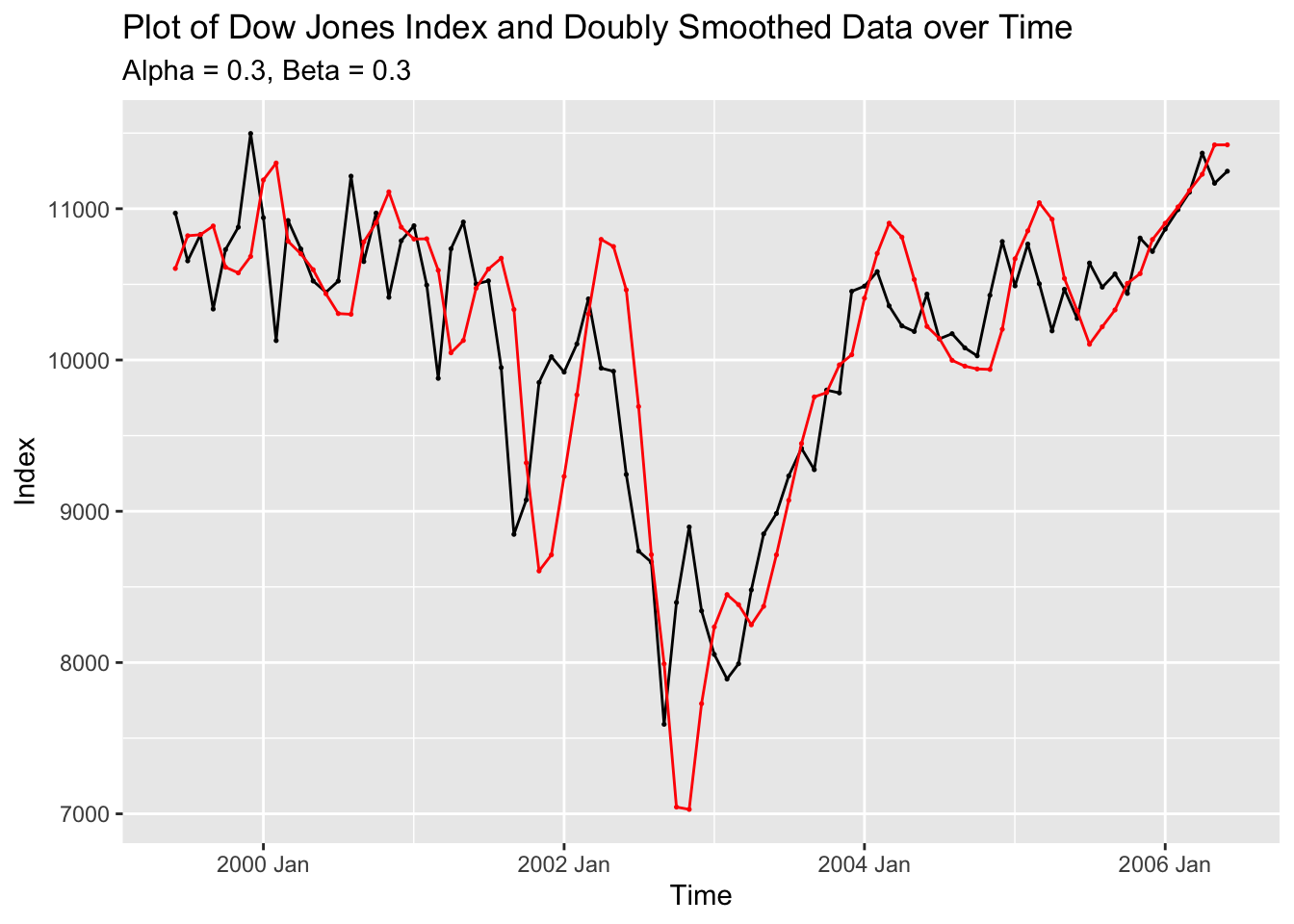

dow_jones.fit2 |> accuracy() |> mutate_if(is.numeric, dig) |> gt()
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) Training 1.065 556.895 394.388 -0.047 4.04 0.458 0.506 0.462
 
plot_residuals(augment(dow_jones.fit2))
## # A tibble: 1 × 3
##   .model                                                       lb_stat lb_pvalue
##   <chr>                                                          <dbl>     <dbl>
## 1 "ETS(index ~ error(\"A\") + trend(\"A\", alpha = 0.3, beta …    18.8 0.0000148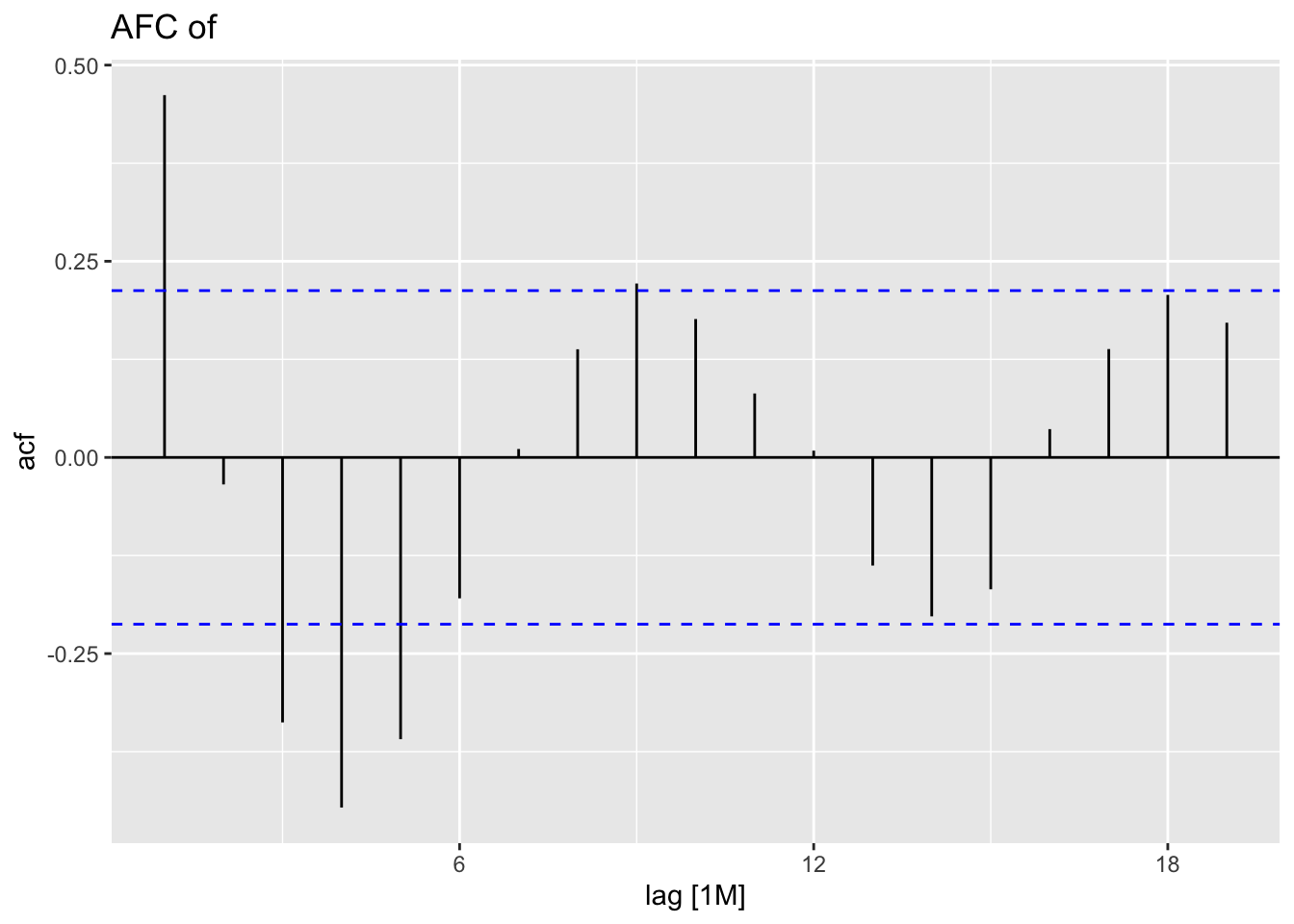

4.10.5 Example 4.4: Forecasting a Constant Process

For this example, we will use the data from Speed.csv. This file contains the weekly average speed during non-rush hours.35 In the code chunk below, I read in the data and declare it as a tsibble.

(speed <- read_csv("data/Speed.csv") |> 
  rename(time = 1, speed = 2) |> 
  as_tsibble(index = time))
## Rows: 100 Columns: 2
## ── Column specification ───────────────────────────────────────
## Delimiter: ","
## dbl (2): Week, Speed
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
## # A tsibble: 100 x 2 [1]
##     time speed
##    <dbl> <dbl>
##  1     1  47.1
##  2     2  45.0
##  3     3  44.7
##  4     4  45.4
##  5     5  45.4
##  6     6  44.8
##  7     7  45.2
##  8     8  45.3
##  9     9  46.9
## 10    10  48.0
## # ℹ 90 more rows

I then manually calculate the optimal value of lambda and compare it to the results from the HoltWinters() function. We will use the first 78 values as the training set and the remaining 22 as the test set. I create a sequence of lambda values from 0.1 to 0.9 in increments of 0.1. Then, I write a custom function, sse.speed, that wraps measacc.fs(), and use the sapply() function to apply the sequence of lambdas to sse.speed. I then save the lambda with the smallest SSE to opt.lambda. I then graph each lambda and the resulting SSE, and denote the optimal lambda with a vertical red line. You can see that the optimal lambda is at the bottom of a parabola. HoltWinters() finds the optimal lambda to be 0.385.

lambda.vec <- seq(0.1, 0.9, 0.1) #Sequence of lambda values from 0.1 to 0.9 in increments of 0.1
# this uses the measures of accuracy function: only take the 1-78 observations and use the remaining ones as the holdout sample. 
# The point is to use the 78 points to make the actual data and compare the forecasts to the remaining 22 points
sse.speed <- function(sc){measacc.fs(speed$speed[1:78], sc)[1]} #Apply "firstSmooth" through measacc
# holdout sample is important to monitor the forecast otherwise there is no measure of forecast performance
sse.vec <- sapply(lambda.vec, sse.speed) #SAPPLY instead of "for" loops for computational purpose
# this saves time in large data sets but functions in the same way
opt.lambda <- lambda.vec[sse.vec == min(sse.vec)] #Optimal lambda that minimizes SSE

tibble(lambda = lambda.vec,
        sse = sse.vec) |>
  ggplot(aes(x = lambda, y = sse)) + 
  geom_point() + 
  geom_line() + 
  geom_vline(aes(xintercept = opt.lambda), color = "red") + 
  labs(title = "SSE vs. Lambda",
       subtitle = "SSE min = 116.69, Lambda = 0.4", 
       x = "Lambda", 
       y = "SSE")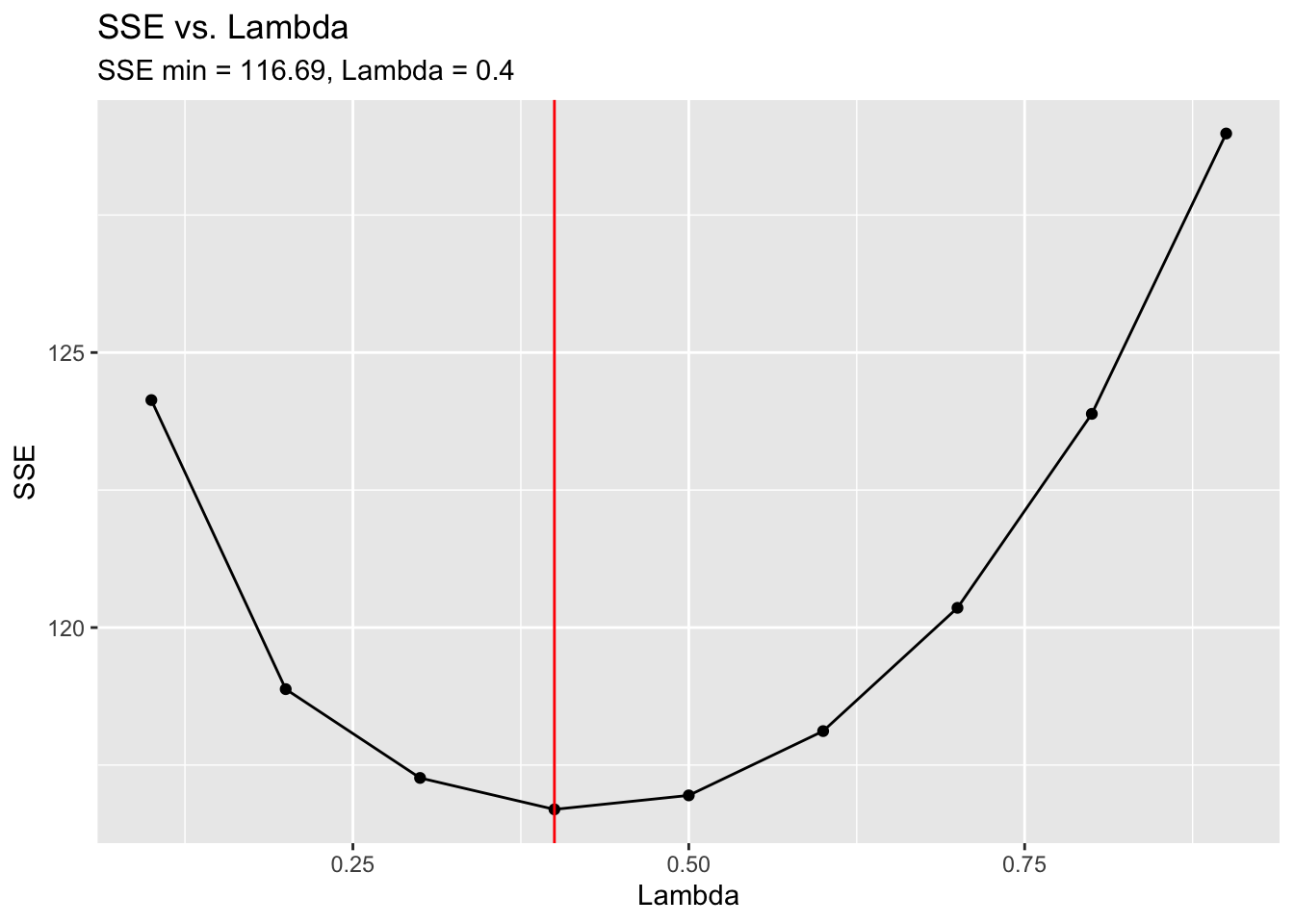

#Alternatively, use the Holt Winters function without specifying alpha parameter to get "best" value of smoothing constant.
(speed.hw <- HoltWinters(speed$speed, beta=FALSE, gamma=FALSE))
## Holt-Winters exponential smoothing without trend and without seasonal component.
## 
## Call:
## HoltWinters(x = speed$speed, beta = FALSE, gamma = FALSE)
## 
## Smoothing parameters:
##  alpha: 0.3846525
##  beta : FALSE
##  gamma: FALSE
## 
## Coefficients:
##       [,1]
## a 45.61032

The methods in the fable package find the optimal alpha parameter to be 0.23. This differs due to the optimization of the first value of the smoother.

speed.fit <- speed |> filter(time <= 78) |>
  model(ETS(speed ~ error("A") + trend("N") + season("N")))

speed.fit |> tidy() |> mutate(estimate = round(estimate, digits = 3)) |> gt()
.model term estimate
ETS(speed ~ error("A") + trend("N") + season("N")) alpha 0.00
ETS(speed ~ error("A") + trend("N") + season("N")) l[0] 45.45
 
accuracy(speed.fit) |> mutate_if(is.numeric, dig) |> gt()
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
ETS(speed ~ error("A") + trend("N") + season("N")) Training 0 1.161 0.919 -0.065 2.016 0.838 0.874 0.321
 
plot_residuals(augment(speed.fit))
## # A tibble: 1 × 3
##   .model                                                     lb_stat lb_pvalue
##   <chr>                                                        <dbl>     <dbl>
## 1 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N\"))"    8.34   0.00388

(speed.forecast <- speed.fit |> forecast(new_data = speed |> filter(time >= 79)))
## # A fable: 22 x 4 [1]
## # Key:     .model [1]
##    .model                                                  time      speed .mean
##    <chr>                                                  <dbl>     <dist> <dbl>
##  1 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    79 N(45, 1.4)  45.4
##  2 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    80 N(45, 1.4)  45.4
##  3 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    81 N(45, 1.4)  45.4
##  4 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    82 N(45, 1.4)  45.4
##  5 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    83 N(45, 1.4)  45.4
##  6 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    84 N(45, 1.4)  45.4
##  7 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    85 N(45, 1.4)  45.4
##  8 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    86 N(45, 1.4)  45.4
##  9 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    87 N(45, 1.4)  45.4
## 10 "ETS(speed ~ error(\"A\") + trend(\"N\") + season(\"N…    88 N(45, 1.4)  45.4
## # ℹ 12 more rows
accuracy(speed.forecast, speed) |> mutate_if(is.numeric, dig) |> gt()
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
ETS(speed ~ error("A") + trend("N") + season("N")) Test -0.334 0.963 0.825 -0.78 1.834 0.753 0.725 0.506
 
autoplot(speed.forecast, speed) +
  labs(title = "Forecast of Mean Speed During Non-Rush Hours",
       x = "Time", 
       y = "Speed")

4.10.6 Example 4.5: Forecasting a Linear Trend Process

In this next example, we use the CPI data that was previously read in to forecast a linear trend process. We use simple exponential smoothing, optimizing the alpha parameter by minimizing the SSE. This is done using the same methods as the last example. The first 108 observations are used as the training set, while the final 12 are the test set.

# Finding the value of the smoothing constant that minimizes SSE using First-order exponential smoothing
lambda.vec <- c(seq(0.1, 0.9, 0.1), .95, .99) # series of possible lambda values
sse.cpi <- function(sc){measacc.fs(cpi.data$index[1:108],sc)[1]}
sse.vec <- sapply(lambda.vec, sse.cpi)
opt.lambda <- lambda.vec[sse.vec == min(sse.vec)]

tibble(lambda = lambda.vec,
        sse = sse.vec) |>
  ggplot(aes(x = lambda, y = sse)) + 
  geom_point() + 
  geom_line() + 
  geom_vline(aes(xintercept = opt.lambda), color = "red") + 
  labs(title = "SSE vs. Lambda",
       subtitle = "SSE min = 28.65, Lambda = 1", 
       x = "Lambda", 
       y = "SSE")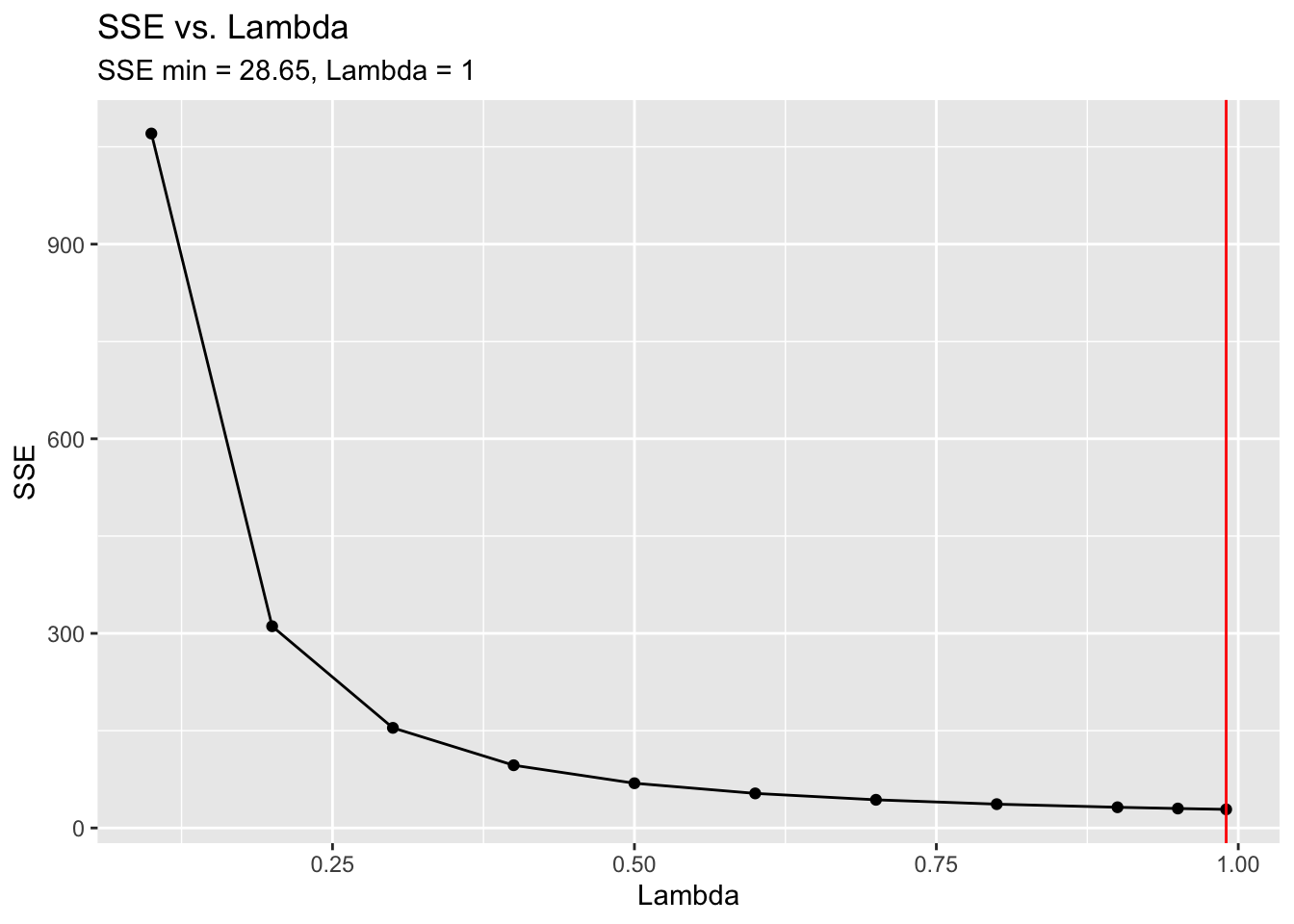

ACF(cpi.data |> filter(year(time) < 2004), index) |> 
  autoplot() + 
  labs(title = "ACF of CPI Data Training Set") #ACF of the data

4.10.6.1 Option A: 1 to 12 Step Ahead Forecast

I manually calculate a 1 to 12 step ahead forecast and read the results into a tibble.

#Now, we forecast using a Second-order exponential smoother with lambda=0.3
lcpi <- 0.3
cpi.smooth1 <- firstsmooth(y=cpi.data$index[1:108],lambda=lcpi)
cpi.smooth2 <- firstsmooth(y=cpi.smooth1, lambda=lcpi)
cpi.hat <- 2*cpi.smooth1 - cpi.smooth2
tau <- 1:12
T <- length(cpi.smooth1)
cpi.forecast <- (2 + tau*(lcpi/(1 - lcpi)))*cpi.smooth1[T] - (1+tau*(lcpi/(1-lcpi)))*cpi.smooth2[T]
# because we are saying tau it will do it for all values of tau
ctau <- sqrt(1 + (lcpi/((2-lcpi)^3))*(10-14*lcpi+5*(lcpi^2)+2*tau*lcpi*(4-3*lcpi)+2*(tau^2)*(lcpi^2)))
alpha.lev <- 0.05
sig.est <- sqrt(var(cpi.data$index[2:108] - cpi.hat[1:107]))
cl <- qnorm(1-alpha.lev/2)*(ctau/ctau[1])*sig.est

cpi.fc <- tibble(time = cpi.data$time[109:120],
       mean = cpi.forecast, 
       upper = cpi.forecast + cl,
       lower = cpi.forecast - cl)

Then I graph the forecast with the original data.

cpi.data |>
  left_join(cpi.fc, by = join_by(time)) |>
  ggplot(aes(x = time, y = index)) +
  geom_point(size = 0.25) + 
  geom_line() + 
  geom_point(aes(y = mean), color = "blue", size = 0.25, na.rm = TRUE) + 
  geom_line(aes(y = mean), color = "blue", na.rm = TRUE) + 
  geom_ribbon(aes(ymax = upper, ymin = lower), fill = "blue", alpha = 0.5) + 
  labs(title = "1 to 12 Step-Ahead Forecast", 
       x = "Time",
       y = "Index")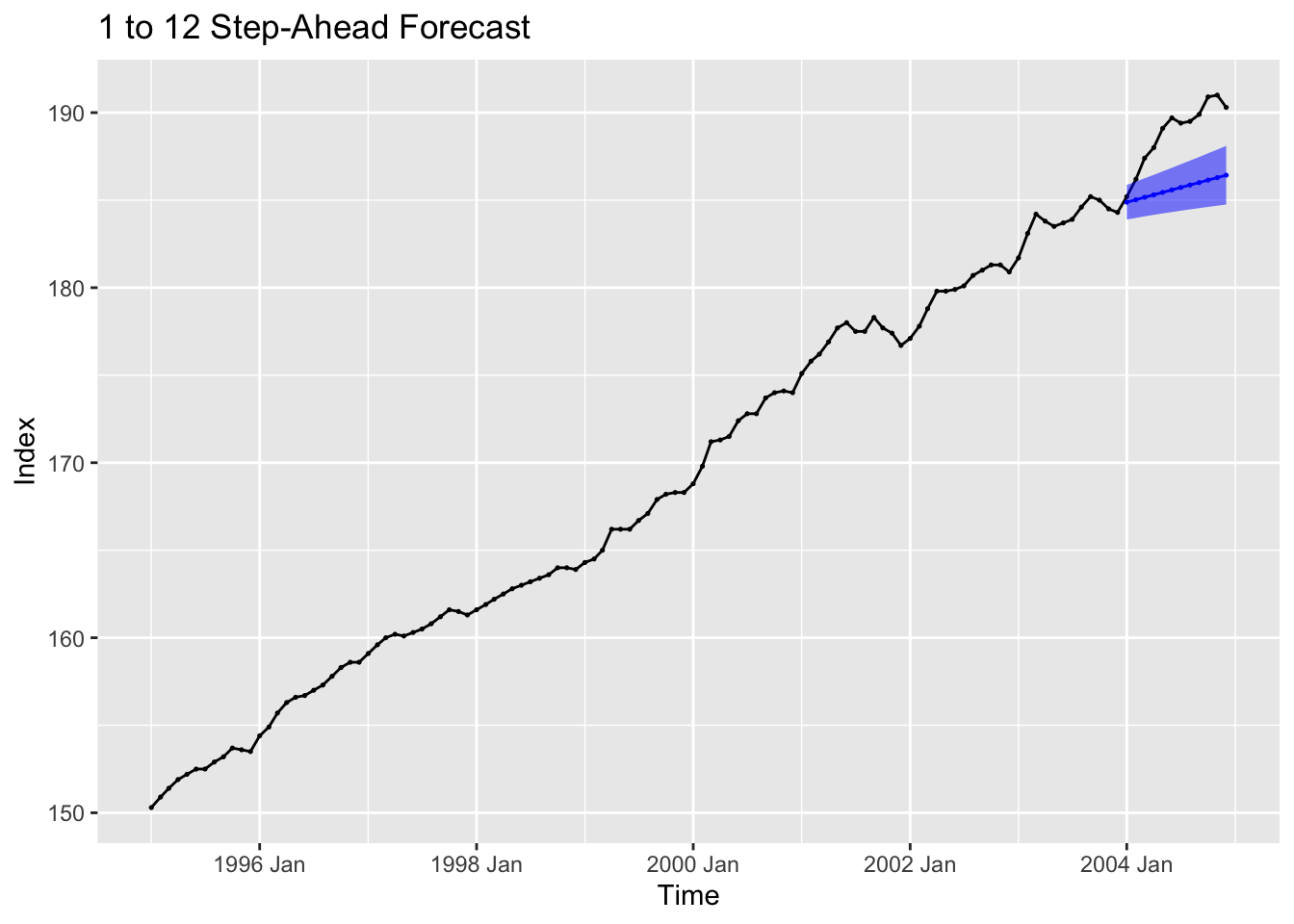

4.10.6.2 Option B: 12 One-Step-Ahead Forecasts

I then calculate 12 one-step ahead forecasts

lcpi <- 0.3
T <- 108
tau <- 12
alpha.lev <- 0.05
cpi.forecast <- rep(0,tau)
cl <- rep(0,tau)
cpi.smooth1 <- rep(0,T+tau)
cpi.smooth2 <- rep(0,T+tau)
for (i in 1:tau) {
  cpi.smooth1[1:(T+i-1)] <- firstsmooth(y=cpi.data$index[1:(T+i-1)], lambda=lcpi)
  cpi.smooth2[1:(T+i-1)] <- firstsmooth(y=cpi.smooth1[1:(T+i-1)], lambda=lcpi)
  cpi.forecast[i] <- (2+(lcpi/(1-lcpi)))*cpi.smooth1[T+i-1]- (1+(lcpi/(1-lcpi)))*cpi.smooth2[T+i-1]
  cpi.hat <- 2*cpi.smooth1[1:(T+i-1)] - cpi.smooth2[1:(T+i-1)]
  sig.est <- sqrt(var(cpi.data[2:(T+i-1),2]- cpi.hat[1:(T+i-2)]))
  cl[i] <- qnorm(1-alpha.lev/2)*sig.est
}

cpi.fc2 <- tibble(time = cpi.data$time[109:120],
       mean = cpi.forecast, 
       upper = cpi.forecast + cl,
       lower = cpi.forecast - cl)

I graph the results in the code chunk below.

cpi.data |>
  left_join(cpi.fc2, by = join_by(time)) |>
  ggplot(aes(x = time, y = index)) +
  geom_point(size = 0.25) + 
  geom_line() + 
  geom_point(aes(y = mean), color = "blue", size = 0.25, na.rm = TRUE) + 
  geom_line(aes(y = mean), color = "blue", na.rm = TRUE) + 
  geom_ribbon(aes(ymax = upper, ymin = lower), fill = "blue", alpha = 0.5) +
  labs(title = "12 One-Step-Ahead Forecast", 
       x = "Time",
       y = "Index")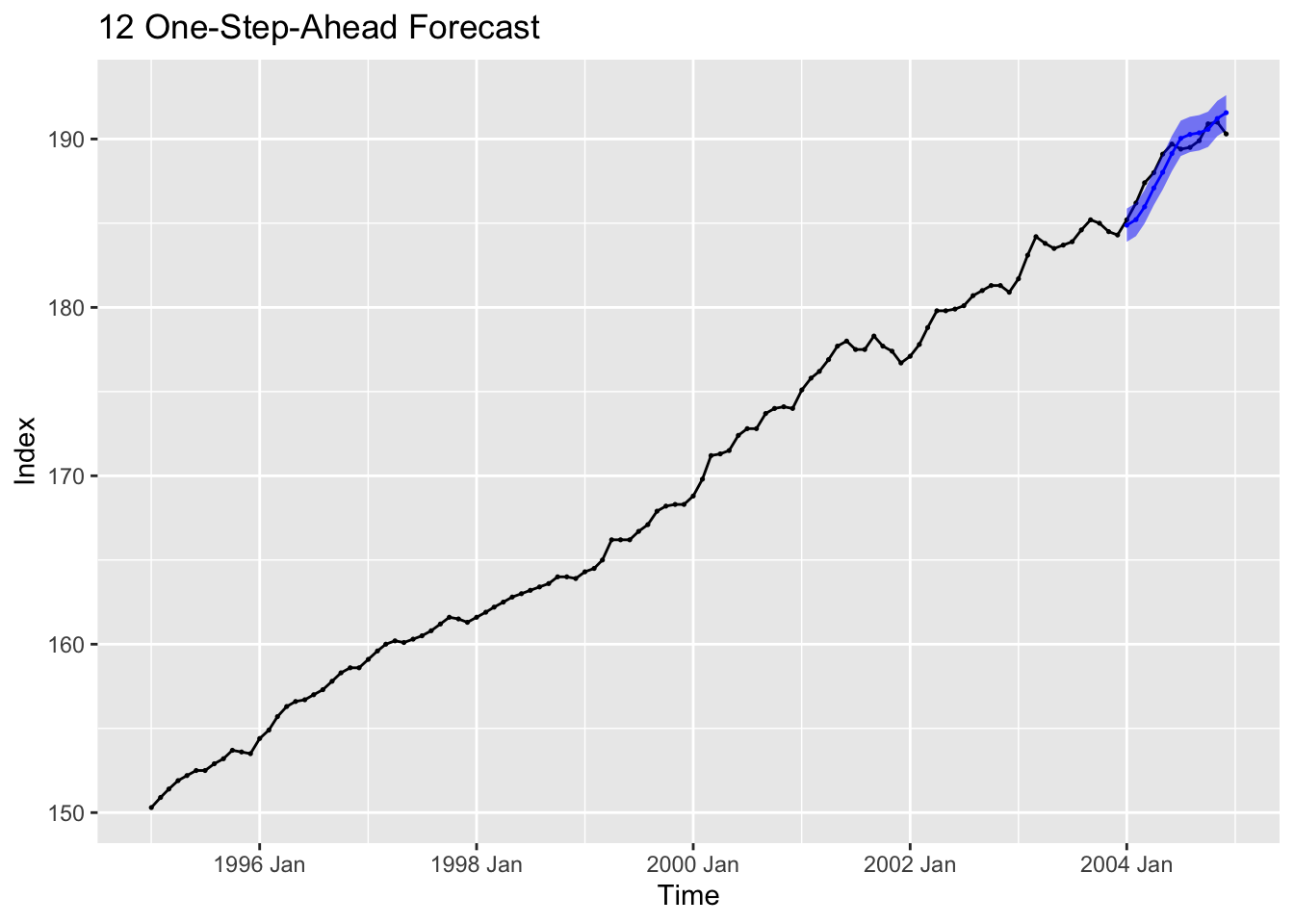

In fable, it is only possible to automatically do a 1 to 12 step ahead forecast. In the code chunk below, I estimate a 12 step ahead forecast using an analogous model in fable.

cpi.fit2 <- cpi.data |> filter(year(time) < 2004) |>
  model(ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N"))) 

cpi.fit2 |> tidy() |> mutate(estimate = round(estimate, digits = 3)) |> gt()
.model term estimate
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) alpha 0.300
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) beta 0.300
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) l[0] 149.952
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) b[0] 0.628
 
cpi.fc3 <- cpi.fit2 |> 
  forecast(new_data = cpi.data |> filter(year(time) > 2003)) 

cpi.fc3 |> accuracy(cpi.data |> filter(year(time) > 2003)) |>  mutate_if(is.numeric, dig) |> gt()
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")) Test 5.075 5.54 5.075 2.676 2.676 NaN NaN 0.723
 
cpi.fc3 |>
  autoplot(cpi.data)

To calculate 12 one-step-ahead forecasts using fable, I use a for loop to iteratively get all one step ahead forecasts for T+1 to T+tau. I then graph the results of this process against the test set.

one_step_for <- vector(mode = "list", length = 12) # create vectors to store the one step ahead forecasts
one_step_upper <- vector(mode = "list", length = 12)
one_step_lower <- vector(mode = "list", length = 12)

T <- 108 # define T
for (i in (T+1):(T+tau)){ # iterate 12 times, i = current period to forecast for
  cpi.fit3 <- cpi.data[1:T,] |> # create a model with training data to one before i
    model(ETS(index ~ error("A") + trend("A", alpha = 0.3, beta = 0.3) + season("N")))
  
  cpi.forecast2 <-  cpi.fit3 |> # create a one step ahead forecast
    forecast(new_data = cpi.data[(T+1),])
  
  one_step_for[i - 108] <- cpi.forecast2$.mean # record the mean
  interval <- hilo(cpi.forecast2$index) # split the distribution into upper and lower bounds
  one_step_upper[i - 108] <- interval$upper # record upper and lower
  one_step_lower[i - 108] <- interval$lower
  T <- T + 1 # update T
}

cpi.fc.tibble <- tibble(mean = one_step_for, # create a tibble containing mean and upper and lower bounds
                        lower = one_step_lower,
                        upper = one_step_upper) |> 
  mutate_all(as.numeric) |> 
  mutate(time = cpi.data$time[109:120])

cpi.data |> # plot the results
  left_join(cpi.fc.tibble, by = join_by(time)) |>
  ggplot(aes(x = time, y = index)) +
  geom_point(size = 0.25) +
  geom_line() + 
  geom_point(aes(y = mean), color = "blue", size = 0.25, na.rm = TRUE) + 
  geom_line(aes(y = mean), color = "blue", na.rm = TRUE) + 
  geom_ribbon(aes(ymin = lower, ymax = upper), fill = "blue", alpha = 0.5) + 
  labs(title = "12 One-Step Ahead Forecasts", 
       subtitle = "alpha = 0.3, beta = 0.3",
       x = "Time",
       y = "Index")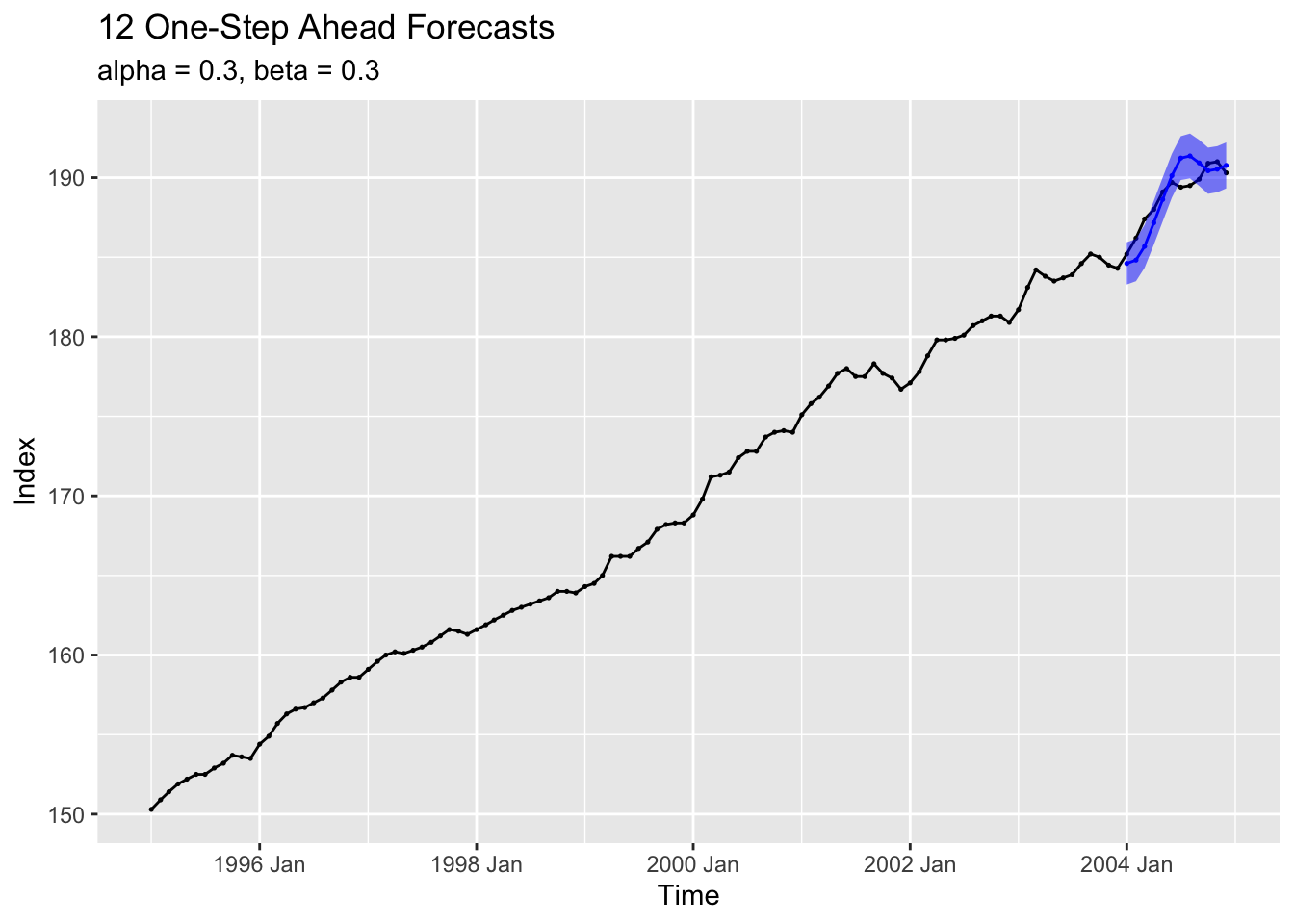

4.10.7 Example 4.6: Adaptive Updating of the Discount Factor, Lambda

The Trigg-Leach method adaptively updates the discount factor. In the code chunk below, I define a custom function for the Trigg-Leach smoother.

#First, we define the Trigg-Leach Updating function:
tlsmooth<-function(y, gamma, y.tilde.start=y[1], lambda.start=1){
  T <- length(y)
  
  #Initialize the vectors
  Qt <- vector()
  Dt <- vector()
  y.tilde <- vector()
  lambda <- vector()
  err <- vector()
  
  #Set the starting values for the vectors
  lambda[1] = lambda.start
  y.tilde[1] = y.tilde.start
  Qt[1] <- 0
  Dt[1] <- 0
  err[1] <- 0
  
  for (i in 2:T){
    err[i] <- y[i] - y.tilde[i-1]
    Qt[i] <- gamma*err[i] + (1-gamma)*Qt[i-1]
    Dt[i] <- gamma*abs(err[i]) + (1-gamma)*Dt[i-1]
    lambda[i] <- abs(Qt[i]/Dt[i])
    y.tilde[i] = lambda[i]*y[i] + (1-lambda[i])*y.tilde[i-1]
  }
  return(cbind(y.tilde, lambda, err, Qt, Dt))
}

Then, I run this function and first_smooth() on the dow_jones data.

#Obtain the exponential smoother for Dow Jones Index
dji.smooth1 <- firstsmooth(y=dow_jones$index, lambda=0.4)

#Now, we apply the Trigg-Leach Smoothing function to the Dow Jones Index:
out.tl.dji <- tlsmooth(dow_jones$index, 0.3)

Plotting the results of both these methods with the original data, it is clear that the adaptive updating of the smoothing parameter leads to a better fit with this data.

#Plot the data together with TL and exponential smoother for comparison
dow_jones |>
  ggplot(aes(x = time, y = index)) + 
  geom_point(aes(color = "Original Data"), size = 0.5) + 
  geom_line(aes(color = "Original Data")) +
  geom_point(aes(y = dji.smooth1, color = "Simple Smooth"), size = 0.5) + 
  geom_line(aes(y = dji.smooth1, color = "Simple Smooth")) + 
  geom_point(aes(y = out.tl.dji[,1], color = "Trigg-Leach Smooth"), size = 0.5) + 
  geom_line(aes(y = out.tl.dji[,1], color = "Trigg-Leach Smooth")) + 
  scale_color_manual(values = c('Original Data' = "black", 
                                "Simple Smooth" = "blue",
                                "Trigg-Leach Smooth" = "red")) + 
  labs(title = "Plot of Dow Jones, First Smoothed, and Trigg-Leach Smoothed Data",
       x = "Time",
       y = "Index")

This method only applies to a simple exponential smoother and is not included in the fable package, so it must be done using custom functions.

4.10.8 Example 4.7: Exponential Smoothing for Additive Seasonal Model

In this section we will use clothing sales data contained in ClothingSales.csv.36 In the code chunk below, I read in the data and create a tsibble object to store it.

(clothing <- read_csv("data/ClothingSales.csv") |> mutate(year = case_when(
  str_sub(Date, start = 5, end = 5) == "9" ~ str_c("19", str_sub(Date, start = 5, end = 6)),
  substr(Date, 5, 5) == "0" ~ str_c("20", str_sub(Date, start = 5, end = 6)),
  str_sub(Date, start = 1, end = 1) == "0" ~ str_c("20", str_sub(Date, start = 1, end = 2))
  )) |>
  mutate(month = case_when(str_sub(Date, 1, 1) == "0" ~ str_sub(Date, start = 4, end = 6),
                           str_sub(Date, 1, 1) != "0" ~ str_sub(Date, start = 1, end = 3)
                           )) |>
  mutate(time = yearmonth(str_c(year,"-",month))) |>
  select(time, Sales) |>
  rename(sales = Sales) |> 
  as_tsibble(index = time))
## Rows: 144 Columns: 2
## ── Column specification ───────────────────────────────────────
## Delimiter: ","
## chr (1): Date
## dbl (1): Sales
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
## # A tsibble: 144 x 2 [1M]
##        time sales
##       <mth> <dbl>
##  1 1992 Jan  4889
##  2 1992 Feb  5197
##  3 1992 Mar  6061
##  4 1992 Apr  6720
##  5 1992 May  6811
##  6 1992 Jun  6579
##  7 1992 Jul  6598
##  8 1992 Aug  7536
##  9 1992 Sep  6923
## 10 1992 Oct  7566
## # ℹ 134 more rows

The holdout sample for this example is the first 132/144 observations. In the code chunk below, I use the HoltWinters() function to create an additive model where alpha = 0.2, beta. 0.2, and gamma = 0.2. I then plot that model against the original series and create forecasts, which I plot against the test sample.

clo.hw1 <- HoltWinters(clothing |> filter(year(time) < 2003), alpha=0.2, beta=0.2, gamma=0.2, seasonal="additive")
# create the additive model
# lose 12 observations
clothing |> 
  filter(year(time) < 2003 & year(time) > 1992) |> # filter data so it is the proper time frame
  ggplot(aes(x = time, y = sales)) + 
  geom_point(aes(color = "Original"), size = 0.5) + 
  geom_line(aes(color = "Original")) + 
  geom_point(aes(y = clo.hw1[["fitted"]][,1], color = "Fitted"), size = 0.5) + 
  geom_line(aes(y = clo.hw1[["fitted"]][,1], color = "Fitted")) + 
  scale_color_manual(values = c("Fitted" = "red", "Original" = "black")) + 
  labs(title = "Clothing Sales Data Additive Seasonal Model",
       subtitle = "Alpha = 0.2, Beta = 0.2, Gamma = 0.2", 
       x = "Time", 
       y = "Sales",
       color = "Data")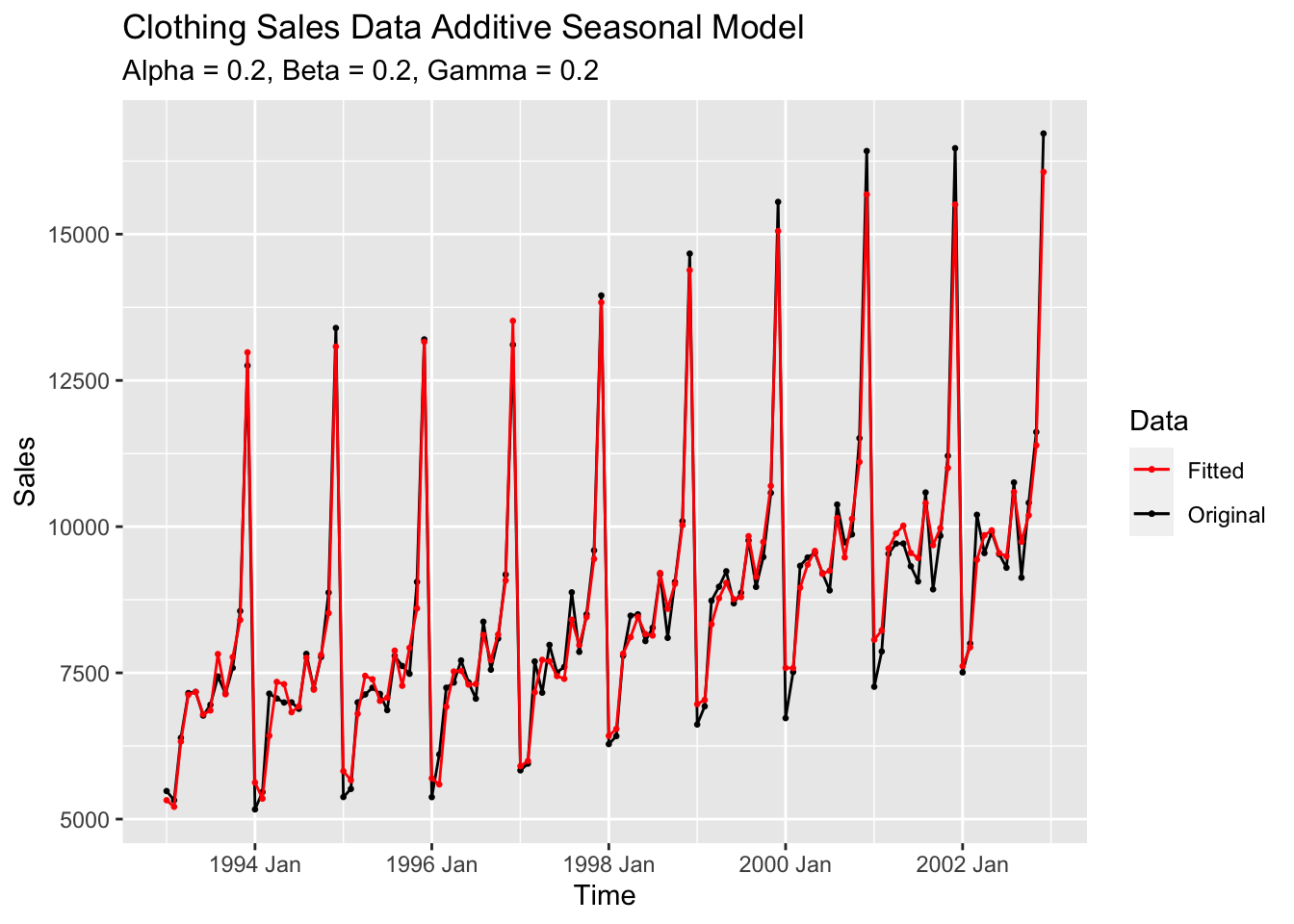

y2.forecast <- predict(clo.hw1, n.ahead=12, prediction.interval=TRUE)
# create forecasts

forecast <- tsibble(time = clothing$time[133:144],
        fit = y2.forecast[,1],
        upper = y2.forecast[,2],
        lower = y2.forecast[,3], 
        index = time) # make tibble to store forecasts

clothing |>
  left_join(forecast, by = join_by(time)) |> #join forecasts with data
  ggplot(aes(x = time, y = sales)) +
  geom_point(size = 0.5) + 
  geom_line() + 
  geom_line(aes(y = fit), color = "blue", na.rm = TRUE) + 
  geom_point(aes(y = fit), color = "blue", na.rm = TRUE) + 
  geom_ribbon(aes(ymin = lower, ymax = upper), fill = "blue", alpha = 0.5) + 
  labs(title = "Clothing Sales Data Additive Seasonal Model Forecast",
       subtitle = "Alpha = 0.2, Beta = 0.2, Gamma = 0.2", 
       x = "Time", 
       y = "Sales")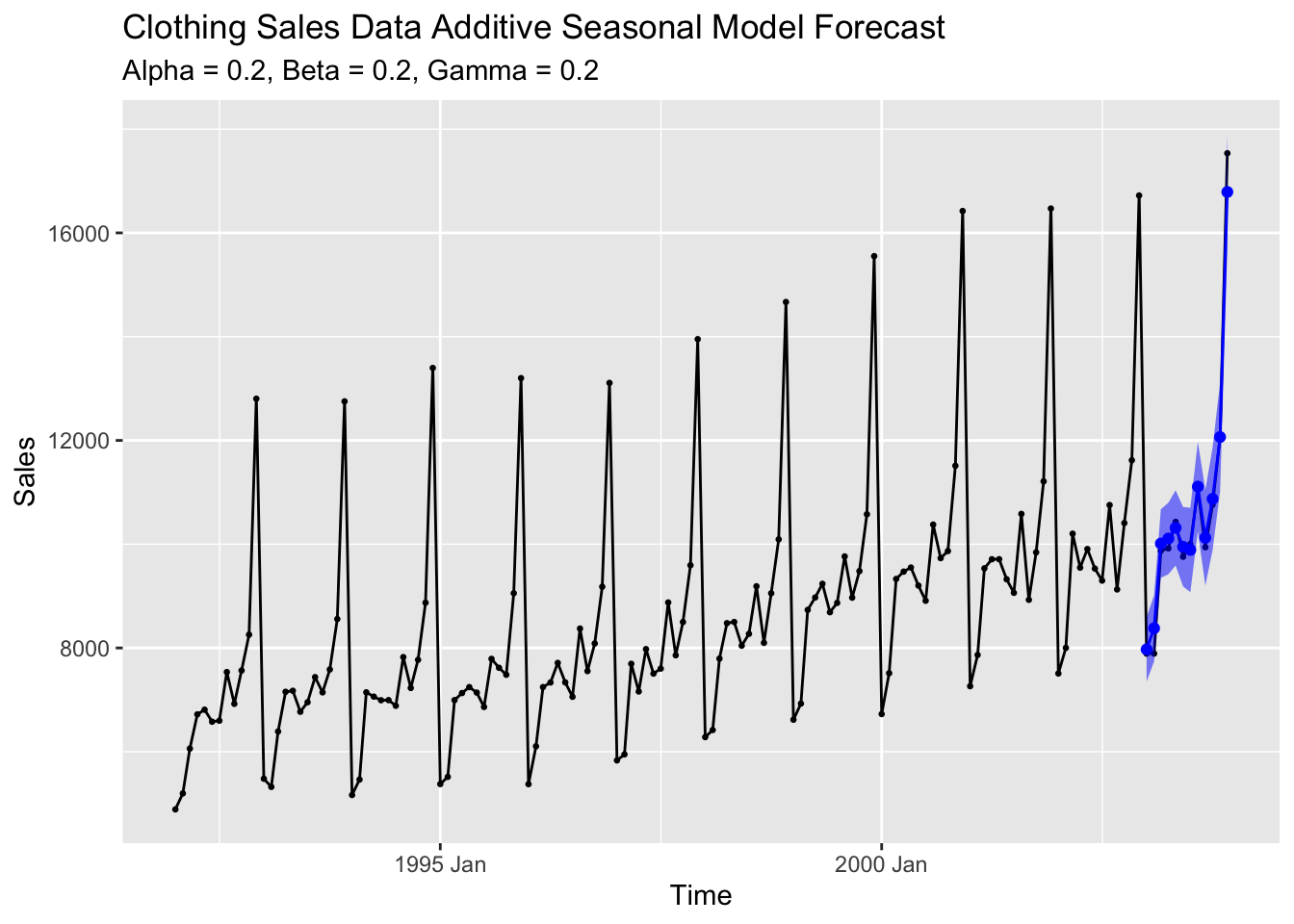

4.10.9 Example 4.8: Exponential Smoothing for Multiplicative Seasonal Model

For this example we will use liquor sales data from LiquorSales.csv.37 In the code chunk below, I read in the data and create a tsibble object to store it.

(liquor <- read_csv("data/LiquorSales.csv") |> 
  mutate(year = case_when(
    str_sub(Date, start = 5, end = 5) == "9" ~ str_c("19", str_sub(Date, start = 5, end = 6)),
    substr(Date, 5, 5) == "0" ~ str_c("20", str_sub(Date, start = 5, end = 6)),
    str_sub(Date, start = 1, end = 1) == "0" ~ str_c("20", str_sub(Date, start = 1, end = 2))
    )) |>
  mutate(month = case_when(str_sub(Date, 1, 1) == "0" ~ str_sub(Date, start = 4, end = 6),
                           str_sub(Date, 1, 1) != "0" ~ str_sub(Date, start = 1, end = 3)
                           )) |>
  mutate(time = yearmonth(str_c(year,"-",month))) |>
  select(time, Sales) |> 
  rename(sales = Sales) |> 
  as_tsibble(index = time))
## Rows: 156 Columns: 2
## ── Column specification ───────────────────────────────────────
## Delimiter: ","
## chr (1): Date
## dbl (1): Sales
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
## # A tsibble: 156 x 2 [1M]
##        time sales
##       <mth> <dbl>
##  1 1992 Jan  1519
##  2 1992 Feb  1551
##  3 1992 Mar  1606
##  4 1992 Apr  1686
##  5 1992 May  1834
##  6 1992 Jun  1786
##  7 1992 Jul  1924
##  8 1992 Aug  1874
##  9 1992 Sep  1781
## 10 1992 Oct  1894
## # ℹ 146 more rows

I then create an additive and multiplicative model of the whole data set, as well as a multiplicative model of just the holdout sample of the first 144 observations. I create 12 step-ahead forecasts for the model of the training set and put the results in a tibble.

liq.hw.add <- HoltWinters(liquor, alpha=0.2, beta=0.2, gamma=0.2, seasonal="additive")

liq.hw.mult<-HoltWinters(liquor, alpha=0.2, beta=0.2, gamma=0.2, seasonal="multiplicative")

liq.hw1 <- HoltWinters(liquor |> filter(year(time) < 2004), alpha=0.2, beta=0.2, gamma=0.2, seasonal="multiplicative")

y2.forecast <- predict(liq.hw1, n.ahead=12, prediction.interval = TRUE)

forecast2 <- tsibble(time = liquor$time[145:156],
        fit = y2.forecast[,1],
        upper = y2.forecast[,2],
        lower = y2.forecast[,3], 
        index = time)

I then plot the additive and multiplicative model each in their own plots against the original data, and plot the forecasts against the test set.

liquor |>
  filter(year(time) > 1992) |>
  ggplot(aes(x = time, y = sales)) + 
  geom_point(aes(color = "Original Data"), size = 0.5) + 
  geom_line(aes(color = "Original Data")) + 
  geom_point(aes(y = liq.hw.add$fitted[,1], color = "Additive Model"), size = 0.5) + 
  geom_line(aes(y = liq.hw.add$fitted[,1], color = "Additive Model")) + 
  scale_color_manual(values = c("Original Data" = "black", "Additive Model" = "red")) + 
  labs(title = "Plot of Liquor Sales Data and Additive Model vs. Time", 
       x = "Time", 
       y = "Sales")

liquor |>
  filter(year(time) > 1992) |>
  ggplot(aes(x = time, y = sales)) + 
  geom_point(aes(color = "Original Data"), size = 0.5) + 
  geom_line(aes(color = "Original Data")) + 
  geom_point(aes(y = liq.hw.mult$fitted[,1], color = "Multiplicative Model"), size = 0.5) + 
  geom_line(aes(y = liq.hw.mult$fitted[,1], color = "Multiplicative Model")) + 
  scale_color_manual(values = c("Original Data" = "black", "Multiplicative Model" = "blue")) + 
  labs(title = "Plot of Liquor Sales Data and Multiplicative Model vs. Time", 
       x = "Time", 
       y = "Sales")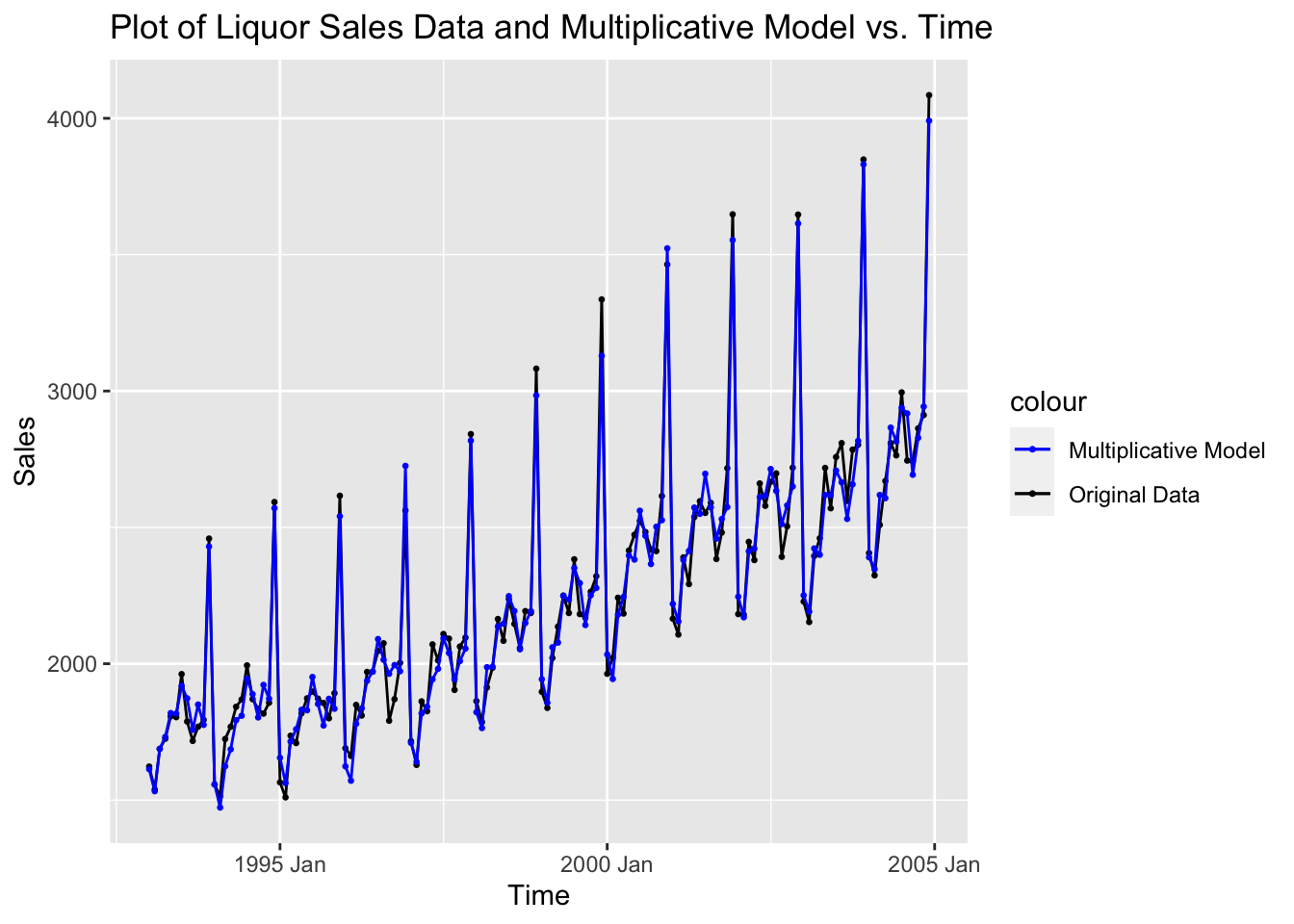

liquor |>
  left_join(forecast2, by = join_by(time)) |>
  ggplot(aes(x = time, y = sales)) +
  geom_point(size = 0.5) + 
  geom_line() + 
  geom_line(aes(y = fit), color = "blue", na.rm = TRUE) + 
  geom_point(aes(y = fit), color = "blue", na.rm = TRUE) + 
  geom_ribbon(aes(ymin = lower, ymax = upper), fill = "blue", alpha = 0.5)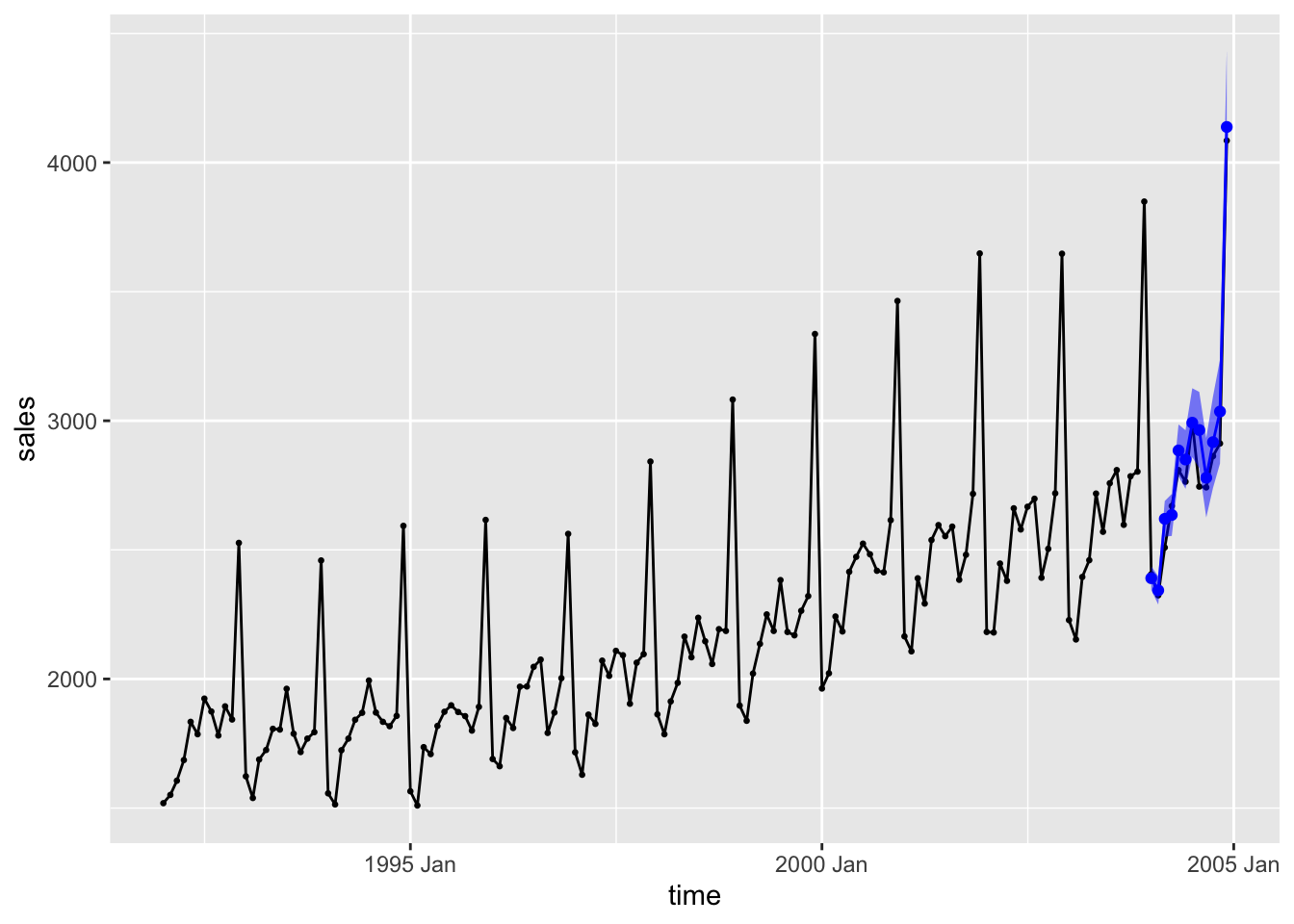

4.10.10 Comparing an Additive and Multiplicative ETS Models

This section compares the possible ETS models within a single model object in fable. We use the liquor sales data from the last example as the data in this section. In the model object, I create three different models, an optimized model with all additive components, an optimized model with all multiplicative components, and a model that is the best model chosen from all possible ETS() models. The holdout sample will be all data before 2004 (1:144), and the test set will be the 2004 data (145:156).

liquor.fit <- liquor |> 
  filter(year(time) < 2004) |>
           model(additive = ETS(sales ~ error("A") + trend("A") + season("A")),
                 multiplicative = ETS(sales ~ error("M") + trend("M") + season("M")),
                 opt = ETS(sales))

To compare the models at first glance, I use the custom function below to generate reports for each one.

gen_report <- function(models){
  for (i in 1: length(models)){
    print(colnames(models)[i])
    report(models[i])
  }
}
gen_report(liquor.fit)
## [1] "additive"
## Series: sales 
## Model: ETS(A,A,A) 
##   Smoothing parameters:
##     alpha = 0.3014984 
##     beta  = 0.0001003563 
##     gamma = 0.6985013 
## 
##   Initial states:
##      l[0]     b[0]     s[0]    s[-1]     s[-2]    s[-3]    s[-4]   s[-5]
##  1852.093 6.344784 835.0637 50.29692 -27.55822 -96.8937 32.12562 96.7324
##      s[-6]    s[-7]     s[-8]     s[-9]    s[-10]    s[-11]
##  -2.986356 25.68023 -143.6287 -137.9088 -344.6557 -286.2675
## 
##   sigma^2:  5402.729
## 
##      AIC     AICc      BIC 
## 1970.323 1975.180 2020.810 
## [1] "multiplicative"
## Series: sales 
## Model: ETS(M,M,M) 
##   Smoothing parameters:
##     alpha = 0.2025417 
##     beta  = 0.01421412 
##     gamma = 0.0001043186 
## 
##   Initial states:
##      l[0]     b[0]     s[0]    s[-1]     s[-2]     s[-3]    s[-4]    s[-5]
##  1820.413 1.002463 1.387258 1.018877 0.9894544 0.9581219 1.019136 1.051209
##      s[-6]    s[-7]     s[-8]     s[-9]   s[-10]    s[-11]
##  0.9957197 1.012082 0.9332928 0.9313566 0.843961 0.8595313
## 
##   sigma^2:  8e-04
## 
##      AIC     AICc      BIC 
## 1905.049 1909.906 1955.536 
## [1] "opt"
## Series: sales 
## Model: ETS(M,A,M) 
##   Smoothing parameters:
##     alpha = 0.1975246 
##     beta  = 0.01101548 
##     gamma = 0.0004288403 
## 
##   Initial states:
##      l[0]      b[0]    s[0]    s[-1]    s[-2]     s[-3]    s[-4]    s[-5]
##  1819.605 0.4247737 1.38356 1.021844 0.991333 0.9542633 1.022034 1.046424
##      s[-6]    s[-7]     s[-8]     s[-9]    s[-10]    s[-11]
##  0.9957946 1.014296 0.9328883 0.9313987 0.8427128 0.8634506
## 
##   sigma^2:  8e-04
## 
##      AIC     AICc      BIC 
## 1903.879 1908.736 1954.366

The completely optimized model has the lowest AIC, AICc, and BIC indicating that it has the most promise of the models we are evaluating. It uses multiplicative errors and seasonal components with an additive trend component. The both the multiplicative model and the optimal model have beta and gamma parameters close to zero, indicating that these components have little effect on the model as a whole. Next, I generate a table of the parameters of each model as well as a table of different measures of accuracy for each model.

liquor.fit |> tidy() |> mutate(estimate = round(estimate, digits = 3)) |> gt()
.model term estimate
additive alpha 0.301
additive beta 0.000
additive gamma 0.699
additive l[0] 1852.093
additive b[0] 6.345
additive s[0] 835.064
additive s[-1] 50.297
additive s[-2] -27.558
additive s[-3] -96.894
additive s[-4] 32.126
additive s[-5] 96.732
additive s[-6] -2.986
additive s[-7] 25.680
additive s[-8] -143.629
additive s[-9] -137.909
additive s[-10] -344.656
additive s[-11] -286.268
multiplicative alpha 0.203
multiplicative beta 0.014
multiplicative gamma 0.000
multiplicative l[0] 1820.413
multiplicative b[0] 1.002
multiplicative s[0] 1.387
multiplicative s[-1] 1.019
multiplicative s[-2] 0.989
multiplicative s[-3] 0.958
multiplicative s[-4] 1.019
multiplicative s[-5] 1.051
multiplicative s[-6] 0.996
multiplicative s[-7] 1.012
multiplicative s[-8] 0.933
multiplicative s[-9] 0.931
multiplicative s[-10] 0.844
multiplicative s[-11] 0.860
opt alpha 0.198
opt beta 0.011
opt gamma 0.000
opt l[0] 1819.605
opt b[0] 0.425
opt s[0] 1.384
opt s[-1] 1.022
opt s[-2] 0.991
opt s[-3] 0.954
opt s[-4] 1.022
opt s[-5] 1.046
opt s[-6] 0.996
opt s[-7] 1.014
opt s[-8] 0.933
opt s[-9] 0.931
opt s[-10] 0.843
opt s[-11] 0.863
 
liquor.fit |> accuracy() |> mutate_if(is.numeric, dig) |> gt()
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
additive Training 0.262 69.300 54.351 -0.140 2.530 0.582 0.594 -0.107
multiplicative Training 1.022 57.165 45.501 -0.012 2.122 0.487 0.490 -0.005
opt Training 5.923 56.727 45.482 0.218 2.122 0.487 0.487 -0.014

The next step is to plot each model against the original series.

augment(liquor.fit |> select(additive)) |>
  ggplot(aes(x = time, y = sales)) + 
  geom_point(aes(color = "Original"),size = 0.25) +
  geom_line(aes(color = "Original")) + 
  geom_point(aes(y = .fitted, color = "Fitted"),size = 0.25) + 
  geom_line(aes(y = .fitted, color = "Fitted")) + 
  scale_color_manual(values = c("Fitted" = "red", "Original" = "black")) +
  labs(title = "Plot of ETS(A,A,A) Model",
       subtitle = "alpha = 0.301, beta = 0.000, gamma = 0.699",
       color = "Data",
       x = "Time",
       y = "Sales")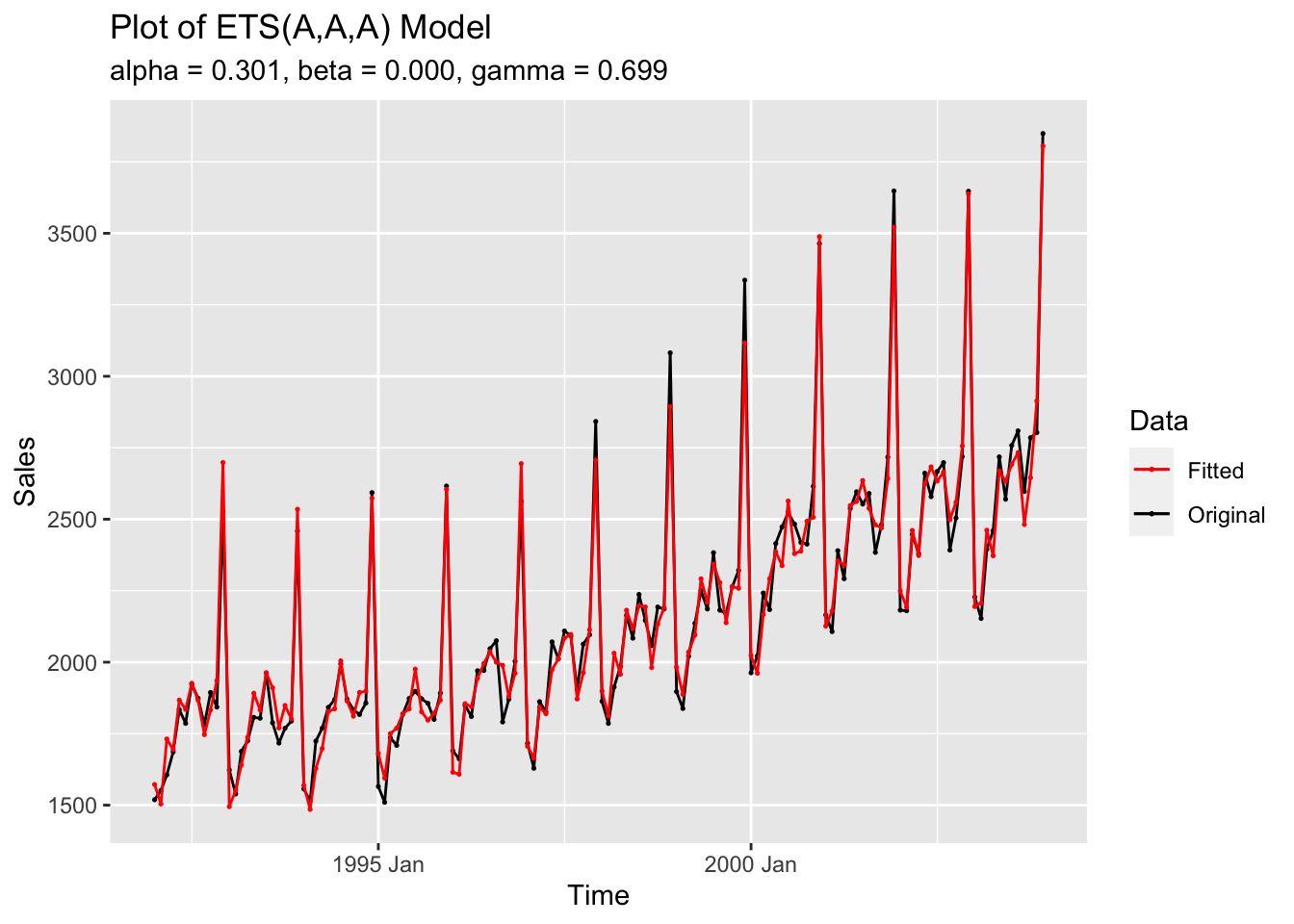

augment(liquor.fit |> select(multiplicative)) |>
  ggplot(aes(x = time, y = sales)) + 
  geom_point(aes(color = "Original"),size = 0.25) +
  geom_line(aes(color = "Original")) + 
  geom_point(aes(y = .fitted, color = "Fitted"),size = 0.25) + 
  geom_line(aes(y = .fitted, color = "Fitted")) + 
  scale_color_manual(values = c("Fitted" = "red", "Original" = "black")) +
  labs(title = "Plot of ETS(M,M,M) Model",
       subtitle = "alpha = 0.203, beta = 0.014, gamma = 0.000",
       color = "Data",
       x = "Time",
       y = "Sales")

augment(liquor.fit |> select(opt)) |>
  ggplot(aes(x = time, y = sales)) + 
  geom_point(aes(color = "Original"),size = 0.25) +
  geom_line(aes(color = "Original")) + 
  geom_point(aes(y = .fitted, color = "Fitted"),size = 0.25) + 
  geom_line(aes(y = .fitted, color = "Fitted")) + 
  scale_color_manual(values = c("Fitted" = "red", "Original" = "black")) +
  labs(title = "Plot of ETS(M,A,M) Model",
       subtitle = "alpha = 0.198, beta = 0.011, gamma = 0.000",
       color = "Data",
       x = "Time",
       y = "Sales")

Next, I plot the residuals for each model using plot_residuals().

plot_residuals(augment(liquor.fit |> select(additive)), title = "ETS(A,A,A) Model")
## # A tibble: 1 × 3
##   .model   lb_stat lb_pvalue
##   <chr>      <dbl>     <dbl>
## 1 additive    1.69     0.194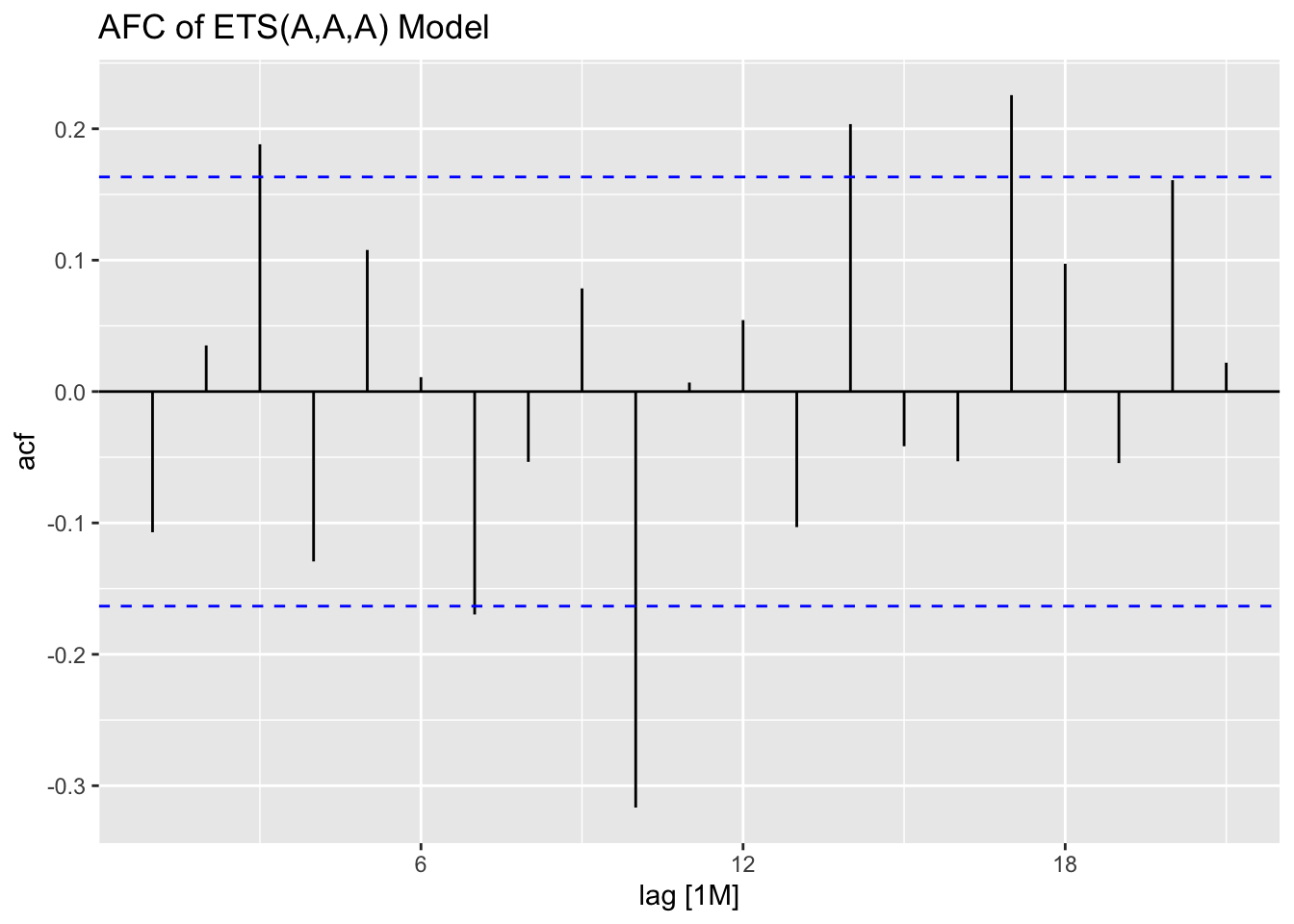

plot_residuals(augment(liquor.fit |> select(multiplicative)), title = "ETS(M,M,M) Model")
## # A tibble: 1 × 3
##   .model         lb_stat lb_pvalue
##   <chr>            <dbl>     <dbl>
## 1 multiplicative 0.00391     0.950

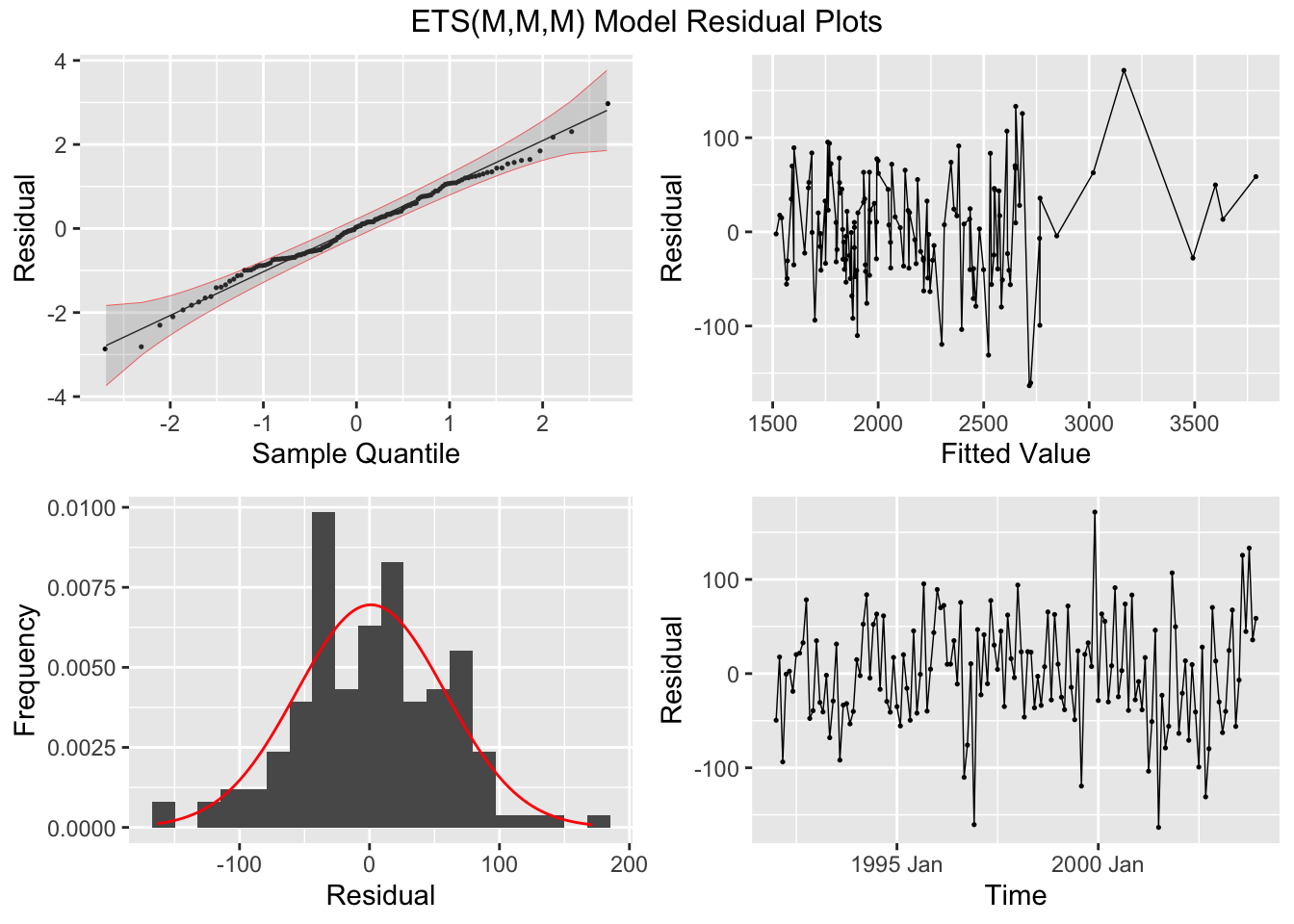
plot_residuals(augment(liquor.fit |> select(opt)), title = "ETS(M,A,M) Model")
## # A tibble: 1 × 3
##   .model lb_stat lb_pvalue
##   <chr>    <dbl>     <dbl>
## 1 opt     0.0304     0.861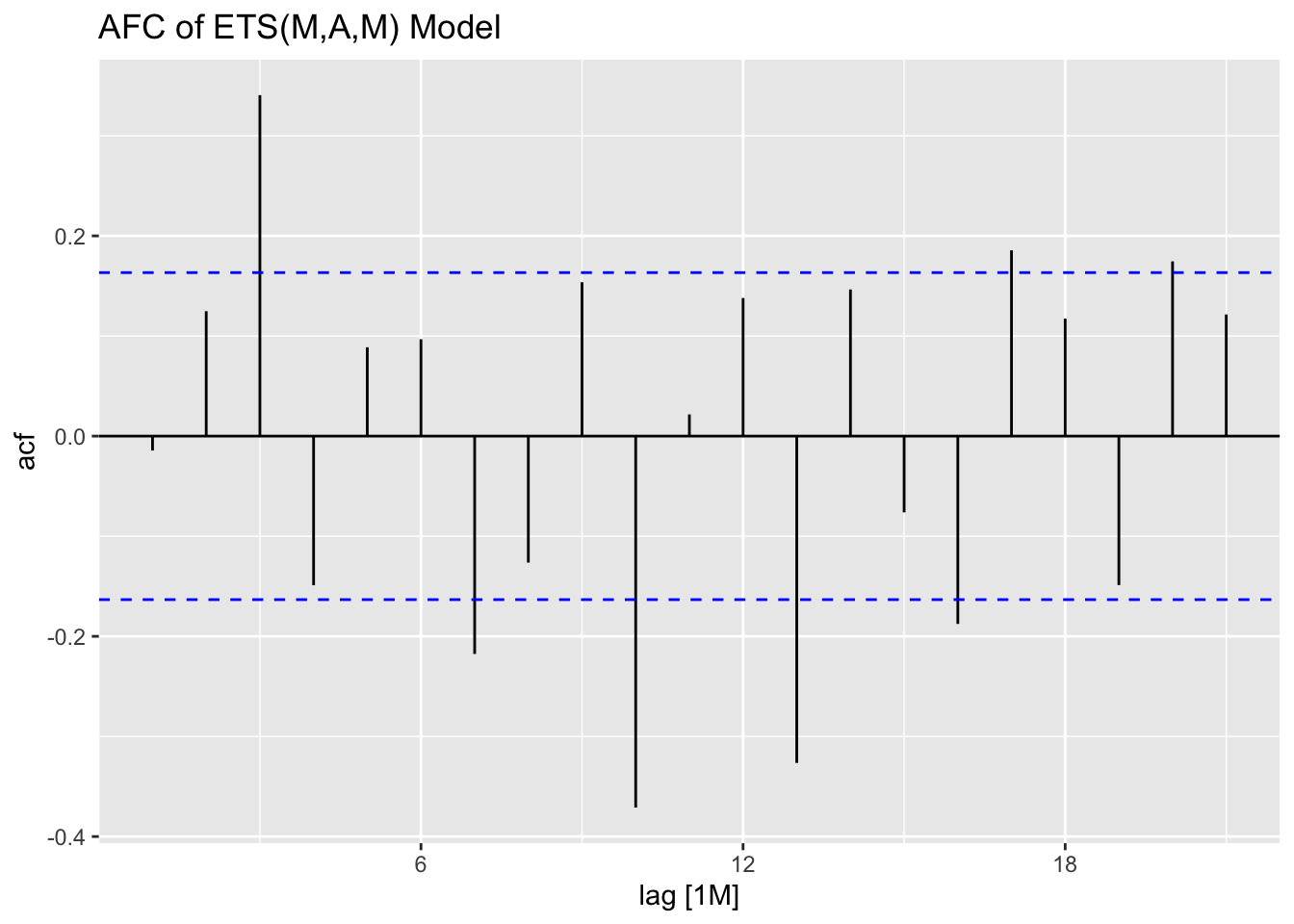

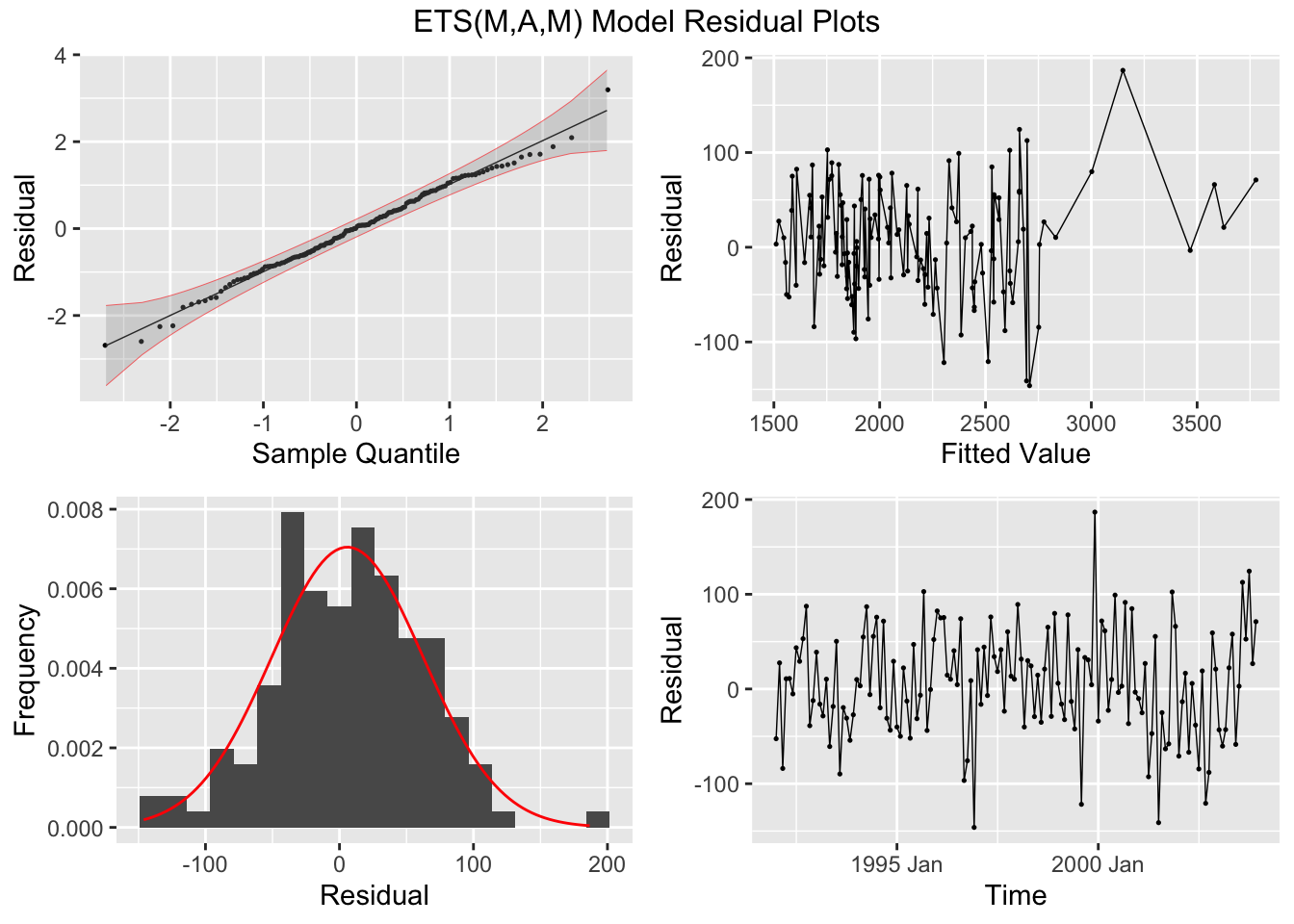
Then, I generate forecasts for each model, plot the forecasts for each model against each other, and make a table of the measure of accuracy for the test set. Looking at the results of the accuracy table, the. multiplicative model outperformed the other two, but all these models generate comparable forecasts.

liquor.fc <- forecast(liquor.fit, new_data = liquor |> filter(year(time) == 2004))

liquor.fc |> autoplot(liquor[145:156,]) + facet_wrap(~.model)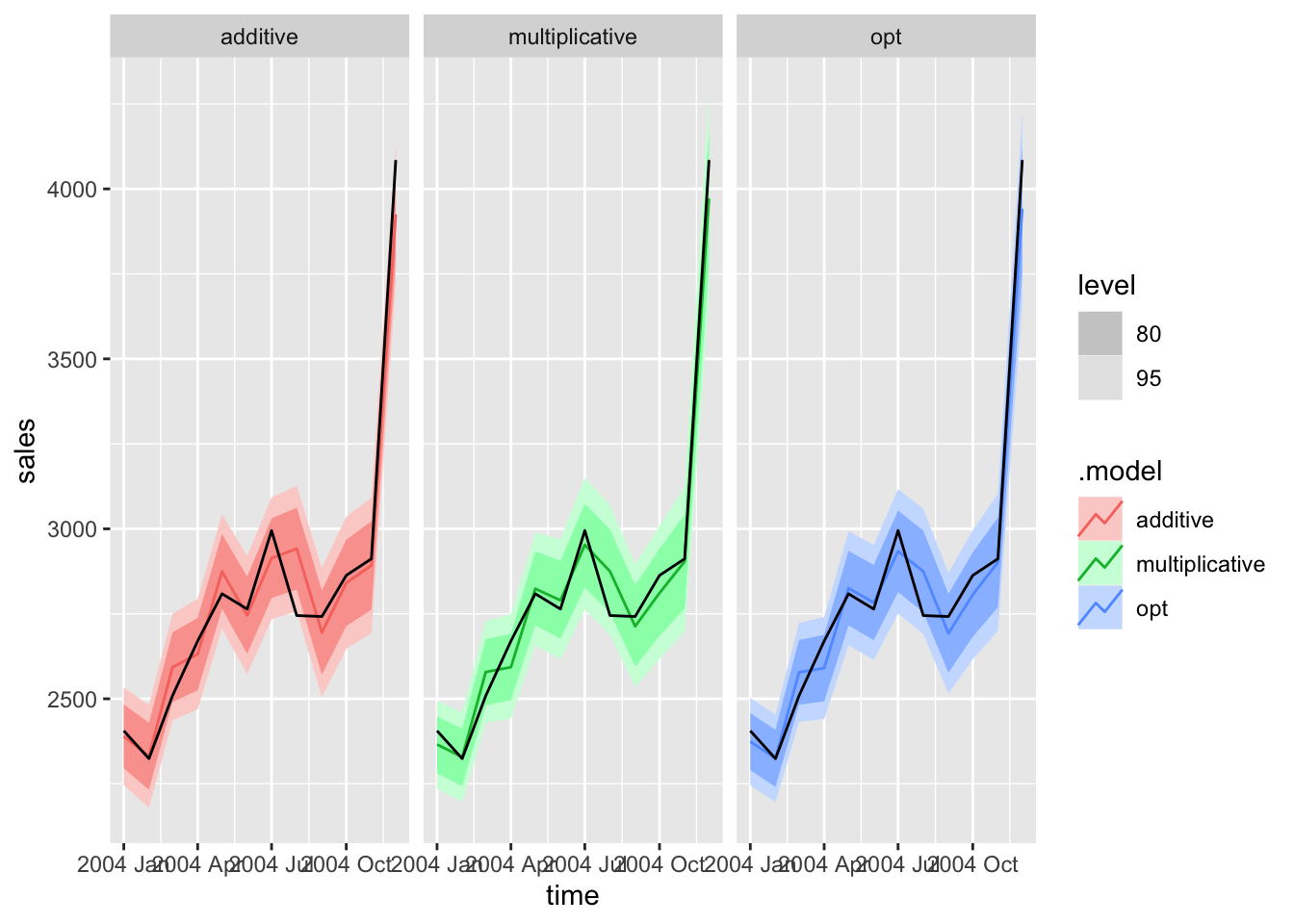

accuracy(liquor.fc, liquor) |> mutate_if(is.numeric, dig) |> gt()
.model .type ME RMSE MAE MPE MAPE MASE RMSSE ACF1
additive Test 4.141 85.361 63.019 -0.048 2.143 0.675 0.732 -0.288
multiplicative Test 9.641 63.457 50.456 0.223 1.752 0.540 0.544 -0.280
opt Test 16.428 70.465 55.576 0.433 1.897 0.595 0.604 -0.315

References

Hyndman, Rob J, and George Athanasopoulos. Forecasting Principles and Practice. Vol. 3. Melbourne, Australia: OTexts, 2021.
Montgomery, Douglas C, Cheryl L. Jennings, and Murat Kulahci. Introduction to Time Series Analysis and Forecasting. Vol. 2. Hoboken, New Jersey: John Wiley & Sons, 2016.

  1. Montgomery, Jennings, and Kulahci.↩︎

  2. Montgomery, Jennings, and Kulahci.↩︎

  3. Hyndman and Athanasopoulos, Forecasting Principles and Practice.↩︎

  4. Montgomery, Jennings, and Kulahci, Introduction to Time Series Analysis and Forecasting.↩︎

  5. Montgomery, Jennings, and Kulahci.↩︎

  6. Montgomery, Jennings, and Kulahci.↩︎