BLOQUE 4: Simulación de variables aleatorias

En este bloque vamos a aprender técnicas de simulación de números aleatorios. De esta forma, aprenderemos-mediante la experimentación- conceptos de variables aleatorias, y veremos una nueva técnica de estimación llamada “bootstrap”.

Clase 1. Introducción a los generadores de números aleatorios

Vamos a aprender cómo las máquinas generan números aleatorios. ¿Para qué los necesitamos? Como ha visto en este texto, algunos de los algoritmos más famosos con los que ha trabajado tienen como punto de partida una selección aleatoria de elementos de la muestra. Para poder hacer eso, [R] necesita saber cómo buscar dichos números aleatorios. Para ello, vamos a aprender un método de generación de variables aleatorias que se denomina generador congruencial.

Repaso de aritmética modular

Como seguro que ya sabe, en informática, la operación módulo \((mod)\) obtiene el resto de la división de un número entre otro. Dados dos números positivos, \(a\) (el numerador) y \(b\) (el denominador), \(a\) \(mod\) \(b\) es el resto de la división de a entre b. Por ejemplo, la expresión \(5\) \(mod\) \(2\) se evalúa a 1 porque 5 dividido entre 2 da un cociente de 2 y un resto de 1 (es decir \({\color{red}5}=2\times{\color{blue}2}+1)\), mientras que \(9\) \(mod\) \(3\) se evaluaría a 0. porque la división de 9 entre 3 tiene un cociente de 3 y da un resto de 0. ¿Y cómo se evalúa \(3\:mod\;9?\) En este caso, \(3=0\times9+3\), por lo que cuando el numerador es menor que el denominador, el módulo es el numerador.

Un generador congruencial

Queremos tener una máquina que simule a un niño de San Ildefonso. Imagine que tiene el conjunto \(\{0,1,2,3,4,5,6,7,8\}\) y le gustaría tener un niño de San Ildefonso autómata que fuera extrayendo números al azar. ¡Hay una manera muy sencilla!

\[\begin{equation} X_{n+1}=(aX_{n}+c)\:mod\:m\label{eq:congruencial} \end{equation}\]

donde

\(m>0\) es el módulo

\(0<a<m\) es el multiplicador

\(0\leq c<m\) es el incremento

\(0\leq X_{0}<m\) es la semilla.

Supongamos que \(a=2,m=9\) y \(c=0\). Supongamos que \(X_{0}=1.\) ¿Cómo obtenemos el resto de números aleatorios?

\[ X_{1}=(2X_{0}+0)\:mod\:9 \]

es decir, \(X_{1}=2\:mod\:9=2\)

¿Y el siguiente?

\[ X_{2}=(2\times2+0)\:mod\:9=4 \]

Ejercicio Complete el siguiente script para que [R] genere los números aleatorios

 #parámetros iniciales
m <- 9 
a <- 2 
c <- 0  
x <- 1  
aleat<-rep(0,20) #queremos obtener 20 resultados
aleat[1]<-1 #inicializamos el vector resultados
for (i in 2:20) {   
 $ x <- (a * x + c) %% m
  aleat[i] <- x }   #almacenamos los números

Si imprime la salida, obtendrá lo siguiente

1 2 4 8 7 5 \({\color{red}{1 2 4 8 7 5}}\)\({\color{green}{1 2 4 8 7 5}}\)\({\color{blue}{1 2...}}\)

Como ve, esta salida tiene

  • los seis primeros son, efectivamente, valores aleatorios
  • Hay una estructura cíclica, lo que imposibilita que sea lo que esperamos
  • Cada vez que ejecute el script, saldrá exactamente lo mismo.

¿Qué podemos hacer?

el resultado obtenido depende de los valores para \(m\),\(a\),\(c\) y la semilla. De esta forma, este generador de números aleatorios no es tan “aleatorio”. En realidad, no es aleatorio en el sentido “puro” de la palabra. Es más bien “pseudoaleatorio” porque:

  • Si empieza con la misma semilla y parámetros, obtendrá los mismos valores
  • Si pide una cantidad suficiente de extracciones “aleatorias” volverá a repetirse el ciclo como ocurrió anteriormente.

Hay, documentados, algunos valores famosos para estos parámetros (puede encontrarlos en Wikipedia, por ejemplo, al buscar “generador congruencial”).

Ejercicio propuesto Investigue cómo genera un ordenador números aleatorios. ¿De dónde saca la semilla? Diseñe un algoritmo para obtener números aleatorios de una uniforme (0,1). Para ello, complete este código

 #parámetros iniciales

m <- 2 ** 32 
a <- 1103515245 
c <- 12345  #parámetros iniciales
x <- 1234 
aleat<-rep(0,20) 
aleat[1]<-x #inicializamos el vector resultados
for (i in 1:20) {   
  x <- (a * x + c) %% m 
  aleat[i] <- x/m } #almacenamos los números

Fíjese que, si genera una cantidad grande de estos números, obtendrá lo que esperamos teóricamamente: una distribución donde cualquier valor en el intervalo \(0\leq x \leq 1\) tiene la misma probabilidad de ser elegido. Compruébelo.

Como habrá observado, la semilla (es decir, el valor inicial elegido) modificará la secuencia que obtenga. Esto quiere decir que si queremos obtener la misma secuencia, por motivos relacionados con el experimento que estemos llevando a cabo, entonces deberemos utilizar la misma semilla.

En [R] puede simular una uniforme mediante la función runif. Observará que, cada vez que lo lance, el resultado será distinto. Eso es así porque [R] usa como semilla un código obtenido mediante la señal horaria de su PC. Si quiere obtener siempre la misma simulación, deberá establecer una semilla (con la secuencia set.seed())

Esta instrucción le proporcionará siempre la misma secuencia "pseudoaleatoria" de valores distribuidos según una uniforme (0,1).


set.seed(1234)
runif(10)

Clase 2: La distribución normal. Entendiendo el Teorema Central del Límite

Ya hemos aprendido a simular distribuciones uniformes. Muchas de las distribuciones de probabilidad conocidas se pueden simular a través de la uniforme. Por ejemplo, la distribución normal (0,1), puede simularse mediante la transformación de Box-Muller, puede probarse que se genera de la siguiente manera, a través de dos variables uniforme e independientemente distribuidas

\[ N=\sqrt{-2log(u_1)}\times \cos(2\pi u_2) \] donde \(N\) es un valor, aleatorio, proveniente de una normal \(N(0,1)\), y \(u_1\),\(u_2\) son realizaciones aleatorias de sendas distribuciones uniformes \(U(0,1)\).

u1<-runif(100)
u2<-runif(100)
N<-sqrt(-2*log(u1))*cos(2*pi*u2)

En el siguiente ejercicio, se puede ver cómo la simulación, según aumenta el tamaño muestral, es más precisa y se acerca más a lo esperado.

par(mfrow=c(2,2))
u<-runif(100)
v<-runif(100)
N<-sqrt(-2*log(u))*cos(2*pi*v)
hist(N, main="n=100")

u<-runif(1000)
v<-runif(1000)
N<-sqrt(-2*log(u))*cos(2*pi*v)
hist(N,main="n=1000")

u<-runif(10000)
v<-runif(10000)
N<-sqrt(-2*log(u))*cos(2*pi*v)
hist(N,main="n=10000")

u<-runif(100000)
v<-runif(100000)
N<-sqrt(-2*log(u))*cos(2*pi*v)
hist(N,main="n=100000")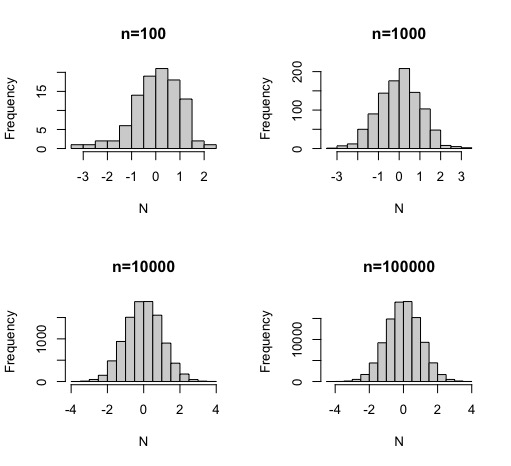

FIG 1: simulación de una normal con diferentes tamaños muestrales

Ahora bien, rescatemos ahora un resultado, el del Teorema Central del Límite que, a menudo, suele malinterpretarse.

El Teorema Central del Límite

En general, suele haber cierta confusión con la interpretación del Teorema Central del Límite, uno de los más famosos, celebrados e importantes en Estadística. Por simplificación, mucha gente cree que este teorema dice algo así como si una muestra es muy grande, la distribución de los datos será normal . Lo cual, se mire como se mire, es incorrecto. De hecho,lo puede comprobar muy fácilmente

Ejercicio: Simule distribuciones uniformes (0,1) para muestras cada vez mayores. Obtenga el histograma y discuta si la distribución, según aumenta la muestra, está normalmente distribuida

par(mfrow=c(2,2))

U<-runif(100)
hist(U, main="n=100")

U<-runif(1000)
hist(U, main="n=1000")

U<-runif(10000)
hist(U, main="n=10000")


U<-runif(100000)
hist(U, main="n=100000")

como verá, por mucho que amplíe la muestra la distribución uniforme seguirá siendo una distribución uniforme

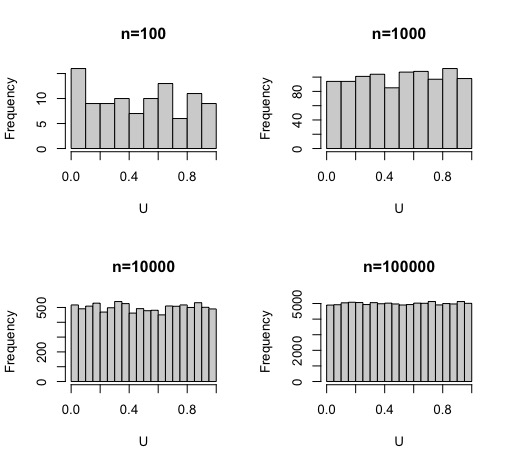
FIG 2: simulación de una normal con diferentes tamaños muestrales

Veamos, entonces, qué resultado proporciona el teorema.

TCL

Sean \(X_{1},...,X_{n}\) \(n\) variables aleatorias independientes e idénticamente distribuidas de media \(\mu\) y varianza, \(\sigma\), finita. Sea \(\overline{X}_{n}=\frac{X_{1}+X_{2}+...+X_{n}}{n}\) la media muestral, entonces, si \(N\rightarrow\infty\) se cumple que \[ \overline{X}_{n}\approx N\left(\mu,\frac{\sigma^{2}}{n}\right) \]

donde \(\approx\) significa se aproxima . Este teorema, entonces, quiere decir de una manera más coloquial:

  • No importa la distribución de partida de la variable aleatoria \(X\) (valen tanto continuas (exponencial, uniforme, etc…) como discretas (binomial, Poisson, etc…) si el muestreo es aleatorio, se satisface el teorema.
  • Es importante el se aproxima del texto . Esto quiere decir, que la distribución de la media no es normal, sino que puede utilizarse la distribución normal como un resultado aproximado para lo que se necesite calcular.

Quizás esta infografía le sirva para entender, básicamente, la idea del teorema

FIG 3: El TCL(1)

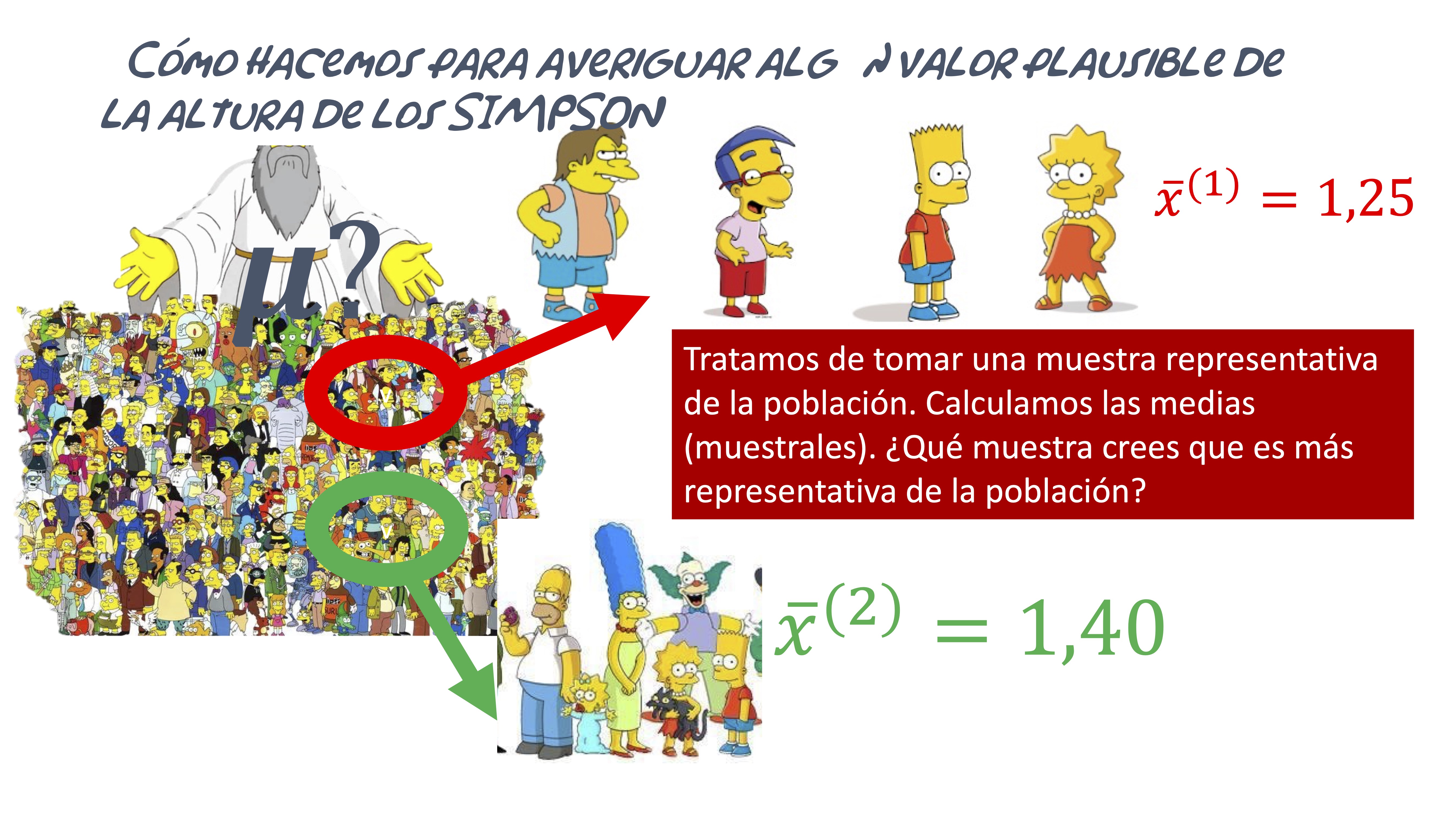
FIG 4: El TCL(2) FIG 5: El TCL(3): aquí es importante ver que tenemos dos tamaños que nos importan: n se refiere la cantidad de individuos que hay en cada submuestra y N se refiere al número de submuestras

Esto mismo, lo puede simular utilizando [R]. Para ello:

  • simule \(N\) muestras de tamaño fijo (en general, \(N\) debe ser grande para poder ver el histograma adecuadamente) (\(n={1,5,100,500}\)) de uniformes \(U(0,1)\). -A continuación, obtenga los promedios muestrales de cada una y dibuje el histograma. Pruebe que, según \(n\) se hace grande, la distribución de los promedios muestrales se acerca a una normal.

Puede escribir el script generando una matriz como esta:

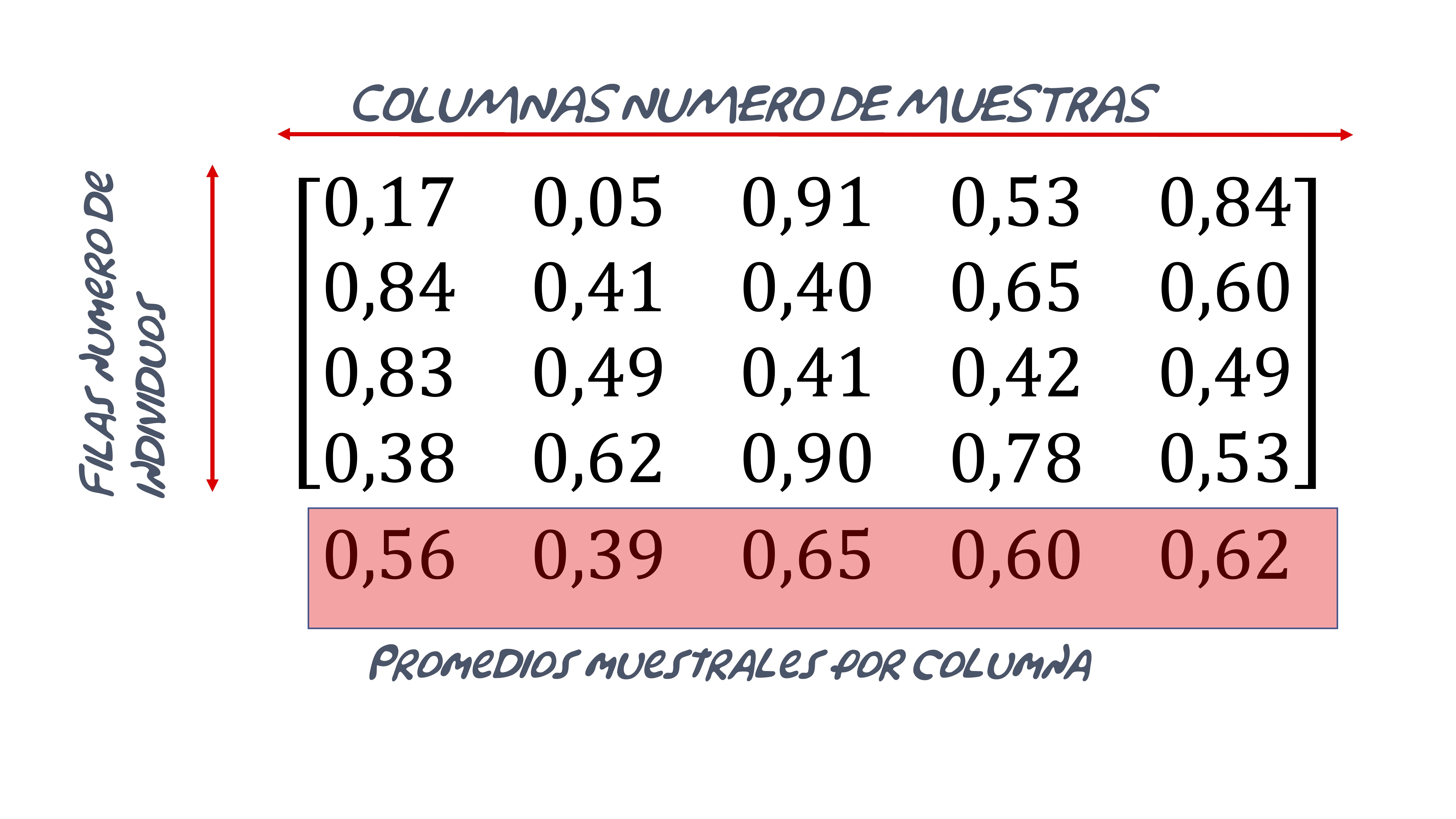
FIG 6: El TCL(4)

De esta forma, obtendrá la FIG7 donde se puede ver cómo la campana de Gauss se empieza a conformar con una muestra superior a 40 elementos

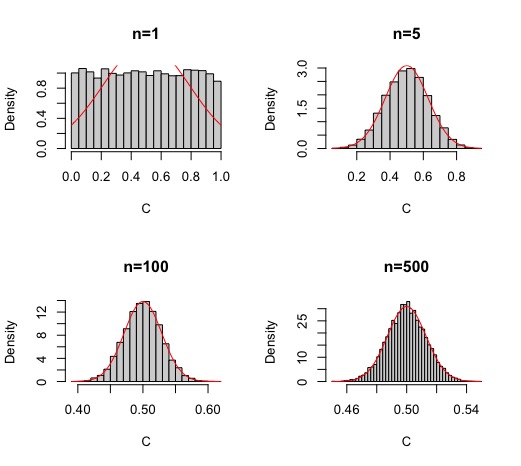FIG 7: El TCL simulado con una uniforme como distribución original de la variable aleatoria con n=10 Para ello, habrá tenido que escribir un código similar a este

par(mfrow=c(2,2))
M1<-matrix(runif(10000*1),nrow=1)
C<-colMeans(M1)    
hist(C,breaks=30,prob=TRUE,main="n=1")
curve( dnorm(x,mean=0.5,sd=sqrt(1/(12*1))), add=TRUE, col='red' )


M1<-matrix(runif(10000*5),nrow=5)
C<-colMeans(M1)    
hist(C,prob=TRUE,main="n=5",breaks=30)
curve( dnorm(x,mean=0.5,sd=sqrt(1/(12*5))), add=TRUE, col='red' )

M1<-matrix(runif(10000*100),nrow=100)
C<-colMeans(M1)    
hist(C,prob=TRUE,main="n=100",breaks=30)
curve( dnorm(x,mean=0.5,sd=sqrt(1/(12*100))), add=TRUE, col='red' )


M1<-matrix(runif(10000*500),nrow=500)
C<-colMeans(M1)    
hist(C,prob=TRUE,main="n=500",breaks=50)
curve( dnorm(x,mean=0.5,sd=sqrt(1/(12*500))), add=TRUE, col='red' )
  • Por otro lado, como sabemos que \(X\rightarrow U(a,b)\), entonces \(E(X)=\frac{b+a}{2}\) y que \(V(X)=\frac{\left(b-a\right)^{2}}{12}\), entonces,

\[ \overline{X}_{n}\approx N\left(\frac{b+a}{2},\frac{\left(b-a\right)^{2}}{12\times n}\right) \] en este caso, pruebe que \[ \overline{X}_{N}\approx N\left(0.5,\frac{1}{12\times n}\right) \]

Para ello, tendrá que obtener la media y la varianza de lo que ha simulado y cercionarse de que se obtiene dicho resultado. En la FIG7 se ha incluido dicha curva.

Clase 3: Usos de la simulación (1): entender conceptos de estadística y probabilidad

En esta clase, vamos a discutir dos ideas centrales en estadística y probabilidad que, es probable, que siga interpretando con errores o no sea capaz de definir de manera adecuada.

El intervalo de confianza

Suponga que quiere estimar el valor promedio de una variable aleatoria \(X\) de una población, es decir, quiere estimar \(\mu\), utilizando un intervalo de confianza. Asuma que la población se distribuye como una normal \(X\rightarrow N(\mu,\sigma^{2})\) entonces, según la teoría de muestreo tradicional, el intervalo de confianza para la media poblacional será:

\[ IC\left(\mu\right)_{\left(1-\alpha\right)\%}\equiv\left(\overline{x}-N(0,1)\sqrt{\frac{\sigma^2}{N}},\overline{x}+N(0,1)\sqrt{\frac{\sigma^2}{N}}\right) \]

donde el \(N(0,1)\) es el percentil correspondiente de la normal dado el nivel de significación \(\alpha\) (o de confianza \(1-\alpha\). ¿Qué cosas son importantes del intervalo?

Ejercicio Piense, por un momento, cómo definiría usted la idea de intervalo de confianza.

  • Es un intervalo aleatorio : eso quiere decir que, por cada muestra que recoja, el valor inferior y superior de este va a cambiar
  • Como ve en la FIG 1, cada muestra que utilice sobre un mismo experimento, le permitirá obtener un intervalo diferente. En algunos de esos intervalos, el parámetro poblacional estará contenido en este y en otros, no.

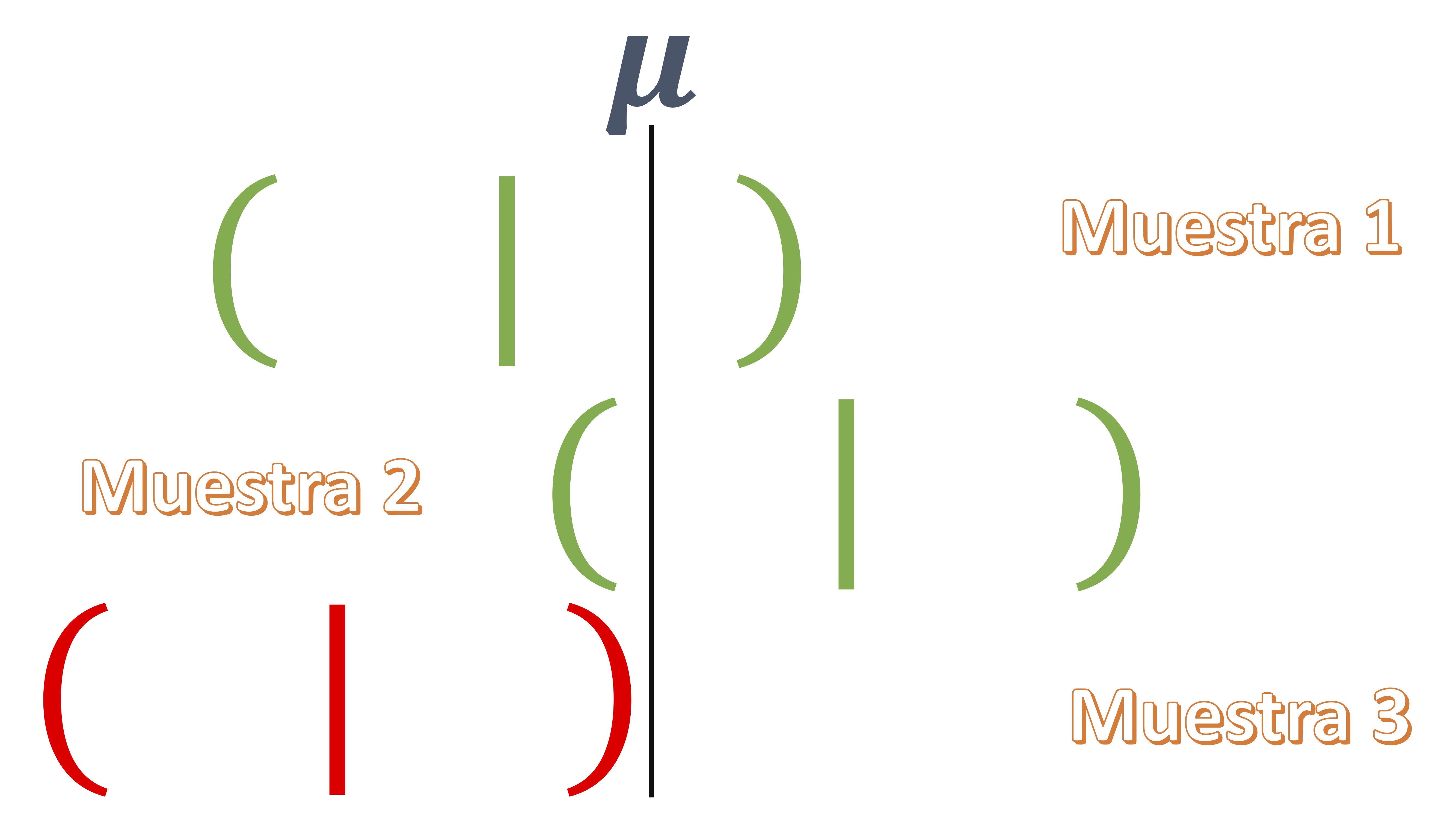
FIG 1: La idea de construir diferentes intervalos de confianza para un mismo parámetro poblacional

Entonces, lo que queremos decir es que:

  • La idea de intervalo de confianza-al 95%, por ejemplo- implica que de cada 100 experimentos que realice en las mismas condiciones, en 95 de ellos estará el verdadero parámetro poblacional desconocido.
  • En la vida real, se cuenta con una sola muestra (debido a lo caro que resulta la extracción de esta) y, por tanto, usted nunca sabrá si está ante el intervalo que contiene al verdadero parámetro poblacional o no.
  • Por eso se llama de confianza. Porque usted confía en que el intervalo contenga el parámetro. Claro, ante mayor valor de la confianza, más ancho será el intervalo y, por tanto, más frecuente será que esté dicho parámetro poblacional dentro de este. Sin embargo, cuanto más ancho sea un intervalo, menos informativo será para usted (es como decir que un intevalo de confianza al 99% de la nota de la asignatura está entre 1 y 9.5)

Ejercicio Simule muestras aleatorias (por ejemplo, 50) de una población normal con la media y desviación típica deseadas. Calcule los límites inferior y superior de cada uno de los 50 intervalos de confianza (al 95%, por ejemplo) que genere y obtenga una variable dicotómica que tome valor 1 si el valor de la media poblacional elegido está contenido o no en el intervalo. Obtenga el porcentaje de veces que está contenido. Esa es la confianza.

n<-50
vec<-vector()
N<-200
for (i in 1:N){
y <- rnorm(n,mean=1,sd=0.5)  #generamos muestras de 50 individuos normales con media 1 y desv típica 0.5
x_bar<-mean(y)  #obtenemos la media muestral de cada muestra
sd_bar<-sd(y)/sqrt(n) #obtenemos la desviación típica de la media muestral (error estándar)
CI_low<-x_bar-1.96*sd_bar #obtenemos el límite inferior del intervalo
CI_high<-x_bar+1.96*sd_bar #obtenemos el límite superior del intervalo
vec[i]<-CI_low<1 & CI_high>1} #generamos una variable que nos dice si el valor poblacional está o no dentro del intervalo

¿Qué ha aprendido?

La interpretación del intervalo de confianza es más sutil y, quizás, menos práctica de lo que pensaba. En realidad, cuando calcula un intervalo con una sola muestra, la probabilidad de que el verdadero parámetro poblacional esté dentro del intervalo es 1 o 0. Puede hacer una interpretación mucho más laxa “un intervalo de confianza nos proporciona un conjunto de valores compatibles con el parámetro poblacional”. Obviamente, cuanto más ancho sea el intervalo, más imprecisa será su inferencia. Cuanto más estrecho, más riesgo corre de excluir al verdadero parámetro poblacional. Esto entronca con lo aprendido en capítulos anteriores: la inferencia no debería consistir en una dicotomía entre “rechazar” y “no rechazar” hipótesis.

Es decir esta pregunta es de interés:

¿Cómo interpretamos, entonces, un intervalo de confianza si en la vida real sólo tenemos UNA MUESTRA?

  1. Después de analizar la esperanza de vida en España, se concluye que un intervalo de confianza al 95% para dicho parámetro es \(\left(77.8,79.1\right)\) años. ¿Podemos decir, entonces, decir:
  • En torno al 95% de la gente en Españaa tiene una esperanza de vida entre 77.8 y 79.1 años

No, pese a que es muy común interpretar así el intervalo de confianza. Recuerde que 77.8 y 79.1 son valores aleatorios. Si hubiéramos contado con otra muestra, esos límites habrían cambiado (por ejemplo, \(\left(77.3,80.2\right)\) . Tampoco sabemos cuál es el verdadero parámetro, por lo que no podemos obtener qué porcentaje de gente, en la población, tiene como esperanza de vida entre 77.8 y 79.1 años.

  • Hay una probabilidad del 95% de que la esperanza de vida promedio valga entre 77.8 y 79.1 años?

La esperanza de vida, como parámetro poblacional, es desconocida, y determinista (es decir, no hay probabilidad asociada con ella: es un valor único). De nuevo, no podemos asociar una probabilidad a dicho parámetro.

Entonces, lo que en realidad podemos decir, que es lo que hemos simulado, es que:

De cada 100 posibles intervalos, 95 de ellos contendrán el verdadero parámetro, es decir, hay un 95% de probabilidad de que el intervalo aleatorio (77.8,79.1) incluya al verdadero parámetro poblacional.

De manera más gráfica, puede ejecutar el siguiente script de regalo, donde se simulan muestras provenientes de poblaciones \(N(1,\sigma=0.5)\). El objetivo es obtener 100 intervalos y ver cuántos de ellos no contienen a la media poblacional (que conocemos, porque la hemos impuesto nosotros).

install.packages("BSDA")
library(BSDA)
N = 100
curve(expr = dnorm(x, mean = 1, sd = 0.5), from = -1, to = 3,
      main = "95% Simulación de intervalos de confianza",
      xlab = "valores x", ylab = "densidad",
      lwd=2, col="blue") #creamos una curva normal
abline(v = 1, col = "purple", lwd = 2) #esta línea indica el valor de la media poblacional (que es 1)
contador <- 0
#el siguiente bucle genera N intervalos de confianza basados en N muestras aleatorias
#y marca con rojo aquellos intervalos que no contienen la media poblacional
for (i in 1:N) {
  col <- rgb(0,0,0,0.5)
  simula.interv <- rnorm(n = 20, mean = 1, sd = 0.5) 
  myCI <- z.test(simula.interv, sigma.x = 0.5, conf.level = 0.95)$conf.int
  if (min(myCI) > 1 | max(myCI) < 1) {
    contador <- contador + 1
    col <- rgb(1,0,0,1)
  }
  segments(min(myCI), 1.5 * i / N,
           max(myCI), 1.5 * i / N,
           lwd = 1, col = col)
}

del que obtendrá la FIG2

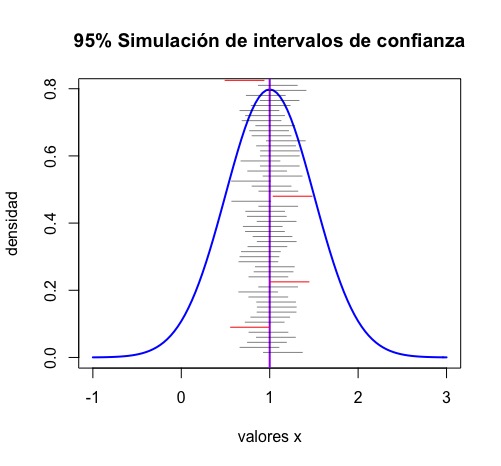FIG 2: La idea de construir diferentes intervalos de confianza para un mismo parámetro poblacional fíjese cómo, en rojo, se mustran los intervalos de confianza (de los 100 generados) que no contienen al verdadero parámetro poblacional. Es una aproximación, en teoría deberíamos haber obtenido 5, ya que la confianza es del 95%. Si lo repite con \(N\) mayor, verá cómo según crece \(N\), más se acerca al resultado teórico.

El p valor

Piense en el caso anterior, en el que queríamos estimar el valor promedio de una variable aleatoria \(X\), es decir, quiere estimar \(\mu\), utilizando un intervalo de confianza. Asuma que la población se distribuye como una normal \(X\rightarrow N(\mu,\sigma^{2})\).

Quiere testar la hipótesis típica:

\[ H_{0}:\mu=0 \] \[ H_{1}:\mu\neq0 \]

Para ello, dadas las asunciones que hemos hecho antes, tendremos que el estadístico de contraste, \(t\), será

\[ t=\frac{\bar{x}-\mu_{H_{0}}}{\frac{s}{\sqrt{n}}}\approx N(0,1) \]

donde \(s\) es la desviación típica muestral. El p-valor del contraste se obtiene como

\[ 2\times Pr\left(N(0,1)\geq\left|\frac{\bar{x}-\mu_{H_{0}}}{\frac{s}{\sqrt{n}}}\right|\right) \]

es decir, es la probabilidad de encontrar un estadístico \(t\) más extremo (en valor absoluto) que el obtenido con esta muestra, asumiendo que la hipótesis nula es cierta. ¿Qué significa lo de asumiendo que la hipótesis nula es cierta? Pues que en la expresión del estadístico

\(\left(\frac{\bar{x}-{\color{red}\mu_{H_{0}}}}{\frac{s}{\sqrt{n}}}\right)\)

se introduce el valor de la nula (en este caso, cero). En el fondo, estamos tratando de medir el grado de compatibilidad de nuestros datos con nuestro modelo (el modelo aquí es tan sencillo como decir que \(\mu=0\)). De nuevo, el p-valor necesita una interpretación probabilística que, consiste en:

p-valor

El p-valor es también una variable aleatoria. Nos permite analizar cómo de compatibles es la muestra con la hipótesis que se contrasta. Sin embargo, tenga en cuenta que detrás de una hipótesis hay una selección de un modelo concreto (con sus correspondientes restricciones) y la elección de unos datos concretos. De hecho, volvemos a la situación de partida: cuando obtiene el p-valor de un contraste- y bajo los supuestos de que el modelo es el adecuado- no sabe si ha obtenido aquella muestra donde rechazaría la hipótesis de manera correcta o lo contrario.

Ejercicio Simule un conjunto de muestras de tamaño \(n\) a su elección y con distribución normal de parámetros \(\mu\neq0\) y \(\sigma^2\), también a su elección. Obtenga los p valores de dos contrastes: el de media poblacional nula (que deberá rechazar puesto que su media poblacional es distinta de cero) y el de media poblacional cero (que no deberá rechazar). Analice la distribución del p valor en ambos casos y, por tanto, la frecuencia con la que rechaza indebidamente o no rechaza indebidamente.

n<-50
p_value<-vector()
N<-200
for (i in 1:N){
  y <- rnorm(n,mean=1,sd=4)  #generamos muestras de 50 individuos normales con media 0 y desv típica 0.5
  x_bar<-mean(y)  #obtenemos la media muestral de cada muestra
  sd_bar<-sd(y)/sqrt(n) #obtenemos la desviación típica de la media muestral (error estándar)
  tstat<-(x_bar-0)/(sd_bar) #calculamos el t-stadístico con la nula mu=0
 p_value[i]<-2*(1-pnorm(abs(tstat), mean=0, sd=1))} #obtenemos el p valor



hist(p_value,main="Aquí deberíamos rechazar")
abline(v = 0.05, col = "purple", lwd = 2)

mean(p_value>0.05)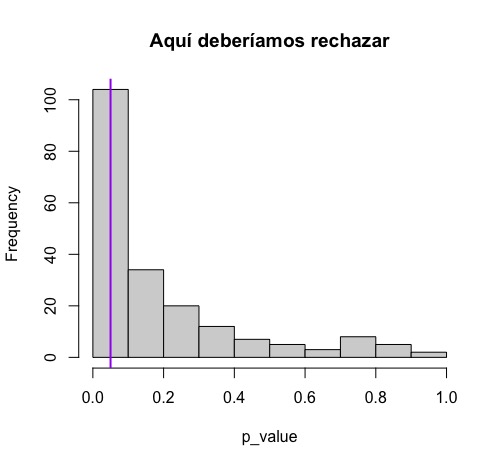

FIG 3: Distribución de los diferentes p valores cuando deberíamos rechazar la nula

Como verá en la FIG3, en el 59% de las veces, no rechazaríamos la nula de que \(\mu=0\), al 5% de significación, esto es, obtenemos en el 59% de los contrastes un p-valor mayor al 0.05. Sin embargo, deberíamos rechazarla siempre. Esto se debe, entonces, a un alto “error de tipo 2” (no rechazar la nula cuando es falsa) y estamos en un caso de baja potencia. El p-valor no detecta baja potencia en el contraste.

p-valor

Por eso, en el primer semestre discutimos el riesgo de utilizar el p-valor como único dato para la toma de decisiones. Recuerde el gráfico de p-valores que realizábamos para entender qué conjunto de hipótesis no habríamos rechazado.

Por lo tanto:

  • El p-valor debe tomarse como una medida-informal-de compatibilidad de nuestros datos con el modelo.
  • El p-valor no es un criterio sólido científico que pueda sustituir cualquier otro análisis en favor de “rechazar” o “no rechazar” una hipótersis
  • La propia construcción y definición del p-valor debería hacerle reflexionar sobre su uso indiscriminado.