Chapter 2 BLOQUE 4: ampliación de simulación

Clase 1: Simulación de un modelo de regresión

Está cerca de entender un método que requiere de la simulación para la obtención de resultados. Sin embargo, antes va a aprender a simular datos sintéticos para poner a prueba ciertos resultados que conoce de los modelos de regresión lineal. ¿En qué consistirá esta simulación? Vayamos paso a paso.

Usted cuenta con una población que-en la vida real-suele estar formada por infinitos individuos y que, para R va a ser un modelo. En este caso, es un modelo de regresión lineal, por ejemplo:

\[ y=3+5x+u, \]

donde \(u\rightarrow N(0,\sigma=3)\). Usted no puede crear los infinitos elementos de esa población. Sin embargo, puede simular una muestra de dicha población. Por ejemplo, puede simular \(n=50\) elementos de dicha población. Es decir, su marco conceptual es el de la FIG1

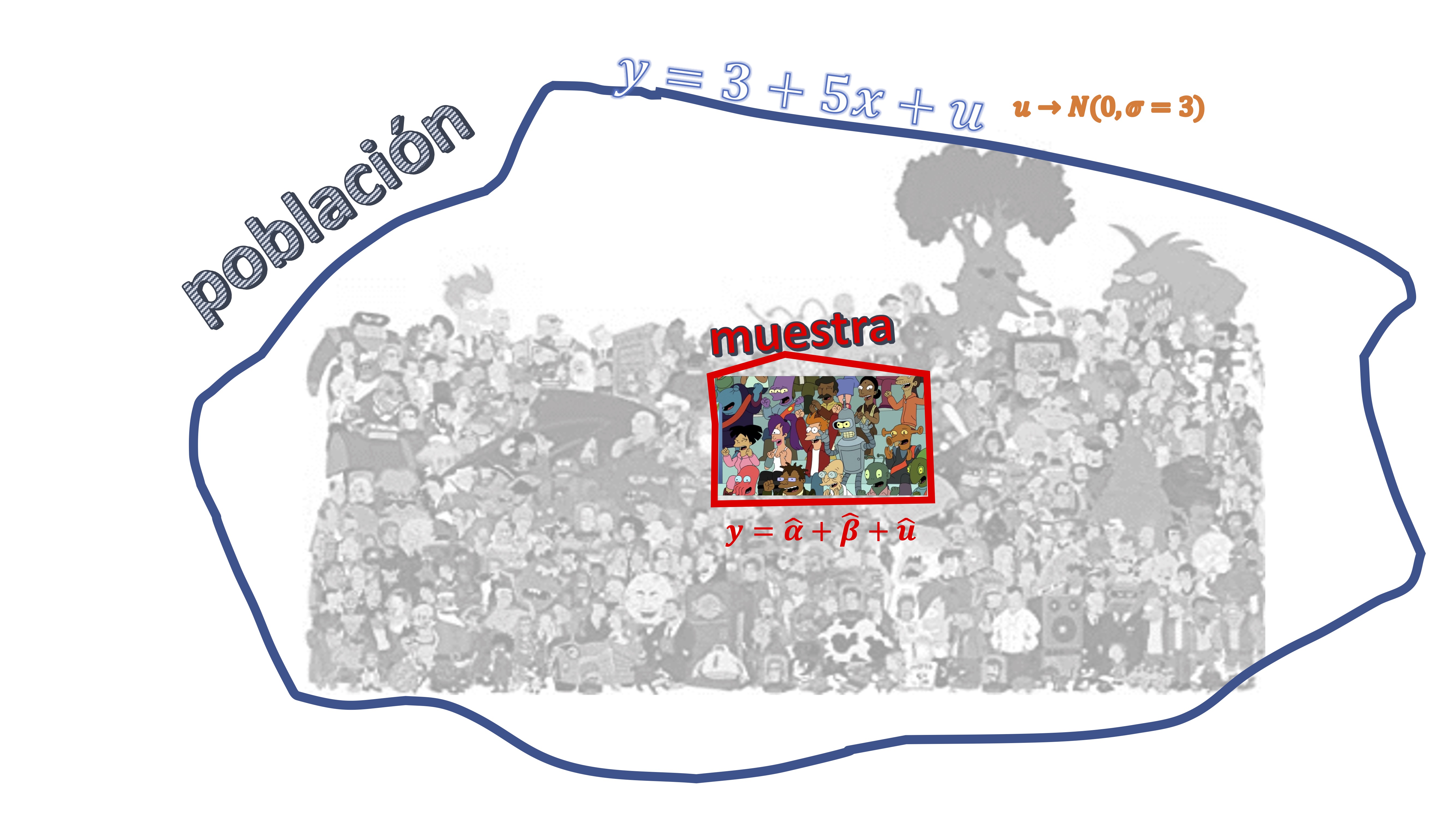FIG 1: la idea de “muestra” y “población” en un modelo de regresión Para ello, explore el siguiente:

Experimento 1

Simule primero el error del modelo (mediante una normal de media cero y varianza 3)

u<-rnorm(n,0,sd=3)

-Simule valores para la variable \(x\). Recuerde que, bajo los supuestos generales del modelo de regresión lineal, \(x\) no es aleatoria y-por tanto, para fines de simulación-puede fijar los números de esa variable como desee.

x<-runif(n)

Escriba la ecuación de regresión y ya tiene 50 elementos extraídos al azar de dicha población.

y<-3+5*x+u

A continuación, puede utilizar el estimador de mínimos cuadrados (lm, en R) para tratar de recuperar los coeficientes del modelo poblacional

M0<-lm(y~x)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.6615     0.7422   3.586 0.000785 ***
x             4.8682     1.2149   4.007 0.000213 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.547 on 48 degrees of freedom
Multiple R-squared:  0.2507,    Adjusted R-squared:  0.2351 
F-statistic: 16.06 on 1 and 48 DF,  p-value: 0.0002132

¿Qué ha ocurrido?

Como verá, los coeficientes que obtiene, no tienen por qué ser

\[ \alpha=3,\beta=5 \]

puesto que usted ha cogido una única muestra al azar-representativa de la población- y, por tanto, lo que ha obtenido es una posible realización del experimento. Entonces ¿la estadística no me promete que-cada vez que haga el experimento- obtenga el verdadero valor de los parémetros? ¡No! la estadística lo que le promete es que, bajo ciertas propiedades de (en este caso, de la más importante es que la \(x\) y la \(u\) no estén relacionadas, esto es, sean independientes y el error aleatorio sea i.i.d) el estimador lineal de los parámetros será insesgado, es decir,

\[ E\left[\widehat{\alpha}\right]=\alpha \]

\[ E\left[\widehat{\beta}\right]=\beta \]

O lo que es lo mismo, si usted pudiera hacer este experimento infinitas veces, en promedio, las estimaciones que obtendría le proporcionarían el verdadero parámetro poblacional. Es decir, como ve en la FIG2,

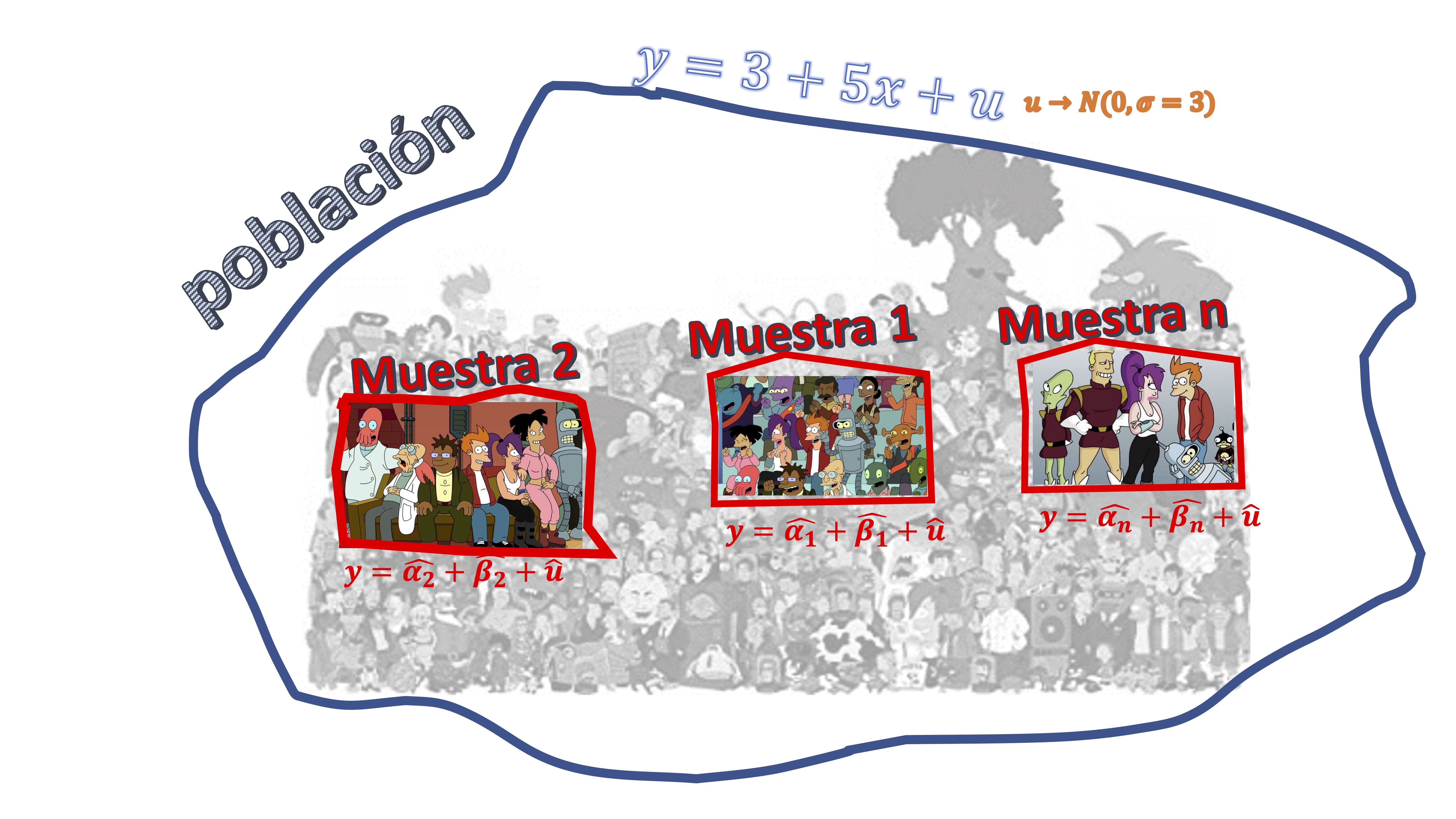
FIG 2: la idea de diferentes “muestras” y “población” en un modelo de regresión

sería lo equivalente en nuestro experimento a tomar un conjunto de muestras de tamaño \(n\) de nuestra población y hacer (en este caso hemos decidido 10.000 veces) el mismo experimento que antes para obtener 10000 posibles realizaciones de \(\widehat{\alpha},\widehat{\beta}.\)

Experimento 2 Este es el código que le permite obtener los 10.000 posibles valores paramétricos

b<-vector()
a<-vector()
n<-50
for(i in 1:10000) {
  u<-rnorm(n,0,sd=3)
  x<-runif(n)
  y<-3+5*x+u
  M1<-lm(y~x)
  a[i]<-M1$coefficients[1]
  b[i]<-M1$coefficients[2]
  
}

par(mfrow=c(1,2))
hist(a, main="histograma para a")
abline(v =3, col = "purple", lwd = 2)
hist(b, main="histograma para b")
abline(v =5, col = "blue", lwd = 2)

De esta forma, obtendrá los histogramas de la FIG3,

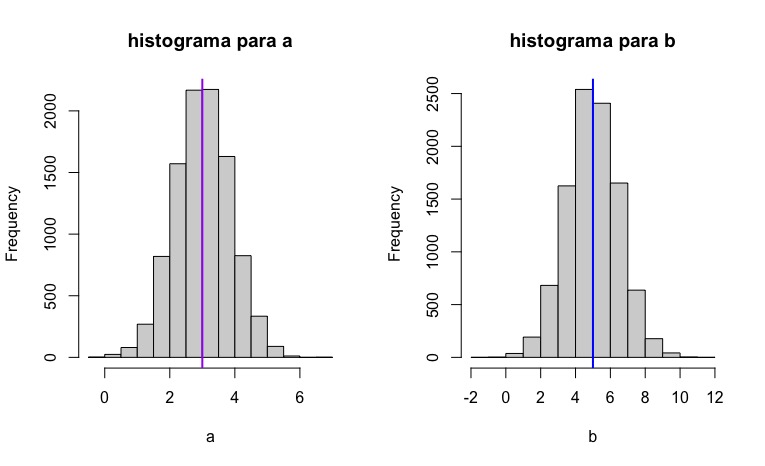FIG 3: obtención de los coeficientes insesgados que representan la idea de la insesgadez: en promedio, nuestros estimadores están apuntando al verdadero valor poblacional, aunque-como ya sabe- lo normal es obtener el resultado de una única muestra (es decir, una única realización del experimento aleatorio) y utilizar dichos valores como si fueran los poblaciones. Ya que es la mejor estimación que puede tener.

¿Qué ha aprendido?

Este ejercicio de simulación le ha permitido comprobar cómo se comporta un estimador de un modelo de regresión si satisface las hipótesis habituales. Pese a que-en teoría- la propiedad de insesgadez es deseable y funciona, en la práctica usted sólo ha estimado el posible valor del parámetro utilizando una única muestra (que es lo equivalente al experimento 1) pese a que lo desesable, pero imposible, es el experimento 2.

Ahora bien, como se habrá dado cuenta, hemos especificado que-para que este experimento salga bien- debemos asegurarnos de que la variable \(x\) y la variable \(u\) sean independientes. Si no lo son, entonces, en general

\[ E\left[\widehat{\beta}\right]\neq\beta \]

es decir, los estimadores de las pendientes son sesgados. Esto es un problema, puesto que no podemos confiar, entonces, en la estimación obtenida.

Ejercicio resuelto. Investigue cómo generar una normal multivariante para las variables \(x,u\) de tal manera que, indicando la correlación deseada entre \(x,u\) pueda evaluar cómo es el tamaño del sesgo según dicha correlación es mayor (por ejemplo, hágalo para correlación de un 10%, de un 30% y de un 70% entre el error y la variable explicatova)

solución

install.packages("dplyr")
install.packages("tidyr")
install.packages("faux")


library(dplyr)
library(tidyr)
library(faux)


#correlación del 10%#

#usamos cmat para introducir la correlación. Se hace en los dos valores
#centrales del vector

a10<-vector()
b10<-vector()
n<-50
for(i in 1:10000) {
  
  cmat <- c(1, .1,.1, 1)
  bvn <- rnorm_multi(n, 2, 0, 1, cmat, 
                     varnames = c("x", "u"))
  x<-bvn$x
  u<-bvn$u
  y<-3+5*x+u
  M1<-lm(y~x)
  a10[i]<-M1$coefficients[1]
  b10[i]<-M1$coefficients[2]
}




#correlación del 30%#
a30<-vector()
b30<-vector()
n<-50
for(i in 1:10000) {
  
  cmat <- c(1, .3,.3, 1)
  bvn <- rnorm_multi(n, 2, 0, 1, cmat, 
                     varnames = c("x", "u"))
  x<-bvn$x
  u<-bvn$u
  y<-3+5*x+u
  M1<-lm(y~x)
  a30[i]<-M1$coefficients[1]
  b30[i]<-M1$coefficients[2]
}

#correlación del 70%#
a70<-vector()
b70<-vector()
n<-50
for(i in 1:10000) {
  
  cmat <- c(1, .7,.7, 1)
  bvn <- rnorm_multi(n, 2, 0, 1, cmat, 
                     varnames = c("x", "u"))
  x<-bvn$x
  u<-bvn$u
  y<-3+5*x+u
  M1<-lm(y~x)
  a70[i]<-M1$coefficients[1]
  b70[i]<-M1$coefficients[2]
}


par(mfrow=c(3,2))
hist(a10, xlim = c(2,6), main="histograma para a, corr=0.1")
abline(v =3, col = "purple", lwd = 2)
hist(b10,xlim=c(2,6), main="histograma para b,corr=0.1")
abline(v =5, col = "blue", lwd = 2)

hist(a30,xlim=c(2,6), main="histograma para a,corr=0.3")
abline(v =3, col = "purple", lwd = 2)
hist(b30,xlim=c(2,6), main="histograma para b,corr=0.3")
abline(v =5, col = "blue", lwd = 2)


hist(a70,xlim=c(2,6), main="histograma para a,corr=0.7")
abline(v =3, col = "purple", lwd = 2)
hist(b70,xlim=c(2,6), main="histograma para b,corr=0.7")
abline(v =5, col = "blue", lwd = 2)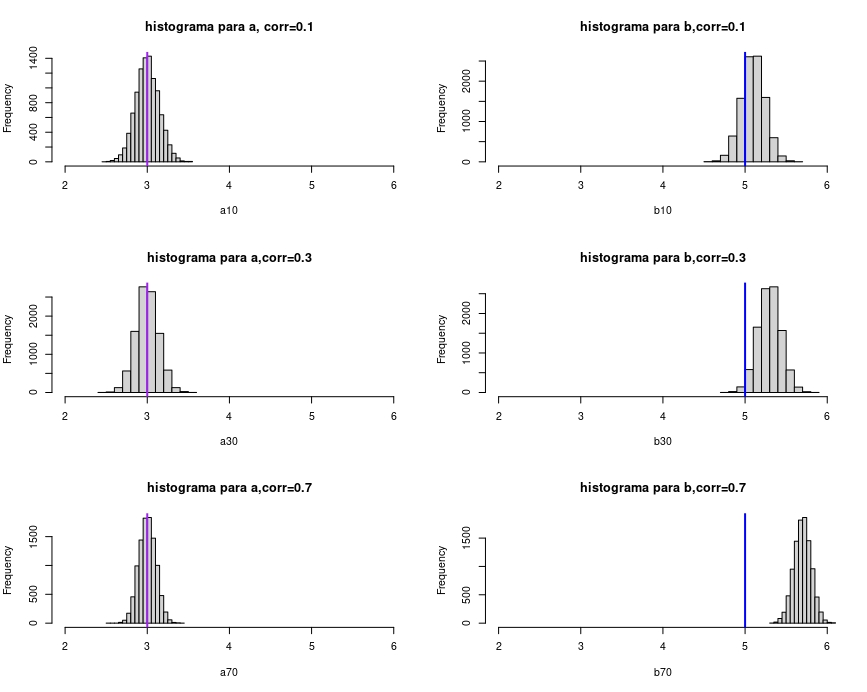

FIG 4: obtención de los coeficientes sesgados

Como puede ver en la FIG 4, cuanto mayor sea la correlación entre el error y la variable explicativa, mayor es el sesgo cometido (de tal forma que el estimador se aleja del verdadero valor poblacional)

Ejercicio

Piense ahora en su proyecto del primer cuatrimestre. Si estimó modelos de regresión ¿tiene motivos para pensar que podría haber estimado coeficientes sesgados?

Clase 2: la técnica del bootstrapping

Todo lo que ha aprendido en las clases anteriores tenía un objetivo: entender la idea del bootstrapping. Debemos añadir, sin embargo, otra de las utilidades de la simulación para cerrar el círculo. Con la simulación también podemos resolver problemas de probabilidad.

El muestreo con reemplazamiento

Esto ya lo ha hecho cuando resolvía los tediosos problemas de probabilidad con bolas de colores. En la FIG1, tenemos un ejemplo de muestreo con “reemplazamiento”. Tiene sus bolas originales, y la probabilidad de obtener una de cada color. Si quiere, por ejemplo, saber qué probabilidad tiene de sacar dos veces bola azul si una vez saca una bola la vuelve a depositar en la urna (reemplazamiento), tiene que darse cuenta de que son sucesos independientes y, por tanto \(P(azul|azul)=P(azul)\times P(azul)=\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}\).

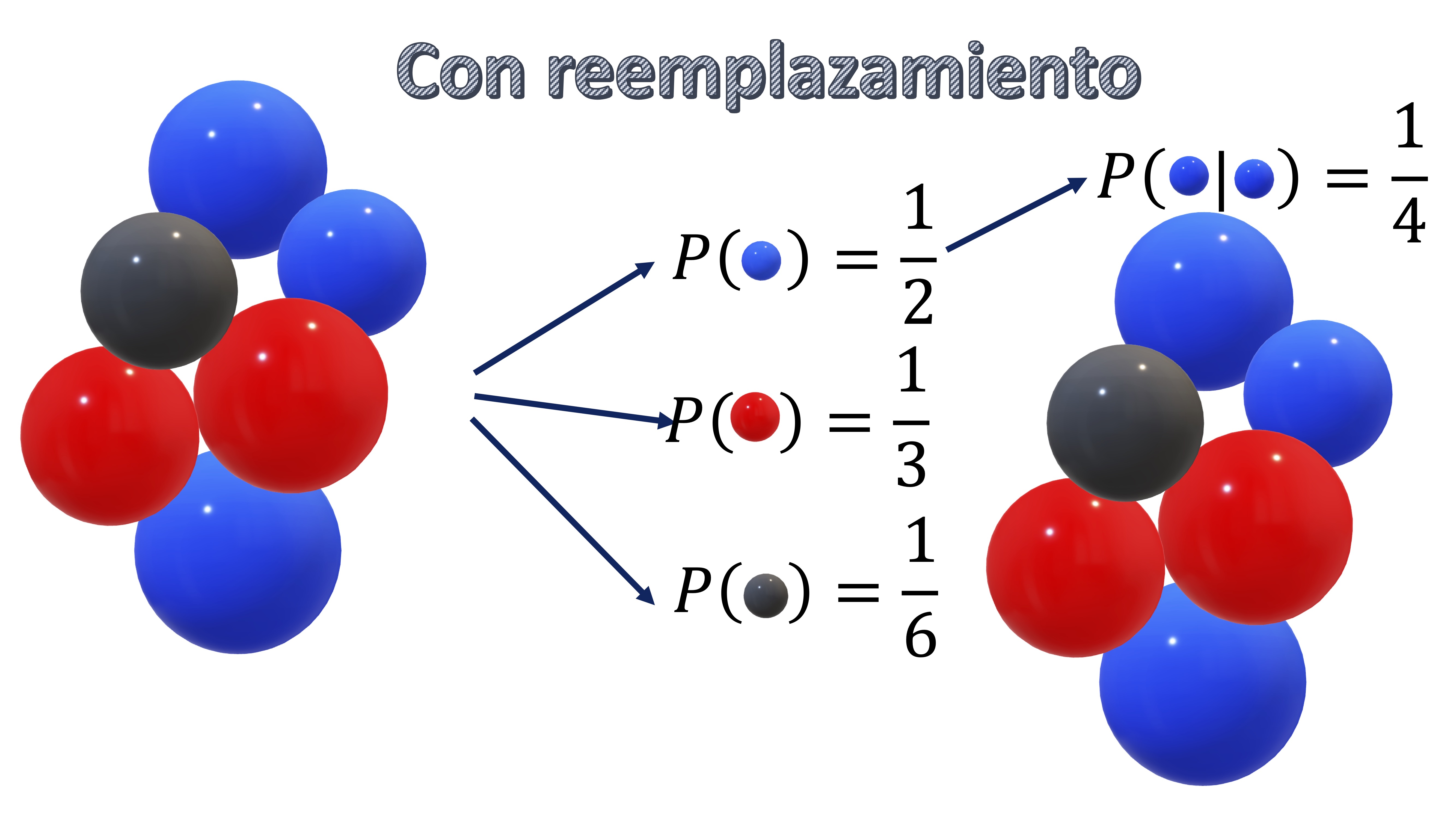
FIG 1: muestreo con reemplazamiento

Esto lo puede simular en R. Por ejemplo, cree un vector donde \(1\) sea azul, \(2\) sea rojo y \(3\) sea negro.

x=c(1,1,1,2,2,3)

Utilizando la función sample, podrá simular cualquier salida de la urna. Por ejemplo, aquí le estamos diciendo que saque dos bolas con reemplazamiento (es decir, R saca una bola, vuelve a depositarla en la urna, y saca de nuevo otra)

sample(x, 2, replace = TRUE)

Tomando el resultado frecuentista de que

\[ P(azul|azul)=\frac{veces\: que\: salen\:2\: bolas\: azules}{veces\:totales} \]

generamos un código que nos permita obtener-simulando un conjunto de casos posibles- el número de favorables. Deberá aproximarse dicho resultado a la probabilidad real que es 0.25.

for(i in 1:10000) {
  
  y<-sample(x, 2, replace = TRUE)
  if (y[1]==1 && y[2]==1){
  count<-count+1}
}

Prob=count/10000

> Prob
[1] 0.2475

Muestreo sin reemplazamiento

Lo mismo ocurrirá si hace el muestreo sin reemplazamiento. en este caso, la probabilidad de obtener azul una vez se ha obtenido azul no es independiente, puesto que el número de bolas será distinto. Entonces, tendrá que ocurrir lo que ve en la FIG2

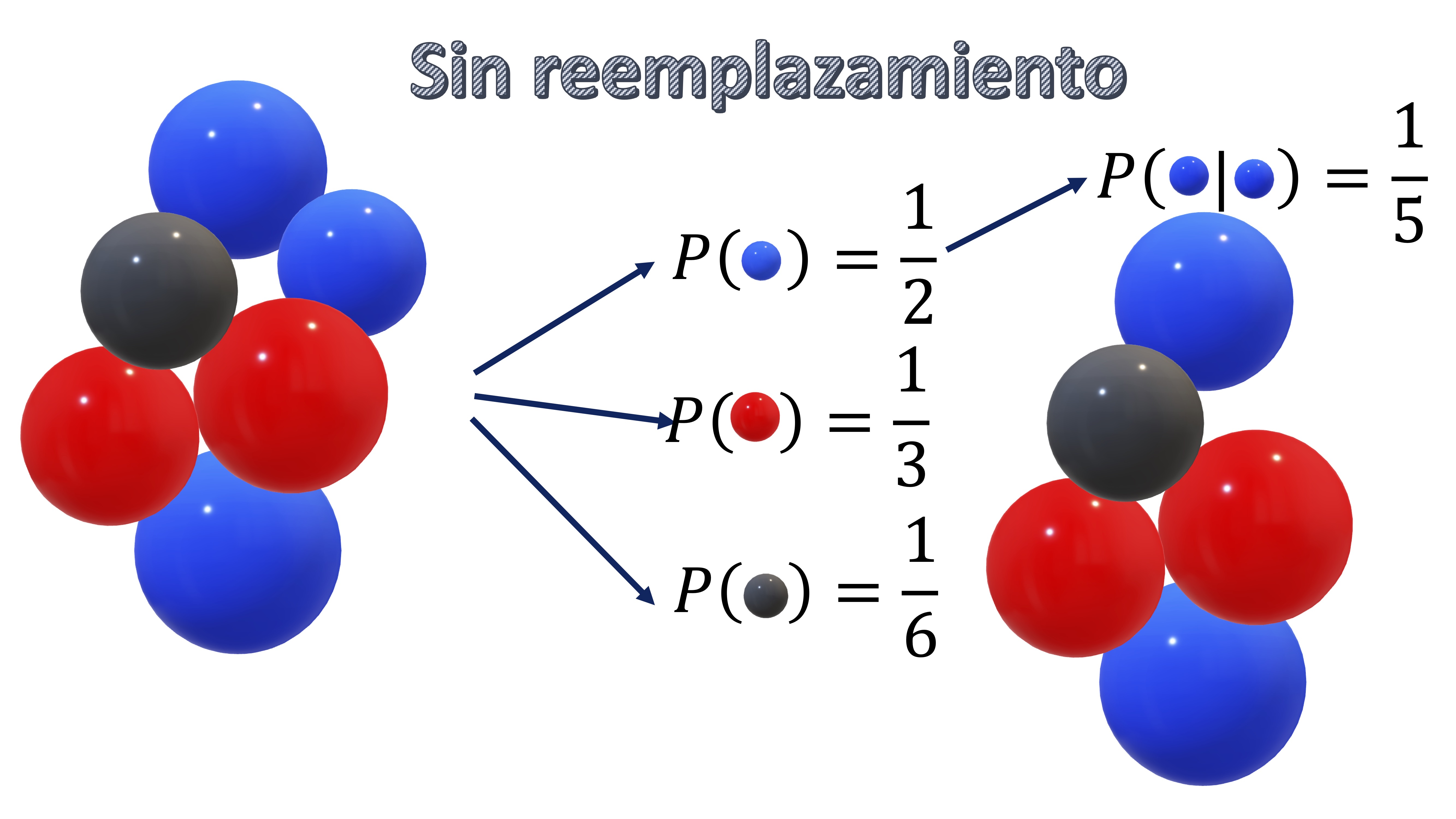
FIG 2: muestreo sin reemplazamiento

x=c(1,1,1,2,2,3)

count<-0

for(i in 1:10000) {
  
  y<-sample(x, 2, replace = FALSE)
  if (y[1]==1 && y[2]==1){
    count<-count+1}
}


Prob=count/10000

> Prob
[1] 0.2035

La idea del bootstrapping consiste en lo siguiente: usted tiene unos datos originales, por ejemplo, la muestra de la FIG3

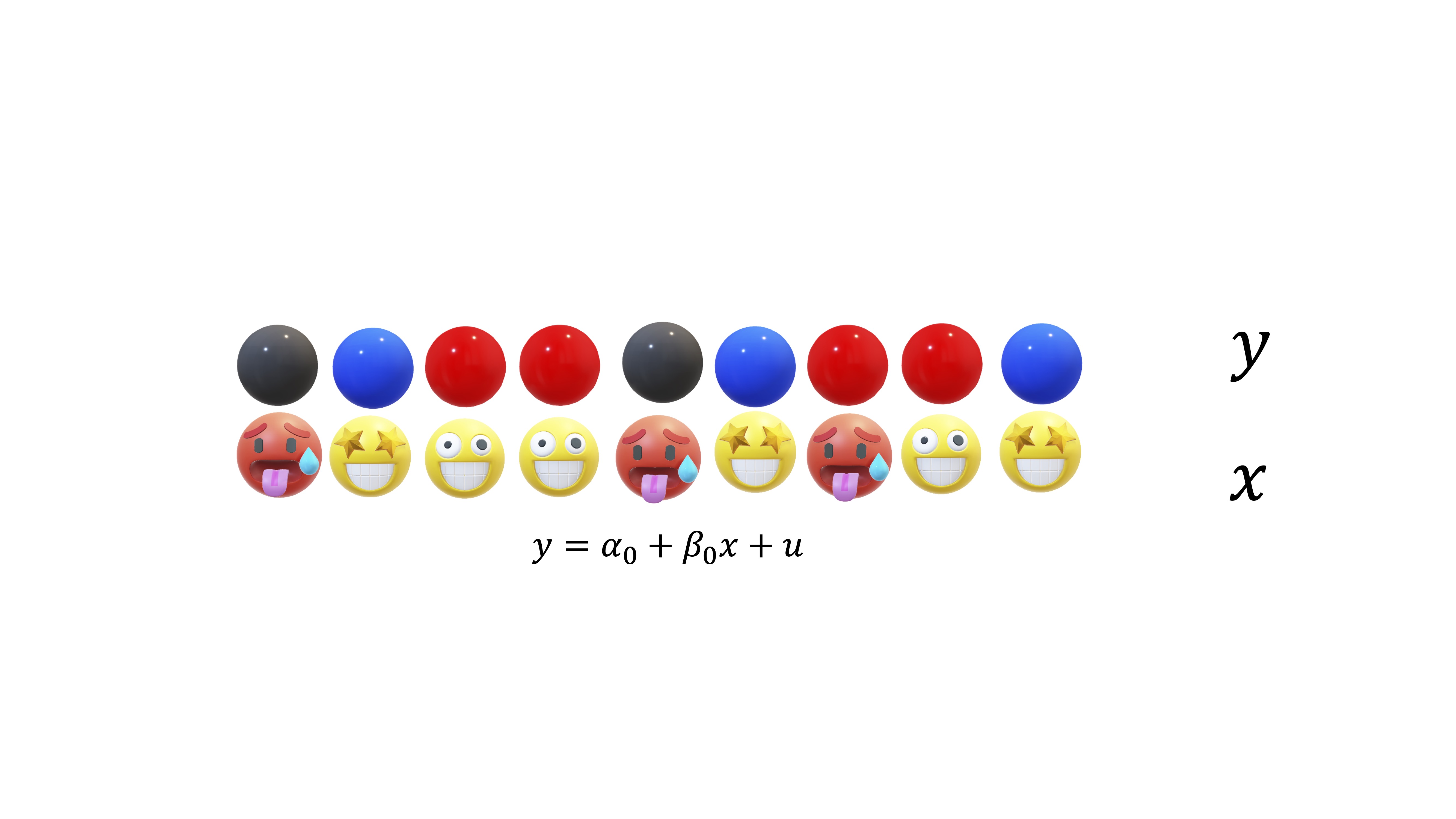
FIG 3: una muestra para estimar un modelo de regresión

Ahora, usted obtiene una estimación para \(\alpha\) y para \(\beta\) y se pregunta ¿podría tener una distribución? Entonces, va a asumir que esa muestra es su población (es una asunción, no es la realidad) y, entonces, va a hacer muestreos con reemplazamiento de los pares que tiene, de tal forma que pueda estimar modelos de regresión alternativos

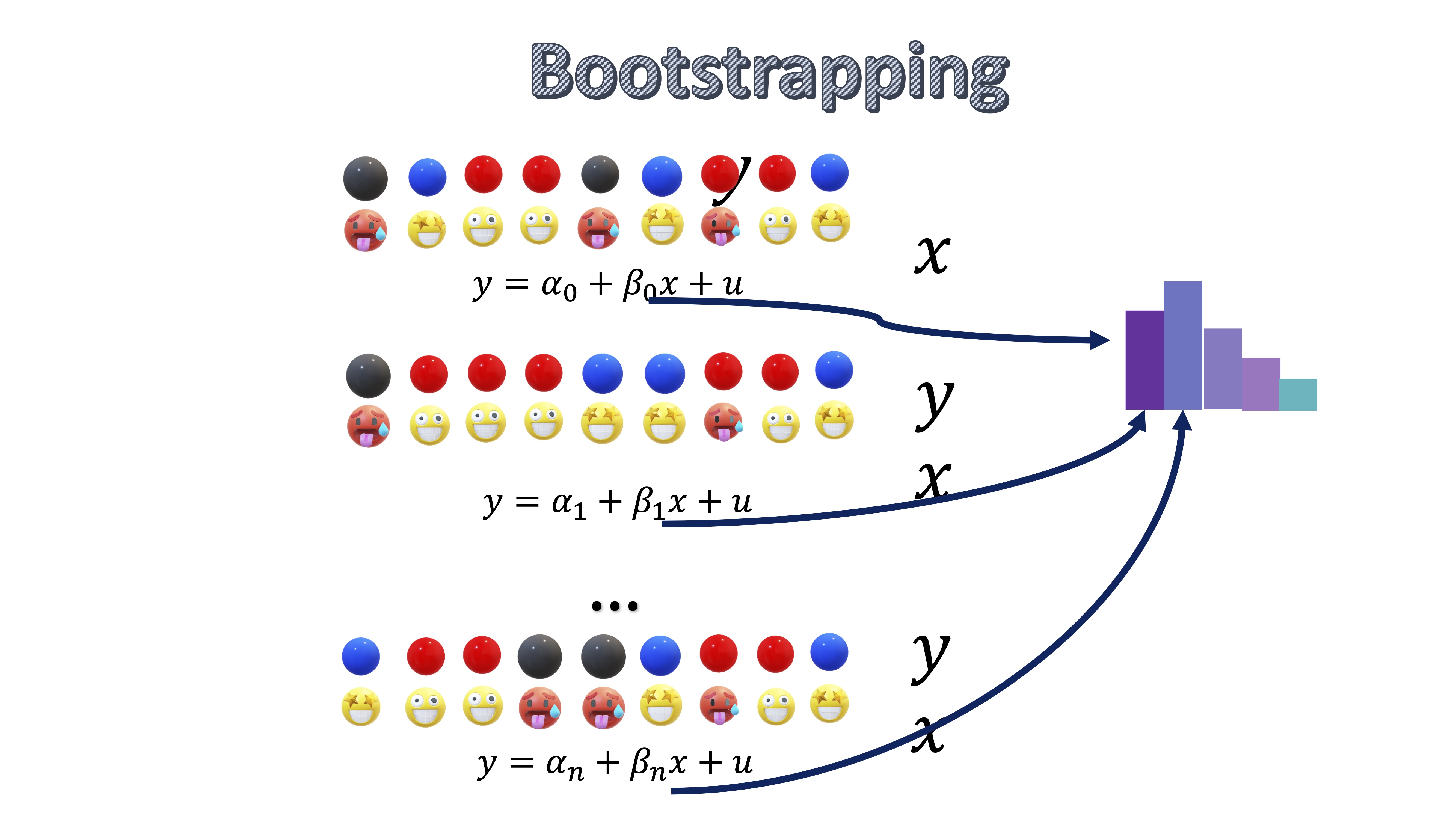
FIG 4: la idea del bootstrapping

Como ve, cada iteración que hace, es como si sorteara en la urna qué elementos de la muestra se utilizan y en qué proporción. Habrá elementos (bolas) que no saque en una iteración y otras que las saque muchas veces. Como ve, lo que está haciendo es generar muchas muestras alternativas a partir de una única muestra.

Esta técnica es útil para:

Obtener intervalos de confianza para parámetros cuando el modelo no lo permite (piense en modelos complicados, donde no se puede obtener una expresión analítica de las varianzas)

Obtener intervalos de confianza para parámetros cuando los errores no siguen una distribución normal (y la muestra es pequeña)

Obtener intervalos de confianza para predicciones

Vea cómo utilizarla. Por ejemplo, generamos un modelo de regresión lineal donde todo funciona. Entonces, el script del bootstrap es el siguiente

#declaramos los vectores donde guardaremos las estimaciones
b<-vector()
a<-vector()
#generamos la muestra aleatoria del modelo de regresión
set.seed(123)
n<-100
u<-rnorm(n,0,sd=3)
x<-runif(n)
y<-3+5*x+u
#estimamos un primer modelo base
M0<-lm(y~x)

for(i in 1:10000) {

 id<-sample(c(1:n), n, replace = TRUE)  
  X<-x[id]
  Y<-y[id]
  M1<-lm(Y~X)
  a[i]<-M1$coefficients[1]
  b[i]<-M1$coefficients[2]
  
}



par(mfrow=c(1,2))
hist(a, main="histograma para a")
abline(v =3, col = "purple", lwd = 2)
hist(b, main="histograma para b")
abline(v =5, col = "blue", lwd = 2)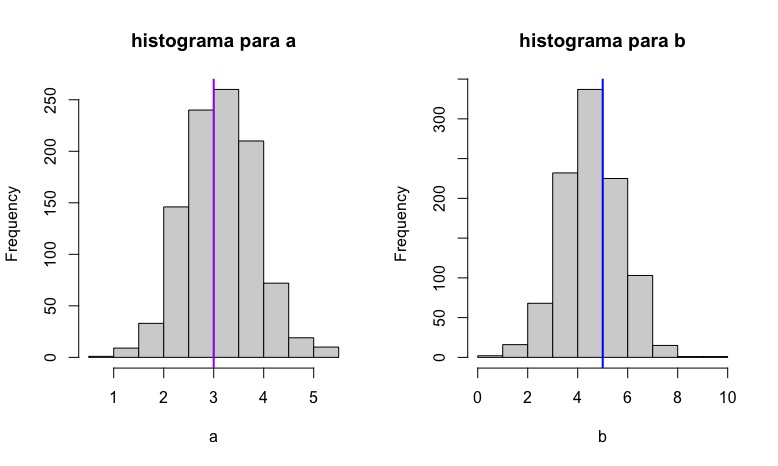

FIG 5: Primer ejemplo del bootstrap De hecho, puede comprobar cómo los intervalos de confianza que obtiene son similares. Mediante el modelo :

#esta es la regresión inicial# 
> summary(M0)

Call:
lm(formula = y ~ x)


Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   3.0196     0.5325   5.671 1.44e-07 ***
x             5.5177     0.9384   5.880 5.69e-08 ***

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.086 on 48 degrees of freedom
Multiple R-squared:  0.2106,    Adjusted R-squared:  0.1941 
F-statistic:  12.8 on 1 and 48 DF,  p-value: 0.0008027

Donde un Intervalo de confianza para el parámetro \(\beta\) se obiene como

\[ IC\left(\beta\right)_{\left(1-\alpha\right)\%}\equiv\left(5.51-1.96\times0.9384,5.51+1.96\times0.9384\right)=(3.6707,7.349) \]

Como puede ver, si calculamos el IC mediante los resultados del bootstrap, tendremos

> quantile(b, c(.025, .5, .975)) 
    2.5%      50%    97.5% 
3.690361 5.502940 7.38899

que es un intervalo similar. Ahora bien, ¿qué ocurre si los errores no se distribuyen de forma normal? En este caso, pedimos que los errores se distribuyan de manera uniforme.

b<-vector()
a<-vector()
set.seed(123)
n<-50
u<-runif(n,-3,3)
x<-runif(n)
y<-3+5*x+u
M0<-lm(y~x)

for(i in 1:10000) {
  
  id<-sample(c(1:n), n, replace = TRUE)  
  X<-x[id]
  Y<-y[id]
  M1<-lm(Y~X)
  a[i]<-M1$coefficients[1]
  b[i]<-M1$coefficients[2]
  
}

En este caso, es importante notar que la hipótesis principal para obtener intervalos de confianza de parámetros en modelos de regresión lineal, como ya se vio, es que los errores se distribuyan normal. Partiendo del modelo original de regresión, obtenido con los datos simulados (con error NO normal), calculamos el intervalo de confianza para los parámetros obtenido como si los errores fueran normales

#esta es la regresión inicial# 
> summary(M0)

Call:
lm(formula = y ~ x)


Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.8818     0.5051   5.705 7.05e-07 ***
x             5.5005     0.9183   5.990 2.60e-07 ***
---
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.086 on 48 degrees of freedom
Multiple R-squared:  0.2106,    Adjusted R-squared:  0.1941 
F-statistic:  12.8 on 1 and 48 DF,  p-value: 0.0008027

Donde un Intervalo de confianza para el parámetro \(\beta\) se obiene como

\[ IC\left(\beta\right)_{\left(1-\alpha\right)\%}\equiv\left(5.50-1.96\times0.9183,5.50+1.96\times0.9183\right)=(3.7001,7.2998) \]

mientras que el intervalo, calculado con la muestra bootstrap, será

> quantile(b, c(.025, .5, .975)) 
    2.5%      50%    97.5% 
3.598279 5.506940 7.382569

que difiere del calculado asumiendo normalidad y que, en el caso de distribuciones de errores con mayor asmetría, etc… podría dar resultados mucho más diferentes.

Ejemplo resuelto de predicción con Bootstrapp aplicado a una muestra real

Objetivo Aplicar la técnica del bootstrap a unos datos reales y entender la utilidad.

Con los datos de los Simpson, pretendemos estimar los coeficientes de un modelo de regresión,

\[ audiencia_i=\beta_0+\beta_1 rating_i+\beta_2season_i+\beta_3homer_i+u_i \]

donde \(u_i\) es un error aleatorio con media cero y varianza constante.

Mediante bootstrap, obtendremos una estimación de la función de densidad de los parámetros

library(readr)
SIMPSONS<- read_table2("SIMPSONS_FINAL.csv", locale = locale(decimal_mark = ","))
SIMPSONS<-na.omit(SIMPSONS)
audiencia<-SIMPSONS$millions_audiene
rating<-SIMPSONS$rating_imdb
Season<-SIMPSONS$season
Homer<-SIMPSONS$Homer
n<-dim(SIMPSONS)[1]

a<-vector()
b<-vector()
c<-vector()
d<-vector()

for(i in 1:10000) {
  
  id<-sample(c(1:n), n, replace = TRUE)  
  X1<-rating[id]
  X2<-Season[id]
  X3<-Homer[id]
  Y<-audiencia[id]
  M1<-lm(Y~X1+X2+X3)
  a[i]<-M1$coefficients[1]
  b[i]<-M1$coefficients[2]
  c[i]<-M1$coefficients[3]
  d[i]<-M1$coefficients[4]
}

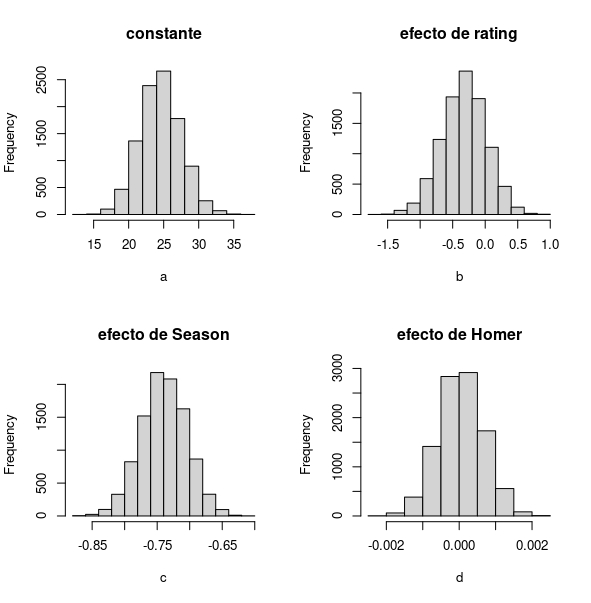FIG 6: Resultado del Bootstrap con el modelo de los Simpson Como ya ha entendido, en este curso tratamos de evitar los contrastes de hipótesis habituales para dar respuesta a preguntas que, en realidad, son complejas. ¿Cómo podremos usar el bootstrap para ilustrar el impacto cuantitativo de las variables de interés?

Puede entonces,

Analizar cuál es la distribución del posible efecto en la audiencia de un incremento “promedio” de las variables Homer y rating

Para ello, piense que no es lo mismo aumentar una unidad en la variable Homer que una unidad en la variable rating. Recuerde que para cada una de las variables puede obtener su desviación típica, puesto que le informa de la variación promedio de dichas variables en la muesrtra.

Si multiplica dicho impacto promedio por los coeficientes obtenidos en el bootstrap, tendrá la distribución del efecto de cada una de estas variables sobre la audiencia

¿Cuál parece tener mayor efecto sobre la audiencia? Haga un gráfico con los dos efectos (en valor absoluto) y analice cuál podría tener mayor impacto sobre la audiencia

im_rat<-sd(rating)
im_Homer<-sd(Homer)

hist( abs(im_rat*b), col=rgb(0,0,1,1/4), xlim=c(0,1),main="Histograma de los efectos potenciales")  # first histogram
hist( abs(im_Homer*d), col=rgb(1,0,0,1/4), xlim=c(0,1), add=T)  # second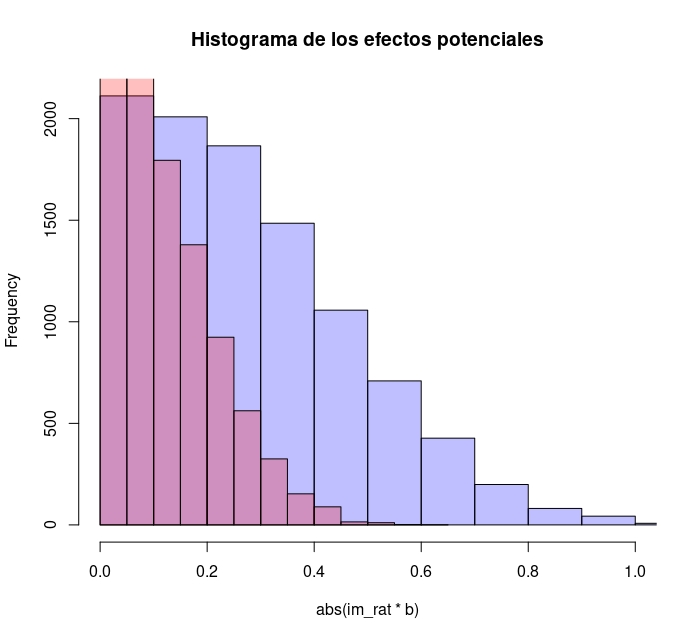

FIG 8: Distribución del efecto “promedio” de ambas variables

La variable rating (morada) tiene un impacto potencial, sobre la audiencia, mucho más remarcable que las apariciones de Homer.

Por otro lado, puede hacer predicción condicional. Por ejemplo, ¿cuál será la distribución de la predicción para la audiencia de la temporada 27 en un episodio con un 6 de nota media y con 200 líneas de guión de Homer?

#predicción para la temporada 27 de la audiencia de un episodio con un 6 de nota media de Rating y 200 líneas de 
#guion de Homer

pred_simpsons<-a+b*6+c*27+d*200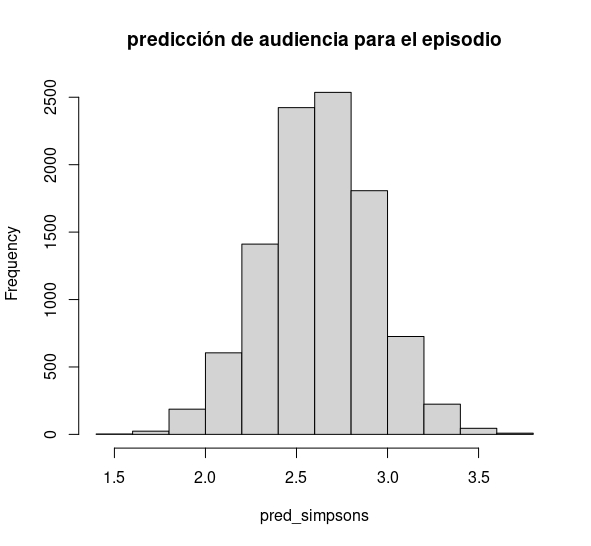

FIG 7: Predicción “bootstrap” de la audiencia del episodio ¿Cómo comentaría este resultado?

** Fin del Bloque**

En este bloque ha aprendido a entender una técnica de mucha utilidad en el mundo de la ciencia de datos: la simulación. Con suerte, además, habrá tenido la oportunidad de seguir discutiendo conceptos que lleva ya, años, viendo en estadística y que, quizás, no define y entiende con precisión.

FIG