BLOQUE 5: Introducción al aprendizaje automático

clase 1: métodos de reducción de la dimensión

Clase 4: Componentes Principales

El análisis de componentes principales tiene una clara idea geométrica basada en un concepto clave: la proyección ortogonal. Primero, explicaremos visualmente la idea de proyección ortogonal para, a continuación, ir usando esas ideas con el objetivo de entender el método. La forma de desarrollarlo estará basada en intuiciones para, al final, disponer de un apéndice que le permita entender, con algo más de profundidad (si está interesado), las expresiones que se utilizan en el texto principal.

NOTA!

Aquí empieza la parte que no se verá en la explicación de clase, pero es importante interiorizar para entenderlo

Algunas ideas de álgebra y geometría

Las ideas que aquí se cuentan son, en realidad, un ejemplo gráfico y divulgativo. De esta manera, tanto los conceptos centrales de proyección ortogonal y de diagonalización de matrices, se enuncian de forma aplicada y se anima al lector/a que acuda a un texto de matemáticas (si tiene más interés en asentar esas ideas). Un buen texto es “Álgebra Lineal y sus Aplicaciones” de David C. Lay.

• Vector. La definición típica de vector es “un segmento de recta orientado”. Por ejemplo, el vector \(\overrightarrow{x}=\left[\begin{array}{c} 1\\ 2 \end{array}\right]\) nos dice que tenemos que orientarnos dado un paso en sentido el eje \(x\) (es decir, a la derecha) y dando dos pasos en sentido del eje \(y\) (es decir, hacia arriba). Sin embargo, el vector no dice nada de dónde debemos empezar, esto es, el punto de aplicación: todos estos vectores son el mismo:

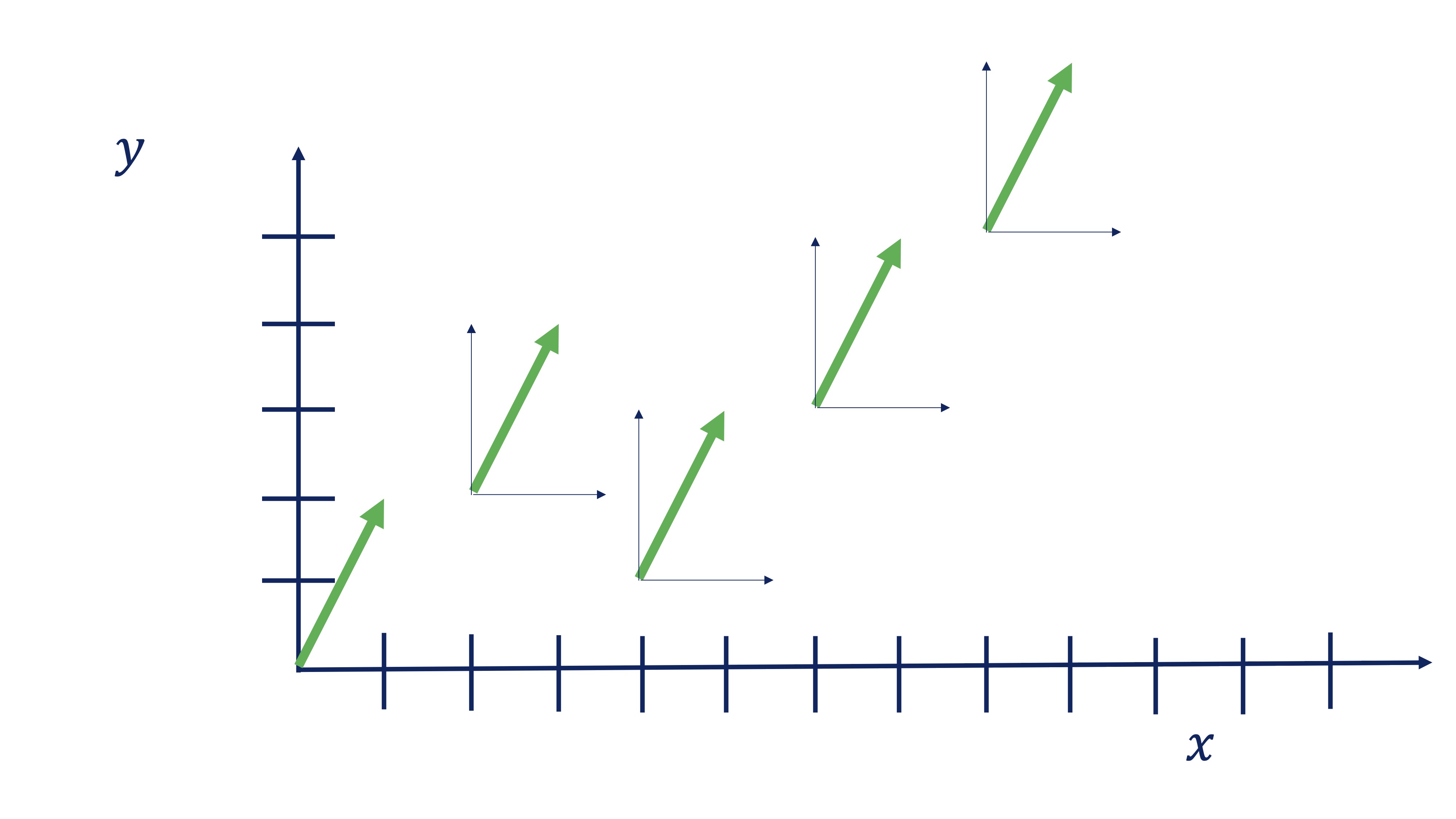
FIG 1: El mismo vector en distintos puntos de aplicación

La definición de segmento de recta orientado, quizás no le permita hacerse una idea de para qué usará los vectores. En nuestro caso, un vector será un almacenador de información. De hecho, el ojo humano suele “vectorizar” el análisis de datos. Mire, si no, el precio de la acción de Coca-Cola:

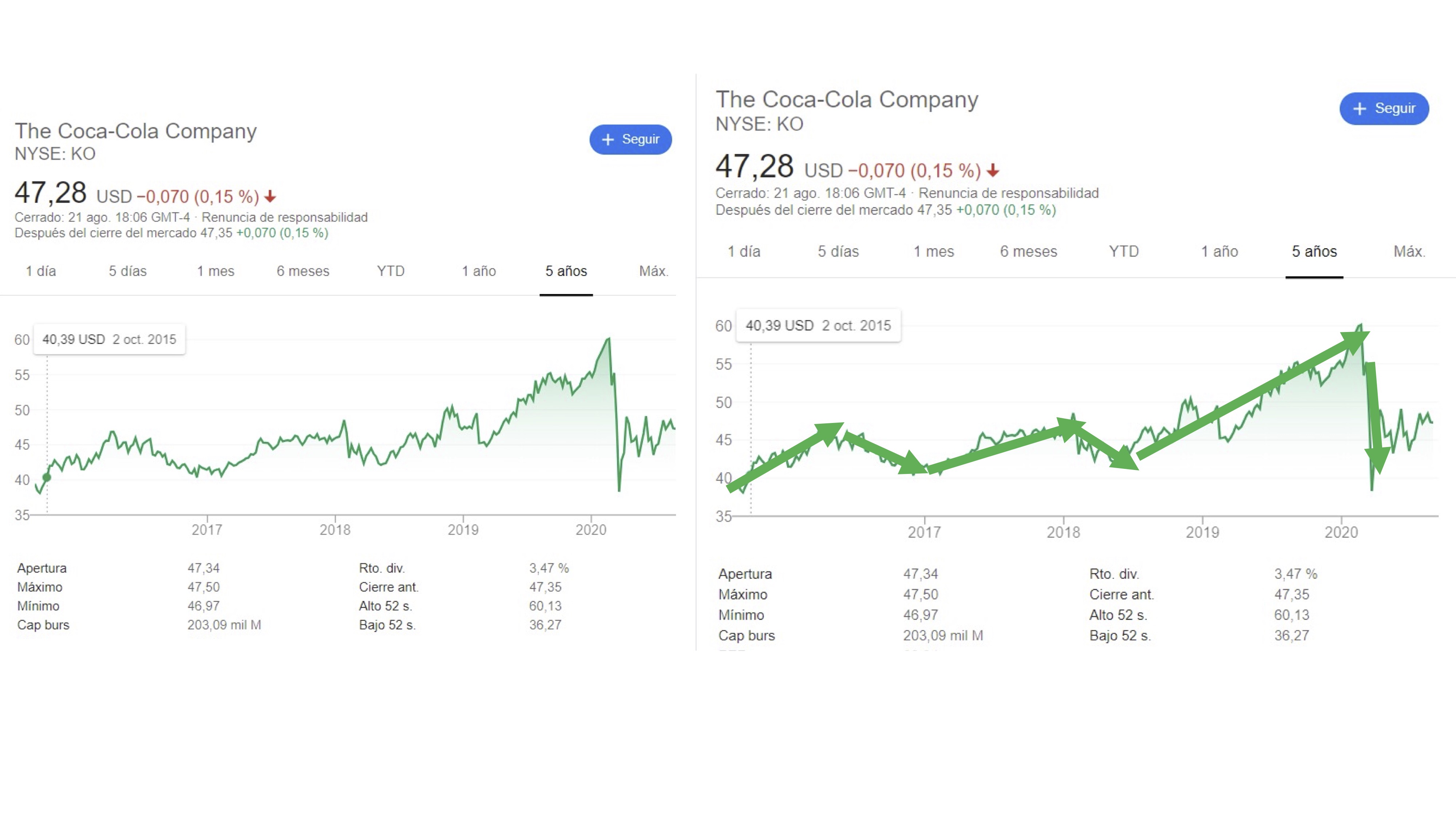
FIG 2: El precio de la acción de “Coca Cola” vectorizado

Como puede ver, nuestro ojo no está preparado para procesar todas las pequeñas discrepancias de la evolución de los datos. Seguro que prefiere tener una idea más general de los movimientos de la bolsa usando esas flechitas que llamamos vectores.

Por ejemplo, si almacenamos en un vector, \(\overrightarrow{v}\) la siguiente información sobre el precio de las acciones de Coca Cola:

\[ \overrightarrow{v}=\left[\begin{array}{cc} \#meses, & variaci\acute{o}n\:precio\end{array}\right], \]

tendremos algo así:

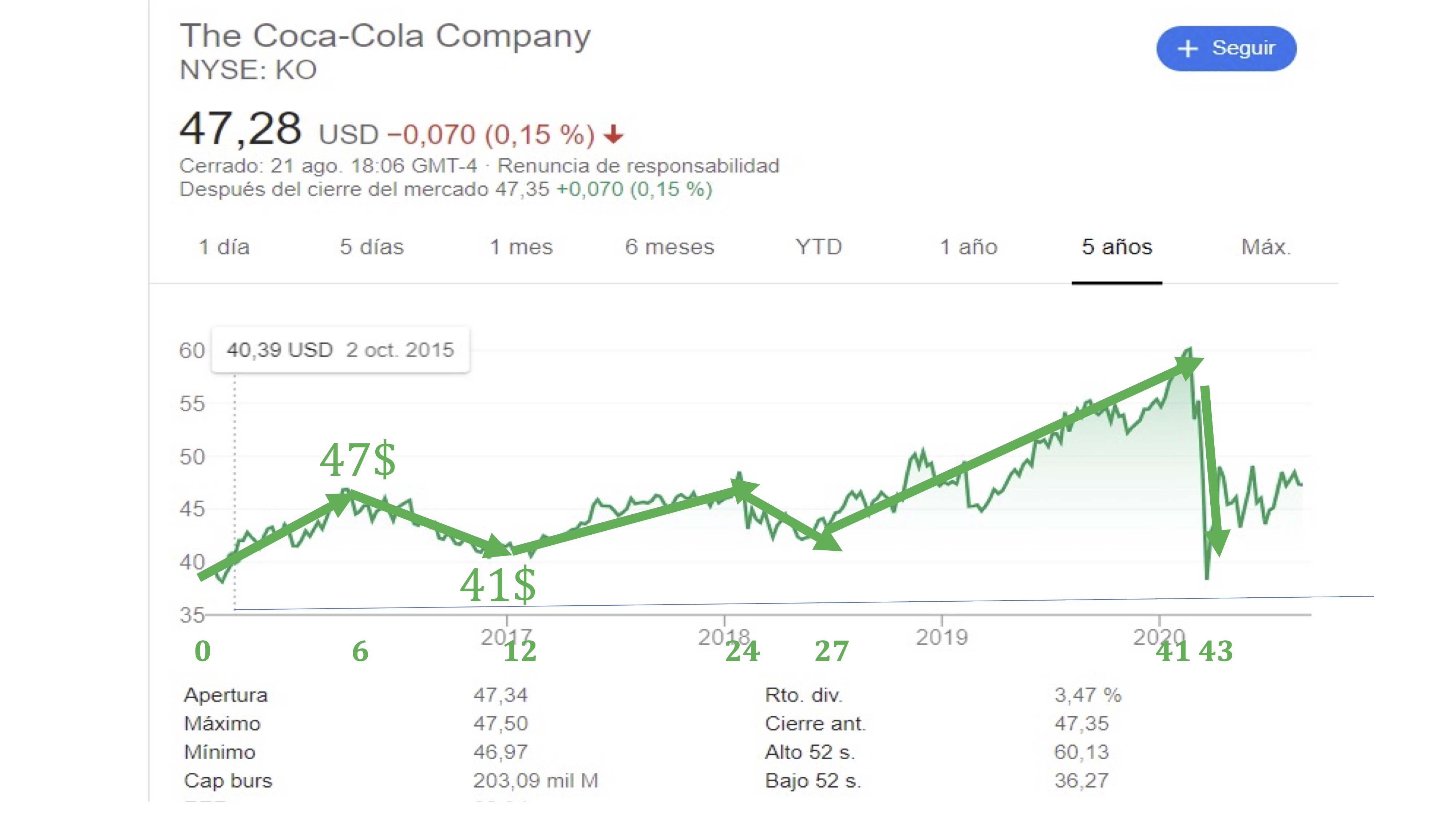
FIG 3: un caso concreto para ver la idea de vector

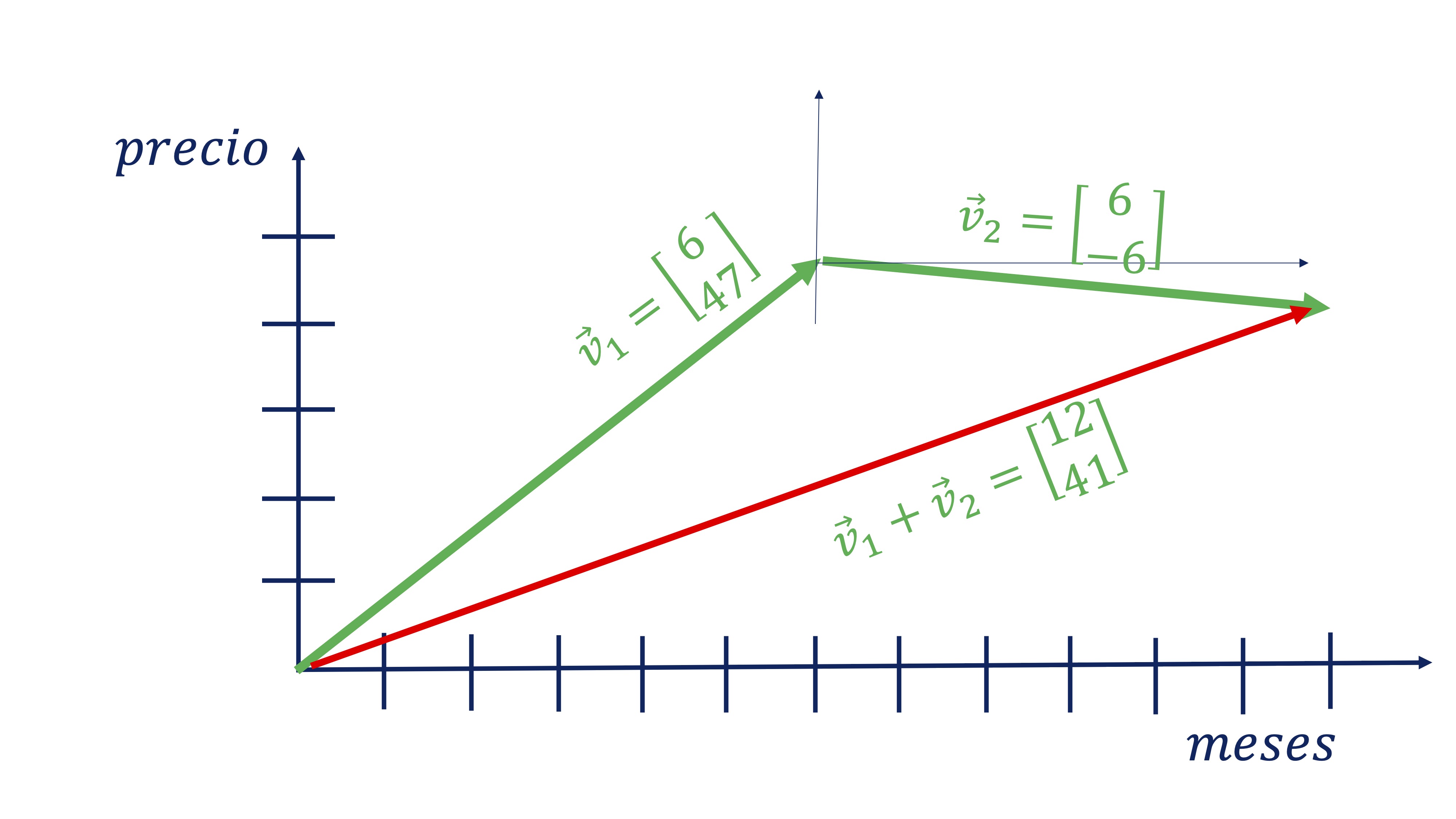Donde, además, la suma de los dos vectores tiene sentido ya que nos da en el primer componente el tiempo que ha pasado y en el segundo el precio en dicho momento (vector rojo).

Recuerde que, en general, denotamos un vector como \(\overrightarrow{v}\) (la flecha superior indica que es un vector) y ponemos sus componentes en columna: \(\overrightarrow{v}=\left[\begin{array}{c} -2\\ 3 \end{array}\right]\). Además, recuerde que si quiere tener el vector como una fila, lo ha de trasponer: \(\overrightarrow{v}^{T}=\left[\begin{array}{cc} -2 & 3\end{array}\right]\), usando la letra \(T\) en el exponente para indicarlo. Si tenemos otro vector \(\overrightarrow{w}=\left[\begin{array}{c} 3\\ 2 \end{array}\right]\), definimos el producto escalar de ambos vectores como:

\[ \overrightarrow{v}^{t}\overrightarrow{w}=\left[\begin{array}{cc} -2 & 3\end{array}\right]\left[\begin{array}{c} 3\\ 2 \end{array}\right]=(-2\times3)+(3\times2)=0 \]

(como ve, se define “producto escalar” porque al multiplicarlos obtenemos siempre un número-un escalar). Como en nuestro caso, si el producto escalar de dos vectores es 0, eso indica que son perpendiculares (es decir, conforman un ángulo de 90º). Los dibujamos para que vea que, efectivamente, ocurre:

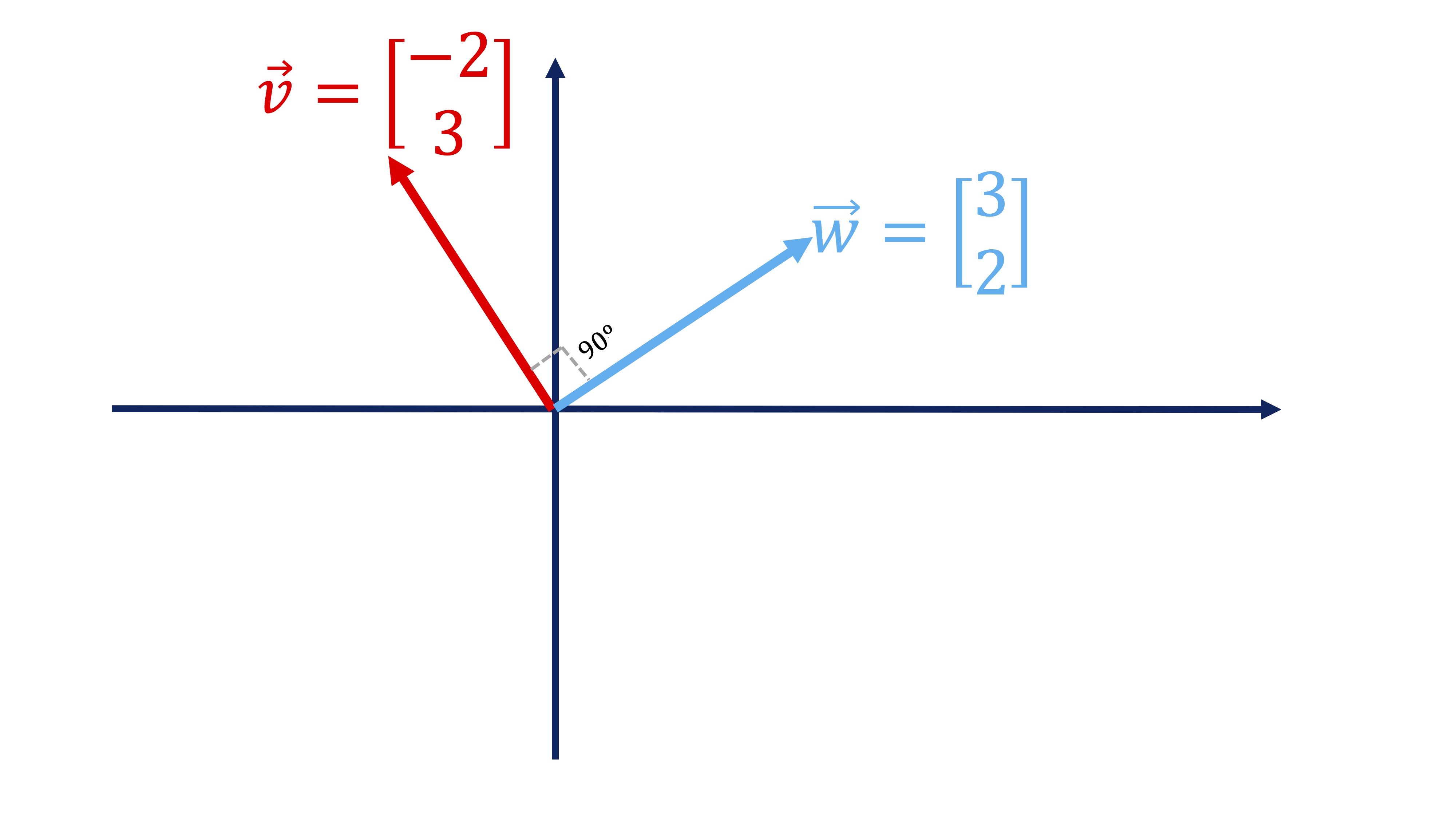
FIG 5: Dos vectores son perpendiculares (su producto escalar es cero)

-Matriz Respecto a una matriz, puede verla como una generalización de la idea de vector. Sigue siendo un buen almacén de información que, en este caso, es como si estuviera formada por un montón de vectores apilados. Por ejemplo, esta matriz guarda en columnas el número de observación (id), los meses, y la variación del precio (\(\Delta precio\)):

Id	Meses	\(\Delta precio\)
1	6	47
2	6	-6
…	…	…

Es decir,

\[ X=\left[\begin{array}{ccc} 1 & 6 & 47\\ 2 & 6 & -6 \end{array}\right], \]

esta matriz decimos que es de dimensión \(2\times3\), ya que tiene 2 filas y 3 columnas. De manera más formal, se puede escribir así: \(X\in\mathcal{M}_{2\times3}\), que indica que \(X\) pertenece al espacio de las matrices de dimensión \(2\times3.\)

Recuerde que para que dos matrices puedan multiplicarse se debe poder realizar el producto escalar, visto anteriormente con los vectores, para cada fila y columna. Es decir, \(X=\left[\begin{array}{cc} 1 & 0\\ 3 & 1\\ 5 & 2 \end{array}\right]\), \(Y=\left[\begin{array}{cc} 1 & 2\\ 0 & 1 \end{array}\right]\), pueden multiplicarse así \(XY\) porque el número de columnas de la primera matriz es igual al número de filas de la segunda, pero no pueden multiplicarse así: \(YX\):

\[ XY=\left[\begin{array}{cc} 1 & 0\\ 3 & 1\\ 5 & 2 \end{array}\right]\left[\begin{array}{cc} 1 & 2\\ 0 & 1 \end{array}\right]=\left[\begin{array}{cc} 1 & 2\\ 3 & 7\\ 5 & 12 \end{array}\right] \]

\[ YX=\left[\begin{array}{cc} 1 & 2\\ 0 & 1 \end{array}\right]\left[\begin{array}{cc} 1 & 0\\ 3 & 1\\ 5 & 2 \end{array}\right]=? \]

• MATRIZ DE VARIANZAS Y COVARIANZAS. Una aplicación del producto de matrices, que encontrará habitualmente, es la matriz de varianzas y covarianzas. Recuerde que la varianza de una variable es \(var(x)=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}{n-1}\) y la covarianza entre dos variables es \(cov(x,y)=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{n-1}\) y podemos construir una matriz con esa información:

\[\begin{equation} C=\left[\begin{array}{cc} var(x) & cov(x,y)\\ cov(x,y) & var(y) \end{array}\right]\label{eq:matrizC} \end{equation}\]

(dese cuenta de que es una matriz simétrica). \(C\) se puede obtener con cálculos más rápidos mediante operaciones con matrices. Vamos a imaginar que la \(X\) es ahora nuestra matriz de datos, donde la columna 1 es la variable \(x\) y la columna 2 es la variable \(y\), de tal forma que las filas son las observaciones por individuos:

Id	\(x\)	\(y\)
1	1	0
2	3	1
3	5	2

para poder seguir con la fórmula, vamos a transformar la matriz y le vamos a restar a cada columna su media:

Id	\(x-\bar{x}\)	\(y-\bar{y}\)
1	-2	-1
2	0	0
3	2	1

de tal forma que tenemos que \(\widetilde{X}=\left[\begin{array}{cc} -2 & -1\\ 0 & 0\\ 2 & 1 \end{array}\right]\) es la matriz \(X\) donde le hemos restado las medias (se dice que es la matriz \(X\) en desviaciones con respecto a sus medias). Si ahora hacemos esta cuenta:

\[ \frac{1}{n-1}\widetilde{X}^{t}\widetilde{X}=\frac{1}{3}\left[\begin{array}{ccc} -2 & 0 & 2\\ -1 & 0 & 1 \end{array}\right]\left[\begin{array}{cc} -2 & -1\\ 0 & 0\\ 2 & 1 \end{array}\right]=\frac{1}{2}\left[\begin{array}{cc} 8 & 4\\ 4 & 2 \end{array}\right]=\left[\begin{array}{cc} 4 & 2\\ 2 & 1 \end{array}\right] \]

donde \(N\) representa el número de elementos muestrales, nos proporciona la matriz de varianzas y covarianzas.

    x1<-c(1,3,5)
    x2<-c(0,1,2)
    X<-data.frame(x1,x2)
    C<-cov(X)
    #equivalente a hacer
    x1<-x1-mean(x1)
    x2<-x2-mean(x2)
    X<-as.matrix(data.frame(x1,x2))
    C<-(1/(dim(X)[1]-1))*(t(X))%*%X

Por lo tanto, concluímos que:

• Una matriz \(W\) cuyas filas son observaciones por individuo y las columnas son variables, si está expresada en desviaciones con respecto a la media, su matriz de varianzas y covarianzas resulta ser:

Ejercicio: pruebe que si las variables están estandarizadas (es decir los elementos de \(W\) no sólo están desviados con respecto a la media, sino que se los divide por su desviación típica), al hacer \(\frac{1}{N-1}W^{t}W,\) lo que obtenemos es la matriz de correlaciones.

La noción de proyección ortogonal

Otra de las preguntas de interés en álgebra son las que están relacionadas con la proyección ortogonal. Aquí vamos a ver un ejemplo sencillo, con el que trabajaremos a mano. Pero antes, necesitamos saber qué es un vector proporcional a otro. Diremos que un vector \(\overrightarrow{w}\) es proporcional a otro \(\overrightarrow{v}\) (y se escribe con esta notación \(\overrightarrow{w}\propto\overrightarrow{v},\) leyéndose \(\propto\) como “es proporcional a”) si se cumple que:

\[ \overrightarrow{w}=\lambda\overrightarrow{v}, \]

con \(\lambda\in\mathbb{R}.\) En la figura siguiente, tiene un ejemplo donde -una manera de verlo- el vector \(\overrightarrow{v}_{2}\propto\overrightarrow{v}_{1}\), con \(\lambda=2\), indicando que siguen la misma dirección y sentido, solo que \(\overrightarrow{v}_{2}\) es más grande. \(\overrightarrow{v}_{3}\propto\overrightarrow{v}_{1}\), con \(\lambda=-1/2\), indicando que siguen la misma dirección y sentido contrario (y es más pequeño). Como ve, los vectores proporcionales comparten dirección.

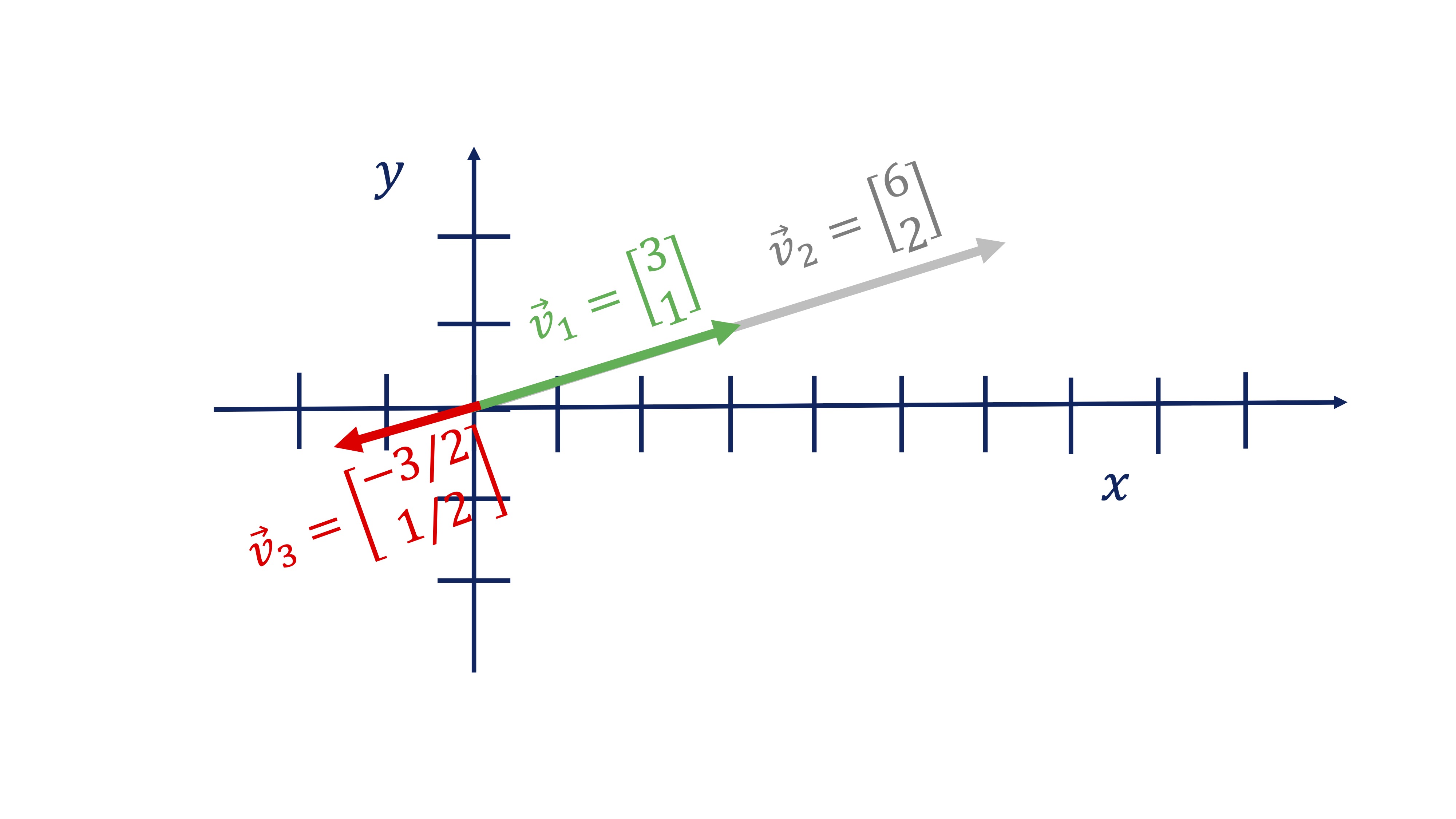
FIG 6: Tres vectores proporcionales

La idea de proyección ortogonal necesita tnener clara la de vector proporcional. De hecho, la idea de proyectar el vector \(\overrightarrow{w}\) sobre el vector \(\overrightarrow{v}\) consiste en lo siguiente:

**buscar un vector proporcional a \(\overrightarrow{v}\) que esté lo más cerca posible de \(\overrightarrow{w}:\)

Piense que hay infinitos vectores proporcionales a \(\overrightarrow{v}\) pero sólo uno de estos será el más cercano a \(\overrightarrow{w}.\) ¿Cuál cree que es en la figura siguiente?

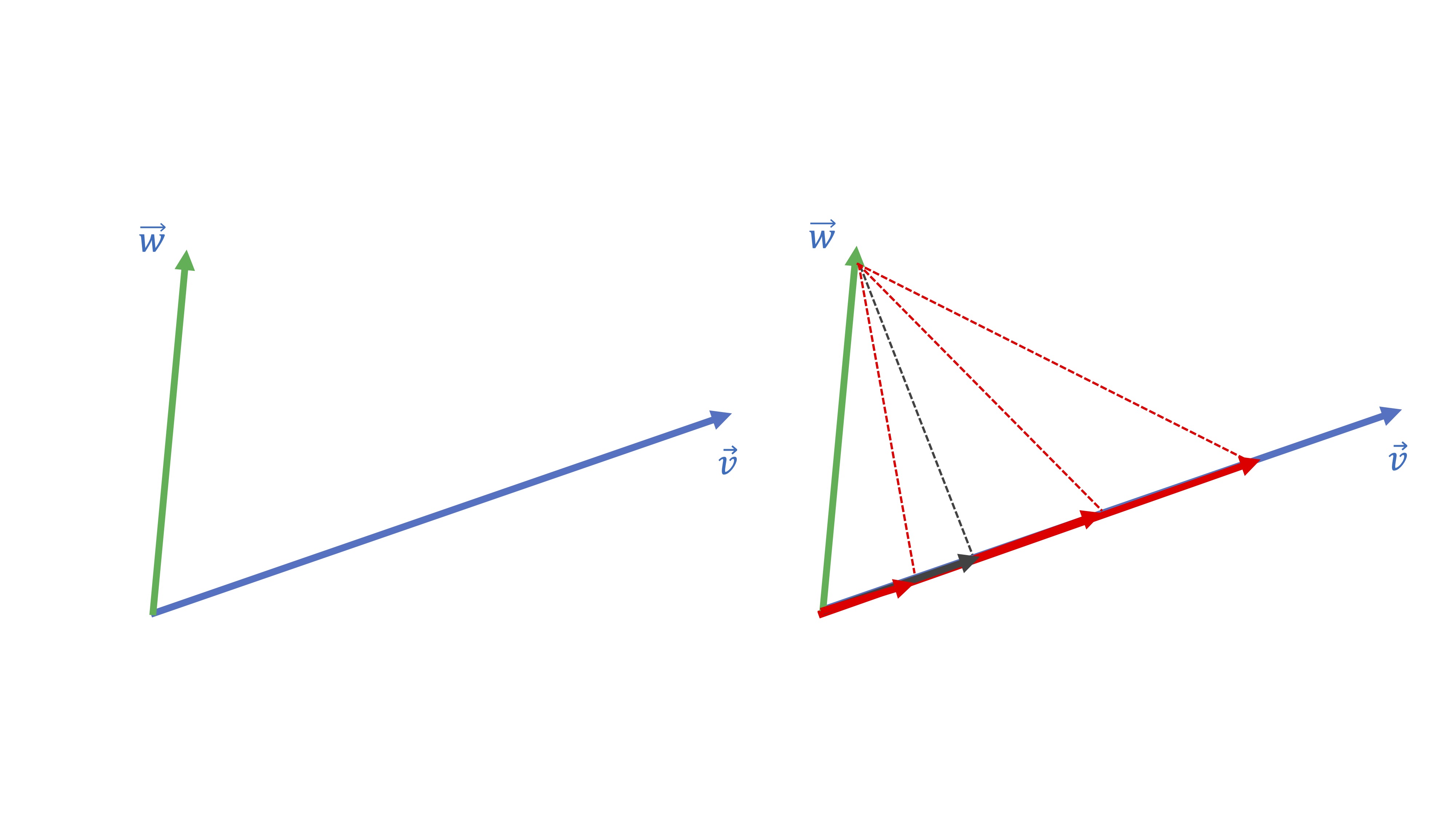
FIG 7: ¡El vector perpendicular es el que está más cerca!

Seguramente, habrá caído en la cuenta de que el más cercano es el gris:

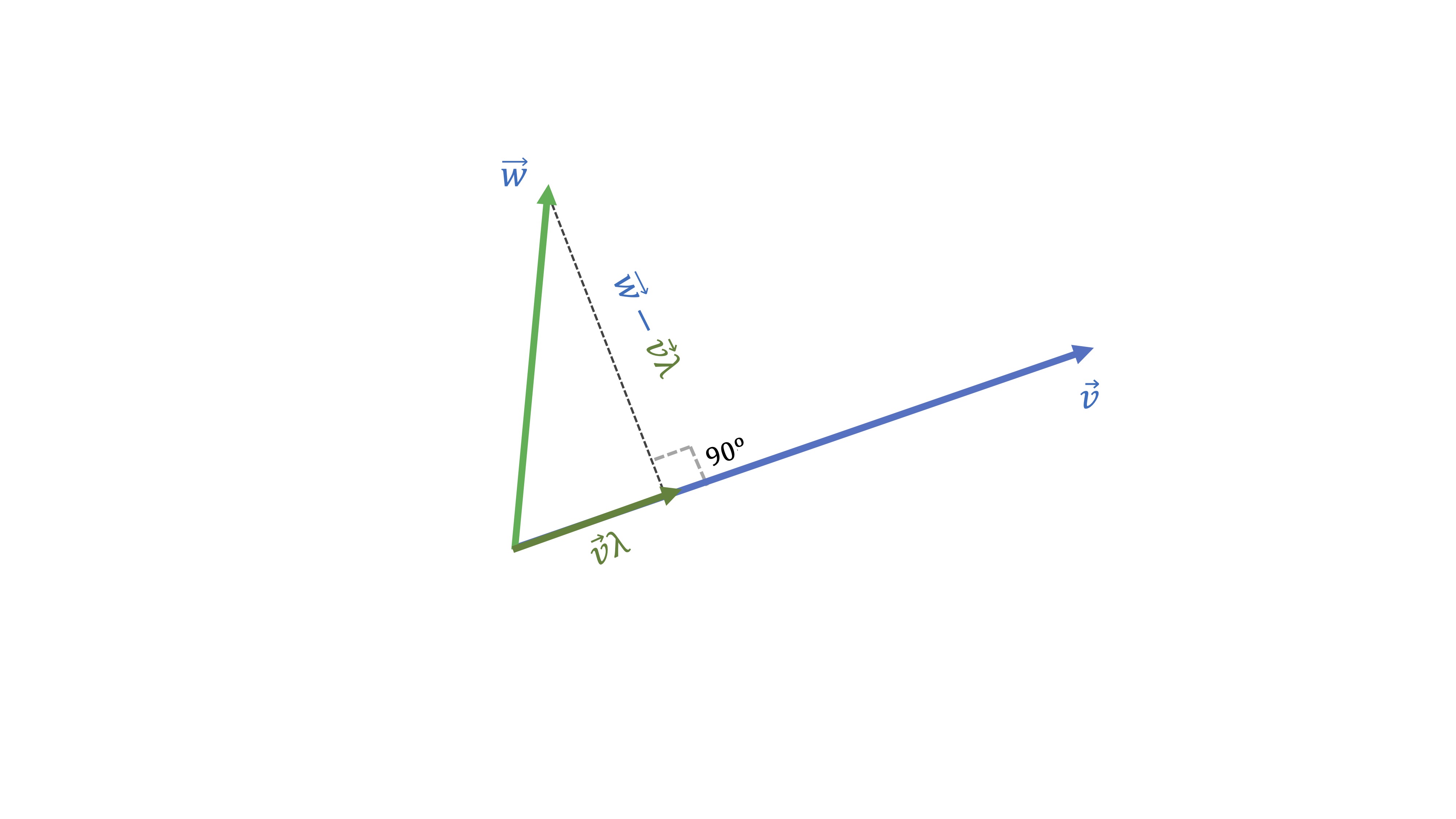
FIG 8: ¡El vector perpendicular es el que está más cerca!

Nuestro objetivo será encontrar qué vector proporcional a \(\overrightarrow{v}\) (es decir, \(\overrightarrow{v}\lambda\), donde \(\lambda\) es un escalar) está más cerca de \(\overrightarrow{w}.\) Ese “más cerca” quiere decir que la distancia entre los dos vectores sea la mínima posible. Como puede ver, esa es la distancia que genera el segmento ortogonal al vector \(\overrightarrow{v}\). Como ya hemos dicho, han de ser ortogonales, es decir, han de cumplir:

\[ \left(\overrightarrow{w}-\overrightarrow{v}\lambda\right)^{t}\overrightarrow{v}=0\Rightarrow\lambda=\frac{\overrightarrow{w}^{t}\overrightarrow{v}}{\overrightarrow{v}^{t}\overrightarrow{v}} \]

Veamos un ejemplo “a mano”.

• Si queremos proyectar el vector \(\overrightarrow{w}=\left[\begin{array}{c} 3\\ 1 \end{array}\right]\) sobre el vector \(\overrightarrow{v}=\left[\begin{array}{c} 1\\ 0 \end{array}\right]\), tendremos que

\[ \lambda=\frac{\overrightarrow{w}\cdot\overrightarrow{v}}{\overrightarrow{v}\cdot\overrightarrow{v}}=\frac{\left[\begin{array}{cc} 3 & 1\end{array}\right]\left[\begin{array}{c} 1\\ 0 \end{array}\right]}{\left[\begin{array}{cc} 1 & 0\end{array}\right]\left[\begin{array}{c} 1\\ 0 \end{array}\right]}=\frac{3}{1}=3 \]

Por lo que el vector más parecido a \(\overrightarrow{w}=\left[\begin{array}{c} 3\\ 1 \end{array}\right]\) pero que es proporcional a \(\overrightarrow{v}=\left[\begin{array}{c} 1\\ 0 \end{array}\right]\) es \(3\overrightarrow{v}=\left[\begin{array}{c} 3\\ 0 \end{array}\right]\). Dibújelo para cercionarse.

Autovalores y autovectores

Ya estamos terminando de la parte introductoria de álgebra. Nos queda, eso sí, justo lo más necesario para poder entender la idea de los componentes principales. Ciertas matrices cuadradas tienen una propiedad muy utilizada y muy famosa en álgebra: se dice que son diagonalizables si, por ejemplo, la matriz \(X=\left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\), admite esta descomposición:

\[ \left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\left(\begin{array}{c} -0.57\\ -0.57\\ -0.57 \end{array}\right)=6\left(\begin{array}{c} -0.57\\ -0.57\\ -0.57 \end{array}\right) \]

Cuando esto ocurre, lo que tenemos es \[ X\overrightarrow{v}=\lambda\overrightarrow{v}, \]

donde \(\overrightarrow{v}\) se denomina autovector y \(\lambda\) autovalor. De hecho, esta matriz, \(X\) va a tener tres autovalores (y sus correspondientes autovectores) no necesariamente distintos. Para calcularlos, vamos a usar R.

   X<-matrix(c(1,2,3,6,0,0,2,2,2),3,3,byrow=TRUE)
   ev<-eigen(X)
  #donde ev nos proporciona los resultados que buscamos

eigen() decomposition
$values
[1]  6 -2 -1

$vectors
           [,1]       [,2]       [,3]
[1,] -0.5773503 -0.3015113  0.1441708
[2,] -0.5773503  0.9045340 -0.8650248
[3,] -0.5773503 -0.3015113  0.4805693

Llegamos, entonces, al resultado que decíamos

\[ \left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\left(\begin{array}{c} -0.57\\ -0.57\\ -0.57 \end{array}\right)=6\left(\begin{array}{c} -0.57\\ -0.57\\ -0.57 \end{array}\right),\]

\[ \left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\left(\begin{array}{c} -0.30\\ 0.90\\ -0.30 \end{array}\right)=\left(\begin{array}{c} 0.30\\ -0.90\\ 0.30 \end{array}\right),\left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\left(\begin{array}{c} 0.14\\ 0.86\\ 0.48 \end{array}\right)=-2\left(\begin{array}{c} 0.14\\ 0.86\\ 0.48 \end{array}\right) \]

¿Cualquier matriz cuadrada admite esta descomposición?. No toda matriz cuadrada es diagonalizable: sin embargo, las que vamos a utilizar en este contexto (que, en esencia, serán matrices de varianzas y covarianzas y de correlaciones) sí admiten esta descomposición por ser simétricas. Además,

• La suma de los autovalores es igual a la suma de los elementos de la diagonal principal de la matriz

• Los autovectores son perpendiculares. Esto implica que la correlación entre ellos es cero

NOTA!

Hasta aquí acaba la parte que no se verá en la explicación

El método de los componentes principales (PCA)

Ya es momento de entender en qué consiste el método de “componentes principales”. Para ello, necesitaremos acudir a la proyección ortogonal y a la descomposición en autovalores y autovectores de una matriz simétrica.

Partimos de una nube de puntos

Vamos a dibujar esta matriz de datos,

Id	\(x\)	\(y\)
1	4.5	3
2	1	-1
3	-1	-2
4	-3	-1.5
5	-1.5	1.5
6	0	0

donde contamos con \(6\) observaciones y dos variables \((x,y)\), en una nube de puntos.

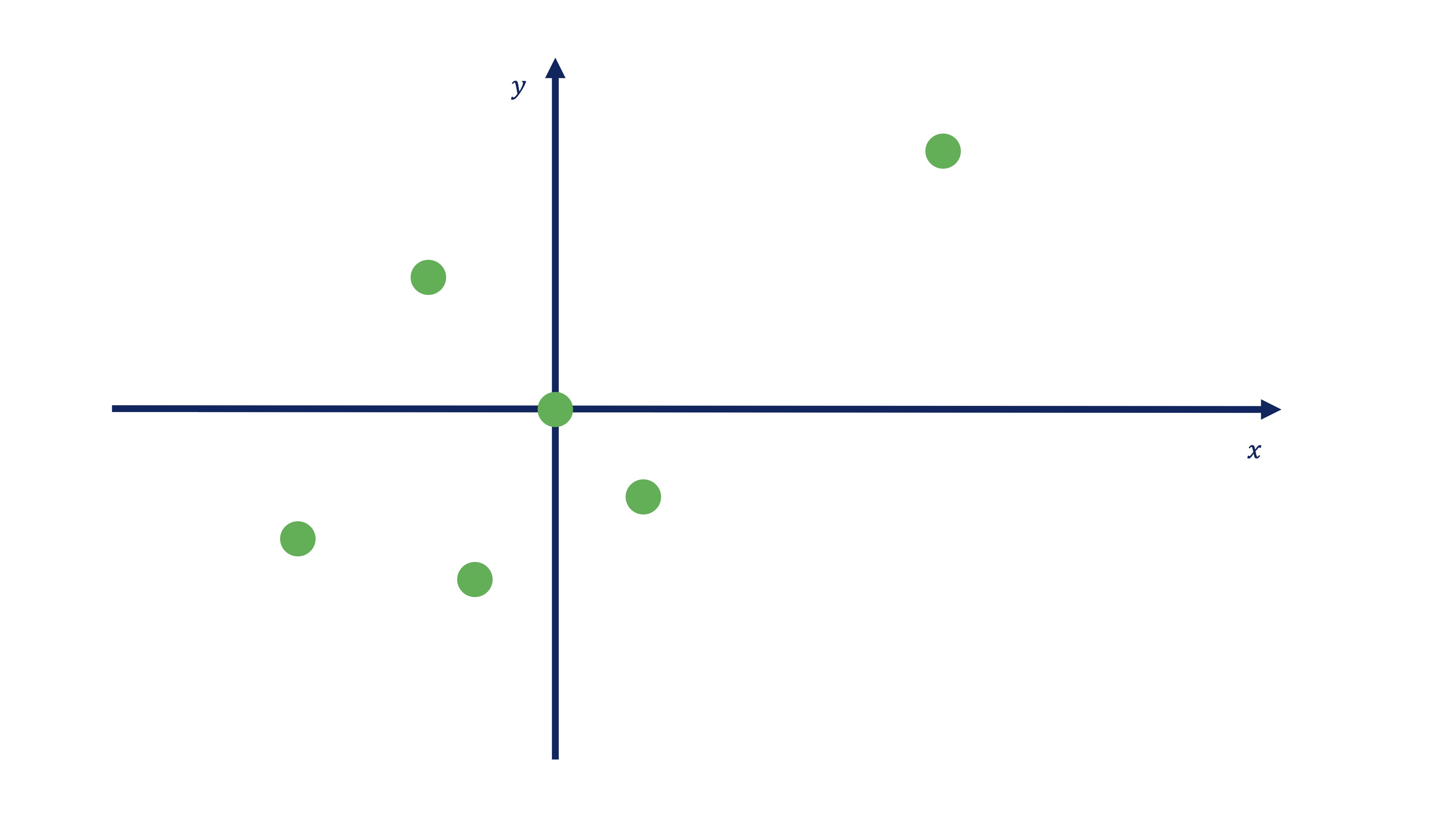
FIG 9: Dibujo de la nube de puntos

Como ve, estos puntos tienen una cierta relación lineal (es decir, un valor alto del coeficiente de correlación). La idea de los componentes principales consiste en pensar lo siguiente:

Si las variables son parecidas (tienen una correlación alta) quisiera intentar quedarme con una combinación de las dos y así pasar de tener dos variables a tener una

Es decir, idea lo que busca es reducir la dimensión (en columnas) de un conjunto de datos con un cierto número de variables relacionadas entre sí. En resumen, el objetivo de PCA, será el siguiente:

análisis de Componentes Principales!

Reducir el número de variables \(m\) de un conjunto de datos a un número \(k\) tal que \(k<<m\).

¿Cómo reducimos el número de variables? Para ello, tenemos que usar una técnica geométrica conocida como la proyección. La pregunta que nos hacemos es la siguiente: ¿Cómo transformamos la información de cada individuo, que-en este caso- está en dos dimensiones a una nueva información que esté en una dimensión? Esto ya lo hace, por ejemplo, cuando calcula un promedio. Imaginemos que las variables 1 y 2 están medidas en las mismas unidades y que, por tanto, tiene sentido obtener un promedio. El promedio de dos variables \(x,y\) consiste en \(\frac{x+y}{2}\), es decir

\[ nueva\:variable_{i}=0.5x_{i}+0.5y{}_{i}\:\:i=1,..,6 \]

Id	\(x\)	\(y\)	nueva variable
1	4.5	3	3.75
2	1	-1	0
3	-1	-2	-1.5
4	-3	-1.5	-2.25
5	-1.5	1.5	0
6	0	0	0

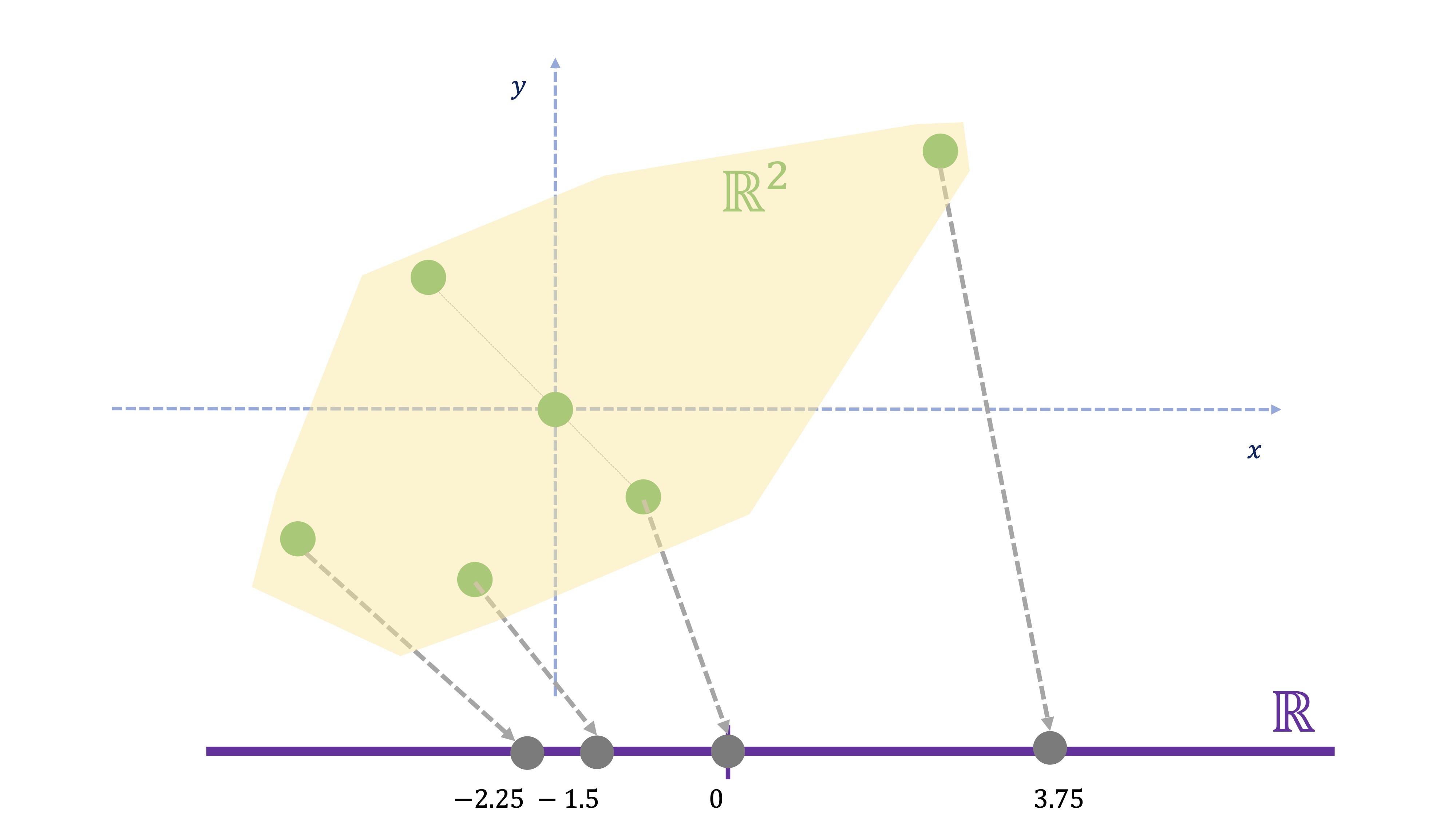
FIG 10: El promedio como proyección

Si se da cuenta (FIG 10), la nueva variable se representa sólo sobre un eje, ya que hemos resumido la información de las dos variables de cada individuo al promedio. Es decir: hemos proyectado un punto en \(\mathbb{R}^{2}\) (por ejemplo \((5.5,3)\) en \(\mathbb{R}\) (es decir, su proyección es 4.25). Ahora bien:

• ¿Y si las variables están relacionadas pero medidas en unidades distintas (años, euros, etc…)? El promedio no tiene sentido

• ¿El promedio es la mejor proyección?

Para ello nació el análisis de componentes principales

Como hemos visto, sólo en casos muy concretos es sensato utilizar el promedio como un “reductor” de la dimensión de nuestra información disponible. En realidad, si seguimos trabajando en este caso con información bidimensional, nos interesará proyectar los puntos sobre una recta (como hicimos antes con el promedio) pero que tenga, en general unos “pesos” para cada variable, elegidos mediante algún criterio sensato.

Entonces nos preguntamos: ¿Cómo buscar los valores \(C1,a1\) en esta expresión?

\[ C1_{i}=a1_{1}x_{i}+a1_{2}y_{i} \]

donde \(a1_{1},a1_{2}\) son los pesos asociados a cada variable, los cuales nos permitirán resumir lo mejor posible la información conjunta de las variables \(x,y\) en una nueva variable que llamaremos \(C1\)? Lo que vamos a hacer aquí lo contaremos de una manera sencilla (pensando sobre un gráfico) aunque en el apéndice se desarrolla el álgebra necesaria para entenderlo todo. Tenemos que buscar una recta sobre la que proyectar los puntos de tal forma que esos puntos estén lo más cerca posible a la recta. Seguro que ya ha averiguado que aquí:

buscamos una proyección ortogonal.

Vamos a imaginarnos, entonces, que somos capaces de encontrar una recta que nos permita realizar la proyección ortogonal de todos los puntos a esa recta (y que nos permite, entonces, pasar de \(\mathbb{R}^{2}\rightarrow\mathbb{R}\)). Usando, por ahora, la imaginación, nos podríamos acercar a algo así:

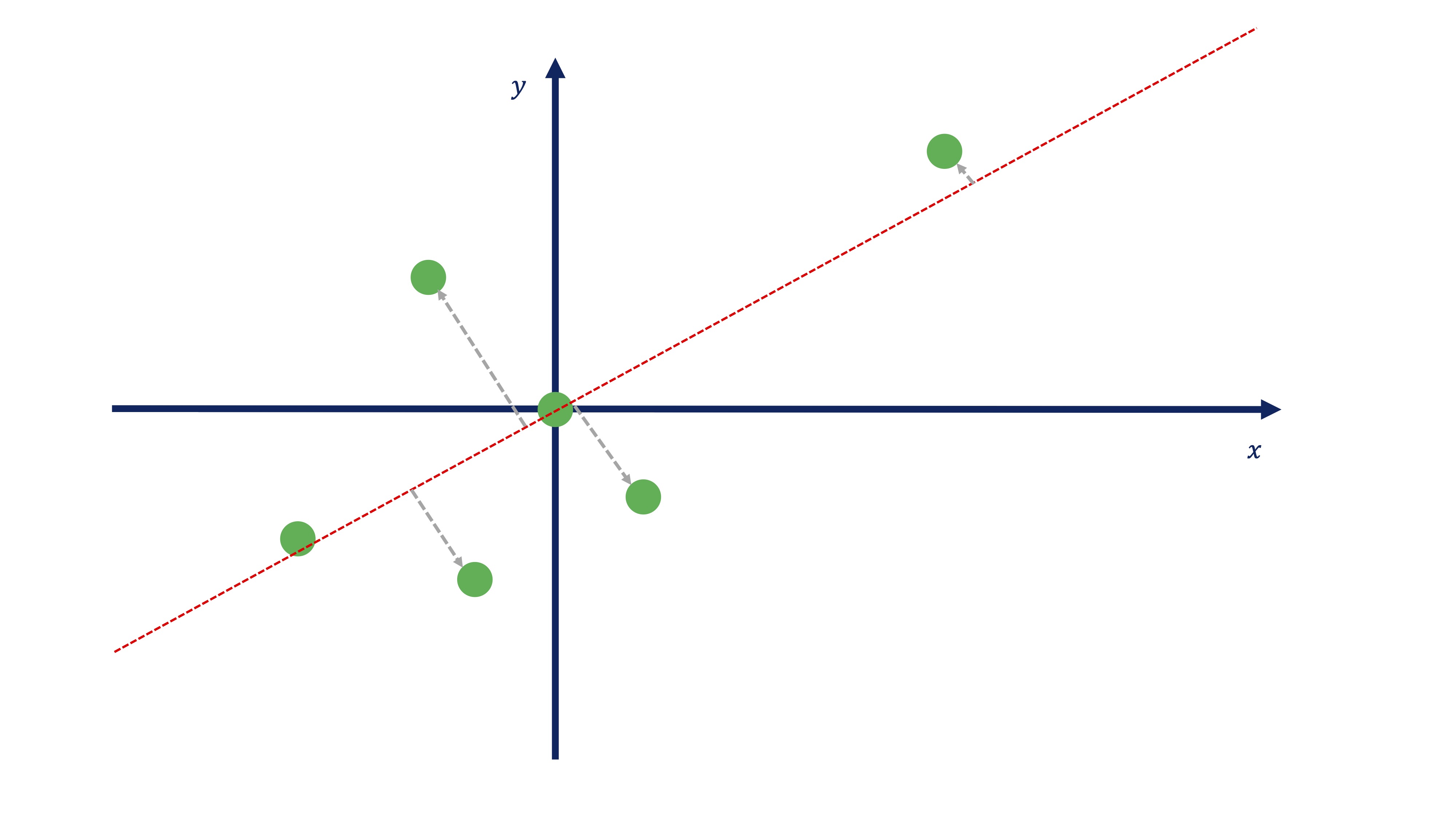
FIG 11: Una proyección ortogonal

A lo mejor, alguien ha pensado esta otra recta (o similar):

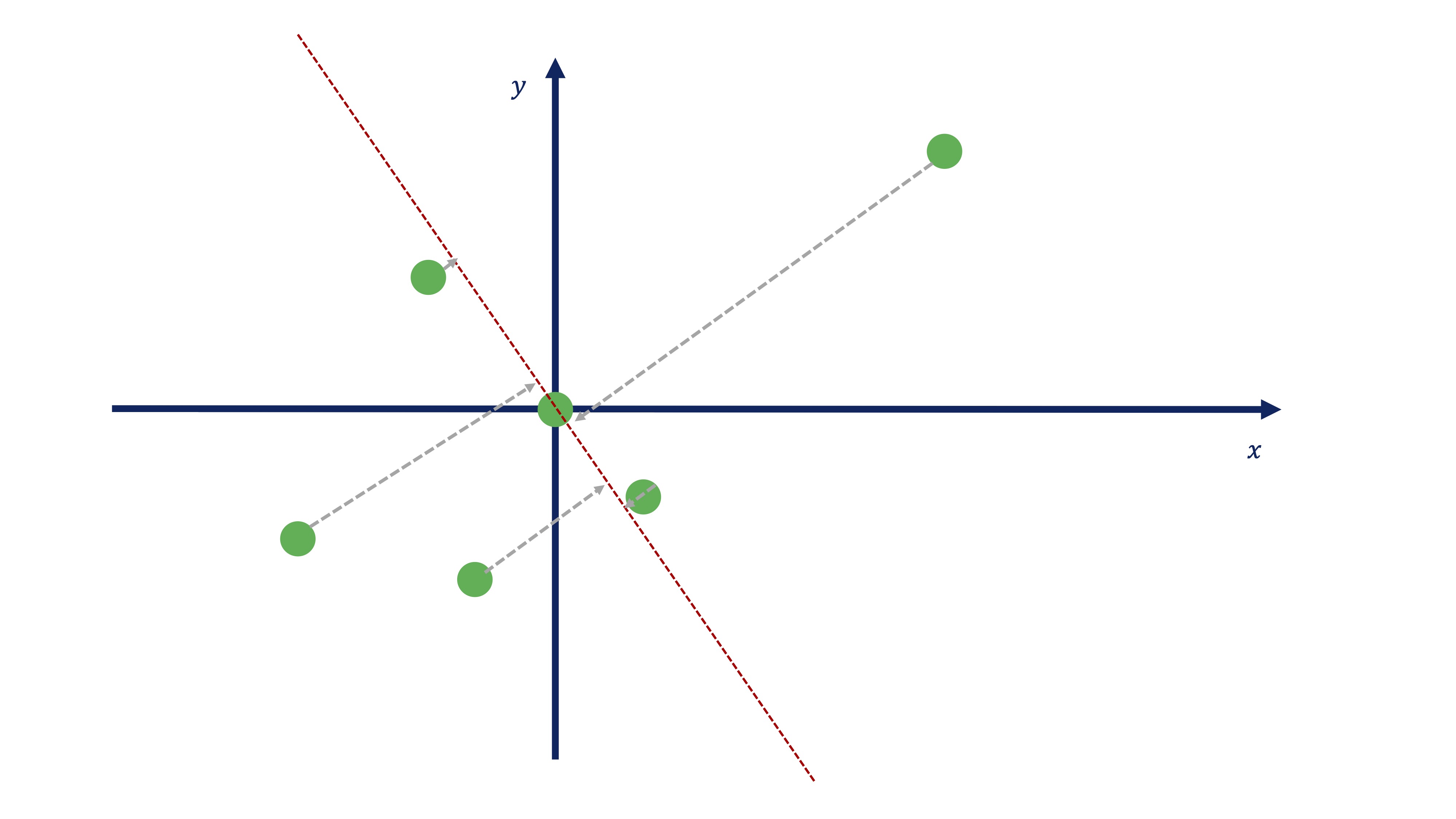
FIG 12: El promedio como proyección

Ambas se llaman DIRECCIONES PRINCIPALES. Antes de tomar una decisión sobre qué dirección principal es más interesante, tendremos que plantearnos cómo se obtienen esos coeficientes que nos permiten parametrizar las direcciones. En el apéndice matem?tico se prueba que se obtienen mediante la diagonalización de la matriz de varianzas y covarianzas de los datos.

Es decir, tenemos que \[ X=\left[\begin{array}{cc} 4.5 & 3\\ 1 & -1\\ -1 & -2\\ -3 & -1.5\\ -1.5 & 1.5\\ 0 & 0 \end{array}\right] \]

cuya matriz de varianzas y covarianzas es:

\[ C(X)=\left(\begin{array}{cc} 6.7 & 3.35\\ 3.35 & 3.70 \end{array}\right) \]

    x1<-c(4.5,1,-1,-3,-1.5,0)   #Genera las dos variables
    x2<-c(3,-1,-2,-1.5,1.5,0)
    X<-data.frame(x1,x2)    #dale estructura de datos
    RES<-(princomp(X)) #usamos componentes principales

usando la función princomp podemos obtener lo que necesitmos.

RES$loadings #nos proporciona los autovectores

Loadings:
   Comp.1 Comp.2
x1  0.839  0.544
x2  0.544 -0.839

RES$scores #nos proporciona cada componente (C1,C2))
            Comp.1        Comp.2
[1,]  5.407863e+00 -7.084558e-02
[2,]  2.954918e-01  1.382998e+00
[3,] -1.926752e+00  1.134737e+00
[4,] -3.333365e+00 -3.723922e-01
[5,] -4.432378e-01 -2.074498e+00
[6,] -1.509219e-17  2.329373e-17

Así, el primer autovector nos dará la dirección principal primera. Fíjese, si representamos el vector \(\overrightarrow{a}_{1}=\left(\begin{array}{c} 0.8392\\ 0.5438 \end{array}\right)\), conjuntamente con los datos:

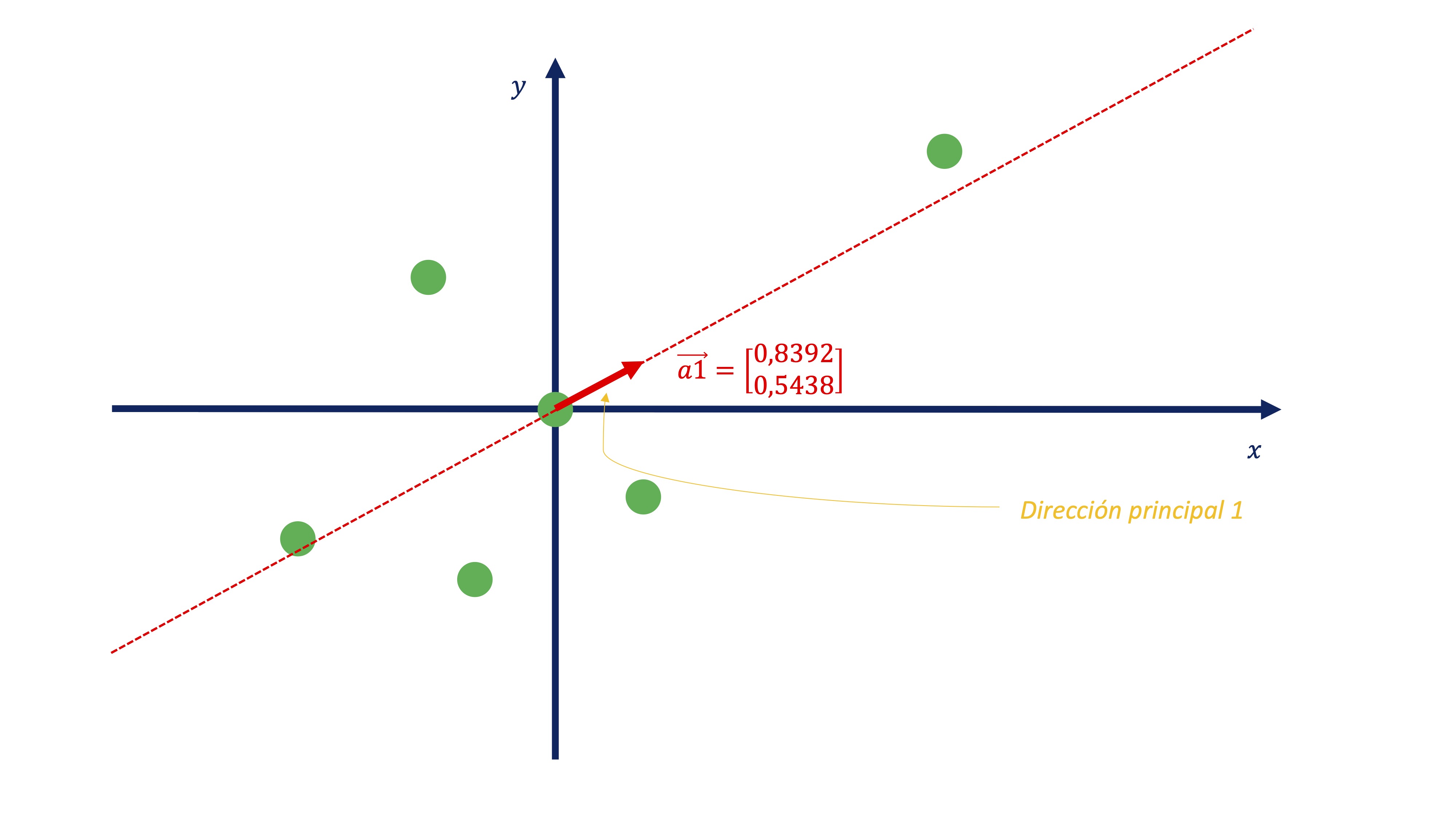
FIG 13: La primera dirección principal

nos permite encontrar cuál es esa recta. De tal forma que usando esos coeficientes, obtenemos dicha proyección:

\[ C1_{i}=0.8392x_{i}+0.5438y_{i} \]

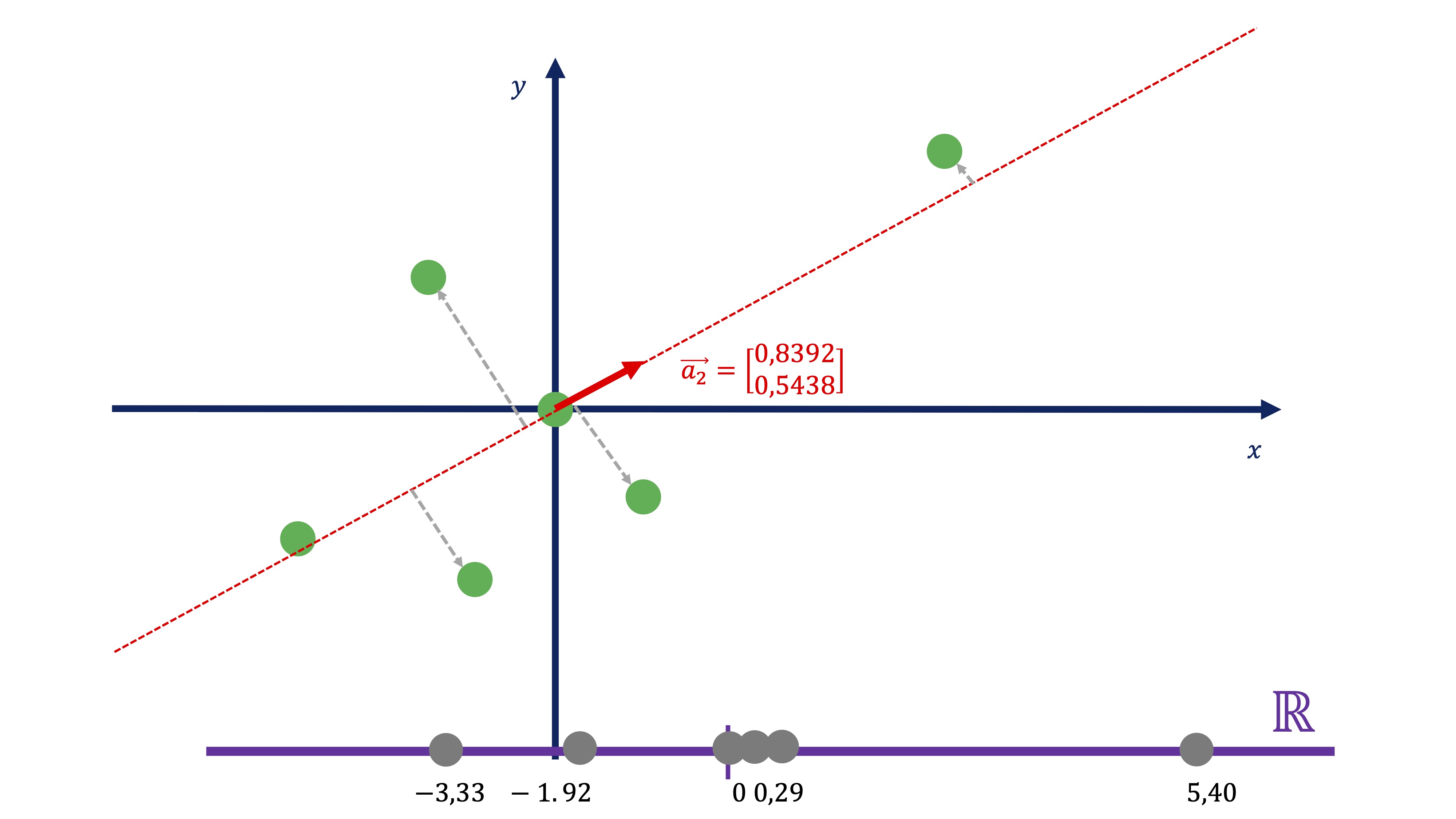
FIG 14: Calculamos el componente como la proyección

Entonces, usando la expresión de la dirección principal 1, podemos obtener el “resumen” de las dos variables en una nueva, que llamamos \(C1\). Esta nueva variable no tiene unas unidades de medida claras, pues es la combinación de dos variables que pueden no tener las mismas unidades. Podemos entenderla como un “índice” de tal forma que el valor que toma \(C1\) como tal no es importante, sino su variación a través de la muestra.

De igual manera, podemos obtener el segundo componente

\[ C2_{i}=-0.5438x_{i}+0.8392y_{i} \]

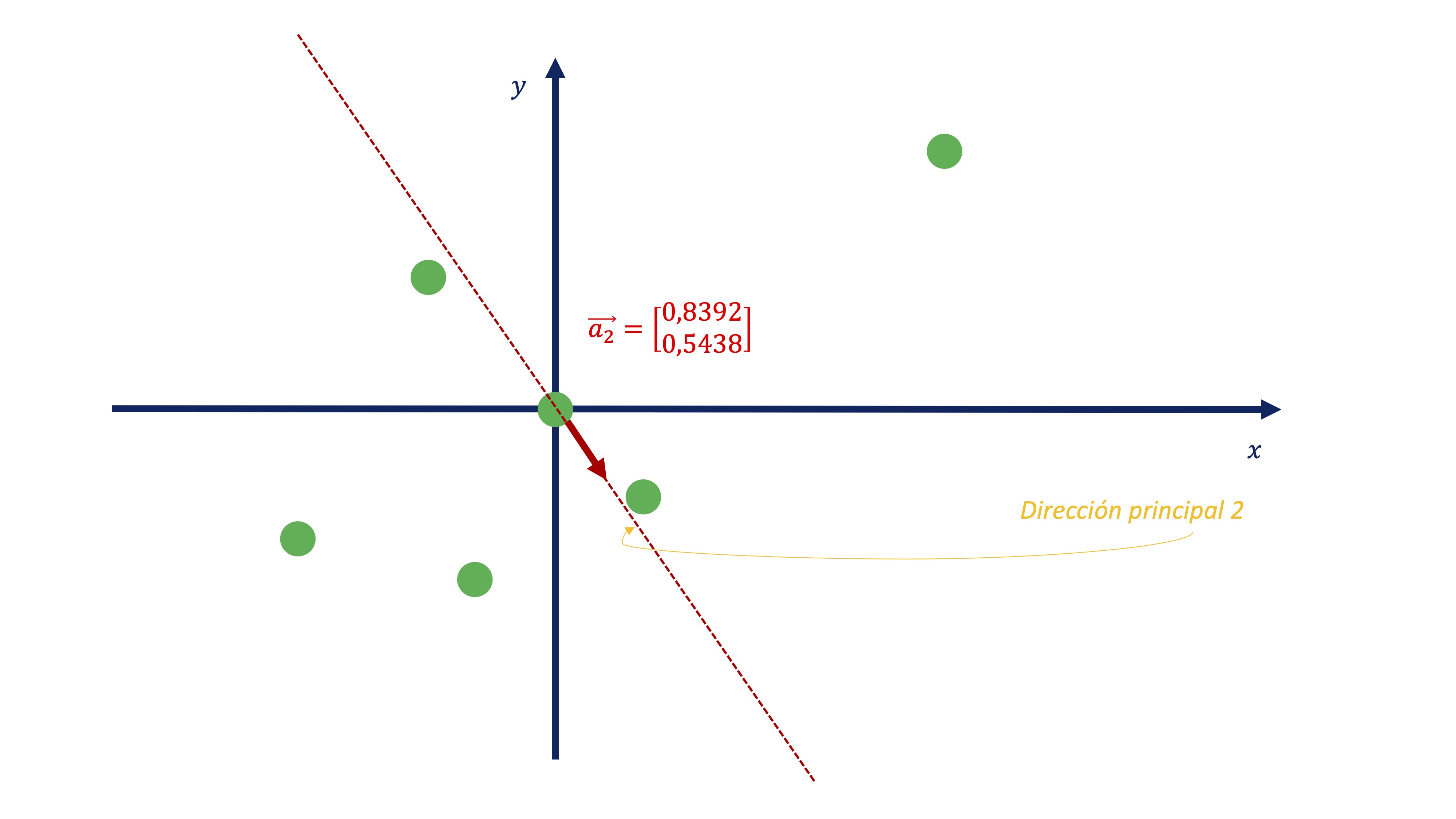
FIG 15: Este sería el segundo componente

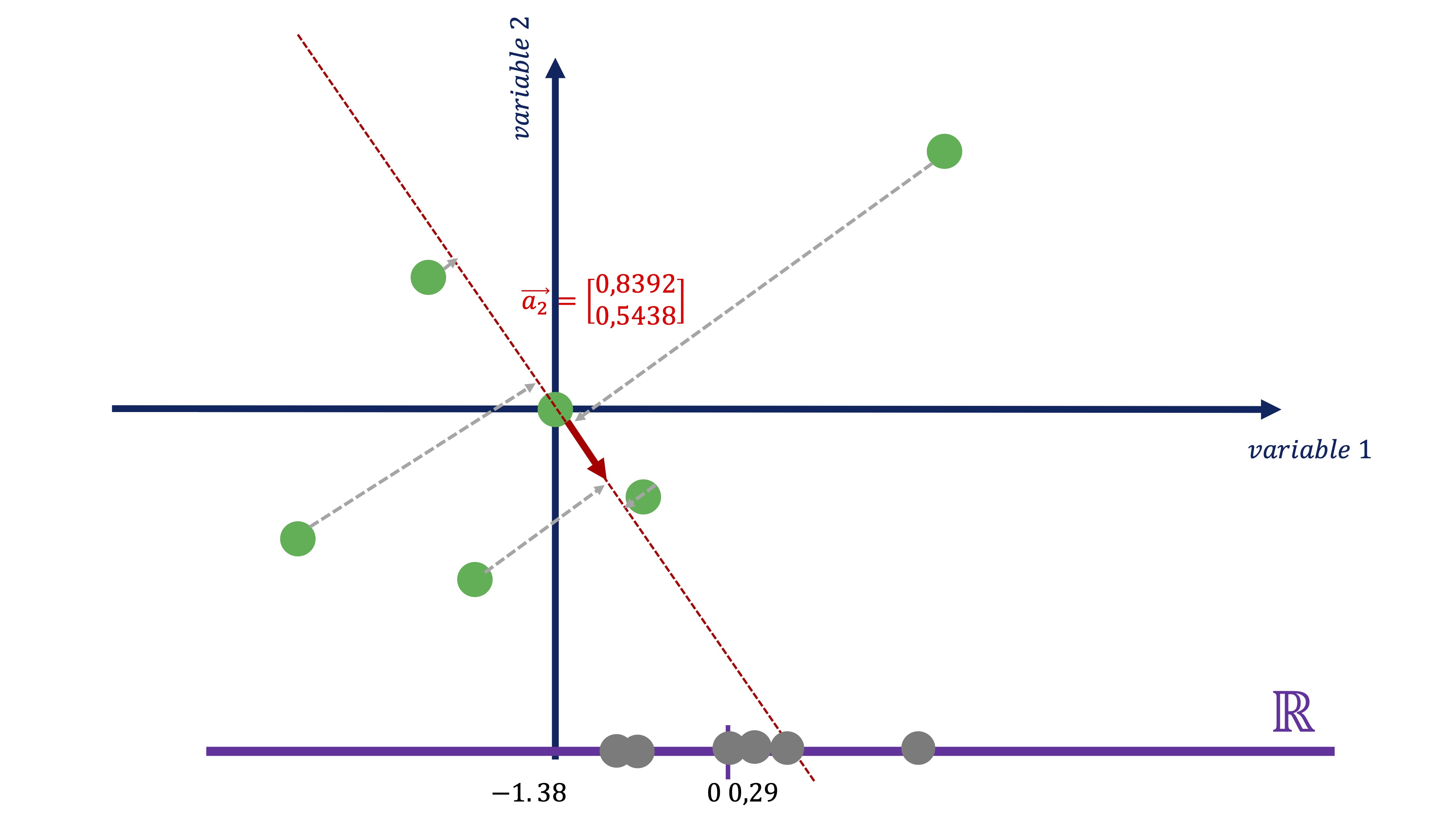
FIG 16: …y esta la proyección

Como vemos (FIG 14, FIG 16) parece más exitoso quedarse con el primer componente antes con el segundo, puesto que el primero parece recoger de una manera más acertada la variabilidad que muestran los datos

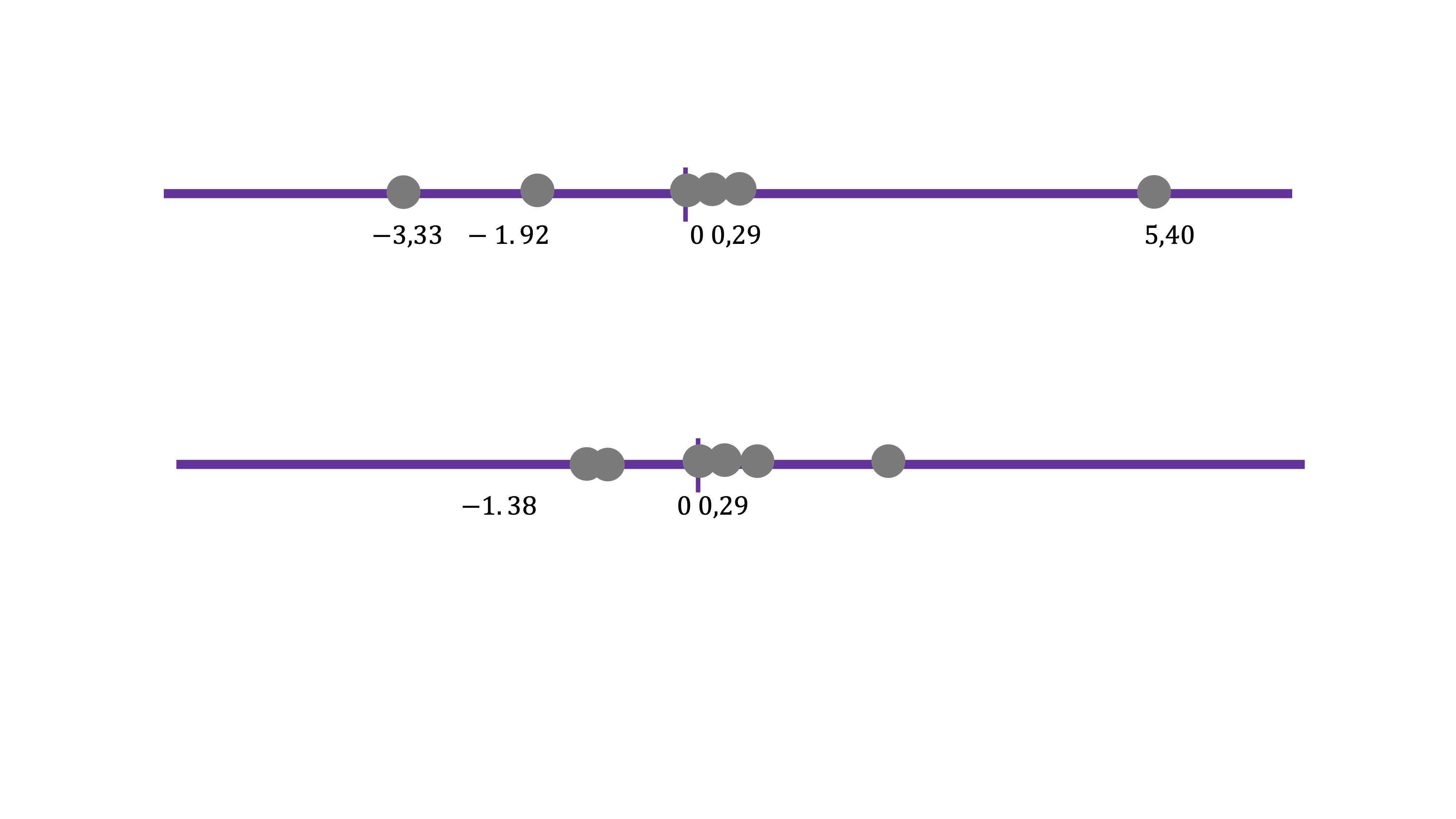
FIG 15: Estos son los dos componentes (el primero tiene mucha más varianza que el segundo, recoge mejor los movimientos conjuntos que vimos en la nube de puntos de la FIG9 )

Conclusiones hasta ahora

Tanto los autovalores como los autovectores van a tener una interpretación que nos ayudaá a entender mejor cómo se toman decisiones en el análisis PCA. >- Autovalores

 princomp(covmat=cov(X))$sd^2 #obtención de los autovalores
 Comp.1  Comp.2 
8.87049 1.52951 

 C<-cov(X)  #y, por otro lado, la matriz de varianzas y covarianzas de los datos
 C
     x1   x2
x1 6.70 3.35
x2 3.35 3.70

Para empezar, la suma de los autovalores es igual a la suma de los elementos de la diagonal principal de \(C\) (propiedad 1} que vimos en el apartado de diagonalización de la matriz C). De esta manera: \(6.7+3.7=10.4\) es igual a \(8.87+1.53=10.4\). Esto es interesante, puesto que podemos considerar la suma de los elementos de la diagonal principal de \(C\) como la “varianza total” con la que contamos en los datos. Entonces, es fácil ver que, de la varianza total el primer componente ya representa \(8.87/10.4=0.85\) un 85% de la variación total. Nos parece, entonces, un buen resumen de la información disponible.

• Respecto a la interpretación de los componentes como “índices” lo verá claro en la aplicación con datos reales relacionados con el informe PISA.

• Si las variables tienen mucha diferencia en las varianzas, entonces se puede recomendar hacer la descomposición mediante la matriz de correlaciones. Esta postura es criticada, por cuanto se pierde la información de las varianzas.

Aplicación con datos reales: el informe PISA

Por hacer

2.0.1 Apéndice

¿De dónde se obtiene la expresión de componentes principales mediante la diagonalización de una matriz de varianzas y covarianzas?

Queremos minimizar la distancia entre las observaciones (\(X\)) y la proyección \(\left(XV\right)\), donde \(X\in M^{n\times k}\),\(V\in M^{k\times k}\)

\[ \min_{V}\left\Vert X-XV\right\Vert ^{2}, \]

con la restricción (para asegurarnos unicidad de solución) \(\left\Vert V\right\Vert =I.\) Asumiremos que la matriz \(X\) tiene sus observaciones en desviaciones respecto a la media. Nótese que, en este caso, nuestra incógnita es una matriz, \(V\), cuyas columnas conformarán lo que llamaremos coeficientes de la proyección para cada componente . Ahora bien, nótese también que, utilizando propiedades de vectores y matrices, la expresión anterior puede reescribirse como \[ \min_{V}\left(X-XV\right)^{T}\left(X-XV\right), \] que resulta ser

\[ \min_{V}X^{T}X-2V^{T}XX^{T}V+V^{T}XX^{T}V, \] que es equivalente (deshaciéndonos de \(X^{T}X\), porque no desempeña ningún papel, ya que no depende de \(V\))

\[ \min_{V}-V^{T}XX^{T}V, \]

donde minimizar “menos” una cantidad es equivalente a maximizarla:

\[ \max_{V}V^{T}XX^{T}V, \]

sin olvidar que \(\left\Vert V\right\Vert =I\) sigue siendo la restricción. Nótese que, las variables \(X\) están escritas en desviación a su media y que, por tanto, \(\mathbb{E}\left(XX^{T}\right)=Var-cov(X)=\Sigma\), es decir, queremos maximizar

\[ \max_{V}V^{T}\Sigma V, \]

Para resolver este problema, planteamos el lagrangiano \[ L(V,\lambda)=V^{T}\Sigma V-\overrightarrow{\lambda}^{T}\left(V^{T}V-I\right) \]

y derivando con respecto a \(V\), tenemos que la CPO es \[ 2\Sigma V-2\overrightarrow{\lambda}V=0\Rightarrow\Sigma V=\overrightarrow{\lambda}^{T}V \] y esta condición es, exactamente, el resultado de la diagonalización de matrices:\(V\) es una matriz que almacena los autovectores y \(\overrightarrow{\lambda}\) es un vector que almacena los autovalores.

clase 2: así resuelven problemas de optimización los ordenadores

El aprendizaje automático que, en inglés, se conoce como machine learning pertenece a una rama de la inteligencia artificial, cuyo objetivo es desarrollar técnicas que permitan que las computadoras aprendan. Diremos que una computadora aprende cuando su consecución de objetivos mejora con la experiencia y mediante el uso de información externa, es decir, datos. En el aprendizaje automático una computadora observa datos, construye un modelo basado en esos datos y utiliza ese modelo a la vez como una hipótesis acerca del mundo y una pieza de software que puede resolver problemas.

Pese a que las técnicas que ha visto en el semestre anterior están también absorbidas por la inteligencia artificial, se presenta en este capítulo una técnica de las más famosas y celebradas en esta área: las redes neuronales. Para entender los fundamentos de estos mecanismos, deberá recordar antes ciertos conceptos de cálculo diferencial para, posteriormente, ser capaz de escribir funciones sencillas. Nos centraremos, de hecho, en intentar entener- primeramente- cómo busca óptimos de funciones un computador. Posteriormente, lo aprendido será básico para entender la idea de una red neuronal.

Recuerde que este es un curso de fundamentos y que, por tanto, aquí va a aprender los cimientos sobre los que se asientan multitud de aplicaciones de interés.

Piense en la función

\[ f(x)=x^2 \]

¿Cómo busca la máquina el mínimo global?

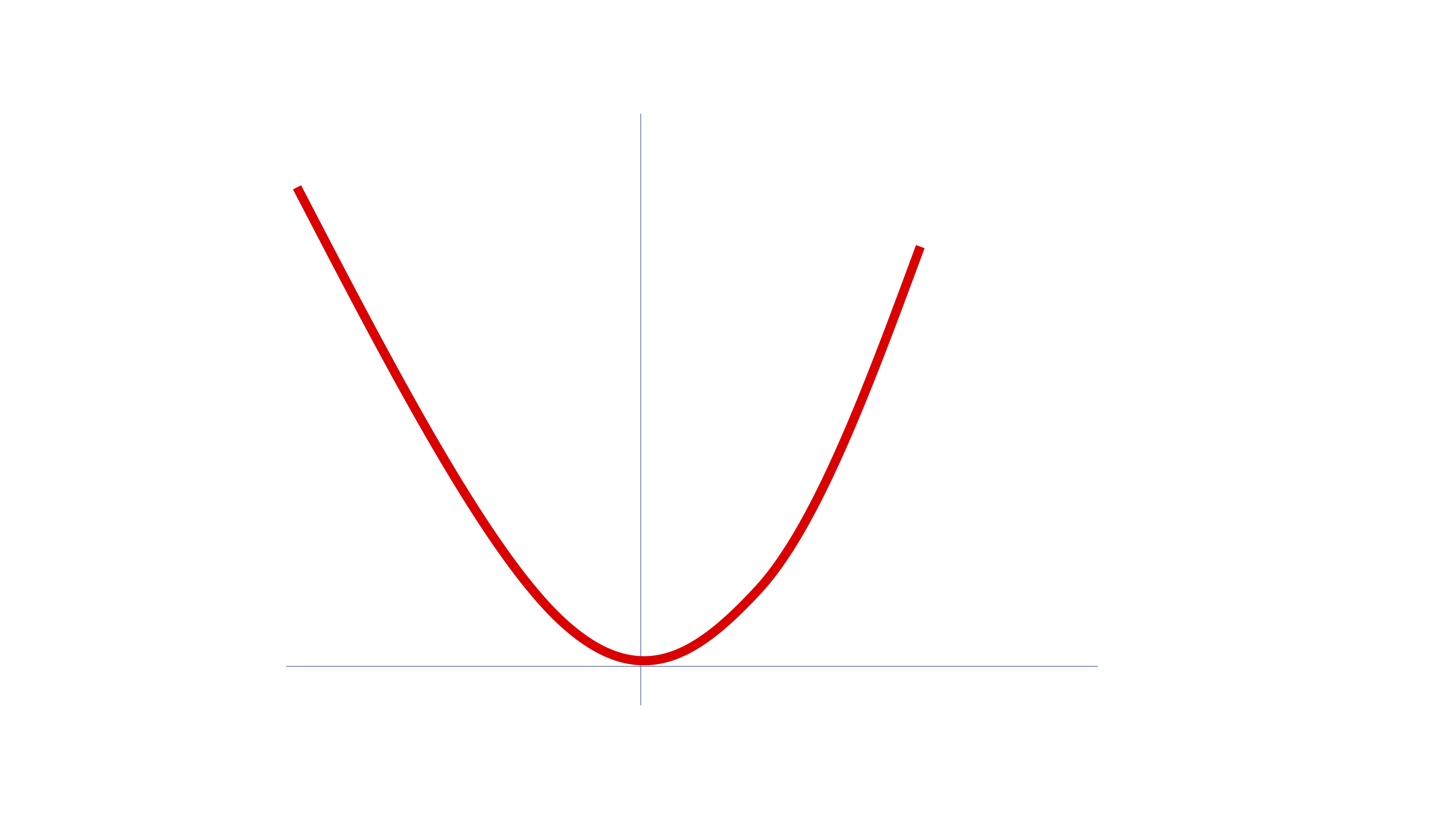
FIG 1: ¿Cómo lo hace la máquina? (I)

Las máquinas harán algo parecido a lo que hacen los humanos. Intentarán buscar un punto \(x\in\mathbb{R}\) donde se anule la derivada. Para ello, como en la FIG 2, se situarán sobre un punto cualquiera de la función (por ejemplo, \(x_{0}\)).

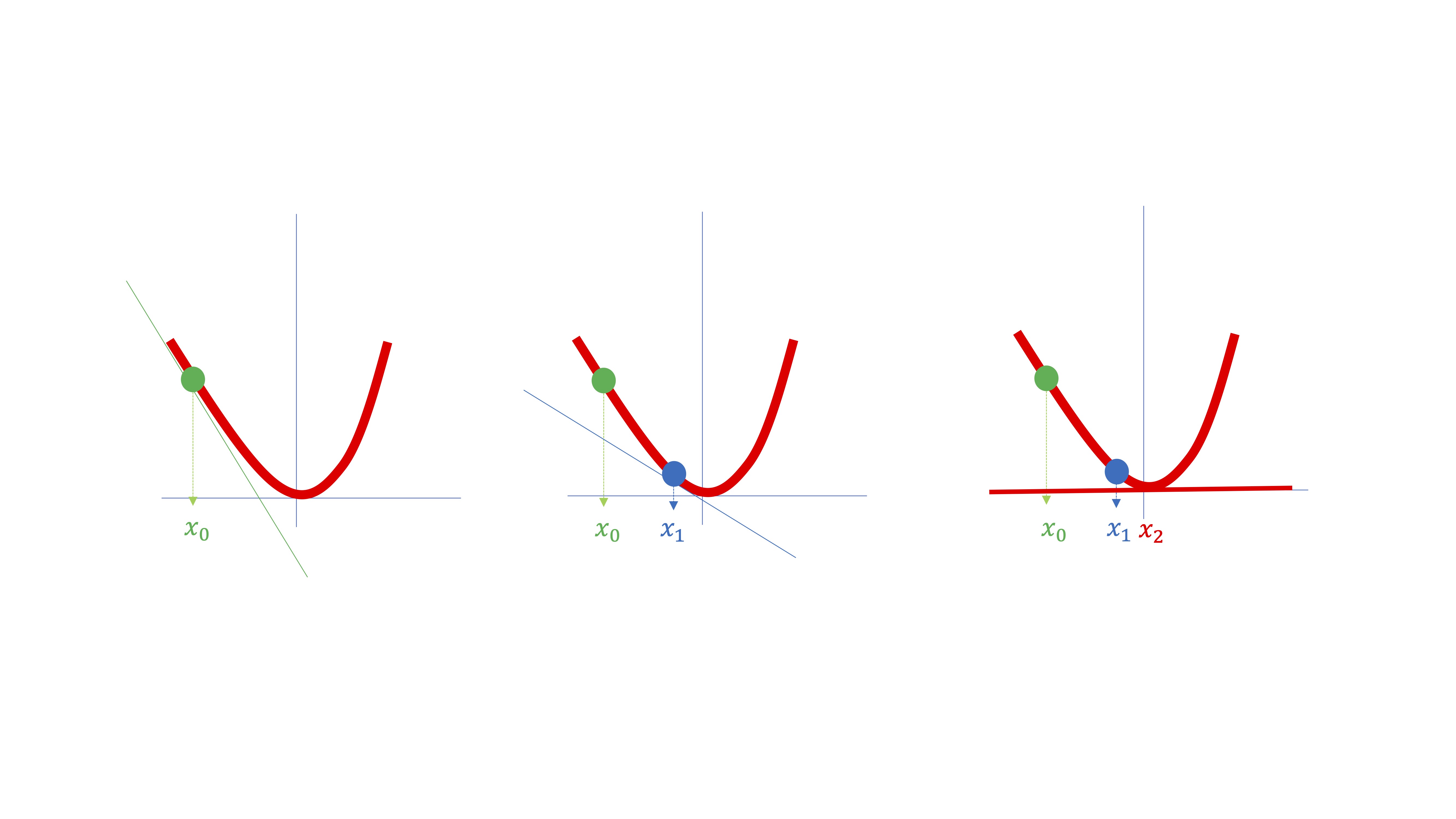
FIG 2: Cómo lo hace la máquina?

Entonces, la máquina obtendrá la derivada de la función evaluada en ese punto \(f'(x_{0})\) y tratará de buscar un nuevo punto \(x_{1}\), por ejemplo, donde la derivada sea menor, ya que pretende conseguir ese punto \(x\in\mathbb{R}\) en el que la derivada de la función se anule (es decir, en la FIG 2 sería \(x_{2}\)).

De una manera más formal, puede pensar en el polinomio de Taylor de primer orden. Recuerde que es una herramienta útil con la que aproximar, mediante una recta, una función diferenciable en puntos \(x\) cercanos a \(x_{0}\): que es, básicamente, lo que se dibuja en la FIG 2. Dicho polinomio consiste en

\[ f(x)\simeq f(x_{0})+f'(x_{0})(x-x_{0}) \]

llamaremos a \(h=(x-x_{0})\), es decir, un “pequeño” incremento de \(x\) (en la FIG 2 sería como pasar de \(x_{0}\rightarrow x_{1}\)).

\[ f(x)\simeq f(x_{0})+f'(x_{0})h. \]

Utilizando esta expresión, el método de buscar el mínimo de la función consistirá, por tanto, en

• Empiece en un punto aleatorio \(x_{0}\)
• Calcule la derivada de la función evaluada en ese punto \(f'(x_{0})\)
• Muévase al siguiente punto en sentido contrario a la derivada: \(x_{1}\rightarrow x_{0}-f'(x_{0})\)…

• …pero para que no sea muy exagerado, muévase un poquito (elija \(h\rightarrow0\)) es decir \(x_{1}\rightarrow x_{0}-hf'(x_{0})\)

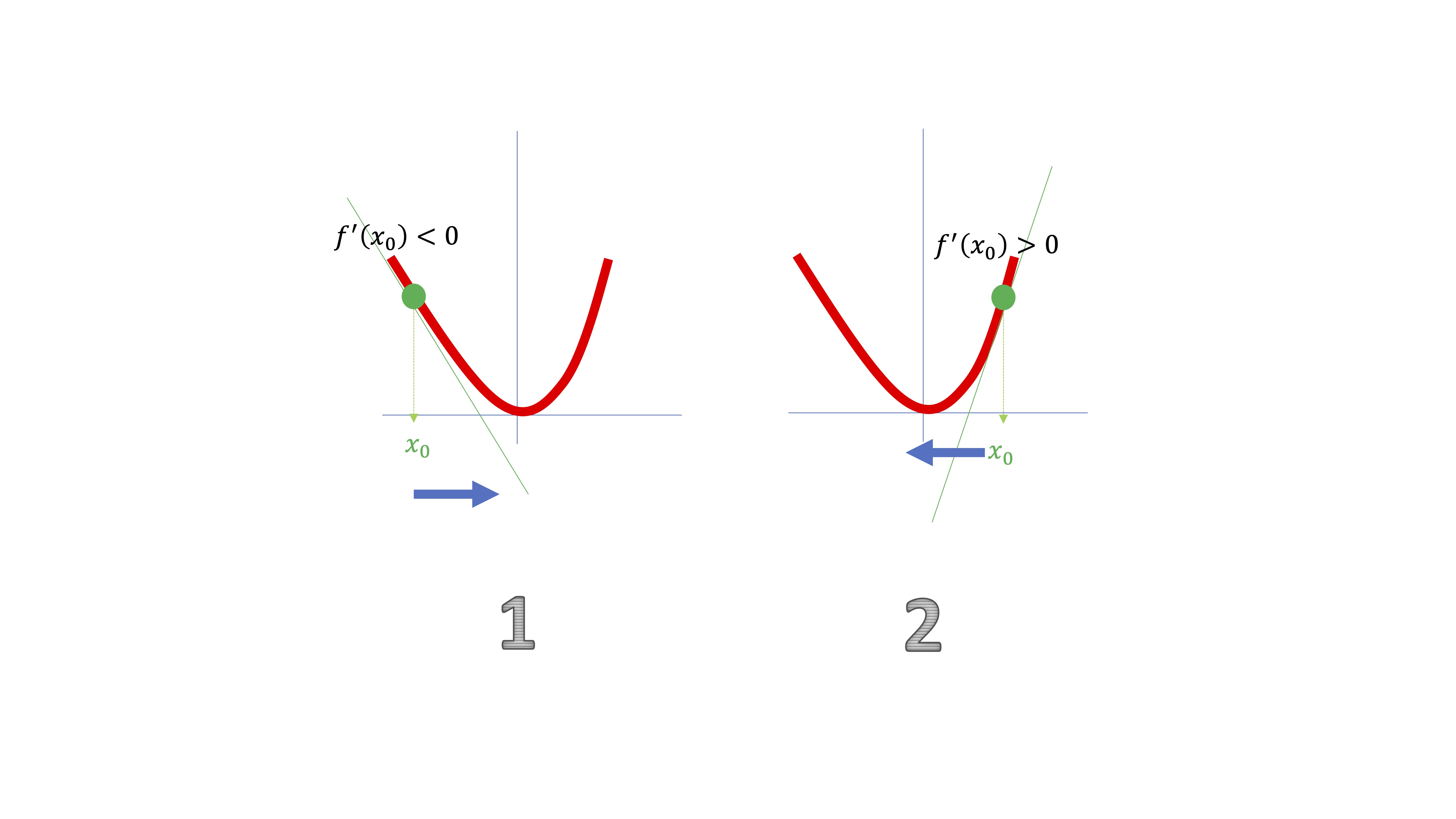
FIG 3: ¿Cómo lo hace la máquina?(III)

donde, como ve, en la situación #1, la derivada le da una información muy útil: la función está decreciendo en un entorno del punto \(x_{0}\). Ahora bien, como verá, necesitará moverse “ligeramente” a la derecha, por lo que deberá ir en sentido \(-hf'(x_{0})\). En la situación #2, pasará al contrario.

Para que avance ligeramente de un punto a otro, deberá introducir un valor para \(h\) muy cercano a cero que se denominará “tasa de aprendizaje” de tal forma que para pasar de un punto a otro utilizará la expresión \[ x_{1}\rightarrow x_{0}-h f'(x_{0}) \]

con \(h\rightarrow 0\).

Ejercicio resuelto Diseñe un algoritmo en R para minimizar la función \(y=x^2\). Para ello, deberá crear una función (objetivo) y su derivada. Deberá, asimismo, definir un valor de tolerancia (para tener un criterio de parada de este). Entones, a partir de un punto inicial, deberá iterar en el algoritmo mediante la regla \(x_{new}\rightarrow x_{0}-h f'(x_{old})\), donde debe definir \(h\) como un parámetro pequeño y deberá evaluar, a cada paso, \(\vert f(x_{new})-f(x_{old})\vert\). Cuando esa diferencia sea menor que el valor de tolerancia, deberá parar el algoritmo. ¿Dónde encuentra el mínimo? ¿Cómo influye la tolerancia y el valor \(h\) en la búsqueda de ese mínimo?

 # defina una función objetivo, por ejemplo, y=x^2
 fobj<- function(x) {
   x[1]^2
 }
 
# almacene la derivada de la función, en este caso, y'=2x
 der<- function(x) {
   2*x[1]
 }
 
# fije un valor de tolerancia para detener el algoritmo
 tol<-0.000001
 
#inicie en un punto (el que quiera)
 y<-vector()
 w<-vector()
 y[1]=2
 h<-0.01 #defina el parámetro de "aprendizaje"
 dist<-1+tol #defina un valor inicial para la función que evaluará la diferencia entre valores de la función objetivo
 i<-1
 while (dist > tol) {
   y[2]<-y[1]-h*der(y[1]) #esta es la iteración basada en Taylor
   dist<-abs(fobj(y[1])-fobj(y[2])) #aquí se mira si la función objetivo cambia mucho o no
   y[1]<-y[2]
   w[i]<-y[1] 
   i<-i+1
   
   
 }

¿Por qué funciona el método en el que \(x_{1}\rightarrow x_{0}-h f'(x_{0})\)? Un argumento heurístico

Si aproximamos con Taylor la función \(f(x_{0}-hf'(x_{0}))\), en torno a \(x_{0}\), con \(h\rightarrow0\), obtenemos

\[ f(x_{0}-hf'(x_{0}))\simeq f(x_{0})-h f'(x_{0})f'(x_{0}) \]

es decir

\[ f(\underbrace{x_{0}-h f'(x_{0})}_{x_{1}=x_{0}+h})\simeq f(x_{0})-\underbrace{h f'(x_{0})}_{h}f'(x_{0}) \]

de donde tenemos que \[ f(x_{0}-hf'(x_{0}))-f(x_{0})\simeq-h f'(x_{0})^{2} \]

Siendo \(-hf'(x_{0})^{2}<0\), por lo que \(f(x_{1})-f(x_{0})\) será negativo y, por tanto, estaremos camino del mínimo. De aquí, entonces, se puede intuir que utilizando esta estrategia \[ x_{1}\rightarrow x_{0}-h f'(x_{0}) \]

La función mejora (es decir, se hace menor) localmente. Hasta que llega al mínimo tras un conjunto finito de pasos. El resultado dependerá, por tanto, del valor de \(h\).

Ejercicio Pruebe en el algoritmo del ejercicio resuelto anterior cómo la elección de \(h\) muy grande podría provocar que este no converja y no encuentre el mínimo global. Pruebe, sin embargo, que la elección demasiado “pequeña” podría hacer que tarde mucho tiempo en encontrar el mínimo.

¿Cómo trabaría la computadora si la función que quiere optimizar tiene dos variables? Imagine que quiere buscar el mínimo de

\[ f_{1}\left(x_{1},x_{2}\right)=x_{1}^{2}+x_{2}^{2} \]

¿se podrían utilizar las estrategias que se han esbozado anteriormente? Habrá que adaptarlas. Para ello, recuerde cómo se visualizaban, en el plano, funciones de dos variables (que, como recordará, son funciones tridimensionales)

Visualización de una función en dos variables

Partamos de las siguientes dos funciones

\[ f_{1}\left(x_{1},x_{2}\right)=x_{1}^{2}+x_{2}^{2}, \]

\[ f_{2}\left(x_{1},x_{2}\right)=log(x_{1}^{2}+x_{2}^{2}) \]

Puede visualizarlas usando primero google (o Geogebra).

FIG 4: Así es \(f_1\)

FIG 5: Así es \(f_2\)

Como verá, ambas figuras vistas desde arriba (es decir, desechando el eje \(z\)) presentan un aspecto común. Eso es porque ambas funciones tienen las mismas curvas de nivel

Definamos una curva de nivel como los puntos del dominio de la función (en este caso, \((x_1,x_2)\)) que nos proporcionan un valor, \(C\), como imagen de la función. Es decir

\[ Nivel=\left\{ \left(x_{1},x_{2}\right)\in D\::\:f(x_{1},x_{2})=C\right\} \]

De esta forma, dando diferentes valores a \(C\) se pueden esbozar las curvas de nivel de esta y poder entender hacia dónde crece/decrece.

• En este caso concreto, note que la imagen de \(f_{1}\) siempre es \(Im(f_{1})\geq0\) ( ya que la función sólo puede tomar valores iguales o mayores que cero), por lo que las curvas de nivel

\[ Nivel_{1}=\left\{ \left(x_{1},x_{2}\right)\in D\::\:x_{1}^{2}+x_{2}^{2}=C,C\geq0\right\} \]

tendremos, entonces, circunferencias concéntricas de radio \(\sqrt{C}\) (que son las que ves en la FIG 4).

Piense ¿Cómo se obtienen las curvas de nivel de \(f_2\)?

Recuerde, por otro lado, que las derivadas parciales primeras de una función de \(n\) variables se almacenan en el gradiente. Es decir, el vector gradiente de la función \(f(x_{1},...,x_{n})\) es un vector en \(\mathbb{R}^{n}\) tal que

\[ \nabla f(x_{1},...,x_{n})=\left[\frac{\partial f}{\partial x_{1}},...,\frac{\partial f}{\partial x_{n}}\right] \]

Trate ahora de entender una propiedad interesante, y muy útil, del gradiente de la función, con un ejemplo.

---

Ejemplo sobre el gradiente Sea la función

\[ f(x,y)=ln(4x-y) \]

Suponga que está en el punto inicial \(x_{0},y_{0}=(1,3)\). Calcule el gradiente de la función como

\[ \nabla f(x,y)=\left[\frac{4}{4x-y},\frac{-1}{4x-y}\right] \]

que, evaluado en el punto \((1,3)\):

\[ \nabla f(x_{0},y_{0})=\left[4,-1\right] \]

Ahora obtenga las curvas de nivel de la función:

\[ C=ln(4x-y)\Rightarrow e^{C}=4x-y \]

FIG 6: En realidad son rectas

Como ve, la función crece según nos vamos en sentido sureste en el plano \(xy\). ¿Se puede mejorar esta descripción?. Ahora puede preguntarse ¿cuál de estos vectores es la que permite avanzar hacia el siguiente “valor mayor” de la función de forma más rápida? Vea diferentes candidatos

FIG 7: Diferentes maneras de acercarse al siguiente nivel de la función

estarás de acuerdo que el mejor candidato es el marcado con verde. Esa es la dirección más rápida que encontrará para avanzar al siguiente punto de la función. Pues fíjese, ese vector es proporcional a otro que hemos obtenido antes:

FIG 8: ¡El gradiente!

¡el gradiente! En efecto. De hecho, puede probarse que

El gradiente en un punto marca la dirección de aumento más rápido de la función

---

Clase 3: así resuelven los problemas de optimización los ordenadores (II)

Es momento de aplicar la idea visa en la #clase 1 a un problema que ya ha visto en otras ocasiones: el de los mínimos cuadrados. Como recuerda, es un problema de optimización que da lugar a la estimación de los parámetros en un modelo de regresión. En este caso, tenemos observaciones para \(\left\{ y_{i},x_{i}\right\}\) y buscamos los valores de \(\hat{\beta}_{0},\hat{\beta}_{1}\) que mejor ajusten, de manera lineal, la relación entre ambas variables. Para ello, recuerde, este es el modelo poblacional

\[ y_{i}=\beta_{0}+\beta_{1}x_{i}+u_{i} \]

su objetivo es minimizar la suma de residuos al cuadrado, es decir, sea esta la función a la que debemos buscar el valor de \(\hat{\beta}_{0},\hat{\beta}_{1}\)

\[ y_{i}=\hat{\beta}_{0}+\hat{\beta}_{1}x_{i}+\hat{u}_{i}, \] el problema de minimización que pretendemos resolver consiste en

\[ \min_{\hat{\beta}_{0},\hat{\beta}_{1}}SR=\min_{\hat{\beta}_{0},\hat{\beta}_{1}}\sum_{i=1}^{n}\hat{u}_{i}^{2}=\min_{\hat{\beta}_{0},\hat{\beta}_{1}}\sum_{i=1}^{n}\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}\right)^{2} \]

Donde el gradiente de la función objetivo resulta ser

\[ \nabla SR=\left[-2\sum_{i=1}^{n}\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}\right),-2\sum_{i=1}^{n}\left(y_{i}-\hat{\beta}_{0}-\hat{\beta}_{1}x_{i}\right)x_{i}\right]^{T} \]

El método del gradiente, aplicado a una función con \(n\) variables es, en esencia, similar al anterior. Recuerde que la aproximación de Taylor de primer orden, para una función de dos variables \(f(x,y)\), en el entorno de un punto \(\left(x_{0},y_{0}\right)\) es \[ f(x,y)\approx f(x_{0},y_{0})+\frac{\partial f}{\partial x}\left(x_{0},y_{0}\right)h_{x}+\frac{\partial f}{\partial y}\left(x_{0},y_{0}\right)h_{y} \]

De nuevo, \(h_{x}=\left(x-x_{0}\right),h_{y}=\left(y-y_{0}\right).\) Asumiendo que \(h_{x},h_{y}\rightarrow0\) deberá trabajar como en el caso con una variable:

• Parte de un punto inicial \(\left(x_{0},y_{0}\right)\)
• Busca un candidato mejor a mínimo \(\left(x_{1},y_{1}\right)\rightarrow\left(x_{0},y_{0}\right)-h\left[\frac{\partial f}{\partial x}\left(x_{0},y_{0}\right),\frac{\partial f}{\partial y}\left(x_{0},y_{0}\right)\right]\)

Donde \(h\) es un número peque?o (y común para ambas variables). Como ve, está utilizando el gradiente de la función \((\left[\frac{\partial f}{\partial x}\left(x_{0},y_{0}\right),\frac{\partial f}{\partial y}\left(x_{0},y_{0}\right)\right])\) multiplicado por \(-h\) para poder ir en el sentido de mayor decrecimiento de esta (que es \(-\nabla f(x,y)).\)

#genere un modelo de regresión con datos 
x<-rnorm(100,1,1)
y<-3+2*x+rnorm(100,0,1)


#Cree la función objetivo y el gradiente de la función objetivo
fobj2<- function(b) { sum(y-b[1]-b[2]*x)^2 } #escriba la función objetivo donde y,x son datos
der<- function(b) { c(-2*sum(y-b[1]-b[2]*x),-2*sum((y-b[1]-b[2]*x)*x))} #escriba el gradiente de la función objetivo


tol<-0.000001 #declare un parámetro de tolerancia

bold<-vector()
bnew<-vector()
bold[1]=30 
bold[2]=20 #Dé valores iniciales a los parámetros
h<-0.001  #dé un valor al parámetro de aprendizaje
dist<-1+tol
i<-1
while (dist > tol) { 
  grad<-der(bold)  #evalúe el gradiente en el punto "old"
  bnew[1]<-bold[1]-h*(grad[1]) #actualice los valores
  bnew[2]<-bold[2]-h*(grad[2]) 
  dist<-abs(fobj2(bnew)-fobj2(bold)) #analice el cambio en la función objetivo
  bold<-bnew
  i<-i+1}

Ejercicios Prueba, de nuevo, la convergencia del método si \(h\) toma valores grandes. Razona sobre la importancia de controlar el tamaño de \(h\) para la convergencia del método. Qué ocurre si \(h=0.00000001\)? ¿Qué otros factores pueden afectar a la velocidad de convergencia?

Clase 3: Los modelos de redes neuronales

Ideas sobre la composición de funciones que debe conocer

Las funciones compuestas surgen debido a las dependencias que pueden existir entre las variables de un modelo matemático. Por ejemplo, en la ecuación (2.1) diremos que la variable \(y\) depende de la variable \(x\) pero, a su vez, la variable \(x\) depende de la variable \(t:\)

\[\begin{equation} y=f(x)\;\;x=g(t) \tag{2.1} \end{equation}\]

De este modo, podríamos decir igualmente-si nos interesa especialmente dicho análisis- que la variable \(y\) depende de la variable \(t\). Para escribir esto, ya que que la relación entre \(x\) e \(y\) viene dada por \(f\) y la relación entre \(x\) y \(t\) viene dada por \(g\), diremos que \(f\) es una función compuesta por la \(g\). lo resumimos así: \(f\circ g\), o también:

\[ y=f(g(t)). \]

De hecho, otra manera de escribirlo, de acuerdo con la figura FIG 1, es mediante una función \(F\) (por ejemplo) de tal forma que:

\[ y=F(t). \]

¿Cómo se analiza el cambio de \(y\) cuando se modifica \(t\)? Gráficamente, se puede ver en la FIG 1 que: si se cambia \(t\), ese cambio afecta a la \(x\) y la \(x\) afecta a la \(y\).

Ahora bien, si nuestra pregunta consiste en analizar cómo operar para ver cómo cambia la \(y\) ante un cambio en \(t\), vamos a pensar la respuesta utilizando la idea de la diferencial. Sabemos que

\[ \triangle y=f'(x)\triangle x+\epsilon\triangle x \]

(y sabemos que \(\epsilon \rightarrow 0\) cuando \(\triangle x \rightarrow 0\)) Como queremos analizar cuánto cambia la \(y\) ante cambios “marginales” en \(t\), dividimos en ambos miembros por \(\triangle t\)

\[ \frac{\triangle y}{\triangle t}=f'(x)\frac{\triangle x}{\triangle t}+\frac{\epsilon\triangle x }{\triangle t} \]

Nota que si \(\triangle t\rightarrow 0\), entonces, usando la definición de derivada, tenemos

\[ \frac{\mathrm{d}y}{\mathrm{d}t}=f'(x)\lim_{\triangle t\rightarrow0}\frac{\triangle x}{\triangle t}+\lim_{\triangle t\rightarrow0}\frac{\epsilon \triangle x}{\triangle t} \]

que nos lleva, finalmente, a la expresión, dado que \(\epsilon \rightarrow 0\)

\[ \frac{\mathrm{d}y}{\mathrm{d}t}=\frac{\mathrm{d}y}{\mathrm{d}x}\frac{\mathrm{d}x}{\mathrm{d}t}+0\frac{\mathrm{d}x}{\mathrm{d}t} \]

Y esta es la regla que ya conoce en funciones de una variable:

\[ \frac{\mathrm{d}y}{\mathrm{d}t}=\frac{\mathrm{d}y}{\mathrm{d}x}\frac{\mathrm{d}x}{\mathrm{d}t} \]

> Por ejemplo, tiene que \(f(x)=\ln\left(x\right)\) y \(x=g(t)=3t^{2}+2\) entonces, al componerlas, obtienes \[ y=\ln\left(3t^{2}+2\right). \] Por lo que \[ \frac{\mathrm{d}y}{\mathrm{d}t}=f'(x)\frac{\mathrm{d}x}{\mathrm{d}t} \], es decir \(\frac{\mathrm{d}y}{\mathrm{d}t}=\frac{1}{x} 6t\) pero \(x=3t^{2}+2\), por lo que \[ \frac{\mathrm{d}y}{\mathrm{d}t}=\frac{1}{3t^{2}+2}6t \]

que es la regla de derivación del logaritmo neperiano de una función compuesta, como ha estudiado en bachillerato. Ahora es el momento de analizar algunos casos para funciones de \(n\) variables. Por simplicidad, aquí lo haremos para el caso de \(n=2\).

caso 1:composición del tipo \(z=F(t)\)

En este caso, tenemos una función de dos variables, tal que, por ejemplo, \(z=f(x,y)\) pero, a su vez, \(x=g(t)\) y \(y=h(t)\). A través de \(x,y\) podemos ver cómo un cambio en \(t\) modifica el valor de \(z\). Es decir, la composición actúa como \(z=F(t)\) (mire, para ello, la FIG 2). Ahora nos interesa calcular la derivada \(F'(t)\) (o \(\frac{\mathrm{d}z}{\mathrm{d}t},...)\) con el objeto de analizar cuánto cambia la variable \(z\) ante un incremento marginal de la variable \(t\). Es muy importante que vea que, como la composición resulta en una función sólo de \(t\), la simbología de la derivada es distinta. Esta no es parcial, ya que es una función finalmente de una variable, y se ha de usar la \(\mathrm{d}\) romana.

Este primer ejemplo, podemos verlo en la siguiente gráfica:

Como ve, la variable \(t\), al incrementarse, afecta tanto a \(x\) como a \(y\). Una vez estas dos variables cambian, se traduce en un cambio de la variable \(z\). Se puede obtener la derivada de la función mediante la regla de la cadena (la misma regla que ya se sabe) \[ \frac{\mathrm{d}z}{\mathrm{d}t}=\frac{\partial f}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}t}+\frac{\partial f}{\partial y}\frac{\mathrm{d}y}{\mathrm{d}t} \]

Este esquema le permite ver cómo se obtienen la derivada deseada

puede ver que, si va en la misma rama, realiza el producto de las derivadas (teniendo en cuenta si estas son parciales o no). Cuando salta de rama, estas se suman.

caso 2:composición \(z=F(t,s)\)

En este caso, tiene una función donde \(z=f(x,y)\) pero, a su vez, \(x=g(t,s)\) y \(y=g(t,s)\). A través de \(x,y\) puede ver cómo un cambio en \(t\) o en \(s\) modifica el valor \(z\). Es decir, la composición actúa como \(z=F(t,s).\) Ahora, por tanto, queremos calcular las derivadas parciales \(F_{t}'(t,s)\) o \(F_{s}'(t,s)\) o también \(\frac{\mathrm{\partial}z}{\mathrm{\partial}t},\frac{\mathrm{\partial}z}{\mathrm{\partial}s}\). Fíjese que ahora cambiamos la derivada por la parcial, puesto que la función \(F\) depende de dos argumentos.

Este primer ejemplo, podemos verlo en la siguiente gráfica de la FIG 4

Usando la regla de la cadena, estas serían las derivadas parciales de la función

\[ \frac{\partial z}{\partial t}=\frac{\partial f}{\partial x}\frac{\partial g}{\partial t}+\frac{\partial f}{\partial y}\frac{\partial h}{\partial t} \]

\[ \frac{\partial z}{\partial s}=\frac{\partial f}{\partial x}\frac{\partial g}{\partial s}+\frac{\partial f}{\partial y}\frac{\partial h}{\partial s} \]

y esta es la regla de la cadena

De hecho, puede obtener el gradiente de la función \(F\), es decir:

\(\nabla F(t,s)=[\frac{\partial f}{\partial x}(x_{0},y_{0})\frac{\partial g}{\partial t}(t_{0},s_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\frac{\partial h}{\partial t}(t_{0},s_{0}), \frac{\partial f}{\partial x}(x_{0},y_{0})\frac{\partial g}{\partial s}(t_{0},s_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\frac{\partial h}{\partial s}(t_{0},s_{0})]\)

El enfoque que se va a dar a los modelos de redes neuronales se aleja del tradicional en el que se explican estos modelos como una “imitación” del funcionamiento del cerebro. Hay cantidad de textos que explican cómo estos modelos replican, en cierta forma, la manera en que las neuronas reciben la información y la propagan.

En nuestro caso, se pretenderá entender que una red neuronal es un modelo que, a través de técnicas de aprendizaje automático, trata de aprender de un conjunto de datos abordando la no linealidad en el proceso que genera estos datos.

Para ello, se presentarán diferentes esquemas que le permitirán ir entendiendo, paso a paso, la idea fundamental de los modelos de redes neuronales. Como ya se ha aprendido, la simulación puede ser una herramienta potente de aprendizaje. Se propondrán, de hecho, esquemas iniciales y sencillos con datos simulados, de tal forma que pueda ejecutarlos paso a paso para comprobar lo que se está explicando.

El esquema que se presenta en esta clase se denomina “perceptrón multicapa” (de nuevo, la palabra perceptrón hace alusión al cerebro) y consiste en un esquema como el de la FIG 1

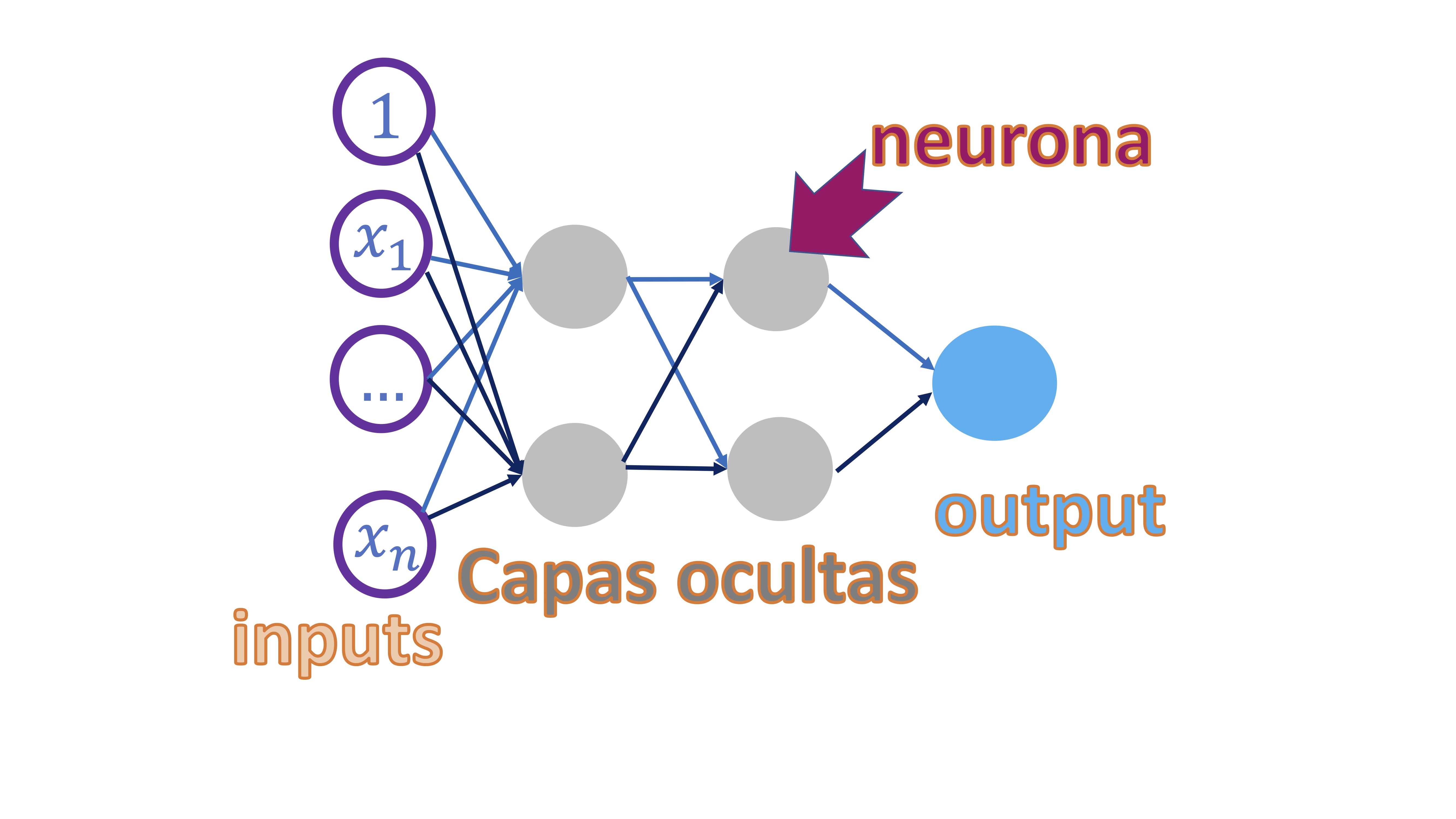
FIG 1: El perceptrón multicapa

como decimos, hay multitud de esquemas de redes neuronales. Este, tomado de “towardsdatascience”, es el más completo que hemos encontrado. Nótese que lo que hemos traducido como “perceptrón multicapa” en la FIG 2 se conoce como “Deep Feed Forward”.

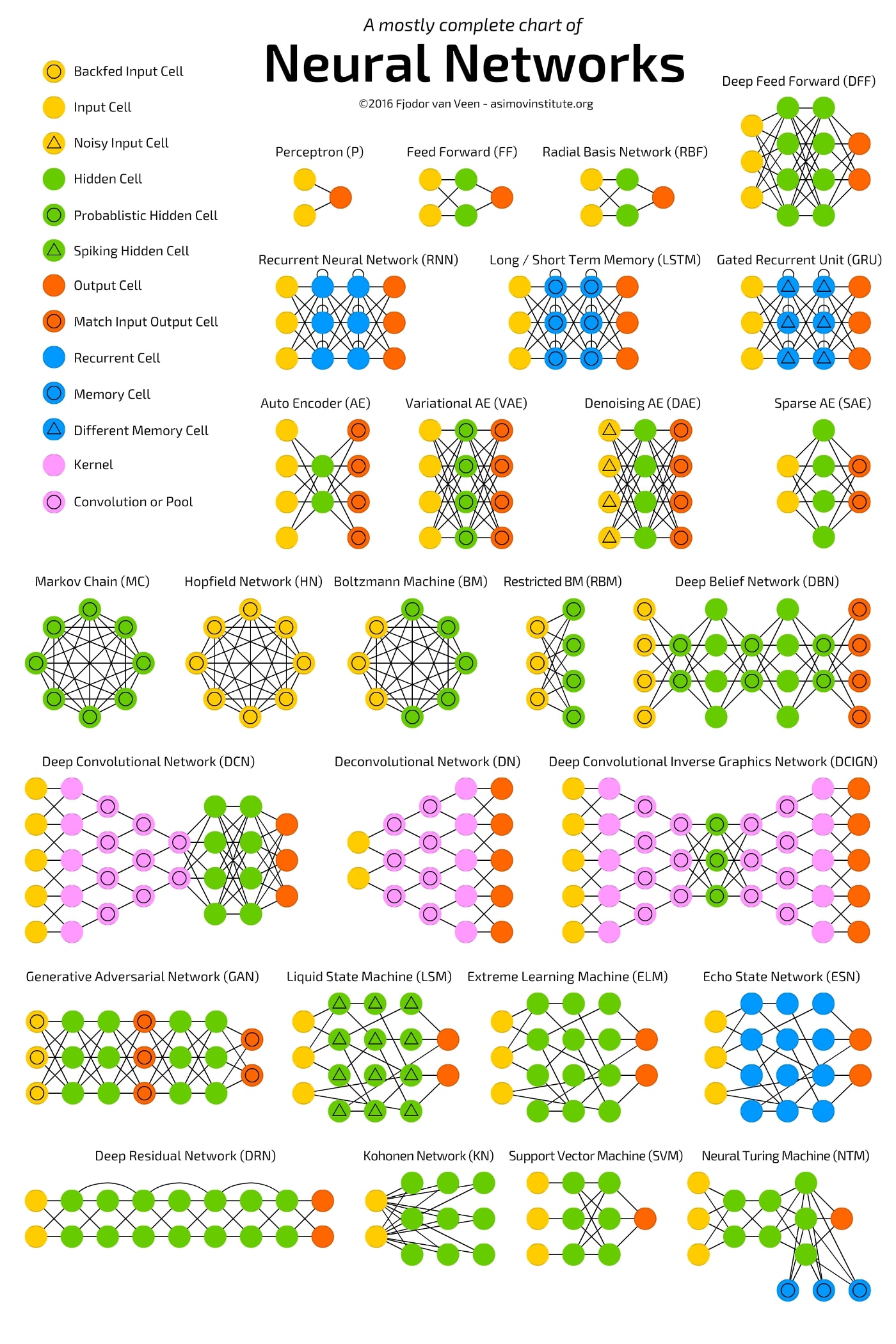
FIG 2: Clasificación de los modelos de redes neuronales (fuente: towardsdatascience)

El perceptrón multicapa consiste en una red en la que el punto de partida es un conjunto de “inputs” que, en su caso, serán variables explicativas (piense en su proyecto del primer cuatrimestre). Cada observación de cada input se conecta con el siguiente elemento, que se llama neurona, y que- en este caso- se organizan por “capas” que van dotándole a la red de más complejidad. Las neuronas tendrán lo que, habitualmente, se denomina función de activación y que es lo que permite que se conecten los nodos entre sí. Veremos que, matemática, lo que estaremos construyendo es una composición de funciones y que, además, esto le permitirá ser capaz de modelar la ya comentada no linealidad entre las variables. El final de todo este proceso es conectar los inputs con el output final (que será la variable/variables que usted quiere predecir) de tal forma que, mediante la complejidad del modelo, pueda capturar relaciones que otros modelos más rígidos no serán capaces.

Ojo con el sobreajuste

Sin embargo, estos modelos son famosos por sobreajustar los datos, implicando que error o ruido se confunda con señal.

Ejemplo 1: Un modelo lineal

Lo primero que se va a hacer es visualizar un sencillo modelo lineal. Verá que, en ese caso, la propia red neuronal le ofrecerá, como resultado de salida, los mismos parámetros que proporciona la estimación mínimo cuadrática. Sin embargo, este ejemplo le permitirá entender de manera más concreta el esquema de red neuronal que se propuso antes sin entrar en mucho detalle.

-El esquema es muy sencillo. Suponga que tiene un input (además de una constante) y que, directamente, quiere ir al output sin pasar por ninguna capa oculta. Además, la función que relaciona el input con el output es lineal

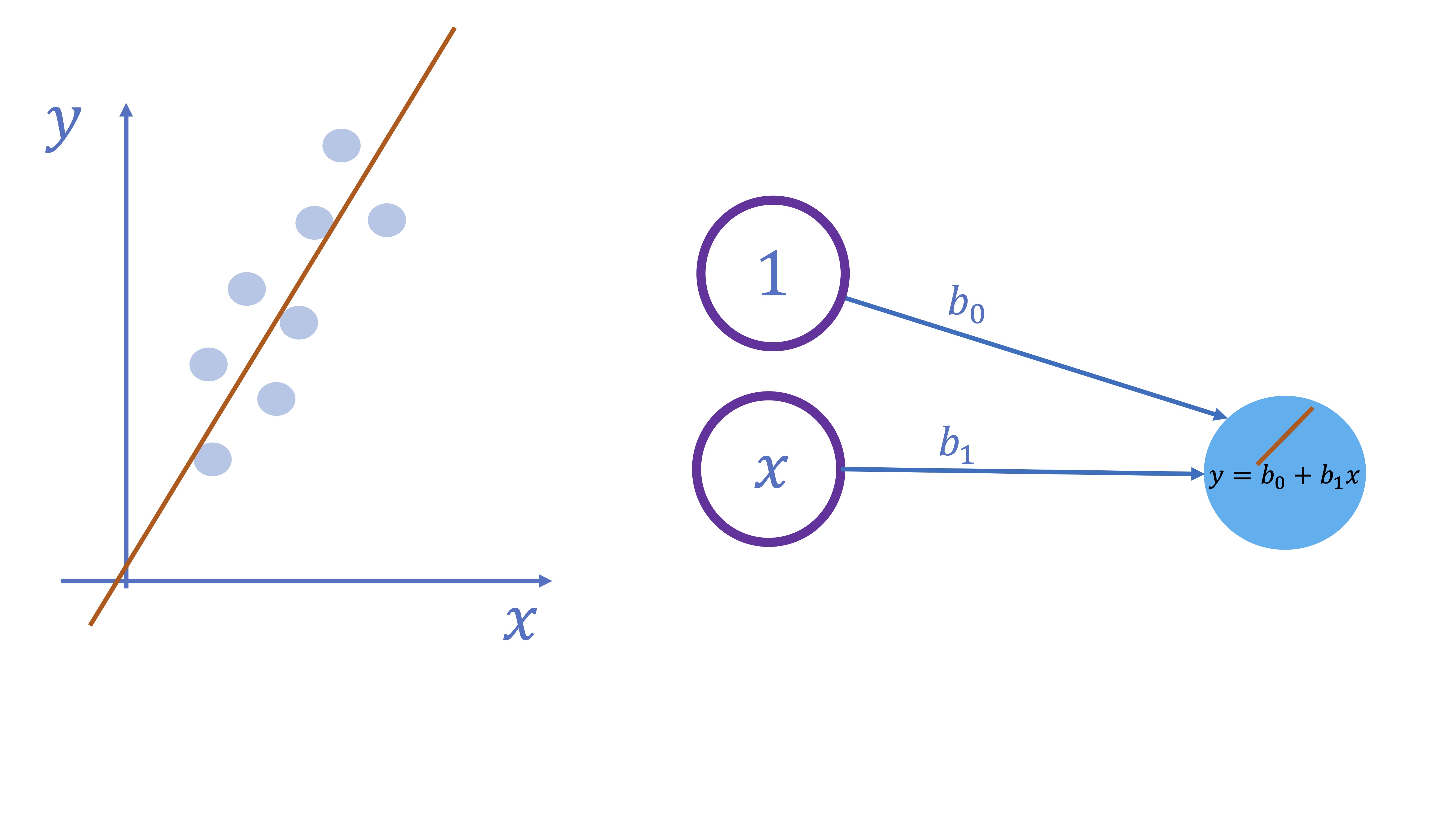
FIG 3: Una red neuronal lineal

Simulando en R, como se muestra a continuaci?n:

#librerías/paquetes que necesita
install.packages("quantmod")
library(quantmod)
install.packages("neuralnet")
library(neuralnet) 
install.packages('kimisc')
library(kimisc)



#genera un modelo del que conoce los parámetros
x1<-rnorm(100,1,1) 
u<-rnorm(100,0,1) 
y<-2+5*x1+u 
#almacena las variables en un DF
DATOS.L<-data.frame(y,x1) 
#entrena una red neuronal MP con 0 capas ocultas
red<-neuralnet(y~x1,hidden=0,data=DATOS.L)  
plot(red) 

lo que da lugar a lo que esperaba: al no tener capas ocultas y la función que vincula el input con el output es lineal, los parámetros son los del modelo de regresión

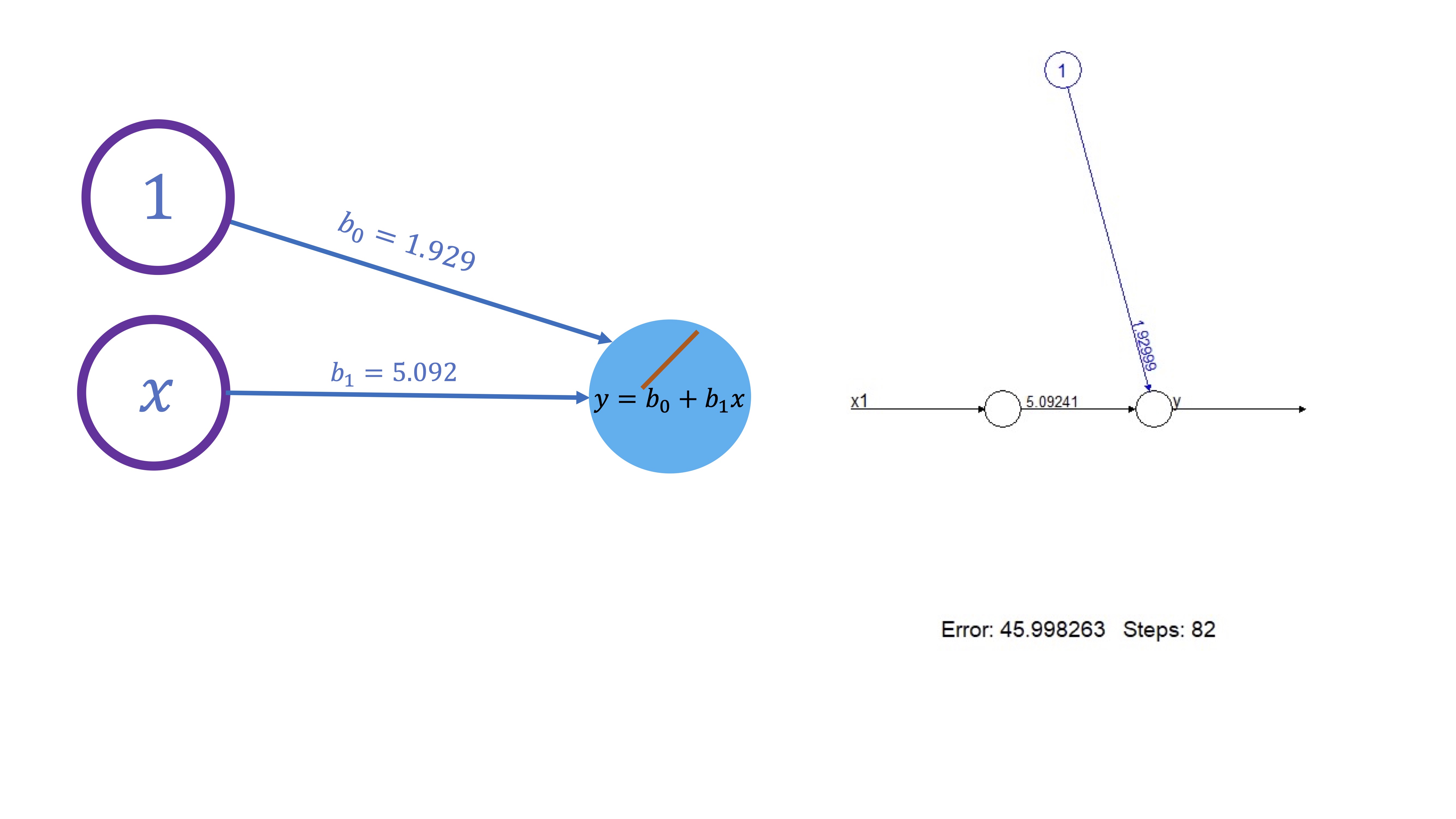
FIG 4: Una red neuronal lineal

de hecho, si estima los parámetros del correspondiente modelo de regresión, obtendrá lo mismo

mod<-lm(y~x1)
summary(mod)

Este modelo es muy sencillo y, por tanto, no tiene ninguna aplicación práctica más que la de poder comprobar que todo funciona como se espera.

Ejercicio resuelto

Complique el modelo lineal de forma innecesaria (añadiendo, por ejemplo, dos neuronas) y escriba la ecuación correspondiente del modelo.

Obtenemos este modelo:

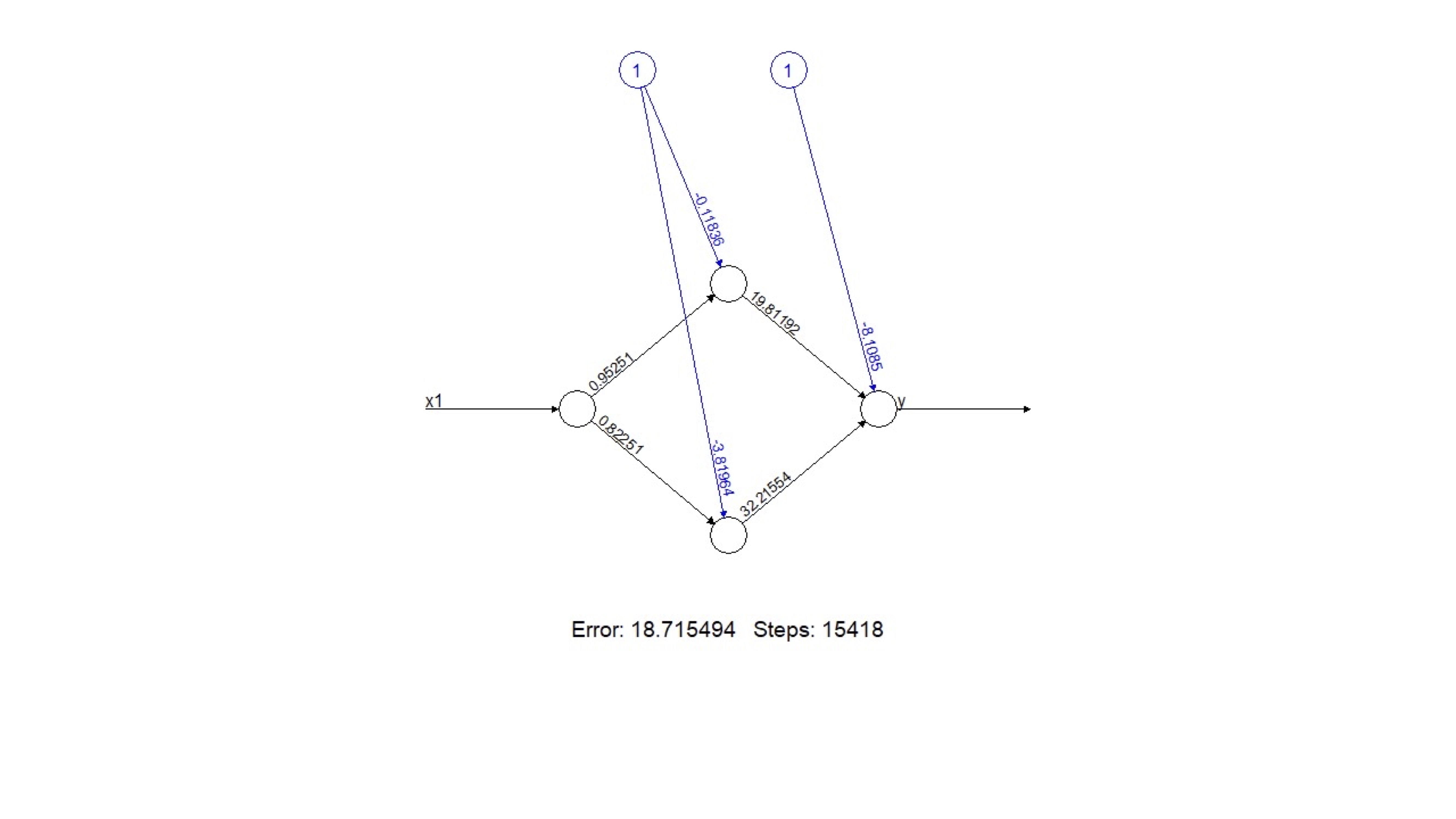Las ecuaciones serán:

• Salida: \(y=-8.10+19.81N_{1}+32.21N_{2}\)
• Capa interna con dos neuronas \(N_{1}=-0.118+0.9525x_{1},N_{2}=-3.81+0.8251x_{1}\)

• Modelo final: \(y=-8.10+1.81\left(-0.118+0.9525x_{1}\right)+32.21\left(-3.81+0.8251x_{1}\right)\)

De esta forma, para cada valor de \(x_{1}\), podemos aplicar esta expresión que nos proporciona el valor final de la \(y\).

¿Qué ha aprendido?

Aquí puede ver cómo la inclusión de neuronas implica una composición matemática de funciones

Ejemplo 2: un modelo logístico

De nuevo, se puede trabajar sobre un modelo no lineal sencillo y conocido previamente (como puede ser un logístico). Este, sería equivalente a un esquema como el siguiente

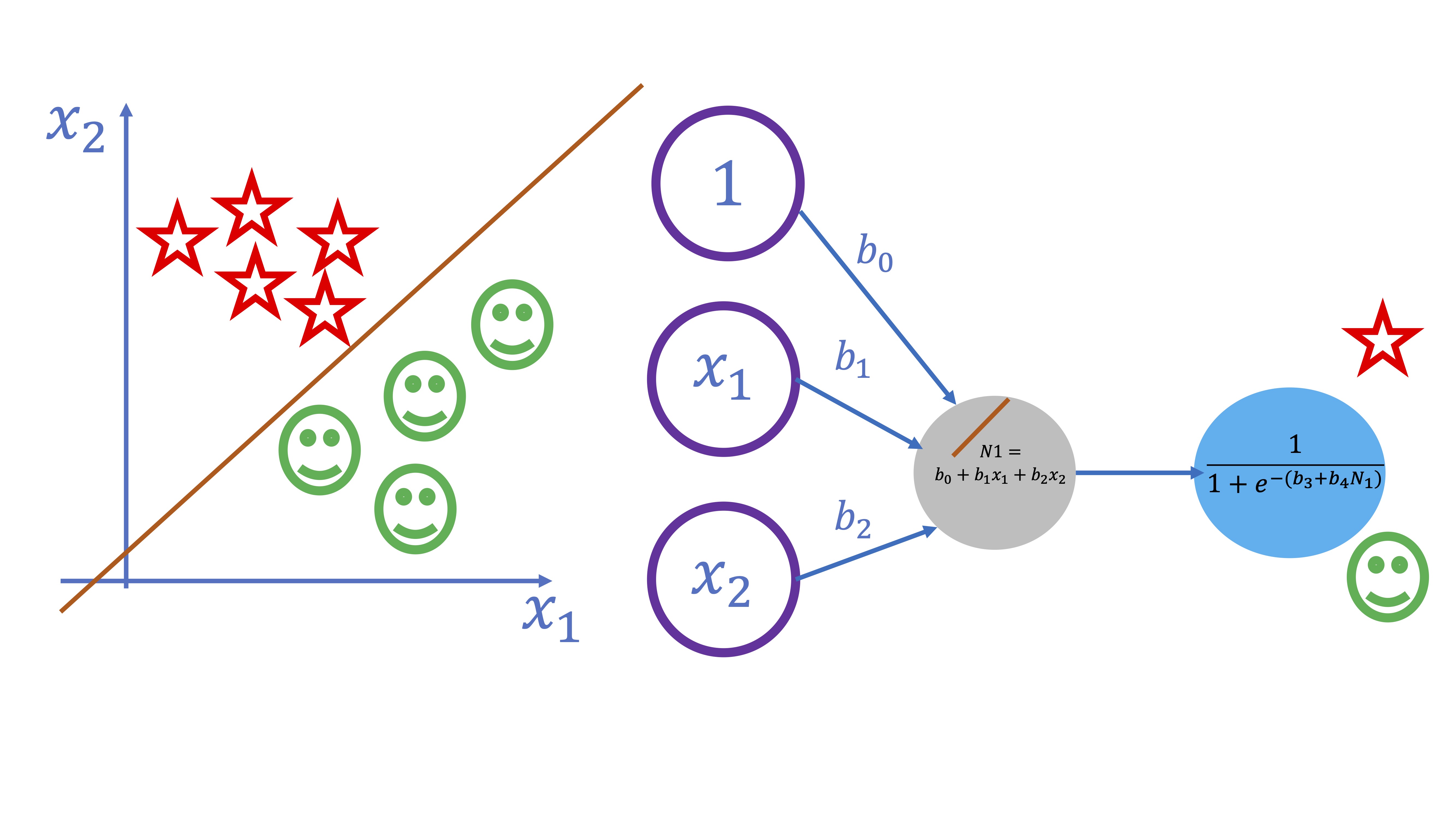
FIG 6: Un modelo logístico donde tenemos dos clases (estrellas y emoticonos)

En este ejemplo se pretende separar dos clases (los smiles y las estrellas) atendiendo a los valores que toman las variables \(x_{1}\) y \(x_{2}\). Como verá la FIG 6, ambos conjuntos son fácilmente separables a través de una recta. Eso sí, como el OUTPUT es una variable cualitativa, necesitaremos que la salida del modelo sea la probabilidad de pertenecer a una u otra clase. Es por ello que la función “output” deberá ser la función logística, es decir:

\[ y=\frac{1}{1+e^{-(\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2})}} \]

Para entender con claridad esto, simulemos datos que proceden de dos variables explicativas continuas y una variable explicada dicotómica. Concretamente, siguiendo este script:

x1<-rnorm(100,0,1) #Simulamos las variables continuas
x2<-rnorm(100,0,1) 
z = 1 + 2*x1 - 3*x2 #nos invetamos la ecuación linel que separa 
pr = 1/(1+exp(-z)) #obtenemos la probabilidad a través de la logística
y = rbinom(1000,1,pr) #creamos una variable dicotómica a través de nuestros resultados
DATOS.B = data.frame(y=y,x1=x1,x2=x2) #almacenamos los datos en un "dataframe"
qplot(x1, x2, colour =y, data = DATOS.B) #lo dibujamos para ver que cuadra

puede generar algo como lo que verá en la FIG 7

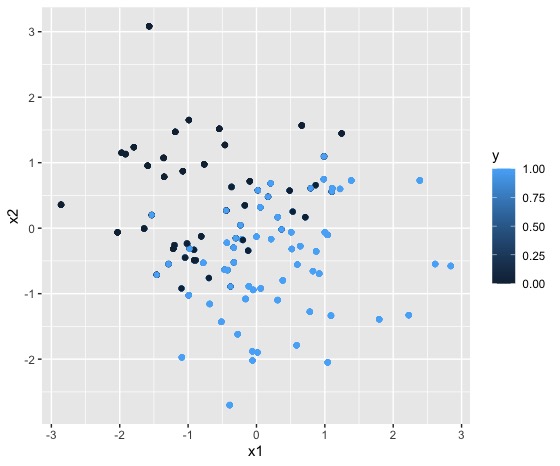si ahora entrena el modelo

red<-neuralnet(y~x1+x2,hidden=0,data=DATOS.B,linear.output=FALSE) 

plot(red)

obtendrá

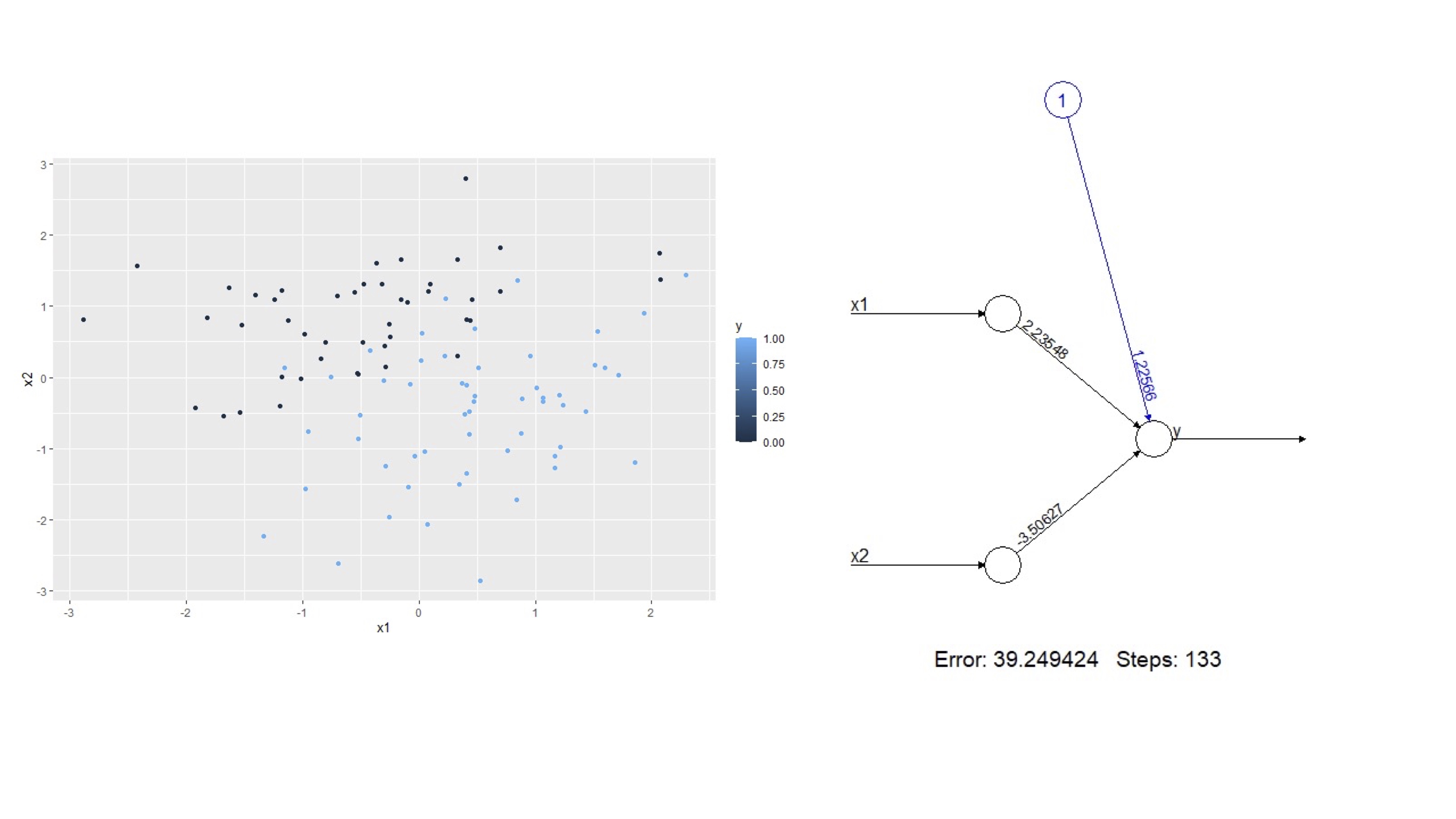
FIG 7: El modelo entrenado en R

es importante notar que la función de activación sigue siendo lineal (\(\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}\)) pero la salida (es decir, la función output, es logística -lo cual se indica con un FALSE en linear. output). Observe que, si ajusta, un modelo binomial a los datos, obtendrá unos coeficientes similares a los que proporciona la red que ha entrenado

glm(y~x1+x2,data=DATOS.B, family=binomial)

no son los mismos, puesto que ya no es un modelo lineal y cada uno de ellos tiene una rutina distinta de estimación de los parámetros.

Clase 4: Modelos complejos de redes neuronales

Empecemos con un ejercicio

---

Genere el modelo \(y_i=2-3x_i+u_i\) con \(i=1,...,500\) y \(u\rightarrow N(0,1)\) Cree una rutina de validación cruzada de tal forma que obtenga una distribución del error de predicción con los siguientes modelos:

• Una regresión lineal
• Una regresión cuadrática
• Un modelo de red neuronal sin neuronas
• Un modelo de red neuronal con 2 neuronas

¿qué ha aprendido sobre la complejidad?

---

Hasta ahora se ha trabajado con estructuras de red neuronal demasiado sencillas que, en realidad, no aportan ninguna utilidad al modelado, ya que han servido para entender las ideas básicas de una red neuronal. A continución proponemos problemas donde la red neuronal pasa a ser decisiva. Por ejemplo, en el siguiente gráfico

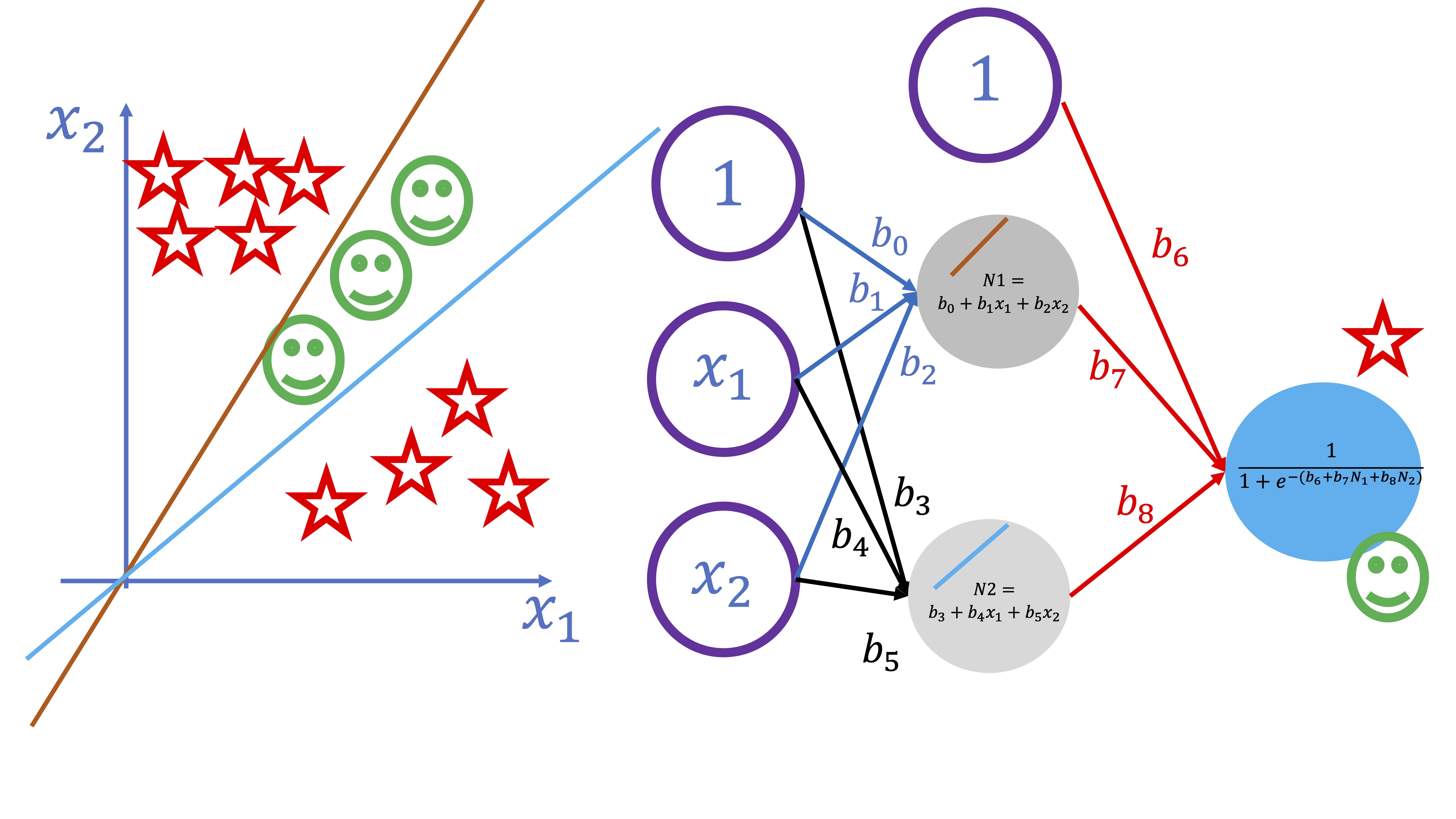Como ve, queremos clasificar una variable con dos posibles resultados,la estrella y la sonrisa, ante los valores que toman \(x_{1},x_{2}\). En este caso, hay cierta mezcla entre las sonrisas y las estrellas, de tal forma que un modelo logit no sería capaz de hacer una buena separación (en la clase anterior ha podido repasar cómo funciona el modelo logit) Para ello, necesitará dos neuronas que, primeramente, construyan las dos rectas que separan las regiones de interés (nótese en el dibujo cómo se remarcan en colores ambas rectas). Una vez las obtenga, deberá combinarlas y obtener una probabilidad (por lo que deberá usar ahí la función logística).

---

Ejercicio

Sean los siguientes datos \(y=(1,1,1,0,0,0,0,0,1,1,1,1)\) \(x_1=(1,1.5,0.75,3,3.5,3.5,4,4,5,5.5,7,7.5)\) \(x_2=(7,7.5,6,5,5.5,5.25,4.75,4.5,1,0.75,0.75,1.1)\)

• Modele \(y=f(x_1,x_2)\) mediante un modelo logit y una red neuronal con 1 y 2 neuronas.
• Evalúe la capacidad de ajuste de ambos modelos mediante una matriz de confusión

---

La solución podemos verla utilizando este código

y<-c(1,1,1,0,0,0,0,0,1,1,1,1)
x1<-c(1,1.5,0.75,3,3.5,3.5,4,4,5,5.5,7,7.5)
x2<-c(7,7.5,6,5,5.5,5.25,4.75,4.5,1,0.75,0.75,1.1)
DATOS.C<-data.frame(y,x1,x2)
qplot(x1, x2, colour =y, data = DATOS.C) #lo dibujamos para ver que cuadra




red1<-neuralnet(y~x1+x2,hidden=1,data=DATOS.C,linear.output=FALSE) 

red2<-neuralnet(y~x1+x2,hidden=2,data=DATOS.C,linear.output=FALSE) 

glm(y~x1+x2,data=DATOS.C, family=binomial)

En la FIG 2 se puede ver lo que se pretende ajustar,

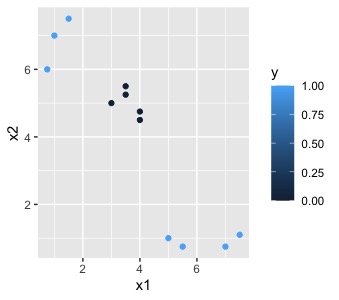
FIG 2: Un modelo más complejo

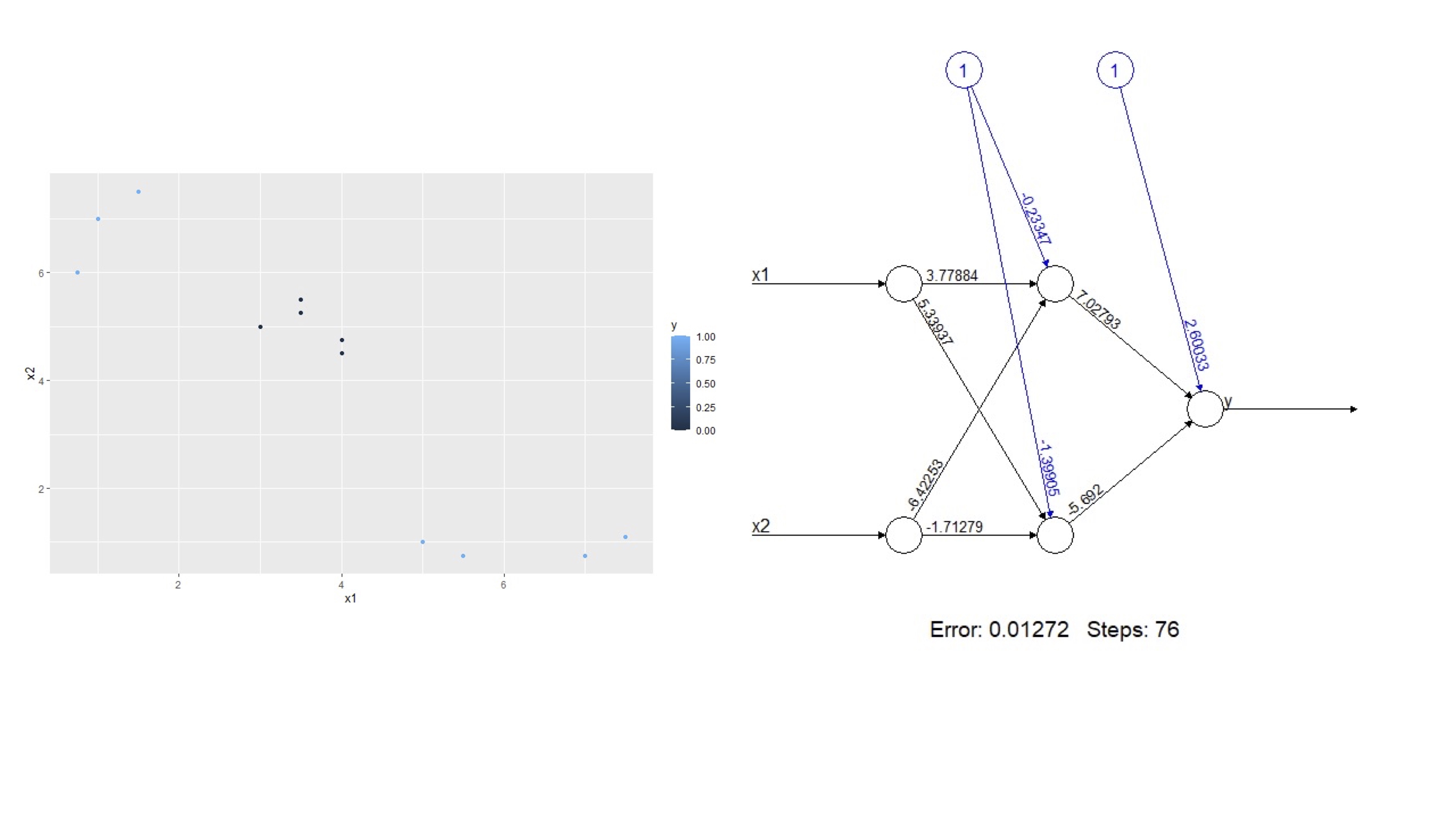
FIG 3: Un modelo más complejo

Note que este resultado puede escribirse como sigue:

• Salida: \(y=\frac{1}{1+e^{-(2.70+7.02N_{1}-5.69N_{2})}}\)
• Capa interna \(N_{1}=-0.23+3.77x_{1}+5.34x_{2},N_{2}=-1.39+5.33x_{1}-6.42x_{2}\)
• Modelo: \(y=\frac{1}{1+e^{-(2.70+7.02\left[-0.23+3.77x_{1}+5.34x_{2}\right]-5.69\left[-1.39+5.33x_{1}-6.42x_{2}\right])}}\)

y que ya no podría obtenerse una representación similar utilizando un logit.

¿Qué modelo proporciona un mejor ajuste?

Podemos seguir aumentando la complejidad. Por ejemplo, en este otro caso, queremos encontrar la función que separa estos elementos que, como vemos, presentan una nueva complicación: no vale separar sólo con dos rectas, hay que buscar otra recta adicional y, posteriormente, juntarlas. Para ello, se debe añadir otra neurona:

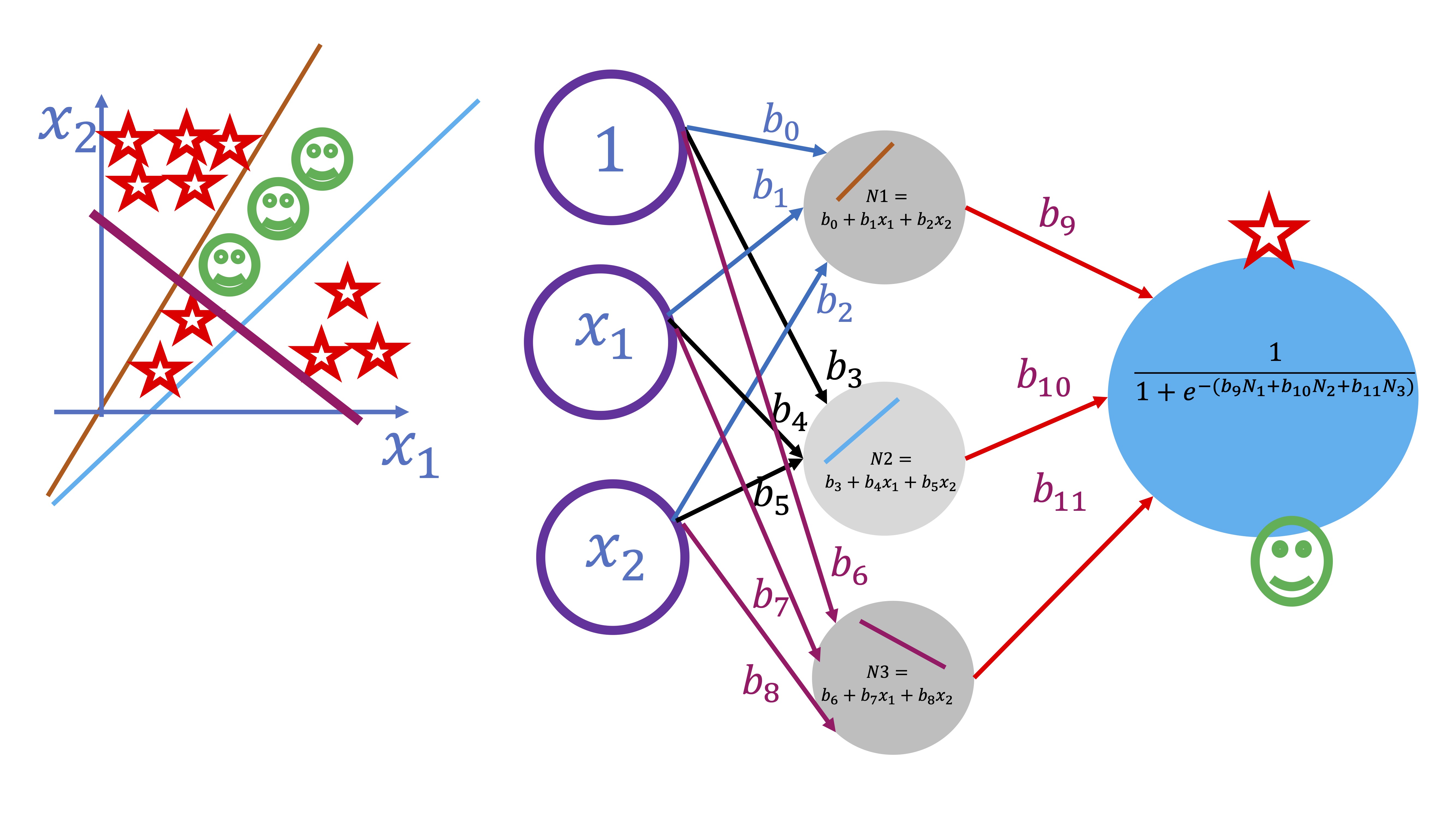
FIG 4: Un modelo más complejo

y conectarlas posteriormente, como se puede ver en la figura. Añadir neuronas, por tanto, genera una estructura más compleja que permite ir entrenando el modelo correspondiente.

Pero ¿Y si se incrementan las capas ocultas? Las capas ocultas surgen cuando se busca crear una estructura más compleja al interactuar las neuronas de la primera capa. Como se ve en la FIG 5, en este caso, al cortarse ciertas rectas, se generan subconjuntos donde cambia la clase de la variable \(y\). Esas interacciones se modelan creando una capa nueva.

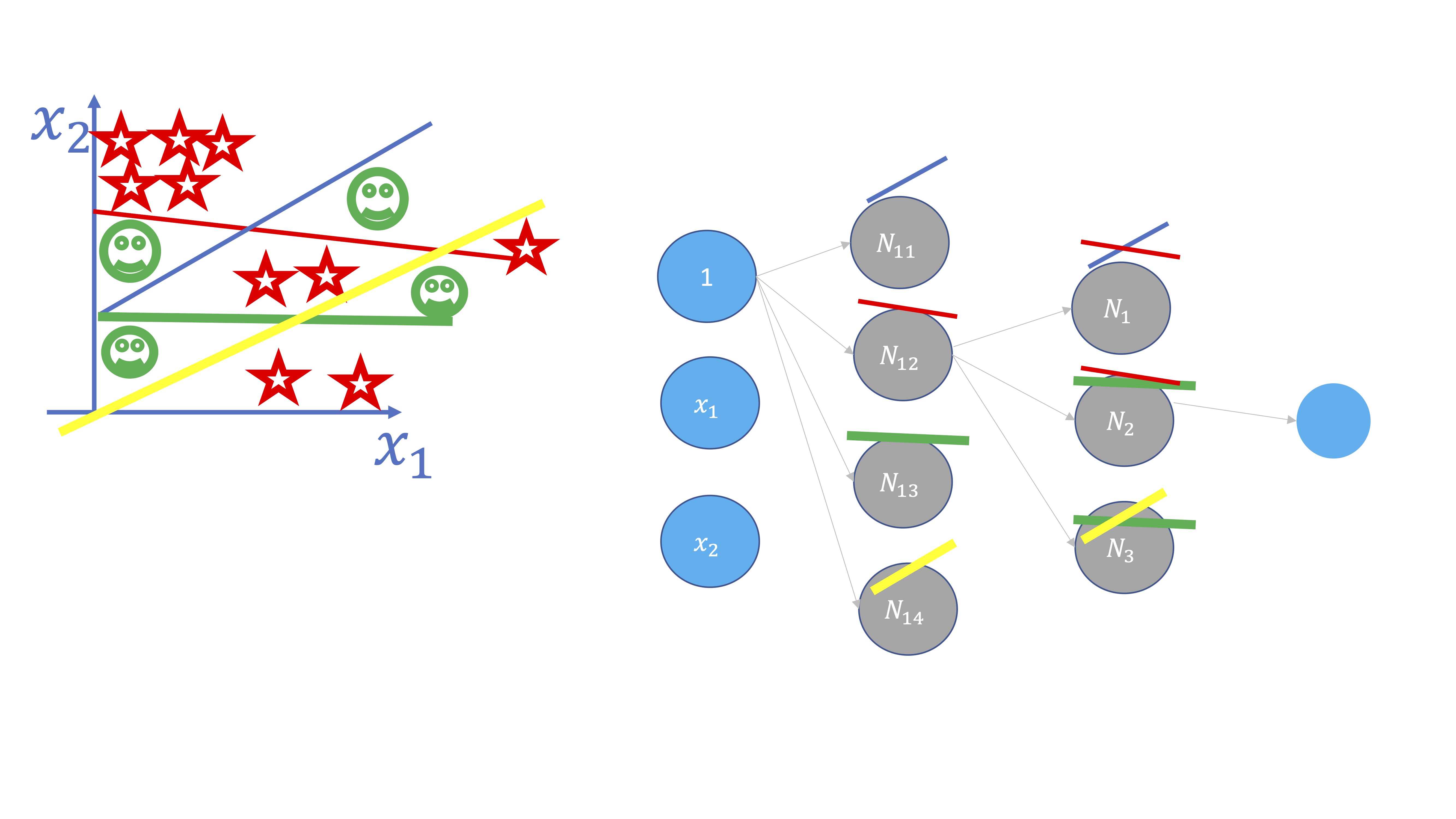
FIG 5: Un modelo más complejo

Por lo tanto:

• Se añaden neuronas cuando se quieren crear ‘barreras’ separadoras en el modelo
• Se crean capas ocultas cuando las “barreras” trazadas interactúan entre ellas (se cortan)

Puede entenderse bien con el siguiente ejemplo: se pretende ajustar el siguiente problema de clasificación

y<-c(1,1,1,0,0,0,0,0,1,1,1,1)
x1<-c(1,1.5,0.75,3,3.5,3.5,4,4,5,5.5,7,7.5)
x2<-c(7,7.5,6,5,5.5,5.25,4.75,4.5,1,0.75,0.75,1.1)
DATOS.C<-data.frame(y,x1,x2)
qplot(x1, x2, colour =y, data = DATOS.C) #lo dibujamos para ver que cuadra




red1<-neuralnet(y~x1+x2,hidden=1,data=DATOS.C,linear.output=FALSE) 

red2<-neuralnet(y~x1+x2,hidden=2,data=DATOS.C,linear.output=FALSE) 

glm(y~x1+x2,data=DATOS.C, family=binomial)

• Evalúe qué modelo ajusta mejor los datos.

Ejercicio propuesto

Utilice estos datos para analizar qué configuración de redes neuronales podría ajustar mejor

x1<-c(1,1.5,0.75,3,3.5,3.5,4,4,5,5.5,7,7.5,2,3,2.75,1.5,4,4,4.15,4,6,6.5,6,7,2,2,3,3,4,4,6,6.25,5.75,6)
x2<-c(7,7.5,6,5,5.5,5.25,4.75,4.5,1,0.75,0.75,1.1,2,2.5,2,2.25,2,2.1,2.2,2.3,5.5,5.5,5.5,5.5,5.5,4,4.5,5.5,5.25,4,3,3,3,3)
y=c(1,1,1,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,0,0,1,1,0,1,0,0,0,0)

El siguiente script le permitirá ver cómo la complejidad en la relación entre las variables \(x_1,x_2\) con la variable \(y\) nos obliga a introducir 3 capas ocultas (mediante el comando hidden). En el primer ejemplo (red1) se usan sólo 2 neuronas y podrá ver en la tabla CM cómo la red neuronal clasifica incorrectamente bastantes observaciones. Al aumentar tanto las neuronas como las capas, (red2), puede ver que la clasificación es “casi” perfecta.

DATOS.D<-data.frame(y,x1,x2)
qplot(x1,x2,colour=y, data=DATOS.D)+geom_point(size=3)

red1<-neuralnet(y~x1+x2,rep=6,hidden=c(2),data=DATOS.D, linear.output = FALSE)
y1<-predict(red1, newdata=DATOS.F[,2:3])
qplot(x1,x2,colour=y1, data=DATOS.D)+geom_point(size=3)

y1_n<-y1>0.5
CM<- table(y1_n, y)


set.seed(1234)
red2<-neuralnet(y~x1+x2,hidden=c(10,10,10),data=DATOS.D, linear.output = FALSE)
y1_2<-predict(red2, newdata=DATOS.D[,2:3])
qplot(x1,x2,colour=y1_2, data=DATOS.D)+geom_point(size=3)

y2_n<-y1_2>0.50
CM<- table(y2_n, y)

Sin embargo, esto nos puede llevar a un claro problema: el sobreajuste/sobreentrenamiento. Con redes neuronales es fácil ser capaz de alcanzar altos niveles de ajuste de los modelos a los datos, sin embargo, por dicho motivo, es fácil estar asumiendo ruido del modelo como si fuera señal y, por lo tanto, incurrir en errores importantes de predicción fuera de la muestra.

Clase 5: Entrenamiento de modelos de redes neuronales(I)

Para entender cómo se entrenan los modelos y, por tanto, se obtienen las estimaciones para cada uno de los parámetros de la red, podemos ver el modelo de red neuronal como una composición de funciones. Por ejemplo, en la FIG 1, podemos ver el esquema de dependencias que da lugar a la composición de funciones

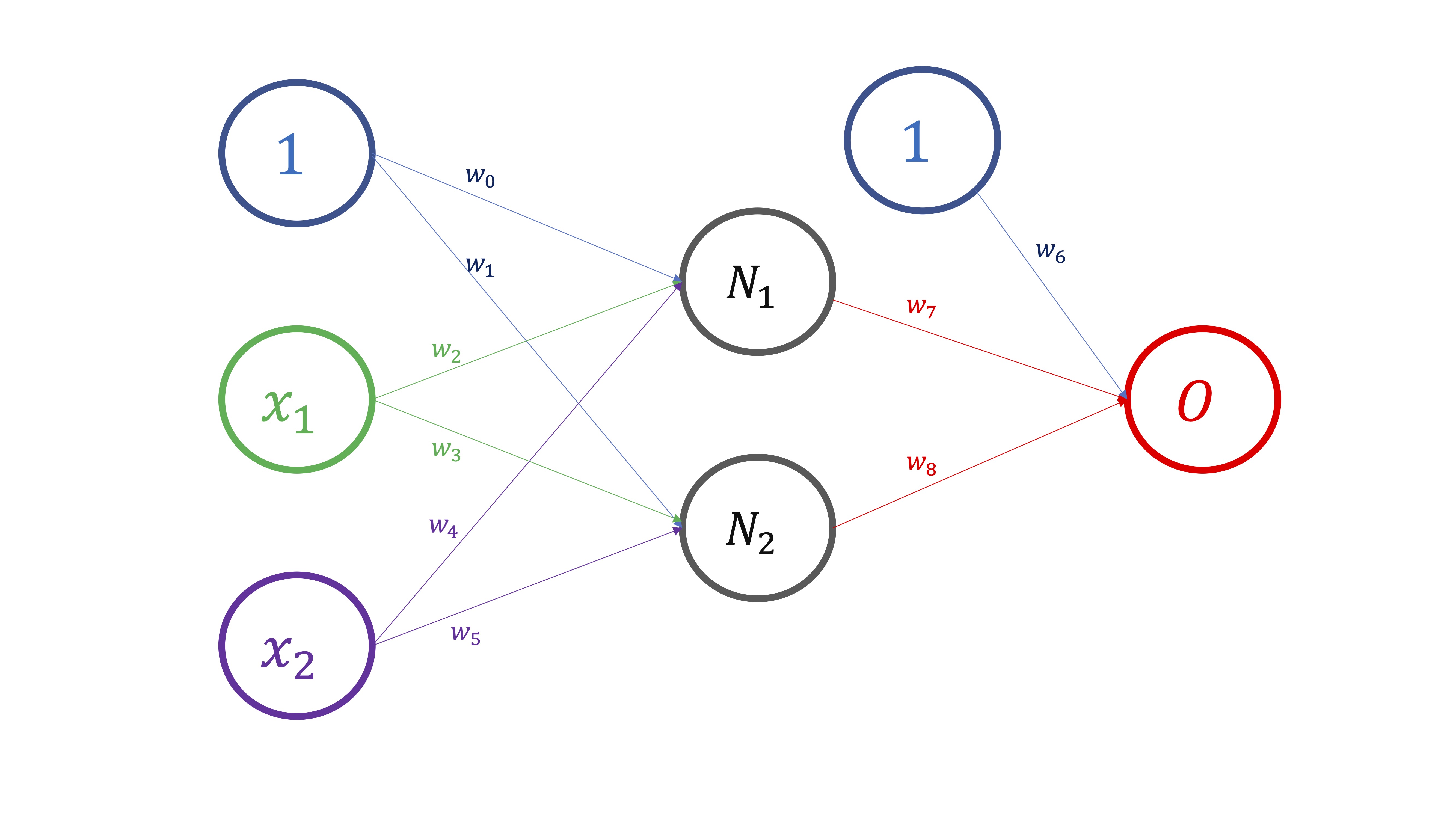Para empezar, dados unos valores para \((x_1,x_2)\), necesitamos conocer los valores de los pesos \(w_0,w_1,...,w_5\) y así obtener \(N_1,N_2\). Ahí tenemos, por tanto, que \[ (w_0,w_2,w_4;1,x_1,x_2)\mapsto N_1 \] \[ (w_1,w_3,w_5;1,x_1,x_2)\mapsto N_2 \]

Una vez obtenemos estas dos neuronas, \((N_1,N_2)\), obtenemos el “output”, de tal forma que

\[ (w_6,w_7,w_8;1,N_1,N_2)\mapsto O \]

y, entonces, comparamos el output que nos da el modelo, \(O\), con las verdaderas observaciones \(O_{real}\) de tal forma que

\[ Error=(O_{real}-O)^2 \] Ahora, si hacemos esto para las \(T\) observaciones de que dispongamos en la muestra, obtendremos como medida del error, el error cuadrático medio,esto es,

\[ ECM=\frac{\sum(O_{real}-O)_{i}^{2}}{T} \]

el algoritmo para obtener esos pesos se conoce como retropropagación y, básicamente, funciona así:

• Dé pesos iniciales aleatorios (en este caso, \(w_{0}=0.1,w_{1}=0.1,...,w_{8}=0.6\))

• PROPAGACIÓN HACIA DELANTE Compute (a través de la composición de funciones) la predicción del output (FIG2).

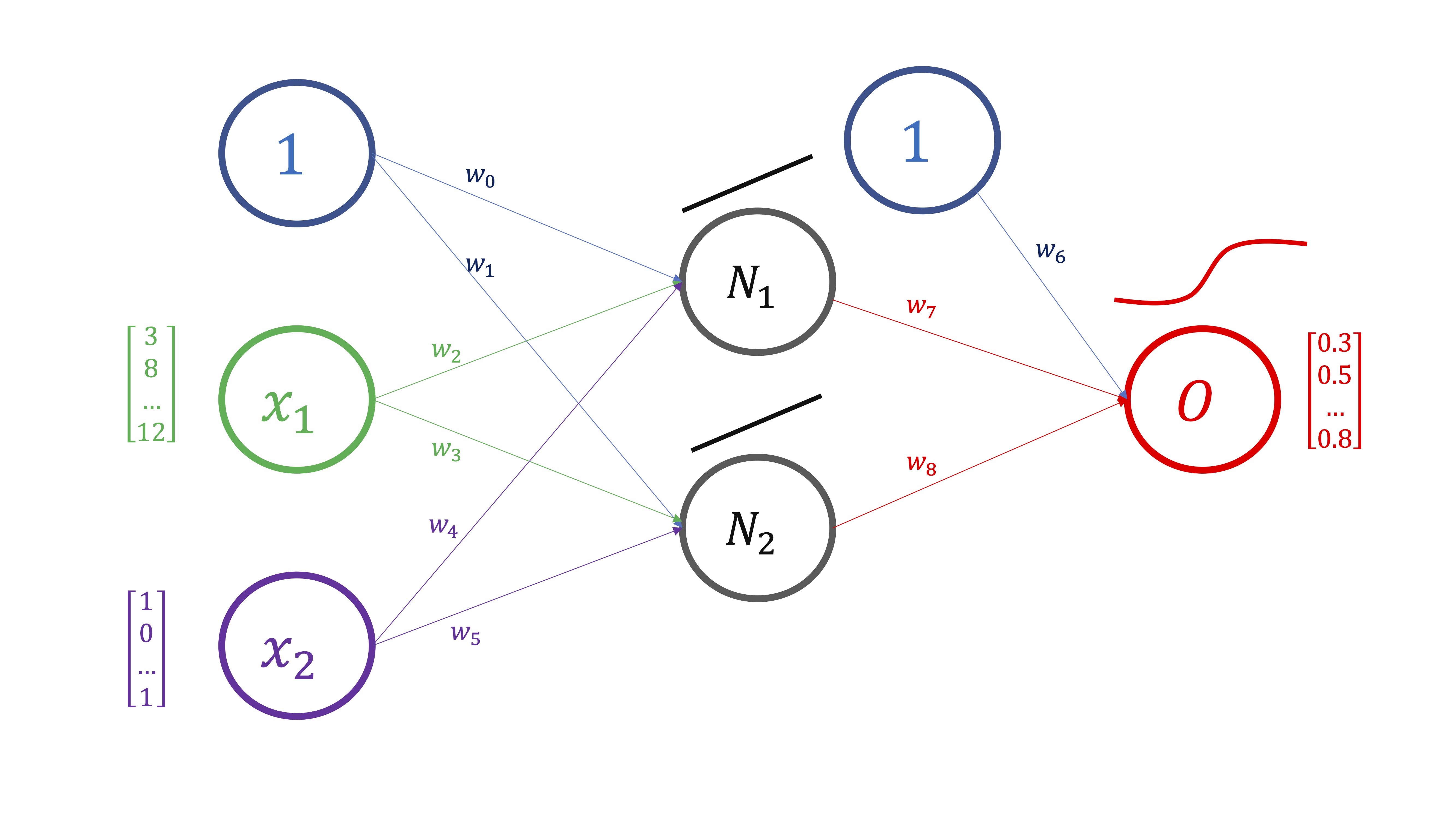
FIG 2: Esquema donde tenemos \(T\) observaciones de las variables \(x_1,x_2,O\)

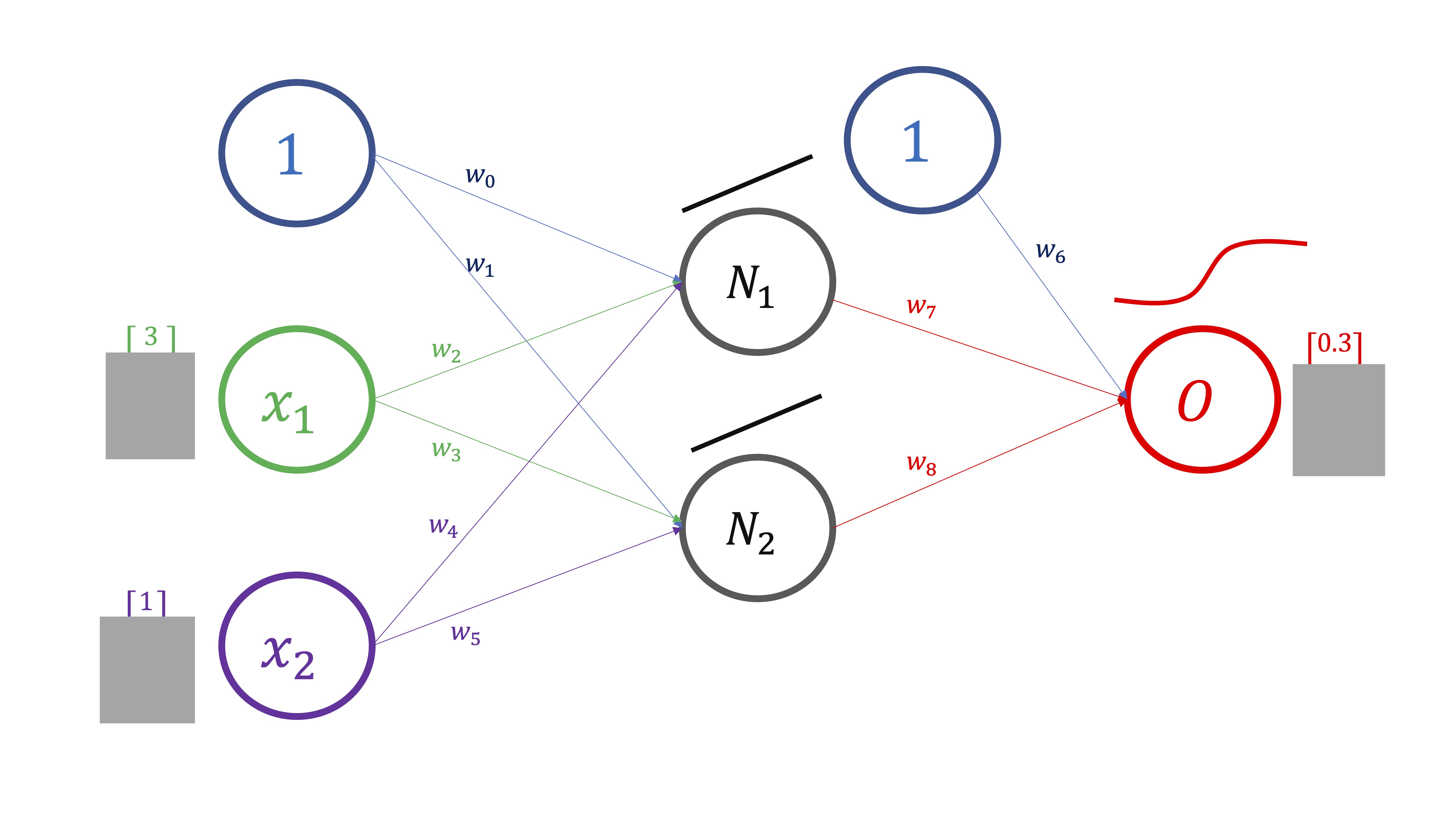
FIG 3: Aunque aquí, por simplicidad, usaremos la primera observación de cada variable

En este caso (FIG3), lo haremos para un sólo valor de los inputs y del output, pero en realidad se hace para todo el vector de datos:

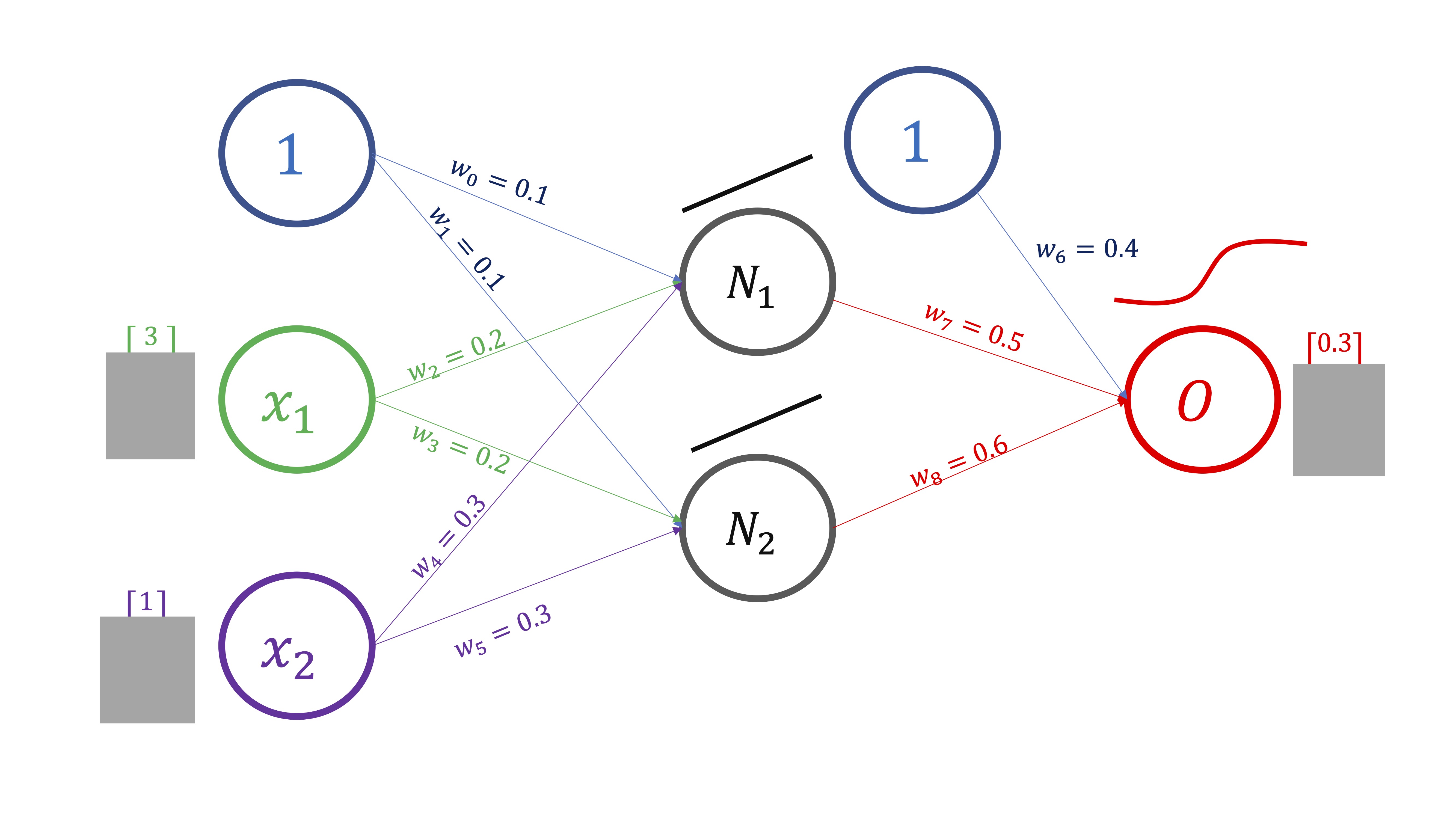
FIG 4: pesos iniciales obtenidos de manera aleatoria

\[ \begin{cases} N_{1}=w_{0}+w_{2}x_{1}+w_{4}x_{2} & \Rightarrow N_{1}=0.1+0.2\times3+0.3\times1=1\\ N_{2}=w_{1}+w_{3}x_{1}+w_{5}x_{2} & \Rightarrow N_{2}=0.1+0.2\times3+0.3\times1=1\\ \hat{O}=\frac{1}{1+e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}} & \Rightarrow\hat{O}=\frac{1}{1+e^{-\left(0.4+0.5\times1+0.6\times1\right)}}=0.81 \end{cases} \]

Ya tiene una predicción hecha por el modelo para \(O_{real}\) . Puede calcular el error que comete. Este modelo predice \(O=0.81\) pero, en realidad, \(O_{real}=0.3\)

• Evalúe el error cuadrático medio (\(ECM=\frac{\sum_{i=1}^{^{T}}\left(O_{i}-\hat{O_{i}}\right)^{2}}{T})\) que, en este caso, para simplificar \(N=1\) y obtiene \(ECM=\left(0.3-0.81\right)^{2}=0.26\). El objetivo ahora es minimizar este error. Para ello, deberá buscar nuevos pesos que mejoren el \(ECM.\) Es decir, quiere

\[ \min_{w_{0},w_{1},....,w_{8}}ECM \]

Este problema de minimización, que es complejo- pues involucra a una función compuesta de otras funciones (y que aquí se ha simplificado para que pueda entenderlo)- se debe hacer de manera iterativa utilizando, por ejemplo, el método del gradiente. Es decir, supongamos que quiere mejorar la estimación de \(w_{7}\), tendrá que seguir la regla ya aprendida en clases anteriores:

\[ w_{7}^{new}=w_{7}^{old}-h\frac{\partial ECM}{\partial w_{7}} \]

de tal forma que \(h\rightarrow0\)

Fíjese:

\[ \begin{cases} N_{1}=w_{0}+w_{2}x_{1}+w_{4}x_{2}\\ N_{2}=w_{1}+w_{3}x_{1}+w_{5}x_{2}\\ O=\frac{1}{1+e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}}\\ ECM=\frac{\sum_{i=1}^{^{T}}\left(O_{real,i}-O_{i}\right)^{2}}{T} & \Rightarrow ECM=\frac{\sum_{i=1}^{^{T}}\left(O_{real,i}-\frac{1}{1+e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}}\right)^{2}}{T} \end{cases} \]

De tal forma, que si necesita calcular

\[ \frac{\partial ECM}{\partial w_{7}} \]

deberá utilizar la regla de la cadena:

\[ \frac{\partial ECM}{\partial w_{7}}=2\left(O_{real}-O\right)^{2}\left(\frac{e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}N_{1}}{\left(1+e^{-\left(w_{6}+w_{7}N_{1}+w_{8}N_{2}\right)}\right)^{2}}\right) \] y, sustituyendo, \[ \frac{\partial ECM}{\partial w_{7}}=2\times0.26\left(\frac{0.22\times1}{0.81^{2}}\right)=0.17 \]

por lo que \[ w_{7}^{new}=0.5-h\times0.17 \]

El nuevo valor del parámetro, como verá, dependerá del valor de \(h\) el cual, ya vimos, afecta al proceso de convergencia (y, por tanto, de obtención del resultado del método de optimización).

• RETROPROPAGACIÓN Una vez tiene actualizados todos los parámetros utilizando este procedimiento (llamado Backward) deberá volver a obtener los nuevos valores de \(O\), es decir, predicciones nuevas de la variable output y optimizar, de nuevo, el error. Esto es lo que se conoce como “retropropagación”.

El algoritmo consiste en dar de manera iterativa los pasos de “propagación hacia delante (forward)” y de “retropropagación (backpropagation)” hasta que se considere que el \(ECM\) ha alcanzado un mínimo (generalmente, local).

Clase 6: Entrenamiento de modelos de redes neuronales(II)

El objetivo ahora es tratar de buscar un mecanismo para decidir los valores que tendrán los hiperparámetros de nuestra red neuronal. Llamaremos hiperparámetros a aquellos que debemos definir nosotros. A un nivel básico, el número de capas ocultas y el de neuronas por capa. Aunque, dependiendo de la función que utilice para entrenar sus modelos, puede requerir fijar más parámetros (por ejemplo, el valor de \(h\) en el algoritmo de “retropropagación”, o el número máximo de iteraciones, etc…).

La mejor manera de evitar el temido sobreajuste, será mediante un mecanismo de validación cruzada. sin embargo, la contrapartida estriba en el coste computacional que tienen los modelos de redes neuronales. Veamos un ejemplo con los datos anteriores.

x1<-c(1,1.5,0.75,3,3.5,3.5,4,4,5,5.5,7,7.5,2,3,2.75,1.5,4,4,4.15,4,6,6.5,6,7,2,2,3,3,4,4,6,6.25,5.75,6)
x2<-c(7,7.5,6,5,5.5,5.25,4.75,4.5,1,0.75,0.75,1.1,2,2.5,2,2.25,2,2.1,2.2,2.3,5.5,5.5,5.5,5.5,5.5,4,4.5,5.5,5.25,4,3,3,3,3)
y=c(1,1,1,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,1,1,1,1,0,0,1,1,0,1,0,0,0,0)



DATOS.D<-data.frame(y,x1,x2)
qplot(x1,x2,colour=y, data=DATOS.D)+geom_point(size=3)

será interesante, hacer un juicio basado en información visual. Trate de ver, mediante gráficos, la relación que tienen las variables que considera más relevantes

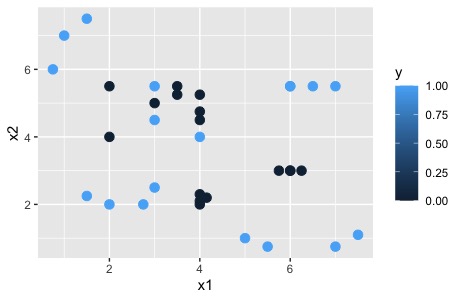En este caso, puede ver que hay cierta confusión en la relación entre \(x1,x2\) y \(O\), sugiriendo que necesitará más de una capa oculta para modelar la no-linealidad de dicha relación. Puede ser sensato analizar el mejor modelo basado en una, dos y-como máximo- 3 capas ocultas y un conjunto de neuronas que, como mínimo serán 3 (dos variables input y una constante). El máximo es desconocido, pero podemos probar con el conjunto \({3,5,7}\), como mucho.

error<-mat.or.vec(50, 9) #creamos un vector que almacenará 50 errores y 9 configuraciones distintas
neurons<-c(3,5,7) #creamos un vector que contiene los diferentes valores del número de neuronas
for(i in 1:50){     #Iniciamos los subíndices: este es el de la iteración
  for (j in 1:3){   #este es el subíndice del número de neuronas
    random <- sample(1:nrow(DATOS.D), size = floor(.7*nrow(DATOS.D))) # Elegimos la muestra de entrenamiento al azar
    train<-DATOS.D[random,]
    test <-DATOS.D[-random, ] #por lo que la muestra de test es la contraria
    red1<-neuralnet(y~x1+x2,hidden=c(neurons[j]),data=train, linear.output = FALSE) #configuración con 1 capa oculta
    red2<-neuralnet(y~x1+x2,hidden=c(neurons[j],neurons[j]),data=train, linear.output = FALSE) #configuración con 2 capas ocultas
    red3<-neuralnet(y~x1+x2,hidden=c(neurons[j],neurons[j],neurons[j]),data=train, linear.output = FALSE) #configuración con 3 capas ocultas
    
    O_red1<-predict(red1, newdata=test,type="response") 
    O_red2<-predict(red2, newdata=test,type="response")
    O_red3<-predict(red3, newdata=test,type="response")
    
    O_red1_n<-as.numeric(O_red1>0.5)
    O_red2_n<-as.numeric(O_red2>0.5)
    O_red3_n<-as.numeric(O_red3>0.5)
    O_real<-(test$y)
   
    X<-data.frame(O_red1_n,O_red2_n,O_red3_n,O_real)  
    xt1<-table(factor(X[,1],levels=0:1),factor(X[,4],levels=0:1))
    xt2<-table(factor(X[,2],levels=0:1),factor(X[,4],levels=0:1))
    xt3<-table(factor(X[,3],levels=0:1),factor(X[,4],levels=0:1))
    
    error[i,j]<-(xt1[1,2]+xt1[2,1])/length(O_red1_n) #medimos los errores de clasificación
    error[i,j+3]<-(xt2[1,2]+xt2[2,1])/length(O_red2_n) 
    error[i,j+6]<-(xt3[1,2]+xt3[2,1])/length(O_red3_n) 
    
    
    
     }}

La matriz “error” nos proporciona, por columnas:

1. 2 neuronas 1 capa oculta

2. 5 neuronas 1 capa oculta

3. 7 neuronas 1 capa oculta

4. 2 neuronas 2 capas ocultas

5. 5 neuronas 2 capas ocultas

6. 7 neuronas 2 capas ocultas

7. 2 neuronas 3 capas ocultas

8. 5 neuronas 3 capas ocultas

9. 7 neuronas 3 capas ocultas

Para cada una de estas configuraciones, tenemos mediciones del error. Puede comprobar que la columna 6 es la que tiene un menor error promedio (es decir, utilizando 7 neuronas y 2 capas ocultas).

Ejercicio Trabaje con su conjunto de datos, entrenando un modelo de red neuronal. Juegue a combinar los modelos que ha utilizado hasta ahora incluyendo el de red neuronal (la combinación más sencilla: promedio de ambos modelos)