BLOQUE 6: Introducción al análisis de series temporales

Clase 1. Introducción al análisis de Series Temporales a través de los procesos estocásticos

Los datos de series temporales consisten en una secuencia de \(N\) observaciones (datos, en general, relativos a comportamientos humanos agregados) ordenados cronológicamente (y, en general, equiespaciados). Un instrumento importante para analizar series temporales son los gráficos donde, en el eje de abscisas, se representa la variable “tiempo” y en el eje de ordenadas la magnitud que se está considerando. Además, conviene acostumbrarse a hacer una buena inspección gráfica para obtener las ideas más relevantes que compondrán la serie.

Por ejemplo, apoyémonos en ciertos gráficos de series temporales obtenidos del INE, Yahoo finanzas y Google para tener una primera idea de lo que buscamos en las series.

  • Frecuencia

La frecuencia de una serie indica cada cuánto tiempo se representa la información disponible. En el INE abundan, por ejemplo, las series anuales y trimestrales (por el coste que supone recoger información con mayor frecuencia). Las series bursátiles son diarias y las de consumo eléctrico pueden ser horarias.

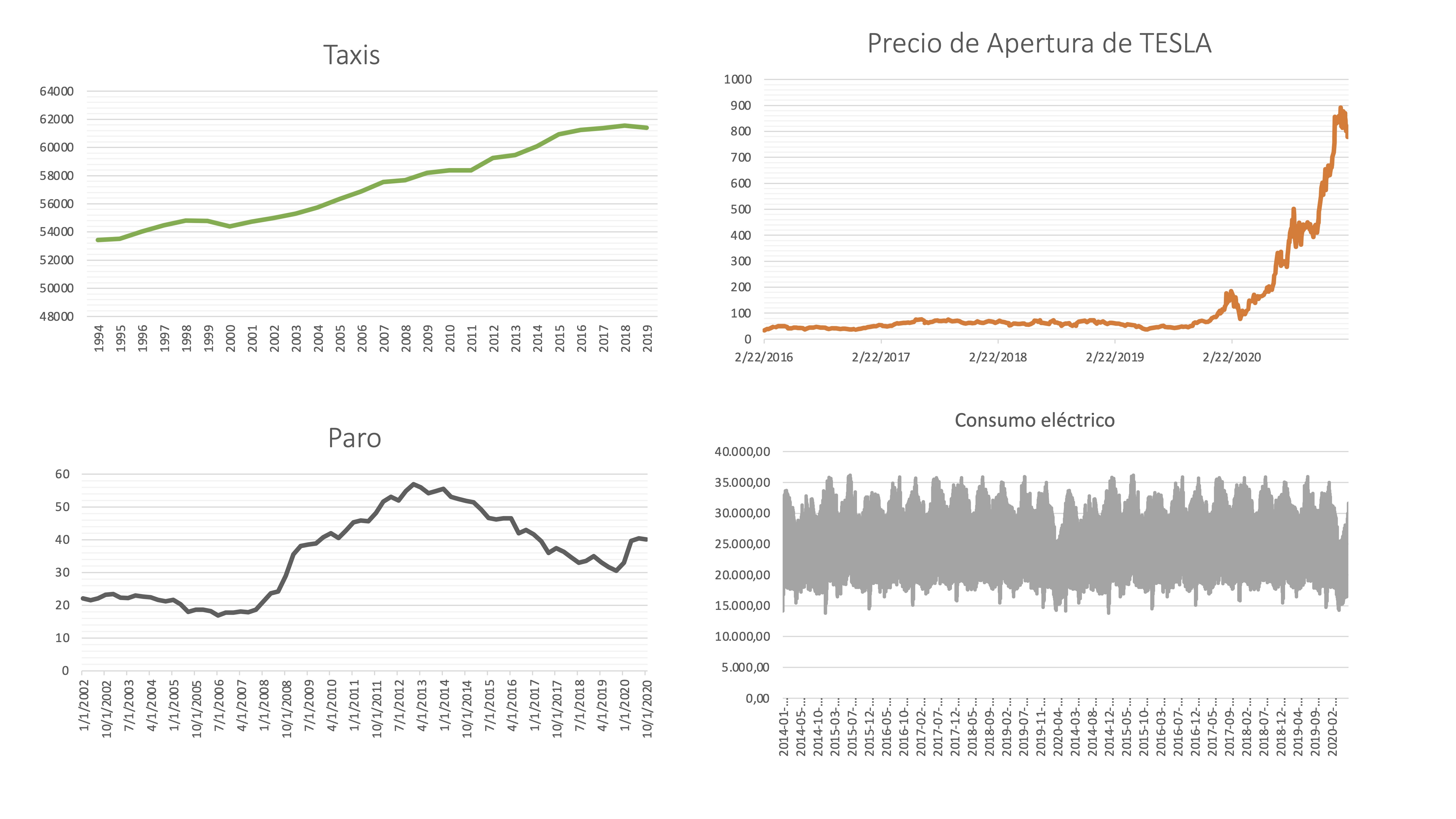
FIG 1: Diferentes series temporales

  1. Taxis, con frecuencia anual, representa el número de taxis en circulación en España.

  2. Precio Apertura TESLA, con frecuencia diaria, representa el precio de la acción de esta empresa.

  3. Paro, con frecuencia trimestral, representa la tasa de paro de individuos menores de 25 años.

  4. Consumo eléctrico, con frecuencia horaria, representa el consumo en MW hora.

  • Estacionalidad

Es una característica que pueden tener las series recogidas con frecuencia superior al año. Está relacionada con el concepto “estación del año” y tiene que ver con que el comportamiento humano se adapta a las estaciones y, por tanto, se suele modificar. En el ejemplo anterior, la tasa de paro tiene cierto comportamiento estacional (subidas sistemáticas del paro al acabar verano y navidades), y la serie de consumo eléctrico. Sin embargo, la serie del precio de TESLA no parece tener estacionalidad (de hecho, si esto fuera así, sería más predecible el mercado de acciones, ¿no?).

Ejemplo

En esta serie de turistas mensuales se puede ver claramente la pauta estacional

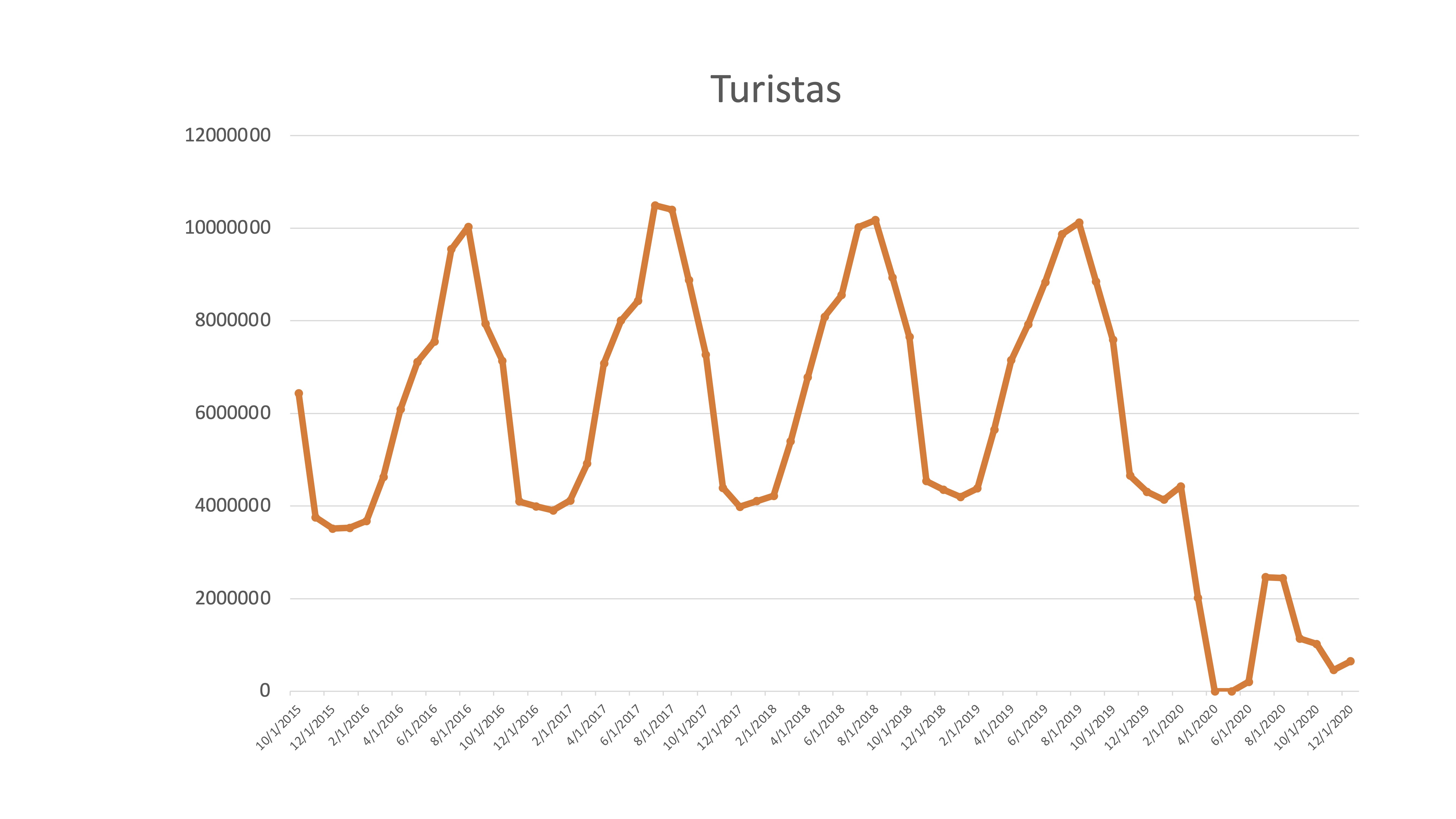
FIG 2: Serie temporal de turistas en España

que, obviamente, se ha modificado con claridad desde el mes de marzo de 2020. Hasta ese momento ¿no era una serie muy previsible? ¿Cómo predeciremos el comportamiento de la serie?

  • Estacionariedad en media

una serie temporal es estacionaria en media cuando la media es un buen “resumen” de la serie, es decir, es representativa. Una forma de ver si una serie es estacionaria en media, mediante el gráfico, es ver si las observaciones cortan o no, de manera reiterada dicha media.

Ejemplo

Dos series temporales: el número de taxis y su variación. La serie de Taxis, como vemos, tiene una tendencia creciente, por lo que la media no puede ser representativa. Note que, sin embargo, su variación (calculada como \(y_{t}-y_{t-1})\) si que parece estar razonablemente bien resumida por su media.

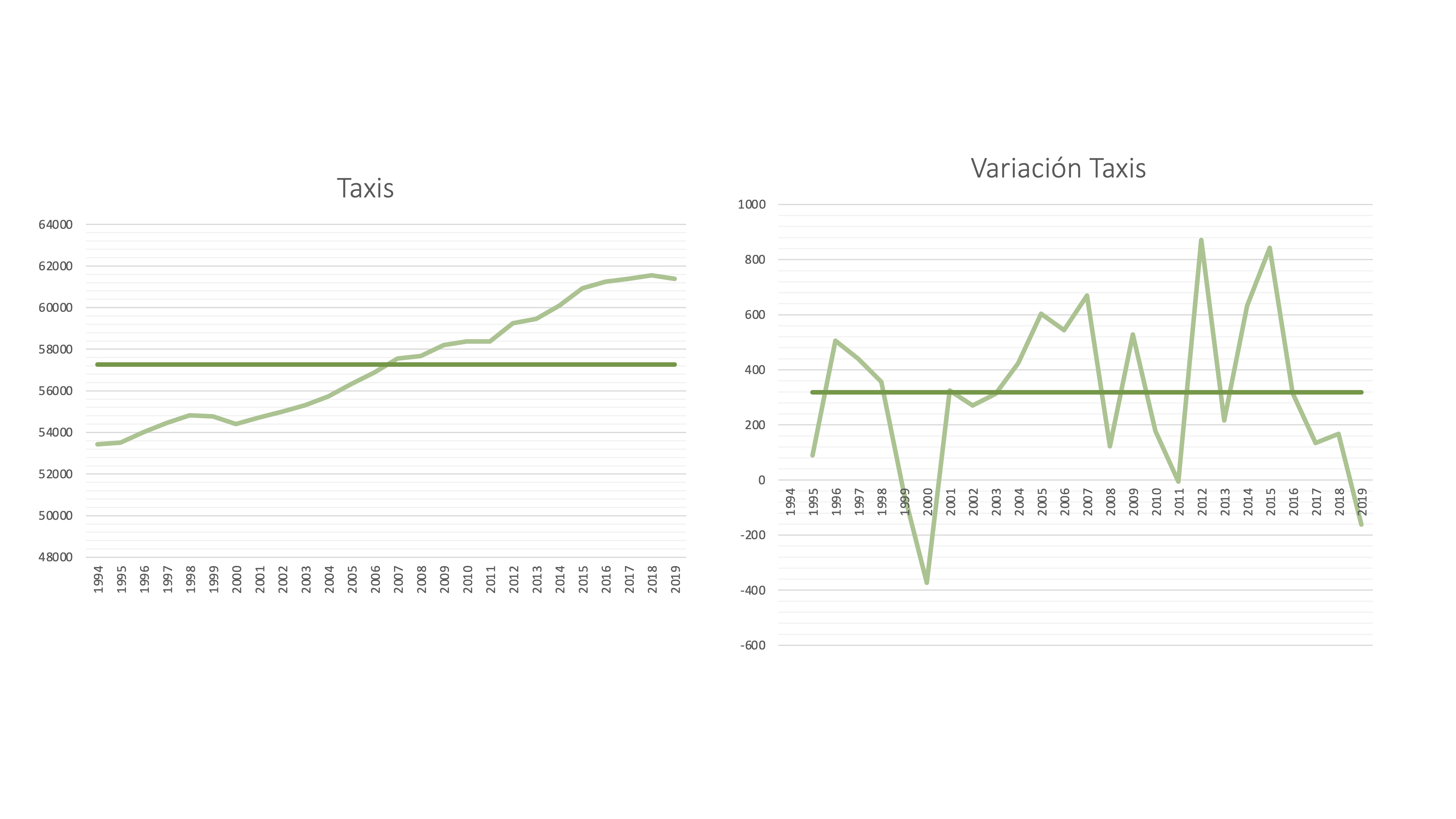
FIG 3: La serie de “taxis” en España

Nota: una serie con estacionalidad no puede ser estacionaria en media: puesto que la media en cada estación es distinta.

  • Estacionariedad en varianza

También nos interesará analizar si la varianza de la serie es razonablemente estable (estacionaria) o no. Para ello, debemos observar si la evolución de la serie está acotada, de manera aproximada, por un rango similar en todo su dominio temporal

Ejemplo

Por ejemplo, la serie de variación porcentual de stocks y de consumo eléctrico parecen tener una variabilidad constante, ya que se podría resumir con una sola “caja”. Sin embargo, la tasa de paro parece que va cambiando su fluctuación según aumentan los valores del nivel de la serie, por lo que esta no parece estacionaria en varianza.

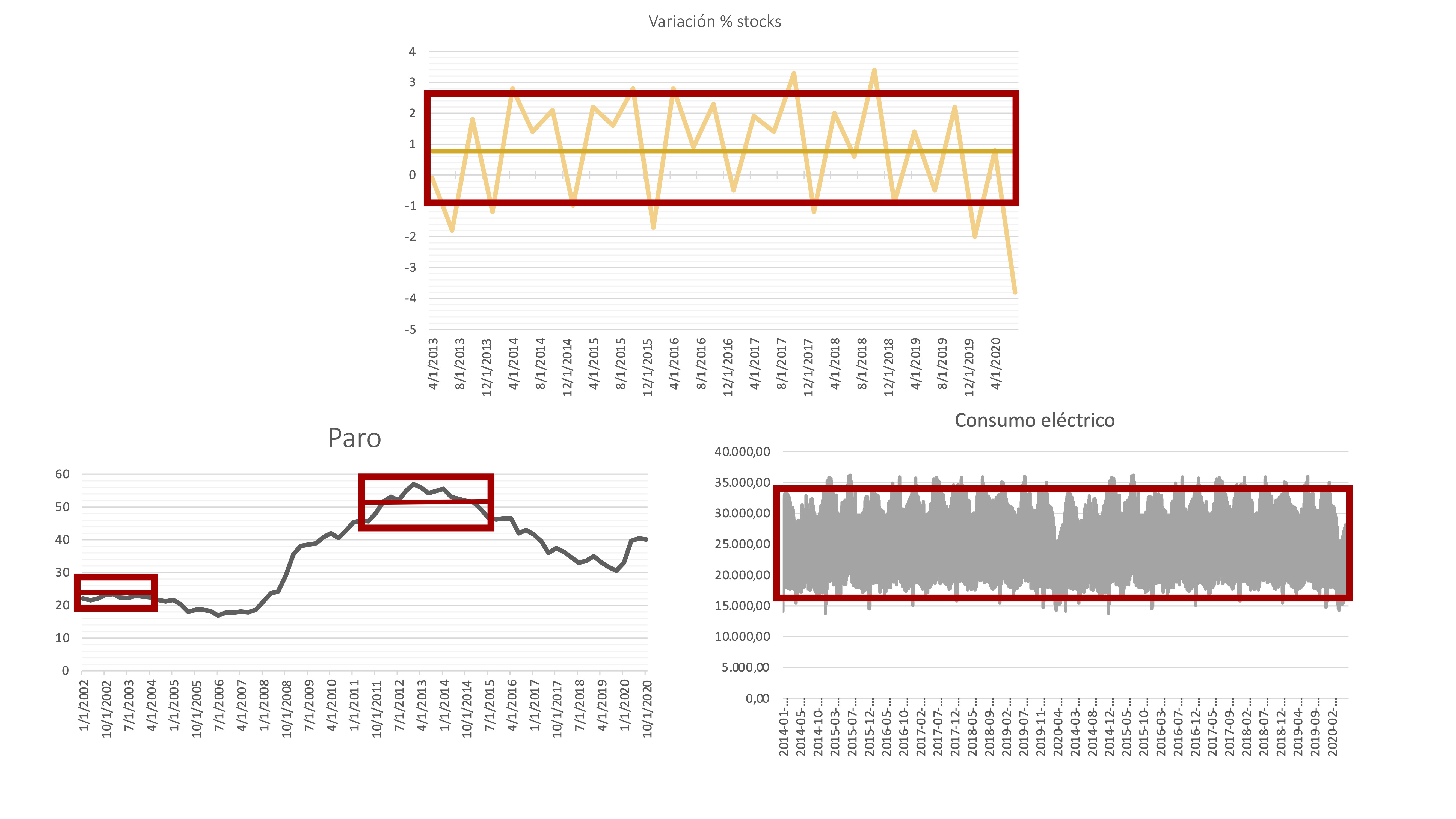
FIG 4: Aálisis temporal de la varianza

Introducción a los Procesos Estocásticos

Los modelos teóricos o poblacionales que usaremos en este capítulo proceden de la teoría de los procesos estocásticos. Un proceso estocástico puede definirse, de forma “ligera”, como una secuencia de variables aleatorias ordenadas cronológicamente. Un proceso estocástico gobernado por la variable \(x\) se escribe así \(\left\{ x_{t}\right\} _{t\geq0}\). Como a cualquier variable aleatoria, podremos calcular sus medias, varianzas, covarianzas, etc… para poder caracterizarlo.

Sin embargo, vamos empezar intuiyendo la idea de un proceso estocástico de manera visual, relacionándolo con la idea de serie temporal.

En la FIG5, mostramos la idea subyacente del proceso estocástico. Debemos imaginarnos que en cada momento temporal (\(t=\{0,1,2,....\}\)) el proceso \(\left\{ x_{t}\right\} _{t\geq0}\) está conformado por una distribución de probabilidades. Diremos que un proceso es estacionario si está conformado por aquel cuyas distribuciones de probabilidades para la variable aleatoria \(x\) no cambian para ningún \(t\). Lo contrario para un proceso no estacionario, donde las distribuciones de probabilidad pueden tener distintas medias, varianzas, kurtosis, asimetrías, etc…

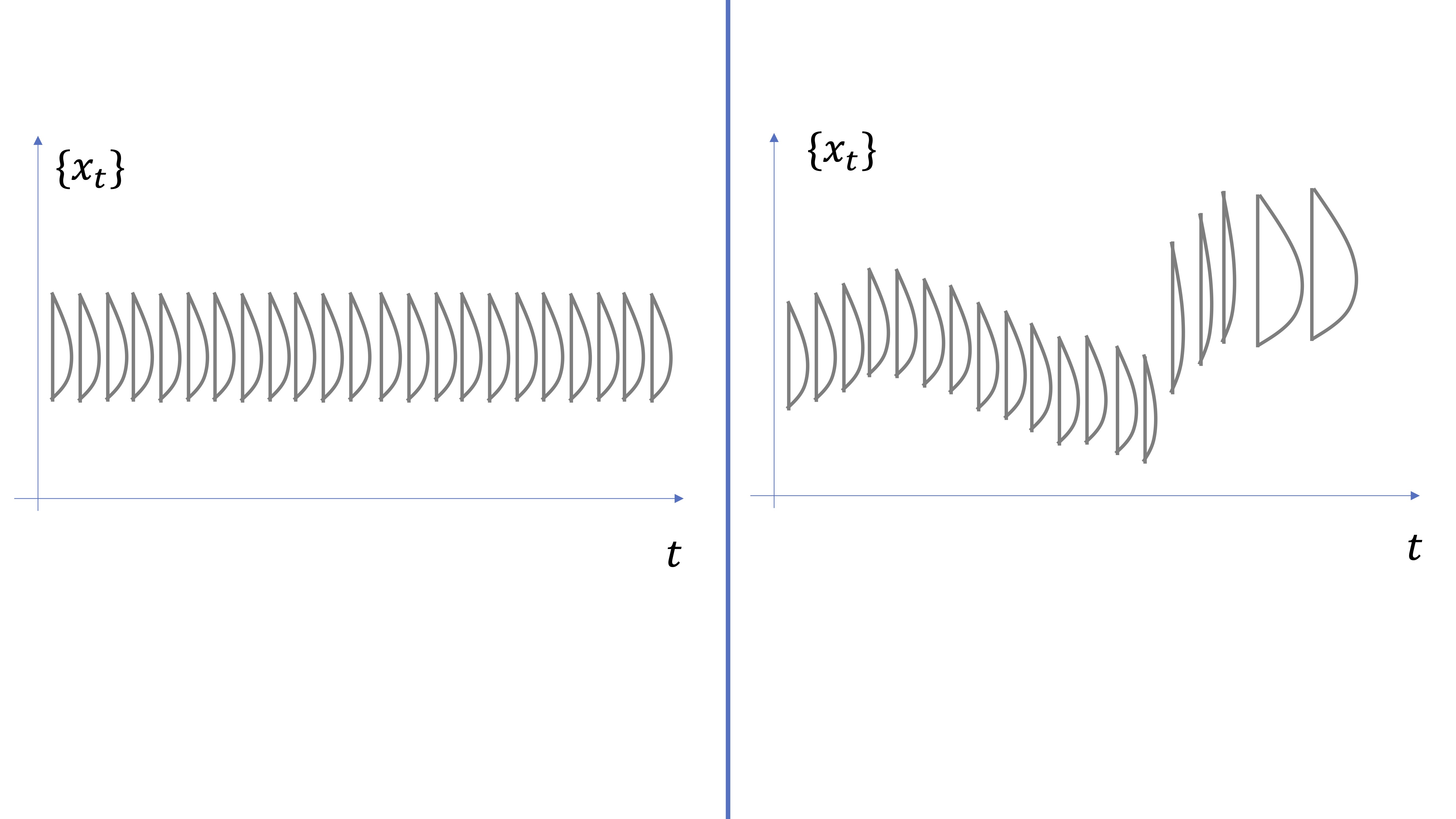
FIG 5: Idea de proceso estocástico

De hecho, podemos considerar una serie temporal (que es lo que observamos en la vida real) como una realización posible de la variable aleatoria: es decir, como si en cada momento \(t\), un ente desconocido hiciera un sorteo y decidiera el valor de la serie temporal (ver FIG6).

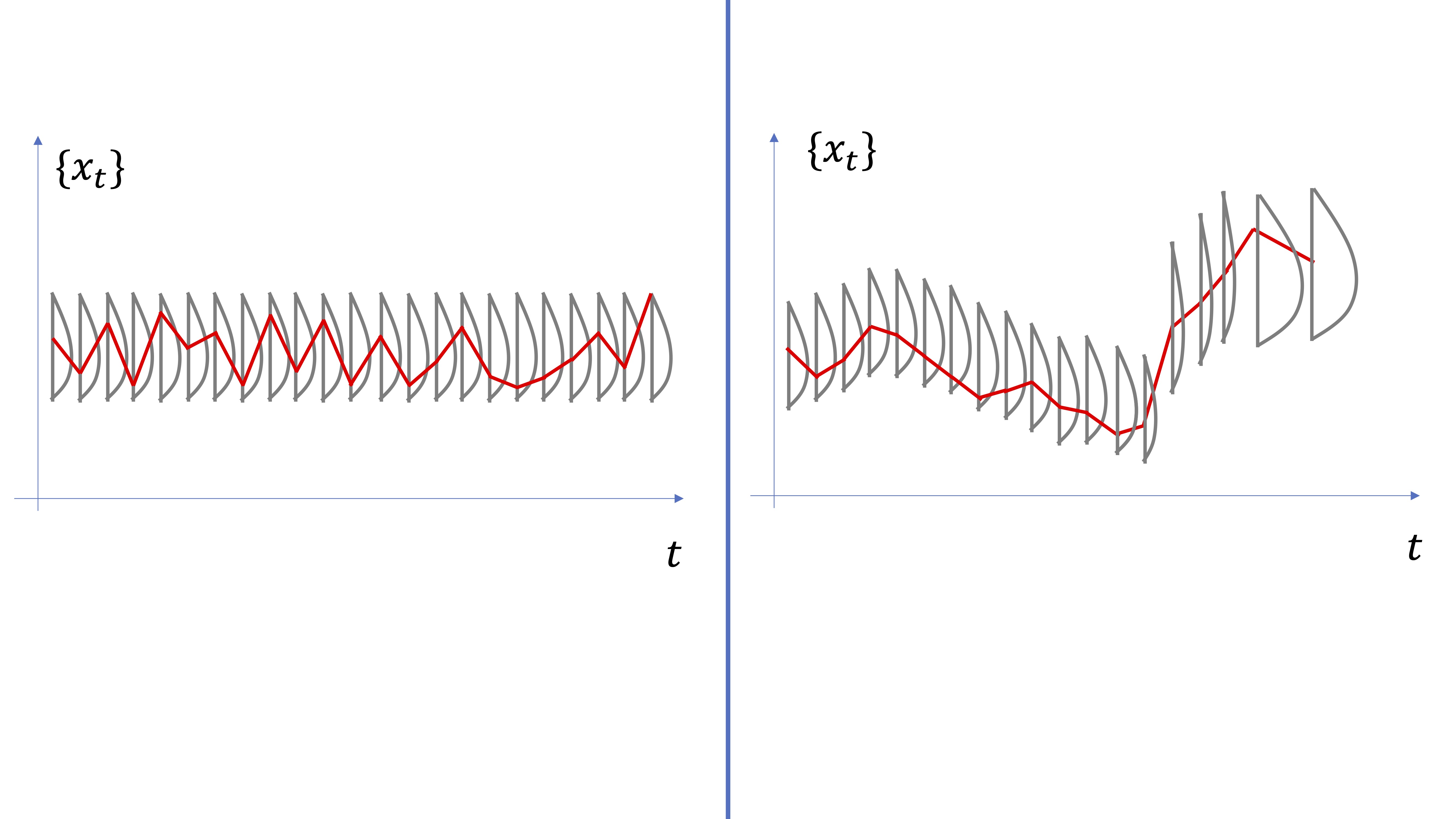
FIG 6: Una serie temporal vista como una “realización aleatoria” del proceso

Entonces, un proceso estacionario necesitará que la distribución conjunta de este permanezca invariante en el tiempo (por ejemplo, que la distribución conjunta de \(x_{t_{1}},x_{t_{2}},x_{t_{3}},...,x_{t_{n}}\) sea la misma que la de \(x_{t_{1}+h},x_{t_{2}+h},x_{t_{3}+h},...,x_{t_{n}+h}\) para cualquier \(h\neq0\). Sin embargo, es muy complicado verificar esto en la práctica (cuando sólo se tiene una serie temporal como testigo de todo el proceso). Es por ello que, en general, definiremos el concepto de estacionariedad en sentido débil, que requerirá:

  • Media y vairanza constantes
  • Autocovarianza constante

Dos procesos estocásticos muy célebres

De nuevo, vamos a usar la simulación para entender conceptos relacionados con procesos estocásticos.

Proceso 1: ruido blanco

El concepto “ruido blanco” proviene de la ingeniería y consiste en una secuencia de valores imprevisibles, equivalentes a cuando se va la televisi?n a “negro” y vemos estas secuencias aleatorias de puntos blancos y negros.

FIG 7: La idea de un ruido blanco

Llevándolo a un concepto estadístico, diremos que un ruido blanco es un proceso estocástico definido como \[ x_{t}=a_{t} \]

donde \[ a_{t}\rightarrow i.i.d(\mu,\sigma^{2}) \]

y donde \(i.i.d\) significa “independiente e idénticamente distribuido como”. E indicamos, en este caso, una media y varianza de la distribución (trabajaremos, habitualmente, con distribuciones como la Normal, que queda definida correctamente con estos dos parámetros).

Es fácil, en este caso, hacer un análisis de las propiedades teóricas del proceso. En general, estudiaremos la media, la varianza y la covarianza (esta última, en la próxima clase) Por ahora, nos centraremos en la media y varianza del proceso. Recuerde que, como estamos con variables aleatorias (es decir, un modelo poblacional) deberemos usar el operador esperanza (\(E\)) y varianza (\(V\)). Sea el proceso \[ x_{t}=a_{t} \]

con \[ a_{t}\rightarrow i.i.d(\mu=0,\sigma^{2}=2) \]

Tenemos: \[ E\left(x_{t}\right)=E(a_{t})=0 \]

\[ V\left(x_{t}\right)=V(a_{t})=2 \]

Proceso 2: paseo aleatorio

El paseo aleatorio está ampliamente documentado en la literatura estadística.

Lo definiremos como \[ x_{t}=x_{t-1}+a_{t} \]

donde \[ a_{t}\rightarrow i.i.d(\mu,\sigma^{2}) \]

Como puede observar, es un proceso con “inercia” y “persistencia”: el valor en el momento \(t\) depende del valor en el momento \(t-1\) más un ruido blanco.

y, además, podemos analizar sus propiedades teóricas.

Sea el proceso \[ x_{t}=x_{t-1}+a_{t} \]

con \[ a_{t}\rightarrow i.i.d(\mu=0,\sigma^{2}=2) \]

Para calcular la esperanza y la varianza es conveniente escribirlo en función de las \(a\):

\[ x_{1}=x_{0}+a_{1}\Rightarrow x_{1}=a_{1} \]

\[ x_{2}=x_{1}+a_{2}\Rightarrow x_{2}=a_{1}+a_{2} \]

\[ x_{3}=x_{2}+a_{3}\Rightarrow x_{3}=a_{1}+a_{2}+a_{3} \]

de manera general, \[ x_{T}=a_{1}+a_{2}+...+a_{T} \]

Tenemos, por tanto, \[ E\left(x_{t}\right)=E(a_{1}+a_{2}+...+a_{t})=0 \]

\[ V\left(x_{t}\right)=V(a_{1}+a_{2}+...+a_{t})=V(a_{1})+V(a_{2})+...+V(a_{t}) \]

donde hemos usado que la varianza de una suma es la suma de las varianzas si las variables son \(i.i.d\) (y las \(a_{t}\) lo son)

\[ V\left(x_{t}\right)=t\sigma^{2}=2t \]

que, como ve, encaja con lo que hemos obtenido en los histogramas.

Clase 2: La función de autocovarianzas

Ejercicios

  • Simule en R un ruido blanco

Simule en R un proceso estocástico “ruido blanco”. Para ello, calcule 300 realizaciones de este con tamaño muestral 200. Diremos, además, que \[ a_{t}\rightarrow i.i.d(\mu=0,\sigma^{2}=2) \] \[ x_{0}=0 \]

N=200
M=300

X=matrix( rnorm(N*M,mean=0,sd=1), N, M)

Al ejecutar ts.plot(x), tendremos una imagen del proceso estocástico:

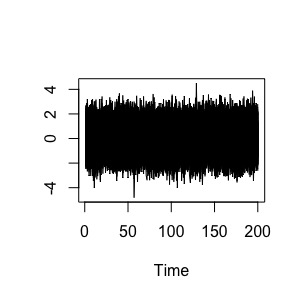
FIG 1: Un ruido blanco “simulado”

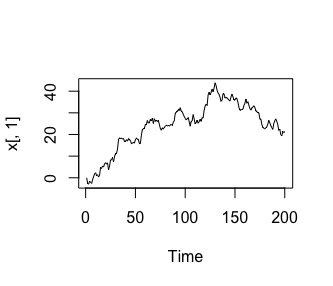
son las 300 series temporales de longitud “200 momentos temporales” apiladas. Una de esas 300 series temporales, sería esta:

ts.plot(X[,1])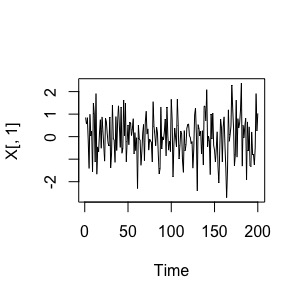

FIG 2: Una realización posible del proceso estocástico “ruido blanco”

esto (FIG9) es lo que se llama una serie temporal procedente de un proceso de ruido blanco. Como verá, puede inferir claramente la estacionariedad en media y varianza que, se como se especificó teóricamente, tiene el proceso teórico

puede comprobar, de hecho, que los histogramas de la distribución del proceso tienen esta media y varianza en cualquier momento de este:

par(mfrow=c(2, 2))
hist(X[1,], 
     main="Histograma del proceso en t=1", 
     border="blue", 
     col="green",
     xlim=c(-3,3),
     las=1, 
     breaks=5)
hist(X[15,], 
     main="Histograma del proceso en t=15", 
     border="blue", 
     col="red",
     xlim=c(-3,3),
     las=1, 
     breaks=5)

hist(X[50,], 
     main="Histograma del proceso en t=50", 
     border="blue", 
     col="yellow",
     xlim=c(-3,3),
     las=1, 
     breaks=5)

hist(X[200,], 
     main="Histograma del proceso en t=200", 
     border="blue", 
     col="purple",
     xlim=c(-3,3),
     las=1, 
     breaks=5)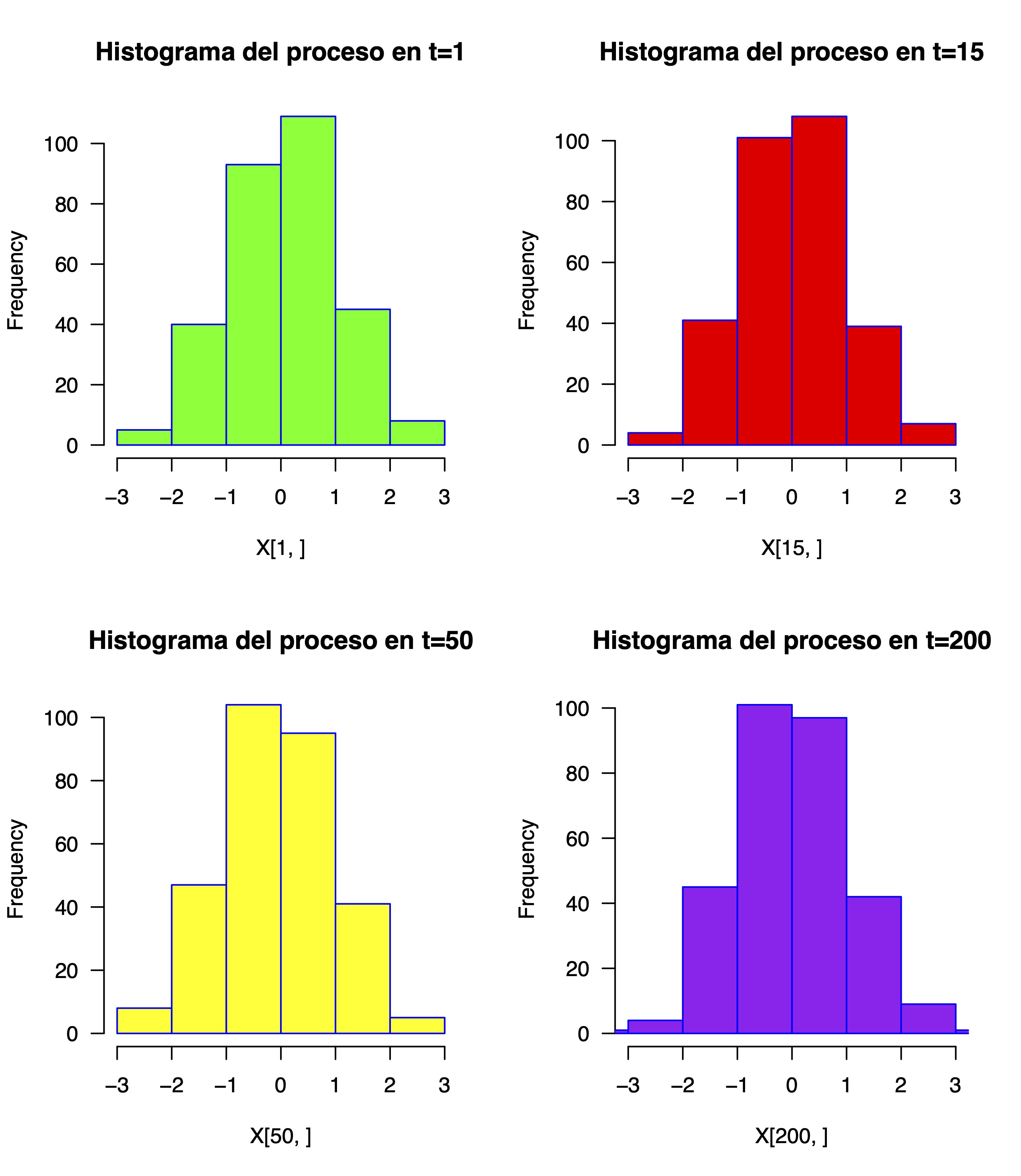

FIG 3: distribuciones a lo largo del tiempo del “ruido blanco”

  • Simule, en R, un paseo aleatorio

Simule en R un proceso estocástico “paseo aleatorio”. Para ello, calcule 300 realizaciones de este con tamaño muestral 200. Diremos, además, que \[ a_{t}\rightarrow i.i.d(\mu=0,\sigma^{2}=2) \] \[ x_{0}=0 \]

x<-matrix(0 , 200,300)
for (i in 1:199){
  for (j in 1:300){ 
    x[i+1,j]<-x[i,j]+rnorm(1,mean=0,sd=sqrt(2))
    }}

Al ejecutar ts.plot(x), tendrá una imagen del proceso estocástico que ha simulado:

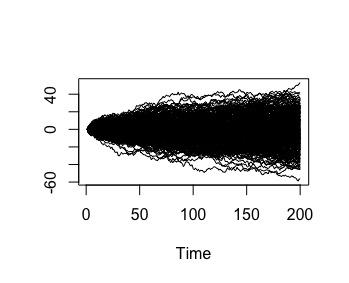FIG 4: El proceso estocástico “paseo aleatorio” simulado son las 300 series temporales de longitud 200 momentos apiladas. Una de esas 300 series temporales, sería esta:

FIG 12: Una realización posible del proceso estocástico “paseo aleatorio” que, como vemos, podemos inferir claramente la NO estacionariedad en media y en varianza (si usa las ideas que vimos anteriormente). Aunque, cómo no, quizás no lo vea o le cueste. De nuevo, puede ver los histogramas en diferentes momentos del tiempo

par(mfrow=c(2, 2))
hist(x[2,], 
     main="Histograma del proceso en t=2", 
     border="blue", 
     col="green",
     xlim=c(-10,10),
     las=1, 
     breaks=50)
hist(x[15,], 
     main="Histograma del proceso en t=15", 
     border="blue", 
     col="red",
     xlim=c(-10,10),
     las=1, 
     breaks=50)

hist(x[50,], 
     main="Histograma del proceso en t=50", 
     border="blue", 
     col="yellow",
     xlim=c(-50,50),
     las=1, 
     breaks=50)

hist(x[200,], 
     main="Histograma del proceso en t=200", 
     border="blue", 
     col="purple",
     xlim=c(-50,50),
     las=1, 
     breaks=50)

que da lugar a la FIG13

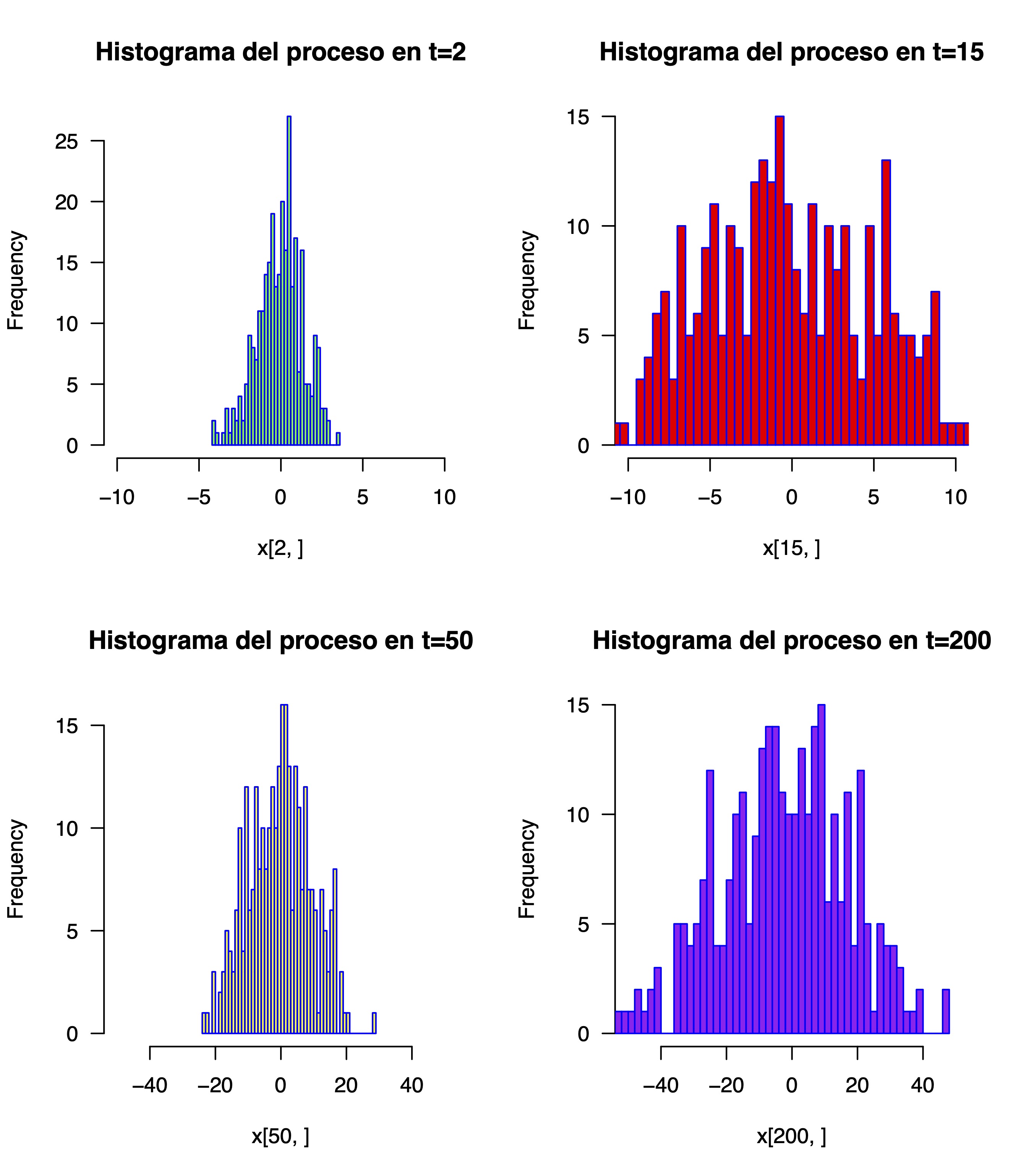
FIG 5: diferentes histogramas del proceso estocástico “paseo aleatorio”

Importante

Una de las ideas del análisis de series temporales es tratar de reconocer el proceso estocástico que está detrás de los datos mediante la observación de las características de la serie temporal.

La función de autocovarianzas

Una forma de analizar cómo influye el pasado de un proceso estocástico sobre el momento \(t\) es a través de la función de “auto”covarianzas.

Recuerde

Sean dos variables aleatorias, \(X,Y\), su covarianza mide el tipo de relación lineal entre estas. \[ cov(X,Y)=E\left[X-E\left(X\right)\right]\left[Y-E\left(Y\right)\right] \]

y esta cantidad puede ser :

  • 0, si no tienen relación lineal (lo que no implica que no tengan otro tipo de relación)

  • 0, si esta relación es positiva

  • <0 si es negativa.

Además, recuerde la propiedad de la linealidad:

\[ cov(aX,bY)=ab\times cov(X,Y) \]

Finalmente, note que además \[ cov(X,X)=E\left[X-E\left(X\right)\right]\left[X-E\left(X\right)\right]=var(X) \]

Por otro lado, si queremos medir el grado de relación lineal debemos emplear la correlación entre variables. Esta se obtiene a través de la covarianza y se suele denotar por \(\rho\) (que se lee “rho”):

\[ \rho(X,Y)=\frac{cov(X,Y)}{DT(X)DT(Y)}, \] que está acotada \(-1\leq\rho\leq1\). Nota que, por tanto, \[ \rho(X,X)=\frac{cov(X,X)}{DT(X)DT(X)}=\frac{var(X)}{var(X)}=1. \]

En el caso que nos ocupa, definiremos la función de “autocovarianza”. Esta mide el grado de relación lineal de un proceso con su pasado/futuro. Diremos que es la función (que denotaremos por \(\gamma\)) tal que \[ \gamma(x_{t},x_{t-k})=\gamma_{k}=cov(x_{t},x_{t-k}) \]

La varianza del proceso, por tanto, vendrá dada por \[ \gamma(x_{t},x_{t})=\gamma_{0}=cov(x_{t},x_{t}) \] y, de la misma manera que antes, denominaremos la autocorrelación como \[ \rho(x_{t},x_{t-k})=\rho_{k}=\frac{\gamma(x_{t},x_{t-k})}{\sqrt{\gamma(x_{t},x_{t})\gamma(x_{t-k},x_{t-k})}} \]

y, de nuevo, estará acotada entre -1 y 1.

Un proceso estocástico es “debilmente” estacionario si, además de la estacionariedad en media y varianza lo es en autocovarianza. Para ser estacionario en autocovarianza, esta no debe depender de \(t\), sino de \(k\). Enseguida vemos cómo el paseo aleatorio no es estacionario en autocovarianza.

Vamos a explorar la autocovarianza de los dos procesos con los que hemos trabajado hasta ahora. Para entender bien esta función, primero vamos a explorarla en los procesos simulados para, posteriormente, obtenerla de forma analítica.

La autocovarianza en el ruido blanco

Si recordamos la definición de “ruido blanco”, este proceso se dice que es independiente e idénticamente distribuido. Esto quiere decir que no seremos capaces de predecir lo que va a ocurrir con el proceso por la mera observación de este en el pasado. Para que lo recuerde:

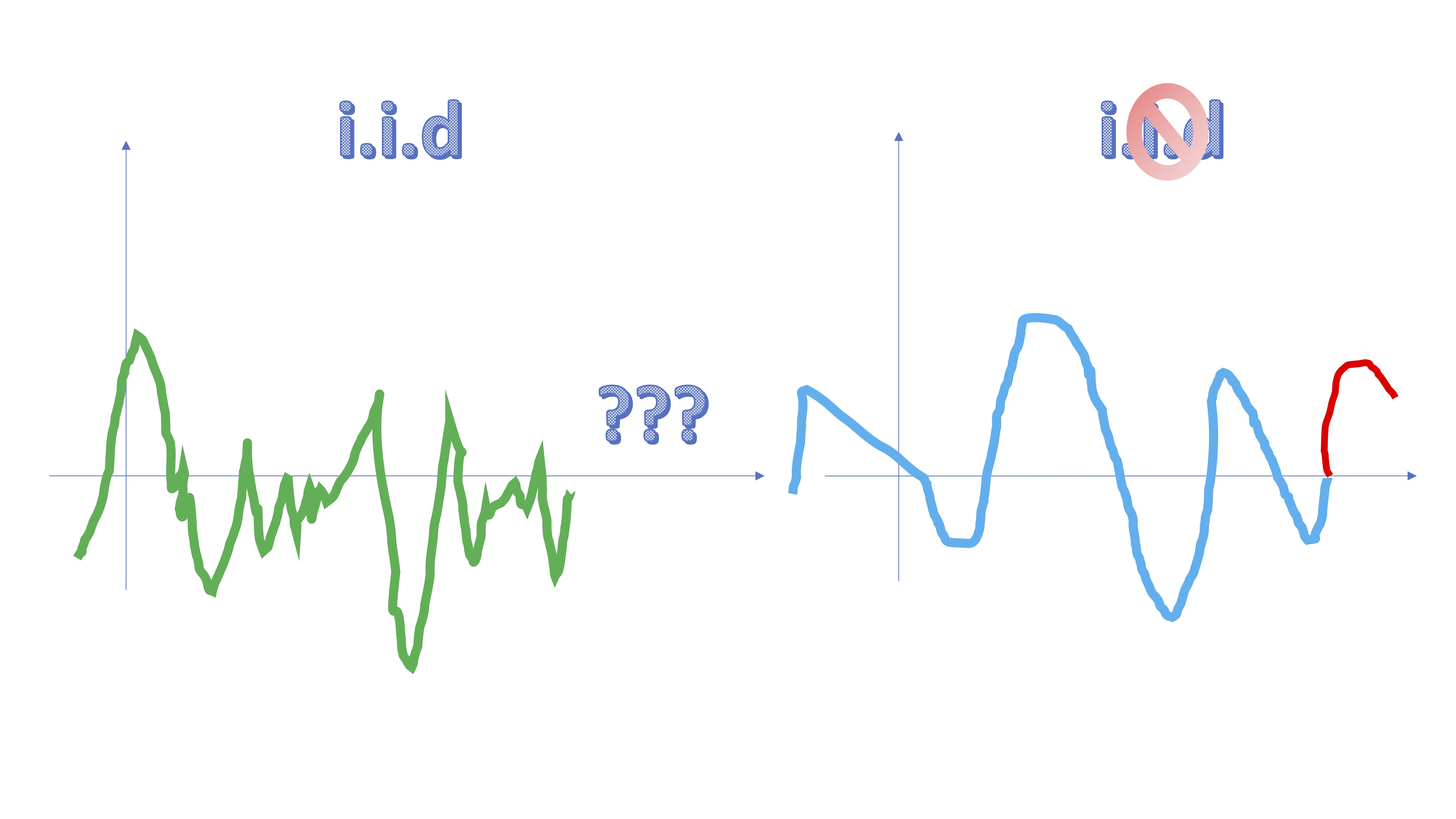FIG 6: Proceso i.i.d versus otro no i.i.d como ve, en la gráfica verde es difícil saber qué ocurrirá con está en el futuro. En la azul, parece más probable aventurarse a decir algo.

De esta forma, esperamos que de un ruido blanco, al ser i.i.d, tengamos

\[ \gamma(y_{t},y_{t-k})=0 \]

para todo \(t\),y todo \(k\).

  • Función de autocovarianzas de un ruido blanco

Nuestro modelo es \[ y_{t}=a_{t} \] \[ a_{t}\rightarrow i.i.d(\mu=0,\sigma^{2}) \]

entonces, \[ \gamma_{1}=cov(y_{t},y_{t-1})=cov(a_{t},a_{t-1})=0 \] (por ser i.i.d).

Como verá, para cualquier valor de \(k\) obtendrá lo mismo. La función de autocorrelación podremos obtenerla, con una muestra de datos,en R mediante el comando \(acf(x)\). En este caso,

\[ \rho_{0}=1 \]

\[ \rho_{k}=0,k>1. \]

(para nosotros será “0” si el palo está dentro de las bandas azules obtenidas por R).

N=100
y=rnorm(N,mean=0,sd=1)
acf(y)

la cual resulta ser la de la FIG7

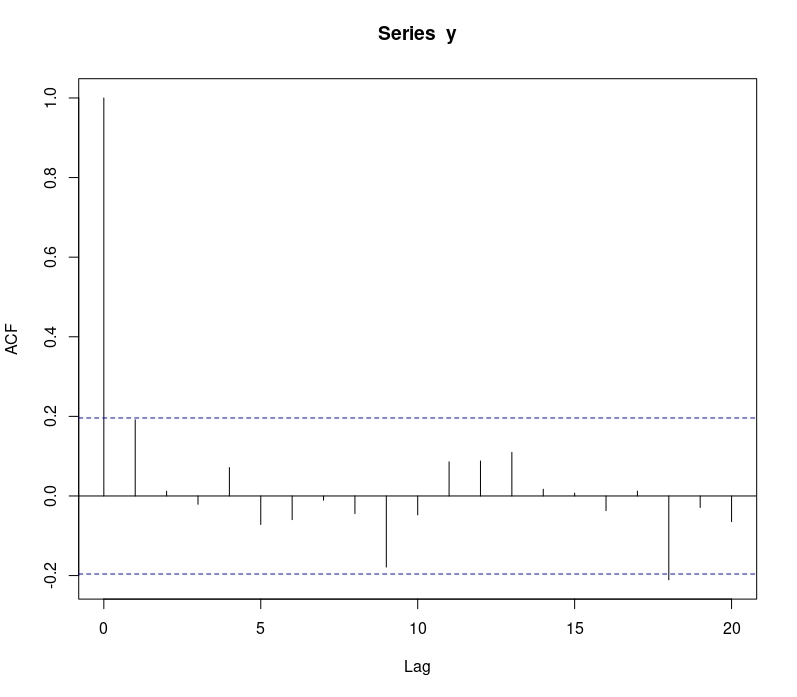
FIG 7: ACF de un ruido blanco

el “lag” 0 se corresponde con la correlación del proceso con él mismo a tiempo \(t\), por lo que debe ser 1. El resto de correlaciones se corresponden con la relación del proceso a tiempo \(t\) frente a tiempo \(t-1\),\(t-2\),… como ya sabemos teóricamente, estas correlaciones deben ser cero. Numéricamente lo serán al estar dentro de las bandas azules.

La autocovarianza del paseo aleatorio

Por otro lado, analicemos la del paseo aleatorio de la misma manera que hemos hecho con el ruido blanco. Nuestro modelo es \[ x_{t}=x_{t-1}+a_{t} \] \[ a_{t}\rightarrow i.i.d(\mu=0,\sigma^{2}) \]

entonces, podemos escribir el proceso como (mira la clase 2) \[ x_{t}=a_{1}+a_{2}+...+a_{t} \]

de tal forma que \[ x_{t-k}=a_{1}+a_{2}+...+a_{t-k} \] y, por tanto,

\[ \gamma_{1}=cov(y_{t},y_{t-1})=cov(a_{1}+a_{2}+...+a_{t-1}+ \color{red}{a_{t}},a_{1}+a_{2}+...+a_{t-1})=(t-1)\sigma^{2} \]

Nota que este resultado sale de que \(cov(a_{1},a_{1})=cov(a_{2},a_{2})=....=cov(a_{t-1},a_{t-1})=\sigma^{2}\). Asimismo:

\[ \gamma_{2}=cov(y_{t},y_{t-2})=cov(a_{1}+a_{2}+...+a_{t-2}+ a_{t-1}+ a_{t},a_{1}+a_{2}+...+a_{t-2})=(t-2)\sigma^{2} \]

por lo que, de manera general,

\[ \gamma_{k}=cov(y_{t},y_{t-k})=(t-k)\sigma^{2} \]

La autocorrelación será, en este caso, \[ \rho_{k}=\frac{\gamma_{k}}{DT(y_{t})DT(y_{t-k})}=\frac{(t-k)\sigma^{2}}{\sqrt{t\sigma^{2}(t-k)\sigma^{2}}}=\frac{t-k}{\sqrt{t(t-k)}}, \]

como ve, no es estacionaria porque depende del tiempo \(t\), no solo de \(k\). Para ver cómo es la ACF que nos proporciona R de un proceso ruido blanco, podemos generarlo y calcularla

z<-matrix(0 , 200)
for (i in 1:199){
    z[i+1]<-z[i]+rnorm(1,mean=0,sd=sqrt(2))
    }

acf(z)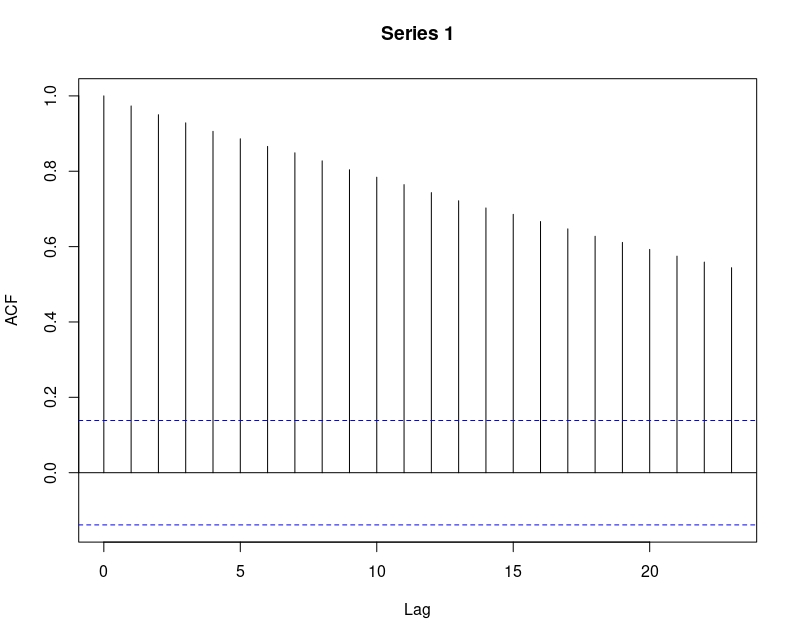

FIG 8: ACF de un paseo aleatorio este es diametralmente opuesto al anterior. Como ve, la inercia temporal es muy grande. El pasado más lejano influye mucho sobre el momento \(t\). En general, los procesos que tengan una ACF de este estilo (con mucha persistencia temporal), diremos que son no estacionarios.

Clase 3: el proceso AR(1)

Un conjunto de procesos estocásticos famosos, que nos serán de gran utilidad para predecir series temporales son los modelos ARMA. En esencia, un modelo ARMA(p,q) consiste en lo siguiente:

\[ y_{t}=c+\underset{AR(p)}{\underbrace{\phi_{1}y_{t-1}+\phi_{2}y_{t-2}+...+\phi_{p}y_{t-p}}+}\underset{MA(q)}{\underbrace{\epsilon_{t}+\theta_{1}\epsilon_{t-1}+\theta_{2}\epsilon_{t-2}+...+\theta_{q}\epsilon_{t-q}}} \]

donde \(c\) es una constante, \(\phi_{i}\),\(i=1,...,p\) (se lee “phi”) son los parámetros que miden el impacto de los retardos de la variable \(y_{t}\) sobre esta. Por eso se llama “autorregresivo”: la propia serie (auto) en el pasado explica a la serie hoy (regresivo). Por otro lado, tenemos \(\epsilon_{t},\epsilon_{t-1},...\) que son términos ruido blanco. Esta parte, como vemos, indica que los errores cometidos en el pasado tratando de predecir \(y_{t}\) pueden ayudar a predecir el futuro. Vamos ahora a trabajar con una versión restringida de este modelo: el famoso AR(1)

  • Características del AR(1)

Definiendo el modelo AR(1) como

\[ y_{t}=c+\phi_{1}y_{t-1}+\epsilon_{t}, \]

donde \(\epsilon_{t}\rightarrow i.i.d(0,\sigma^{2})\). Vamos a deducir ahora la media, varianza y autocovarianza. De esta forma, podremos entender cuándo este proceso es estacionario (en sentido débil).

Media del AR(1)

Utilizaremos el operador esperanza

\[ E(y_{t})=E(c+\phi_{1}y_{t-1}+\epsilon_{t}) \]

y la propiedad de que la esperanza de una suma es la suma de las esperanzas \[ E(y_{t})=E(c)+\phi_{1}E(y_{t-1})+E(\epsilon_{t}), \]

donde:

  • La esperanza de una constante es ella misma \(E(c)=c\)
  • Los parámetros salen fuera del operador esperanza multiplicando \(E(\phi_{1}y_{t-1})=\phi_{1}E(y_{t-1})\)
  • La esperanza de \(\epsilon_{t}\) es cero por hipótesis \(E(\epsilon_{t})=0\)

Entonces, llegamos a que

\[ E(y_{t})=c+\phi_{1}E(y_{t-1}) \]

Como queremos que el proceso sea estacionario en media, debemos imponer que esta sea constante para cualquier \(t\), por lo que

\[ \mu=c+\phi_{1}\mu\Rightarrow\mu=\frac{c}{1-\phi_{1}} \]

Como podemos deducir enseguida, necesitamos que el parámetro \(\phi_{1}\neq1\). Si no, la media no tendríaa sentido. Además, fíjese que si \(\phi_{1}=1,\) estamos ante un paseo aleatorio (que es no estacionario). Definamos ahora la varianza

Varianza de un AR(1)

Utilizaremos el operador varianza

\[ V(y_{t})=V(c+\phi_{1}y_{t-1}+\epsilon_{t}) \]

donde la varianza de la suma no es, en general, la suma de las varianzas. Aunque si las variables aleatorias son independientes, entonces sí: como es el caso \[ V(y_{t})=V(c)+\phi_{1}^{2}V(y_{t-1})+V(\epsilon_{t}), \]

donde:

  • La varianza de una constante es cero \(V(c)=0\)
  • Los parámetros salen fuera del operador varianza multiplicando al cuadrado \(V(\phi_{1}y_{t-1})=\phi_{1}^{2}V(y_{t-1})\)
  • La varianza de \(\epsilon_{t}\) es \(\sigma^{2}\) por hipótesis \(V(\epsilon_{t})=\sigma^{2}\)

Entonces, llegamos a que \[ V(y_{t})=\phi_{1}^{2}V(y_{t-1})+\sigma^{2} \]

Como queremos que el proceso sea estacionario en varianza, debemos imponer que esta sea constante para cualquier \(t\), por lo que \[ \gamma_{0}=\phi_{1}^{2}\gamma_{0}+\sigma^{2}\Rightarrow\gamma_{0}=\frac{\sigma^{2}}{1-\phi_{1}^{2}} \]

donde observe que hemos puesto \(\gamma_{0}=V(y_{t})=V(y_{t-1})=...\)

De aquí ya podemos sacar una condición para que el proceso sea estacionario en media y varianza (tomando, por supuesto, el criterio más restrictivo). Si habíamos visto que, en el caso de la media, debíamos tener \(\phi_{1}\neq1\), en el caso de la varianza, nos sugiere que \(\left|\phi_{1}\right|<1\). Esta, entonces, será la condición de estacionariedad en media y varianza del proceso.

Finalmente, debemos obtener la función de autocovarianzas/autocorrelación. Para ello, iteraremos para ciertos valores de \(k\)

k=1

\[ \gamma_{1}=cov(y_{t},y_{t-1})=cov(\phi_{1}y_{t-1}+\epsilon_{t},y_{t-1})=\phi_{1}\gamma_{0} \]

de donde hemos utilizado:

  • \(cov(y_{t-1},y_{t-1})=var(y_{t-1})=\gamma_{0}\) por estacionario.
  • \(cov(\epsilon_{t},y_{t-1})=0\) no puedo predecir un error en el futuro (\(\epsilon_{t})\) con la informaci?n que tenemos en \(t-1\) \end{enumerate}

k=2

\[ \gamma_{2}=cov(y_{t},y_{t-2})=cov(\phi_{1}y_{t-1}+\epsilon_{t},y_{t-2})=\phi_{1}\gamma_{1}=\phi_{1}^{2}\gamma_{0} \]

donde hemos usado que

  • \(cov(y_{t-1},y_{t-2})=\gamma_{1}\) ya que entre \(t-1\)y \(t-2\) hay un periodo de desfase y, como es estacionario, da igual en qué momento se produzca.
  • De la ecuación anterior, ya teníamos que \(\gamma_{1}=\phi\gamma_{0}\) y se lo enchufamos.

Es fácil ver que, en general, en un AR(1), tenemos que \[ \gamma_{k}=\phi_{1}^{k}\gamma_{0},k=1,2,... \]

Finalmente, la autocorrelación puede calcularse de manera muy sencilla, dividiendo por la varianza del proceso: \[ \rho_{1}=\gamma_{1}/\gamma_{0}=\phi_{1}\gamma_{0}/\gamma_{0}=\phi_{1} \]

\[ \rho_{2}=\gamma_{2}/\gamma_{0}=\phi_{1}^{2}\gamma_{0}/\gamma_{0}=\phi_{1}^{2} \]

Es fácil ver que, para cualquier \(k\), tendremos

\[ \rho_{k}=\phi_{1}^{k},k=1,2,... \]

Entonces,

un proceso AR(1) se caracteriza por una función ACF en decaimiento exponencial (claro, como }}\(\left|\phi_{1}\right|<1\), la ACF decaerá rápidamente hacia cero).

Vamos ahora a simular en R un proceso AR(1) para comprobar las características de las que hablamos. Para ello, simulemos, por ejemplo:

\[ y_{t}=5+0.75y_{t-1}+\epsilon_{t} \]

donde \(\epsilon_{t}\rightarrow i.i.d(0,\sigma^{2}=3).\) Hagamos, además, que \(y_{0}=0\). Puede adaptar el script de simulación del paseo aleatorio.

 z<-matrix(0 , 200)
for (i in 1:199){
      z[i+1]<-5+0.75*z[i]+rnorm(1,mean=0,sd=3)
}
 
 ts.plot(z)
 acf(z)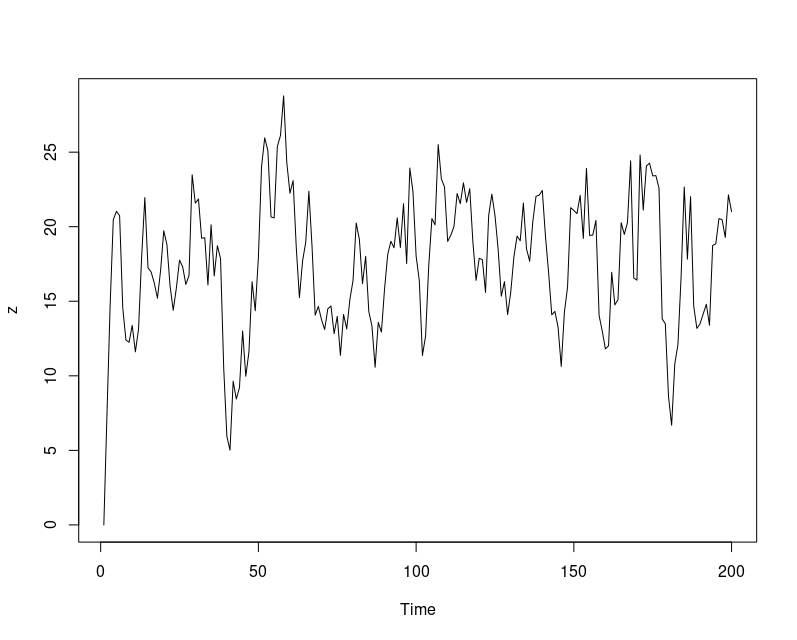

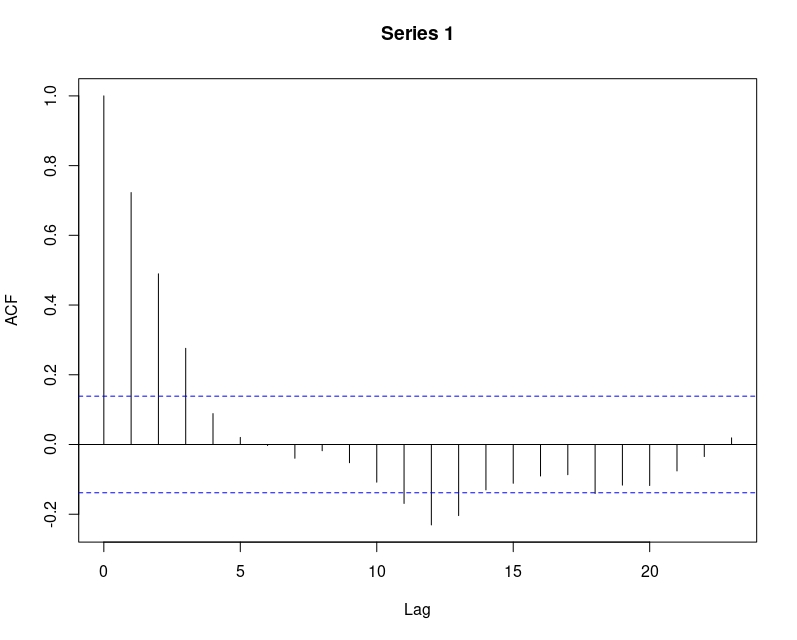
FIG 1: Serie Temporal de un AR(1) FIG 2: ACF de un AR(1)

Como se puede ver, en la gráfica temporal (FIG1), esta parece estarionaria en media (la cual es, atendiendo al modelo \(\mu=\frac{5}{0.25}=20\). Puede comprobar que si ejecuta en R: mean(z) obtendrá un resultado cercano a 20. La varianza también parece razonablemente constante y, además, la ACF (FIG2) tiene un decaimiento rápido desde 0.75 (aproximadamente, cuando Lag=1) hasta cero al cuarto retardo.

Entonces,

Se puede probar que, en general, cualquier modelo AR(p) se identifica por tener una ACF con decaimiento exponencial rápido.

Ejercicio

Simule otros modelos AR y obtenga las ACF

\[ y_{t}=5+0.75y_{t-1}-0.35y_{t-2}+\epsilon_{t} \]

\[ y_{t}=5+0.25y_{t-1}-0.35y_{t-2}+0.15y_{t-3}+\epsilon_{t} \]

Clase 4: el proceso MA(1)

Volvemos a los procesos ARMA para fijarnos en el MA(1)

\[ y_{t}=c+\epsilon_{t}+\theta\epsilon_{t-1} \]

De nuevo, calculamos la esperanza y varianza del proceso (usando la misma lógica que en la clase 3):

  • La esperanza

\[ E(y_{t})=E(c+\epsilon_{t}+\theta\epsilon_{t-1})=c \]

  • la varianza:

\[ V(y_{t})=V\left(c+\epsilon_{t}+\theta\epsilon_{t-1}\right)=\sigma^{2}+\theta^{2}\sigma^{2}=(1+\theta^{2})\sigma^{2} \]

No necesita condiciones para ser estacionario (recuerde: en media y varianza), como podemos ver directamente en la expresión obtenida.

Se ve claro:

Un MA es estacionario por construccion ¡Es la suma de procesos que son estacionarios!

Calculemos ahora la función de autocorrelación. Primero, a través de la función de autocovarianzas

\[ \gamma_{1}=cov(y_{t},y_{t-1})=cov(c+\epsilon_{t}+{\theta\epsilon_{t-1}},c+\epsilon_{t-1}+\theta\epsilon_{t-2})=\theta\sigma^{2} \] Observe que, sin embargo,

\[ \gamma_{2}=cov(y_{t},y_{t-2})=cov(c+\epsilon_{t}+\theta\epsilon_{t-1},c+\epsilon_{t-2}+\theta\epsilon_{t-3})=0 \]

y podemos deducir, entonces, que \[ \gamma_{k}\begin{cases} \theta\sigma^{2} & k=1\\ 0 & k>1 \end{cases} \]

Esto nos lleva a la ACF

\[ \rho_{k}\begin{cases} \frac{\theta\sigma^{2}}{(1+\theta^{2})\sigma^{2}}=\frac{\theta}{(1+\theta^{2})} & k=1\\ 0 & k>1 \end{cases} \]

clave:

ya puede diferenciar un proceso AR de un MA usando la ACF:

  • El AR va a tener un decaimiento rápido (exponencial)
  • El MA tendrá tantos valores fuera de bandas como su orden. En este caso, 1.

recuerde que la expresión “fuera de bandas” indica que el coeficiente se considera lo suficientemente grande como para ser tenido en cuenta.

Clase 5: aprendizajes sobre modelos ARMA

Primero, empiece con este ejercicio, donde simulará los siguientes procesos, y se hará con una idea de qué pinta tienen las ACF y PACF de los procesos más relevantes

  • \(y_t=5+0.3y_{t-1}+\epsilon_{t}\)
  • \(y_t=5+\epsilon_{t}-0.8\epsilon_{t-1}\)
  • \(y_t=5+0.7y_{t-1}-0.4y_{t-2}+0.5y_{t-3}+\epsilon_{t}\)
  • \(y_t=5+\epsilon_{t}-0.8\epsilon_{t-1}+0.5\epsilon_{t-2}-0.25\epsilon{t-3}\)
  • \(y_t=5+0.95y_{t-1}+\epsilon_{t}-0.8\epsilon_{t-1}\)

¿cómo clasificaría este último modelo?

En realidad, tiene que haberse dado cuenta de lo siguiente:

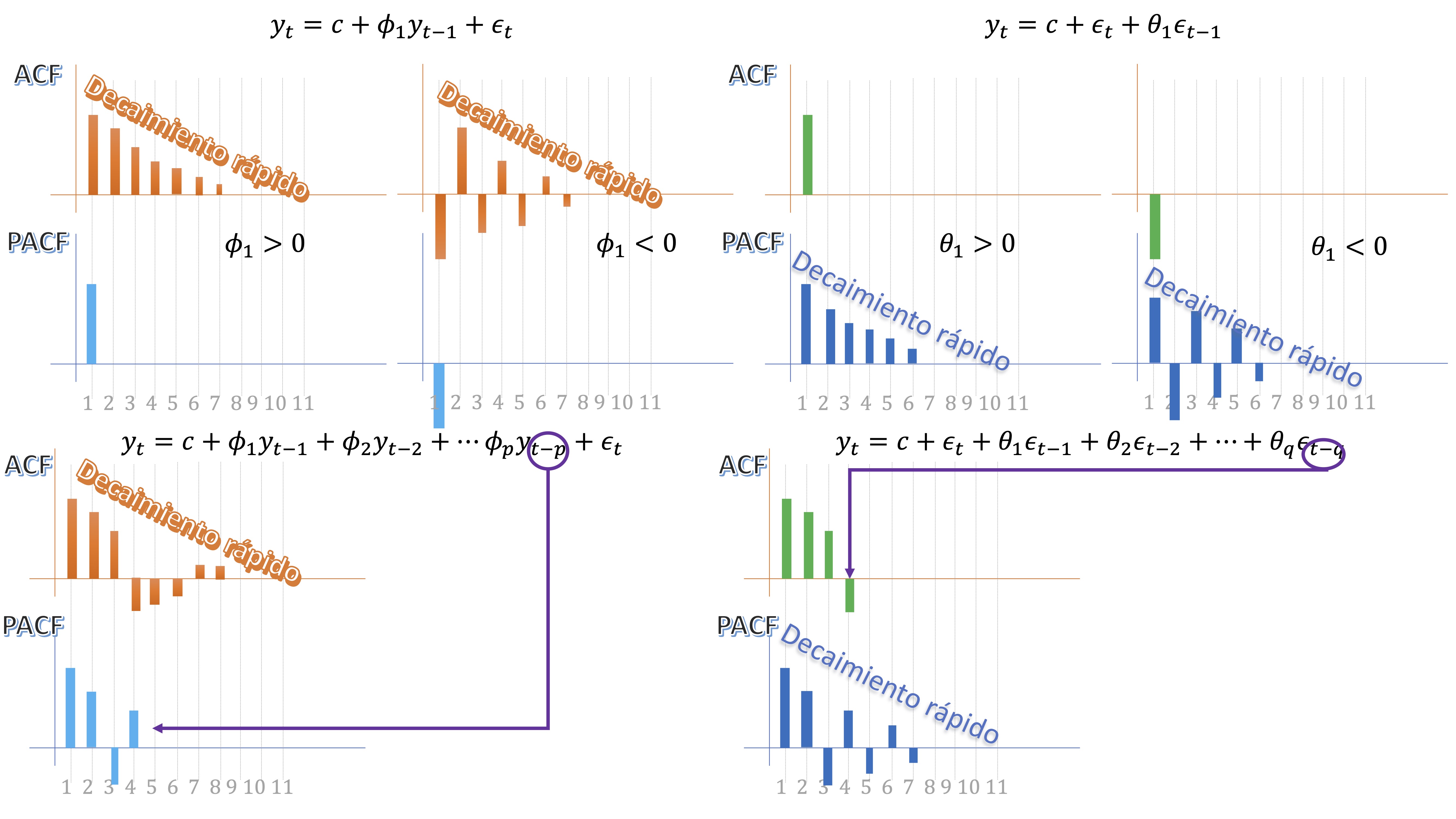FIG 1: la ACF y PACF de modelos AR y MA En los modelos AR(p) estacionarios, la ACF tiene un decaimiento rápido a cero, mientras que la PACF tiene “p” valores distintos de cero. En los modelos MA(q), ocurre a la inversa: la ACF tiene q palos distintos de cero, mientras que la PACF muestra un decaimiento rápido.

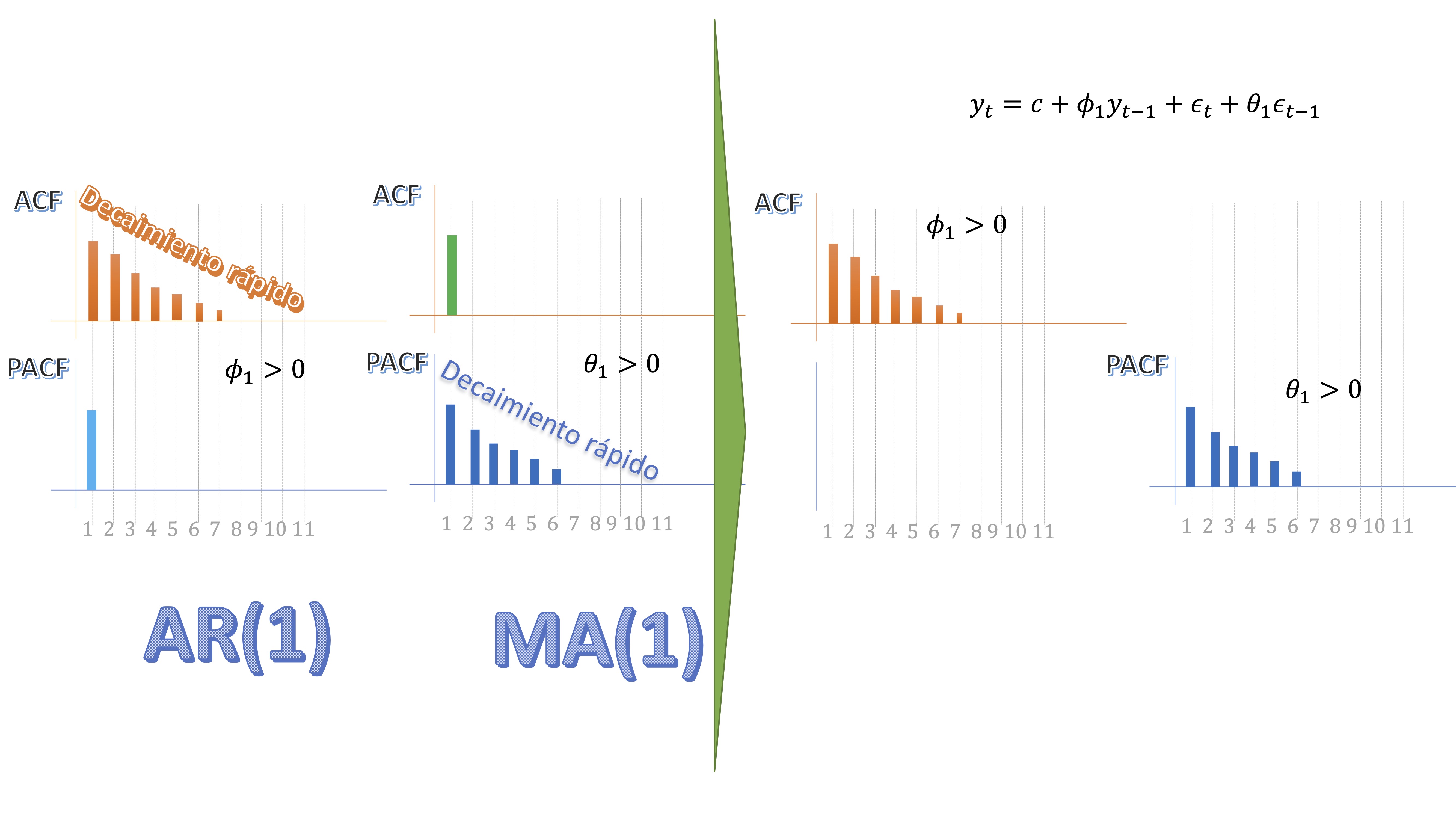FIG 2: la ACF y PACF de modelos ARMA sin embargo, los modelos mixtos (ARMA) tendrán, lógicamente, ACF y PACF en decaimiento rápido, ya que heredan las de los correspondientes AR y MA. Esto lo ha visto al simular el último proceso. Aquí tiene los scripts:

 #modelo AR(1)

z<-matrix(0 , 500)
for (i in 1:499){
  z[i+1]<-5+0.3*z[i]+rnorm(1,mean=0,sd=0.5)
}
par(mfrow=c(1,2))
acf(z[100:500])
pacf(z[100:500])


#Modelo MA(1)


a=rnorm(500,mean=0,sd=0.5) 
a_1=Lag(a,1) 
x=na.omit(a-0.8*a_1) 
par(mfrow=c(1,2))
acf(x)
pacf(x)


#Modelo AR(3)


y<-matrix(0 , 500)
y[1]=rnorm(1,mean=0,sd=0.5)
y[2]=rnorm(1,mean=0,sd=0.5)
y[3]=rnorm(1,mean=0,sd=0.5)
for (i in 3:499){
  y[i+1]<-5+0.70*y[i]-0.4*y[i-1]+0.5*y[i-2]+rnorm(1,mean=0,sd=1)
}

par(mfrow=c(1,2))
acf(y[100:500])
pacf(y[100:500])


#Modelo MA(3)

a=rnorm(500,mean=0,sd=0.5) 
a_1=Lag(a,1) 
a_2=Lag(a,2) 
a_3=Lag(a,3) 
w=na.omit(5+a-0.8*a_1+0.5*a_2-0.25*a_3) 
par(mfrow=c(1,2))
acf(w)
pacf(w)


#modelo ARMA(1,1)
a=rnorm(500,mean=0,sd=1) 
m<-matrix(0 , 500)
for (i in 1:499){

  m[i+1]<-5+0.95*m[i]+a[i+1]-0.8*a[i]
}

par(mfrow=c(1,2))
acf(m[100:500])
pacf(m[100:500])

En la clase anterior, aprendimos que un proceso AR(1), para que sea estacionario, debe satisfacer que el parámetro \(\phi_1\) en valor absoluto sea menor que 1. Sin embargo, vimos que el modelo MA(1) no requería ninguna condición sobre el parámetro para que este fuera estacionario. Sin embargo, vamos a ver una característica necesaria que es la invertibilidad. Para que el MA(1) sea invertible (veremos qué quiere decir), necesitaremos imponer una condición sobre el parámetro \(\theta_1\)

Ejercicio

Simule los siguientes procesos de Media Móvil

\[ y_{t}=3+\epsilon_{t}+0.5\epsilon_{t-1} \]

y, por otro lado,

\[ w_{t}=3+\epsilon_{t}+2\epsilon_{t-1} \]

\(a_{t}\rightarrow iid(0,2).\)

haga, para ello 1000 iteraciones temporales. Calcule la ACF ¿qué observa? Utilice la fórmula de la función ACF de la clase anterior.

sol Habrá comprobado que ambos procesos tienen el parámetro \(\theta\) diferentes pero, sin embargo, proporcionan la misma ACF y PACF. Verá que, usando esta expresión \[ \rho_{k}\begin{cases} \frac{\theta}{(1+\theta^{2})} & k=1\\ 0 & k>1 \end{cases} \]

para \(\theta=2\) y para \(\theta=0.5\) obtiene lo mismo. ¿Con cuál nos quedamos?

Observemos un detalle de interés

\[\begin{equation} y_{t}=\epsilon_{t}+\theta\epsilon_{t-1} \end{equation}\]

Escribimos la misma ecuación en \(t-1\) y despejamos \(\epsilon_{t-1}\) \[ y_{t-1}=\epsilon_{t-1}+\theta\epsilon_{t-2}\Rightarrow{\color{blue}{\epsilon_{t-1}}=y_{t-1}-\theta\epsilon_{t-2}} \]

insertando en el MA(1) original, tenemos

\[\begin{equation} y_{t}=\epsilon_{t}+\theta\left[y_{t-1}-\theta\epsilon_{t-2}\right] \end{equation}\]

despejamos, de nuevo, \(\epsilon_{t-2}\) \[ y_{t-2}=\epsilon_{t-2}+\theta\epsilon_{t-3}\Rightarrow{\color{blue}{\epsilon_{t-2}}=y_{t-2}-\theta\epsilon_{t-3}} \]

entonces \[ y_{t}=\epsilon_{t}+\theta\left[y_{t-1}-\theta\left[y_{t-2}-\theta\epsilon_{t-3}\right]\right] \]

y, sucesivamente, tendremos

\[\begin{equation} y_{t}=\theta y_{t-1}-\theta^{2}y_{t-2}+\theta^{3}y_{t-3}....+\epsilon{}_{t} \end{equation}\]

Observa

Hemos escrito un MA(1) de manera AR(infinita), es decir, parece que hay una conexión entre los procesos MA y AR

Ahora, veamos un caso práctico:

Ejercicio resuelto

reescriba estos MA(1) utilizando lo aprendido anteriormente

\[ y_{t}=\epsilon_{t}+0.5\epsilon_{t-1} \]

\[ y_{t}=\epsilon_{t}+2\epsilon_{t-1} \]

El primero de ellos lo escribimos como:

\[ y_{t}=0.5y_{t-1}-0.25y_{t-2}+0.125y_{t-3}+...+\epsilon_{t} \]

y el segundo como \[ w_{t}=2y_{t-1}-4y_{t-2}+8y_{t-3}+...+\epsilon_{t} \]

Estos procesos cuentan historias bien distintas:

  • \(y_{t}\) recibe un impacto de su pasado más cercano. Esto quiere decir que para predecir \(y_{t}\) necesitamos conocer como mucho 4 datos anteriores.
  • \(w_{t}\) según aumentan los retardos, mayor es el impacto de estos sobre el proceso. De esta forma si, por ejemplo, la tasa de paro siguiera un proceso como el de \(w_{t}\), entonces, para predecir el paro del trimestre que viene tendríaamos que conocer el de la Edad Media. Y eso no tiene sentido.

Esto nos lleva a la siguiente característica

clave:

Los procesos MA que nos interesan son aquellos para los que la secuencia AR (infinita) que se puede obtener de estos decaiga rápidamente y, por tanto, sólo influya el pasado más cercano del proceso).

Es decir, nos interesará que la secuencia de parámetros asociados a los retardos \(\left\{ \theta,\theta^{2},...\right\}\) converja a cero. Y para que esta secuencia sea convergente (entonces, tenga sentido) debemos imponer que \(\left|\theta\right|<1\) y diremos que, entonces, el MA es invertible. La invertibilidad del proceso MA(1) nos ayuda, además, a entender cómo modelar en la práctica:

clave:

Si me encuentro con un AR grande, entonces, puedo resumirlo como un MA(1). Esta interpretación del MA es muy interesante: ayuda a que los modelos AR tengan pocos parámetros

Analicemos ahora un AR(1) estacionario \[ y_{t}=\phi y_{t-1}+\epsilon_{t} \]

Si \(t=1\), tenemos \[ y_{1}=\phi y_{0}+\epsilon_{1} \]

Si \(t=2\), tendremos, por tanto, \[ y_{2}=\phi y_{1}+\epsilon_{2} \]

pero, si sustituimos, \[ y_{2}=\phi\left[\phi y_{0}+\epsilon_{1}\right]+\epsilon_{2}=\phi^{2}y_{0}+\phi\epsilon_{1}+\epsilon_{2} \]

si sigue haciendo estas sustituciones, tendrá:

\[ y_{t}=\epsilon_{t}+\phi\epsilon_{t-1}+\phi^{2}\epsilon_{t-2}+\phi^{3}\epsilon_{t-3}+... \]

clave:

Es decir, un AR(1) se puede poner como un MA(grande). De esta forma, si detecta que un proceso sigue un MA(grande), parece más interesante modelarlo como un AR(1)

Gran ejercicio propuesto

simule un AR(6), por ejemplo,

\(y_{t}=-0.80y_{t-1}-0.64y_{t-2}-0.512y_{t-3}-0.41y_{t-4}-0.32y_{t-5}-0.26y_{t-6}+\epsilon_{t}\)

y compruebe la ACF y la PACF. ¿Tendría sentido modelarlo como algún proceso MA?

Haga lo mismo con este MA(6), por ejemplo,

\(y_{t}=\epsilon_{t}+0.70\epsilon_{t-1}+0.49\epsilon_{t-2}+0.343\epsilon_{t-3}+0.24\epsilon_{t-4}+0.16\epsilon_{t-5}+0.11\epsilon_{t-6}\)

Clase 6: Su primer modelo ARMA

En la clase de hoy vamos a trabajar con datos de la economía española. En este caso: la inflación. Esta es la web donde puede descargárselos

https://www.bde.es/webbde/es/estadis/infoest/sindi.html

La idea es tratar de intentar utilizar los modelos que ha aprendido previamente, para ajustarlos a datos reales. Es importante que recuerde no ser dogmático en el análisis de datos. Hay que tratar de entender que modelamos para ser capaces de generalizar lo que ocurre con los datos, por lo que no suele ser muy exitoso tratar de que todo funcione exactamente como viene en sus apuntes del grado. Antes de empezar, recordemos que los modelos que hemos aprendido han de cumplir el requisito de estacionariedad en sentido débil, esto es, estacionarios en media y en varianza.

La primera diferencia

Una manera de tratar de conseguir que una serie temporal sea estacionaria en media, con el objeto de que pueda encajar en alguno de nuestros modelos previos, es transformarla mediante una primera diferencia. Se denota con el operador \(\Delta\) (delta mayúscula) y hace lo siguiente:

\[ \Delta y_{t}=y_{t}-y_{t-1} \]

Es decir, sea una serie \(y_{t}\) no estacionaria en media, el operador primera diferencia tratará de generar una nueva serie que presente un comportamiento más estable. Por ejemplo, \[ y_{t}=\left\{ 2,3,4,5,8,9,12,15,10,13,16,19,19,20\right\} \]

si dibuja esta secuencia verá que no es estacionaria en media. Sin embargo, la secuencia

\[ \Delta y_{t}=\left\{ *,1,1,1,3,1,3,3,-5,3,3,0,1\right\} \]

si la dibuja, verá que parece más sensato pensar que es estacionaria en media. Cuando una serie temporal se “convierte” en estacionaria al hacerle una primera diferencia se dice que es una serie “integrada de orden 1”. Es decir, diremos que \(y_{t}\sim I(1).\) En muchas series económicas y sociales, esto parece funcionar bien. Si, por ejemplo, la serie necesitara otra diferencia más, entonces diremos que es “integrada de orden 2” (algo poco habitual). Ojo, una segunda diferencia consiste en \[ \Delta\Delta y_{t}=\Delta^{2}y_{t}=\Delta\left(y_{t}-y_{t-1}\right)=y_{t}-y_{-1}-y_{t-1}+y_{t-2}=y_{t}-2y_{t-1}+y_{t-2} \]

y no en un error muy común en los alumnos que es decir que \(\Delta^{2}y_{t}=y_{t}-y_{t-2}.\) Eso es incorrecto.

  • ¿Cómo detecto si una serie temporal no es estacionaria en media?

Mire siempre el gráfico y razone sobre él: ¿tiene una tendencia? Entonces, no es estacionario en media. ¿Cortan pocas veces las observaciones a la media? Entonces, tampoco, ya que esta no será representativa de la serie.

library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)


inf <- read_excel("Datos_inflacion_21.xlsx")
inf.t=ts(inf[,2],frequency=12,start=c(1962,1))
ts.plot(inf.t)

Observando el gráfico de la variable inflación, en la FIG 1

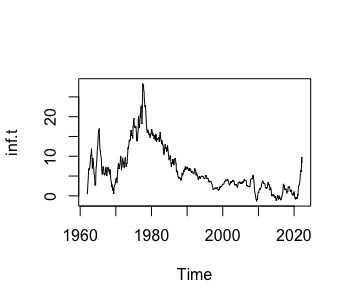FIG 1: la serie temporal de la inflación podemos observar que tiene un comportamiento errático que no es propio de un proceso estacionario. Recordemos, además, quelos procesos no estacionarios (recuerde el paseo aleatorio) presentaban una ACF en decaimiento lento. Podemos ver su ACF:

acf(inf.t)

que, efectivamente, muestra (FIG2) un decaimiento lento lo que sugiere ser un proceso no estacionario en media.

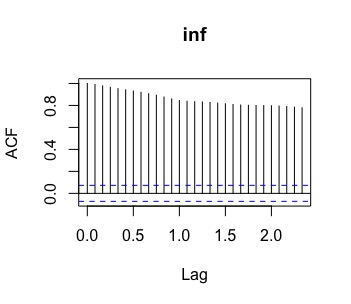
FIG 2: ACF de la serie temporal de la inflación

la transformación logarítmica

Es muy común que la desviación típica de una serie temporal crezca con su nivel (o tendencia). Si pasa eso, es que hay una relación multplicativa entre la tendencia de la serie y el error. De forma muy simplificada, ocurrirá que

\[ y_{t}=t\epsilon_{t} \]

donde \(t\) es un comportamiento tendencial lineal (\(t=\left\{ 1,2,3,4,....\right\} )\) y \(\epsilon_{t}\rightarrow i.i.d(\mu,\sigma)\). Entonces, fíjese que

\[\begin{equation} dt(y_{t})=t\sigma \end{equation}\]

por lo que la desviación típica de la \(y_{t}\) crecerá de forma lineal con la variable de tendencia. Una manera, entonces de conseguir que la varianza de la serie no sea proporcional al nivel de esta será, por tanto, aplicar logaritmos (dadas sus propiedades “linealizadoras” de procesos multiplicativos) \[ \ln y_{t}=\ln t+\ln\epsilon_{t} \]

de tal forma que la varianza de la serie \(\ln y_{t}\) ahora será estable.

Ejercicio resuelto:

simule la serie \[ y_{t}=t\epsilon_{t} \]

donde \(\epsilon_{t}\rightarrow i.i.d(1,0.1)\). Realice un gráfico de esta y verifique que la transformación logarítmica estabiliza su varianza

e<-rnorm(200,mean=1,sd=0.1)
t<-seq(1,200) 
x=t*e 
ts.plot(x)
ts.plot(log(x))

Donde se puede ver, claramente, cómo la varianza de la serie crece según avanza la variable “tiempo”. Al introducir el logaritmo neperiano, es fácil ver que la varianza se tiende a estabilizar.

Una manera de reconocer si una serie temporal necesita o no logaritmo es mediante un sencillo gráfico en el que pueda enfrentarse el nivel de la serie y su desviación típica. Si esta relación es proporcional, entonces satisfacerá- de manera aproximada- la ecuación multiplicativa anterior. Para ello, sólo deberemos elegir un número arbitrario de particiones que haremos en la muestra de la serie y, para cada partición, calcularemos la media y la desviación típica locales. Veamos cómo se puede hacer para la serie que hemos creado previamente: en el script siguiente, decidimos hacer 10 particiones (por tanto, de 20 observaciones cada una) y después calculamos la media y la desviación típica para cada partición

T<-length(x) 

Ind<-rep(seq(1,20), each = 10)  #creo un indicador cada 30 observaciones
DF<-data.frame(x,Ind) #creo un set de datos con la variable y el indicador

Mean<-vector() 
SD<-vector()  

for (i in 1:10){ 

  newdata <- subset(DF, Ind==i) 
  Mean[i]=mean(newdata$x) 
  SD[i]=sd(newdata$x)} 
  plot(Mean,SD)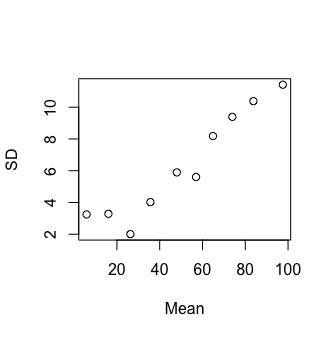

FIG 3: el gráfico media-desviación típica

Como vemos en la FIG3, según crece la media de la serie (localmente) la desviación típica también lo hace (de forma razonablemente lineal).

Si transforma la serie mediante un logaritmo, verá cómo este efecto se atenúa

T<-length(x) 

Ind<-rep(seq(1,20), each = 10)  #creo un indicador cada 30 observaciones
DF<-data.frame(x,Ind) #creo un set de datos con la variable y el indicador

Mean<-vector() 
SD<-vector()  

for (i in 1:10){ 

  newdata <- subset(DF, Ind==i) 
  Mean[i]=mean(log(newdata$x)) 
  SD[i]=sd(log(newdata$x))} 
  plot(Mean,SD)

Ejercicio

¿Es la serie de la inflación en España estacionaria en varianza?

Adapte el código anterior.

T<-length(inf.t) 

Ind<-rep(seq(1,37), each = 20)  #creo un indicador cada 30 observaciones
Ind<-Ind[1:T]
DF<-data.frame(inf.t,Ind) #creo un set de datos con la variable y el indicador

Mean<-vector() 
SD<-vector()  

for (i in 1:37){ 
  
  newdata <- subset(DF, Ind==i) 
  Mean[i]=mean(newdata$inf) 
  SD[i]=sd(newdata$inf)}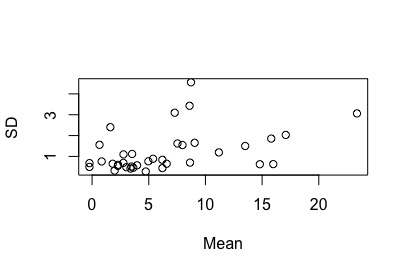

FIG 4: el gráfico media-desviación típica para la inflación

No está tan claro, aunque parece tener cierta relación creciente la media con la desviación típica, no podremos utilizar la transformación logarítmica porque la serie toma valores negativos (y el logaritmo no está definido para dichos valores).

entonces: Parece recomendable modelar la primera diferencia de la serie temporal, es decir \(\triangle(inf_t)\) que puede interpretarse como la variación mensual de la serie original

Llega el momento de decidir el modelo ARMA adecuado

Realizamos la transformación necesaria según nuestro análisis previo y obtenemos

y<-diff(inf.t)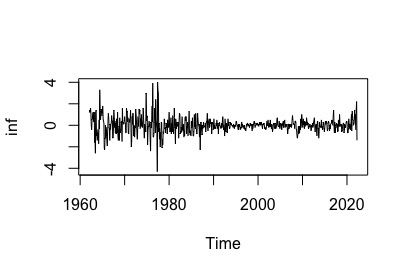

FIG 5: primera diferencia de la inflación la serie parece: >- estacionaria en torno al valor central 0 >- con cierta varianza mayor antes de 1980.

Puede ser razonable obviar los datos de 1960 a 1980 por considerar que podrían representar otro régimen más volátil de la economía. Realizaremos, entonces, el estudio con los datos desde 1980 en adelante. Analicemos la ACF,PACF de la serie.

Entonces:

¿No estoy perdiendo información si elimino datos? Tenga cuidado, porque al entrenar un modelo, usted está tratando de resumir la información de su muestra. La frase “cuantos más datos, mejor” deberá tomarla con pinzas. Si el proceso que genera los datos es susceptible de ser distinto en diferentes submuestras, quizás le interese no utilizar dos regímenes distintos para resumir la información con un modelo. Estará promediando un régimen muy volátil con otro mucho más estable. ¿Tiene sentido?

ny<-window(inf.t, start = c(1980,1), end = c(2022,4))
y<-diff(ny)

par(mfrow=c(1,2))
acf(y)
pacf(y)

Obtenemos el siguiente gráfico: ¿qué observa?

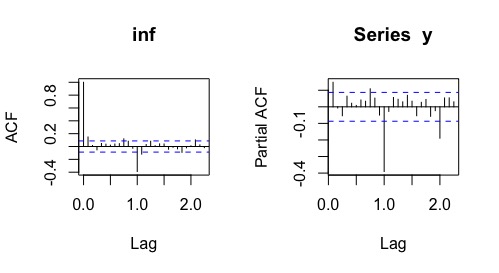
FIG 5: el gráfico ACF-PACF de la inflación en España

Clase 7: análisis de la estacionalidad

Una característica que está presente en las series temporales es la estacionalidad. No lo confunda con estacionariedad

FIG 1: No confunda

La estacionalidad es, en general, una consecuencia de los hábitos humanos. Tiene que ver con “estación” del año y de cómo redistribuímos nuestros hábitos en función del calendario. Por definición, entonces, una serie estacional no será estacionaria en media: claro, la media de la serie será, localmente, distinta en cada estación. Por ejemplo, en la serie de turistas se ve claramente el componente estacional:

FIG 2: No confunda

donde puede verse que, dependiendo del mes del año, el promedio se sitúa en un nivel remarcablemente distinto a otros meses. Entonces, diremos que la serie temporal es estacional de periodo \(s\). Generalmente, la estacionalidad vendrá dada por la cantidad de observaciones en las que se divida el año. Por ejemplo, las series trimestrales es de esperar que tengan un componente trimestral de periodo \(s=4\): es decir, los primeros trimestres tenderán a tener un comportamiento común, los segundos, etc… De igual modo, pasará con las series mensuales (\(s=12)\) y, ¡cuidado! con las series diarias (\(s=365)\) donde la complicación aumenta: puesto que puede haber un efecto “día del año, día del mes, día de la semana…”. Las series diarias ofrecen mucha complicación por la riqueza de efectos que pueden incorporar.

El componente estacional se puede detectar, generalmente, a simple vista (como en la gráfica de turistas). Recuerde que nosotros hemos definido unos procesos (ARMA) que han de ser estacionarios en media y varianza. Es por ello que, entonces, desearemos poder trabajar con series estacionarias en media. Entonces, tendremos que “deshacernos” de la estacionalidad de la serie. Para esto hay multitud de métodos a nuestra disposición.

Modelos ARMA estacionales

En la parte estacional del modelo se puede encontrar también un modelo ARMA Eso ocurre cuando el correlograma (es decir la ACF y la PACF) nos permite identificar un proceso AR o MA para la parte estacional (es decir, para los periodos \(s\),\(2s\),\(3s\),….. Se identifican de la misma manera. Por ejemplo, un AR(1) para un proceso estacional de periodo \(s,\)se escribir? as?: \(AR(1)_{s}\) y su ecuación será:

\[ y_{t}=c+\Phi_{1}y_{t-s}+\epsilon_{t} \]

donde \(\epsilon_{t}\rightarrow iid(0,\sigma^{2}).\) Ahora tiene un retardo de periodo \(s\). Por ejemplo, con datos mensuales, ser?

\[ y_{t}=c+\Phi_{1}y_{t-12}+\epsilon_{t} \]

Por otro lado, un media móvil de orden 1 estacional de periodo \(s\), lo escribiremos como \[ y_{t}=c+\epsilon_{t}+\Theta_{1}\epsilon_{t-s} \]

Se identifican de la misma manera que los procesos anteriores

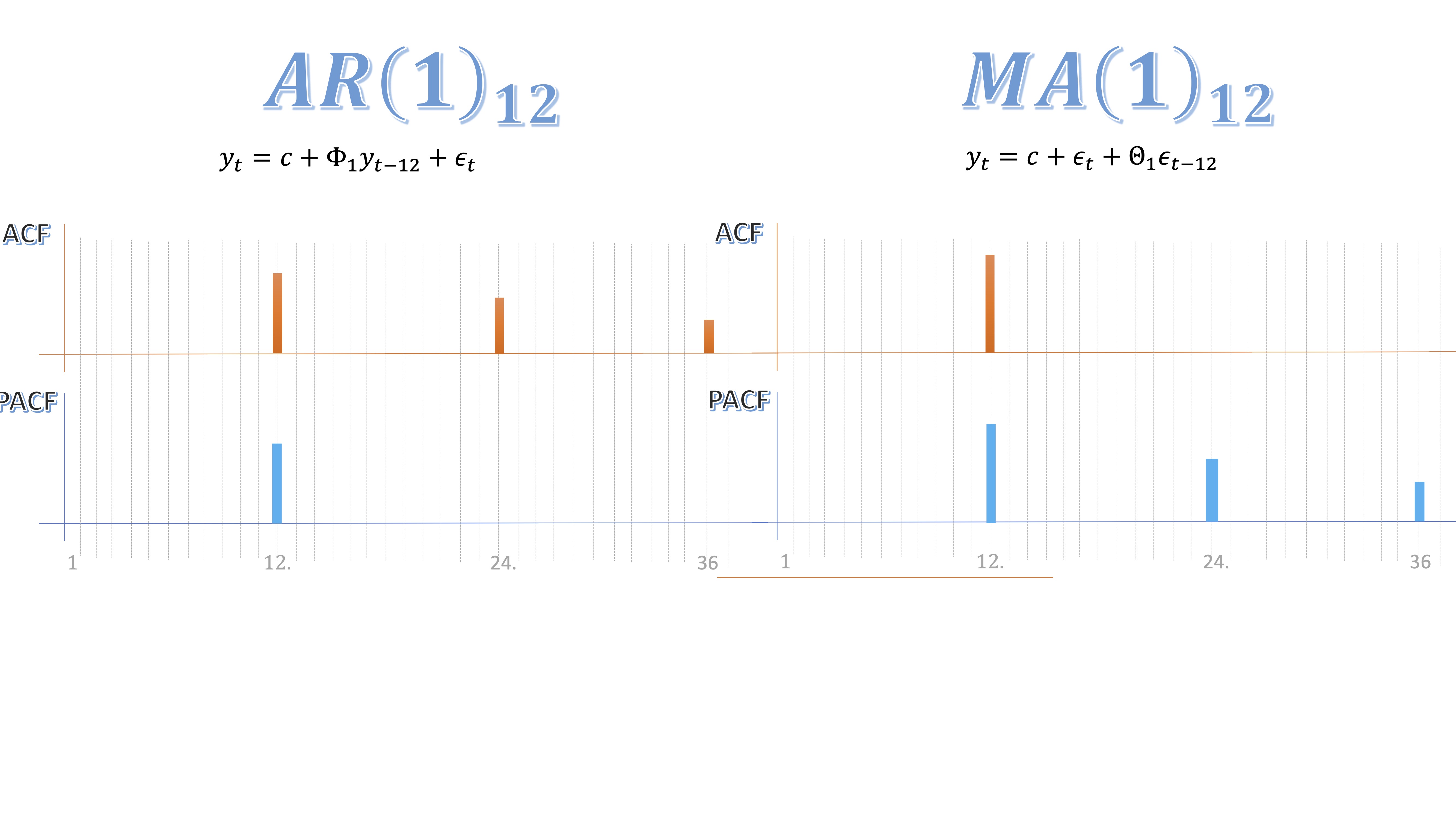
FIG 3: Dos modelos ARMA estacionales

  • El AR(1) estacional (en este caso, de periodo 12) , se identifica con una ACF que decae rápidamente en los periodos 12,24,36,etc… y una PACF con un valor distinto de cero en el periodo 12.
  • El MA(1) estacional (en este caso, de periodo 12), se identifica con el inverso (PACF en decaimiento rápido y un valor distinto de cero en la ACF).

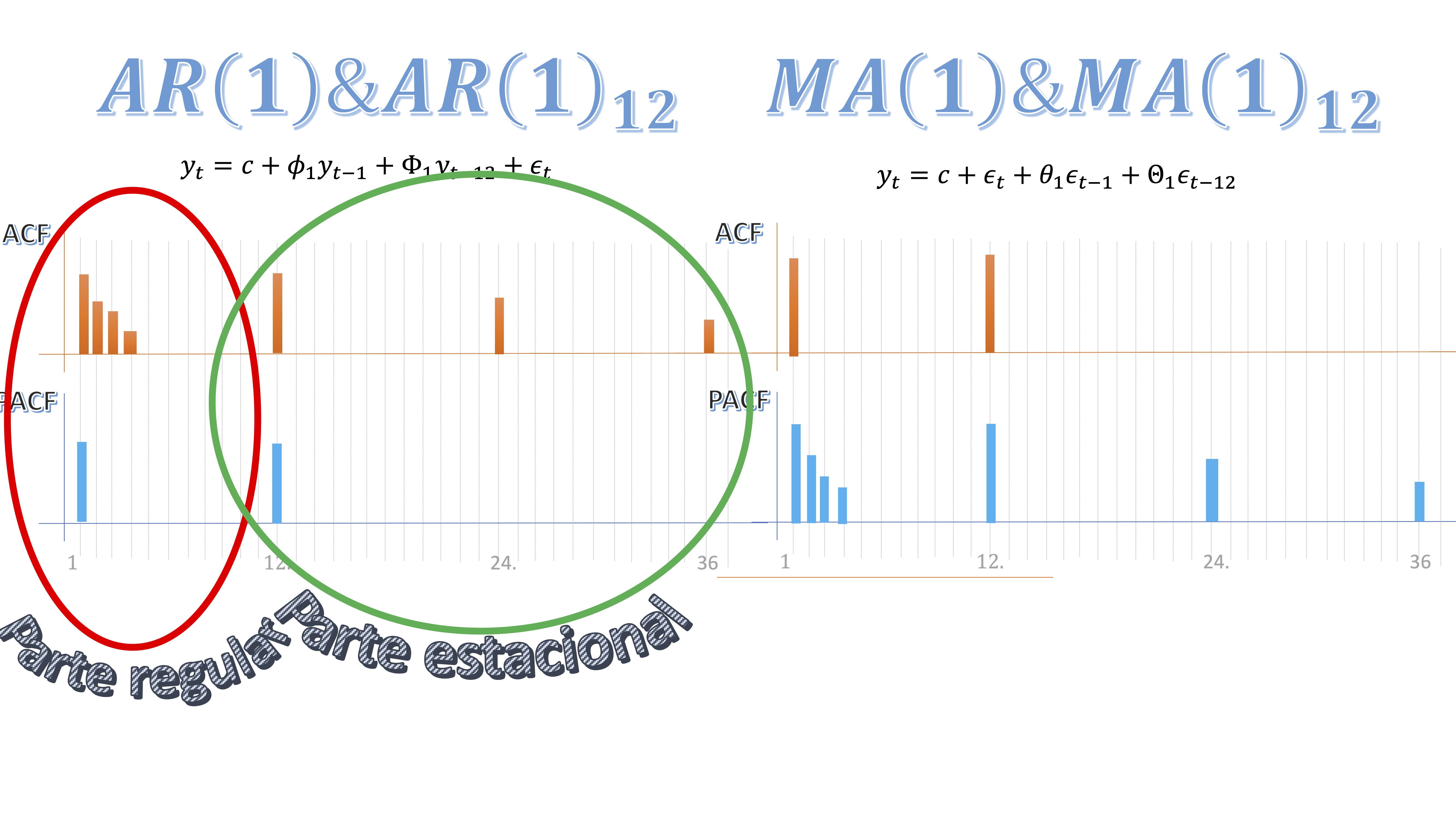
FIG 4: No confunda

Sin embargo, lo normal es tener que identificar el modelo tanto en la parte, llamémosla, regular (es decir, la inercia que tiene la serie en los meses cercanos) junto con la estacional (la pauta que se repite cada \(s\) meses).

Lo recomendable, entonces, será seguir este modo de proceder:

  • Evalúe la estacionariedad en media y varianza. Tome las decisiones correspondientes
  • Analice la estacionalidad mediante el correlograma. Estime el correspondiente modelo estacional
  • LOS RESIDUOS de dicho modelo son la serie sin estacionalidad. Ahora analice el correlograma de esos residuos y decida el modelo para la parte regular.
  • Estime el modelo conjuntamente con la serie original
  • Analice los residuos: si son ruido blanco, el modelo será adecuado.

Piense:

Queremos residuos ruido blanco porque esto, entonces, indicará que ya no tenemos más señal en la serie temporal y “lo que queda” es el conjunto de “shocks” impredecibles que sufrió la serie en el pasado.

Continuemos con el ejemplo de la inflación española

#cargamos los datos y nos quedamos con la muestra desde 1980#
inf <- read_excel("Datos_inflacion_21.xlsx")
inf.t=ts(inf[,2],frequency=12,start=c(1962,1))
ts.plot(inf.t)
n_inf<-window(inf.t, start = c(1980,1), end = c(2022,4)) 

dtrend=diff(D12n_inf) #aplicamos la primera diferencia

par(mfrow=c(1,2)) #estudiamos el correlograma
acf(na.omit(dtrend),lag.max=55)
pacf(na.omit(dtrend),lag.max=55)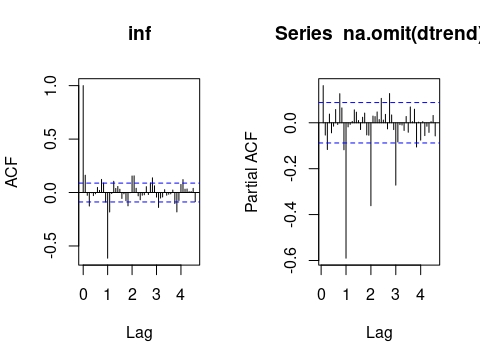

FIG 5: ACF-PACF inflación en primeras diferencias Podrá ver que la PACF tiene decaimiento rápido en la parte estacional (donde se corresponde con Lag=1,2,3,4) y un valor “grande” en la ACF en Lag=1. Esto se corresponde con un modelo MA(1) estacional de periodo 12 (es decir, \(MA(1)_{12}\))

#estimamos el modelo. En "order" se indica el primer valor de la parte AR regular (todavía no lo sabemos), el número de diferencias (sabemos que es 1) y la parte MA regular. En Seasinal se escribe, de igual modo, el modelo ARMA. En este caso, es un MA(1):#
AM1<-Arima(n_inf,order=c(0,1,0), seasonal=c(0,0,1))
par(mfrow=c(1,2))
acf(na.omit(AM1$residuals),lag.max=55)
pacf(na.omit(AM1$residuals),lag.max=55)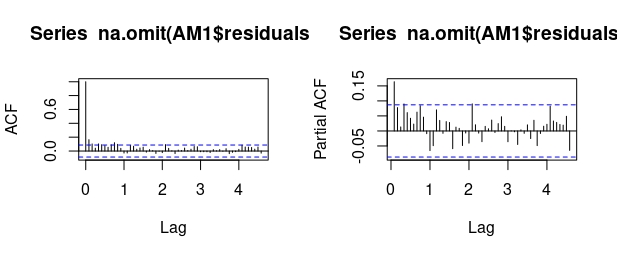

FIG 6: ACF-PACF de los residuos En la FIG6, no parece que se tenga claro qué modelo entrenar. Lo más probable es que sea un AR(1): en la PACF hay un palo (con un valor pequeño, cercano a 0.15) y la ACF decae rápidp (tiene dos valores fuera de las bandas, aunque hay que fijarse mucho). Propongamos un modelo AR(1) para la parte regular, y estimemos de nuevo:

#estimamos el modelo. En "order" se indica el primer valor de la parte AR regular (todavía no lo sabemos), el número de diferencias (sabemos que es 1) y la parte MA regular. En Seasinal se escribe, de igual modo, el modelo ARMA. En este caso, es un MA(1):#
AM1<-Arima(n_inf,order=c(1,1,0), seasonal=c(0,0,1))
par(mfrow=c(1,2))
acf(na.omit(AM1$residuals),lag.max=55)
pacf(na.omit(AM1$residuals),lag.max=55)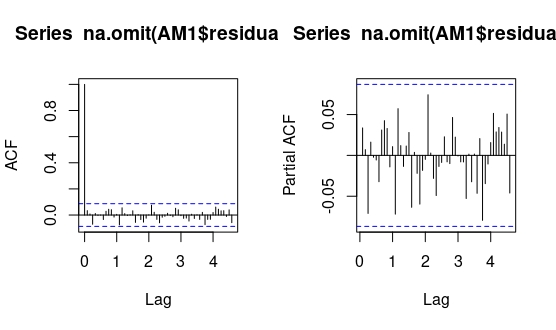

FIG 7: ACF-PACF de los residuos

Si se fija en la FIG7, ya no hace falta seguir. Los residuos son ruido blanco. El modelo para la inflación parece ser un ARIMA(1,1,0) para la parte regular un un ARIMA(0,0,1) para la parte estacional. Finalmente, entrenamos el modelo y obtenemos la predicción

autoplot(forecast(AM1))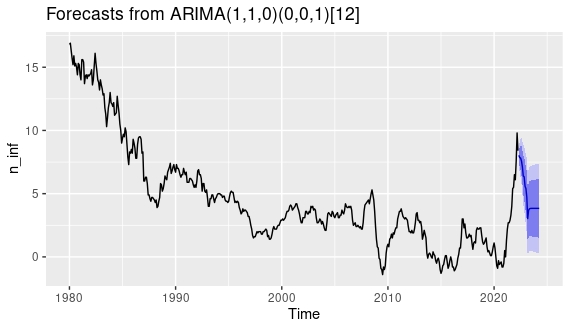

FIG 8: predicción final

En las siguientes clases, discutiremos más sobre predicción. Sin embargo, hay que anotar que:

  • Se ha pasado muy de puntillas sobre la estacionalidad. Hay muchas maneras de trabajar con ellas: busque información, puesto que hay métodos para filtrarla (desde simples dummies estacionales, que son muy rígidas, a modelos basados en el filtro de Kalman, mucho más adaptativas)
  • Se ha pasado muy de puntillas sobre los modelos ARIMA estacionales: estos pueden ser aditivos o multiplicativos. Los multiplicativos son los más comunes y, además, suelen ser a veces difíciles de identificar (puesto que interactúan con la parte regular del modelo). Ante dudas en su proyecto, consulte a su profesor, a un vídeo de youtube-si su profesor le da miedo- o a cualquier fuente de la que se fíe (vale un vidente).

Clase 8: información externa

En el proceso de modelado, también es importante ser capaces de incorporar información del entorno. Sin embargo, no es algo sencillo, puesto no sólo nos vale con tener una(s) variable(s) que estén relacionadas con nuestra variabel de interés (por ejemplo,el turismo está muy relacionado con un montón de variables económicas). Si usted quiere predecir el número de turistas basado en una variable económica: también tendrá que predecir dicha variable económica. Vamos a entender alguno de estos aspectos utilizando la serie de turistas justo antes de la crisis del COVID.

#tomamos datos desde el principio de la muestra hasta febrero de 2020
TUR_n<-window(TUR.t, start = c(2015,10), end = c(2020,2))
#estudiamos la ACFy PACF...
par(mfrow=c(1,2))
acf(na.omit(TUR_n),lag.max=36)
pacf(na.omit(TUR_n),lag.max=36)
#...de la que sospechamos un AR(1) estacional (de periodo 12). Estimamos el modelo
M1<-Arima((TUR_n), seasonal=c(1,0,0),method="ML")
#los residuos de dicho modelo se interpretan como la serie de turistas desestacionalizada
TUR_desestacionaslizados<-M1$residuals
#Analizamos la ACF y PACF...
par(mfrow=c(1,2))
acf(na.omit(TUR_desestacionaslizados),lag.max=36)
pacf(na.omit(TUR_desestacionaslizados),lag.max=36)
#...y vemos que en la parte regular podemos encontrarnos con un AR(2). Lo estimamos
M2<-Arima(TUR_desestacionaslizados,order=c(2,0,0),method="ML")

#Analizamos el correlograma:
par(mfrow=c(1,2))
acf(na.omit(M2$residuals),lag.max=36)
pacf(na.omit(M2$residuals),lag.max=36)

#como dicho correlograma ya nos muestra que los residuos son ruido blanco, estimamos el modelo conjunto: ARIMA(2,0,0)xARIMA(1,0,0)12

Mf<-Arima(TUR_n,order=c(2,0,0),seasonal=c(1,0,0),method="ML")

#nos guardamos, además, los datos reales para comparar
TUR_n2<-window(TUR.t, start = c(2015,10), end = c(2020,12))


#y hacemos la predicción a horizonte 10 meses

par(mfrow=c(1,2))
plot(forecast(Mf,h=10),main="model")
ts.plot(TUR_n2,main="real")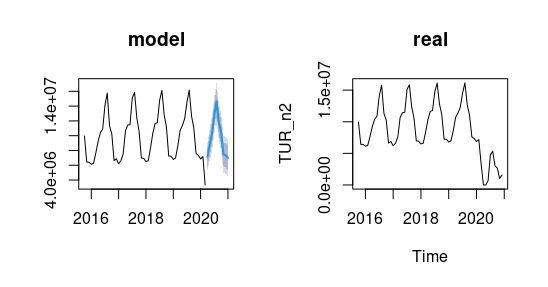

FIG 1:Ejemplo de un gran error de predicción por, obviamente, no saber la que se venía encima ¿Cómo reaccionar para la siguiente predicción? Puede intentar incorporar algo de información en el modelo.

Definiremos una variable escalón \(E_{t}^{t^{*}}\), que se activa a partir de un momento \(t^{*}\), como aquella que se modela como \[ E_{t}^{t^{*}}\begin{cases} 1 & t\geq t^{*}\\ 0 & t<t^{*} \end{cases} \]

de tal forma que, con esta variable dummy, estamos generando un escalón:

Note que ha de ver \(E_{t}\) como una variable cualquiera, que tome valor 1 en un momento del tiempo simplemente significa que el nivel de la serie temporal cambia en ese periodo (de forma positiva o negativa)

En esta gráfica del turismo, como vemos, el nivel decrece, por lo que la variable \(E_{t}^{t^{*}}\) deberá ir multiplicada por un coeficiente negativo (que indique la caóda en dicho nivel).

Entonces:

Es importante notar que siempre conviene tener información extramuestral acerca de qué pasó en la serie temporal para tener dicha caída de nivel. Es decir, siempre que quiera intervenir la serie con un efecto escalón (u otro, aunque este es el más común) debe tener clara la justificación. Ya que, si no, podría estar sesgando los resultados del modelo.

En el caso de que hayamos detectado un claro efecto escalón y conocemos a partir de cuándo se produce, podemos modelarlo así

\[\begin{equation} y_{t}=\alpha_{0}+\alpha_{1}E_{t}^{t^{*}}+u_{t}\label{eq:escalon} \end{equation}\]

de esta forma, previo a \(t^{*}\), \(E_{t}^{t^{*}}=0\) y, por lo tanto, la serie, en promedio, valdrá:

\[ E(y_{t})=\alpha_{0} \]

mientras que, cuando entremos en \(t^{*}\) -y periodos siguientes- \(E_{t}^{t^{*}}=1\) , de tal forma que la serie, en promedio, valdrá

\[ E(y_{t})=\alpha_{0}+\alpha_{1} \]

por lo que el signo de \(\alpha_{1}\) indicará si el nivel del escalón es positivo o negativo.

Algo más

Por otro lado, si el proceso \(\left\{ y_{t}\right\}\) sigue un modelo ARMA(p,q), tendremos que estimar un modelo del tipo:

\[ y_{t}=\alpha_{0}+\alpha_{1}E_{t}^{t^{*}}+\phi_{1}y_{t-1}+...+\phi_{p}y_{t-p}+u_{t}+\theta_{1}u_{t-1}+...+\theta_{q}u_{t-q} \]

y, si además, el proceso requiere una primera diferencia para ser estacionario, fíjese que el modelo denotado por la ecuación (\(\ref{eq:escalon}\)) se convierte en

\[ \Delta y_{t}=\alpha_{1}\Delta E_{t}^{t^{*}}+\Delta u_{t} \]

De la misma manera que, si sigue un proceso ARMA, y este ha de ir en primeras diferencias, deberá entrenarse así: \[ \Delta y_{t}={\color{red}\alpha_{1}\Delta E_{t}^{t^{*}}}+\phi_{1}\Delta y_{t-1}+....+\phi_{p}\Delta y_{t-p}+\epsilon_{t}+\theta_{1}\epsilon_{t-1}+...+\theta_{q}\epsilon_{t-q} \]

donde \(\epsilon_{t}=\Delta u_{t}\). Esto, lo que implica es que, como pasa con la estacionalidad, a veces cuesta identificar el modelo ARMA cuando todavia no se ha identificado el escalón. Para ello, es recomendable seguir estos pasos:

  • Decida, con información “extramuestral” dónde están esos posibles efectos escalón (hable con su cliente, su equipo, busque noticias, etc…)
  • Cree las variables escalón y estime, por MCO, la regresión \(y_{t}=\alpha_{0}+\alpha_{1}E_{t}^{t_{1}^{*}}+...+\alpha_{m}E_{t}^{t_{m}^{*}}u_{t}\) , donde hay \(m\) escalones que suceden en periodos de tiempo \(t_{1}^{*},...,t_{m}^{*}\).
  • Quédese con los residuos, ya que estos darán lugar a la serie \(y_{t}\) sin escalones
  • Identifique el proceso ARMA correspondiente con la ACF y PACF de los residuos
  • Estime el modelo ARMA completo, incluyendo la variable escalón.

Ahora, entonces, además de incorporar un dato más (el de marzo de 2020), también una variable escalón desde dicho mes, para capturar la caída de nivel de la serie

## Generamos la variable "dummy" que tomará valor 1 en marzo de 2020 y siguientes
dummy[which(TUR[,1] < "2020-03-01")] <- 0
dummy[which(TUR[,1] >= "2020-03-01")] <- 1

## Le damos carácter de serie temporal
dummy.t=ts(dummy,frequency=12,start=c(2015,10))

## Obtenemos las variables para modelar con información hasta abril de 2020 (un mes más que antes)
TUR_n<-window(TUR.t, start = c(2015,10), end = c(2020,4))
dummy_n<-window(dummy.t, start = c(2015,10), end = c(2020,4))

## Estimamos el modelo ARMA correspondiente incluyendo "xreg", es decir, "external regressor"
Mf<-Arima(TUR_n, order=c(2,0,0),seasonal=c(1,0,0),xreg=dummy_n,method="ML")

## Guardamos la variable real de turismo para representar
TUR_n2<-window(TUR.t, start = c(2015,10), end = c(2020,12))

#obtenemos la variable Dummy escalón para hacer la predicción
dummy_n<-window(dummy.t, start = c(2020,5), end = c(2021,2))

par(mfrow=c(1,2))
plot(forecast(Mf,xreg=dummy_n), main="model")
ts.plot(TUR_n2, main="real")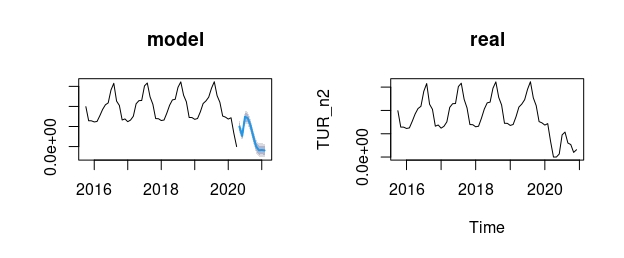

FIG 2:Ejemplo de mejora en el error de predicción al incorporar la nueva variable (con un mes de retraso, obviamente)

Ahora, la pregunta es ¿Hasta cuándo dejo de incluir el efecto del escalón? Lógicamente, dependerá de lo que esté modelando y-por supuesto-dependerá de su habilidad para comprender qué y cómo está modelando. No hay una respuesta a esa pregunta.

Clase 9: Juicio a la capacidad predictiva de los modelos

En series temporales también se puede realizar validación cruzada. La particularidad de estos datos (el orden ha de ser cronológico) hace que no se pueda realizar como con datos de individuos (donde se puede realizar un conjunto de remuestreos aleatorios y seleccionar un amplio número de submuestras con las que entrenar el modelo). En este caso, además, se une el hecho habitual de que las series temporales no son excesivamente amplias.

Lo normal para hacer validación cruzada consiste en elegir una muestra de datos de entrenamiento (desde el principio o desde una observación adecuada para nuestros objetivos), entrenar el conjunto de modelos correspondientes para esa muestra y, posteriormente, realizar predicciones al horizonte correspondiente y validarlas con los datos no utilizados en el entrenamiento.

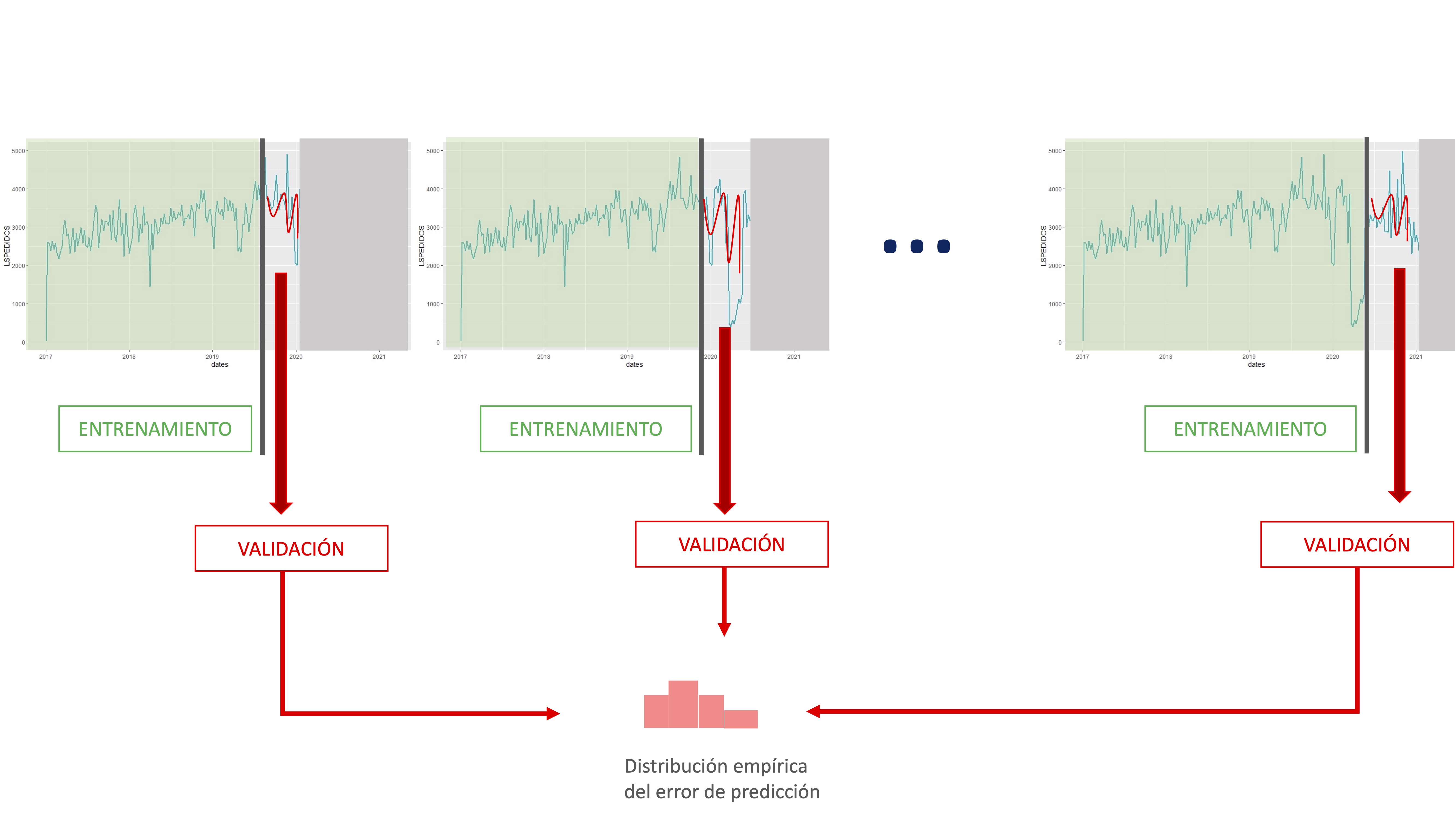
FIG 1:La validación cruzada en series temporales

De esta manera, vamos obteniendo información asociada a la habilidad predictiva de cada modelo mediante el almacenamiento de sus errores de predicción. Presentamos, a continuación, un esquema numérico para la realización de la validación cruzada. El ejemplo lo vamos a realizar con la serie de inflación

inf <- read_excel("Datos_inflacion_21.xlsx")
inf.t=ts(inf[,2],frequency=12,start=c(1962,1))
ts.plot(inf.t)
n_inf<-window(inf.t, start = c(1980,1), end = c(2022,4))
#Elijo cuantos datos quiero tener para empezar
k <- 300
#obtengo el total de datos de la muestra
n<-length(n_inf) 
#genero dos vectores vacíos para almacenar errores
error1<-vector() 
error2<-vector() 
#Creo un bucle que va a ir elaborando predicciones a horizonte 1

for(i in 1:(n-k-1)) {
  #extrae la muestra con la que entrenará
  xshort <- n_inf[1:(k+i)] 
  #extrae el dato real con el que comparar
  xnext <- n_inf[(k+i+1)]
  
  TS.xshort = ts(xshort, frequency = 12, start=c(1980,01)) 
  #entrena dos modelos: el que identificamos previamente y otro automático que tiene R
  t1<-Arima(TS.xshort, order=c(1,1,0) ,seasonal=c(0,0,1), include.drift=TRUE) 
  t2<-auto.arima(TS.xshort)
  fcast1 <- forecast(t1) 
  fcast2 <- forecast(t2) 
  error1[i]<-((xnext)-(fcast1$mean))/(xnext)
  error2[i]<-((xnext)-(fcast2$mean))/(xnext) }

¿Con qué modelo quedarse?

En general, no hay un criterio claro que nos permita decantarnos por un único modelo. Puede darse el caso de que los candidatos predigan de forma similar (donde podría ser interesante promediar las predicciones de cada uno de los modelos elegidos) o que haya interesantes diferencias entre ellos. En general, parece sensato buscar alguna forma de combinar los modelos. Una propuesta para combinarlos puede ser desde hacer una media aritmética de las predicciones o, por ejemplo, una media ponderada en función de cuál prediga mejor.

Clase 10: elaboración de predicciones probabilísticas

Uno de los intereses que tiene un ejercicio de predicción es ser capaces de otorgar una probabilidad (o verosimilitud) a un escenario. Esto le permitirá entrar en un debate más sano que aquel en el que se proporciona una predicción central sin dar información sobre la incertidumbre que se tiene sobre dicha predicción.

Una manera de poder hacer esto es mediante la técnica del bootstrapping. Usted, a partir de un modelo inicial, podrá generar un conjunto grande de estimaciones alternativas de los parámetros de los modelos sin tener que asumir distribuciones (generalmente rígidas) sobre la distribución de los errores o de los parámetros de los modelos.

Sin embargo, el bootstrapping con series temporales tiene una particularidad: no debe mueestrear (con reemplazamiento) directamente en la serie temporal, puesto que una de las características de máximo interés en una serie temporal es el orden. Es decir, si su serie temporal es esta:

FIG 1:Un ejemplo de una serie temporal un muestreo con reemplazamiento erróneo sería, por ejemplo, hacer esto:

FIG 2:Un ejemplo de un muestreo con reemplazamiento

de repente, el orden de la serie se ha perdido…y podrían pasar cosas desastrosas como esto:

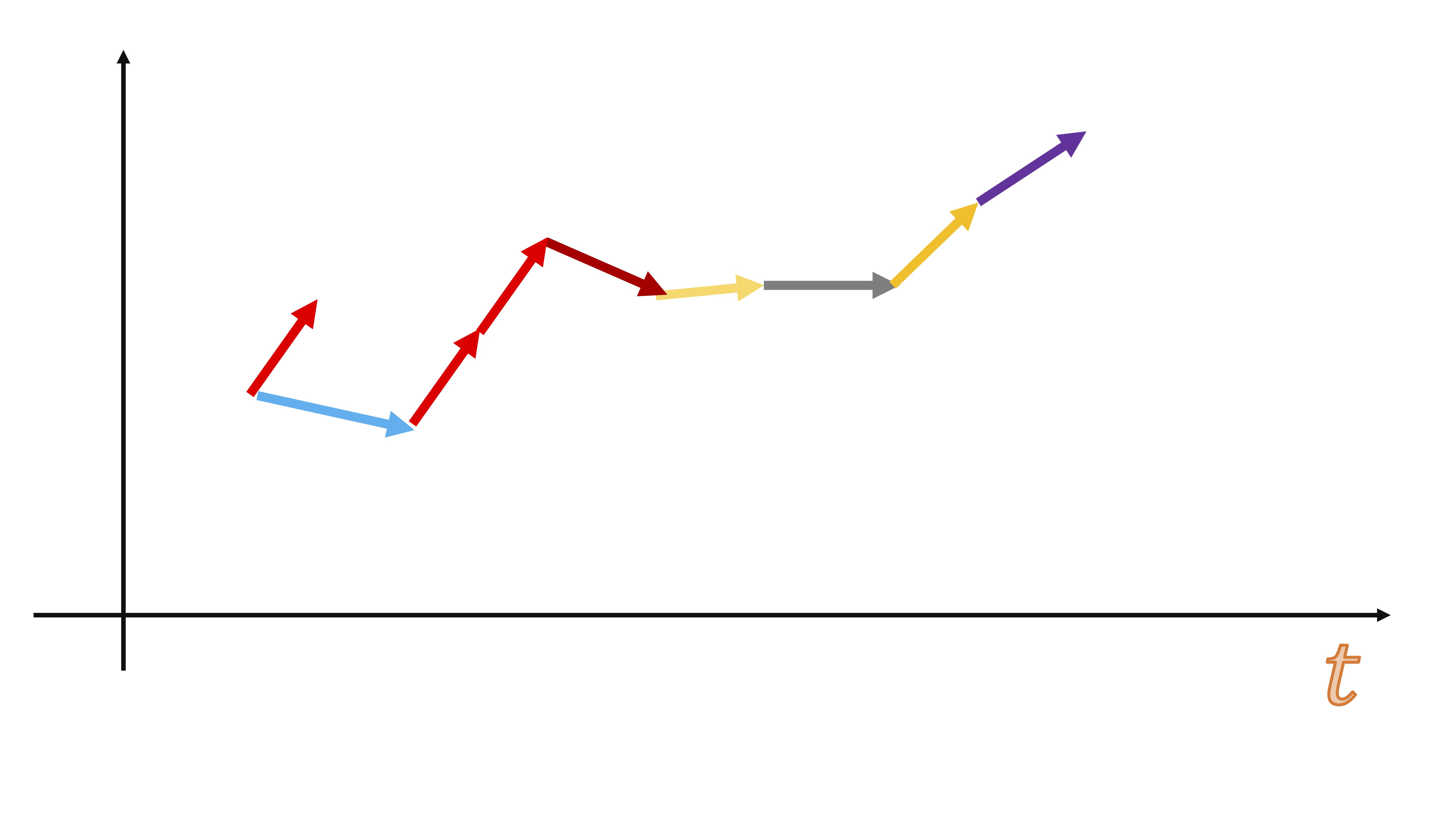FIG 3:Un ejemplo de un muestreo con reemplazamiento es decir, sería equivalente a tener datos de paro (inflación, beneficios, ventas, etc…) y juntar mezclarlos aleatoriamente ¿qué podría analizar de eso? nada, puesto que en una serie temporal su tendencia es uno de los componentes más importantes.

La idea del bootstrapping en series temporales es la siguiente:

  • Usted parte de su serie temporal

FIG 4:Un ejemplo de una serie temporal >- Ajuste el modelo ARIMA que corresponda

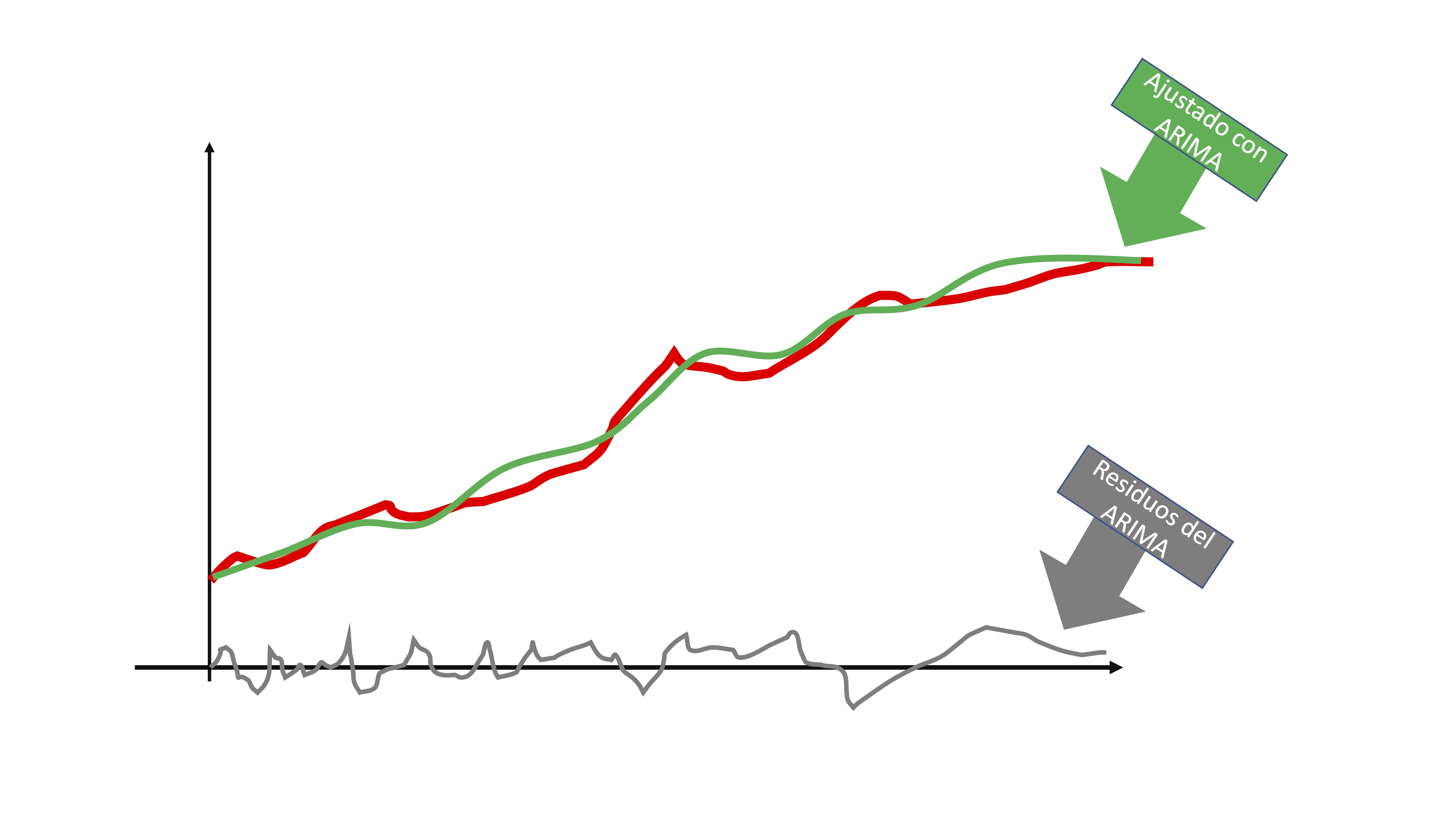FIG 5:modelo ARIMA ajustado entonces, obtendrá dos elementos: la línea verde de la FIG5 que sería la serie que es capaz de predecir con su modelo y la línea gris que son los residuos. Puede interpretar los residuos, al ser i.i.d, como una secuencia de shocks o sorpresas que no puede captar el modelo por ser completamente aleatorio.

  • Remuestree con reemplazamiento esos residuos

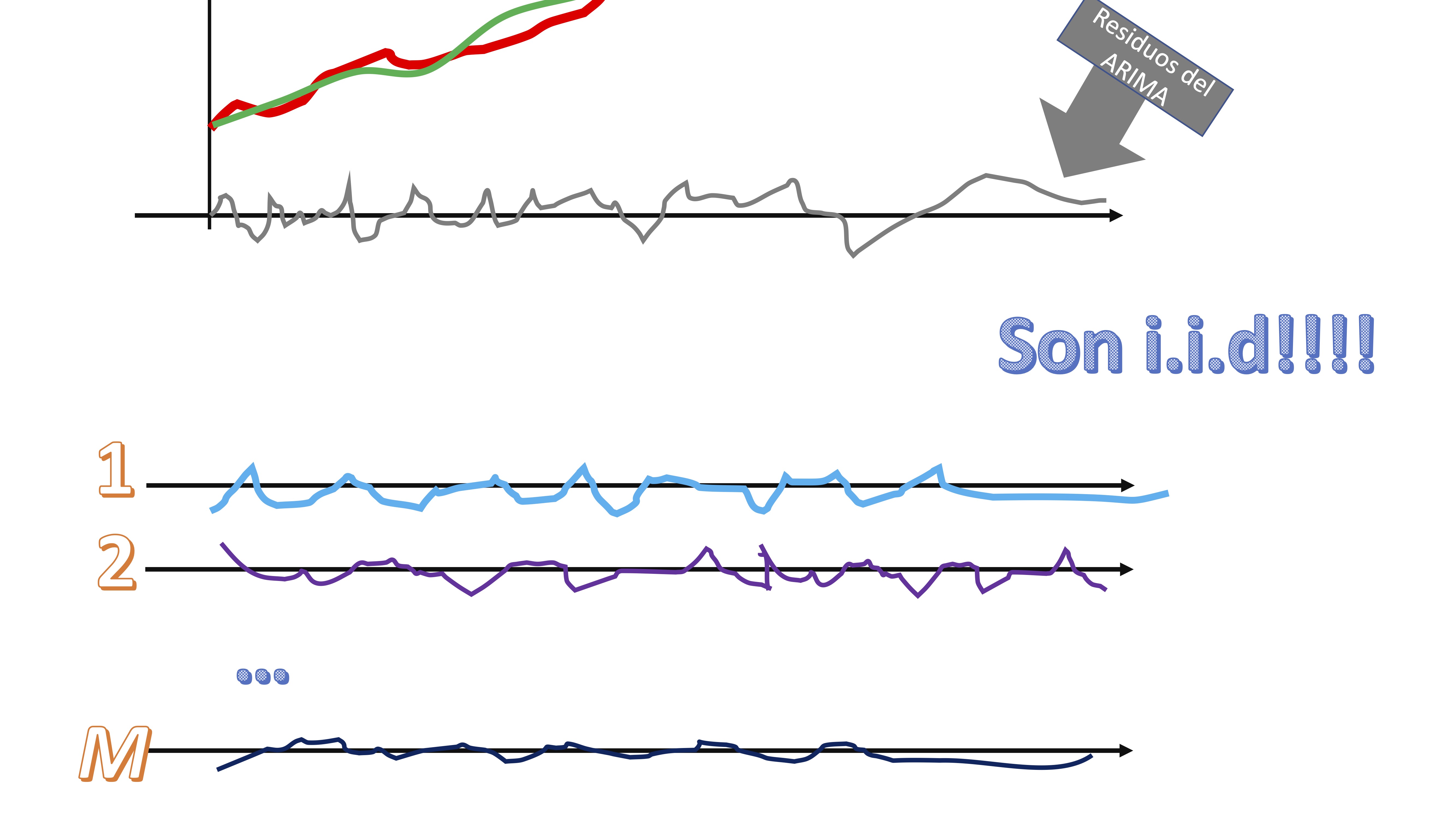FIG 6:Un ejemplo de un muestreo con reemplazamiento claro, los residuos, al ser i.i.d, su orden nos da igual. Tendremos, entonces \(M\) secuencias de “shocks” que podrían haber ocurrido a la serie original.

  • Súmele cada secuencia de shocks a la serie ajustada por el modelo ARIMA y tendrá diferentes versiones de la serie original, afectadas por shocks alternativos

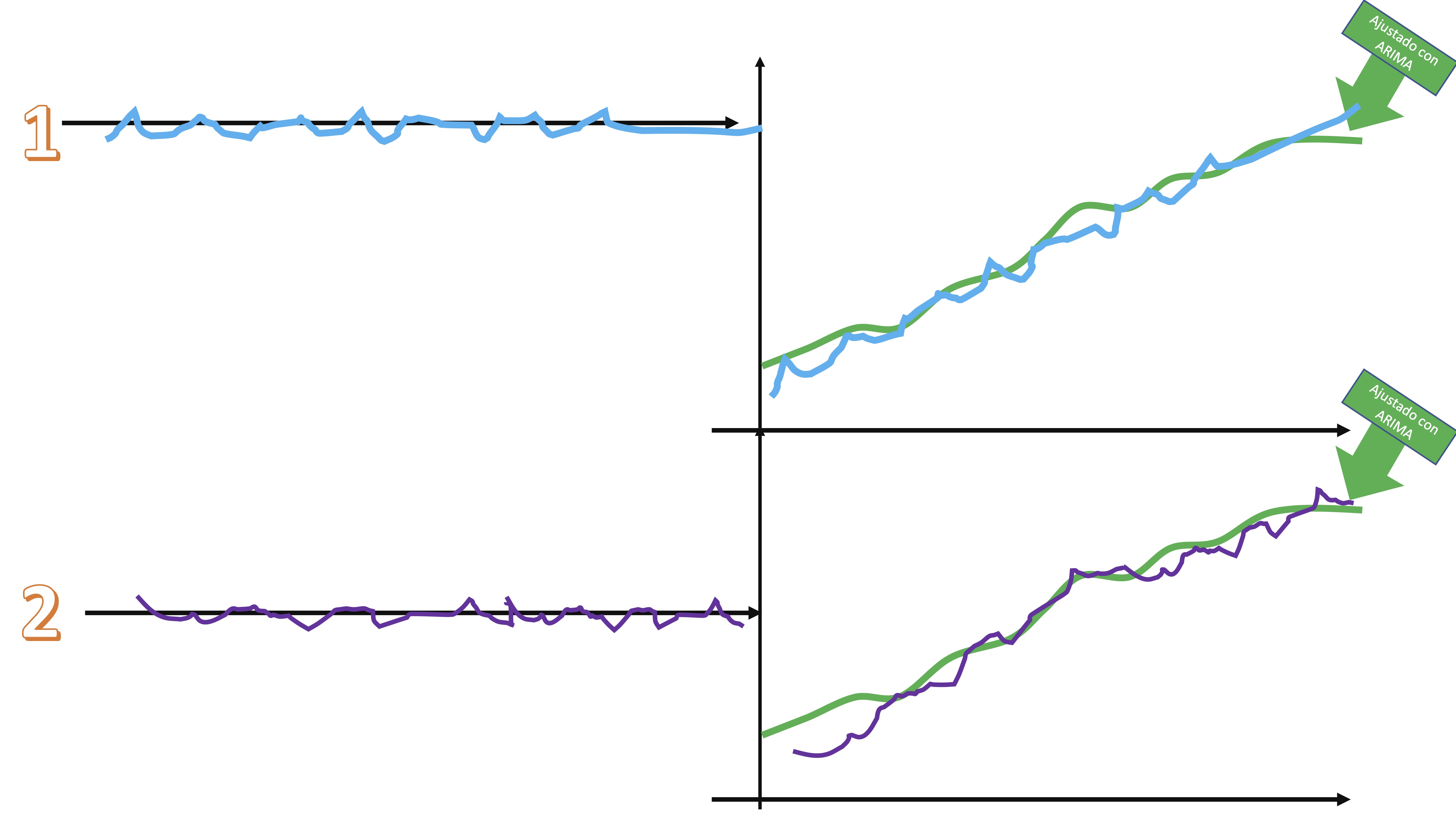FIG 7:Un ejemplo de dos series nuevas Las características principales de la serie no se pierden, pero sí son versiones “perturbadas” de la serie original.

Estime los correspondientes \(M\) modelos ARIMA y obtenga las predicciones. De esta manera, al finalizar, podrá tener distribuciones de la variable aleatoria prevista.

Así puede hacerse en R. Vamos a generar una predicción dos meses adelante (recuerde que la predicción con modelos ARIMA sólo está justificada para horizontes cortoplacistas)

library(readxl)
install.packages("xts")
library(xts)
install.packages("fpp")
library(fpp)
install.packages("forecast")
library(forecast)

#cargamos los datos hasta la última observación disponible
inf <- read_excel("Datos_inflacion_21.xlsx")
inf.t=ts(inf[,2],frequency=12,start=c(1962,1))
ts.plot(inf.t)
n_inf<-window(inf.t, start = c(1980,1), end = c(2022,4))


# generamos una matriz donde guardaremos los 5000 posibles escenarios para los dos horizontes temporales que vamos a usar
FORECAST<-matrix(0,5000,2)
#estimamos el modelo ARIMA que ya reconocimos en su momento
AM1<-Arima(n_inf,order=c(1,1,0), seasonal=c(0,0,1))
#obtenemos los datos ajustados
fitted<-AM1$fitted
#obtenemos los residuos, que es lo que remuestrearemos
res<-AM1$residuals
n<-length(res)
for (i in 1:(5000)){
 
  AM1<-Arima(n_inf,order=c(1,1,0), seasonal=c(0,0,1))
  #almacenamos las predicciones para cada horizonte (1,2)
  FORECAST[i,1]<-forecast(AM1,h=2)$mean[1]
  FORECAST[i,2]<-forecast(AM1,h=2)$mean[2]
  #remuestreamos el error a través de los residuos
  new_error<-sample(res, n, replace = TRUE) 
  #importante: para no sesgar los resultados, nos aseguramos que
  #el error tenga media cero
  m_error<-mean(new_error)
  new_error<-new_error-m_error
  #damos estructura de serie temporal al nuevo error
  new_error.t=ts(new_error,frequency=12,start=c(1980,1))
  #generaamos la nueva serie temporal
  n_inf<-fitted+new_error.t
   
}

Entonces, podemos obtener predicciones para los dos meses a partir de los que tenemos información.

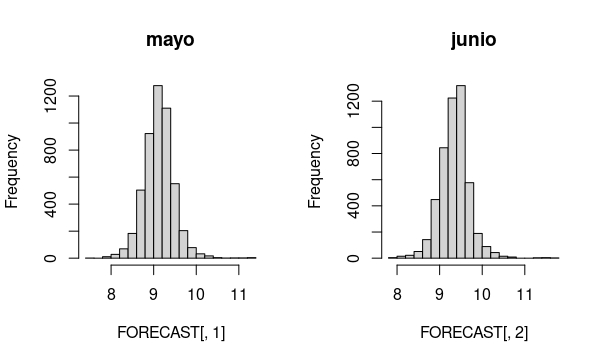FIG 8:Un ejemplo de la predicción para mayo y para junio De aquí podemos hacernos preguntas. Por ejemplo,

  • ¿Qué probabilidad hay de que la inflación en el mes de mayo esté entre el 8.5 y el 9%?

Deberemos contar cuántas veces la predicción está en esa zona y dividirlo por el total de simulaciones (5000 en este caso)

Prob<-sum(FORECAST[,1]>=8.5&FORECAST[,1]<=9)/length(FORECAST[,1])

Obtenemos que hay un 31% de probabilidad de dicho escenario. Por cierto, una recomendación: no debería pronunciarse excesivamente sobre si un 31% es mucho o poco. Este hilo de Twitter de Kiko Llaneras lo explica muy bien: https://twitter.com/kikollan/status/1294926143758508033

Al final, no perdamos de vista que un 25% de probabilidad para un suceso “es tan raro o tan frecuente como sacar cruz dos veces o ver a Messi fallar un penalti”.

Aquí se acaba el curso. Siento que haya sido tan aburrido como para que la asistencia fuera la que ha sido. De hecho, la asistencia de un gran porcentaje de ustedes ha sido tan infrecuente como que el profesor de la asignatura, que nunca ve fútbol, vea a Messi acertar un penalti

Extra: La función de predicción de los modelos AR,MA

A continuación, vamos a analizar cómo obtener predicciones de los modelos que se han presentado anteriormente. Lo vamos a hacer únicamente para un AR(1) y un MA(1) ya que, una vez entendido el proceso de predecir, el resto se realiza de la misma forma (y resulta engorroso, dado lo que se puede aprender de ello). La predicción se entenderá como una esperanza condicionada \(E(*|I_{t})\) de la información de la que se dispone en un momento del tiempo. Esa información la llamaremos \(I_{t}\) con el subíndice indicando hasta qué momento disponemos de esta. Es un conjunto de datos, de tal forma que \(I_{t}=\{y_{t},y_{t-1},y_{t-2},....,y_{0},u_{t},u_{t-1},....,u_{0}\}\). Entonces, la expresión

\[ E\left(y_{t+h}|I_{t}\right) \]

significará: “la predicción que podemos hacer con toda la infomación que tenemos en tiempo \(t\), a horizonte \(t+h\) del proceso \(\left\{ y_{t}\right\}\)”.

Modelo AR(1)

Sea el modelo

\[\begin{equation} y_{t}=c+\phi y_{t-1}+u_{t},\label{eq:AR1} \end{equation}\]

con \(u_{t}\overset{i.i.d}{\sim}(0,\sigma^{2})\), definiremos la predicción a horizonte \(h=1\) como

\[ E\left[y_{t+1}|I_{t}\right]=E\left[c|I_{t}\right]+\phi E\left[y_{t}|I_{t}\right]+\left[u_{t+1}|I_{t}\right] \]

  • \(E\left[c|I_{t}\right]=c\) La esperanza de una constante es ella misma
  • \(E\left[y_{t}|I_{t}\right]=y_{t}\) La esperanza de la serie en el momento \(t\) es ella misma: ¡la conocemos!
  • \(E\left[u_{t+1}|I_{t}\right]=0\) La esperanza de un error futuro es cero. Es el mejor valor que podemos dar

por tanto, la mejor predicción para el periodo siguiente será \[ E\left[y_{t+1}|I_{t}\right]=c+\phi y_{t} \]

y el error de previsión que se comete es la diferencia entre la previsión y el modelo teórico (\(\ref{eq:AR1}\)) . Llamaremos \(e(1)\) al error de previsión a horizonte \(1\) \[ e(1)={\underbrace{c+\phi y_{t}+u_{t+1}}_{te\acute{o}rico}}{\underbrace{-c-\phi y_{t}}_{previsi\acute{o}n}}=u_{t+1}. \]

Por otro lado, la varianza del error de previsión a horizonte 1, será \[ V\left[e\left(1\right)\right]=V\left[u_{t+1}\right]=\sigma^{2}. \]

Un intervalo de predicción aproximado -con la expresión “aproximado”, se pretende indicar que: (1) si el error del modelo se distribuye Normal, y la muestra es pequeña, se deberá utilizar la distribución \(t\) para la obtención de los valores críticos. Si la muestra es grande (más de 100 elementos), dicha distribución se aproximará , vía TCL, por una normal. (2) Si el error no se distribuye normal (pero es i.i.d) pueden usarse argumentos del TCL para aproximar el valor crítico necesario por una Normal- será \[ y_{t+1}\in\left[\underbrace{c+\phi y_{t}}_{previsi\acute{o}n}\pm\underbrace{N(0,1)}_{valor\:cr\acute{\imath}tico}\underbrace{\sigma}_{desv\:t\acute{\imath}pica\:error\:previsi\acute{o}n}\right]. \]

A horizonte 2 (pero con el conjunto de información situado en el periodo \(t\)), tendremos lo siguiente

\[ E\left[y_{t+2}|I_{t}\right]=E\left[c|I_{t}\right]+\phi E\left[y_{t+1}|I_{t}\right]+\left[u_{t+2}|I_{t}\right] \]

De nuevo,

  • \(E\left[c|I_{t}\right]=c\)
  • \(E\left[y_{t+1}|I_{t}\right]=c+\phi y_{t}\)
  • \(E\left[u_{t+2}|I_{t}\right]=0\)

por tanto, la mejor predicción a horizonte 2 será \[ E\left[y_{t+2}|I_{t}\right]=c+\phi\left[c+\phi y_{t}\right]=c+\phi c+\phi^{2}y_{t} \]

y el error de previsión que se comete es la diferencia entre la previsión y el modelo teórico (\(\ref{eq:AR1}\)). Llamaremos \(e(2)\) al error de previsión a horizonte \(2\) \[ e(2)={c+\phi c+\phi^{2}y_{t}+\phi u_{t+1}}+u_{t+2}}-{c-\phi c-\phi^{2}y_{t}}=\phi u_{t+1}+u_{t+2} \]

la varianza del error de previsión a horizonte 2, será \[ V\left[e\left(2\right)\right]=V\left[\phi u_{t+1}+u_{t+2}\right]=\sigma^{2}(1+\phi^{2}) \]

y un intervalo de predicción aproximado será, entonces \[ y_{t+2}\in\left[c+\phi c+\phi^{2}y_{t}\pm N(0,1)\sigma\sqrt{1+\phi^{2}}\right] \]

(Mire el que se ha hecho a horizonte 1, para comprender este).

Si seguimos haciendo cuentas, podemos ver cómo la función de predicción (es decir, aquella que nos informa de la predicción a cada periodo del horizonte \(h\)) será

\[ E\left[y_{t+h}|I_{t}\right]=c(1+\phi+\phi^{2}+...+\phi^{h-1})+\phi^{h}y_{t} \]

de tal forma que, a largo plazo (es decir, si \(h\rightarrow\infty)\), diremos que \[ E\left[y_{t+h}|I_{t}\right]=\frac{c}{1-\phi}\:\:h\rightarrow\infty \]

es decir, la predicción a largo plazo de un modelo AR(1) converge a la media incondicional del proceso. El error de previsión a horizonte \(h\), será un media móvil de periodo \(h\), es decir

\[ e(h)=\phi u_{t+1}+\phi^{2}u_{t+2}+...+\phi^{h}u_{t+h} \]

Asimismo, la varianza del error de previsión será, entonces, \[ V\left[e(h)\right]=\phi^{2}\sigma^{2}+\phi^{4}\sigma^{4}+... \]

donde, si \(h\rightarrow\infty\), entonces, a largo plazo, la varianza convergerá a \[ V(e(h))=\frac{\sigma^{2}}{1-\phi^{2}}\:h\rightarrow\infty \]

De tal forma que el intervalo de confianza a largo plazo para la previsión, lo realizamos con la media y la varianza del proceso:

\[ y_{t+h}\in\left[\frac{c}{1-\phi}\pm N(0,1)\frac{\sigma}{\sqrt{1-\phi^{2}}}\right]\:\:h\rightarrow\infty \]

Como puede ver, el principal interés de un modelo ARMA es la predicción a corto plazo utilizando la información disponible en el momento \(t\). A largo plazo, la predicción de dicho modelo converge a la media y varianza del proceso que, en principio, es una predicción más pero no está basada en informacián adicional (por ejemplo, relación con otras variables)

Respecto a un modelo MA(1), podemos hacer algo similar. Exponemos el modelo y su esperanza condicionada a horizonte 1

\[\begin{equation} y_{t}=c+u_{t}+\theta u_{t-1}\label{eq:AR1-1} \end{equation}\]

\[ E\left[y_{t+1}|I_{t}\right]=E\left[c|I_{t}\right]+E\left[u_{t+1}|I_{t}\right]+\theta E\left[u_{t}|I_{t}\right], \] de donde sabemos que

por tanto, la mejor predicci?n para el periodo siguiente \[ E\left[y_{t+1}|I_{t}\right]=c+\theta u_{t} \]

y el error de previsi?n que se comete, de nuevo, consiste en restar (\(\ref{eq:AR1-1}\)) y la predicci?n. Llamaremos \(e(1)\) al error de previsi?n a horizonte \(1\) \[ e(1)={\color{blue}c+u_{t+1}+\theta u_{t}}{\color{red}-c-\theta u_{t}}=u_{t+1} \]

la varianza del error de previsi?n a horizonte 1, ser? \[ V\left[e\left(1\right)\right]=V\left[u_{t+1}\right]=\sigma^{2} \]

y un intervalo de predicci?n aproximado ser? \[ y_{t+1}\in\left[c+\theta u_{t}\pm N(0,1)\sigma\right] \]

A horizonte 2 (pero detenidos en el periodo \(t\)), tendremos lo siguiente

\[ E\left[y_{t+2}|I_{t}\right]=E\left[c|I_{t}\right]+E\left[u_{t+2}|I_{t}\right]+\theta E\left[u_{t+1}|I_{t}\right] \]

por tanto, la mejor predicci?n a horizonte 2 ser? \[ E\left[y_{t+2}|I_{t}\right]=c \]

y el error de previsi?n que se comete es la diferencia entre la previsi?n y el modelo te?rico (\(\ref{eq:AR1-1}\)) y la predicci?n. Llamaremos \(e(2)\) al error de previsi?n a horizonte \(2\) \[ e(2)=c+u_{t+2}+\theta u_{t+1}-{\color{red}c}=u_{t+2}+\theta u_{t+1} \]

la varianza del error de previsi?n a horizonte 2, ser? \[ V\left[e\left(2\right)\right]=V\left[u_{t+2}+\theta u_{t+1}\right]=\sigma^{2}(1+\theta^{2}) \]

y un intervalo de predicci?n aproximado \[ y_{t+2}\in\left[c\pm N(0,1)\sigma\sqrt{1+\theta^{2}}\right] \]

Si seguimos haciendo cuentas, podemos ver c?mo la funci?n de predicci?n (es decir, aquella que nos informa de la predicci?n a cada periodo del horizonte \(h\)>1) ser?

\[ E\left[y_{t+h}|I_{t}\right]=c \]

de tal forma que, a largo plazo (es decir, si \(h\rightarrow\infty)\), diremos que \[ E\left[y_{t+h}|I_{t}\right]=c\:\:h\rightarrow\infty \]

es decir, la predicci?n a largo plazo de un modelo MA(1) converge a la media incondicional del proceso (recuerda de la clase 5). De hecho, converge a ese valor cuando \(h\) es mayor que el orden del media m?vil (en este caso, es de orden 1, por lo que a horizonte 2 ya converge a la predicci?n de largo plazo). Por otro lado, el error de previsi?n a horizonte \(h\), ser? un media m?vil de periodo \(1\), es decir

\[ e(h)=u_{t+h}+\theta u_{t+h-1} \]

Asimismo, la varianza del error de previsi?n ser?, entonces, \[ V\left[e(h)\right]=\sigma^{2}(1+\theta^{2}) \]

donde, si \(h>1\), entonces, a largo plazo, ser? \[ V(e(h))=\sigma^{2}(1+\theta^{2})\:h>1 \]

De tal forma que el intervalo de confianza a largo plazo para la previsi?n, lo realizamos con la media y la varianza del proceso:

\[ y_{t+h}\in\left[c\pm N(0,1)\sigma\sqrt{1+\theta^{2}}\right]\:\:h>1 \]