BLOQUE 1: Introducción a la minería de datos

Clase 1. La realización de preguntas en ciencia (de datos)

Estos apuntes están pensados para desarrollar ciertas habilidades del futuro científico de datos. Contrariamente a lo que pensará, no es una profesión concebida únicamente para desarrollar nuevas metodologías de análisis de datos (lo cual no ocurre todos los días), ni en ser capaz de saberse más líneas de código de memoria o hacer scripts de [R] o Python sin despeinarse. Una primera misión del científico de datos consistirá en tener una filosofía de trabajo basada, fundamentalmente, en establecer un conjunto de preguntas de interés y, como consecuencia de ello, tener un conjunto de habilidades analíticas y técnicas para indagar en las posibles respuestas.

Desde ya, el científico de datos tendrá que asumir que:

• las preguntas que realice deberán formularse con la mayor precisión posible
• no siempre la respuesta está clara: esta profesión implica entender la incertidumbre asociada a un resultado que viene dada por los datos disponibles
• las respuestas, muchas veces, son compatibles con diversas hipótesis iniciales
• no hay una única técnica para abordar un proyecto (o una parte de un proyecto), ni consiste en hacer el trabajo tirando de recetas. En estadística, en general, no hay técnicas prohibidas, sino que es más conveniente ser capaz de entender las limitaciones de estas a la hora de aplicarlas a un conjunto de datos.
• sin embargo, esta profesión puede ser todo lo estimulante que uno quiera: los datos siempre son un reto y una buena excusa para pensar, discutir y, por qué no, sentir el placer de entender algo más este mundo.

Por lo tanto, lo primero por lo que vamos a empezar es por aprender a realizar preguntas. ¿Pero es que no sabemos hacerlas? Sí sabemos! De hecho, sabemos más de lo que creemos, pero debemos entender la sutileza entre una buena pregunta en ciencia y una pregunta con pocas posibilidades. De nuevo, lo que viene a continuación es un conjunto de ideas de cómo deberíamos plantearnos una pregunta adecuada. No son mandamientos, por lo que son discutibles y revisables. Imaginemos que tenemos un conjunto de datos sobre ventas y gastos realizados en publicidad de una marca.

Preguntas concretas: Lo normal es empezar pensando: una pregunta puede ser ¿cómo afecta el gasto en publicidad en mis ventas?. El problema de esa pregunta es que, en general, es demasiado amplia y ya sabemos la respuesta “afecta mucho” (seguramente). Ante una pregunta vaga, una respuesta vaga. Debemos pensar en otras opciones. Si el cliente nos pregunta ¿cómo afecta el gasto en publicidad? Nosotros tenemos el deber de reformularla y, por supuesto, confirmar si son enfoques válidos. Es decir, no debemos tener miedo en repreguntar

Por ejemplo:

• ¿Cuántas semanas dura el impacto de un incremento en el gasto en publicidad sobre las ventas?

• ¿Tiene algún umbral mínimo y máximo el efecto del gasto en publicidad sobre las ventas?

• ¿Se producen efectos cruzados entre un incremento del gasto en publicidad y una estrategia en precio sobre las ventas?

Estas preguntas se diferencian de la primera en que tratan de enfocarse en un aspecto concreto de la posible relación entre el gasto en publicidad y las ventas. Dirigen a la persona a realizar un conjunto de anílisis acotados y, por supuesto, a poder tener más claro en qué tipo de datos y de experimentos deberá concentrarse.

Preguntas cuantificables, medibles: De nuevo, hay que enfocar la pregunta a forzar una respuesta cuantitativa. Los métodos con que se trabaja en este campo pretenden cuantificar efectos e indagar en la incertidumbre asociada a esas mediciones. Por tanto, hay que ir en esa línea.

• ¿Cómo de probable es que la elasticidad precio de mi producto sea mayor que la unidad?

• ¿En qué porcentaje se reducirán las ventas el año que viene con el cierre de dos centros de producción?

• ¿Cómo de rentable es la publicidad en la marca asociada al coste estacional de dicha inversión?

Evitar un clásico: análisis de los determinantes de… es muy común creer que, en general, con estas metodologías uno puede responder con claridad a la pregunta de cuáles son los determinantes de un hecho de interés (las ventas de un producto, el precio de la electricidad, etc…). Lamentablemente, esa pregunta no suele ser interesante porque, en general, se requiere un modelo teórico claro que testar-el cual, especificará de antemano dichos determinantes- y el analista, en todo caso, será quien cuantifique dichos impactos. Sin embargo, esta pregunta suele ser pretenciosa y difícil de abordar, si no imposible, con las técnicas existentes, en general.

¿Qué viene primero: el set de datos o la pregunta? En realidad, eso no es muy importante. Una pregunta puede venir estimulada por un análisis del conjunto de datos disponible y de ideas previas del analista. Lo contrario también es factible: una pregunta dada permitirá hacer acopio de los datos necesarios para tratar de responderla.

EJERCICIO

Piense en preguntas que le estimulen y busque, entre las bases de datos que hay en internet, un posible conjunto de datos para intentar responderlas. Dele varias vueltas a la luz de los datos que ha encontrado

Clase 2 Aspectos relevantes en la modelización estadística (I): el análisis descriptivo

(por escribir la introducción y/ ejemplos)

Imagine que se encuentra la siguiente relación entre dos variables:

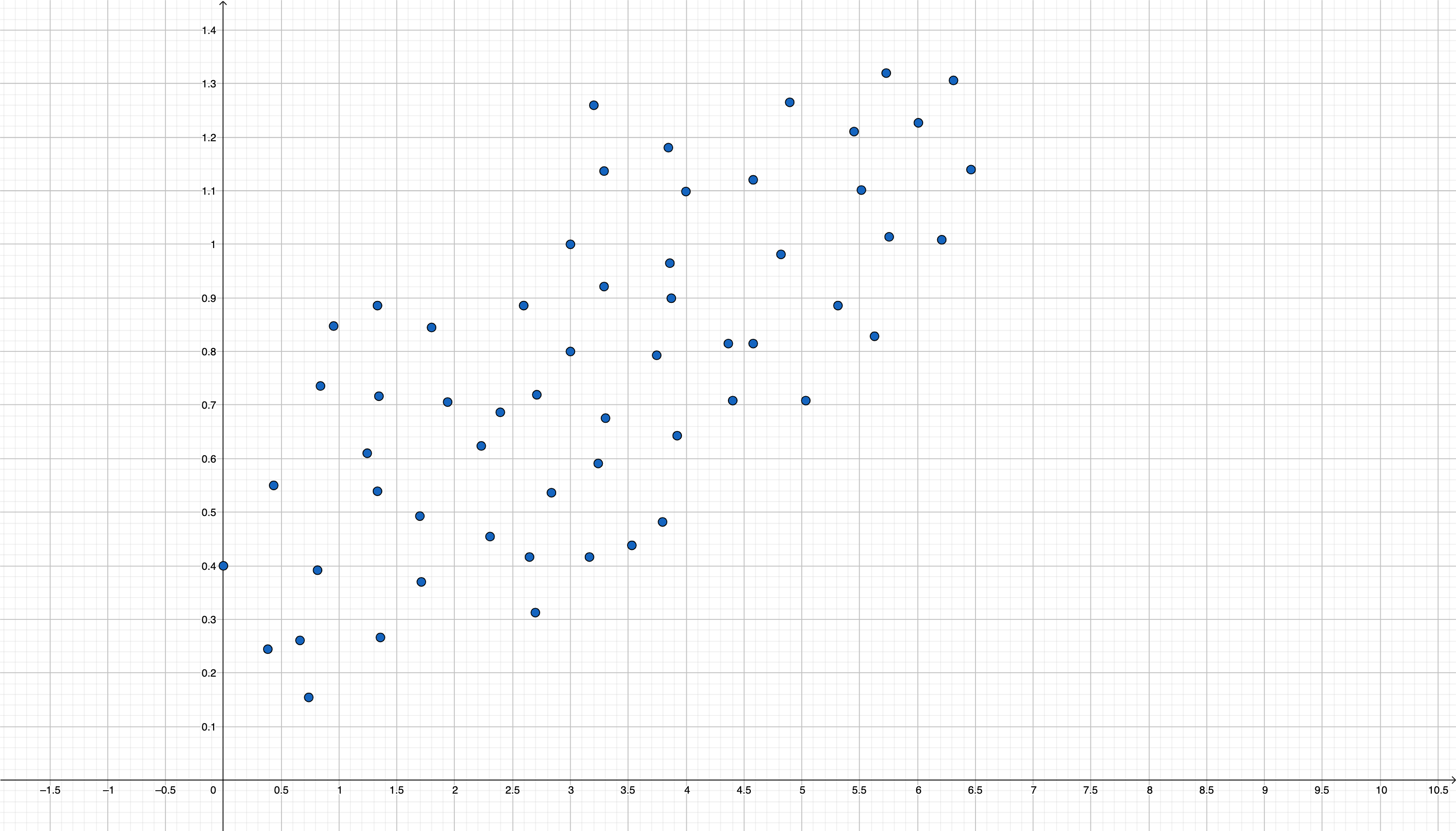
FIG 1. Posible nube de puntos que relaciona virus con consumo de vitamina C

vamos a asumir que el eje \(x\) se corresponde con dosis de vitamina C y el eje \(y\) se corresponde con cantidad de virus en el cuerpo.

A simple vista uno puede pensar que la relación entre el consumo de vitamina C y la cantidad de virus es positiva. Es decir, el consumo de vitamina C no es favorable para reducir la cantidad de virus en el organismo.

Esto, a priori, suena extraño:

OJO

Un análisis de datos debería estar acompañado de cierto modelo teórico (basado, en general, en evidencias científicas previas) sobre la posible relación entre las variables. Nosotros aspiraremos a cuantificar dichos efectos o, en su caso, a realizar predicciones basadas en esas teorías.

En este caso, en realidad estaremos ante lo que se conoce como la pradoja de “Simpson-Yule”. La relación que estamos viendo en el gráfico procede de muestras asociadas a poblaciones distintas. De esta forma, si separamos dichas poblaciones (quizás usando una variable de interés omitida), podamos encontrar la verdadera relación entre las variables

En este caso, podemos pensar que hay grupos con distinto nivel de “inmunidad” y que, por tanto, necesitan mayores cantidades de vitamina C. Una posible relación que no puede verse a simple vista sería

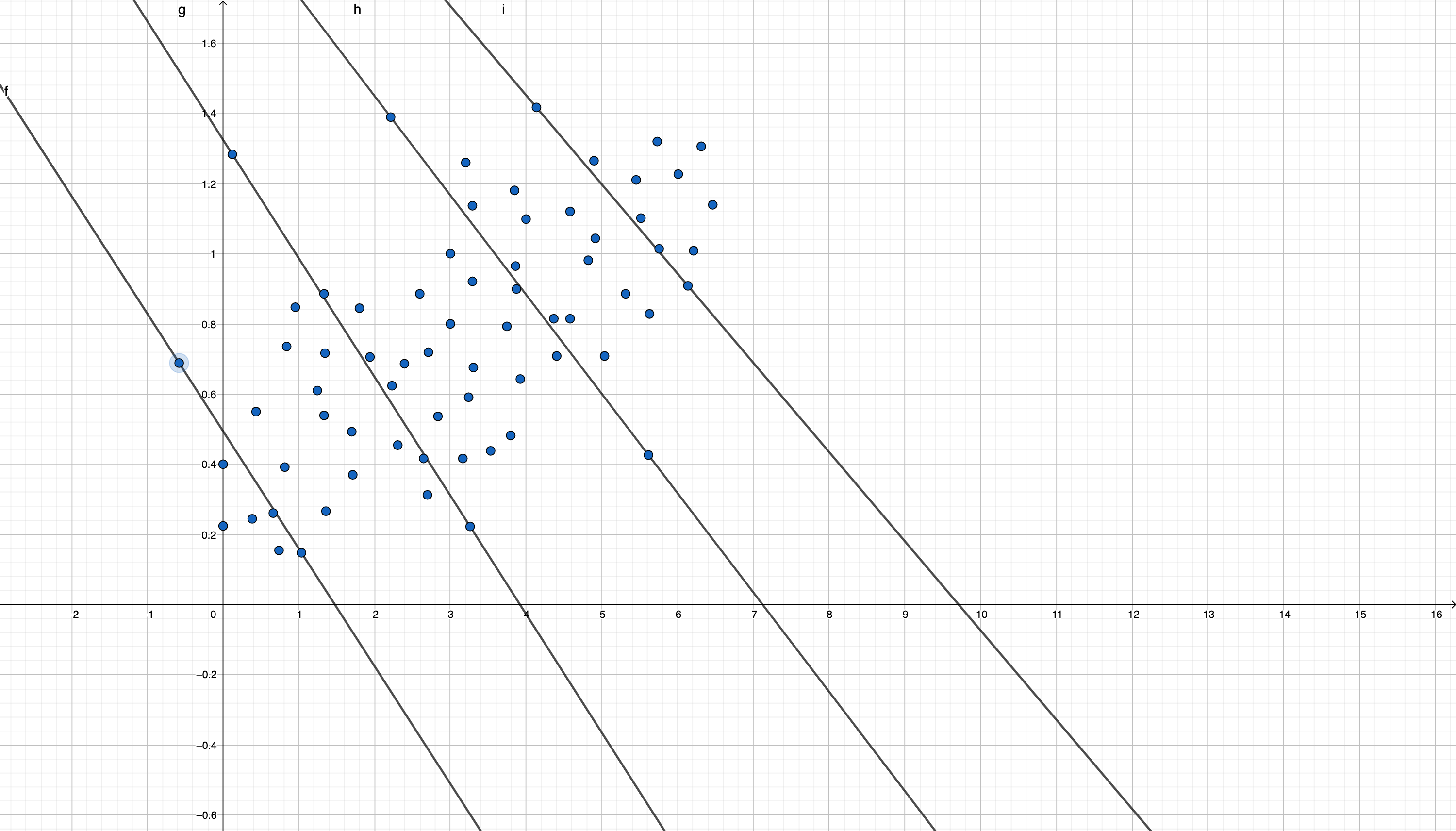En estos subgrupos la relación entre consumo de vitamina C y cantidad de virus será, ahora, negativa.

Es complicado, en general, tener claras estas cosas en un primer contacto con los datos. El analista/científico/consultor ha de pararse a pensar sobre todas estas posibilidades antes de avanzar en el trabajo. En el curso se irá discutiendo la habilidad de ciertas metodologías para detectar posibles “paradojas”. Sin embargo, no hay una regla clara y cada caso es posible que sea un mundo.

• Si le interesa leer más acerca de la paradoja de Simpson-Yule, tiene a su disposición:

1. Este hilo de Twitter https://twitter.com/dadosdelaplace/status/1420294893797355526?lang=es
2. Esta entrada en un blog https://blogs.elpais.com/alternativas/2017/07/caf%C3%A9-salud-y-la-paradoja-de-simpson.html
3. Esta noticia de un periódico: https://elpais.com/ciencia/2021-07-26/infecciones-en-vacunados-de-covid-19-la-utilizacion-sin-contexto-de-datos-estadisticos-conduce-a-conclusiones-falsas.html

Clase 3 Aspectos relevantes en la modelización estadística (II): la causalidad

En general, cuando pretendemos acercarnos a un conjunto de datos con la idea de analizarlos, una vez formulamos la pregunta que tenemos en mente, solemos tener muy claro qué variable queremos predecir y cuáles serán los predictores. De una manera abstracta, tendremos algo as?:

\[ (x_{1},x_{2},...,x_{n},u)\mapsto y \]

de tal forma que estamos indicando que un conjutno de inputs \(x_{1},x_{2},...,x_{n}\) y un error aleatorio \(u\) tienen impacto sobre la variable “output” \(y\). Da lo mismo qué función vincule a esas variables, puesto que lo que vamos a contar aquí se puede generalizar a la mayor parte de metodologías que aprenderemos durante el curso.

Vamos a ver diferentes ejemplos que tienen, como objetivo, llamarnos la atención sobre el entrenamiento de modelos de manera sistemática.

1.0.1 Los datos de la Liga de Fútbol

Disponemos de datos (football-data.co.uk/spainm.php) de la liga española en la temporada 2019/20. Una pregunta de interés para cualquier analista (para ser usada, por ejemplo, en beneficio personal en apuestas \(\clubsuit\)) tendrá que ver con la capacidad de predecir adecuadamente el resultado de un conjunto de partidos de fútbol. En nuestro caso, pretendemos saber si

Podemos predecir los goles de los equipos (local FTHG y visitante FTAG), utilizando-para ello- el resultado conocido en el primer tiempo del partido

Un primer paso necesario para realizar cualquier análisis es conocer bien el conjunto de los datos con los que trabajaremos. Es habitual preguntarse <> tienen las posibles variables predictoras con la variable que intentamos predecir. Ojo con la palabra correlación:

El coeficiente de correlación (llamado habitualmente \(\rho\)) mide el grado de relación lineal entre dos variables, donde \(-1\leq\rho\leq1\). Por lo tanto:

• No es cierto que dos variables con correlación baja no están relacionadas (cualquier relación no lineal- por ejemplo, parabólica, logarítmica, etc…- tendrá un coeficiente de correlación bajo)
• No es cierto que dos variables con correlación alta implicará que una tenga un alto poder predictivo sobre la otra (no deberíamos confundir la causalidad con que exista una relación estadística-regularidad empírica- entre variables).

Para ello, indaguemos en la relación entre las variables del fichero de <>.

Una forma inicial para analizar relaciones entre pares de variables (en este caso, los goles frente a las posibles variables predictoras como los tiros a puerta durante el partido) es mediante el análisis gráfico. Por ejemplo, un gráfico de nube de puntos:

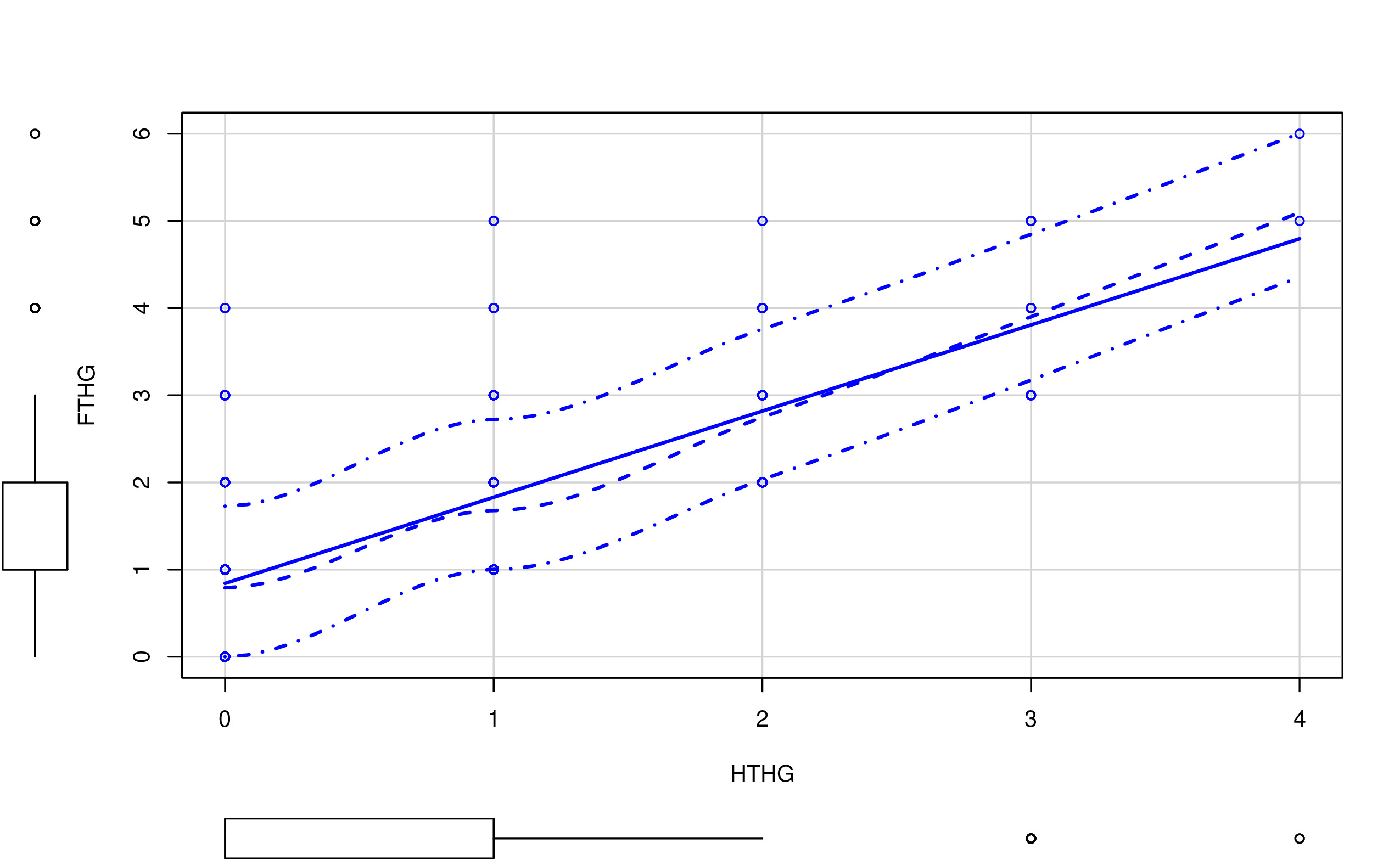
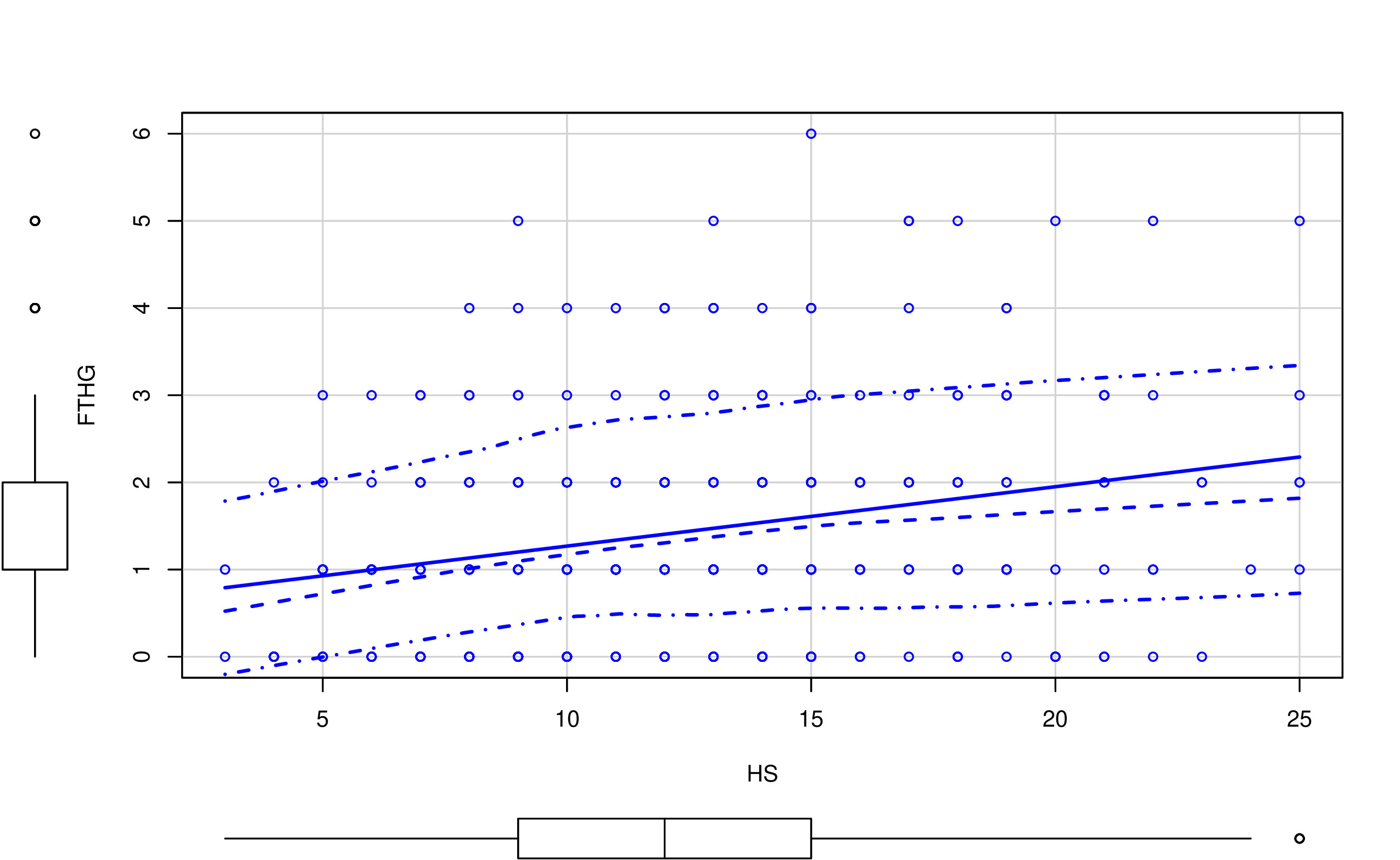
En las FIG1 y FIG2, puedes ver dos tipos de relaciones distintas: por un lado, HTHG y FTHG parecen claramente una relación lineal (y positiva), mientras que HS y FTHG no parecen tener una relación lineal tan clara. De hecho, parece más una relación dónde, para cierto valor de HS, FTHG ya no crece (se satura). Por otro lado, merece la pena destacar:

• Con variables discretas (como puede ser este caso) la nube de puntos está menos justificada. No quiere decir que no se pueda usar (recuerde que en estadística está prohibido prohibir el uso de técnicas)

• Este diagrama de “nube de puntos” añade la distribución univariante de la variable (en forma de diagrama de cajas). Es importante tener también esa información puesto que, antes de entrenar cualquier modelo, uno tiene que conocer perfectamente el tipo de variables que tiene y los valores que cabría encontrarse.

• Por otro lado, tenga cuidado con un gráfico como el de la FIG3. Como ya decimos, podría hacer pasar relaciones importantes (no lineales) entre variables como si estas no existieran.

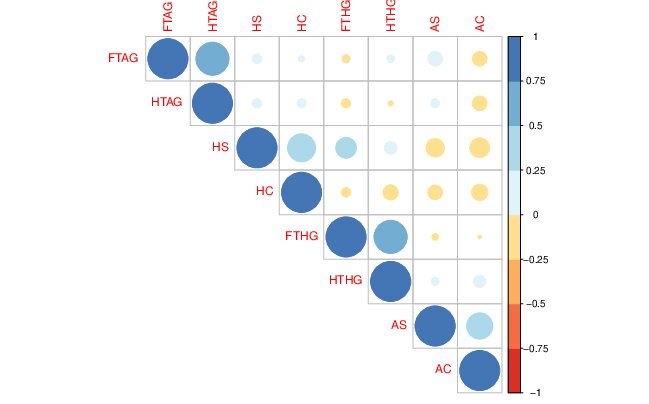
FIG 3. Gráfico de correlaciones.

Este código te permitirá hacer un análisis similar:

LIGA <- read_csv("LaLIGA_FINAL_1920.csv")

install.packages("car")
install.packages("corrplot")
library("car")
library("corrplot")



futbol<-data.frame(LIGA["FTHG"],LIGA["FTAG"],LIGA["HTHG"],LIGA["HTAG"],LIGA["HS"],LIGA["AS"],LIGA["HC"],LIGA["AC"])plot(LIGA["FTHG"],LIGA["HS"])
scatterplot(futbol$HS,futbol$FTHG) # Hace el gráfico de nube de puntos

M<-cor(futbol)
corrplot(M)

Sin embargo, podría ser que todo lo que estamos empezando a hacer, a modo de análisis preliminar, no sirva para mucho:

ARGUMENTO 1

Quiere vivir de predecir resultados de fútbol, apostando y, por lo tanto, ganando dinero a expuertas por ello. ¿Usaría estos datos para entrenar un modelo predictivo? Seguro que no tarda un minuto en responder que NO.

No tiene ningún sentido ser capaz de averiguar el resultado de un partido teniendo, como predictores, los resultados a mitad del partido. Las apuestas se cierran antes de que el partido empiece. Además, ¿de verdad necesita un modelo para predecir el resultado de un partido si ya conoces lo que ha ocurrido hasta el descanso?

ARGUMENTO 2

Regularidad empírica versus causalidad: es habitual encontrar variables que tengan una relación lineal (o no lineal) alta, ¿significa eso algo? desafortunadamente, suele indicar que dichas variables ocurren simultaneamente (quizás bajo la influencia de una variable común que afecta a ambas), aunque también podría ser una relación causal.

El riesgo de tratar con “regularidades empíricas” es que, pese a que tengas un modelo con-aparentemente- buenas propiedades, no será muy útil. Piensa, de nuevo, en el caso del fútbol.

La selección de variables es una tarea clave. No consiste en buscar simplemente variables con un aparente grado de relación, sino hay que pensar en la estructura causal. ¿Qué variable(s) ocurre(n) antes en el tiempo? Cuando quiera predecir tendrá la información disponible de las variables predictoras?

De hecho, con el conjunto de variables que tenemos, no podríamos formular ningún modelo predictivo, ya que todas estas conforman datos de estadísticas relativas al encuentro que se suceden, prácticamente, a la vez. En casos como estos, donde hay simultaneidad entre las variables, resulta difícil acceder a buenas variables predictivas. Esto ocurre también en bases de datos de clientes, por ejemplo, donde las variables predictivas suelen ser un subconjunto bastante inferior al conjunto original de variables. Hacer ciencia de datos no consiste en “probar todas” las relaciones aprovechando la capacidad de cálculo del ordenador. Consiste en sentarse antes con las unidades de negocio correspondientes y tratar de entender qué información del cliente se tiene con antelacón para ser capaz de ver cómo predecir sus movimientos.

Un tema muy importante que, quizás, no se le dedica todo el esfuerzo que se debiera. Seguro que no es la primera vez que te planteas estas cuestiones. Podemos remontarnos al filósofo David Hume, que decía:

CAUSALITY

we may define a cause to be an object, followed by another, and where all the objects similar to the first are followed by objects similar to the second. Or in other words where, if the first object had not been, the second never had existed. According to Hume, causal events are ontologically reducible to noncausal events, and causal relations are not directly observable, but can be known by means of the experience of constant conjunctions (see A Treatise of Human Nature 1739-40, vol. I, book I, part III, section 2-6, 14, 15)

podemos traducirlo, para entendernos, como sigue:

Si el evento A causa al B (\(A\rightarrow B)\), entonces, A antecede en el tiempo a B y la distribución de probabilidades de B cambia si A entra en acción.

Sin embargo, este tema es bastante peliagudo. En ciencias sociales, donde no se experimenta en laboratorios, no está tan claro qué variables causan a cuáles. Por ejemplo, si quiere analizar el efecto que tiene el ratio alumno/profesor sobre la nota de estos, podría pensar que el ratio causa la nota. Pero ¿Y si los alumnos que sacan buenas notas y, por tanto, pueden elegir van a colegios con menores ratios?

Esto, en general, es un tema complicado. En este curso trataremos de usar la lógica y, siempre que se pueda, hacer asunciones sensatas a este respecto.

Predictores perfectos

Imagine que tiene el siguiente set de datos que puede crear con [R]

y<-c(0,0,0,0,1,1,1) 
x1<-c(1,2,3,3,5,6,7)
x2<-c(7,3,4,2,1,0,2)

y, a continuación, analice la posible relación entre la \(y\) y ambas variables \(x_1\) y \(x_2\).

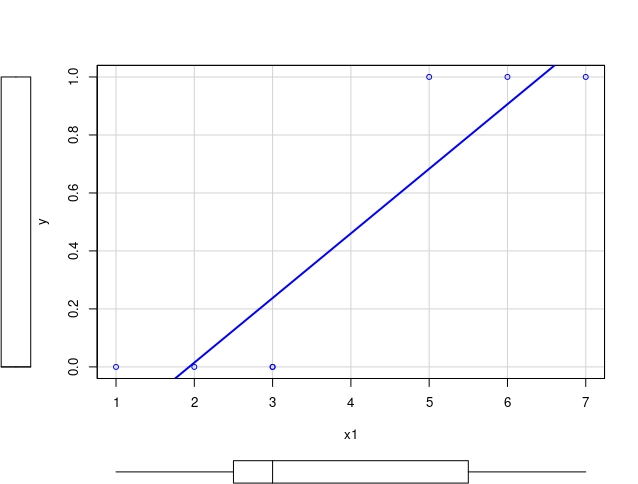
FIG 3.

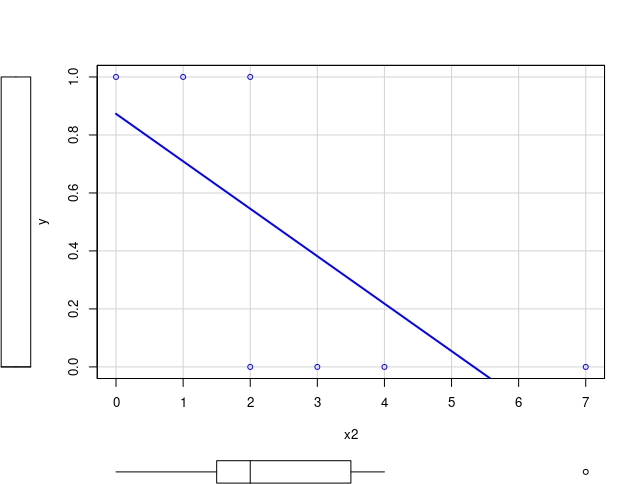
FIG 4.

La variable respuesta o (target) es binaria, ya que se corresponde con una medición de una variable cualitativa (por ejemplo, aprobar/suspender). Si realiza un gráfico de nube de puntos, obtendrá FIG 3 y FIG 4. Podemos observar que:

• la recta de regresión no está prohibida (aún cuando la variable que pretendemos explicar no sea continua) ya que, en este caso, parece que discrimina adecuadamente los 0 y los 1. Generalmente, interpretaremos el resultado de ajustar una recta de regresión como una probabilidad (si estimas la regresión utilizando el comando “lm”, obtendrás para el primer caso) \[ \hat{y}=-0.43+0.22x_{1} \] por ejemplo, si \(x_{1}=6\Rightarrow y|(x_{1}=6)=0.89\) y si elegimos 0.5 como valor umbral para clasificar, diremos que le corresponde una \(y=1\), si \(x_{1}=3\Rightarrow y|(x_{1}=3)=0.23\), por lo que le corresponderá un valor \(y=0.\) Sin embargo, el problema que tiene es que las predicciones se pueden salir de lo sensato (piense qué ocurre si \(x_{1}=1,\) por ejemplo).

• podría ser más sensato ajustar algún modelo que contemple este detalle. Existen varios en la literatura. Los más conocidos son el probit (basado en la función de distribución de una normal) y el logit(basado en la función de distribución logística).

Los modelos probit/logit tienen como función link, es decir -la función que une las observaciones de las variables explicativas con la explicada-, una de la familia de las sigmoideas (con forma de S):

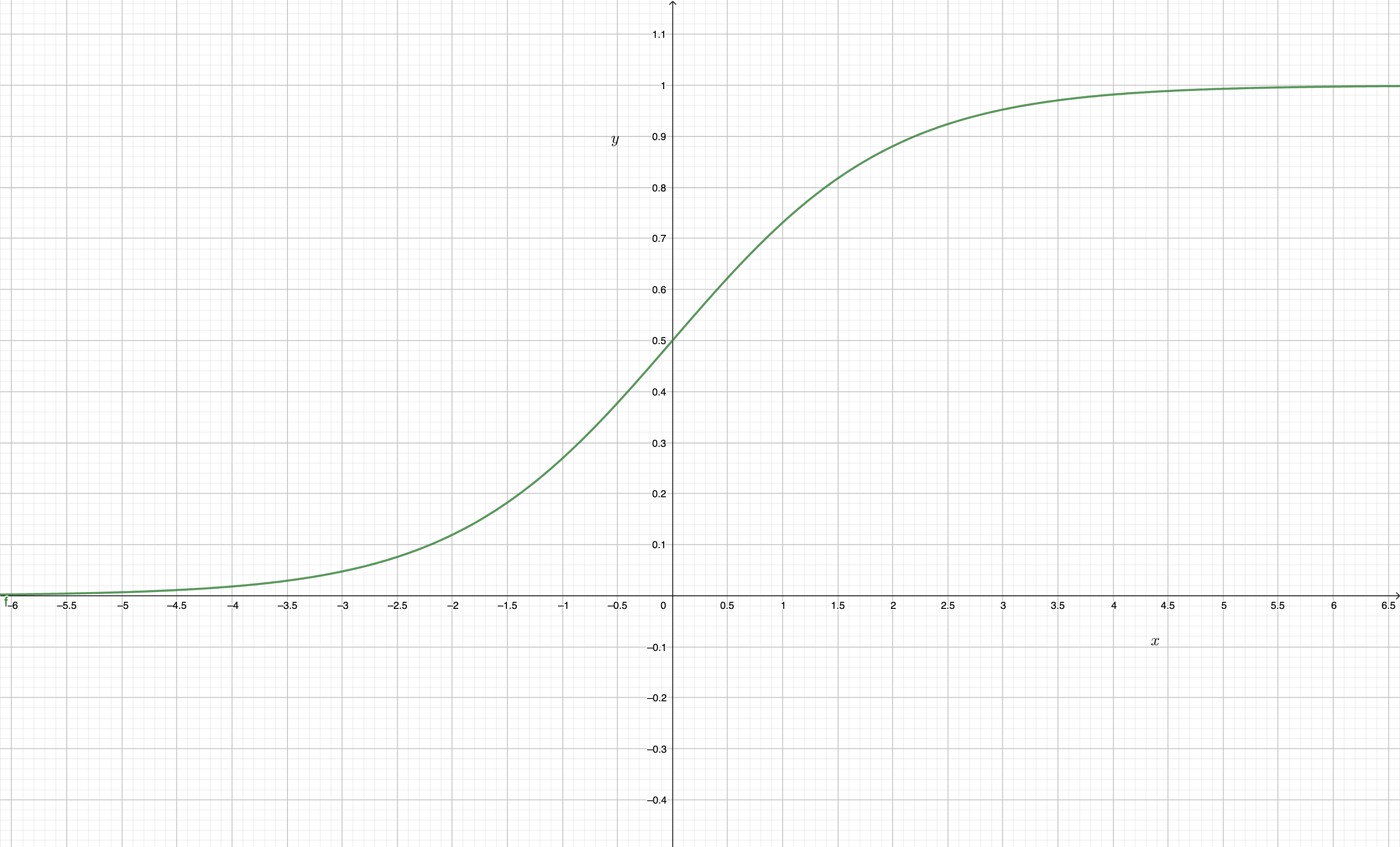
FIG 5: la función sigmoidea (con forma de S) \(f(x)=1/(1+e^{-x})\).

y, como ve, acota tanto la parte superior como inferior de la imagen de la función. Aunque es posible que estos modelos puedan resultar inútiles.

ARGUMENTO 1

si se fija con detenimiento, la variable \(y\) toma valores 0 cuando \(x_{1}\) toma valores inferiores o iguales a 3. Lo contrario cuando \(x_{1}>3\). Cuando pasa esto, se conoce como un problema de <>

Esta idea puede verse desde otra perspectiva:

ARGUMENTO 2

Regularidad empírica versus causalidad: esto suele ocurrir cuando la variable \(y\) y la \(x_{1}\) son la misma variable (imagine que \(y\) es una variable que clasifica individuos que están aprobados o suspensos y \(x_{1}\) es la nota del examen final), o son dos variables que ocurren simultaneamente y, por tanto, no hay una estructura causal adecuada. Es lógico que alguien que saque una mala nota en el examen figure como suspenso. Nos están dando información redundante.

Puede probar a estimar el modelo y comprobará que los resultados de la tabla son algo anormales, ¿no? ¿qué significa “Warning message: glm.fit: fitted probabilities numerically 0 or 1 occurred”?

m1<-glm(y~x1,family=binomial)


Warning message:
glm.fit: fitted probabilities numerically 0 or 1 occurred 

Coefficients:
             Estimate Std. Error z value Pr(>|z|)
(Intercept)    -94.47  190877.72   0.000        1
x1              23.54   46641.45   0.001        1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 9.5607e+00  on 6  degrees of freedom
Residual deviance: 3.3855e-10  on 5  degrees of freedom
AIC: 4

NOTA En el caso del modelo de regresión, \(\hat{y}=-0.43+0.22x_{1}\) la pendiente (0.22) se interpreta como la contrbución marginal sobre la probabilidad de que \(y=1\) ante un incremento unitario en \(x_{1}\). En el caso del segundo modelo, la interpretación del coefciente \(23.54\) no es inmediata: se suele interpretar como un “peso” sobre la probabilidad. Como comprenderá, si diferencia la función logística \(y=\frac{1}{1+e^{-(-94.47+23.54 x_{1})}}\) (y obtiene, por tanto, la derivada con respecto a \(x_{1})\) el impacto sobre la probabilidad dependerá del valor de \(x_{1}\). De hecho, si hubiera más variables, el impacto dependería también del valor del resto de variables. El motivo: es un modelo no lineal.

Desconfíe, por tanto, de esas variables con alta correlación (siendo una la explicada y otra una de las explicativas). Podrían no ser buenas a la hora de predecir.

Ejercicio: Con la base de datos de ensayos clínicos trate de predecir cómo de probable es que alguien con diabetes desarrolle anemia. Hágalo con las primeras 145 observaciones. Piense sobre la posible relación causa efecto (puede buscar en internet) y sobre lo que ha obtenido. ¿Qué le sugiere el resultado restringiendo la muestra? ¿y sin restringir?

Clase 4 Aspectos relevantes en la modelización estadística (IV): el concepto de significación estadística y su uso mecánico

Esto es importante:

IDEA

El uso mecánico del p-valor, como mecanismo “científico” para tomar decisiones estadísticas basadas en modelos, afortunadamente, está generando mucha controversia entre los científicos de datos más relevantes. Las revistas “Nature” y “Science” llevan años publicando artículos de gran impacto llamando la atención sobre este hecho. Vamos a explicar en qué consiste esta crítica en el contexto de un modelo de regresión para, a continuación, discutir sobre ello.

Tengamos como referencia una salida de un modelo de regresión cualquiera:

Call:
lm(formula = y ~ x1)

Residuals:
       1        2        3        4        5        6 
 0.20792 -0.01485 -0.23762 -0.23762  0.31683  0.09406 
       7 
-0.12871 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) -0.43069    0.19276  -2.234  0.07576 . 
x1           0.22277    0.04422   5.037  0.00398 **
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2376 on 5 degrees of freedom
Multiple R-squared:  0.8354,    Adjusted R-squared:  0.8025 
F-statistic: 25.38 on 1 and 5 DF,  p-value: 0.003976

es muy común que el investigador acuda enseguida a la última columna (la del p-valor) y mire el número de asteriscos. En función de ese resultado, enseguida dirá: “el efecto es muy significativo”, “la variable es relevante”. Pronunciarse sobre algo así es controvertido y está sujeto a muchos condicionantes. Tantos, como se verá a continuación, que merecerá la pena pensar si esa es la mejor forma de trabajar para responder a una pregunta con interés científico o social.

Pero, para ello, resulta conveniente analizar con detalle algunos conceptos que ya se han estudiado previamente.

El análisis de regresión: se basa, fundamentalmente, en disponer de un modelo poblacional (sea este el de una regresión simple, fácilmente generalizable a un modelo múltiple)

\[ y_{i}=\beta_{0}+\beta_{1}x_{i}+u_{i}\:\:\:i=1,...,T \]

donde el término de error aleatorio

\[ u\sim N(0,\sigma) \]

idea: si pudiéramos tener todos los elementos de una población de tamaño \(T\) (lo cual es, en general, imposible, ya que \(T\rightarrow\infty\)), entonces, \(\beta_{0},\beta_{1}\) serían unos parámetros fijos (no sujetos a ninguna ley probabilística) y, por lo tanto, no tendríamos ninguna incertidumbre en torno a su verdadero valor.

Sin embargo, esto no es posible y debemos recoger una muestra, de tamaño \(N\) y estimar un modelo tal que:

\[ y_{i}=\hat{\beta}_{0}+\hat{\beta}_{1}x_{i}+\hat{u}_{i},\:i=1,...,N \] donde \[ \widehat{u}_{i}\sim iid(0,\hat{\sigma}) \]

En este caso, los parámetros del modelo se “estiman” usando para ello funciones a partir de la muestra (llamadas estimadores). Al “estimar”, estamos asumiendo que podemos equivocarnos y, por lo tanto, cuantificamos no sólo el valor estimado sino la dispersión promedio que esperamos. Bajo ciertas condiciones en el desarrollo del experimento (entre ellas, un tamaño muestral grande), esperamos que \(\hat{\beta_{1}}\sim N(\beta,dt(\hat{\beta}_{1}))\), es decir, la distribución del estimador se aproximará a una normal, centrada en el parámetro poblacional (desconocido) y con desviación típica estimada con los datos. Recuerde, en esencia estos resultados del modelo de regresión simple que iremos invocando en la explicación

Concepto	Expresión
\(\hat{\beta}_{1}\)	\(\frac{cov(x,y)}{var(x)}\)
\(dt(\)\(\hat{\beta}_{1}\))	\(\sqrt{\frac{\hat{\sigma}_{u}^{2}}{N\hat{\sigma}_{x}^{2}}}\)
\(t-value\)	\(\frac{\hat{\beta}_{1}}{dt\left(\hat{\beta}_{1}\right)}\)

• \({\hat{\beta_{1}}}\) es la estimación del parámetro poblacional \(\beta_{1}\), cuyo estimador es \(\frac{cov(x,y)}{var(x)}\). Al ser la pendiente de una recta, mide el incremento promedio de la variable \(y\) al incrementar la variable \(x\) en una unidad. Al estimar este parámetro (que, como ve, es proporcional a la covarianza entre \(x\) e \(y\)) está asumiendo que la relación es lineal y que la covarianza se mantiene estable para toda la muestra de tamaño \(N\) (lo que es demasiado asumir, sobre todo con muestras muy heterogéneas).

En general, parece que habitualmente no se analiza con mucha dedicación este valor. Veremos que, en realidad, deberíamos empezar a dedicarle más tiempo y creatividad.

• \(dt(\hat{\beta}_{1})\)…es la desviación típica estimada del parámetro (lo que se conoce como error estándar, al ser una desviación típica de un estimador). Este resultado nos permite analizar el grado de precisión con el que somos capaces de estimar el parámetro \(\beta_{1}\) que, recordemos, es un parámetro poblacional desconocido del que pretende tener una estimación en un contexto de incertidumbre.

Si recuerda, la estimación por intervalo, aproximadamente, con un 95% de confianza consistía en

\[ IC(\beta_{1})_{0.95}=\left(\hat{\beta}_{1}-1.96dt(\hat{\beta}_{1}),\hat{\beta}_{1}+1.96dt(\hat{\beta}_{1})\right) \]

Por lo que, cuanto más grande sea esa desviación típica, mayor imprecisión (ya que cabrán muchos más valores plausibles del parámetro). ¿De qué depende, entonces, la imprecisión? Veamos paso a paso:

• \(\uparrow N\Rightarrow\sqrt{\frac{\hat{\sigma}_{u}^{2}}{{\color{red}\uparrow N}\hat{\sigma}_{x}^{2}}}\Rightarrow{\color{green}\downarrow dt(\hat{\beta}_{1})}\) Parece sensato: a mayor tamaño muestral, más y más precisión. Piensa, entonces, qué ocurre en casos donde la muestra es especialmente grande: si \(N\rightarrow\infty\), tendremos un exceso de precisión. Veremos que un exceso de precisión, si se realizan contrastes de forma automática, también constituye un problema.

• \(\downarrow\hat{\sigma}_{u}^{2}\Rightarrow\sqrt{\frac{{\color{red}\downarrow\hat{\sigma}_{u}^{2}}}{n\hat{\sigma}_{x}^{2}}}\Rightarrow{\color{green}\downarrow dt(\hat{\beta}_{1})}\) De nuevo, es sensato: a menor error en el modelo, mayor precisión. ¿Qué cuantifica el error del modelo? En general, la precisión con la que se captura la relacion (lineal) entre ambas variables. Si no es lineal, por ejemplo, o el modelo está incorrectamente especificado, habrá más error.

• \(\uparrow\hat{\sigma}_{x}^{2}\Rightarrow\sqrt{\frac{\hat{\sigma}_{u}^{2}}{n{\color{red}\uparrow\hat{\sigma}_{x}^{2}}}}\Rightarrow{\color{green}\downarrow dt(\hat{\beta}_{1})}\) Finalmente: a mayor varianza de la variable \(x\), mayor precisión.¿Por qué? Recuerde que lo que queremos es que la \(x\) ejerza de variable, es decir, haga bien su papel de fluctuar. Cuanto más fluctúe, más precisos seremos en la medición del efecto de la \(x\) sobre la \(y\), si esta relación es adecuada.

Entonces, ahora nos preguntamos qué mide la columna de la tabla de regresión que se denomina \(t-value\). Como verá, es un ratio entre el parámetro estimado y la precisión con la que este se estima. Por tanto, el \(t-value\) será:

• GRANDE SI: el efecto estimado es grande (ante una precisión fija)
• GRANDE SI: el efecto estimado es pequeño (pero con mucha precisión)
• PEQUEÑO SI: el efecto estimado es pequeño (ante una precisión fija)
• PEQUEÑO SI: el efecto estimado es grande (pero con mucha precisión)

Esto va a ser clave cuando discutamos el enfoque habitual del contraste de hipótesis

Antes, vamos a reflexionar sobre cómo se realizan contrastes de hipótesis.

Como es habitual, el científico de datos se preguntará, por la significatividad estadística de un parámetro (es decir, si en la población este parámetro es cero), mediante la siguiente hipótesis nula

\[ Ho\::\:\beta_{1}=0 \]

frente a la alternativa

\[ H_{1}\::\:\beta_{1}\neq0. \]

Es importante notar que las hipótesis se realizan sobre parámetros poblacionales (que, en el caso de la estadística frecuentista son desconocidos pero fijos, no aleatorios: son un único valor). Pero para hacer este contraste nos basamos en que, si la muestra es grande (en este curso obviaremos las muestras pequeñas, por simplicidad), entonces

\[ \hat{\beta}_{1}\sim N\left(\beta_{1},dt(\hat{\beta}_{1})\right), \]

es decir, el estimador se centra en el verdadero valor (desconocido) del parámetro y su dispersión viene dada por \(dt(\hat{\beta}_{1}).\) Por otro lado, si asumimos la hipótesis nula como cierta (es decir, imponemos que se cumple), esperaríamos que \[ \hat{\beta}_{1}\sim N\left({\color{red}0},dt(\hat{\beta}_{1})\right), \]

donde se asume normalidad en la distribución del estimador (al cumplir las hipótesis del TCL, que aquí se obvian para no complicar más la discusión)

FIG 1: Distribución del estadístico de contraste bajo la nula.

En la FIG1, vemos dicha distribución de \(\hat{\beta}_{1}\) que, como prometimos, está centrada en 0 y la desviación típica que hemos estimado define cómo será la apertura de la campana de la distribución (como se esboza en el dibujo: recuerde que dos desviaciones típicas encierran, aproximadamente, el 95% de la distribución). Nuestro objetivo, por tanto, es ver (mediante el uso del punto crítico a un nivel de significación o de “exigencia”, para entendernos) dónde se sitúa el parámetro \(\hat{\beta}_{1}\). Cuanto más lejos esté del valor \(0\), que es el de nuestra hipótesis, más razones tendremos para rechazar la hipótesis y, por lo tanto, más motivos tendremos para rechazarlo. Para ello, la teoría estadística determina que debemos elegir un nivel de significaci?n (o confianza, recuerda que “\(\%\)confianza=1-\(\%\)significación” que, en realidad, revela lo exigente que podemos ser con nuestros datos, ya que para ciertos niveles de confianza (o significación) rechazaremos y para otros, no:

FIG 2: La distribución de acuerdo con el nivel de significación.

En realidad, es más común estandarizar la normal, de tal forma que

\[ \hat{\beta}_{1}\sim N\left({\color{red}0},dt(\hat{\beta}_{1})\right)\Rightarrow\frac{\hat{\beta}_{1}-0}{dt(\hat{\beta}_{1})}\sim N(0,1) \]

y a la cantidad \[ T=\frac{\hat{\beta}_{1}}{dt(\hat{\beta}_{1})} \]

Supongamos que hemos estimado una regresión y obtenemos \(\hat{\beta}_{1}=0.037\) y \(dt(\hat{\beta}_{1})=0.04\), con un \(t-value=0.93\)

se le denomina estadístico de contraste. Como ves, se distribuye como una normal (0,1) y, entonces, es muy fácil trabajar con ello, al estar tabulado. Por ejemplo, si obtenemos un \(t-value=0.93\), consultando en las tablas de la normal, podemos ver (utilizando los puntos críticos) que usando los niveles de significación/confianza habituales, no rechazamos la nula.

FIG 3: Toma de decisión ante un estadístico de contraste.

En este repaso, informal, sobre la inferencia estadística, lo normal es acabar con la pregunta: ¿se puede hacer de una manera más ágil este proceso? La respuesta es: sí. En vez de mirar el punto crítico para cada nivel de significación, lo que podemos hacer es buscar directamente a partir de qué nivel de significación rechazaríamos la nula. Deberemos buscar, entonces, qué nivel de significación elegir para “rechazar”

FIG 4: La idea del p-valor.

Lo que estamos haciendo, en realidad, es buscar esta probabilidad

\[ 2\times P(N(0,1)>0.93)\simeq0.35 \]

Nótese que multplicamos por 2 porque buscamos el resultado a dos colas.

Es decir, tendríamos que hacer el test con un nivel de significación mayor que 0.35 (o nivel de confianza de 0.65) para rechazar la nula. La implicación de esto es que, a los niveles de significación habituales (1%,5% y 10%) no rechazamos la hipótesis nula.

REFLEXIONE

Si relee todo de nuevo, verá que, en realidad, el p-valor está muy influido tanto por la estimación del parámetro como por la precisión con la que este se estima. Entonces, hay cuatro casos de los que dos de ellos nos alertan de un posible error por el que no rechazaríamos la nula cuando deberíamos: un efecto fuerte (\(\hat{\beta}_{1}\) grande) y poca precisión en la estimación, o del error de rechazarla cuando no deberíamos: mucha precisión en la estimación y un efecto débil.

Ejercicio Razone y exprese por escrito qué debería ocurrir en la muestra para ser capaces de encontrarnos un p-valor lo más pequeño posible para, así, rechazar la hipótesis nula.

RECUERDE

Si está interesado en contrastar cualquier otro valor, recuerde que la nula y la alternativa se escriben así

\[ Ho\::\:\beta_{1}=\beta^{*} \]

frente a la alternativa

\[ H_{1}\::\:\beta_{1}\neq\beta^{*}. \]

y el estadístico de contraste, ante una muestra grande

\[ t-ratio=\frac{\hat{\beta}_{1}-\beta^{*}}{dt(\hat{\beta}_{1})}\sim N(0,1) \]

Clase 5 Aspectos relevantes en la modelización estadística (V): el p valor

Recuerde lo que “hace” el p-valor. Imagine que ha estimado una regresión y obtiene \(\hat{\beta}_{1}=0.037\) y \(dt(\hat{\beta}_{1})=0.04\), con un \(t-value=0.93\). Según la definición de la sociedad estadística americana (ASA):

El p-valor según la ASA

A p-value is the probability under a specified statistical model that a statistical summary of the data (e.g., the sample mean difference between two compared groups) would be equal to or more extreme than its observed value.

En la FIG 1, discutimos la obtención del p-valor, en este caso, asociado a la hipótesis nula \[ H_{0}:\beta=0 \] frente a la alternativa

\[ H_{0}:\beta>0 \]

FIG 1: La idea del p-valor (de nuevo).

La idea es ¿cómo de probable sería si-con otra muestra- tratamos de encontrar una estimación mayor que 0.037, asumiendo que la hipótesis nula es cierta?

Hasta ahora, hemos tratado de reflexionar sobre la naturaleza de los constrastes estadísticos. ¿Cree que debería utilizar el p-valor de manera indiscriminada?

• Piense, entonces, sobre la naturaleza de los test y la precisión con la que miden los efectos buscados
• Piense sobre la potencia del test (habilidad de rechazar hipótesis muy distintas a las planteadas)
• Piense sobre el efecto de “precisión extrema” y la posibilidad de rechazar casi cualquier hipótesis nula

Por ejemplo, realice el siguiente ejercicio y reflexione:

Ejercicio

Se tienen datos de ventas de un producto y del precio. Se estima el siguiente modelo de regresión, donde el coeficiente asociado a la variable precio se puede interpretar como la elasticidad precio:

\[ ln(ventas)=5.32-0.97ln(precio)+\hat{u} \]

Además, el error estándar asociado al parámetro de interés es \(0.65\)

1. Realice un contraste de significatividad al uso (para ello, obtenga el p-valor)
2. Interprete la importancia económica del parámetro
3. Realice un intervalo de confianza al 95% y reflexione sobre la potencia del contraste

Ahora, suponga que se estima el siguiente modelo

\[ ln(ventas)=5.32-0.37ln(precio)+\hat{u} \]

Además, el error estándar asociado al parámetro de interés es \(0.08\)

1. Realice un contraste de significatividad al uso (para ello, obtenga el p-valor)
2. Interprete la importancia económica del parámetro
3. ¿qué concluye de ambos casos?

Este mecanismo que parece “bastante científico” está siendo muy criticado. Y veremos que con razón.

FIG 2: Sobre el p-valor y los mecanismos de contraste estándar.

FIG 3: Evite mirar a la columna del p-valor y piense más en el conjunto: efecto estimado versus precisión.

FIG 4: Piense en los intervalos de confianza.

FIG 5: En definitiva: evite el exceso de automatización en la toma de decisiones.

De hecho, en 2016, la ASA (American Statistical Association: https://www.amstat.org/) presentó los “seis principios” sobre el p valor y la inferencia estadística:

• Los p valores “pueden” indicar cómo de incompatibles son los datos con un modelo estadístico especificado es decir, podría ser que un p valor grande simplemente esté advirtiendo de que el modelo elegido no es adecuado, esto es, no es compatible con nuestros datos.
• Los p valores no miden la probabilidad de que la hipótesis nula sea cierta o de que los resultados del efecto estimado sean fruto de la aleatoriedad No olvidemos que el p -valor asume que la hipótesis nula es cierta, por lo que no puede calcular la probabilidad de dicha hipótesis.
• Conclusiones científicas o de negocios no deberían estar basadas en un p-valor La expansión, nada sensata, de la regla \(P\leq 0.05\) que dictamina si una variable tiene efecto sobre otra (o es significativa) de manera dicotómica, sin tener en cuenta posibles contextos y resultados de los efectos puede ser pernicioso y contraproducente.
• Inferencia adecuada requiere un análisis pormenorizado y transparente Hay muchas técnicas para hacer “p hacking”. Si sólo se presentan los resultados donde el p-valor apoya una conclusión, se está ocultando el verdadero mecanismo de la toma de decisiones
• Un p valor no mide la importancia del efecto que se está buscando analizar La significatividad estadística no es equivalente a la significatividad científica, humana o económica. p-valores pequeños no implican, necesariamente, efectos relevantes. De hecho, efectos similares pueden tener distintos p valores atendiendo a la precisión con la que estos se estiman.
• Un p valor no proporciona evidencia a favor de una hipótesis sobre un modelo un p valor grande, no implica evidencia a favor de una hipótesis nula. Podría haber multitud más de hipótesis que no se rechazarían.

Aquí tiene la fuente original de este resumen: https://amstat.tandfonline.com/doi/full/10.1080/00031305.2016.1154108#.YUiYN2YzaH0

¿Cómo deberíamos trabajar, entonces?. Aquí vienen algunas propuestas que tratan de ser sencillas y sensatas ante lo complicado que es pronunciarse a la hora de trabajar con datos.

Supongamos que estima un modelo, en este caso, con la base de datos de los Simpson

por ejemplo, analicemos mediante una regresión la nota en IMBD de los episodios, dada la importancia de los cuatro protagonistas

SIMPSONS_FINAL <- read_table2("SIMPSONS_FINAL.csv", locale = locale(decimal_mark = ","))

#calculamos las importancias (en %) de cada personaje en cada episodio
Total_words<-rowSums(SIMPSONS_FINAL[ , c(2,3,4,5,6,7,8,9,10)], na.rm=TRUE)
Imp_Homer<-(SIMPSONS_FINAL$Homer/Total_words)*100
Imp_Bart<-(SIMPSONS_FINAL$Bart/Total_words)*100
Imp_Apu<-(SIMPSONS_FINAL$Apu/Total_words)*100

#entrenamos el modelo de regresión

summary(lm(SIMPSONS_FINAL$rating_imdb~Imp_Homer+Imp_Bart+Imp_Apu))

Call:
lm(formula = SIMPSONS_FINAL$rating_imdb ~ Imp_Homer + Imp_Bart + 
    Imp_Apu)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.7738 -0.5234 -0.1296  0.5648  1.9213 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 7.053826   0.119040  59.256  < 2e-16 ***
Imp_Homer   0.005769   0.002187   2.637  0.00859 ** 
Imp_Bart    0.008407   0.002834   2.966  0.00314 ** 
Imp_Apu     0.009182   0.005945   1.544  0.12303    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.7258 on 560 degrees of freedom
  (4 observations deleted due to missingness)
Multiple R-squared:  0.01984,   Adjusted R-squared:  0.01459 
F-statistic: 3.778 on 3 and 560 DF,  p-value: 0.01054

Como vemos, si seguimos a pies juntillas lo que -muchas veces- se nos dice de forma mecánica: Homber y Bart presentan un efecto significativo mientras que Apu, no. sin embargo, vamos a pensar:

1. El coeficiente asociado a Apu es ligeramente superior a Homer y a Bart y, sin embargo, este resulta no significativo. ¿Cómo puede ser? Esto es una incongruencia que, habitualmente, se deja pasar de lado.

2. SI RECHAZO LA NULA:

**recuerda que puede ocurrir que esté mediendo con mucha precisión (baja desviación típica de la beta estimada) y que el efecto sea bajo [por lo que rechazaría casi cualquier hipótesis] o que el efecto sea relevante (en magnitud). Para ello, echemos cuentas

• 1: ¿Es mucho el impacto de Homer? Dice que si aumenta una unidad la importancia, entonces la nota del episodio aumentará en 0.0058 unidades. Para saber cuánto implica, deberemos responder a lo siguiente ¿cuánto se incrementa, en promedio, la variable explicativa? Esa medida la proporciona la desviación típica de la variable asociada. Por ejemplo, la desviación típica de “Homer” es 16.38. Es decir, esperamos que la fluctuación promedio de la variable “importancia de Homer” sea 16.38 puntos sobre 100. Entonces, el impacto que tendrá una fluctuación promedio de la importancia de Homer sobre la nota, será

\[ Efecto\:\: Promedio=0.0058\times 16.38=0.095 \]

• 2: En el caso de Bart, la desviación típica de su importancia es \(12.73\). Esto implica que su efecto promedio, de acuerdo con el coeficiente estimado será

\[ Efecto\:\: Promedio=0.0084\times 12.73=0.1069 \]

¿Son altos o bajos estos efectos? Se puede tratar de comprobar con una desviación típica de la variable que estamos tratando de explicar: la nota en imbd. ¿Cuánto varía la nota en promedio? Su desviación típica es 0.72. Es decir, tanto los efectos de Homer y Bart, aun siendo “significativamente estadísticos” no parecen ser muy relevantes, ya que sus movimientos en términos de notas no representan un porcentaje alto de la nota.

2. SI NO RECHAZO LA NULA:

• 1 Hemos visto que la importancia de Apu parece no relevante estadísticamente. Si bien, como vimos, su impacto numérico parece mayor que el de Homer y Bart. Cabría preguntarse si estamos en un contexto de baja precisión. Para ello, podemos construir un intervalo de confianza aproximado para el parámetro: \(\beta_{APU}\in (0.09182 \pm 1.96\times 0.005945)\), es decir \(\beta_{APU}\in (-0.002,0.02)\)

• 2 Dado que la desviación típica muestral de la importancia de APU es de 5.25, este intervalo implica que en el rango de efectos de APU sobre la nota en imbd \(efecto_{APU}\in (-0.019,0.11)\) que, de nuevo, está en el rango de efectos similares a los de Bart y Homer y que, por tanto, no parece tampoco muy destacado.
• 3 Por otro lado, fíjese en la FIG6, donde se muestran los p valores para el contraste de diferentes hipótesis alternativas a \(\beta=0\). En este caso, no parece que estemos ante un problema grande de baja potencia (no se rechazarían hipótesis muy dispares). Es, simplemente, que el efecto no parece muy grande.

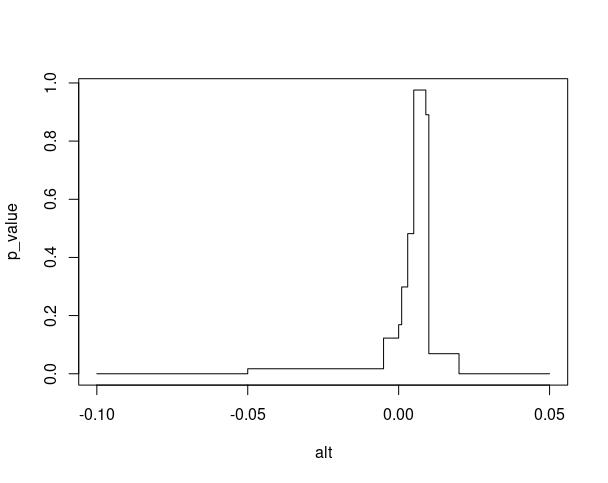
FIG 6: Gráfico de p valores para el coeficiente de APU.

Es decir, una conclusión de este modelo es que ninguno de los efectos tratados parece especialmente relevante, al margen de la inferencia estadística “tradicional”. No parece que la importancia de ninguno de los personajes consiga mejorar el impacto que tiene en la audiencia.

Ejercicio

Realiza, con R, un gráfico similar al mostrado anteriormente para el ejercicio de las elasticidades precio y demanda para ambos casos

Código empleado para la FIG 6

#guardo el modelo en un objeto llamado "m1"
m1<-(lm(SIMPSONS_FINAL$rating_imdb~Imp_Homer+Imp_Bart+Imp_Apu))

#propongo un conjunto de alternativas bien distintas (incluyo también la de beta=0)
alt<-c(-0.1,-0.05,-0.005, 0, 0.001, 0.003, 0.005, 0.009, 0.01,0.02,0.04,0.05)
#almaceno la beta estimada y su desviación típica y genero un vector de p-valores vacío
beta_est<-summary(m1)$coefficients[4,1]
desv_beta<-summary(m1)$coefficients[4,2]
p_value<-vector()

#en este bucle obtengo los p-valores del contraste (a dos colas)
for (i in 1:length(alt)){
  
  t_test<-(beta_est-alt[i])/desv_beta
  p_value[i]<-2*(pnorm(-abs(t_test)))
  
}

plot(alt,p_value,type = "S")

Por ejemplo, si utilizamos el script anterior para analizar el ejercicio donde se planteaban unas funciones de ventas dependiendo del precio del producto :

CASO 1

\[ ln(ventas)=5.32-0.97ln(precio)+\hat{u} \]

con error estándar asociado al parámetro de interés es \(0.65\)

CASO 2

\[ ln(ventas)=5.32-0.37ln(precio)+\hat{u} \]

con el error estándar asociado al parámetro de interés de \(0.08\), tendremos lo siguiente

alt<-c(-3, -2.75,-2,-1.5, -1, -0.5,0,0.5,1, 1.5)
beta_est<--0.97
desv_beta<-0.65
p_value<-vector()

for (i in 1:length(alt)){
  
  t_test<-(beta_est-alt[i])/desv_beta
  p_value[i]<-2*(pnorm(-abs(t_test)))
  
}

plot(alt,p_value,type = "S")

donde recuerda que “alt” son valores alternativos para contrastar distintas hipótesis nulas. El bucle realiza los contrastes y busca el correspondiente p-valor del test (por ejemplo,para el primer caso, testea \(H_0 : \beta=-3, H_1 :\beta\neq -3\)) y obtiene el p valor del contraste. La figura que resulta es la siguiente:

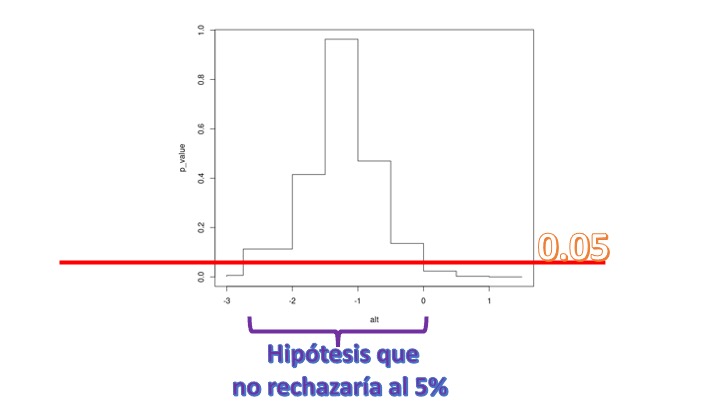de tal forma que en el eje \(y\), tenemos los distintos p-valores del cada constraste y en el eje \(x\) el valor de la \(\beta\) para la hipótesis nula. Como vemos, si elegimos el 5% de nivel de significación, no rechazaría muchas hipótesis. No rechazaría que \(\beta=-2.5\), pero tampoco rechazaría que \(\beta=-1\) y ni siquiera que \(\beta=0\). Son hipótesis con un significado económico muy distinto: en el primer caso no rechazo que el bien sea elástico, en el segundo caso con elasticidad unitaria y en el tercero inelástico. Como vemos, aquí realizar un test resulta pernicioso: pese a que intuímos que el impacto del precio sobre el producto tiene importancia, si realizamos un test de significatividad podríamos concluir lo contrario. Y lo que es peor: podríamos concluir cosas muy dispares.

Si realiza lo mismo para el CASO 2, verá que ahora el test es muy rotundo. Rechaza la nula de que \(\beta=0\) pero, en realidad, rechaza un montón más de hipótesis nulas: esto se debe a que la precisión con la que estamos estimando es muy alta (medida por el valor de la desviación típica del estimador). En ese contexto, tampoco nos conviene hacer un test. Rechazaremos casi siempre. Es mucho mejor pensar, como nos propone la ASA, sobre la relevancia o no del efecto. En este caso, como ya dijimos, no parece muy relevante.

Importante, fin de bloque. Cosas que debe saber:

• Plantear adecuadamente una pregunta de investigación
• Conocer las principales “paradojas” iniciales que uno puede hallar en el estudio aplicado con datos
• Tener una idea clara del conjunto de pasos iniciales que se deben dar en un estudio con datos (y practicarlo)
• Entender que la idea de “analizar” la significatividad de una variable trasciende a la idea de mirar un p-valor y conocer las principales críticas a este uso lanzadas por los científicos

Por otra parte >- Debería tener clara la base de datos con la que va a realizar el proyecto y la pregunta que quiere responder >- Debería haber realizado un análisis previo similar a los propuestos en la intranet del curso.