BLOQUE 3: Técnicas de modelos NO supervisados en datos de Sección Cruzada
Muchas veces le puede interesar reducir la dimensión asociada al número de variables con el que cuenta. Es posible, por ejemplo, que le interese agrupar la información con la que cuenta para crear una nueva variable sintética. Imagine, por ejemplo, que tiene 10 variables que aluden a la clase social y la formación del individuo: quizás quiera tener una única variable que clasifique a los individuos según la información conjunta contenida en ese bloque de variables. Sin embargo, no va a poder entrenar un modelo y validarlo: usted usa la técnica sin saber, a priori, lo que va a obtener. Por eso, a estas técnicas se las conoce como no supervisadas. No puede realizar comprobaciones cuantitativas mediante test y validación. Sólo podrá usar su lógica para ver si lo que obtiene es sensato o no. Generalmente, estas técnicas son pasos intermedios para tener una base de datos más sintética que le ayude en el proceso de modelar su pregunta de interés.
Clase 1. “K means”
Este análisis busca realizar agrupaciones de observaciones condicionadas por el valor que tomen ciertas variables disponiles. Imagine que tiene una nube de puntos asociada a dos variables: \(x_1,x_2\). Visualmente, seguro que es capaz de hacer dos grupos ¿no?
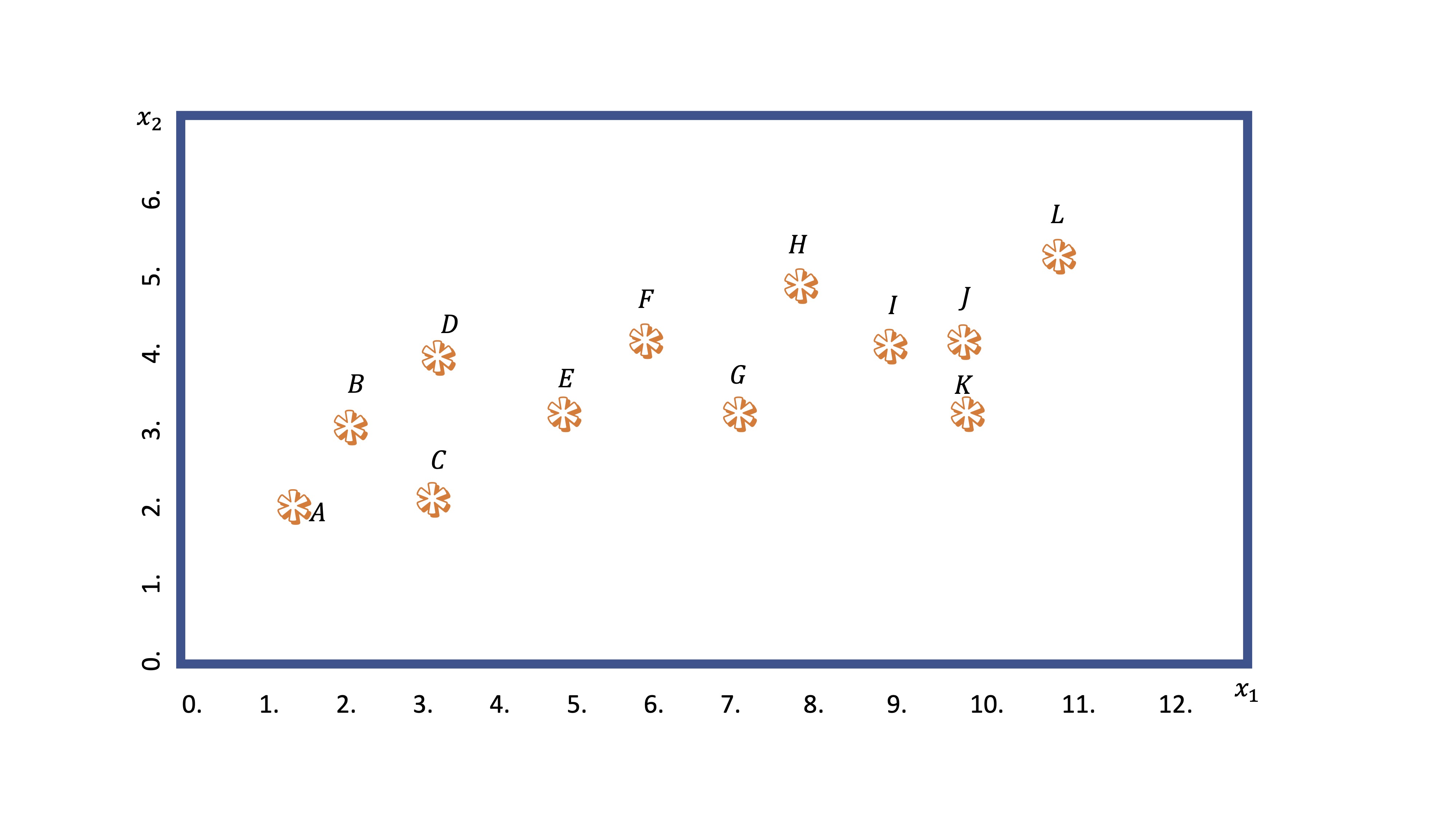
FIG 1: Un ejemplo de variable que queremos agrupar
¿Cómo lo hará la máquina? Veamos el algoritmo en los diferentes pasos:
- Primero: busca dos puntos (generalmente de manera aleatoria). Nosotros elegiremos los más distantes entre sí. Esos puntos se llamarán centroides de los cluster.
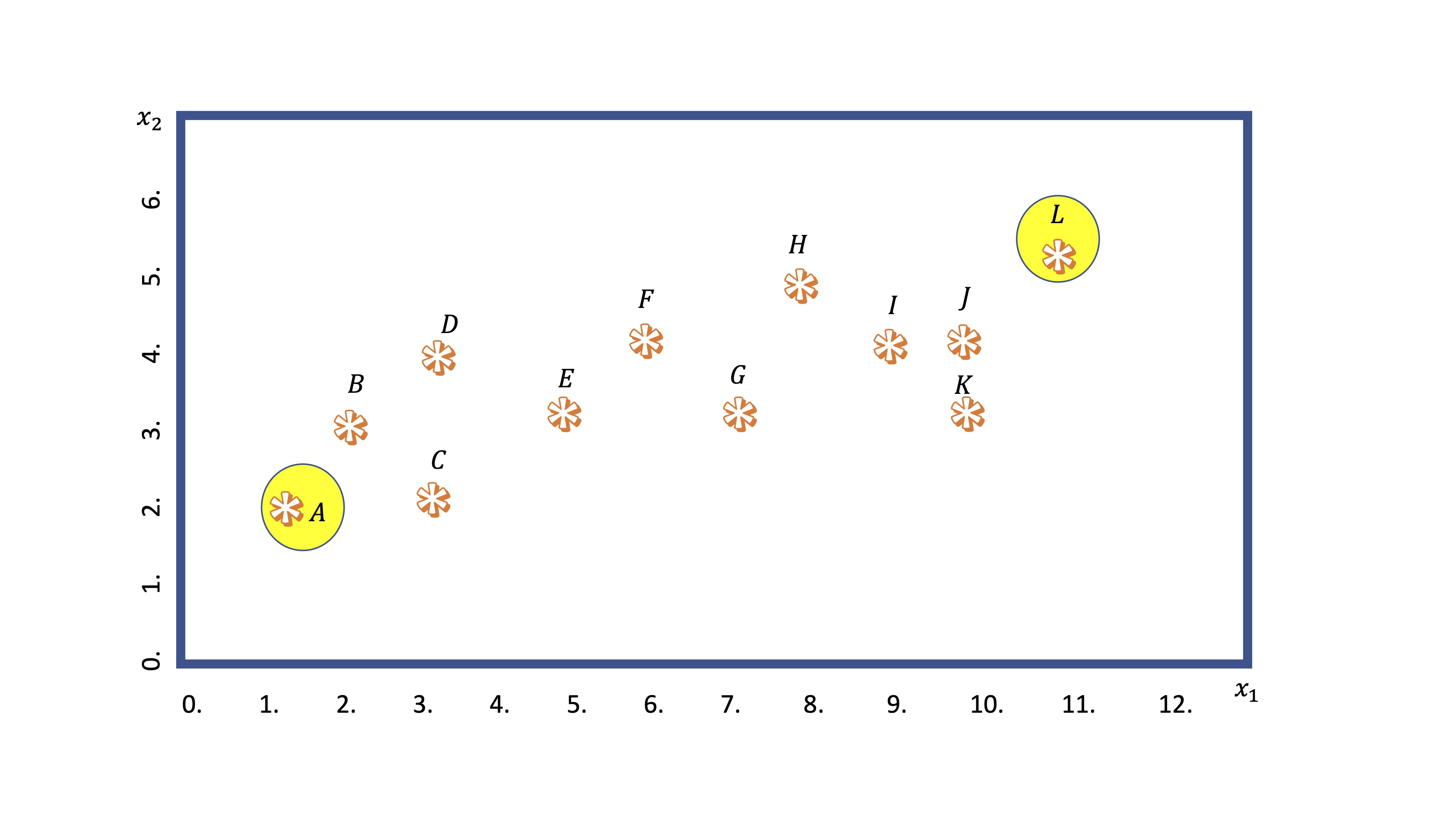
FIG 2: centroides iniciales
El centroide 1, el punto A, tiene coordenadas \(A(1,2)\), mientras que el centroide 2, el punto L, tiene coordenadas \(L(11,5.5)\). Esas son ahora las referencias de los grupos.
- Segundo: Calcula la distancia (mediante alguna medida general, como la norma euclídea) de cada punto a los centroides
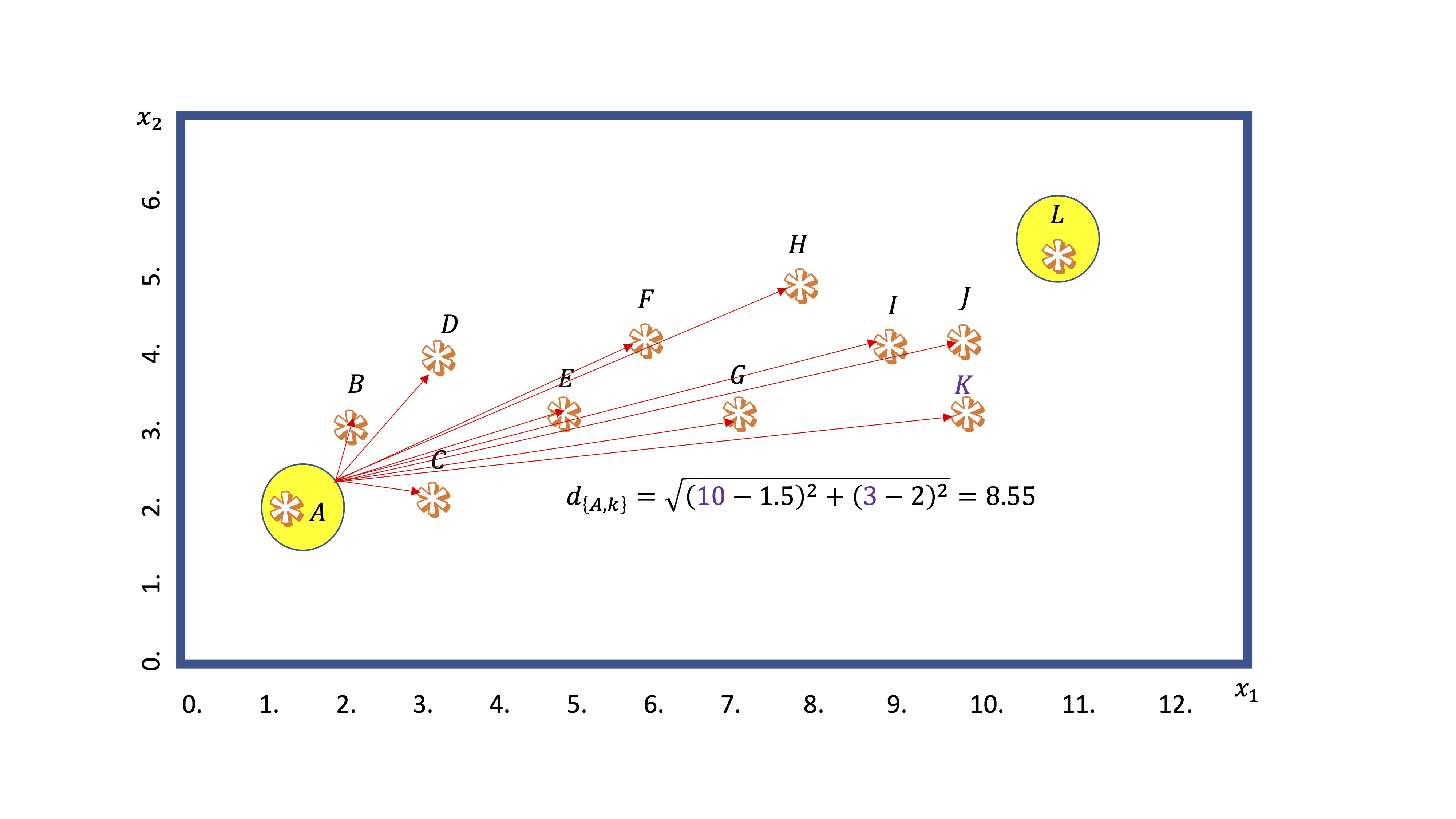
FIG 3: Un ejemplo del cálculo de la distancia
En este ejemplo, calculamos la distancia del centroide A al punto K. Obtenemos \(8.55\). Por otro lado, del centroide L al mismo punto:
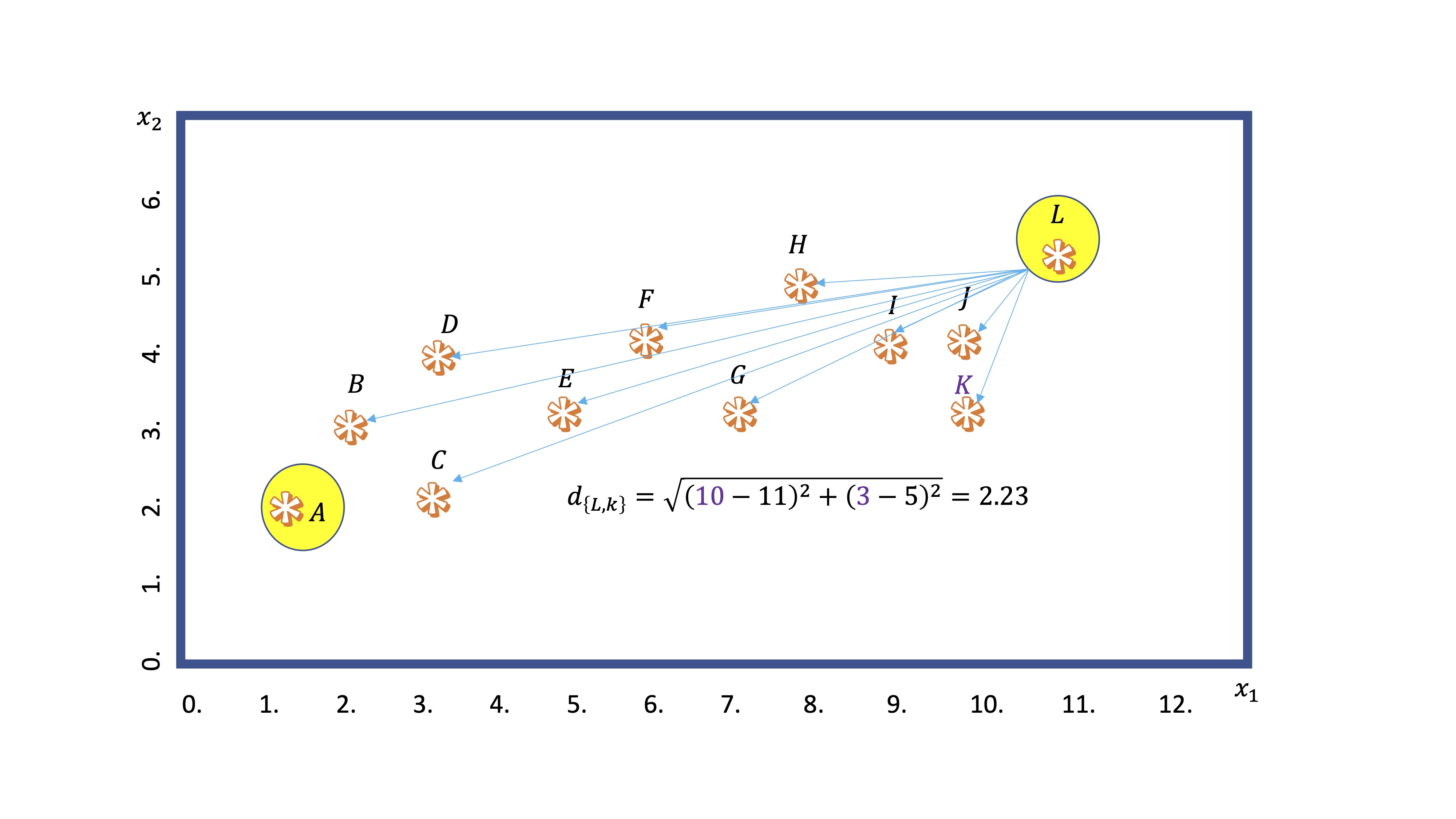
FIG 4: Un ejemplo del cálculo de la distancia
y vemos que es menor. Entonces, el algoritmo dejará al punto K dentro del nodo que “preside” L.
- Tercero: establece una agrupación por clusters en función de la distancia de cada punto a los centroides elegidos
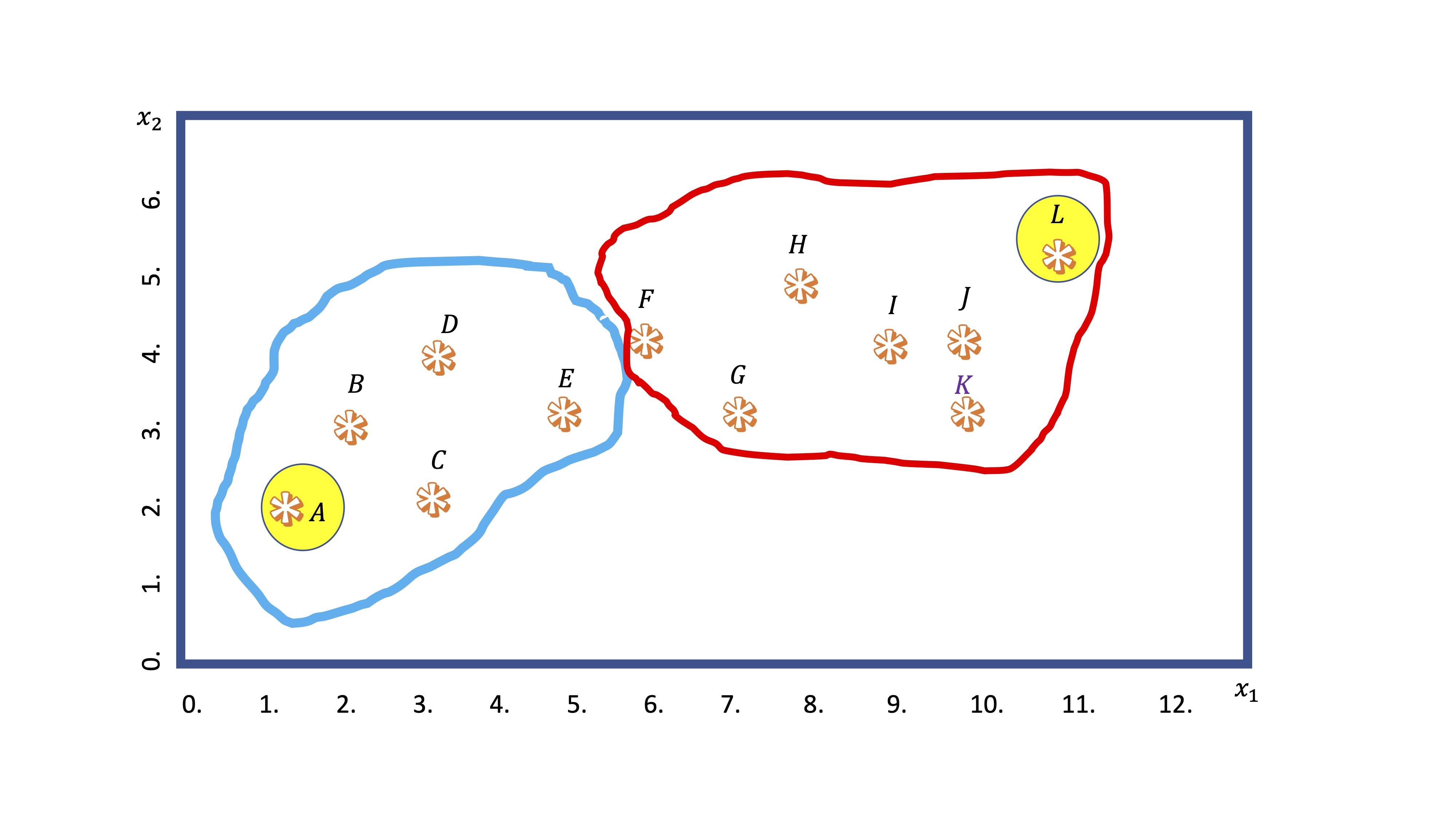
FIG 5: Los primeros clusters!
Sin embargo, con los nuevos grupos hechos, ahora recalcula los centroides (haciendo la media de las coordenadas \(x_1,x_2\) de cada punto dentro del grupo). De hecho, el nuevo centroide puede ya no ser ningún punto de los que se encuentran en el grupo.
- Cuarto: entonces, recalcula la distancia de todos los puntos a los centroides y, en base a ese dato, los grupos van a reorganizarse (observaciones en las fronteras de cada grupo irán cambiándose)
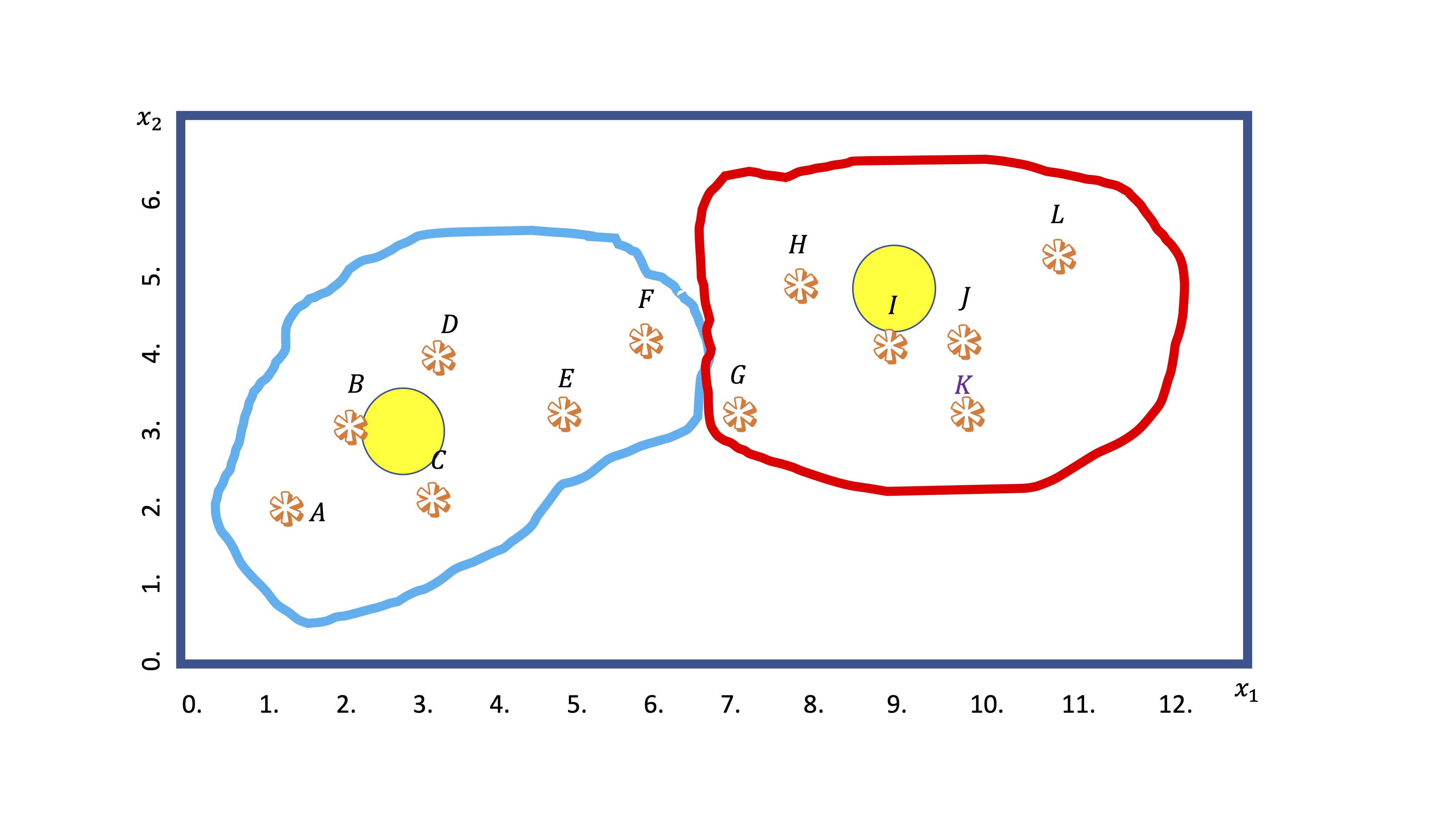
FIG 6: La observación F se cambia de chaqueta
El algoritmo iterará hasta que la clasificación se estabilice. ¿Qué criterio seguiremos para decidir cuántos grupos/cluster hacer?
Elección de número de grupos “k”. Habitualmente, el algoritmo calcula la “suma de cuadrados” de cada uno de los grupos utilizando los centroides como valores de referencia. De esta manera, realiza la suma de cuadrados de las distancias de cada coordenada a su valor central en cada grupo. El objetivo es minimizar la suma total. Esa suma siempre será decreciente, por lo que se elegirá el número de grupos \(k\), donde un incremento adicional de \(k\) haga que el error caiga marginalmente. Lo veremos con un ejemplo:
Introducimos los datos que han generado las figuras anteriores
x1<-c(1.5,2,3,3,5,6,7,8,9,10,10,11)
x2<-c(2,3,2,4,3,4,3,5,4,4,3,6)
dataset<-data.frame(x1,x2)Ahora creamos un bucle que va a ir incrementando la cantidad de clusters (\(k\)) y calculando las sumas de cuadrados (whitinss, en la función empleada)
S <- vector() #inicializo mi vector de dispersiones
for(i in 1:8){
kresult<-kmeans(dataset, i, nstart=100)$withinss
S[i]<-sum(kresult)
} #calculo mediante kmeans la S para cada knote que nstart=100 quiere decir que deberá empezar 100 veces, de manera aleatoria, los centroides. Es una manera de estabilizar el algoritmo y hacer que el resultado no dependa de la selección original de centroides.
ggplot() +
geom_point(aes(x = 1:8, y = S), color = "blue") +
geom_line(aes(x = 1:8, y = S), color = "blue") +
ggtitle("Selección de clusters") +
xlab("Cantidad de Centroides k") +
ylab("S")El gráfico de la FIG7 nos sugiere, de hecho, hacer entre 4 y 5 clusters.
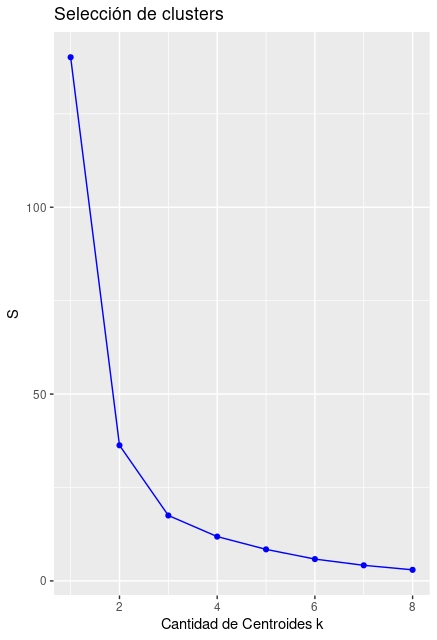
FIG 7: Gráfico para la selección del número de clusters
Aunque, a todas luces, parece demasiado exagerado hacer 4 clusters. Será usted, como usuario, quien deba elegir lo más conveniente (debería, por ejemplo, utilizar algún criterio extramuestral). Con este script puede dibujar los resultados:
install.packages("factoextra")
library(factoextra)
kmeans <- kmeans(dataset, 2, iter.max = 1000, nstart = 25)
fviz_cluster(kmeans, data = dataset)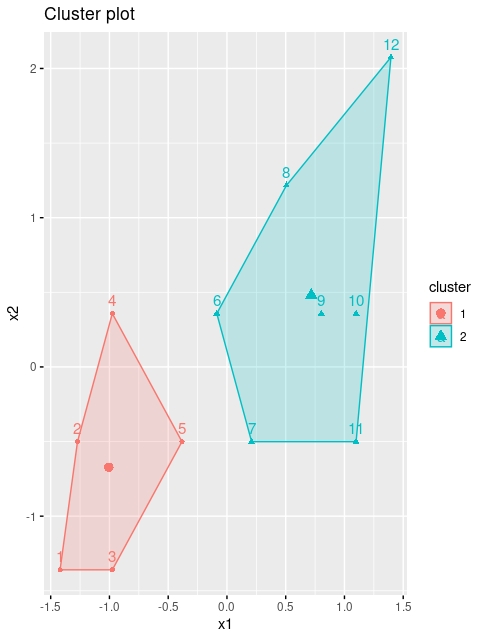
FIG 8: Con \(k=2\)
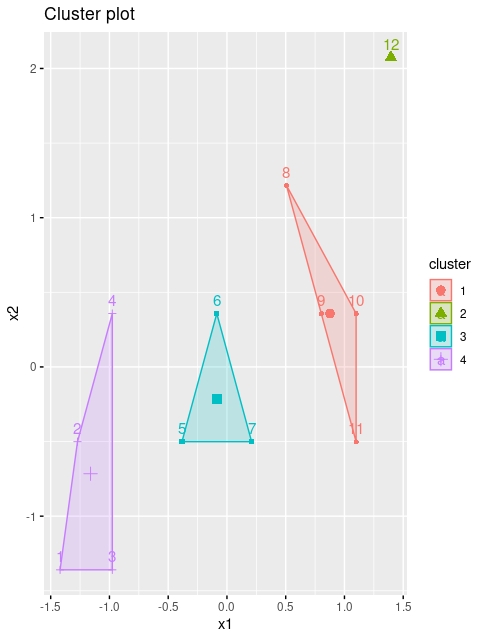 Ahora bien, lo normal es no tener acceso a estos gráficos porque usted quiera hacer los cluster con más de dos variables (no olvide que el objetivo es reducir el tamaño del conjunto de variables disponible). Entonces, le interesará acceder a la información que proporciona la función kmeans
Ahora bien, lo normal es no tener acceso a estos gráficos porque usted quiera hacer los cluster con más de dos variables (no olvide que el objetivo es reducir el tamaño del conjunto de variables disponible). Entonces, le interesará acceder a la información que proporciona la función kmeans
K-means clustering with 2 clusters of sizes 5, 7
#por un lado, le proporciona las coordenadas de los centroides. Eso le ayudará a entender el significado de estos, ya que son los promedios de cada variable en el cluster.
Cluster means:
x1 x2
1 2.90 2.80
2 8.71 4.14
#por otro lado, le proporciona la "etiqueta" del cluster al que pertenece cada observación. Esta será una nueva variable para usted que resume las anteriores. Tendrá que darle un significado, basado en los valores de los centroides
Clustering vector:
[1] 1 1 1 1 1 2 2 2 2 2 2 2
#Y estas son las sumas de cuadrados de cada cluster
Within cluster sum of squares by cluster:
[1] 10.0 26.3
(between_SS / total_SS = 74.1 %)Ejercicio Realice un ejercicio de cluster con los datos de audiencia y puntuación de los Simpson de tal forma que trate de ver si encuentra mayor capacidad predictiva de los personajes en el resultado de esa nueva variable caracterizada por los clusters que encuentre. Trate de explicar el significado de los cluster.
Clase 2. “K means (algunos comentarios)”
Si ha tratado de hacer el ejercicio de la clase anterior, habrá visto algo curioso respecto a los clusters. Vamos a ello:
- Ha seleccionado las variables audiencia y rating de los episodios, y ha ejecutado la sentencia que le permite ver cuántos clusters son convenientes:
#Cargo los datos
SIMPSONS<-na.omit(SIMPSONS)
audiencia<-SIMPSONS$millions_audiene
rating<-SIMPSONS$rating_imdb
#creo un data frame y elimino los NAs
dataset<-data.frame(audiencia,rating)
dataset<-na.omit(dataset)
S <- vector() #inicializo mi vector de dispersiones
for(i in 1:8){
kresult<-kmeans(dataset, i, nstart=100)$withinss
S[i]<-sum(kresult)
} #calculo mediante kmeans la S para cada k
ggplot() +
geom_point(aes(x = 1:8, y = S), color = "blue") +
geom_line(aes(x = 1:8, y = S), color = "blue") +
ggtitle("Selección de clusters") +
xlab("Cantidad de Centroides k") +
ylab("S")
FIG 1: Diagrama para la selección de clusters
-Donde, según la FIG 1, parece sensato elegir cuatro clusters (o, como mucho, 5). Seleccionamos cuatro porque seguimos con la intuición de que los episodios se pueden separar en cuatro categorías (muy vistos y mal valorados, poco vistos y mal valorados, muy vistos y bien valorados,poco vistos y bien valorados).
Entonces, solicitamos la separación con \(K=4\), y obtenemos
kmeans <- kmeans(dataset, 4, iter.max = 1000, nstart = 25)
fviz_cluster(kmeans, data = dataset,stand=FALSE)
K-means clustering with 4 clusters of sizes 172, 65, 123, 189
Cluster means:
audiencia rating
1 10.87 7.27
2 24.95 8.07
3 16.76 8.01
4 6.44 6.95
- Si los vemos gráficamente, detectamos un posible problema:
 >-como vemos, parece ser la variable audiencia la que determina los clusters, esto es, la variable rating no parece determinar la separación. De hecho, si vemos la información que nos ofrece [R], la variable rating fluctúa poco (en un grupo es 7.27, en otro 8.07, en otro 8.01 y en el último 6.95).
>-como vemos, parece ser la variable audiencia la que determina los clusters, esto es, la variable rating no parece determinar la separación. De hecho, si vemos la información que nos ofrece [R], la variable rating fluctúa poco (en un grupo es 7.27, en otro 8.07, en otro 8.01 y en el último 6.95).
Recuerde que si ejecuta esto en su ordenador, le saldrá algo parecido pero no igual, debido a la aleatoriedad en los puntos de partida del algoritmo.
Ahora bien, ¿parece sensata dicha separación? Dese cuenta de que, en este algoritmo, se calculan las distancias al centroide utilizando las unidades de medida de las variables. Por lo tanto, si estas son dispares, las distancias las marcará la variable con unidades mayores (en este caso, la audiencia). Por eso, es conveniente tratar de homogeneizar las variables en un caso como esto. Lo que puede hacer es :
Estandarizar las variables
Una variable \(x\) con media \(\bar{x}\) y desviación típica \(\sigma_{x}\) se puede transformar a una variable con media cero y desviación típica 1 mediante la operación \(\frac{(x-\bar{x})}{\sigma_{x}}\). Sin embargo, eso no quiere decir que esté convirtiendo a la variable en Normal (error común), simplemente la está cambiando de escala.
- Ahora, realizamos la operación de estandarización y volvemos a obtener los cluster
audiencia<-(audiencia - mean(audiencia)) / sd(audiencia)
rating<-(rating - mean(rating)) / sd(rating)
dataset<-data.frame(audiencia,rating)
dataset<-na.omit(dataset)
kmeans <- kmeans(dataset, 4, iter.max = 1000, nstart = 25)
fviz_cluster(kmeans, data = dataset,stand=FALSE)
FIG 3: posibles clusters obtenidos con las variables estandarizadas
Ahora podemos separar a los episodios de los simpson en 4 grupos. El morado parecen aquellos con poca audiencia y peor valorados, el verde con mucha audiencia y valoración. El rojo parece que son poca audiencia y muy bien valorados y el grupo 3 parece un intermedio entre el grupo 1 y el 4. Si bien es cierto, esta separación parece que cuenta con más variabildiad en la variable rating.
Esto nos muestra que, en caso de tener unidades de medida distintas, conviene estandarizar las variables que, eso sí, pasan a tener todas la misma varianza (el problema de la estandarización). Podemos ilustrar las bondades de estandarizar
Atendiendo a estos datos simulados con, claramente, distintas unidades de medida
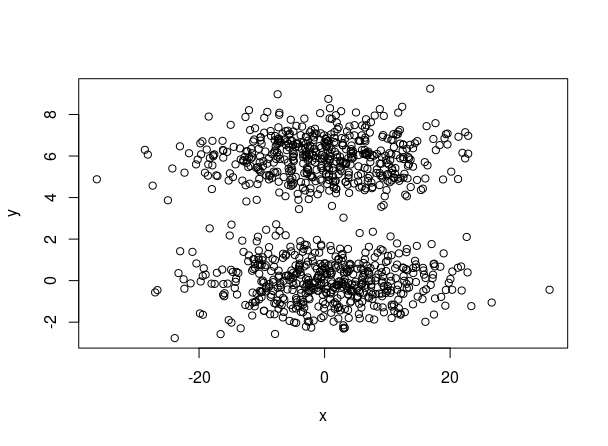
FIG 4: dos clusters simulados
de los que aquí puede disponer del código para simularlos:
x = rnorm(1000) * 10
y = c(rnorm(500), rnorm(500) + 6)
plot(x,y)Se obtienen los siguientes resultados de la función “kmeans” utilizando 2 clusters
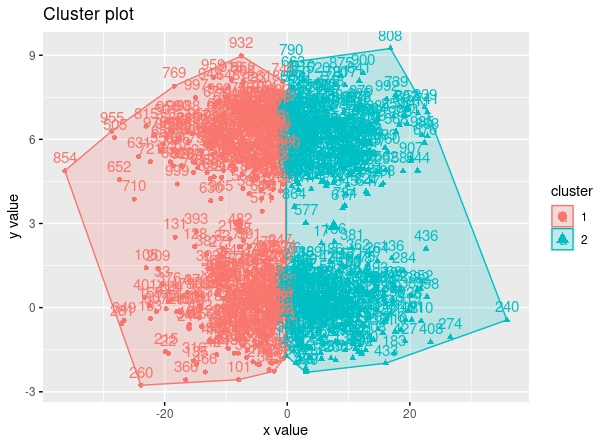
FIG 5: dos clusters simulados, entrenados “malamente” con k means
Sin embargo, tras estandarizarlos, obtenemos una solución más existosa
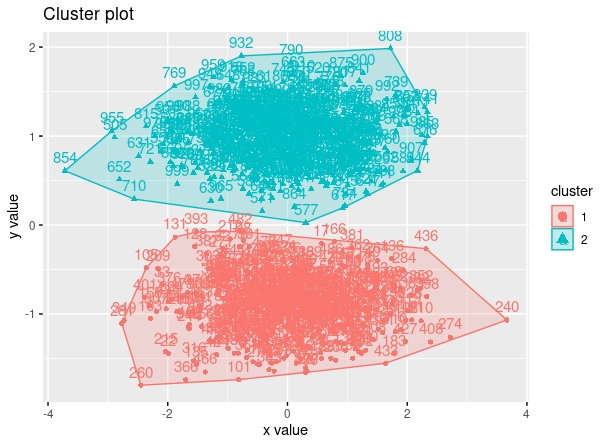
FIG 5: dos clusters simulados, entrenados con k means
Ahora bien, ¿es siempre la solución estandarizar? En el manual FRIEDMAN, Jerome H. The elements of statistical learning: Data mining, inference, and prediction. springer open, 2017.
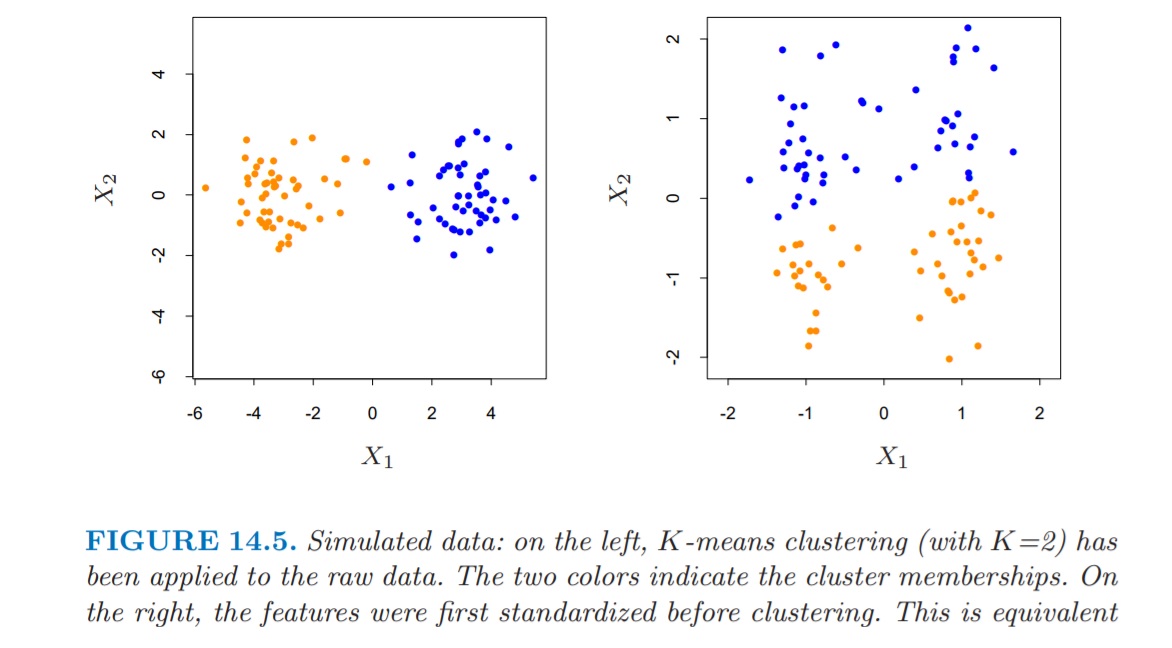
FIG 6: del libro “elements of statistical learning”
donde, como vemos, tras la estandarización, los clusters correspondientes sufren modificaciones al cambiar la dispersión respecto al eje de ordenadas.
- Sin embargo, parece razonable confiar en la estandarización siempre que las unidades de medida sean muy diferentes y nos interese realizar un cluster con dichas variables.
Clase 3. “El dendrograma”
Otra manera de busar clusters es, en vez de en el conjunto de observaciones, en el conjunto de variables (es decir, en vez de por filas, por columnas). Para ello, elegiremos la correlación como una medida de “similaridad” de variables. Aunque, obviamente, la correlación sólo mide similaridad de carácter lineal. Es decir: puede haber relaciones entre variables que este método no capte. Aunque lo usaremos, en general, por su sencillez y flexibilidad.
Suponga que tiene un conjunto de datos, con cinco variables (V1,V2,V3,V4,V5) del que obtiene su matriz de correlaciones, como se ve en la FIG 1, parte 1
FIG 1: De la matriz de correlaciones a la matriz de distancias
- En el punto (1), se muestra la matriz de correlaciones. En este caso, interpretaremos las correlaciones POSITIVAS y ALTAS como variables que están cerca y NEGATIVAS y ALTAS variables que están muy lejos. Como queremos una medida de distancia-positiva- que recoja esta idea, podemos utilizar \(d_{i,j}=1-\rho_{i,j}\), es decir, la distancia entre la variable \(i\) y la variable \(j\) consistirá en 1 menos la correlación.
- En el punto (2) se obtienen dichas distancias.
- Empecemos eligiendo el par de variables que tienen menor distancia que son V4 y V5. Las unimos en un gráfico que llamaremos dendrograma (no “dendograma”) y que se construye indicando, en el eje de ordenadas, dicha distancia. El eje de abcisas es “mudo”.
Ahora, pasemos a la FIG2
- En el punto (4) hemos creado una nueva categoría que es la unión de la variable 4 y la 5 y obtenemos las distancias del resto de variables a esta nueva categoría. Se coge la mayor de entre las dos posibles. Ahora la menor distancia es entre V2 y V3 y hacemos la correspondiente marca en el dendrograma.
- En el punto (5) hemos creado el nuevo grupo y recalculamos distancias hasta que, finalmente, llegamos al último punto
FIG 3: Construimos el dendrograma
Este gráfico nos permite agrupar las variables de forma jerárquica. Por ejemplo, si queremos hacer dos grupos, el gráfico nos dice, claramente, que uno de ellos estará formado por las variables V1,V4 y V5 y el otro por V2 y V3. Si quisiéramos hacer tres grupos, entonces, uno de ellos sería el formado por V1, el otro por V4 y V5 y el último por V2 y V3. Y así sucesivamente, descendiendo de manera imaginaria en el eje de ordenadas.
Es fácil obtener el dendrograma para los datos de los Simpson. Mediante este script y la función “hclust”
Homer<-(SIMPSONS$Homer)
Bart<-(SIMPSONS$Bart)
Lisa<-(SIMPSONS$Lisa)
Marge<-(SIMPSONS$Marge)
Apu<-SIMPSONS$Apu
Flanders<-SIMPSONS$Flanders
Krusty<- SIMPSONS$Krusty
Milhause<-SIMPSONS$Milhause
SIMPSONS_char<-data.frame(Homer,Bart,Lisa,Marge,Apu,Flanders,Krusty,Milhause)
dd <- as.dist((1 - cor(SIMPSONS_char)))
round(1000 * dd)
plot(hclust(dd))llegamos a la FIG 4, donde se pueden ver distintas agrupaciones posibles:
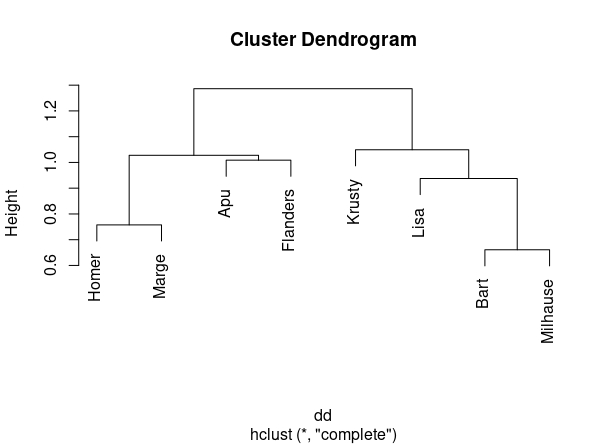 Si queremos:
Si queremos:
- Dos cluster: Homer+Marge+Apu+Flanders y Krusty+Lista+Bart+Milhause
- Tres cluster: Homer+Marge y Apu+Flanders y Krusty+Lista+Bart+Milhause
- Cuatro cluster: Homer+Marge, Apu+Flanders, Krusty, Lisa+Bart+Milhause
y así, sucesivamente.
Ejercicio de interés ¿Pueden estas asociaciones de personajes explicar los resultados de los cluster de episodios?
Clase 4: Componentes Principales
El análisis de componentes principales tiene una clara idea geométrica basada en un concepto clave: la proyección ortogonal. Primero, explicaremos visualmente la idea de proyección ortogonal para, a continuación, ir usando esas ideas con el objetivo de entender el método. La forma de desarrollarlo estará basada en intuiciones para, al final, disponer de un apéndice que le permita entender, con algo más de profundidad (si está interesado), las expresiones que se utilizan en el texto principal.
NOTA!
Aquí empieza la parte que no se verá en la explicación de clase, pero es importante interiorizar para entenderlo
Algunas ideas de álgebra y geometría
Las ideas que aquí se cuentan son, en realidad, un ejemplo gráfico y divulgativo. De esta manera, tanto los conceptos centrales de proyección ortogonal y de diagonalización de matrices, se enuncian de forma aplicada y se anima al lector/a que acuda a un texto de matemáticas (si tiene más interés en asentar esas ideas). Un buen texto es “Álgebra Lineal y sus Aplicaciones” de David C. Lay.
- Vector. La definición típica de vector es “un segmento de recta orientado”. Por ejemplo, el vector \(\overrightarrow{x}=\left[\begin{array}{c} 1\\ 2 \end{array}\right]\) nos dice que tenemos que orientarnos dado un paso en sentido el eje \(x\) (es decir, a la derecha) y dando dos pasos en sentido del eje \(y\) (es decir, hacia arriba). Sin embargo, el vector no dice nada de dónde debemos empezar, esto es, el punto de aplicación: todos estos vectores son el mismo:
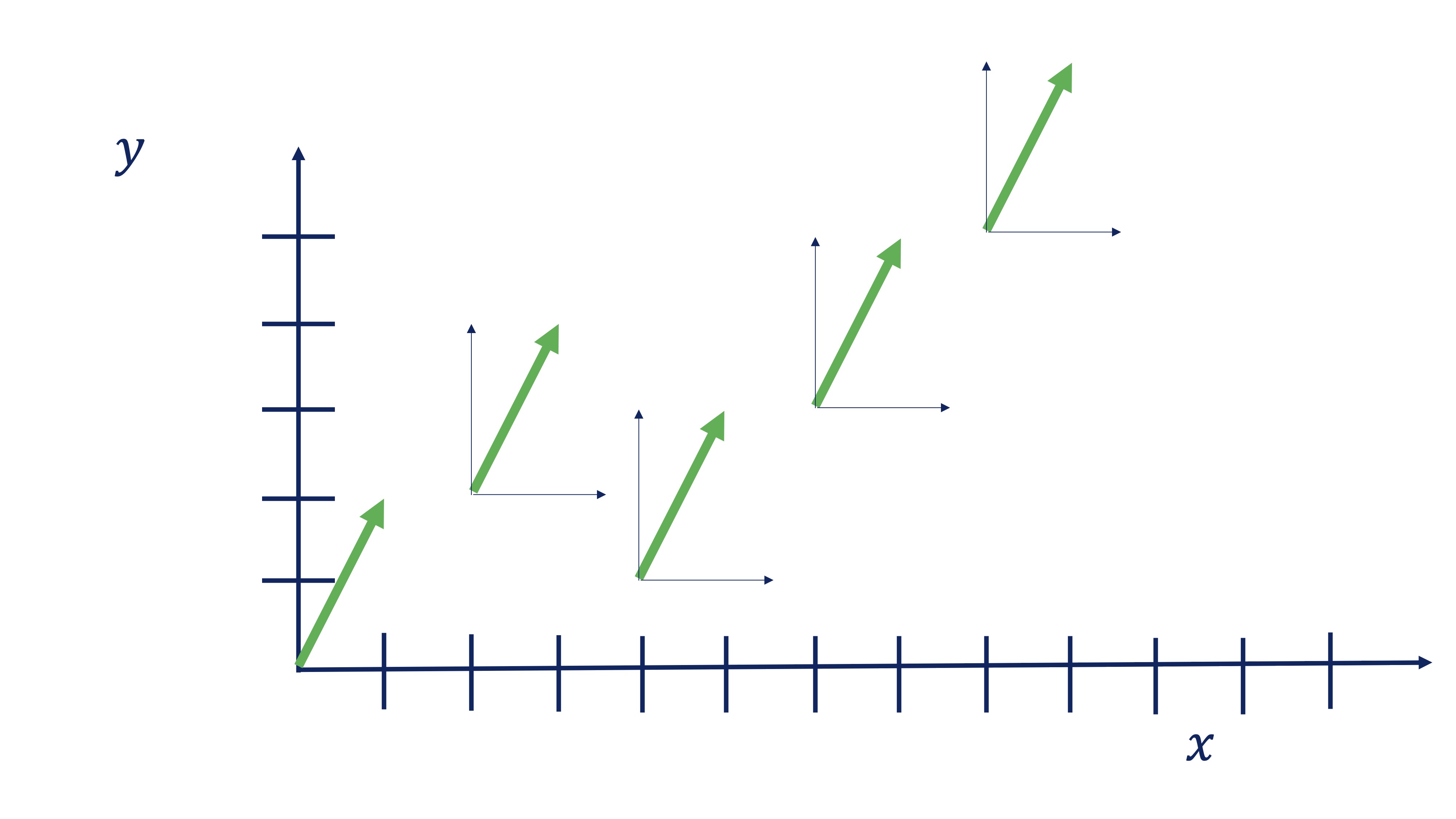
FIG 1: El mismo vector en distintos puntos de aplicación
La definición de segmento de recta orientado, quizás no le permita hacerse una idea de para qué usará los vectores. En nuestro caso, un vector será un almacenador de información. De hecho, el ojo humano suele “vectorizar” el análisis de datos. Mire, si no, el precio de la acción de Coca-Cola:
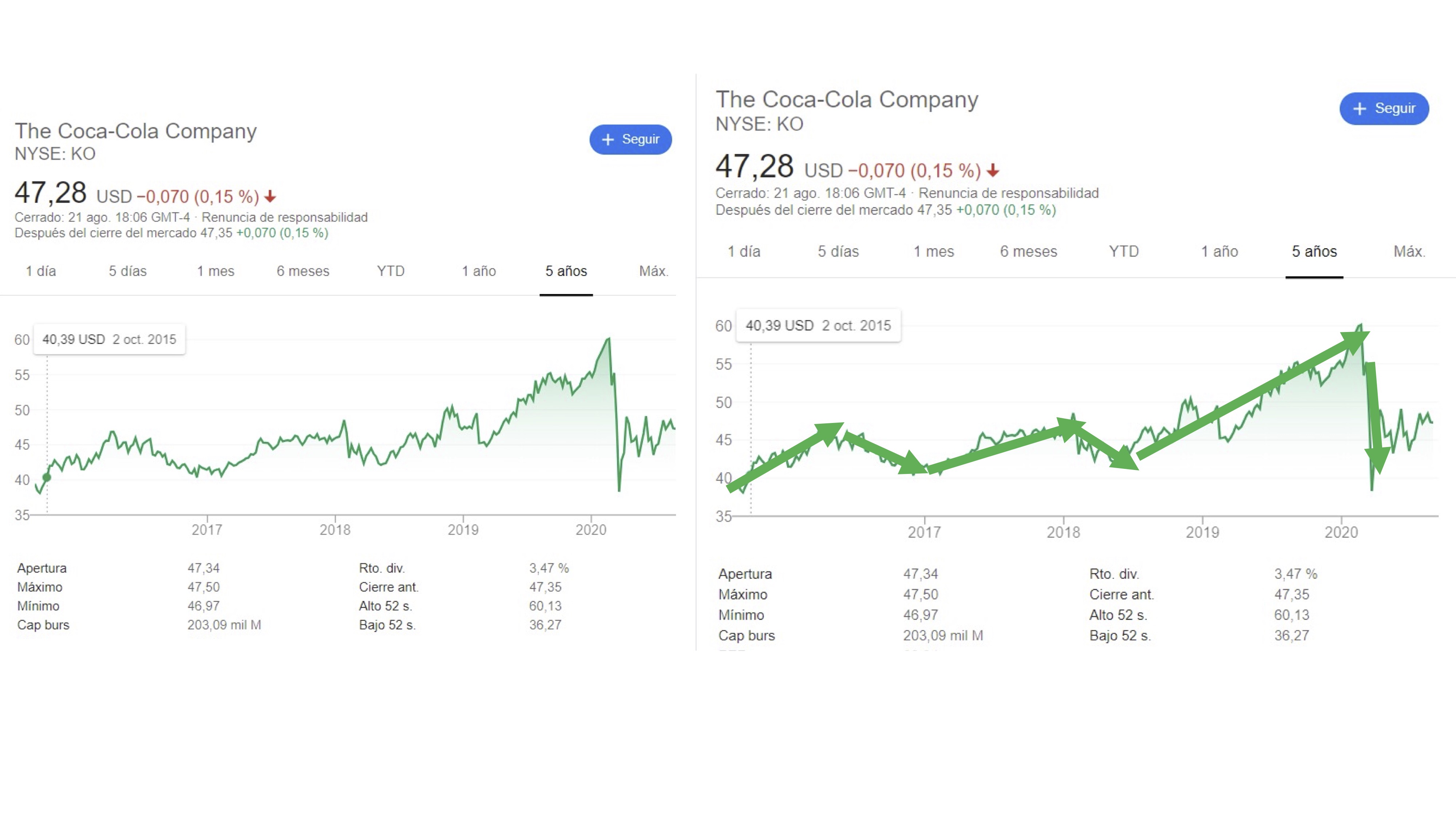
FIG 2: El precio de la acción de “Coca Cola” vectorizado
Como puede ver, nuestro ojo no está preparado para procesar todas las pequeñas discrepancias de la evolución de los datos. Seguro que prefiere tener una idea más general de los movimientos de la bolsa usando esas flechitas que llamamos vectores.
Por ejemplo, si almacenamos en un vector, \(\overrightarrow{v}\) la siguiente información sobre el precio de las acciones de Coca Cola:
\[ \overrightarrow{v}=\left[\begin{array}{cc} \#meses, & variaci\acute{o}n\:precio\end{array}\right], \]
tendremos algo así:
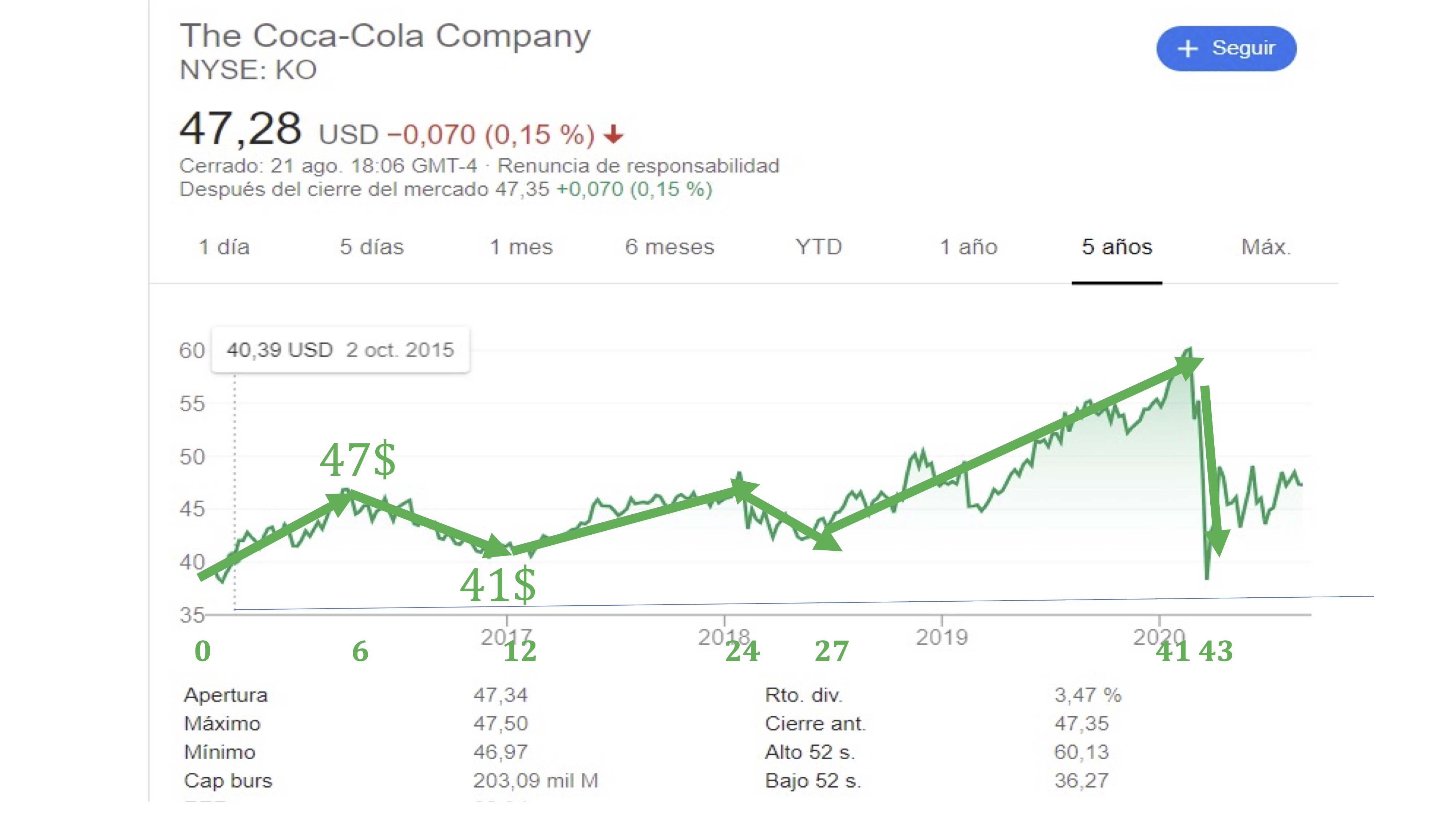
FIG 3: un caso concreto para ver la idea de vector
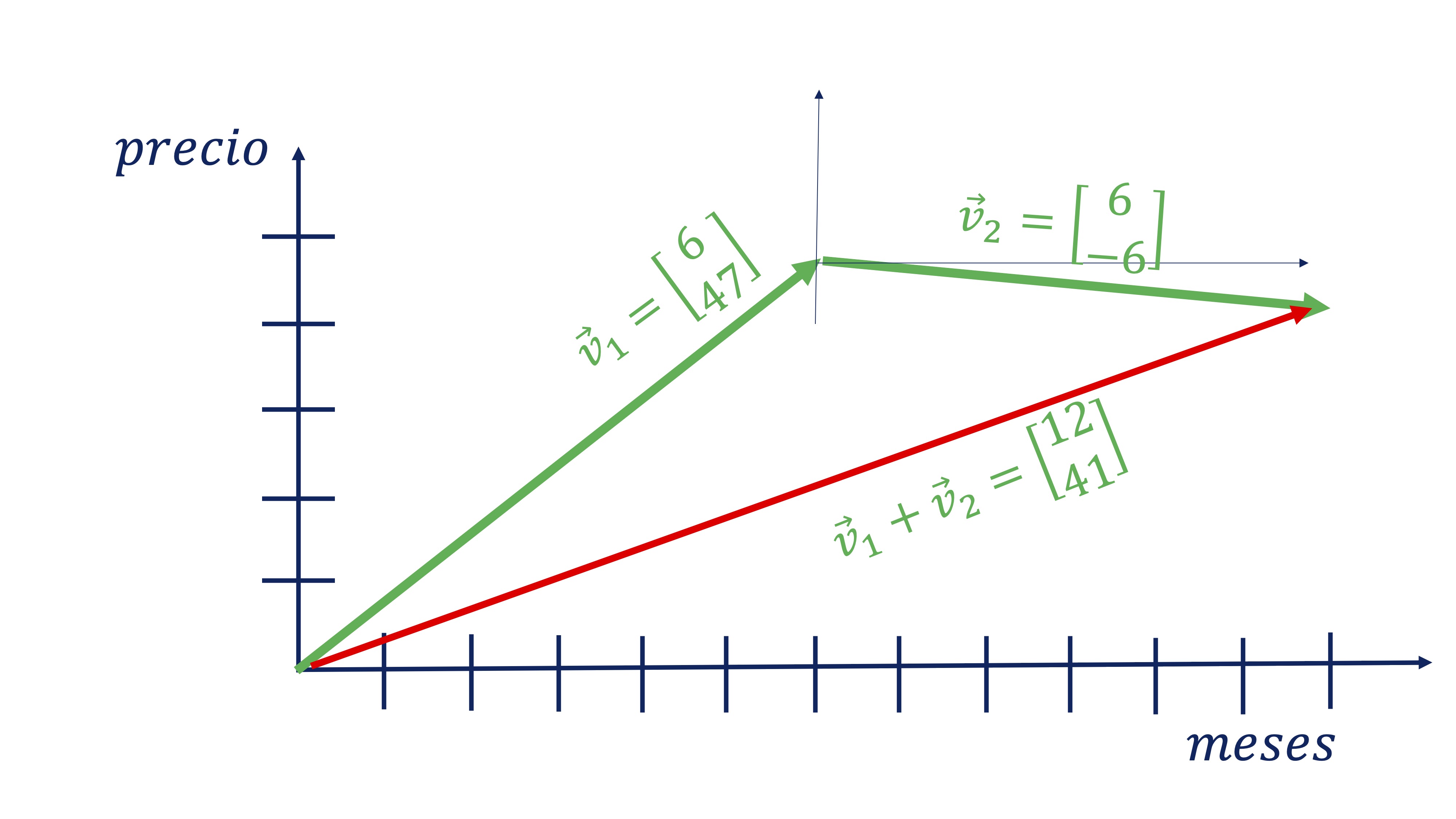 Donde, además, la suma de los dos vectores tiene sentido ya que nos
da en el primer componente el tiempo que ha pasado y en el segundo
el precio en dicho momento (vector rojo).
Donde, además, la suma de los dos vectores tiene sentido ya que nos
da en el primer componente el tiempo que ha pasado y en el segundo
el precio en dicho momento (vector rojo).
Recuerde que, en general, denotamos un vector como \(\overrightarrow{v}\) (la flecha superior indica que es un vector) y ponemos sus componentes en columna: \(\overrightarrow{v}=\left[\begin{array}{c} -2\\ 3 \end{array}\right]\). Además, recuerde que si quiere tener el vector como una fila, lo ha de trasponer: \(\overrightarrow{v}^{T}=\left[\begin{array}{cc} -2 & 3\end{array}\right]\), usando la letra \(T\) en el exponente para indicarlo. Si tenemos otro vector \(\overrightarrow{w}=\left[\begin{array}{c} 3\\ 2 \end{array}\right]\), definimos el producto escalar de ambos vectores como:
\[ \overrightarrow{v}^{t}\overrightarrow{w}=\left[\begin{array}{cc} -2 & 3\end{array}\right]\left[\begin{array}{c} 3\\ 2 \end{array}\right]=(-2\times3)+(3\times2)=0 \]
(como ve, se define “producto escalar” porque al multiplicarlos obtenemos siempre un número-un escalar). Como en nuestro caso, si el producto escalar de dos vectores es 0, eso indica que son perpendiculares (es decir, conforman un ángulo de 90º). Los dibujamos para que vea que, efectivamente, ocurre:
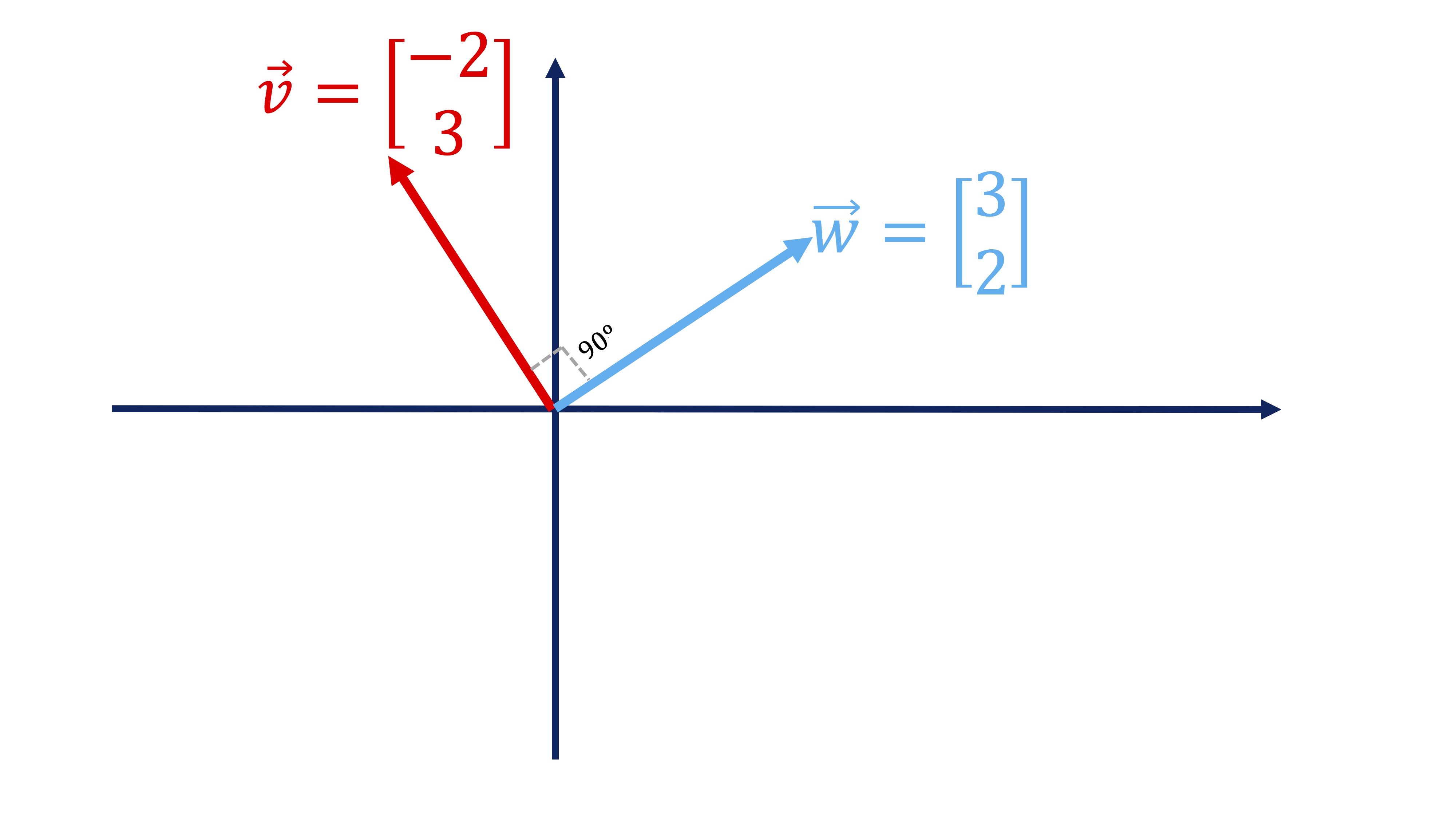
FIG 5: Dos vectores son perpendiculares (su producto escalar es cero)
-Matriz Respecto a una matriz, puede verla como una generalización de la idea de vector. Sigue siendo un buen almacén de información que, en este caso, es como si estuviera formada por un montón de vectores apilados. Por ejemplo, esta matriz guarda en columnas el número de observación (id), los meses, y la variación del precio (\(\Delta precio\)):
| Id | Meses | \(\Delta precio\) |
|---|---|---|
| 1 | 6 | 47 |
| 2 | 6 | -6 |
| … | … | … |
Es decir,
\[ X=\left[\begin{array}{ccc} 1 & 6 & 47\\ 2 & 6 & -6 \end{array}\right], \]
esta matriz decimos que es de dimensión \(2\times3\), ya que tiene 2 filas y 3 columnas. De manera más formal, se puede escribir así: \(X\in\mathcal{M}_{2\times3}\), que indica que \(X\) pertenece al espacio de las matrices de dimensión \(2\times3.\)
Recuerde que para que dos matrices puedan multiplicarse se debe poder realizar el producto escalar, visto anteriormente con los vectores, para cada fila y columna. Es decir, \(X=\left[\begin{array}{cc} 1 & 0\\ 3 & 1\\ 5 & 2 \end{array}\right]\), \(Y=\left[\begin{array}{cc} 1 & 2\\ 0 & 1 \end{array}\right]\), pueden multiplicarse así \(XY\) porque el número de columnas de la primera matriz es igual al número de filas de la segunda, pero no pueden multiplicarse así: \(YX\):
\[ XY=\left[\begin{array}{cc} 1 & 0\\ 3 & 1\\ 5 & 2 \end{array}\right]\left[\begin{array}{cc} 1 & 2\\ 0 & 1 \end{array}\right]=\left[\begin{array}{cc} 1 & 2\\ 3 & 7\\ 5 & 12 \end{array}\right] \]
\[ YX=\left[\begin{array}{cc} 1 & 2\\ 0 & 1 \end{array}\right]\left[\begin{array}{cc} 1 & 0\\ 3 & 1\\ 5 & 2 \end{array}\right]=? \]
- MATRIZ DE VARIANZAS Y COVARIANZAS. Una aplicación del producto de matrices, que encontrará habitualmente, es la matriz de varianzas y covarianzas. Recuerde que la varianza de una variable es \(var(x)=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}{n-1}\) y la covarianza entre dos variables es \(cov(x,y)=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{n-1}\) y podemos construir una matriz con esa información:
\[\begin{equation} C=\left[\begin{array}{cc} var(x) & cov(x,y)\\ cov(x,y) & var(y) \end{array}\right]\label{eq:matrizC} \end{equation}\]
(dese cuenta de que es una matriz simétrica). \(C\) se puede obtener con cálculos más rápidos mediante operaciones con matrices. Vamos a imaginar que la \(X\) es ahora nuestra matriz de datos, donde la columna 1 es la variable \(x\) y la columna 2 es la variable \(y\), de tal forma que las filas son las observaciones por individuos:
| Id | \(x\) | \(y\) |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 3 | 1 |
| 3 | 5 | 2 |
para poder seguir con la fórmula, vamos a transformar la matriz y le vamos a restar a cada columna su media:
| Id | \(x-\bar{x}\) | \(y-\bar{y}\) |
|---|---|---|
| 1 | -2 | -1 |
| 2 | 0 | 0 |
| 3 | 2 | 1 |
de tal forma que tenemos que \(\widetilde{X}=\left[\begin{array}{cc} -2 & -1\\ 0 & 0\\ 2 & 1 \end{array}\right]\) es la matriz \(X\) donde le hemos restado las medias (se dice que es la matriz \(X\) en desviaciones con respecto a sus medias). Si ahora hacemos esta cuenta:
\[ \frac{1}{n-1}\widetilde{X}^{t}\widetilde{X}=\frac{1}{3}\left[\begin{array}{ccc} -2 & 0 & 2\\ -1 & 0 & 1 \end{array}\right]\left[\begin{array}{cc} -2 & -1\\ 0 & 0\\ 2 & 1 \end{array}\right]=\frac{1}{2}\left[\begin{array}{cc} 8 & 4\\ 4 & 2 \end{array}\right]=\left[\begin{array}{cc} 4 & 2\\ 2 & 1 \end{array}\right] \]
donde \(N\) representa el número de elementos muestrales, nos proporciona la matriz de varianzas y covarianzas.
x1<-c(1,3,5)
x2<-c(0,1,2)
X<-data.frame(x1,x2)
C<-cov(X)
#equivalente a hacer
x1<-x1-mean(x1)
x2<-x2-mean(x2)
X<-as.matrix(data.frame(x1,x2))
C<-(1/(dim(X)[1]-1))*(t(X))%*%XPor lo tanto, concluímos que:
- Una matriz \(W\) cuyas filas son observaciones por individuo y las columnas son variables, si está expresada en desviaciones con respecto a la media, su matriz de varianzas y covarianzas resulta ser:
Ejercicio: pruebe que si las variables están estandarizadas (es decir los elementos de \(W\) no sólo están desviados con respecto a la media, sino que se los divide por su desviación típica), al hacer \(\frac{1}{N-1}W^{t}W,\) lo que obtenemos es la matriz de correlaciones.
La noción de proyección ortogonal
Otra de las preguntas de interés en álgebra son las que están relacionadas con la proyección ortogonal. Aquí vamos a ver un ejemplo sencillo, con el que trabajaremos a mano. Pero antes, necesitamos saber qué es un vector proporcional a otro. Diremos que un vector \(\overrightarrow{w}\) es proporcional a otro \(\overrightarrow{v}\) (y se escribe con esta notación \(\overrightarrow{w}\propto\overrightarrow{v},\) leyéndose \(\propto\) como “es proporcional a”) si se cumple que:
\[ \overrightarrow{w}=\lambda\overrightarrow{v}, \]
con \(\lambda\in\mathbb{R}.\) En la figura siguiente, tiene un ejemplo donde -una manera de verlo- el vector \(\overrightarrow{v}_{2}\propto\overrightarrow{v}_{1}\), con \(\lambda=2\), indicando que siguen la misma dirección y sentido, solo que \(\overrightarrow{v}_{2}\) es más grande. \(\overrightarrow{v}_{3}\propto\overrightarrow{v}_{1}\), con \(\lambda=-1/2\), indicando que siguen la misma dirección y sentido contrario (y es más pequeño). Como ve, los vectores proporcionales comparten dirección.
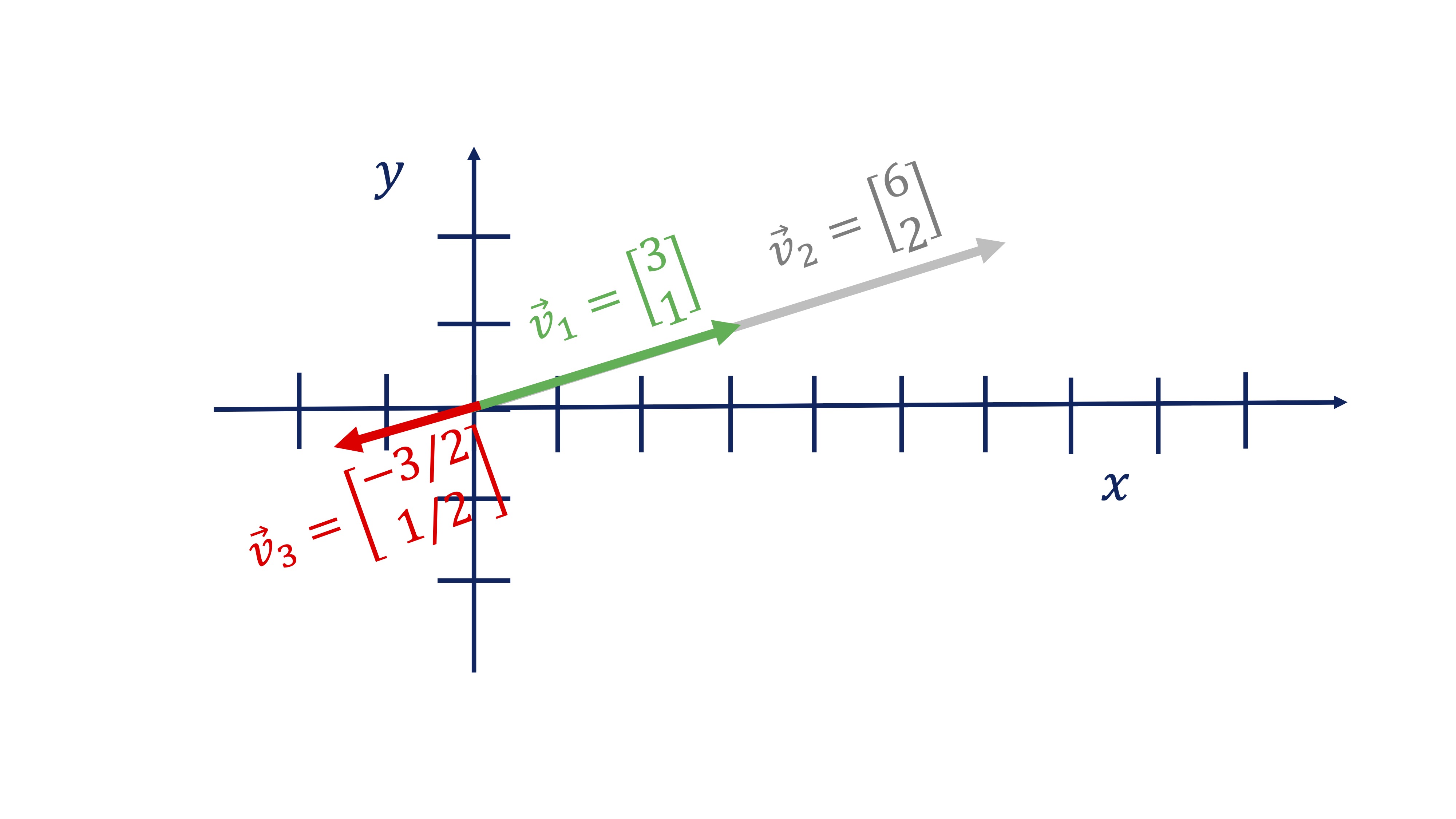
FIG 6: Tres vectores proporcionales
La idea de proyección ortogonal necesita tnener clara la de vector proporcional. De hecho, la idea de proyectar el vector \(\overrightarrow{w}\) sobre el vector \(\overrightarrow{v}\) consiste en lo siguiente:
**buscar un vector proporcional a \(\overrightarrow{v}\) que esté lo más cerca posible de \(\overrightarrow{w}:\)
Piense que hay infinitos vectores proporcionales a \(\overrightarrow{v}\) pero sólo uno de estos será el más cercano a \(\overrightarrow{w}.\) ¿Cuál cree que es en la figura siguiente?
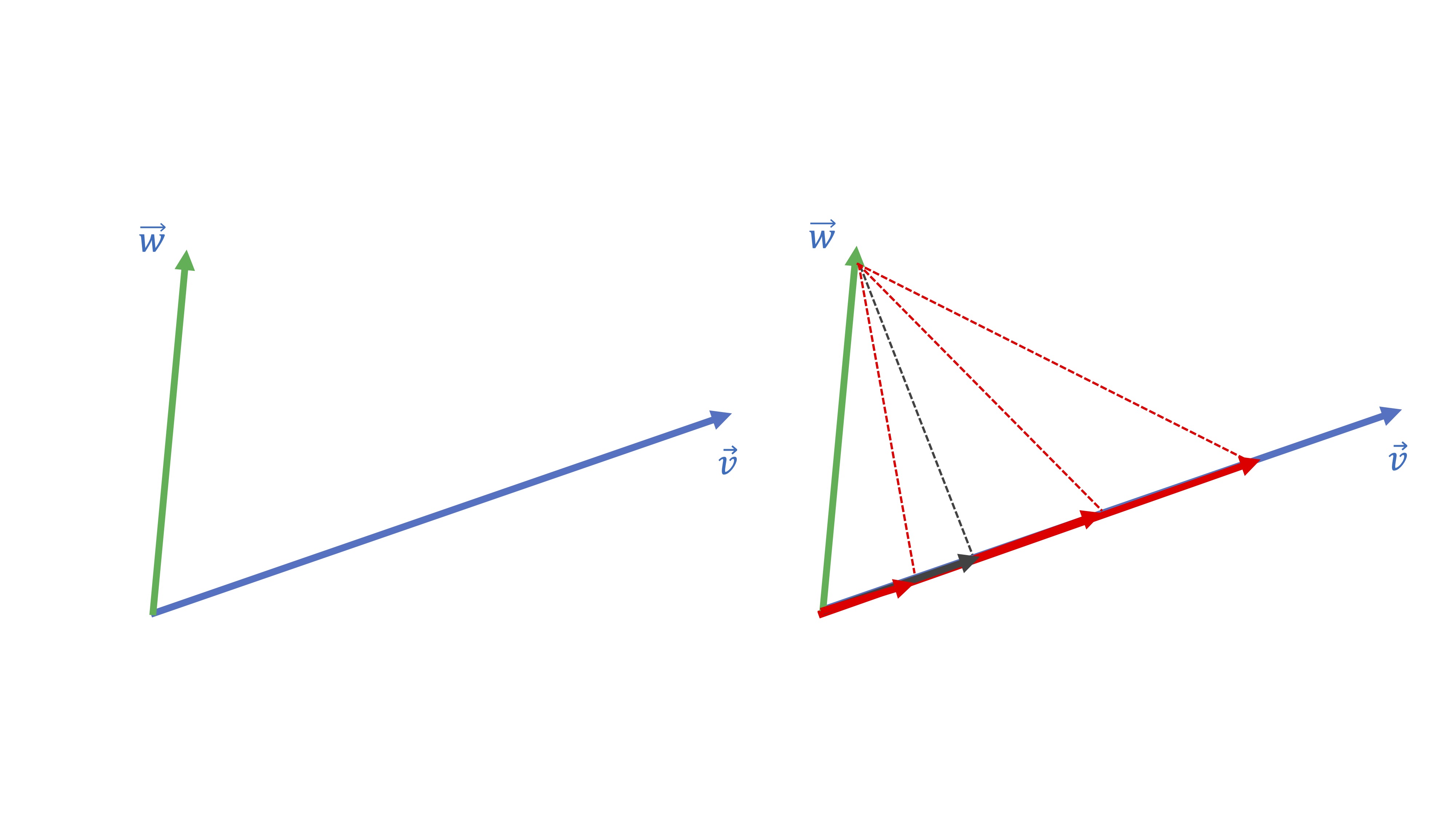
FIG 7: ¡El vector perpendicular es el que está más cerca!
Seguramente, habrá caído en la cuenta de que el más cercano es el gris:
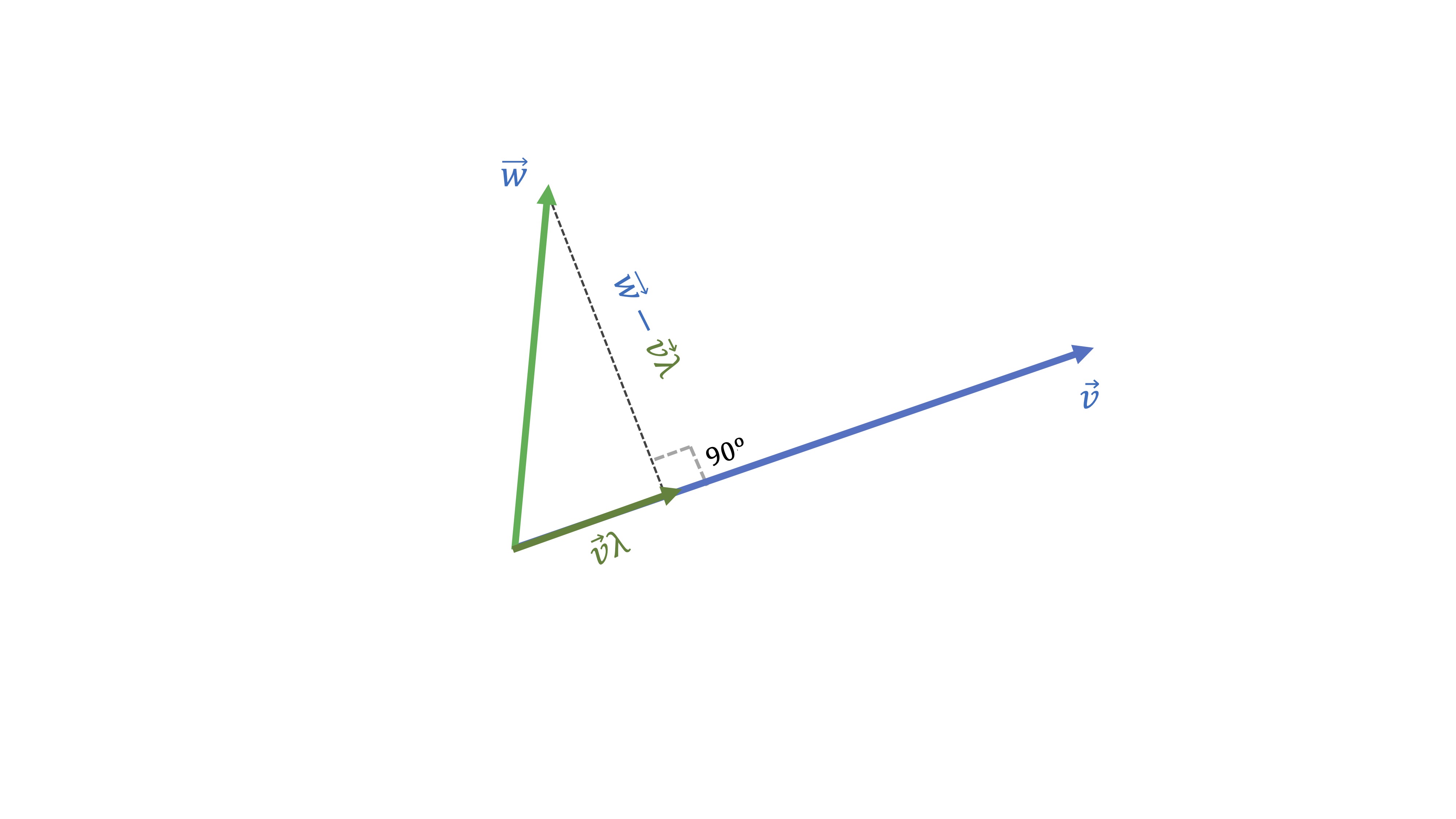
FIG 8: ¡El vector perpendicular es el que está más cerca!
Nuestro objetivo será encontrar qué vector proporcional a \(\overrightarrow{v}\) (es decir, \(\overrightarrow{v}\lambda\), donde \(\lambda\) es un escalar) está más cerca de \(\overrightarrow{w}.\) Ese “más cerca” quiere decir que la distancia entre los dos vectores sea la mínima posible. Como puede ver, esa es la distancia que genera el segmento ortogonal al vector \(\overrightarrow{v}\). Como ya hemos dicho, han de ser ortogonales, es decir, han de cumplir:
\[ \left(\overrightarrow{w}-\overrightarrow{v}\lambda\right)^{t}\overrightarrow{v}=0\Rightarrow\lambda=\frac{\overrightarrow{w}^{t}\overrightarrow{v}}{\overrightarrow{v}^{t}\overrightarrow{v}} \]
Veamos un ejemplo “a mano”.
- Si queremos proyectar el vector \(\overrightarrow{w}=\left[\begin{array}{c} 3\\ 1 \end{array}\right]\) sobre el vector \(\overrightarrow{v}=\left[\begin{array}{c} 1\\ 0 \end{array}\right]\), tendremos que
\[ \lambda=\frac{\overrightarrow{w}\cdot\overrightarrow{v}}{\overrightarrow{v}\cdot\overrightarrow{v}}=\frac{\left[\begin{array}{cc} 3 & 1\end{array}\right]\left[\begin{array}{c} 1\\ 0 \end{array}\right]}{\left[\begin{array}{cc} 1 & 0\end{array}\right]\left[\begin{array}{c} 1\\ 0 \end{array}\right]}=\frac{3}{1}=3 \]
Por lo que el vector más parecido a \(\overrightarrow{w}=\left[\begin{array}{c} 3\\ 1 \end{array}\right]\) pero que es proporcional a \(\overrightarrow{v}=\left[\begin{array}{c} 1\\ 0 \end{array}\right]\) es \(3\overrightarrow{v}=\left[\begin{array}{c} 3\\ 0 \end{array}\right]\). Dibújelo para cercionarse.
Autovalores y autovectores
Ya estamos terminando de la parte introductoria de álgebra. Nos queda, eso sí, justo lo más necesario para poder entender la idea de los componentes principales. Ciertas matrices cuadradas tienen una propiedad muy utilizada y muy famosa en álgebra: se dice que son diagonalizables si, por ejemplo, la matriz \(X=\left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\), admite esta descomposición:
\[ \left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\left(\begin{array}{c} -0.57\\ -0.57\\ -0.57 \end{array}\right)=6\left(\begin{array}{c} -0.57\\ -0.57\\ -0.57 \end{array}\right) \]
Cuando esto ocurre, lo que tenemos es \[ X\overrightarrow{v}=\lambda\overrightarrow{v}, \]
donde \(\overrightarrow{v}\) se denomina autovector y \(\lambda\) autovalor. De hecho, esta matriz, \(X\) va a tener tres autovalores (y sus correspondientes autovectores) no necesariamente distintos. Para calcularlos, vamos a usar R.
X<-matrix(c(1,2,3,6,0,0,2,2,2),3,3,byrow=TRUE)
ev<-eigen(X)
#donde ev nos proporciona los resultados que buscamos
eigen() decomposition
$values
[1] 6 -2 -1
$vectors
[,1] [,2] [,3]
[1,] -0.5773503 -0.3015113 0.1441708
[2,] -0.5773503 0.9045340 -0.8650248
[3,] -0.5773503 -0.3015113 0.4805693Llegamos, entonces, al resultado que decíamos
\[ \left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\left(\begin{array}{c} -0.57\\ -0.57\\ -0.57 \end{array}\right)=6\left(\begin{array}{c} -0.57\\ -0.57\\ -0.57 \end{array}\right),\]
\[ \left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\left(\begin{array}{c} -0.30\\ 0.90\\ -0.30 \end{array}\right)=\left(\begin{array}{c} 0.30\\ -0.90\\ 0.30 \end{array}\right),\left(\begin{array}{ccc} 1 & 2 & 3\\ 6 & 0 & 0\\ 2 & 2 & 2 \end{array}\right)\left(\begin{array}{c} 0.14\\ 0.86\\ 0.48 \end{array}\right)=-2\left(\begin{array}{c} 0.14\\ 0.86\\ 0.48 \end{array}\right) \]
¿Cualquier matriz cuadrada admite esta descomposición?. No toda matriz cuadrada es diagonalizable: sin embargo, las que vamos a utilizar en este contexto (que, en esencia, serán matrices de varianzas y covarianzas y de correlaciones) sí admiten esta descomposición por ser simétricas. Además,
- La suma de los autovalores es igual a la suma de los elementos de la diagonal principal de la matriz
- Los autovectores son perpendiculares. Esto implica que la correlación entre ellos es cero
NOTA!
Hasta aquí acaba la parte que no se verá en la explicación
El método de los componentes principales (PCA)
Ya es momento de entender en qué consiste el método de “componentes principales”. Para ello, necesitaremos acudir a la proyección ortogonal y a la descomposición en autovalores y autovectores de una matriz simétrica.
Partimos de una nube de puntos
Vamos a dibujar esta matriz de datos,
| Id | \(x\) | \(y\) |
|---|---|---|
| 1 | 4.5 | 3 |
| 2 | 1 | -1 |
| 3 | -1 | -2 |
| 4 | -3 | -1.5 |
| 5 | -1.5 | 1.5 |
| 6 | 0 | 0 |
donde contamos con \(6\) observaciones y dos variables \((x,y)\), en una nube de puntos.
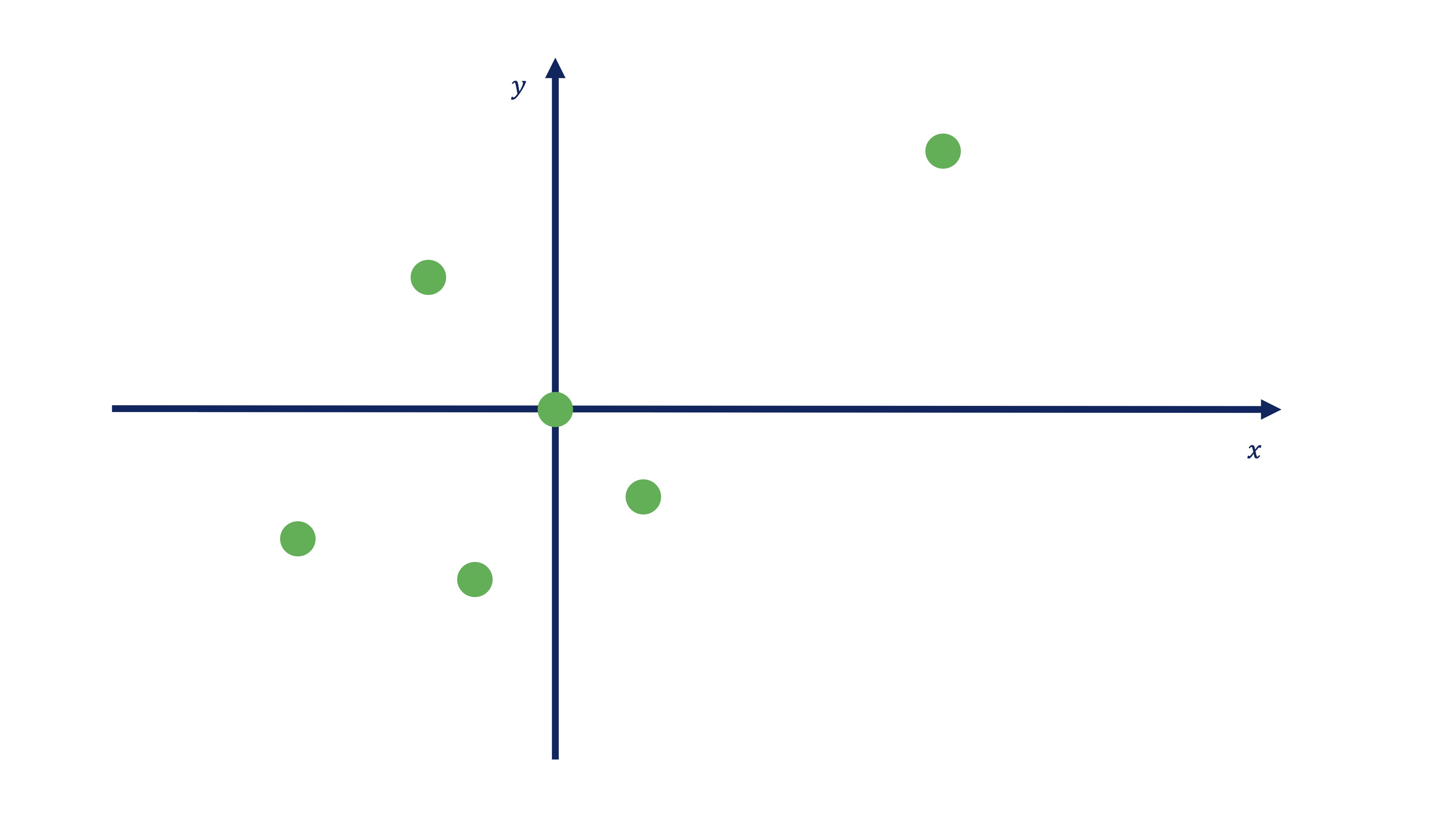
FIG 9: Dibujo de la nube de puntos
Como ve, estos puntos tienen una cierta relación lineal (es decir, un valor alto del coeficiente de correlación). La idea de los componentes principales consiste en pensar lo siguiente:
Si las variables son parecidas (tienen una correlación alta) quisiera intentar quedarme con una combinación de las dos y así pasar de tener dos variables a tener una
Es decir, idea lo que busca es reducir la dimensión (en columnas) de un conjunto de datos con un cierto número de variables relacionadas entre sí. En resumen, el objetivo de PCA, será el siguiente:
análisis de Componentes Principales!
Reducir el número de variables \(m\) de un conjunto de datos a un número \(k\) tal que \(k<<m\).
¿Cómo reducimos el número de variables? Para ello, tenemos que usar una técnica geométrica conocida como la proyección. La pregunta que nos hacemos es la siguiente: ¿Cómo transformamos la información de cada individuo, que-en este caso- está en dos dimensiones a una nueva información que esté en una dimensión? Esto ya lo hace, por ejemplo, cuando calcula un promedio. Imaginemos que las variables 1 y 2 están medidas en las mismas unidades y que, por tanto, tiene sentido obtener un promedio. El promedio de dos variables \(x,y\) consiste en \(\frac{x+y}{2}\), es decir
\[ nueva\:variable_{i}=0.5x_{i}+0.5y{}_{i}\:\:i=1,..,6 \]
| Id | \(x\) | \(y\) | nueva variable |
|---|---|---|---|
| 1 | 4.5 | 3 | 3.75 |
| 2 | 1 | -1 | 0 |
| 3 | -1 | -2 | -1.5 |
| 4 | -3 | -1.5 | -2.25 |
| 5 | -1.5 | 1.5 | 0 |
| 6 | 0 | 0 | 0 |
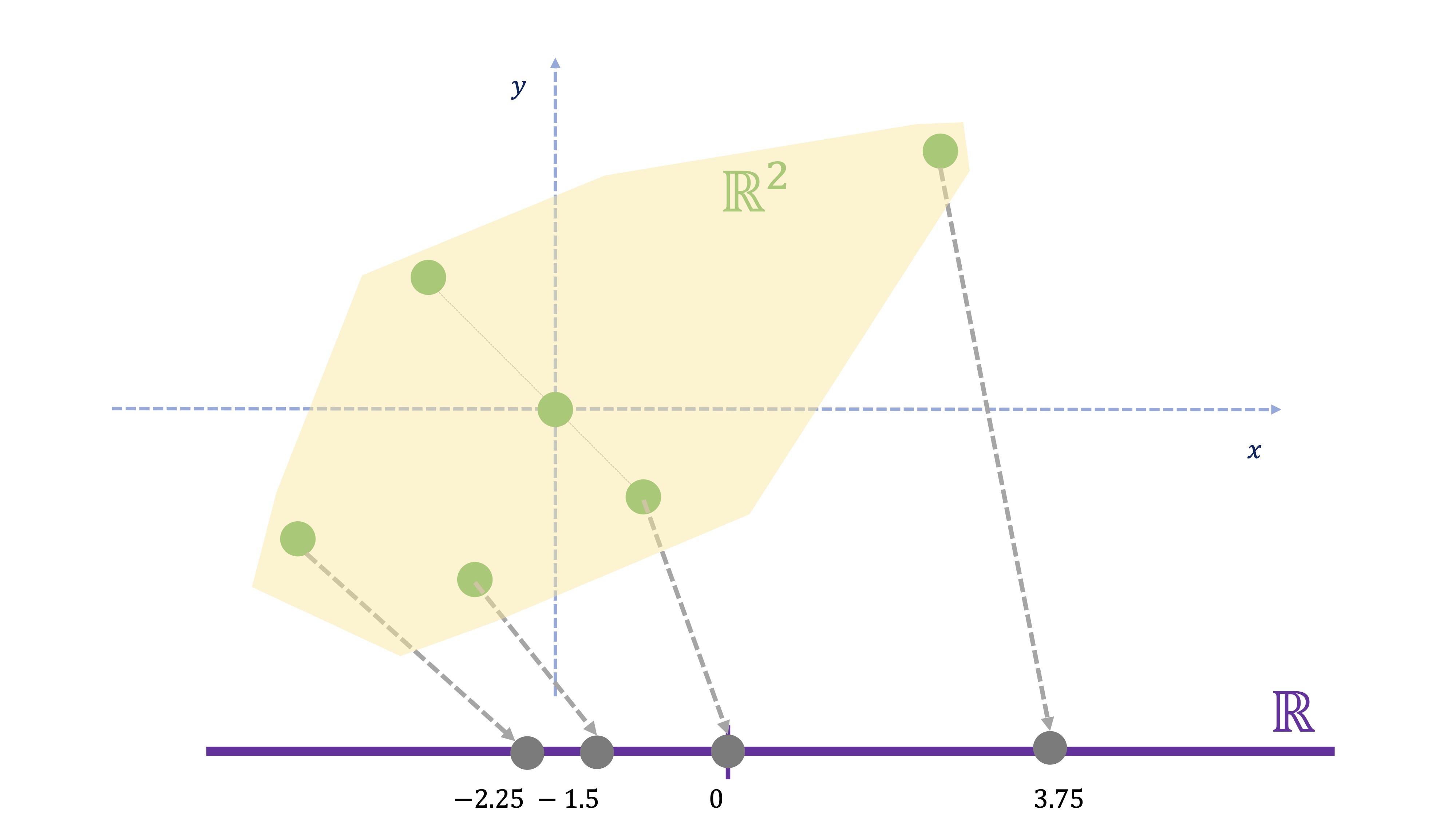
FIG 10: El promedio como proyección
Si se da cuenta (FIG 10), la nueva variable se representa sólo sobre un eje, ya que hemos resumido la información de las dos variables de cada individuo al promedio. Es decir: hemos proyectado un punto en \(\mathbb{R}^{2}\) (por ejemplo \((5.5,3)\) en \(\mathbb{R}\) (es decir, su proyección es 4.25). Ahora bien:
- ¿Y si las variables están relacionadas pero medidas en unidades distintas (años, euros, etc…)? El promedio no tiene sentido
- ¿El promedio es la mejor proyección?
Para ello nació el análisis de componentes principales
Como hemos visto, sólo en casos muy concretos es sensato utilizar el promedio como un “reductor” de la dimensión de nuestra información disponible. En realidad, si seguimos trabajando en este caso con información bidimensional, nos interesará proyectar los puntos sobre una recta (como hicimos antes con el promedio) pero que tenga, en general unos “pesos” para cada variable, elegidos mediante algún criterio sensato.
Entonces nos preguntamos: ¿Cómo buscar los valores \(C1,a1\) en esta expresión?
\[ C1_{i}=a1_{1}x_{i}+a1_{2}y_{i} \]
donde \(a1_{1},a1_{2}\) son los pesos asociados a cada variable, los cuales nos permitirán resumir lo mejor posible la información conjunta de las variables \(x,y\) en una nueva variable que llamaremos \(C1\)? Lo que vamos a hacer aquí lo contaremos de una manera sencilla (pensando sobre un gráfico) aunque en el apéndice se desarrolla el álgebra necesaria para entenderlo todo. Tenemos que buscar una recta sobre la que proyectar los puntos de tal forma que esos puntos estén lo más cerca posible a la recta. Seguro que ya ha averiguado que aquí:
buscamos una proyección ortogonal.
Vamos a imaginarnos, entonces, que somos capaces de encontrar una recta que nos permita realizar la proyección ortogonal de todos los puntos a esa recta (y que nos permite, entonces, pasar de \(\mathbb{R}^{2}\rightarrow\mathbb{R}\)). Usando, por ahora, la imaginación, nos podríamos acercar a algo así:
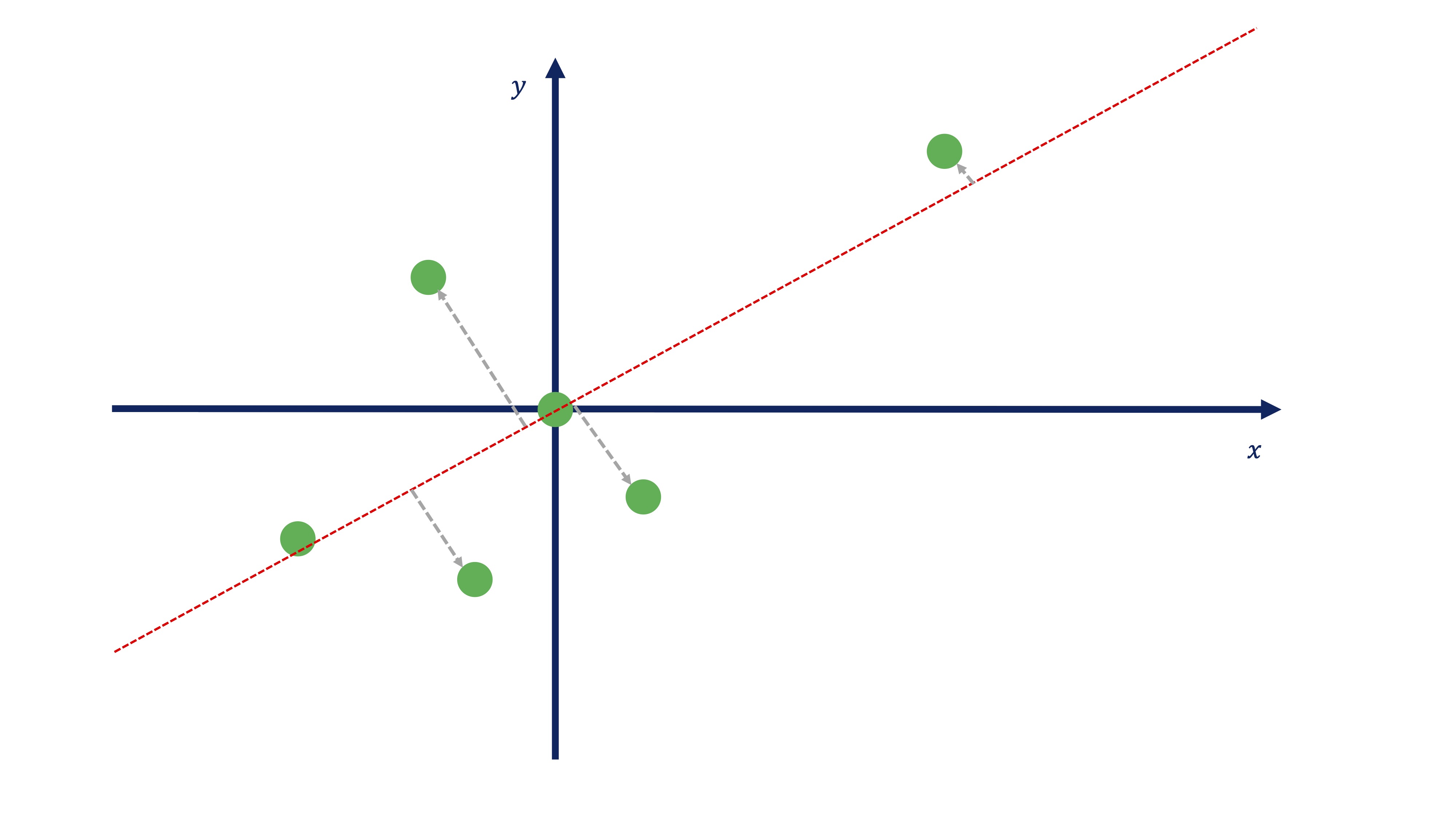
FIG 11: Una proyección ortogonal
A lo mejor, alguien ha pensado esta otra recta (o similar):
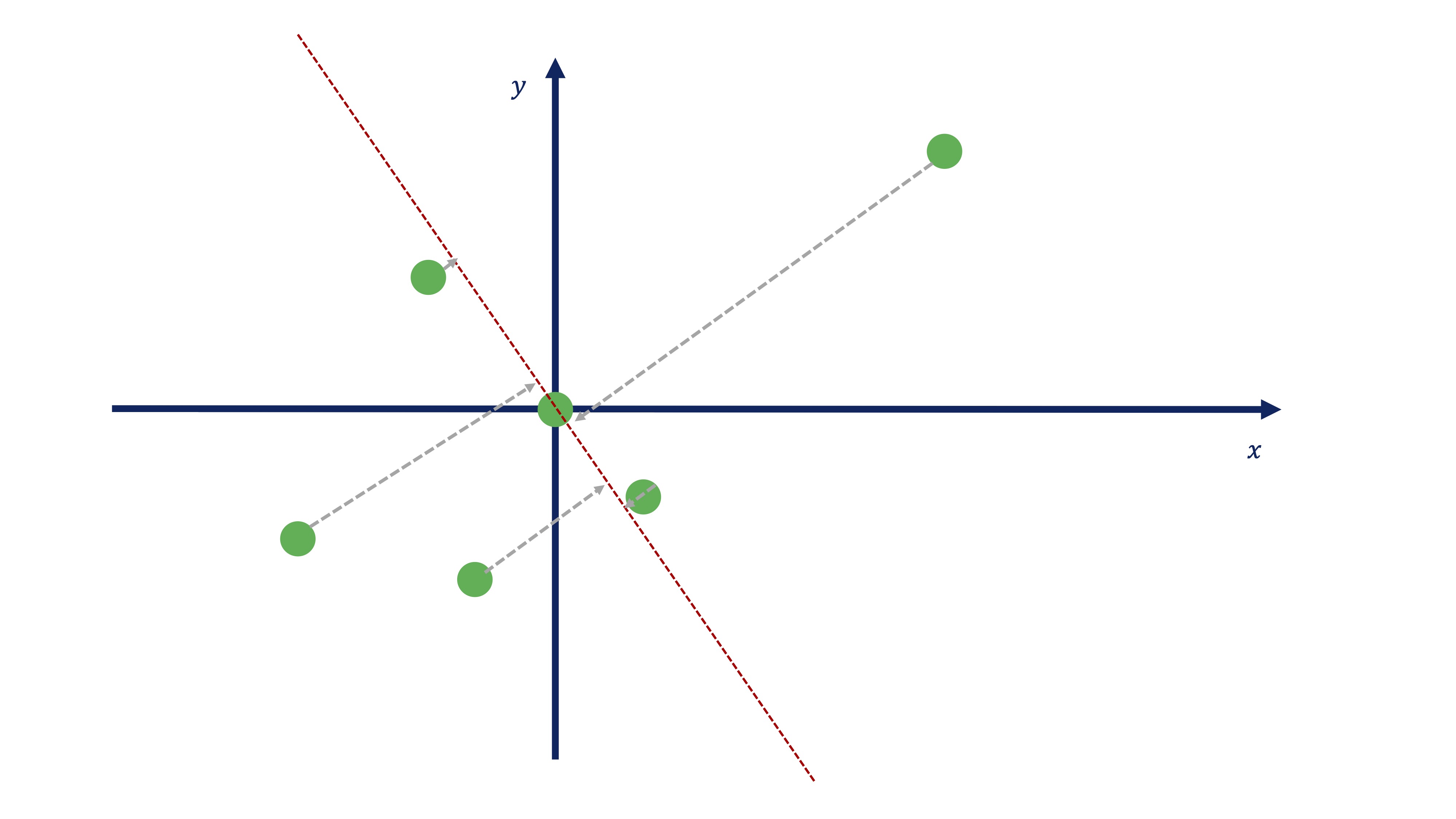
FIG 12: El promedio como proyección
Ambas se llaman DIRECCIONES PRINCIPALES. Antes de tomar una decisión sobre qué dirección principal es más interesante, tendremos que plantearnos cómo se obtienen esos coeficientes que nos permiten parametrizar las direcciones. En el apéndice matem?tico se prueba que se obtienen mediante la diagonalización de la matriz de varianzas y covarianzas de los datos.
Es decir, tenemos que \[ X=\left[\begin{array}{cc} 4.5 & 3\\ 1 & -1\\ -1 & -2\\ -3 & -1.5\\ -1.5 & 1.5\\ 0 & 0 \end{array}\right] \]
cuya matriz de varianzas y covarianzas es:
\[ C(X)=\left(\begin{array}{cc} 6.7 & 3.35\\ 3.35 & 3.70 \end{array}\right) \]
x1<-c(4.5,1,-1,-3,-1.5,0) #Genera las dos variables
x2<-c(3,-1,-2,-1.5,1.5,0)
X<-data.frame(x1,x2) #dale estructura de datos
RES<-(princomp(X)) #usamos componentes principalesusando la función princomp podemos obtener lo que necesitmos.
RES$loadings #nos proporciona los autovectores
Loadings:
Comp.1 Comp.2
x1 0.839 0.544
x2 0.544 -0.839
RES$scores #nos proporciona cada componente (C1,C2))
Comp.1 Comp.2
[1,] 5.407863e+00 -7.084558e-02
[2,] 2.954918e-01 1.382998e+00
[3,] -1.926752e+00 1.134737e+00
[4,] -3.333365e+00 -3.723922e-01
[5,] -4.432378e-01 -2.074498e+00
[6,] -1.509219e-17 2.329373e-17Así, el primer autovector nos dará la dirección principal primera. Fíjese, si representamos el vector \(\overrightarrow{a}_{1}=\left(\begin{array}{c} 0.8392\\ 0.5438 \end{array}\right)\), conjuntamente con los datos:
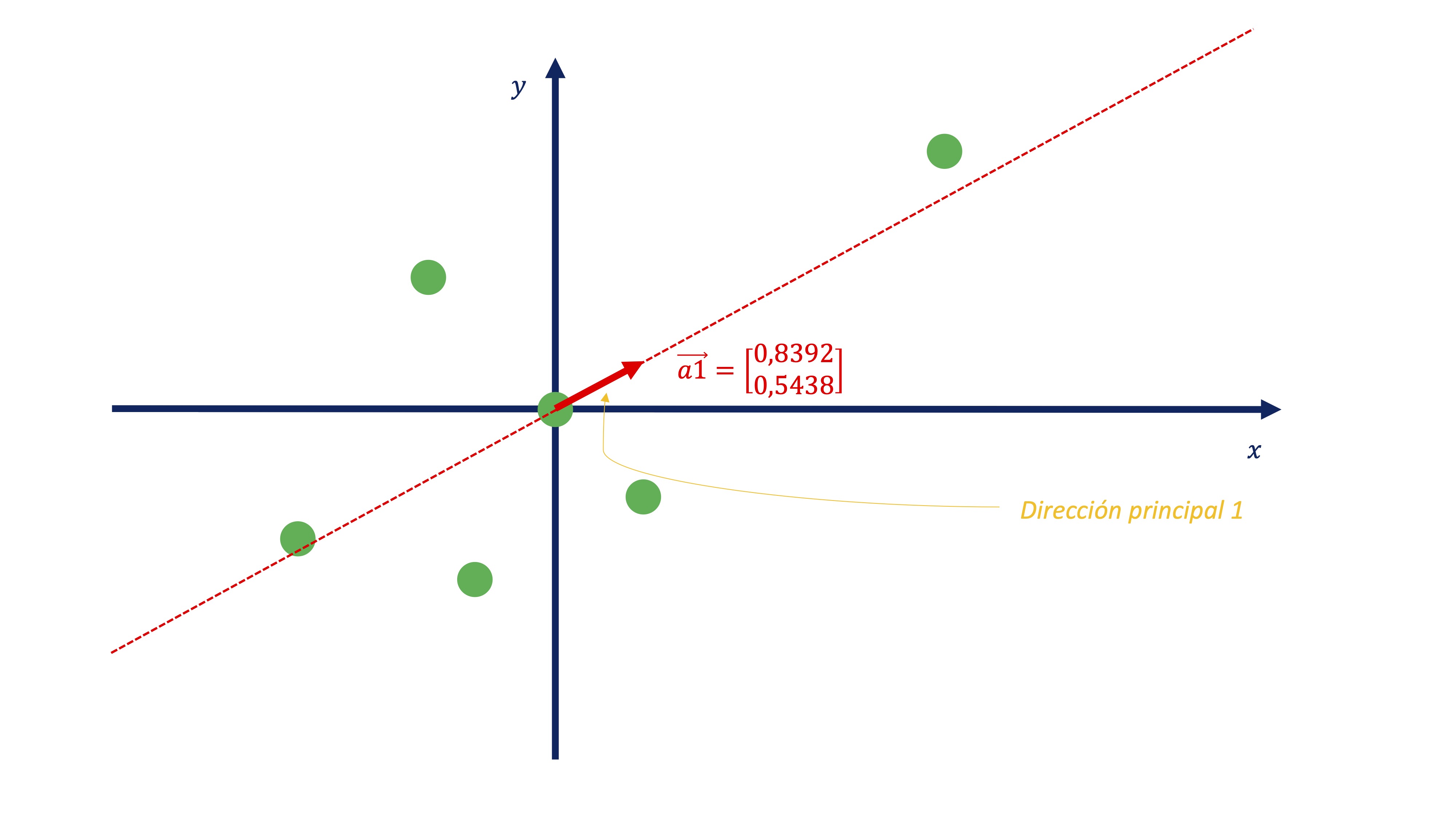
FIG 13: La primera dirección principal
nos permite encontrar cuál es esa recta. De tal forma que usando esos coeficientes, obtenemos dicha proyección:
\[ C1_{i}=0.8392x_{i}+0.5438y_{i} \]
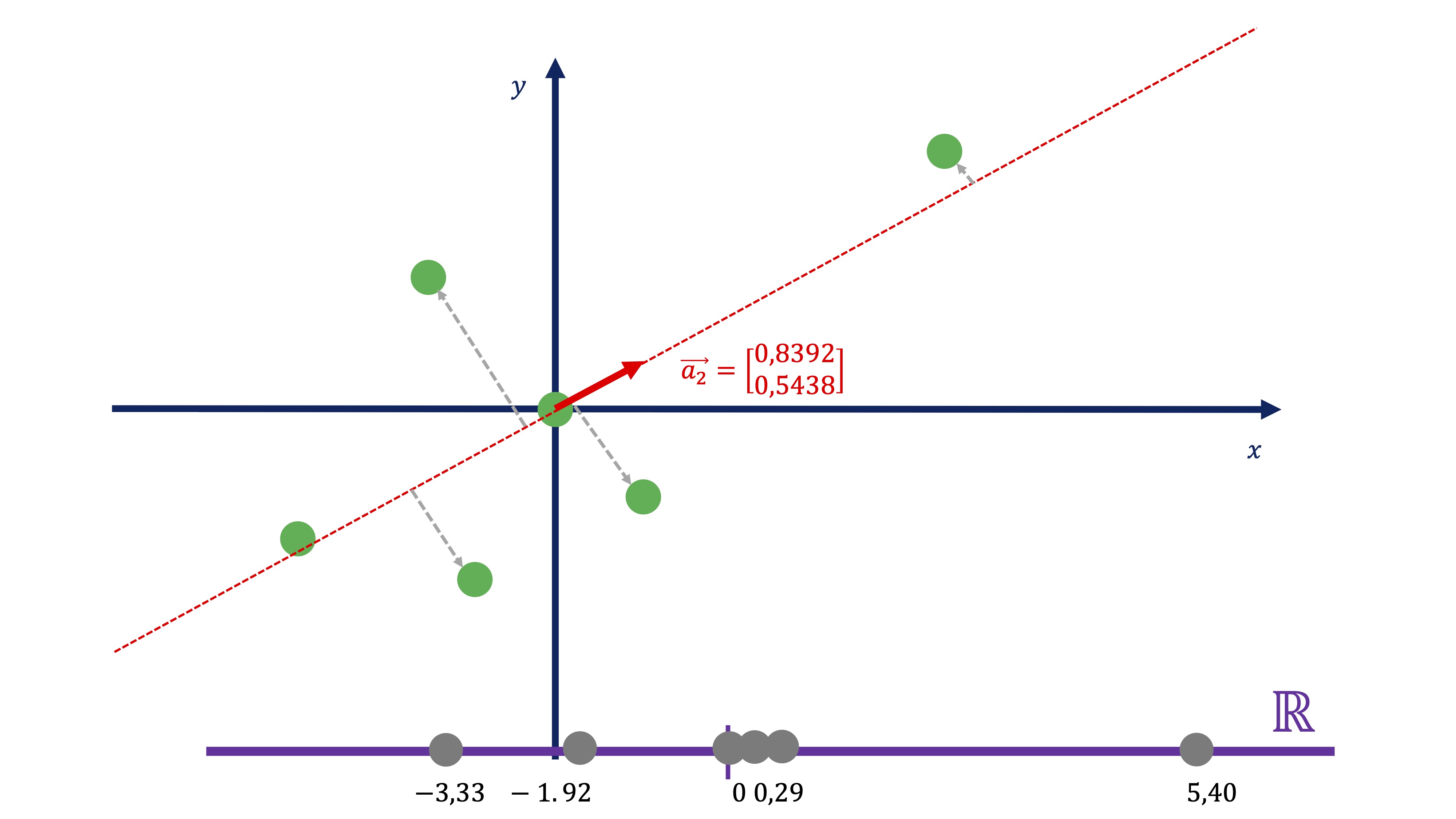
FIG 14: Calculamos el componente como la proyección
Entonces, usando la expresión de la dirección principal 1, podemos obtener el “resumen” de las dos variables en una nueva, que llamamos \(C1\). Esta nueva variable no tiene unas unidades de medida claras, pues es la combinación de dos variables que pueden no tener las mismas unidades. Podemos entenderla como un “índice” de tal forma que el valor que toma \(C1\) como tal no es importante, sino su variación a través de la muestra.
De igual manera, podemos obtener el segundo componente
\[ C2_{i}=-0.5438x_{i}+0.8392y_{i} \]
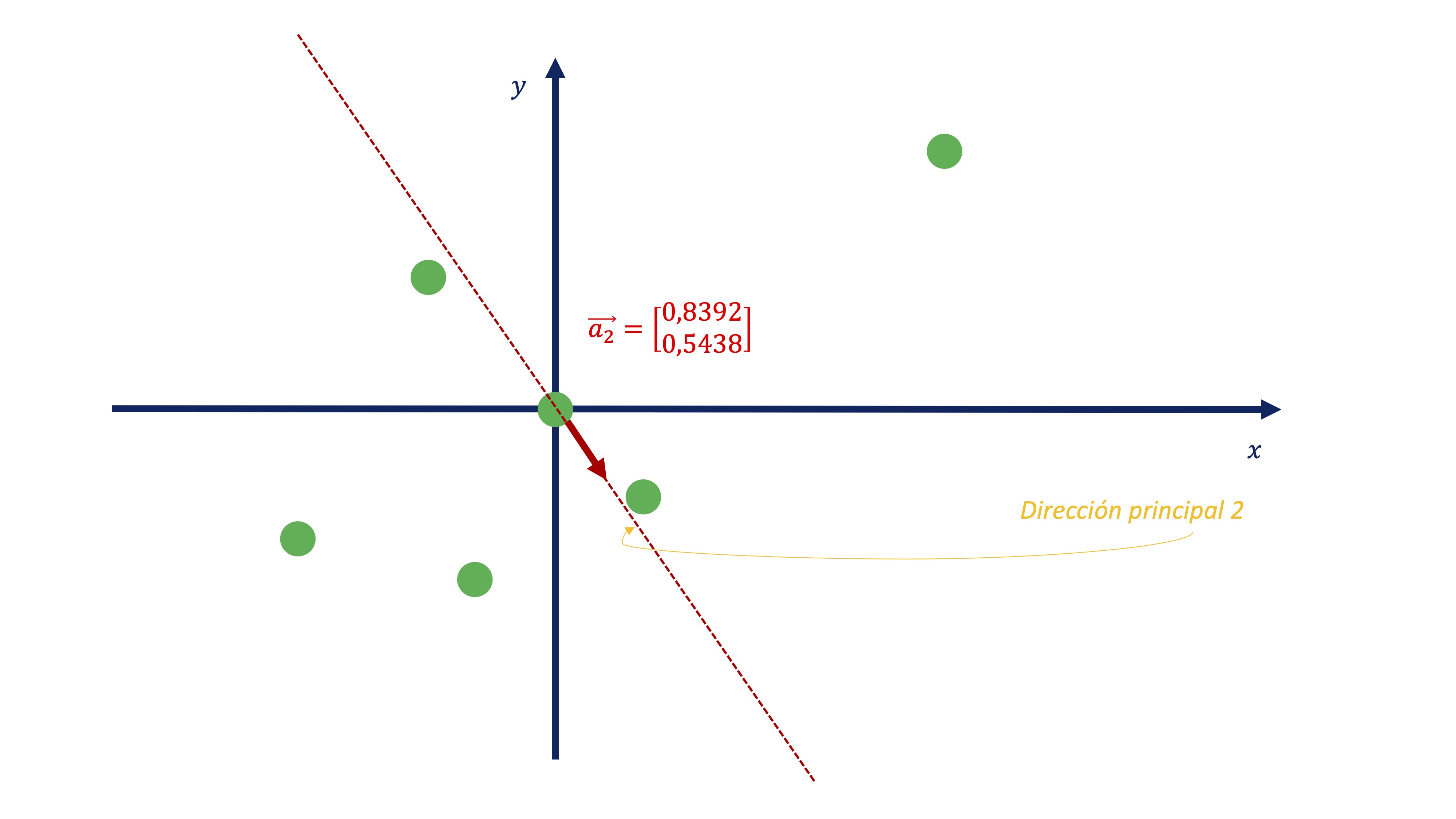
FIG 15: Este sería el segundo componente
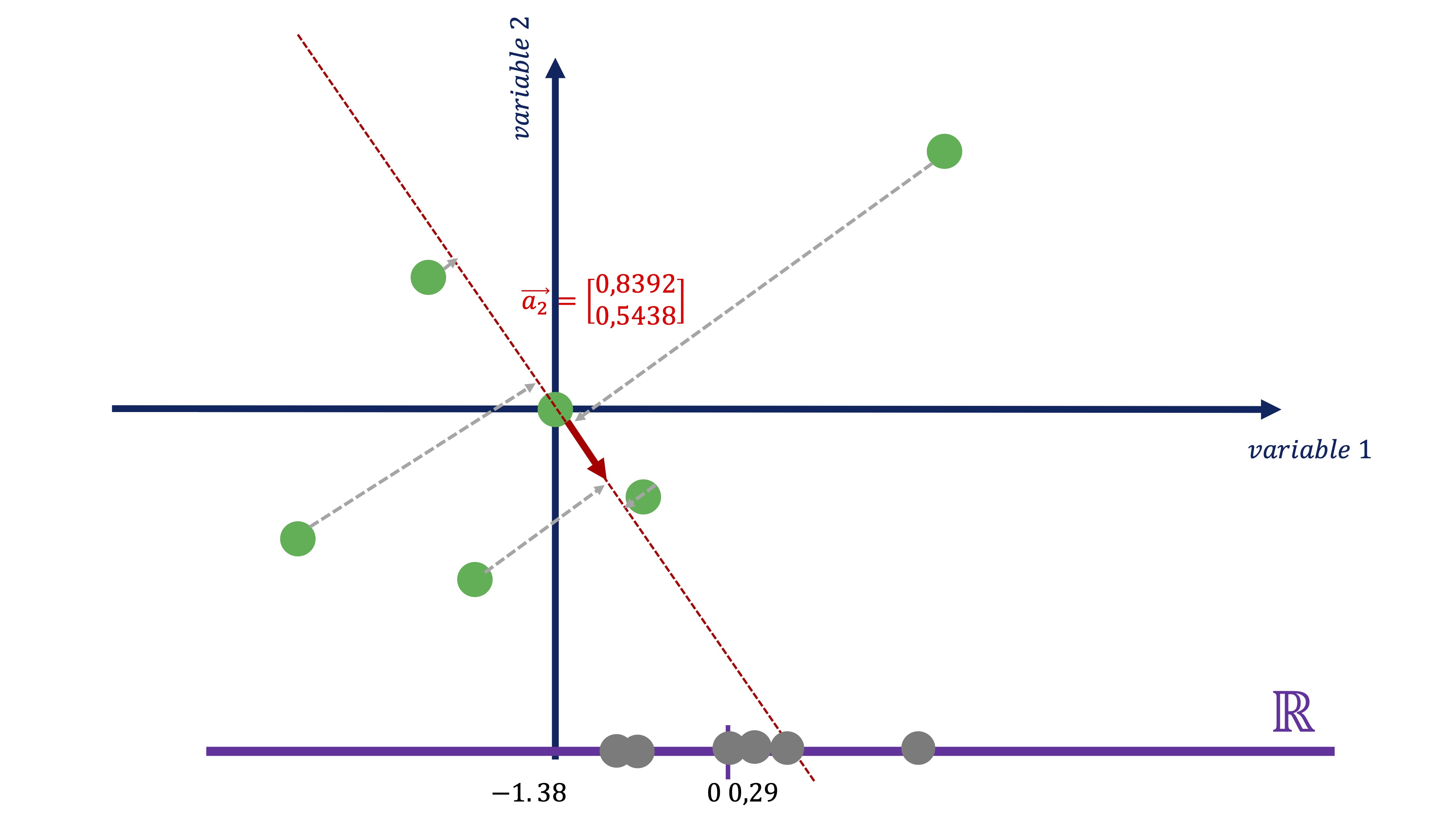
FIG 16: …y esta la proyección
Como vemos (FIG 14, FIG 16) parece más exitoso quedarse con el primer componente antes con el segundo, puesto que el primero parece recoger de una manera más acertada la variabilidad que muestran los datos
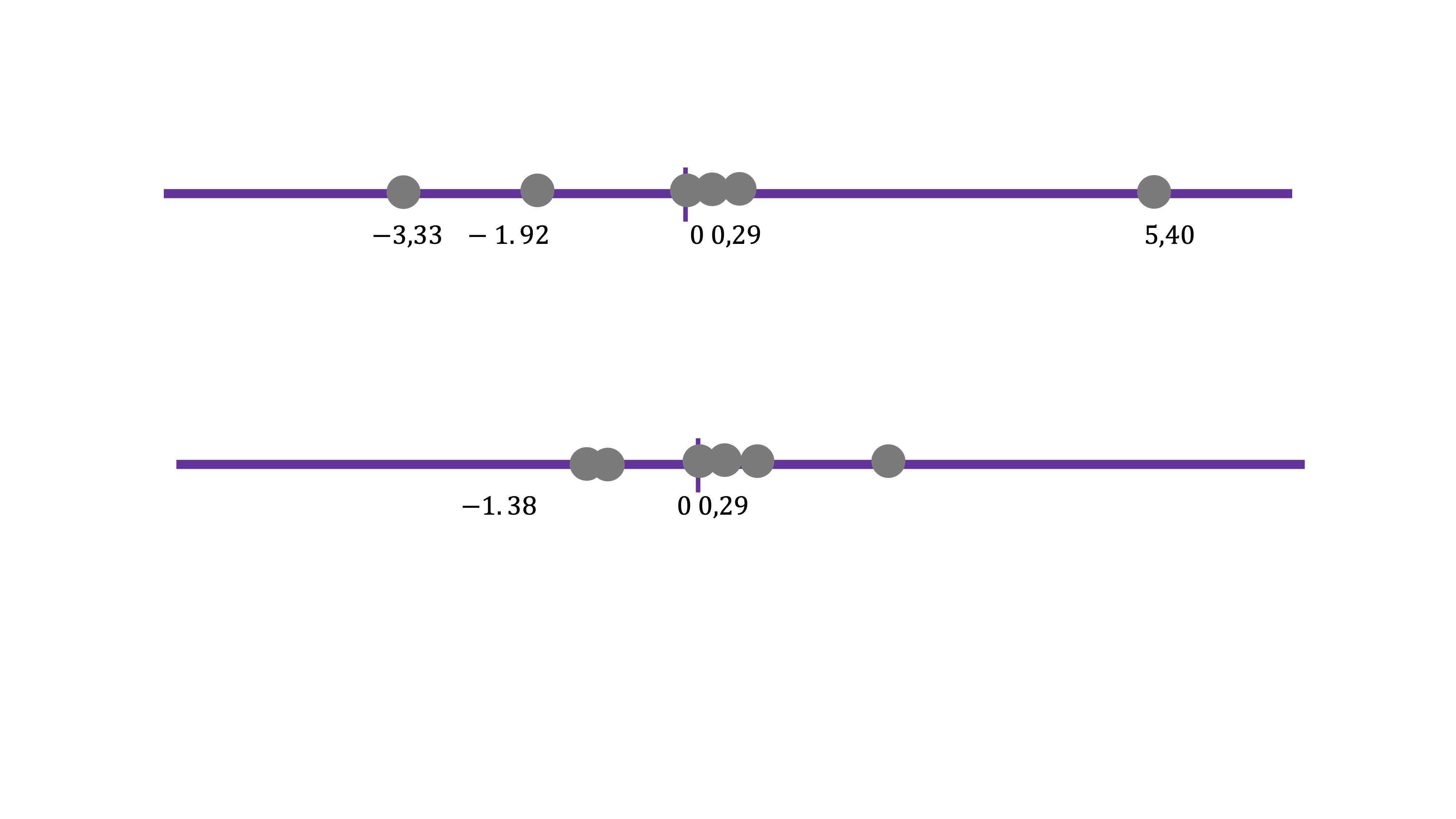
FIG 15: Estos son los dos componentes (el primero tiene mucha más varianza que el segundo, recoge mejor los movimientos conjuntos que vimos en la nube de puntos de la FIG9 )
Conclusiones hasta ahora
Tanto los autovalores como los autovectores van a tener una interpretación que nos ayudaá a entender mejor cómo se toman decisiones en el análisis PCA. >- Autovalores
princomp(covmat=cov(X))$sd^2 #obtención de los autovalores
Comp.1 Comp.2
8.87049 1.52951
C<-cov(X) #y, por otro lado, la matriz de varianzas y covarianzas de los datos
C
x1 x2
x1 6.70 3.35
x2 3.35 3.70Para empezar, la suma de los autovalores es igual a la suma de los elementos de la diagonal principal de \(C\) (propiedad 1} que vimos en el apartado de diagonalización de la matriz C). De esta manera: \(6.7+3.7=10.4\) es igual a \(8.87+1.53=10.4\). Esto es interesante, puesto que podemos considerar la suma de los elementos de la diagonal principal de \(C\) como la “varianza total” con la que contamos en los datos. Entonces, es fácil ver que, de la varianza total el primer componente ya representa \(8.87/10.4=0.85\) un 85% de la variación total. Nos parece, entonces, un buen resumen de la información disponible.
- Respecto a la interpretación de los componentes como “índices” lo verá claro en la aplicación con datos reales relacionados con el informe PISA.
- Si las variables tienen mucha diferencia en las varianzas, entonces se puede recomendar hacer la descomposición mediante la matriz de correlaciones. Esta postura es criticada, por cuanto se pierde la información de las varianzas.
1.2.2 Apéndice
¿De dónde se obtiene la expresión de componentes principales mediante la diagonalización de una matriz de varianzas y covarianzas?
Queremos minimizar la distancia entre las observaciones (\(X\)) y la proyección \(\left(XV\right)\), donde \(X\in M^{n\times k}\),\(V\in M^{k\times k}\)
\[ \min_{V}\left\Vert X-XV\right\Vert ^{2}, \]
con la restricción (para asegurarnos unicidad de solución) \(\left\Vert V\right\Vert =I.\) Asumiremos que la matriz \(X\) tiene sus observaciones en desviaciones respecto a la media. Nótese que, en este caso, nuestra incógnita es una matriz, \(V\), cuyas columnas conformarán lo que llamaremos coeficientes de la proyección para cada componente . Ahora bien, nótese también que, utilizando propiedades de vectores y matrices, la expresión anterior puede reescribirse como \[ \min_{V}\left(X-XV\right)^{T}\left(X-XV\right), \] que resulta ser
\[ \min_{V}X^{T}X-2V^{T}XX^{T}V+V^{T}XX^{T}V, \] que es equivalente (deshaciéndonos de \(X^{T}X\), porque no desempeña ningún papel, ya que no depende de \(V\))
\[ \min_{V}-V^{T}XX^{T}V, \]
donde minimizar “menos” una cantidad es equivalente a maximizarla:
\[ \max_{V}V^{T}XX^{T}V, \]
sin olvidar que \(\left\Vert V\right\Vert =I\) sigue siendo la restricción. Nótese que, las variables \(X\) están escritas en desviación a su media y que, por tanto, \(\mathbb{E}\left(XX^{T}\right)=Var-cov(X)=\Sigma\), es decir, queremos maximizar
\[ \max_{V}V^{T}\Sigma V, \]
Para resolver este problema, planteamos el lagrangiano \[ L(V,\lambda)=V^{T}\Sigma V-\overrightarrow{\lambda}^{T}\left(V^{T}V-I\right) \]
y derivando con respecto a \(V\), tenemos que la CPO es \[ 2\Sigma V-2\overrightarrow{\lambda}V=0\Rightarrow\Sigma V=\overrightarrow{\lambda}^{T}V \] y esta condición es, exactamente, el resultado de la diagonalización de matrices:\(V\) es una matriz que almacena los autovectores y \(\overrightarrow{\lambda}\) es un vector que almacena los autovalores.