BLOQUE 1: Modelización y visualización

• Este bloque pretende recoger el testigo a muchas de las ideas matemáticas con las que ya has trabajado en bachillerato y primaria. Sin embargo, vamos a darles un nuevo enfoque: ¿por qué no intentamos que una función nos sirva para hacer predicciones (de la misma manera que se hace en el mundo científico)? ¿Por qué no aprendemos nuevas maneras de visualizar información en el que se involucran varias variables?
• Combinaremos el aprendizaje con sesiones de clase invertida (es decir, el alumno/a debe trabajar en la clase previamente a esta, de tal forma que pueda haber discusión sobre los puntos complicados de la sesión y los ejercicios propuestos) y clase magistral (el docente desarrollará las ideas clave en una clase más tradicional)
• Este texto (que no debería sustituir a un buen libro de cálculo) es una referencia a modo de notas de clase que, además, contiene enlaces a vídeos de youtube preparados por el autor para motivar y reforzar ideas

Referencias de interés

• Stewart, J. (2009). Calculus: Concepts and contexts. Cengage Learning.
• STEWART, James; CLEGG, Daniel K.; WATSON, Saleem. Calculus: early transcendentals. Cengage Learning, 2020.
• SYDSAETER, Knut; HAMMOND, Peter. Matemáticas para el análisis económico. Pearson Educación, 1996.
• SIMON, Carl P., et al. Mathematics for economists. New York: Norton, 1994.
• SMITH, Robert T.; MINTON, Roland B.; RAFHI, Ziad AT. Cálculo de varias variables: trascendentes tempranas. McGraw-Hill Interamericana, 2019.

Clase 1 (invertida): el concepto de función en \(1\) y \(n\) variables

Clase invertida!

Esta es una sesión de clase invertida. Deberás verte el vídeo que tienes a continuación y tratar de hacer los ejercicios. En el aula se discutirá sobre lo que se ha aprendido y se ampliarán los conceptos que no queden claros. Esto es así porque gran parte de lo que se va a aprender nuevo es una extensión de lo que ya se debería saber.

Una función es una regla (llamada, generalmente, \(f,g,h,....\)) que asigna a los valores de un conjunto llamado dominio un único valor de un conjunto llamado imagen. En este curso trabajaremos, en general con funciones \(\mathscr{\mathbb{R}}^{n}\rightarrow\mathbb{R}\), indicando que el dominio es un conjunto \(n-\) dimensional de números reales (muy a menudo \(n=1,2\)) y \(\mathbb{R}\) es la, famosísima, recta real.

• Asegúrate que entiendes qué significan \(\mathbb{R}^{2}\) y \(\mathbb{R}^{3}\)
• ¿Te convence el vídeo?

En este curso trabajaremos, en general, con los números reales \(n\) dimensionales, lo que ya constituye un avance frente a lo que has aprendido en cursos pasados.

[]

Ejemplo de una función de una variable: Sea la función \[ f(x)=\frac{1}{x-1} \] Como ves, el dominio son todos los valores reales salvo el 1, puesto que la función, cuando el denominador vale 0, no está definida; y lo escribimos así \[ D=\left\{ x\in\mathbb{R}|x\neq1\right\} \] El recorrido (o rango, o imagen) son los posibles valores que puede tomar la \(y.\) En este caso, será todo \(\mathbb{R}\) salvo el valor 0.

Puedes usar Geogebra para hacer los gráficos de muchas de las funciones que se presentarán en este curso. Por ejemplo, aquí representamos la función anterior:

FIG1. La función real de variable real de la Anotación 1 ¿sabrías hacerla a mano?.

Si tenemos \(n\) variables, que es lo nuevo de este curso, la idea será similar: necesitamos una regla que le asigne un único output a un conjunto de \(n\) variables input.

Función de n variables: Una función de variables se define como \[ y=f(x_{1},x_{2},...,x_{n}) \]

\(y\)	\(x_{1},...,x_{n}\)
endógena	exógenas
explicada	explicativas
dependiente	independientes

Y necesitamos \(n\) variables porque los modelos que estudiarás en Ciencias Sociales suelen basarse en un conjunto amplio de factores que explican un hecho. Entonces:

Decimos que \(f\,:\,D\subset\mathbb{R}^{n}\rightarrow\mathbb{R}\) si la regla o función \(f\) asigna a cada valor del dominio \(D\) (que es un subconjunto de los numeros reales \(n\) dimensionales) un valor real. En este texto usaremos, generalmente, funciones de dos variables, es decir:

\[ y=f\left(x_{1},x_{2}\right), \]

donde \(f\,:\,D\subset\mathbb{R}^{2}\rightarrow\mathbb{R}.\)

Pero, por supuesto, podríamos tener una función de \(n\) variables

\[ y=f\left(x_{1},x_{2},...,x_{n}\right), \]

donde \(f\,:\,D\subset\mathbb{R}^{n}\rightarrow\mathbb{R}.\)

Ejemplo: piensa sobre las funciones aparecen en el vídeo: \[ ResultadosPISA=f(gasto) \] es una función \(\mathbb{R\rightarrow R}\), por otro lado, \[ IMC=\frac{peso}{altura^{2}} \] es una función \(\mathbb{R}^{2}\rightarrow\mathbb{R}\), mientras que la última función

\[ M=C_{0}\frac{\left(1+\frac{i}{m}\right)^{n\times m}\left(\frac{i}{m}\right)}{\left(1+\frac{i}{m}\right)^{n\times m}-1} \]

es \(\mathbb{R}^{4}\rightarrow\mathbb{R}\). Asegúrte de que entiendes lo que esto significa, de acuerdo con lo que se dice en el vídeo.

[]

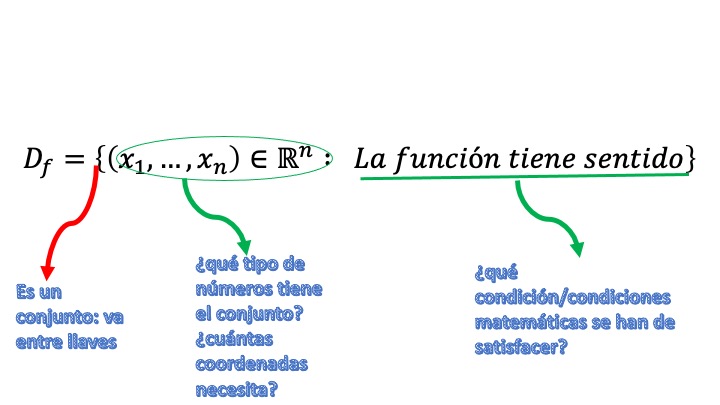
El dominio de una función es el conjunto de valores de la(s) variable(s) independientes para los que la función está definida y tiene sentido.

-Si la función es \(f\::\:\mathscr{\mathbb{R}}\rightarrow\mathbb{R},\) (por ejemplo, \(y=f(x))\) el dominio se puede escribir como \(D=\left\{ x\in\mathbb{R}\::\:f\;\mathrm{est\acute{a}\:definida}\right\}\).

Lo que estás diciendo es que _el dominio consiste en valores de la variable \(x\), tales que pertenecen al conjunto de los números reales, siempre que la función tenga sentido matemático. Donde pone f está definida, deberás poner tú qué condiciones debe cumplir para que lo esté. Por ejemplo, \(y=ln(x+1)\), \(D=\left\{ x\in\mathbb{R}\::\:x>-1\right\}\).

-Si la función es \(f\::\:\mathscr{\mathbb{R}}^{2}\rightarrow\mathbb{R}\), (por ejemplo, \(y=f(x_{1},x_{2}))\), el domino se escribe como \(D=\left\{ (x_{1},x_{2})\in{\mathbb{R}^{2}}\::\:f\;\mathrm{está\:definida}\right\}\). Por ejemplo, \(y=ln(x_{1}+x_{2})\), \(D=\left\{ (x_{1},x_{2})\in\mathbb{R}^{2}\::\:x_{1}>-x_{2}\right\}\).

Fíjate cómo indicamos \(\mathbb{R}^{2}\) como el conjunto donde vamos a buscar los valores para las variables independientes.

• Si la función con la que estás trabajando tiene sentido económico, físico, biológico,… es conveniente que pienses sobre posibles restricciones adicionales en el dominio, indicando que usarás dicha restricción.

Puedes llamarlo Dominio Natural o Económico (por ejemplo, si la función de demanda de un bien depende de dos precios, \(y=-2x_{1}+3x_{2}\), entonces \(D_{N}=\left\{ (x_{1},x_{2})\in\mathbb{R}^{2}\::\:x_{1},x_{2}>0\right\}\), mientras que \(D=\left\{ (x_{1},x_{2})\in\mathbb{R}^{2}\right\}\), puesto que no existen los precios negativos (dominio natural) pero la función tendría sentido matemático para cualquier valor real de las variables exógenas.

En el vídeo anterior aparece otra función de dos variables muy famosa, que conoces, y que -a lo mejor- no te habías parado a pensar en que lo era: el índice de masa corporal.

FIG 2. Este es el IMC que te encuentras en la farmacia. En los ejercicios trabajaremos sobre él.

El índice de masa corporal (IMC) es una función que tiene su dominio en dos dimensiones (el par \((p,a)\)) y cuya imagen es un único valor real (el valor del índice para cada individuo). Es decir, \(f\::D\subset\mathbb{R}^{2}\rightarrow\mathbb{R}:\)

\[\begin{equation} IMC=\frac{p}{a^{2}} \tag{1.1} \end{equation}\]

En este caso, la función se puede escribir de esta forma:

\[ IMC=f(p,a) \]

Si te das cuenta, la variable output o endógena es el IMC, mientras que \(p,a\) son los inputs o exógenas de la función. Pertenecen a valores en \(\mathbb{R}^{2}\). ¿Pero cualquier para en \(\mathbb{R}^{2}\) será válido? Por ejemplo, valdrá decir que el peso de un individuo es -15 kg y su altura -1,75 metros?

¿Cuál será el dominio? En principio, si analizamos la función de una manera fría sin saber qué es \(p\) ni \(a\), tenemos que pensar qué valores de la función harían que no esté correctamente definida. En este caso, si \(a=0\), el IMC no estará definido, puesto que no podemos dividir por cero. Por lo que el dominio de la función será:

\[ D=\left\{ \left(p,a\right)\in\mathbb{R}^{2}|a\neq0\right\} \]

(que se lee: el dominio de la función es el conjunto de todos los valores reales en dos dimensiones de \(p\) y \(a\) tales que \(a\neq0\))

Sin embargo, este dominio parece no tener sentido. ¿Puede ser el peso de un individuo -8 kilogramos en el planeta Tierra tal y como están las cosas? ¡NO! Por ello, definimos el dominio natural de una función que será aquel que tenga sentido económico, de una manera amplia (por económico también entendemos social, psicológico, biológico, etc…). En nuestro caso, dado que el peso y la altura son siempre valores positivos, el domino natural:

\[ D_{N}=\left\{ \left(p,a\right)\in\mathbb{R}^{2}|p>0,a>0\right\} \]

Por tanto, el dominio, al final, es el subconjunto de los números reales \(n\)-dimensionales (en este caso, \(n\)=2) para los cuales la función tiene sentido. El rango (recorrido o imagen) lo buscaremos en el conjunto: \(\mathbb{R}\)). La imagen es el resultado de aplicarle la expresión de la función al conjunto de \(n\) valores cualesquiera que pertenezcan al dominio.

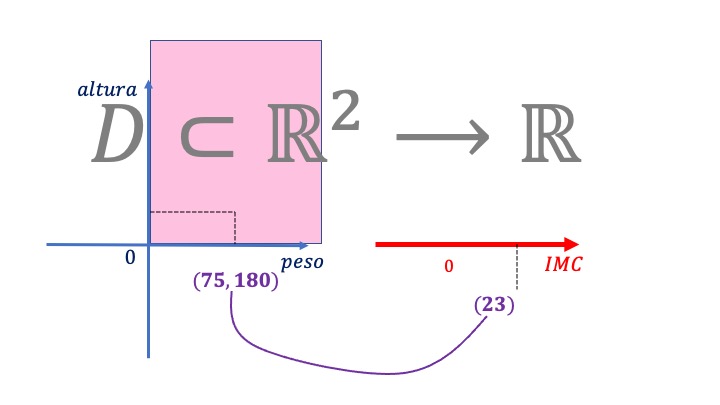
FIG3 Esta es la idea esquemática del IMC. El dominio está en dos dimensiones, mientras que la imagen en una dimensión.

1.3.1 ¿Para qué necesitamos las funciones?

Como se apunta en el vídeo, en general las funciones son una herramienta muy natural para poder expresar un comportamiento humano, económico, social, sanitario, etc… Permiten dotar de lógica a un modelo con el objetivo de poder obtener predicciones. Piensa que uno de los grandes fines de la ciencia es ser capaces de poder decir qué va a ocurrir y, además, disponer de herramientas para optimizar resultados. Puedes hacer esta lectura breve que, como verás, tiene mucho de actual

https://theconversation.com/covid-19-pandemia-de-modelos-matematicos-136212

Ejercicio 1

Piensa, o busca por internet, en contextos en los que creas que se usan modelos matemáticos basados en funciones. Propón alguno en clase.

Ejercicio 2

En el siguiente gráfico aparecen varias curvas en el plano. Identifica cuáles se corresponden con funciones de la forma \(y=f(x)\), cuáles se corresponden con funciones de la forma \(x=f(y)\) y si, mediante alguna modificación (al dominio), se puede extraer alguna función de donde, en principio, no la hay.

Gráfico para el Ejercicio 2

Ejercicio 3

En los siguientes diagramas se proponen diferentes posibles funciones. El sentido de la flecha indica cuál es el dominio y cuál el conjunto imagen (\(dominio\rightarrow imagen)\). Discute si son o no funciones y bajo qué condiciones (por ejemplo, una restricción en el dominio) pueden serlo:

Gráfico para el Ejercicio 3

Ejercicio 4

Halla el dominio y la imagen de las siguientes funciones:

1. \(h(t)=\frac{1}{3}t^{3}+t^{2}+1\)

2. \(f(x)=\sqrt{10-2x}\)

solución \(D_{f}=\left\{x\in\mathbb{R}\::\:x\leq5\right\}\), \(Im_{f}=[0,\infty)\)

3. \(y(k)=\frac{2k-1}{k^{2}-k}\)

4. \(j(x)=\sqrt{9-x^{2}}\)

5. \(g(p)=\left(\frac{p-1}{\left(p-2\right)\left(p-3\right)}\right)^{1/2}\)

Ejercicio 5

Sea \(W(q)\) la función definida por

\[ W(q)=\frac{3q+6}{q-2} \]

• Calcula su dominio
• Muestra que el 5 pertenece al conjunto imagen de la función ¿Está también el 3 en dicho conjunto?

Ejercicio 6

Halla el dominio de las siguientes funciones definidas en \(\mathbb{R}^{2}\rightarrow\mathbb{R}\)

1. \(f(x,y)=x-3y\)

2. \(g(x,y)=\ln(x-3y)\)

solución \(D_{g}=\left\{ (x,y)\in\mathbb{R}^{2}\::\:x-3y>0\right\}\)

3. \(h(x,y)=x+4y^{2}\)

4. \(i(x,y)=\frac{x}{y-2}\)

5. \(j(x,y)=4(x-1)^{2}+9(y-2)^{2}\)

6. \(k(x,y)=(x-1)^{1/2}(y-2)\)

7. \(l(x,y)=\ln y+x\)

8. \(m(x,y)=\ln(y+e^{-x})\)

Ejercicio 7

La función \(x(p,q)=\frac{20-p+q}{p}\) representa la demanda \(x\) de un bien, dado su precio \(p\) y el precio de otro bien, \(q\). Halla su dominio natural (o económico) y dibuja los puntos \((p,q)\) del dominio natural (o económico) para los que la demanda es mayor o igual a 3 unidades.

-Indicación para la segunda parte: deberás resolver \(\frac{20-p+q}{p}\geq3\) y dibujar la desigualdad que encuentres. Puedes comprobarlo con Geogebra

Ejercicio resuelto

Imagina una función \(f\), cuyo dominio está conformado por el peso y la altura de un individuo y la imagen es el IMC del individuo y, además, toma los siguientes valores:

• 0, si el individuo está en su peso
• 1, si el individuo está en una situación de sobrepeso
• -1, si el individuo tiene un IMC por debajo de lo normal.

Explica cómo sería el dominio e imagen de la función. Razona si es una función definida como \(f\::\mathbb{R}^{2}\rightarrow\mathbb{R}\). En caso de no serlo, especifica de manera adecuada la función. Busca, además, una manera sensata de dar el resultado para un individuo cuyo peso son 68 kilogramos y su altura es 1.80 metros.

solución:

la función no es del tipo \(f\::\mathbb{R}^{2}\rightarrow\mathbb{R}\) sino de este otro \(f\::\mathbb{R}_{++}^{2}\rightarrow\mathbb{R}^{2}\), ¡ojo! esto no quiere decir que tenga dos imágenes en un mismo conjunto. Tiene una imagen en el conjunto IMC y otro en el conjunto \(\left\{ 0,1,-1\right\}\) que evalúa su resultado. La función es tal que \[ D=\left\{ (p,a)\in\mathbb{R}_{++}^{2}\right\} \]

\[ Im=\left\{ (IMC,y)\in\mathbb{R}^{2}\::\:IMC>0,y=\left\{ -1,0,1\right\} \right\} \] De tal forma que \(f(68,1.80)=(20.98,0)\).

Ejercicio 8

Expresa el dominio natural de la siguiente función de la que se habla en el vídeo 1, encontrada en Ponferrada (León). Para ello, vuelve al vídeo, mira los detalles de cada variable y piensa en qué conjunto está bien definido.

\[ M=C_{0}\frac{\left(1+\frac{i}{m}\right)^{n\times m}\left(\frac{i}{m}\right)}{\left(1+\frac{i}{m}\right)^{n\times m}-1} \]

Recuerda los conjuntos de números que conocemos:

Naturales: para contar. \(\mathbb{N}=\{0,1,2,3,....\}\)

Enteros: una ampliación de los naturales \(\mathbb{Z}=\left\{....,-3,-2,-1,0,1,2,3,....\right\}\)

Racionales: \(\mathbb{Q}=\left\{\frac{p}{q},p\in\mathbb{Z},q\in\mathbb{Z}\setminus\left\{ 0\right\} \right\}\)

Irracionales \(\mathbb{I}=\left\{e,\pi,\sqrt{2},...\right\}\)

Reales \(\mathbb{R}=\mathbb{N}\cup\mathbb{Z}\cup\mathbb{Q}\cup\mathbb{I}\)

Clase 2 (magistral): repaso de gráficas funciones de variable real (I)

La función más sencilla con la que has trabajado en toda tu educación previa es la recta:

\[ y=ax+b \]

donde la \(y\) es la variable dependiente y la \(x\) es la variable independiente.

¿Cómo se interpreta \(b\)?

Es la ordenada en el origen. Es el valor de la \(y\) cuando \(x=0\).

¿Cómo se interpreta \(a\)?

Es la pendiente. Cuánto cambia \(y\) ante incrementos de \(x\) en una unidad.

• Si \(a>0,\) el incremento de \(y\) ante incrementos de \(x\) es positivo (\(x,y\) son proporcionales)
• Si \(a<0,\)el incremento de \(y\) ante incrementos de \(x\) es negativo (\(x,y\) son inversamente proporcionales)

¿Para qué se utiliza en Economía?

Cuando queremos hacer modelos sencillos para entender la, compleja y difícil de conocer al detalle, realidad.

La ecuación de una recta se puede obtener dependiendo de la información que se nos proporcione

Nombre	información que me dan	Ecuación
punto-pendiente	\(a,(x_{0},y_{0})\)	\(y-y_{0}=a(x-x_{0})\)
Dos puntos	\((x_{0},x_{1}),\left(y_{0},y_{1}\right)\)	\(y-y_{0}=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}(x-x_{0})\)
Intersección con los ejes	\(x=a,y=b\)	\(\frac{x}{a}+\frac{y}{b}=1\)

Diremos que dos rectas \(y=c+m_{1}x\), \(y=d+m_{2}x\) son paralelas si las pendientes son iguales (\(m_{1}=m_{2})\). Son perpendiculares si el producto de sus pendientes es -1 \((m_{1}m_{2}=-1)\). Dibuja, en geogebra dos rectas paralelas y perpendiculares y asegúrate de que se cumple.

Ejercicio 1

Halla la pendiente y la ordenada en el origen de las siguientes rectas. Dibújalas.

1. \(20x-24y-30=0\)

2. \(2x-3=0\)

3. \(4y+5=0\)

-Escribe una ecuación para una recta que pase por el punto \((-3,2)\) y que sea paralela a \(3x-5y+8=0\). Dibújalas.

-Escribe una ecuación para una recta que pasa por el punto \((2,-4)\) y es perpendicular a \(x-4y+8=0\). Dibújalas.

-Un punto \(A\) es colineal a una recta \(r\), si el punto está en la recta (\(A\subset r).\) Estudia si los siguientes puntos son colineales: \(A(-5,3),B(-1,8),C(3,0).\) Busca una manera de encontrar dos puntos colineales a cualquier recta.

Clase 3 (magistral): repaso de gráficas funciones de variable real (II)

Funciones polinómicas

Parábola. \(y=ax^2+bx+c\). Tenemos dos casos

\(a<0\) con forma: \({\color{red}\cap}\)

\(a>0\) con forma: \({\color{teal}\cup}\)

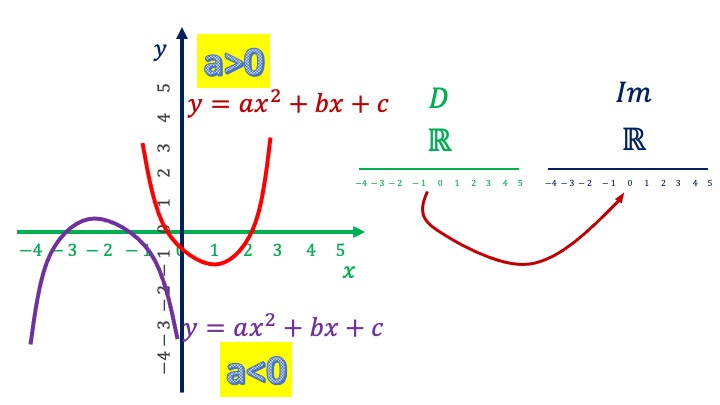
Las parábolas

Recuerda

• vértices: \(x=\frac{-b}{2a}\) \(y=f(\frac{-b}{2a})\).
• corte con el eje de las \(x\) : \(\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\)
• corte con el eje de la \(y\), hacemos \(x=0\) y obtenemos el valor correspondiente.

cúbicas. \(y=a+bx+cx^{2}+dx^{3}\). Tenemos dos casos

\(d<0\) con forma: \({\cup\cap}\)

\(d>0\) con forma: \({\cap\cup}\)

Las cúbicas

Más adelante, cuando veamos aplicaciones de las derivadas, veremos cómo dibujarlas con mayor precisión. Es cierto que el dibujo de gráficas polinomiales se va complicando con el grado del polinomio y es necesario conocer más herramientas de cálculo para hacerlo adecuadamente.

Potenciales . Funciones del tipo \(f(x)=x^{n}\). Con diferentes tipos de valores para \(n\). Mira los pies de cada una de las imágenes para identificarlas

\(n\) par y positivo , \(n=\left\{ 2,4,6,....\right\}\)

\(n\) impar y positivo , \(n=\left\{ 3,5,7,....\right\}\)

\(n\) par y negativo , \(n=\{-2,-4,...\}\)

\(n\) impar y negativo \(n=\{-1,-3.-5...\}\)

\(n\) positivo y racional

En este vídeo puedes repasar ideas de estas funciones polinómicas que te hemos presentado

Ejercicio 3

Sea la función \(f(x)=ax^2+bx+c\). Sabiendo que los puntos \((1,-3)\), \((0,-6)\), \((3,15)\), son puntos de su gráfica: calcula los valores de \(a,b,c\)

Ejercicio 4

Dibuja las gráficas de \(f(x)=x^2\), \(g(x)=(x-2)^2\), \(h(x)=x^2+3\) ¿Cómo se relacionan dichas gráficas?

Ejercicio 5

Una forma muy cómoda de escribir una parábola es así: \(y=(x-2)(x-8)\) ¿Por qué? ¡ya nos da las raíces de la ecuación de segundo grado!. Dibújala.

Ejercicio 6

Escribe de forma simplificada y, posteriormente, dibuja las siguientes funciones potenciales

• \(f(a)=(((a^{1/2})^{2/3})^{3/4})^{4/5}\)

• \(g(x)=(((3x)^{-1})^{-2}(2x^{-2})^{-1})/x^{-3}\)

Logaritmo y exponencial

El logaritmo -en base \(a\)- es una función tal que

\[ log_{a}y=x\Longleftrightarrow a^{x}=y \]

Esta relación indica, además, que la función inversa al logaritmo es la función exponencial (y viceversa): \[ y=a^{x} \]

Donde \(a>0\).

Es muy común el uso del logaritmo en base \(e\), es decir, el logaritmo neperiano. De tal forma que

\[ \ln y=x\Longleftrightarrow e^{x}=y \]

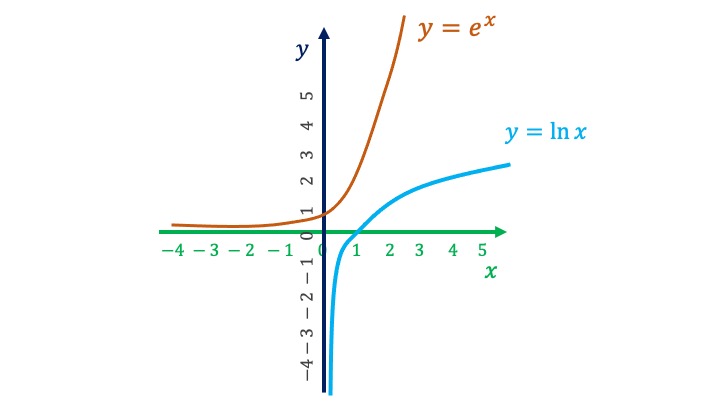
En esta figura se puede ver la propiedad de que ambas funciones son inversas

Ejercicio 7

Recupera las propiedades del logaritmo y de la exponencial. Haz una lista con ellas y tenla siempre a mano.

Ejercicio 8

Una libreta de ahorros con un capital inicial de \(600\) euros, produce un \(3\)% de interés anual

Escribe una función que represente el capital que se obtendrá en el año \(t\) y responde

• a: ¿Cuánto tiempo tendrá que pasar para que reciba \(655.63\) euros?
• b: ¿Qué ocurre con el capital si \(t\) se vuelve “muy grande?”

Ejercicio 9

Después de desactivar una bomba, el agente especial 00.0 regresa a casa y se entera de que su mejor amigo “Siggy,” ha sido asesinado. La policía dice que el cuerpo fue encontrado a la 1 de la madrugada del jueves, en un frigorífico a 10ºF. También le dijeron que la temperatura del cadáver, cuando lo encontraron, era de 40ºF. Se sabe que la temperatura de un cuerpo, después de muerto, sigue la función

\[ T=T_{a}+(98.6-T_a)(0.97)^t \]

Donde \(T_a\) es la temperatura del aire que rodea el cuerpo y \(t\) son las horas. El agente sabe que el asesinato fue cometido o por Ernest Stabros o por André Scélérat. Si el primero estuvo en la cárcel hasta el miércoles y el segundo fue visto en Las Vegas desde el mediodía del miércoles hasta el viernes: ¿quién cometió el crimen?

pista:necesitas obtener \(t\) para los datos de los que dispones

Ejercicio 10

Demuestra las siguientes igualdades

• a: \(ln(x)-x=ln(x/e^{x})\)
• b: \(ln (x) - ln(y) + ln(z) =ln(xz/y)\)
• c: \(3 +2ln(x)=ln(e^{3}x^2)\)

Simplifica las expresiones siguientes

• a: \(e^{lnx}-ln{e^x}\)
• b: \(ln(x^4 e^{-x})\)
• c: \(e^{ln{x^2}-2ln{x}}\)

Uno de sus usos es simplificar las unidades y escalas de medida. Por ejemplo, mira esta información de El País sobre los datos del Coronavirus:

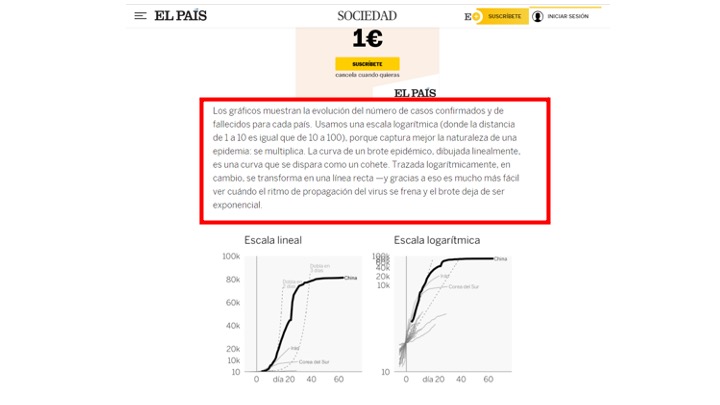
¡el logaritmo sale en la prensa!

Lo que viene a decir este recorte de prensa es que si el virus avanza siguiendo una función exponencial como esta \(f(x)=ae^{bx}\), con \(a,b\in \mathbb{R}\), si se introduce la transformación logarítmica a los datos, esta debería convertirse en una recta. Mira cómo:

\[ y=ae^{bx} \]

\[ \ln y=\ln a+\ln e^{bx} \]

\[ \ln y=\ln a+bx \]

\[ \ln y=a^{*}+bx, \]

En este vídeo tienes un buen resumen de la función logaritmo y la exponencial

Cónicas

Las cónicas esenciales que necesitaremos este año van a ser las circunferencias y las elipses. Ambas son curvas que se dibujan en el plano (en \(\mathbb{R}^2\)) pero que, como ves, no constituyen una función (sabrías por qué?) ¿Ves? Este es un ejemplo, de tantos, de una “fórmula” que no es una función.

circunferencia . Su expresión canónica es \((x-x_{0})^2+(y-y_{0})^2=r^2\), de tal forma que \((x_{0},y_{0})\) es el punto central de la circunferencia. La ecuación dice que todos los puntos equidistan de ella a la misma distancia, llamada \(r\) o radio. Por lo tanto, dibujar una circunferencia con esta expresión es muy sencillo: tienes tanto el centro como el radio. No tiene pérdida.

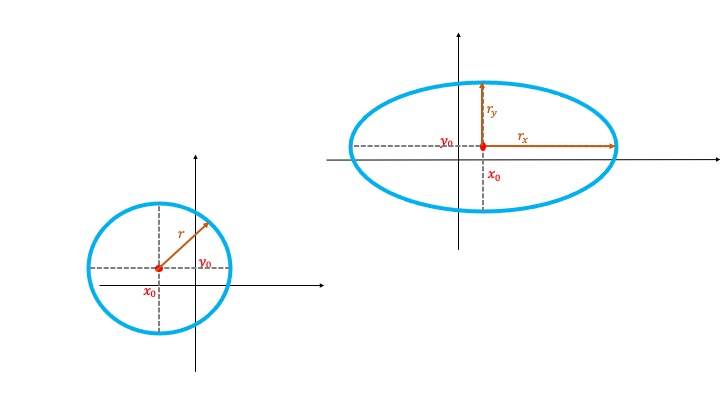
La circunferencia y la elipse

elipse . Su expresión canónica es \(\frac{(x-x_{0})^2}{r_x^2}+\frac{(y-y_{0})^2}{r_y^2}=1\), de tal forma que \((x_{0},y_{0})\) es el punto central de la elipse. Como ya sabes, una elipse es una circunferencia “achatada.” Para dibujarla, necesitas de nuevo conocer su centro y, en el denominador de la expresión \((x-x_{0})^2\) te encontrarás con el cuadrado del semieje mayor (es decir, \(r_x\)), mientras que en el denominador de \((y-y_{0})^2\) te encontrarás con el cuadrado del semieje menor (es decir, \(r_y\)). Con esa información puedes dibujarla como en la figura. Es importante que notes que *la ecuación debe estar igualada a 1. Si no, deberás dividir en ambos lados por el mismo valor.

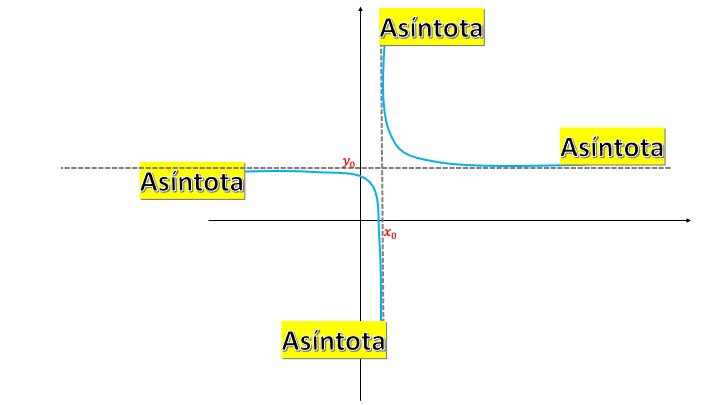
La hipérbola equilátera

hipérbola equilátera . Finalmente, otra de las cónicas de interés. Esta sí es una función cuya expresión es \((x-x_0)(y-y_0)=K\), donde \(K\) es una constante. Tiene, como asíntotas, las rectas \(x=x_0\) e \(y=y_0\). Y se sitúa en el primer y tercer cuadrante si \(K>0\) y en el segundo y cuarto si \(K<0\)

En este vídeo tienes un buen resumen de las cónicas. Además, hay ejercicios resueltos que te ayudarán a practicar.

• Ojo, todas estas gráficas no sólo son relevantes para esta parte del curso, sino que las necesitaremos de nuevo para dibujar curvas de nivel y, además, en Matemáticas II.

Clase 4 (invertida): modelización para responder preguntas

Clase invertida!

Esta es una sesión de clase invertida. Deberás verte el vídeo que tienes a continuación y tratar de hacer los ejercicios. En el aula se discutirá sobre lo que se ha aprendido y se ampliarán los conceptos que no queden claro. Esto es así porque gran parte de lo que se va a aprender nuevo es una extensión de lo que ya se debería saber.

Ejercicio 1

Del modelo que se presenta en el minuto 1.30 del vídeo 5:

\[ Esperanza\:de\:vida=a+b\times a\tilde{n}o\equiv y=a+bx \]

calcula el valor para \(a\) y \(b\) usando los puntos \((x_{0},y_{0}),(x_{1},y_{1})\equiv(1948,66.3)(2019,81.3)\). Discute por qué \(a\) es diferente a la obtenida en el vídeo, pero \(b\) es igual. ¿Obtienes la misma predicción de la esperanza de vida para el año 2039? Justifica por qué.

Ejercicio 2

Los antropólogos usan un modelo lineal para relacionar la longitud del fémur humano con la altura del individuo. Esto es importante, ya que permite, ante el hallazgo parcial de un esqueleto, predecir la altura que tenía el individuo. Usa los siguientes datos para proporcionar un modelo que nos permita realizar dicha predicción (puedes hacerlo con Excel, por ejemplo, o a mano).

Longitud Fémur	Altura
50.1	178.5
44.5	168.3
48.3	173.6
42.7	165
45.2	164.8
39.5	155.4
44.7	163.7
38	155.8

Arqueólogos trabajando en Pompeya, cuando hallaron un caballo petrificado

• Un individuo tiene un fémur con longitud 43 cmts ¿Qué altura aproximada tendrá?
• Se encuentra a un individuo con longitud de fémur 58 ctms con una altura de 180 ctms. ¿Qué sugiere este resultado sobre el uso del modelo?

(Adaptado de Stewart)

Ejercicio 3

Ahora debes dar valores a los parámetros de la función que nos permite obtener la esperanza de vida al nacer según el año (En este caso, \(a,b,c,d...\)), usando los datos disponibles en el fichero Excel, y la siguiente función definida a trozos

\[ f(x)=\begin{cases} f_1(x) & x<1900\\ f_2(x) & x\geq1900 \end{cases} \]

una función en la que \(x\) es el año y \(f(x)\) es la esperanza de vida. Analiza:

• Si es o no continua la función que has encontrado.
• En caso de no ser continua, reformula \(f(x)\) y parametrízala para que lo sea.

• Discute la idoneidad de usar este modelo para predecir la esperanza de vida en 1300, por ejemplo, y en el año 2100.

Ejercicio 4

Una compañía que ofrece préstamos en 24 horas utiliza un modelo de concesión de los créditos basado en dos variables de interés del individuo candidato a recibir el préstamo: los meses que lleva contratado en la empresa actual y su nómina. En base a la devolución de los préstamos en el último año, han realizado el siguiente gráfico:

Muestra de la empresa de Marketing

de tal manera que SÍ indica las características (meses de contrato y salario) del individuo que devolvió el préstamo y NO, lo contrario.

• Busca la función que relaciona meses de contrato y salario. Usa esa función (curvilínea) para determinar los meses de contrato que necesita un individuo para que, cobrando 1278 euros al mes, se le conceda el préstamo.

• Los responsables de Marketing consideran que la regla de decisión es demasiado estricta y penaliza a demasiados clientes. Busca otra regla algo más permisiva (una recta) y determina los meses de contrato que necesitaría un individuo que cobra 1278 euros al mes para que se le conceda el préstamo. Si se hubiera usado esa regla en el pasado, ¿qué porcentaje de individuos habrían sido impagos pese a concederles el préstamo?

Una empresa competidora tiene esta otra muestra.

Muestra de la empresa de Marketing

¿Podrías definir una función de tal forma que se discrimine perfectamente los síes y los noes?

Clase 5 (magistral): las curvas de nivel

Una vez hemos recordado cómo representar funciones reales de variable real (recuerda que son funciones que tienen una variable explicativa y que se representan en un espacio de 2 dimensiones), ahora vamos a ver cómo representar una función con dos variables. Volvamos al IMC, del que recuerdas, se escribe

\[\begin{equation} IMC=\frac{p}{a^{2}} \tag{1.1} \end{equation}\]

Es una función donde cada intersección de un valor del peso y de la altura (lo que se llama par ordenado) proporciona un IMC (usando la fórmula que te damos en la ecuación (1.1). Sin embargo, siempre es útil tener una impresión visual de las funciones con las que trabajamos (como ya sabes). Pensemos sobre esta función cuyo dominio tiene dos variables y su imagen tiene una, como en la FIG3

FIG3 Esta es la idea esquemática del IMC. El dominio está en dos dimensiones, mientras que la imagen en una dimensión.

Ahora bien, ¿cuáles serán las novedades?

• El gráfico ahora tiene tres ejes (de forma general \(x_{1},x_{2},y\)) con el objetivo de pintar la función \(y=f(x_{1},x_{2}).\) Es decir, el gráfico de una función \(\mathbb{R}^{2}\rightarrow\mathbb{R}\) está definido en tres dimensiones: una para cada variable
• El gráfico de la función son los puntos \((x_{1},x_{2},y=f(x_{1},x_{2})\) tales que \(\left(x_{1},x_{2}\right)\) pertencen al dominio \(D\). Esto lo escribimos así: \(G(f)=\left\{ x_{1},x_{2},f(x_{1},x_{2})|\left(x_{1},x_{2}\right)\in D\right\}\)
• Imagina que la función que tenemos es \(f(x_1,x_2)=x_1+x_2-0.2\). Entonces, un punto de la función será \(x_{1}=0.6,x_{2}=0.4\) con \(f(x_{1},x_{2})=0.8.\). En la FIG4 dibujamos ese punto (de los infinitos que dan lugar a la función)
• En la FIG 5, hacemos lo mismo pero ahora yo con la función para calcular el IMC \(Graf(f)=\left\{ p,a,f(p,a)|\left(p,a\right)\in D\right\}\)

FIG4 Así se representa un punto en 3 dimensiones.

FIG5 Así se representa la función IMC.

Sin embargo, dibujar funciones en 3D está muchas veces fuera de nuestro alcance, a no ser que tengamos a mano un ordenador (O Google: si pones en el buscador una función, automáticamente te saca el gráfico. Prueba, por ejemplo, en escribir z=x/y^2 y dar a buscar ¿qué sale? ) Sin embargo, a veces podremos esbozar la pinta del gráfico. Para ello, podemos aprovechar que conocemos la pinta que tienen las funciones elementales y ver que esta función es una ``mezcla’’ de dos fuciones famosas:

\[ f(p,a)=\frac{p}{a^{2}} \]

Para ello, primeramente nos olvidamos de que existe la variable \(a\). ¡Que deje de ser una variable y que sea una constante!. Por ejemplo, digamos que \(C=\frac{1}{a^{2}}.\) Al hacer eso, nos estamos olvidando del eje asociado a la variable altura y estamos representando esta función:

\[ f(p)=Cp \]

Que, como ves, es una ecuación lineal con pendiente \(C\). Por eso las líneas amarillas de la FIG 6 son rectas. Esas rectas quieren decir que ``si nos olvidamos de la variable altura, la función tiene pinta de recta con respecto a la variable peso’’.

FIG6 Si miramos la gráfica del IMC olvidándonos primero la altura y luego el peso.

Por otro lado, si nos olvidamos de la variable \(p\), y decimos que sea una constante, tendremos esta función con respecto a \(a\):

\[ f(a)=\frac{C}{a^{2}} \]

En este caso, tú, que eres un gran conocedor de las funciones elementales, habrás detectado que es una de tipo potencial (y con una relación inversa con el IMC). De ahí, las líneas marcadas en rosa. Y así quedaría esbozada la función.

Ejercicio 1

Mira este ejercicio de examen ¿sabrías hacerlo? Mira bien los valores de los ejes y recuerda la ecuación de una recta y de una parábola :)

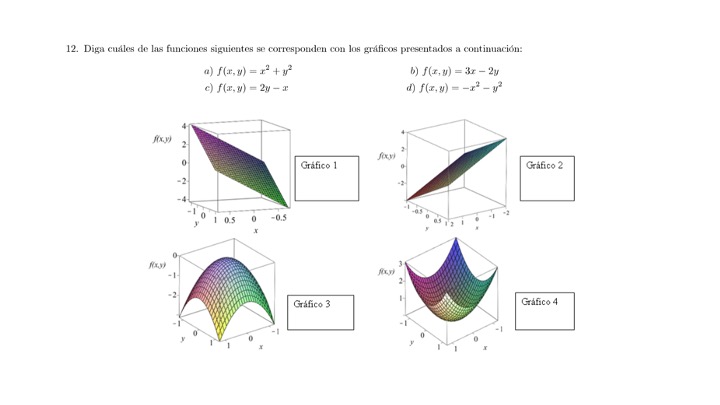
Ejercicio de Examen.

Las curvas de nivel

Son una nueva herramienta de análisis visual que, aunque no lo creas, llevas mucho tiempo viéndolas hasta por la televisión. Mira el siguiente vídeo para familiarizarte con las curvas de nivel

Como ya vimos, es complicado tratar de dibujar funciones en 3D. Pero tiene que haber alguna manera de que entendamos los aspectos más importantes de una función sin que nos cueste mucho esfuero. ¡La hay! Es una técnica de representación que se utiliza en muchos contextos. Las curvas de nivel. ¿Recuerdas haberlas visto?

FIG7 Todas las noches en tu TV.

Efectivamente, en "El Tiempo’’ siempre las ponen. Esas curvas unen coordenadas del planeta Tierra que tienen la misma presión atmosférica. ¡Espera un momento! vamos a volver a los datos del IMC. Si te fijas, pesar 75 kilos y medir 1.75 te da el mismo IMC que si pesas 80 kilos y mides 1.80, es decir, un IMC de 25. Por lo tanto, podemos buscar esos valores de peso y altura que te dan el mismo IMC

FIG8 Curvas de nivel de la función IMC generadas por ordenador: en el vídeo te explicamos de dónde vienen.

Pues ya podemos definir una curva de nivel. Consiste en los puntos del dominio que nos proporcionan un valor, \(C\in\ Im(f)\) (es decir, constante y que pertenezca a la imagen de la función) o lo que es lo mismo

\[ Nivel=\left\{ \left(x_{1},x_{2}\right)\in D\::\:f(x_{1},x_{2})=C\right\} \]

De esta forma, dando diferentes valores a \(C\) podemos esbozar el comportamiento de nuestra función. Por ejemplo, si damos valor \(C=20\), en el ejemplo del IMC, tendremos que

\[ 20=\frac{p}{a^{2}}\Rightarrow p=20a^{2} \]

si te fijas, \(p=20a^{2}\) es una parábola (es como si tuvieras \(y=20x^{2}\)) por eso, las curvas de nivel de la figura 8 tienen esa pinta de curva.

FIG8 Curvas de nivel de la función IMC, remarcando la de nivel 20 y el sentido de crecimiento de la función.

Una vez dibujas la curva de nivel 20, puedes darte cuenta enseguida de que si aumentas el valor de \(C\), en este caso la parábola se irá haciendo cada vez más estrecha (claro, \(p=25a^{2}\) te devuelve un valor mayor para \(p\) por cada \(a\), comparada con \(p=20a^{2})\). De esta forma, ya puedes dibujar unas flechas que indiquen hacia dónde crece la función (es decir, hacia dónde tiene mayor nivel).

Mira, ahora, estas funciones:
\[ f_{1}\left(x_{1},x_{2}\right)=x_{1}^{2}+x_{2}^{2} \] \[ f_{2}\left(x_{1},x_{2}\right)=Ln\left(x_{1}^{2}+x_{2}^{2}\right) \] Puedes pintarlas primero usando google. Con poner en el buscador z=x^2 + y^2 y z=ln(x^2 + y^2) puedes ver qué pinta tienen. Si mueves el cursor, podrás obtener la visión de la función ``desde arriba’’. Esa vista cenital te permite ver la proyección de la función en 3D sobre el plano. Y, por tanto, puedes deducir la pinta que tendrán las curvas de nivel.

FIG9 Curvas de nivel de la función \(z=x^2+y^2\), obtenidas de Google

FIG10 Curvas de nivel de la función \(z=ln(x^2+y^2)\), obtenidas de Google.

Analíticamente, nota que la imagen de \(f_{1}\) siempre es \(Im(f_{1})\geq0\) ( ya que la función sólo puede tomar valores iguales o mayores que cero), por lo que las curvas de nivel \[ Nivel_{1}=\left\{ \left(x_{1},x_{2}\right)\in D\::\:x_{1}^{2}+x_{2}^{2}=C,C\geq0\right\} \] tendremos, entonces, circunferencias concéntricas de radio \(\sqrt{C}.\) Por otro lado, para las curvas de \(f_{2}\) , la imagen será \(Im(f_{2})=\mathbb{R}\) aunque en el dominio, \(x_{1}^{2}+x_{2}^{2}>0\). Esto hace que \[ Nivel_{2}=\left\{ \left(x_{1},x_{2}\right)\in D\::\:x_{1}^{2}+x_{2}^{2}=e^{C},C\in\mathbb{R}\right\} \] y serán circunferencias concéntricas de radio \(\sqrt{e^{C}}\)

¿Por qué tienen la misma pinta las curvas de nivel? Pues porque \(f_{2}\) es una transformación monótona de \(f_{1}\). Eso implica que el logaritmo neperiano respeta el orden dado (esto es, si \(f_{1}(x_{1},x_{2})>f_{1}(y_{1},y_{2})\), entonces,\(f_{2}(x_{1},x_{2})>f_{2}(y_{1},y_{2})\)).

Ejercicio 2

Dibuja 3 curvas de nivel de cada función e indica con una flecha el sentido hacia el que crece.

• \(f(x,y)=x^{2}+(y-1)^{2}\)
• \(g(x,y)=\frac{1}{9}x^{2}+(y-1)^{2}\)
• \(h(x,y)=2x^{2}+y\)
• \(j(x,y)=2+y-\sqrt{x}\)
• \(l(x,y)=y-\ln(x)\)
• \(m(x,y)=(x-2)y\)
• \(n(x,y)=(x+1)^{2}+(y+3)^{2}\)
• \(p(x,y,)=\sqrt{2x+y}\)

Ejercicio 3

Dibuja las curvas de nivel de las siguientes funciones \(f(x,y)=3x+y,g(x,y)=\ln(3x+y),h(x,y)=e^{3x+y}\) ¿qué observas?

Ejercicio 4

Volvamos a la función del Banco de Ponferrada (vídeo 1): \[ M=C_{0}\frac{\left(1+\frac{i}{m}\right)^{n\times m}\left(\frac{i}{m}\right)}{\left(1+\frac{i}{m}\right)^{n\times m}-1}, \]

como seguro que ya has entendido, de esta función (que a valores del número de años, meses, tipo de interés y capital inicial te dice cuánto tienes que pagar al mes del préstamo) no podemos obtener una gráfica en 3D (puesto que estaría en 5D), ni un conjunto de curvas de nivel (que estarían en 4D). Vamos a suponer que fijamos ciertos valores: \(n=1\), \(m=12\), de tal forma que la función se reescribe así

\[ M=C_{0}\frac{\left(1+\frac{i}{12}\right)^{12}\left(\frac{i}{12}\right)}{\left(1+\frac{i}{12}\right)^{12}-1}, \]

Si sólo podemos pagar una mensualidad de \(M=100\) euros, obtén el conjunto de los tipos de interés y capitales iniciales que nos podemos permitir (inténtalo primero a mano, haz unas cuentas y acude a Excel, que te vendrá como agua de mayo).

Recuerda que los tipos de interés están en tanto por uno (es decir, \(i\in(0,1)\)).

Las curvas de nivel van a ser una herramienta que estaremos utilizando constantemente. Deberías practicar mucho con ellas y entender perfectamente las claves de estas.

Clase 6 (invertida): modelización con sistemas de Ecuaciones

OJO, clase invertida!

Esta es una clase invertida. Debes visualizar el vídeo a continuación y tratar de pensar sobre los ejercicios que se te proponen.

Ejercicio 1 (minutos 0:00 a 2:36 del vídeo)

En el vídeo se empieza, de forma sencilla, recordando la idea de un sistema de ecuaciones. En el siguiente ejercicio, dibuja los siguientes sistemas con la intención de que digas cuántas soluciones tiene. Utiliza las propiedades de la recta que estudiaste en clases anteriores para intentar ver cómo se construyen sistemas con una, ninguna o infinitas soluciones

\(\begin{cases} 2x+3y=12\\ x+y=5 \end{cases}\)

\(\begin{cases} 2x+3y=12\\ 4x+6y=24 \end{cases}\)

\(\begin{cases} 2x+3y=12\\ 2x+3y=7 \end{cases}\)

Ejercicio 2 (minutos 2:36 a 4:26 del vídeo)

Di cuáles de los siguientes sistemas son lineales. Discute la solución de todos ellos utilizando GEOGEBRA (no uses ningún método de solución analítica)

• \(\begin{cases} x+y-3z=0\\ -x+y+z=0\\ x-3y-z=0 \end{cases}\)

• \(\begin{cases} 3x+y-\frac{1}{2}z=3\\ 2x+y=1\\ z=2 \end{cases}\)

• \(\begin{cases} x+y-3z=1\\ -x+y+z=0\\ 2x+2y-6z=2 \end{cases}\)

• \(\begin{cases} z=5/(xy)\\ x+y+z=3\\ x+2y-z=10 \end{cases}\)

¿Por qué preferimos los sistemas lineales a los no lineales? :)

Escritura matricial de un sistema de ecuaciones

Recuerda que una matriz es un instrumento matemático para organizar y manipular la información disponible y, además, es un elemento clave en el Álgebra Lineal . Se suele notar con letras mayúsculas. Por ejemplo, decimos que la matriz \(A\) es de dimensión \(m\times n\) si está formada por entradas con \(m\) filas y \(n\) columnas:

\[ A=\left[\begin{array}{cccc} a_{11} & a_{12} & ... & a_{1n}\\ a_{21} & a_{22} & ... & a_{2n}\\ ... & ... & ... & ...\\ a_{m1} & a_{m2} & ... & a_{mn} \end{array}\right] \]

Usaremos las matrices para escribir los sistemas de ecuaciones. Para ello, tenemos que ver cómo se multiplica una matriz por un vector: recuerda que es el sumatorio del producto de los elementos de las filas de la matriz de la izquierda con los de las columnas de la matriz de la derecha (no se puede cambiar el orden)

\[ \left[\begin{array}{cccc} {\color{red}a_{11}} & {\color{red}a_{12}} & {\color{red}...} & {\color{red}a_{1n}}\\ {\color{blue}a_{21}} & {\color{blue}a_{22}} & {\color{blue}...} & {\color{blue}a_{2n}}\\ ... & ... & ... & ...\\ {\color{lime}a_{m1}} & {\color{lime}a_{m2}} & {\color{lime}...} & {\color{lime}a_{mn}} \end{array}\right]\left[\begin{array}{c} {\color{red}b_{1}}\\ {\color{red}b_{2}}\\ {\color{red}...}\\ {\color{red}b_{n}} \end{array}\right]=\left[\begin{array}{c} {\color{red}a_{11}b_{1}+a_{12}b_{2}+...+a_{1n}b_{n}}\\ {\color{blue}a_{21}b_{1}+a_{22}b_{2}+...+a_{2n}b_{n}}\\ {\color{red}...}\\ {\color{lime}a_{m1}b_{1}+a_{m2}b_{2}+...+a_{mn}b_{n}} \end{array}\right] \]

Ejercicio 3

Realiza estos productos (en caso de que sea posible)

• \(\left[\begin{array}{ccc} 2 & 0 & -1\\ 3 & 1 & 0\\ 2 & 0 & 2 \end{array}\right]\left[\begin{array}{c} 1\\ 1\\ 0 \end{array}\right]\)

• \(\left[\begin{array}{ccc} 2 & 0 & -1\\ 3 & 1 & 0\\ 2 & 0 & 2 \end{array}\right]\left[\begin{array}{c} 1\\ 1 \end{array}\right]\)

• \(\left[\begin{array}{c} 1\\ 1\\ 0 \end{array}\right]\left[\begin{array}{ccc} 2 & 0 & -1\\ 3 & 1 & 0\\ 2 & 0 & 2 \end{array}\right]\)

¿Qué concluyes sobre las propiedades del producto de matrices? ?Es siempre posible multiplicar dos matrices?

Finalmente llegamos a donde queríamos: escribir un sistema de ecuaciones en forma matricial. Por ejemplo, del sistema que se propone en el vídeo sobre la empresa que dona parte de su beneficio y paga impuestos:

\[ \begin{cases} x+0.1y+0.1z=10000\\ 0.05x +z=5000\\ 0.4x+y+0.4z=40000 \end{cases} \]

Ahora, tendremos por un lado la matriz de coeficientes \(A\) , por otro, el vector de incógnitas

\(\left[\begin{array}{c} x\\ y\\ z \end{array}\right]\)

y, finalmente, el vector de términos independientes \(\left[\begin{array}{c} 10000\\ 5000\\ 40000 \end{array}\right].\) Escribimos, usando las propiedades anteriores:

\[ A \left[\begin{array}{ccc} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 28\\ 0\\ 1 \end{array}\right]. \]

Ahora, debemos rellenar la matriz \(A\) para que diga lo que deseamos:

\[ \left[\begin{array}{ccc} 1 & 0.1 & 0.1\\ 0.05 & 0 & 1\\ 0.4 & 1 & 0.4 \end{array}\right]\left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 10000\\ 5000\\ 40000 \end{array}\right]. \]

Hemos reescrito el sistema en forma matricial. Trabajaremos con ello a partir de ahora.

Ejercicio 4

Supón que una economía tiene tres industrias punteras: bloggers, instagramers y modistas (que hacen la ropa que sugieren bloggers e instagramers). Supón que la producción de cada sector se distribuye entre los diversos sectores como en la siguiente tabla:

De Bloggers	De Instagrammers	De modistas	Comprada por:
\(0\)	\(0.4\)	\(0.6\)	Bloggers
\(0.6\)	\(0.1\)	\(0.2\)	Instagrammers
\(0.4\)	\(0.5\)	\(0.2\)	Modistas

Las entradas en una columna representan el porcentaje de la producción total de un sector concreto (por eso suman 1). Por ejemplo, la primera columna dice que la producción de Bloggers va en un 60% a los instagrammers y en un 40% a los Modistas.

• Si los precios de producción de cada sector son \(p_b\),\(p_i\),\(p_m\), respectivamente, ¿cuáles son los precios de equilibrio que hacen que los ingresos de un sector igualen a los gastos?

Fíjate, si leemos por filas, obtenemos que de la primera fila, el sector de los Bloggers recibe (y, por tanto, paga) un \(40%\) de la producción de los instagrammers y un \(60%\) d elos modistas. La industria de los bloggers, por tanto, deberá distribuir sus costes como sigue:

\[ p_b=0.4p_i+0.6p_m \]

• Expresa el resto de ecuaciones del sistema y propón su expresión matricial. No lo resuelvas por ahora.

Clase 7 (magistral): Metodología para la resolución de sistemas de Ecuaciones

Una vez sabemos escribir sistemas de ecuaciones en forma matricial, vamos a trabajar con ellos. Empecemos con los que tienen matriz de coeficientes cuadrada (es decir, la dimensión de \(A\) es \(n\times n\)).

\[ \left[\begin{array}{cccc} a_{11} & a_{12} & ... & a_{1n}\\ a_{21} & a_{22} & ... & a_{2n}\\ ... & ... & ... & ...\\ a_{n1} & a_{n2} & ... & a_{nn} \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ ...\\ x_{n} \end{array}\right]=\left[\begin{array}{c} b_{1}\\ b_{2}\\ ...\\ b_{n} \end{array}\right], \]

En forma matricial, podemos escribirlos de forma compacta utilizando las letras en “rojo”:

\[ \underset{{\color{red}A}}{\left[\begin{array}{cccc} a_{11} & a_{12} & ... & a_{1n}\\ a_{21} & a_{22} & ... & a_{2n}\\ ... & ... & ... & ...\\ a_{n1} & a_{n2} & ... & a_{nn} \end{array}\right]}\underset{{\color{red}X}}{\left[\begin{array}{c} x_{1}\\ x_{2}\\ ...\\ x_{n} \end{array}\right]}=\underset{{\color{red}B}}{\left[\begin{array}{c} b_{1}\\ b_{2}\\ ...\\ b_{n} \end{array}\right]}, \]

es decir, el sistema será

\[ AX=B \]

(nota que, en lenguaje matricial, no ponemos ningún signo para denotar el producto).

Como has visto en el vídeo, si el determinante de \(A\) es distinto de cero, podemos hacer uso de la matriz inversa:

• La inversa de una matriz cuadrada \(A\), con \(det(A)\neq0\) es una matriz, llamada \(A^{-1}\), que verifica \[ AA^{-1}=A^{-1}A=I \]

donde \(I\) es la matriz identidad:

\(I=\left[\begin{array}{cccc} 1 & 0 & ... & 0\\ 0 & 1 & ... & 0\\ ... & 0 & \ddots & ...\\ 0 & 0 & ... & 1 \end{array}\right].\)

De nuestro sistema previo, tenemos entonces que despejar \(X\), que es la incógnita del sistema. Si usamos la propiedad de la inversa: \[ A^{-1}AX=A^{-1}B \]

Por lo que la solución del sistema será: \[ X=A^{-1}B \]

¿Cómo obtenemos a mano la inversa de una matriz? Debes, primero, verificar que:

• la matriz \(A\) es cuadrada
• \(det(A)\neq0\)

Definimos el determinante de \(A\) como \(det(A)\) o \(\left|A\right|\), como el resultado de:

• \(\left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right|=a_{11}a_{22}-a_{21}a_{12}\)

• \(\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right|={a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}}-{(a_{31}a_{22}a_{13}+a_{21}a_{12}a_{33}+a_{11}a_{23}a_{32})}\)

• No vamos a aportarte nada nuevo de lo que ya sabes del bachillerato

• Se puede hacer para matrices \(n\times n\) usando el método de los menores. En este curso no necesitaremos tales cálculos.
• Aprenderemos a hacerlo con Excel

Por cierto, el determinante tiene muchas propiedades. Las contaremos cuando las vayamos necesitando.

Ahora, utilizando el determinante, podemos calcular- a mano- la inversa de una matriz:

• caso 1: \(2\times2\). Es muy fácil De la matriz \(A=\left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right]\)

1. calculamos el determinante \(\left|A\right|\), si es distinto de cero

2. la inversa es: \(A^{-1}=\frac{1}{\left|A\right|}\left[\begin{array}{cc} a_{22} & -a_{12}\\ -a_{21} & a_{11} \end{array}\right]\)

• caso 2: \(3\times3.\) Usaremos la matriz de adjuntos

De la matriz \(A=\left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right]\)

La inversa será \(A^{-1}={\frac{1}{\left|A\right|}}(adjA)^{t}\)

• ¿Qué es \(adj(A)\)? : es un conjunto de determinantes tomados de submatrices de orden 2 de acuerdo con la siguiente expresión: \(Adj(A)_{ij}=(-1)^{i+j}M_{ij}\), donde \(M_{ij}\) es el determinante que se obtiene de la submatriz donde se eliminan la fila \(i\) y la columna \(j\). Por ejemplo, de la matriz

\(A=\left[\begin{array}{ccc} 1 & 2 & 1\\ 2 & 1 & -1\\ -1 & 0 & 2 \end{array}\right]\)

el \(\left[adj(A)\right]_{11}\) significa que eliminamos la fila 1 y la columna 1 y calculamos el determinante:

\(\left[adj(A)\right]_{11}=\left|\begin{array}{cc} 1 & -1\\ 0 & 2 \end{array}\right|=2\)

Nota que la expresión \((-1)^{i+j}\) implica que los determinantes van afectados por un signo: \(sign(Adj(A))=\left[\begin{array}{ccc}+ & - & +\\ - & + & -\\ + & - & + \end{array}\right]\)

• Mezclando todo, tenemos la matriz de adjuntos \(adj(A).\) Finalmente, la trasponemos.

La traspuesta de una matriz \(B^{t}\) intercambia las filas y columnas de la matriz. Por ejemplo, \(\left[\begin{array}{cc} 5 & 1\\ 2 & 3\\ 0 & -1 \end{array}\right]^{t}=\left[\begin{array}{ccc} 5 & 2 & 0\\ 1 & 3 & -1 \end{array}\right]\).

Usamos el símbolo \(t\).

Hemos necesitado definir la traspuesta, porque aparece en la definición de inversa: \(A^{-1}={\frac{1}{\left|A\right|}(adjA)^{{\color{red}t}}}\)

Entonces, finalmente, la inversa de \(A=\left[\begin{array}{ccc} 1 & 2 & 1\\ 2 & 1 & -1\\ -1 & 0 & 2 \end{array}\right]\)

se obtendrá de la siguiente forma:

• Calcula el determinante \(\left|A\right|=(2+2+0)-(-1+0+8)=-3\)
• calcula los adjuntos \[ adjA=\left[\begin{array}{ccc} 2 & -2 & 1\\ -4 & 3 & -2\\ -3 & 3 & -3 \end{array}\right] \]

• Obtén su traspuesta \[ adjA^{t}=\left[\begin{array}{ccc} 2 & -4 & -3\\ -2 & 3 & 3\\ 1 & -2 & -3 \end{array}\right] \]

• Tienes la inversa! \[ A^{-1}=\frac{1}{-3}\left[\begin{array}{ccc} 2 & -4 & -3\\ -2 & 3 & 3\\ 1 & -2 & -3 \end{array}\right]=\left[\begin{array}{ccc} -2/3 & 4/3 & 1\\ 2/3 & -1 & -1\\ -1/3 & 2/3 & 1 \end{array}\right] \]

El rango de una matriz (necesario para el teorema de existencia)

El rango de la matriz \(A\) es el orden (dimensión) de la mayor submatriz con determinante distinto de cero. Por ejemplo, de la siguiente matriz \(A\),

\[ A=\left[\begin{array}{ccc} 2 & 0 & 4\\ 1 & 1 & 5\\ -1 & 0 & -2 \end{array}\right] \]

como \(A\) es una matriz \(3\times3\), el rango debería ser, como mucho, 3. Sin embargo: \[ \left|A\right|=0 \]

entonces, deberemos analizar las submatrices. Por ejemplo, hay un montón de \(2\times2\) submatrices de \(A\)

\[ A=\left[\begin{array}{ccc} {\color{magenta}2} & {\color{magenta}0} & 4\\ {\color{magenta}1} & {\color{magenta}1} & 5\\ -1 & 0 & -2 \end{array}\right],\left[\begin{array}{ccc} 2 & {\color{magenta}0} & {\color{magenta}4}\\ 1 & {\color{magenta}1} & {\color{magenta}5}\\ -1 & 0 & -2 \end{array}\right],\left[\begin{array}{ccc} 2 & 0 & 4\\ {\color{magenta}1} & {\color{magenta}1} & 5\\ {\color{magenta}-\color{magenta}1} & {\color{magenta}0} & -2 \end{array}\right],\left[\begin{array}{ccc} 2 & 0 & 4\\ 1 & {\color{magenta}1} & {\color{magenta}5}\\ -1 & {\color{magenta}0} & {\color{magenta}-\color{magenta}2} \end{array}\right],\left[\begin{array}{ccc} {\color{magenta}2} & {\color{magenta}0} & 4\\ 1 & 1 & 5\\ {\color{magenta}-\color{magenta}1} & {\color{magenta}0} & -2 \end{array}\right],... \]

como puedes ver, al menos hay una matriz de orden 2 con determinante distinto de cero. Esto implica que el rango de \(A\) es 2 . Diremos, entonces, que \(rg(A)=2\).

Con sólo encontrar una submatriz con determinante distinto de cero, ya puedes parar.

Ejercicio 1

Busca el rango de las siguientes matrices:

• \(A=\left(\begin{array}{ccc} 1 & -1 & 0\\ 2 & 1 & 1\\ 1 & -4 & -1 \end{array}\right)\)

• \(B=\left(\begin{array}{ccc} 1 & 0 & 1\\ 2 & 1 & 1\\ 0 & -1 & 1\\ 3 & 1 & 2 \end{array}\right)\)

• \(C=\left(\begin{array}{cccc} 0 & 1 & -1 & 2\\ 0 & -1 & 1 & -2\\ 2 & 1 & -1 & 1 \end{array}\right)\)

Finalmente: ¡TEOREMA DE EXISTENCIA DE SOLUCIONES!

Cualquier sistema de ecuaciones se puede escribir usando su matriz “ampliada.” Creamos una nueva matriz, por ejemplo \(\overline{A}\), pegando la matriz de coeficientes y el vector de términos independientes como sigue:

\[ \overline{A}=\left[\left.{A}\right|\color{red}B\right]. \]

Por ejemplo, del sistema: \[ \begin{cases} x+y+z=28\\ x+y-3z=0\\ x-y=-1 \end{cases} \]

su matriz ampliada es

\[ \overline{A}=\left[\begin{array}{ccc} 1 & 1 & 1\\ 1 & 1 & -3\\ 1 & -1 & 0 \end{array}\begin{array}{c} {\color{red}2\color{red}8}\\ {\color{red}0}\\ {\color{red}-\color{red}1} \end{array}\right] \]

Introducimos ahora un teorema que nos permite usar la matriz ampliada para decidir qué tipo de soluciones tiene un sistema:

Teorema de Existencia de Soluciones para Sistemas de Ecuaciones Lineales

Un sistema de ecuaciones con \(n\) variables es:

• Compatible determinado: si rg\((A)=\) rg (\(\overline{A})\)= \(n\)
• compatible indeterminado: si rg (\(A)=\) rg (\(\overline{A}\))\(<n\)
• Incompatible si rg\((A)<\) rg (\(\overline{A})\)

Ejercicio2

Clasifica los sistemas siguientes usando el teorema

• \(\begin{cases} 2x+3y=12\\ 2x+y=4 \end{cases}\)

• \(\begin{cases} x+y=12\\ 2x+2y=24 \end{cases}\)

-\(\begin{cases} 2x+3y=12\\ 2x+3y=7 \end{cases}\)

Nota, por ejemplo, que la matriz ampliada del sistema 3 es: \(\left(\begin{array}{ccc} 2 & 3 & 12\\ 2 & 3 & 7 \end{array}\right)\) el rango de la matriz de coeficientes es 1, pero el rango de la ampliada es 2.

Un método de solución:REGLA DE CRAMER

Esta regla nos ayudará a resolver sistemas de \(n\) ecuaciones con \(n\) variables tal que: \[ \begin{cases} a_{11}x_{1}+a_{12}x_{2}+...+a_{1n}x_{n}=b_{1}\\ a_{21}x_{1}+a_{22}x_{2}+...+a_{2n}x_{n}=b_{2}\\ ...\\ a_{n1}x_{1}+a_{n2}x_{2}+...+a_{nn}x_{n}=b_{n} \end{cases} \]

para obtener la solución, para cada \(x_{i}\), donde \(i=1,2,...,n\),

\[ x_{i}=\frac{\left|\begin{array}{cccccc} a_{11} & a_{12} & ... & {\color{red}b_{1}} & {\color{red}...} & a_{1n}\\ a_{21} & a_{22} & ... & {\color{red}b_{2}} & {\color{red}...} & a_{2n}\\ ... & ... & ... & {\color{red}...} & {\color{red}...} & ...\\ a_{n1} & a_{n2} & ... & {\color{red}b_{n}} & {\color{red}{\color{red}...}} & a_{nn} \end{array}\right|}{\left|\begin{array}{cccccc} a_{11} & a_{12} & ... & a_{1i} & {\color{red}...} & a_{1n}\\ a_{21} & a_{22} & ... & a_{2i} & {\color{red}...} & a_{2n}\\ ... & ... & ... & {\color{red}...} & {\color{red}...} & ...\\ a_{n1} & a_{n2} & ... & a_{ni} & {\color{red}{\color{red}...}} & a_{nn} \end{array}\right|} \]

Si el sistema es Compatible Determinado:

\[ \begin{cases} a_{11}x+a_{12}y+a_{13}z=b_{1}\\ a_{21}x+a_{22}y+a_{23}z=b_{2}\\ a_{31}x+a_{32}y+a_{33}z=b_{3} \end{cases} \]

donde \(A=\left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right],\) tendremos

\[ x=\frac{\left|\begin{array}{ccc} {\color{green}b_{1}} & a_{12} & a_{13}\\ {\color{green}b_{2}} & a_{22} & a_{23}\\ {\color{green}b_{3}} & a_{32} & a_{33} \end{array}\right|}{\left|A\right|},y=\frac{\left|\begin{array}{ccc} a_{11} & {\color{green}b_{1}} & a_{13}\\ a_{21} & {\color{green}b_{2}} & a_{23}\\ a_{31} & {\color{green}b_{3}} & a_{33} \end{array}\right|}{\left|A\right|},z=\frac{\left|\begin{array}{ccc} a_{11} & a_{12} & {\color{green}b_{1}}\\ a_{21} & a_{22} & {\color{green}b_{2}}\\ a_{31} & a_{32} & {\color{green}b_{3}} \end{array}\right|}{\left|A\right|} \]

Sólo consiste en calcular determinantes!

Ejercicio 3

Resuelve este sistema usando la regla de Cramer

\[ \begin{cases} x+y+z=28\\ x+y-3z=0\\ x-y=1 \end{cases} \]

Si el sistema es compatible indeterminado, lo veremos con un ejemplo. Sea el siguiente sistema de ecuaciones:

\[ \begin{cases} x+2y+z=2\\ 2x\:\:\:\,+2z=4\\ x+y+z=2 \end{cases} \] si obtenemos la matriz ampliada \[ \left[\left.\begin{array}{ccc} 1 & 2 & 1\\ 2 & 0 & 2\\ 1 & 1 & 1 \end{array}\right|\begin{array}{c} 2\\ 4\\ 2 \end{array}\right] \] por un lado, \(\left|\begin{array}{ccc} 1 & 2 & 1\\ 2 & 0 & 2\\ 1 & 1 & 1 \end{array}\right|=0\), y tenemos sub-matrices de orden 2 con determinante distinto de cero (por ejemplo, \(\left|\begin{array}{cc} 1 & 2\\ 2 & 0 \end{array}\right|=-4)\). Observa cómo el rango de la ampliada es también 2 (para ello, calcula los determimantes de \(\left[\begin{array}{ccc} 1 & 2 & 2\\ 2 & 0 & 4\\ 1 & 1 & 2 \end{array}\right],\left[\begin{array}{ccc} 1 & 1 & 2\\ 2 & 2 & 4\\ 1 & 1 & 2 \end{array}\right]\) y observa que todos son cero!). Así que el sistema tiene infinitas soluciones. Esto nos dice que nos sobra una ecuación y que, por tanto, nos podemos deshacer de ella. Nos deshacemos de la tercera ecuación y elegimos la variable \(z\) como parámetro: \[ \begin{cases} x+2y=2-z\\ 2x\:\:\:\,=4-2z \end{cases} \] usamos Cramer para resolverlo: \[ x=\frac{\left|\begin{array}{cc} 2-z & 2\\ 4-2z & 0 \end{array}\right|}{\left|\begin{array}{cc} 1 & 2\\ 2 & 0 \end{array}\right|}=\frac{-8+4z}{-4}=2-z \] \[ y=\frac{\left|\begin{array}{cc} 1 & 2-z\\ 2 & 4-2z \end{array}\right|}{\left|\begin{array}{cc} 1 & 2\\ 2 & 0 \end{array}\right|}=\frac{0}{-4}=0 \]

por lo que la solución será:

\[ x=2-z,y=0, \]

y \(z\in\mathbb{R}\)

Ejercicio 4

Busca el planteamiento del Ejercicio 4 de la clase anterior, discútelo y resuélvelo.

Ejercicio EBAU Madrid 2021

Se considera el sistema de ecuaciones lineales dependiente del parámetro real \(a\)

\[ \begin{cases} x+y-z=-1\\ x-y+a^2z=3\\ 2x-y+z=4 \end{cases} \]

• Discute el sistema en función de los valores del parámetro \(a\).
• Resuelve el sistema, a mano, para \(a=1\).
• Resuelve el sistema, usando Excel, para \(a=2\)