Capítulo 6 Como analisar a performance de Modelos de Regressão?

Neste capítulo serão abordadas formas de mensurar a qualidade do ajuste de modelos de regressão, assim como formas de investigar a existência ou não de sobreajuste.

6.1 Medida de qualidade do ajuste

Para os problemas de regressão a variável resposta \(Y\) é uma variável quantitativa. Suponha que um modelo de regressão \(k\) realizou a previsões \(\hat{y}_i^k\) para a \(i\)-ésima observação da variável \(Y\). Suponha \(y_i\) o real valor observado para a \(i\)-ésima observação da variável \(Y\).

i Valor observado Previsão para o Modelo 1 Previsão para o Modelo 2 Previsão para o Modelo 3
1 \(y_1\) \(\hat y_1^1\) \(\hat y_1^2\) \(\hat y_1^3\)
2 \(y_2\) \(\hat y_2^1\) \(\hat y_2^2\) \(\hat y_2^3\)
3 \(y_3\) \(\hat y_3^1\) \(\hat y_3^2\) \(\hat y_3^3\)
… … … … …
N \(y_N\) \(\hat y_N^1\) \(\hat y_N^2\) \(\hat y_N^3\)

No contexto deste curso os Modelos apresentados na tabela acima podem ser modelos de árvores de regressão, floresta aleatória, gradiente bossting e ainda estes modelos com diferentes valores para os hiperparâmetros. Para comparar o desempenho dos diferentes modelos de regressão são usadas medidas baseadas na diferença entre valor real observado \(y_i\) e valor estimado estimado \(\hat{y}_i\), chamada de resíduo. Uma vez conhecidos os resíduos é possível usar o SSE (soma dos erros ao quadrado) ou MSE (média dos erros ao quadrado) para comparar a qualidade do ajuste dos diferentes modelos.

\[ SSE^k = \sum_{i=1}^N (\hat{y}_i^k - y_i)^2 \qquad \qquad MSE^k = \dfrac{1}{N} \sum_{i=1}^N (\hat{y}_i^k - y_i)^2 = \dfrac{SSE}{N} \]

Suponha o MSE como medida de comparação. Esta medida pode ser calculada para os valores da base de treino e também da base de teste. Assim é possível construir a seguinte tabela.

Modelo MSE na base de treino MSE na base de teste
1 \(MSE^1_{treino}\) \(MSE^1_{teste}\)
2 \(MSE^2_{treino}\) \(MSE^2_{teste}\)
3 \(MSE^3_{treino}\) \(MSE^3_{teste}\)

O modelo com menor MSE na base de teste será aquele aparentemente com melhor desempenho. Observar o valor do MSE na base de treino também pode trazer informações importantes, como por exemplo, se um modelo apresenta sobreajuste. Quando um modelo apresenta MSE na base de treino bem menor que o MSE na base de teste, principalmente quando comparado com os outros modelos, percebemos a ocorrência do sobreajuste (overfiting).

Vamos Praticar

Primeiro, como sempre, carregar os pacotes necessários e a base de dados de treino.

library(tidyverse)
library(rpart)
library(randomForest)
library(xgboost)
base_treino = readRDS(file="arquivos-de-trabalho/base_treino_final.rds")

Neste exemplo será considerada somente como variável resposta a nota da redação. Por esse motivo, as demais variáveis respostas serão retiradas da base. Além destas, também serão retiradas as variáveis de identificação das escolas.

base_treino = base_treino |> select(-c(CO_ESCOLA_EDUCACENSO,
                                       NO_ESCOLA_EDUCACENSO,
                                       NU_MEDIA_CN,
                                       NU_MEDIA_CH,
                                       NU_MEDIA_LP,
                                       NU_MEDIA_MT,
                                       NU_TAXA_PARTICIPACAO,
                                       NU_PARTICIPANTES))

Carregar modelos de regressão

A proposta é comparar os modelos de regressão já ajustados para prever a nota de redação de uma escola. Para aproveitar o trabalho já realizado, em vez de ajustar os modelos serão carregados os objetos salvos na ocasião de ajuste dos modelos em capítulos anteriores.

tree_RD = readRDS(file="arquivos-de-trabalho/tree_RD.rds")
rf_RD = readRDS(file = "arquivos-de-trabalho/rf_RD.rds")
xgb_RD = readRDS(file = "arquivos-de-trabalho/xgb_RD.rds")

Previsão na base de treino

O cálculo da previsão da nota de redação será feito com a função predict e o newdata recebe a mesma base de treino.

prev_treino_tree_RD = predict(tree_RD,newdata = base_treino)
prev_treino_rf_RD = predict(rf_RD,newdata = base_treino)

Para o caso do XGBoost vale lembrar que a função xgboot recebe como entrada uma matriz, e não um data.frame, somente com as covariáveis do problema.

X_treino = base_treino |> select(-NU_MEDIA_RED)
M_X_treino = model.matrix(~. , data = X_treino)[,-1]
prev_treino_xgb_RD = predict(xgb_RD,newdata = M_X_treino)

MSE na base de treino

Em seguida calcula-se o valor do MSE na base de treino.

MSE_treino_tree_RD = mean((prev_treino_tree_RD - base_treino$NU_MEDIA_RED)^2)
MSE_treino_rf_RD = mean((prev_treino_rf_RD - base_treino$NU_MEDIA_RED)^2)
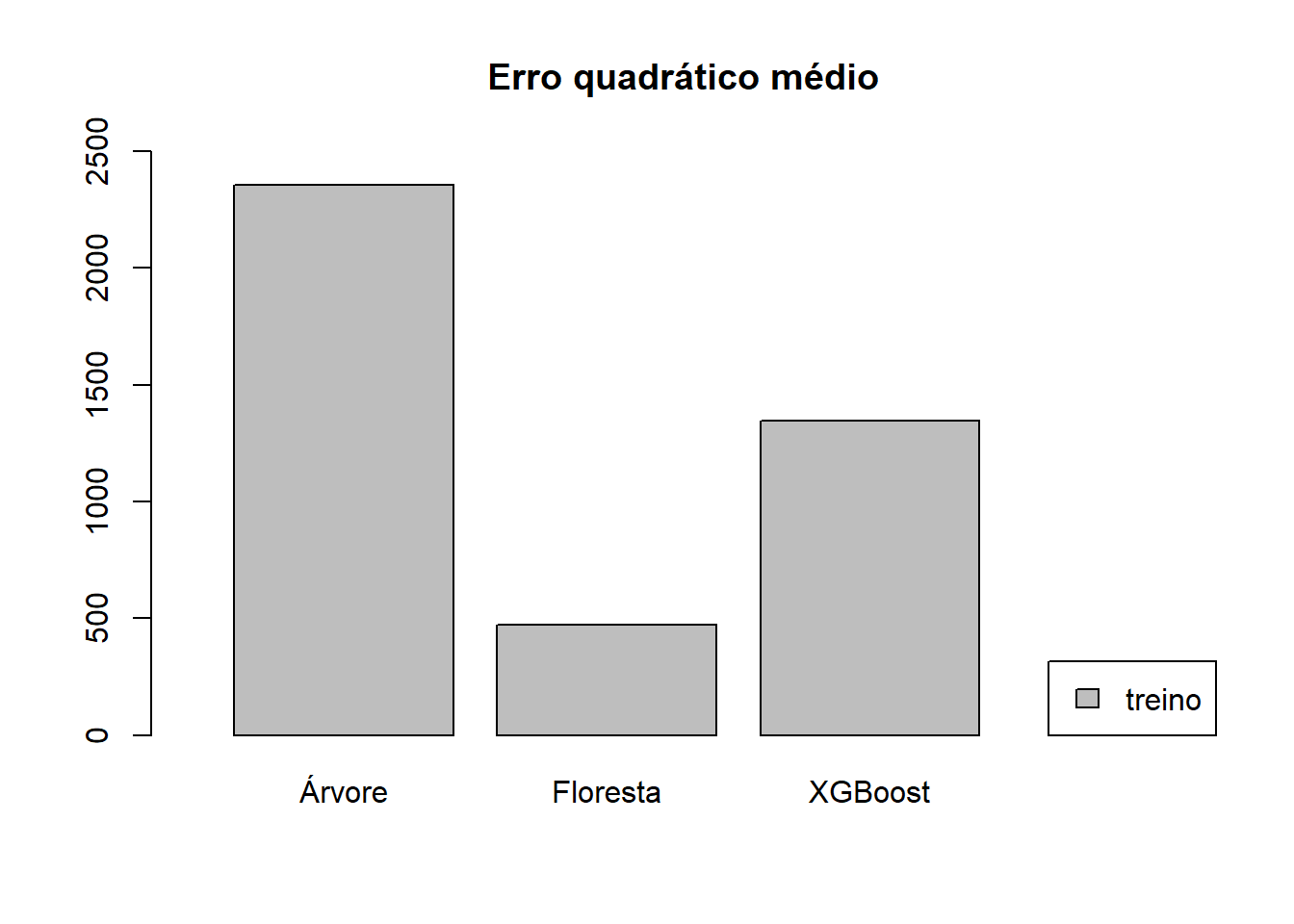
MSE_treino_xgb_RD = mean((prev_treino_xgb_RD - base_treino$NU_MEDIA_RED)^2)

Vejamos agora os resultados obtidos para os três modelos.

Tabela 6.1: Erro quadrático médio na base de treino
Árvore de Decisão Floresta Aleatória XGBoost
MSE no treino 2354.907 473.64 1348.059

Previsão na base de teste

Antes de realizar a previsão na base de teste é preciso carregar e arrumar a base de teste de acordo com as mudanças feitas na base de treino.

base_teste = readRDS(file="arquivos-de-trabalho/base_teste.rds")
base_teste = base_teste |> select(-c(NU_MEDIA_OBJ, 
                                     NU_MEDIA_TOT,
                                     NU_ANO,
                                     NU_TAXA_APROVACAO,
                                     CO_UF_ESCOLA,
                                     CO_MUNICIPIO_ESCOLA,
                                     NO_MUNICIPIO_ESCOLA))
base_teste = base_teste  |>
  mutate(NU_TAXA_REPROVACAO = replace_na(NU_TAXA_REPROVACAO, mean(base_treino$NU_TAXA_REPROVACAO, na.rm = TRUE)),
         NU_TAXA_ABANDONO = replace_na(NU_TAXA_ABANDONO, mean(base_treino$NU_TAXA_ABANDONO, na.rm = TRUE)),
         PC_FORMACAO_DOCENTE = replace_na(PC_FORMACAO_DOCENTE, mean(base_treino$PC_FORMACAO_DOCENTE, na.rm = TRUE))
         )
base_teste = base_teste |> select(-c(CO_ESCOLA_EDUCACENSO,
                                       NO_ESCOLA_EDUCACENSO,
                                       NU_MEDIA_CN,NU_MEDIA_CH,
                                       NU_MEDIA_LP,NU_MEDIA_MT,
                                       NU_TAXA_PARTICIPACAO,
                                       NU_PARTICIPANTES))

Para realizar as previsões na base de teste será usada também a função predict, mas dessa vez o argumento newdata recebe base_teste. Aqui novamente para o XGBoost é preciso criar uma matriz para o argumento newdata deste método.

prev_teste_tree_RD = predict(tree_RD,newdata = base_teste)
prev_teste_rf_RD = predict(rf_RD,newdata = base_teste)
X_teste = base_teste |> select(-NU_MEDIA_RED)
M_X_teste = model.matrix(~. , data = X_teste)[,-1]
prev_teste_xgb_RD = predict(xgb_RD,newdata = M_X_teste)

MSE na base de teste

O cálculo do MSE na de teste é realizado de forma análoga ao cálculo já feito para a base de treino.

MSE_teste_tree_RD = mean((prev_teste_tree_RD - base_teste$NU_MEDIA_RED)^2)
MSE_teste_rf_RD = mean((prev_teste_rf_RD - base_teste$NU_MEDIA_RED)^2)
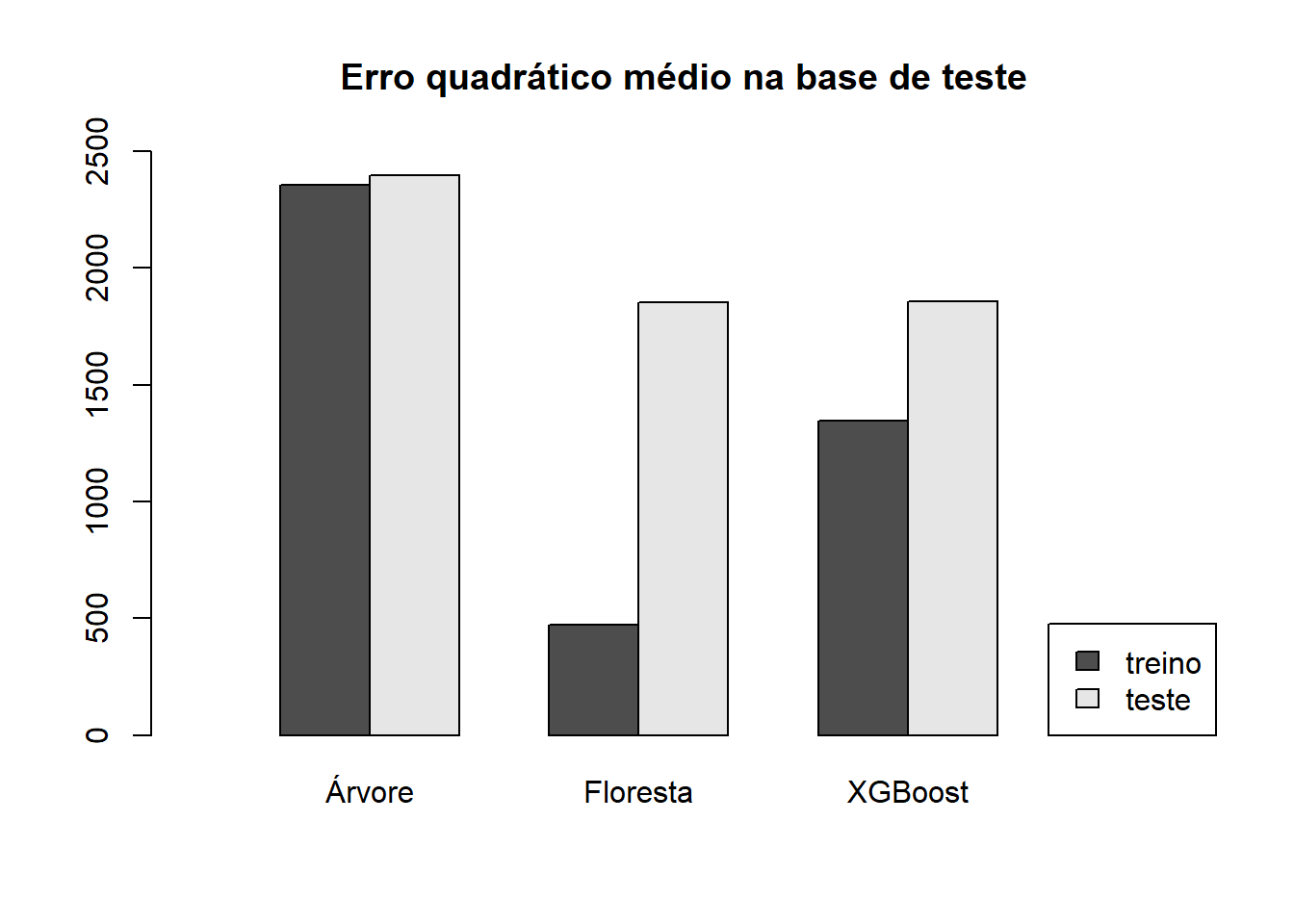
MSE_teste_xgb_RD = mean((prev_teste_xgb_RD - base_teste$NU_MEDIA_RED)^2)

Agora já é possível comparar os desempenhos dos modelos tanto na base de treino quando na base de teste.

Tabela 6.2: Erro quadrático médio
Árvore Floresta XGBoost
MSE no treino 2354.907 473.640 1348.059
MSE no teste 2398.215 1852.735 1855.455

6.2 Validação Cruzada

A validação cruzada (k-fold cross-validation) é um processo de análise do ajuste do modelo que pode ser feito na base de treino, antes de verificar o seu desempenho na base de teste. Este processo é útil para se encontrar valores para os hiperparâmetros e melhor analisar o desempenho dos métodos.

Neste processo primeiro é feita uma partição da base de treino em \(k\) pedaços. Isto é, parte é defnida por algumas linhas da base de treino, partes diferentes não têm linhas em comum e todas as partes unidas representam todas as linhas da base. Uma vez a base de treino dividida, o modelo é ajustado utilizando-se como treino \(k-1\) partes e verificando seu desempenho na parte que ficou de fora do treinamento. Esse processo é feito \(k\) vezes e calcula-se as medidas de desempenho em cada uma delas. Ao final do processo, em vez de um valor do MSE na base de treino, teremos \(k\) valores do MSE na base de treinamento e \(k\) valores do MSE na base de validação.

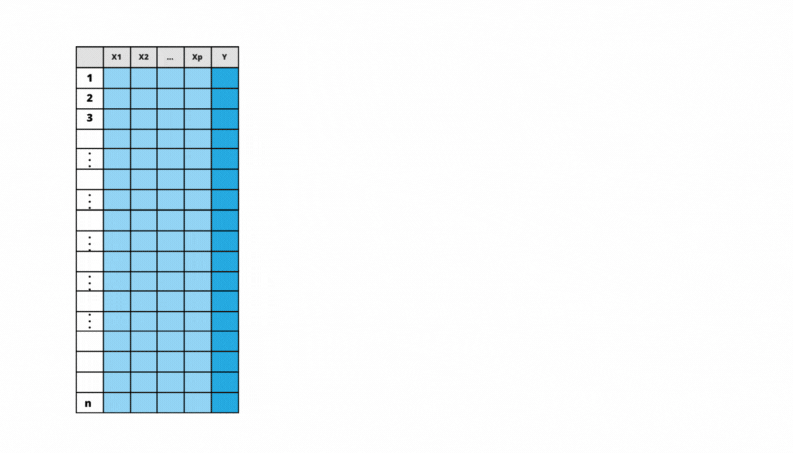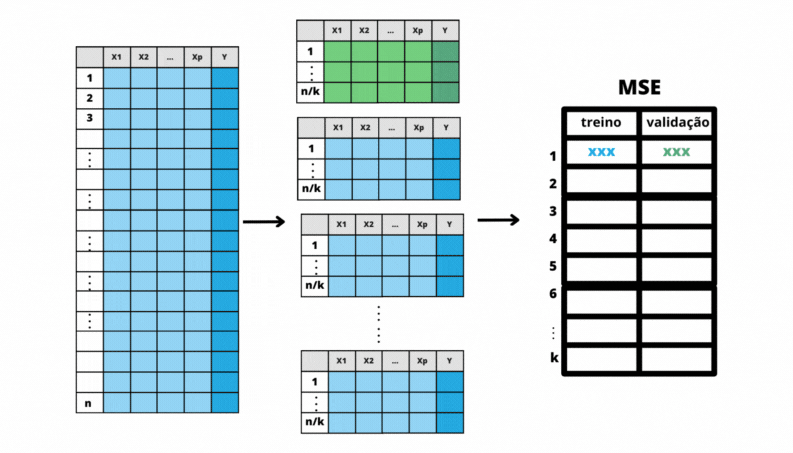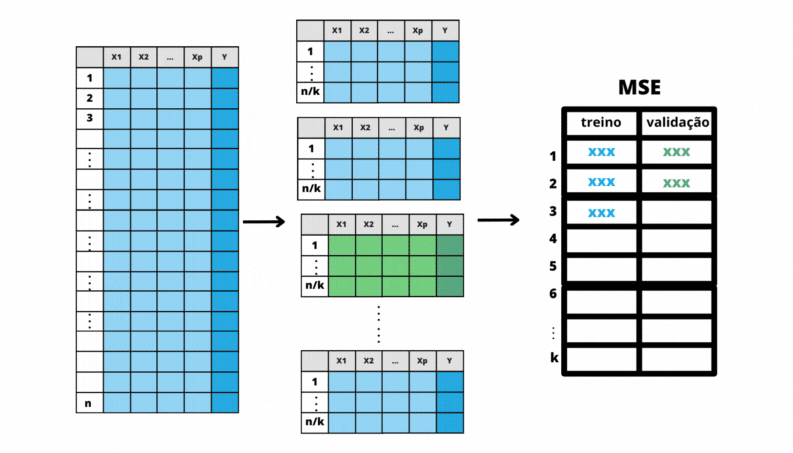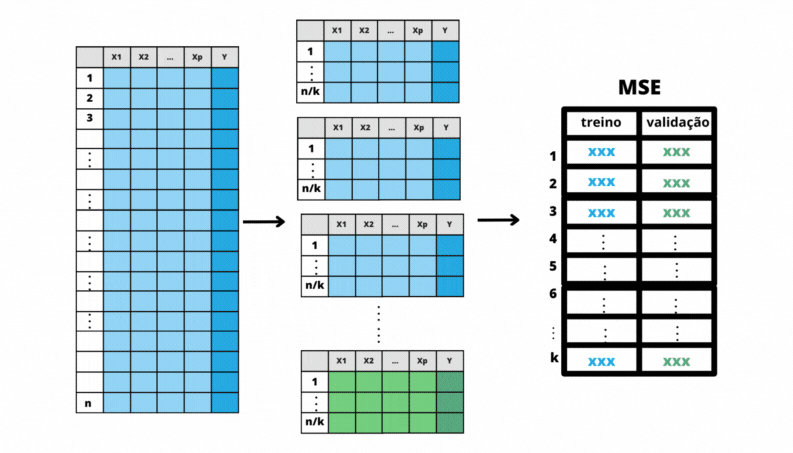
Validação Cruzada

Figura 6.1: Validação Cruzada

  1. Divide a base de treino em \(k\) partes;

  2. Faz \(i=1\);

  3. Considere a parte \(i\) como base de validação e o restante da base de dados como base de treino.

  4. Ajuste cada modelo para a base de treino.

  5. Calcule o MSE na base de validação para cada modelo ajustado na base de treino.

  6. Faz \(i = i + 1\) e se \(i \le k\), volte para o passo 3.

Realizar a validação cruzada para se chegar ao melhor modelo de regressão é uma avaliação bem mais ampla do que simplesmente testar o modelo no treino e no teste. No final, em vez de comparar o valor do MSE na base de treino e teste, serão comparados \(k\) valores do MSE na base de treino e de validação. Nesse caso fica mais interessante e informativo comparar estatísticas para estes valores. A análise destes valores resulta num melhor compreendimento dos desempenhos dos modelos e uma escolha mais acertiva sobre qual deles adotar no problema em questão.

Vamos Praticar

O primeiro passo para se executar uma validação cruzada é separar a base em \(k\) partes. Neste exemplo será usado \(k=10\), nesse caso será realizado 10-fold Cross Validation. O pacote caret(Kuhn 2022) , já usado para a separação em treino e teste, será usado também para a partição da base em \(k\) partes de mesmo tamanho.

library(caret)
set.seed(1234567890)
K = 10
n=nrow(base_treino)
indices_folds = createFolds(1:n,k=K)

O código acima cria o objeto indices_folds que é uma lista de tamanho \(k=10\). Cada posição desta lista guarda um vetor de índices referente às linhas da base em cada fold.

Escolha dos hiperparâmetros para a Árvore de Regressão

A validação cruzada será usada aqui para analisar o desempenho do modelo de Árvores de Regressão para diferentes valores dos seus hiperparâmetros. Os hiérparâmeros considerados nesta comparação são os parâmeros que definem os critérios de parada. Foram eles: minsplit, que indica o número mínimo aceitado por nó da árvore; cp, que indica a melhora mínima, em percentual, aceita e uma divisão da árvore; e maxdepth, que é a profundidade máxima da árvore. Mais detalhes consulte o help a partir do comando ?rpart.control.

O código a seguir mostra os valores considerados para cada um dos três parâmetros.

#arvore de regressao
param = list(minsplit = c(20,10,50),
             cp = c(0.01, 0.005, 0.02),
             maxdepth = c(30,20,10))

param_combination_tree = expand.grid(param, stringsAsFactors = FALSE)

O objeto param_combination_tree é um data.frame que guarda todas as combinações dos valores definidos para cada parâmetro.

param_combination_tree
##    minsplit    cp maxdepth
## 1        20 0.010       30
## 2        10 0.010       30
## 3        50 0.010       30
## 4        20 0.005       30
## 5        10 0.005       30
## 6        50 0.005       30
## 7        20 0.020       30
## 8        10 0.020       30
## 9        50 0.020       30
## 10       20 0.010       20
## 11       10 0.010       20
## 12       50 0.010       20
## 13       20 0.005       20
## 14       10 0.005       20
## 15       50 0.005       20
## 16       20 0.020       20
## 17       10 0.020       20
## 18       50 0.020       20
## 19       20 0.010       10
## 20       10 0.010       10
## 21       50 0.010       10
## 22       20 0.005       10
## 23       10 0.005       10
## 24       50 0.005       10
## 25       20 0.020       10
## 26       10 0.020       10
## 27       50 0.020       10

Agora começa a validação cruzada para o modelo de árvores. Para cada combinação dos parâmetros definida pelas linhas de param_combination_tree serão ajustados \(k\) modelos de árvores os valores do MSE, que é a medida de qualidade do ajuste adotada, será guardada em duas matrizes. A primeira, MSE_treino_tree, guarda em cada linha o MSE na base de treino para cada combinação dos parâmetros, as colunas indicam a iteração da validação cruzada. O mesmo vale para MSE_valida_tree, mas aqui será o MSE na base de validação.

MSE_treino_tree = matrix(NA,nrow = nrow(param_combination_tree),ncol = K)
MSE_valida_tree = matrix(NA,nrow = nrow(param_combination_tree),ncol = K)

for(i in 1:nrow(param_combination_tree)){
  
  for(f in 1:K){
  
    valida = base_treino |> dplyr::slice(indices_folds[[f]])
    treino = base_treino |> dplyr::slice(-indices_folds[[f]])
    
    tree <- rpart(NU_MEDIA_RED ~ ., 
                  data = treino,
                  control = rpart.control(minsplit = param_combination_tree$minsplit[i], 
                                          cp = param_combination_tree$cp[i], 
                                          maxdepth = param_combination_tree$maxdepth[i]))
    
    prev_treino = predict(tree,newdata = treino)
    prev_valida = predict(tree,newdata = valida)
    
    MSE_treino_tree[i,f] = mean((prev_treino - treino$NU_MEDIA_RED)^2)
    MSE_valida_tree[i,f] = mean((prev_valida - valida$NU_MEDIA_RED)^2)
  }
}

A tabela a seguir apresenta os valores o erro médio quadrático (MSE) na base de treinamento. Estes são os valores guardados em MSE_treino_tree. As primeiras colunas indicam a combinação dos parâmetros considerada em cada linha.

(#tab:VC_MSE_tree_treino)MSE na base de treinamento
minsplit cp maxdepth Parte 1 Parte 2 Parte 3 Parte 4 Parte 5 Parte 6 Parte 7 Parte 8 Parte 9 Parte 10
20 0.010 30 2391.8 2337.4 2341.2 2342.0 2362.0 2342.2 2326.0 2359.6 2335.0 2348.5
10 0.010 30 2391.8 2337.4 2341.2 2342.0 2362.0 2342.2 2326.0 2359.6 2335.0 2348.5
50 0.010 30 2391.8 2337.4 2341.2 2342.0 2362.0 2342.2 2326.0 2359.6 2335.0 2348.5
20 0.005 30 2263.2 2217.4 2251.2 2218.9 2234.3 2213.6 2202.2 2231.6 2240.4 2222.1
10 0.005 30 2263.2 2217.4 2251.2 2218.9 2234.3 2213.6 2202.2 2231.6 2240.4 2222.1
50 0.005 30 2263.2 2217.4 2251.2 2218.9 2234.3 2213.6 2202.2 2231.6 2240.4 2222.1
20 0.020 30 2745.4 2708.7 2694.6 2690.8 2723.9 2709.5 2580.7 2715.1 2702.7 2698.1
10 0.020 30 2745.4 2708.7 2694.6 2690.8 2723.9 2709.5 2580.7 2715.1 2702.7 2698.1
50 0.020 30 2745.4 2708.7 2694.6 2690.8 2723.9 2709.5 2580.7 2715.1 2702.7 2698.1
20 0.010 20 2391.8 2337.4 2341.2 2342.0 2362.0 2342.2 2326.0 2359.6 2335.0 2348.5
10 0.010 20 2391.8 2337.4 2341.2 2342.0 2362.0 2342.2 2326.0 2359.6 2335.0 2348.5
50 0.010 20 2391.8 2337.4 2341.2 2342.0 2362.0 2342.2 2326.0 2359.6 2335.0 2348.5
20 0.005 20 2263.2 2217.4 2251.2 2218.9 2234.3 2213.6 2202.2 2231.6 2240.4 2222.1
10 0.005 20 2263.2 2217.4 2251.2 2218.9 2234.3 2213.6 2202.2 2231.6 2240.4 2222.1
50 0.005 20 2263.2 2217.4 2251.2 2218.9 2234.3 2213.6 2202.2 2231.6 2240.4 2222.1
20 0.020 20 2745.4 2708.7 2694.6 2690.8 2723.9 2709.5 2580.7 2715.1 2702.7 2698.1
10 0.020 20 2745.4 2708.7 2694.6 2690.8 2723.9 2709.5 2580.7 2715.1 2702.7 2698.1
50 0.020 20 2745.4 2708.7 2694.6 2690.8 2723.9 2709.5 2580.7 2715.1 2702.7 2698.1
20 0.010 10 2391.8 2337.4 2341.2 2342.0 2362.0 2342.2 2326.0 2359.6 2335.0 2348.5
10 0.010 10 2391.8 2337.4 2341.2 2342.0 2362.0 2342.2 2326.0 2359.6 2335.0 2348.5
50 0.010 10 2391.8 2337.4 2341.2 2342.0 2362.0 2342.2 2326.0 2359.6 2335.0 2348.5
20 0.005 10 2263.2 2217.4 2251.2 2218.9 2234.3 2213.6 2202.2 2231.6 2240.4 2222.1
10 0.005 10 2263.2 2217.4 2251.2 2218.9 2234.3 2213.6 2202.2 2231.6 2240.4 2222.1
50 0.005 10 2263.2 2217.4 2251.2 2218.9 2234.3 2213.6 2202.2 2231.6 2240.4 2222.1
20 0.020 10 2745.4 2708.7 2694.6 2690.8 2723.9 2709.5 2580.7 2715.1 2702.7 2698.1
10 0.020 10 2745.4 2708.7 2694.6 2690.8 2723.9 2709.5 2580.7 2715.1 2702.7 2698.1
50 0.020 10 2745.4 2708.7 2694.6 2690.8 2723.9 2709.5 2580.7 2715.1 2702.7 2698.1

Para melhor analisar esses números podem ser usadas estatísticas referentes aos \(k\) valores para cada combinação de parâmetros. Isto é, por linha, em vez de olharmos para todos os 10 valores, vamos olhar para: o menor valor, o maior valor, o valor médio, e qualquer outra estatística que a gente julge interessante. Esses resultados são obtidos pelo comando a seguir e apresentados em tabelas.

result_treino_tree = apply(MSE_treino_tree, MARGIN = 1, summary)
Tabela 6.3: Estatísticas para o MSE na base de treinamento
Parâmetros 1 Parâmetros 2 Parâmetros 3 Parâmetros 4 Parâmetros 5 Parâmetros 6 Parâmetros 7 Parâmetros 8 Parâmetros 9 Parâmetros 10 Parâmetros 11 Parâmetros 12 Parâmetros 13 Parâmetros 14 Parâmetros 15 Parâmetros 16 Parâmetros 17 Parâmetros 18 Parâmetros 19 Parâmetros 20 Parâmetros 21 Parâmetros 22 Parâmetros 23 Parâmetros 24 Parâmetros 25 Parâmetros 26 Parâmetros 27
Min. 2326.0 2326.0 2326.0 2202.2 2202.2 2202.2 2580.7 2580.7 2580.7 2326.0 2326.0 2326.0 2202.2 2202.2 2202.2 2580.7 2580.7 2580.7 2326.0 2326.0 2326.0 2202.2 2202.2 2202.2 2580.7 2580.7 2580.7
1st Qu. 2338.3 2338.3 2338.3 2217.7 2217.7 2217.7 2695.5 2695.5 2695.5 2338.3 2338.3 2338.3 2217.7 2217.7 2217.7 2695.5 2695.5 2695.5 2338.3 2338.3 2338.3 2217.7 2217.7 2217.7 2695.5 2695.5 2695.5
Median 2342.1 2342.1 2342.1 2226.9 2226.9 2226.9 2705.7 2705.7 2705.7 2342.1 2342.1 2342.1 2226.9 2226.9 2226.9 2705.7 2705.7 2705.7 2342.1 2342.1 2342.1 2226.9 2226.9 2226.9 2705.7 2705.7 2705.7
Mean 2348.6 2348.6 2348.6 2229.5 2229.5 2229.5 2697.0 2697.0 2697.0 2348.6 2348.6 2348.6 2229.5 2229.5 2229.5 2697.0 2697.0 2697.0 2348.6 2348.6 2348.6 2229.5 2229.5 2229.5 2697.0 2697.0 2697.0
3rd Qu. 2356.9 2356.9 2356.9 2238.9 2238.9 2238.9 2713.7 2713.7 2713.7 2356.9 2356.9 2356.9 2238.9 2238.9 2238.9 2713.7 2713.7 2713.7 2356.9 2356.9 2356.9 2238.9 2238.9 2238.9 2713.7 2713.7 2713.7
Max. 2391.8 2391.8 2391.8 2263.2 2263.2 2263.2 2745.4 2745.4 2745.4 2391.8 2391.8 2391.8 2263.2 2263.2 2263.2 2745.4 2745.4 2745.4 2391.8 2391.8 2391.8 2263.2 2263.2 2263.2 2745.4 2745.4 2745.4

O mesmo pode ser feito para os resultados do MSE na base de validação.

(#tab:VC_MSE_tree_valida)MSE na base de validação
minsplit cp maxdepth Parte 1 Parte 2 Parte 3 Parte 4 Parte 5 Parte 6 Parte 7 Parte 8 Parte 9 Parte 10
20 0.010 30 2023.6 2537.4 2479.9 2496.1 2297.0 2387.2 2519.1 2327.8 2445.3 2438.6
10 0.010 30 2023.6 2537.4 2479.9 2496.1 2297.0 2387.2 2519.1 2327.8 2445.3 2438.6
50 0.010 30 2023.6 2537.4 2479.9 2496.1 2297.0 2387.2 2519.1 2327.8 2445.3 2438.6
20 0.005 30 1944.0 2385.3 2368.1 2372.1 2210.0 2284.0 2390.8 2249.1 2355.6 2345.0
10 0.005 30 1944.0 2385.3 2368.1 2372.1 2210.0 2284.0 2390.8 2249.1 2355.6 2345.0
50 0.005 30 1944.0 2385.3 2368.1 2372.1 2210.0 2284.0 2390.8 2249.1 2355.6 2345.0
20 0.020 30 2386.6 2717.1 2843.5 2878.4 2582.3 2710.4 2720.6 2659.6 2771.4 2813.9
10 0.020 30 2386.6 2717.1 2843.5 2878.4 2582.3 2710.4 2720.6 2659.6 2771.4 2813.9
50 0.020 30 2386.6 2717.1 2843.5 2878.4 2582.3 2710.4 2720.6 2659.6 2771.4 2813.9
20 0.010 20 2023.6 2537.4 2479.9 2496.1 2297.0 2387.2 2519.1 2327.8 2445.3 2438.6
10 0.010 20 2023.6 2537.4 2479.9 2496.1 2297.0 2387.2 2519.1 2327.8 2445.3 2438.6
50 0.010 20 2023.6 2537.4 2479.9 2496.1 2297.0 2387.2 2519.1 2327.8 2445.3 2438.6
20 0.005 20 1944.0 2385.3 2368.1 2372.1 2210.0 2284.0 2390.8 2249.1 2355.6 2345.0
10 0.005 20 1944.0 2385.3 2368.1 2372.1 2210.0 2284.0 2390.8 2249.1 2355.6 2345.0
50 0.005 20 1944.0 2385.3 2368.1 2372.1 2210.0 2284.0 2390.8 2249.1 2355.6 2345.0
20 0.020 20 2386.6 2717.1 2843.5 2878.4 2582.3 2710.4 2720.6 2659.6 2771.4 2813.9
10 0.020 20 2386.6 2717.1 2843.5 2878.4 2582.3 2710.4 2720.6 2659.6 2771.4 2813.9
50 0.020 20 2386.6 2717.1 2843.5 2878.4 2582.3 2710.4 2720.6 2659.6 2771.4 2813.9
20 0.010 10 2023.6 2537.4 2479.9 2496.1 2297.0 2387.2 2519.1 2327.8 2445.3 2438.6
10 0.010 10 2023.6 2537.4 2479.9 2496.1 2297.0 2387.2 2519.1 2327.8 2445.3 2438.6
50 0.010 10 2023.6 2537.4 2479.9 2496.1 2297.0 2387.2 2519.1 2327.8 2445.3 2438.6
20 0.005 10 1944.0 2385.3 2368.1 2372.1 2210.0 2284.0 2390.8 2249.1 2355.6 2345.0
10 0.005 10 1944.0 2385.3 2368.1 2372.1 2210.0 2284.0 2390.8 2249.1 2355.6 2345.0
50 0.005 10 1944.0 2385.3 2368.1 2372.1 2210.0 2284.0 2390.8 2249.1 2355.6 2345.0
20 0.020 10 2386.6 2717.1 2843.5 2878.4 2582.3 2710.4 2720.6 2659.6 2771.4 2813.9
10 0.020 10 2386.6 2717.1 2843.5 2878.4 2582.3 2710.4 2720.6 2659.6 2771.4 2813.9
50 0.020 10 2386.6 2717.1 2843.5 2878.4 2582.3 2710.4 2720.6 2659.6 2771.4 2813.9 
result_valida_tree = apply(MSE_valida_tree, MARGIN = 1, summary)
Tabela 6.4: Estatísticas para o MSE na base de validação
Parâmetros 1 Parâmetros 2 Parâmetros 3 Parâmetros 4 Parâmetros 5 Parâmetros 6 Parâmetros 7 Parâmetros 8 Parâmetros 9 Parâmetros 10 Parâmetros 11 Parâmetros 12 Parâmetros 13 Parâmetros 14 Parâmetros 15 Parâmetros 16 Parâmetros 17 Parâmetros 18 Parâmetros 19 Parâmetros 20 Parâmetros 21 Parâmetros 22 Parâmetros 23 Parâmetros 24 Parâmetros 25 Parâmetros 26 Parâmetros 27
Min. 2023.6 2023.6 2023.6 1944.0 1944.0 1944.0 2386.6 2386.6 2386.6 2023.6 2023.6 2023.6 1944.0 1944.0 1944.0 2386.6 2386.6 2386.6 2023.6 2023.6 2023.6 1944.0 1944.0 1944.0 2386.6 2386.6 2386.6
1st Qu. 2342.7 2342.7 2342.7 2257.8 2257.8 2257.8 2672.3 2672.3 2672.3 2342.7 2342.7 2342.7 2257.8 2257.8 2257.8 2672.3 2672.3 2672.3 2342.7 2342.7 2342.7 2257.8 2257.8 2257.8 2672.3 2672.3 2672.3
Median 2442.0 2442.0 2442.0 2350.3 2350.3 2350.3 2718.9 2718.9 2718.9 2442.0 2442.0 2442.0 2350.3 2350.3 2350.3 2718.9 2718.9 2718.9 2442.0 2442.0 2442.0 2350.3 2350.3 2350.3 2718.9 2718.9 2718.9
Mean 2395.2 2395.2 2395.2 2290.4 2290.4 2290.4 2708.4 2708.4 2708.4 2395.2 2395.2 2395.2 2290.4 2290.4 2290.4 2708.4 2708.4 2708.4 2395.2 2395.2 2395.2 2290.4 2290.4 2290.4 2708.4 2708.4 2708.4
3rd Qu. 2492.1 2492.1 2492.1 2371.1 2371.1 2371.1 2803.3 2803.3 2803.3 2492.1 2492.1 2492.1 2371.1 2371.1 2371.1 2803.3 2803.3 2803.3 2492.1 2492.1 2492.1 2371.1 2371.1 2371.1 2803.3 2803.3 2803.3
Max. 2537.4 2537.4 2537.4 2390.8 2390.8 2390.8 2878.4 2878.4 2878.4 2537.4 2537.4 2537.4 2390.8 2390.8 2390.8 2878.4 2878.4 2878.4 2537.4 2537.4 2537.4 2390.8 2390.8 2390.8 2878.4 2878.4 2878.4

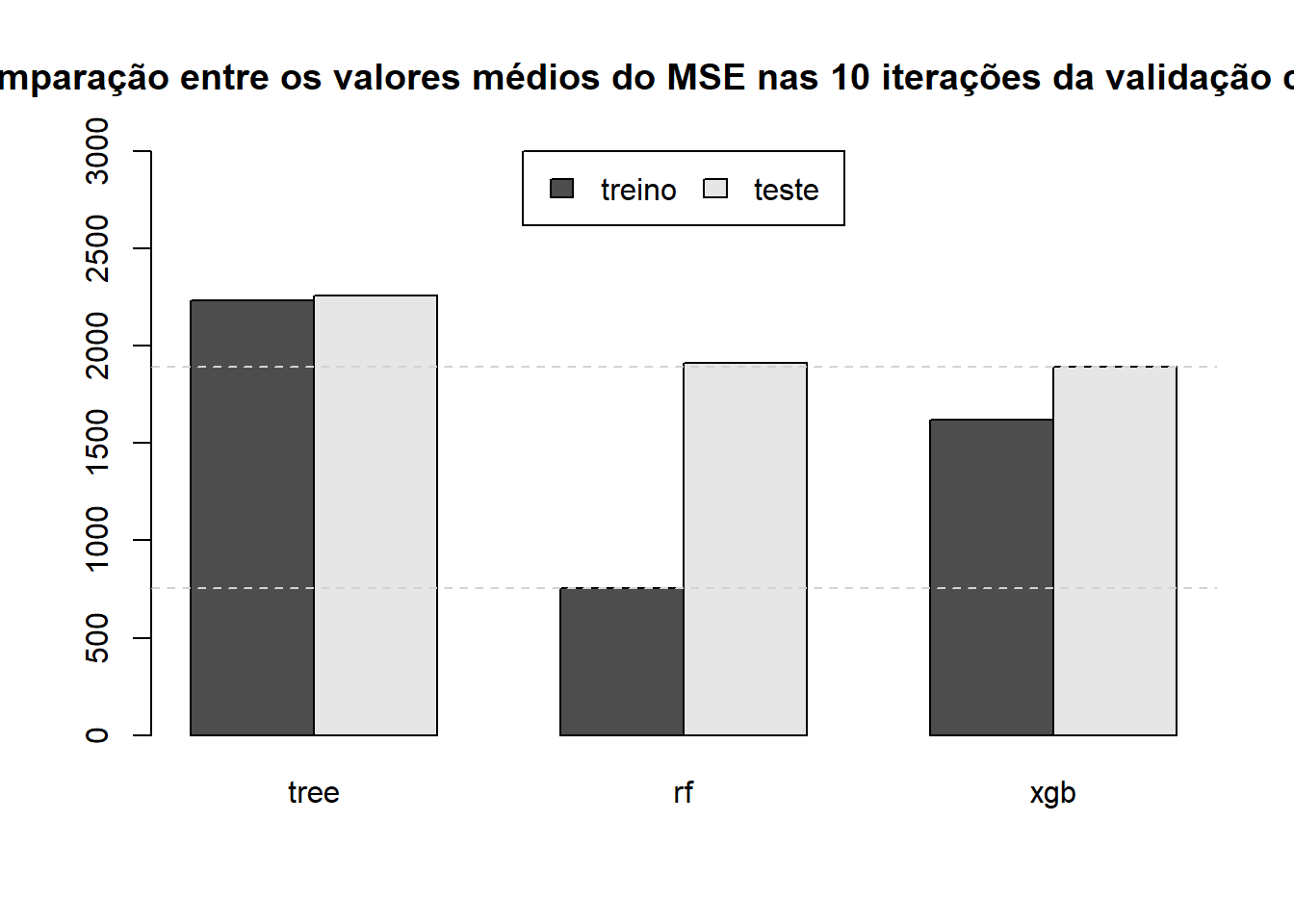
Por fim é possível comparar os diferentes modelos de árvores de regressão, definidos por diferentes hiperparâmetros. Essa comparação será feita a partir do valor médio dos MSE entre as 10 iterações da validação cruzada, tanto na medida de treino quanto na medida de teste.

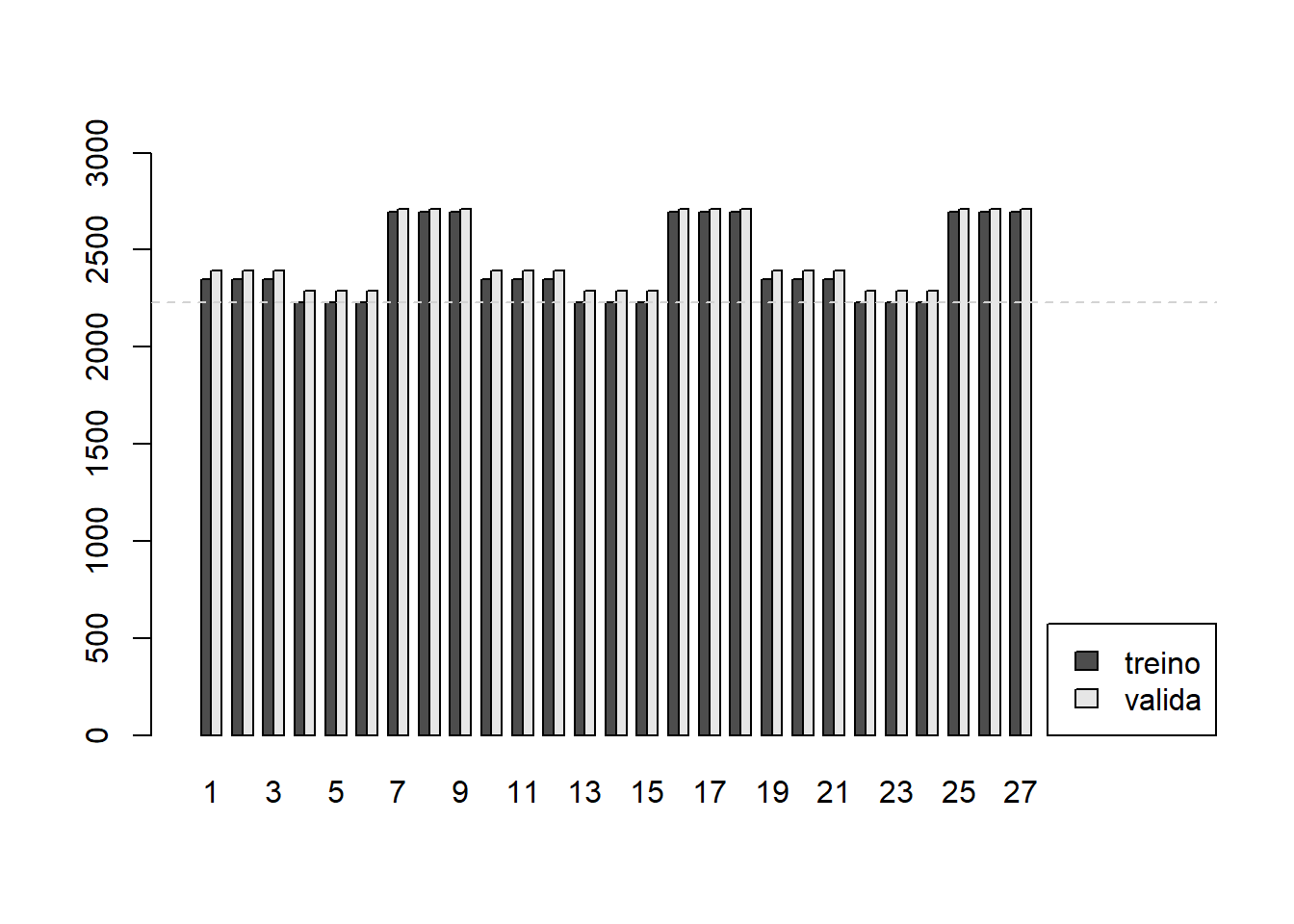
Escolha dos hiperparâmetros para a Floresta Aleatória

A validação cruzada será usada agora para analisar o desempenho do modelo de Floresta Aleatória para diferentes valores dos seus hiperparâmetros. Os hiérparâmeros considerados nesta comparação são: mtry, que indica o número de ´covariáveis sorteadas a cada partição das árvores; e ntree, que é o número de árvores na floresta. O código a seguir mostra os valores considerados para cada um dos dois parâmetros.

param = list(mtry = c(2,3,4),
             ntree = c(100,500))

param_combination_rf = expand.grid(param, stringsAsFactors = FALSE)

O objeto param_combination_rf guarda todas as combinações dos valores definidos para cada parâmetro.

param_combination_rf
##   mtry ntree
## 1    2   100
## 2    3   100
## 3    4   100
## 4    2   500
## 5    3   500
## 6    4   500

A validação cruzada aqui executada é semelhante aquela feita para o modelo de Árvores de Regressão.

MSE_treino_rf = matrix(NA,nrow = nrow(param_combination_rf),ncol = K)
MSE_valida_rf = matrix(NA,nrow = nrow(param_combination_rf),ncol = K)

for(i in 1:nrow(param_combination_rf)){
  
  for(f in 1:K){
    
    valida = base_treino |> dplyr::slice(indices_folds[[f]])
    treino = base_treino |> dplyr::slice(-indices_folds[[f]])

    rf <- randomForest(NU_MEDIA_RED ~ .,
                  data = treino,
                  mtry = param_combination_rf$mtry[i],
                  ntree = param_combination_rf$ntree[i]
                  )

    prev_treino = predict(rf,newdata = treino)
    prev_valida = predict(rf,newdata = valida)

    MSE_treino_rf[i,f] = mean((prev_treino - treino$NU_MEDIA_RED)^2)
    MSE_valida_rf[i,f] = mean((prev_valida - valida$NU_MEDIA_RED)^2)
  }
}

A tabela a seguir apresenta os valores o erro médio quadrático (MSE) na base de treinamento. Estes são os valores guardados em MSE_treino_rf. As primeiras colunas indicam a combinação dos parâmetros considerada em cada linha.

(#tab:VC_MSE_rf_treino)MSE na base de treinamento
mtry ntree Parte 1 Parte 2 Parte 3 Parte 4 Parte 5 Parte 6 Parte 7 Parte 8 Parte 9 Parte 10
2 100 771.1 762.4 746.0 759.9 736.7 765.1 736.8 751.7 744.7 740.3
3 100 485.1 477.0 483.8 485.8 476.6 482.5 474.9 485.3 484.9 475.1
4 100 412.8 404.1 411.7 407.5 407.6 404.9 404.4 409.0 410.1 401.4
2 500 758.4 739.2 744.5 746.5 749.3 744.3 734.0 746.7 750.1 735.2
3 500 481.4 469.0 473.6 474.0 471.5 474.6 468.9 477.7 476.8 470.1
4 500 404.7 393.7 397.0 400.3 397.3 397.6 394.4 398.6 400.9 394.9

Para melhor analisar esses números podem ser usadas estatísticas referentes aos \(k\) valores para cada combinação de parâmetros.

result_treino_rf = apply(MSE_treino_rf, MARGIN = 1, summary)
Tabela 6.5: Estatísticas para o MSE na base de treinamento
Parâmetros 1 Parâmetros 2 Parâmetros 3 Parâmetros 4 Parâmetros 5 Parâmetros 6
Min. 736.7 474.9 401.4 734.0 468.9 393.7
1st Qu. 741.4 476.7 404.5 740.5 470.5 395.4
Median 748.8 483.2 407.5 745.5 473.8 397.4
Mean 751.5 481.1 407.3 744.8 473.8 397.9
3rd Qu. 761.7 485.1 409.8 748.6 476.2 399.9
Max. 771.1 485.8 412.8 758.4 481.4 404.7

O mesmo pode ser feito para os resultados do MSE na base de validação.

(#tab:VC_MSE_rf_valida)MSE na base de validação
mtry ntree Parte 1 Parte 2 Parte 3 Parte 4 Parte 5 Parte 6 Parte 7 Parte 8 Parte 9 Parte 10
2 100 1591.2 2001.3 1963.0 1954.0 1819.8 1923.8 2029.4 1865.3 1903.1 2016.2
3 100 1551.5 1976.3 1901.9 1906.0 1784.8 1897.6 1993.6 1811.6 1865.4 1954.0
4 100 1535.5 1986.6 1874.2 1880.4 1758.1 1874.7 1990.7 1808.6 1849.7 1946.6
2 500 1591.6 1984.6 1947.9 1948.2 1782.4 1904.1 2001.4 1839.8 1908.4 1996.2
3 500 1542.0 1966.5 1887.8 1876.0 1752.7 1880.2 1983.1 1807.4 1842.2 1941.6
4 500 1531.9 1974.8 1861.4 1864.1 1750.0 1865.4 1983.1 1788.8 1829.2 1936.5 
result_valida_rf = apply(MSE_valida_rf, MARGIN = 1, summary)
Tabela 6.6: Estatísticas para o MSE na base de validação
Parâmetros 1 Parâmetros 2 Parâmetros 3 Parâmetros 4 Parâmetros 5 Parâmetros 6
Min. 1591.2 1551.5 1535.5 1591.6 1542.0 1531.9
1st Qu. 1874.7 1825.0 1818.9 1855.9 1816.1 1798.9
Median 1938.9 1899.8 1874.5 1928.1 1878.1 1862.7
Mean 1906.7 1864.3 1850.5 1890.5 1848.0 1838.5
3rd Qu. 1991.7 1942.0 1930.0 1975.5 1928.2 1918.7
Max. 2029.4 1993.6 1990.7 2001.4 1983.1 1983.1

Escolha dos hiperparâmetros para o XGBoost

A validação cruzada será usada novamente para analisar os valores dos seus hiperparâmetros, agora para o XGBoost. Os hiérparâmeros considerados nesta comparação são: eta, que é a taxa de aprendizagem; subsample, que é a proporção da base sorteada para a construção de cada árvore de correção; e nrounds, o número de árvores construídas.

param = list(eta = c(0.1,0.05,0.15),
             subsample = c(0.5, 0.4, 0.6),
             nrounds = c(100, 200))

param_combination_xgb = expand.grid(param, stringsAsFactors = FALSE) 
mat_treino = model.matrix(~. , data = base_treino |> select(-NU_MEDIA_RED))[,-1]

O objeto param_combination_xgb guarda todas as combinações dos valores definidos para cada parâmetro. A validação cruzada aqui executada é semelhante às duas já realizadas anteriormente.

MSE_treino_xgb = matrix(NA,nrow = nrow(param_combination_xgb),ncol = K)
MSE_valida_xgb = matrix(NA,nrow = nrow(param_combination_xgb),ncol = K)

for(i in 1:nrow(param_combination_xgb)){
  print(i)
  for(f in 1:K){
    print(f)
    valida = mat_treino[indices_folds[[f]],]
    treino = mat_treino[-indices_folds[[f]],]
    
    y_treino = (base_treino |> dplyr::slice(-indices_folds[[f]]))$NU_MEDIA_RED
    y_valida = (base_treino |> dplyr::slice(indices_folds[[f]]))$NU_MEDIA_RED
    
    xgb <- xgboost(data = treino,
                   label = y_treino,
                   objective = "reg:squarederror",
                   nrounds = param_combination_xgb$nrounds[i],
                   subsample = param_combination_xgb$subsample[i],
                   eta = param_combination_xgb$eta[i])
    
    
    prev_treino = predict(xgb,newdata = treino)
    prev_valida = predict(xgb,newdata = valida)
    
    MSE_treino_xgb[i,f] = mean((prev_treino - y_treino)^2)
    MSE_valida_xgb[i,f] = mean((prev_valida - y_valida)^2)
  }
}

A tabela a seguir apresenta os valores o erro médio quadrático (MSE) na base de treinamento. Estes são os valores guardados em MSE_treino_xgb. As primeiras colunas indicam a combinação dos parâmetros considerada em cada linha.

(#tab:VC_MSE_xgb_treino)MSE na base de treinamento
eta subsample nrounds Parte 1 Parte 2 Parte 3 Parte 4 Parte 5 Parte 6 Parte 7 Parte 8 Parte 9 Parte 10
0.10 0.5 100 1350.6 1331.7 1334.8 1323.6 1340.5 1324.8 1318.2 1326.5 1327.8 1322.6
0.05 0.5 100 1616.6 1581.5 1584.8 1592.5 1588.1 1581.7 1581.2 1596.0 1596.4 1570.0
0.15 0.5 100 1191.7 1157.0 1155.7 1167.8 1164.9 1162.6 1156.4 1150.7 1173.8 1153.3
0.10 0.4 100 1388.0 1345.7 1367.1 1358.3 1351.0 1360.8 1343.0 1355.9 1366.7 1337.3
0.05 0.4 100 1638.1 1595.8 1606.0 1617.0 1614.5 1608.6 1596.7 1620.0 1616.6 1591.2
0.15 0.4 100 1224.4 1193.7 1209.7 1213.6 1223.3 1209.8 1194.3 1212.8 1220.1 1214.8
0.10 0.6 100 1334.0 1287.9 1320.1 1324.4 1323.0 1301.3 1301.8 1304.7 1318.3 1292.5
0.05 0.6 100 1596.9 1562.6 1568.1 1568.3 1583.9 1582.0 1563.3 1571.7 1572.9 1553.2
0.15 0.6 100 1148.3 1139.6 1153.2 1144.6 1135.6 1127.6 1142.0 1151.4 1146.1 1140.4
0.10 0.5 200 1022.0 979.2 999.3 997.7 996.3 1003.5 992.5 1009.7 1000.4 997.5
0.05 0.5 200 1340.9 1308.9 1315.5 1317.1 1316.1 1328.6 1302.9 1312.9 1306.3 1317.6
0.15 0.5 200 820.5 783.2 805.0 810.2 797.6 785.9 785.3 795.5 797.9 813.7
0.10 0.4 200 1065.8 1011.8 1033.1 1042.0 1046.7 1030.2 1031.1 1034.4 1022.7 1030.3
0.05 0.4 200 1364.5 1323.0 1343.3 1344.2 1335.8 1341.4 1330.4 1338.1 1334.3 1328.7
0.15 0.4 200 874.7 817.8 838.0 849.9 853.3 834.5 844.2 844.2 863.6 849.9
0.10 0.6 200 976.6 955.5 975.4 970.7 974.4 960.6 978.3 977.7 969.7 974.3
0.05 0.6 200 1320.6 1288.1 1292.2 1296.5 1312.4 1305.6 1302.9 1310.2 1299.4 1293.6
0.15 0.6 200 775.2 760.7 761.4 769.9 752.6 770.4 770.6 760.1 786.4 770.1

Para melhor analisar esses números podem ser usadas estatísticas referentes aos \(k\) valores para cada combinação de parâmetros.

result_treino_xgb = apply(MSE_treino_xgb, MARGIN = 1, summary)
Tabela 6.7: Estatísticas para o MSE na base de treinamento
Parâmetros 1 Parâmetros 2 Parâmetros 3 Parâmetros 4 Parâmetros 5 Parâmetros 6 Parâmetros 7 Parâmetros 8 Parâmetros 9 Parâmetros 10 Parâmetros 11 Parâmetros 12 Parâmetros 13 Parâmetros 14 Parâmetros 15 Parâmetros 16 Parâmetros 17 Parâmetros 18
Min. 1318.2 1570.0 1150.7 1337.3 1591.2 1193.7 1287.9 1553.2 1127.6 979.2 1302.9 783.2 1011.8 1323.0 817.8 955.5 1288.1 752.6
1st Qu. 1323.9 1581.6 1155.9 1347.0 1599.0 1209.7 1301.4 1564.5 1139.8 996.6 1309.9 788.3 1030.2 1331.4 839.5 970.0 1294.3 760.9
Median 1327.2 1586.5 1159.8 1357.1 1611.6 1213.2 1311.5 1570.0 1143.3 998.5 1315.8 797.8 1032.1 1337.0 847.1 974.4 1301.1 770.0
Mean 1330.1 1588.9 1163.4 1357.4 1610.4 1211.6 1310.8 1572.3 1142.9 999.8 1316.7 799.5 1034.8 1338.4 847.0 971.3 1302.1 767.8
3rd Qu. 1334.0 1595.1 1167.1 1365.2 1616.9 1218.7 1322.3 1579.7 1147.8 1002.7 1317.5 808.9 1040.1 1342.8 852.5 976.3 1309.1 770.6
Max. 1350.6 1616.6 1191.7 1388.0 1638.1 1224.4 1334.0 1596.9 1153.2 1022.0 1340.9 820.5 1065.8 1364.5 874.7 978.3 1320.6 786.4

O mesmo pode ser feito para os resultados do MSE na base de validação.

(#tab:VC_MSE_xgb_valida)MSE na base de validação
eta subsample nrounds Parte 1 Parte 2 Parte 3 Parte 4 Parte 5 Parte 6 Parte 7 Parte 8 Parte 9 Parte 10
0.10 0.5 100 1597.5 1944.5 1894.3 1833.4 1793.0 1904.7 1982.2 1805.6 1884.3 1963.8
0.05 0.5 100 1595.8 1961.4 1939.5 1961.0 1823.0 1857.9 2021.9 1849.9 1924.4 2013.5
0.15 0.5 100 1605.5 2011.0 1903.5 1860.4 1880.3 1896.1 1972.8 1877.3 1927.3 2006.1
0.10 0.4 100 1602.1 1965.1 1924.8 1844.2 1832.5 1853.4 1992.3 1840.9 1916.5 1979.4
0.05 0.4 100 1626.2 1974.8 1941.4 1969.1 1784.4 1903.4 2011.4 1846.2 1921.7 2030.6
0.15 0.4 100 1628.3 1972.8 1927.6 1910.4 1815.3 1913.7 2020.1 1853.8 1937.4 1948.7
0.10 0.6 100 1599.9 1919.7 1916.8 1853.8 1754.1 1896.2 1968.6 1818.9 1875.8 1971.8
0.05 0.6 100 1587.0 1968.2 1921.5 1950.6 1813.8 1871.6 2000.1 1836.3 1922.3 2019.6
0.15 0.6 100 1567.4 1968.5 1935.2 1831.6 1832.0 1910.6 1939.5 1811.6 1876.6 1994.7
0.10 0.5 200 1556.5 1943.7 1963.1 1887.3 1819.9 1912.3 1967.8 1805.9 1910.4 1998.7
0.05 0.5 200 1534.6 1900.8 1863.4 1827.5 1755.5 1872.0 1950.3 1796.7 1848.7 1956.9
0.15 0.5 200 1630.4 2014.8 1973.4 1975.4 1880.0 2081.8 2060.1 1853.7 1919.5 2083.5
0.10 0.4 200 1575.5 1990.1 1967.3 1936.5 1783.3 1914.1 1939.3 1841.2 1908.8 2013.4
0.05 0.4 200 1545.8 1928.9 1872.9 1831.6 1769.3 1855.4 1949.1 1808.1 1877.6 1983.8
0.15 0.4 200 1652.0 2129.2 1995.4 1981.5 1886.5 2074.6 2051.1 2007.9 1937.8 2194.0
0.10 0.6 200 1580.9 2014.2 1918.9 1874.0 1780.6 1970.1 1972.4 1811.0 1887.9 1995.7
0.05 0.6 200 1520.4 1950.8 1877.2 1846.4 1759.5 1854.1 1934.1 1765.2 1848.7 1948.2
0.15 0.6 200 1664.9 2056.2 1958.2 1903.4 1821.3 1961.0 2025.6 1883.1 1981.3 2004.0 
result_valida_xgb = apply(MSE_valida_xgb, MARGIN = 1, summary)
Tabela 6.8: Estatísticas para o MSE na base de validação
Parâmetros 1 Parâmetros 2 Parâmetros 3 Parâmetros 4 Parâmetros 5 Parâmetros 6 Parâmetros 7 Parâmetros 8 Parâmetros 9 Parâmetros 10 Parâmetros 11 Parâmetros 12 Parâmetros 13 Parâmetros 14 Parâmetros 15 Parâmetros 16 Parâmetros 17 Parâmetros 18
Min. 1597.5 1595.8 1605.5 1602.1 1626.2 1628.3 1599.9 1587.0 1567.4 1556.5 1534.6 1630.4 1575.5 1545.8 1652.0 1580.9 1520.4 1664.9
1st Qu. 1812.5 1851.9 1878.1 1841.7 1860.5 1867.9 1827.6 1845.1 1831.7 1836.8 1804.4 1889.9 1858.1 1813.9 1948.7 1826.7 1785.5 1888.1
Median 1889.3 1931.9 1899.8 1884.9 1931.6 1920.7 1886.0 1921.9 1893.6 1911.3 1856.1 1974.4 1925.3 1864.1 2001.7 1903.4 1851.4 1959.6
Mean 1860.3 1894.8 1894.0 1875.1 1900.9 1892.8 1857.6 1889.1 1866.8 1876.5 1830.6 1947.3 1887.0 1842.2 1991.0 1880.6 1830.5 1925.9
3rd Qu. 1934.5 1961.3 1961.4 1955.0 1973.3 1945.9 1919.0 1963.8 1938.4 1958.3 1893.6 2048.8 1960.3 1916.0 2068.7 1971.8 1919.9 1998.3
Max. 1982.2 2021.9 2011.0 1992.3 2030.6 2020.1 1971.8 2019.6 1994.7 1998.7 1956.9 2083.5 2013.4 1983.8 2194.0 2014.2 1950.8 2056.2

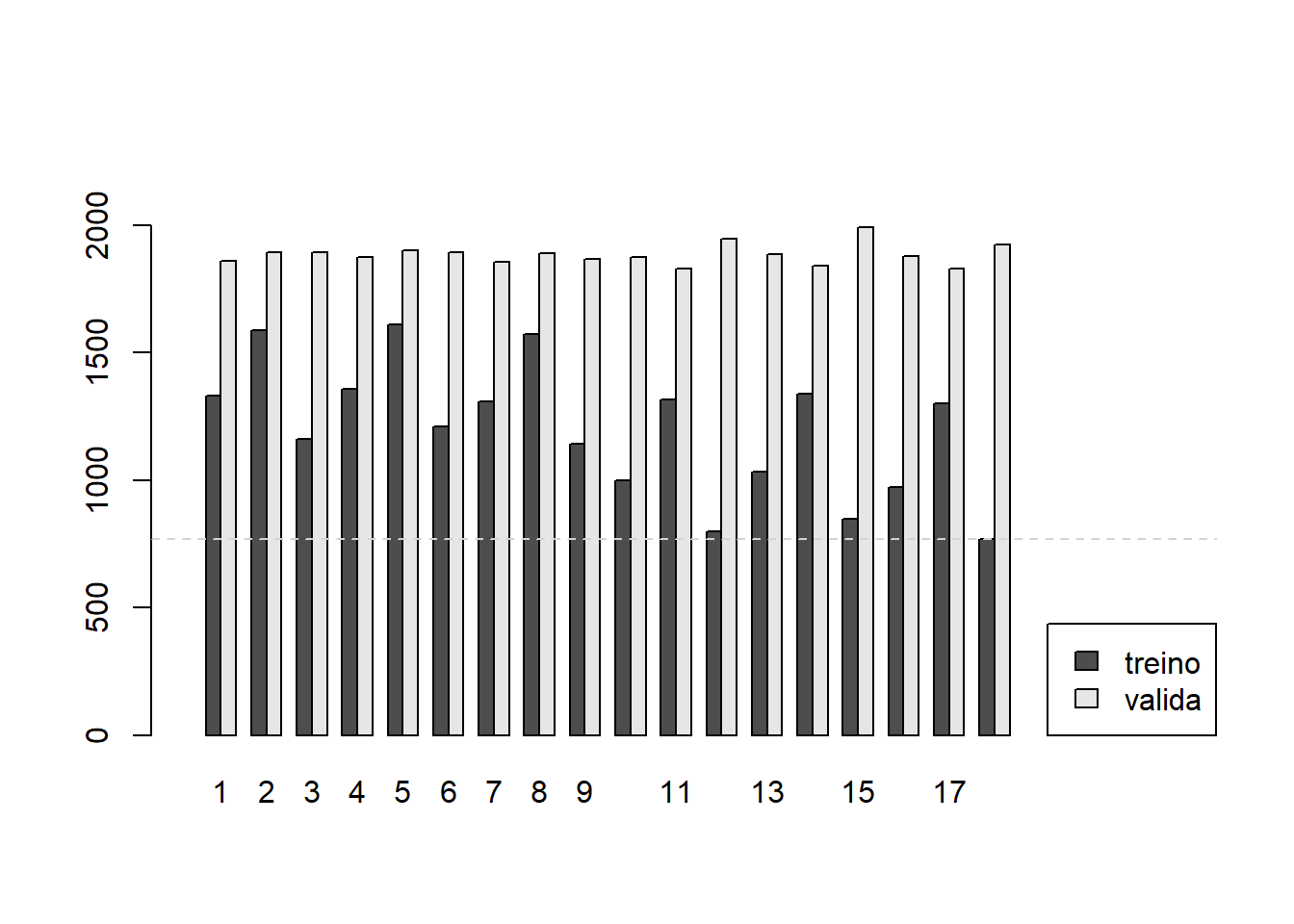
6.3 Comparação entre os modelos de Árvore de Regressão, Floresta Aleatória e XGBoost

Vamos considerar para cada modelo treinado a melhor combinação de parâmetros.

treino_tree = result_treino_tree[,4]
valida_tree = result_valida_tree[,4]

treino_rf = result_treino_rf[,1]
valida_rf = result_valida_rf[,1]

treino_xgb = result_treino_xgb[,5]
valida_xgb = result_valida_xgb[,5]
mat = matrix(c(treino_tree,treino_rf,treino_xgb),
             byrow = FALSE,ncol=3)
colnames(mat) = c("tree","rf","xgb")
rownames(mat) = rownames(result_treino_xgb)
mat  |>
  kbl(caption = "´Estatísticas para o MSE na base de treino para os melhores modelos de Árvore de Regressão, Floresta Aleatória e XGBoost")  |>
  kable_styling(bootstrap_options = "striped", full_width = F, position = "left")
Tabela 6.9: ´Estatísticas para o MSE na base de treino para os melhores modelos de Árvore de Regressão, Floresta Aleatória e XGBoost
tree rf xgb
Min. 2202.218 736.6918 1591.195
1st Qu. 2217.729 741.4094 1599.003
Median 2226.856 748.8028 1611.569
Mean 2229.472 751.4585 1610.447
3rd Qu. 2238.882 761.7413 1616.877
Max. 2263.169 771.1445 1638.111 
matv = matrix(c(valida_tree,valida_rf,valida_xgb),
             byrow = FALSE,ncol=3)
colnames(matv) = c("tree","rf","xgb")
rownames(matv) = rownames(result_valida_xgb)
matv  |>
  kbl(caption = "´Estatísticas para o MSE na base de validação para os melhores modelos de Árvore de Regressão, Floresta Aleatória e XGBoost")  |>
  kable_styling(bootstrap_options = "striped", full_width = F, position = "left")
Tabela 6.10: ´Estatísticas para o MSE na base de validação para os melhores modelos de Árvore de Regressão, Floresta Aleatória e XGBoost
tree rf xgb
Min. 1944.010 1591.247 1626.174
1st Qu. 2257.810 1874.725 1860.489
Median 2350.297 1938.881 1931.554
Mean 2290.393 1906.707 1900.914
3rd Qu. 2371.070 1991.726 1973.344
Max. 2390.767 2029.401 2030.590

6.4 Estimativas finais na base de teste

Vamos ver agora como será o desemenho em treino e teste dos modelos finais. Espera-se uma diferença semelhante àquela encontrada na validação cruzada.

tree <- rpart(NU_MEDIA_RED ~ ., 
                data = base_treino,
                control = rpart.control(minsplit = param_combination_tree$minsplit[4], 
                                        cp = param_combination_tree$cp[4], 
                                        maxdepth = param_combination_tree$maxdepth[4]))
prev_treino_tree_RD = predict(tree,newdata = base_treino)
MSE_treino_tree_RD = mean((prev_treino_tree_RD - base_treino$NU_MEDIA_RED)^2)
prev_teste_tree_RD = predict(tree,newdata = base_teste)
MSE_teste_tree_RD = mean((prev_teste_tree_RD - base_teste$NU_MEDIA_RED)^2)
saveRDS(object = tree,file="tree_final.rds")
 rf <- randomForest(NU_MEDIA_RED ~ .,
                  data = base_treino,
                  mtry = param_combination_rf$mtry[1],
                  ntree = param_combination_rf$ntree[1]
                  )

prev_treino_rf_RD = predict(rf,newdata = base_treino)
MSE_treino_rf_RD = mean((prev_treino_rf_RD - base_treino$NU_MEDIA_RED)^2)
prev_teste_rf_RD = predict(rf,newdata = base_teste)
MSE_teste_rf_RD = mean((prev_teste_rf_RD - base_teste$NU_MEDIA_RED)^2)
saveRDS(object = rf,file="rf_final.rds")
xgb <- xgboost(data = mat_treino,
               label = base_treino$NU_MEDIA_RED ,
               objective = "reg:squarederror",
               nrounds = param_combination_xgb$nrounds[5],
               subsample = param_combination_xgb$subsample[5],
               eta = param_combination_xgb$eta[5])
    

prev_treino_xgb_RD = predict(xgb,newdata = mat_treino)
MSE_treino_xgb_RD = mean((prev_treino_xgb_RD - base_treino$NU_MEDIA_RED)^2)
prev_teste_xgb_RD = predict(xgb,newdata = M_X_teste)
MSE_teste_xgb_RD = mean((prev_teste_xgb_RD - base_teste$NU_MEDIA_RED)^2)
saveRDS(object = xgb,file="xgb_final.rds")

References

———. 2022. Caret: Classification and Regression Training. https://CRAN.R-project.org/package=caret.