Capítulo 7 Como analisar a performance de Modelos de Classificação?
Neste capítulo serão abordadas formas de mensurar a qualidade do ajuste de modelos de classificação, assim como formas de investigar a existência ou não de sobreajuste.
library(tidyverse)
library(rpart)
library(randomForest)
library(xgboost)
base_treino = readRDS(file="arquivos-de-trabalho/base_treino_final.rds")
base_treino = base_treino |>
mutate(NOTA_RED = ifelse(base_treino$NU_MEDIA_RED>=600,"boa","regular")) |>
select(-c(CO_ESCOLA_EDUCACENSO,
NO_ESCOLA_EDUCACENSO,
NU_MEDIA_CN,NU_MEDIA_CH,
NU_MEDIA_LP,NU_MEDIA_MT,
NU_TAXA_PARTICIPACAO,
NU_PARTICIPANTES,
NU_MEDIA_RED))
base_treino$NOTA_RED = as.factor(base_treino$NOTA_RED)7.1 Classificação Binária
Começamos supondo que já temos modelos de classificação. Para o caso deste texto, vamos usar como exemplo a previsão da nota de redação de cada escola entre “boa” e “regular”.
tree_RED = readRDS(file="arquivos-de-trabalho/tree_RED.rds")
rf_RED = readRDS(file = "arquivos-de-trabalho/rf_RED.rds")
xgb_RED = readRDS(file = "arquivos-de-trabalho/xgb_RED.rds")Suponha que um modelo de classificação \(k\) realizou a previsão \(\hat{y}_i^k\) para a i-ésima observação da variável \(Y\). Como se trata de um modelo de classificação binário, as classes serão 0 ou 1 e a previsão \(\hat{y}_i^k\) é um valor no intervalo \((0,1)\) que indica o quanto provavél a observação está de pertencer à classe de referência, que é a classe 1.
Começamos com a previsão na base de treino. Primeiro para os modelos de árvore e de floresta aleatóra.
prev_treino_tree = predict(tree_RED,
newdata = base_treino,
type = "prob")
prev_treino_rf = predict(rf_RED,
newdata = base_treino,
type = "prob")E depois para o modelo XGBoost, que tem uma sintaxe diferente dos anteriores.
M_treino = model.matrix(~., data = base_treino)[,-1]
X_treino = M_treino[,-45]
Y_treino = M_treino[,45]
prev_treino_xgb = predict(xgb_RED,newdata = X_treino,type = "prob")Podemos também encontrar previsões para os dados de teste. Nesete caso primeiro devem ser lidos e tratados os dados de teste para então realizar as previsões.
base_teste = readRDS(file="arquivos-de-trabalho/base_teste.rds")
base_teste = base_teste |> select(-c(NU_MEDIA_OBJ,
NU_MEDIA_TOT,
NU_ANO,
NU_TAXA_APROVACAO,
CO_UF_ESCOLA,
CO_MUNICIPIO_ESCOLA,
NO_MUNICIPIO_ESCOLA))
base_teste = base_teste |>
mutate(NU_TAXA_REPROVACAO = replace_na(NU_TAXA_REPROVACAO, mean(base_treino$NU_TAXA_REPROVACAO, na.rm = TRUE)),
NU_TAXA_ABANDONO = replace_na(NU_TAXA_ABANDONO, mean(base_treino$NU_TAXA_ABANDONO, na.rm = TRUE)),
PC_FORMACAO_DOCENTE = replace_na(PC_FORMACAO_DOCENTE, mean(base_treino$PC_FORMACAO_DOCENTE, na.rm = TRUE))
)
base_teste = base_teste |>
mutate(NOTA_RED = ifelse(base_teste$NU_MEDIA_RED>=600,"boa","regular")) |>
select(-c(CO_ESCOLA_EDUCACENSO,
NO_ESCOLA_EDUCACENSO,
NU_MEDIA_CN,NU_MEDIA_CH,
NU_MEDIA_LP,NU_MEDIA_MT,
NU_TAXA_PARTICIPACAO,
NU_PARTICIPANTES,
NU_MEDIA_RED))Previsão na base de teste.
prev_teste_tree = predict(tree_RED,
newdata = base_teste,
type = "prob")
prev_teste_rf = predict(rf_RED,newdata = base_teste,type = "prob")
M_teste = model.matrix(~., data = base_teste)[,-1]
X_teste = M_teste[,-45]
Y_teste = M_teste[,45]
prev_teste_xgb = predict(xgb_RED,newdata = X_teste,type = "prob")7.1.1 Medidas de qualidade do ajuste
Existem algumas possíveis medidas de desempenho para modelos de classificação. As duas mais usuais são a Entropia Cruzada e a Área embaixo da Curva ROC.
7.1.1.1 Entropia Cruzada
Uma vez conhecidas as previsões para a variável resposta, considerando que essas previsões serão uma probbailidade da observação pertencer a classe de referência, é possível calcular a EC (entropia cruzada) e usar essa medida como comparação de qualidade do ajuste.
\[ EC = - \dfrac{1}{N} \sum_{i=1}^N \left( y_i\ln(\hat{y}_i) + (1-y_i)\ln(1-\hat{y}_i) \right) \]
Veja que quando \(\hat{y}_i\) está próximo da classe real a parcela \(i\) do somatório é bem pequena e quando \(\hat{y}_i\) está próxima da classificação errada, a parcela \(i\) do somatório é bem grande. Quanto menor a EC, melhor o ajuste do modelo.
EC = function(real,previsao){
n = length(real)
ec = -sum(ifelse(real_treino==1,log(previsao),log(1-previsao)))/n
return(ec)
}Veja que a conta acima pode ser feita considerando tanto a base de treino quanto a base de teste. Em geral vamos medir a EC para as duas bases.
Valores da EC para a base de treino.
real_treino = ifelse(base_treino$NOTA_RED == "regular",1,0)
EC_treino_tree = EC(real_treino,prev_treino_tree [,2])
EC_treino_rf = EC(real_treino,prev_treino_rf [,2])
EC_treino_xgb = EC(real_treino,prev_treino_xgb )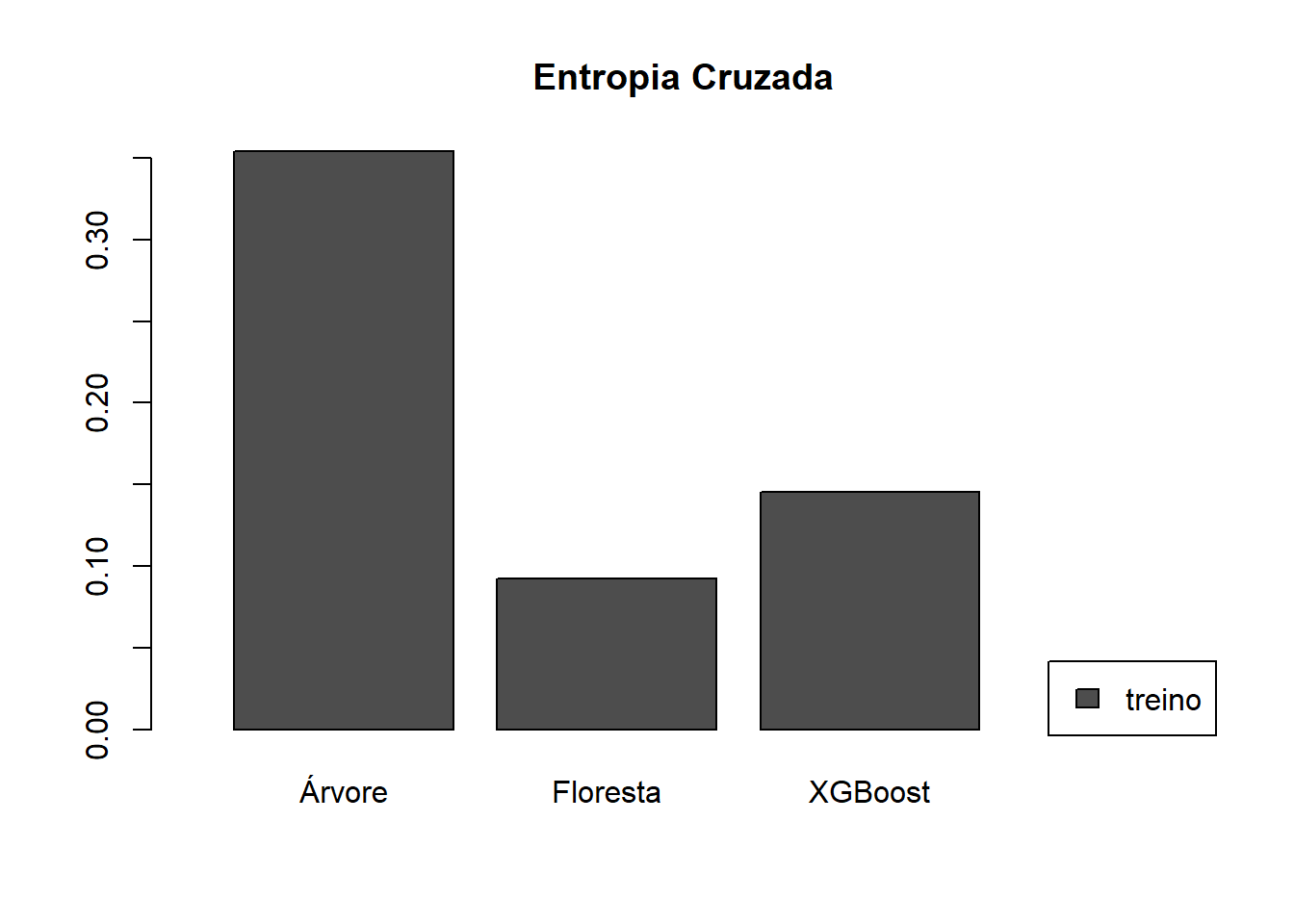
Valores da EC para a base de teste.
#referencia = classe regular
real_teste = ifelse(base_teste$NOTA_RED == "regular",1,0)
EC_teste_tree = EC(real_teste,prev_teste_tree [,2])
EC_teste_rf = EC(real_teste,prev_teste_rf [,2])
EC_teste_xgb = EC(real_teste,prev_teste_xgb )## Árvore Floresta XGBoost
## EC no treino 0.3541748 0.09241238 0.1453029
## EC no teste 2.9102760 Inf 4.6709746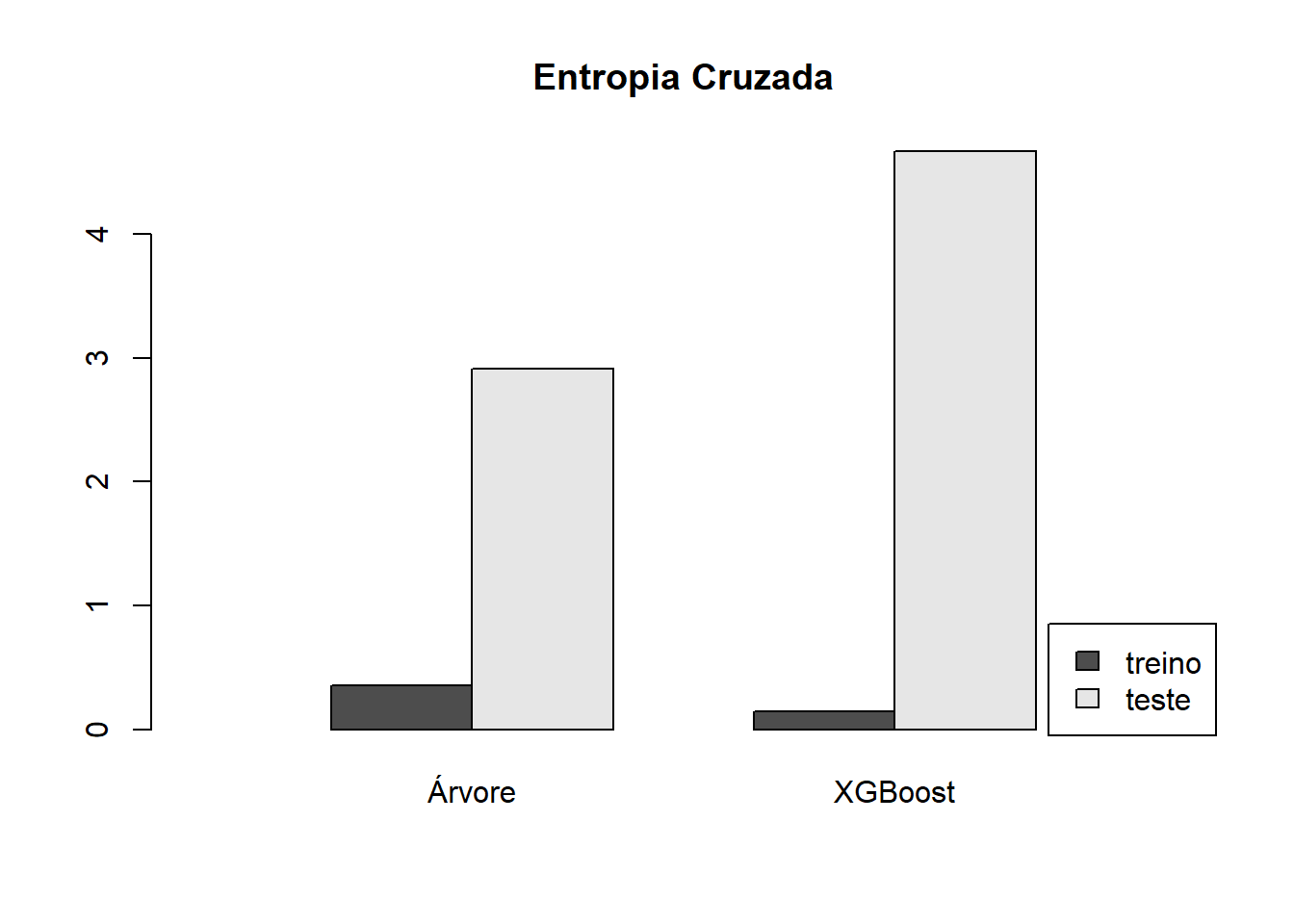
7.1.1.2 Curva ROC
Mas qual valor escolher para \(q\)? A escolha do valor de corte \(q\) pode ser feita a partir da curva ROC. A curva ROC é uma curva parametrizada pelo valor \(q\) definida por:
\[ ROC(q) = (1-Especificidade(q)\ , \ Sensibilidade(q)) \ , \quad q \in (0,1) \]
A figura a seguir mostra como em geral é a curva ROC.
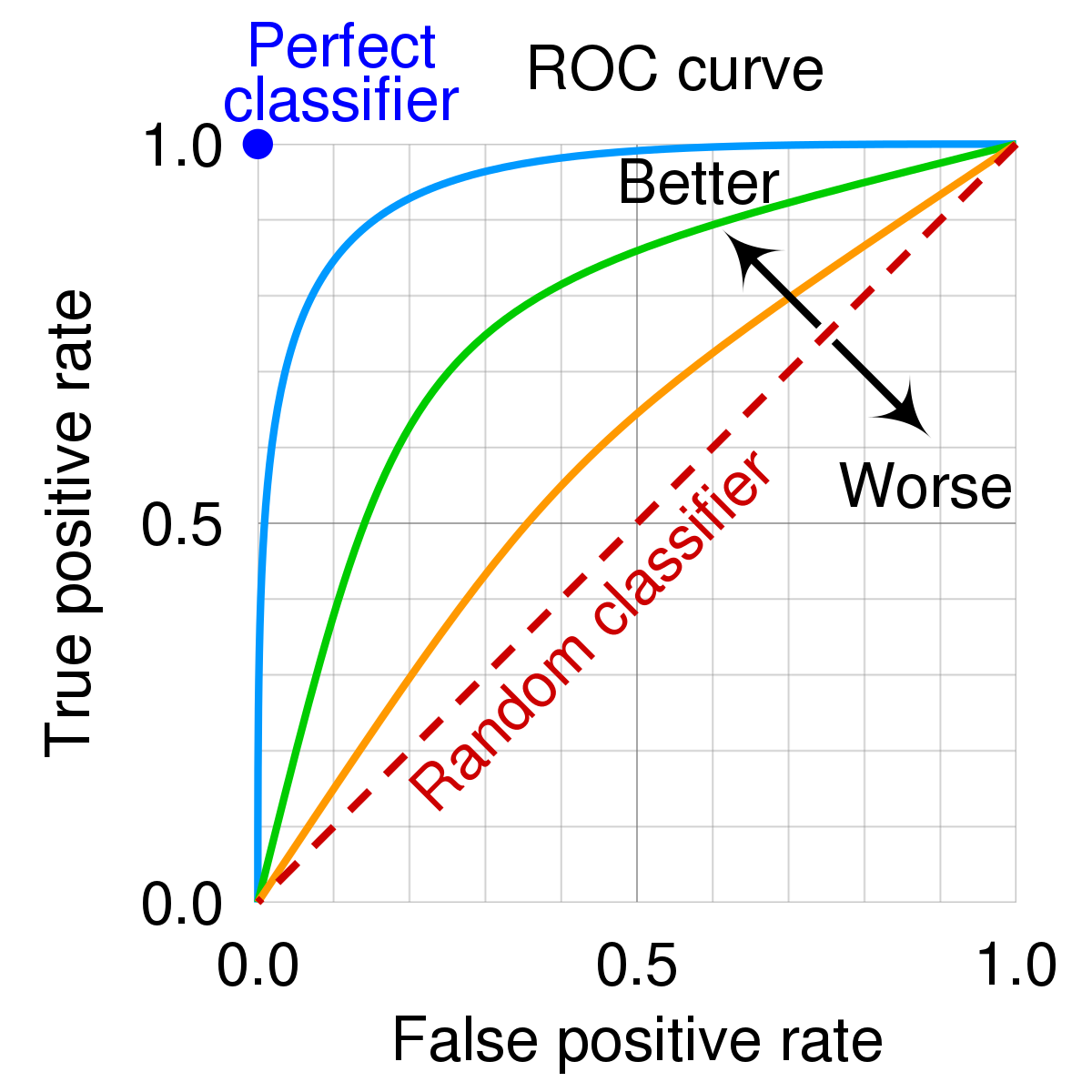
Figura 7.1: Curva ROC
Vamos escolher o valor de \(q\) que gerou o ponto mais acima e à esquerda. O valor da área embaixo da curva ROC (AUC) também é uma medida de qualidade do ajuste bastante usada.
library(pROC)
roc_tree_treino = roc(response = real_treino,
predictor = prev_treino_tree[,2])
plot.roc(roc_tree_treino,print.auc = TRUE)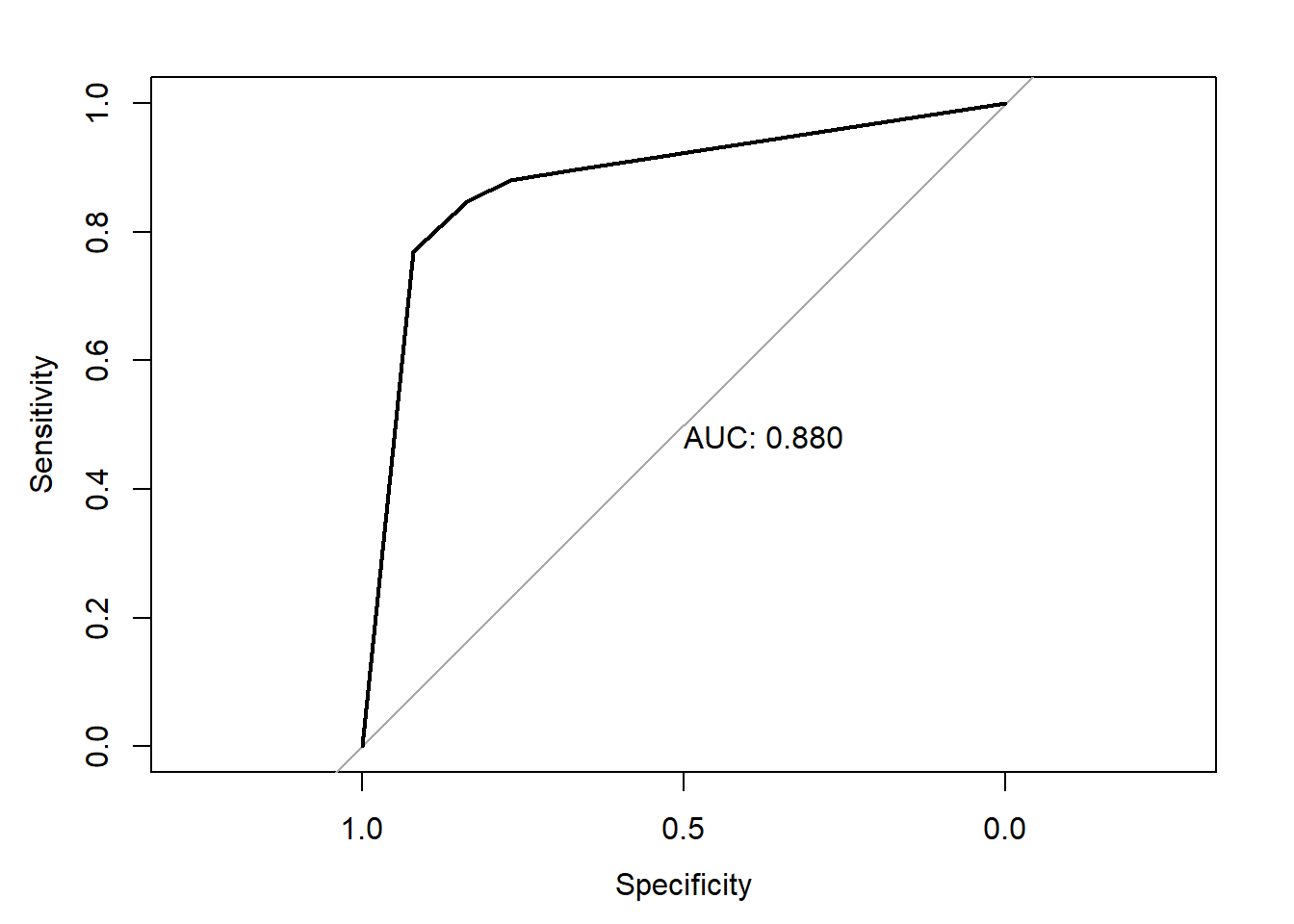
roc_rf_treino = roc(response = real_treino,
predictor = prev_treino_rf[,2])
plot.roc(roc_rf_treino,print.auc = TRUE)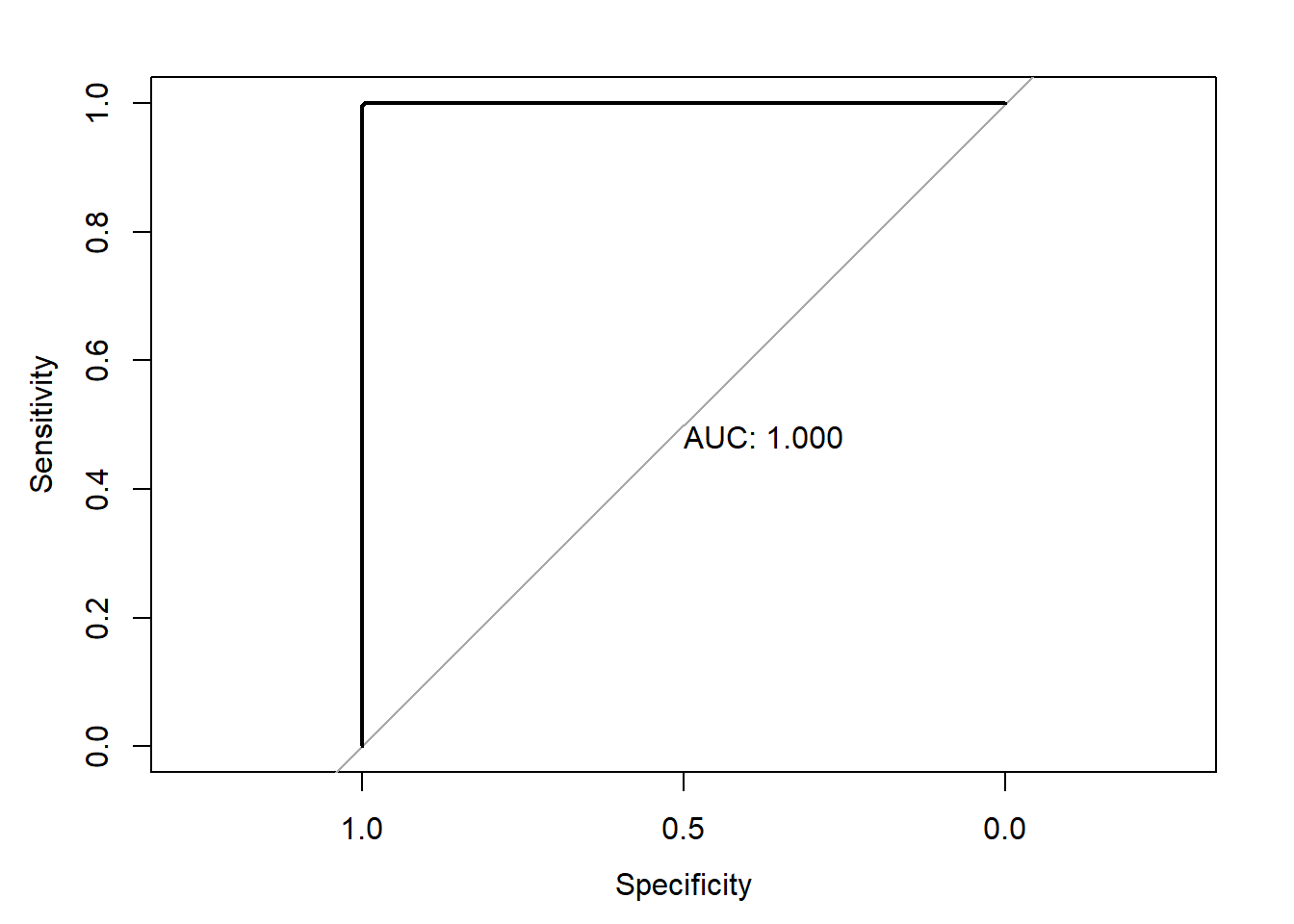
## Area under the curve: 1roc_xgb_treino = roc(response = real_treino,
predictor = prev_treino_xgb )
plot.roc(roc_xgb_treino,print.auc = TRUE)
## Area under the curve: 0.9906A medida de AUC também pode ser encntrada para a base de teste.
roc_tree_teste = roc(response = real_teste,
predictor = prev_teste_tree [,2])
plot.roc(roc_tree_teste,print.auc = TRUE)
## Area under the curve: 0.8746roc_rf_teste = roc(response = real_teste,
predictor = prev_teste_rf [,2])
plot.roc(roc_rf_teste,print.auc = TRUE)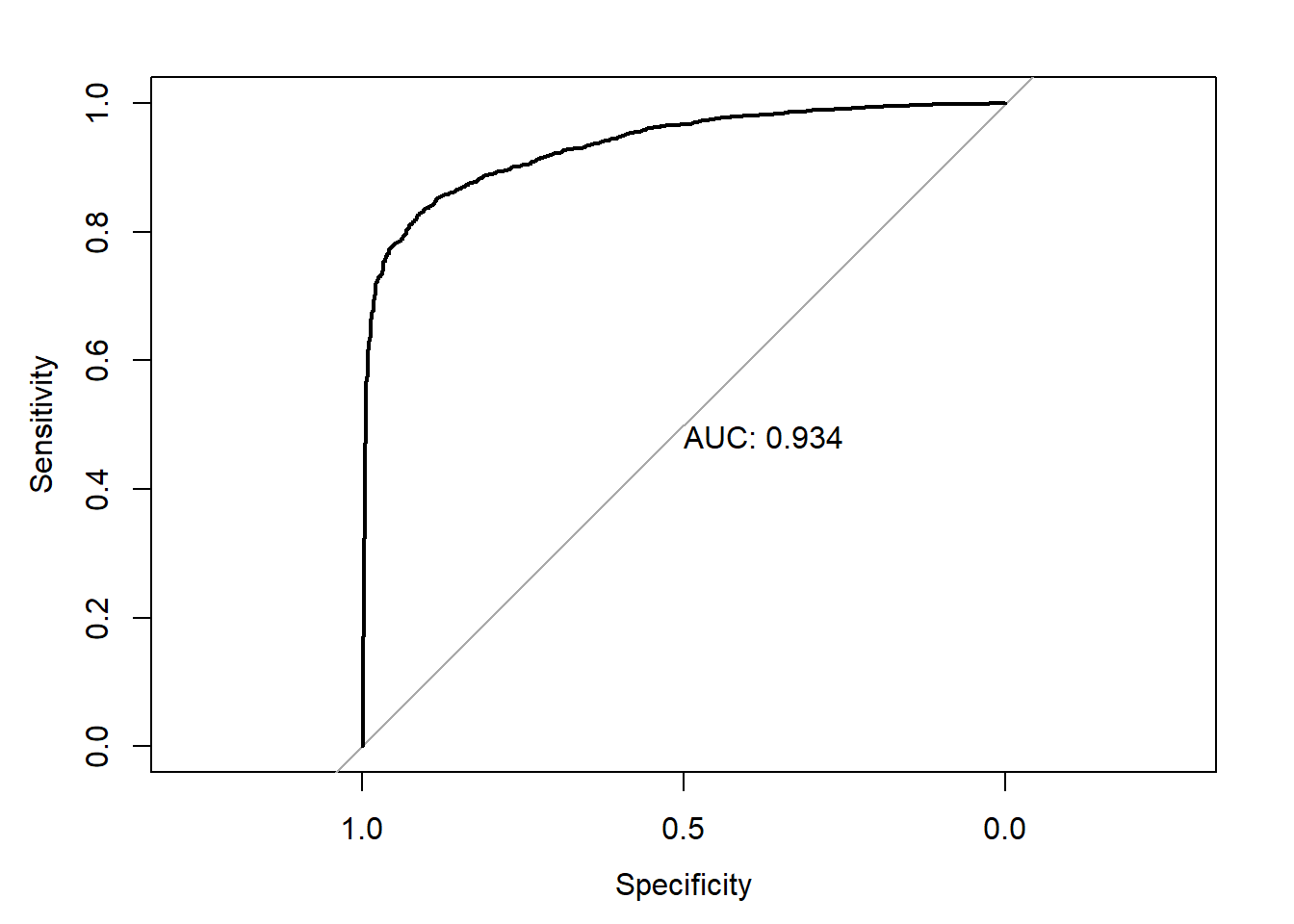
## Area under the curve: 0.9342roc_xgb_teste = roc(response = real_teste,
predictor = prev_teste_xgb )
plot.roc(roc_xgb_teste,print.auc = TRUE)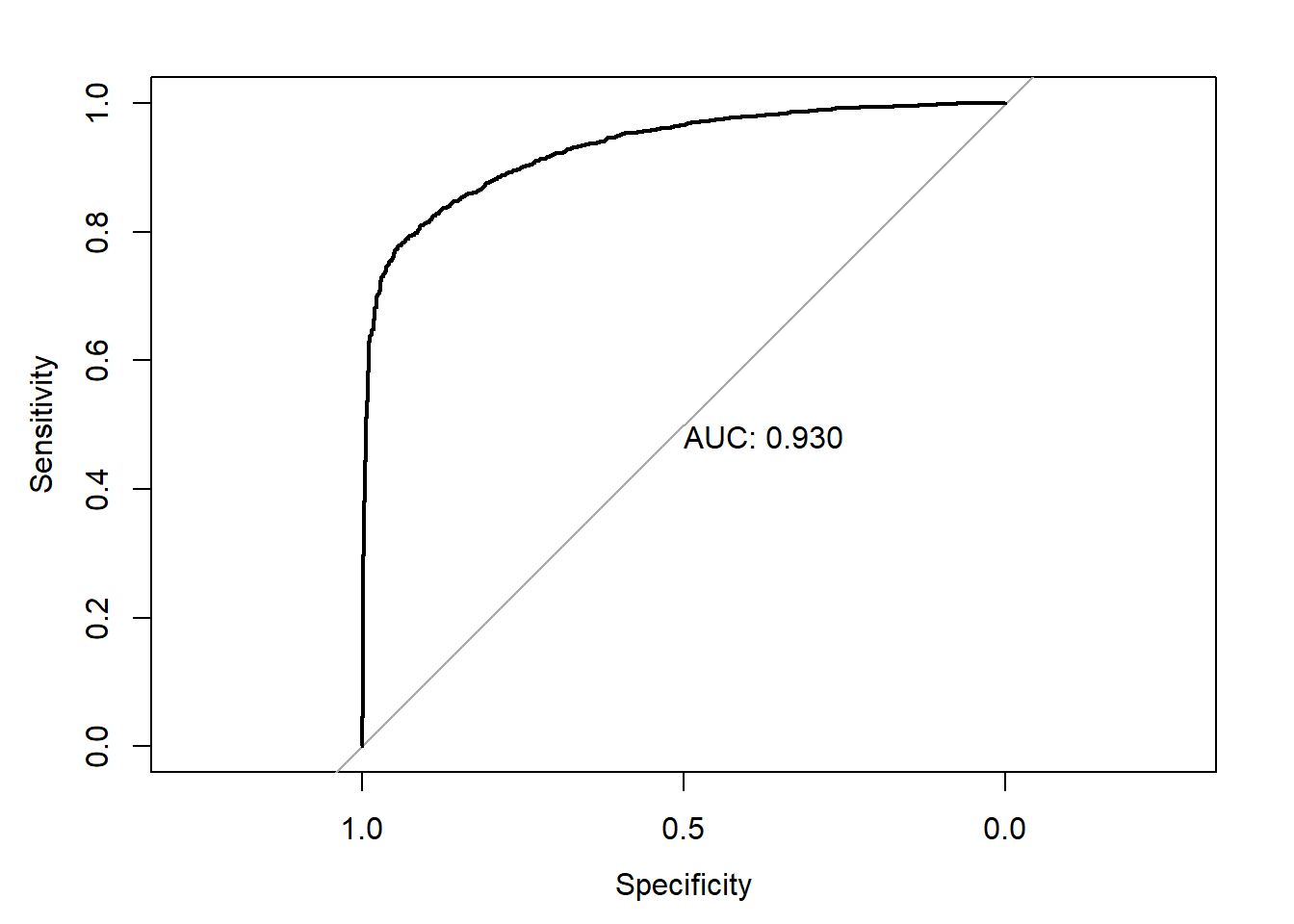
## Area under the curve: 0.93df2 = data.frame(arvore = roc_tree_teste$auc,
floresta = roc_tree_teste$auc,
xgboost = roc_tree_teste$auc)
rownames(df2) = c("AUC no teste")
colnames(df2) = c("Árvore","Floresta","XGBoost")
rbind(df,df2)## Árvore Floresta XGBoost
## AUC no treino 0.8797110 0.9999862 0.9906083
## AUC no teste 0.8745771 0.8745771 0.8745771barplot(as.matrix(rbind(df,df2)),
beside = TRUE,
ylim=c(0,1),
xlim = c(0,11),
legend.text = c("treino","teste"),
names.arg = c("Árvore","Floresta","XGBoost"),
args.legend = list(x="bottomright"),
main = "Entropia Cruzada")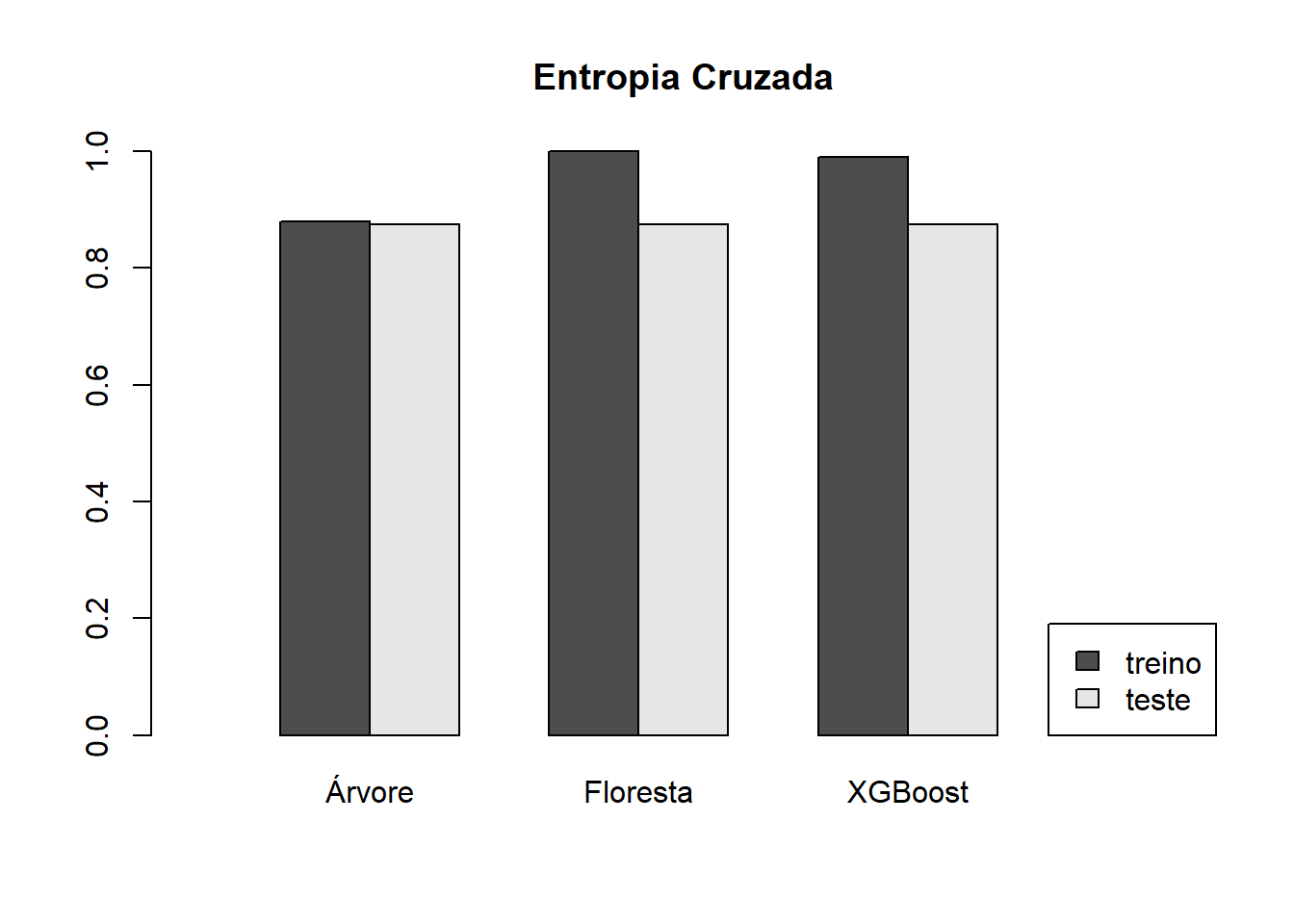
7.1.2 Validação Cruzada para Classificação
7.1.2.1 Árvres de Classificação
param = list(minsplit = c(20,10,50),
cp = c(0.01, 0.005, 0.02),
maxdepth = c(30,20,10))
param_combination_tree = expand.grid(param, stringsAsFactors = FALSE) AUC_treino_tree = matrix(NA,nrow = nrow(param_combination_tree),ncol = K)
AUC_valida_tree = matrix(NA,nrow = nrow(param_combination_tree),ncol = K)
for(i in 1:nrow(param_combination_tree)){
print(i)
for(f in 1:K){
print(f)
valida = base_treino |> dplyr::slice(indices_folds[[f]])
treino = base_treino |> dplyr::slice(-indices_folds[[f]])
tree <- rpart(NOTA_RED ~ .,
data = treino,
method = "class",
control = rpart.control(minsplit = param_combination_tree$minsplit[i],
cp = param_combination_tree$cp[i],
maxdepth = param_combination_tree$maxdepth[i]))
prev_treino = predict(tree,newdata = treino,type="prob")
prev_valida = predict(tree,newdata = valida,type="prob")
classe_treino = treino$NOTA_RED
classe_valida = valida$NOTA_RED
AUC_treino_tree[i,f] = (roc(response = classe_treino, predictor = prev_treino[,2]))$auc
AUC_valida_tree[i,f] = (roc(response = classe_valida, predictor = prev_valida[,2]))$auc
}
}result_treino_tree =
apply(AUC_treino_tree, MARGIN = 1, summary)
result_valida_tree =
apply(AUC_valida_tree, MARGIN = 1, summary)mat = matrix(c(
result_treino_tree["Mean",],
result_valida_tree["Mean",]),
byrow = TRUE,
nrow=2)
barplot(mat,
names.arg = 1:nrow(param_combination_tree),
beside = T,
ylim = c(0,1),
xlim = c(0,90),
main="AUC para Validação Cruzada do Árvore",
legend.text = c("treino","valida"),
args.legend = list(x="bottomright"))
abline(h=min(mat),lty=2,col="lightgray")
7.1.2.2 Floresta Aleatória
param = list(mtry = c(2,3,4),
ntree = c(100,500))
param_combination_rf = expand.grid(param, stringsAsFactors = FALSE)AUC_treino_rf = matrix(NA,nrow = nrow(param_combination_rf),ncol = K)
AUC_valida_rf = matrix(NA,nrow = nrow(param_combination_rf),ncol = K)
for(i in 1:nrow(param_combination_rf)){
print(i)
for(f in 1:K){
print(f)
valida = base_treino |> dplyr::slice(indices_folds[[f]])
treino = base_treino |> dplyr::slice(-indices_folds[[f]])
rf <- randomForest(NOTA_RED ~ .,
data = treino,
mtry = param_combination_rf$mtry[i],
ntree = param_combination_rf$ntree[i])
prev_treino = predict(rf,newdata = treino,type="prob")
prev_valida = predict(rf,newdata = valida,type="prob")
classe_treino = treino$NOTA_RED
classe_valida = valida$NOTA_RED
AUC_treino_rf[i,f] = (roc(response = classe_treino, predictor = prev_treino[,2]))$auc
AUC_valida_rf[i,f] = (roc(response = classe_valida, predictor = prev_valida[,2]))$auc
}
}result_treino_rf =
apply(AUC_treino_rf, MARGIN = 1, summary)
result_valida_rf =
apply(AUC_valida_rf, MARGIN = 1, summary)
7.1.2.3 XGBoost
param = list(eta = c(0.1,0.05,0.15),
subsample = c(0.5, 0.4, 0.6),
nrounds = c(100, 200))
param_combination_xgb = expand.grid(param, stringsAsFactors = FALSE) AUC_treino_xgb = matrix(NA,nrow = nrow(param_combination_xgb),ncol = K)
AUC_valida_xgb = matrix(NA,nrow = nrow(param_combination_xgb),ncol = K)
for(i in 1:nrow(param_combination_xgb)){
print(i)
for(f in 1:K){
print(f)
valida = base_treino |> dplyr::slice(indices_folds[[f]])
treino = base_treino |> dplyr::slice(-indices_folds[[f]])
M_treino = model.matrix(~., data = treino)[,-1]
X_treino = M_treino[,-45]
Y_treino = M_treino[,45]
M_valida = model.matrix(~., data = valida)[,-1]
X_valida = M_valida[,-45]
Y_valida = M_valida[,45]
xgb <- xgboost(data = X_treino,
label = Y_treino,
objective = "binary:logistic",
nrounds = param_combination_xgb$nrounds[i],
subsample = param_combination_xgb$subsample[i],
eta = param_combination_xgb$eta[i])
prev_treino = predict(xgb,newdata = X_treino,type="prob")
prev_valida = predict(xgb,newdata = X_valida,type="prob")
classe_treino = treino$NOTA_RED
classe_valida = valida$NOTA_RED
AUC_treino_xgb[i,f] = (roc(response = classe_treino, predictor = prev_treino))$auc
AUC_valida_xgb[i,f] = (roc(response = classe_valida, predictor = prev_valida))$auc
}
}AUC_treino_xgb = readRDS(file="AUC_treino_xgb.rds")
AUC_valida_xgb = readRDS(file="AUC_valida_xgb.rds")result_treino_xgb =
apply(AUC_treino_xgb, MARGIN = 1, summary)
result_valida_xgb =
apply(AUC_valida_xgb, MARGIN = 1, summary)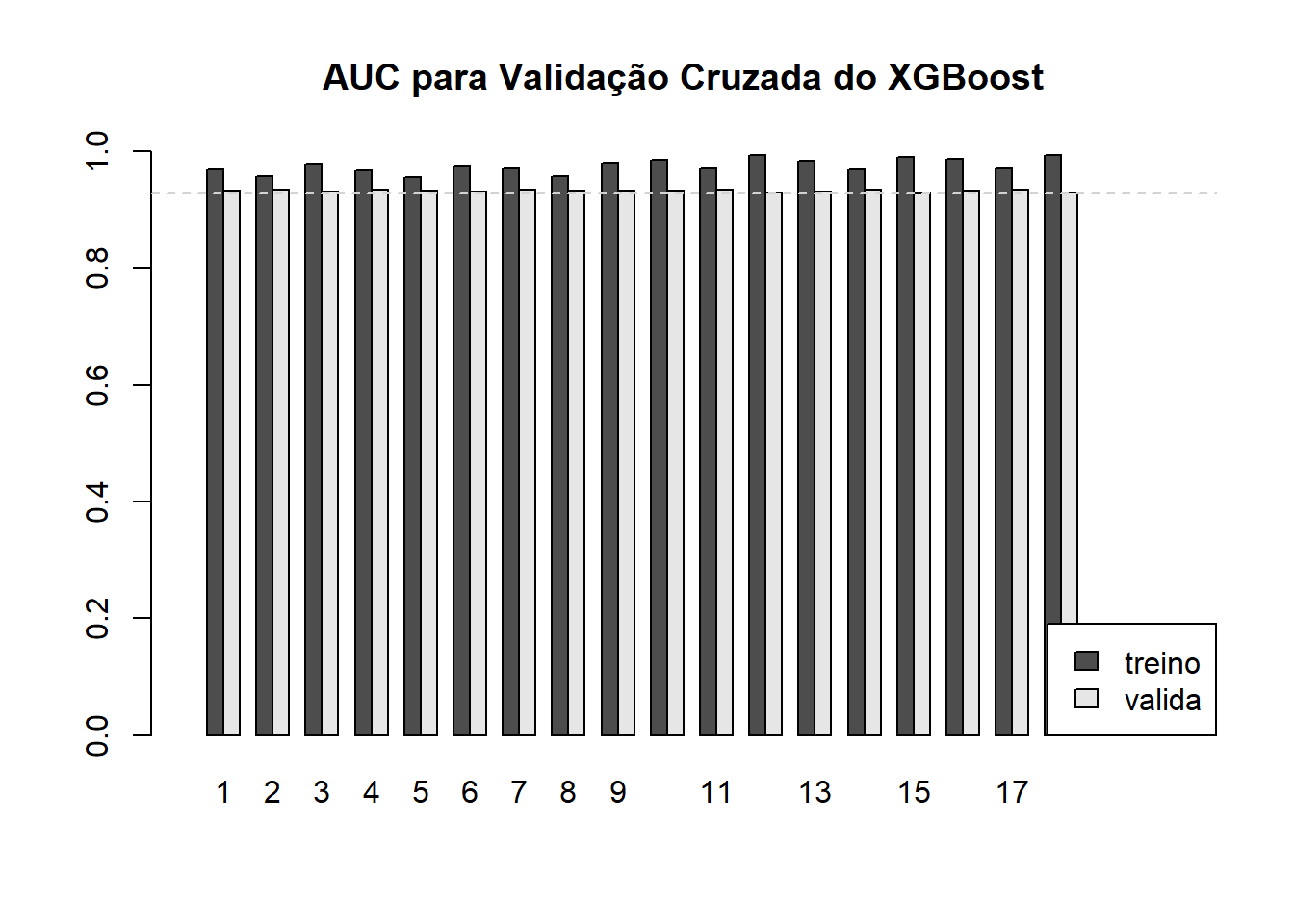
7.1.3 Medidas de qualidade da classificação
Mas como medir a capacidade de classificação?
7.1.3.1 Matriz de Confusão
Os modelos de classificação retornam como previsão para a \(i\)-ésima observação um valor \(\hat{y}_i^k \in (0,1)\). Mas o objetivo final é prever a classe da observação \(i\).
Uma vez escolhido o modelo de classificação que melhor se ajusta aos dados, podemos realizar agora a previsão da classe para a observação \(i\). Suponha o seguinte critério para a escolha da classe prevista:
\[ \hat{c}_i = \left\{ \begin{array}{ll} 0 & \hbox{, se } \hat{y}_i < q\\ 1 & \hbox{, se } \hat{y}_i \ge q\\ \end{array} \right. \]
O valor de \(q\) pode ser determinado a partir da curva ROC para os dados de treino.
Para entender melhor a capacidade de previsão do modelo de classificação queremos encontrar as medidas de Acurácia, Precisão, Sensibilidade, entre outras. Estas medidas serão definidas a partir da matriz de confusão, que é formada pela contagem de classes reais e classes previstas.
| Real 0 | Real 1 | |
| Prev 0 | VN | FN |
| Prev 1 | FP | VP |
VN = verdadeiro negativo = número de observações iguais a 0 que foram previstas como 0.
FN = falso negativo = número de observações iguais a 1 que foram previstas como 0.
FP = falso positivo = número de observações iguais a 0 que foram previstas como 1.
VP = verdadeiro positivo = número de observações iguais a 1 que foram previstas como 1.
Quanto maior o número de observações na diagonal principal da matriz de confusão melhor. A partir desta tabela podemos calcular algumas medidas de desempenho para os modelos de classificação.
7.1.3.2 Acurácia
A acurácia é a taxa de acerto do classificador. Ela é a proporção de predições corretas dentre todas as predições.
\[ Acurácia = \dfrac{V P + V N}{V P + V N + FP + FN} \]
7.1.3.3 Sensibilidade (ou Recall)
A sensibilidade é a taxa de acerto dos casos positivos. Ela é a proporção de casos positivos que foram corretamente classificados como positivos.
\[ Sensibilidade = \dfrac{VP}{VP + FN} \]
7.1.3.4 Especificidade
A especificidade é a taxa de acerto dos casos negativos. Ela é a proporção dos casos negativos que foram corretamente classificados como negativos.
\[ Especificidade = \dfrac{VN}{V N + FP} \]
7.1.3.5 Precisão
A precisão é a taxa de acerto dentras previsões positivas. Ela é a proporção dos acertos entre os casos classificados como positivos.
\[ Precisão = \dfrac{VP}{V P + FP} \]
7.1.3.6 F1-Score
É uma combinação da Precisão e do Recall que na prática é a média harmônica entre a Precisão e o Recall.
\[ F1-score = 2 \dfrac{Precisão \times Recall}{Precisão + Recall} \]
q_tree = coords(roc_tree_treino, "best", ret = "threshold")[1,1]
prev_class_treino_tree =
ifelse(prev_treino_tree[,2] > q_tree,"regular","boa")
tabela = table(prev=prev_class_treino_tree,
real_treino=classe_treino)
CM_treino_tree = confusionMatrix(tabela)
CM_treino_tree## Confusion Matrix and Statistics
##
## real_treino
## prev boa regular
## boa 3056 1936
## regular 266 6442
##
## Accuracy : 0.8118
## 95% CI : (0.8046, 0.8188)
## No Information Rate : 0.7161
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.5981
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Sensitivity : 0.9199
## Specificity : 0.7689
## Pos Pred Value : 0.6122
## Neg Pred Value : 0.9603
## Prevalence : 0.2839
## Detection Rate : 0.2612
## Detection Prevalence : 0.4267
## Balanced Accuracy : 0.8444
##
## 'Positive' Class : boa
## q_rf = coords(roc_rf_treino, "best", ret = "threshold")[1,1]
prev_class_treino_rf =
ifelse(prev_treino_rf[,2] > q_rf,"regular","boa")
tabela = table(prev=prev_class_treino_rf,
real_treino=classe_treino)
CM_treino_rf = confusionMatrix(tabela)
CM_treino_rf## Confusion Matrix and Statistics
##
## real_treino
## prev boa regular
## boa 3320 24
## regular 2 8354
##
## Accuracy : 0.9978
## 95% CI : (0.9967, 0.9985)
## No Information Rate : 0.7161
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.9945
##
## Mcnemar's Test P-Value : 3.814e-05
##
## Sensitivity : 0.9994
## Specificity : 0.9971
## Pos Pred Value : 0.9928
## Neg Pred Value : 0.9998
## Prevalence : 0.2839
## Detection Rate : 0.2838
## Detection Prevalence : 0.2858
## Balanced Accuracy : 0.9983
##
## 'Positive' Class : boa
## q_xgb = coords(roc_xgb_treino, "best", ret = "threshold")[1,1]
prev_class_treino_xgb =
ifelse(prev_treino_xgb > q_xgb,"regular","boa")
tabela = table(prev=prev_class_treino_xgb,
real_treino=classe_treino)
CM_treino_xgb = confusionMatrix(tabela)
CM_treino_xgb## Confusion Matrix and Statistics
##
## real_treino
## prev boa regular
## boa 3173 471
## regular 149 7907
##
## Accuracy : 0.947
## 95% CI : (0.9428, 0.951)
## No Information Rate : 0.7161
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.8734
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Sensitivity : 0.9551
## Specificity : 0.9438
## Pos Pred Value : 0.8707
## Neg Pred Value : 0.9815
## Prevalence : 0.2839
## Detection Rate : 0.2712
## Detection Prevalence : 0.3115
## Balanced Accuracy : 0.9495
##
## 'Positive' Class : boa
## Os resultados podem ser encontrados também para os dados de teste.
prev_class_teste_tree =
ifelse(prev_teste_tree[,2] > q_tree,"regular","boa")
tabela = table(prev=prev_class_teste_tree,
real_treino=classe_teste)
CM_teste_tree = confusionMatrix(tabela)
CM_teste_tree## Confusion Matrix and Statistics
##
## real_treino
## prev boa regular
## boa 1029 632
## regular 87 2150
##
## Accuracy : 0.8155
## 95% CI : (0.803, 0.8276)
## No Information Rate : 0.7137
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.6062
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Sensitivity : 0.9220
## Specificity : 0.7728
## Pos Pred Value : 0.6195
## Neg Pred Value : 0.9611
## Prevalence : 0.2863
## Detection Rate : 0.2640
## Detection Prevalence : 0.4261
## Balanced Accuracy : 0.8474
##
## 'Positive' Class : boa
## prev_class_teste_rf =
ifelse(prev_teste_rf[,2] > q_rf,"regular","boa")
tabela = table(prev=prev_class_teste_rf,
real_treino=classe_teste)
CM_teste_rf = confusionMatrix(tabela)
CM_teste_rf## Confusion Matrix and Statistics
##
## real_treino
## prev boa regular
## boa 844 274
## regular 272 2508
##
## Accuracy : 0.8599
## 95% CI : (0.8486, 0.8707)
## No Information Rate : 0.7137
## P-Value [Acc > NIR] : <2e-16
##
## Kappa : 0.6574
##
## Mcnemar's Test P-Value : 0.9659
##
## Sensitivity : 0.7563
## Specificity : 0.9015
## Pos Pred Value : 0.7549
## Neg Pred Value : 0.9022
## Prevalence : 0.2863
## Detection Rate : 0.2165
## Detection Prevalence : 0.2868
## Balanced Accuracy : 0.8289
##
## 'Positive' Class : boa
## prev_class_teste_xgb =
ifelse(prev_teste_xgb > q_xgb,"regular","boa")
tabela = table(prev=prev_class_teste_xgb,
real_treino=classe_teste)
CM_teste_xgb = confusionMatrix(tabela)
CM_teste_xgb## Confusion Matrix and Statistics
##
## real_treino
## prev boa regular
## boa 909 369
## regular 207 2413
##
## Accuracy : 0.8522
## 95% CI : (0.8407, 0.8632)
## No Information Rate : 0.7137
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.6535
##
## Mcnemar's Test P-Value : 1.969e-11
##
## Sensitivity : 0.8145
## Specificity : 0.8674
## Pos Pred Value : 0.7113
## Neg Pred Value : 0.9210
## Prevalence : 0.2863
## Detection Rate : 0.2332
## Detection Prevalence : 0.3279
## Balanced Accuracy : 0.8409
##
## 'Positive' Class : boa
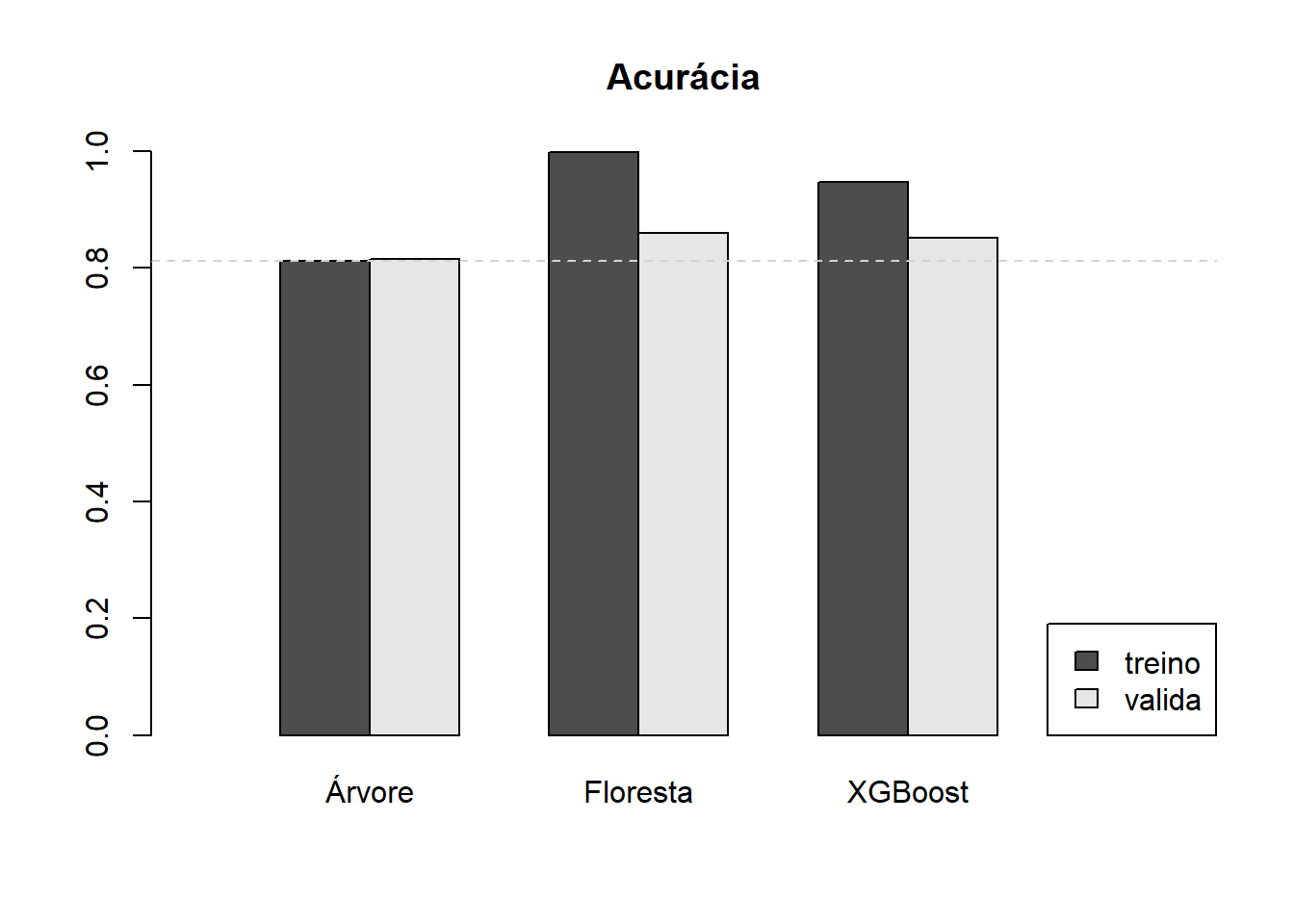
## Usando, por exemplo, a acurácia como medida de comparação, temos o seguinte resultado.
7.2 Classificação Multiclasses
Suponha um problema de classificação que, em vez de cada instância (observação) pertencer a uma de duas possíveis classes, ela pertence a uma entre \(k\) possíveis classes.
base_treino = readRDS(file="arquivos-de-trabalho/base_treino_final.rds")
base_treino = base_treino |>
mutate(NOTA_RED =
ifelse(
base_treino$NU_MEDIA_RED>600,"boa",
ifelse(base_treino$NU_MEDIA_RED<500,"ruim",
"regular"))) |>
select(-c(CO_ESCOLA_EDUCACENSO,
NO_ESCOLA_EDUCACENSO,
NU_MEDIA_CN,NU_MEDIA_CH,
NU_MEDIA_LP,NU_MEDIA_MT,
NU_TAXA_PARTICIPACAO,
NU_PARTICIPANTES,
NU_MEDIA_RED))
base_treino$NOTA_RED = as.factor(base_treino$NOTA_RED)7.2.1 Medidas de qualidade do ajuste
tree_RED = readRDS(file="arquivos-de-trabalho/tree_RED_3.rds")
rf_RED = readRDS(file = "arquivos-de-trabalho/rf_RED_3.rds")
xgb_RED = readRDS(file = "arquivos-de-trabalho/xgb_RED_3.rds")7.2.1.1 Previsão na base de treino
prev_treino_tree = predict(tree_RED,
newdata = base_treino,
type = "prob")
prev_treino_rf = predict(rf_RED,
newdata = base_treino,
type = "prob")
M_treino = model.matrix(~., data = base_treino)[,-1]
X_treino = M_treino[,-c(45,46)]
prev_treino_xgb = predict(xgb_RED,
newdata = X_treino)
prev_treino_xgb =
matrix(predict(xgb_RED, newdata = X_treino),
byrow = TRUE,
ncol=3,
dimnames = list(NULL,c("boa","regular","ruim"))
)7.2.1.2 Entropia Cruzada
Para o caso do problema com mais de duas classes a expressão da entropia cruzada precisa ser generalizada.
\[ EC = - \dfrac{1}{N} \sum_{i=1}^N \sum_{k=1}^K y_{k,i}\ln(\hat{y}_{k,i}) \] sendo, \(N\) o número de instâncias (observações), \(K\) o número de classes, \(y_{k,i}\) a variável indicadora da classe \(k\), isto é, \(y_{k,i} = 1\) se a isntância \(i\) pertence a classe \(k\) e 0 caso contrário, e \(\hat{y}_{k,i}\) o valor de saída para a classe \(k\).
7.2.2 Medidas de qualidade da classificação
7.2.2.1 Previsão da classe na base de treino
classe_treino = base_treino$NOTA_RED
indice_classe = apply(prev_treino_tree,MARGIN = 1,which.max)
prev_class_treino_tree =
ifelse(indice_classe == 1,"boa",ifelse(indice_classe == 2,"regular","ruim"))
tabela = table(prev=prev_class_treino_tree,
real_treino=classe_treino)
CM_treino_tree = confusionMatrix(tabela)
CM_treino_tree## Confusion Matrix and Statistics
##
## real_treino
## prev boa regular ruim
## boa 2745 1271 36
## regular 492 4159 1267
## ruim 41 696 993
##
## Overall Statistics
##
## Accuracy : 0.675
## 95% CI : (0.6664, 0.6834)
## No Information Rate : 0.5236
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.4664
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Statistics by Class:
##
## Class: boa Class: regular Class: ruim
## Sensitivity 0.8374 0.6789 0.43249
## Specificity 0.8448 0.6844 0.92163
## Pos Pred Value 0.6774 0.7028 0.57399
## Neg Pred Value 0.9303 0.6598 0.86931
## Prevalence 0.2802 0.5236 0.19624
## Detection Rate 0.2346 0.3555 0.08487
## Detection Prevalence 0.3463 0.5058 0.14786
## Balanced Accuracy 0.8411 0.6817 0.67706indice_classe = apply(prev_treino_rf,MARGIN = 1,which.max)
prev_class_treino_rf =
ifelse(indice_classe == 1,"boa",ifelse(indice_classe == 2,"regular","ruim"))
tabela = table(prev=prev_class_treino_rf,
real_treino=classe_treino)
CM_treino_rf = confusionMatrix(tabela)
CM_treino_rf## Confusion Matrix and Statistics
##
## real_treino
## prev boa regular ruim
## boa 3274 16 1
## regular 4 6110 7
## ruim 0 0 2288
##
## Overall Statistics
##
## Accuracy : 0.9976
## 95% CI : (0.9965, 0.9984)
## No Information Rate : 0.5236
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.9961
##
## Mcnemar's Test P-Value : 0.001653
##
## Statistics by Class:
##
## Class: boa Class: regular Class: ruim
## Sensitivity 0.9988 0.9974 0.9965
## Specificity 0.9980 0.9980 1.0000
## Pos Pred Value 0.9948 0.9982 1.0000
## Neg Pred Value 0.9995 0.9971 0.9992
## Prevalence 0.2802 0.5236 0.1962
## Detection Rate 0.2798 0.5222 0.1956
## Detection Prevalence 0.2813 0.5232 0.1956
## Balanced Accuracy 0.9984 0.9977 0.9983indice_classe = apply(prev_treino_xgb,MARGIN = 1,which.max)
prev_class_treino_xgb =
ifelse(indice_classe == 1,"boa",ifelse(indice_classe == 2,"regular","ruim"))
tabela = table(prev=prev_class_treino_xgb,
real_treino=classe_treino)
CM_treino_xgb = confusionMatrix(tabela)
CM_treino_xgb## Confusion Matrix and Statistics
##
## real_treino
## prev boa regular ruim
## boa 3026 306 5
## regular 246 5697 530
## ruim 6 123 1761
##
## Overall Statistics
##
## Accuracy : 0.8961
## 95% CI : (0.8904, 0.9015)
## No Information Rate : 0.5236
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.8264
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Statistics by Class:
##
## Class: boa Class: regular Class: ruim
## Sensitivity 0.9231 0.9300 0.7670
## Specificity 0.9631 0.8608 0.9863
## Pos Pred Value 0.9068 0.8801 0.9317
## Neg Pred Value 0.9699 0.9179 0.9455
## Prevalence 0.2802 0.5236 0.1962
## Detection Rate 0.2586 0.4869 0.1505
## Detection Prevalence 0.2852 0.5532 0.1615
## Balanced Accuracy 0.9431 0.8954 0.87667.2.2.2 Leitura da base de teste
base_teste = readRDS(file="arquivos-de-trabalho/base_teste.rds")
base_teste = base_teste |> select(-c(NU_MEDIA_OBJ,
NU_MEDIA_TOT,
NU_ANO,
NU_TAXA_APROVACAO,
CO_UF_ESCOLA,
CO_MUNICIPIO_ESCOLA,
NO_MUNICIPIO_ESCOLA))
base_teste = base_teste |>
mutate(NU_TAXA_REPROVACAO = replace_na(NU_TAXA_REPROVACAO, mean(base_treino$NU_TAXA_REPROVACAO, na.rm = TRUE)),
NU_TAXA_ABANDONO = replace_na(NU_TAXA_ABANDONO, mean(base_treino$NU_TAXA_ABANDONO, na.rm = TRUE)),
PC_FORMACAO_DOCENTE = replace_na(PC_FORMACAO_DOCENTE, mean(base_treino$PC_FORMACAO_DOCENTE, na.rm = TRUE))
)
base_teste = base_teste |>
mutate(NOTA_RED =
ifelse(
base_teste$NU_MEDIA_RED>600,"boa",
ifelse(base_teste$NU_MEDIA_RED<500,"ruim",
"regular"))) |>
select(-c(NU_MEDIA_CN,NU_MEDIA_CH,
NU_MEDIA_LP,NU_MEDIA_MT,
NU_TAXA_PARTICIPACAO,
NU_PARTICIPANTES,
NU_MEDIA_RED,CO_ESCOLA_EDUCACENSO,NO_ESCOLA_EDUCACENSO))
base_teste$NOTA_RED = as.factor(base_teste$NOTA_RED)Previsão na base de teste.
classe_teste = base_teste$NOTA_RED
prev_teste_tree = predict(tree_RED,
newdata = base_teste,
type = "prob")
prev_teste_rf = predict(rf_RED,
newdata = base_teste,
type = "prob")
M_teste = model.matrix(~., data = base_teste)[,-1]
X_teste = M_teste[,-c(45,46)]
prev_teste_xgb = predict(xgb_RED,
newdata = X_teste)
prev_teste_xgb =
matrix(predict(xgb_RED, newdata = X_teste),
byrow = TRUE,
ncol=3,
dimnames = list(seq(1:nrow(X_teste)),c("boa","regular","ruim"))
)indice_classe = apply(prev_teste_tree,MARGIN = 1,which.max)
prev_class_teste_tree =
ifelse(indice_classe == 1,"boa",ifelse(indice_classe == 2,"regular","ruim"))
tabela = table(prev=prev_class_teste_tree,
real_teste=classe_teste)
CM_teste_tree = confusionMatrix(tabela)
CM_teste_tree## Confusion Matrix and Statistics
##
## real_teste
## prev boa regular ruim
## boa 923 438 15
## regular 172 1306 431
## ruim 15 253 345
##
## Overall Statistics
##
## Accuracy : 0.6603
## 95% CI : (0.6452, 0.6752)
## No Information Rate : 0.5123
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.4492
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Statistics by Class:
##
## Class: boa Class: regular Class: ruim
## Sensitivity 0.8315 0.6540 0.43616
## Specificity 0.8375 0.6828 0.91374
## Pos Pred Value 0.6708 0.6841 0.56281
## Neg Pred Value 0.9259 0.6526 0.86423
## Prevalence 0.2848 0.5123 0.20292
## Detection Rate 0.2368 0.3350 0.08851
## Detection Prevalence 0.3530 0.4897 0.15726
## Balanced Accuracy 0.8345 0.6684 0.67495indice_classe = apply(prev_teste_rf,MARGIN = 1,which.max)
prev_class_teste_rf =
ifelse(indice_classe == 1,"boa",ifelse(indice_classe == 2,"regular","ruim"))
tabela = table(prev=prev_class_teste_rf,
real_teste=classe_teste)
CM_teste_rf = confusionMatrix(tabela)
CM_teste_rf## Confusion Matrix and Statistics
##
## real_teste
## prev boa regular ruim
## boa 846 273 3
## regular 264 1550 454
## ruim 0 174 334
##
## Overall Statistics
##
## Accuracy : 0.7004
## 95% CI : (0.6857, 0.7147)
## No Information Rate : 0.5123
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.4951
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Statistics by Class:
##
## Class: boa Class: regular Class: ruim
## Sensitivity 0.7622 0.7762 0.42225
## Specificity 0.9010 0.6223 0.94400
## Pos Pred Value 0.7540 0.6834 0.65748
## Neg Pred Value 0.9049 0.7258 0.86519
## Prevalence 0.2848 0.5123 0.20292
## Detection Rate 0.2170 0.3976 0.08568
## Detection Prevalence 0.2878 0.5818 0.13032
## Balanced Accuracy 0.8316 0.6992 0.68312indice_classe = apply(prev_teste_xgb,MARGIN = 1,which.max)
prev_class_teste_xgb =
ifelse(indice_classe == 1,"boa",ifelse(indice_classe == 2,"regular","ruim"))
tabela = table(prev=prev_class_teste_xgb,
real_teste=classe_teste)
CM_teste_xgb = confusionMatrix(tabela)
CM_teste_xgb## Confusion Matrix and Statistics
##
## real_teste
## prev boa regular ruim
## boa 840 275 5
## regular 268 1527 440
## ruim 2 195 346
##
## Overall Statistics
##
## Accuracy : 0.696
## 95% CI : (0.6813, 0.7104)
## No Information Rate : 0.5123
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.4901
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Statistics by Class:
##
## Class: boa Class: regular Class: ruim
## Sensitivity 0.7568 0.7646 0.43742
## Specificity 0.8996 0.6276 0.93659
## Pos Pred Value 0.7500 0.6832 0.63720
## Neg Pred Value 0.9028 0.7174 0.86736
## Prevalence 0.2848 0.5123 0.20292
## Detection Rate 0.2155 0.3917 0.08876
## Detection Prevalence 0.2873 0.5734 0.13930
## Balanced Accuracy 0.8282 0.6961 0.68701
Breiman, Leo. 2001. “Random Forests.” Machine Learning 45: 5–32.
Chen, Tianqi, Tong He, Michael Benesty, Vadim Khotilovich, Yuan Tang, Hyunsu Cho, Kailong Chen, et al. 2023. Xgboost: Extreme Gradient Boosting. https://CRAN.R-project.org/package=xgboost.
Ding, Yong, Lingxiao Fan, and Xue Liu. 2021. “Analysis of Feature Matrix in Machine Learning Algorithms to Predict Energy Consumption of Public Buildings.” Energy and Buildings 249: 111208.
Dubey, Saurabh C, Ketan S Mundhe, and Aditya A Kadam. 2020. “Credit Card Fraud Detection Using Artificial Neural Network and Backpropagation.” In 2020 4th International Conference on Intelligent Computing and Control Systems (ICICCS), 268–73. IEEE.
Dudkina, Tetiana, Ievgen Meniailov, Kseniia Bazilevych, Serhii Krivtsov, and Anton Tkachenko. 2021. “Classification and Prediction of Diabetes Disease Using Decision Tree Method.” In IT&AS, 163–72.
FERNANDES, GABRIELA FERREIRA. 2021. “Aplicação de Modelos de Regressão Para a Previsão de Preço de Residência.” Bacharelado em Estatística. Niterói: Universidade Federal Fluminense.
Friedman, Jerome H. 2001. “Greedy Function Approximation: A Gradient Boosting Machine.” Annals of Statistics, 1189–1232.
Goswami, Vasudha, Vijay Malviya, and Pratyush Sharma. 2020. “Detecting Spam Emails/SMS Using Naive Bayes, Support Vector Machine and Random Fores.” In Proceeding of the International Conference on Computer Networks, Big Data and IoT (ICCBI - 2019), LNDECT 49:306–13. Springer.
James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning. Vol. 112. Springer.
Kuhn, Max. 2008. “Building Predictive Models in r Using the Caret Package.” Journal of Statistical Software 28: 1–26.
———. 2022. Caret: Classification and Regression Training. https://CRAN.R-project.org/package=caret.
Liaw, Andy, and Matthew Wiener. 2002. “Classification and Regression by randomForest.” R News 2 (3): 18–22. https://CRAN.R-project.org/doc/Rnews/.
Lotfy, Nesma. 2021. “Regression Tree Modelling to Predict Total Average Extra Costs in Household Spending During COVID-19 Pandemic.” Bulletin of the National Research Centre 45: 1–7.
LUZ, LUCCAS MARTINS DA. 2021. “Avaliação Do Perfil Das Internações Hospitalares Emergenciais Em Idosos Com Doenças Respiratórias e de Possíveis Fatores Associados Ao Desfecho.” Bacharelado em Estatística. Niterói: Universidade Federal Fluminense.
Milborrow, Stephen. 2022. Rpart.plot: Plot ’Rpart’ Models: An Enhanced Version of ’Plot.rpart’. https://CRAN.R-project.org/package=rpart.plot.
Natekin, Alexey, and Alois Knoll. 2013. “Gradient Boosting Machines, a Tutorial.” Frontiers in Neurorobotics 7: 21.
Navaney, Pavas, Gaurav Dubey, and Ajay Rana. 2018. “SMS Spam Filtering Using Supervised Machine Learning Algorithms.” In 8th International Conference on Cloud Computing, Data Science & Engineering, 43–48.
OLIVEIRA, YAGO CORREA DE. 2021. “Modelando a Relação Entre Desempenho Escolar, Infraestrutura e Outros Indicadores Em Educação.” Bacharelado em Estatística. Niterói: Universidade Federal Fluminense.
PORTO, PAULO VICTOR CUNHA. 2021. “Métodos Estatísticos de Classificação: Abordagem Aplicada Ao Diagnóstico de Casos de Câncer de Mama.” Bacharelado em Estatística. Niterói: Universidade Federal Fluminense.
Purba, Kristo Radion, David Asirvatham, and Raja Kumar Murugesan. 2020. “Analysis and Prediction of Instagram Users Popularity Using Regression Techniques Based on Metadata, Media and Hashtags Analysis.”
R Core Team. 2022. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Schloerke, Barret, Di Cook, Joseph Larmarange, Francois Briatte, Moritz Marbach, Edwin Thoen, Amos Elberg, and Jason Crowley. 2021. GGally: Extension to ’Ggplot2’. https://CRAN.R-project.org/package=GGally.
SOARES, KAROLINA DECNOP. 2021. “Avaliação de Modelos Estatísticos Para a Precificação de Seguros de Automóveis Na Cidade Do Rio de Janeiro.” Bacharelado em Estatística. Niterói: Universidade Federal Fluminense.
SOUZA, ADRIELLY AGDA COSTA DE. 2021. “Estratégias Estatísticas Para Busca de Fatores Associados à Colelitíase Pós-Bariátrica.” Bacharelado em Estatística. Niterói: Universidade Federal Fluminense.
SOUZA, JULIA OLIVEIRA DIAS DE. 2021. “Associação Entre as Características Da Mãe e Do Recém-Nascido e a Prevalência de Prematuridade No Estado Do Rio de Janeiro: Um Estudo Utilizando Modelo de Regressão Log-Linear de Poisson.” Bacharelado em Estatística. Niterói: Universidade Federal Fluminense.
Therneau, Terry, and Beth Atkinson. 2022. Rpart: Recursive Partitioning and Regression Trees. https://CRAN.R-project.org/package=rpart.
VARANDA, GABRIEL HERCULANO. 2021. “Modelagem Das Taxas de Óbitos Por Acidentes de Transportes Nas Unidades Federativas Do Brasil.” Bacharelado em Estatística. Niterói: Universidade Federal Fluminense.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019. “Welcome to the tidyverse.” Journal of Open Source Software 4 (43): 1686. https://doi.org/10.21105/joss.01686.
Wickham, Hadley, Romain François, Lionel Henry, and Kirill Müller. 2022. Dplyr: A Grammar of Data Manipulation. https://CRAN.R-project.org/package=dplyr.
Wickham, Hadley, Jim Hester, and Jennifer Bryan. 2022. Readr: Read Rectangular Text Data. https://CRAN.R-project.org/package=readr.