Capítulo 3 Árvores de Decisão

Esse capítulo tem como objetivo apresentar o Modelo de Árvore de Decisão, tanto para Regressão quanto para Classificação.

Um modelo de Árvore de Decisão é um algoritmo de Aprendizado de Máquina supervisionado usado para resolver problemas de Classificação ou de Regressão. Ele é chamado de “Árvore de Decisão” porque o algoritmo cria uma estrutura de dados de árvore binária, que é construída a partir de decisões tomadas a partir dos dados de treinamento.

A ideia básica do modelo de Árvore de Decisão é dividir o conjunto de dados de um certo nó em subconjuntos menores, de acordo com características relevantes dos dados que chegaram no nó em questão. Estas divisões são feitas de maneira hierárquica, começando pelo nó raiz, que recebe a base de treino completa.

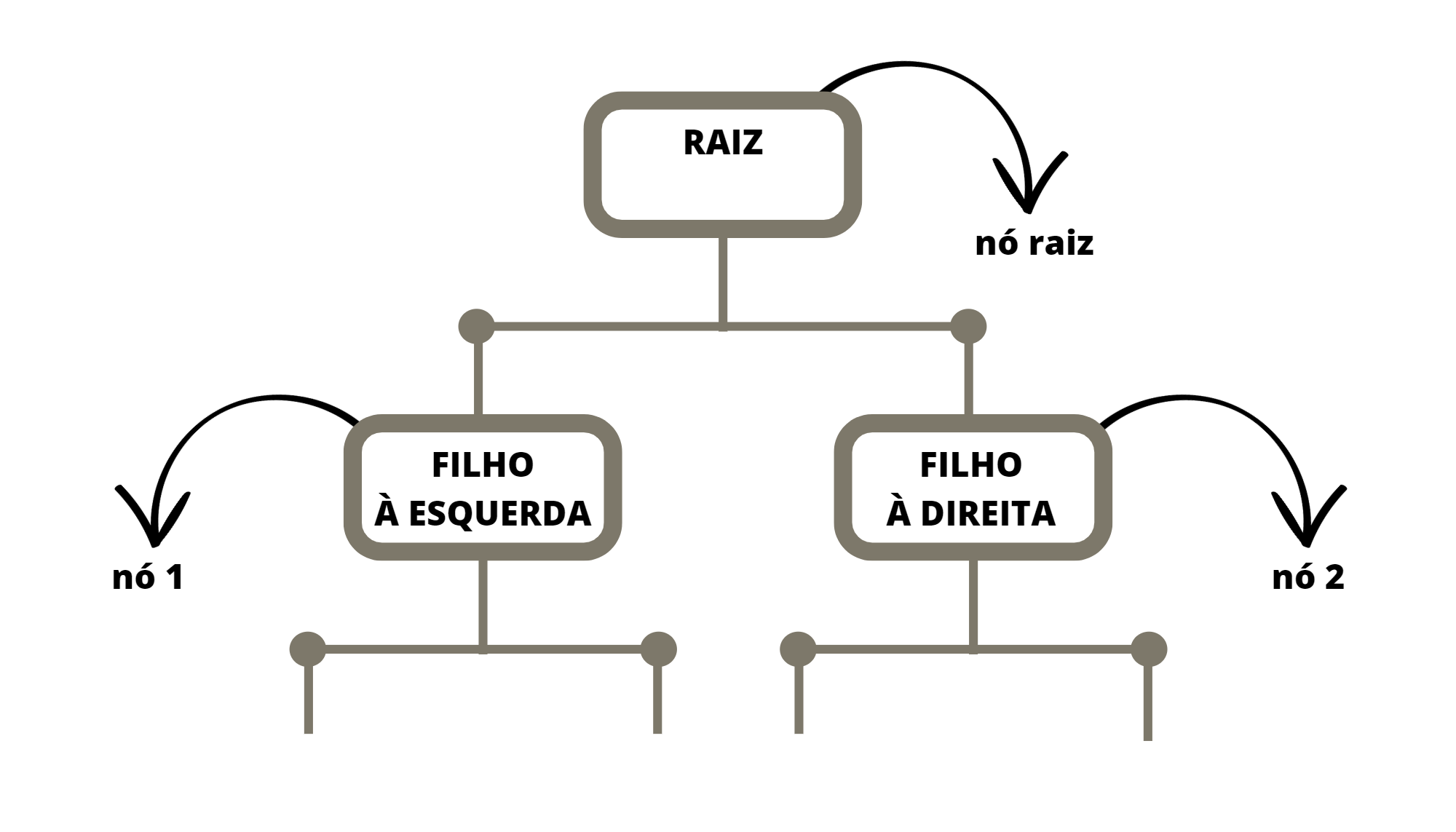
Figura 3.1: Estrutura da Árvore de Decisão

É chamado de raiz o primeiro nó de uma árvore de decisão. Este nó recebe todos as instâncias da base de treino e é a partir dele que começa a divisão. O nó raiz dá origem a dois filhos, o filho à direita e o filho à esquerda. Cada filho pode ser um nó, caso ele tenha dois outros filhos, ou uma folha, caso ele não tenha filhos. Cada nó define uma partição dos dados de entrada e cada folha define uma região no domínio.

Suponha uma base de dados supervisionada cuja variável alvo é \(Y\) e as covariáveis são \(X_1\), \(X_2\), \(\ldots\) \(X_p\). Suponha também a base de dados é formada por \(n\) observações. Desta forma \(Y_i\) é o valor da variável alvo para a observação \(i\) e \(X_{i,j}\) é o valor da covariável \(j\) para a observação \(i\). Posto isso, segue a idéia principal da árvore para prever o valor de \(Y\).

No nó raiz “chegam” todos as observações. Busca-se então a covariável \(X_j\) e o valor de \(cte\) tais que, a partição da base definida pelas observações \(A_1 = \{ i | X_{i,j} \le cte \}\) e \(A_2 = \{ i | X_{i,j} > cte \}\) apresente a menor “impureza” entre todos as possíveis partições formadas com diferentes valores de \(j\) e \(cte\). Essa medida de impureza depende se a árvore é de classificação ou de reggressão.

Uma das principais vantagens do modelo de árvore de decisão é sua capacidade de lidar com dados categóricos e numéricos, bem como sua interpretabilidade. As árvores de decisão podem ser facilmente visualizadas e compreendidas, o que ajuda a explicar as decisões tomadas pelo modelo.

No entanto, as árvores de decisão também têm algumas limitações. Elas podem ser sensíveis a pequenas variações nos dados de treinamento, o que pode levar a problemas de sobreajuste (overfiting). Para mitigar isso, técnicas como a poda da árvore ou o uso de conjuntos de árvores, como o algoritmo Random Forest, podem ser aplicadas.

No R o pacote para trabalhar com árvores de decisão é o rpart (Therneau and Atkinson 2022) e a função que cria as estruturas de árvore também se chama rpart.

3.1 Árvores de Classificação

As árvores de classificação são métodos baseados em árvores de decisão para o caso da variável alvo ser qualitativa. Neste caso a medida de impureza que define as partições e o método de prever a variável alvo precisam ser pensados para o problema de classificação.

As animações apresentadas nas Figuras 3.2 e 3.3 ilustram um problema de classificação com duas covariáveis. A variável alvo, aqui qualitativa, é representada pela cor do ponto: vermelho ou azul.

Figura 3.2: Ilustração da construção de uma Árvore de Decisão

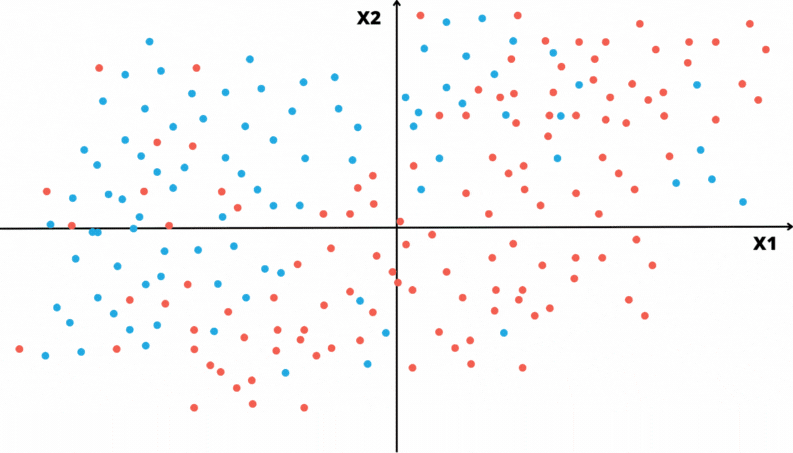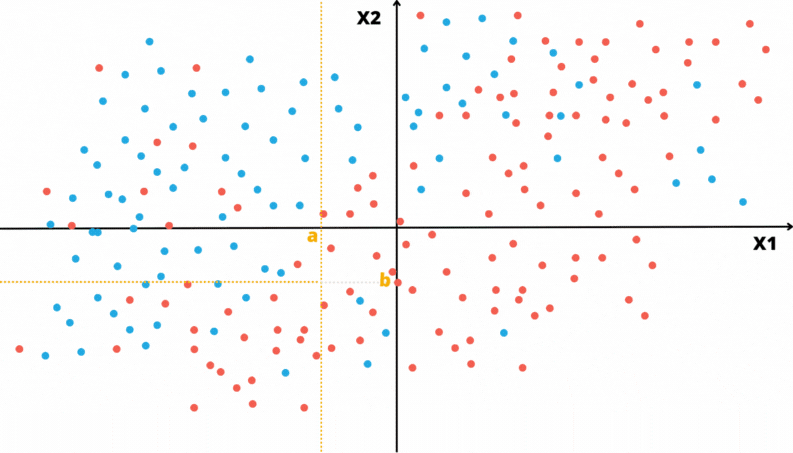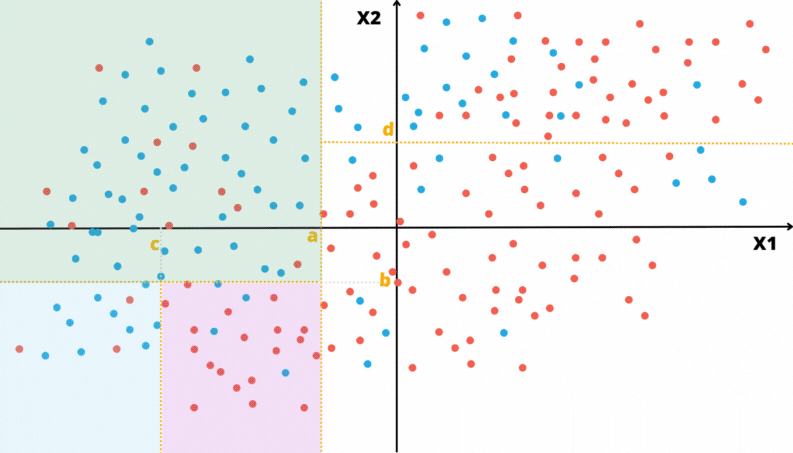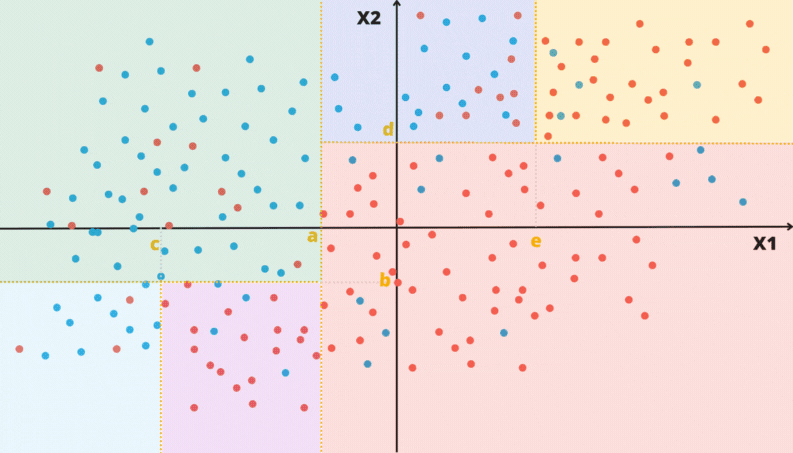
Figura 3.3: Ilustração da partição do domínio por uma Árvore de Decisão

3.1.1 Medida de impureza

Índice de GINI para problemas com duas classes

No caso dos problemas de classificação a medida de impureza comumente usada é o índice de GINI. O índice de GINI fornece uma medida de impureza para um dada região. Se o problema for de duas classes, essa medida é definida por

\[ G_R = 1 - q^2 - (1-q)^2 \]

sendo \(q\) a proporção das observações da classe de referência dentro da região \(R\).

A Figura 3.4 apresenta diferentes regiões com diferentes proporção entre duas classes. Considere a classe vermelha como a de referência.

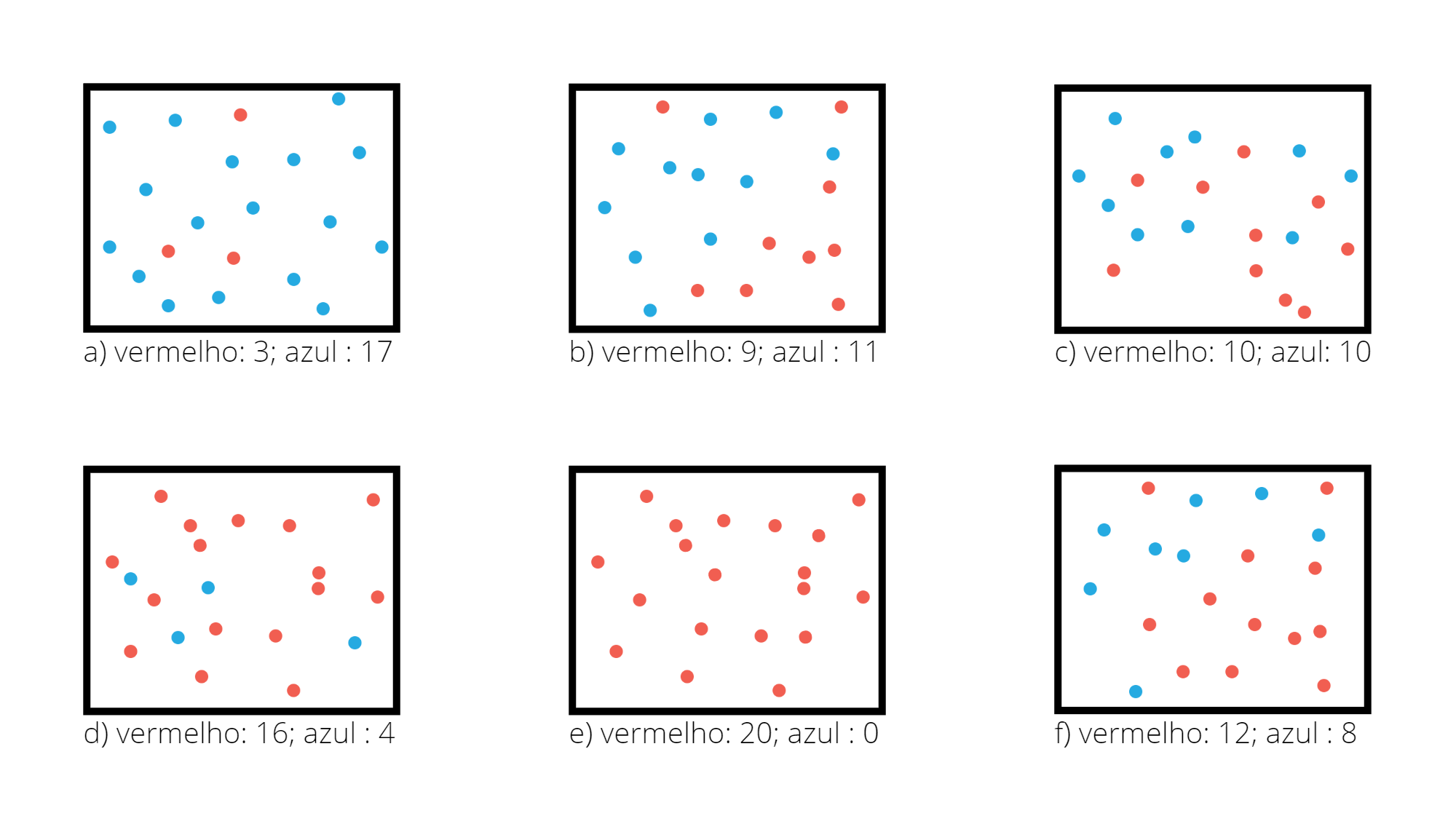
Figura 3.4: Exemplo do Índice de Gini em diferentes regiões

Para a região da Figura 3.4.a o valor do índice de Gini é \(0,255\).

q = 3/20
1 - q^2 - (1-q)^2

## [1] 0.255

Para a região da Figura 3.4.b o valor do índice de Gini é \(0,495\).

q = 9/20
1 - q^2 - (1-q)^2

## [1] 0.495

Para a região da Figura 3.4.c o valor do índice de Gini é \(0,5\).

q = 10/20
1 - q^2 - (1-q)^2

## [1] 0.5

Para a região da Figura 3.4.d o valor do índice de Gini é \(0,32\).

q = 16/20
1 - q^2 - (1-q)^2

## [1] 0.32

Para a região da Figura 3.4.e o valor do índice de Gini é \(0,0\).

q = 20/20
1 - q^2 - (1-q)^2

## [1] 0

Para a região da Figura 3.4.f o valor do índice de Gini é \(0,48\).

q = 12/20
1 - q^2 - (1-q)^2

## [1] 0.48

Se a região contiver apenas valores de uma das classes, isso seria uma região com impureza nula, \(q=1\) ou \(q=0\) e com isso \(G_R = 0\). O caso oposto, considerado com maior impureza, seria quando a região contém uma proporção igual de observações das duas classes, neste caso \(q=0,5\) e \(G_R = 1 - 0,25 - 0,25 = 0,5\). Para o caso de existirem apenas duas classes, o valor máximo do índice de Gini é \(0,5\) e ele ocorre quando \(q=0,5\).

Índice de GINI para problemas com três classes ou mais

Se o problema for multi-classes, a expressão do índice de Gini será generalizada. Suponha um problema de \(k\) classes. O índice de Gini na região \(R\) é definido por

\[ G_R = 1 - \sum_{i=1}^k q_i^2 \]

sendo \(q_i\) a proporção das observações da região \(R\) que pertencem à classe \(i\).

A Figura 3.5 apresenta diferentes regiões com diferentes proporção entre quatro classes.

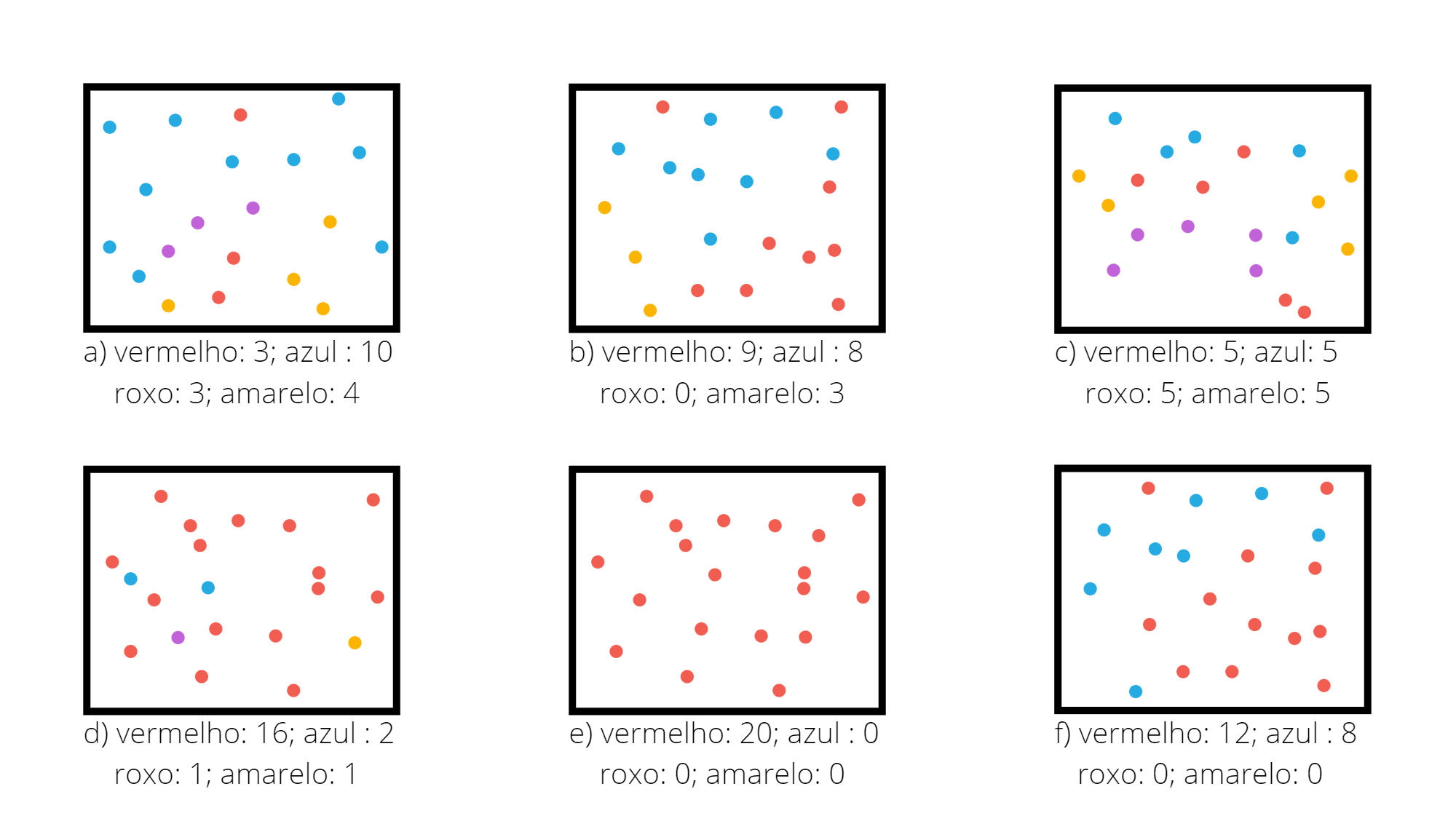
Figura 3.5: Exemplo do Índice de Gini em diferentes regiões

Para a região da Figura 3.5.a o valor do índice de Gini é \(0,684125\).

q1 = 3/20
q2 = 10/20
q3 = 3/20
q4 = 4/20
1 - q1^2 - q2^2 - q3^3 - q4^2

## [1] 0.684125

Para a região da Figura 3.5.b o valor do índice de Gini é \(0,615\).

q1 = 9/20
q2 = 8/20
q3 = 0/20
q4 = 3/20
1 - q1^2 - q2^2 - q3^2 - q4^2

## [1] 0.615

Para a região da Figura 3.5.c o valor do índice de Gini é \(0,75\).

q1 = 5/20
q2 = 5/20
q3 = 5/20
q4 = 5/20
1 - q1^2 - q2^2 - q3^2 - q4^2

## [1] 0.75

Para a região da Figura 3.5.d o valor do índice de Gini é \(0,345\).

q1 = 16/20
q2 = 2/20
q3 = 1/20
q4 = 1/20
1 - q1^2 - q2^2 - q3^2 - q4^2

## [1] 0.345

Para a região da Figura 3.4.e o valor do índice de Gini é \(0,0\).

q1 = 20/20
q2 = 0/20
q3 = 0/20
q4 = 0/20
1 - q1^2 - q2^2 - q3^2 - q4^2

## [1] 0

Para a região da Figura 3.4.f o valor do índice de Gini é \(0,48\).

q1 = 12/20
q2 = 8/20
q3 = 0/20
q4 = 0/20
1 - q1^2 - q2^2 - q3^2 - q4^2

## [1] 0.48

No método de Árvores de Classificação toda vez que uma partição é realizada e para isso são escolhidos os valores de \(X_j\) e \(cte\), estes valores são escolhidos de forma que minimizam a soma dos índices de Gini das duas partições criadas. Por exemplo, suponha que no nó em questão chegaram as observações \(A\). Quando é escolhido \(j\) e \(cte\) é definida uma partição para \(A\) de forma que \(A_1 = \{ X_i \in A \ | \ x_{i,j} \le cte \}\) e \(A_2 = \{ X_i \in A \ | \ x_{i,j} > cte \}\). São então calculados os índices de Gini em \(A_1\) e \(A_2\), denominados \(G_{A_1}\) e \(G_{A_2}\). A escolha de \(X_j\) e \(cte\) é feita de forma a minimizar a soma \(G_{A_1} + G_{A_2}\).

3.1.2 Algoritmo

1. Define-se os critérios de parada, que em geral são: um valor limite para o indice de Gini; a quantidade de elementos que chegaram ao nó; ou a profundidade da árvore.

2. Considere \(X\) o conjunto dos dados de entrada e \(X_j\) as covariáveis do problema.

3. Escolhe-se a variável \(j\) e o valor \(s\) tais que minimizam a soma dos índices Gini nas regiões \(R_1 = \{X|X_j < s\}\) e \(R_2 = \{X|X_j \ge s\}\).

Sejam \(Y_1\) os valores das variáveis alvo dos pontos de \(X\) que pertencem à \(R_1\) e \(Y_2\) os valores das variáveis alvo dos pontos de \(X\) que pertencem à \(R_2\).

4. Verifique se um dos critérios de parada foi atingido pelos elementos de \(Y_1\). Se sim, este nó é uma folha e FIM. Se não, faça \(X = R_1\) e volte para o passo 3.

5. Verifique se um dos critérios de parada foi atingido pelos elementos de \(Y_2\). Se sim, este nó é uma folha e FIM. Se não, faça \(X = X_2\) e volte para o passo 3.

3.1.3 Como realizar previsões

Uma vez a árvore construída, ela pode ser usada para prever a classse da variável alvo de novas observações. O dado de entrada percorre a árvore, seguindo os ramos que correspondem às características das covariáveis, até alcançar uma folha. Veja Figura 3.6.

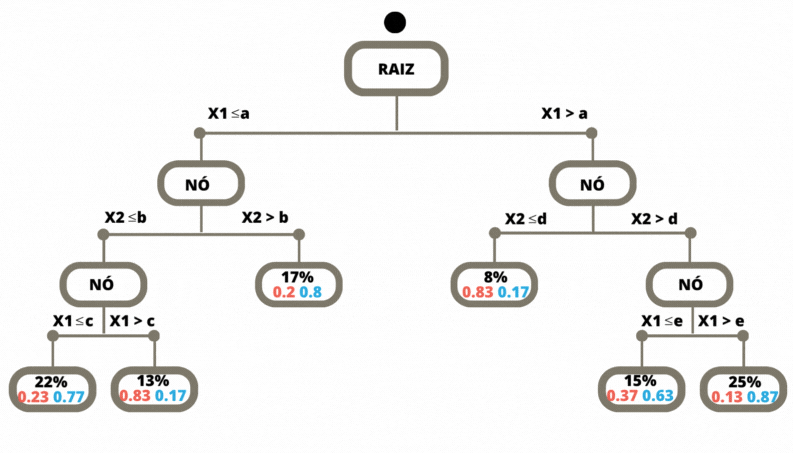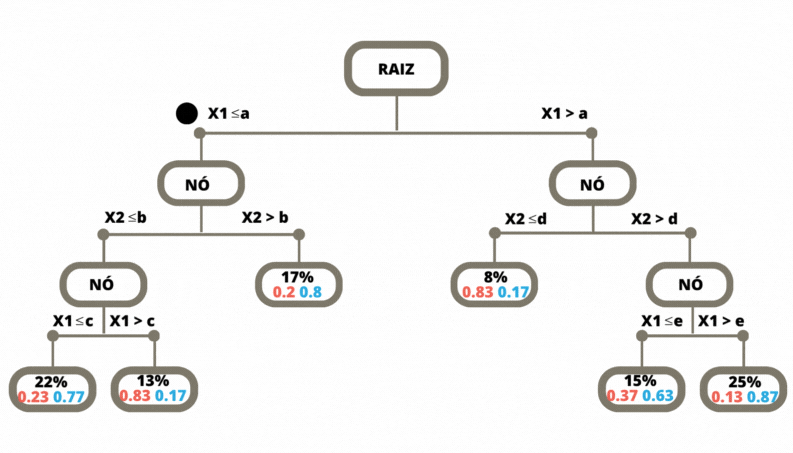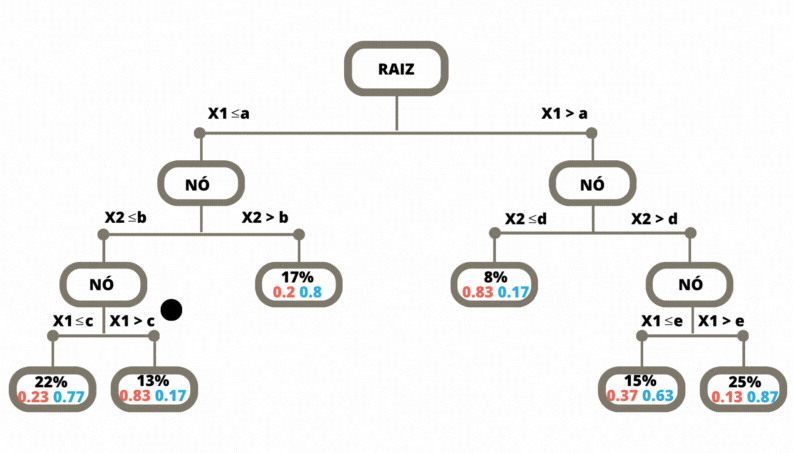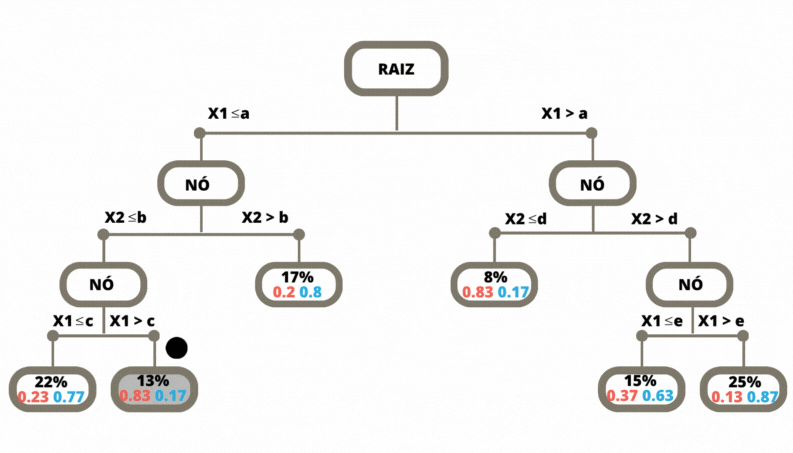
Figura 3.6: Previsão em uma Árvore de Classificação

Os métodos de classificação, em geral, não retornam a classe prevista e sim um número no intervalo \([0,1]\) para cada classe, que indica a probabilidade daquela classe ser a classe correta. Para as árvores de decisão a nova observação, para a qual não conhecemos a sua classe, percorre a árvore de acordo com os valores das suas covariáveis (atributos). Ao chegar em uma folha é verificado então, considerando os dados de treinamento, a proporção de cada uma das classes que chegaram nesta mesma folha. Para este exemplo o método retorna os valores \((0.83, 0.17)\).

3.1.4 Vamos praticar

Segue-se analisando a base com informações sobre as escolas. Aquele arquivo que foi salvo depois do Capítulo 2 pode ser recuperado e a base de treino final obtida.

library(tidyverse)
#install.packages("rpart")
library(rpart)
base_treino = readRDS(file="arquivos-de-trabalho/base_treino_final.rds")

Classificação Binária

O Primeiro problema proposto será classificar a nota de uma escola entre “boa” e “regular”. Ou seja, analisar as características relevantes em uma escola que diferenciam aquelas com a nota “boa” das com nota “regular”.

Nota em Redação

Vamos começar considerando como variável de interesse a nota das escolas em redação.

summary(base_treino$NU_MEDIA_RED)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   345.0   508.4   547.2   564.0   609.6   920.0

Metade das escolas apresentaram nota abaixo de 547 e que a nota média foi perto de 563. A partir destes valores vamos assumir que uma nota em redação maior ou igual a 600 é uma boa nota, enquanto uma nota abaixo de 600 é uma nota regular (ou ruim).

Definição da variável alvo

Para seguir com essa análise é preciso criar uma variável alvo, qualitativa, que indica se a nota média de cada escola em redação é “boa” ou “regular” de acordo com o critério estabelecido.

base_treino_RED = base_treino |> 
  mutate(NOTA_RED = ifelse(base_treino$NU_MEDIA_RED>=600,"boa","regular")) |>
  select(-c(NU_TAXA_PARTICIPACAO,
            NU_MEDIA_CN,
            NU_MEDIA_CH,
            NU_MEDIA_LP, 
            NU_MEDIA_MT,
            NU_MEDIA_RED,
            CO_ESCOLA_EDUCACENSO,
            NO_ESCOLA_EDUCACENSO
            ))
base_treino_RED$NOTA_RED = as.factor(base_treino_RED$NOTA_RED)
summary(base_treino_RED$NOTA_RED)

##     boa regular 
##    3322    8378

A grande maioria das escolas apresentou nota média em redação regular.

Ajuste do Modelo

O modelo é ajustado com a função rpart, do pacote rpart (Therneau and Atkinson 2022).

tree_RED <- rpart(NOTA_RED ~ ., 
              data = base_treino_RED, 
              method = "class")

Para que possamos usar este resultado no futuro e não seja preciso realizar o código para chegar nele, vamos salvar o objeto tree_RED com a extensão rds.

saveRDS(tree_RED,file = "arquivos-de-trabalho/tree_RED.rds")

O pacote rpart.plot (Milborrow 2022) gera gráficos mais bonitos do que os básicos do pacote rpart (Therneau and Atkinson 2022).

#install.packages("rpart.plot")
library("rpart.plot")
rpart.plot(tree_RED,type=5,cex=1)

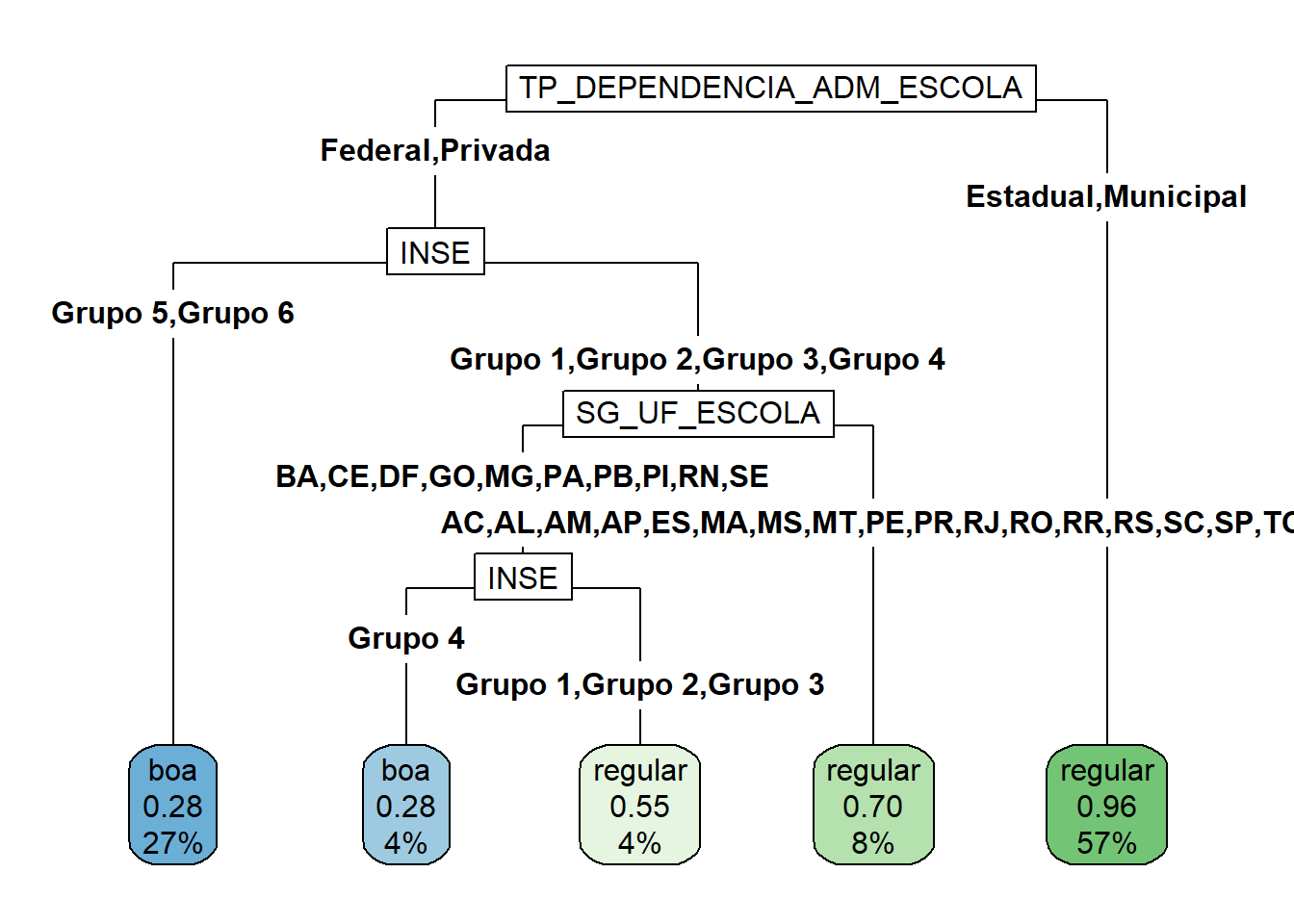
Variáveis Importantes

Ainda é possível obter as variáveis mais relevantes para o problema com a função varImp do pacote caret (Kuhn 2022). A importância (overall) de uma variável é calculada com base na redução do índice de Gini quando esta variável é removida da base. Para isso são feitas combinações das covariáveis e, para cada combinação, uma árvore é gerada. Então calcula-se a média do índice de Gini nas regiões definidas pelas árvores que usaram a covariável no ajuste. Depois calcula-se a média do índice de Gine das regiões definidas pelas árvores criadas sem esta covariável. A diferença entre as duas médias é o valor do overall (Kuhn 2008). Quando maior este valor, maior a importância da variável para o problema.

imp <- caret::varImp(tree_RED, scale = FALSE)
importancia = tibble(overall = imp$Overall,
                     var = rownames(imp))
importancia |> arrange(desc(overall))

## # A tibble: 11 × 2
##    overall var                      
##      <dbl> <chr>                    
##  1  1876.  TP_DEPENDENCIA_ADM_ESCOLA
##  2  1738.  INSE                     
##  3  1088.  NU_TAXA_ABANDONO         
##  4   316.  NU_TAXA_REPROVACAO       
##  5   307.  NU_MATRICULAS            
##  6   187.  PC_FORMACAO_DOCENTE      
##  7   134.  SG_UF_ESCOLA             
##  8    83.2 PORTE_ESCOLA             
##  9    14.5 NU_TAXA_PERMANENCIA      
## 10     0   TP_LOCALIZACAO_ESCOLA    
## 11     0   NU_PARTICIPANTES_NEC_ESP

# Visualizar a importância das variáveis

Interpretação

Agora é papel do pesquisador interpretar toda a informação que foi passada.

A conclusão direta que se tem deste resultado é que o fato de uma escola ser estadual ou municipal aumenta, e muito, as chances da nota média de seus alunos em redação ficar abaixo de 600. O fato da escola ser estadual ou municipal é tão relevante para a nota média de seus alunos em redação que nem é preciso saber, por exemplo, o estado desta escola.

Entre as escolas federais e privadas existem características que diferenciam uma das outras e contribuem para a nota média dos alunos no ENEM ser acima ou abaixo de 600. A primeira característica relevante para diferencias as escolas com notas altas das escolas com notas médias baixas no ENEM é o INSE - Indicador de Nível Socioeconômico da escola. Quanto maior o número do grupo, maior é este indicador, maior será o nível socioeconômico da escola. Mais uma vez é notório que as escolas que atendem a classe mais privilegiada têm seu desempenho médio na nota de redação superior que as demais.

Quase 90% das escolas federais ou privadas que pertencem ao Grupo 6, aquele com maior indicador socioeconômico, apresentaram nota média na redação maior que 600. Para os demais grupos socioeconômicos outras variáveis são importantes nesta análise, como o estado de origem da escola e a PC_FORMACAO_DOCENTE, que é um indicador de adequação da formação docente da escola.

Uma outra observação relevante é que, apesar da NU_TAXA_ABANDONO não ser uma variável de divisão na árvore, ela apareceu como a terceira mais importante. Além disso, o fator de importância das três variáveis mais importantes são bem maiores que o fator de importância das demais. Esta variável deve ser tratada com atenção.

Este resultado poderia, por exemplo, ser útil nas tomadas de políticas públicas. Sem dúvida as escolas estaduais e municipais precisam de mais investimento. Além disso, destacamos a importência da formação dos docentes.

Previsão para novas observações

E se quiséssemos usar a árvore criada para realizar previsões, ou seja, dadas as características de uma escola qual seria a nota média dos alunos desta escola na redação do ENEM?

Por exemplo, qual a previsão de nota média no ENEM a escola descrita a seguir?

• “SG_UF_ESCOLA” = RJ

• “TP_DEPENDENCIA_ADM_ESCOLA” = Estadual

• “TP_LOCALIZACAO_ESCOLA” = Urbana

• “NU_MATRICULAS” = 87

• “NU_PARTICIPANTES_NEC_ESP” = 1

• “INSE” = Grupo 3

• “PC_FORMACAO_DOCENTE” = 48,1

• “NU_TAXA_PERMANENCIA” = 67.4

• “NU_TAXA_REPROVACAO” = 6,1

• “NU_TAXA_ABANDONO” = 0

• “PORTE_ESCOLA” = De 61 a 90 alunos

Para realizar uma previsão na árvore é preciso criar um data.frame ou tibble com o mesmo padrão das linhas da base de treino. Os nomes das variáveis têm que ser os mesmos.

escola = tibble(
SG_UF_ESCOLA = "RJ",
TP_DEPENDENCIA_ADM_ESCOLA = "Estadual",
TP_LOCALIZACAO_ESCOLA = "Urbana",
NU_MATRICULAS = 87,
NU_PARTICIPANTES = 49,
NU_PARTICIPANTES_NEC_ESP = 1,
INSE = "Grupo 3",
PC_FORMACAO_DOCENTE = 48.1,
NU_TAXA_PERMANENCIA = 67.4,
NU_TAXA_REPROVACAO = 6.1,
NU_TAXA_ABANDONO = 0,
PORTE_ESCOLA = "De 61 a 90 alunos")
  
predict(tree_RED, newdata = escola, type = "prob")

##          boa   regular
## 1 0.03965414 0.9603459

Nota em Matemática

Será que a análise com a nota em outra prova, como por exemplo a de Matemática, apresenta resultados parecidos ou diferentes deste?

summary(base_treino$NU_MEDIA_MT)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   372.4   442.9   471.3   492.4   527.8   845.7

Para a prova de matemática uma nota será considerada “boa” se ela ficou acima de 500 e regular caso contrário.

Definição da Variável Alvo

base_treino_MAT = base_treino |> 
  mutate(NOTA_MAT = ifelse(base_treino$NU_MEDIA_MT>500,"boa","regular")) |>
  select(-c(NU_TAXA_PARTICIPACAO,
            NU_MEDIA_CN,
            NU_MEDIA_CH,
            NU_MEDIA_LP, 
            NU_MEDIA_MT,
            NU_MEDIA_RED,
            CO_ESCOLA_EDUCACENSO,
            NO_ESCOLA_EDUCACENSO
            ))
base_treino_MAT$NOTA_MAT = as.factor(base_treino_MAT$NOTA_MAT)
summary(base_treino_MAT$NOTA_MAT)

##     boa regular 
##    4074    7626

Ajuste do Modelo

tree_MAT <- rpart(NOTA_MAT ~ ., 
              data = base_treino_MAT, 
              method = "class")
saveRDS(tree_MAT,file="arquivos-de-trabalho/tree_MAT.rds")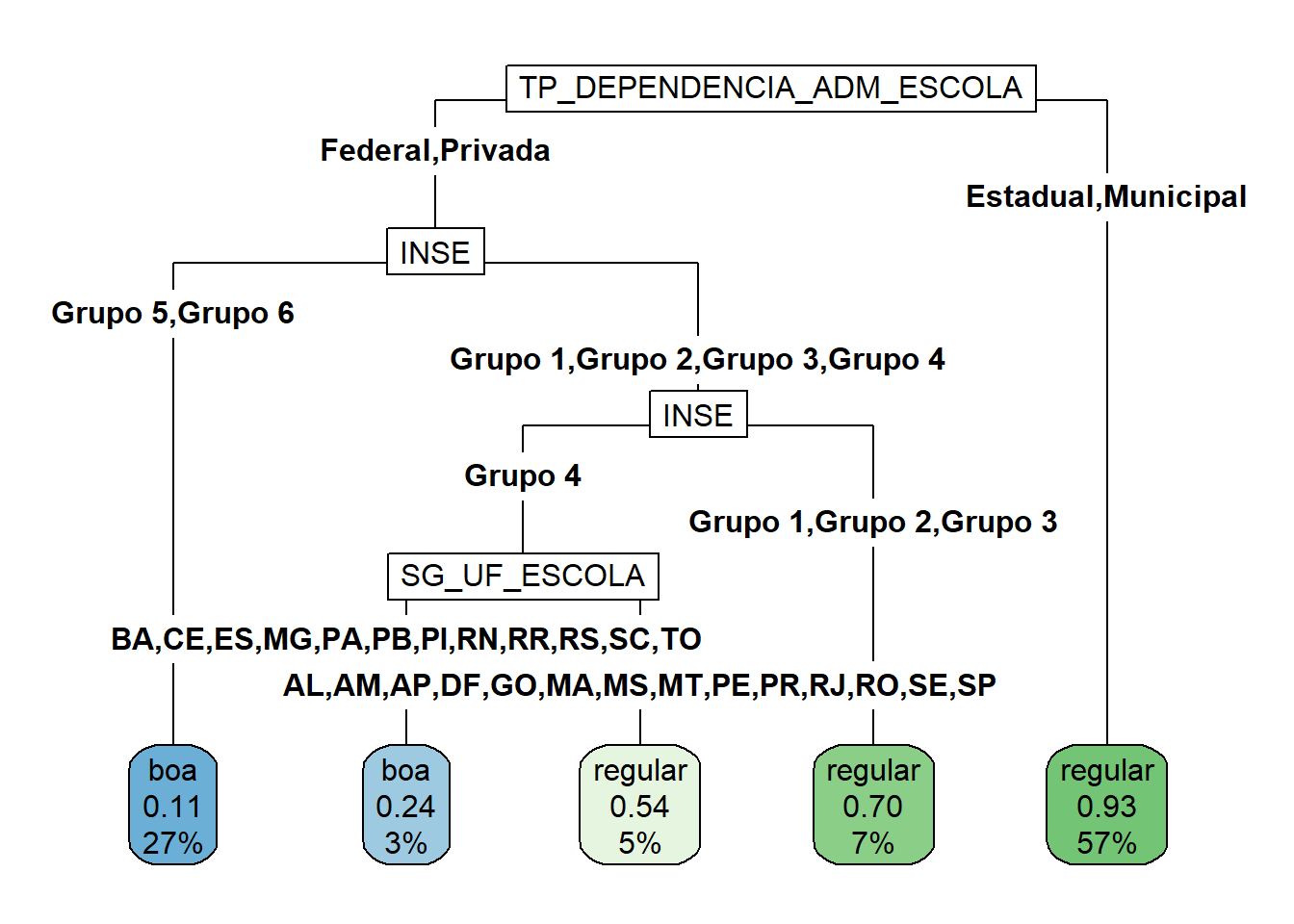

rpart.plot(tree_MAT,type=5,cex=1)

Variáveis Importantes

imp <- caret::varImp(tree_MAT, scale = FALSE)
importancia = tibble(overall = imp$Overall,
                     var = rownames(imp))
importancia |> arrange(desc(overall))

## # A tibble: 12 × 2
##    overall var                      
##      <dbl> <chr>                    
##  1  2881.  INSE                     
##  2  2495.  TP_DEPENDENCIA_ADM_ESCOLA
##  3  1545.  NU_TAXA_ABANDONO         
##  4   442.  NU_TAXA_REPROVACAO       
##  5   338.  NU_MATRICULAS            
##  6   321.  SG_UF_ESCOLA             
##  7   246.  PC_FORMACAO_DOCENTE      
##  8   144.  NU_PARTICIPANTES         
##  9    50.4 NU_TAXA_PERMANENCIA      
## 10     0   TP_LOCALIZACAO_ESCOLA    
## 11     0   NU_PARTICIPANTES_NEC_ESP 
## 12     0   PORTE_ESCOLA

predict(tree_MAT, newdata = escola, type = "prob")

##          boa   regular
## 1 0.06753131 0.9324687

Classificação multi-classes

Agora, em vez de classificar a nota da escola em uma prova como "boa" ou "regular", será incluída uma categoria intermediária: "ruim".

Nota de Redação

summary(base_treino$NU_MEDIA_RED)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   345.0   508.4   547.2   564.0   609.6   920.0

Definição da variável alvo

A nota de redação de uma escola será considerada boa se ela for maior que 600, ruim se ela for menor que 500 e regular caso contrário.

base_treino_RED_3 = base_treino |>
  mutate(NOTA_RED = 
           ifelse(
             base_treino$NU_MEDIA_RED>600,"boa",
             ifelse(base_treino$NU_MEDIA_RED<500,"ruim",
             "regular"))) |>
  select(-c(NU_TAXA_PARTICIPACAO,
            NU_MEDIA_CN,
            NU_MEDIA_CH,
            NU_MEDIA_LP, 
            NU_MEDIA_MT,
            NU_MEDIA_RED,
            CO_ESCOLA_EDUCACENSO,
            NO_ESCOLA_EDUCACENSO
  ))
base_treino_RED_3$NOTA_RED = as.factor(base_treino_RED_3$NOTA_RED)
summary(base_treino_RED_3$NOTA_RED)

##     boa regular    ruim 
##    3278    6126    2296

Ajuste do modelo

tree_RED_3 <- rpart(NOTA_RED ~ ., 
              data = base_treino_RED_3, 
              method = "class")
saveRDS(tree_RED_3,file="arquivos-de-trabalho/tree_RED_3.rds")

Esse processo com três classe já fica bem mais custoso do que o com duas classes.

rpart.plot(tree_RED_3,type=5,cex=1)

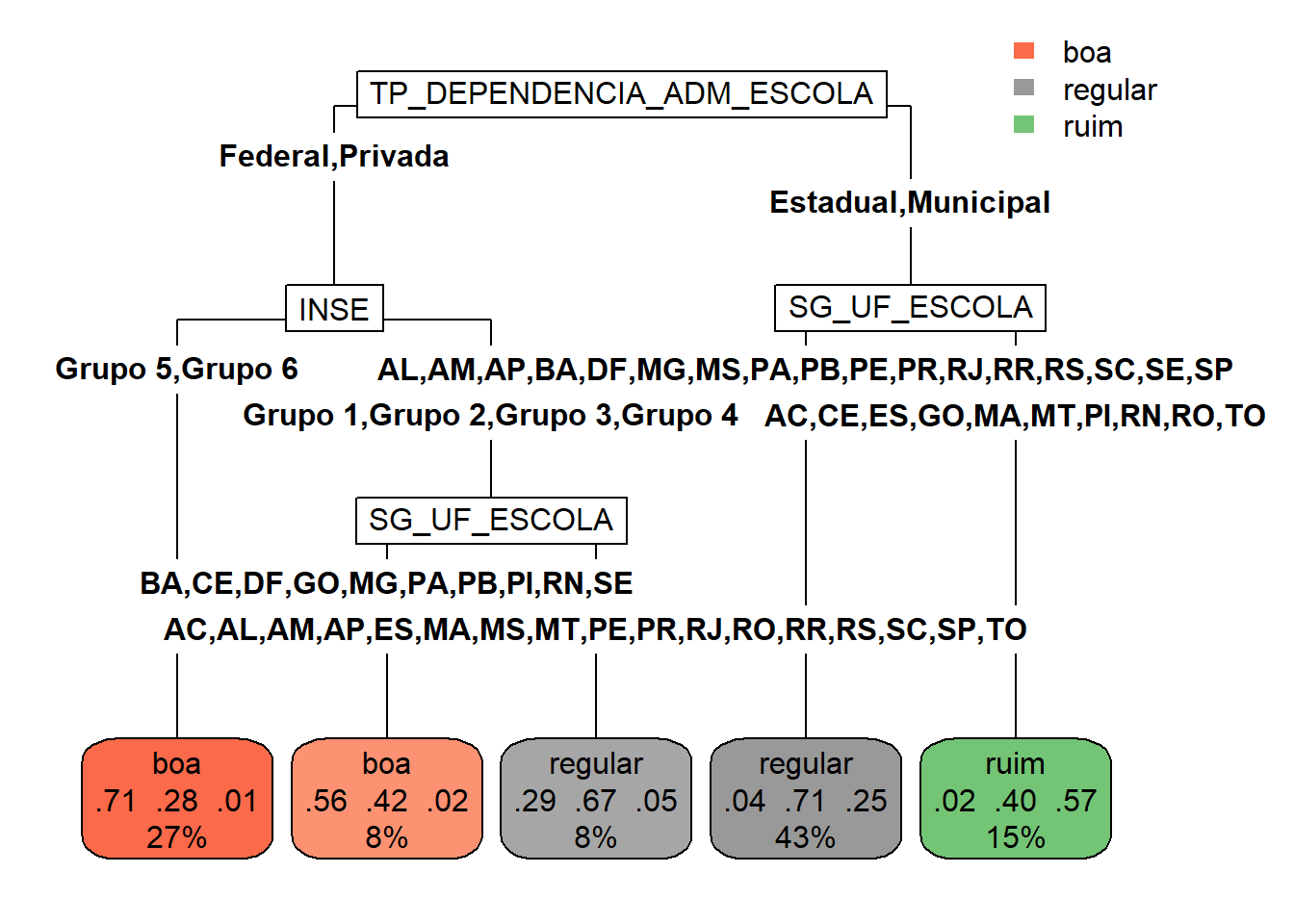
Variáveis Importantes

As variáveis mais relevantes para o problema são apresentadas com o código a seguir, o mesmo para os problemas de duas classes.

imp <- caret::varImp(tree_RED_3, scale = FALSE)
importancia = tibble(overall = imp$Overall,
                     var = rownames(imp))
importancia |> arrange(desc(overall))

## # A tibble: 11 × 2
##    overall var                      
##      <dbl> <chr>                    
##  1  1483.  INSE                     
##  2  1377.  TP_DEPENDENCIA_ADM_ESCOLA
##  3   857.  NU_TAXA_ABANDONO         
##  4   581.  SG_UF_ESCOLA             
##  5   273.  NU_TAXA_REPROVACAO       
##  6   268.  PC_FORMACAO_DOCENTE      
##  7    90.6 NU_MATRICULAS            
##  8    72.9 PORTE_ESCOLA             
##  9    15.8 NU_TAXA_PERMANENCIA      
## 10     0   TP_LOCALIZACAO_ESCOLA    
## 11     0   NU_PARTICIPANTES_NEC_ESP

Previsão para novas observações

predict(tree_RED_3, newdata = escola, type = "prob")

##          boa   regular      ruim
## 1 0.04439534 0.7097228 0.2458819

Nota de Matemática

Agora para a nota em matemática.

summary(base_treino$NU_MEDIA_MT)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   372.4   442.9   471.3   492.4   527.8   845.7

Definição da variável alvo

A nota de matemática será considerada boa se ela for maior que 520, ruim se ela for menor que 450 e regular caso contrário.

base_treino_MAT_3 = base_treino |>
  mutate(NOTA_MAT = 
           ifelse(
             base_treino$NU_MEDIA_MT>520,"boa",
             ifelse(
               base_treino$NU_MEDIA_MT<450,"ruim","regular"))) |> 
  select(-c(NU_TAXA_PARTICIPACAO,
            NU_MEDIA_CN,
            NU_MEDIA_CH,
            NU_MEDIA_LP, 
            NU_MEDIA_MT,
            NU_MEDIA_RED,
            CO_ESCOLA_EDUCACENSO,
            NO_ESCOLA_EDUCACENSO
  ))
base_treino_MAT_3$NOTA_MAT = as.factor(base_treino_MAT_3$NOTA_MAT)
summary(base_treino_MAT_3$NOTA_MAT)

##     boa regular    ruim 
##    3219    4761    3720

Ajuste do Modelo

tree_MAT_3 <- rpart(NOTA_MAT ~ ., 
              data = base_treino_MAT_3, 
              method = "class")
saveRDS(tree_MAT_3,file="arquivos-de-trabalho/tree_MAT_3.rds")

Esse processo com três classe já fica bem mais custoso do que o com duas classes.

rpart.plot(tree_MAT_3,type=5,cex=1)

Variáveis Importantes

imp <- caret::varImp(tree_MAT_3, scale = FALSE)
importancia = tibble(overall = imp$Overall,
                     var = rownames(imp))
importancia |> arrange(desc(overall))

## # A tibble: 12 × 2
##    overall var                      
##      <dbl> <chr>                    
##  1  2605.  INSE                     
##  2  2381.  TP_DEPENDENCIA_ADM_ESCOLA
##  3  1610.  NU_TAXA_ABANDONO         
##  4  1428.  SG_UF_ESCOLA             
##  5   261.  NU_TAXA_REPROVACAO       
##  6   248.  PC_FORMACAO_DOCENTE      
##  7    65.1 NU_TAXA_PERMANENCIA      
##  8    39.3 NU_PARTICIPANTES         
##  9     0   TP_LOCALIZACAO_ESCOLA    
## 10     0   NU_MATRICULAS            
## 11     0   NU_PARTICIPANTES_NEC_ESP 
## 12     0   PORTE_ESCOLA

Previsão

predict(tree_MAT_3, newdata = escola, type = "prob")

##          boa   regular      ruim
## 1 0.03051911 0.6317741 0.3377068

3.1.5 Atividade

Trabalhar novamente com a base Bike Sharing Dataset.

Problema de Classificação Binária

I. Prever, para um dado dia, uma vez conhecidas as características relacionadas ao clima e calendário, se a quantidade de bicicletas alugadas será abaixo de 4.000. Essa pode ser uma informação importante para, por exemplo, organizar os dias de manutenção das bicicletas.

A seguir um roteiro para esta atividade.

1. Abra um novo scrip do R;
2. Carregue o arquivo com a base de treino para Bike Sharing Dataset, que é resultado da última atividade.
3. Criar a nova alvo
4. Ajustar um modelo de árvores de classificação

Problema multi-classe

2. Prever, para um dado dia, uma vez conhecidas as características relacionadas ao clima e calendário, se a quantidade de bicicletas alugadas será abaixo de 4.000, acima de 6.000 ou entre esses dois valores.

O roteiro anterior serve também para esta atividade.

3.2 Árvores de Regressão

As árvores de regressão são métodos baseados em árvores de decisão para o caso da variável alvo ser quantitativa. O método de construção da árvore é muito parecido com aquele apresentado para árvores de classificação, mas neste caso o índice de Gine não é adequado e é preciso definir outra medida de impureza.

Outra diferença é na forma de previsão, que para as árvores de regressão será a média dos valores da variável resposta em cada folha.

As animações apresentadas nas Figuras 3.7 e 3.8 ilustram um problema de regressão com duas covariáveis. A variável alvo é quantitativa e está representada pela escala de cor. Por exemplo, quanto mais perto do vermelho, maior o valor; quanto mais perto do azul, menor o valor.

Figura 3.7: Ilustração da construção de uma Árvore de Decisão

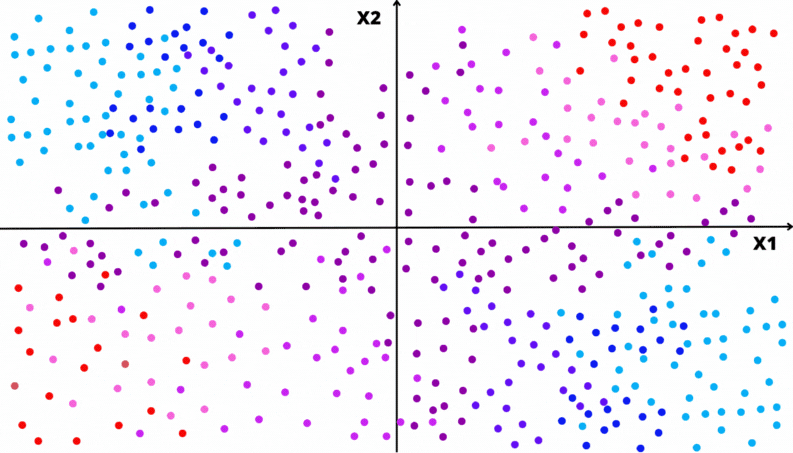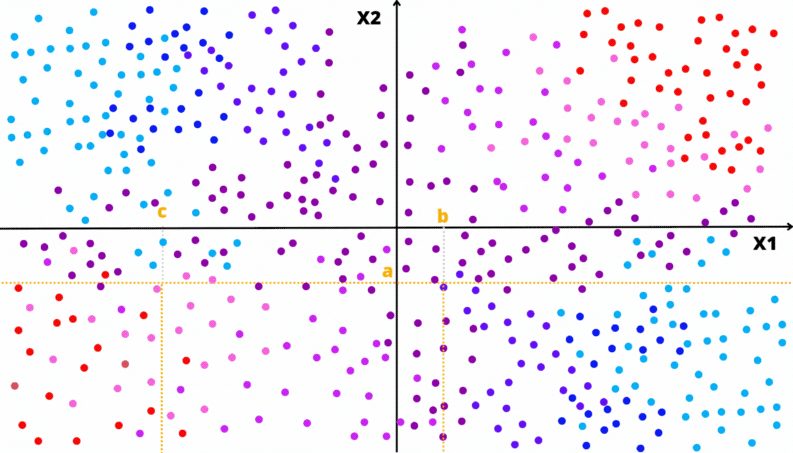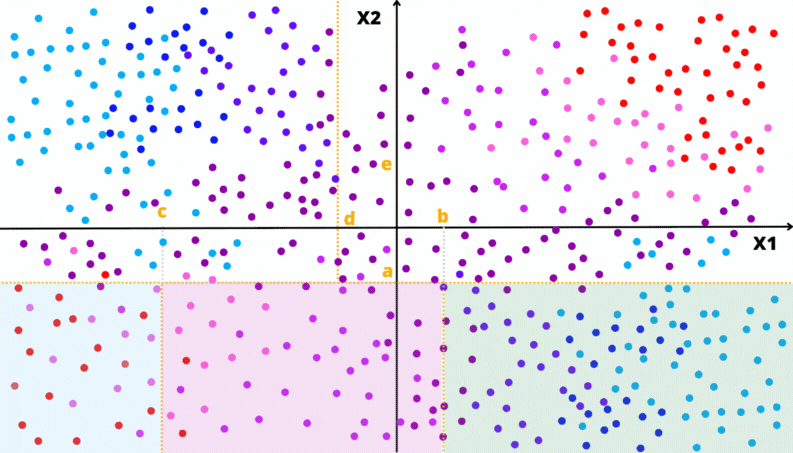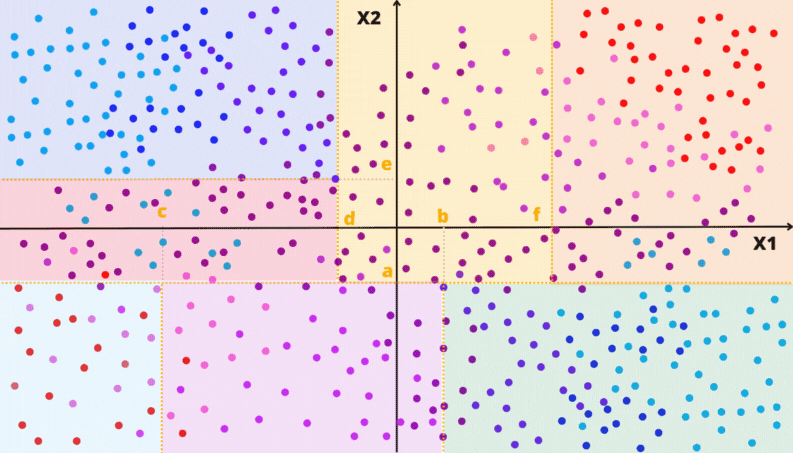
Figura 3.8: Ilustração da partição do domínio por uma Árvore de Decisão

3.2.1 Medida de impureza

Para um conjunto de variávels quantitativas as maneiras mais comuns de medir a impureza dos valores são o MSE (Mean Squase Erro) ou o RSS (Residual Sum of Squares), este inclusive usado no material (James et al. 2013).

Seja \(Y\) a variável alvo e \(Y_i\) a \(i\)-ésima observação dela. Considere também \(R\) uma região do \(\mathbb{R}^p\), \(I\) os índices dos dados de entrada que pertencem à \(R\) e \(n\) a quantidade de elementos em \(I\), isto é, o número de pontos da base de entrada que pertencem à \(R\). A média dos valores da base de entrada em \(R\) pode ser definida por: \[ \bar{Y} = \sum_{i \in I} \dfrac{Y_i}{n}. \] E, para o caso das árovers de regressão, os valores de \(MSE\) e do \(RSS\) na região \(R\) são:

\[ MSE_R = \dfrac{\sum_{i \in I} (Y_i - \bar{Y})^2}{n} \ \ \ \ \text{e} \ \ \ \ RSS_R = \sum_{i \in I} (Y_i - \bar{Y})^2 \]

Entendemos que um método de regressão é bom quando os valores de \(MSE\) ou \(SSE\) são baixos. Ou seja, para dois modelos de classificação pra mesma base de dados e variável alvo, aquele com menor valor de \(MSE\) e \(RSS\) será o mais adequado para o problema.

3.2.2 Algoritmo

1. Define-se os critérios de parada, que em geral são: um valor limite para o MSE ou RSS; a quantidade de elementos que chegaram ao nó; ou a profundidade da árvore.

2. Considere \(X\) o conjunto dos dados de entrada e \(X_j\) as covariáveis do problema.

3. Escolhe-se a variável \(j\) e o valor \(s\) tais que minimizam a soma dos MSE (ou RSS) nos conjuntos \(R_1 = \{X|X_j < s\}\) e \(R2 = \{X|X_j \ge s\}\).

Sejam \(Y_1\) os valores das variáveis alvo dos pontos de \(X\) que pertencem à \(R_1\) e \(Y_2\) os valores das variáveis alvo dos pontos de \(X\) que pertencem à \(R_2\)

4. Verifique se um dos critérios de parada foi atingido pelos elementos de \(Y_1\). Se sim, este nó é uma folha e FIM. Se não, faça \(X = R_1\) e volte para o passo 3.

5. Verifique se um dos critérios de parada foi atingido pelos elementos de \(Y_2\). Se sim, este nó é uma folha e FIM. Se não, faça \(X = X_2\) e volte para o passo 3.

3.2.3 Como realizar previsão

Uma vez que a árvore de regressão é construída, ela pode ser utilizada para fazer previsões para novos exemplos. Isso é feito percorrendo a árvore a partir da raiz até chegar a uma folha correspondente. O valor previsto é geralmente a média dos valores da variável alvo das amostras de treinamento que pertencem a essa folha.

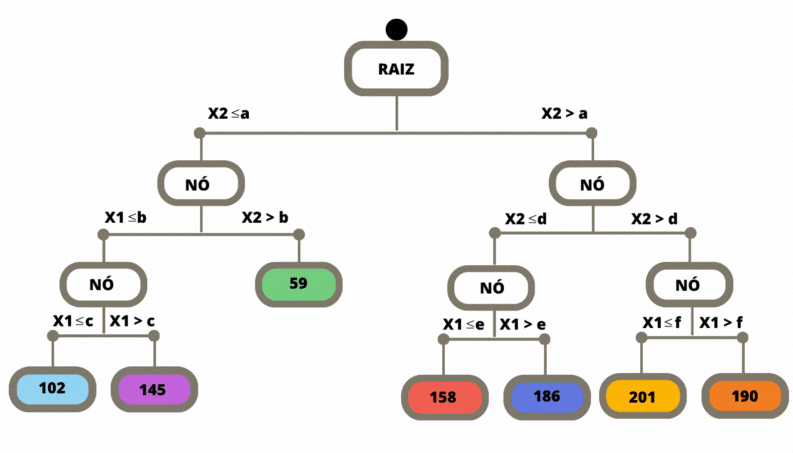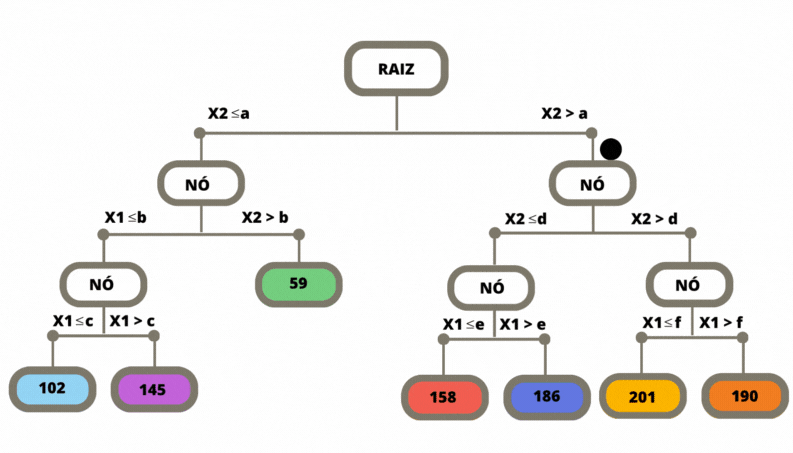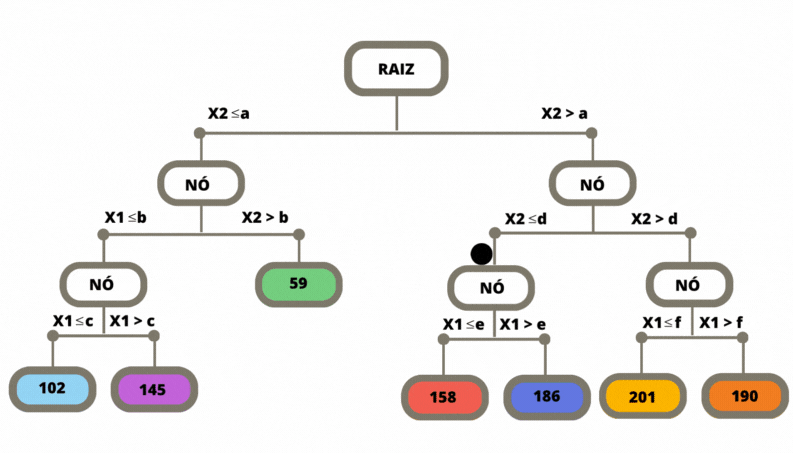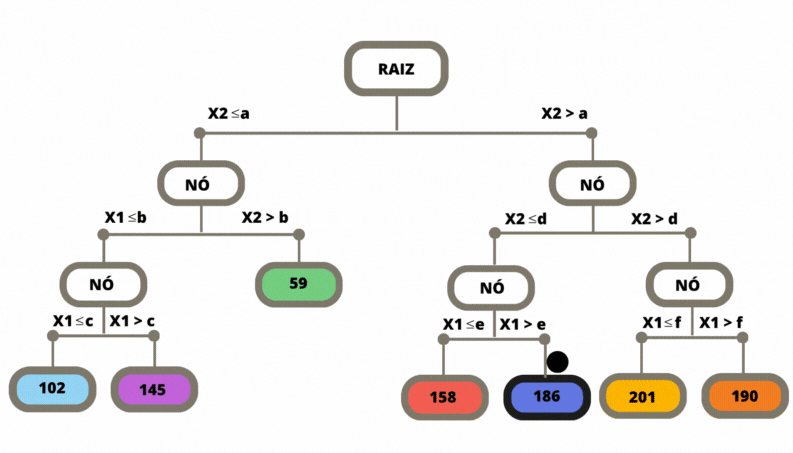
Figura 3.9: Previsão em uma Árvore de Classificação

3.2.4 Vamos praticar

Segue-se analisando a base com informações sobre as escolas. O arquivo que foi salvo depois do Capítulo 2 pode ser recuperado e a base de treino final obtida.

library(tidyverse)
#install.packages("rpart")
library(rpart)
base_treino = readRDS(file="arquivos-de-trabalho/base_treino_final.rds")

O problema proposto será prever a nota de uma escola em uma determinada prova.

Nota em Redação

Vamos começar considerando como variável de interesse a nota das escolas em redação.

summary(base_treino$NU_MEDIA_RED)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   345.0   508.4   547.2   564.0   609.6   920.0

Definição da variável alvo

A variável alvo para este problema será aquela que guarda a média das notas dos alunos de cada escola em redação.

Ajuste do Modelo

O modelo é ajustado com a função rpart, do pacote rpart (Therneau and Atkinson 2022) e é indicado que o problema é de regressão através do argumento method = "reg".

Lembre-se de retirar da base de treino as demais variáveis alvo e também as variáveis de identificação.

tree_RD <- rpart(NU_MEDIA_RED ~ ., 
              data = base_treino |>
                select(-c(CO_ESCOLA_EDUCACENSO,
                          NO_ESCOLA_EDUCACENSO,
                          NU_PARTICIPANTES,
                          NU_TAXA_PARTICIPACAO,
                          NU_MEDIA_CN, 
                          NU_MEDIA_CH, 
                          NU_MEDIA_MT, 
                          NU_MEDIA_LP))) 
saveRDS(tree_RD,file="arquivos-de-trabalho/tree_RD.rds")

Carregar o pacote rpart.plot (Milborrow 2022) gera gráficos mais bonitos.

#install.packages("rpart.plot")
library("rpart.plot")
rpart.plot(tree_RD,type=5,cex=1)

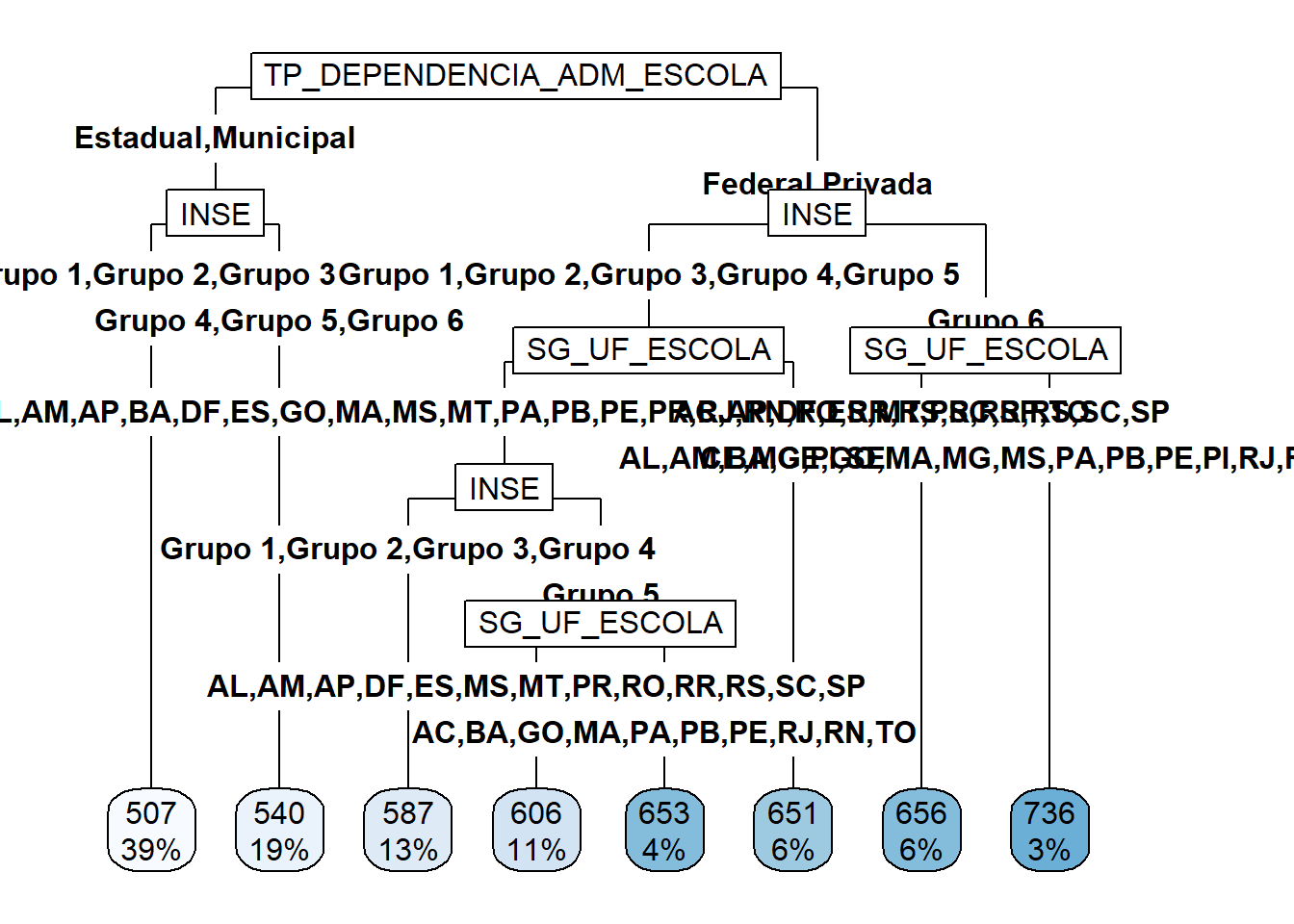
Variáveis Importantes

Ainda é possível obter as variáveis mais relevantes para o problema com a função varImp do pacote caret (Kuhn 2022). A importância (overall) de uma variável é calculada com base na redução do índice de Gini quando esta variável é removida da base. Para isso são feitas combinações das covariáveis e, para cada combinação, uma árvore é gerada. Então calcula-se a média dos \(MSE\) ou \(SSE\) das árvores geradas com a covariável no ajuste. Depois calcula-se a média dos \(MSE\) ou \(SSE\) das árovores geradas sem a covariável no ajuste. A diferença entre as duas médias é o valor do overall (Kuhn 2008). Quando maior este valor, maior a importância da variável para o problema.

imp <- caret::varImp(tree_RD, scale = FALSE)
importancia = tibble(overall = imp$Overall,
                     var = rownames(imp))
importancia |> arrange(desc(overall))

## # A tibble: 11 × 2
##    overall var                      
##      <dbl> <chr>                    
##  1  0.788  INSE                     
##  2  0.664  SG_UF_ESCOLA             
##  3  0.489  TP_DEPENDENCIA_ADM_ESCOLA
##  4  0.379  PC_FORMACAO_DOCENTE      
##  5  0.351  NU_TAXA_ABANDONO         
##  6  0.236  NU_MATRICULAS            
##  7  0.201  PORTE_ESCOLA             
##  8  0.0607 NU_TAXA_REPROVACAO       
##  9  0.0149 NU_TAXA_PERMANENCIA      
## 10  0      TP_LOCALIZACAO_ESCOLA    
## 11  0      NU_PARTICIPANTES_NEC_ESP

# Visualizar a importância das variáveis

Previsão para novas observações

E se quiséssemos usar a árvore criada para realizar previsões, ou seja, dadas as características de uma escola qual seria a nota média dos alunos desta escola na redação do ENEM?

Vamos adotar valores para as covariáveis do problema para 5 escolas hipotéticas. Para realizar uma previsão na árvore é preciso criar um data.frame ou tibble com o mesmo padrão das linhas da base de treino. Os nomes das variáveis têm que ser os mesmos.

escolas = tibble(
SG_UF_ESCOLA = c("RJ","SP","MG","AM","RS"),
TP_DEPENDENCIA_ADM_ESCOLA = c("Estadual","Privada","Estadual","Municipal","Federal"),
TP_LOCALIZACAO_ESCOLA = c("Urbana","Urbana","Urbana","Rural","Urbana"),
NU_MATRICULAS = c(87,44,102,21,80),
NU_PARTICIPANTES_NEC_ESP = c(1,2,0,0,1),
INSE = c("Grupo 3","Grupo 6","Grupo 4","Grupo 2","Grupo 4"),
PC_FORMACAO_DOCENTE = c(48.1 , 75.7 , 68.8 , 51.2 , 70.3),
NU_TAXA_PERMANENCIA = c(67,100,92,87,75),
NU_TAXA_REPROVACAO = c(6.1,3.3, 9.1, 8.7,5.6),
NU_TAXA_ABANDONO = c(0,0,1, 2, 3),
PORTE_ESCOLA = c("De 61 a 90 alunos","Maior que 90 alunos","De 61 a 90 alunos","De 31 a 60 alunos","Maior que 90 alunos"))

escolas

## # A tibble: 5 × 11
##   SG_UF_…¹ TP_DE…² TP_LO…³ NU_MA…⁴ NU_PA…⁵ INSE  PC_FO…⁶ NU_TA…⁷ NU_TA…⁸ NU_TA…⁹
##   <chr>    <chr>   <chr>     <dbl>   <dbl> <chr>   <dbl>   <dbl>   <dbl>   <dbl>
## 1 RJ       Estadu… Urbana       87       1 Grup…    48.1      67     6.1       0
## 2 SP       Privada Urbana       44       2 Grup…    75.7     100     3.3       0
## 3 MG       Estadu… Urbana      102       0 Grup…    68.8      92     9.1       1
## 4 AM       Munici… Rural        21       0 Grup…    51.2      87     8.7       2
## 5 RS       Federal Urbana       80       1 Grup…    70.3      75     5.6       3
## # … with 1 more variable: PORTE_ESCOLA <chr>, and abbreviated variable names
## #   ¹​SG_UF_ESCOLA, ²​TP_DEPENDENCIA_ADM_ESCOLA, ³​TP_LOCALIZACAO_ESCOLA,
## #   ⁴​NU_MATRICULAS, ⁵​NU_PARTICIPANTES_NEC_ESP, ⁶​PC_FORMACAO_DOCENTE,
## #   ⁷​NU_TAXA_PERMANENCIA, ⁸​NU_TAXA_REPROVACAO, ⁹​NU_TAXA_ABANDONO
## # ℹ Use `colnames()` to see all variable names

predict(tree_RD, newdata = escolas, type = "vector")

##        1        2        3        4        5 
## 507.0903 656.4227 539.8623 507.0903 587.1707

3.2.4.0.1 Medidas de erro

Para medir a impureza em cada folha precisamos saber quais pontos da base chegaram na folha em questão. A folha mais à esquerda foi nomeada por 3, pois a numeração é feita sempre da raíz para as folhas e da esquerda para a direita.

O comando abaixo mostra quantos pontos estão em cada uma das folhas, que foram numeradas pelos números 3, 4, 8, 10, 11, 12, 14 e 15.

table(tree_RD$where)

## 
##    3    4    8   10   11   12   14   15 
## 4515 2193 1481 1345  477  677  706  306

Primeiro são guardados os valores da variável alvo para as observações que terminaram na primeira folha, aquela de número 3.

indices = which(tree_RD$where == 3)
Y = base_treino |> slice() |> 
  select(NU_MEDIA_RED)
Y = Y$NU_MEDIA_RED

Depois definimos os valores previstos para cada um desses pontos, que será a média deles.

(Y_ = mean(Y))

## [1] 563.9521

Veja que este número está impresso na primeira folha da árvore.

Por é possível calcular a média dos erros ao quadrado e a soma dos erros ao quadrado.

(MSE = mean((Y - Y_)^2))

## [1] 6029.432

(RSS = sum((Y - Y_)^2))

## [1] 70544352

Nota de Matemática

Agora as mesmas análises serão reproduzidas para a nota de matemática.

Definição da variável alvo

A variável alvo para este problema será aquela que guarda a média das notas dos alunos de cada escola em matemática.

Ajuste do Modelo

A variável alvo para este problema será aquela que guarda a média das notas dos alunos de cada escola em redação.

summary(base_treino$NU_MEDIA_MT)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   372.4   442.9   471.3   492.4   527.8   845.7

tree_MT <- rpart(NU_MEDIA_MT ~ ., 
                 data = base_treino |>
                   select(-c(CO_ESCOLA_EDUCACENSO,
                             NO_ESCOLA_EDUCACENSO,
                             NU_PARTICIPANTES,
                             NU_TAXA_PARTICIPACAO,
                             NU_MEDIA_CN, 
                             NU_MEDIA_CH, 
                             NU_MEDIA_RED, 
                             NU_MEDIA_LP)))
saveRDS(tree_MT,file="arquivos-de-trabalho/tree_MT.rds")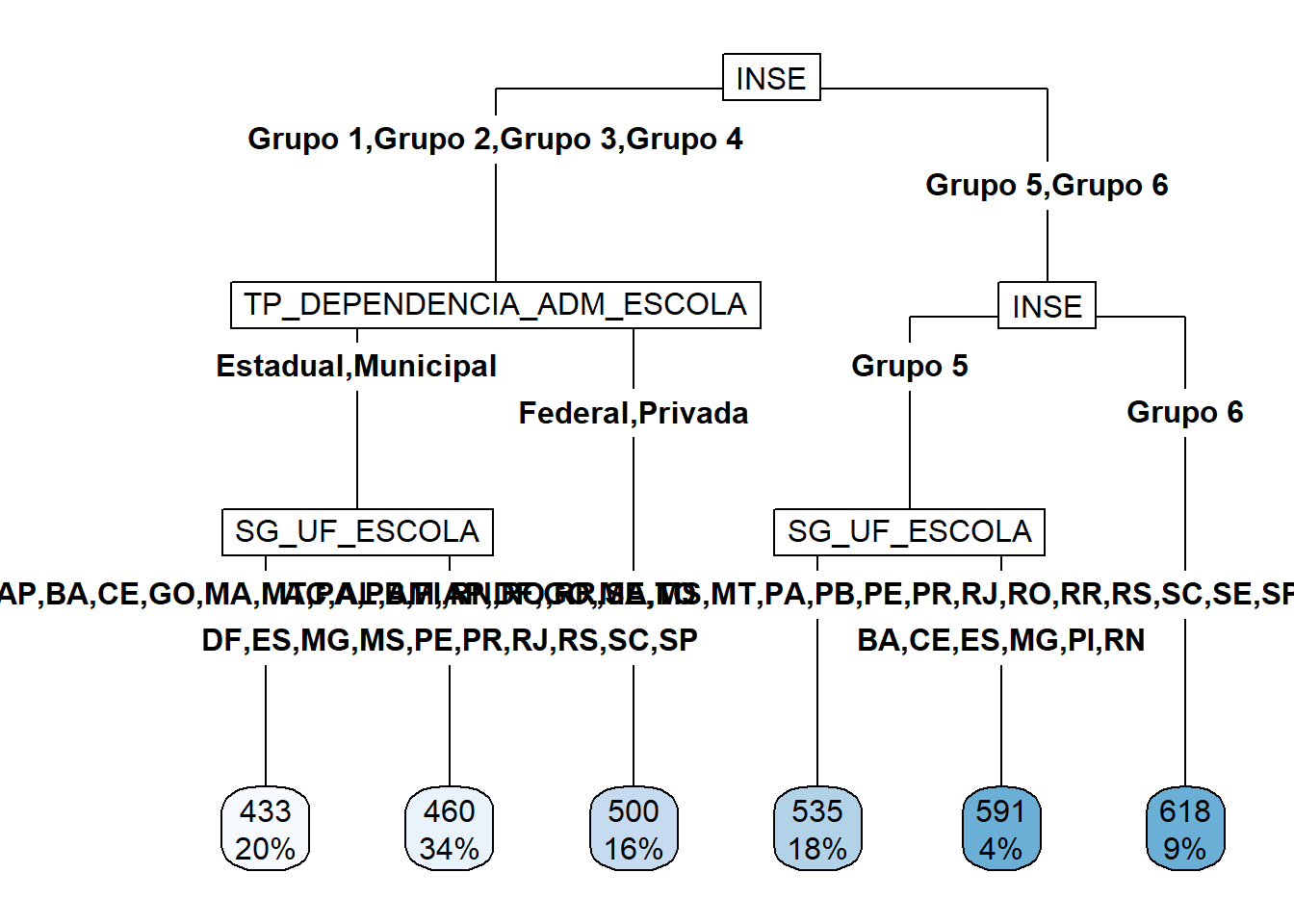

rpart.plot(tree_MT,type=5,cex=1)

Variáveis Importantes

imp <- caret::varImp(tree_MT, scale = FALSE)
importancia = tibble(overall = imp$Overall,
                     var = rownames(imp))
importancia |> arrange(desc(overall))

## # A tibble: 11 × 2
##    overall var                      
##      <dbl> <chr>                    
##  1  1.06   INSE                     
##  2  0.918  TP_DEPENDENCIA_ADM_ESCOLA
##  3  0.623  NU_TAXA_ABANDONO         
##  4  0.569  SG_UF_ESCOLA             
##  5  0.0992 NU_TAXA_REPROVACAO       
##  6  0.0990 PC_FORMACAO_DOCENTE      
##  7  0.0529 NU_TAXA_PERMANENCIA      
##  8  0      TP_LOCALIZACAO_ESCOLA    
##  9  0      NU_MATRICULAS            
## 10  0      NU_PARTICIPANTES_NEC_ESP 
## 11  0      PORTE_ESCOLA

Previsão para novas observações

predict(tree_MT, newdata = escolas, type = "vector")

##        1        2        3        4        5 
## 460.1370 617.5129 460.1370 433.0279 499.8683

3.2.4.0.2 Medidas de erro

Observar o número de pontos por folha.

table(tree_MT$where)

## 
##    4    5    6    9   10   11 
## 2369 3991 1858 2048  416 1018

Criar uma base de dados somente com as observações que chegam na folha 5.

indices = which(tree_MT$where == 5)
Y = base_treino |> 
  slice(indices) |> 
  select(NU_MEDIA_MT)
Y = Y$NU_MEDIA_MT
mean(Y)

## [1] 460.137

Calcular a média da variável resposta destas observações.

Y_ = mean(Y)

Por fim, as medidas de erro para esta folha.

(MSE = mean((Y - Y_)^2))

## [1] 731.6874

(RSS = sum((Y - Y_)^2))

## [1] 2920164

3.2.5 Atividade

Trabalhar novamente com a base Bike Sharing Dataset.

Problema de Regressão

I. Prever, para um dado dia, uma vez conhecidas as características relacionadas ao clima e calendário, a quantidade de bicicletas alugadas.

A seguir um roteiro para esta atividade.

1. Abra um novo scrip do R;
2. Carregue o arquivo com a base de treino para Bike Sharing Dataset, que é resultado da última atividade.
3. Ajustar um modelo de árvores de classificação

2. Criar exemplos hipotéticos para as covariáveis e encontrar a previsão dada pela a árvore para o número de bicicletas alugadas nos dias em questão.

3.3 Referênicas

References

James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning. Vol. 112. Springer.

Kuhn, Max. 2008. “Building Predictive Models in r Using the Caret Package.” Journal of Statistical Software 28: 1–26.

———. 2022. Caret: Classification and Regression Training. https://CRAN.R-project.org/package=caret.

Milborrow, Stephen. 2022. Rpart.plot: Plot ’Rpart’ Models: An Enhanced Version of ’Plot.rpart’. https://CRAN.R-project.org/package=rpart.plot.

Therneau, Terry, and Beth Atkinson. 2022. Rpart: Recursive Partitioning and Regression Trees. https://CRAN.R-project.org/package=rpart.