Capítulo 5 Gradiente Boosting
Assim como a Floresta Aleatória de Breiman (Breiman 2001), o Gradiente Boosting de Friedman (Friedman 2001) é um método para dados supervisionados que combina muitas árvores para gerar uma única previsão. Mas a maneira que as árvores são construídas e a previsão final são bem diferentes entre os dois métodos.
Como já visto no capítulo anterior, a Floresta Aleatória é um método de aprendizagem de conjunto (ensemble learning) que combina várias árvores de decisão para fazer previsões. Cada árvore de decisão é treinada em uma amostra aleatória do conjunto de dados, usando a técnica bootstrapping (amostragem com reposição). Além disso, em cada divisão de uma árvore de decisão da floresta, apenas um subconjunto aleatório de variáveis é considerado para escolher a melhor divisão. No final, as previsões de cada árvore são combinadas para se obter a previsão final.
Podemos dizer que as árvores da Floresta Aleatória são construídas “em paralelo”, são árvores independentes e as previsões de todas elas, que podem ser feitas ao mesmo tempo, resulta no modelo final. Já o Boosting constrói as árvores “em série”, de forma sequencial. Cada nova árvore é treinada para corrigir os erros cometidos pelas árvores anteriores. As árvores não são independentes e o resultado final precisa passar por cada uma das árvores, na ordem em que elas foram construídas, para ser obtido.
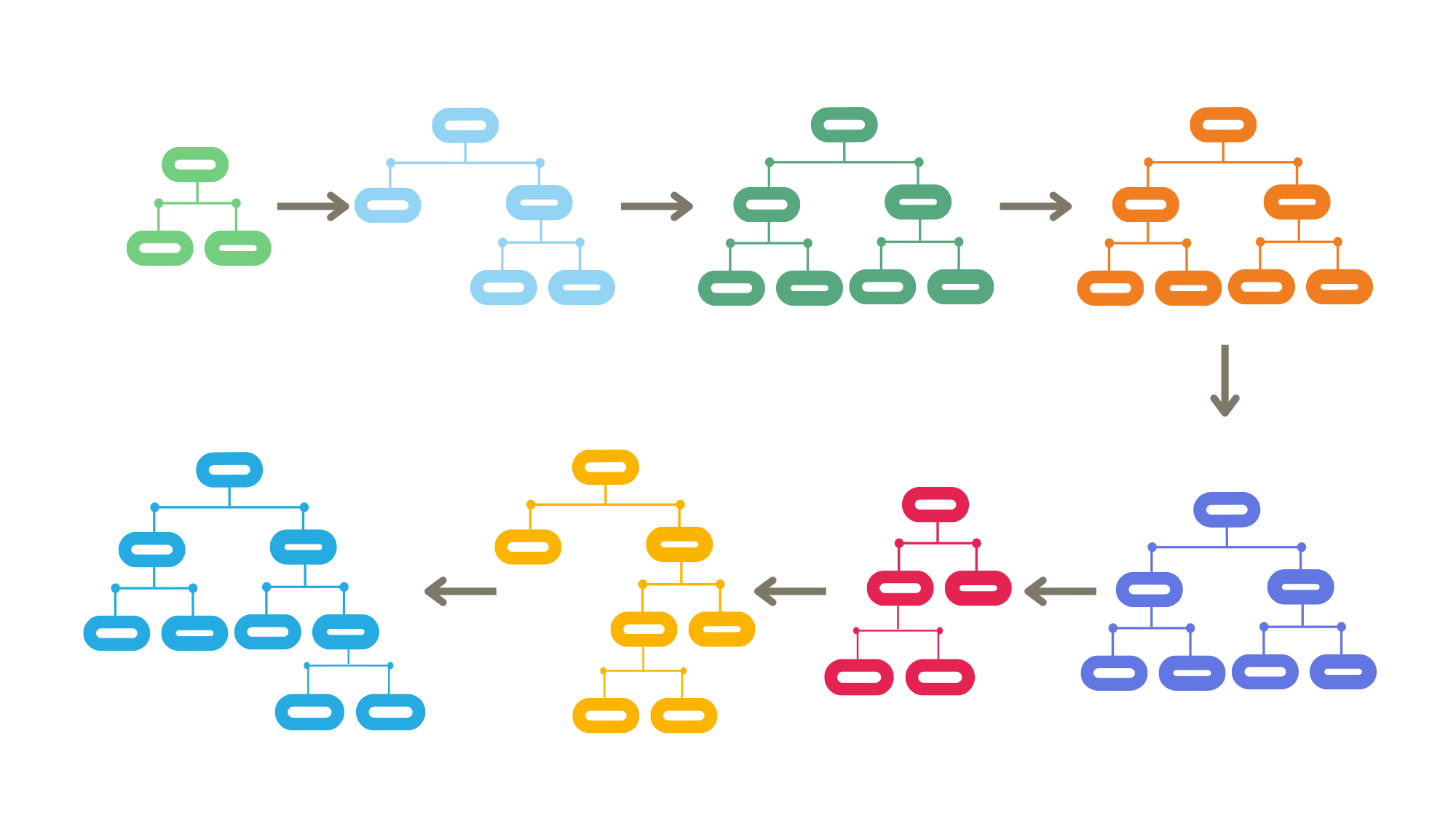
Figura 5.1: Gradiente Boosting
5.1 Boosting
Os métodos de aprendizado Boosting são uma classe de algoritmos de aprendizado de máquina que combinam vários modelos fracos para formar um modelo forte e de alta precisão. A ideia central do Boosting é treinar os modelos de forma sequencial, onde cada novo modelo é construído para corrigir os erros cometidos pelos modelos anteriores.
O Boosting é conhecido por sua capacidade de melhorar gradualmente a precisão do modelo à medida que novos modelos são adicionados. Ele é especialmente eficaz em problemas complexos e difíceis, onde um único modelo fraco não é suficiente para obter um bom desempenho.
5.2 O Método
De forma bem geral, o Gradiente Boosting começa com um primeiro método de aprendizado bem simples, conhecido como aprendizado fraco. Este método pode ser uma árvore com uma única partição ou até mesmo a média amostral, para o caso de regressão, ou a proporção das classes, para o caso de classificação. vamos chamar o aprendizado fraco de \(A_0\), que retorna uma previsão para cada observação \(\mathbf{x}_i\), denominado \(A_0(\mathbf{x}_i)\). Considerando o método apenas com o aprendizado fraco, a previsão para o observação \(\mathbf{x}_i\) será dada por:
\[F_0(\mathbf{x}_i) = A_0(\mathbf{x}_i)\] sendo \(F_0(\mathbf{x}_i)\) a previsão do Gradiente Boosting para a observação \(\mathbf{x}_i\) no momento inicial.
Em seguida são calculados os erros cometidos na base de treino. Chama-se \(e^0_i\) o erro da observação \(i\) no momento inicial do método.
\[ e^0_i = y_i - F_0(\mathbf{x}_i) \]
Uma nova árvore é ajustada, mas agora a variável resposta é o erro \(\mathbf{e^0}\). Vamos chamar essa árvore de \(A_1\), que é a primeira árvore construída para prever o erro. Denomina-se \(A_1(\mathbf{x}_i)\) a previsão dada por \(A_1\) para cada observação \(\mathbf{x}_i\). Com estas duas árvores o método fornece como previsão para a observação \(\mathbf{x}_i\)
\[ F_1(\mathbf{x}_i) = F_0(\mathbf{x}_i) + A_1(\mathbf{x}_i) \]
Sendo \(F_1(\mathbf{x}_i)\) a previsão dada pelo Gradiente Boosting na primeira iteração. Novamente é encontrado o erro cometido pelo método:
\[ e^1_i = y_i - F_1(\mathbf{x}_i). \] O erro sempre será a diferença entre o valor observado e o valor previsto pela última iteração do método. Mais uma árvore é ajustada, agora para prever os erros \(\mathbf{e^1}\). O processo é repetido até que se tenha construído as \(M\) árvores previstas pelo algoritmo.
Veja que é sempre possível escrever a previsão do método na iteração \(m\) em termos da sua previsão na iteração anterior:
\[ F_m(\mathbf{x}_i) = F_{m-1}(\mathbf{x}_i) + A_m(\mathbf{x}_i) \]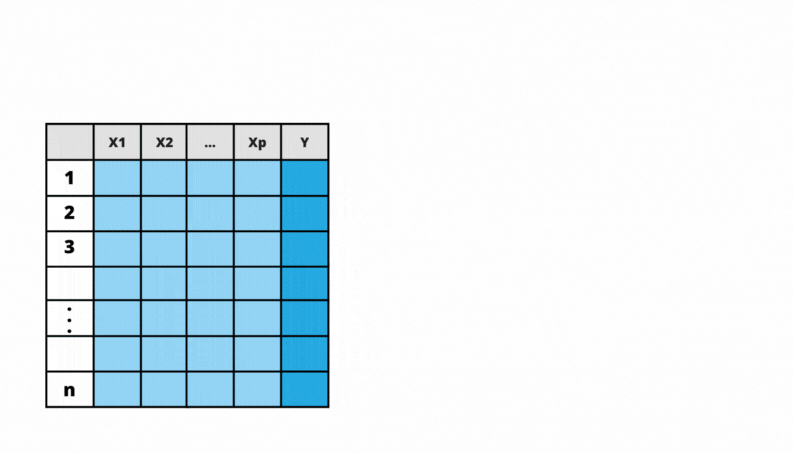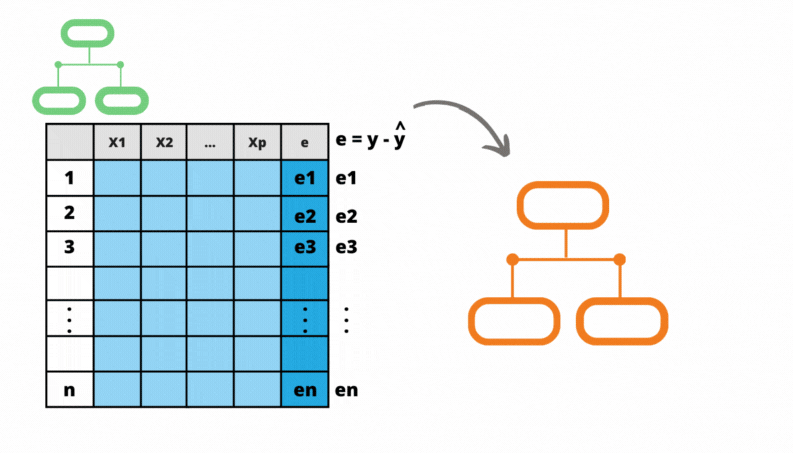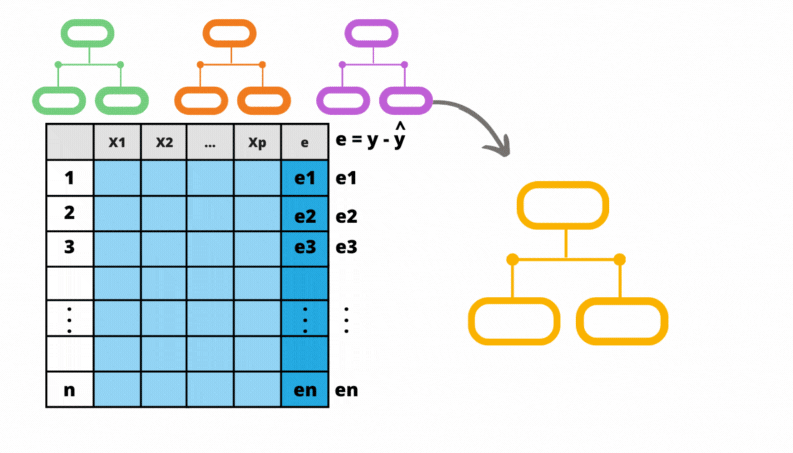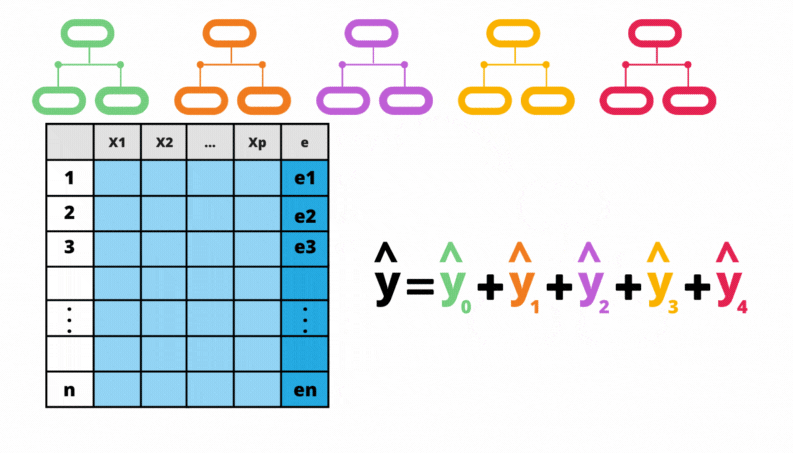
Figura 5.2: Gradiente Boosting
5.3 Regularização
A maior preocupação ao construir um modelo de aprendizado de máquina a partir de dados é a capacidade de generalização do modelo. Se o algoritmo de aprendizado não for aplicado corretamente, o modelo pode facilmente superajustar os dados. Esta também é uma preocupação para o método do Gradiente Boosting (Natekin and Knoll 2013).
5.3.1 Subamostragem
A técnicas mais simples de regularização é a subamostragem. A ideia é introduzir algum grau de aleatoriedade no procedimento de ajuste. Para isso, para cada árvore construída apenas uma parte aleatória dos dados de treinamento é usada, normalmente os dados de treinamento são amostrados sem reposição.
Esta etapa gera um hiperparâmetro chamado de “fração de amostragem” (bag. fraction), que especifica a proporção dos dados a serem usados em cada iteração. Por exemplo, \(\lambda = 0,1\) corresponde a usar 10% dos dados em cada iteração para o ajuste de cada árvore. Constuma-se usar \(\lambda=0,5\), mas o valor ideal para este parãmetro pode ser definido a partir de uma validação cruzada. Uma propriedade útil do subsampling é que ele se adapta naturalmente aos conjuntos grandes de dados, quando não há razão para usar todas as enormes quantidades de dados de uma só vez.
5.3.2 Taxa de Aprendizagem (shrinkage)
A abordagem clássica para controlar a complexidade do modelo é a introdução de uma taxa de aprendizado \(\nu \in (0,1]\). Esta taxa é usada para reduzir o impacto das correções dos erros e reduzir o tamanho dos passos incrementais em cada etapa. A intuição por trás dessa técnica é: chegamos à um resultado melhor com muitos pequenos passos do que com poucos grandes passos. Além disso, se uma das iterações se mostrar errônea, seu impacto negativo pode ser facilmente corrigido em etapas subsequentes.
\[ F_m(\mathbf{x}_i) = F_{m-1}(\mathbf{x}_i) + \nu A_m(\mathbf{x}_i) \]
5.4 Regressão x Classificação
Parece natural pensar no Gradiente Boosting para Regressão: temos árvores de regressão em sequência onde cada uma conserta o erro, que é um valor numérico contínua, da etapa anterior. E para o caso da classificação? O que seria o erro que será usado como variável alvo na etapa seguinte?
No método Gradient Boosting para classificação o modelo de aprendizado fraco, \(A_0\), será um modelo de classificação que retorna como previsão um número entre 0 e 1, que indica a chance da classe referência ser a classe escolhida. O erro então é calculado como a diferença entre a previsão dada por \(A_0\) e o valor de variável indicadora que representa a classe. Assim se \(A_0 \approx 1\) e a classe referência for a verdadeira, o erro será pequeno. Por outro lado, se \(A_0 \approx 1\) e a classe referência for falsa, o erro será grande.
No momento da construção de \(A_1\), a primeira árvore de correção dos erros, a variável alvo não será mais uma categoria e sim um valor contínuo que indica o erro. Daí por diante todas as árvores construídas pelo método são de regressão, mesmo o método sendo para classificação.
No entanto, é importante observar que, apesar de usar árvores de regressão para corrigir os erros, o Gradient Boosting é amplamente utilizado para problemas de classificação, onde o objetivo é prever rótulos de classe discretos. Isso é possível porque, após a etapa de treinamento do Gradient Boosting, a combinação das previsões de todas as árvores é usada para atribuir à cada instâncias um valor entre 0 e 1 que indica a classe prevista.
5.5 Algoritmo
Considere uma base de dados supervisionada, onde \(Y\) é a variável resposta (qualitativa ou quantitativa) e \(X_j\), \(j=1, 2, \ldots, p\) são as \(p\) covariáveis. Para cada observação \(i\), \(i=1, 2, \ldots, n\), isto é, para cada linha \(i\) da base, temos \(Y_i\) o valor da variável resposta para a observação \(i\) e \(X_{i,j}\) o valor ca covariável \(j\) para a observação \(i\). Posto isso, segue o algoritmo para o Método de Floresta Aleatória.
Escolhem-se os valores para os hiperparâmetros \(\lambda\), \(M\) e \(\nu\).
Ajuste o modelo fraco \(A_0\): \(F(\mathbf{x}_i) = A_0(\mathbf{x}_i)\).
Faça \(m=1\).
Calcule os erros \(e_i = y_i - F(\mathbf{x}_i)\).
Faça uma seleção aleatória simples, sem reposição, de \(\lambda \times 100\%\) da base de treino.
Ajuste uma árvore de regressão \(A_m\) para prever os erros \(e_i\) usando como base de treino o sorteio da etapa anterior.
Atualize: \(F(\mathbf{x}_i) = F(\mathbf{x}_i) + \nu A_m(\mathbf{x}_i)\).
Se \(m<M\), volte para o passo 3.
5.6 XGBoost
O XGBoost (Extreme Gradient Boosting) é uma implementação otimizada e aprimorada do algoritmo de gradiente boosting. o XGBoost também é baseado em um conjunto de árvores de decisão onde cada árvore é construída sequencialmente, corrigindo os erros residuais das árvores anteriores. Ele foi projetado para ser mais eficiente, rápido e preciso em comparação com outras implementações de gradient boosting.
Melhorias na Regularização: O XGBoost incorpora técnicas avançadas de regularização para evitar o overfitting e melhorar a capacidade de generalização do modelo. Isso inclui a adição de termos de penalidade nas funções de perda e a utilização de técnicas como a poda de árvores para evitar o crescimento excessivo.
Melhorias no tempo de execução: O XGBoost utiliza técnicas eficientes de otimização para melhorar o desempenho do modelo. Isso inclui amostragem estocástica de dados durante o treinamento e a aplicação de algoritmos de aproximação para acelerar o processo de ajuste dos parâmetros. O XGBoost também possui a capacidade de paralelizar o treinamento das árvores, aproveitando ao máximo os recursos computacionais disponíveis e acelerando o processo de ajuste do modelo.
Assim como no gradiente boosting, o XGBoost também requer o ajuste adequado de hiperparâmetros para obter os melhores resultados. Isso inclui o número de árvores, a taxa de aprendizagem, a profundidade máxima da árvore e a força da regularização, entre outros.
O XGBoost ganhou popularidade na comunidade de ciência de dados e competições de machine learning devido à sua eficiência, precisão e flexibilidade. Ele foi usado com sucesso em muitos problemas do mundo real e demonstrou um desempenho impressionante em diversas tarefas de modelagem.
5.7 Vamos praticar
Primeiro, sempre, carregar os pacotes necessários para manipulação da base de dados e a base já tratada.
# Carregar pacotes e base de treino
library(tidyverse)
library(rpart)
base_treino = readRDS(file="arquivos-de-trabalho/base_treino_final.rds")Para criar modelos de Gradiente Boosting será usado o pacote gbm (Chen et al. 2023).
Assim como para a Floresta Aleatória, para o Gradiente Boosting é fundamental fixar a semente para garantir a reprodutibilidade do código.
Serão replicados os mesmos exemplos feitos para os métodos já apresentados.
Regressão
Primeiro será ajustado um modelo para prever a nota em redação das escolas. A função a ser usada é a xgboost, do pacote de mesmo nome.
Um passo importante que precisa ser feito ao usar esta função é a transformação da base de dados, que é um data.frame, em matriz. A função xgboost não aceita data.frame como base de dados. E esta matriz deve conter somente as covariáveis.
X_treino = base_treino |> select(-c(NU_TAXA_PARTICIPACAO,
NU_MEDIA_CN,
NU_MEDIA_CH,
NU_MEDIA_LP,
NU_MEDIA_MT,
NU_MEDIA_RED,
CO_ESCOLA_EDUCACENSO,
NO_ESCOLA_EDUCACENSO,
NU_PARTICIPANTES))
M_X_treino = model.matrix(~. , data = X_treino)[,-1]Ajuste do Modelo
É preciso informar o objetivo do método, que neste exemplo é realizar uma regressão. Por isso objective = "reg:squarederror". Neste momento também é possível indicamos valores para os hiperparâmetros aprendidos na aula de hoje: nrounds, número de árvores; subsample, proporção da base referente à subamostra; e eta, a taxa de aprendizagem.
Variáveis Importantes
As variáveis importantes para esse modelo podem ser encontradas apartir do comando a seguir.
## Feature Gain Cover Frequency
## 1: TP_DEPENDENCIA_ADM_ESCOLAEstadual 5.871463e-01 0.0442016849 0.0203992104
## 2: INSEGrupo 6 5.813755e-02 0.0480205323 0.0164509761
## 3: PC_FORMACAO_DOCENTE 5.431931e-02 0.1052648347 0.1566132924
## 4: NU_MATRICULAS 4.777774e-02 0.1096735103 0.1710901513
## 5: NU_TAXA_PERMANENCIA 4.301560e-02 0.1199057347 0.1465233604
## 6: NU_TAXA_ABANDONO 3.526397e-02 0.0604876132 0.0758938364
## 7: NU_TAXA_REPROVACAO 2.929084e-02 0.0680919608 0.1151568326
## 8: INSEGrupo 5 1.938949e-02 0.0504977513 0.0188637859
## 9: SG_UF_ESCOLAMG 1.282486e-02 0.0170025948 0.0140381663
## 10: SG_UF_ESCOLASP 1.121327e-02 0.0260697522 0.0184250932
## 11: SG_UF_ESCOLACE 1.070294e-02 0.0269233804 0.0140381663
## 12: INSEGrupo 4 9.757994e-03 0.0269209985 0.0149155517
## 13: INSEGrupo 3 7.098748e-03 0.0119028585 0.0138188199
## 14: SG_UF_ESCOLAPR 6.094916e-03 0.0182971799 0.0092125466
## 15: SG_UF_ESCOLAPI 5.867498e-03 0.0145456224 0.0092125466
## 16: SG_UF_ESCOLARJ 5.619310e-03 0.0124644011 0.0133801272
## 17: SG_UF_ESCOLABA 5.250396e-03 0.0240314059 0.0098705857
## 18: NU_PARTICIPANTES_NEC_ESP 4.599596e-03 0.0134168799 0.0221539811
## 19: TP_LOCALIZACAO_ESCOLARural 4.365905e-03 0.0091275991 0.0140381663
## 20: TP_DEPENDENCIA_ADM_ESCOLAPrivada 4.142200e-03 0.0076135777 0.0092125466
## 21: INSEGrupo 2 3.970958e-03 0.0137851876 0.0129414345
## 22: SG_UF_ESCOLASC 3.694992e-03 0.0129970628 0.0078964685
## 23: TP_DEPENDENCIA_ADM_ESCOLAMunicipal 2.884194e-03 0.0120877567 0.0054836587
## 24: SG_UF_ESCOLARS 2.779124e-03 0.0078654680 0.0092125466
## 25: SG_UF_ESCOLAES 2.548280e-03 0.0117519029 0.0081158149
## 26: SG_UF_ESCOLAPB 2.351754e-03 0.0227442644 0.0067997368
## 27: SG_UF_ESCOLAGO 2.272406e-03 0.0065071659 0.0081158149
## 28: SG_UF_ESCOLADF 2.242796e-03 0.0108824944 0.0052643123
## 29: SG_UF_ESCOLASE 2.084472e-03 0.0169439395 0.0052643123
## 30: SG_UF_ESCOLAPE 2.017845e-03 0.0066730086 0.0070190831
## 31: SG_UF_ESCOLAPA 1.986872e-03 0.0174691576 0.0054836587
## 32: PORTE_ESCOLADe 31 a 60 alunos 1.893989e-03 0.0058178917 0.0081158149
## 33: SG_UF_ESCOLATO 1.500989e-03 0.0072926111 0.0035095416
## 34: SG_UF_ESCOLARN 1.263245e-03 0.0106830068 0.0039482343
## 35: SG_UF_ESCOLAMA 1.189801e-03 0.0039025131 0.0039482343
## 36: SG_UF_ESCOLAMS 1.141071e-03 0.0037601921 0.0035095416
## 37: PORTE_ESCOLADe 61 a 90 alunos 9.357530e-04 0.0017870515 0.0046062733
## 38: SG_UF_ESCOLARO 6.111924e-04 0.0043366219 0.0021934635
## 39: SG_UF_ESCOLAMT 2.339125e-04 0.0019603377 0.0015354244
## 40: SG_UF_ESCOLAAM 2.266033e-04 0.0004701357 0.0017547708
## 41: SG_UF_ESCOLAAL 2.026644e-04 0.0031096244 0.0013160781
## 42: SG_UF_ESCOLARR 5.712264e-05 0.0010626436 0.0002193463
## 43: SG_UF_ESCOLAAP 3.149244e-05 0.0016500898 0.0004386927
## Feature Gain Cover FrequencyA tabela apresentada mostra as variáveis ordenadas de acordo com sua importância no modelo, geralmente medido com base na redução média de ganho (Gain) ou na frequência em que a variável é selecionada para splits nas árvores do modelo (Frequency).
Já a coluna Cover representa a cobertura das variáveis, que representa a proporção de instâncias (observações) que são atribuídas a uma determinada ramificação do split. Quanto maior a cobertura média, maior a importância atribuída à variável, pois ela tem um impacto mais amplo na divisão dos dados e afeta uma proporção maior das instâncias de treinamento.
Previsão para novas observações
Será usado o mesmo exemplo hipotético para mostrar como realizar previsões.
SG_UF_ESCOLA =
factor(x = c("RJ","SP","MG","AM","RS"),
levels = levels(base_treino$SG_UF_ESCOLA))
TP_DEPENDENCIA_ADM_ESCOLA =
factor( x = c("Estadual","Privada","Estadual","Municipal","Federal"),
levels = levels(base_treino$TP_DEPENDENCIA_ADM_ESCOLA))
TP_LOCALIZACAO_ESCOLA =
factor(x = c("Urbana","Urbana","Urbana","Rural","Urbana"),
levels = levels(base_treino$TP_LOCALIZACAO_ESCOLA))
INSE = factor(x = c("Grupo 3","Grupo 6","Grupo 4","Grupo 2","Grupo 4"),
levels = levels(base_treino$INSE))
PORTE_ESCOLA = factor(x = c("De 61 a 90 alunos","Maior que 90 alunos","De 61 a 90 alunos","De 31 a 60 alunos","Maior que 90 alunos"),
levels = levels(base_treino$PORTE_ESCOLA))
NU_MATRICULAS = c(87,44,102,21,80)
NU_PARTICIPANTES_NEC_ESP = c(1,2,0,0,1)
PC_FORMACAO_DOCENTE = c(48.1 , 75.7 , 68.8 , 51.2 , 70.3)
NU_TAXA_PERMANENCIA = c(67,100,92,87,75)
NU_TAXA_REPROVACAO = c(6.1,3.3, 9.1, 8.7,5.6)
NU_TAXA_ABANDONO = c(0,0,1, 2, 3)
escola = tibble(SG_UF_ESCOLA ,
TP_DEPENDENCIA_ADM_ESCOLA,
TP_LOCALIZACAO_ESCOLA ,
NU_MATRICULAS ,
NU_PARTICIPANTES_NEC_ESP ,
INSE ,
PC_FORMACAO_DOCENTE ,
NU_TAXA_PERMANENCIA ,
NU_TAXA_REPROVACAO ,
NU_TAXA_ABANDONO ,
PORTE_ESCOLA)A função predict realiza a previsão tanto para a Floresta Aleatória quanto para o Gradiente Boosting. A questão principal nesta etapa é que agora é preciso passar a base para previsão também como uma matriz, e não mais como um data.frame.
## [1] 516.4885 678.7314 557.3550 519.2161 603.7460Classificação Binária
Vamos repetir o processo de criar a nova variável resposta categória seguindo os critérios estipulados. A questão principal aqui é que a função xgboost quando usada para problemas de classificação não recebe como label um objeto do tipo factor, o objeto passado como entrada no label precisa ser um vetor de números inteiros, começando em 0, que indica para cada observação qual a sua classe. Vamos usar 0 para a classe “boa” e 1 para a classe “regular”.
Ajuste do Modelo
A diferença na chamada da função xgboost para o caso de classificação é que agora objective = "binary:logistic", isso para o caso de classificação binária.
Variáveis Importantes
## Feature Gain Cover Frequency
## 1: TP_DEPENDENCIA_ADM_ESCOLAEstadual 4.802224e-01 0.042149112 0.0118257860
## 2: PC_FORMACAO_DOCENTE 7.974839e-02 0.171635497 0.1967118546
## 3: NU_TAXA_PERMANENCIA 6.976822e-02 0.085005589 0.1811364292
## 4: NU_MATRICULAS 6.894161e-02 0.094540097 0.1658494376
## 5: NU_TAXA_REPROVACAO 5.735357e-02 0.090861460 0.1658494376
## 6: NU_TAXA_ABANDONO 5.046417e-02 0.060809008 0.0628785694
## 7: INSEGrupo 6 4.772872e-02 0.040640077 0.0089414479
## 8: INSEGrupo 5 3.046937e-02 0.042095458 0.0199019325
## 9: SG_UF_ESCOLASP 2.026366e-02 0.020420889 0.0135563888
## 10: INSEGrupo 4 1.002468e-02 0.013514009 0.0187481973
## 11: SG_UF_ESCOLAMG 9.468728e-03 0.013898909 0.0060571099
## 12: SG_UF_ESCOLACE 7.979172e-03 0.026797479 0.0086530141
## 13: SG_UF_ESCOLAPR 7.447557e-03 0.025042171 0.0077877127
## 14: SG_UF_ESCOLABA 6.275196e-03 0.022950126 0.0086530141
## 15: NU_PARTICIPANTES_NEC_ESP 5.206231e-03 0.016034087 0.0147101240
## 16: INSEGrupo 3 4.976101e-03 0.008026098 0.0095183155
## 17: INSEGrupo 2 4.935309e-03 0.024543203 0.0066339775
## 18: TP_DEPENDENCIA_ADM_ESCOLAMunicipal 4.595423e-03 0.012889423 0.0043265071
## 19: SG_UF_ESCOLARJ 4.368800e-03 0.004544968 0.0066339775
## 20: SG_UF_ESCOLAPA 2.671588e-03 0.011144665 0.0051918085
## 21: PORTE_ESCOLADe 31 a 60 alunos 2.666116e-03 0.003834448 0.0092298817
## 22: SG_UF_ESCOLAPI 2.472692e-03 0.016099126 0.0051918085
## 23: SG_UF_ESCOLASC 2.421963e-03 0.008946211 0.0074992789
## 24: SG_UF_ESCOLARS 2.380385e-03 0.007568013 0.0057686761
## 25: SG_UF_ESCOLAPE 2.148076e-03 0.006695830 0.0057686761
## 26: SG_UF_ESCOLADF 2.072943e-03 0.012848845 0.0031727718
## 27: SG_UF_ESCOLAPB 1.429605e-03 0.017837302 0.0037496395
## 28: SG_UF_ESCOLAGO 1.422557e-03 0.003409774 0.0037496395
## 29: TP_DEPENDENCIA_ADM_ESCOLAPrivada 1.421908e-03 0.005073314 0.0043265071
## 30: PORTE_ESCOLADe 61 a 90 alunos 1.385891e-03 0.001356467 0.0046149409
## 31: SG_UF_ESCOLAES 1.226177e-03 0.010330238 0.0023074704
## 32: TP_LOCALIZACAO_ESCOLARural 1.073445e-03 0.012152979 0.0034612057
## 33: SG_UF_ESCOLASE 1.061063e-03 0.016599827 0.0034612057
## 34: SG_UF_ESCOLARN 8.256432e-04 0.006834440 0.0020190366
## 35: SG_UF_ESCOLAMA 5.564185e-04 0.014595197 0.0031727718
## 36: SG_UF_ESCOLAAM 5.054708e-04 0.002190402 0.0011537352
## 37: SG_UF_ESCOLARO 4.815149e-04 0.003935343 0.0011537352
## 38: SG_UF_ESCOLAMS 4.325084e-04 0.003898224 0.0011537352
## 39: SG_UF_ESCOLAAL 4.308892e-04 0.004680250 0.0017306028
## 40: SG_UF_ESCOLAMT 3.700720e-04 0.004067212 0.0017306028
## 41: SG_UF_ESCOLAAP 2.233091e-04 0.008973396 0.0017306028
## 42: SG_UF_ESCOLATO 8.247229e-05 0.000530836 0.0002884338
## Feature Gain Cover FrequencyClassificação Multiclasses
Agora é preciso cirar um vetor com 3 classes, que serão indicadas pelos números 0, 1 e 2. Vamos usar 0 para a classe “boa”, 1 para a classe “regular” e 3 para a classe “ruim”.
Ajuste do Modelo
Dessa vez mais duas mudanças serão feitas na chamada da função xgboost. Agora objective = "multi:softprob", para indicar que o problema é multiclasse, e ainda é preciso informar o número de classes com num_class = 3.
Variáveis Importantes
## Feature Gain Cover Frequency
## 1: TP_DEPENDENCIA_ADM_ESCOLAEstadual 3.422294e-01 0.0311139176 1.109057e-02
## 2: PC_FORMACAO_DOCENTE 1.026770e-01 0.2089576599 1.794736e-01
## 3: NU_MATRICULAS 8.968033e-02 0.1051127640 1.632779e-01
## 4: NU_TAXA_PERMANENCIA 8.063775e-02 0.0957322582 1.653024e-01
## 5: NU_TAXA_ABANDONO 7.062189e-02 0.0887977109 1.063287e-01
## 6: NU_TAXA_REPROVACAO 6.999436e-02 0.1021706619 1.548279e-01
## 7: INSEGrupo 6 5.037140e-02 0.0326579883 7.921838e-03
## 8: INSEGrupo 5 3.219277e-02 0.0301292099 1.311504e-02
## 9: INSEGrupo 4 2.880049e-02 0.0167628956 1.390723e-02
## 10: SG_UF_ESCOLASP 1.578912e-02 0.0152425588 1.161870e-02
## 11: SG_UF_ESCOLACE 1.232426e-02 0.0150884218 7.745797e-03
## 12: INSEGrupo 3 1.078866e-02 0.0180635770 1.434733e-02
## 13: NU_PARTICIPANTES_NEC_ESP 1.052829e-02 0.0156523888 2.649415e-02
## 14: SG_UF_ESCOLAMG 8.914341e-03 0.0066937502 6.777572e-03
## 15: INSEGrupo 2 6.309761e-03 0.0086954126 9.330165e-03
## 16: SG_UF_ESCOLARJ 6.236533e-03 0.0057417421 5.897368e-03
## 17: SG_UF_ESCOLABA 5.871788e-03 0.0125518490 8.097879e-03
## 18: SG_UF_ESCOLAPR 5.202066e-03 0.0122020651 4.665082e-03
## 19: TP_DEPENDENCIA_ADM_ESCOLAMunicipal 4.122744e-03 0.0093160282 5.017164e-03
## 20: SG_UF_ESCOLARS 3.957043e-03 0.0139667645 6.161429e-03
## 21: TP_LOCALIZACAO_ESCOLARural 3.483742e-03 0.0067113663 6.689552e-03
## 22: SG_UF_ESCOLAPI 3.172906e-03 0.0117224457 2.904674e-03
## 23: SG_UF_ESCOLAGO 2.982999e-03 0.0101344713 3.608837e-03
## 24: SG_UF_ESCOLATO 2.923264e-03 0.0096577136 2.640613e-03
## 25: SG_UF_ESCOLAES 2.765462e-03 0.0088330423 4.313001e-03
## 26: SG_UF_ESCOLASC 2.673710e-03 0.0101935225 7.217675e-03
## 27: SG_UF_ESCOLAPB 2.615286e-03 0.0130009039 3.872899e-03
## 28: SG_UF_ESCOLAPE 2.609138e-03 0.0041224890 4.665082e-03
## 29: PORTE_ESCOLADe 31 a 60 alunos 2.603833e-03 0.0017770785 7.393715e-03
## 30: SG_UF_ESCOLAPA 2.579817e-03 0.0092010997 4.577062e-03
## 31: PORTE_ESCOLADe 61 a 90 alunos 2.513673e-03 0.0013020945 6.777572e-03
## 32: SG_UF_ESCOLAMA 2.048503e-03 0.0139190717 3.696858e-03
## 33: TP_DEPENDENCIA_ADM_ESCOLAPrivada 1.614098e-03 0.0022505014 3.168735e-03
## 34: SG_UF_ESCOLAMS 1.579929e-03 0.0029320139 2.464572e-03
## 35: SG_UF_ESCOLADF 1.385560e-03 0.0141121790 2.024470e-03
## 36: SG_UF_ESCOLAAL 1.131610e-03 0.0075959889 2.640613e-03
## 37: SG_UF_ESCOLARO 9.448022e-04 0.0060424521 2.024470e-03
## 38: SG_UF_ESCOLASE 9.068242e-04 0.0078759131 2.112490e-03
## 39: SG_UF_ESCOLAMT 8.127745e-04 0.0016197672 2.112490e-03
## 40: SG_UF_ESCOLARN 6.816419e-04 0.0071183695 1.848429e-03
## 41: SG_UF_ESCOLAAM 4.181206e-04 0.0009675050 7.921838e-04
## 42: SG_UF_ESCOLAAP 2.779078e-04 0.0041486348 9.682246e-04
## 43: SG_UF_ESCOLARR 2.446834e-05 0.0001117517 8.802042e-05
## Feature Gain Cover FrequencyPrevisão para novas observações
## [1] 0.045517765 0.732763350 0.221718878 0.641780496 0.357111365 0.001108135
## [7] 0.064953960 0.852914155 0.082131900 0.005642034 0.772220075 0.222137928
## [13] 0.436463267 0.551206231 0.012330489A saída da função predict são as probabilidades de cada uma das 3 classes para cada uma das novas observações. Mas essa apresentação é bem confusa e desorganizada. Segue uma sugestão para uma saída mais amigável.
matrix(predict(xgb_RED_3, newdata = M_escola),
byrow = TRUE,
ncol=3,
dimnames = list(seq(1:5),c("boa","regular","ruim"))
)## boa regular ruim
## 1 0.045517765 0.7327634 0.221718878
## 2 0.641780496 0.3571114 0.001108135
## 3 0.064953960 0.8529142 0.082131900
## 4 0.005642034 0.7722201 0.222137928
## 5 0.436463267 0.5512062 0.0123304895.8 Atividade
Trabalhar novamente com a base Bike Sharing Dataset.
- Ajuste um modelo XGBoost para prever a quantidade de bicicletas alugadas (regressão).
- Identifique as variáveis importantes para o modelo.
- Faça uma previsão com valores hipotéticos.
- Ajuste um modelo XGBoost para prever se a quantidade de bicicletas alugadas será ou não menor que 4.000 (classificação binária).
- Identifique as variáveis importantes para o modelo.
- Faça uma previsão com valores hipotéticos.
- Ajuste um modelo XGBoost para prever se a quantidade de bicicletas ficará em qual das três faixas: [0,4.000), [4.000,6.000) ou [6.000,\(\infty\)) (multiclasses).
- Identifique as variáveis importantes para o modelo.
- Faça uma previsão com valores hipotéticos.