Capítulo 2 Leitura, limpeza e organização dos dados

Neste capítulo os conceitos serão abordados através de exemplos práticos. Para isso usaremos a base de dados do ENEM 2015, disponível pelo site do INEP 6. Esta base contém informações por escola.

Questões interessantes que podemos tentar responder a partir desta base de dados:

  • Quais as principais características das escolas que influenciam, positivamente ou negativamente, no resultado dos seus alunos no ENEM?

  • Quais as características das escolas que indicam menor taxa de participação no ENEM?

  • Dada uma escola qualquer, qual a probabilidade da nota média dos seus alunos em todas as provas ser maior que 500?

Responder essas perguntas pode ser importante para tomadas de decisão sobre como usar os recursos nas escolas, tanto recursos públicos quanto particulares.

2.1 Como ler os dados no R

A primeira etapa sempre será verificar se o diretório corrente é aquele que você está trabalhando, onde foi salvo o arquivo com dados a serem lidos. Para isso, o comando

getwd()

verifica o diretório corrente. Caso queira alterar o diretório corrente, use

setwd("aqui coloca o endereço do diretório")

É preciso que o diretório corrente do R seja o mesmo onde estão salvos o script.R e a base de dados.

A base de dados está salva no formato csv no arquivo MICRODADOS_ENEM_ESCOLA_2015.csv. O primeiro passo é a leitura desta base dentro do Programa R (R Core Team 2022). Para trabalhar com os dados, vamos instalar o pacote tidyverse (Wickham et al. 2019), que na sua instalação também instala os pacotes dplyr(Wickham et al. 2022) e readr(Wickham, Hester, and Bryan 2022).

library(tidyverse)

Para leitura da base pode-se usar as funções read_csv, read_csv2 ou read_delim , todas retornam um objeto fo tipo tibble. Em particupar, a última delas possibilita escolher o caractere para separação das colunas, com a definição do argumento delim, e para separação de casas decimais, a partir do decimal_mark. Como a base está com as colunas separadas por ; e a casa decimal por ,, será usada a função read_csv2para a sua leitura.

base = read_csv2(file="MICRODADOS_ENEM_ESCOLA_2015.csv")

É importante ressaltar que, geralmente, junto com uma base pública é disponibilizado um arquivo de dicionário. É nele que estão as explicações de cada variável da base. Para a base MICRODADOS_ENEM_ESCOLA_2015.csv o arquivo dicionário é Dicionário_Microdados_Enem_Escola.xlsx.

2.2 Classificação das variáveis da base

2.2.1 Quanto ao seu tipo

O primeiro passo, em qualquer análise de dados, é entender cada variável da base. Para isso elas serão classificadas entre as seguintes possibilidades:

Tabela 2.1: Classificação das variáveis quanto ao seu tipo
Classificação Descrição
Identificação Aquelas cuja única função é identificar a unidade amostral (linha). Esta variável assume um valor diferente para cada linha da base.
Quantitativa Aquelas que atribuem à cada unidade amostral uma característica de quantidade.
Qualitativa Aquelas que atribuem a cada unidade amostral uma característica, que pode ser de diferentes naturezas: textual, lógica ou até mesmo numérica. Mas sempre indica uma categoria e não uma quantidade.

Vejamos uma rápida apresentação de cada variável a partir da função glimpse.

glimpse(base)
## Rows: 15,598
## Columns: 27
## $ NU_ANO                    <dbl> 2015, 2015, 2015, 2015, 2015, 2015, 2015, 20…
## $ CO_UF_ESCOLA              <dbl> 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, …
## $ SG_UF_ESCOLA              <chr> "RO", "RO", "RO", "RO", "RO", "RO", "RO", "R…
## $ CO_MUNICIPIO_ESCOLA       <dbl> 1100205, 1100205, 1100205, 1100205, 1100205,…
## $ NO_MUNICIPIO_ESCOLA       <chr> "Porto Velho", "Porto Velho", "Porto Velho",…
## $ CO_ESCOLA_EDUCACENSO      <dbl> 11000058, 11000171, 11000198, 11000244, 1100…
## $ NO_ESCOLA_EDUCACENSO      <chr> "CENTRO DE ENSINO CLASSE A", "CENTRO EDUCACI…
## $ TP_DEPENDENCIA_ADM_ESCOLA <dbl> 4, 4, 4, 4, 4, 2, 2, 4, 2, 2, 2, 2, 2, 2, 4,…
## $ TP_LOCALIZACAO_ESCOLA     <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1,…
## $ NU_MATRICULAS             <dbl> 137, 20, 39, 55, 26, 97, 44, 34, 75, 41, 24,…
## $ NU_PARTICIPANTES_NEC_ESP  <dbl> 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,…
## $ NU_PARTICIPANTES          <dbl> 130, 17, 37, 49, 23, 96, 38, 29, 59, 22, 21,…
## $ NU_TAXA_PARTICIPACAO      <dbl> 94.89, 85.00, 94.87, 89.09, 88.46, 98.97, 86…
## $ NU_MEDIA_CN               <dbl> 591.64, 458.46, 529.05, 508.74, 523.38, 505.…
## $ NU_MEDIA_CH               <dbl> 652.34, 533.51, 583.87, 586.45, 591.66, 582.…
## $ NU_MEDIA_LP               <dbl> 604.53, 472.62, 547.11, 531.35, 563.45, 527.…
## $ NU_MEDIA_MT               <dbl> 627.66, 459.72, 507.22, 529.87, 528.93, 492.…
## $ NU_MEDIA_RED              <dbl> 732.00, 507.82, 652.43, 591.84, 583.48, 580.…
## $ NU_MEDIA_OBJ              <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, …
## $ NU_MEDIA_TOT              <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, …
## $ INSE                      <chr> "Grupo 6", "Grupo 4", "Grupo 5", "Grupo 5", …
## $ PC_FORMACAO_DOCENTE       <dbl> 67.5, 58.3, 67.7, 56.0, 72.7, 53.6, 73.9, 46…
## $ NU_TAXA_PERMANENCIA       <dbl> 78.46, 70.59, 40.54, 81.63, 52.17, 85.42, 63…
## $ NU_TAXA_APROVACAO         <dbl> 96.1, 94.6, 90.1, 88.7, 84.5, 89.2, 73.9, 88…
## $ NU_TAXA_REPROVACAO        <dbl> 3.9, 5.4, 9.9, 10.5, 13.1, 10.8, 22.2, 9.9, …
## $ NU_TAXA_ABANDONO          <dbl> 0.0, 0.0, 0.0, 0.8, 2.4, 0.0, 3.9, 1.4, 0.3,…
## $ PORTE_ESCOLA              <chr> "Maior que 90 alunos", "De 1 a 30 alunos", "…

Nesta base as variáveis podem ser identificadas de acordo com a tabela a seguir.

Classificação Variáveis
Identificação CO_ESCOLA_EDUCACENSO , NO_ESCOLA_EDUCACENSO
Quantitativas NU_MATRICULAS , NU_PARTICIPANTES_NEC_ESP , NU_PARTICIPANTES , NU_TAXA_PERMANENCIA , NU_TAXA_APROVACAO , NU_TAXA_REPROVACAO , NU_TAXA_ABANDONO , PC_FORMACAO_DOCENTE , NU_TAXA_PARTICIPACAO , NU_MEDIA_CN , NU_MEDIA_CH , NU_MEDIA_LP , NU_MEDIA_MT , NU_MEDIA_RED , NU_MEDIA_OBJ , NU_MEDIA_TOT
Qualitativas NU_MATRICULAS , NU_PARTICIPANTES_NEC_ESP , NU_PARTICIPANTES , NU_TAXA_PERMANENCIA , NU_TAXA_APROVACAO , NU_TAXA_REPROVACAO , NU_TAXA_ABANDONO , C_FORMACAO_DOCENTE , NU_TAXA_PARTICIPACAO , NU_MEDIA_CN , NU_MEDIA_OBJ , NU_MEDIA_TOT , NU_MEDIA_CH , NU_MEDIA_LP , NU_MEDIA_MT , NU_MEDIA_RED

O CO_ESCOLA_EDUCACENSO, apesar de ser representada por um número, é uma variável que indica uma identidade e não uma quantidade. Por isso é importante que o R não reconheça esta variável como um número. Veja na segunda coluna da saída da função glimpse, na linha referente à variável CO_ESCOLA_EDUCACENSO, aparece <dbl>, o que indica que o R entendeu que esta variável como um double. Em breve este problema será resolvido.

As variáveis quantitativas foram todas corretamente lidas como double. Já as variáveis qualitativa, algumas delas, como TP_DEPENDENCIA_ADM_ESCOLA , por exemplo, por terem a sua categoria representada por um número foram erradamente lidas pelo R como um double.

Veja mais um problema na base.

base$NO_MUNICIPIO_ESCOLA[1:50]
##  [1] "Porto Velho"        "Porto Velho"        "Porto Velho"       
##  [4] "Porto Velho"        "Porto Velho"        "Porto Velho"       
##  [7] "Porto Velho"        "Porto Velho"        "Porto Velho"       
## [10] "Porto Velho"        "Porto Velho"        "Porto Velho"       
## [13] "Porto Velho"        "Porto Velho"        "Porto Velho"       
## [16] "Porto Velho"        "Porto Velho"        "Porto Velho"       
## [19] "Porto Velho"        "Porto Velho"        "Porto Velho"       
## [22] "Porto Velho"        "Porto Velho"        "Porto Velho"       
## [25] "Porto Velho"        "Porto Velho"        "Porto Velho"       
## [28] "Porto Velho"        "Porto Velho"        "Porto Velho"       
## [31] "Porto Velho"        "Porto Velho"        "Porto Velho"       
## [34] "Porto Velho"        "Porto Velho"        "Nova Mamor\xe9"    
## [37] "Nova Mamor\xe9"     "Buritis"            "Candeias do Jamari"
## [40] "Itapu\xe3 do Oeste" "Costa Marques"      "Guajar\xe1-Mirim"  
## [43] "Guajar\xe1-Mirim"   "Guajar\xe1-Mirim"   "Guajar\xe1-Mirim"  
## [46] "Guajar\xe1-Mirim"   "Guajar\xe1-Mirim"   "Guajar\xe1-Mirim"  
## [49] "Ariquemes"          "Ariquemes"

Variáveis com texto em protuguês muitas vezes têm acentos e caracteres especiais, precisamos verificar se estes foram lidos corretamente. Caso não tenha sido lido, mudamos o encoding na função de leitura da base e este problema será resolvido.

base = read_csv2(file="MICRODADOS_ENEM_ESCOLA_2015.csv",
                 locale = locale(encoding = "latin1"))

base$NO_MUNICIPIO_ESCOLA[1:50]

Agora só falta corrigir o tipo das variáveis. Vamos fazer com que todas as variáveis de identificação sejam do tipo "character" e todas as variáveis qualitativas para o tipo factor.

base$CO_ESCOLA_EDUCACENSO = as.character(base$CO_ESCOLA_EDUCACENSO)
base$NU_ANO = factor(base$NU_ANO)

base$CO_UF_ESCOLA = factor(base$CO_UF_ESCOLA)
  
base$SG_UF_ESCOLA = factor(base$SG_UF_ESCOLA)
  
base$CO_MUNICIPIO_ESCOLA = factor(base$CO_MUNICIPIO_ESCOLA)

base$NO_MUNICIPIO_ESCOLA = factor(base$NO_MUNICIPIO_ESCOLA)

  
base$TP_DEPENDENCIA_ADM_ESCOLA = factor(base$TP_DEPENDENCIA_ADM_ESCOLA,
                                               levels = c(1,2,3,4),
                                               labels = c("Federal", "Estadual" ,"Municipal","Privada")
                                               ) 
base$TP_LOCALIZACAO_ESCOLA = factor(base$TP_LOCALIZACAO_ESCOLA,
                                               levels = c(1,2),
                                               labels = c("Urbana", "Rural")
                                               ) 
base$INSE = factor(base$INSE)

base$PORTE_ESCOLA = factor(base$PORTE_ESCOLA)

glimpse(base)
## Rows: 15,598
## Columns: 27
## $ NU_ANO                    <fct> 2015, 2015, 2015, 2015, 2015, 2015, 2015, 20…
## $ CO_UF_ESCOLA              <fct> 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, …
## $ SG_UF_ESCOLA              <fct> RO, RO, RO, RO, RO, RO, RO, RO, RO, RO, RO, …
## $ CO_MUNICIPIO_ESCOLA       <fct> 1100205, 1100205, 1100205, 1100205, 1100205,…
## $ NO_MUNICIPIO_ESCOLA       <fct> Porto Velho, Porto Velho, Porto Velho, Porto…
## $ CO_ESCOLA_EDUCACENSO      <chr> "11000058", "11000171", "11000198", "1100024…
## $ NO_ESCOLA_EDUCACENSO      <chr> "CENTRO DE ENSINO CLASSE A", "CENTRO EDUCACI…
## $ TP_DEPENDENCIA_ADM_ESCOLA <fct> Privada, Privada, Privada, Privada, Privada,…
## $ TP_LOCALIZACAO_ESCOLA     <fct> Urbana, Urbana, Urbana, Urbana, Urbana, Urba…
## $ NU_MATRICULAS             <dbl> 137, 20, 39, 55, 26, 97, 44, 34, 75, 41, 24,…
## $ NU_PARTICIPANTES_NEC_ESP  <dbl> 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,…
## $ NU_PARTICIPANTES          <dbl> 130, 17, 37, 49, 23, 96, 38, 29, 59, 22, 21,…
## $ NU_TAXA_PARTICIPACAO      <dbl> 94.89, 85.00, 94.87, 89.09, 88.46, 98.97, 86…
## $ NU_MEDIA_CN               <dbl> 591.64, 458.46, 529.05, 508.74, 523.38, 505.…
## $ NU_MEDIA_CH               <dbl> 652.34, 533.51, 583.87, 586.45, 591.66, 582.…
## $ NU_MEDIA_LP               <dbl> 604.53, 472.62, 547.11, 531.35, 563.45, 527.…
## $ NU_MEDIA_MT               <dbl> 627.66, 459.72, 507.22, 529.87, 528.93, 492.…
## $ NU_MEDIA_RED              <dbl> 732.00, 507.82, 652.43, 591.84, 583.48, 580.…
## $ NU_MEDIA_OBJ              <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, …
## $ NU_MEDIA_TOT              <lgl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, …
## $ INSE                      <fct> Grupo 6, Grupo 4, Grupo 5, Grupo 5, Grupo 5,…
## $ PC_FORMACAO_DOCENTE       <dbl> 67.5, 58.3, 67.7, 56.0, 72.7, 53.6, 73.9, 46…
## $ NU_TAXA_PERMANENCIA       <dbl> 78.46, 70.59, 40.54, 81.63, 52.17, 85.42, 63…
## $ NU_TAXA_APROVACAO         <dbl> 96.1, 94.6, 90.1, 88.7, 84.5, 89.2, 73.9, 88…
## $ NU_TAXA_REPROVACAO        <dbl> 3.9, 5.4, 9.9, 10.5, 13.1, 10.8, 22.2, 9.9, …
## $ NU_TAXA_ABANDONO          <dbl> 0.0, 0.0, 0.0, 0.8, 2.4, 0.0, 3.9, 1.4, 0.3,…
## $ PORTE_ESCOLA              <fct> Maior que 90 alunos, De 1 a 30 alunos, De 31…

2.2.2 Quanto ao seu objetivo

Outra classificação interessante de ser feita entre as variáveis, diferentes das de identificação, é definir quais variáveis são determinísticas e quais são aleatórias. Veja que algumas das variáveis são facilmente observadas antes mesmo da prova do ENEM, por exemplo, o número de alunos matriculados ("NU_MATRICULAS") e o porte da escola ("PORTE_ESCOLA"). Estas são variáveis que de alguma maneira caracterizam as escolas.

Outras variáveis já são aleatórias, que depende do desempenho dos alunos no ENEM, como as notas das escolas no ENEM. Estas são aquelas que pretendemos explicar em termos das que conhecemos. Será que uma escola grande tem mais chance de ter uma boa nota no ENEM quando comparada com uma escola pequena, ou seria o contrário? Como será a influência da taxa de abandono de uma escola com o seu desempenho no ENEM?

Costumamos chamar as variáveis determinísticas de covariáveis, ou variáveis independentes. Já as aleatórias, chamamos de variável de interesse, variável alvo ou desfecho.

Tabela 2.2: Classificação das variáveis quanto ao seu objetivo
Classificação Variáveis
Covariáveis “NU_ANO”, “NU_MATRICULAS”, “NU_PARTICIPANTES_NEC_ESP”, “NU_TAXA_PERMANENCIA”, “NU_TAXA_APROVACAO”, “NU_TAXA_REPROVACAO”, “NU_TAXA_ABANDONO”, “PC_FORMACAO_DOCENTE”, “CO_UF_ESCOLA”, “SG_UF_ESCOLA”, “CO_MUNICIPIO_ESCOLA”, “NO_MUNICIPIO_ESCOLA”, “TP_DEPENDENCIA_ADM_ESCOLA”, “TP_LOCALIZACAO_ESCOLA”, “INSE” e “PORTE_ESCOLA”
Variáveis alvo “NU_PARTICIPANTES”, “NU_TAXA_PARTICIPACAO”, “NU_MEDIA_CN”, “NU_MEDIA_LP”, “NU_MEDIA_MT”, “NU_MEDIA_RED”, “NU_MEDIA_OBJ” e “NU_MEDIA_TOT”

2.3 Separação da base em treino e de teste

Em qualquer problema de Aprendizado de Máquinas é adequado separar a base de dados em duas partes: base de treino e base de teste. A base de treino é composta pela maioria das linhas da base original, geralmente em torno de 70% ou 80%, e é a partir dela que faremos todas as análises estatísticas. A base de teste , a menor parte, em torno de 20% ou 30%, será usada apenas para avaliar o desempenho dos modelos fora da base de treinamento. Dessa maneira é possível mensurar se o modelo está de fato aprendendo ou se está ocorrendo sobreajuste.

No pacote caret (Kuhn 2022) existe a função createDataPartition que realiza a partição da base. Essa função retorna uma seleção aleatória dos índices da base de tamanho indicada pelo argumento de entrada p.

library(caret)
set.seed(123456789)

O código acima somente carrega o pacote e define o valor da semente pelo comendo set.seed. Isso é recomendado fazer sempre que o código tiver alguma seleção aleatória, pois assim é possível replicar o código como da primeira vez se for necessário.

N = nrow(base) #numero de linhas da base
indices_treino = createDataPartition(1:N,p=0.75)[[1]]
base_treino = base |> slice(indices_treino)
base_teste  = base |> slice(-indices_treino)

Vamos verificar se a partição realizada respeitou 75% para base de treino e 25% para a base de teste.

n_treino = dim(base_treino)[1]
n_teste = dim(base_teste)[1]
#verificando a proporcao entre as bases 
(n_treino/(n_treino+n_teste))
## [1] 0.7500962
(n_teste/(n_treino+n_teste))
## [1] 0.2499038

Toda análise realizada a partir de agora será feita considerando os dados da base de treino.

2.4 Limpeza da base de dados

Antes de ajustar/treinar qualquer modelo precisamos analisar com cuidado a base de dados para garantir que não teremos problemas futuros. Os principais passos dessa análise de dados são:

  • breve análise a partir da função summary;

  • procurar dados faltantes;

  • procurar covariáveis com variância quase zero (ou zero);

  • procurar covariáveis com alta correlação.

2.4.1 Dados faltantes

É preciso verificar se a base possui dados faltantes. Caso afirmativo, teremos que tomar uma decisão: eliminar a linha (escola), eliminar a coluna (variável) ou imputar valores para as entradas com dados faltantes.

A função summary mostra se alguma variável está toda preenchida com `NA.

summary(base_treino)
##   NU_ANO       CO_UF_ESCOLA   SG_UF_ESCOLA  CO_MUNICIPIO_ESCOLA
##  2015:11700   35     :2495   SP     :2495   3550308:  510      
##               31     :1279   MG     :1279   3304557:  362      
##               33     :1076   RJ     :1076   2304400:  219      
##               43     : 858   RS     : 858   5300108:  149      
##               23     : 632   CE     : 632   3106200:  136      
##               41     : 524   PR     : 524   2927408:  121      
##               (Other):4836   (Other):4836   (Other):10203      
##      NO_MUNICIPIO_ESCOLA CO_ESCOLA_EDUCACENSO NO_ESCOLA_EDUCACENSO
##  São Paulo     :  510    Length:11700         Length:11700        
##  Rio de Janeiro:  362    Class :character     Class :character    
##  Fortaleza     :  219    Mode  :character     Mode  :character    
##  Brasília      :  149                                             
##  Belo Horizonte:  136                                             
##  Salvador      :  121                                             
##  (Other)       :10203                                             
##  TP_DEPENDENCIA_ADM_ESCOLA TP_LOCALIZACAO_ESCOLA NU_MATRICULAS   
##  Federal  : 247            Urbana:11277          Min.   : 10.00  
##  Estadual :6629            Rural :  423          1st Qu.: 29.00  
##  Municipal:  79                                  Median : 58.00  
##  Privada  :4745                                  Mean   : 85.92  
##                                                  3rd Qu.:113.00  
##                                                  Max.   :835.00  
##                                                                  
##  NU_PARTICIPANTES_NEC_ESP NU_PARTICIPANTES NU_TAXA_PARTICIPACAO  NU_MEDIA_CN   
##  Min.   : 0.0000          Min.   : 10.00   Min.   : 50.00       Min.   :388.6  
##  1st Qu.: 0.0000          1st Qu.: 23.00   1st Qu.: 62.31       1st Qu.:456.5  
##  Median : 0.0000          Median : 42.00   Median : 76.92       Median :476.6  
##  Mean   : 0.5626          Mean   : 62.84   Mean   : 76.16       Mean   :490.8  
##  3rd Qu.: 1.0000          3rd Qu.: 80.00   3rd Qu.: 90.38       3rd Qu.:519.0  
##  Max.   :27.0000          Max.   :658.00   Max.   :100.00       Max.   :720.4  
##                                                                                
##   NU_MEDIA_CH     NU_MEDIA_LP     NU_MEDIA_MT     NU_MEDIA_RED   NU_MEDIA_OBJ  
##  Min.   :460.9   Min.   :397.1   Min.   :372.4   Min.   :345.0   Mode:logical  
##  1st Qu.:537.3   1st Qu.:484.4   1st Qu.:442.9   1st Qu.:508.4   NA's:11700    
##  Median :559.0   Median :509.7   Median :471.3   Median :547.2                 
##  Mean   :566.8   Mean   :515.4   Mean   :492.4   Mean   :564.0                 
##  3rd Qu.:594.1   3rd Qu.:545.3   3rd Qu.:527.8   3rd Qu.:609.6                 
##  Max.   :709.2   Max.   :649.9   Max.   :845.7   Max.   :920.0                 
##                                                                                
##  NU_MEDIA_TOT        INSE      PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA
##  Mode:logical   Grupo 1: 753   Min.   :  0.00      Min.   :  0.00     
##  NA's:11700     Grupo 2:1030   1st Qu.: 49.70      1st Qu.: 69.23     
##                 Grupo 3:3578   Median : 62.00      Median : 80.47     
##                 Grupo 4:2856   Mean   : 60.44      Mean   : 75.98     
##                 Grupo 5:2464   3rd Qu.: 73.10      3rd Qu.: 88.89     
##                 Grupo 6:1018   Max.   :100.00      Max.   :100.00     
##                 NA's   :   1   NA's   :14                             
##  NU_TAXA_APROVACAO NU_TAXA_REPROVACAO NU_TAXA_ABANDONO
##  Min.   : 38.9     Min.   : 0.000     Min.   : 0.000  
##  1st Qu.: 80.8     1st Qu.: 2.800     1st Qu.: 0.000  
##  Median : 90.5     Median : 6.700     Median : 0.900  
##  Mean   : 87.4     Mean   : 8.822     Mean   : 3.776  
##  3rd Qu.: 96.2     3rd Qu.:12.700     3rd Qu.: 6.000  
##  Max.   :100.0     Max.   :60.200     Max.   :51.600  
##  NA's   :65        NA's   :65         NA's   :65      
##               PORTE_ESCOLA 
##  De 1 a 30 alunos   :3147  
##  De 31 a 60 alunos  :2893  
##  De 61 a 90 alunos  :1827  
##  Maior que 90 alunos:3833  
##                            
##                            
##

Podemos identificar que as variábeis NU_MEDIA_OBJ e NU_MEDIA_TOT estão com todos os valores como NA. Nesse, as duas variáveis serão retiradas da base.

base_treino = base_treino  |> select(-c(NU_MEDIA_OBJ, NU_MEDIA_TOT))

Mas será aque ainda existem dados faltantes?

library(naniar)
gg_miss_var(x = base_treino)
Dados Faltantes

Figura 2.1: Dados Faltantes 

vis_miss(x = base_treino)
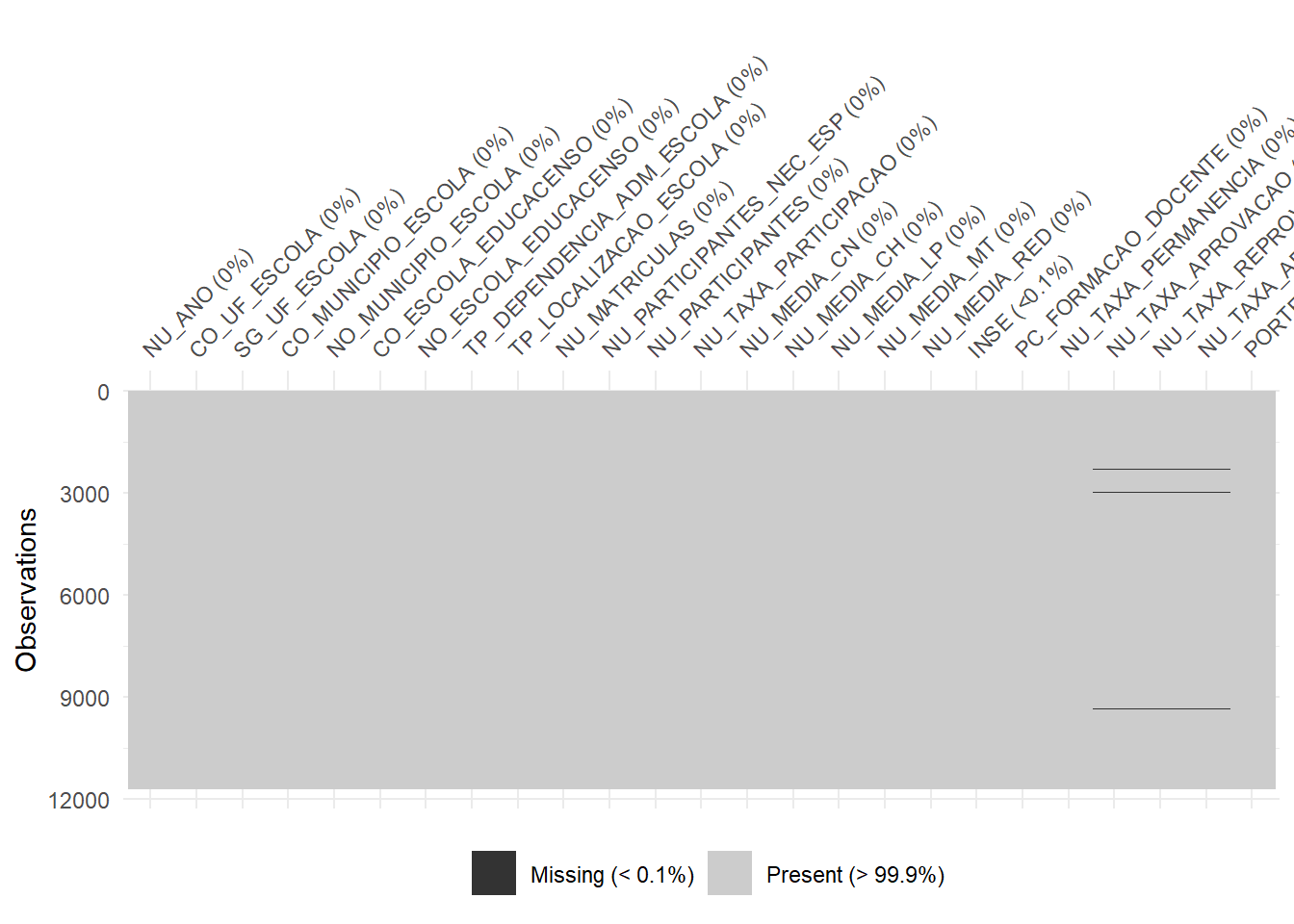
Dados Faltantes

Figura 2.2: Dados Faltantes 

base_treino  |> miss_var_summary()
## # A tibble: 25 × 3
##    variable            n_miss pct_miss
##    <chr>                <int>    <dbl>
##  1 NU_TAXA_APROVACAO       65  0.556  
##  2 NU_TAXA_REPROVACAO      65  0.556  
##  3 NU_TAXA_ABANDONO        65  0.556  
##  4 PC_FORMACAO_DOCENTE     14  0.120  
##  5 INSE                     1  0.00855
##  6 NU_ANO                   0  0      
##  7 CO_UF_ESCOLA             0  0      
##  8 SG_UF_ESCOLA             0  0      
##  9 CO_MUNICIPIO_ESCOLA      0  0      
## 10 NO_MUNICIPIO_ESCOLA      0  0      
## # … with 15 more rows
## # ℹ Use `print(n = ...)` to see more rows

2.4.1.1 Dados faltantes para a variável de interesse

Caso seja encontrada alguma linha da base, para o nosso exemplo alguma escola, com dados faltantes para uma das varáveis de interesse, as linhas correspondentes devem ser eliminadas, uma vez que não pode-se imputar valores para ela.

Observando novamente a saída do comando summarypercebemos que as únicas variáveis de interesse com dados faltantes eram NU_MEDIA_OBJ e NU_MEDIA_TOT, que já foram retiradas da base. Assim não temos dados faltantes em nenhuma variável de interesse depois da última alteração.

2.4.1.2 Dados faltantes para as covariáveis

Analisando os gráficos apresentados nesta seção podemos perceber que as variáveis NU_TAXA_APROVACAO, NU_TAXA_REPROVACAO e nem para NU_TAXA_ABANDONO têm valores faltantes para as mesmas linhas da base de dados, ou seja, para as mesmas escolas. Se excluirmos essas escolas da base de treino, o método criado não terá capacidade de analisar outras escolas, da base de teste, com as mesmas informações faltantes.

Uma alternativa, que pouco muda o ajuste do modelo e permite que ele seja usado mesmo quando existem valores faltantes na base, é imputar valores para os dados faltantes. Em geral usa-se a média, no caso das variáveis quantitativas, ou a moda, no caso das variáveis qualitativas. Se fosse uma variável qualitativa com muitos valores faltantes, ainda existe a possibilidade de se criar uma nova categoria, como por exemplo "não respondeu".

Segue as linhas de comando para imputação dos valores faltantes. Primeiro as variáveis quantitativas e por último a única variável qualitativa com valores faltantes, INSE.

base_treino = base_treino  |>
  mutate(NU_TAXA_APROVACAO = replace_na(NU_TAXA_APROVACAO, mean(NU_TAXA_APROVACAO, na.rm = TRUE)),
         NU_TAXA_REPROVACAO = replace_na(NU_TAXA_REPROVACAO, mean(NU_TAXA_REPROVACAO, na.rm = TRUE)),
         NU_TAXA_ABANDONO = replace_na(NU_TAXA_ABANDONO, mean(NU_TAXA_ABANDONO, na.rm = TRUE)),
         PC_FORMACAO_DOCENTE = replace_na(PC_FORMACAO_DOCENTE, mean(PC_FORMACAO_DOCENTE, na.rm = TRUE))
         )
moda = names(table(base_treino$INSE))[which.max(table(base_treino$INSE))]
base_treino = base_treino  |> mutate(INSE = replace_na(INSE,moda))

Verificando que não há mais dados faltantes.

base_treino  |> miss_var_summary()
## # A tibble: 25 × 3
##    variable                  n_miss pct_miss
##    <chr>                      <int>    <dbl>
##  1 NU_ANO                         0        0
##  2 CO_UF_ESCOLA                   0        0
##  3 SG_UF_ESCOLA                   0        0
##  4 CO_MUNICIPIO_ESCOLA            0        0
##  5 NO_MUNICIPIO_ESCOLA            0        0
##  6 CO_ESCOLA_EDUCACENSO           0        0
##  7 NO_ESCOLA_EDUCACENSO           0        0
##  8 TP_DEPENDENCIA_ADM_ESCOLA      0        0
##  9 TP_LOCALIZACAO_ESCOLA          0        0
## 10 NU_MATRICULAS                  0        0
## # … with 15 more rows
## # ℹ Use `print(n = ...)` to see more rows

2.4.2 Covariáveis com variância (quase) zero

Para procurar as variáveis com variância (quase) zero vamos analisar a variabilidade de cada variável. Nesse momento é importante tratar de forma diferente as variáveis quantitativas das qualitativas, por isso foram criados os objetos qualitativas e quantitativas, que guardam os nomes das covariáveis quantitativas e qualitativas. Ele facilitará o código a seguir.

A variabilidade das variáveis quantitativas será dada pela variância amostral, que pode ser encontrada a partir do comando var.

diag(var(base_treino  |>  select(where(is.numeric)) ))
##            NU_MATRICULAS NU_PARTICIPANTES_NEC_ESP         NU_PARTICIPANTES 
##              7118.322823                 1.829308              3858.560551 
##     NU_TAXA_PARTICIPACAO              NU_MEDIA_CN              NU_MEDIA_CH 
##               236.777373              2227.860448              1595.884448 
##              NU_MEDIA_LP              NU_MEDIA_MT             NU_MEDIA_RED 
##              1732.500132              4716.964468              6029.947170 
##      PC_FORMACAO_DOCENTE      NU_TAXA_PERMANENCIA        NU_TAXA_APROVACAO 
##               297.007113               390.706286               119.106033 
##       NU_TAXA_REPROVACAO         NU_TAXA_ABANDONO 
##                62.774436                30.303195

Nenhuma variável quantitativa com variância nula.

Agora o caso das variáveis qualitativas. Para medir a variabilidade destas variáveis vamos contar a quantidade de categorias que cada uma delas apresenta. Só será descartada aquelas que apresentarem apenas uma categoria.

summary(base_treino  |>  select(where(is.factor)))
##   NU_ANO       CO_UF_ESCOLA   SG_UF_ESCOLA  CO_MUNICIPIO_ESCOLA
##  2015:11700   35     :2495   SP     :2495   3550308:  510      
##               31     :1279   MG     :1279   3304557:  362      
##               33     :1076   RJ     :1076   2304400:  219      
##               43     : 858   RS     : 858   5300108:  149      
##               23     : 632   CE     : 632   3106200:  136      
##               41     : 524   PR     : 524   2927408:  121      
##               (Other):4836   (Other):4836   (Other):10203      
##      NO_MUNICIPIO_ESCOLA TP_DEPENDENCIA_ADM_ESCOLA TP_LOCALIZACAO_ESCOLA
##  São Paulo     :  510    Federal  : 247            Urbana:11277         
##  Rio de Janeiro:  362    Estadual :6629            Rural :  423         
##  Fortaleza     :  219    Municipal:  79                                 
##  Brasília      :  149    Privada  :4745                                 
##  Belo Horizonte:  136                                                   
##  Salvador      :  121                                                   
##  (Other)       :10203                                                   
##       INSE                   PORTE_ESCOLA 
##  Grupo 1: 753   De 1 a 30 alunos   :3147  
##  Grupo 2:1030   De 31 a 60 alunos  :2893  
##  Grupo 3:3579   De 61 a 90 alunos  :1827  
##  Grupo 4:2856   Maior que 90 alunos:3833  
##  Grupo 5:2464                             
##  Grupo 6:1018                             
##

Veja que a variável NU_ANO apresenta uma única categoria. Todas as observações são referentes ao mesmo ano. Dessa forma esta variável não agrega informação e será retirada da base.

base_treino = base_treino  |>  select(-NU_ANO)

2.4.3 Análise de Multicolinearidade

A Análise de Multicolinearidade é o processo de seleção de variáveis para garantir que as covariáveis da base não apresentam alta correlação entre si. Esse processo consiste em procurar variáveis altamente correlacionadas e, no caso destas existirem, escolher algumas para ficarem na base e outras para saírem, de forma que a base final não contenha covariáveis com correlação maior que 80%.

A principal questão nesta etapa é como medir a associação entre as covariáveis. O cálculo da correlação amostral, a partir da função cor do R, só deve ser feito entre variáveis quantitativas. Entre pares de variáveis qualitativas e entre uma variável qualitativa e outra quantitativa é preciso utilizar outra medida de associação, como será visto mais pra frente.

2.4.3.1 Entre pares de covariáveis quantitativas

Primeiro a análise das associações entre as variáveis quantitativas, duas a duas. A medida de associação utilizada será a correlação, a partir da função cor. As variáveis de interesse não serão consideradas nesta etapa.

mat_cor = base_treino  |> 
  select(where(is.numeric))  |> 
  select(-c(NU_TAXA_PARTICIPACAO, 
            NU_PARTICIPANTES,
            NU_MEDIA_CN, 
            NU_MEDIA_LP, 
            NU_MEDIA_MT, 
            NU_MEDIA_RED, 
            NU_MEDIA_CH))   |> 
  cor()
mat_cor
##                          NU_MATRICULAS NU_PARTICIPANTES_NEC_ESP
## NU_MATRICULAS              1.000000000               0.40071034
## NU_PARTICIPANTES_NEC_ESP   0.400710336               1.00000000
## PC_FORMACAO_DOCENTE        0.152880742               0.06447547
## NU_TAXA_PERMANENCIA       -0.006362418               0.01192405
## NU_TAXA_APROVACAO         -0.283616144              -0.18180816
## NU_TAXA_REPROVACAO         0.228583994               0.15421657
## NU_TAXA_ABANDONO           0.233283453               0.13848074
##                          PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA
## NU_MATRICULAS                    0.152880742       -0.0063624179
## NU_PARTICIPANTES_NEC_ESP         0.064475474        0.0119240509
## PC_FORMACAO_DOCENTE              1.000000000        0.0290660572
## NU_TAXA_PERMANENCIA              0.029066057        1.0000000000
## NU_TAXA_APROVACAO               -0.005119007        0.0050907666
## NU_TAXA_REPROVACAO               0.048549624       -0.0063308905
## NU_TAXA_ABANDONO                -0.059728155       -0.0009807009
##                          NU_TAXA_APROVACAO NU_TAXA_REPROVACAO NU_TAXA_ABANDONO
## NU_MATRICULAS                 -0.283616144         0.22858399     0.2332834533
## NU_PARTICIPANTES_NEC_ESP      -0.181808162         0.15421657     0.1384807443
## PC_FORMACAO_DOCENTE           -0.005119007         0.04854962    -0.0597281554
## NU_TAXA_PERMANENCIA            0.005090767        -0.00633089    -0.0009807009
## NU_TAXA_APROVACAO              1.000000000        -0.87648766    -0.7210265409
## NU_TAXA_REPROVACAO            -0.876487660         1.00000000     0.2983883659
## NU_TAXA_ABANDONO              -0.721026541         0.29838837     1.0000000000

Uma maneira gráfica de visualizar essas correlações, e ainda ganhar uma análise descritiva de brinde, é a partir do comando ggpairs.

library(GGally)
base_treino  |>
  select(where(is.numeric))  |>
  select(-c(NU_TAXA_PARTICIPACAO,
            NU_PARTICIPANTES,
            NU_MEDIA_CN,
            NU_MEDIA_LP,
            NU_MEDIA_MT,
            NU_MEDIA_RED,
            NU_MEDIA_CH))  |>
ggpairs()

O resultado indica uma forte correlação entre NU_TAXA_APROVACAO e NU_TAXA_REPROVACAO, NU_TAXA_APROVACAO e NU_TAXA_ABANDONO. veja queNU_TAXA_REPROVACAO e NU_TAXA_ABANDONO não apresentam grande correlação entre elas. Por esse motivo será descartada da base a variávei NU_TAXA_APROVACAO.

base_treino = base_treino  |> select(-NU_TAXA_APROVACAO)

2.4.3.2 Entre pares de covariáveis qualitativas

Para mensurar a associação entre duas variáveis qualitativas será usado o Coeficiente de Contingência Modificado. Primeiro serão feitas as contas para um par específico de covariáveis e depois a conta será generalizada para todos os pares.

Considere as covariáveis qualitativas TP_LOCALIZACAO_ESCOLA e PORTE_ESCOLA. Antes da apresentação do coeficiente de contingência, veja a tabela de contingência para essas duas variáveis.

library(expss)
tabela = base_treino |> 
  select(TP_LOCALIZACAO_ESCOLA,PORTE_ESCOLA) |> 
  table()
(#tab:tabela_cont)Tabela de Contingência para as variáveis ‘tipo de localização’ e ‘porte’ da escola
De 1 a 30 alunos De 31 a 60 alunos TOTAL Maior que 90 alunos TOTAL
Urbana 2976 2767 1763 3771 11277
Rural 171 126 64 62 423
3147 2893 1827 3833 11700

Vamos chamar de valor observado para a \(i\) da primeira variável e a categoria \(j\) da segunda variável o número que indica quantos indivíduos da base satisfazem tanto a categoria \(i\) quando a categoria \(j\), representado por \(O_{i,j}\). Este valor está na tabela acima, por exemplo, 2970 escolas da base de treino estão na zona rural e têm porte entre 1 e 30 alunos no último ano do ensino médio.

Se as covariáveis são independentes espera-se encontrar em cada célula \((i,j)\) a proporção em relação a todos os valores da categoria \(i\) igual a proporção que todos os valores da categoria \(j\) representam para toda a amostra, que será chamado de \(E_{i,j}\).

\[ E_{i,j} = \text{total linha i} \times \dfrac{ \text{total coluna j}}{\text{total da tabela}} \]

Por exemplo, o valor esperado para a célula \((1,1)\) da tabela é:

\[ E_{1,1} = 3.145 \times \dfrac{11.286}{11.700} = 3.033,715 \] Já o valor observado para a célula \((1,1)\) é \(O_{1,1} = 2.970,00\).

As frequências esperadas são comparadas com as observadas e a partir desta comparação é calculada uma estatística, chamada de Qui-Quadrado, \(\chi^2\), definida por:

\[ \chi^2 = \sum_{i=1}^L \sum_{j=1}^C \dfrac{(O_{i,j} - E_{i,j})^2}{E_{i,j}} \]

Quanto maior for o valor de \(\chi^2\), maior será o grau de associação entre as variáveis. O valor da estatística qui-quadrado pode ser encontrada pela função chisq.test.

aux = chisq.test(tabela, correct = FALSE)
q = aux$statistic
q
## X-squared 
##  78.37618

O Coeficiente de Contingência Modificado, definido a seguir, varia de zero (completa independência) até 1 (associação perfeita).

\[ C^\star = \sqrt{\dfrac{\chi^2}{\chi^2 + N}}\sqrt{\dfrac{k}{k-1}} \]

sendo \(\chi^2\) a estatística Qui-Quadrado, \(N\) é o número total de observações da tabela de contingências, \(k\) é o menor número entre o número de linhas e colunas da tabela de contingências.

N = nrow(base_treino)
k = min(nrow(tabela),nrow(tabela))
C = sqrt(q/(q+N))*sqrt(k/(k-1))
C
## X-squared 
## 0.1153624

O resultado indica que as variáveis TP_LOCALIZACAO_ESCOLA e PORTE_ESCOLA apresentam baixa associação. O gráfico de barras empilhadas destas duas variáveis é uma forma de vizualizar a relação entre elas.

par(mfrow=c(1,2))
base_treino  |>
  select(TP_LOCALIZACAO_ESCOLA,PORTE_ESCOLA)  |>
  table()  |> 
  prop.table(margin = 2)   |> cbind(a="") |>
  barplot(col=c("#7D786A","#74CE7F","white"),
          main ="Localização da escola por porte",
          names.arg = c("[1,30]","[31,60]","[61,90]","+90",""),
          las = 2
          )
legend("right", 
       horiz = FALSE, 
       legend = levels(base_treino$TP_LOCALIZACAO_ESCOLA), 
       fill = c("#7D786A","#74CE7F"))

base_treino  |>
  select(PORTE_ESCOLA,TP_LOCALIZACAO_ESCOLA)  |>
  table()  |> 
  prop.table(margin = 2)   |> cbind(a="") |>
  barplot(col=c("#E1E1E1","#FBB400","#F17D21","#F15E51","white"),
          names.arg = c(levels(base_treino$TP_LOCALIZACAO_ESCOLA),""),
          main="Porte da escola por local")
legend("right",c("[1,30]","[31,60]","[61,90]","+90"), 
       horiz = FALSE, 
       fill = c("#E1E1E1","#FBB400","#F17D21","#F15E51"))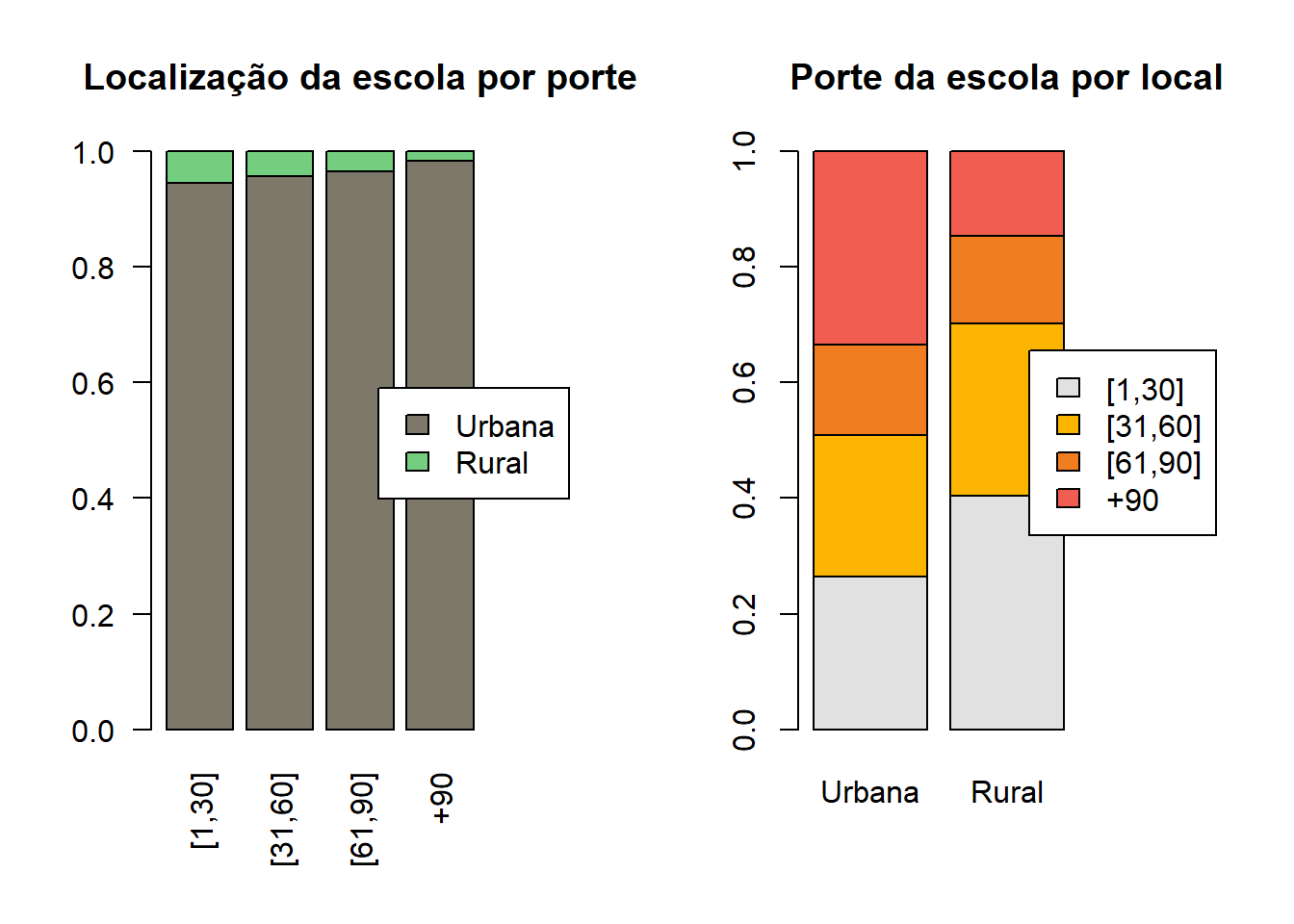

Repetir o procedimento descrito acima para todo par de variáveis qualitativas pode ser bem custoso e demorado. O código a seguir automatiza esta conta e cria uma matriz com o coeficiente de contingência para todos os possíveis pares de variáveis qualitativas da base.

base_quali = base_treino  |> select(where(is.factor)) 
base_quali = apply(base_quali,
                   MARGIN = 2,
                   FUN = "as.character")

n = ncol(base_quali)
mat_coef_cont = matrix(NA,ncol = n, 
                       nrow = n)
colnames(mat_coef_cont) = colnames(base_quali)
rownames(mat_coef_cont) = colnames(base_quali)
N = nrow(base_quali)

for(i in 1:n){
  for(j in 1:n){
    
    tabela = table(base_quali[,i],base_quali[,j])
    dim(tabela)
    
    aux = chisq.test(tabela, correct = FALSE)
    q = aux$statistic
    
    k = min(nrow(tabela),
            ncol(tabela))
    
    mat_coef_cont[i,j] = sqrt(q/(q+N))*sqrt(k/(k-1))
  }
}
mat_coef_cont
##                           CO_UF_ESCOLA SG_UF_ESCOLA CO_MUNICIPIO_ESCOLA
## CO_UF_ESCOLA                 1.0000000    1.0000000           1.0000000
## SG_UF_ESCOLA                 1.0000000    1.0000000           1.0000000
## CO_MUNICIPIO_ESCOLA          1.0000000    1.0000000           1.0000000
## NO_MUNICIPIO_ESCOLA          0.9995445    0.9995445           1.0000000
## TP_DEPENDENCIA_ADM_ESCOLA    0.2982486    0.2982486           0.7830383
## TP_LOCALIZACAO_ESCOLA        0.1410659    0.1410659           0.7757372
## INSE                         0.6674883    0.6674883           0.9009905
## PORTE_ESCOLA                 0.2594393    0.2594393           0.7856970
##                           NO_MUNICIPIO_ESCOLA TP_DEPENDENCIA_ADM_ESCOLA
## CO_UF_ESCOLA                        0.9995445                 0.2982486
## SG_UF_ESCOLA                        0.9995445                 0.2982486
## CO_MUNICIPIO_ESCOLA                 1.0000000                 0.7830383
## NO_MUNICIPIO_ESCOLA                 1.0000000                 0.7740119
## TP_DEPENDENCIA_ADM_ESCOLA           0.7740119                 1.0000000
## TP_LOCALIZACAO_ESCOLA               0.7704964                 0.2258141
## INSE                                0.8958194                 0.6443970
## PORTE_ESCOLA                        0.7788526                 0.5164087
##                           TP_LOCALIZACAO_ESCOLA      INSE PORTE_ESCOLA
## CO_UF_ESCOLA                          0.1410659 0.6674883    0.2594393
## SG_UF_ESCOLA                          0.1410659 0.6674883    0.2594393
## CO_MUNICIPIO_ESCOLA                   0.7757372 0.9009905    0.7856970
## NO_MUNICIPIO_ESCOLA                   0.7704964 0.8958194    0.7788526
## TP_DEPENDENCIA_ADM_ESCOLA             0.2258141 0.6443970    0.5164087
## TP_LOCALIZACAO_ESCOLA                 1.0000000 0.2461237    0.1153624
## INSE                                  0.2461237 1.0000000    0.3346274
## PORTE_ESCOLA                          0.1153624 0.3346274    1.0000000

Os resultados indicam, como já esperado, uma grande associação entre as variáveis CO_UF_ESCOLA, SG_UF_ESCOLA, CO_MUNICIPIO_ESCOLA e NO_MUNICIPIO_ESCOLA. Estas quatro variáveis caracterizam a localização da escola. Como são muitas as categorias para os municípios, entre estas quatro variáveis será mantida apenas a SG_UF_ESCOLA.

base_treino = base_treino  |> select(-c(CO_UF_ESCOLA,CO_MUNICIPIO_ESCOLA,NO_MUNICIPIO_ESCOLA))

As variáveis qualitativas restantes na base não apresentam associação grande o suficiente para justificar mais alguma retirada.

2.4.3.3 Entre uma covariáveis quantitativa e outra qualitativa

Por fim, as associações entre uma variável quantitativa e outra qualitativa será calculado a partir da medida \(R^2\). Essa medida é obtida da seguinte maneira. Primeiro é calculada a variância amostral da variável quantitativa restrita a cada categoria da variável qualitativa. Considere \(X\) a variável qualitativa e \(Y\) a quantitativa.

\[ \sigma^2_c = Var(Y , X = c) \]

Em seguida é feita a conta da variância média, que é a média das variâncias calculadas acima ponderada pelo número de observações em cada categoria de \(c\).

\[ \sigma^2_{med} = \sum_{c \in C} \dfrac{\sigma^2_c \times n_c}{n}, \]

sendo \(C\) o conjunto com as possíveis categorias de \(X\), \(n_c\) o número de observações com \(X=c\) e \(n\) o número total de observações. O valor de \(R^2\) será

\[ R^2 = 1 - \dfrac{\sigma^2_{med}}{\sigma^2} \]

onde \(\sigma^2\) é a variância da variável quantitativa considerando toda a amostra.

Vejamos como ficaria o valor de \(R^2\) para as variáveis \(X =\) SG_UF_ESCOLA e $Y = $ NU_PARTICIPANTES.

resumo = base_treino  |> 
  group_by(SG_UF_ESCOLA)  |> 
  summarise(variancia = var(NU_PARTICIPANTES),
            n = n() #função que contabiliza o número de linhas
  )
resumo
## # A tibble: 27 × 3
##    SG_UF_ESCOLA variancia     n
##    <fct>            <dbl> <int>
##  1 AC               7308.    40
##  2 AL               3326.   161
##  3 AM              11477.   120
##  4 AP               9402.    44
##  5 BA               3756.   516
##  6 CE               5719.   632
##  7 DF              13988.   149
##  8 ES               4399.   286
##  9 GO               3347.   461
## 10 MA               5521.   247
## # … with 17 more rows
## # ℹ Use `print(n = ...)` to see more rows
Var_med = sum((resumo$variancia*resumo$n))/sum(resumo$n)
R2 = 1 - Var_med/var(base_treino$NU_PARTICIPANTES)
R2
## [1] 0.06398418

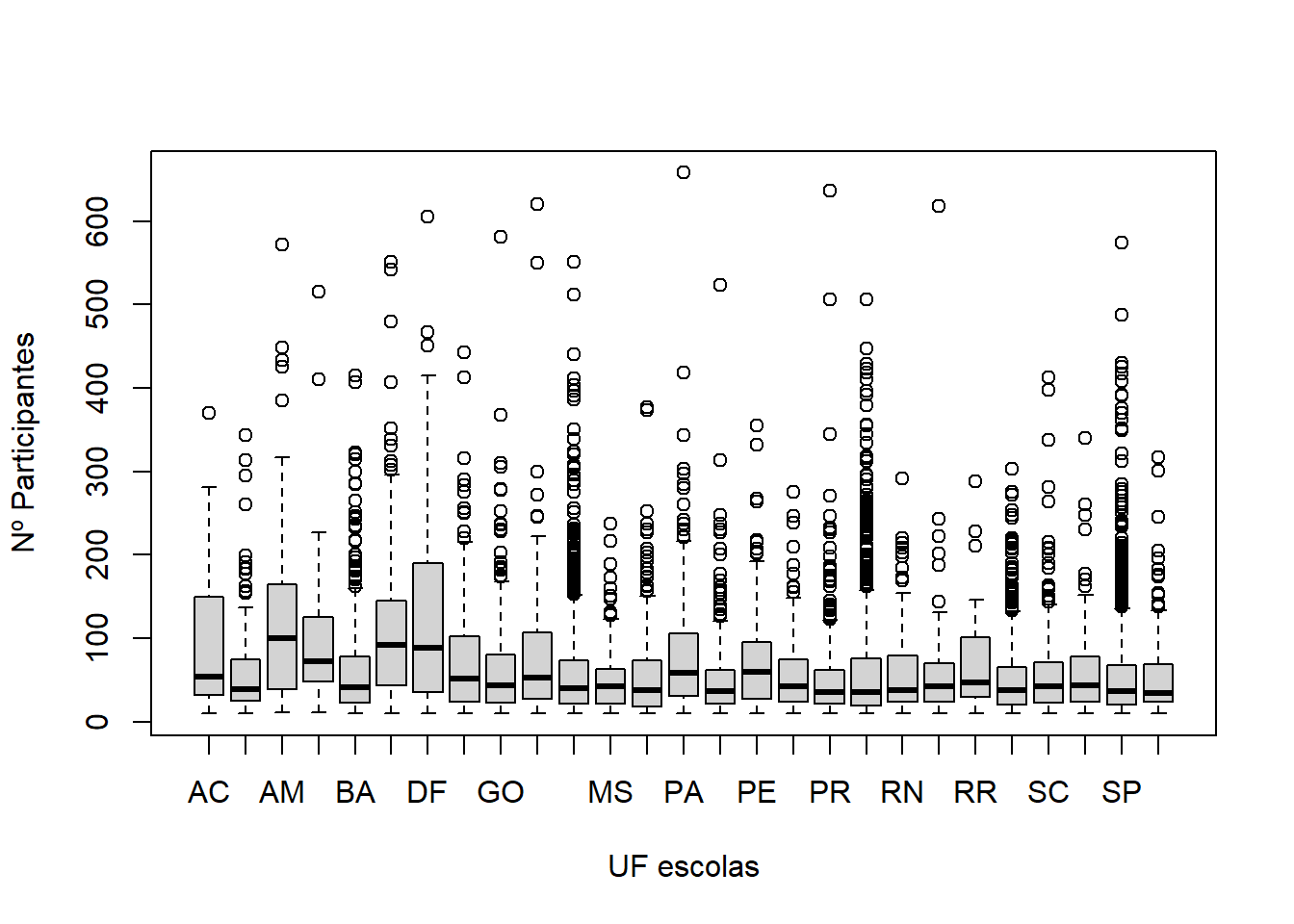
Valores baixos de \(R^2\), perto de zero, indicam baixa associação entre as variáveis. Valores altos de \(R^2\), perto de um, indicam alta associação. Conclui-se então que as variáveis SG_UF_ESCOLA e NU_PARTICIPANTES apresentam baixa associação. O gráfico do boxplot da variável quantitativa para cada categoria da qualitativa é uma possível análise visual a respeito da associação das duas variáveis.

boxplot(
  base_treino$NU_PARTICIPANTES ~ base_treino$SG_UF_ESCOLA,
  xlab = "UF escolas",
  ylab = "Nº Participantes"
    )

Assim como foi automatizado o cálculo do coeficiente de contingência, o cálculo do \(R^2\) será automatizado.

names_quali = names(base_treino  |> select(where(is.factor)))
index_quali = which(names(base_treino) %in% names_quali )
names_quanti = names(base_treino  |> select(where(is.numeric))  |> 
  select(-c(NU_TAXA_PARTICIPACAO, NU_PARTICIPANTES, NU_MEDIA_CN, NU_MEDIA_LP, NU_MEDIA_MT, NU_MEDIA_RED, NU_MEDIA_CH) ))
index_quanti = which(names(base_treino) %in% names_quanti )

R2_mat = matrix(NA,
                nrow = length(index_quali),
                ncol = length(index_quanti))
rownames(R2_mat) = names_quali
colnames(R2_mat) = names_quanti
for(l in 1:length(index_quali)){
  for(c in 1:length(index_quanti)){
    i = index_quali[l]
    j = index_quanti[c]
    resumo = base_treino  |> group_by_at(i)  |>
      summarise(n=n(),
                variancia = var(eval(as.symbol(names(base_treino)[j])))
      )
    Var_med = sum((resumo$variancia*resumo$n))/sum(resumo$n)
    R2_mat[l,c] = 1 - Var_med/var(base_treino[,j])

  }
}
R2_mat
##                           NU_MATRICULAS NU_PARTICIPANTES_NEC_ESP
## SG_UF_ESCOLA                0.049086208              0.052409797
## TP_DEPENDENCIA_ADM_ESCOLA   0.149521403              0.057232094
## TP_LOCALIZACAO_ESCOLA       0.006236224              0.001853315
## INSE                        0.058096488              0.017493387
## PORTE_ESCOLA                0.599035395              0.096215392
##                           PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA
## SG_UF_ESCOLA                      0.234033134         0.048356114
## TP_DEPENDENCIA_ADM_ESCOLA         0.015142705         0.032986538
## TP_LOCALIZACAO_ESCOLA             0.007723438         0.003363637
## INSE                              0.082371015         0.007873919
## PORTE_ESCOLA                      0.031177327         0.007327728
##                           NU_TAXA_REPROVACAO NU_TAXA_ABANDONO
## SG_UF_ESCOLA                    0.1256118765     0.1608382436
## TP_DEPENDENCIA_ADM_ESCOLA       0.1516780308     0.2666830599
## TP_LOCALIZACAO_ESCOLA           0.0006946453     0.0007267075
## INSE                            0.0848976039     0.2192047992
## PORTE_ESCOLA                    0.0657965820     0.0769356917

A matriz acima não apresenta nenhum valor acima de 0,7. Podemos então concluir que a associação entre as variáveis quantitativas e qualitativas, duas a duas, é baixa.

2.5 Uma breve Análise Descritiva

Antes de salvar a base de treino final vale fazer uma breve análise descritiva. Primeiro a partir da função summary.

summary(base_treino)
##   SG_UF_ESCOLA  CO_ESCOLA_EDUCACENSO NO_ESCOLA_EDUCACENSO
##  SP     :2495   Length:11700         Length:11700        
##  MG     :1279   Class :character     Class :character    
##  RJ     :1076   Mode  :character     Mode  :character    
##  RS     : 858                                            
##  CE     : 632                                            
##  PR     : 524                                            
##  (Other):4836                                            
##  TP_DEPENDENCIA_ADM_ESCOLA TP_LOCALIZACAO_ESCOLA NU_MATRICULAS   
##  Federal  : 247            Urbana:11277          Min.   : 10.00  
##  Estadual :6629            Rural :  423          1st Qu.: 29.00  
##  Municipal:  79                                  Median : 58.00  
##  Privada  :4745                                  Mean   : 85.92  
##                                                  3rd Qu.:113.00  
##                                                  Max.   :835.00  
##                                                                  
##  NU_PARTICIPANTES_NEC_ESP NU_PARTICIPANTES NU_TAXA_PARTICIPACAO  NU_MEDIA_CN   
##  Min.   : 0.0000          Min.   : 10.00   Min.   : 50.00       Min.   :388.6  
##  1st Qu.: 0.0000          1st Qu.: 23.00   1st Qu.: 62.31       1st Qu.:456.5  
##  Median : 0.0000          Median : 42.00   Median : 76.92       Median :476.6  
##  Mean   : 0.5626          Mean   : 62.84   Mean   : 76.16       Mean   :490.8  
##  3rd Qu.: 1.0000          3rd Qu.: 80.00   3rd Qu.: 90.38       3rd Qu.:519.0  
##  Max.   :27.0000          Max.   :658.00   Max.   :100.00       Max.   :720.4  
##                                                                                
##   NU_MEDIA_CH     NU_MEDIA_LP     NU_MEDIA_MT     NU_MEDIA_RED        INSE     
##  Min.   :460.9   Min.   :397.1   Min.   :372.4   Min.   :345.0   Grupo 1: 753  
##  1st Qu.:537.3   1st Qu.:484.4   1st Qu.:442.9   1st Qu.:508.4   Grupo 2:1030  
##  Median :559.0   Median :509.7   Median :471.3   Median :547.2   Grupo 3:3579  
##  Mean   :566.8   Mean   :515.4   Mean   :492.4   Mean   :564.0   Grupo 4:2856  
##  3rd Qu.:594.1   3rd Qu.:545.3   3rd Qu.:527.8   3rd Qu.:609.6   Grupo 5:2464  
##  Max.   :709.2   Max.   :649.9   Max.   :845.7   Max.   :920.0   Grupo 6:1018  
##                                                                                
##  PC_FORMACAO_DOCENTE NU_TAXA_PERMANENCIA NU_TAXA_REPROVACAO NU_TAXA_ABANDONO
##  Min.   :  0.00      Min.   :  0.00      Min.   : 0.000     Min.   : 0.000  
##  1st Qu.: 49.70      1st Qu.: 69.23      1st Qu.: 2.900     1st Qu.: 0.000  
##  Median : 62.00      Median : 80.47      Median : 6.800     Median : 1.000  
##  Mean   : 60.44      Mean   : 75.98      Mean   : 8.822     Mean   : 3.776  
##  3rd Qu.: 73.10      3rd Qu.: 88.89      3rd Qu.:12.700     3rd Qu.: 6.000  
##  Max.   :100.00      Max.   :100.00      Max.   :60.200     Max.   :51.600  
##                                                                             
##               PORTE_ESCOLA 
##  De 1 a 30 alunos   :3147  
##  De 31 a 60 alunos  :2893  
##  De 61 a 90 alunos  :1827  
##  Maior que 90 alunos:3833  
##                            
##                            
##

Outra análise possível é a partir da função ggpairs do pacote GGally (Schloerke et al. 2021). Esta é uma função custosa, pode demorar para rodar. Além disso, ela gera muitos gráficos em uma única janela e se forem usadas muitas variáveis fica pequena demais cada figura. Por esse motivo esta função será rodada apenas para as variáveis quantitativas, que são as variáveis com melhor resultado da função.

2.6 Como salvar a base final

Todo o processo realizado neste capítulo foi bem custoso e resultou em uma base de treino pronta para ser trabalhada. Para garantir que o trabalho realizado não precisará ser repetido, a base final deve ser salva. Assim, quando for necessário utilizar esta base, em algum trabalho, basta carregar a base final salva.

saveRDS(base_treino,file="arquivos-de-trabalho/base_treino_final.rds")
write_csv2(base_treino,file="arquivos-de-trabalho/base_treino_final.csv")


saveRDS(base_teste,file="arquivos-de-trabalho/base_teste.rds")
write_csv2(base_teste,file="arquivos-de-trabalho/base_teste.csv")

2.7 Atividade

Reproduzir todo esse processo em uma nova base de dados. A base de dados utilizada nesta atividade será Bike Sharing Dataset, com informações diárias de uma mesma cidade sobre o clima e sobre o número de bicicletas utilizadas em um sistema de alugueis de bicicleta.

2.8 Referências

References

———. 2022. Caret: Classification and Regression Training. https://CRAN.R-project.org/package=caret.
R Core Team. 2022. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Schloerke, Barret, Di Cook, Joseph Larmarange, Francois Briatte, Moritz Marbach, Edwin Thoen, Amos Elberg, and Jason Crowley. 2021. GGally: Extension to ’Ggplot2’. https://CRAN.R-project.org/package=GGally.
Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019. “Welcome to the tidyverse.” Journal of Open Source Software 4 (43): 1686. https://doi.org/10.21105/joss.01686.
Wickham, Hadley, Romain François, Lionel Henry, and Kirill Müller. 2022. Dplyr: A Grammar of Data Manipulation. https://CRAN.R-project.org/package=dplyr.
Wickham, Hadley, Jim Hester, and Jennifer Bryan. 2022. Readr: Read Rectangular Text Data. https://CRAN.R-project.org/package=readr.

  1. https://www.gov.br/inep/pt-br/acesso-a-informacao/dados-abertos/microdados/enem-por-escola↩︎