12 Jawaban 4
Distribusi \(t\) bisa didapatkan dari hasil transformasi distribusi \(\chi^2\) dan \(N(0,1)\) melalui persamaan dibawah ini:
\(X = \frac{Z}{\sqrt{\frac{Y}{2}}}\)
Sehingga berdasarkan persamaa tersebut kita bisa menuliskan program R untuk membangkitkan distribusi \(t(2)\) sebagai berikut
#banyaknya amatan
n <- 1000
set.seed(15)
z <- rnorm(n,mean = 0,sd = 1)
y <- rchisq(n,df = 2)
x <- z/sqrt(y/2)
head(x)## [1] 0.4249926 2.2981978 -0.3956900 0.8938340 0.9930945 -1.4325087- Menamplikan histogram di R
set.seed(5)
v <- rt(n,df=2)
par(mfrow=c(1,2))
hist(x,main="t(2) dari Direct")
hist(v,main="t(2) dari rt")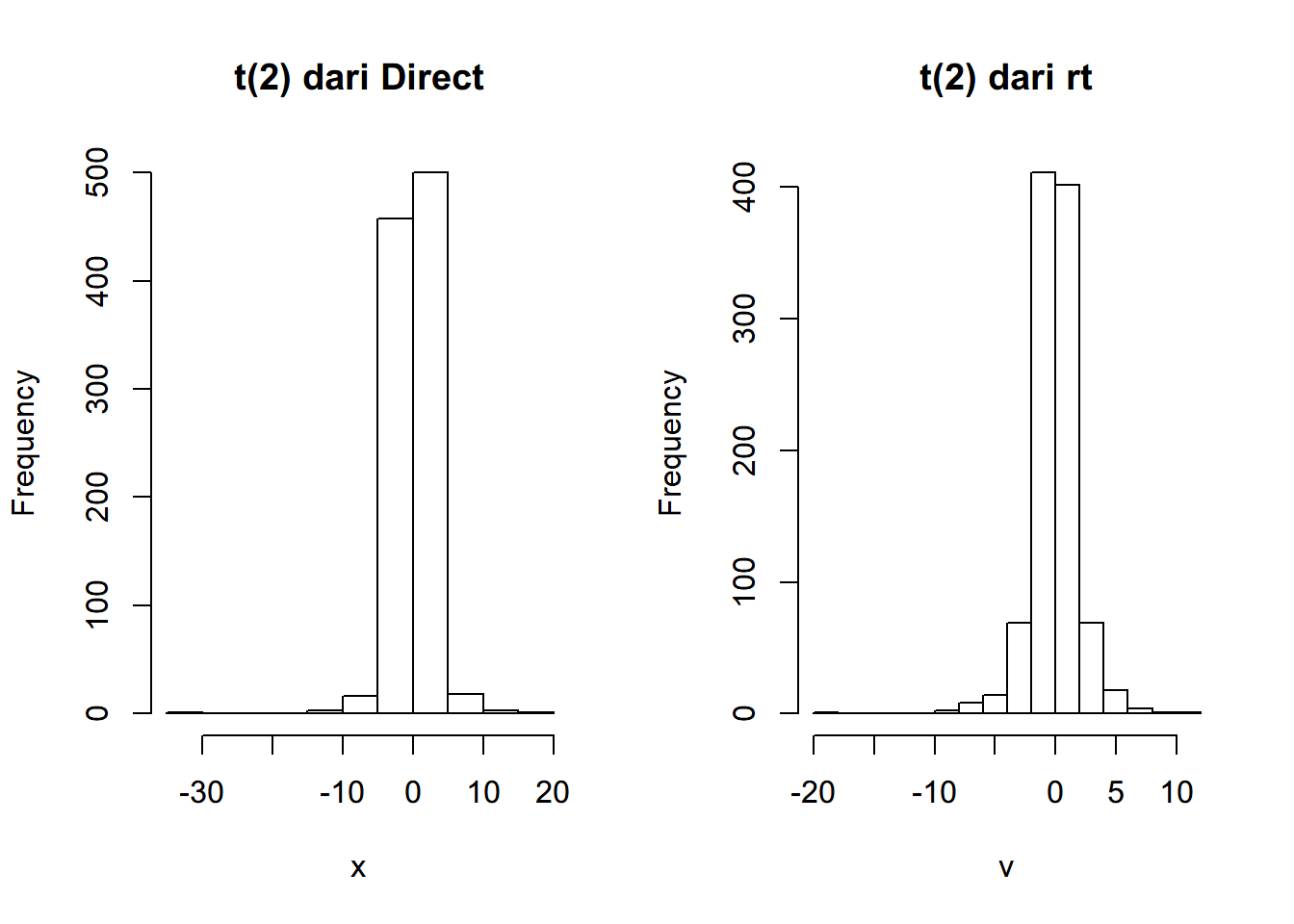
12.1 Algoritme pembangkitan bilangan acak untuk Regresi Linear
Algoritme pembangkitan bilangan acak untuk Regresi Linear adalah sebagai berikut:
- Bangkitkan residual berdasarkan distribusi normal \(\epsilon \sim N(0,\sigma)\)
- Bangkitkan peubah penjelas \(X_{i}\) yang saling bebas.
- Bangkitkan peubah respon \(Y\) dengan menggunakan model regresi