Capítulo 7 Estadística descriptiva con RStudio

Habiendo construido y configurado una base de datos ad hoc para nuestros análisis, en el presente capítulo se presenta un modo de calcular frecuencias, medidas de tendencia central, de posición y de dispersión a nivel de la estimación puntual y del parámetro poblacional.³²

Para efectos de este manual distinguiremos aquellos estadísticos que se calculan desde una muestra (probabilística o no probabilística) de aquellos que se obtienen vía registros administrativos o de censos. Específicamente, en el caso de estadísticos que se estiman a partir de una muestra probabilística avanzaremos desde la estimación puntual al cálculo del parámetro poblacional (con su respectivo intervalo de confianza, nivel de confianza y error de estimación). Esto último nos permitirá estimar los valores que la estimación puntual alcanza en la población (que representa la muestra) y si existen diferencias estadísticamente significativas a nivel del parámetro entre dos grupos (prueba de hipótesis).

El presente capitulo se ordena como sigue: en el primer apartado se indicará cómo realizar la estimación puntual de diferentes estadísticos descriptivos usando R (medidas de tendencia central, distribuciones de frecuencia y medidas de posición, medidas de dispersión y forma de distribuciones) y su exportación a planillas de cálculo para su presentación en reportes de investigación académica o profesional; en el segundo apartado se presentará la forma de realizar inferencia estadística, construyendo intervalos de confianza de parámetros, a partir de estimaciones puntuales, y calculando indicadores insesgados a partir de factores de expansión.

7.1 Estimación puntual de estadísticos descriptivos usando R

7.1.1 Medidas de tendencia central: cálculo de la media, mediana y moda

El cálculo de la media es sencillo en cuanto a los códigos y aritmética necesarios. En las dos siguientes líneas de comandos se observa el cálculo de una media simple y luego de una media recortada. En ambos casos se utiliza el comando mean, indicando la variable sobre la cual se desea hacer el cálculo, acompañado del argumento na.rm = TRUE para excluir del cálculo a los casos dados como perdidos (valores NA que ya fueron codificados al preparar las variables). Para el caso de la media recortada, se agrega el argumento trim, que permite indicar la proporción de casos que se eliminan en cada extremo de la distribución.³³ Así, se obtiene la estimación puntual de ambos estadísticos.

Ejercicio 7.1

mean(CEP$satisfaccion_vida, na.rm = TRUE)

## [1] 7.311174

mean(CEP$satisfaccion_vida, na.rm = TRUE, trim = 0.025)

## [1] 7.390625

Como se observa en el ejercicio 7.1 la media aritmética arroja un valor de 7,31 en una una escala de 1 a 10, mientras la media recortada al 5% presenta un valor de 7,39 (ambos valores se redondean al segundo decimal). Como fue anticipado, la interpretación de estos resultados (y sus diferencias) se explorarán en el siguiente apartado.

Para el caso de la mediana, se trata de un comando similar. Se utiliza el comando median, indicando la variable sobre la cual se desea hacer el cálculo, acompañado del argumento na.rm = TRUE para excluir del cálculo a los casos dados como perdidos (valores NA que ya fueron codificados al preparar las variables). De esa forma se obtiene la estimación puntual de este estadístico.

Ejercicio 7.2

median(CEP$satisfaccion_vida, na.rm = TRUE)

## [1] 7

Como se ve en el ejercicio 7.2, el valor de la mediana es 7, lo que indica que la mitad de los casos indica tener una satsfacción con la propia vida menor a 7, considerando una escala de 1 a 10.

Para el cálculo de la moda, debe haberse instalado previamente el paquete modeest y haberlo cargado en la sesión de trabajo; esto permitirá contar con una función que calculará de forma automática el o los valores más frecuentes de la distribución, herramienta que no existe en los paquetes básicos de R. Así, como se ve en el ejercicio 7.3, se utiliza el comando mfv³⁴ para calcular la moda de la variable edad. El resultado de este comando indica el valor, o los valores, con más frecuencia dentro de la distribución de casos de la variable señalada.

Ejercicio 7.3

#Ejecutar previamente "install.packages("modeest")"
library(modeest)
mfv(CEP$edad) #Indica el o los valores con más frecuencia

## [1] 50

En este caso, la moda de la variable edad es 50 años, lo que indica que el valor que más se repite en la distribución de casos de tal variable corresponde a tal respuesta.

7.1.2 Medidas de posición: cálculo de frecuencias absolutas y relativas, cuantiles

El cálculo de tablas de frecuencias absolutas para una variable se efectúa mediante el comando table, indicando como argumento de la función la variable sobre la cual se ejecuta el cálculo. En este sub apartado, trabajaremos con la variable ordinal de nuestra base de datos que refiere a una evaluación de la economía (CEP$eval_econ_factor) por parte de la persona encuestada.

Ejercicio 7.4

tabla <- table(CEP$eval_econ_factor)
tabla

## 
## Positiva   Neutra Negativa 
##      471      730      209

De forma muy sucinta, los resultados del ejercicio 7.4 muestran un importante predominio de opiniones “neutras” con 730 casos, seguida por una concentración de 471 casos en respuestas “positivas” y 209 casos en respuestas “negativas”.

Para facilitar la comparación con otros datos, estos resultados pueden expresarse como frecuencias relativas. Para el cálculo de frecuencias relativas, se usa el objeto tabla de frecuencias simples ya construido (tabla): como se ve en el ejercicio 7.5, sobre tal objeto, se ejecuta la función prop.table que construye una nueva tabla en la que cada celda es la división simple entre la cantidad de casos de la categoría y el total de casos.

Ejercicio 7.5

#Frecuencias relativas (proporciones)
prop.table(tabla)

## 
##  Positiva    Neutra  Negativa 
## 0.3340426 0.5177305 0.1482270

De tal forma, los resultados del ejercicio 7.5 confirman lo ya observado con frecuencias absolutas. En este caso, los valores se presentan como proporciones de una unidad (1). Así, se observa que la categoría “neutra” concentra la mayor cantidad de casos con aproximadamente la mitad de los mismos (0,52), mientras que la categoría “positiva” concentra un tercio de las respuestas (0,33).

Ahora bien, para facilitar aún más la lectura y divulgación de estos resultados resultará de utilidad convertir estas frecuencias relativas en porcentajes. Como se observa en el ejercicio 7.6, para construir una tabla de porcentajes se multiplica el resultado de calcular la tabla de proporciones por 100; si a ello además se le agrega la función round, es posible configurar un resultado redondeado a dos decimales.

Ejercicio 7.6

#Frecuencias relativas (porcentajes)
prop.table(tabla)*100

## 
## Positiva   Neutra Negativa 
## 33.40426 51.77305 14.82270

round((prop.table(tabla)*100),2)

## 
## Positiva   Neutra Negativa 
##    33.40    51.77    14.82

De tal modo, los resultados del ejercicio 7.6 permiten afirmar que la mayor cantidad de respuestas se concentran en una evaluación “neutra” con el 51,8% del total, seguido por evaluaciones positivas que representan un 33,4% del total de respuestas, y finalmente las respuestas que reflejan evaluaciones negativas, que alcanzan un 14,8% de los casos.

Una última configuración que resulta de utilidad para el examen de distribuciones de frecuencias es la modalidad de cantidades acumuladas. Este tipo de tablas se construye a partir de tablas de frecuencias absolutas y relativas (sea en su modalidad proporcional o porcentual). En el ejercicio 7.7 se aplica la función cumsum a las diferentes modalidades de tablas de frecuencias construidas a partir del objeto tabla, que almacena una tabla de frecuencias absolutas. Esta función (cumsum) permite construir tablas de frecuencias acumuladas, a partir del cálculo de cada distribución de frecuencias ya construidas en los ejercicios anteriores.

Ejercicio 7.7

#Frecuencias absolutas acumuladas
cumsum(tabla)

## Positiva   Neutra Negativa 
##      471     1201     1410

#Frecuencias relativas acumuladas
cumsum(prop.table(tabla))

##  Positiva    Neutra  Negativa 
## 0.3340426 0.8517730 1.0000000

#Porcentaje acumulado redondado en dos decimales
round(cumsum(prop.table(tabla)*100),2)

## Positiva   Neutra Negativa 
##    33.40    85.18   100.00

Así los resultados del ejercicio 7.7, permiten observar que una amplia mayoría de los casos presenta una evaluación neutra o positiva de la economía nacional con el 85,2% de los casos (en términos relativos), lo que equivale a 1.201 casos en términos absolutos. Sólo un 14,8% de las respuestas se concentran en una evaluación negativa de la economía.

Una última forma de describir la concentración de casos de una distribución es mediante los cuantiles. Tales estadísticos permiten describir la concentración de casos según cualquier posición relativa de los datos en la distribución, que resulte de interés. Para el cálculo de cuantiles la función quantile permite calcular los casos equivalentes a diferentes proporciones de la distribución (ejercicio 7.8). El primer argumento de la función es la variable a considerar, en este caso CEP$atisfaccion_chilenos, que refiere a la evaluación que la persona cree los chilenos tiene de su vida, en una escala de 1 a 10; luego, mediante el argumento prob se indica en formato vector los cuantiles a calcular (expresados como proporción). Si existen casos perdidos (codificados como NA) se debe indicar el argumento na.rm = TRUE.

Ejercicio 7.8

quantile(CEP$satisfaccion_chilenos, prob = c(0.25, 0.5, 0.75), na.rm = TRUE)

## 25% 50% 75% 
##   4   5   6

De tal forma, en el ejercicio 7.8 se solicita al software el cálculo del cuartil 1 (percentil 25 o caso que corta el 25% de la distribución), el cuartil 2 (percentil 50, mediana o caso que corta el 50% de la distribución) y el cuartil 3 (percentil 75, o caso que corta el 75% de la distribución). Los resultados obtenidos en el ejercicio 7.6 permiten concluir que solamente el 25% superior de los casos cree que los chilenos tienen una evaluación de su vida mayor o igual a 6, mientras que la mitad de los casos cree que los chilenos tienen una evaluación de su vida igual o menor a 5, en una escala del 1 al 10.

7.1.3 Medidas de dispersión: rango, varianza, desviación estándar y coeficiente de variación

En relación a las medidas de dispersión se partirá por cálculo del rango. Los valores mínimo y máximo de la distribución pueden calcularse de manera simultánea con la función range, indicando como argumentos la variable de interés y adicionando también el argumento na.rm = TRUE en el caso de que hubieran sido codificados como NA los valores perdidos. Como se observa en el ejercicio 7.9, los valores mínimo y máximo pueden calcularse de forma independiente, con las funciones min y max respectivamente, que siguen la misma lógica que la función range. En este caso se trabajará sobre la variable CEP$edad.

Ejercicio 7.9

range(CEP$edad, na.rm = TRUE)

## [1] 18 97

min(CEP$edad, na.rm = TRUE)

## [1] 18

max(CEP$edad, na.rm = TRUE)

## [1] 97

max(CEP$edad, na.rm = TRUE) - min(CEP$edad, na.rm = TRUE)

## [1] 79

Luego, para conocer el rango de los valores se debe restar el valor máximo al mínimo. Los resultados del ejercicio 7.9 indican que, para el caso de la variable edad el rango es de 79 años, siendo su valor mínimo 18 años y su valor máximo 97 años.

Otras dos medidas de uso generalizado para describir la dispersión de una variable son la varianza y la desviación estándar. El cálculo de ambas medidas, sigue la misma lógica en lo que refiere a la estructura de la función utilizada. Respectivamente, las funciones utilizadas son var para varianza y sd, para desviación estándar. Como se observa en el ejercicio 7.10 también debe incluirse el argumento na.rm = TRUE en el caso de que hubieran sido codificados como NA los valores perdidos. En este ejercicio se trabaja sobre la variable CEP$atisfaccion_chilenos, que refiere a la evaluación que la persona cree los chilenos tiene de su vida, en una escala de 1 a 10.

Ejercicio 7.10

var(CEP$satisfaccion_chilenos, na.rm = TRUE)

## [1] 3.017771

sd(CEP$satisfaccion_chilenos, na.rm = TRUE)

## [1] 1.737173

Atendiendo a los resultados del ejercicio 7.10 puede observarse que la dispersión de la variable que representa la evaluación que cada entrevistado/a cree que los chilenos tienen sobre su propia vida es de 3,02 unidades atendiendo a la varianza y de 1,73 unidades atendiendo a la desviación estándar.

Otra medida que debemos aprender a calcular para nuestros análisis es el coeficiente de variación. Como se observa en el siguiente ejercicio (7.11), el coeficiente de variación puede calcularse de manera sencilla, ejecutando una división simple entre la desviación estándar y la media de la variable de interés. Sin embargo, también existe la función coefficient.variation (del paquete FinCal) que permite calcular este estadístico indicando como argumento la media y desviación estándar de la variable de interés. En este caso tales valores se incluyen indicando la función para calcularlos: de tal modo se evitan errores humanos al momento de especificar los valores, ya sea por tipeo del valor o por su aproximación decimal. En este ejercicio trabajamos con la variable edad.

Ejercicio 7.11

sd(CEP$edad)/mean(CEP$edad)

## [1] 0.3566407

#Asegurarse de ejecutar previamente el comando "install.packages("FinCal")"
library(FinCal)
coefficient.variation(sd=sd(CEP$edad), avg = mean(CEP$edad))

## [1] 0.3566407

De este modo, los resultados del ejercicio 7.11 muestran que la variable edad presenta una dispersión del 35,67% según el valor obtenido en el coeficiente de variación.³⁵

7.1.4 Forma de una distribución: simetría, curtosis y normalidad

Un último grupo de estadísticos que resulta de importancia para el análisis estadístico de variables refiere a aquellos que dan cuenta de la forma general que asume la distribución de una variable. En específico, mostraremos en este apartado el cálculo e interpretación de estadísticos que dan cuenta de la simetría, curtosis y normalidad de una variable.

En el siguiente ejercicio (7.12) se muestra cómo calcular los coeficientes de simetría y curtosis mediante las funciones skew y kurtosi presentes en el paquete psych.

Ejercicio 7.12

library(psych)
skew(CEP$satisfaccion_vida)

## [1] -0.5335721

kurtosi(CEP$satisfaccion_vida)

## [1] -0.1461258

Como se observa en los resultados del ejercicio 7.12, los coeficientes de simetría y curtosis para la variable satisfaccion_vida son de -0,53 y -0.15 unidades de forma respectiva. Dado que tales valores están expresados en la unidad de medida de la variable en cuestión, no son útiles para comparar variables de diferentes unidades de medición. Es por eso que en el ejercicio 7.13 se calculan los coeficientes de simetría y curtosis estandarizados: para ello, se divide la simetría calculada, por la raíz cuadrada del valor 6 (este número es una constante en la fórmula) dividido en la cantidad de casos de la variable (en este caso, 1.401).

Ejercicio 7.13

skew(CEP$satisfaccion_vida)/sqrt(6/1401)

## [1] -8.153359

kurtosi(CEP$satisfaccion_vida)/sqrt(6/1401)

## [1] -2.232906

Un criterio general para determinar si los coeficientes de simetría y curtosis reflejan una variable semejante a una distribución normal es que ambos valores se encuentren entre -2 y 2. Como puede observarse en los resultados, ambos coeficientes escapan a tal rango por lo que se observa una distribución poco similar a una normal.

Finalmente, la forma más certera para evaluar si la distribución de datos de una variable se comporta según los parámetros que asume una distribución normal es aplicando un test estadístico específicamente orientado a tal evaluación. Para ello, se diferencia el test de Shapiro Wilk y el de Kolmogorov Smirnov. El primero se adecua a muestras pequeñas (menores a 50 casos), mientras que el segundo sirve para muestras de entre 50 y 1.000 casos.

El ejercicio 7.14 muestra la aplicación de tales pruebas sobre la variable edad. En específico, se utilizan las funciones shapiro.test y ks.test del paquete básico de R (stats). Su ejecución es bastante sencilla pues sólo requieren como argumento la variable sobre la cual se aplicará la prueba.

Ejercicio 7.14

#Prueba de Shapiro Wilk (muestras pequeñas)
shapiro.test(CEP$edad)

## 
##  Shapiro-Wilk normality test
## 
## data:  CEP$edad
## W = 0.97588, p-value = 1.037e-14

#Prueba Kolmogorov Smirnov (muestras grandes)
ks.test(CEP$edad, "pnorm", mean(CEP$edad, na.rm=T), sd(CEP$edad,na.rm=T))

## Warning in ks.test(CEP$edad, "pnorm", mean(CEP$edad, na.rm = T),
## sd(CEP$edad, : ties should not be present for the Kolmogorov-Smirnov test

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  CEP$edad
## D = 0.056969, p-value = 0.0001935
## alternative hypothesis: two-sided

Para interpretar uno u otro estadístico, debemos hacerlo atendiendo a la cantidad de casos de la variable en cuestión. En este caso, la variable edad presenta 1.424 casos. Esto provoca que ninguno de los resultados sea confiable pues las pruebas tienden a fallar cuando no se cumple el supuesto del margen de casos tolerado.

No obstante, vale la pena recordar que para determinar normalidad univariada se busca un valor p mayor a 0,05 para no rechazar la hipótesis nula de igualdad entre la distribución normal teórica y la distribución empírica de datos que estamos evaluado. Si los resultados fueran válidos en términos estadísticos, en ambas situaciones deberíamos rechazar la normalidad pues se aprueba la hipótesis alternativa dado que ambas pruebas presentan valores p menores a 0,05.

7.1.5 Tablas para informes e interpretación de resultados

En el presente apartado se presenta una forma para poder exportar resultados construidos en R a un formato compatible con softwares de tipo planilla de datos como Excel de Microsoft Office o Calc de Libre u Open Office. Es importante recalcar que aquí se enseña una forma simple para exportar resultados, que no se apoya en paquetes especializados en tales procedimientos. Una aproximación general a formas más avanzadas de construcción de reportes de resultados con formato, se presenta en el capítulo 9 de este manual.

En términos generales, el método de tratamiento de datos que presentaremos a continuación supone tres operaciones: en primer lugar, los resultados calculados deben existir en forma de matriz de datos en el entorno de trabajo; en segundo término, tales objetos deben imprimirse a un archivo de tipo CSV (para lo cual emplearemos la función write.csv2), el cual podrá ser abierto con alguno de los softwares tipo planilla de cálculo ya mencionados; así, en tercer lugar, tales datos podrán manipularse y editarse, ajustando su formato según lo que se desee, siendo fácilmente exportables hacia procesadores de texto.

7.1.5.1 Distribuciones de frecuencias

En primera instancia se guardarán como objetos las tablas de frecuencias ya existentes en nuestro entorno de trabajo de R (creadas en apartados anteriores de este capítulo). En el ejercicio 7.15 se observa la creación de tres objetos que contendrán, de forma respectiva, una tabla de frecuencias absolutas, una tabla de frecuencias relativas (porcentajes) y una tabla de frecuencia relativa acumulada (porcentajes) para la variable evaluación de la economía chilena (eval_econ_factor).

Ejercicio 7.15

f <- table(CEP$eval_econ_factor)
f_porc <- round((prop.table(tabla)*100),2)
f_porc_acum <- round(cumsum(prop.table(tabla)*100),2)

Luego, con la función write.csv2 tales tablas pueden imprimirse, de forma individual, a archivos de tipo CSV. Como se observa en la continuación del ejercicio 7.15, al ejecutar esta función se indica el objeto a imprimir como planilla y luego con el argumento file se indica (entre comillas) el nombre del archivo a crear con su respectiva extensión (.csv en este caso).

Ejercicio 7.15 (continuación)

write.csv2(f, file = "Tabla 1.csv")
write.csv2(f_porc, file= "Tabla 2.csv")
write.csv2(f_porc_acum, file= "Tabla 3.csv")

El resultado de la anterior operación será la creación de tres archivos de tipo CSV en la ubicación definida como carpeta de trabajo para la sesión de R. La aparición de tales archivos en la carpeta de trabajo que hemos definido para nuestra sesión de R se observan en la imagen a continuación.

Imagen 7.1: Exportación de resultados a archivos CSV

A partir de estos archivos - como se observa en la siguiente imagen - es posible unificar y editar las tablas en un formato adecuado para su inserción en reportes de investigación académica o profesional. No se profundiza aquí en el manejo de datos en softwares tipo planilla de cálculo, pero las simples operaciones copiar y pegar permiten consolidar los diferentes resultados en una sola tabla. Las tres primeras tablas de la imagen 7.2 son los datos impresos por R en archivos CSV independientes; la cuarta tabla es una tabla configurada manualmente mediante Microsoft Excel, lista para ser copiada y pegada en cualquier procesador de texto.

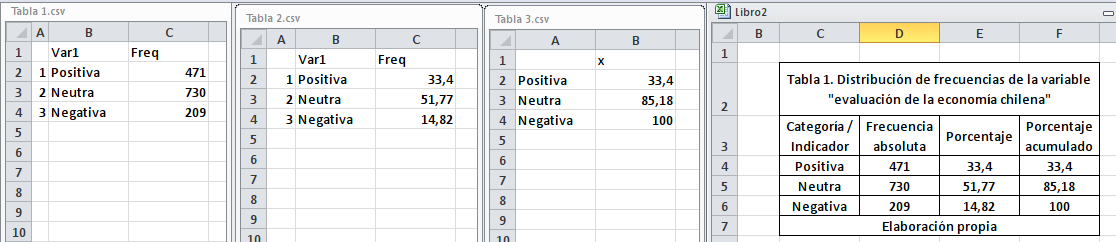
Imagen 7.2: Tabla de frecuencias en archivo CSV

Ahora bien, es importante recalcar cómo se debe realizar la interpretación de una tabla de resultados como la presentada (a continuación se incorpora en un formato adecuado para este documento interactivo).

Distribución de frecuencias de la variable Evaluación de la Economía Chilena
Categoría/Indicador	Frecuencia absoluta	Porcentaje	Porcentaje acumulado
Positiva	471	33,4	33,4
Neutra	730	51,77	85,18
Negativa	209	14,82	100

Reiterando lo señalado para los resultados del ejercicio 7.7, se observa que una amplia mayoría de los casos presenta una evaluación neutra o positiva de la economía nacional con el 85,2% de los casos (en términos relativos), lo que equivale a 1.201 casos en términos absolutos. Dentro de ello destaca que un tercio (33,4% o 471 casos) de las personas declaran una opinión neutra. Finalmente, es posible señalar que sólo un 14,8% de las respuestas (209 casos) se concentran en una evaluación negativa de la economía.

7.1.5.2 Estadísticos descriptivos

A continuación, se explicarán dos formas para calcular de manera agregada diversos estadísticos descriptivos de interés, para la posterior construcción de una tabla exportable a formato planilla que contenga tales valores.

Una primera forma es utilizando la función summary, que se ejecuta con la variable de interés como principal argumento (en este caso, la variable CEP$satisfaccion_vida). A diferencia del cálculo de estadísticos de forma individual, en este caso no es necesario indicar mediante argumento el tratamiento de los casos codificados como NA pues esta función reconoce de manera automática tales valores lógicos y los excluye del análisis.

Mediante este simple comando (ejercicio 7.16) se obtiene una tabla de estadísticos de resumen: valores mínimo y máximo, primer cuartil, mediana, media, tercer cuartil y cantidad de valores codificados como perdidos (valores NA).

Ejercicio 7.16

summary(CEP$satisfaccion_vida)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##   1.000   6.000   7.000   7.311   9.000  10.000      10

Ahora bien, para exportar estos resultados a una planilla de cálculo se deberán ejecutar diversas operaciones que se muestran en el siguiente ejemplo (7.17). Primero, los resultados del comando summary se guardan como un objeto específico (al cual se le asigna el nombre de descriptivos).

Ejercicio 7.17

#Guardar summary como objeto
descriptivos <- summary(CEP$satisfaccion_vida)

Luego, si se le aplican las funciones names y as.numeric a tal objeto (descriptivos) se obtiene un vector que contiene los encabezados de los resultados y otro vector que contiene su valores numéricos: en la continuación del ejercicio 7.17 se observa el resultado de aplicar ambas funciones sobre el objeto mencionado, que muestran en primer lugar los encabezados de la tabla y luego sus valores.

Finalmente, usando la función as.data.frame se configura como matriz de datos el resultado de unir como filas - mediante la función rbind (unir como filas, o row bind en inglés) el encabezado de los estadísticos descriptivos y sus valores numéricos. Tal objeto se nombra como descr_sat_vida y se configura como un objeto de tipo data.frame.

Ejercicio 7.17 (continuación)

#Ver nombres y valores del objeto
names(descriptivos)

## [1] "Min."    "1st Qu." "Median"  "Mean"    "3rd Qu." "Max."    "NA's"

as.numeric(descriptivos)

## [1]  1.000000  6.000000  7.000000  7.311174  9.000000 10.000000 10.000000

#Configurar como matriz de datos
descr_sat_vida <- as.data.frame(rbind(names(descriptivos), as.numeric(descriptivos)))
View(descr_sat_vida)

El resultado del ejercicio (como se observa en la imagen 7.3) muestra cómo ya hemos configurado el resultado en formato matriz de datos.

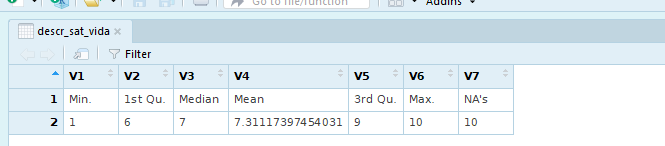
Imagen 7.3: Comando summary configurado como matriz de datos

Así, a partir de esta matriz se puede crear un nuevo archivo tipo planilla de cálculo con estos resultados. Que quedará guardado en la carpeta de trabajo con el nombre de “Tabla 4.csv”.

Ejercicio 7.17 (continuación)

#Exportar matriz a archivo CSV
write.csv2(descr_sat_vida, file = "Tabla 4.csv")

Como se observa en la imagen 7.4, la planilla superior es la exportada desde R, mientras la inferior es la que resulta luego de una edición simple enfocada en editar los encabezados de la tabla y editar el formato de la misma destacando todos los bordes de la tabla y centrando sus valores (entre otras ediciones).

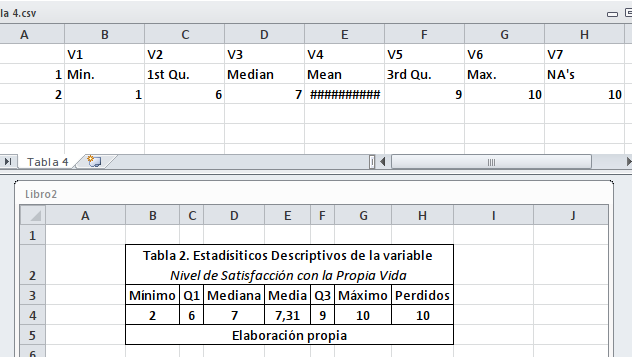
Imagen 7.4: Resultados de summary exportados a archivo CSV

Ahora bien, la función summary no calcula todos los estadísticos que pueden ser de interés. Para construir una tabla completamente personalizada es necesario calcular cada valor que sea de interés y disponerlo en una matriz de datos para así poder guardar una tabla en formato planilla de cálculo.

Como se observa en el ejercicio 7.18, cada valor construido se concatena como un sólo vector (descriptivos_satvida) de valores numéricos, que será una fila de la planilla a construir (la que contendrá los valores de cada estadístico). Adicionalmente, se construye un vector llamado nombres con los encabezados de cada estadístico a escribir en la tabla, que se utilizará como fila de títulos de la planilla de cálculo a exportar.

Ejercicio 7.18

#Cálculo simple de estadíticos descriptivos
min <- min(CEP$satisfaccion_vida, na.rm = TRUE)
q1 <- quantile(CEP$satisfaccion_vida, probs = 0.25, na.rm = TRUE)
media <- mean.default(CEP$satisfaccion_vida, na.rm = TRUE)
media_rec <- mean.default(CEP$satisfaccion_vida, trim = 0.025, na.rm = TRUE)
mediana <- median.default(CEP$satisfaccion_vida, na.rm = TRUE)
moda <- mfv(CEP$satisfaccion_vida)
var <- var(CEP$satisfaccion_vida, na.rm = TRUE)
desvest <- sd(CEP$satisfaccion_vida, na.rm = TRUE)
q3 <- quantile(CEP$satisfaccion_vida, probs = 0.75, na.rm = TRUE)
max <- max(CEP$satisfaccion_vida, na.rm = TRUE)
s <- skew(CEP$satisfaccion_vida)
c <- kurtosi(CEP$satisfaccion_vida)

#Valores de estadísticos como vector
descriptivos_satvida <- as.numeric(c(min, q1, media, media_rec, mediana, moda,
                          var, desvest, q3, max, s, c))

#Encabezados de cada estadístico como un vector
nombres <- c("Mínimo", "Q1", "Media", "Media recortada", "Mediana", "Moda",
             "Varianza", "Desviación Estándar", "Q3", "Máximo", "Simetría", "Curtosis")

Con esta información ya es posible configurar una planilla de estadísticos descriptivos completamente personalizada. Para ello, como se muestra en la continuación del ejercicio 7.18, se configura una matriz de datos (función as.data.frame) a partir de los vectores de encabezados de los estadísticos (nombres) y los valores de tales coeficientes (descriptivos_satvida), que se almacena como un objeto de nombre descr2. Finalmente, esta matriz de datos se exporta a una planilla de cálculo mediante la función write.csv2.

Ejercicio 7.18 (continuación)

descr2 <- as.data.frame(rbind(nombres,descriptivos_satvida))

write.csv2(descr2, file = "Tabla 5.csv")

Todo esto resulta en una planilla como la que se observa en la imagen 7.5, editable para la construcción de reportes formales.

Imagen 7.5: Tabla de estadísticos muestrales personalizada y exportada a CSV

En base a una edición muy simple en software tipo planilla de cálculo, se puede llegar a darle un formato como el que se observa en la imagen 7.6, útil para su presentación en reportes formales de resultados.

Imagen 7.6: Tabla de estadísticos con edición de formato, lista para ser incorporada a procesador de texto

Estadísticos Descriptivos de la variable Nivel de Satisfacción con la Propia Vida
Estadístico	Valor
Mínimo	1,0
Q1	6,0
Media	7,31
Media recortada	7,39
Mediana	7,0
Moda	10,0
Varianza	4,46
Desviación Estándar	2,11
Q3	9,0
Máximo	10,0
Simetría	-0,53
Curtosis	-0,15

En la tabla de estadísticos descriptivos presentada destacan diferentes elementos. En primera instancia, los valores mínimo (1) y máximo (10) indican que el rango de las respuestas observadas abarca todas las respuestas posibles de la pregunta del cuestionario.

En segunda instancia, el valor de la media (7,31) es bastante similar al de la mediana, lo que indica que la mitad de las personas de la distribución le asigna la nota 7 a la satisfacción con su propia vida, en la escala de 1 a 10 ya señalada.

En tercera instancia, se puede señalar - respecto a la dispersión de los datos - que la desviación estándar es de 2,11 unidades.

Finalmente, sobre la forma de la distribución se destacan dos elementos: dado que el coeficiente de simetría es negativo (-0,53), se está ante una variable de tipo asimétrica hacia la izquierda de la distribución de casos, en la cual los casos tienden a concentrase hacia la derecha de la media, es decir, en las puntuaciones más altas de la distribución de respuestas; dado que el coeficiente de curtosis es negativo (-0,15), estamos ante una distribución platicúrtica, en la que existe una menor concentración de casos en torno a la media y presenta una forma más “achatada”.

7.2 Inferencia estadística univariada: de la estimación puntual al parámetro

En el apartado anterior se revisaron procedimientos para estimar de forma puntual estadísticos univariados provenientes de una muestra probabilística. En el presente apartado se explicará como calcular intervalos de confianza para parámetros a partir de muestras probabilísticas. Concretamente se indicarán los procedimientos para calcular intervalos de confianza para medias y proporciones. En primera instancia se presenta los procedimientos más simples que presenta el lenguaje R, adecuados para diseños de muestras del tipo aleatorio simple; en segundo término, se expondrá como calcular estimadores insesgados a partir del uso de factores de expansión, y cómo estimar intervalos de confianza apropiados ante la utilización de diseños muestrales complejos.

7.2.1 Cálculo de intervalos de confianza para proporciones

Para calcular el intervalo de confianza de una proporción es de utilidad la función exactci del paquete PropCIs (recordar instalarlo vía install.packages("PropCIs") de manera previa).

La información que necesita esta función es la cantidad de casos que coinciden con la condición de interés (la categoría de la variable cuya frecuencia relativa interesa) y la cantidad que representa a la totalidad de casos de la muestra (n muestral). En este caso, a partir de la encuesta CEP se evaluará la hipótesis de si la mayoría de las y los chilenos declara tener una opinión negativa de la situación económica del país.

Como se observa a continuación en el ejercicio 7.19, solicitando una tabla de frecuencias es posible identificar la cantidad de casos probables que tienen una percepción negativa de la situación económica del país (730). Por otra parte, solicitando la cantidad de filas de la base de datos (usando la función nrow) se conoce el n total de casos (1.424). Con ambos valores es posible aplicar la función exactci; un tercer argumento a indicar es el nivel de confianza (conf.level), que se expresa en términos numéricos y proporcionales (para este caso, un 95% de confianza se expresa como 0.95).

Ejercicio 7.19

library(PropCIs)

table(CEP$eval_econ_factor)

## 
## Positiva   Neutra Negativa 
##      471      730      209

nrow(CEP)

## [1] 1424

exactci(x = 730, n = 1424, conf.level = 0.95)

## 
## 
## 
## data:  
## 
## 95 percent confidence interval:
##  0.4863248 0.5389039

Así, el resultado de esta función es el límite superior e inferior del intervalo de confianza, construido a partir de la probabilidad ya indicada (proporción de personas que declaran tener una percepción positiva de la situación económica del país).

Con este resultado es posible concluir que, con un 95% de confianza, no es posible afirmar que la proporción de personas que declaran tener una percepción positiva de la situación económica del país sea más que la mitad de población nacional, debido a que el parámetro poblacional se sitúa entre el 48,6% y 53,9% de los casos.

7.2.2 Cálculo de intervalos de confianza para medias

Una segunda variante para el cálculo de parámetros poblacionales es la estimación del intervalo de confianza de una media. Para calcular el intervalo de confianza de una media es útil la función ci.mean del paquete Publish (recordar instalarlo vía install.packages("Publish") de manera previa). Su uso se detalla en el ejercicio 7.20.

La información que necesita esta función solamente es la variable a utilizar. En el caso que se observa a continuación, se calcula el intervalo de confianza para la media de la variable nivel de satisfacción con la propia vida.

El resultado es bastante sencillo e indica el valor del estadístico muestral (el valor de la media bajo la etiqueta mean) a la vez que indica el límite superior e inferior del intervalo de confianza para la media poblacional, o parámetro, bajo la etiqueta CI-95%; esto último indica el nivel de confianza utilizado para la construcción del intervalo.

Ejercicio 7.20

library(Publish)

ci.mean(CEP$satisfaccion_vida) #Nivel de confianza por defecto.

##  mean CI-95%     
##  7.31 [7.20;7.42]

Como se observa en los resultados del ejercicio 7.20, al ejecutar el comando con su configuración por defecto, este utiliza un 95% de confianza. Con este valor se puede afirmar con un 95% de confianza que la media poblacional, es decir el promedio de satisfacción que los chilenos declaran tener respecto a su propia vida, se encuentra entre los valores 7,2 y 7,42, en una escala de 1 a 10.

Ahora bien, si al comando básico se le agrega el argumento alpha es posible definir el valor complementario al nivel de confianza, es decir la proporción de error aceptable para la estimación. En la continuación del ejercicio 7.20 se define el valor 0,2 o 20%.

Ejercicio 7.20 (continuación)

ci.mean(CEP$satisfaccion_vida, alpha = 0.2) #Definición manual del nivel de confianza.

##  mean CI-80%     
##  7.31 [7.24;7.38]

Lo realizado en la continuación del ejercicio 7.20 implica que, observando los resultados, se puede afirmar con un nivel de confianza del 80% que el promedio de satisfacción que los chilenos declaran tener respecto a su propia vida, se encuentra entre los valores 7,24 y 7,38, en una escala de 1 a 10.

Un uso muy frecuente para este tipo de cálculos es evaluar si la diferencia entre una misma media para dos grupos es diferente, de manera estadísticamente significativa. Supondremos que se busca calcular el mismo indicador anterior pero efectuando el cálculo de intervalo de confianza para medias, diferenciando según hombres y mujeres.

Como se observa en el código a continuación (ejercicio 7.21), para indicar a la función cual es la variable de clasificación para construir los grupos, se debe indicar la variable de interés seguida a continuación de una virgulilla (mismo signo usado en la ñ, ~) que la separa de la variable de clasificación. Luego se debe indicar el conjunto de datos de donde provienen tales variables con el argumento data. Como antes, si no se le indica el valor del alpha, la función asume por defecto un cálculo con un 95% de confianza.

Ejercicio 7.21

ci.mean(satisfaccion_vida~sexo_factor, data=CEP)

##  sexo_factor mean CI-95%     
##  Hombre      7.46 [7.29;7.62]
##  Mujer       7.22 [7.07;7.37]

Como se observa en los resultados, las medias muestrales permitirán afirmar que hombres y mujeres presentan una evaluación levemente diferente en relación a la satisfacción que declaran tener con su propia vida. Específicamente, la media de esta variables es de 7,46 para los hombres y de 7,22 para las mujeres. Sin embargo, al observar el comportamiento de tales mediciones a nivel poblacional, es posible afirmar que las variables no difieren de manera estadísticamente significativa. Para un nivel de confianza del 95%, la media de esta variable para los hombres se sitúa entre los valores 7,29 y 7,62 para los hombres y entre los valores de 7,07 y 7,37 para las mujeres. Los valores indican que los intervalos se intersectan, es decir, existe una elevada probabilidad de que estos parámetros sean muy similares e incluso iguales. Por lo tanto, no es posible afirmar que tales valores sean diferentes, de manera estadísticamente significativa, pues existe una alta posibilidad de que sean iguales.

7.2.3 Coeficientes de expansión para estimación de parámetros poblacionales

Las investigaciones sociales basadas en un diseño muestral probabilístico (aleatorio simple, estratificado, por conglomerado o diseños complejos) deben utilizar un ponderador en la estimación de variables de interés para alcanzar validez sobre la población objetivo. Lo anterior se relaciona con las probabilidades de selección de las distintas unidades de muestreo y da cuenta del número de personas de la población que representa cada individuo de la muestra. Este ponderador es conocido como factor de expansión.

Los factores de expansión buscan incorporar en las estimaciones puntuales surgidas desde la muestra, las características y el peso que tienen esos atributos en la población. De esa forma, se producen estimadores insesgados, es decir, que están centrados en el parámetro población. Así, denominaremos “sesgo de un estimador” a la diferencia entre la esperanza (o valor esperado) del estimador y el valor observado del parámetro a estimar. Decimos que un estimador es “insesgado” o “centrado” cuando su sesgo es nulo: o sea, cuando el valor esperado es igual al valor observado.

7.2.3.1 Configuración de los datos a utilizar

Para hacer esto más claro, y a la vez indicar cómo se trabaja con coeficientes de expansión en R, lo explicamos con un ejemplo. Específicamente utilizaremos la Encuesta Nacional de Empleo, trimestre móvil Enero-Febrero-Marzo de 2019 publicada por el Instituto Nacional de Estadísticas de Chile. (2019 a).

Según lo que se indica en el libro de códigos asociado a la base de datos, utilizaremos las siguientes variables para ejemplificar el uso de coeficientes de expansión.

Variables a utilizar desde la ENE
Nombre de variable	Definición	Valores	Estado en base
fact	Factor de expansión	Peso de cada caso en la población	Creada por INE
edad	Edad de la persona entrevistada	Cantidad de años	Creada por INE
PET	Población en edad de trabajar	1 representa personas de 15 y más años - 2 representa a personas menores a 15 años	A crear

Como se observa en el siguiente ejemplo (7.22), primero se carga la base de datos con la función read.csv2, para luego recodificar la variable edad en la variable PET³⁶. A esta última variable le agregamos etiquetas mediante la función factor para poder identificar los casos en las salidas de resultados.

Ejercicio 7.22

#Cargar ENE y guardar como objeto
ENE <- read.csv2("ENE 2019 02 EFM.csv", sep = ";", dec = ",")

#Recodificacón edad en PET
library(dplyr)
ENE <- mutate(ENE, PET = car::recode(ENE$edad, 
                                     "0:14=2; else = 1"))
# Etiquetado de categorías
ENE$PET <- factor(ENE$PET, labels = c(">=15", "<15"))
table(ENE$PET)

## 
##  >=15   <15 
## 86197 20254

Como se observa en los resultados del ejercicio 7.22, en la muestra se observa que existen 86.197 personas en edad de trabajar (con una edad igual o mayor a 15 años), mientras 20.254 personas no están en edad de trabajar (menores de 15 años).

Ahora bien, si se observan los resultados oficiales publicados por el INE (2019 b), se observa que la cantidad de personas de 15 años o más, no es 86.197, sino 15.286.507 personas. Para lograr llegar a tal cifra se deben aplicar el factor - o coeficiente - de expansión de la base de datos, para luego de ello calcular la cifra de interés.

7.2.3.2 Utilización del paquete survey para la utilización de coeficientes de expansión

Para aplicar coeficientes de expansión sobre nuestros resultados utilizaremos el paquete survey (Lumley 2019).³⁷ Como se observa en el ejercicio a continuación, se debe crear un nuevo objeto que almacene la base de datos ponderada. En este caso llamaremos a tal objeto con el nombre ENE_ponderada, que almacenará el resultado de aplicar la función svydesign, con el argumento data indicando la base de datos a ponderar (ENE), con el argumento id indicando la unidad de muestreo que en este caso es el valor 1 pues cada caso se muestrea de forma equiprobable, y finalmente se indica el argumento weights indicando la variable que indica el peso que cada observación de la muestra representa en la población. Como puede verse, cada variable se indica luego de una virgulilla (~).

Ejercicio 7.23

#Creación de base de datos ponderada
library(survey)
ENE_ponderada <- svydesign(data = ENE, id=~1, weights = ~fact)

#Características base ponderada
class(ENE_ponderada)

## [1] "survey.design2" "survey.design"

ENE_ponderada

## Independent Sampling design (with replacement)
## svydesign(data = ENE, id = ~1, weights = ~fact)

El resultado de aplicar la función class sobre el objeto que almacena la base de datos ponderada (ENE_ponderada) y ejecutar directamente tal objeto, es la información de que se trata de un objeto del tipo survey.design y que se trata de un diseño de muestreo con reemplazo, es decir, cada caso tuvo siempre la misma probabilidad de ser elegido (diseño equiprobable).

Ahora bien, sobre este objeto, podemos seguir utilizando funciones del mismo paquete survey para calcular algunos resultados. Retomando el ejemplo sobre la Población en Edad de Trabajar, con la función svytotal es posible calcular nuevamente las frecuencias de la variable PET. Como se observa en el ejercicio 7.24, esto se efectúa mediante la función svytotal, a la cual se le indica la variable de interés antecedida por una virgulilla (~PET) y el nombre del objeto que corresponde a uno del tipo survey.design.

Ejercicio 7.24

svytotal(~PET, ENE_ponderada)

##            total    SE
## PET>=15 15286507 68710
## PET<15   3649759 42750

Como se observa en los resultados del ejercicio 7.24, ahora sí logramos calcular las frecuencias reales de ocurrencia de la variable Población en Edad de Trabajar, pues la categoría igual o mayor a 15 años presenta 15.286.507 casos, equivalente a las cifras publicadas de manera oficial por el INE (2019 b).

No se profundiza de manera adicional, pero el cálculo de otro tipo de resultados con una base ponderada es bastante similar a lo ya revisado en relación a frecuencias simples. Para mayores detalles revisar la página web mantenida por el equipo desarrollador del paquete survey (Lumley 2019).

7.2.3.3 Cálculo de intervalos de confianza en diseños muestrales complejos

Para efectuar una correcta utilización de diseños muestrales complejos en análisis de datos sociales orientados hacia la inferencia estadística, es preciso realizar el cálculo de intervalos de confianza utilizando estimadores insesgados. Para ello, debemos ejecutar tal tipo de análisis habiendo ponderado de forma correcta la base de datos mediante la utilización de factores de expansión. Dado que tal procedimiento fue revisado en el apartado anterior, a continuación presentamos de forma específica el modo de calcular intervalos de confianza para medias y proporciones incluido en el paquete survey.

En primer término, en el ejercicio 7.25 se presenta el cálculo del intervalo de confianza para la proporción que representa la población en edad de trabajar (PET). La función svyciprop precisa definir explícitamente la categoría sobre la cual se desea calcular el intervalo de confianza, luego la base ponderada (ENE_ponderada) en la cual se encuentran los datos ponderados para el cálculo y finalmente el método (method) para realizar la estimación.³⁸

Ejercicio 7.25

svyciprop(~I(PET==">=15"), ENE_ponderada, method = "li")

##                         2.5% 97.5%
## I(PET == ">=15") 0.807 0.803  0.81

Como se observa en el resultado del ejercicio 7.25, el cálculo arroja tres números expresados como proporciones. El primero es 0,807 (u 80,7%), que corresponde a la estimación puntual - basada en las frecuencias ponderadas - de la Población en Edad de Trabajar. Luego se observan los valores 0,803 (80,3%) y 0,81 (81,0%) que marcan, según sus encabezados lo indican los límites del intervalo de confianza calculado con un error tipo 1 (o alfa) del 5%.³⁹.

Este resultado permite concluir que, en base a una estimación realizada con un nivel de confianza del 95%, siendo la estimación puntual un 80,7%, el valor del parámetro que expresa la proporción de las personas en edad de trabajar en la población chilena se encuentra entre el 80,3% y 81,0%.

Esto mismo puede replicarse para frecuencias absolutas. En el ejercicio 7.26 se observa una ejemplificación con los mismos datos que hasta ahora han sido usados: las frecuencias de la variable Población en Edad de Trabajar. En primer término se muestra el cálculo de frecuencias expandidas sobre la variable PET: el cálculo arroja el resultado para las dos categorías de la variable. En segundo lugar se aplica la función confint sobre el resultado de frecuencias absolutas expandidas, indicando de forma explítica el nivel de confianza a utilizar con el argumento level.

Ejercicio 7.26

#Frecuencias expandidas para variable edad
svytotal(~PET, ENE_ponderada)

##            total    SE
## PET>=15 15286507 68710
## PET<15   3649759 42750

#IC para frecuencias absolutas
confint(svytotal(~PET, ENE_ponderada), level = 0.95)

##            2.5 %   97.5 %
## PET>=15 15151838 15421176
## PET<15   3565970  3733548

Como se observa en el resultado del ejercicio 7.26, la funció svytotal calcula las frecuencias (expandidas) de la variable PET, indicando que la población en edad de trabajar son 15.286.507 personas, mientras que las personas menores a la edad de trabajar son 3.649.759. Luego, la función confint arroja los intervalos de confianza construidos con un 5% de error alfa o tipo 1: en el caso de las cantidad de personas en edad de trabajar, se observa que el parámetro de tal atributo se encuentra entre 15.151.838 personas y 15.421.176 personas; en el caso de la población en una edad menor a la de trabajar (menos que 15 años) el parámetro de tal atributo se encuentra entre los 3.565.970 personas y los 3.733.548 personas.

Finalmente, en el ejericio 7.27 se presenta, en primera instancia, el cálculo de la media expandida para la variable edad mediante la función svymean. Luego tal cálculo se utiliza para calcular un intervalo de confianza a partir de la estimación puntual, introduciendola como argumento de la función confint e indicando el nivel de confianza a utilizar para la estimación con el argumento level (en este caso, 95% de confianza expresado con la proporción 0.95).

Ejercicio 7.27

# Cálculo de media expandida para la variable edad
svymean(~edad, ENE_ponderada)

##        mean     SE
## edad 38.313 0.1169

# Cálculo de intervalo de confianza para la media expandida de variable edad
confint(svymean(~edad, ENE_ponderada), level = 0.95)

##         2.5 %   97.5 %
## edad 38.08348 38.54182

Como se observa en los resultados del ejericio 7.27 podemos afirmar que la estimación puntual de la variable edad es 38,31 años. Mientras que el parámetro de tal atributo se encuentra entre los 38,08 y 38,54 años, con un nivel de confianza para tal estimación del 95%.

Bibliografía

INE. 2019a. “Base de Datos Encuesta Nacional de Empleo. Trimestre Enero-Febrero-Marzo de 2019.” Archivo en formato CSV. Santiago de Chile: Instituto Nacional de Estadísticas. https://www.ine.cl/estadisticas/laborales/ene.

INE. 2019b. “Población Total de 15 Años Y Más Por Situación En La Fuerza de Trabajo, Nivel Nacional Y Regional, Ambos Sexos.” Santiago de Chile: Instituto Nacional de Estadísticas. https://www.ine.cl/estadisticas/laborales/ene.

Lumley, Thomas. 2019. “Survey Analysis in R.” Survey Package. http://r-survey.r-forge.r-project.org/survey/index.html.

En este apartado no se profundizará en métodos avanzados para optimizar la presentación de resultados: es importante distinguir entre la construcción de resultados estadísticos para su uso en el proceso de investigación, respecto a la construcción de informes y resultados con un formato adecuado para su divulgación. Éste último aspecto lo revisaremos en los dos últimos capítulos de este documento, enfocados en el uso de los paquetes ggplot2 y las funcionalidades para la construcción de informes vía RMarkdown.↩
Es por eso que si se busca contar con una media recortada al 5%, se indica una proporción de 0.025, que se recortará a ambos extremos de la distribución, alcanzando un recorte total de una proporción de casos del 0.05 o 5%.↩
Sigla en inglés correspondiente a la expresión most frequent values o valores más frecuentes en castellano.↩
En el resultado del ejercicio se obtiene un valor proporcional, es decir una fracción de 1. Cuando expresamos el resultado final en formato de porcentaje, simplemente hemos multiplicado tal resultado por 100.↩
El número 1 representa a las personas mayores o iguales a 15 años, mientras que el número 2 representa a las personas menores a 15 años↩
Adicionalmente a la documentación del paquete disponible en el CRAN, existe una página con más ejemplos de cómo se utilizan sus principales funcionalidades, mantenida ya actualizada por su desarrollador (Lumley 2019).↩
En este caso se dejó sin editar la opción li, que es la que viene definida por defecto en la función.↩
Es el nivel de confianza que la función utiliza por defecto↩