5.2 Compatibility intervals and margin of error
When statisticians report sample estimates, they typically provide the value of the estimate along with the quantification of uncertainty in this estimate. This uncertainty measurement gives us an indication of the “precision” of the estimate. For example, consider again the example of the person who lost his keys. In those pictures, recall, the places where he searched for his keys (the red x’s) represents that sample data.
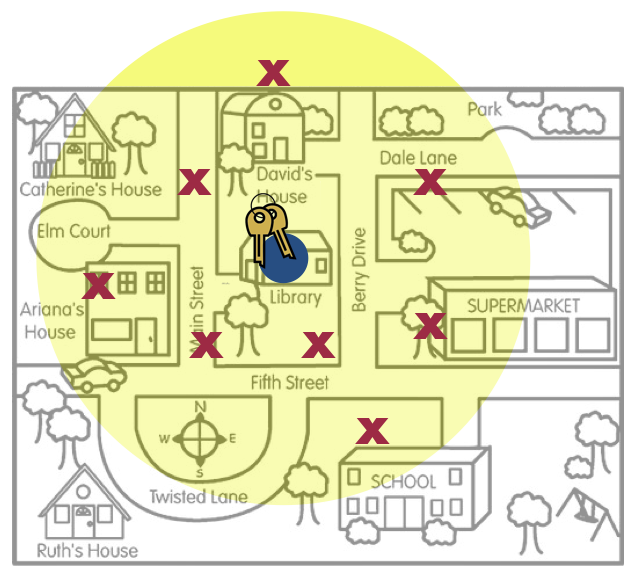
Figure 5.1: This figure is a metaphor for statistical uncertainty.
One estimate that can be made from that data is the “mean” location.24 This location is marked with a big blue dot. This estimate is the one-location best guess about where the actual keys (the population parameter) are located. The yellow area represents the uncertainty; other places where the keys might be aside from the on-location best guess. Interpreting this uncertainty gives him a range of locations where the actual keys might be; the compatibility interval.
5.2.1 Quantification of Uncertainty: Margin of Error
Compatibility intervals are often reported using the sample estimate (statistic) and a margin of error. For example, consider the following poll results reported in the New York Times on June 30, 2011:
As the housing market slumped over the last few years with a speed and magnitude not seen since the Great Depression, aspects of homeownership have been debated as never before. There are tough questions about the role the government should take…includ[ing] how much of a down payment lenders should demand. Whether buyers need to come up with a 20 percent down payment—the standard for decades, but beyond the reach of many families now—is hotly debated. Fifty-eight percent of respondents say lenders should require this, while 36 percent say they should not. The nationwide telephone poll was conducted June 24–28 with 979 adults and has a margin of sampling error of plus or minus three percentage points for all adults.
In this article, the percentage of all adults in the United States who believe that lenders should require a 20% down payment on a house was reported as:
- Sample estimate: 58%
- Margin of error: 3%
Although the compatibility interval isn’t directly reported, it can be computed using the sample estimate and margin of error as,
\[ \mathrm{Sample~Estimate} \pm \mathrm{Margin~of~Error} \]
In this example,
\[ 58\% \pm 3\% = \left[55\%,~61\%\right] \]
Statisticians refer to this as a compatibility interval because it gives an interval of plausible values for the percentage of all adults in the United States who believe that lenders should require a 20% down payment on a house that are compatible with the observed data. Based on the observed data, the best estimate for the “truth” (the population parameter) is that 58% of all adults in the United States believe that lenders should require a 20% down payment on a house. However, because of the uncertainty associated with random sampling, it may be that anywhere between 55% and 61% of all adults in the United States believe that lenders should require a 20% down payment on a house.
In the interpretation above, we associated the amount of uncertainty with variation because of random sampling. It turns out that the margin of error is directly related to the quantification of sampling error. In fact,
\[ \mathrm{Margin~of~Error} = 2 \times \mathrm{SD~of~sampling~distribution} \]
While statistians and polling organizations tend to use two SDs to compute the uncertainty estimate, this is a somewhat arbitrary choice. Some researchers choose one or three SDs of the sampling distribution.
As you interpret compatibility intervals, there are a couple things to keep in mind.
- The compatibility interval is being used to estimate the population parameter.
- The compatibility interval gives a range of compatible values for the population parameter.
To further help you understand ideas related to the standard error and the margin of error, we would like you to read Chapter 10 (What is a Margin of Error?) from a short pamphlet put together by the American Statistical Association’s Section on Survey Research.
- It is available at http://www.prm.nau.edu/prm447/asa%20brochures/margin.pdf.