2 Statistique descriptive

Que faut-il faire pour décrire numériquement et / ou visualiser tel type de variable?

Afin d’illuster certaines fonctions nous allons utiliser le jeu de données suivant:

set.seed(123) 
cat1 <- c(rep("H",25), rep("F",25))
cat2 <- c(rep("Grp1",17), rep("Grp2",17), rep("Grp3",16))
Quanti1 = rnorm(50,4,2)
df <- data.frame(varQuanti = runif(50,0,10), 
                 varQuanti1 = Quanti1,
                 varQuanti2= Quanti1+rnorm(50,0,1),
                 varQuali = sample(cat1, replace=TRUE),
                 varQuali1 = sample(cat1, replace=TRUE),
                 varQuali2 = sample(cat2, replace=TRUE))
# On extrait uniquement les variables quantitatives de df
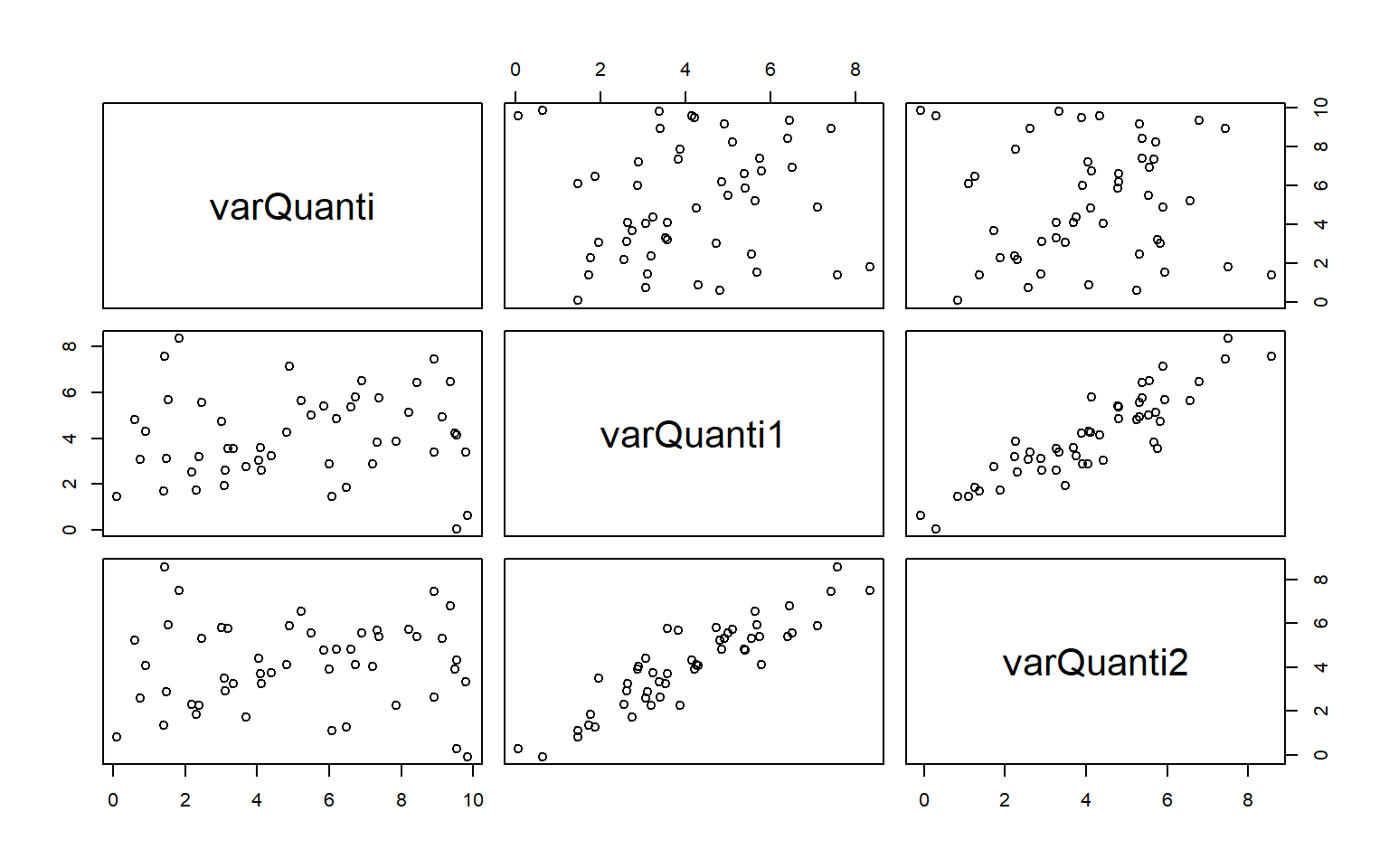
df_quanti <- subset(df, select=c(varQuanti, varQuanti1, varQuanti2))

Ce sont des données fictives, inventées de toute pièce. Il y a 3 variables quantitatives: varQuanti varQuanti1 varQuanti2 ainsi que 3 variables qualitatives varQuali varQuali2 varQuali3. Ces données se trouvent dans un dataframe nommé df et les 3 variables quantitatives uniquement dans df_quanti.

2.1 Numérique

2.1.1 Tendance centrale

  • Moyenne ~> mean()
  • Médiane ~> median()

2.1.2 Variabilité

  • Minimum / maximum ~> min() / max()
  • Range ~> range()
  • Variance ~> var()
  • Ecart-type ~> sd()
  • Covariance ~> cov()

2.1.3 Quantiles

  • Quantile ~> quantile()
quantile(df$varQuanti, p=0.25) # Quantile d'ordre 0.25
  • Ecarte interquartile ~> IQR()

2.1.4 Autres

  • Résumé statistique ~> summary()
res <- summary(df$varQuanti)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.1047 2.596 5.049 5.154 7.358 9.842
  • Table de fréquence ou contingence ~> table()
  • Table de proportion ~> prop.table()
# Fréquence
res <- table(df$varQuali)
F H
22 28 
# Contingence
res <- table(df$varQuali1, df$varQuali2)
  Grp1 Grp2 Grp3
F 2 9 10
H 8 10 11
  • Table de proportion ~> prop.table()
res <- prop.table( table(df$varQuali) )
F H
0.44 0.56
  • Coefficient / matrice de corrélation ~> cor()
# Matrice de corrélation des 3 variables quantitatives
res <- cor(df_quanti)
  varQuanti varQuanti1 varQuanti2
varQuanti 1 0.06801 0.02392
varQuanti1 0.06801 1 0.9014
varQuanti2 0.02392 0.9014 1
  • Matrice de Variance-Covariance ~> cov()
# Matrice de corrélation
res <- cov(df_quanti)
  varQuanti varQuanti1 varQuanti2
varQuanti 8.645 0.3703 0.1364
varQuanti1 0.3703 3.429 3.237
varQuanti2 0.1364 3.237 3.761
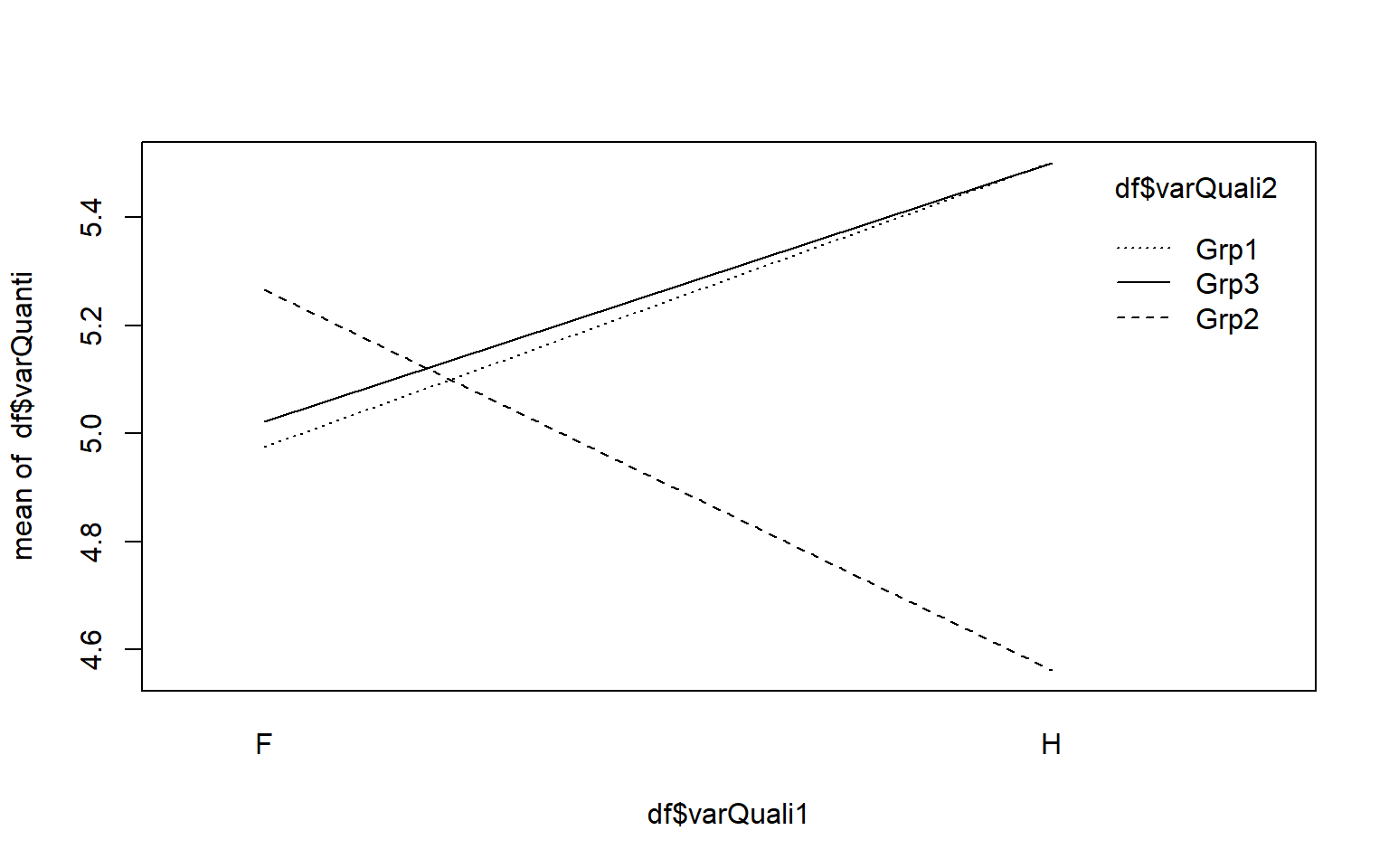
  • Informations par modalités ~> tapply()
res <- tapply(df$varQuanti, df$varQuali, FUN = summary) # summary de df$varQuanti par modalité de df$varQuali

  • F:

    Min. 1st Qu. Median Mean 3rd Qu. Max.
    0.6072 2.226 3.606 4.564 7.358 9.353

  • H:

    Min. 1st Qu. Median Mean 3rd Qu. Max.
    0.1047 3.603 5.746 5.617 7.63 9.842

2.2 Graphique

2.2.1 Scatter plot ~> plot()

plot(varQuanti1 ~ varQuanti2, data = df, main = "Scatter plot")

2.2.2 Matrice de scatter plots ~> pairs()

pairs(df_quanti)

2.2.3 Histogramme ~> hist()

hist(df$varQuanti, freq = TRUE ,
     main = "Histogramme d'une variable uniforme", 
     xlab = "Variable quantitative uniforme")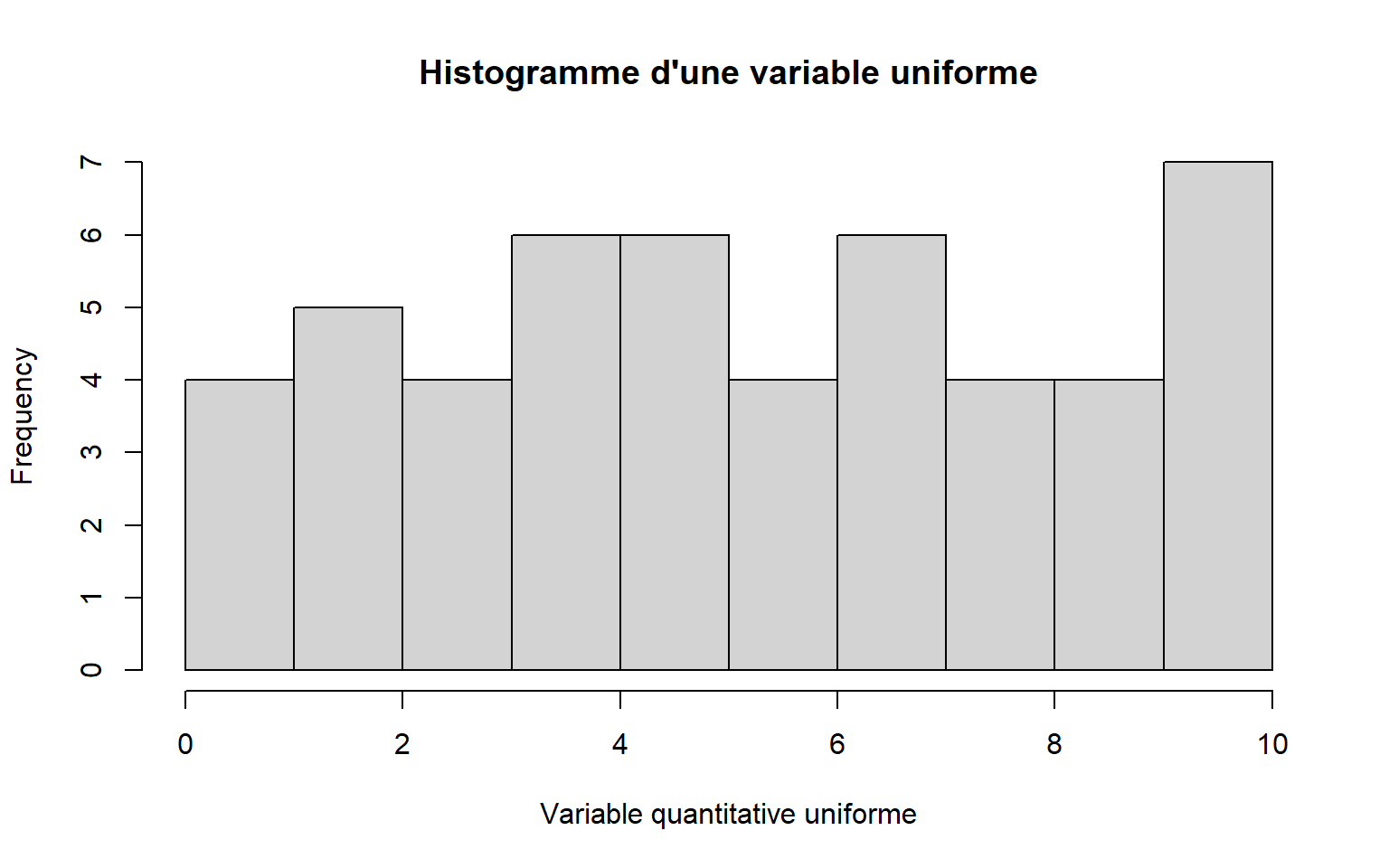

2.2.4 Bar plot ~> barplot()

# Une variable qualitative
barplot(table(df$varQuali2), main = "Bar plot d'une variable qualitative")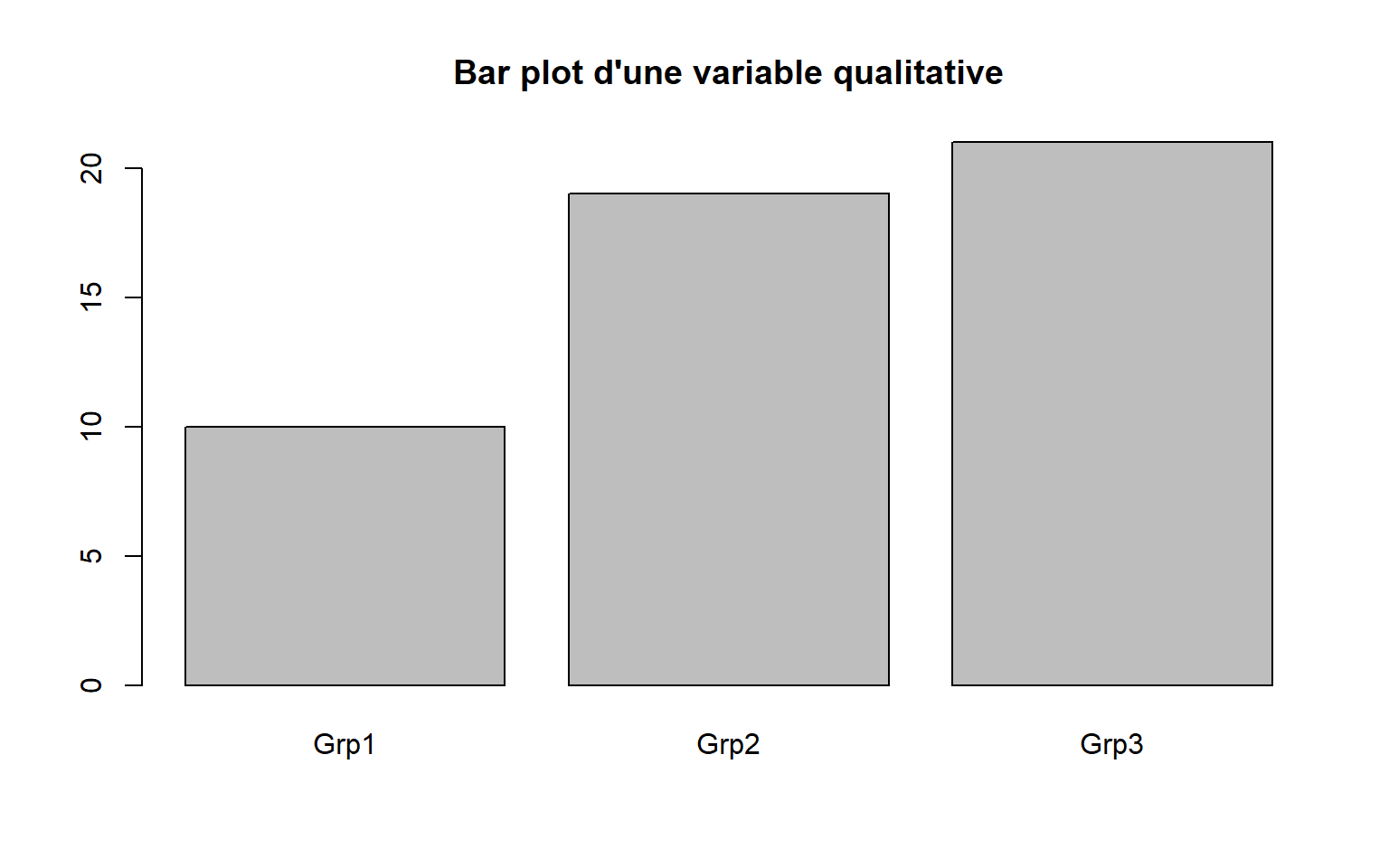

# 2 variables qualitatives
barplot(table(df$varQuali1,df$varQuali2), beside = TRUE, legend = levels(df$varQuali1), 
        main ="Barplot par modalités")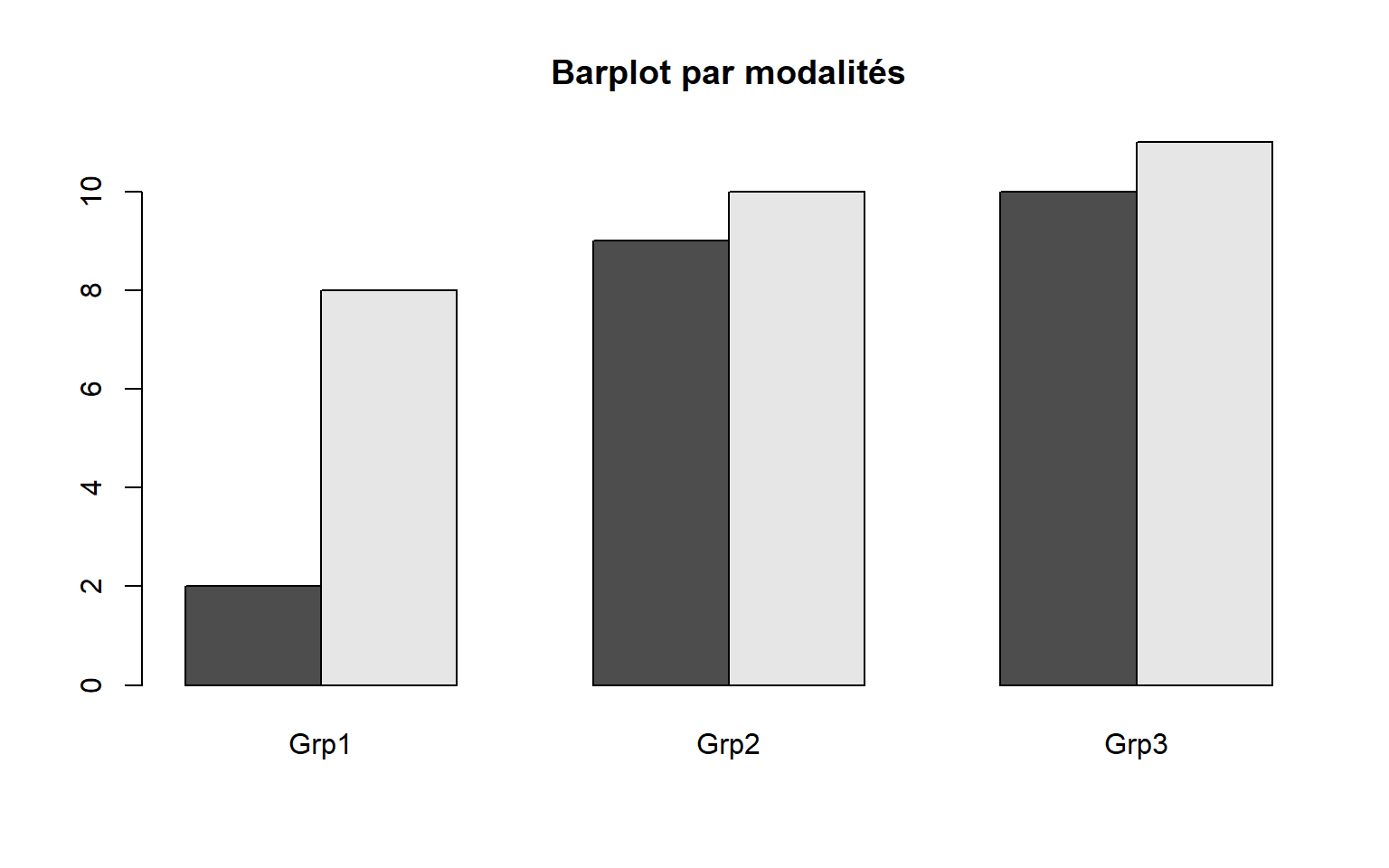

2.2.5 Box plot ~> boxplot()

# Simple
boxplot(df$varQuanti, main= "Boxplot d'une variable quantitative", ylab = "Var quanti")

# Par modalités
boxplot(varQuanti ~ varQuali, data = df,
        main = "Boxplot d'une variable quantitative par modalités",  ylab = "Var quanti")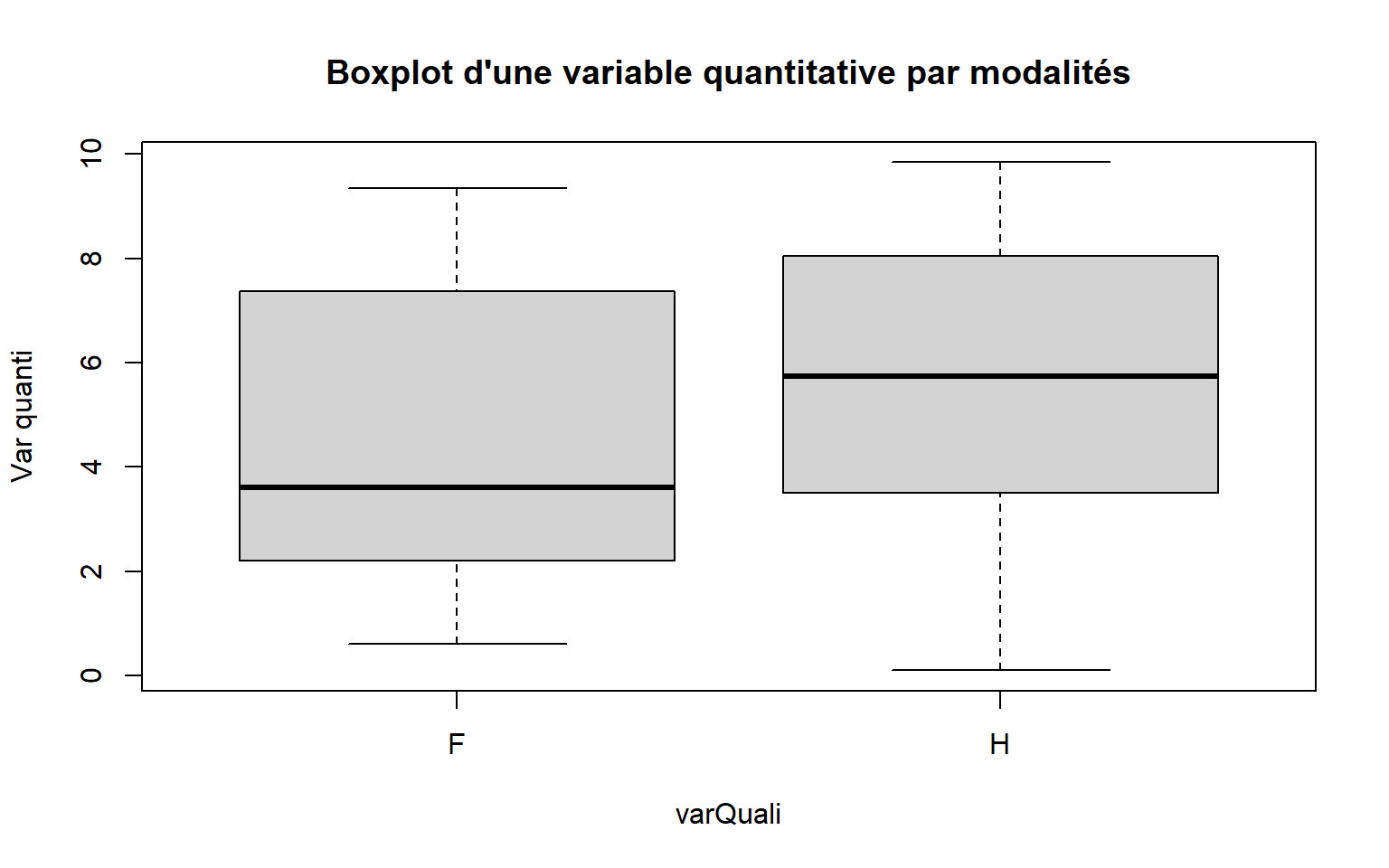

# Par modalités croisées
boxplot(varQuanti ~ varQuali1*varQuali2, data = df, 
        main = "Boxplot d'une variable quanti par modalités croisées",  ylab = "Var quanti")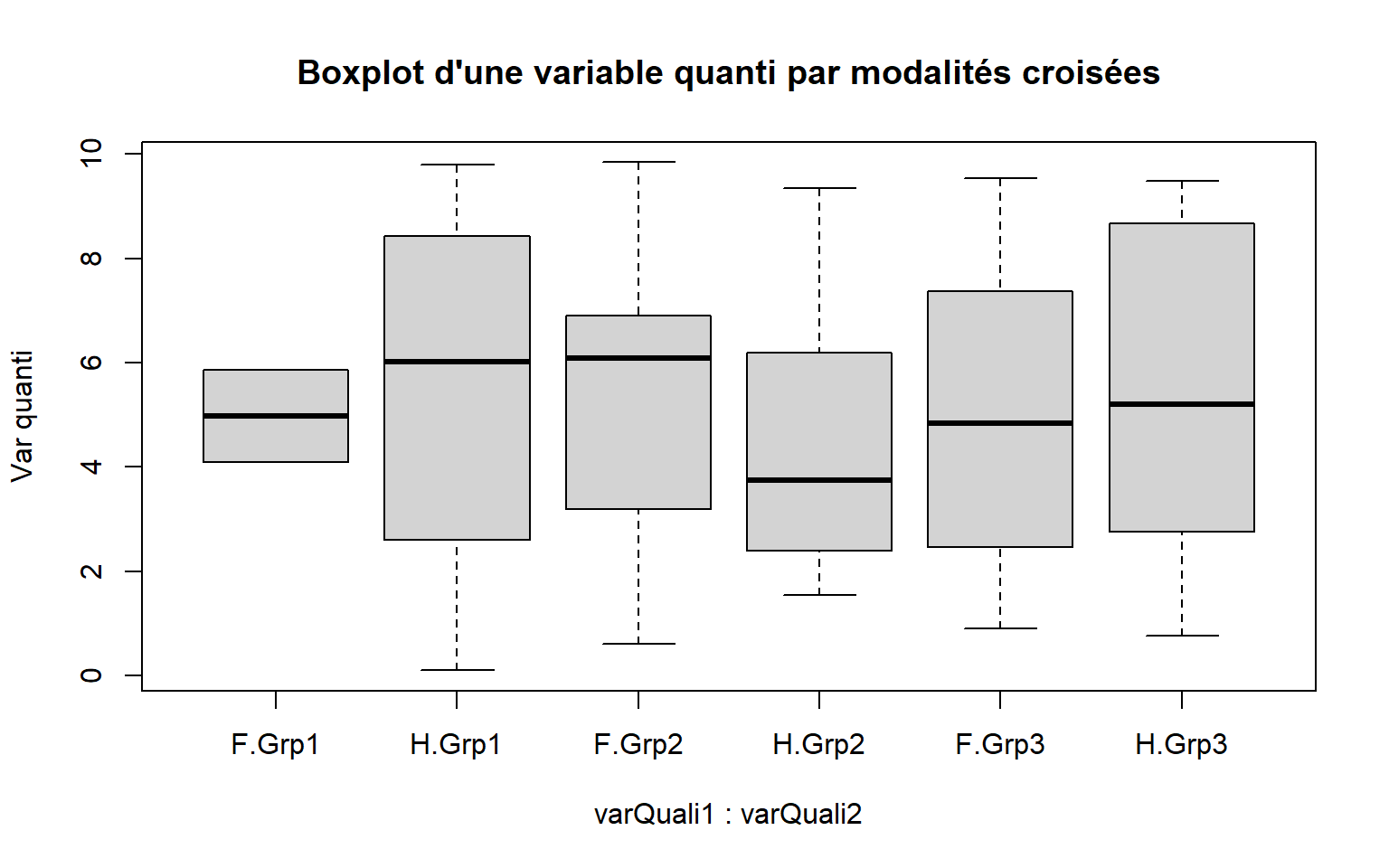

2.2.6 Mosaic plot ~> mosaicplot()

mosaicplot(varQuali1 ~ varQuali2, data = df, 
           main = "Mosaic plot de deux variables qualitatives")

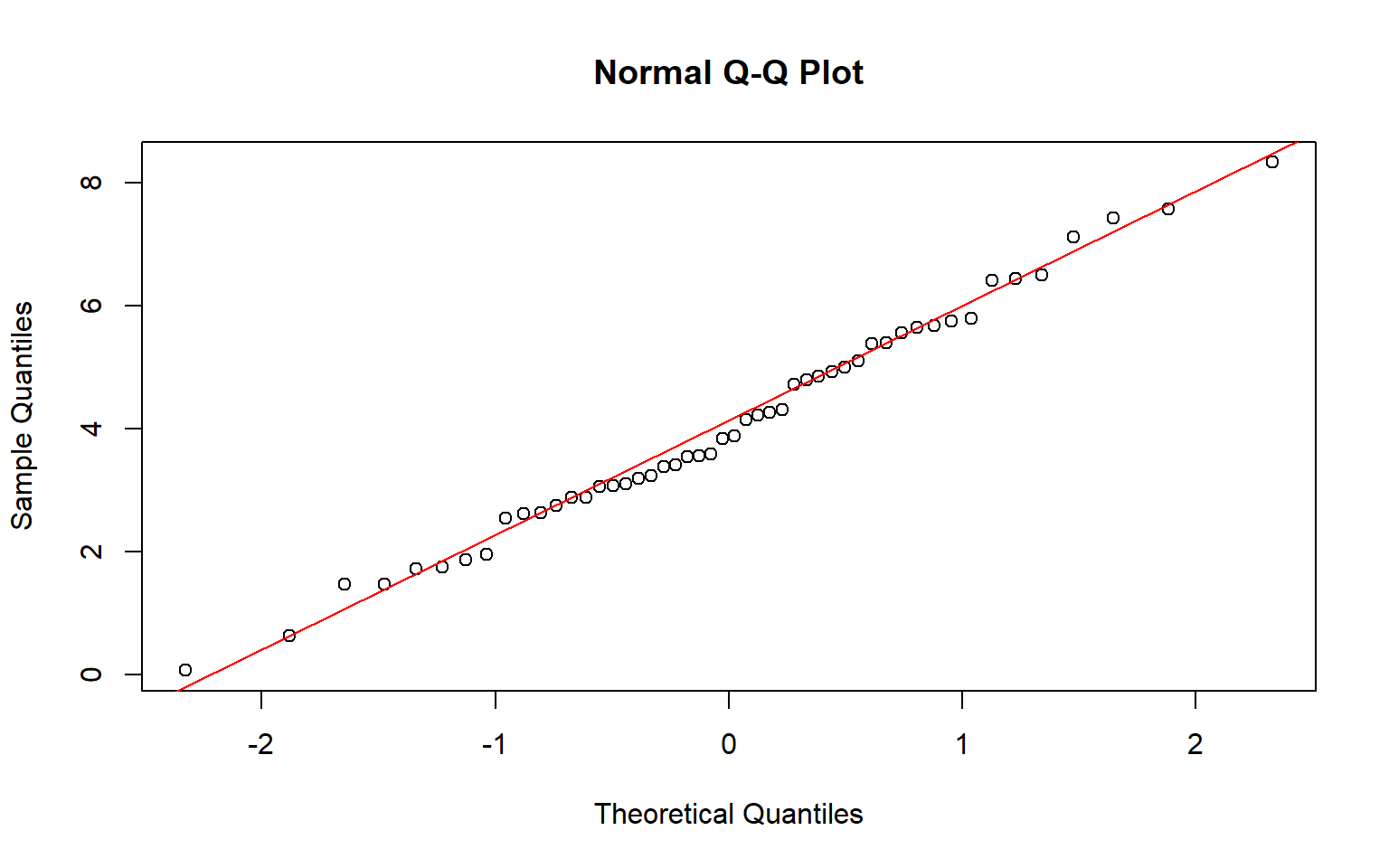
2.2.7 QQ-plot ~> qqnorm() + qqlines()

qqnorm(y = df$varQuanti1)
qqline(y = df$varQuanti1, col = "red")

2.2.8 Graphes des interactions ~> interaction.plot()

Ce graphe présente les moyennes d’une variable quantitative pour toutes les combinaisons des modalités de 2 variables qualitatives.

interaction.plot(x.factor = df$varQuali1, trace.factor = df$varQuali2, response = df$varQuanti)