7 Clustering
Objectif
~> Diviser un ensemble de données en différents groupes sans connaissance a priori sur les groupes (non supervisé). ~> Les observations d’un même groupe sont supposées partager des caractéristiques communes. La distance euclidienne est en général utilisée pour mesurer la proximité entre individus.
7.1 Fonctions utiles pour le clustering
Standardiser les données avant le clustering
Non prévu dans les options de kmeans
Clustering ascendant hiérarchique - CAH
# Clustering hiérarchique = CAH
resCAH <- factoextra::hcut(data, k = .., hc_method = ...,
hc_metric = "euclidean", stand = TRUE)Méthodes de calcul des distances entre groupes hc_method:
“single”, “complete”, “average”, “ward.D”, “ward.D2”.
Clustering kmeans
| Résultats CAH et fonctions liées | |
|---|---|
| Infos sur le clustering | Résultats : resCAH |
~> Nb de groupes proposé par hcut (si non fourni) |
resCAH$nbclust |
| ~> Taille des groupes | resCAH$size |
| ~> N° cluster pour chaque donnée | resCAH$cluster |
| Visualiser le clustering dans l’espace des CPs | factoextra::fviz_cluster(resCAH) |
| Dendrogramme | factoextra::fviz_dend(resCAH, rect = TRUE) |
| Résultats K-Means et fonctions liées | |
|---|---|
| Infos sur le clustering | Résultats:resKM |
| ~> Membres des clusters | Groupes resKM$cluster |
| ~> Centres des clusters | resKM$centers |
| ~> Somme totale des carrés | resKM$totss |
| ~> Sommes des carrés Within | resKM$withinss |
| ~> Total des sommes des carrés Within | resKM$tot.withinss |
| ~> Sommes des carrés Between | resKM$betweenss |
| Visualiser le clustering dans l’espace des CPs | factoextra::fviz_cluster(res, ..) |
7.2 Données du chapitre Clustering
Les données iris sont communément utilisées pour illustrer les bases des méthodes multivariées. Elle fournissent, pour 150 iris, 4 variables liées aux dimensions de la fleur : Sepal.Length, Sepal.Width, Petal.Length, Petal.Width. Ces iris sont de 3 espèces : setosa, versicolor, virginica.
# Jeu de données iris disponible directement dans R dont on sélectionne aléatoirement 45 données
data <- iris[sample(1:150,45),]
# Extraire la variable qualitative avec l'espèce
groupe <- as.factor(data$Species)
# Isoler les 4 variables quantitatives (sans la 5eme colonne de iris)
data <- data[,-5]
# Visualiser les données
plot(data, col = groupe , main="Scatter plots des variables prises 2 à 2", oma=c(3,3,3,12), pch=20)
par(xpd = TRUE)
legend("bottomright", title = "Species", legend = levels(groupe), col = c(1,2,3), cex = 0.8, pch = c(20,20,20))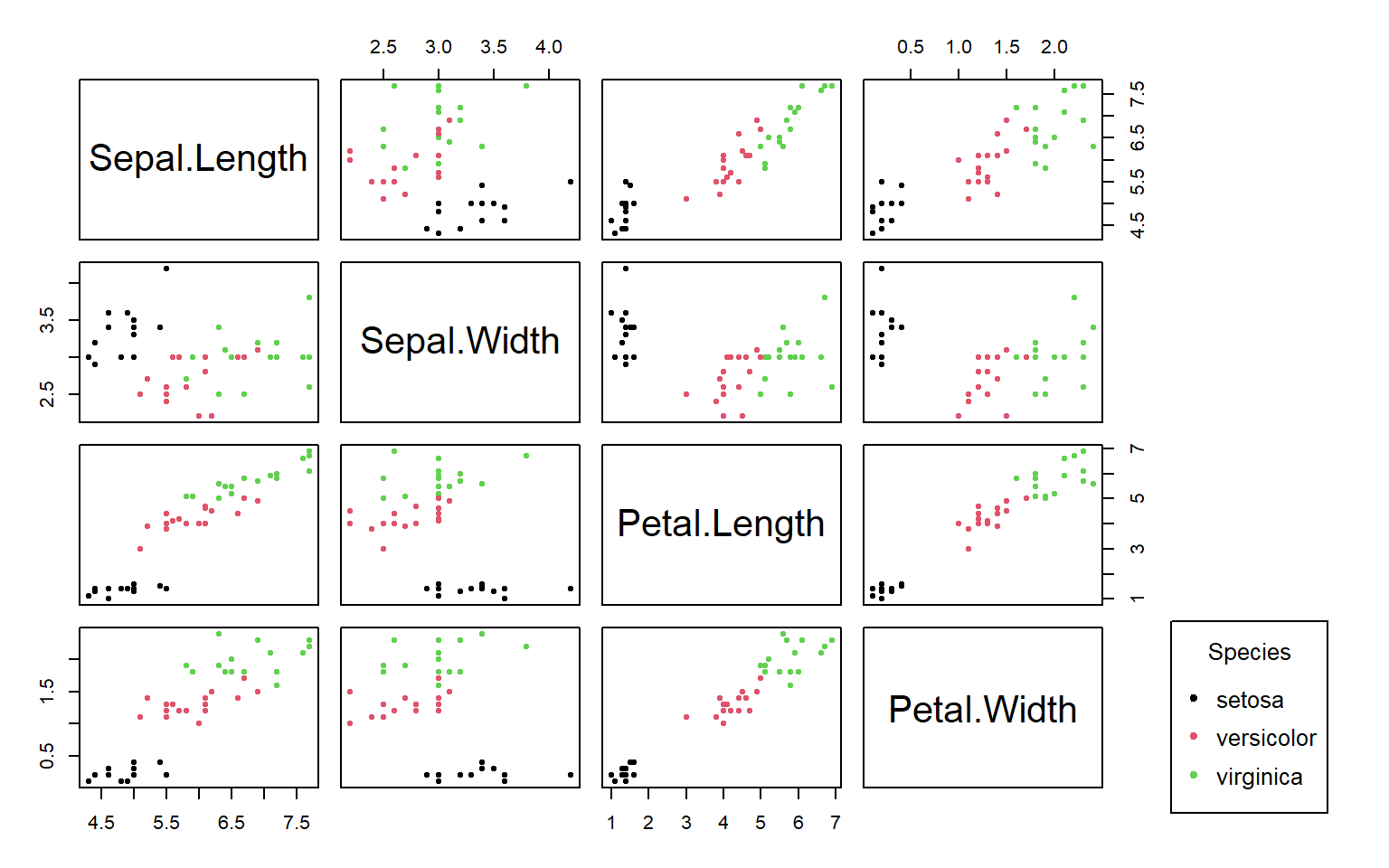
7.3 Application des fonctions hcut() et kmeans()
resCAH <- factoextra::hcut(data, hc_method = "average",
hc_metric = "euclidean", stand = TRUE)
resCAH
Call:
stats::hclust(d = x, method = hc_method)
Cluster method : average
Distance : euclidean
Number of objects: 45 K-means clustering with 3 clusters of sizes 18, 14, 13
Cluster means:
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 -0.0635247 -0.8123590 0.2248319 0.2000685
2 1.1384947 0.2507954 1.0080508 1.0116469
3 -1.1381139 0.8547174 -1.3968989 -1.3664838
Clustering vector:
14 50 118 43 150 148 90 91 143 92 137 99 72 26 7 78 81 147 103 117
3 3 2 3 1 2 1 1 1 1 2 1 1 3 3 2 1 1 2 2
76 32 106 109 136 9 41 74 23 27 60 53 126 119 121 96 38 89 34 93
1 3 2 1 2 3 3 1 3 3 1 2 2 2 2 1 3 1 3 1
69 138 130 63 13
1 2 2 1 3
Within cluster sum of squares by cluster:
[1] 15.29246 12.59662 10.97006
(between_SS / total_SS = 77.9 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" 7.4 Aide au choix du nombre de clusters
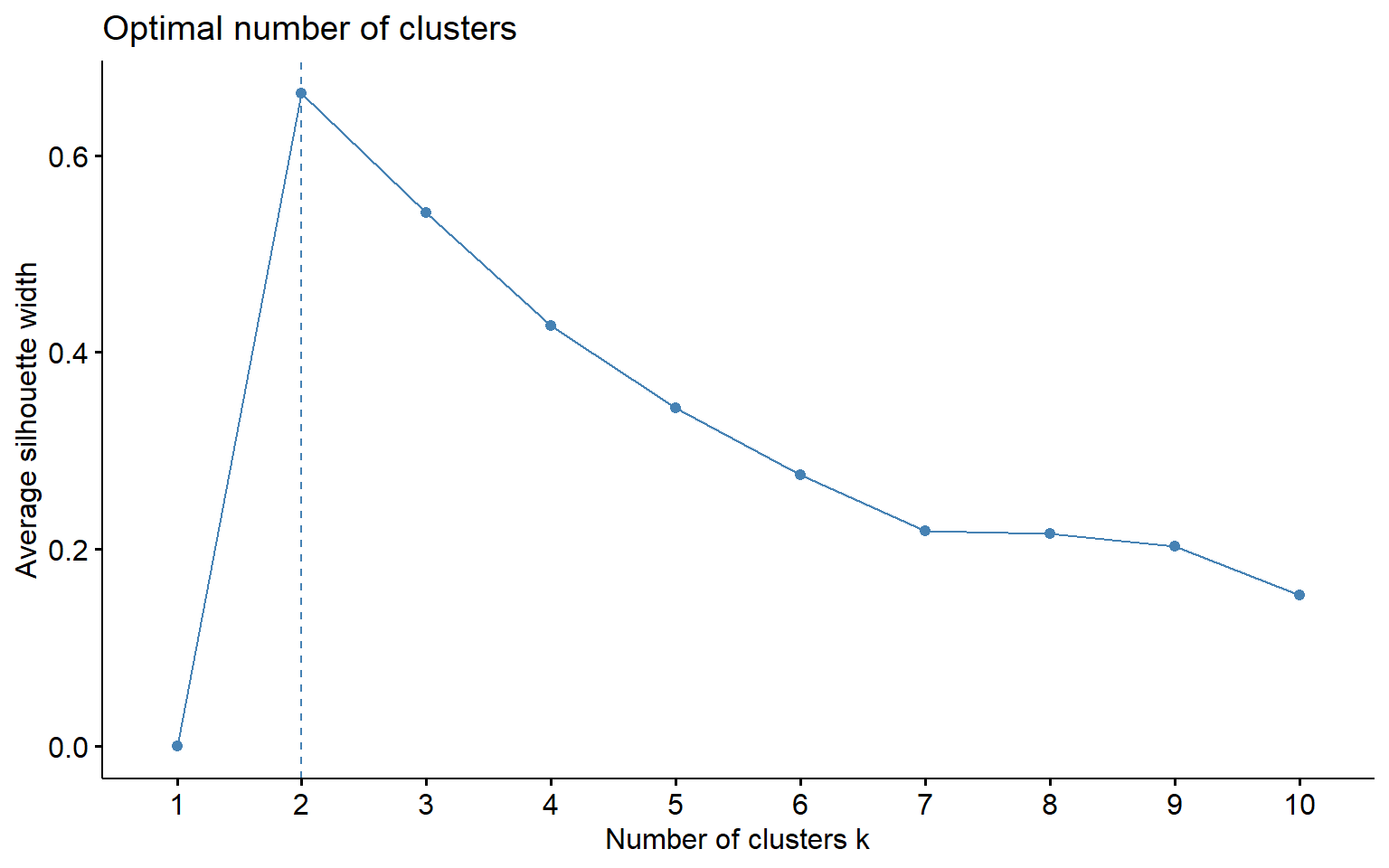
factoextra offre 3 méthodes (wss, silhouette et gap_stat) pour aider au choix du nombre idéal de clusters pour les données analysées. Le dendogramme peut aussi aider en CAH. La fonction Nbclust de la librairie Nbclust offre aussi une panoplie de critères supplémentaires pour répondre à la question.
7.6 Utiliser fviz_cluster()
Présente une projection des données des clusters dans l’espace des premières composantes principales.
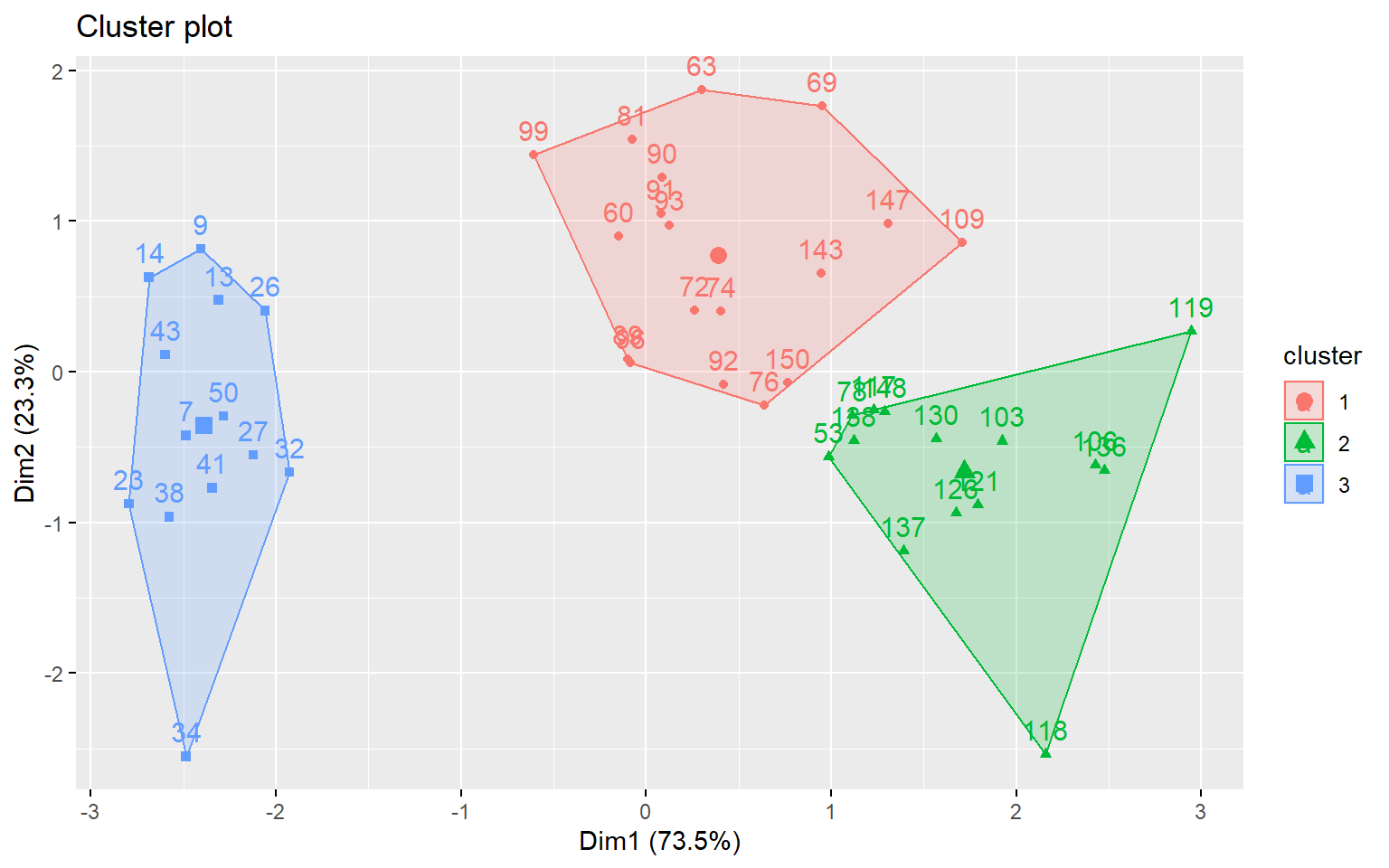
Avec CAH avec 2 clusters
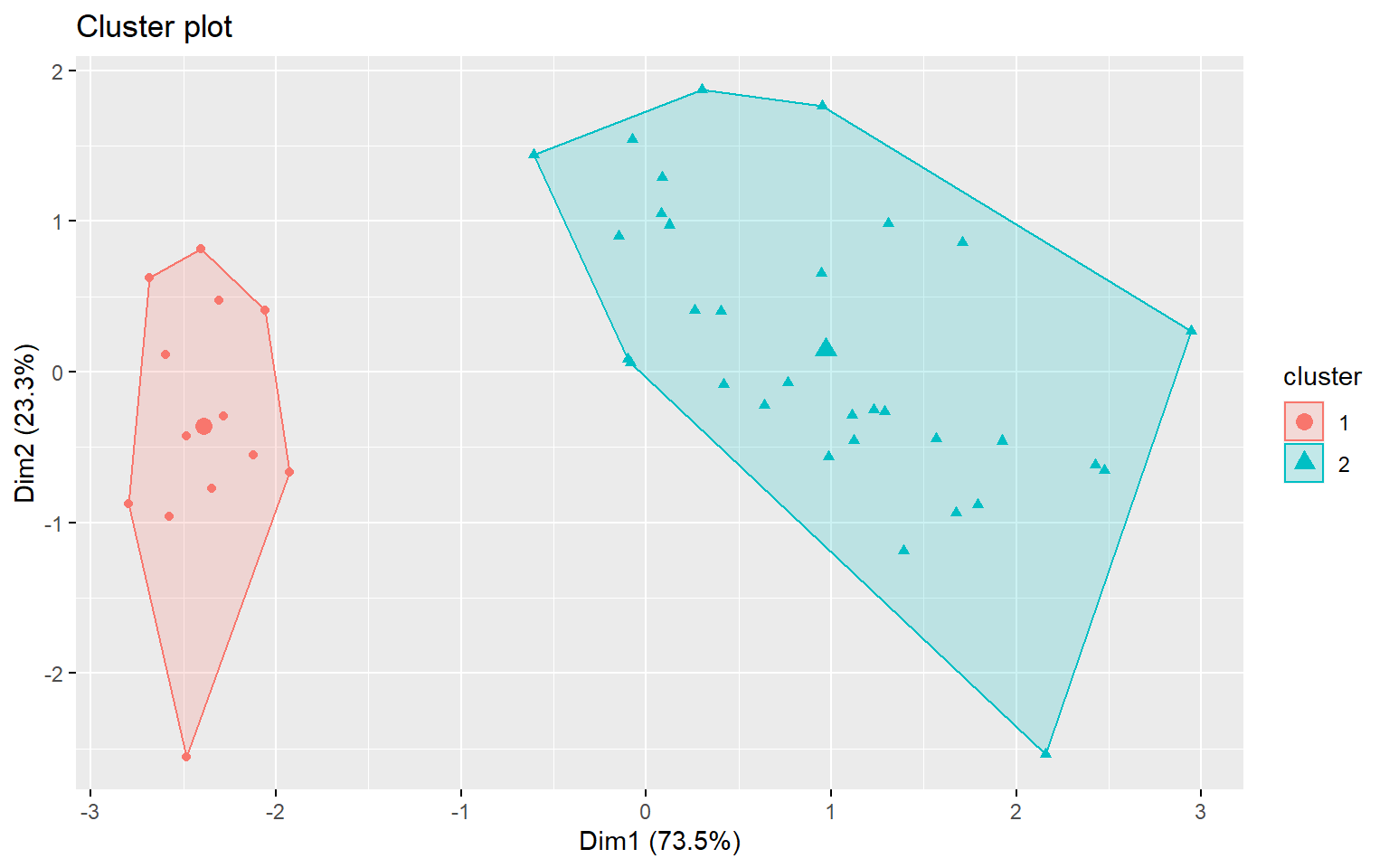
Avec kmeans avec 3 clusters (il faut fournir les données comme argument)