4 Modeles lineaires
Objectif
Expliquer une variable réponse quantitative de distribution normale comme une fonction linéaire de variables explicatives quantitatives et/ou qualitatives + de termes d’ordres plus élevés.
La fonction de modélisation principale utilisée ici est le fonction lm() complétée par une série de fonctions génériques applicables aux résultats de lm. Des fonctions émanant des librairies visreg et emmeans sont aussi proposées pour représenter les résultats des modèles et faire de l’inférence sur des combinaisons linéaires des paramètres.
4.1 Modélisation LM
La fonction lm permet par exemple d’estimer les modèles de base suivants qui font tous partie de la famille des modèles linéaires.
# Régression linéaire simple - X quantitative
mod <- lm( Y ~ X, data = ..)
# Régression linéaire multiple - X1,X2,X3 quantitatives
mod <- lm( Y ~ X1 + X2 + X3, data = ..)
# Régression quadratique - X quantitative
mod <- lm( Y ~ X + I(X^2), data = ..)
# ANOVA 1 - X qualitative
mod <- lm( Y ~ X, data = ..)
# ANOVA 2 croisée - X1,X2 qualitatives
mod <- lm( Y ~ X1 * X2, data = ..)
# Modèle d'analyse de covariance - X1 quantitative, X2 qualitative
mod <- lm( Y ~ X1 * X2, data = ..)Formules dans R
Le premier argument de la fonction lm() est un objet de type formule qui fournit à R la liste des effets à inclure dans le modèle linéaire.
Y ~ 1= modéliser Y en fonction de l’intercept uniquement.Y ~ X= modéliser Y en fonction de X avec intercept.Y ~ -1 + X= modéliser Y en fonction de X sans intercept.Y ~ X1 + X2= modéliser Y en fonction de X1 et X2 avec intercept.Y ~ X1 * X2= modéliser Y en fonction de X1, X2 et de l’interaction X1:X2 avec intercept (équivalent au modèleY ~ X1 + X2 + X1:X2) .Y ~ I(f(X))= modéliser Y en fonction de f(X), une fonction quelconque de X, avec intercept.
Tout cela peut bien entendu être mixé pour créer un modèle bien spécifique. Par exemple pour une régression quadratique sans intercept on utilisera Y ~ -1 + X + I(X^2).
Note La réponse Y peut également être transformée par exemple en logarithme. Il faut utiliser dans ce cas directement log(Y) dans la formule sans l’entourer par la fonction I().
4.2 Visualiser les données avant la modélisation LM
Voici un petit rappel du type de graphiques utiles pour représenter graphiquement des données avant modélisation.
Régression linéaire simple / quadratique ~> scatter plot Y ~ X.
Régression linéaire multiple ~> matrice de scatter plots Y ~ X1, Y ~ X2.
ANOVA 1 ~> boxplot Y ~ X.
ANOVA 2 ~> boxplot Y ~ X1*X2.
Modèle linéaire général ~> scatter plot Y ~ X1 par modalités de X2 où X2 est quantitative ou qualitative.
4.3 Fonctions utiles sur un objet de type mod <- lm(..)
Voici une liste non exhaustive de fonctions qui peuvent être appliquées à l’objet fourni par lm(..) pour obtenir des résultats dérivés du modèle estimé. L’utilisation de certaines de ces fonctions est illustrée ci-dessous.
| Résumé du modèle | summary(mod) |
| Mise à jour du modèle et Signification des coefficients liés |
drop1(mod, ..) + update(mod, ..) |
| Coefficients + Intervalles de Confiance |
coef(mod) + confint(mod) ou car::Confint(mod) |
| Résidus / Réponses prédites | residuals(mod)/fitted(mod) |
| Matrice de Variance-Covariance param. | vcov(mod) |
| Leverages | hatvalues(mod) |
| Matrice X de la régression | mod.matrix(mod) |
| Analyse de la variance (voir remarques plus bas) |
anova(mod) TYPE I car::Anova(mod, type = 2) TYPE II car::Anova(mod, type = 3) TYPE III |
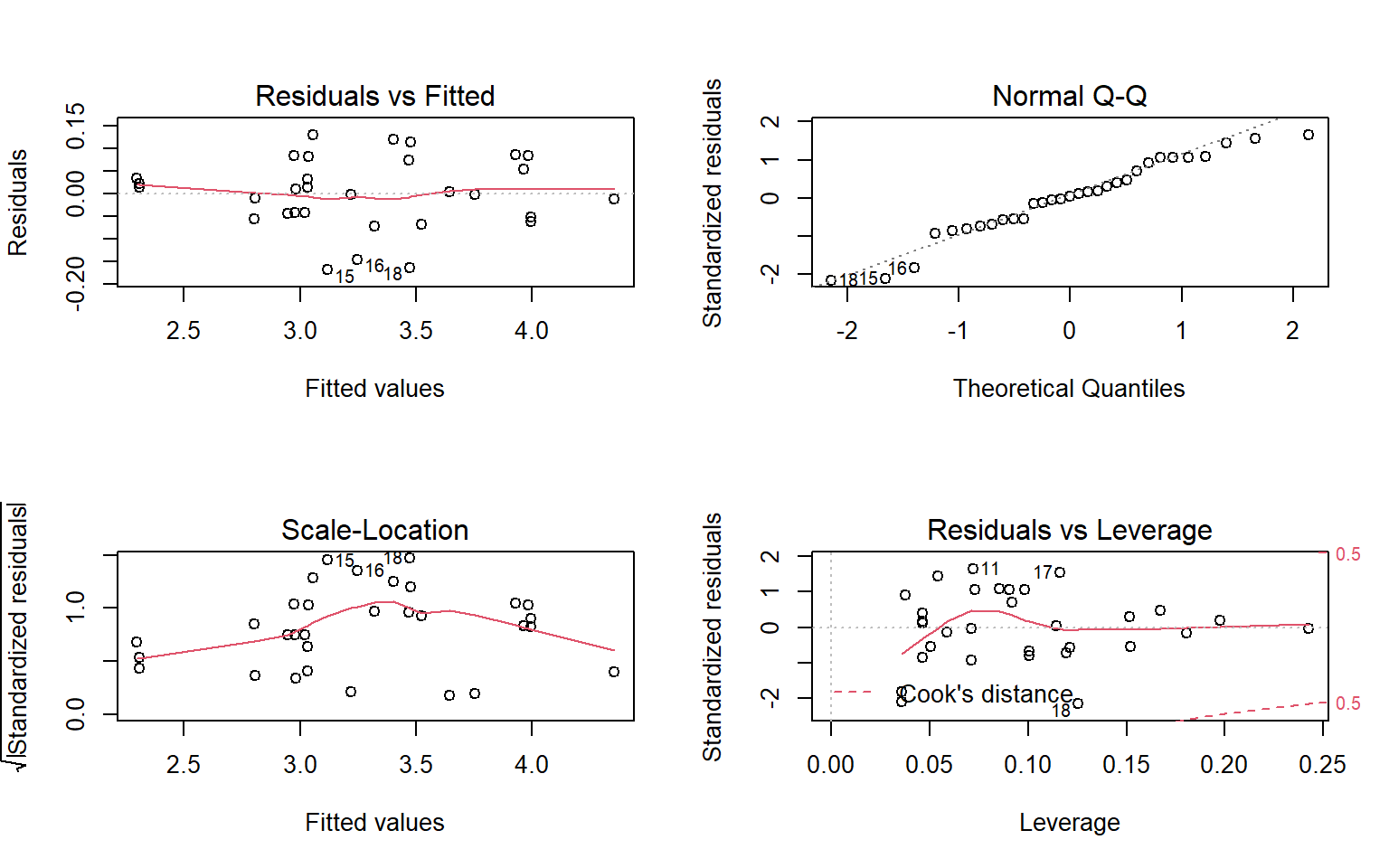
| Graphes des diagnostics | plot(mod) |
| Test d’homogénéité de la variance | car::leveneTest(mod) |
| Visualiser le modèle | visreg::visreg(mod, ..) abline(mod, ...) régression linéaire simple emmeans::emmip(mod, ..) modèle linéaire général |
| Prédictions | predict(mod, ..) |
| Graphe des moyennes | sjPlot::plot_model(mod, type = "eff) |
| Comparaisons de moyennes | emmeans::lsmeans(mod,..) |
| Contrasts linéaires | lsm <- emmeans::lsmeans(mod,..) + emmeans::contrast(lsm, ..) |
| Comparaisons des pentes | emmeans::emtrends(mod,..) |
4.4 Données du chapitre LM
calibration.xlsx |
Estimer une droite de calibration pour relier la surface en dessous du pic d’un chromatogramme en fonction de la concentration (1 variable quantitative) |
Volume_arbres.xlsx |
Modélisation du volume d’un tronc d’arbre en fonction de sa hauteur et de son diamètre (2 variables quantitatives) |
diet_pourR.xlsx |
Estimer un modèle d’ANOVA 1 pour expliquer la perte de poids d’une souris en fonction d’un régime alimentaire suivi (1 var. qualit. à 4 niv.) |
mais.xlsx |
Estimer un modèle d’ANOVA 2 pour expliquer le rendement d’une culture de maïs en fct du type d’engrais et de graine (2 var. qual. à 3 niv.) |
Digestion.xlsx |
Estimer un modèle linéaire général pour expliquer la digestion in-vitro d’un amidon en fonction de 3 variables : le type d’amidon (le standard) (var. qualit. à 3 niv.), le PH et la concentration en Enzyme (2 var. quant.) |
4.5 Utiliser summary() sur lm
Exemple pour les données Volume_arbres
# Modèle complet pour les données Volume_arbres
mod <- lm(lnVolume ~ lnDiam * lnHauteur, data = Volume_arbres)
summary(mod)
Call:
lm(formula = lnVolume ~ lnDiam * lnHauteur, data = Volume_arbres)
Residuals:
Min 1Q Median 3Q Max
-0.165941 -0.048613 0.006384 0.062204 0.132295
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.6869 7.6996 -0.479 0.636
lnDiam 0.7942 3.0910 0.257 0.799
lnHauteur 0.4377 1.7788 0.246 0.808
lnDiam:lnHauteur 0.2740 0.7124 0.385 0.704
Residual standard error: 0.08265 on 27 degrees of freedom
Multiple R-squared: 0.9778, Adjusted R-squared: 0.9753
F-statistic: 396.4 on 3 and 27 DF, p-value: < 2.2e-164.6 Utiliser drop1() / update() sur lm
On a le choix entre un test Chi_Carré, un test F ou une comparaison sur base du critère AIC.
Options pour le test F
La fonction drop1() va toujours commencer par tester les effets d’interaction avant le reste. Un effet principal n’est jamais retiré avant un effet d’ordre plus élevé qui lui est lié.
| Df | Sum of Sq | RSS | AIC | F value | Pr(>F) | |
|---|---|---|---|---|---|---|
| NA | NA | 0.1845 | -150.9 | NA | NA | |
| lnDiam:lnHauteur | 1 | 0.00101 | 0.1855 | -152.7 | 0.1479 | 0.7035 |
Mise à jour du modèle
Ici l’interaction n’est pas significative donc on décide de l’enlever de notre modèle.
Vérification
Call:
lm(formula = lnVolume ~ lnDiam + lnHauteur, data = Volume_arbres)
Residuals:
Min 1Q Median 3Q Max
-0.168561 -0.048488 0.002431 0.063637 0.129223
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.63162 0.79979 -8.292 5.06e-09 ***
lnDiam 1.98265 0.07501 26.432 < 2e-16 ***
lnHauteur 1.11712 0.20444 5.464 7.81e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.08139 on 28 degrees of freedom
Multiple R-squared: 0.9777, Adjusted R-squared: 0.9761
F-statistic: 613.2 on 2 and 28 DF, p-value: < 2.2e-16Maintenant tous les paramètres sont significatifs
4.7 Utiliser anova() / Anova() sur lm
4.7.1 Plan balancé
Rmq Par “balancé” on entend un nombre égal d’observations pour chaque niveau de nos facteurs
Utiliser le modèle classique pour calculer les sommes de carrés de TYPE I (via anova())
4.7.2 Plan non balancé
Ajuster un modèle différent avec le codage “contr.sum”
mod2 <- lm(Production ~ Graines + Engrais + Graines:Engrais,
contrasts = list(Graines=c("contr.sum"), Engrais =c("contr.sum")),
data = mais)Utiliser ce modèle pour calculer les sommes des carrés de TYPE III (via car::Anova())
Anova Table (Type III tests)
Response: Production
Sum Sq Df F value Pr(>F)
(Intercept) 172284 1 40274.299 < 2.2e-16 ***
Graines 432 2 50.532 1.278e-05 ***
Engrais 628 2 73.403 2.676e-06 ***
Graines:Engrais 244 4 14.240 0.0006255 ***
Residuals 39 9
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 14.9 Utiliser abline() sur lm
Pour ajouter une droite de régression sur un simple scatter-plot (ou graphe X-Y). Attention, ne fonctionne de cette façon que pour la régression linéaire simple
# Jeu de données calibration.xlsx
mod <- lm(SURFACE ~ ETHANOL, data = calibration)
plot(SURFACE ~ ETHANOL, data = calibration,
main = "Fonction abline() \n pour une régression linéaire simple")
abline(mod, col = "red")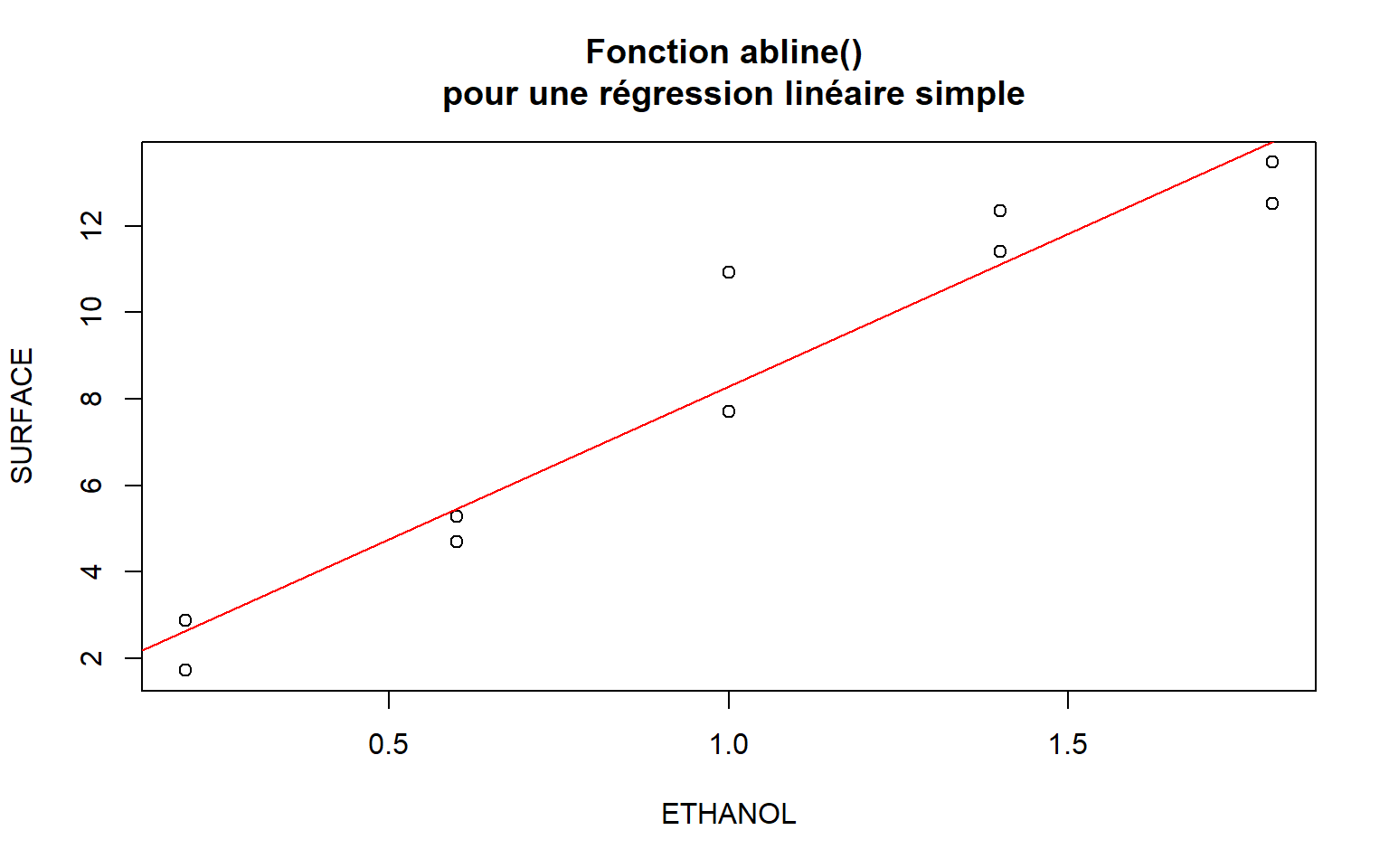
4.10 Utiliser visreg() sur lm
La fonction visreg est très utile pour représenter graphiquement les résultats d’une modélisation. Attention malgré tout : si le nombre de variables du modèle est plus élevé que le nombre de variables représentées, les points sur les graphiques ne sont pas les données de départ mais sont recalculées pour une valeur commune des variables qui ne sont pas sur le graphique (résidus partiels), il est donc conseillé de ne pas les dessiner. Les courbes/moyennes dessinées sont également dépendantes de ces valeurs.
4.10.1 Régression linéaire simple et IC sur la droite
# Jeu de données calibration1.xlsx disponible sur moodle
mod <- lm(SURFACE ~ ETHANOL, data = calibration)
visreg(mod, main = "Fonction visreg() \n pour une régression linéaire simple")
Rmq utilisation similaire pour une régression quadratique.
4.10.2 Régression linéaire multiple
Volume en fonction du Diamètre pour deux niveau de la Hauteur
visreg(mod, xvar = "lnDiam", by = "lnHauteur", breaks = c(4.1,4.5),
overlay = TRUE, band = TRUE, strip.names = c("ln(Hauteur) = 4", "ln(Hauteur) = 4.5"),partial=FALSE, rug=FALSE)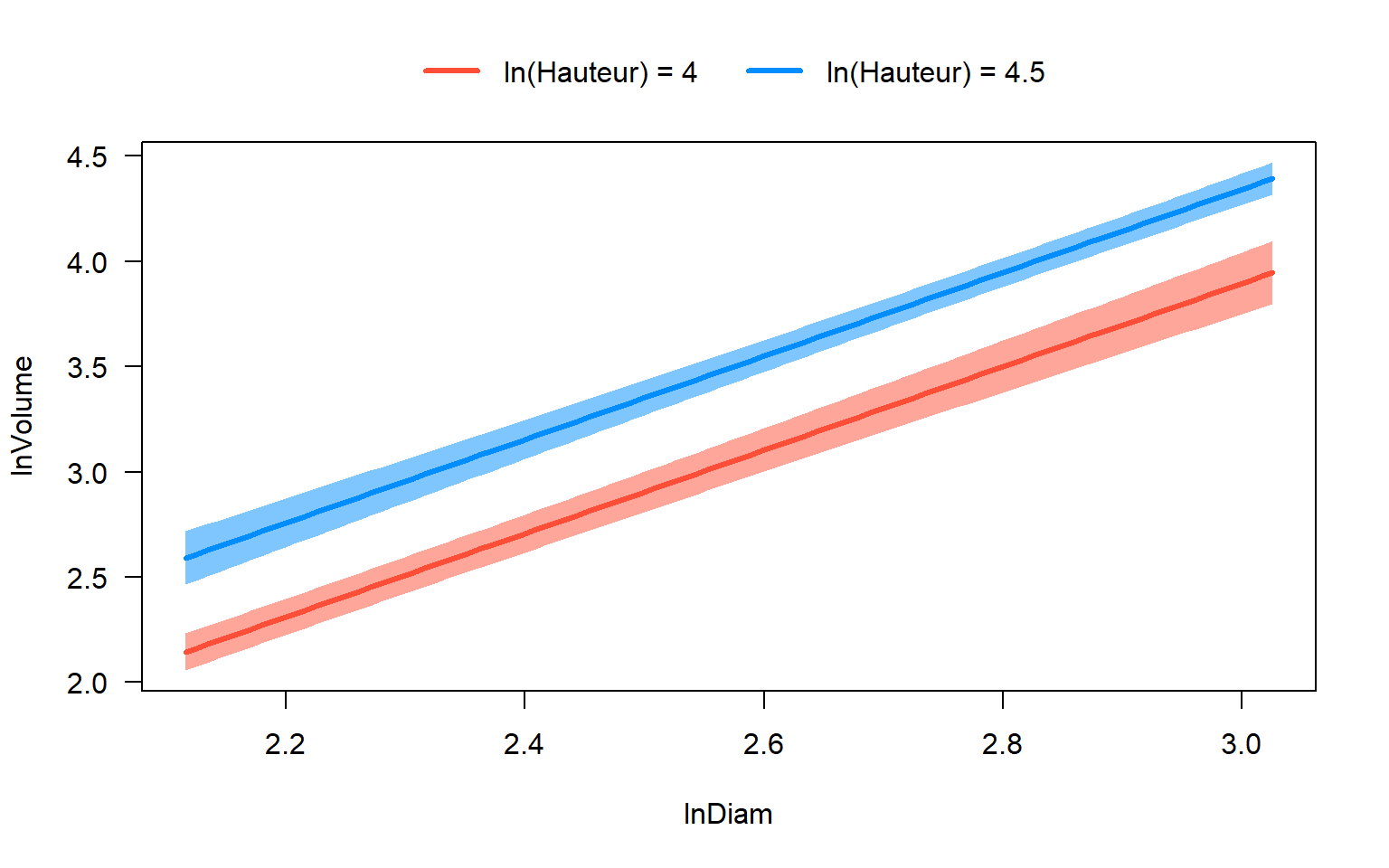
Régression linéaire multiple en 3 dimensions avec visreg2d
visreg2d(mod,"lnDiam", "lnHauteur", plot.type="persp",main="lnVolume en fonction de lnDiam et lnHauteur en 3D")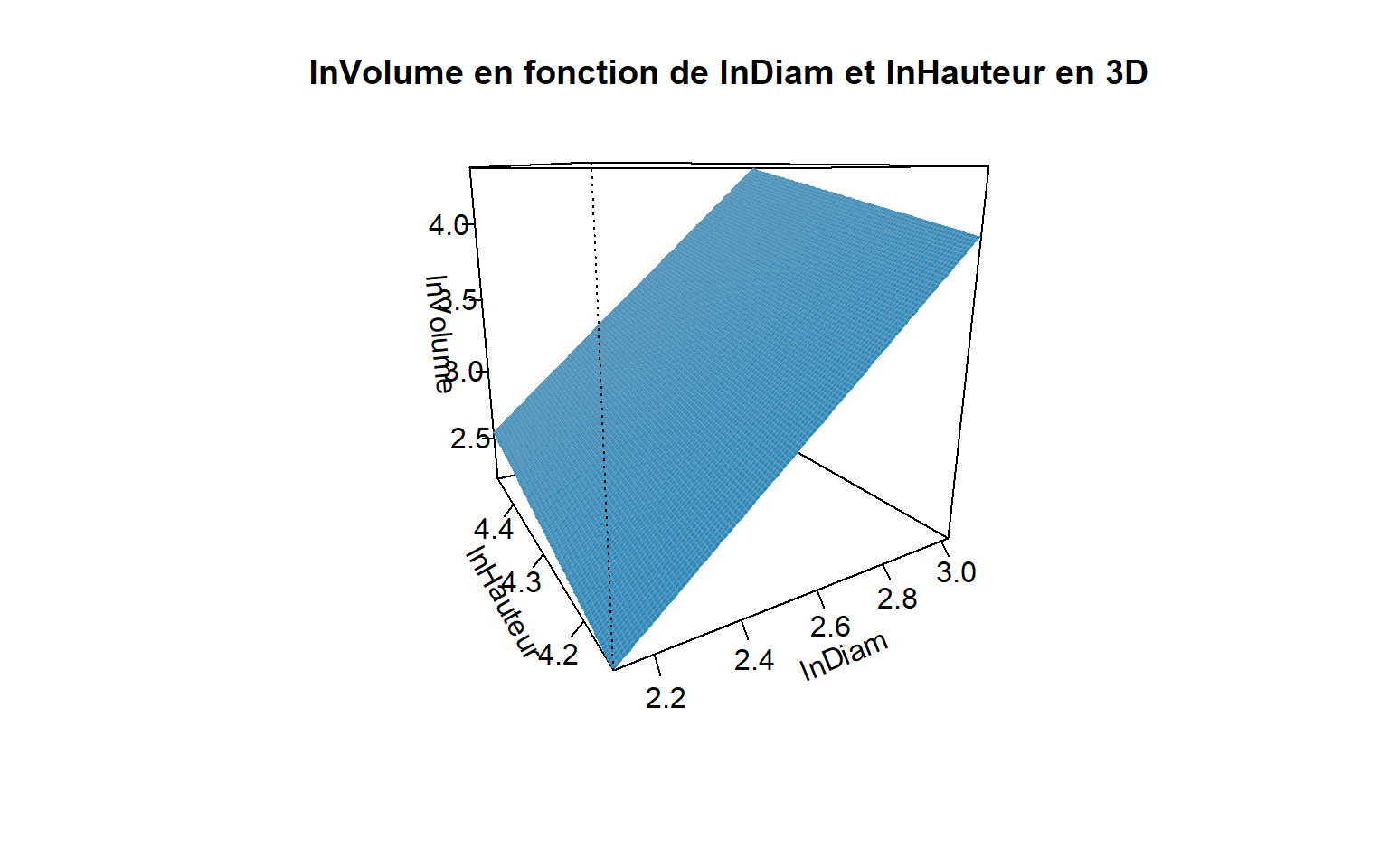
4.10.3 ANOVA 1
# Jeu de données diet_pourR.xlsx
mod <- lm(Dif_poids ~ Produit_T, data = diet_pourR)
visreg(mod, main = "Fonction visreg() \n pour une ANOVA à 1 facteur")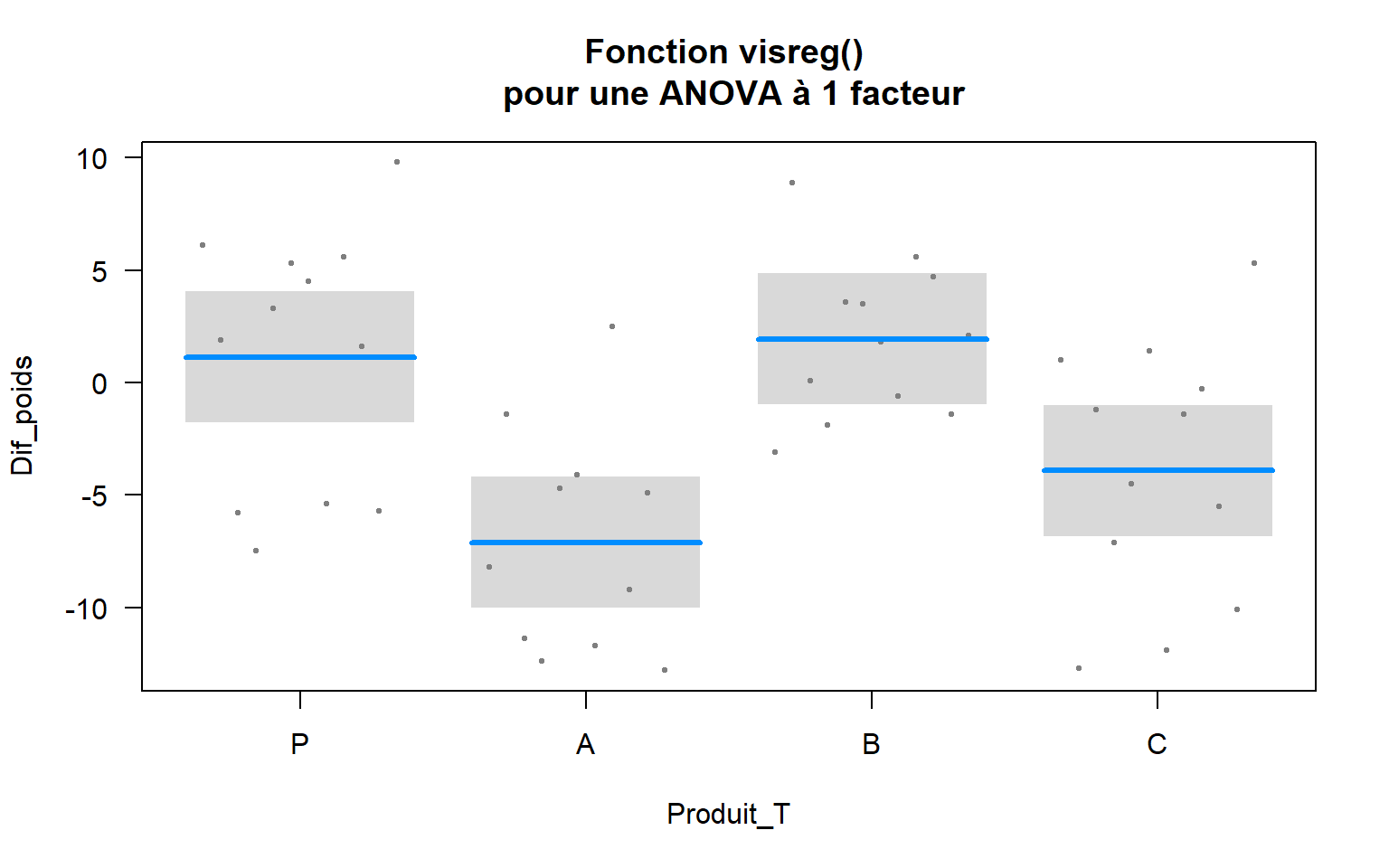
4.10.4 ANOVA 2
# Jeu de données mais.xlsx disponible sur moodle
mod <- lm(Production ~ Graines*Engrais, data = mais)
visreg(mod, "Graines", by = "Engrais",
main = "Fonction visreg() \n pour une ANOVA à 2 facteurs")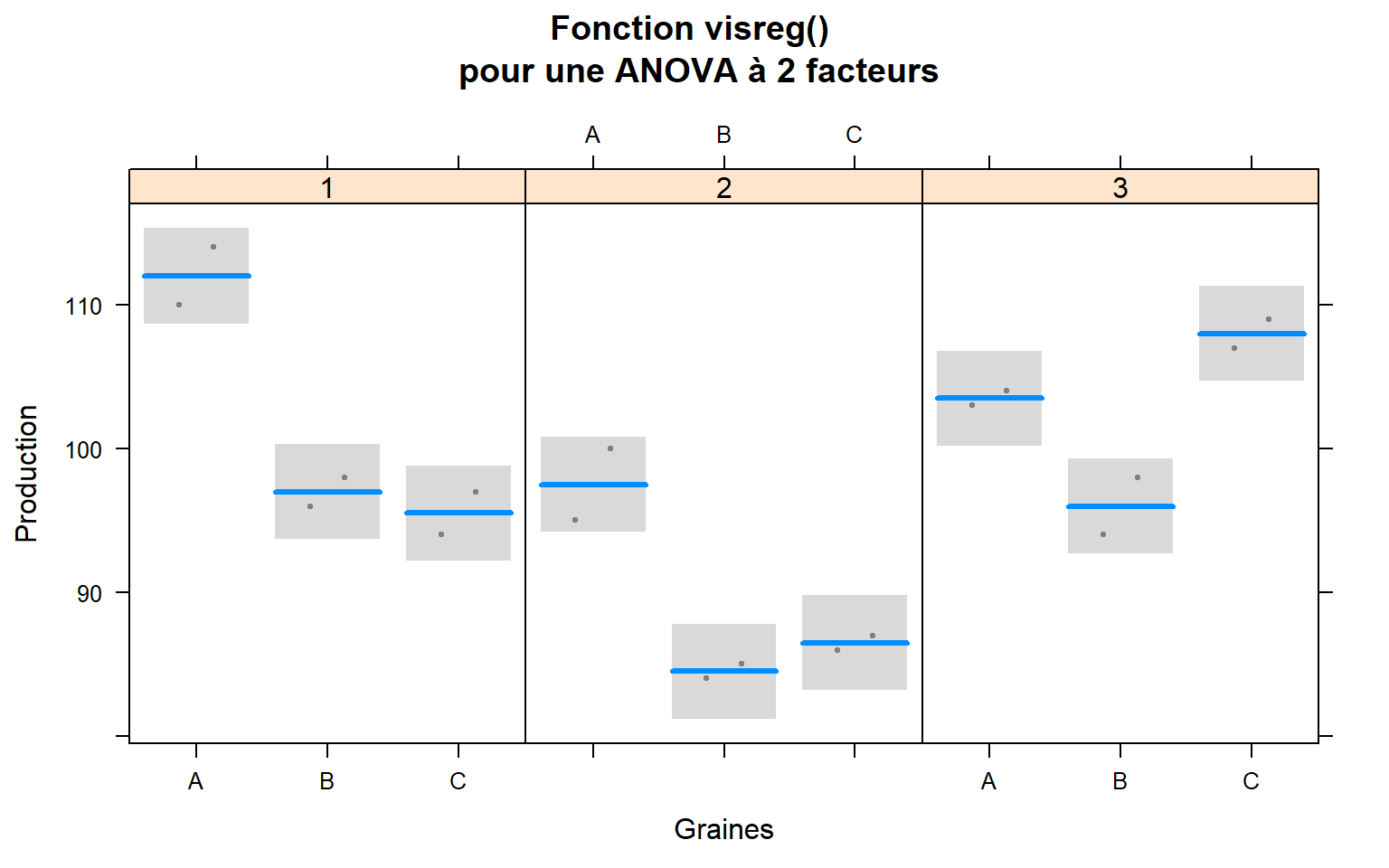
4.10.5 Modèle d’analyse de covariance
# Jeu de données Digestion.xlsx pour CCEnz=0.9 uniquement
digestion09=subset(digestion,subset=(CcEnz==0.9))
mod <- lm(Digestion ~ PH*Standard, data = digestion09)
visreg(mod, xvar = "PH", by = "Standard", overlay=TRUE, band = FALSE,
strip.names=c("Stand=1", "Stand=2", "Stand=3"))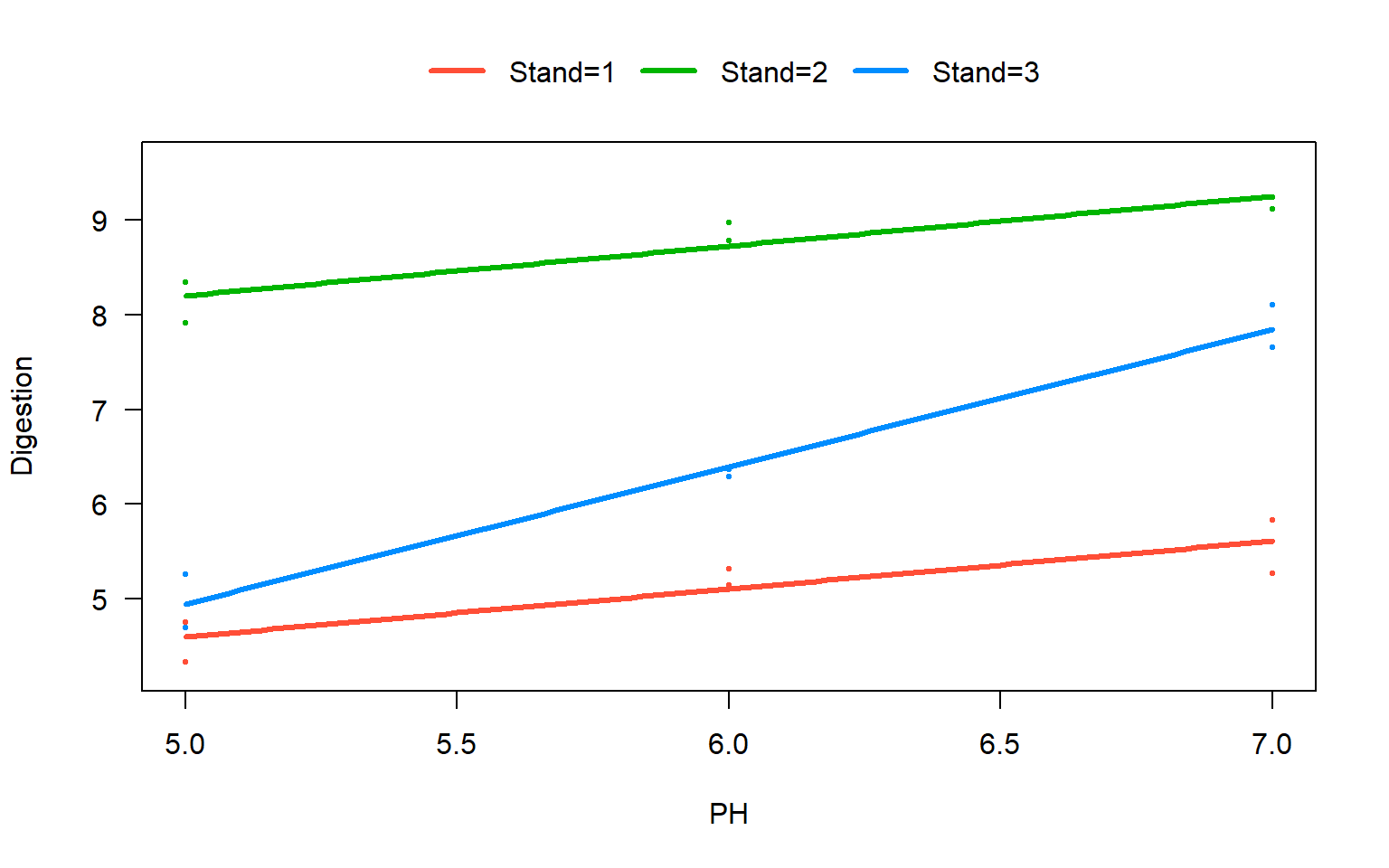
4.11 Utiliser emmip() sur lm
Le fonction emmip() du package emmeans permet de représenter des graphes d’interaction sur base d’un modèle ajusté.
Pratique pour un modèle linéaire général
# Jeu de données Digestion.xlsx disponible sur moodle
mod <- lm(Digestion ~ PH*Standard, data = digestion09)
emmip(mod, Standard ~ PH, cov.reduce = range)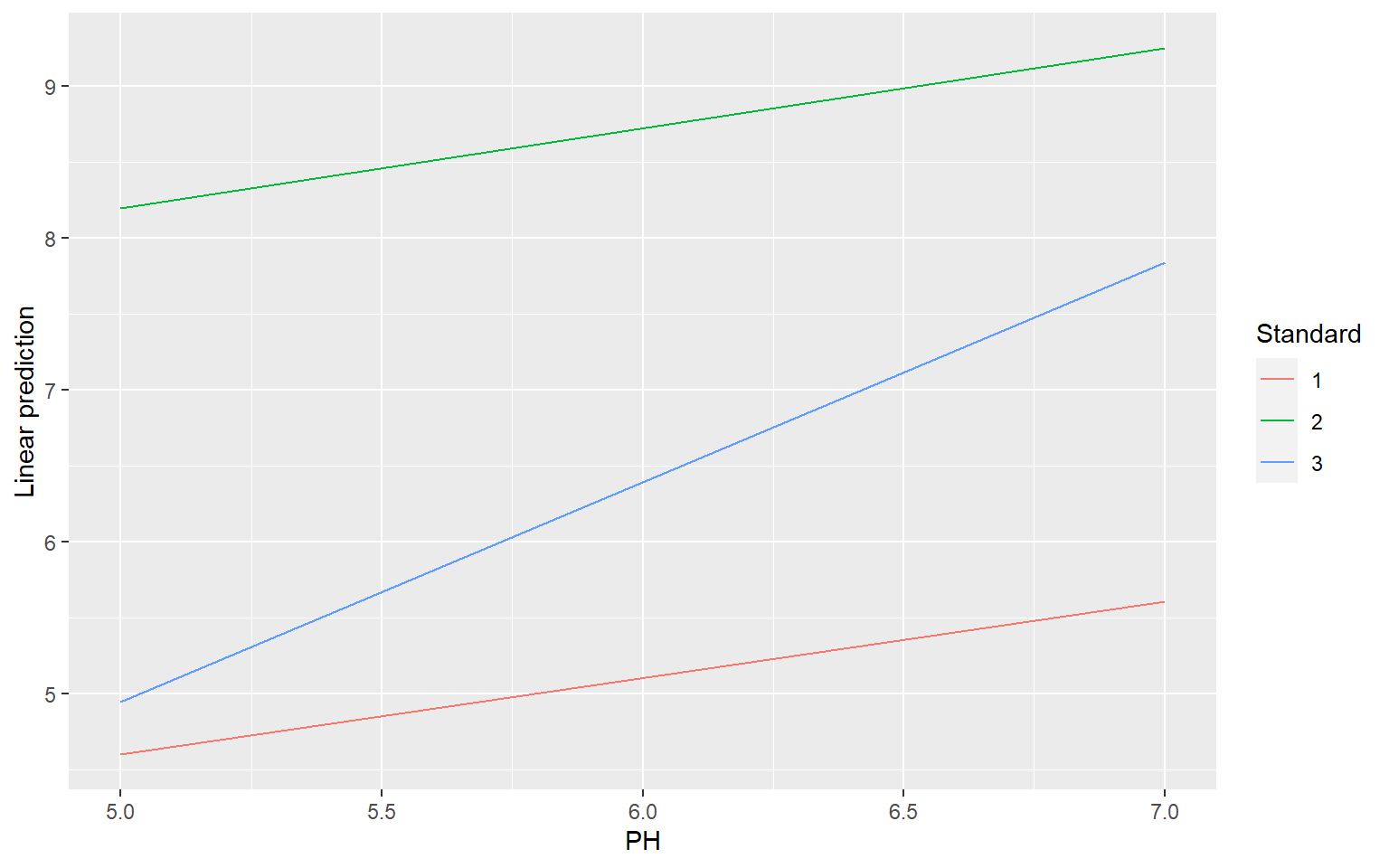
4.12 Utiliser predict() sur lm
Predict calcule la réponse prédite par la modèle pour de nouvelles valeurs des variables explicatives ainsi que des intervalles de confiance ou de prédiction liés.
# Jeu de données Digestion.xlsx disponible sur moodle
mod <- lm(Digestion ~ PH*Standard, data = digestion09)Obtenir les prédictions pour (PH, Standard) = (5,“2”) et (6,“3”)
xnew <- data.frame("PH" = c(5,6),
"Standard" = c("2", "3"))
pred <- predict(mod, newdata = xnew, interval = "prediction")
res <- data.frame(xnew, "Y_Fit" = pred[,1], "Lwr" = pred[,2], "Upr" = pred[,3])
pander(res)| PH | Standard | Y_Fit | Lwr | Upr |
|---|---|---|---|---|
| 5 | 2 | 8.2 | 7.544 | 8.856 |
| 6 | 3 | 6.395 | 5.8 | 6.99 |
4.13 Utiliser lsmeans() et le package emmeans sur lm
lsmeans du package emmeans est utile pour calculer des combinaisons linéaires de paramètres de modèles linéaires et les résultats d’inférence liés (tests et IC). Cette fonction est spécialement utile pour les modèles contenant des variables qualitatives/catégorielles : estimation de moyennes marginales, comparaisons 2 à 2, constrates etc…
4.13.1 Table des moyennes
Pour les modalités de Graines
NOTE: Results may be misleading due to involvement in interactions| Graines | lsmean | SE | df | lower.CL | upper.CL |
|---|---|---|---|---|---|
| A | 104.3 | 0.8444 | 9 | 102.4 | 106.2 |
| B | 92.5 | 0.8444 | 9 | 90.59 | 94.41 |
| C | 96.67 | 0.8444 | 9 | 94.76 | 98.58 |
Pour modalités croisées (interaction)
| Graines | Engrais | lsmean | SE | df | lower.CL | upper.CL |
|---|---|---|---|---|---|---|
| A | 1 | 112 | 1.462 | 9 | 108.7 | 115.3 |
| B | 1 | 97 | 1.462 | 9 | 93.69 | 100.3 |
| C | 1 | 95.5 | 1.462 | 9 | 92.19 | 98.81 |
| A | 2 | 97.5 | 1.462 | 9 | 94.19 | 100.8 |
| B | 2 | 84.5 | 1.462 | 9 | 81.19 | 87.81 |
| C | 2 | 86.5 | 1.462 | 9 | 83.19 | 89.81 |
| A | 3 | 103.5 | 1.462 | 9 | 100.2 | 106.8 |
| B | 3 | 96 | 1.462 | 9 | 92.69 | 99.31 |
| C | 3 | 108 | 1.462 | 9 | 104.7 | 111.3 |
4.13.3 Visualisation des moyennes + IC dans un plot
4.13.4 Utiliser contrast() sur lm
# Jeu de données mais.xlsx disponible sur moodle
lsm <- lsmeans(mod, pairwise ~ Graines*Engrais)
hyp <- list("C1 = A2" = c(0,0,1,-1,0,0,0,0,0),
"A = C" = c(1/3,0,-1/3,1/3,0,-1/3,1/3,0,-1/3))
contrast(lsm$lsmeans, hyp) contrast estimate SE df t.ratio p.value
C1 = A2 -2.00 2.07 9 -0.967 0.3588
A = C 7.67 1.19 9 6.420 0.0001 Rmq pour connaitre l’ordre des coefficients il suffit de faire plot(lsm) et lire de bas en haut les modalités listées sur l’axe y.
4.13.5 Utiliser emtrends() sur lm
Pour faire de l’inférence sur des pentes en analyse de convariance.
mod <- lm(Digestion ~ PH*Standard, data = digestion09)
visreg(mod, xvar = "PH", by = "Standard", overlay=TRUE, band = FALSE,
strip.names=c("Stand=1", "Stand=2", "Stand=3"))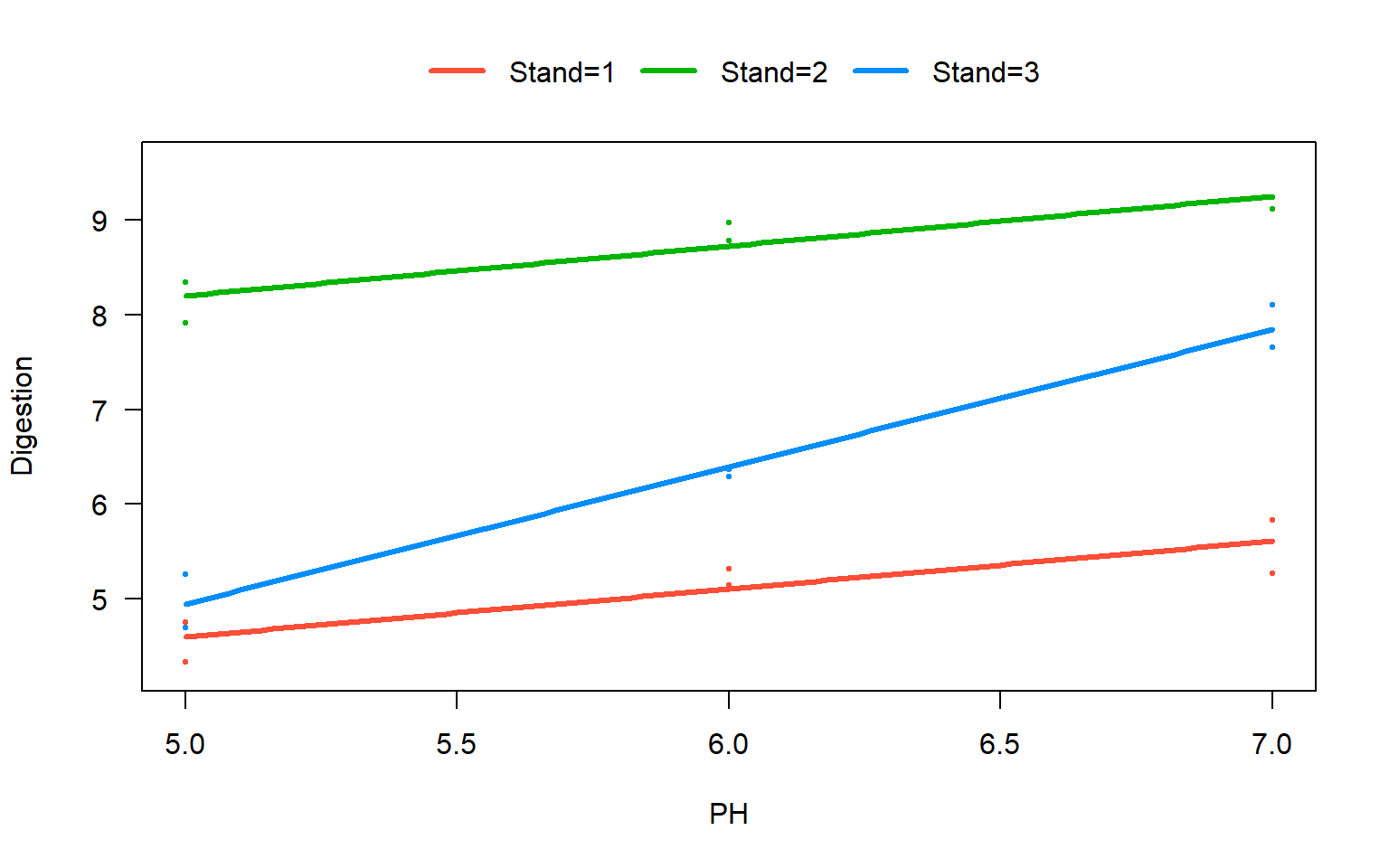
Table des pentes
Standard PH.trend SE df lower.CL upper.CL
1 0.505 0.126 12 0.23 0.78
2 0.525 0.126 12 0.25 0.80
3 1.448 0.126 12 1.17 1.72
Confidence level used: 0.95 Comparaison des pentes 2 à 2
contrast estimate SE df t.ratio p.value
1 - 2 -0.020 0.179 12 -0.112 0.9931
1 - 3 -0.942 0.179 12 -5.271 0.0005
2 - 3 -0.922 0.179 12 -5.160 0.0006
P value adjustment: tukey method for comparing a family of 3 estimates