5 Regression logistique

Objectif

Expliquer une variable réponse binaire en fonction de variables explicatives quantitatives et / ou qualitatives + effets d’ordres plus élevés (interactions…).

La fonction de modélisation principale utilisée ici est la fonction glm() qui permet d’estimer des modèles linéaires généralisés très généraux. Elle s’utilise de façon très semblable à la fonction lm() et , comme pour lm(), de multiples fonctions générique s’appliquent aux résulats de glm().

5.1 Modélisation GLM

Régression logistique simple
X variable explicative qualitative ou quantitative

# si les réponses sous la forme d'un tableau nombre succès / échec / total
mod <- glm( cbind(succes,echec) ~ X, data = .., family = binomial)

# si les réponses sont sous la forme d'un vecteur de 1 et 0 : 1 ligne = 1 individu
mod <- glm( Y ~ X, data = .., family = binomial)

Régression logistique multiple

Quand il y a plusieurs variables explicatives avec ou sans effets d’ordres plus élevés (interactions…), l’équation du modèle s’écrit comme dans le cas des modèles linéaires lm().

5.2 Visualiser les données avant modélisation GLM

Si X quantitative

  • Plot p ~ X où p est la proportion de Y = 1 (=succès).
  • Table de fréquence.

Si X qualitative

  • Barplot Y ~ X
  • Table de fréquence.0

5.3 Fonctions utiles sur un objet de type mod <- glm()

La plupart des fonction disponible sur les modèles de type lm() s’appliquent aussi aux modèles glm().
Pour rappel :

Résumé du modèle summary(mod)
Mise à jour du modèle drop1(mod, ..)
+ update(mod, ..)
Coefficients
+ IC		 coef(mod)
+ confint(mod) ou car::Confint(mod)
Résidus / Valeurs ajustées residuals(mod, ..) / fitted(mod)
Matrice Var-Cov des paramètres vcov(mod)
Matrice X du modèle mod.matrix(mod)
Visualiser la modélisation visreg::visreg(mod, ..)
Prédictions predict(mod, ..)

5.4 Données du chapitre GLM

omega3Cadmium.txt Etude de l’interaction entre nutriments bénéfiques pour la santé Omega3 (1 var. quali. à 2 niv.) et contaminants a priori nocifs Cadmium (1 var. quanti.) sur la survie de cellules.

Ces données ne sont pas des données individuelles mais sont agrégées par groupe.

# Représentation graphique des données
PS=100*data[,"Survie_Oui"]/(data[,"Survie_Oui"]+data[,"Survie_Non"])
OM=as.numeric(data[,"Omega3"])

plot(data[,"Cadmium"],PS,col=OM,pch=OM,xlab="X = Cadmium",ylab="% succès",main="Données pour régression logistique")
legend(1,40,legend=levels(data[,"Omega3"]),col=1:2,pch=1:2)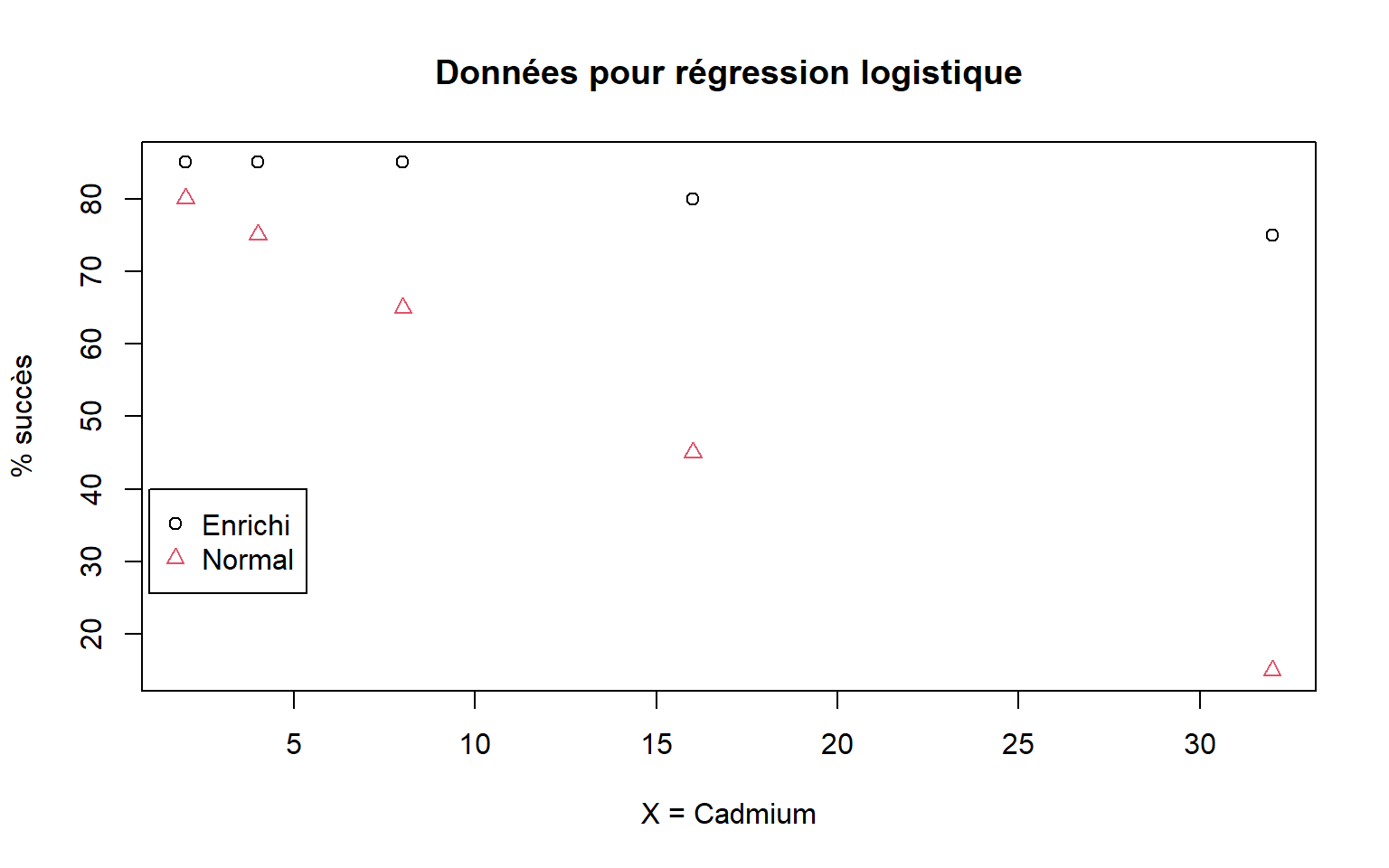

# Régression logistique multiple avec interaction
mod <- glm(cbind(Survie_Oui, Survie_Non) ~ Cadmium*Omega3, data,  family = binomial)

5.5 Utiliser summary() sur glm

summary(mod)

Call:
glm(formula = cbind(Survie_Oui, Survie_Non) ~ Cadmium * Omega3, 
    family = binomial, data = data)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-0.12008  -0.10088   0.01398   0.08504   0.16546  

Coefficients:
                     Estimate Std. Error z value Pr(>|z|)    
(Intercept)           1.82160    0.41425   4.397  1.1e-05 ***
Cadmium              -0.02298    0.02267  -1.014   0.3107    
Omega3Normal         -0.32059    0.54736  -0.586   0.5581    
Cadmium:Omega3Normal -0.08021    0.03323  -2.413   0.0158 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 41.56439  on 9  degrees of freedom
Residual deviance:  0.10979  on 6  degrees of freedom
AIC: 38.758

Number of Fisher Scoring iterations: 4

5.6 Utiliser drop1()/update() sur glm

Utilisation similaire aux modèles linéaires lm(). La seule différence est dans les tests disponibles:

drop1(mod, test = "Chisq")  # Chi_Carré
drop1(mod, test = "Rao")    # Rao
drop1(mod, test = "LRT")    # LRT
drop1(mod, test = "F")      # F
drop1(mod)                  # AIC

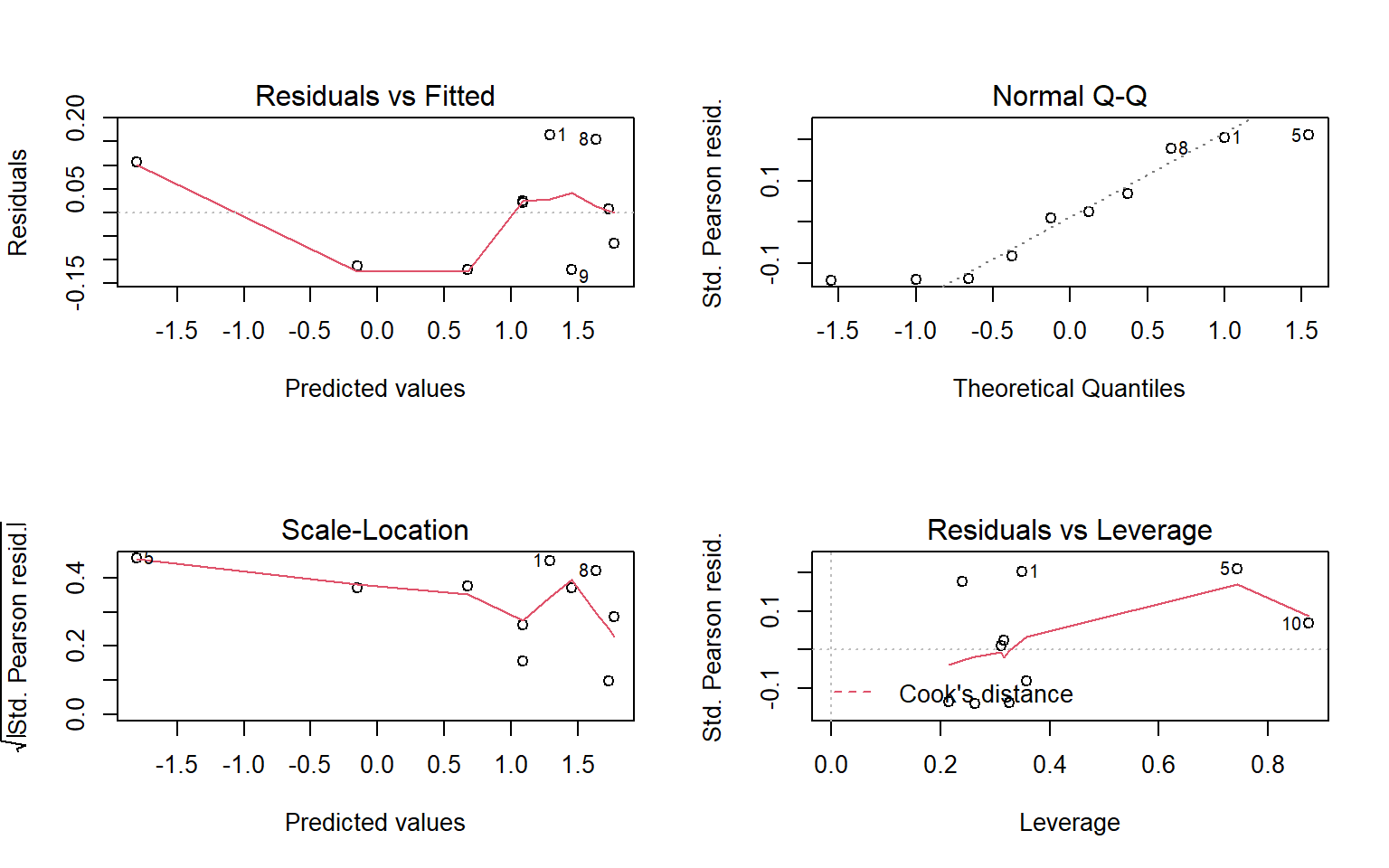
5.7 Utiliser residuals() sur glm

Pour obtenir les valeurs numériques des résidus

residuals(mod, type = "deviance")      # Résidus de déviance
residuals(mod, type = "pearson")      # Résidus de Pearson

Graphe des résidus de pearson 

par(mfrow=c(2,2))
plot(mod)

par(mfrow=c(1,1))

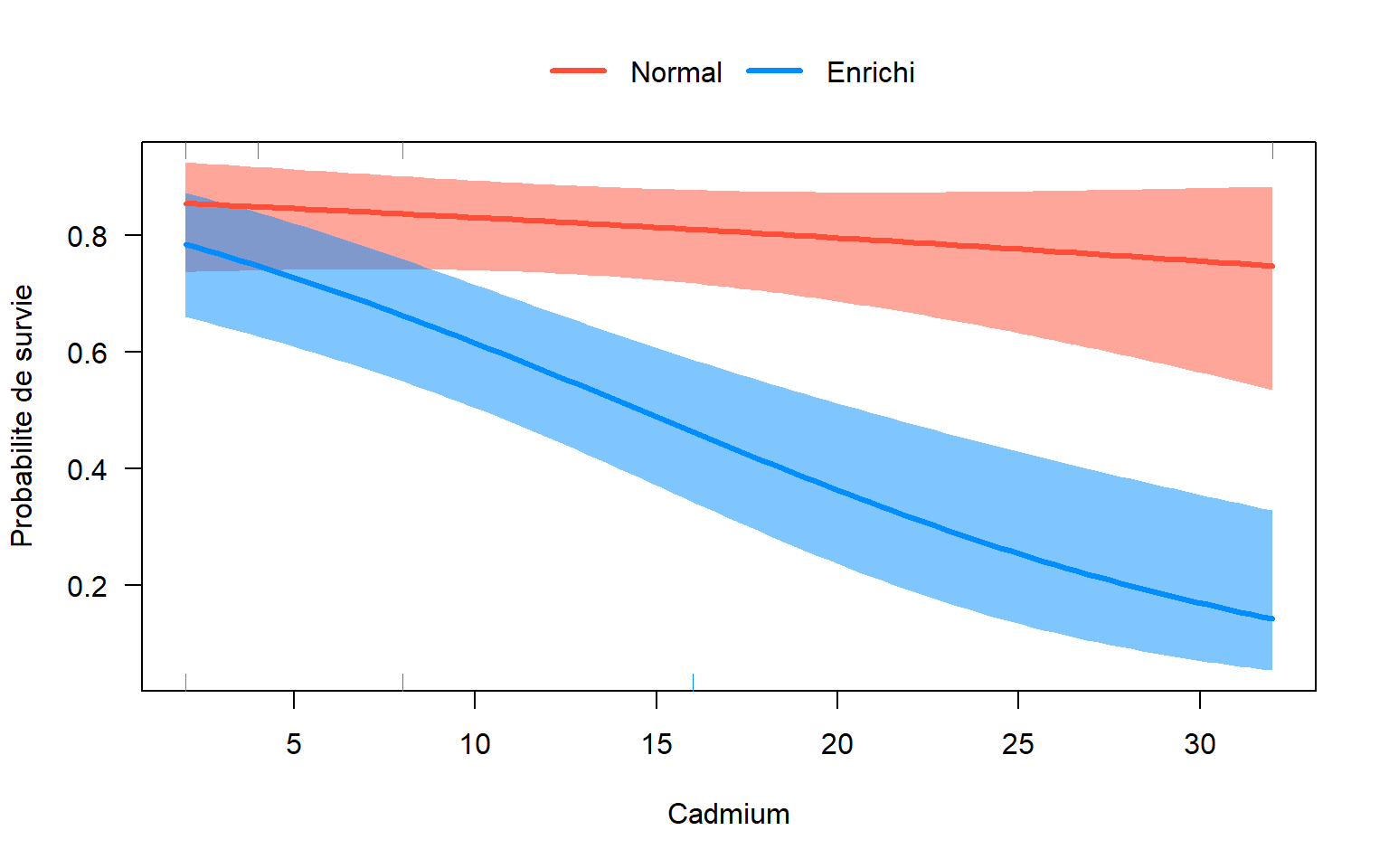
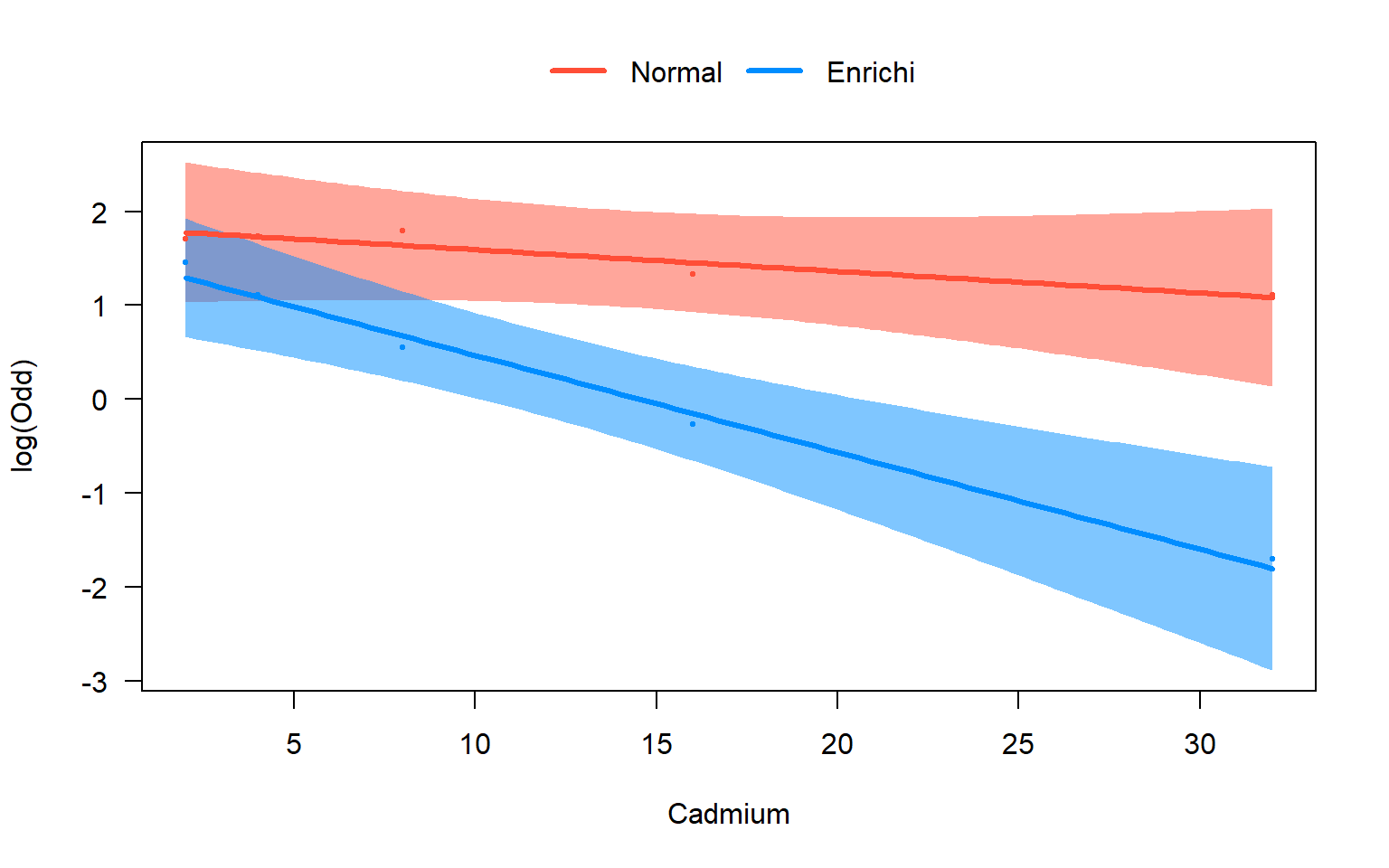
5.8 Utiliser visreg() sur glm

5.8.1 Probabilité de succès

visreg(mod, scale = "response", xvar = "Cadmium", by = "Omega3", band = TRUE,
       ylab = "Probabilite de survie", strip.names=c("Normal", "Enrichi"), overlay= TRUE)

5.8.2 Log(odds)

visreg(mod, xvar = "Cadmium", band = TRUE, by = "Omega3",
      ylab = "log(Odd)", strip.names = c("Normal", "Enrichi"), overlay = TRUE)

5.9 Utiliser predict() sur glm

Obtenir les prédictions pour (Omega3, Cadmium) = (“Normal”, 12) , (“Enrichi”,12)

xnew <- data.frame("Omega3" = c("Normal", "Enrichi"), "Cadmium" = c(12, 12)) 
pred <- predict(mod, newdata = xnew, type = "response", se.fit = TRUE)
res <- data.frame(xnew,
                  "Fit" = pred$fit,
                  "Lwr" = pred$fit - 1.96 * pred$se.fit,
                  "Upr" = pred$fit + 1.96 * pred$se.fit)
pander(res)
Omega3 Cadmium Fit Lwr Upr
Normal 12 0.5653 0.4546 0.676
Enrichi 12 0.8243 0.7487 0.8999