6 Analyse en composantes principales ACP
Objectif
~> Réduire le nombre de variables en transformant des variables corrélées en nouvelles variables décorrélées afin de mieux visualier les données. Les nouvelles variables, les composantes principales, sont des combinaisons linéaires des variables de départ.
Les packages privilégiés à utiliser pour faire de l’ACP sont FactoMiner et factoextra. FactoMinerR propose de multiples méthodes de réductions de dimension dans l’ACP. factoextra propose surtout des méthodes pour extraire et présenter graphiquement les résultats des analyses. FactoMiner n’est pas détaillé dans ce chapitre car l’ACP est déjà disponible dans le package de base de R : stats.
6.1 Fonctions utiles pour l’ACP
Réaliser l’ACP sur une matrice de données quantitatives data:
| Importance des composantes | |
|---|---|
| Résumé | summary(res) |
| Valeurs propres et variances | factoextra::get_eig(res) |
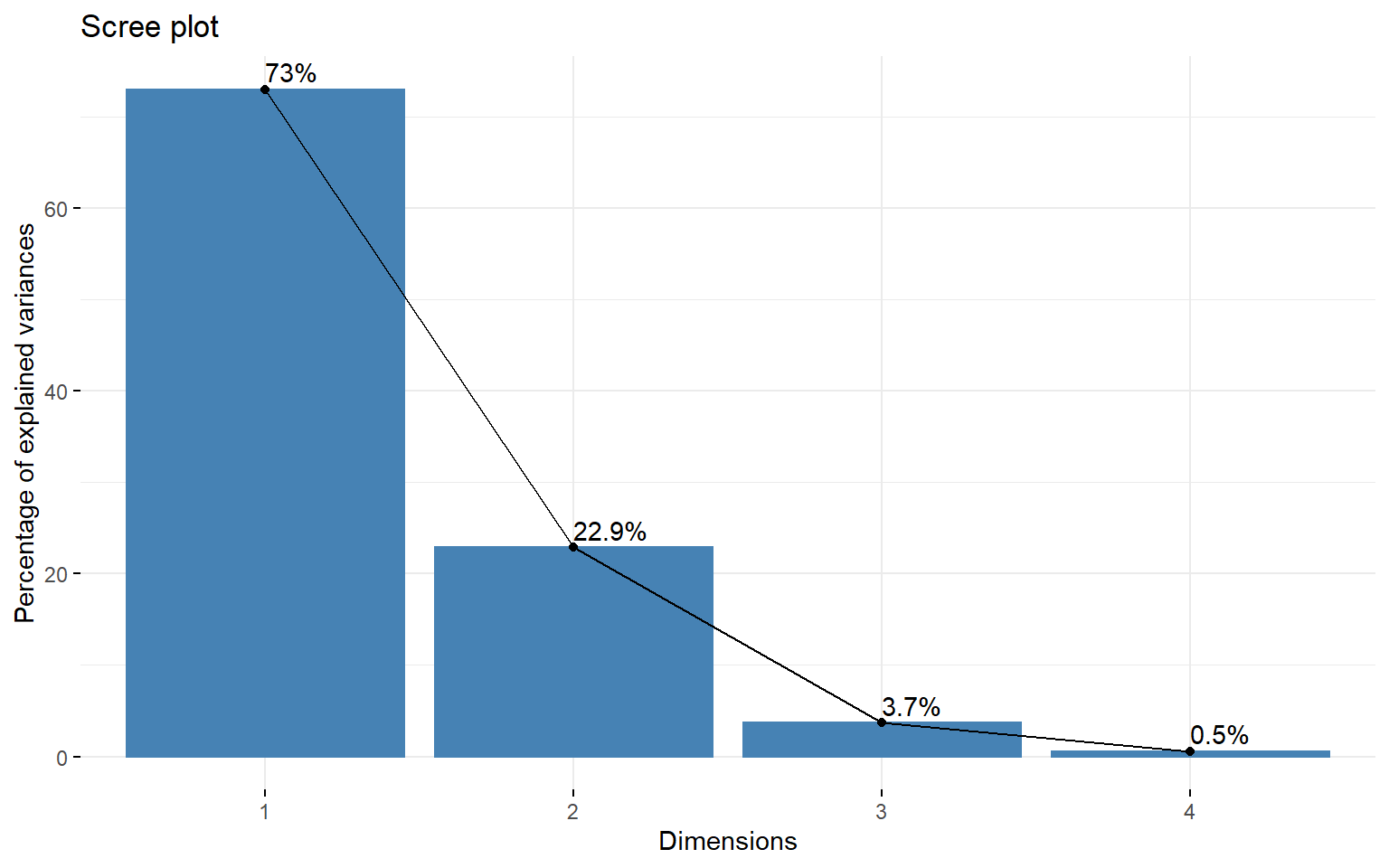
| ScreePlot | factoextra::fviz_screeplot(res, addlabels = TRUE) |
| Variables | |
|---|---|
| Informations | |
| -> Vecteurs propres de X’X | res$rotation |
| -> Autres informations | var <- factoextra::get_pca_var(res) |
| ~~> Corrélation variables/CP | var$cor |
| ~~> Cos2/qualité de représentation | var$cos2 |
| ~~> Contributions | var$contrib |
| Cercle de corrélations | factoextra::fviz_pca_var(res, ..) |
| Visualiser les contributions des variables | factoextra::fviz_contrib(res, choice = "var, ..) |
| Individus | |
|---|---|
| Informations | ind <- factoextra::get_pca_ind(res) |
| (6 premiers individus) | ~> Coordonnées head(ind$coord) |
~> Cos2 / qualité de représentation head(ind$cos2) |
|
~> Contributions head(ind$contrib) |
|
| Score plot ou Carte des individus | factoextra::fviz_pca_ind(res, ..) |
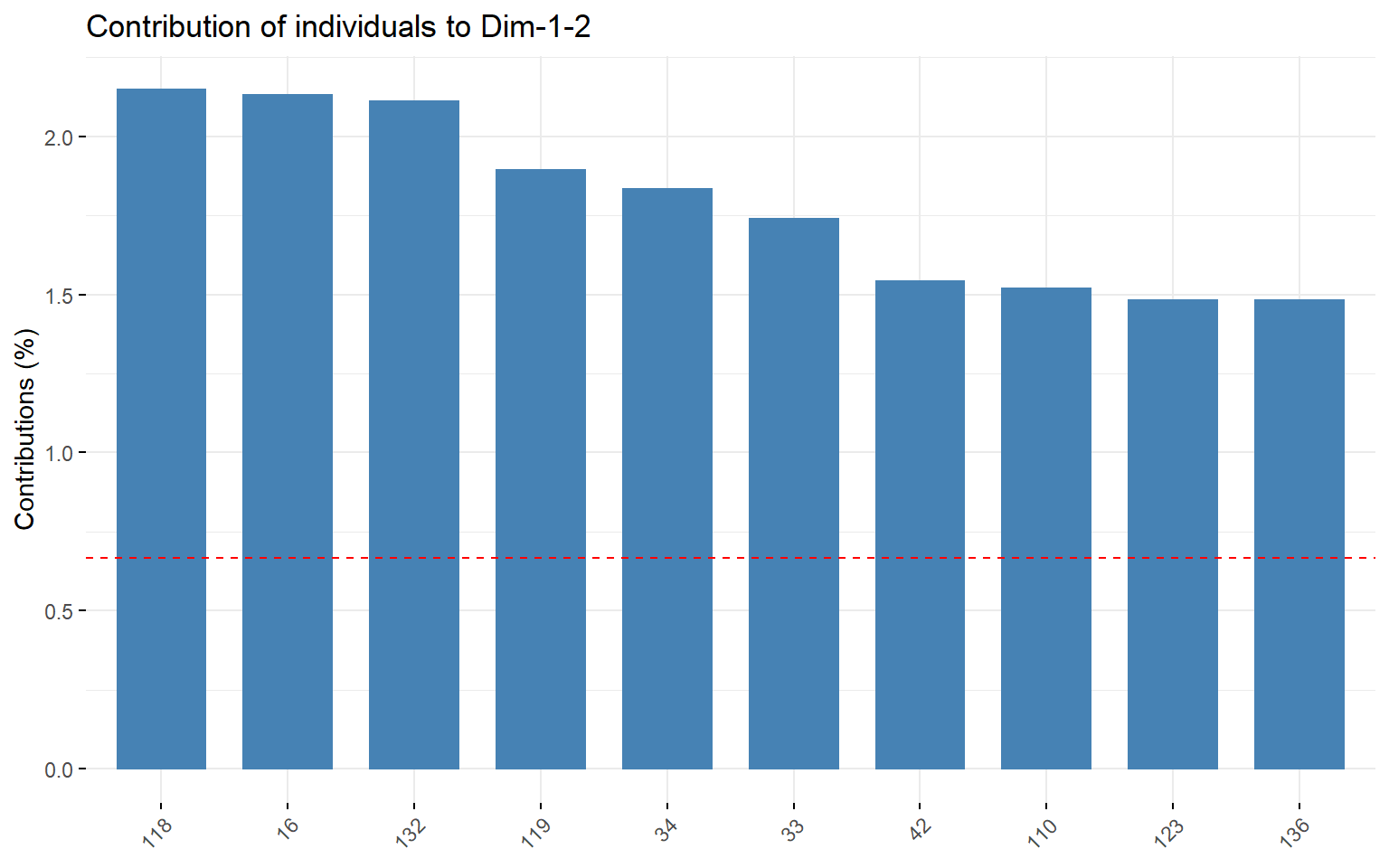
| Visualiser les contributions des individus | factoextra::fviz_contrib(res, choice = "ind", ..) |
| Autres | |
|---|---|
| Biplot variables-individus | factoextra::fviz_pca_biplot(res, ..) |
6.2 Données du chapitre ACP
Les données iris sont communément utilisées pour illustrer les bases des méthodes multivariées. Elle fournissent, pour 150 iris, 4 variables liées aux dimensions de la fleur : Sepal.Length, Sepal.Width, Petal.Length, Petal.Width. Ces iris sont de 3 espèces : setosa, versicolor, virginica.
# Jeu de données iris disponible directement dans R
data <- iris
# Extraire la variable qualitative avec l'espèce
groupe <- as.factor(iris$Species)
# Isoler les 4 variables quantitatives (sans la 5eme colonne de iris)
data <- data[,-5]
# Visualiser les données
plot(data, col = groupe , main="Scatter plots des variables prises 2 à 2", oma=c(3,3,3,12), pch=20)
par(xpd = TRUE)
legend("bottomright", title = "Species", legend = levels(groupe), col = c(1,2,3), cex = 0.8, pch = c(20,20,20))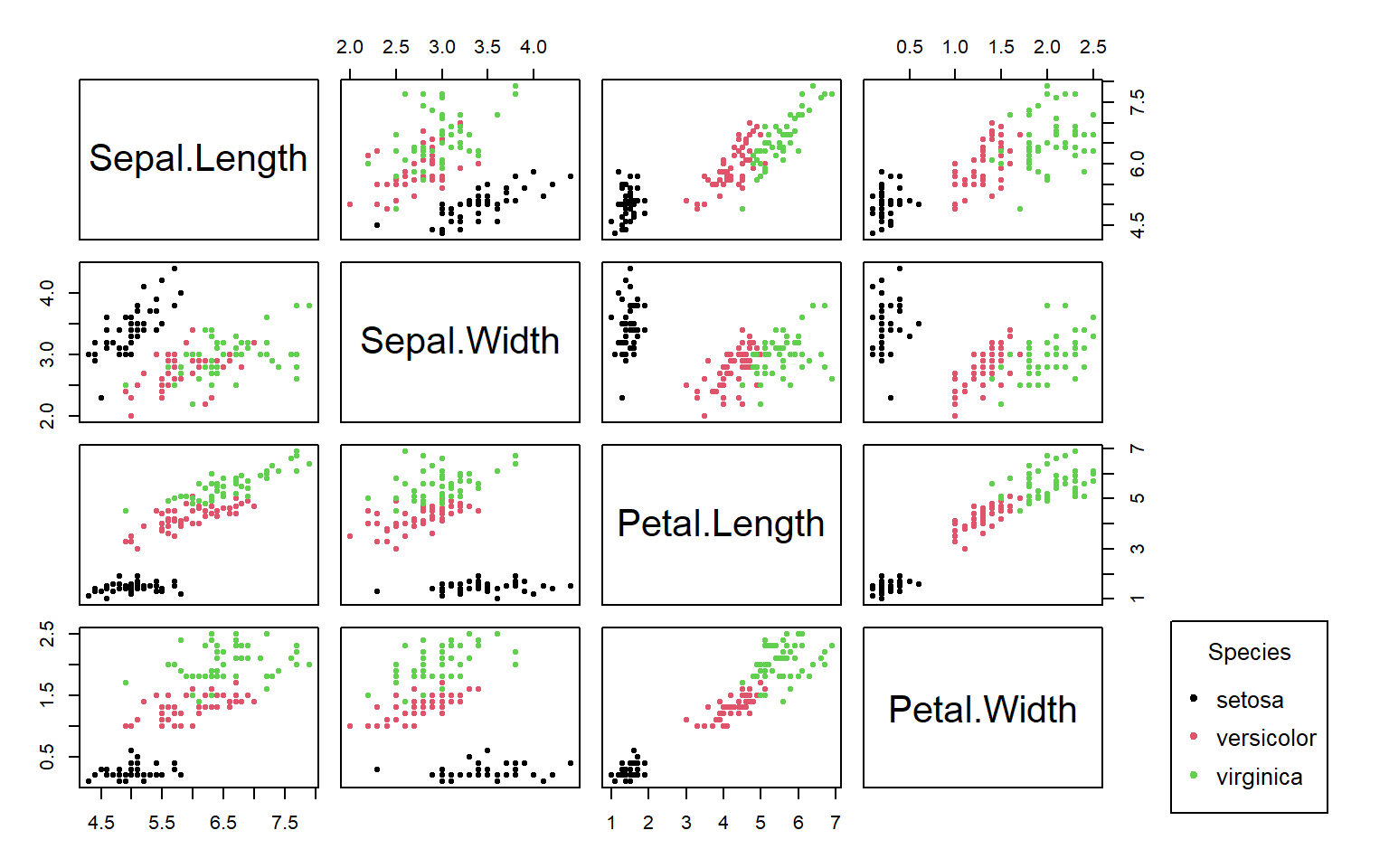
6.3 Utiliser prcomp()
| eigenvalue | variance.percent | cumulative.variance.percent | |
|---|---|---|---|
| Dim.1 | 2.918 | 72.96 | 72.96 |
| Dim.2 | 0.914 | 22.85 | 95.81 |
| Dim.3 | 0.1468 | 3.669 | 99.48 |
| Dim.4 | 0.02071 | 0.5179 | 100 |
6.4 Utiliser fviz_pca_var()
Cercle des corrélations : représentation des corrélations entre les variables de départ et les composantes principales. Les flèches peuvent être colorées en fonction d’une autre variable, ici cos2.
L’option repel permet d’éviter que les noms des variables soient superposés.
fviz_pca_var(res, col.var = "cos2",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"), repel = TRUE )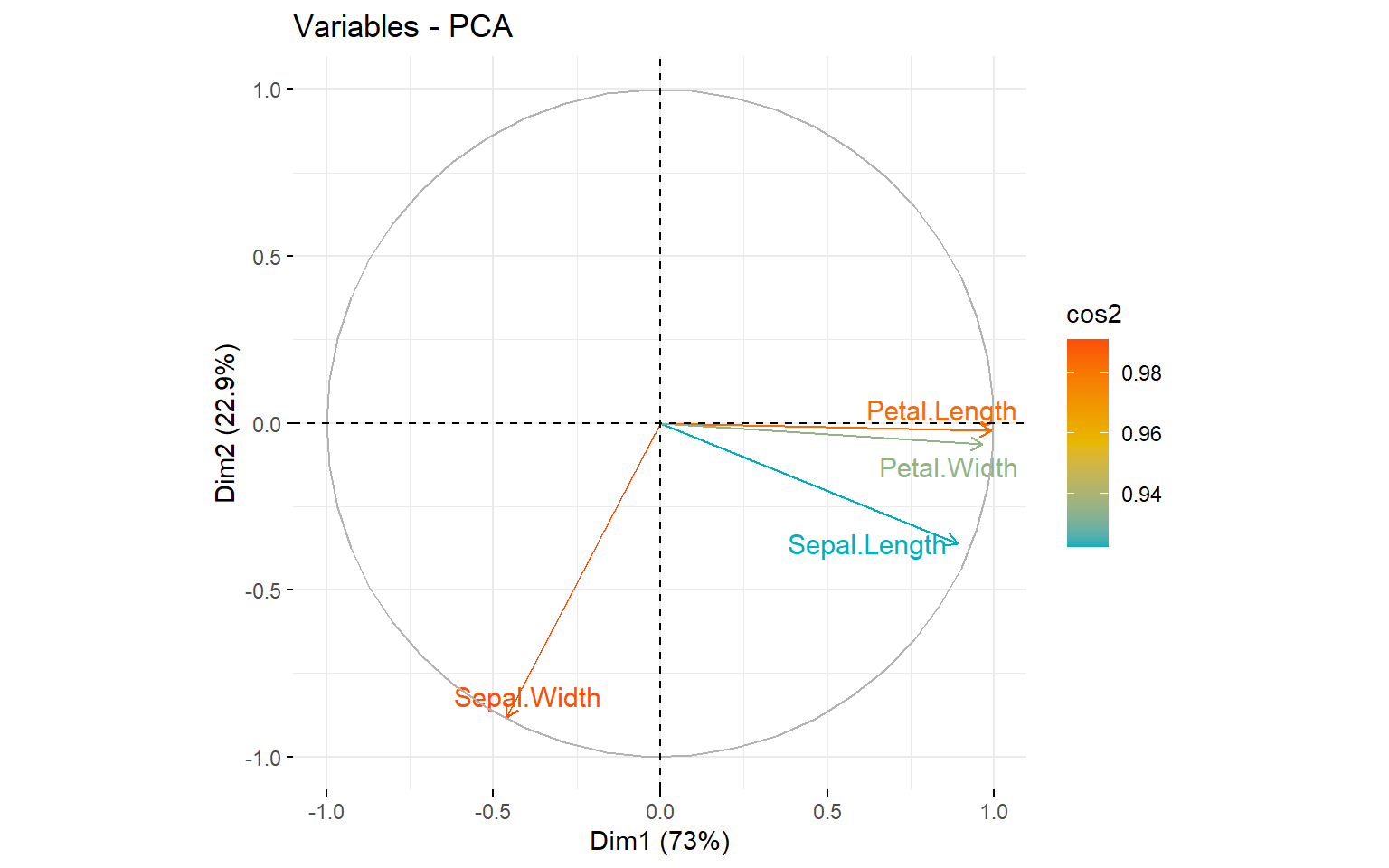
6.5 Utiliser fviz_pca_ind()
Graphe des scores ou carte des individus : Projection des individus sur l’espace des 2 premières composantes principales.
fviz_pca_ind(res, axes = c(1,2), geom.ind = "point", col.ind = groupe,
addEllipses = TRUE, legend.title = "Espèces")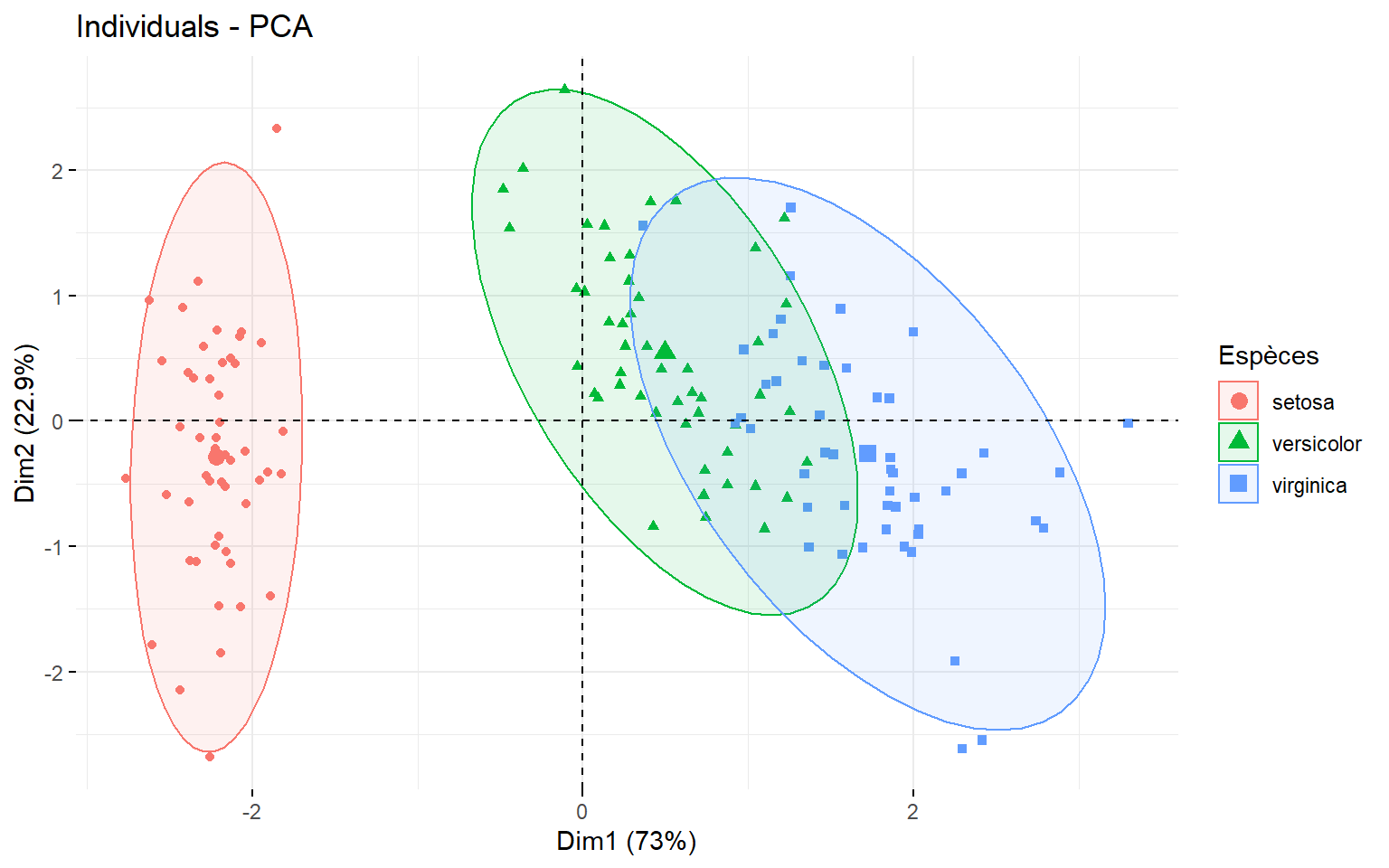
6.6 Utiliser biplot()
biplot : superposition du graphe des scores et des individus
#Biplot variables - individus
fviz_pca_biplot (res, col.ind = groupe, label = "var",
col.var = "black", repel = TRUE, legend.title = "Espèces")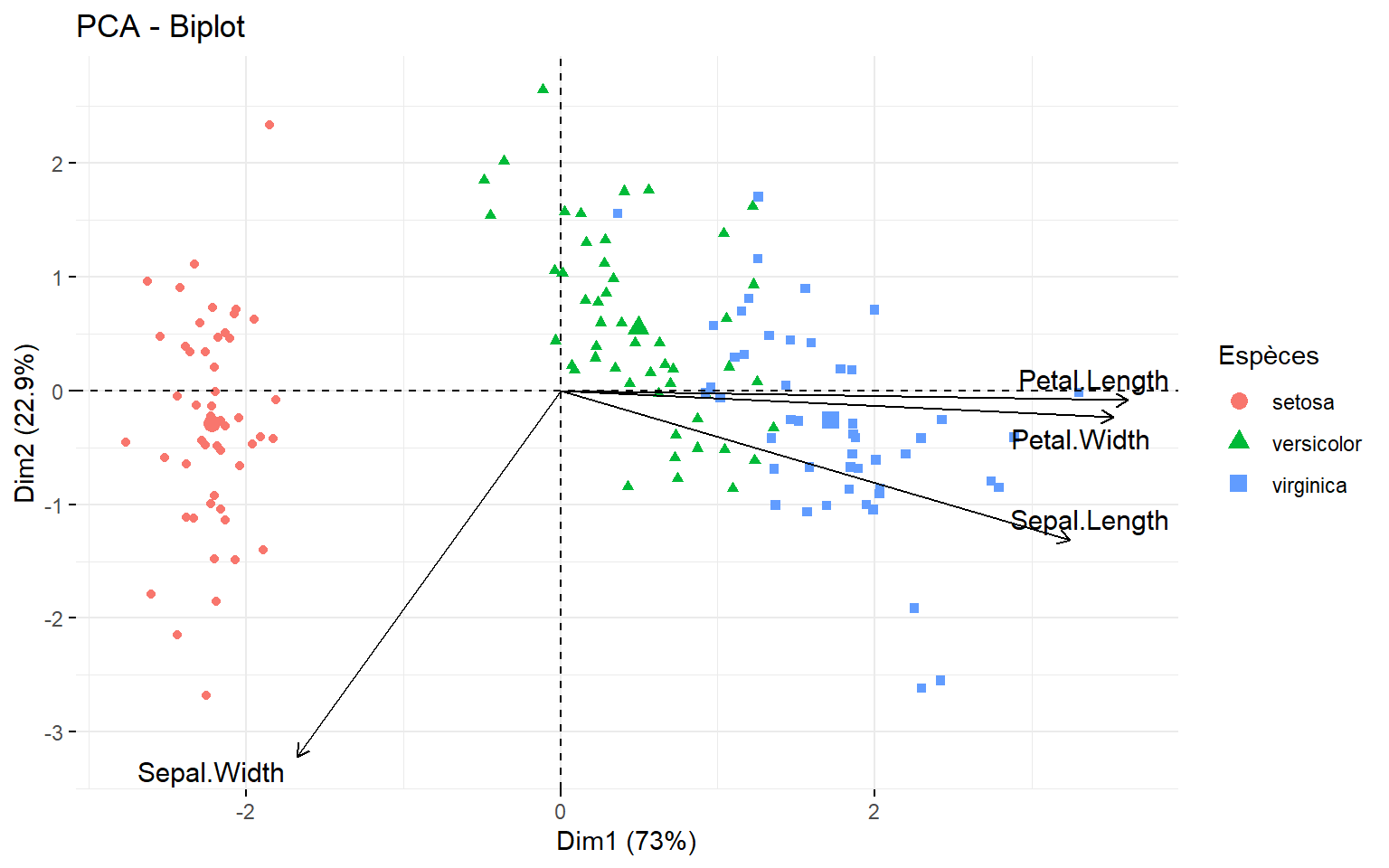
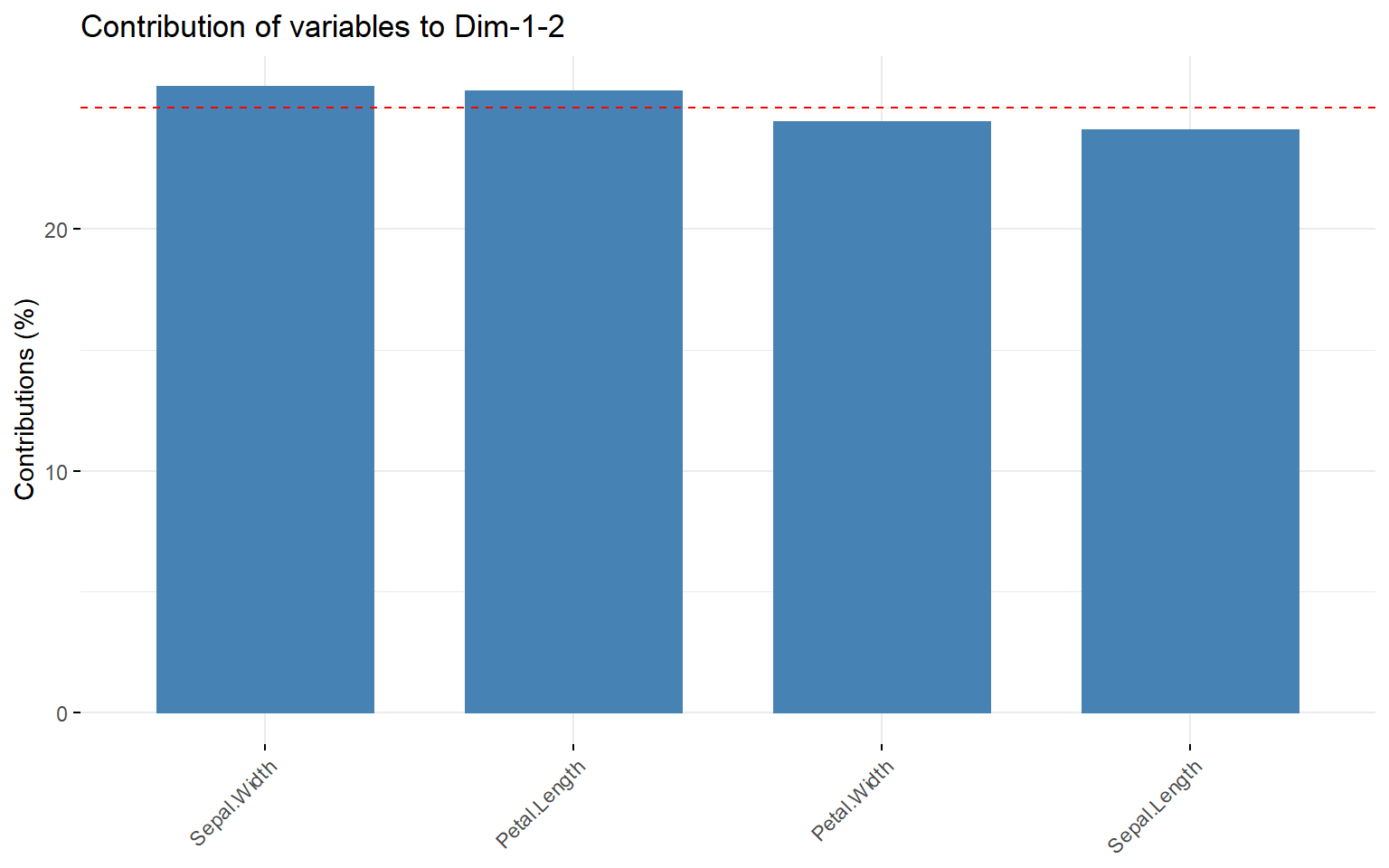
6.7 Utiliser fviz_contrib()
6.7.1 Pour les variables
Afficher les contributions des variables aux CP 1 et 2.