19 Correlation Analysis

We again work with the father/son heights dataset collected by Pearson.

load("data/father_son.rda")
attach(father_son)

19.1 Scatterplot

We saw that a scatterplot is an appropriate plot for paired numerical data.

plot(father, son, pch = 16, xlab = "father's height", ylab = "son's height", asp = 1, cex = 0.5)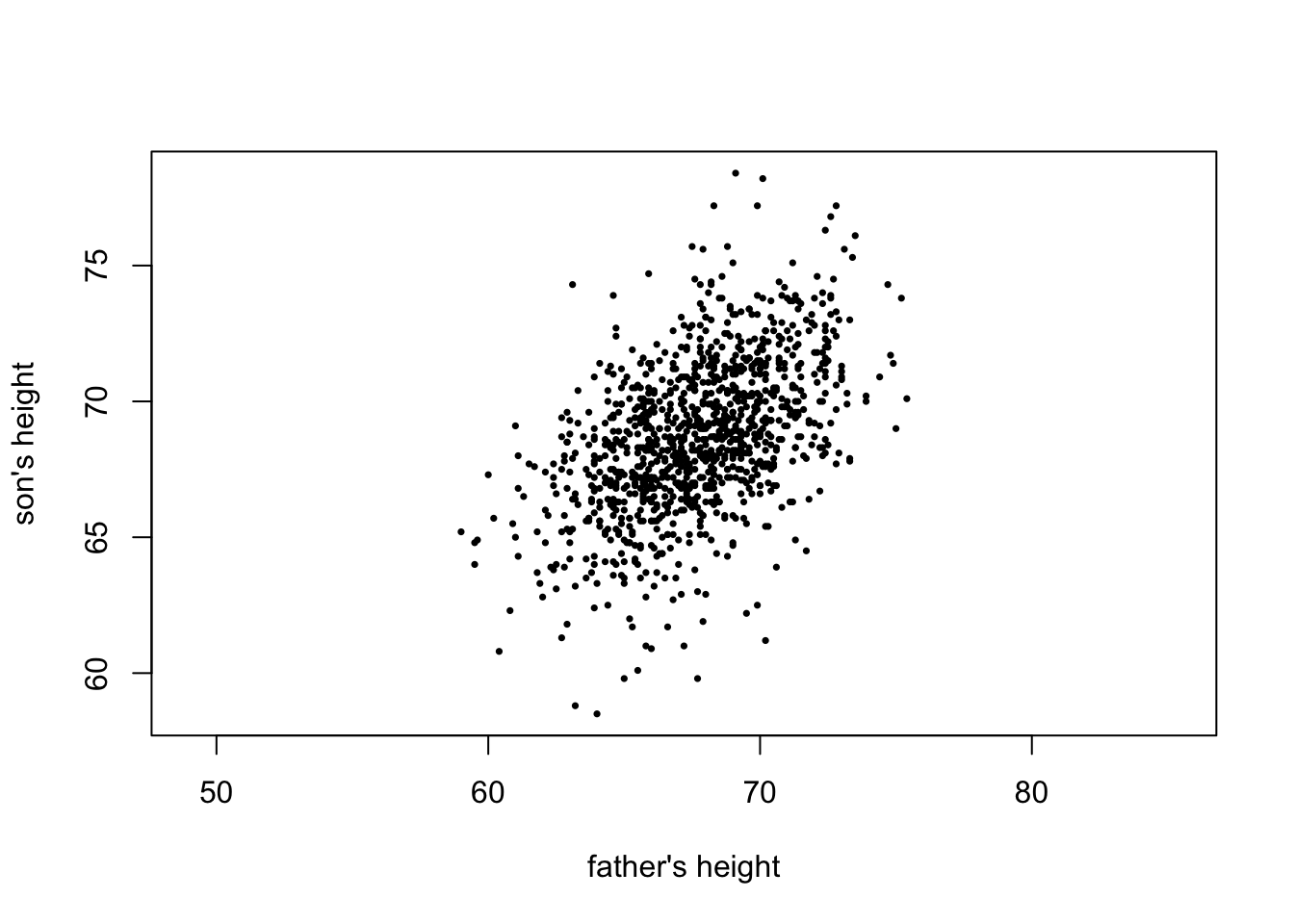 

19.2 Sample correlations

We compute correlations of various types. They are all positive, in congruence with what is observed in the plot.

cor(father, son, method = "pearson")

[1] 0.5012473

cor(father, son, method = "spearman")

[1] 0.505671

cor(father, son, method = "kendall")

[1] 0.3526375

19.3 Correlations tests

Although it is pretty clear from the scatterplot that the heights of a father and his son are positively correlated (or more generally, monotonically associated), for pedagodical reasons we perform the corresponding tests. (Refer to the manual for details on how the p-values are computed.)

cor.test(father, son, method = "pearson")

    Pearson's product-moment correlation

data:  father and son
t = 19.002, df = 1076, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.4551622 0.5446541
sample estimates:
      cor 
0.5012473 

cor.test(father, son, method = "spearman") 

    Spearman's rank correlation rho

data:  father and son
S = 103209762, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
     rho 
0.505671 

cor.test(father, son, method = "kendall")

    Kendall's rank correlation tau

data:  father and son
z = 17.161, p-value < 2.2e-16
alternative hypothesis: true tau is not equal to 0
sample estimates:
      tau 
0.3526375 

19.4 Distance covariance (and test)

We also apply the distance covariance test. (The function returns the Monte Carlo permutation p-value based on R replicates.)

require(energy)
dcov.test(father, son, R = 1e3)

    dCov independence test (permutation test)

data:  index 1, replicates 1000
nV^2 = 742.69, p-value = 0.000999
sample estimates:
     dCov 
0.8300339