8 Árboles
El método del árbol de decisión es una técnica de aprendizaje automático predictivo potente y popular que se utiliza tanto para la clasificación como para la regresión. También se conoce como árboles de clasificación y regresión (CART).
La implementación de R del algoritmo CART se llama RPART (árboles de regresión y particionamiento recursivos) disponible en un paquete con el mismo nombre.
8.1 Carga de los paquetes R
install.packages("tidyverse")
install.packages("caret")
install.packages("rpart")
install.packages("rpart.plot")8.2 Árboles de clasificación
Conjunto de datos: PimaIndiansDiabetes2 [en paquete mlbench], para predecir la probabilidad de ser diabético positivo basándose en múltiples variables clínicas.
Los datos contienen 768 individuos (mujeres) y 9 variables clínicas para predecir la probabilidad de que los individuos sean diabéticos positivos o negativos:
embarazadas: número de embarazos,
glucosa: concentración de glucosa plasmática,
presión: presión arterial diastólica (mm Hg),
tríceps: espesor del pliegue cutáneo del tríceps (mm),
insulina: insulina sérica de 2 horas (mu U / ml),
mass: índice de masa corporal (peso en kg / (altura en m) ) ^ 2),
pedigree: diabetes función del pedigree,
edad: edad (años),
diabetes: variable de clase positiva o negativa.
En R se utiliza la función
rpartcon el argumento:diabetes ~ .donde diabetes es la variable de interés, que en este caso en categorica,~significa que sigue los datos y.significa que toma todas las variables de la base.*
library(tidyverse)
library(caret)
library("rpart.plot")
library(rpart)
library("mlbench")
data ("PimaIndiansDiabetes2" , package = "mlbench")
model1 <-rpart(diabetes ~ ., data = PimaIndiansDiabetes2, method = "class" )
plot(model1)
text(model1, digits = 3 )
R también nos permite ver el conjunto de reglas que define el árbol, en el caso de no poderlo detallar.
data ( "PimaIndiansDiabetes2" , package = "mlbench" )
model1 <-rpart (diabetes ~ ., data = PimaIndiansDiabetes2, method = "class" )
print(model1)## n= 768
##
## node), split, n, loss, yval, (yprob)
## * denotes terminal node
##
## 1) root 768 268 neg (0.65104167 0.34895833)
## 2) glucose< 127.5 485 94 neg (0.80618557 0.19381443)
## 4) age< 28.5 271 23 neg (0.91512915 0.08487085) *
## 5) age>=28.5 214 71 neg (0.66822430 0.33177570)
## 10) insulin< 142.5 164 48 neg (0.70731707 0.29268293)
## 20) glucose< 96.5 51 4 neg (0.92156863 0.07843137) *
## 21) glucose>=96.5 113 44 neg (0.61061947 0.38938053)
## 42) mass< 26.35 19 0 neg (1.00000000 0.00000000) *
## 43) mass>=26.35 94 44 neg (0.53191489 0.46808511)
## 86) pregnant< 5.5 49 15 neg (0.69387755 0.30612245)
## 172) age< 34.5 25 2 neg (0.92000000 0.08000000) *
## 173) age>=34.5 24 11 pos (0.45833333 0.54166667)
## 346) pressure>=77 10 2 neg (0.80000000 0.20000000) *
## 347) pressure< 77 14 3 pos (0.21428571 0.78571429) *
## 87) pregnant>=5.5 45 16 pos (0.35555556 0.64444444) *
## 11) insulin>=142.5 50 23 neg (0.54000000 0.46000000)
## 22) age>=56.5 12 1 neg (0.91666667 0.08333333) *
## 23) age< 56.5 38 16 pos (0.42105263 0.57894737)
## 46) age>=33.5 29 14 neg (0.51724138 0.48275862)
## 92) triceps>=27 22 8 neg (0.63636364 0.36363636) *
## 93) triceps< 27 7 1 pos (0.14285714 0.85714286) *
## 47) age< 33.5 9 1 pos (0.11111111 0.88888889) *
## 3) glucose>=127.5 283 109 pos (0.38515901 0.61484099)
## 6) mass< 29.95 75 24 neg (0.68000000 0.32000000) *
## 7) mass>=29.95 208 58 pos (0.27884615 0.72115385)
## 14) glucose< 157.5 116 46 pos (0.39655172 0.60344828)
## 28) age< 30.5 50 23 neg (0.54000000 0.46000000)
## 56) pressure>=73 29 10 neg (0.65517241 0.34482759)
## 112) mass< 41.8 20 4 neg (0.80000000 0.20000000) *
## 113) mass>=41.8 9 3 pos (0.33333333 0.66666667) *
## 57) pressure< 73 21 8 pos (0.38095238 0.61904762) *
## 29) age>=30.5 66 19 pos (0.28787879 0.71212121) *
## 15) glucose>=157.5 92 12 pos (0.13043478 0.86956522) *8.2.1 Predicciones
Los diferentes conjuntos de reglas establecidos en el árbol se utilizan para predecir el resultado de una nueva prueba de datos. El siguiente código R predice con los siguientes datos:
NuevosDatos <-data.frame(glucose = 98 ,insulin = 148, age=30, pregnant=6, triceps=29, mass=30, pedigree=0.8, pressure=70)
model1 %>% predict(NuevosDatos)## neg pos
## 1 0.1111111 0.8888889Entonces el resultado será:
model1 %>% predict(NuevosDatos)
neg pos
1 0.1111111 0.8888889es decir, el paciente tiene diabetes con una probabilidad de 0.888.
Si por ejemplo, solo quiere utilizar las variables agey glucose se pone en rpart diabetes ~ age+glucose y solo da un árbol con solo estas variables.
data ( "PimaIndiansDiabetes2" , package = "mlbench" )
model2 <-rpart(diabetes ~ age+glucose, data = PimaIndiansDiabetes2, method = "class" )
plot(model2)
text(model2, digits = 3 )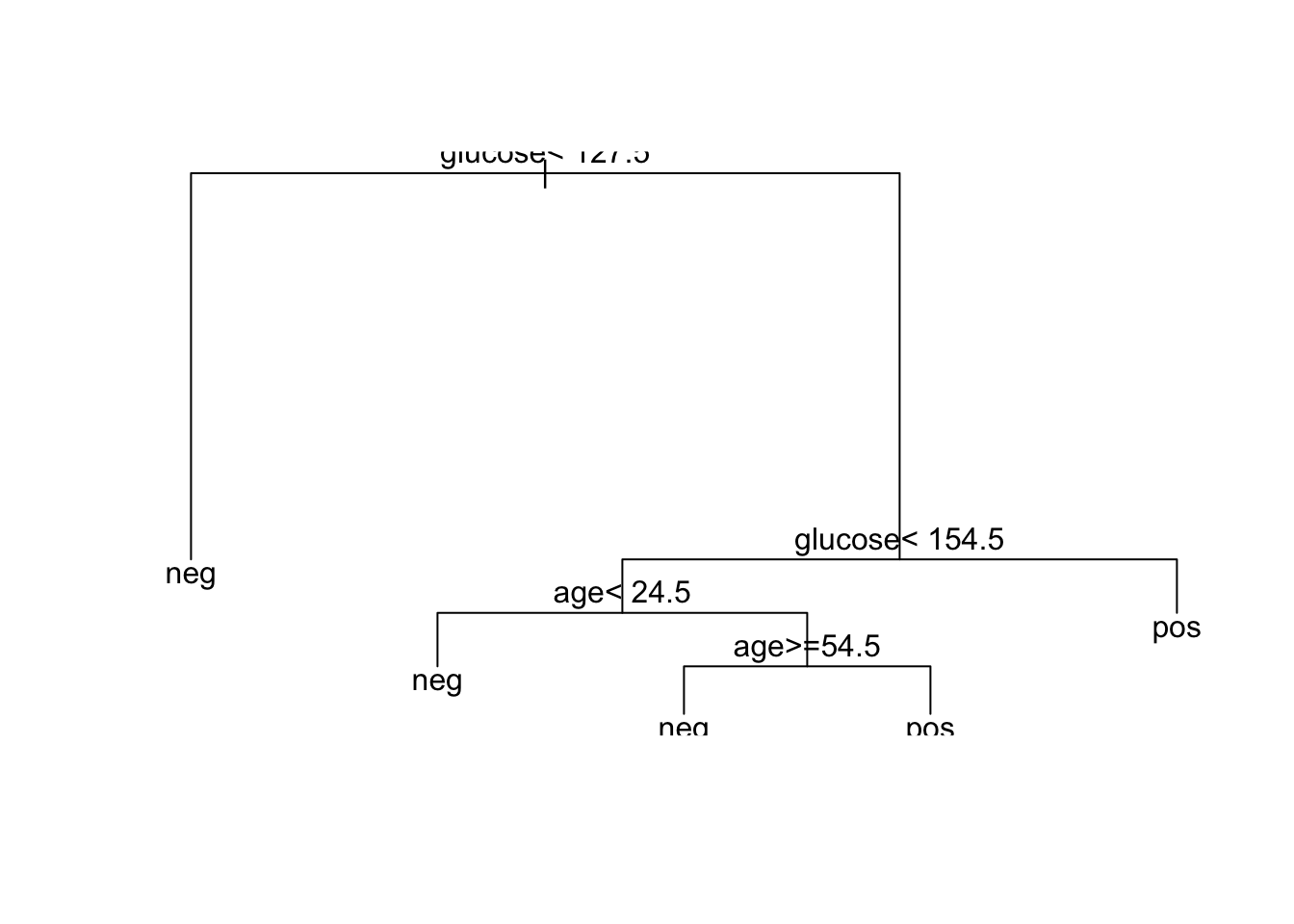
Si el árbol sale feo y no se ve tan chévere, recomiendo el parquete rpart.plot:
library(rpart.plot)
rpart.plot(model2, box.palette="RdBu", shadow.col="gray", nn=TRUE)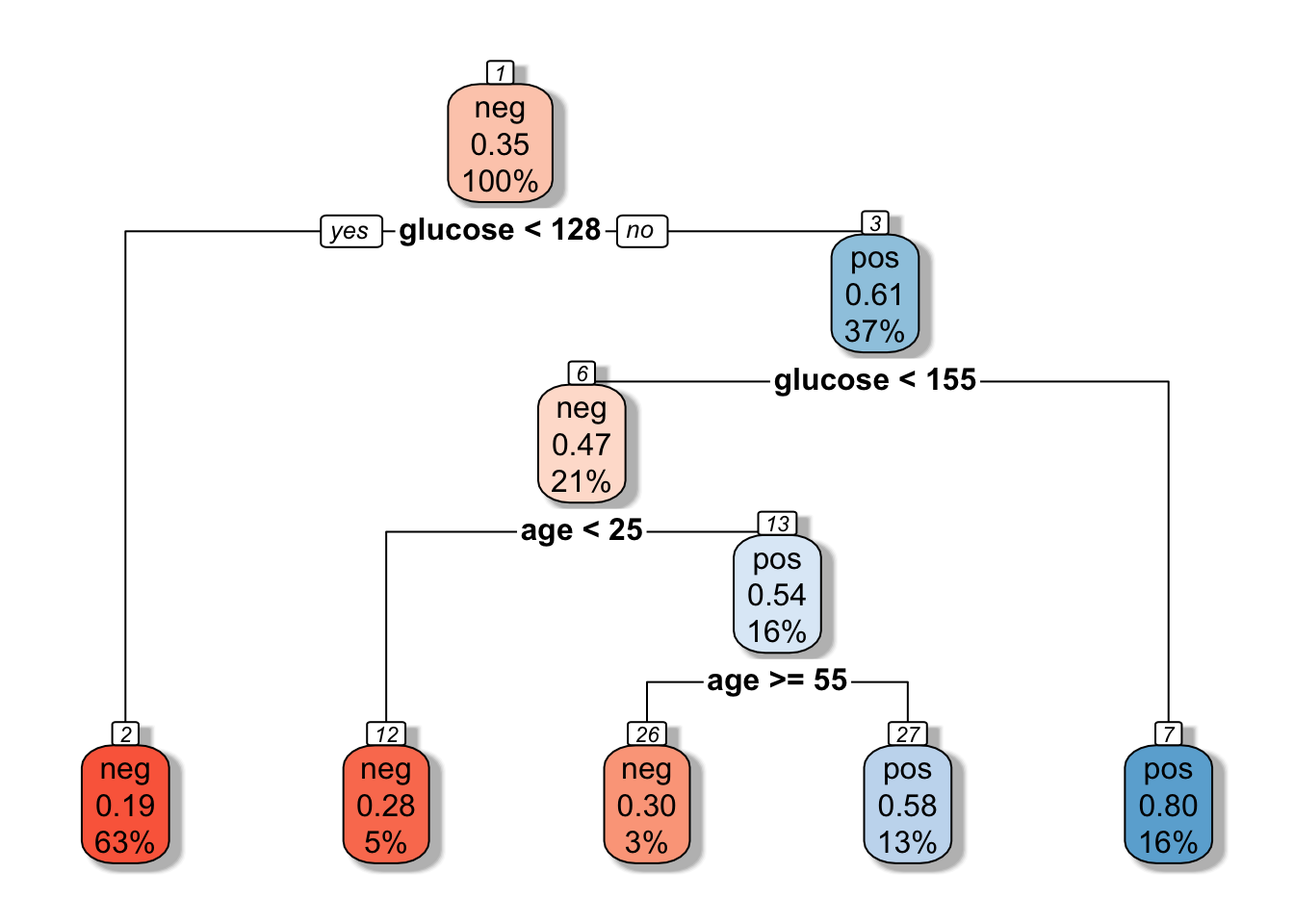
8.2.2 Datos del iris de Edgar Anderson
Este famoso conjunto de datos de iris (de Fisher o Anderson) da las medidas en centímetros de las variables longitud y ancho del sépalo y largo y ancho del pétalo, respectivamente, para 50 flores de cada una de las 3 especies de iris. Las especies son Iris setosa, versicolor y virginica.
iris es un marco de datos con 150 casos (filas) y 5 variables (columnas) denominadas Sepal.Length, Sepal.Width, Petal.Length, Petal.Width y Species.
El siguiente ejemplo representa un modelo de árbol que predice la especie de flor de iris según la longitud (en cm) y el ancho del sépalo y el pétalo
library(tidyverse)
library(caret)
library(rpart)
data ( "iris" )
model <-rpart(Species ~ ., data = iris, method = "class")
par( xpd = NA ) # ayuda a ajustar el gráfico.
rpart.plot(model)
text (model, digits = 3 ) 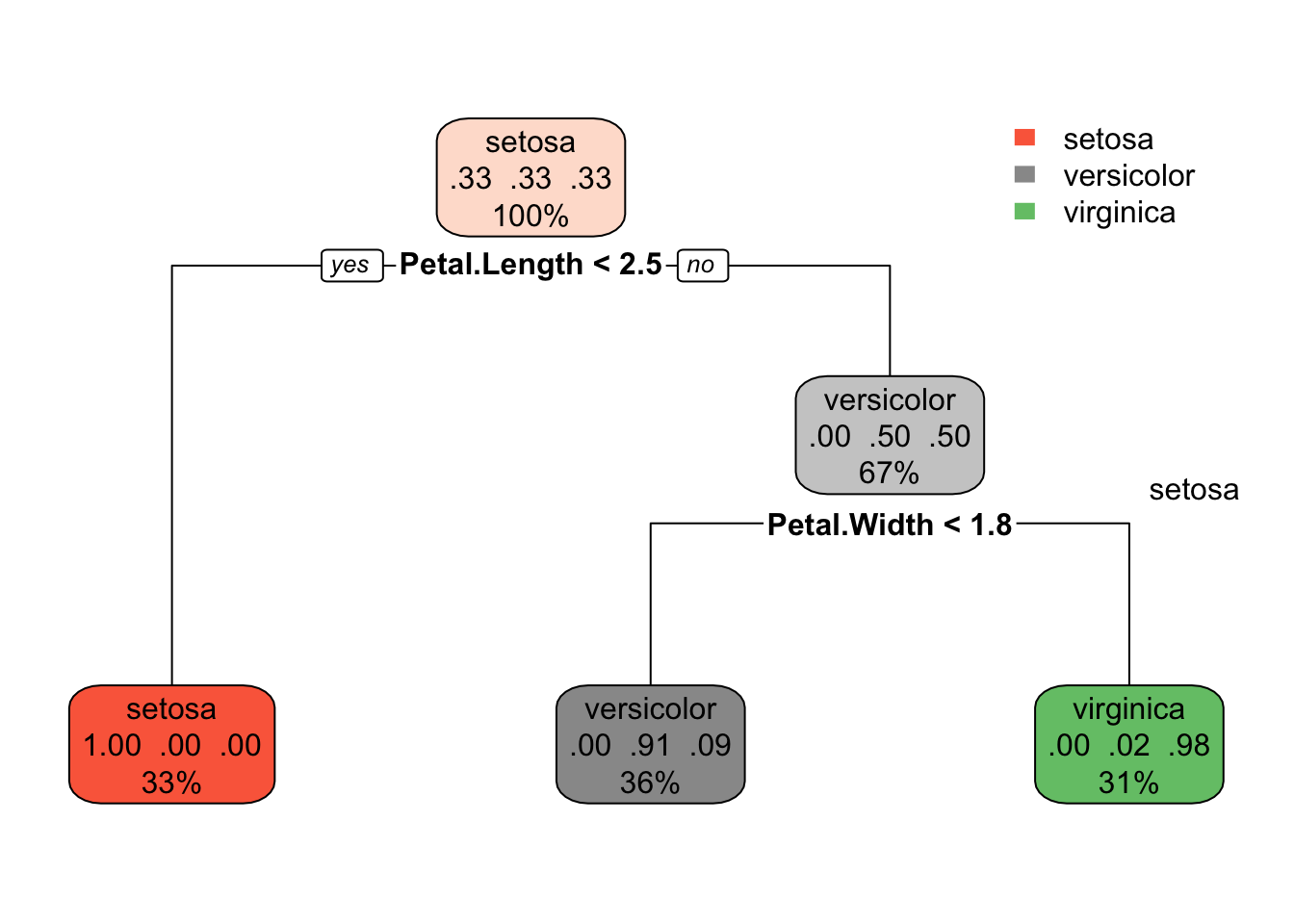
8.3 Árboles de regresión
El código R es idéntico al que hemos visto en apartados anteriores. La única diferencia es que al final del código es method = "anova". No es casualidad, lo que hace es comparar todas las variables con todas.
Ejemplo de conjunto de datos: Usaremos el conjunto de datos de Boston [en el paquete MASS], para predecir el valor mediano de la casa (mdev), en los suburbios de Boston, usando diferentes variables predictoras.
Cargue los datos de datos (“Boston,” paquete = “MASS”). Este marco de datos contiene las siguientes columnas:
crim: tasa de criminalidad per cápita por ciudad.
zn: proporción de terreno residencial dividido en zonas para lotes de más de 25,000 pies cuadrados.
indus: proporción de acres comerciales no minoristas por ciudad.
chas: Variable ficticia de Charles River (= 1 si el tramo limita con el río; 0 en caso contrario).
nox: concentración de óxidos de nitrógeno (partes por 10 millones).
rm: número medio de habitaciones por vivienda.
age: Proporción de unidades ocupadas por sus propietarios construidas antes de 1940.
dis: media ponderada de las distancias a cinco centros de empleo de Boston.
rad: índice de accesibilidad a carreteras radiales.
tax: Tasa de impuesto a la propiedad de valor total por $ 10,000.
ptratio: Proporción alumno-profesor por ciudad.
black: 1000 (Bk - 0.63) ^ 2 donde Bk es la proporción de negros por ciudad. (ESTA VARIABLE ES RACISTA)
lstat: estatus más bajo de la población (porcentaje).
medv: valor medio de las viviendas ocupadas por sus propietarios en $ 1000.
data( "Boston" , package = "MASS" )
model <-rpart(medv ~ ., data = Boston, method = "anova")
rpart.plot(model)
text (model, digits = 3 ) 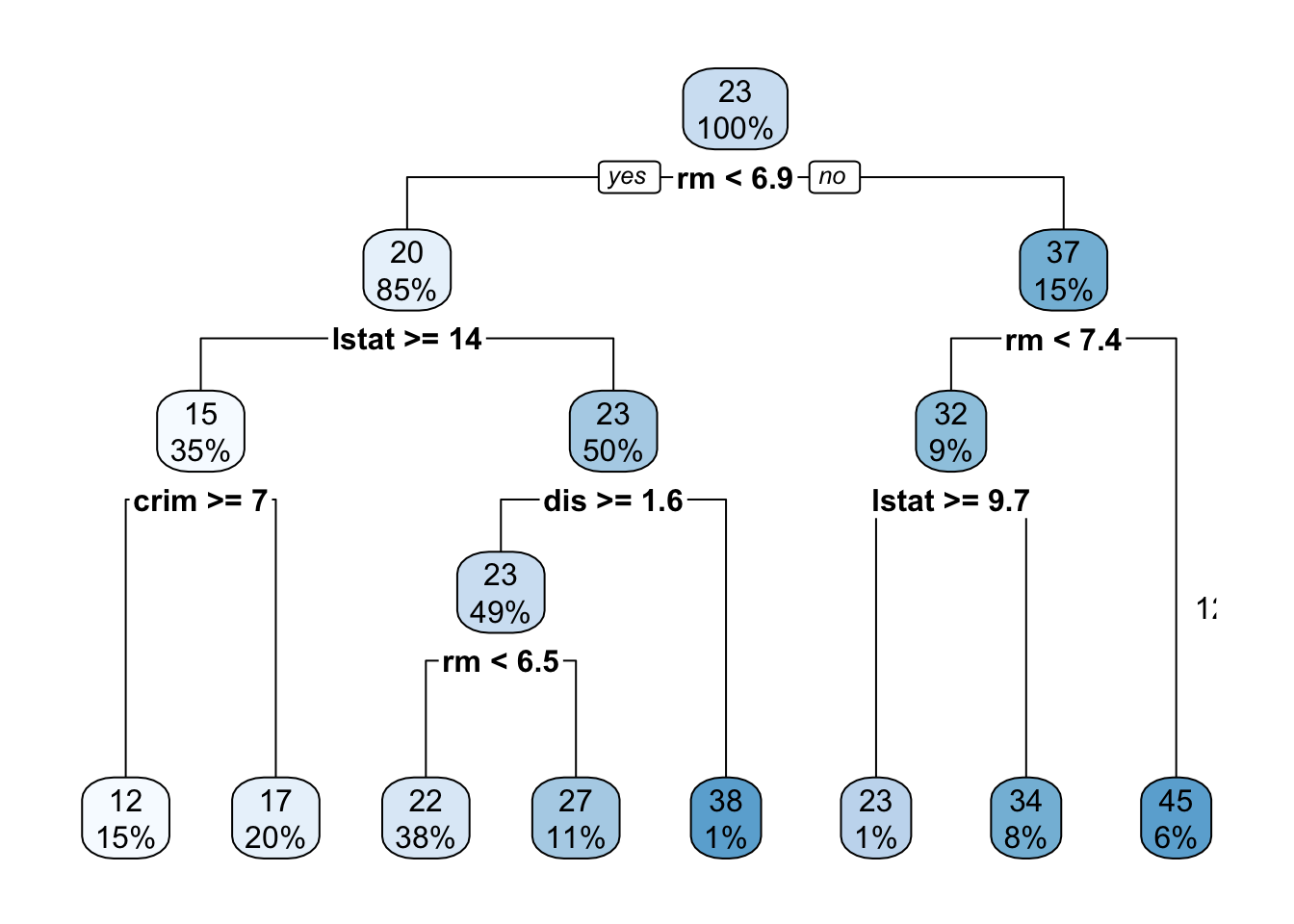
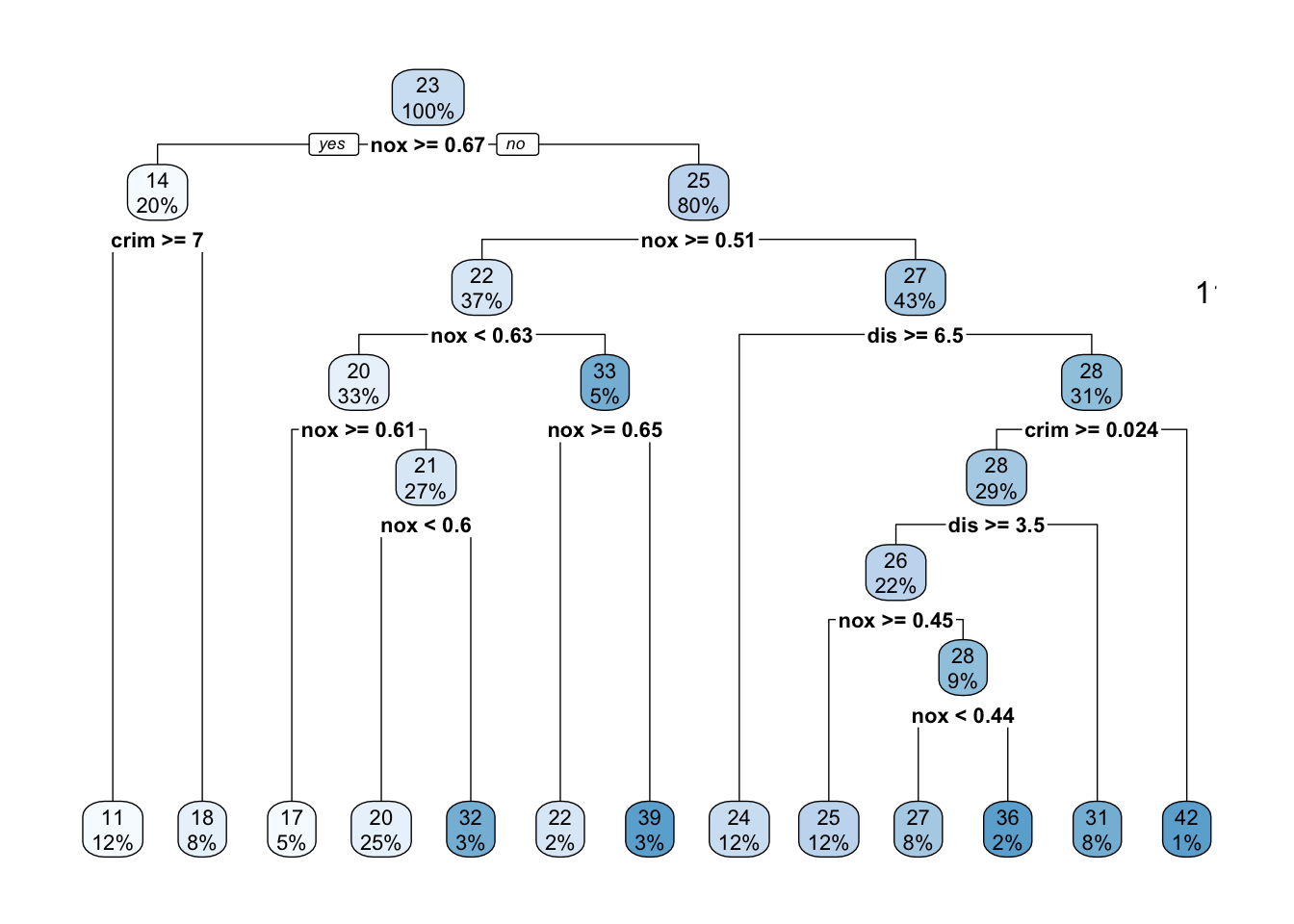
Elimine algunas variables, como la racista. Solo considere crim, nox y dis y ejecute el árbol:
data( "Boston" , package = "MASS" )
model <-rpart(medv ~ crim+nox+dis, data = Boston, method = "anova")
rpart.plot(model)
text (model, digits = 3 )