9 Coeficientes de correlación

9.1 Coeficiente Pearson

Como ya mencionamos, el coeficiente de Pearson es apropiado cuando las variables a comparar con de escala de intervalo o razón ya que toma en cuenta la magnitud relativa de las observaciones.

9.1.1 Ejemplo (Cálculo del Coeficiente de correlación de Pearson)

En este ejemplo, adaptado de (Butler 1985), vamos a suponer que hemos tomado un examen de traducción y otro de comprensión de inglés a doce estudiantes. Los resultados de estos exámenes están en la tabla:

Estudiante	x	y
1	17	15
2	13	13
3	12	8
4	14	17
5	15	16
6	8	9
7	9	14
8	13	10
9	11	16
10	14	13
11	12	14
12	16	17

datos<- data.frame(
  Estudiante = c( 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12),
  x = c( 17, 13, 12, 14, 15, 8, 9, 13, 11, 14, 12, 16),
  y = c( 15, 13, 8, 17, 16, 9, 14, 10, 16, 13, 14, 17)
) 

# Llamamos función
cor(datos$x, datos$y)

## [1] 0.5031258

9.2 Coeficiente Spearman

Si una o ambas variables que estamos comparando son de escala ordinal, el coeficiente apropiado es el de Spearman.

rankings <- data.frame(
  Cafe.A = c(7, 6, 4, 5, 8, 7, 10, 3, 9, 2),
  Cafe.B = c(5, 4, 5, 6, 10, 7, 9, 2, 8, 1)
)

# Llamamos función
cor(rankings$Cafe.A, rankings$Cafe.B, method = "spearman")

## [1] 0.875

9.3 Visualización de datos categóricos

El paquete vcd proporciona una variedad de métodos para visualizar datos categóricos multivariados, inspirados en la maravillosa “Visualización de datos categóricos” de Michael Friendly. Aquí se describen gráficos de asociación y mosaico extendidos. Cada uno proporciona un método para visualizar datos complejos y evaluar las desviaciones de un modelo de independencia específico:

library(vcd)
mosaic(HairEyeColor, shade=TRUE, legend=TRUE)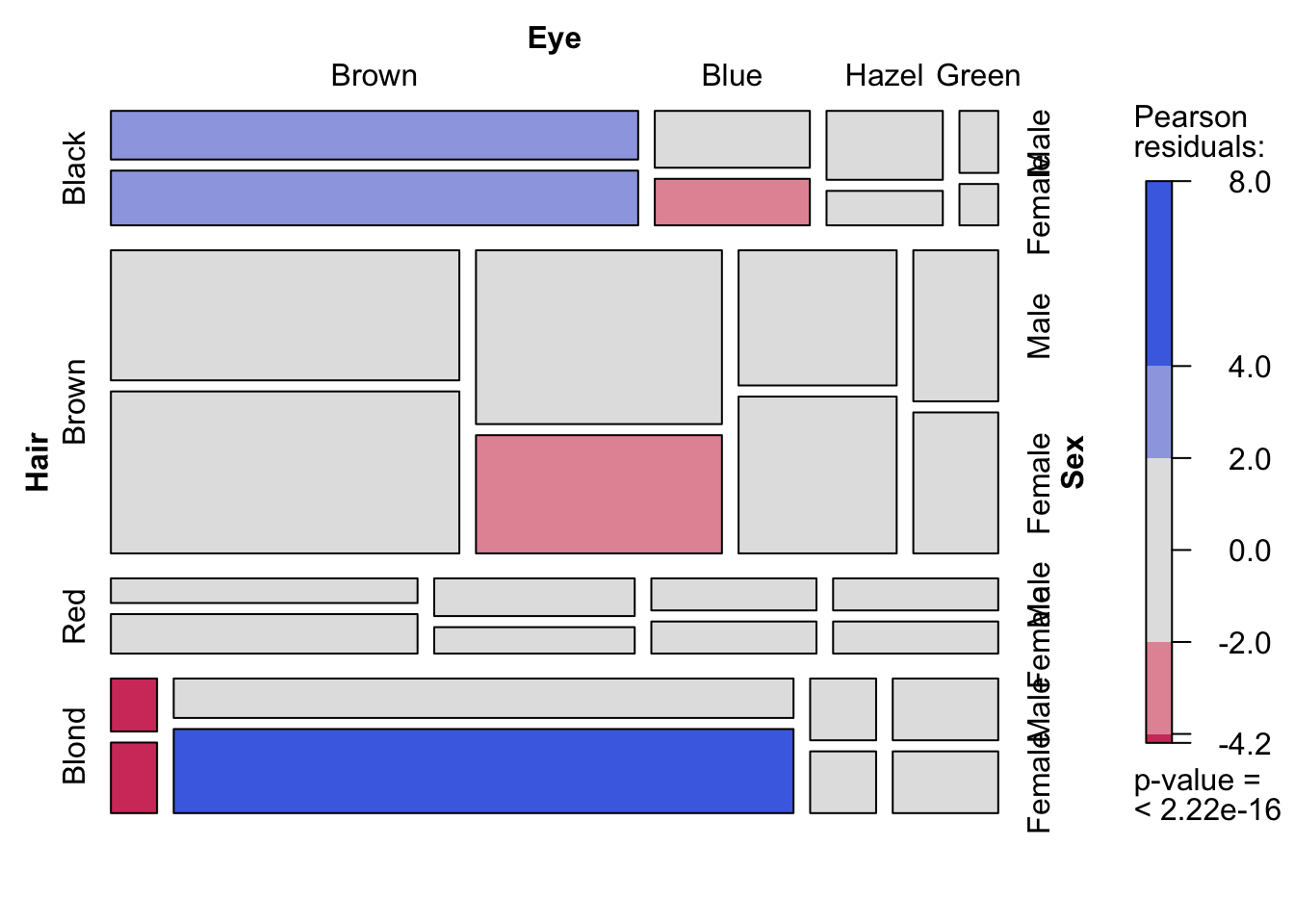

9.4 Mosaico

Es una representación visual de la asociación entre dos o más variables categóricas.

Un diagrama de mosaico es una visualización proporcional al área de las frecuencias observadas, compuesta de mosaicos (correspondientes a las celdas en la tabla de contigencias) creados por divisiones recursivas verticales y horizontales de un rectángulo. El área de cada mosaico es proporcional a la entrada de celda correspondiente.

• Vamos a trabajar:

Descargue los datos de:

DATOS

titanic <- read.csv("Titanic.csv")
mosaic(~ PClass + Sex, data = titanic)

Se puede con tres variables:

titanic <- read_csv("Titanic.csv")
 mosaic(~ PClass + Sex + Survived, data = titanic)

Se le puede poner color:

mosaic(~ PClass + Sex, data = titanic,
       main = "Datos del Titanic", shade = TRUE, legend = TRUE)

O un gráfico de asociación:

assoc(~ PClass + Sex, data = titanic,
       main = "Datos del Titanic", shade = TRUE, legend = TRUE)

Note que los valores de los coeficientes de Pearson, si se ve rojito, es asociación negativa. Por ejemplo, entre female y 3rd tiene correlación negativa. La correlación entre male y 3rd es casi cero, por eso sale gris.