7 ANOVA
Comparar medias en una situación en la que hay más de dos grupos.
En ANOVA unidireccional, los datos se organizan en varios grupos basados en una sola variable de agrupación (también llamada variable factorial).
7.1 Hipótesis de la prueba ANOVA:
- Hipótesis nula: las medias de los diferentes grupos son las mismas
- Hipótesis alternativa: Al menos una media muestral no es igual a las demás.
Tenga en cuenta que, si solo tiene dos grupos, puede usar la prueba t. En este caso, la prueba F y la prueba t son equivalentes
7.2 Supuestos de la prueba ANOVA
Aquí describimos el requisito de la prueba ANOVA. La prueba ANOVA se puede aplicar solo cuando:
Las observaciones se obtienen de forma independiente y aleatoria de la población definida por los niveles de los factores
Los datos de cada nivel de factor se distribuyen normalmente. Estas poblaciones normales tienen una variación común.
my_data <- PlantGrowth
head(my_data)## weight group
## 1 4.17 ctrl
## 2 5.58 ctrl
## 3 5.18 ctrl
## 4 6.11 ctrl
## 5 4.50 ctrl
## 6 4.61 ctrlPara ver los diferentes grupos a comparar, puede utilizar la función level
my_data <- PlantGrowth
levels(my_data$group)## [1] "ctrl" "trt1" "trt2"Si los niveles no están automáticamente en el orden correcto, reordenarlos de la siguiente manera:
my_data <- PlantGrowth
my_data$group <- ordered(my_data$group,
levels = c("ctrl", "trt1", "trt2"))Una buena manera de saber que tan diferentes son los grupos es por medio de los boxplot. Es un análisis descriptivo, se puede ver que tan difernetes son las medias entre los grupos.
my_data <- PlantGrowth
boxplot(weight ~ group, data = my_data,
xlab = "Treatment", ylab = "Weight",
frame = FALSE, col = c("#00AFBB", "#E7B800", "#FC4E07"))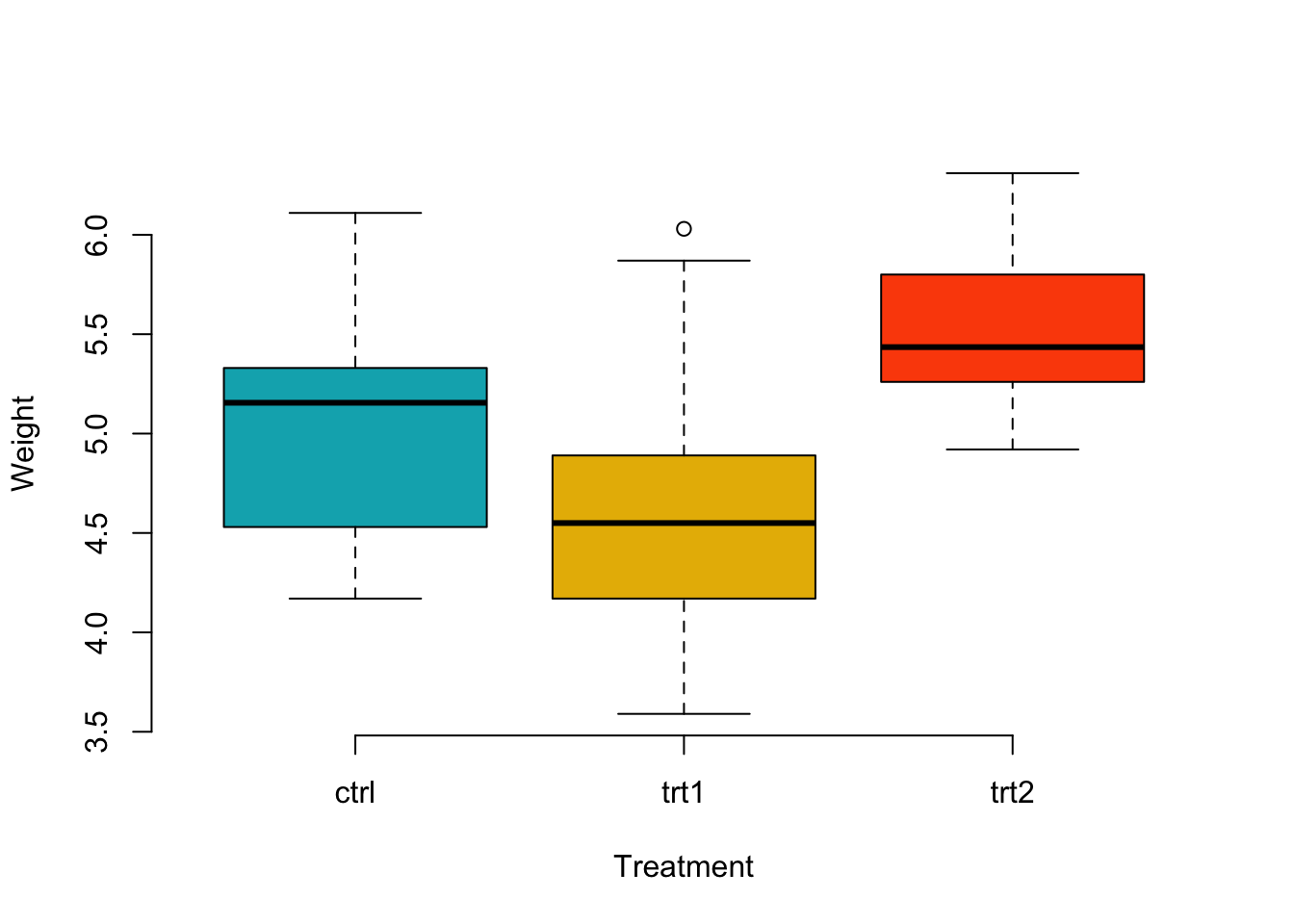
Vamos a aprender a dibujar unos mas bonitos con el paquete ggpubr. Intentelo en su computador.
install.packages("ggpubr")my_data <- PlantGrowth
levels(my_data$group)
library("ggpubr")
ggboxplot(my_data, x = "group", y = "weight",
color = "group", palette = c("#00AFBB", "#E7B800", "#FC4E07"), #estos son colores
order = c("ctrl", "trt1", "trt2"),
ylab = "Weight", xlab = "Treatment")my_data <- PlantGrowth
library("ggpubr")
ggline(my_data, x = "group", y = "weight",
add = c("mean_se", "jitter"),
order = c("ctrl", "trt1", "trt2"),
ylab = "Weight", xlab = "Treatment")7.3 Calcular la prueba ANOVA unidireccional
Queremos saber si existe alguna diferencia significativa entre los pesos medios de las plantas en las 3 condiciones experimentales.
La función R aov() se puede utilizar para responder a esta pregunta. La función summary.aov() se utiliza para resumir el modelo de análisis de varianza.
my_data <- PlantGrowth
res.aov <- aov(weight ~ group, data = my_data)
summary(res.aov)## Df Sum Sq Mean Sq F value Pr(>F)
## group 2 3.766 1.8832 4.846 0.0159 *
## Residuals 27 10.492 0.3886
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La salida incluye el valor de las columnas F y Pr (> F) correspondientes al valor p de la prueba.
7.4 Comparación múltiple por pares entre las medias de los grupos
En la prueba ANOVA de una vía, un valor p significativo indica que algunas de las medias del grupo son diferentes, pero no sabemos qué pares de grupos son diferentes.
Es posible realizar múltiples comparaciones por pares para determinar si la diferencia media entre pares específicos de grupos es estadísticamente significativa.
7.4.1 Comparaciones múltiples por pares de Tukey
Como la prueba ANOVA es significativa, podemos calcular TukeyHSD (Tukey Honest Significant Differences, función R: TukeyHSD ()) para realizar múltiples comparaciones por pares entre las medias de los grupos.
La función TukeyHD() toma el ANOVA ajustado como argumento.
my_data <- PlantGrowth
res.aov <- aov(weight ~ group, data = my_data)
TukeyHSD(res.aov)## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = weight ~ group, data = my_data)
##
## $group
## diff lwr upr p adj
## trt1-ctrl -0.371 -1.0622161 0.3202161 0.3908711
## trt2-ctrl 0.494 -0.1972161 1.1852161 0.1979960
## trt2-trt1 0.865 0.1737839 1.5562161 0.0120064- diff: diferencia entre las medias de los dos grupos
- lwr, upr: el punto final inferior y superior del intervalo de confianza al 95% (predeterminado)
- p adj: valor de p después del ajuste para las comparaciones múltiples.
Se puede ver en la salida que solo la diferencia entre trt2 y trt1 es significativa con un valor p ajustado de 0.012.
7.5 Verifique los supuestos de ANOVA: ¿prueba de validez?
La prueba ANOVA asume que los datos están distribuidos normalmente y la varianza entre grupos es homogénea. Podemos comprobar eso con algunos gráficos de diagnóstico.
7.5.1 Verifique la homogeneidad del supuesto de varianza
La gráfica de residuos versus ajustes se puede usar para verificar la homogeneidad de las varianzas.
En el gráfico siguiente, no hay relaciones evidentes entre los residuos y los valores ajustados (la media de cada grupo), lo cual es bueno. Entonces, podemos asumir la homogeneidad de las varianzas.
my_data <- PlantGrowth
res.aov <- aov(weight ~ group, data = my_data)
plot(res.aov, 1)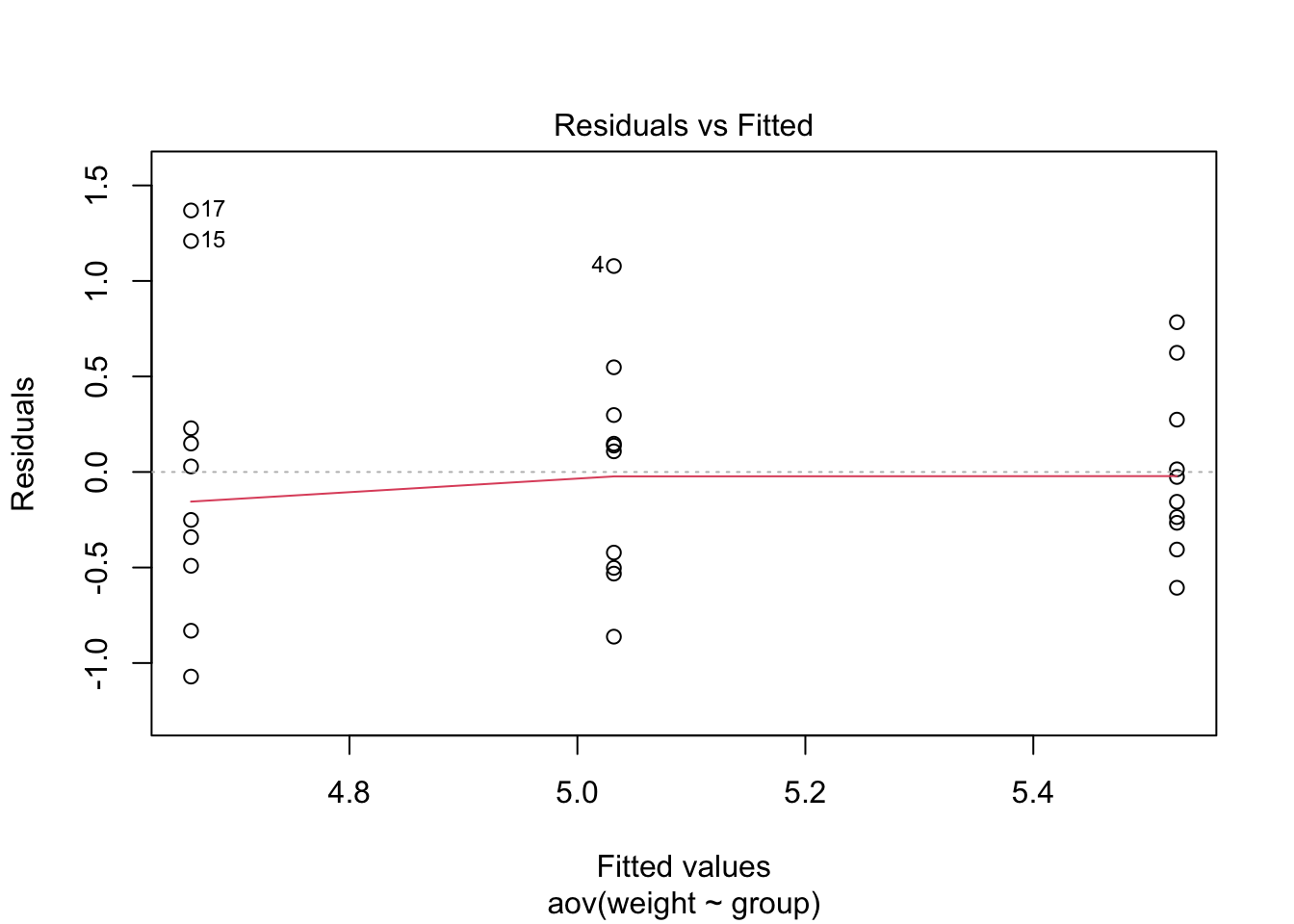
Los puntos 17, 15, 4 se detectan como valores atípicos, lo que puede afectar gravemente a la normalidad y homogeneidad de la varianza. Puede resultar útil eliminar los valores atípicos para cumplir con los supuestos de la prueba.
7.5.2 El supuesto de homogeneidad de la varianza
El ejemplo de las plantas, se puede tener homogeneidad cuando se eliminen los valores atípicos.
¿Cómo hacemos la prueba ANOVA, en una situación en la que se viola el supuesto de homogeneidad de la varianza?
Un procedimiento alternativo (es decir, prueba unidireccional de Welch), que no requiere que se hayan implementado los supuestos en la función oneway.test().
Prueba ANOVA sin suposición de varianzas iguales:
my_data <- PlantGrowth
oneway.test(weight ~ group, data = my_data)##
## One-way analysis of means (not assuming equal variances)
##
## data: weight and group
## F = 5.181, num df = 2.000, denom df = 17.128, p-value = 0.01739En este caso, el valor p se interpreta igual. Así,podemos concluir que existen diferencias significativas.
7.5.3 Verifique el supuesto de normalidad
Gráfico de normalidad de los residuos. En el gráfico siguiente, los cuantiles de los residuos se representan frente a los cuantiles de la distribución normal. También se traza una línea de referencia de 45 grados.
La gráfica de probabilidad normal de residuos se utiliza para verificar el supuesto de que los residuos están distribuidos normalmente. Debe seguir aproximadamente una línea recta.
my_data <- PlantGrowth
res.aov <- aov(weight ~ group, data = my_data)
plot(res.aov, 2)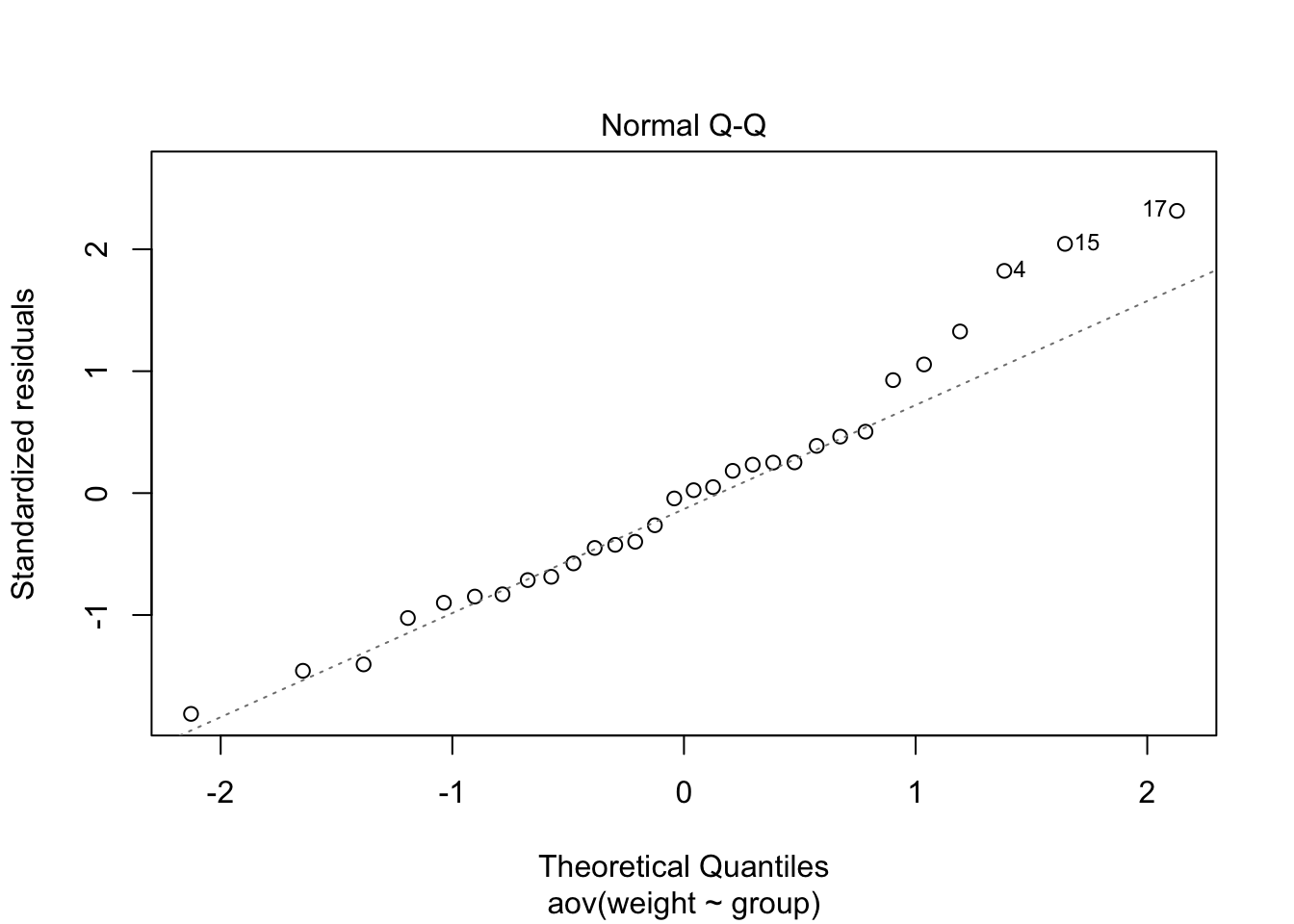
Como todos los puntos caen aproximadamente a lo largo de esta línea de referencia, podemos asumir la normalidad.
La conclusión anterior está respaldada por la prueba de Shapiro-Wilk sobre los residuos de ANOVA (W = 0,96, p = 0,6) que no encuentra indicios de que se viole la normalidad:
my_data <- PlantGrowth
res.aov <- aov(weight ~ group, data = my_data)
aov_residuals <- residuals(object = res.aov )
# pruebaShapiro-Wilk
shapiro.test(x = aov_residuals )##
## Shapiro-Wilk normality test
##
## data: aov_residuals
## W = 0.96607, p-value = 0.4379