10 Regresión lineal
Después de leer este capítulo, podrá:
- Comprender el concepto de modelo.
- Describir dos formas en las que se derivan los coeficientes de regresión.
- Estimar y visualizar un modelo de regresión usando “R.”
- Interpretar coeficientes de regresión y estadísticas en el contexto de problemas del mundo real.
- Utilizar un modelo de regresión para realizar predicciones.
10.1 Modelo
Consideremos un ejemplo simple de cómo la velocidad de un automóvil afecta su distancia de frenado, es decir, qué tan lejos viaja antes de detenerse. Para examinar esta relación, usaremos el conjunto de datos cars que es un conjunto de datos predeterminadoR. Por lo tanto, no necesitamos cargar un paquete primero; está disponible de inmediato.
Para echar un primer vistazo a los datos, puede usar la función View () dentro de RStudio.
View(cars)También podríamos echar un vistazo a los nombres de las variables, la dimensión del marco de datos y algunas observaciones de muestra con str ().
str(cars)## 'data.frame': 50 obs. of 2 variables:
## $ speed: num 4 4 7 7 8 9 10 10 10 11 ...
## $ dist : num 2 10 4 22 16 10 18 26 34 17 ...Como hemos visto antes con los marcos de datos, hay una serie de funciones adicionales para acceder directamente a parte de esta información.
dim(cars)## [1] 50 2nrow(cars)## [1] 50ncol(cars)## [1] 2Aparte de los dos nombres de variables y el número de observaciones, estos datos siguen siendo solo un montón de números, por lo que probablemente deberíamos obtener algo de contexto.
?carsAl leer la documentación, aprendemos que se trata de datos recopilados durante la década de 1920 sobre la velocidad de los automóviles y la distancia resultante que tarda el automóvil en detenerse. La tarea interesante aquí es determinar qué tan lejos viaja un automóvil antes de detenerse, cuando viaja a una cierta velocidad. Entonces, primero trazaremos la distancia de frenado contra la velocidad.
plot(dist ~ speed, data = cars,
xlab = "Speed (in Miles Per Hour)",
ylab = "Stopping Distance (in Feet)",
main = "Stopping Distance vs Speed",
pch = 20,
cex = 2,
col = "grey")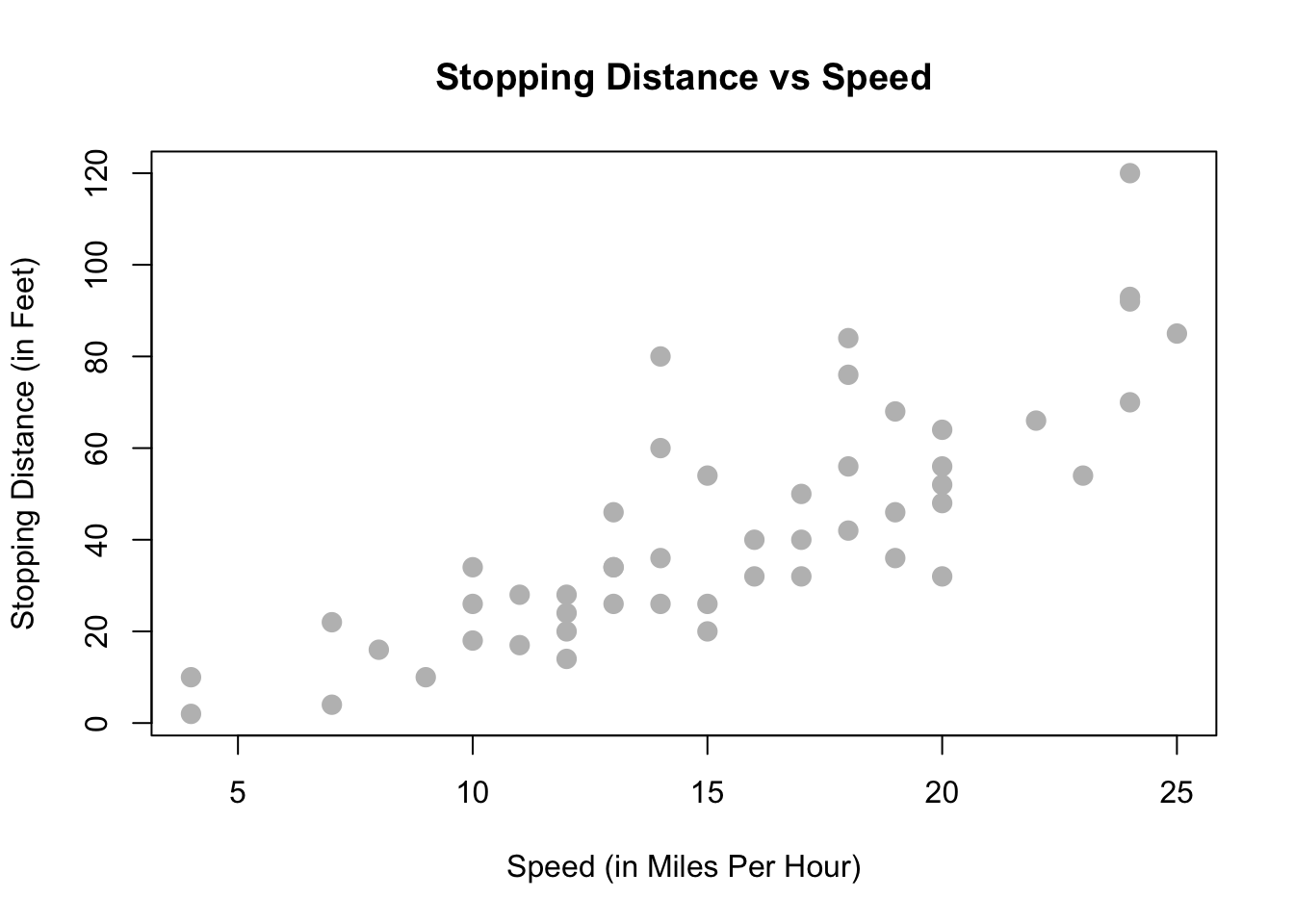
Definamos ahora algo de terminología. Tenemos pares de datos, \((x_i, y_i)\), para \(i = 1, 2, \ldots n\), donde \(n\) es el tamaño de muestra del conjunto de datos.
Usamos \(i\) como índice, simplemente como notación. Usamos \(x_i\) como la variable predictor (explicativa). La variable predictora se utiliza para ayudar a * predecir * o explicar la respuesta (objetivo, resultado) variable, \(y_i\).
En el ejemplo de cars, estamos interesados en usar la variable predictoraspeed para predecir y explicar la variable de respuesta dist.
En términos generales, nos gustaría modelar la relación entre \(X\) y \(Y\) utilizando la formula:
\[ Y = f(X) + \epsilon. \]
La función \(f\) describe la relación funcional entre las dos variables, y el término \(\epsilon\) se usa para dar cuenta del error. Esto indica que si ingresamos un valor dado de \(X\) como entrada, nuestra salida es un valor de \(Y\), dentro de un cierto rango de error. Puedes pensar en esto de varias maneras:
- Respuesta = Predicción + Error
- Respuesta = Señal + Ruido
- Respuesta = Modelo + Inexplicable
- Respuesta = determinista + aleatoria
- Respuesta = Explicable + Inexplicable
¿Qué tipo de función deberíamos usar para \(f(X)\) para los datos de cars?
Podríamos intentar modelar los datos con una línea horizontal. Es decir, el modelo para \(y\) no depende del valor de \(x\). (Alguna función \(f(X) = c\).) En el gráfico siguiente, vemos que esto no parece funcionar muy bien. Muchos de los puntos de datos están muy lejos de la línea naranja que representa \(c\). Este es un ejemplo de desajuste. La solución obvia es hacer que la función \(f (X)\) realmente dependa de \(x\).
plot(dist ~ speed, data = cars,
xlab = "Speed (in Miles Per Hour)",
ylab = "Stopping Distance (in Feet)",
main = "Stopping Distance vs Speed",
pch = 20,
cex = 2,
col = "grey")
underfit_model = lm(dist ~ 1, data = cars)
abline(underfit_model, lwd = 3, col = "darkorange")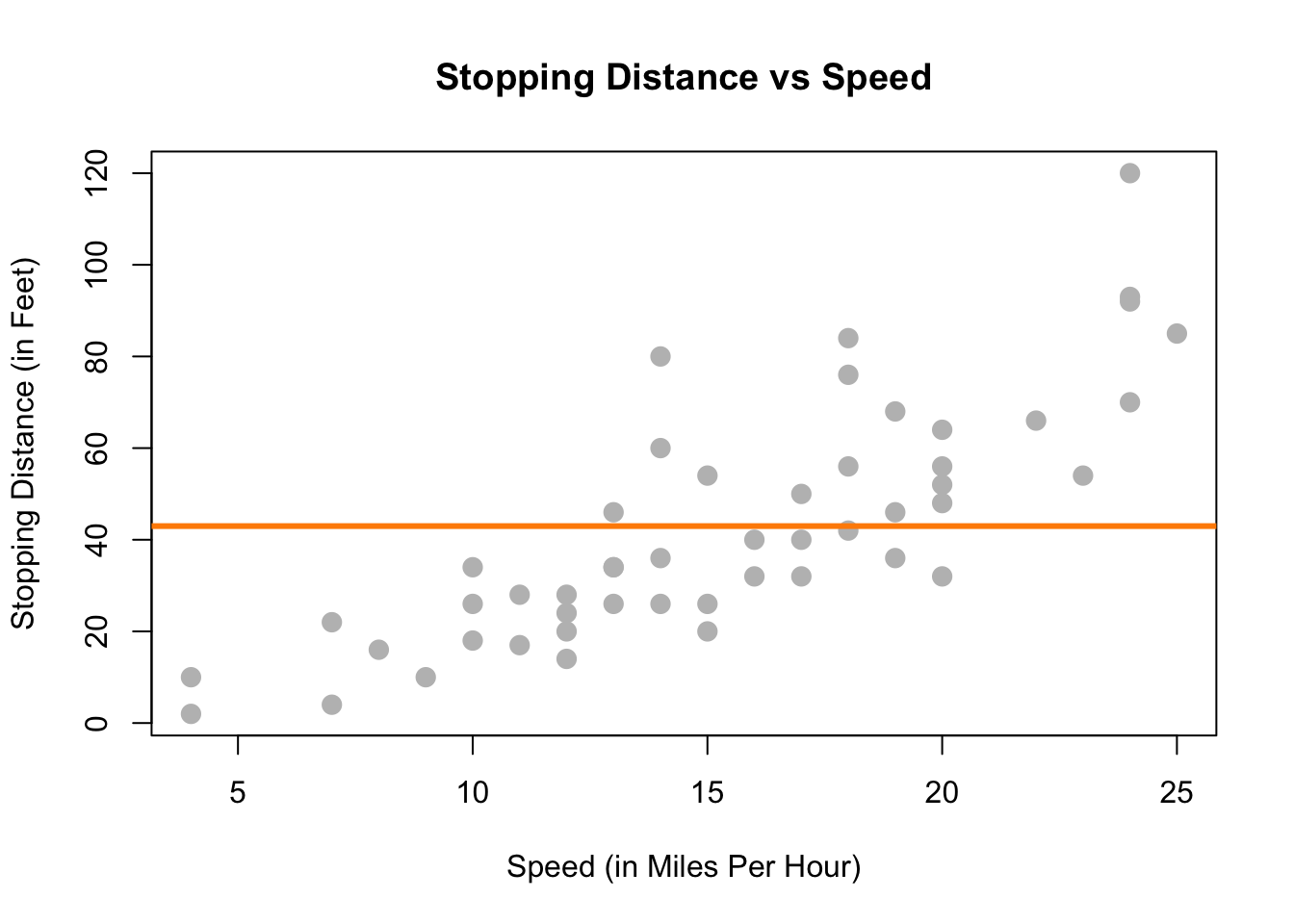
También podríamos intentar modelar los datos con una función muy “ondulada” que intenta atravesar tantos puntos de datos como sea posible. Esto tampoco parece funcionar muy bien. ¡La distancia de frenado para una velocidad de 5 mph no debería estar fuera de la tabla! (Incluso en 1920). Este es un ejemplo de sobreajuste. (Tenga en cuenta que en este ejemplo ninguna función pasará por todos los puntos, ya que hay algunos valores \(x\) que tienen varios valores posibles \(y\) en los datos).
overfit_model = lm(dist ~ poly(speed, 18), data = cars)
x = seq(-10, 50, length.out = 200)
plot(dist ~ speed, data = cars,
xlab = "Speed (in Miles Per Hour)",
ylab = "Stopping Distance (in Feet)",
main = "Stopping Distance vs Speed",
pch = 20,
cex = 2,
col = "grey")
lines(x, predict(overfit_model, data.frame(speed = x)), lwd = 2, col = "darkorange")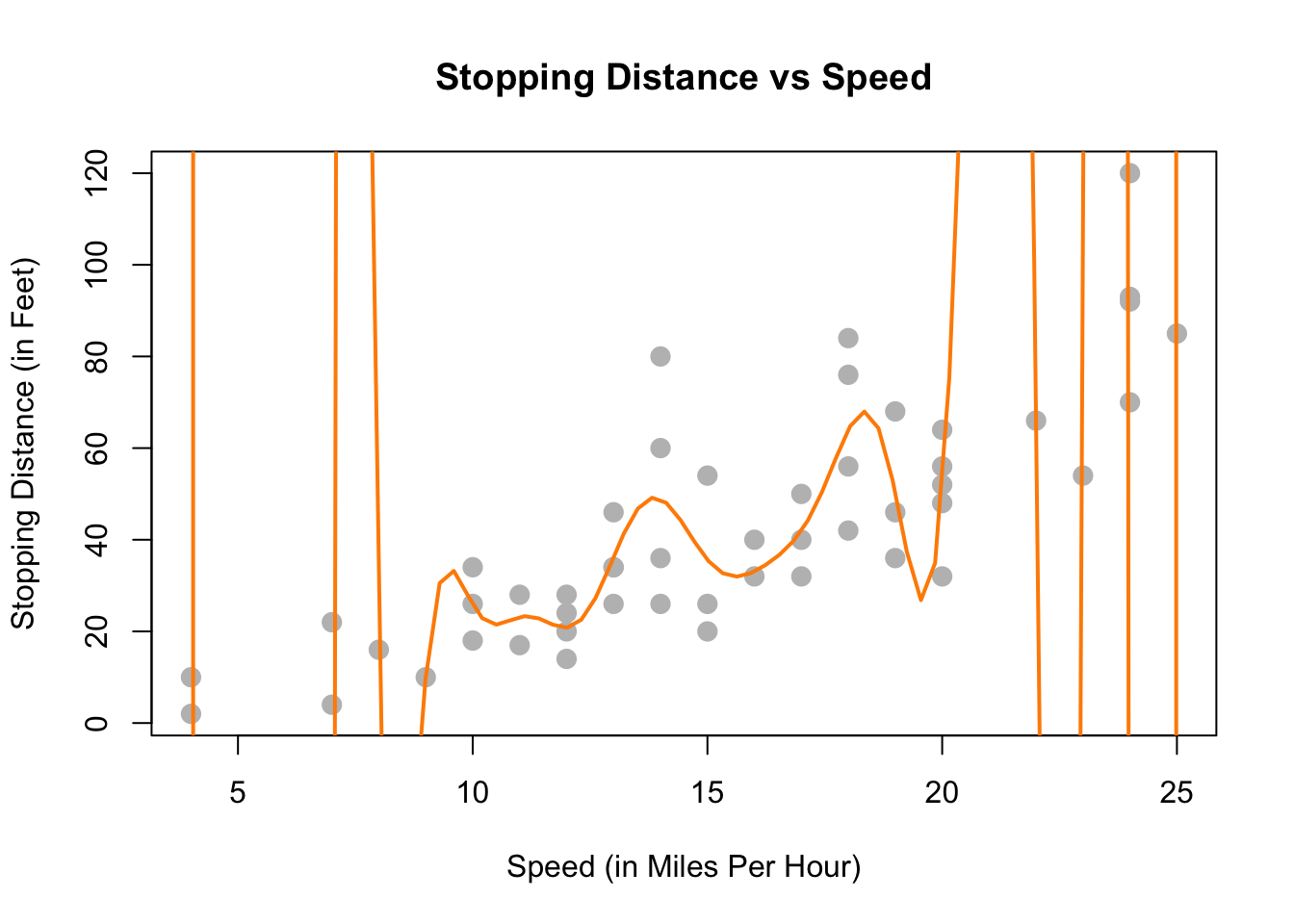
Por último, podríamos intentar modelar los datos con una línea bien elegida en lugar de uno de los dos extremos intentados anteriormente. La línea del gráfico siguiente parece resumir bastante bien la relación entre la distancia de frenado y la velocidad. A medida que aumenta la velocidad, aumenta la distancia necesaria para detenerse. Todavía hay alguna variación en esta línea, pero parece capturar la tendencia general.
stop_dist_model = lm(dist ~ speed, data = cars)
plot(dist ~ speed, data = cars,
xlab = "Speed (in Miles Per Hour)",
ylab = "Stopping Distance (in Feet)",
main = "Stopping Distance vs Speed",
pch = 20,
cex = 2,
col = "grey")
abline(stop_dist_model, lwd = 3, col = "darkorange")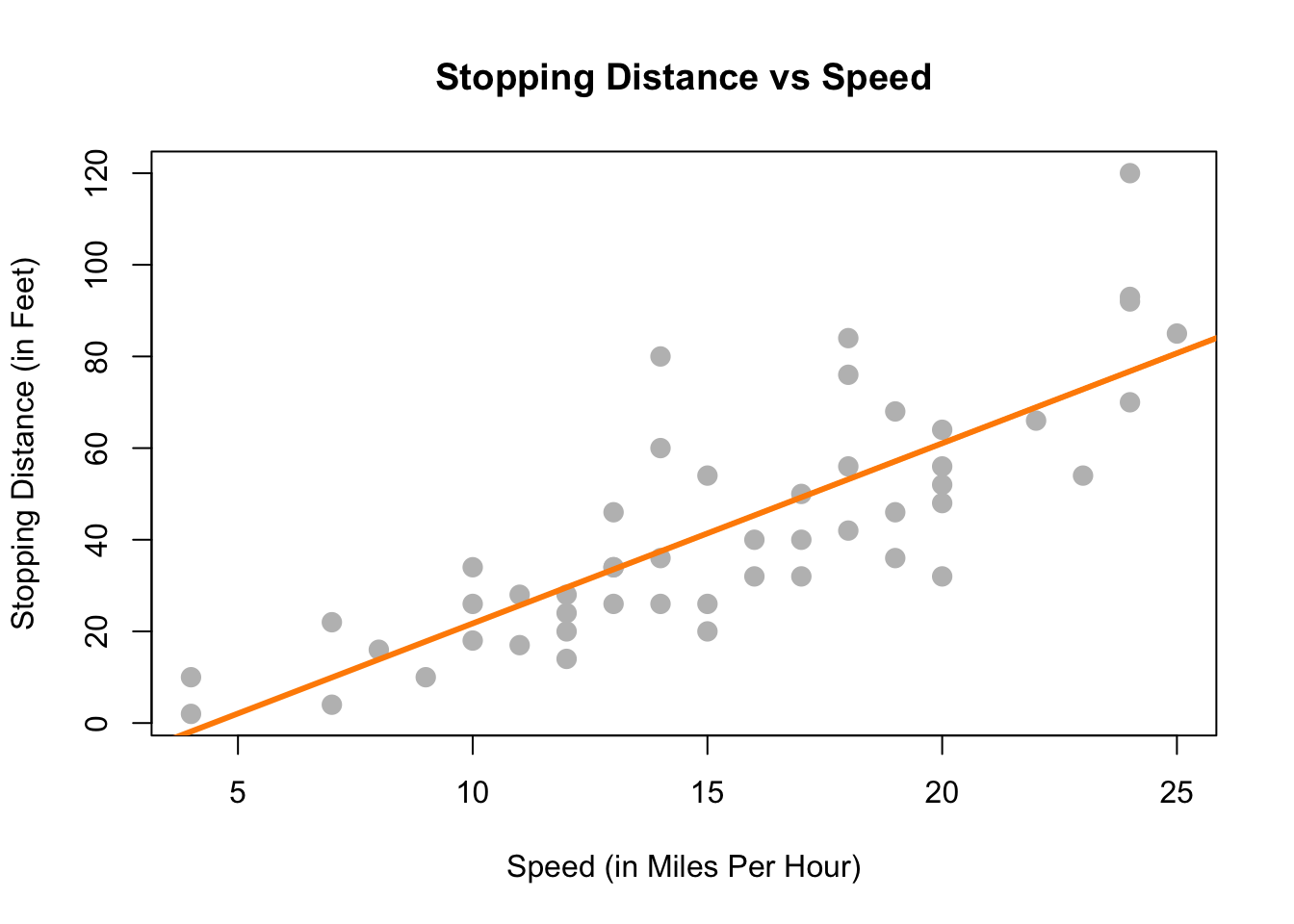
Con esto en mente, nos gustaría restringir nuestra elección de \(f(X)\) a funciones lineales de \(X\). Escribiremos nuestro modelo usando \(\beta_1\) para la pendiente y \(\beta_0\) para la intersección,
\[ Y = \beta_0 + \beta_1 X + \epsilon. \]
10.1.1 Modelo de regresión lineal
Ahora definimos lo que llamaremos el modelo de regresión lineal simple,
\[ Y_i = \beta_0 + \beta_1 x_i + \epsilon_i \]
donde,
\[ \epsilon_i \sim N(0, \sigma^2). \]
A menudo, hablamos directamente sobre las suposiciones que hace este modelo. Se pueden acortar inteligentemente a LINE.
- L inear. La relación entre \(Y\) y \(x\) es lineal, de la forma \(\beta_0 + \beta_1 x\).
- I independiente. Los errores \(\epsilon\) son independientes.
- N ormal. Los errores \(\epsilon\) se distribuyen normalmente. Ese es el “error” alrededor de la línea sigue una distribución normal.
- E qual Varianza. En cada valor de \(x\), la varianza de \(Y\) es la misma, \(\sigma^2\).
También asumimos que los valores de \(x\) son fijos, es decir, no aleatorios. No hacemos una suposición distributiva acerca de la variable predictora.
Como nota al margen, a menudo nos referiremos a la regresión lineal simple como SLR. Alguna explicación del nombre SLR:
- Simple se refiere al hecho de que estamos usando una única variable predictora. Posteriormente usaremos múltiples variables predictoras.
- Lineal nos dice que nuestro modelo para \(Y\) es una combinación lineal de los predictores \(X\). (En este caso solo uno.) Ahora mismo, esto siempre da como resultado un modelo que es una línea, pero más adelante veremos cómo no siempre es así.
- Regresión simplemente significa que estamos intentando medir la relación entre una variable de respuesta \(y\) (una o más) variables predictoras. En el caso de SLR, tanto la respuesta como el predictor son variables numéricas.
10.2 La función lm
El comando lm () se usa para ajustar modelos lineales que en realidad representan una clase más amplia de modelos que la regresión lineal simple, pero usaremos SLR como nuestra primera demostración de lm (). La función lm () será una de nuestras herramientas más utilizadas, por lo que es posible que desee echar un vistazo a la documentación usando ? Lm. Notará que hay mucha información allí, pero comenzaremos con lo más básico. Esta es la documentación a la que querrá volver a menudo.
Continuaremos usando los datos de cars, y esencialmente usaremos la funciónlm ()para verificar el trabajo que habíamos hecho anteriormente.
stop_dist_model = lm(dist ~ speed, data = cars)Esta línea de código se ajusta a nuestro primer modelo lineal. La sintaxis debería resultar familiar. Usamos la sintaxis dist ~ speed para decirle aR que nos gustaría modelar la variable de respuesta dist como una función lineal de la variable predictoraspeed. En general, debería pensar en la sintaxis como “respuesta ~ predictor.” El argumento data = cars le dice aR que las variables dist yspeed son del conjunto de datos cars. Luego almacenamos este resultado en una variable stop_dist_model.
La variable stop_dist_model ahora contiene una gran cantidad de información, y ahora veremos cómo extraer y usar esa información. Lo primero que haremos es simplemente generar lo que esté almacenado inmediatamente en la variable stop_dist_model.
stop_dist_model = lm(dist ~ speed, data = cars)
stop_dist_model##
## Call:
## lm(formula = dist ~ speed, data = cars)
##
## Coefficients:
## (Intercept) speed
## -17.579 3.932Vemos que primero nos dice la fórmula que ingresamos en R, que eslm (fórmula = dist ~ velocidad, datos = autos). También vemos los coeficientes del modelo:
stop_dist_model = lm(dist ~ speed, data = cars)
stop_dist_model$coefficients## (Intercept) speed
## -17.579095 3.932409A continuación, sería bueno agregar la línea ajustada al diagrama de dispersión. Para hacerlo usaremos la función ʻabline () `.
stop_dist_model = lm(dist ~ speed, data = cars)
plot(dist ~ speed, data = cars,
xlab = "Speed (in Miles Per Hour)",
ylab = "Stopping Distance (in Feet)",
main = "Stopping Distance vs Speed",
pch = 20,
cex = 2,
col = "grey")
abline(stop_dist_model, lwd = 3, col = "darkorange")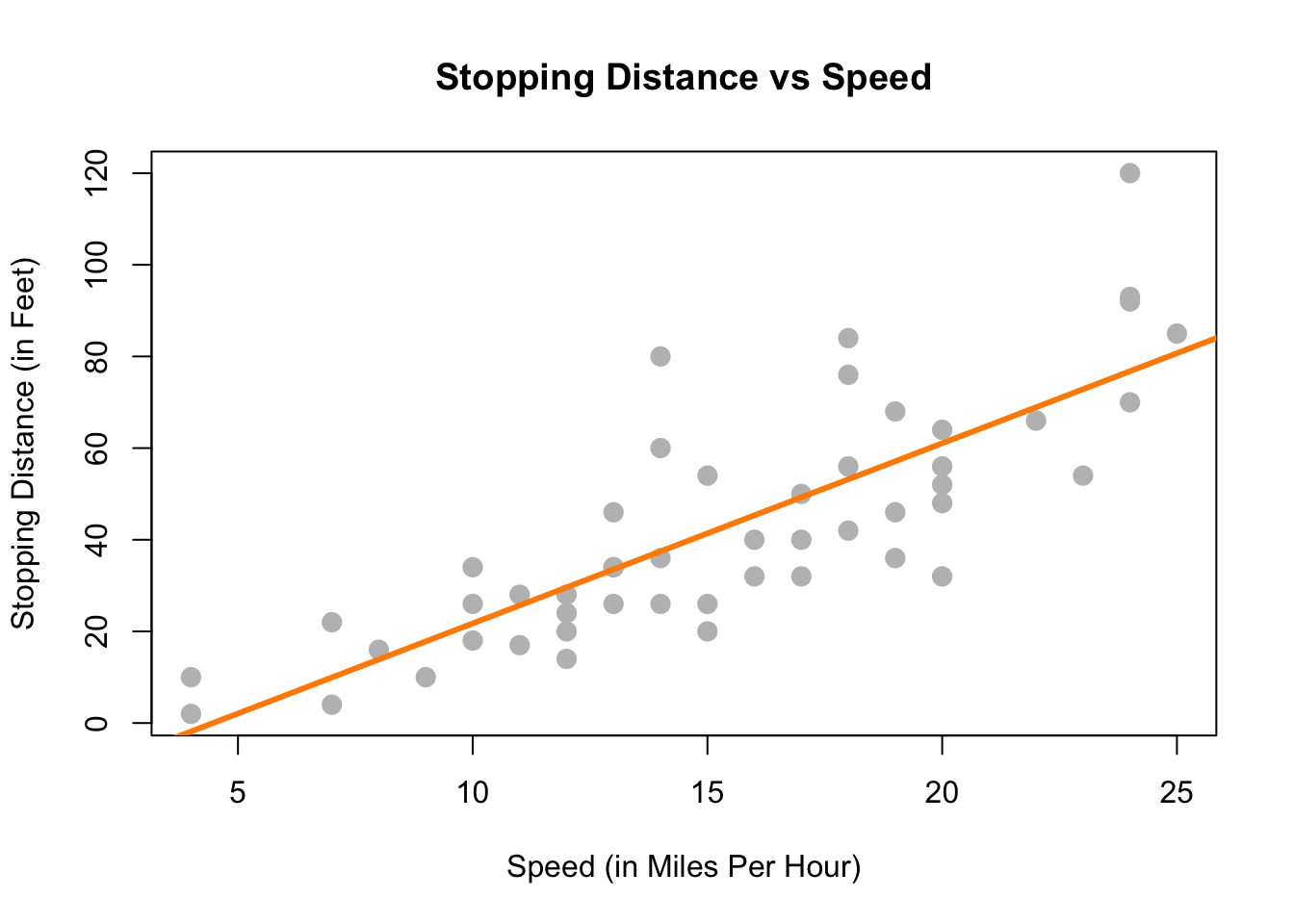
La función ʻabline () se usa para agregar líneas de la forma $a + bx$ a un gráfico. (De ahí ʻab line.) Cuando le damosstop_dist_model como argumento, automáticamente extrae las estimaciones del coeficiente de regresión (\(\hat{\beta} _0\) y \(\hat{\beta} _1\)) y los usa como pendiente e intersección de la línea. Aquí también usamos lwd para modificar el ancho de la línea, así comocol para modificar el color de la línea.
La “cosa” que devuelve la función lm () es en realidad un objeto de la clase lm que es una lista. Los detalles exactos de esto no son importantes a menos que esté seriamente interesado en el funcionamiento interno de R, pero sepa que podemos determinar los nombres de los elementos de la lista usando el comando names ().
stop_dist_model = lm(dist ~ speed, data = cars)
names(stop_dist_model)## [1] "coefficients" "residuals" "effects" "rank" "fitted.values"
## [6] "assign" "qr" "df.residual" "xlevels" "call"
## [11] "terms" "model"Luego podemos usar esta información para, por ejemplo, acceder a los residuos usando el operador $.
stop_dist_model = lm(dist ~ speed, data = cars)
stop_dist_model$residuals## 1 2 3 4 5 6 7 8
## 3.849460 11.849460 -5.947766 12.052234 2.119825 -7.812584 -3.744993 4.255007
## 9 10 11 12 13 14 15 16
## 12.255007 -8.677401 2.322599 -15.609810 -9.609810 -5.609810 -1.609810 -7.542219
## 17 18 19 20 21 22 23 24
## 0.457781 0.457781 12.457781 -11.474628 -1.474628 22.525372 42.525372 -21.407036
## 25 26 27 28 29 30 31 32
## -15.407036 12.592964 -13.339445 -5.339445 -17.271854 -9.271854 0.728146 -11.204263
## 33 34 35 36 37 38 39 40
## 2.795737 22.795737 30.795737 -21.136672 -11.136672 10.863328 -29.069080 -13.069080
## 41 42 43 44 45 46 47 48
## -9.069080 -5.069080 2.930920 -2.933898 -18.866307 -6.798715 15.201285 16.201285
## 49 50
## 43.201285 4.268876Otra forma de acceder a la información almacenada en stop_dist_model son las funcionescoef (),resid ()yfit (). Estos devuelven los coeficientes, los residuos y los valores ajustados, respectivamente.
stop_dist_model = lm(dist ~ speed, data = cars)
coef(stop_dist_model)## (Intercept) speed
## -17.579095 3.932409resid(stop_dist_model)## 1 2 3 4 5 6 7 8
## 3.849460 11.849460 -5.947766 12.052234 2.119825 -7.812584 -3.744993 4.255007
## 9 10 11 12 13 14 15 16
## 12.255007 -8.677401 2.322599 -15.609810 -9.609810 -5.609810 -1.609810 -7.542219
## 17 18 19 20 21 22 23 24
## 0.457781 0.457781 12.457781 -11.474628 -1.474628 22.525372 42.525372 -21.407036
## 25 26 27 28 29 30 31 32
## -15.407036 12.592964 -13.339445 -5.339445 -17.271854 -9.271854 0.728146 -11.204263
## 33 34 35 36 37 38 39 40
## 2.795737 22.795737 30.795737 -21.136672 -11.136672 10.863328 -29.069080 -13.069080
## 41 42 43 44 45 46 47 48
## -9.069080 -5.069080 2.930920 -2.933898 -18.866307 -6.798715 15.201285 16.201285
## 49 50
## 43.201285 4.268876fitted(stop_dist_model)## 1 2 3 4 5 6 7 8 9
## -1.849460 -1.849460 9.947766 9.947766 13.880175 17.812584 21.744993 21.744993 21.744993
## 10 11 12 13 14 15 16 17 18
## 25.677401 25.677401 29.609810 29.609810 29.609810 29.609810 33.542219 33.542219 33.542219
## 19 20 21 22 23 24 25 26 27
## 33.542219 37.474628 37.474628 37.474628 37.474628 41.407036 41.407036 41.407036 45.339445
## 28 29 30 31 32 33 34 35 36
## 45.339445 49.271854 49.271854 49.271854 53.204263 53.204263 53.204263 53.204263 57.136672
## 37 38 39 40 41 42 43 44 45
## 57.136672 57.136672 61.069080 61.069080 61.069080 61.069080 61.069080 68.933898 72.866307
## 46 47 48 49 50
## 76.798715 76.798715 76.798715 76.798715 80.731124Una función R que es útil en muchas situaciones es summary (). Vemos que cuando se llama en nuestro modelo, devuelve una gran cantidad de información. Al final del curso, sabrá para qué se utiliza cada valor aquí. Por ahora, debería notar inmediatamente las estimaciones de los coeficientes y puede reconocer el valor de \(R^2\) que vimos antes.
stop_dist_model = lm(dist ~ speed, data = cars)
summary(stop_dist_model)##
## Call:
## lm(formula = dist ~ speed, data = cars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -29.069 -9.525 -2.272 9.215 43.201
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -17.5791 6.7584 -2.601 0.0123 *
## speed 3.9324 0.4155 9.464 1.49e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.38 on 48 degrees of freedom
## Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
## F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12También podríamos predecir varios valores a la vez.
stop_dist_model = lm(dist ~ speed, data = cars)
predict(stop_dist_model, newdata = data.frame(speed = c(8, 21, 50)))## 1 2 3
## 13.88018 65.00149 179.04134\[ \begin{aligned} \hat{y} &= -17.579, 2 + 3.932, 2 \times 8 = -17.579 + 3.932 * 8, 2 \\ \hat{y} &= -17.579, 2 + 3.932, 2 \times 21 = -17.579 + 3.932 * 21, 2 \\ \hat{y} &= -17.579, 2 + 3.932, 2 \times 50 = -17.579 + 3.932 * 50, 2 \end{aligned} \]
10.3 Las gráficas de diagnóstico
10.3.1 Residuals vs Fitted
Este gráfico muestra si los residuos tienen patrones no lineales. Podría haber una relación no lineal entre las variables predictoras y una variable de resultado y el patrón podría aparecer en este gráfico si el modelo no captura la relación no lineal. Si encuentra residuos igualmente distribuidos alrededor de una línea horizontal sin patrones distintos, es una buena indicación de que no tiene relaciones no lineales. La linea roja debe ser mas o menos recta, no debe estar curvada, entre mas rectica mejor:
stop_dist_model = lm(dist ~ speed, data = cars)
plot(stop_dist_model, which = 1)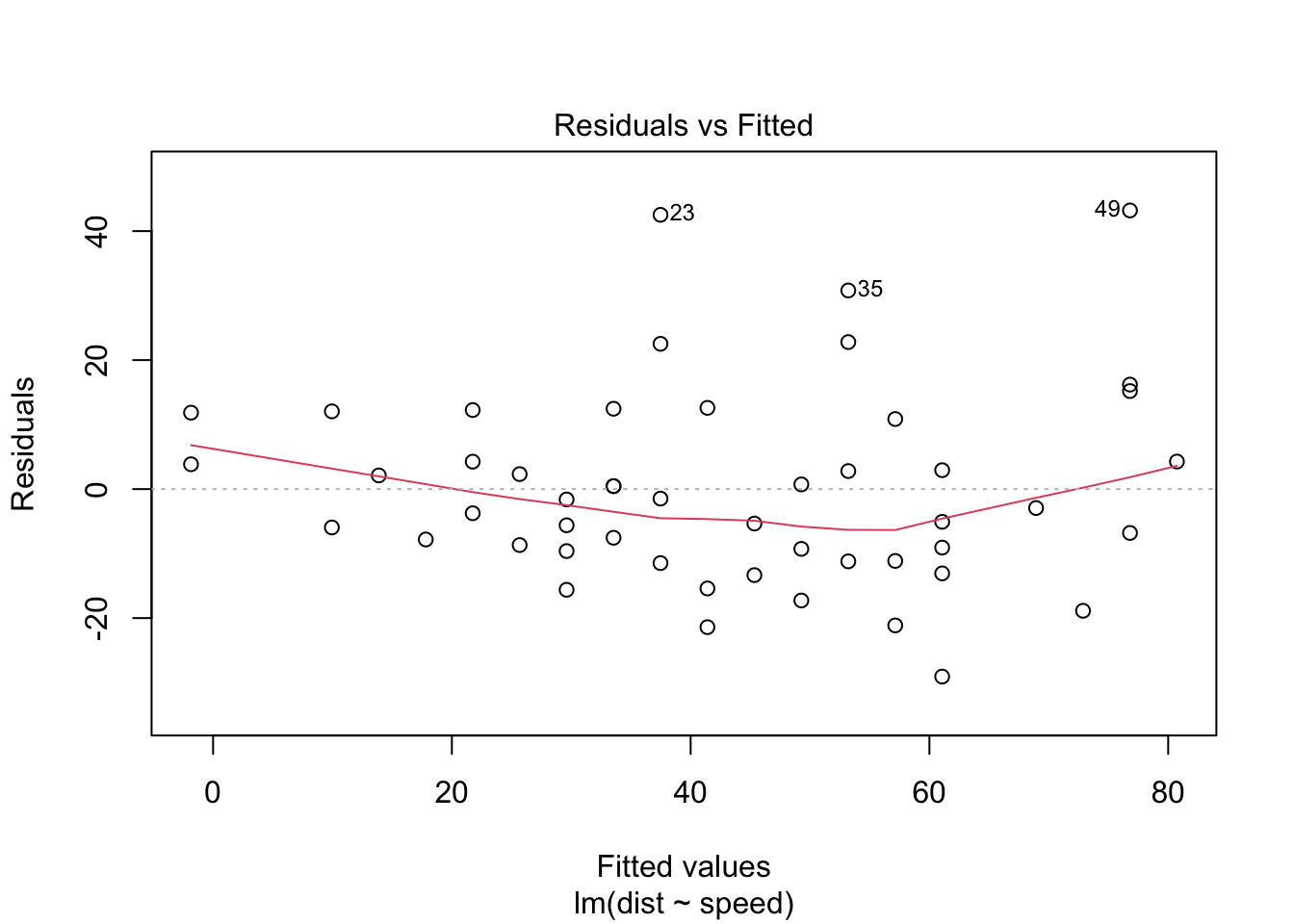
10.3.2 QQ normal
Este gráfico muestra si los residuos se distribuyen normalmente. ¿Los residuos siguen bien una línea recta o se desvían severamente? Es bueno si los residuos están bien alineados en la línea discontinua.
stop_dist_model = lm(dist ~ speed, data = cars)
plot(stop_dist_model, which = 2)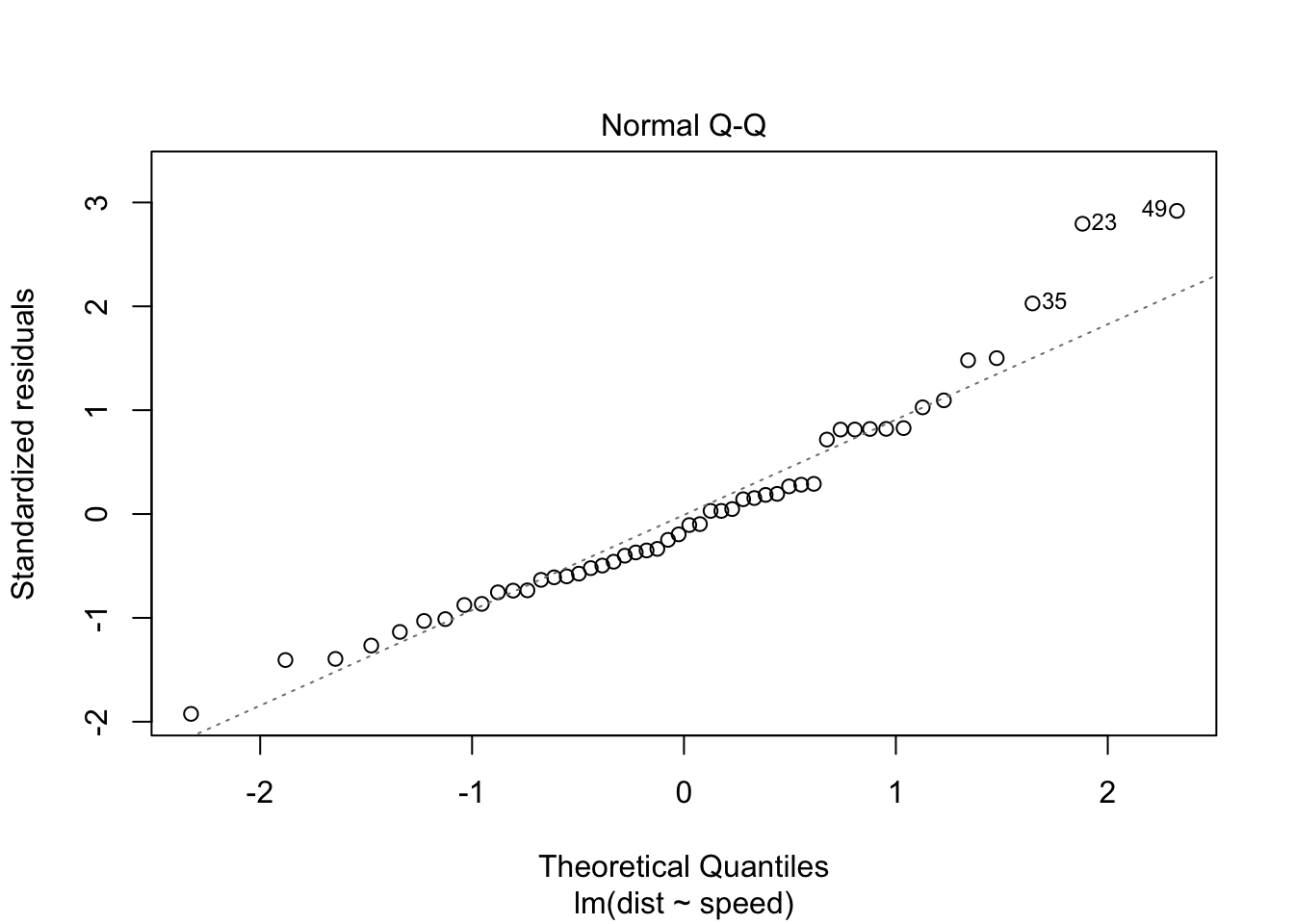
¿Qué piensas? Por supuesto, no serían una línea recta perfecta y esta será su decisión. No es preocupante en este caso.
10.3.3 Scale-Location
También se llama gráfico de ubicación extendida. Este gráfico muestra si los residuos se distribuyen por igual a lo largo de los rangos de predictores. Así es como puede verificar el supuesto de varianza igual (homocedasticidad). Es bueno si ve una línea horizontal con puntos de dispersión iguales (aleatorios).
stop_dist_model = lm(dist ~ speed, data = cars)
plot(stop_dist_model, which = 3)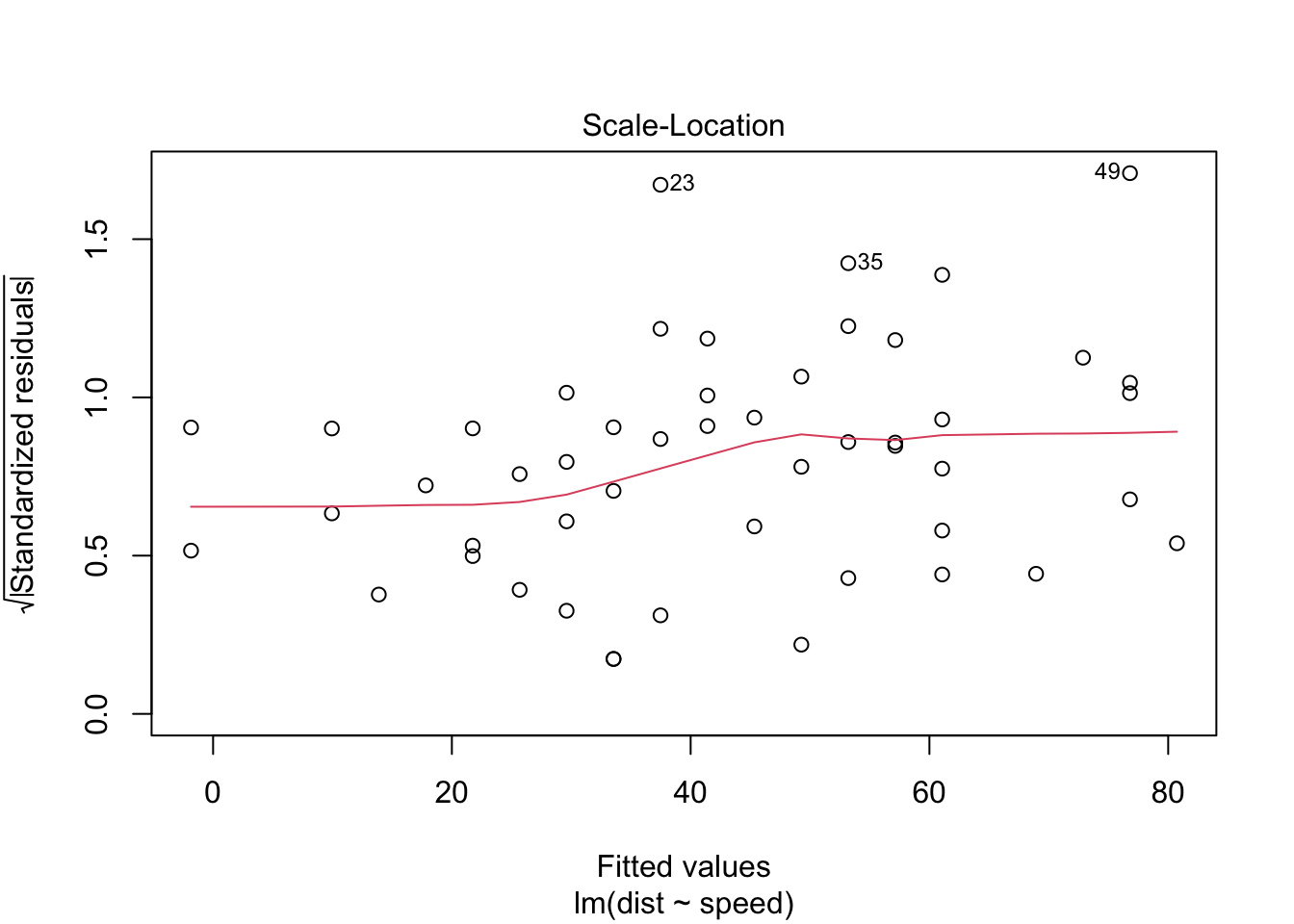
¿Qué piensas? En este caso los residuos aparecen distribuidos aleatoriamente.
10.3.4 Residuals vs Leverage
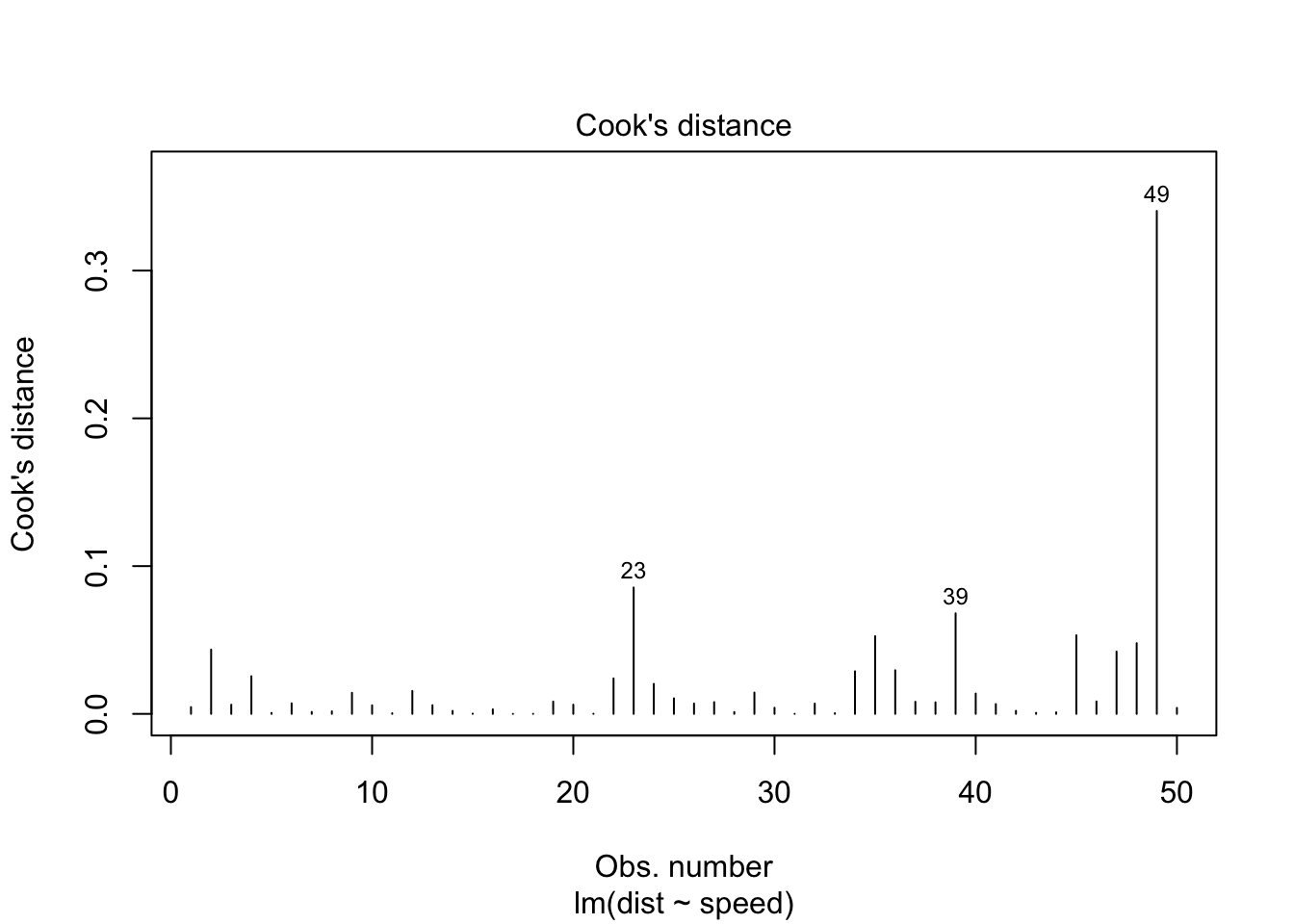
Este gráfico nos ayuda a encontrar casos influyentes. No todos los valores atípicos influyen en el análisis de regresión lineal (independientemente del significado de los valores atípicos). Aunque los datos tienen valores extremos, es posible que no influyan en la determinación de una línea de regresión. Eso significa que los resultados no serían muy diferentes si los incluimos o excluimos del análisis. Siguen la tendencia en la mayoría de los casos y realmente no importan; no son influyentes. Por otro lado, algunos casos pueden ser muy influyentes incluso si parecen estar dentro de un rango razonable de valores. Podrían ser casos extremos contra una línea de regresión y pueden alterar los resultados si los excluimos del análisis. Otra forma de decirlo es que no se llevan bien con la tendencia en la mayoría de los casos.
Los patrones no son relevantes. Estamos atentos a los valores atípicos en la esquina superior derecha o en la esquina inferior derecha. Esos puntos son los lugares donde los casos pueden influir en una línea de regresión. Busque casos fuera de una línea discontinua, la distancia de Cook. Cuando los casos están fuera de la distancia de Cook (lo que significa que tienen puntuaciones de distancia de Cook altas), los casos influyen en los resultados de la regresión. Los resultados de la regresión se alterarán si excluimos esos casos
stop_dist_model = lm(dist ~ speed, data = cars)
plot(stop_dist_model, which = 4)