6 Inferencia Estadística

6.1 Intervalos de Confianza

En este capítulo se muestran las funciones que hay disponibles en R para construir intervalos de confianza para:

la media μ,
la proporción p,
la diferencia de medias $\mu_1-\mu_2$ para muestras independientes y dependientes (o pareadas),
la diferencia de proporciones

6.2 Función t.test

La función t.test se usa para calcular intervalos de confianza para la media y diferencia de medias, con muestras independientes y dependientes (o pareadas). La función y sus argumentos son los siguientes:

t.test(x, y = NULL,
       alternative = c("two.sided", "less", "greater"),
       mu = 0, paired = FALSE, var.equal = FALSE,
       conf.level = 0.95, ...)

Para calcular intervalos de confianza bilaterales para la media a partir de la función t.test es necesario definir 2 argumentos:

x: vector numérico con los datos.
conf.level: nivel de confianza a usar, por defecto es 0.95.

Los demás argumentos se usan cuando se desea obtener intervalos de confianza para diferencia de media con muestras independientes y dependientes (o pareadas).

6.2.1 Intervalo de confianza bilateral para la media μ

Suponga que se quiere obtener un intervalo de confianza bilateral del 90% para la altura promedio de los hombres de la base de datos medidas del cuerpo.

Para calcular el intervalo de confianza, primero se carga la base de datos usando la url apropiada, luego se crea un subconjunto de datos y se aloja en el objeto hombres como sigue a continuación:

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
hombres <- datos[datos$sexo=="Hombre", ]
head(hombres)

##   edad peso altura   sexo muneca biceps
## 1   43 87.3  188.0 Hombre   12.2   35.8
## 2   65 80.0  174.0 Hombre   12.0   35.0
## 3   45 82.3  176.5 Hombre   11.2   38.5
## 4   37 73.6  180.3 Hombre   11.2   32.2
## 5   55 74.1  167.6 Hombre   11.8   32.9
## 6   33 85.9  188.0 Hombre   12.4   38.5

Se revisa que los datos sean simetricos, osea que sigan el supuesto de normalidad:

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
hombres <- datos[datos$sexo=="Hombre", ]

hist(hombres$altura, freq=TRUE,
     main='Histograma para la altura de hombres',
     xlab='Altura (cm)',
     ylab='Frecuencia')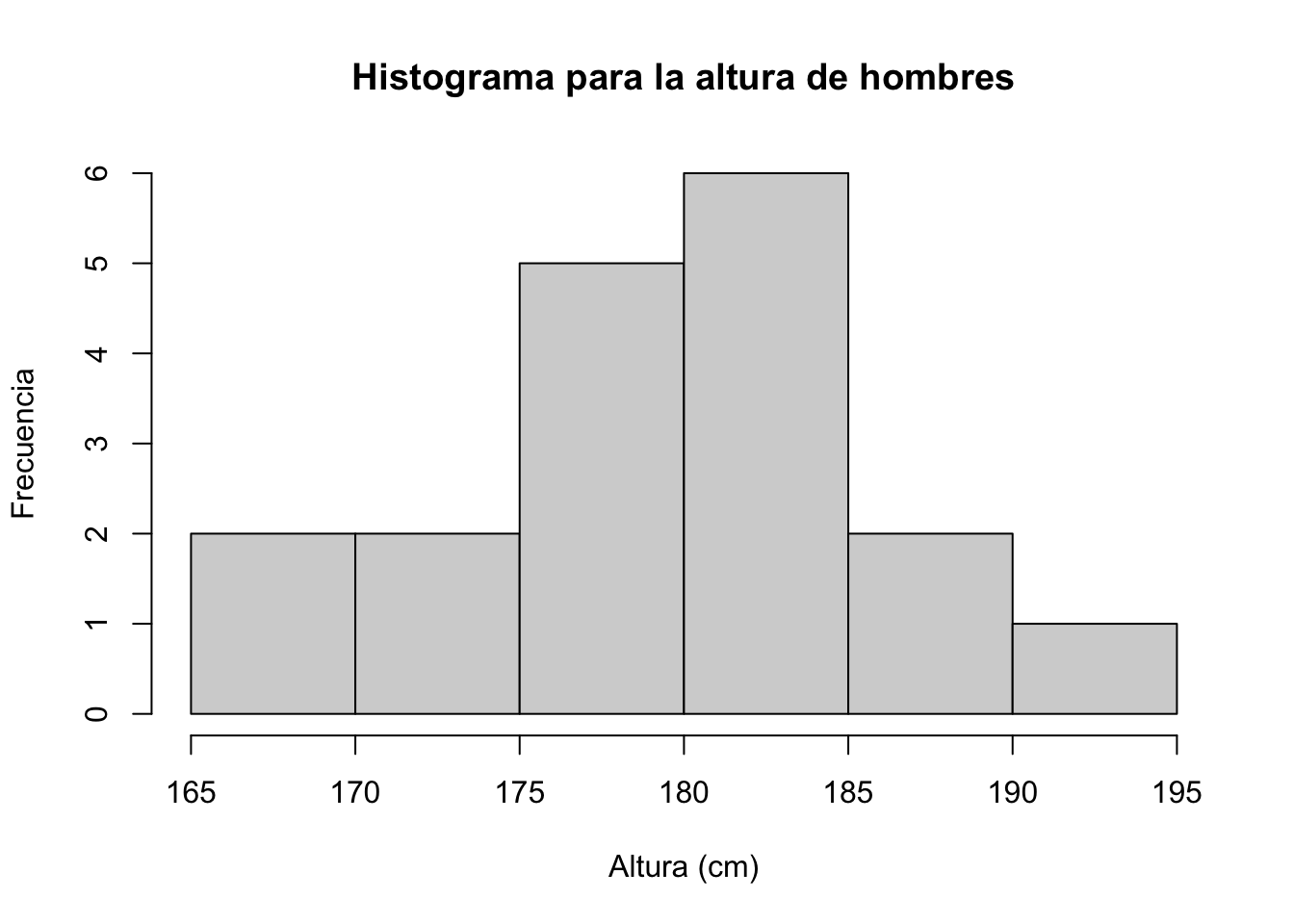

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
hombres <- datos[datos$sexo=="Hombre", ]

t.test(x=hombres$altura, conf.level=0.90)$conf.int

## [1] 176.4384 181.7172
## attr(,"conf.level")
## [1] 0.9

A partir del resultado obtenido se puede concluir, con un nivel de confianza del 90%, que la altura promedio de los estudiantes hombres se encuentra entre 176.4 cm y 181.7 cm.

6.2.2 Ejercicio

Con los datos de DIETA, calcule el intervalo de confianza:

t.test(x=dat$DIETA, conf.level=0.90)$conf.int

6.2.3 Intervalo de confianza bilateral para la diferencia de medias (μ 1 − μ2) de muestras independientes.

Para construir intervalos de confianza bilaterales para la diferencia de medias (μ 1 − μ2) de muestras independientes se usa la función t.test y es necesario definir 5 argumentos:

x: vector numérico con la información de la muestra 1,
y: vector numérico con la información de la muestra 2,
paired=FALSE: indica que el intervalo de confianza se hará para muestras independientes, en el caso de que sean dependientes (o pareadas) este argumento será paired=TRUE,
var.equal=FALSE: indica que las varianzas son desconocidas y diferentes, si la varianzas se pueden considerar iguales se coloca var.equal=TRUE.
conf.level: nivel de confianza.

Ejemplo

Se quiere saber si existe diferencia estadísticamente significativa entre las alturas de los hombres y las mujeres. Para responder esto se va a construir un intervalo de confianza del
$95\%$ para la diferencia de las altura promedio de los hombres y de las mujeres $(\mu_{hombres}-\mu_{mujeres})$

Para construir el intervalo de confianza, primero se carga la base de datos usando la url apropiada, luego se crean dos subconjuntos de datos y se alojan en los objetos hombres y mujeres como sigue a continuación:

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
hombres <- datos[datos$sexo=="Hombre", ]
mujeres <- datos[datos$sexo=="Mujer", ]

Como se cumple el supuesto de normalidad se puede usar la función t.test para construir el intervalo de confianza requerido. A continuación se muestra el código en donde se tiene una lista de hombres y mujeres y es de interes encontrar la diferencia entre las alturas. Note como primero se debe identificar el sexo y en el t.test la altura.

url <- 'https://raw.githubusercontent.com/fhernanb/datos/master/medidas_cuerpo'
datos <- read.table(file=url, header=T)
hombres <- datos[datos$sexo=="Hombre", ]
mujeres <- datos[datos$sexo=="Mujer", ]

t.test(x=hombres$altura, y=mujeres$altura,
       paired=FALSE, var.equal=FALSE,
       conf.level = 0.95)$conf.int

## [1] 10.05574 20.03315
## attr(,"conf.level")
## [1] 0.95

A partir del intervalo de confianza anterior se puede concluir, con un nivel de confianza del
$95 \%$, que la altura promedio de los hombres es superior a la altura promedio de las mujeres, ya que el intervalo de confianza NO incluye el cero y por ser positivos sus limites se puede afirmar con un nivel de confianza del $95\%$ que $\mu_{hombres }> \mu_{mujeres}$.

6.2.3.1 Ejercicio

DATOS CANGA25

Con los datos de CANGA25, calcule el intervalo de confianza del $90\%$ para diferencias entre los pesos de hombres y mujeres. Mucho cuidado, normalmente las bases de datos tiene en la variable sexo, por ejemplo, hombres ó mujeres. En el caso 1 y 2, para mujer y hombre, respectivamente. Bueno, con los simbolos $ puede ubicarlos, identificarlos y llamarlos:

cangadat<-read.csv("canga25.csv", sep=";")
hombres <- cangadat[cangadat$sexo=="2", ]
mujeres <- cangadat[cangadat$sexo=="1", ]

6.3 Función prop.test

La función prop.test se usa para calcular intervalos de confianza para proporciones.

6.3.1 Intervalo de confianza bilateral para la proporción p

Para calcular intervalos de confianza bilaterales para la proporción a partir de la función prop.test es necesario definir 3 argumentos:

x considera el conteo de éxitos,
n indica el número de eventos o de forma equivalente corresponde a la longitud de la variable que se quiere analizar,
conf.level corresponde al nivel de confianza.

El gerente de una estación de televisión debe determinar en la ciudad qué porcentaje de casas tienen más de un televisor. Una muestra aleatoria de 500 casas revela que 275 tienen dos o más televisores. ¿Cuál es el intervalo de confianza del 90% para estimar la proporción de todas las casas que tienen dos o más televisores?

prop.test(x=275, n=500, conf.level=0.90)$conf.int

## [1] 0.5122310 0.5872162
## attr(,"conf.level")
## [1] 0.9

A partir del resultado obtenido se puede concluir, con un nivel de confianza del 90%, que la proporción p de casas que tienen dos o más televisores se encuentra entre 0.5122 y 0.5872.

6.3.1.1 Ejercicio:

Con los datos: DATOS DIABETES1

Encontrar el intervalo de confianza del $97\%$ para la proporción de diabéticos. Debe buscar la forma de encontrar la frecuencia de diabeticos. El total de analizados para ambos grupos es 1000 personas.

prop.test(x=200, n=1000, conf.level=0.97)$conf.int

## [1] 0.1735127 0.2293507
## attr(,"conf.level")
## [1] 0.97

6.3.2 Intervalo de confianza bilateral para la diferencia de proporciones (p 1 − p2)

Se quiere determinar si un cambio en el método de fabricación de una piezas ha sido efectivo o no. Para esta comparación se tomaron 2 muestras, una antes y otra después del cambio en el proceso y los resultados obtenidos son los siguientes.

Num piezas	Antes	Después
Defectuosas	75	80
Analizadas	1500	2000

El intervalo de confianza para este ejercicio con nivel de confianza del 90% es:

prop.test(x=c(75, 80), n=c(1500, 2000), conf.level=0.90)$conf.int

## [1] -0.002314573  0.022314573
## attr(,"conf.level")
## [1] 0.9

6.3.2.1 Ejercicio:

Con los datos: DATOS DIABETES1

Encontrar el intervalo de confianza del $90\%$ para la proporción de diabéticos y No diabéticos. Debe buscar la forma de encontrar la frecuencia de cada uno. El total de analizados para ambos grupos es 1000 personas.

 prop.test(x=c(200, 800), n=c(1000, 1000), conf.level=0.90)$conf.int

## [1] -0.630424 -0.569576
## attr(,"conf.level")
## [1] 0.9

Encontrar el intervalo de confianza del $80\%$ para la proporción de Glucosuria y No Glucosuria.

6.4 Pruebas de hipótesis

En este capítulo se muestran las funciones que hay disponibles en R para realizar prueba de hipótesis para:

la media μ,
la diferencia de medias $\mu_1-\mu_2$ para muestras independientes y dependientes (o pareadas),

6.5 Prueba de hipótesis para μ de una población normal

Se utiliza la función t.test vista en la sección anterior. Pero, es necesario definir 4 argumentos:

x vector de datos,
alternative tipo de hipótesis alterna. Los valores disponibles son two.sided cuando la alterna es
≠, less para el caso < y greater para >,
conf.level corresponde al nivel de confianza,
mu el valor que será probado.

6.5.1 Ejemplo

Para verificar si el proceso de llenado de bolsas de café con 500 gramos está operando correctamente se toman aleatoriamente muestras de tamaño diez cada cuatro horas. Una muestra de bolsas está compuesta por las siguientes observaciones: 502, 501, 497, 491, 496, 501, 502, 500, 489, 490.

¿Está el proceso llenando bolsas conforme lo dice la envoltura? Use un nivel de significancia del 5%.

La prueba de hipótesis se puede realizar usando la función t.test por medio del siguiente código.

\[ H_o: \mu =500 gr\\ H_1: \mu \neq 500 gr \]

La prueba de hipótesis se puede realizar usando la función t.test por medio del siguiente código:

contenido <- c(510, 492, 494, 498, 492,
               496, 502, 491, 507, 496) 

t.test(contenido, alternative='two.sided',
       conf.level=0.95, mu=500)

## 
##  One Sample t-test
## 
## data:  contenido
## t = -1.0629, df = 9, p-value = 0.3155
## alternative hypothesis: true mean is not equal to 500
## 95 percent confidence interval:
##  493.1176 502.4824
## sample estimates:
## mean of x 
##     497.8

Como el valor-P es $0.3155$ y mayor que el nivel de significancia 5%, no se rechaza la hipótesis nula, es decir, las evidencias son suficientes para afirmar que el proceso de llenando está cumpliendo con lo impreso en la envoltura.

6.5.2 Ejercicio

DATOS CANGA25

Se presume que el peso de las personas en promedio es de 80 kilos, ¿que tan cierta es esta afirmación? Suponga un nivel del confianza del 95%.

En este punto, ya debieron notar que la salida de la función t.test es:

## 
##  One Sample t-test
## 
## data:  contenido
## t = -1.0629, df = 9, p-value = 0.3155
## alternative hypothesis: true mean is not equal to 500
## 95 percent confidence interval:
##  493.1176 502.4824
## sample estimates:
## mean of x 
##     497.8

y que claramente dice: alternative hypothesis: true mean is not equal to 500, es decir, el mismo me dice cual es la hipótesis alterna. Por tanto, podemos modificar el código para indicarle cuando realizar pruebas de una o dos colas:

Si la hipótesis alterna es: $H_1: \mu \neq a$ t.test(cangadat$peso, alternative='two.sided', conf.level=0.95, mu=500)
Si la hipótesis alterna es: $H_1: \mu > a$ t.test(cangadat$peso, alternative="greater", conf.level=0.95, mu=500)
Si la hipótesis alterna es: $H_1: \mu < a$ t.test(cangadat$peso, alternative="less", conf.level=0.95, mu=500)

Con los mismo datos canga25. Se presume que el peso de las personas en promedio pesan mas de 10 kilos, ¿que tan cierta es esta afirmación?. Pruebe con un nivel de confianza de 95%.

t.test(cangadat$peso, alternative='greater',  conf.level=0.95, mu=10)

## 
##  One Sample t-test
## 
## data:  cangadat$peso
## t = 20.554, df = 24, p-value < 2.2e-16
## alternative hypothesis: true mean is greater than 10
## 95 percent confidence interval:
##  63.68566      Inf
## sample estimates:
## mean of x 
##     68.56

6.6 Prueba de hipótesis para la diferencia de medias pareadas

Se utiliza la función t.test vista en la sección anterior. El análisis es casi el mismo que el anterior, pero es necesario definir 5 argumentos:

x vector de datos del grupo 1,
y vector de datos del grupo 2,
alternative: tipo de hipótesis alterna. Los valores disponibles son two.sided cuando la alterna es
≠, less para el caso < y greater para >,
conf.level corresponde al nivel de confianza,
mu en este caso, siempre es 0, pues estamos probando siempre para la hipotesis nula:

\[ H_o: \mu_1-\mu_2 = 0\\ \] Y con respecto a la alterna, depende de lo que se desea estudiar.

6.6.1 Ejemplo

Diez individuos participaron de programa para perder peso corporal por medio de una dieta. Los voluntarios fueron pesados antes y después de haber participado del programa y los datos en libras aparecen abajo. ¿Hay evidencia que soporte la afirmación de la dieta disminuye el peso medio de los participantes? Usar nivel de significancia del 5%.

Sujeto	001	002	003	004	005	006	007	008	009
Antes	195	213	247	201	187	210	215	246	294
Después	187	195	221	190	175	197	199	221	278

En este problema interesa estudiar el siguiente conjunto de hipótesis.

\[ H_o: \mu_{antes}-\mu_{despues} = 0\\ H_o: \mu_{antes}-\mu_{despues} > 0 \]

Y el código en R es:

antes <- c(195, 213, 247, 201, 187, 210, 215, 246, 294, 310)
despu <- c(187, 195, 221, 190, 175, 197, 199, 221, 278, 285)
t.test(x=antes, y=despu, alternative="greater", mu=0, 
       paired=TRUE, conf.level=0.95)

## 
##  Paired t-test
## 
## data:  antes and despu
## t = 8.3843, df = 9, p-value = 7.593e-06
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  13.2832     Inf
## sample estimates:
## mean of the differences 
##                      17

De la prueba se obtiene un valor-P pequeño, por lo tanto, podemos concluir que el peso
$\mu_{antes}$ es mayor que $\mu_{despues}$, en otras palabras, la dieta si ayudó a disminuir el peso corporal.

NOTA: Usen paired=FALSE si los tamaños de los grupos son diferentes, si son iguales ponen paired=TRUE

6.6.2 Ejercicio

DATOS CANGA25

Con los datos de CANGA25, deseo saber si el peso de los hombres es diferente que el de las mujeres. Pruebe esto con un 95%.

cangadat<-read.csv("canga25.csv", sep=";")
hombres <- cangadat[cangadat$sexo=="2", ]
mujeres <- cangadat[cangadat$sexo=="1", ]

¿Cual es el código en R?

t.test(x=hombres$peso, y=mujeres$peso, alternative = "two.side", paired=FALSE, mu=0, conf.level = 0.95)

## 
##  Welch Two Sample t-test
## 
## data:  hombres$peso and mujeres$peso
## t = -1.3182, df = 6.0508, p-value = 0.2351
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -32.127493   9.601177
## sample estimates:
## mean of x mean of y 
##  60.00000  71.26316

¿Cual seria la diferencia en el código si se desea probar que la media del pesos de los hombres es MAYOR que el de las mujeres?

t.test(x=hombres$peso, y=mujeres$peso, alternative = "greater", paired=FALSE, mu=0, conf.level = 0.95)

## 
##  Welch Two Sample t-test
## 
## data:  hombres$peso and mujeres$peso
## t = -1.3182, df = 6.0508, p-value = 0.8824
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  -27.84107       Inf
## sample estimates:
## mean of x mean of y 
##  60.00000  71.26316

6.7 Prueba de hipótesis para proporción p

Para calcular prueba de hipótesis de la proporción a partir de la función prop.test es necesario definir 3 argumentos:

x considera el conteo de éxitos,
n indica el número de eventos o de forma equivalente corresponde a la longitud de la variable que se quiere analizar,
alternative tipo de hipótesis alterna. Los valores disponibles son two.sided cuando la alterna es
≠, less para el caso < y greater para >,
p: valor de referencia de la prueba.
conf.level corresponde al nivel de confianza.

El gerente de una estación de televisión debe determinar en la ciudad qué porcentaje de casas tienen más de un televisor. Una muestra aleatoria de 500 casas revela que 275 tienen dos o más televisores. ¿Con un nivel de confianza del 90%, se puede decir que la proporción es mayor que 0.3?

\[ H_o: p = 0.3\\ H_1: p > 0.3 \]

 prop.test(x=275, n=500, alternative="greater", conf.level=0.90, p=0.3)

## 
##  1-sample proportions test with continuity correction
## 
## data:  275 out of 500, null probability 0.3
## X-squared = 147.62, df = 1, p-value < 2.2e-16
## alternative hypothesis: true p is greater than 0.3
## 90 percent confidence interval:
##  0.5203674 1.0000000
## sample estimates:
##    p 
## 0.55

A partir del resultado obtenido se puede concluir, con un nivel de confianza del 90%, que la proporción p de casas es mayor que 0.3, ya que el p-valor fue de 2.2e-16.

6.7.0.1 Ejercicio:

Con los datos: DATOS DIABETES1

Si la hipótesis esta escrita de esta forma, donde p es la proporción de diabeticos,

\[ H_o: p = 0.6\\ H_1: p < 0.6 \] ¿Cúal es el código R para responderla?

prop.test(x=200, n=1000, alternative="less", conf.level=0.90)

## 
##  1-sample proportions test with continuity correction
## 
## data:  200 out of 1000, null probability 0.5
## X-squared = 358.8, df = 1, p-value < 2.2e-16
## alternative hypothesis: true p is less than 0.5
## 90 percent confidence interval:
##  0.0000000 0.2172109
## sample estimates:
##   p 
## 0.2

6.8 Prueba de hipótesis para la diferencia de proporción p1-p2

Para realizar pruebas de hipótesis para la proporción se usa la función prop.test y es necesario definir los siguientes argumentos:

x: vector con el conteo de éxitos de las dos muestras,
n: vector con el número de ensayos de las dos muestras,
alternative tipo de hipótesis alterna. Los valores disponibles son two.sided cuando la alterna es
≠, less para el caso < y greater para >,
p: valor de referencia de la prueba.
conf.level: nivel de confianza para reportar el intervalo de confianza asociado (opcional).

Num piezas	Antes	Después
Defectuosas	75	80
Analizadas	1500	2000

Realizar una prueba de hipótesis con un nivel de confianza del 90%.

En este problema interesa estudiar el siguiente conjunto de hipótesis:

\[ H_o: p_{antes}-p_{despues} = 0\\ H_o: p_{antes}-p_{despues} > 0 \] A estas alturas, ya debería poder escribir el código:

prop.test(x=c(75, 80), n=c(1500, 2000),
          alternative='greater', conf.level=0.90)

## 
##  2-sample test for equality of proportions with continuity correction
## 
## data:  c(75, 80) out of c(1500, 2000)
## X-squared = 1.7958, df = 1, p-value = 0.09011
## alternative hypothesis: greater
## 90 percent confidence interval:
##  0.0002765293 1.0000000000
## sample estimates:
## prop 1 prop 2 
##   0.05   0.04