5 Distribuciones de probabilidad

5.1 Distribuciones de probabilidad en R

El paquete stats de R (que se instala por defecto al instalar R, y se carga en memoria siempre que iniciamos sesión) implementa numerosas funciones para la realización de cálculos asociados a distintas distribuciones de probabilidad.

Entre las utilizadas más comúnmente podemos citar:

Distribuciones discretas:

Distribución	Nombre en
Binomial	`binom`
Poisson	`pois`

Distribuciones contínuas:

Distribución	Nombre en R
Uniforme	`unif`
Normal	`norm`

Examinamos algunas de las operaciones básicas asociadas con las distribuciones de probabilidad.
Hay un gran número de distribuciones de probabilidad disponibles, pero sólo observamos unas pocas.
Para obtener una lista completa de las distribuciones disponibles en R puede utilizar el siguiente comando:

help("Distributions")

Para cada distribución hay cuatro comandos. Los comandos para cada distribución están precedidos de una letra para indicar la funcionalidad:

d: devuelve la función de densidad de probabilidad
p: devuelve la función de densidad acumulada
q: returns the inverse cumulative density function (quantiles)
r: devuelve los números generados aleatoriamente

5.2 Distribución binomial

La distribución binomial es una distribución de probabilidad discreta. Describe el resultado de ensayos independientes de $n$ en un experimento. Se supone que cada ensayo tiene sólo dos resultados, ya sea éxito o fracaso. Si la probabilidad de un ensayo exitoso es de $p$, entonces la probabilidad de tener resultados exitosos de $k$ en un experimento de ensayos independientes de $n$ es dada por la probabilidad de la función de masa:

\[ { f(k,n,p) = \mbox{Pr}(X=k)=\binom{n}{k} p^k (1-p)^{n-k}, \quad k=0,1,2,...,n } \]

La función de distribución acumulativa puede expresarse como:

\[ { F(k;n,p) = \mbox{Pr}(X\leq k) = \sum_{i=0}^{k}\binom{n}{i} p^i (1-p)^{n-i} } \]

x <- 0:12
plot(x, dbinom(x, size=25, prob=0.2), xlab="Número de eventos", ylab="Densidad de Probabilidad", main="Distribución Binomial: eventos = 25, Probabilidad de éxito = 0.2", type="h")
points(x, dbinom(x, size=25, prob=0.2), pch=16)
abline(h=0, col="gray")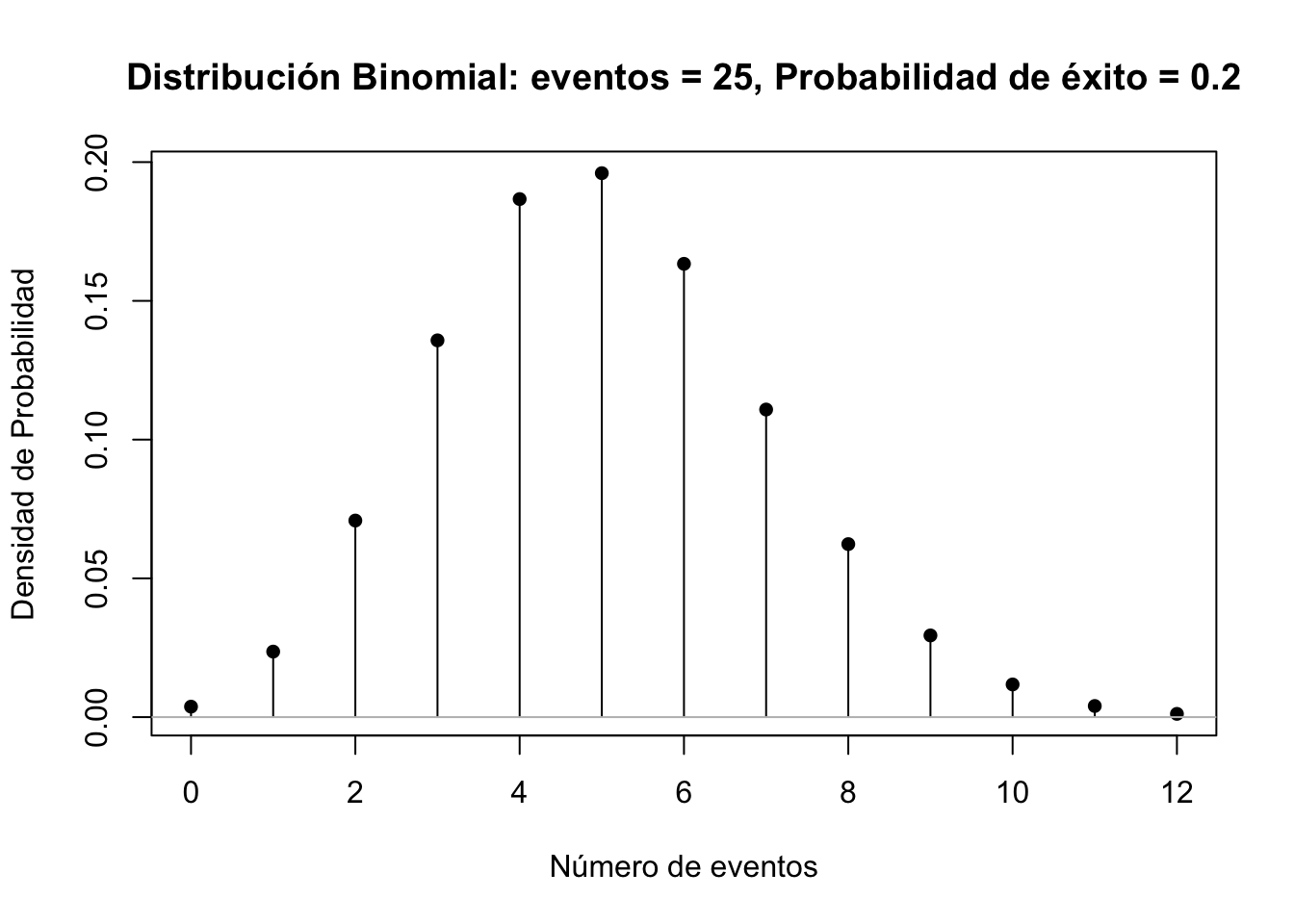

x <- 0:12
x <- rep(x, rep(2, length(x)))
plot(x[-1], pbinom(x, size=25, prob=0.2)[-length(x)], xlab="Número de eventos", ylab="Probabilidad acumulado", main="Distribución Binomial: eventos = 25, Probabilidad de éxito = 0.2", type="l")
abline(h=0, col="gray")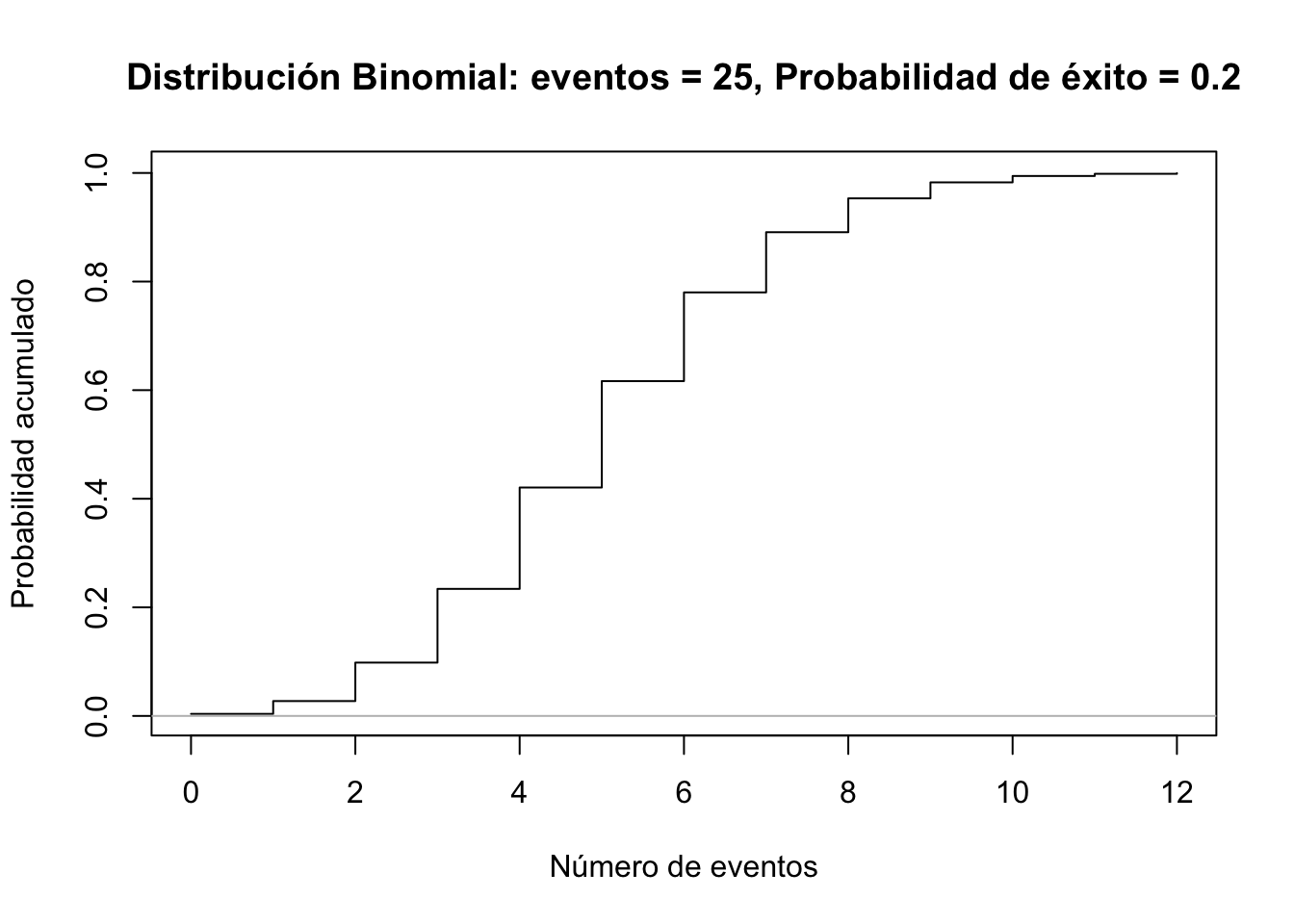

5.2.1 Ejemplo

Suponga que hay doce preguntas de opción múltiple en un examen de matemáticas. Cada pregunta tiene cinco posibles respuestas, y sólo una de ellas es correcta. Encuentre la probabilidad de tener cuatro o menos respuestas correctas si un estudiante intenta responder a cada pregunta al azar.

Solución: Dado que sólo una de cada cinco respuestas posibles es correcta, la probabilidad de responder correctamente una pregunta al azar es de $1/5=0,2$. Podemos encontrar la probabilidad de tener exactamente 4 respuestas correctas por intentos aleatorios de la siguiente manera.

p = 1/5
n = 12
k = 4
dbinom(k,size=n,prob=p)

## [1] 0.1328756

Para encontrar la probabilidad de tener cuatro o menos respuestas correctas mediante intentos aleatorios, aplicamos la función dbinom con k=0,1,2,3,4.

p = 1/5
n = 12
k = 0 
prob0 <- dbinom(k,n,p)
prob0

## [1] 0.06871948

k = 1 
prob1 <- dbinom(k,n,p)
prob1

## [1] 0.2061584

k = 2 
prob2 <- dbinom(k,n,p)
prob2

## [1] 0.2834678

k = 3 
prob3 <- dbinom(k,n,p)
prob3

## [1] 0.2362232

k = 4 
prob4 <- dbinom(k,n,p)
prob4

## [1] 0.1328756

suma<-prob0+prob1+prob2+prob3+prob4
suma

## [1] 0.9274445

o mas fácil con un for:

prob <- NULL
p = 1/5
n = 12
for(k in 0:4){  #aca aprendemos a usar un FOR, traduce para, y lo que hace es que para k=0, k=1, k=2, k=3 y k=4.
prob <- c(prob,dbinom(k,n,p))
prob
}
prob

## [1] 0.06871948 0.20615843 0.28346784 0.23622320 0.13287555

sum(prob)

## [1] 0.9274445

ó simplemente,

p = 1/5
n = 12
sum(dbinom(0:4,n,p))

## [1] 0.9274445

Alternativamente, podemos usar la función de probabilidad acumulada para la distribución binomial pbinom.

p = 1/5
n = 12
pbinom(4,size=n,prob=p)

## [1] 0.9274445

Solución: La probabilidad de que cuatro o menos preguntas sean contestadas correctamente al azar en un cuestionario de opción múltiple de doce preguntas es del 92,7%.

EN CONCLUSION:

Si es: $Pr(X=r)$ se utiliza: dbinom(r, ...).
Si es: $Pr(X\leq r)$ se utiliza: pbinom(r, ...) (Si es $Pr(X<r)$ entonces $Pr(X \leq r-1)$).
Si es: $Pr(X \geq r)$ se utiliza: 1-binom(r, ...) (Por la ley de complemento: $Pr(X \geq r)=1-Pr(X \leq r)$).
lower.tail=TRUE indica que se desea obtener el valor de la función de distribución $P(X<9)$. Si se pusiera lower.tail=FALSE, calcularía $P(X>9)$

5.2.2 Ejercicios:

El departamento de Matemática Aplicada propone un examen de test consistente en 25 cuestiones. Cada cuestión tiene 5 respuestas listadas, siendo correcta sólo una de ellas. Si un estudiante no conoce la respuesta correcta de ninguna cuestión y prueba suerte, queremos saber:

a) ¿Cuál es la probabilidad de responder exactamente 7 respuestas correctas? Para responder a la primera pregunta $Pr(X=7)$:

dbinom(7, size=25, prob=0.2)

## [1] 0.1108419

b) ¿Cuál es la probabilidad de acertar como máximo 9 respuestas?. Se busca $P(X \leq 9)$.

pbinom(9, size=25, prob=0.5)

## [1] 0.1147615

c) Si se aprueba el examen cuando se responden correctamente 13 cuestiones, ¿cuál es la probabilidad de que pase el alumno que ha probado suerte? $Pr(X \geq 13)$:

1-pbinom(12, size=25, prob=0.2)

## [1] 0.000369048

pbinom(12, size=25, prob=0.2, lower.tail = FALSE)

## [1] 0.000369048

5.3 Distribución Poisson

La distribución de Poisson es la distribución de probabilidad de ocurrencias de eventos independientes en un intervalo. Si $\lambda$ es la ocurrencia media por intervalo, entonces la probabilidad de tener ocurrencias $k$ dentro de un intervalo dado es la función de masa de probabilidad dada por:

\[ \mbox{Pr}(\mbox{$k$ eventos en el intervalo}) = \frac{\lambda^k e^{-\lambda}}{k!} \] La para la función de probabilidad acumulativa de Poisson es

\[ P(X\leq x ~|~\lambda ) = \frac{e^{-\lambda} \lambda ^x}{x!}\quad \mbox{para $x=0,1,2,...$} \]

x <- 0:4
plot(x, dpois(x, lambda=0.5), xlab="Número de eventos en tiempo", ylab="Distribución de Probabilidad", main=" Distribución Poisson: Mean = 0.5", type="h")
points(x, dpois(x, lambda=0.5), pch=16)
abline(h=0, col="gray")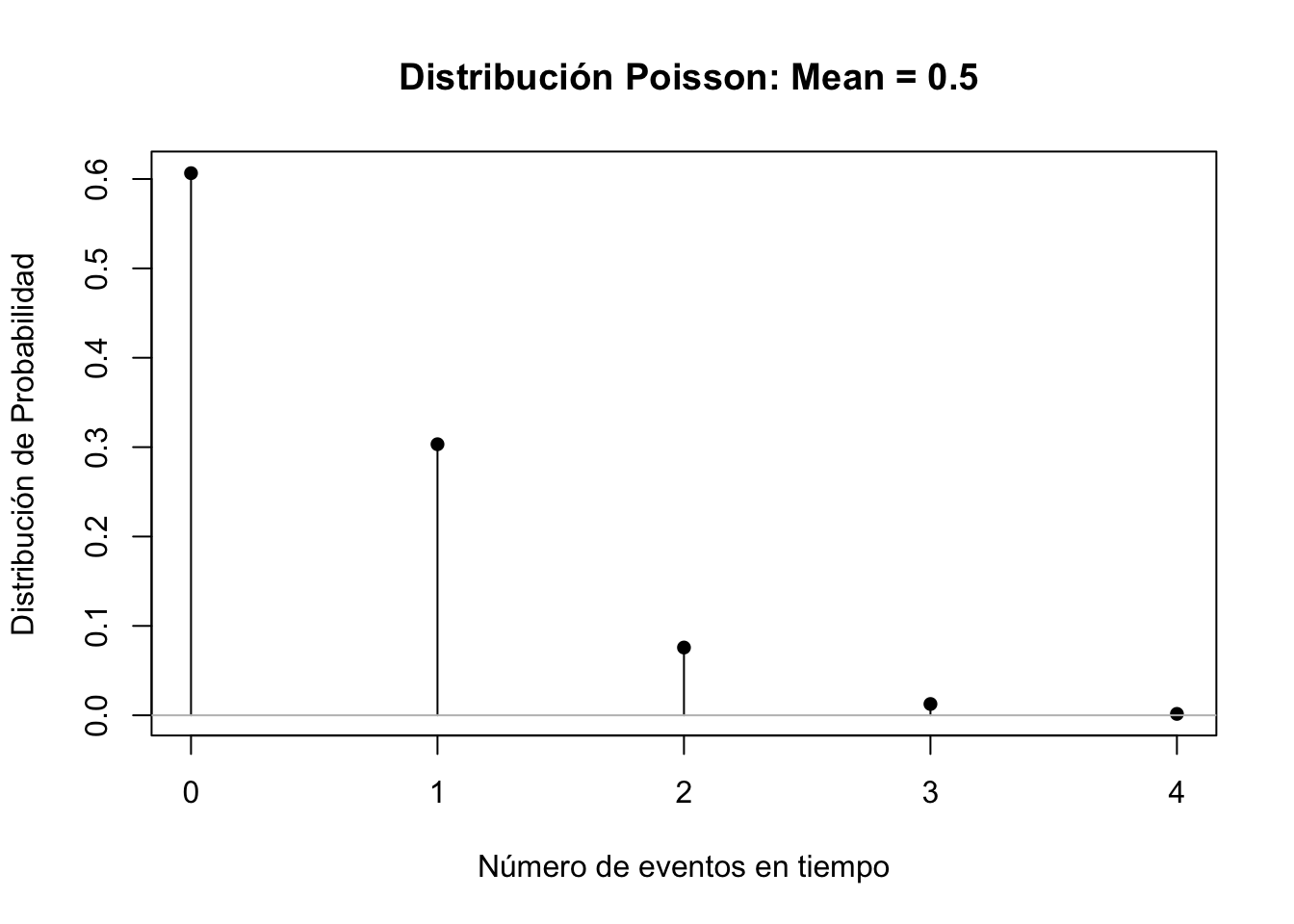

x <- 0:4
x <- rep(x, rep(2, length(x)))
plot(x[-1], ppois(x, lambda=0.5)[-length(x)], xlab="x", ylab="Densidad de Probabilidad",
                main="Distribución Poisson: Mean = 0.5", type="l")
abline(h=0, col="gray")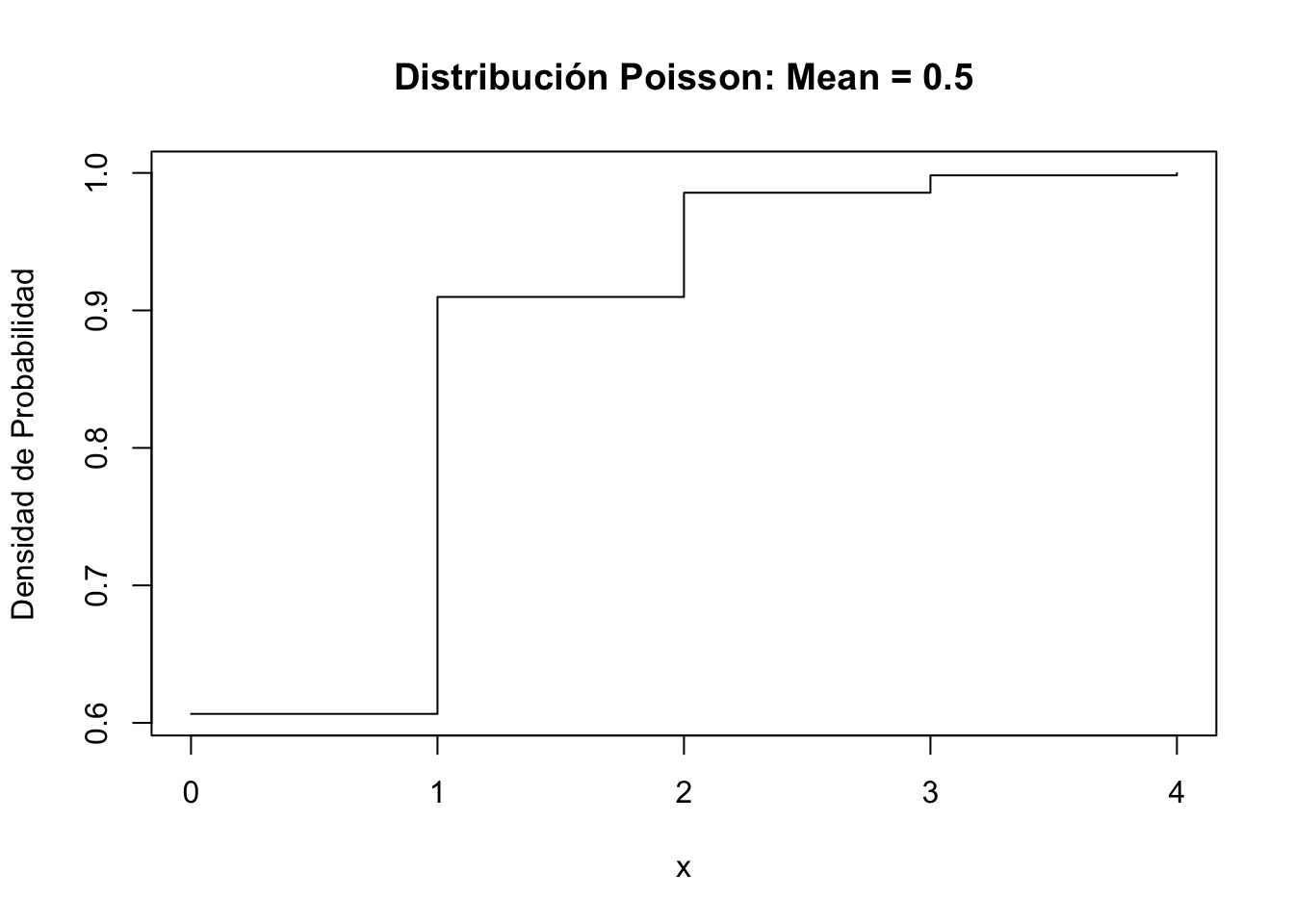

Pregunta:

Supongamos que el número de plantas individuales de una especie dada que esperamos encontrar en un cuadrado de un metro cuadrado sigue la distribución de Poisson con una media de $\lambda=10$
Encuentra la probabilidad de encontrar exactamente 12 plantas por persona.

dpois(12, lambda=10)

## [1] 0.09478033

Pregunta:

Si hay doce coches cruzando un puente por minuto en promedio, encuentre la probabilidad de tener diecisiete o más coches cruzando el puente en un minuto en particular.

¿Cuál es el código en R para calcular esta probabilidad?

ppois(17, lambda=12)

## [1] 0.9370337

5.3.1 Ejercicios:

La centralita telefónica de un hotel recibe un nº de llamadas por minuto que sigue una ley de Poisson con parámetro l=0.5. Determinar las probabilidades:

a) De que en un minuto al azar, se reciba una única llamada.

dpois(1, lambda=0.5)

## [1] 0.3032653

b) De que en un minuto al azar se reciban un máximo de dos llamadas.

ppois(2, lambda=0.5)

## [1] 0.9856123

c) De que en un minuto al azar, la centralita quede bloqueada, sabiendo que no puede realizar más de 3 conexiones por minuto. P(conexiones > 3)

1-ppois(3, lambda=0.5)

## [1] 0.001751623

ppois(3, lambda=0.5, lower.tail = FALSE)

## [1] 0.001751623

d) Se reciban 5 llamadas en dos minutos. P(llamadas=5).

dpois(5, lambda=2)

## [1] 0.03608941

5.4 Distribución Normal

\[ f(x | \mu,\sigma^2) = \frac{1}{\sqrt{2\sigma^2\pi}} e ^{-\frac{(x-\mu)^2}{2\sigma^2}}, \] dónde

\[ Z = \frac{X-\mu}{\sigma} \sim N(0,1) \]

x <- seq ( -6, 6, len=100 ) 
y <- cbind ( dnorm ( x, -2, 1 ), 
dnorm (x, 0, 2 ), 
dnorm ( x, 0, .5), 
dnorm ( x, 2, .3 ),
dnorm ( x, -.5, 3 ) )

matplot ( x, y, type="l", col=1 )
legend ( -6, 1.3, 
paste( "mu =", c(-2,0,0,2,-.5),"; 
sigma =",c(1,2,.5,.3,3) ),  lty=1:5, col=1, cex=.75 )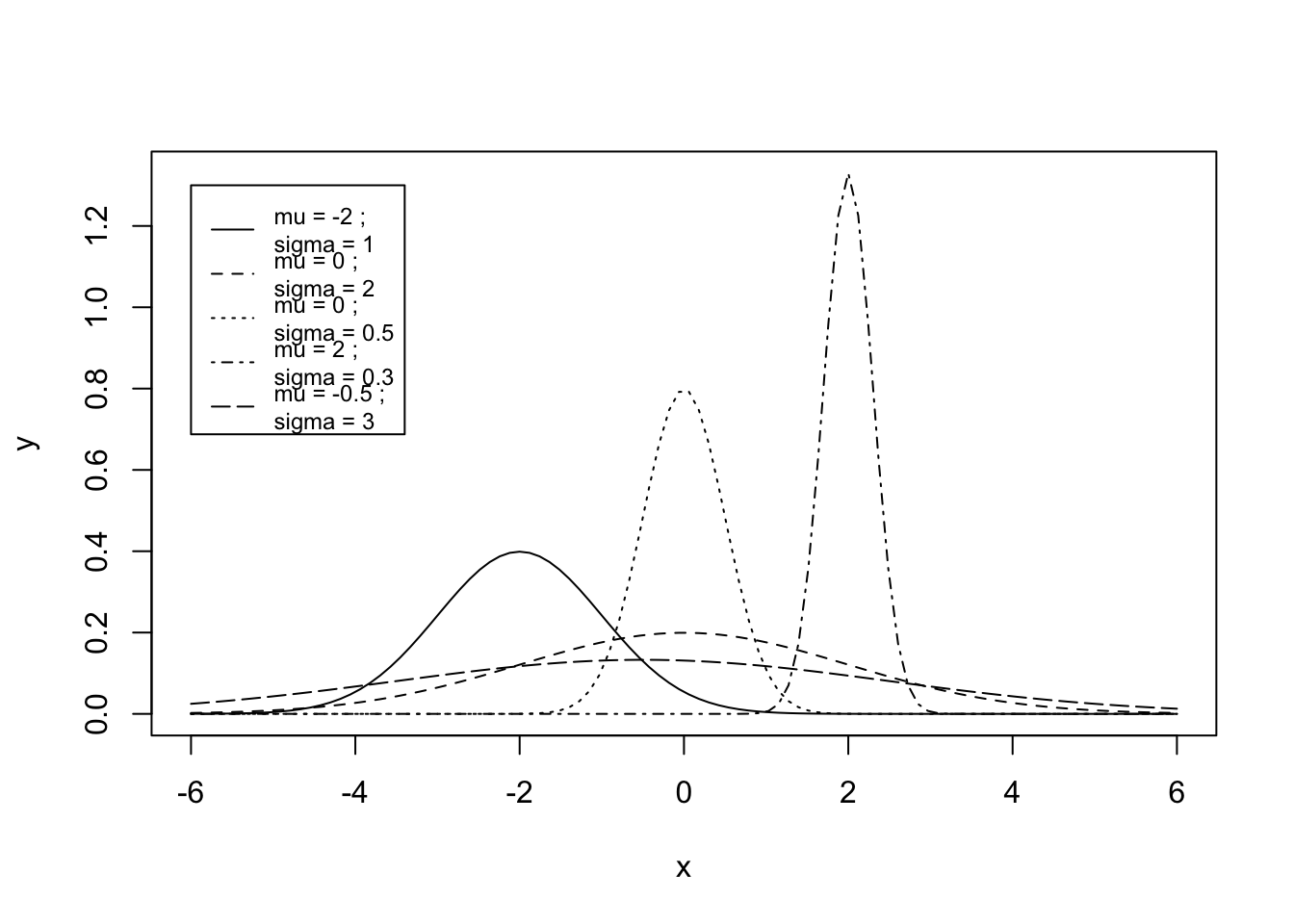

Ejemplo

$X$ es una variable normalmente distribuida con una media de $\mu = 30$ y una desviación estándar de $\sigma = 4$. Encontrar

$P(x<40)$
$P(x>21)$
$P(30<x<35)$

Solucion:

Para $x=40$, la $z$ estandarizada es $(40-30)/4=2.5$ y por tanto:

\[ P(X<40)=P(Z<2.5)=0.9938 \]

pnorm(2.5)

## [1] 0.9937903

pnorm(40,mean=30,sd=4,lower.tail=TRUE)

## [1] 0.9937903

$P(x>21)$

pnorm(21,mean=30,sd=4,lower.tail = FALSE)

## [1] 0.9877755

$P(30<x<35)$

pnorm(35,mean=30,sd=4,lower.tail = TRUE)-pnorm(30,mean=30,sd=4,lower.tail = TRUE)

## [1] 0.3943502

Pregunta

El ingreso a una determinada universidad se determina mediante un examen nacional. Los resultados de esta prueba se distribuyen normalmente con una media de 500 y una desviación estándar de 100. Tom quiere ser admitido en esta universidad y sabe que debe obtener mejores resultados que al menos el 70% de los estudiantes que tomaron el examen. Tom toma el examen y saca 585 puntos. ¿Será admitido en esta universidad?

N = 1000
hist(rnorm(N,500,100),20,col="grey")
abline(v=585,col=2)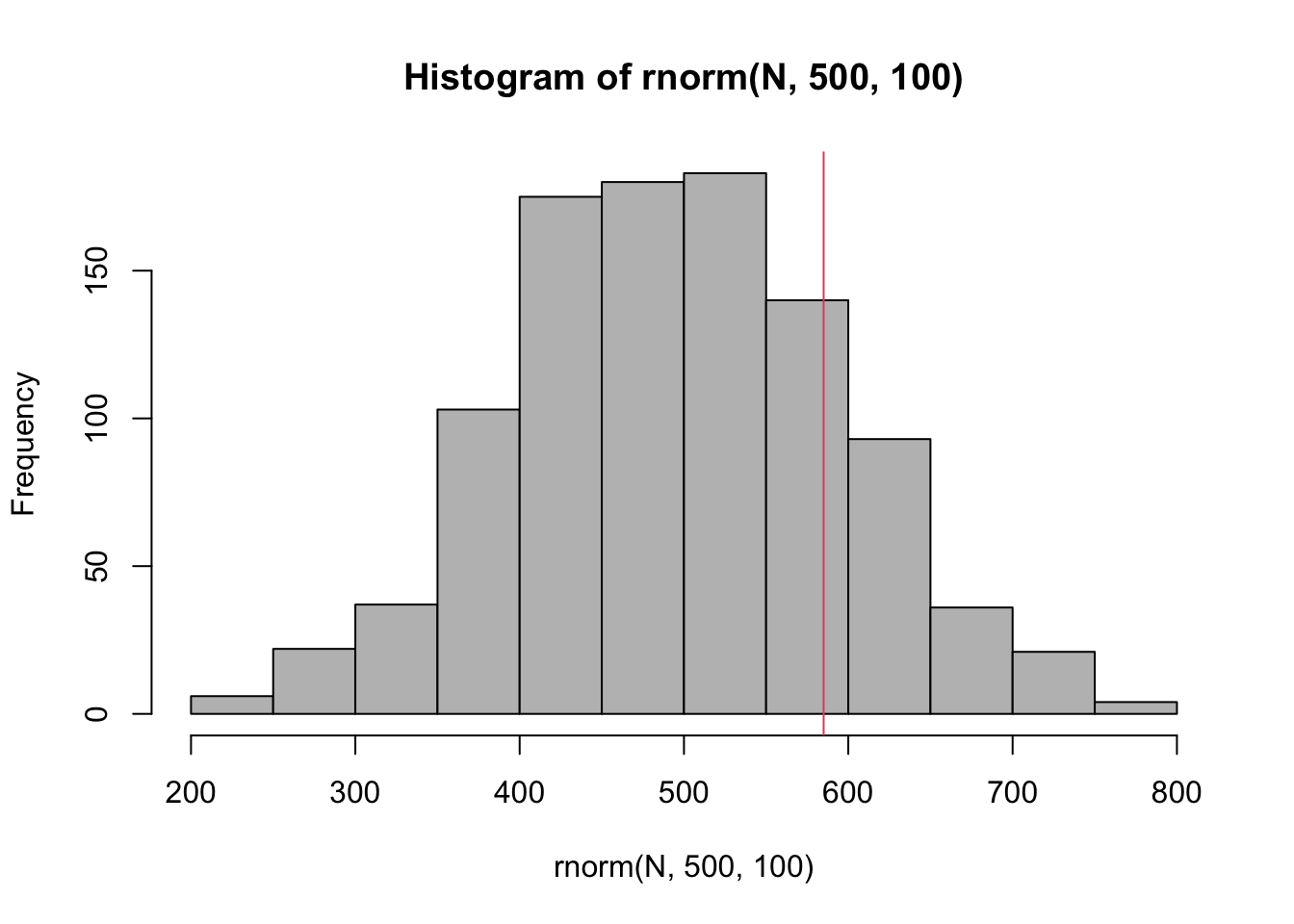

Es (P(X<585) )70%?

pnorm(585,mean=500,sd=100)

## [1] 0.8023375

Tom obtuvo una puntuación mejor que el 80.23% de los estudiantes que tomaron el examen y será admitido en esta universidad.

Ejercicio

Hallar la probabilidad de que la resistencia a la compresión simple X, de una probeta de hormigón sea mayor que 100 Kg/cm2, sabiendo que la resistencia citada es una variable $N(200,40)$ en Kg/cm2.

pnorm(100, mean=200, sd=40, lower.tail=FALSE)

## [1] 0.9937903

Calcular $P(28<X<31)$ en una variable aleatoria normal $N(28,1)$

pnorm(31,mean=28,sd=1,lower.tail = TRUE)-pnorm(28,mean=28,sd=1,lower.tail = TRUE)

## [1] 0.4986501

El contenido de un bote de cerveza se distribuye normalmente con media 30 cl y desviación típica de 2 cl.

a) ¿Cuál es la probabilidad de que un bote determinado tenga más de 33 cl.?

1-pnorm(33, mean=30, sd=2)

## [1] 0.0668072

pnorm(33, mean=30, sd=2, lower.tail=FALSE)

## [1] 0.0668072

b) ¿cual es la probabilidad de que el contenido líquido total sea inferior a a 174cl?

pnorm(175, mean=180, sd=sqrt(4*6))

## [1] 0.1537171