Chapter 3 Expectation, Covariance and Correlation

3.1 Expectation

Norwegian Air run a small five person passenger plane from Oslo to Nordfjordeid. In order to analyse future financial prospects, the company would like to understand fuel consumption of the flight. To calculate fuel consumption, Norwegian air needs to know the total weight of the five passengers. Obviously this quantity will change from flight-to-flight, and so Norwegian Air will have to calculate an expected value for the total weight.

The next flight has a family of \(5\) booked on: a male parent, a female parent and three teenage children. Norwegian air know that the weight of an adult male is modeled by a continuous random variable \(W_{\text{adult male}}\). Similarly \(W_{\text{adult male}}\) is a continuous random variable that models the weight of an adult female and \(W_\text{teenager}\) is a random variable that models the weight of a teenager. Norwegian Air would therefore like to predict the average value of \(W_{\text{adult male}} + W_{\text{adult female}} + 3 W_\text{teenager}\), that is \(\mathbb{E}\left[W_{\text{adult male}} + W_{\text{adult female}} + 3 W_\text{teenager} \right]\).

More generally, given a collection of continuous random variables \(X_1, \ldots, X_n\), what is the expected value of some function \(g \left( X_1, \ldots, X_n \right)\) of these random variables.

In MATH1055, we saw the solution to the analogous discrete problem with \(n=2\): how to calculate the expectation of a function of two discrete random variables.

Let \(X_1\) and \(X_2\) be two discrete random variables, with joint PMF denoted \(p_{X_1,X_2}\). Then, for a function of the two random variables \(g(X_1,X_2)\), we have \[\mathbb{E}[g(X_1,X_2)] = \sum_{(x_1,x_2)} g(x_1,x_2) p_{X_1,X_2}(x_1,x_2).\]

In Theorem 3.1.1, the summation is over all pairs of values \(x_1, x_2\) that \(X_1, X_2\) can take respectively. Since the term inside the summation involves \(p_{X_1,X_2}(x_1,x_2)\), it is enough to only consider pairs \((x_1,x_2)\) for which \(p_{X_1,X_2}(x_1,x_2) \neq 0\), that is, only the pairs that have a change of occurring.

A cafe wants to investigate the correlation between temperature \(X\) in degrees Celsius during winter and the number of customers \(Y\) in the cafe each day. Based on existing data collected by the owner, the joint probability table is

What is the average number of customers per day?

In mathematical language, the question is asking us to calculate \(\mathbb{E}\left[ Y \right]\). Setting \(g(X,Y) = Y\), by Theorem 3.1.1: \[\begin{align*} \mathbb{E}\left[ Y \right] &= \sum_{(x,y)} g(x,y) p_{X,Y}(x,y) \\[5pt] &= 15 \cdot p_{X,Y}(0,15) + 75 \cdot p_{X,Y}(0,75) + 150 \cdot p_{X,Y}(0,150) \\ &\qquad + 15 \cdot p_{X,Y}(10,15) + 75 \cdot p_{X,Y}(10,75) + 150 \cdot p_{X,Y}(10,150) \\ & \qquad \qquad + 15 \cdot p_{X,Y}(20,15) + 75 \cdot p_{X,Y}(20,75) + 150 \cdot p_{X,Y}(20,150) \\[5pt] &= (15 \times 0.07 ) + ( 75 \times 0.11) + (150 \times 0.01) \\ &\qquad + (15 \times 0.23) + (75 \times 0.43) + (150 \times 0.05) \\ & \qquad \qquad + (15 \times 0.04) + (75 \times 0.05) + (150 \times 0.01) \\[5pt] &= 58.35 \end{align*}\]

Theorem 3.1.1 generalises to considering three or more variables. This is possible due to the introduction of joint PMFs in Section 2.4.

Let \(X_1, \ldots, X_n\) be a collection of discrete random variables, with joint PMF denoted \(p_{X_1, \ldots, X_n}\). Then, for a function of the random variables \(g(X_1,\ldots, X_n)\), we have \[\mathbb{E}[g(X_1,\ldots, X_n)] = \sum_{(x_1,\ldots, x_n)} g(x_1,\ldots , x_n) p_{X_1,\ldots, X_n}(x_1,\ldots, x_n).\]

The generalisation of Theorem 3.1.2 to the case of continuous random variables involves integrating over the continuous region of possibilities, rather than summing over the discrete collection of possibilities.

Let \(X_1, \ldots, X_n\) be a collection of continuous random variables, with joint PDF denoted \(f_{X_1, \ldots, X_n}\). Then, for a function of the random variables \(g(X_1 \ldots, X_n)\), we have \[\mathbb{E}[g(X_1,\ldots, X_n)] = \int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} g(x_1,\ldots , x_n) f_{X_1,\ldots, X_n}(x_1,\ldots, x_n) \,dx_1 \cdots \,dx_n.\]

Consider two random variables with joint PDF given by \[f_{X,Y}(x,y) = \begin{cases} 2(x+y), & \text{if } 0 \leq x \leq y \leq 1, \\ 0, & \text{otherwise.} \end{cases}\] Calculate the expected value of \(XY\).

The two-dimensional region on which \(f_{X,Y}(x,y)\) is non-zero is

By applying Theorem 3.1.4, we have that \[\begin{align*} \mathbb{E}[XY] &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} xy \cdot f_{X,Y}(x,y) \,dx \,dy \\[3pt] &= \int_0^1 \int_0^y xy \cdot 2(x+y) \,dx \,dy \\[3pt] &= \int_0^1 \int_0^y 2x^2y + 2x y^2 \,dx \,dy \\[3pt] &= \int_0^1 \left[ \frac{2}{3}x^3 y + x^2 y^2 \right]_0^y \,dy \\[3pt] &= \int_0^1 \frac{2}{3} y^4 + y^4 \,dy \\[3pt] &= \int_0^1 \frac{5}{3} y^4 \,dy \\[3pt] &= \left[ \frac{1}{3} y^5 \right]_0^1 \\[3pt] &= \frac{1}{3}. \end{align*}\]

3.2 Covariance

Consider two random variables \(X\) and \(Y\). We have seen the notion of independence: \(X\) and \(Y\) have no impact on each other. Alternatively there could exist a positive relationship, that is as one of \(X,Y\) increases so does the other, or an inverse relationship, as one of \(X,Y\) increases the other decreases and vice-versa.

The mathematical quantities of covariance studied in this section, and correlation studied in Section 3.3 identify any such relationship and measures its strength.

The covariance of two random variables, \(X\) and \(Y\), is defined by

\[\text{Cov}(X,Y) = E\Big[(X-E[X])(Y-E[Y])\Big]\]

If \(\text{Cov}(X,Y)\) is positive, both random variables generally tend to be large and small at the same time. If \(\text{Cov}(X,Y)\) is negative, then as one random variable is large the other tends to be small. The strength of any such relationship between \(X\) and \(Y\) is not accounted for by the covariance.

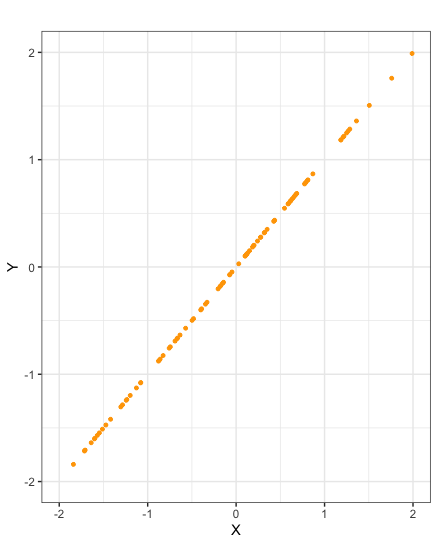
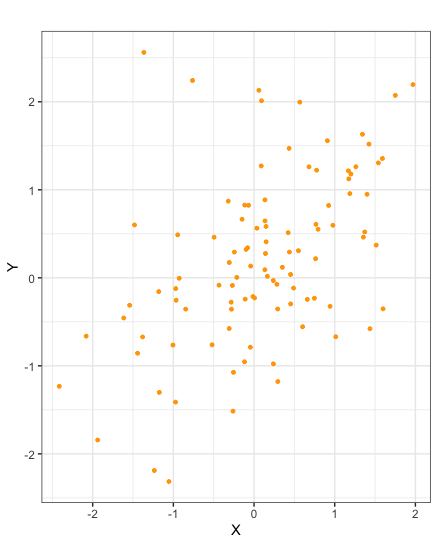
Scatter plots of samples taken from random variables \(X\) and \(Y\) with positive covariance

Scatter plots of samples taken from random variables \(X\) and \(Y\) with negative covariance

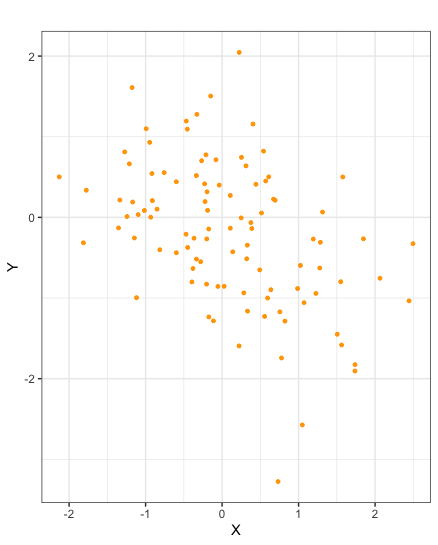
There is a simpler formula than that of Definition 3.2.1 by which to calculate covariance. Specifically it can be shown that covariance is equal to the expected value of the product minus the product of the expected values.

The covariance of two random variables, \(X\) and \(Y\), can by calculated by \[\text{Cov}(X,Y) = E[XY]-E[X]E[Y].\]

Calculate the covariance of the random variables \(X, Y\) in Example 3.1.2 that govern the temperature and number of customers daily in the cafe.

Motivated by the formula \(\text{Cov}(X,Y) = E[XY]-E[X]E[Y]\) for covariance, we seek to calculate \(E[X], E[Y]\) and \(E[XY]\). From Example 3.1.5, we know \(E[Y] = 58.35\). Now calculating \(E[X]\) and \(E[XY]\) using Theorem 3.1.4, obtain

\[\begin{align*} E[X] &= 0 \times P(X=0) + 10 \times P(X=10) + 20 \times P(X=20) \\[3pt] &= 0 \times (0.07 + 0.11 + 0.01) + 10 \times (0.23 + 0.43 + 0.05) + 20 \times (0.04 + 0.05 + 0.01) \\[3pt] &= 9.1, \\[9pt] E[XY] &= \sum\limits_{n \in \mathbb{Z}} n \cdot P(XY =n) \\[3pt] &= \sum\limits_{\begin{array}{c} n=-\infty \\ n: \text{ integer} \end{array}}^{\infty} n \cdot P(XY =n) \\[3pt] &= 0 \times \big( p_{X,Y}(0,15) + p_{X,Y}(0,75) + p_{X,Y}(0,150) \big) + 150 \times p_{X,Y}(10,15) + 300 \times p_{X,Y}(20,15) \\ &\qquad \qquad + 750 \times p_{X,Y}(10,75) + 1500 \times \big( p_{X,Y}(10,150) + p_{X,Y}(20,75) \big) + 3000 \times p_{X,Y}(20,150) \\[3pt] &= 0 \times \left( 0.07 + 0.11 + 0.01 \right) + 150 \times 0.23 + 300 \times 0.04 + 750 \times 0.43 \\ & \qquad \qquad + 1500 \times \left( 0.05 + 0.05 \right) + 3000 \times 0.01 \\[3pt] &= 549. \end{align*}\]

Therefore it follows that

\[ \text{Cov}(X,Y) = 549 - 9.1 \times 58.35 = 18.015.\]

Calculate the covariance of the random variables \(X, Y\) in Example 3.1.5.

Again we seek to apply the formula \(\text{Cov}(X,Y) = E[XY]-E[X]E[Y]\). From Example 3.1.5, we know \(E[XY] = \frac{1}{3}\). Calculating \(E[X]\) and \(E[Y]\) using Theorem 3.1.4, obtain

\[\begin{align*} E[X] &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x \cdot f_{X,Y}(x,y) \,dx \,dy \\[3pt] &= \int_0^1 \int_0^y 2x(x+y) \,dx \,dy \\[3pt] &= \int_0^1 \int_0^y 2x^2 + 2xy \,dx \,dy \\[3pt] &= \int_0^1 \left[ \frac{2}{3}x^3 + x^2 y \right]_0^y \,dy \\[3pt] &= \int_0^1 \frac{2}{3}y^3 + y^3 \,dy \\[3pt] &= \int_0^1 \frac{5}{3} y^3 \,dy \\[3pt] &= \left[ \frac{5}{12}y^4 \right]_0^1 \\[3pt] &= \frac{5}{12}, \\[9pt] E[Y] &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} y \cdot f_{X,Y}(x,y) \,dx \,dy \\[3pt] &= \int_0^1 \int_0^y 2y(x+y) \,dx \,dy \\[3pt] &= \int_0^1 \int_0^y 2xy+2y^2 \,dx \,dy \\[3pt] &= \int_0^1 \left[ x^2 y + 2xy^2 \right]_0^y \,dy \\[3pt] &= \int_0^1 y^3 + 2y^3 \,dy \\[3pt] &= \int_0^1 3y^3 \,dy \\[3pt] &= \left[ \frac{3}{4}y^4 \right]_0^1 \\[3pt] &= \frac{3}{4}. \end{align*}\]

Therefore it follows that

\[ \text{Cov}(X,Y) = \frac{1}{3} - \frac{5}{12}\cdot \frac{3}{4} = \frac{1}{48}.\]

The covariance of two sample populations can be calculated in R. The following code calculates the covariance of a known sample of size \(5\) taken from two random variables \(X\) and \(Y\):

X_samp = c(3,4,7,8,10) 
Y_samp = c(1,21,3,13,15)
cov(X_samp,Y_samp)

Covariance has the following important properties:

If \(X\) and \(Y\) are independent, then \(\text{Cov}(X,Y) = 0\). However if \(\text{Cov}(X,Y) = 0\), then \(X\) and \(Y\) do not necessarily have to be independent;
The covariance of two equal random variables is equal to the variance of that random variable. \[\text{Cov}(X,X) = \text{Var}(X);\]
There is a further relationship between variance and covariance: \[\text{Var}(X+Y) = \text{Var}(X) + \text{Var}(Y) + 2\text{Cov}(X,Y).\] That is to say, that covariance describes the variance of the random variable \(X+Y\) that is not explained by the variances of the random variables \(X\) and \(Y\);

More generally the above relationship between variance and covariance generalises to: \[ \text{Var} \left( \sum_{i=1}^n a_iX_i \right) = \sum_{i=1}^n a_i^2 \text{Var}(X_i) + 2 \sum_{1 \leq i < j \leq n} a_ia_j\text{Cov}(X_i,X_j);3\]
Assume that \(X_1,X_2,\dots,X_n\) are independent so that \(\text{Cov}(X_i,X_j)=0\), and also assume that each \(a_i\) is equal to \(1\). This derives the formula: \[\text{Var} \left( \sum_{i=1}^n X_i \right) = \sum_{i=1}^n \text{Var} (X_i).\]

Suppose \(X\) and \(Y\) are discrete random variables whose probability mass function is given by the following table:

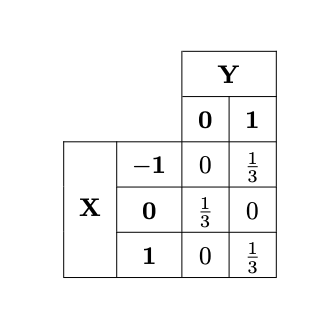
What is the covariance of the two variables? Are they independent?

From the table, one can calculate the probability mass functions for \(X\) and \(Y\):

\[ p_{X} (x) = \begin{cases} \frac{1}{3}, & \text{if } x=-1 \\[5pt] \frac{1}{3}, & \text{if } x=0 \\[5pt] \frac{1}{3}, & \text{if } x=1 \end{cases}\] and \[ p_{Y} (y) = \begin{cases} \frac{1}{3}, & \text{if } y=0 \\[5pt] \frac{2}{3}, & \text{if } y=1 \end{cases}\]

Using \(p_{X}, p_{Y}\) and \(p_{X,Y}\), we can calculate the expectation of \(X\), \(Y\) and \(XY\) respectively:

\[\begin{align*} E[X] &= \sum\limits_{x} x \cdot p_{X}(x) \\ &= \left( -1 \times \frac{1}{3} \right) + \left( 0 \times \frac{1}{3} \right) + \left( 1 \times \frac{1}{3} \right) \\ &= 0 \\[9pt] E[Y] &= \sum\limits_{y} y \cdot p_{Y}(y) \\ &= \left( 0 \times \frac{1}{3} \right) + \left( 1 \times \frac{2}{3} \right) \\ &= 2/3 \\[9pt] E[XY] &=\sum\limits_{(x,y)} x \cdot y \cdot p_{X,Y}((x,y) ) \\ &= \left( -1 \times 0 \times 0 \right) + \left( 0 \times 0 \times \frac{1}{3} \right) + \left( 1 \times 0 \times 0 \right) \\ & \qquad \qquad + \left( -1 \times 1 \times \frac{1}{3} \right) + \left( 0 \times 1 \times 0 \right) + \left( 1 \times 1 \times \frac{1}{3} \right) \\ &= 0 \\ \end{align*}\]

The covariance can then be calculated using Definition 5.1.1:

\[\begin{align*} \text{Cov}(X,Y) &= E[XY] - E[X]E[Y] \\ &= 0-0 \\ &= 0. \end{align*}\]

This does not inform us whether \(X\) and \(Y\) are independent or not. However, note that

\[p_{X,Y}(0,0) = \frac{1}{3} \qquad \text{and} \qquad p_X(0) \cdot p_Y(0) = \frac{1}{3}\cdot \frac{1}{3} = \frac{1}{9}.\] So \(p_{X,Y}(0,0) \neq p_X(0)p_Y(0)\) and therefore, \(X\) and \(Y\) are not independent.

There are some rules which allow us to easily calculate the covariance of linear combinations of random variables.

Let \(a,b\) be real numbers, and \(X,X_1, X_2, Y, Y_1, Y_2\) be random variables. Each of the following rules pertaining to covariance hold in general

\[\begin{align*} \text{Cov}(X+a,Y+b) &= \text{Cov}(X,Y) \\[5pt] \text{Cov}(aX,bY) &= ab\text{Cov}(X,Y) \\[5pt] \text{Cov}(X_1+X_2,Y_1+Y_2) &= \text{Cov}(X_1,Y_1) + \text{Cov}(X_1,Y_2) \\ & \qquad + \text{Cov}(X_2,Y_1) + \text{Cov}(X_2,Y_2) \\[5pt] \end{align*}\]

Consider the cafe from Example 3.1.2. Calculate the covariance of the number of customers the cafe receives in a three day and the average temperature over these three days in degrees Fahrenheit. You may assume that the values \(X\) and \(Y\) on any given day are independent of the values taken by \(X\) and \(Y\) on the other days.

In mathematical language, the total number of customers over a three day period can be modeled by \(3X\). The average temperature in degrees Celsius is modeled by \(\frac{1}{3} \big( Y + Y + Y \big) = \frac{1}{3} \big( 3Y \big) = Y\), which converting into degrees Fahrenheit is \(\frac{9}{5}Y + 32\). Therefore we aim to calculate \(\text{Cov}\left( 3X,\frac{9}{5}Y + 32 \right)\). Applying Lemma 3.2.6 and using the result of Example 3.2.3, obtain

\[\text{Cov}\left( 3X,\frac{9}{5}Y + 32 \right) = 3\cdot \frac{9}{5} \cdot \text{Cov}(X,Y) = 3 \times 1.8 \times 18.015 = 97.281.\]

3.3 Correlation

Suppose two random variables have a large covariance. There are two factors that can contribute to this: the variance of \(X\) and \(Y\) as individual random variables could be high, that is the magnitude of \(X - E[X]\) and \(Y - E[X]\) are particularly large, or the relationship between \(X\) and \(Y\) could be strong. We would like to isolate this latter contribution.

By scaling covariance to account for the variance of \(X\) and \(Y\), one obtains a mathematical quantity, known as correlation, that solely tests the relationship between two random variables, and provides a measure of the strength of this relationship.

If \(\text{Var}(X)>0\) and \(\text{Var}(Y)>0\), then the correlation of \(X\) and \(Y\) is defined by

\[\rho(X,Y) = \frac{\text{Cov}(X,Y)}{\sqrt{\text{Var}(X)\text{Var}(Y)}}.\]

The correlation of two sample populations can be calculated in R. The following code calculates the correlation of a known sample of size \(5\) taken from two random variables \(X\) and \(Y\):

X_samp = c(3,4,7,8,10) 
Y_samp = c(1,21,3,13,15)
cor(X_samp,Y_samp)

Correlation has the following important properties:

\(-1 \leq \rho(X,Y) \leq 1\);
If \(\rho(X,Y) = 1\), then there is a perfect linear positive correlation between \(X\) and \(Y\). If \(\rho(X,Y) = -1\), then there is a perfect linear inverse correlation between \(X\) and \(Y\);
If \(X\) and \(Y\) are independent, then \(\rho(X,Y)=0\). Note, again, that the converse is not true.

These properties can be explored in the following app.

While a correlation \(\rho(X,Y)=1\) indicates a perfect positive linear relationship between \(X\) and \(Y\), it is important to note that the correlation does not indicate the gradient of this linear relationship. Specifically an increase in \(X\) does not indicate an equal increase in \(Y\). A similar statement holds for correlation \(\rho(X,Y)=-1\).

Scatter plots of samples taken from random variables \(X\) and \(Y\) with correlation \(1\)

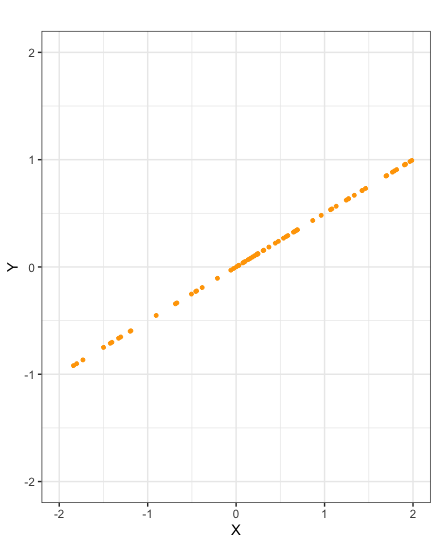
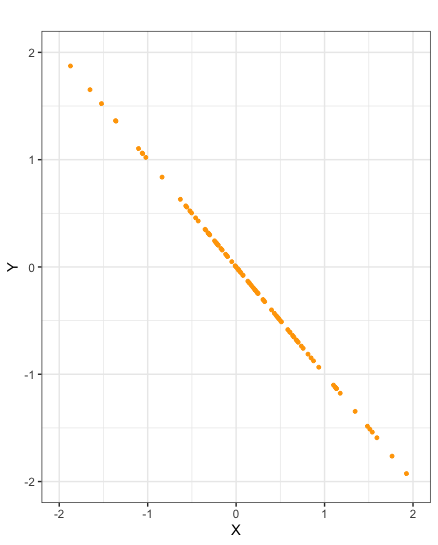
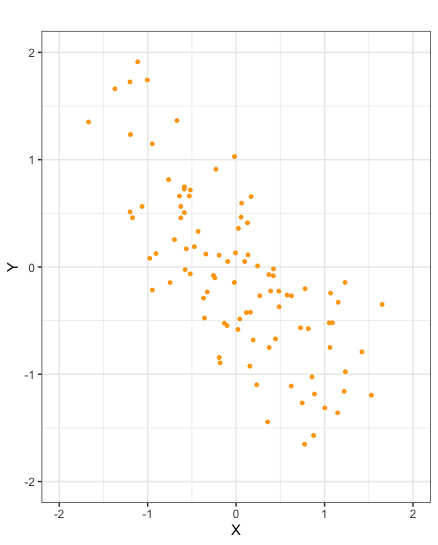
Scatter plots of samples taken from random variables \(X\) and \(Y\) with correlation \(-1\)

Similarly to covariance, there are identities that help us to calculate the correlation of linear combinations of random variables.

Let \(a,b\) be real numbers, and \(X,Y\) be random variables. Both of the following rules pertaining to correlation hold in general:

\[\begin{align*} \rho(X+a, Y+b) &= \rho(X,Y) \\[5pt] \rho (aX,bY) &= \begin{cases} \rho(X,Y), & \text{if } ab>0, \\[3pt] -\rho(X,Y), & \text{if } ab<0. \end{cases} \end{align*}\]

Let \(X_i \sim Exp(\lambda_i)\) where \(\lambda_i >0\) for \(i=0,1,2\) be a collection of independent random variables. Set

\[\begin{align*} Y_1 &= X_0 + X_1 \\[3pt] Y_2 &= X_0 + X_2 \end{align*}\]

Calculate the correlation \(\rho(Y_1,Y_2)\) of \(Y_1\) and \(Y_2\).

Calculate

\[\text{Var}(Y_1) = \text{Var}(X_0 + X_1) = \text{Var}(X_0) + \text{Var}(X_1) = \frac{1}{\lambda_0^2} + \frac{1}{\lambda_1^2}.\]

Similarly

\[\text{Var}(Y_2) = \frac{1}{\lambda_0^2} + \frac{1}{\lambda_2^2}.\]

Now

\[\begin{align*} \text{Cov}(Y_1,Y_2) &= \text{Cov}(X_0 + X_1, X_0 + X_2) \\[3pt] &= \text{Cov}(X_0,X_0) + \text{Cov}(X_1,X_0) + \text{Cov}(X_0,X_2) + \text{Cov}(X_1,X_2) \\[3pt] &= \text{Var}(X_0) + 0 + 0 + 0 \\[3pt] &= \frac{1}{\lambda_0^2}. \end{align*}\]

Therefore

\[\begin{align*} \rho(Y_1, Y_2) &= \frac{\text{Cov}(Y_1,Y_2)}{\sqrt{\text{Var}(Y_1)\text{Var}(Y_2)}} \\[5pt] &= \frac{ \frac{1}{\lambda_0^2} }{ \sqrt{ \left(\frac{1}{\lambda_0^2} + \frac{1}{\lambda_1^2} \right) \left(\frac{1}{\lambda_0^2} + \frac{1}{\lambda_2^2} \right)} } \\[5pt] &= \frac{\lambda_0^2 \lambda_1 \lambda_2 \cdot \frac{1}{\lambda_0^2} }{\lambda_0^2 \lambda_1 \lambda_2 \cdot \sqrt{ \left(\frac{1}{\lambda_0} + \frac{1}{\lambda_1} \right) \left(\frac{1}{\lambda_0} + \frac{1}{\lambda_2} \right)} } \\[5pt] &= \frac{\lambda_1 \lambda_2}{\sqrt{(\lambda_0^2 + \lambda_1^2)(\lambda_0^2 + \lambda_2^2)}}. \end{align*}\]